Structure generation
|
|
|
- Sara Andrews
- 5 years ago
- Views:
Transcription
1 Structure generation Generation of generalized cubic graphs N. Van Cleemput
2 Exhaustive isomorph-free structure generation Create all structures from a given class of combinatorial structures without isomorphic copies Combinatorial enumeration is not always sufficient.
3 Exhaustive isomorph-free structure generation all graphs with 10 vertices all cubic multigraphs with 20 vertices all molecules for the formula C 20 H 10 all permutations of 12 elements all tilings of the plane with 2 face orbits all union-closed families of sets on a ground set with 5 elements
4 Historic highlights of structure generation Theaetetus (±400 BC): 5 platonic solids Narayana Pandit (14th century): all permutation of n elements (probably not for very large n) Jan de Vries (1889): all cubic graphs on up to 10 vertices Donald W. Grace (1965): all polyhedra with up to 11 faces Alexandru T. Balaban (1966): all cubic graphs on up to 10 vertices (1967: 12 vertices) This list is not exhaustive!
5 Why is structure generation useful? test conjectures build intuition search for specific structures count structures
6 A case study Generation of generalized cubic graphs
7 Which structures will be generated? connected, cubic variety of simple graphs multigraphs graphs with loops graphs with semi-edges any combination of these
8 Which structures will be generated? Name Type Counts as Loop 2 v Multi-edge v w 2 Semi-edge v 1
9 Which structures will be generated? P LS LM SM L S M C
10 Motivation Study of maps flag graphs of maps / hypermaps symmetry type graphs / Delaney-Dress graphs arc graphs of oriented maps Voltage graphs
11 Motivation - Delaney-Dress graph Rhombohedron all 6 faces are congruent rhombi has D 3d symmetry (Trigonal trapezohedron)
12 Motivation - Delaney-Dress graph
13 Motivation - Delaney-Dress graph a b c d a b c d
14 Motivation - Delaney-Dress graph a b c a b c
15 Motivation - Delaney-Dress graph a a
16 Motivation - Delaney-Dress graph
17 Motivation - Delaney-Dress graph
18 Motivation - Delaney-Dress graph
19 Motivation - Delaney-Dress graph A B C
20 Motivation - Delaney-Dress graph
21 Generation of pregraphs
22 Translation to multigraphs Pregraph primitives Translate cubic pregraphs to multigraphs with degrees 1 and 3. Notation: (G) is the primitive of G.
23 Translation to multigraphs P LS LM SM P L S M G 1,3 M C C
24 Which are the construction operations?
25 Which are the construction operations?
26 Exhaustive? Can we generate all structures with these operations? From which graphs should we start?
27 Reductions Look at the inverse of the construction operations. Prove that each structure can be reduced Irreducible structures are the start graphs
28 Reductions Each cubic pregraph primitive containing a parallel edge can be reduced by reduction 3 or 4 to a cubic pregraph primitive with fewer vertices, except when it is the theta graph or the buoy graph.
29 Reductions There exists a parallel edge uv: u and v are adjacent to two different vertices x and y u and v are adjacent to one vertex x: x is adjacent to z z is adjacent to two different other vertices z 1 and z 2 z is adjacent to one other vertex z 1 x u v y
30 Reductions There exists a parallel edge uv: u and v are adjacent to two different vertices x and y u and v are adjacent to one vertex x: x is adjacent to z z is adjacent to two different other vertices z 1 and z 2 z is adjacent to one other vertex z 1 u v x z
31 Reductions There exists a parallel edge uv: u and v are adjacent to two different vertices x and y u and v are adjacent to one vertex x: x is adjacent to z z is adjacent to two different other vertices z 1 and z 2 z is adjacent to one other vertex z 1 u v x z z 1 z 2
32 Reductions There exists a parallel edge uv: u and v are adjacent to two different vertices x and y u and v are adjacent to one vertex x: x is adjacent to z z is adjacent to two different other vertices z 1 and z 2 z is adjacent to one other vertex z 1 u v x z z 1
33 Reductions Number of vertices decreases in each step, so this process halts. theta graph buoy graph simple cubic pregraph primitives
34 Reductions Each simple cubic pregraph primitive containing a vertex of degree 1 can be reduced by reduction 1 or 2 to a simple cubic pregraph primitive with fewer edges, except when it is K 2.
35 Reductions There exists a vertex u of degree 1, adjacent to a vertex v of degree 3. The vertex v is adjacent to two other different vertices x and y. u x v y
36 Reductions Number of edges decreases in each step, so this process halts. K 2 cubic graph
37 Reductions The buoy graph reduces to K 2 by applying reduction 1 and 3.
38 The irreducible graphs Each pregraph primitive can be reduced to a cubic simple graph, K 2 or the theta graph.
39 The irreducible graphs Target class C G 1,3 M Irreducible graphs C C C C P
40 The irreducible graphs degree 1 vertices don t count towards the order of the graph when translating from G 1,3 to S (and similar) number of degree 3 vertices never decreases when applying the construction operations
41 The irreducible graphs L, M, LM with n vertices C with n vertices. S, LS, SM, LSM with n vertices C with n vertices, but intermediate G 1,3 and P with 2n + 2 vertices
42 Avoiding isomorphic copies isomorphism rejection by list canonical representatives and Read/Faradžev-type orderly algorithms McKay s canonical construction path method homomorphism principle double coset method closed structures...
43 McKay s canonical construction path method non-isomorphic irreducible graphs..
44 Avoid the same graph from the same parent 3 O.2
45 Avoid the same graph from different parents O.1 = O.3
46 Avoid the same graph from different parents O.3 = O.3
47 Avoid the same graph from different parents O.2 different parents! = O.2
48 McKay s canonical construction path method non-isomorphic irreducible graphs.. define canonical parent avoid by isomorphism check
49 The canonical parent For each cubic pregraph primitive: define canonical double edge define canonical vertex of degree 1
50 The canonical parent A cubic pregraph primitive G is constructed from its canonical parent if or G contains a double edge last operation was operation 3 or 4 new double edge is in the orbit of the canonical double edge G is a cubic simple pregraph primitive the new vertex of degree 1 is in the orbit of the canonical vertex of degree 1
51 Canonicity Let G denote the set of all labelled graphs Canonical representative function c is a function c : G G G G : c(g) = G G, G G : G = G c(g) = c(g ) Canonical representative is the unique element in an isomorphism class that is fixed by c Canonical labelling is an isomorphism φ : G c(g)
52 The canonical vertex of degree 1 Canonical vertex of degree 1 is the vertex of degree 1 with the smallest canonical label.
53 The canonical vertex of degree 1 Computing the canonical labelling is slow (although it is fast).
54 The canonical vertex of degree 1 Assign to each vertex v of degree 1 a pair of numbers (n(v), l(v)) n(v) is number of vertices at distance at most 4 of v l(v) is canonical label of v Canonical vertex of degree 1 is the vertex of degree 1 with the lexicographically smallest pair.
55 The canonical vertex of degree 1 Generation of all simple cubic pregraph primitives with 18 vertices Total operation count % only 1 vertex of degree % rejected by colour % accepted by colour % rejected by nauty % accepted by nauty %
56 The canonical double edge Similar to canonical vertex of degree 1.
57 Exhaustive isomorph-free generation If for one representative of each isomorphism class of simple cubic pregraph primitives on up to n vertices with n 3 < n vertices of degree 3 operation O 1 is applied to one pair of degree-1 vertices in each orbit of pairs of degree-1 vertices, operation O 2 is applied to one bridge in each orbit of bridges, and the resulting graph is accepted if and only if it has at most n vertices the new vertex of degree 1 is in the orbit of the canonical vertex of degree 1 then exactly one representative of each isomorphism class of simple cubic pregraph primitives on up to n vertices with n < n vertices of degree 3 and n 1 > 0 vertices of degree 1 is accepted.
58 Isomorphism-free generation Two isomorphic graphs G 1 and G 2 with respective new vertices of degree 1 v 1 and v 2. Let γ be an isomorphism from G 1 to G 2. γ(v 1 ) is in the same orbit as v 2 under the automorphism group of G 2. A vertex of degree 1 cannot be reduced by both O 1 and O 2, so v 1 and v 2 were obtained by applying the same operation.
59 Isomorphism-free generation w x v 1 w x G O 1 w 1 x 1 G 1 y z v 2 y z G O 1 y 2 z 2 G 2
60 Isomorphism-free generation v 1 w x O 2 w 1 x 1 G G 1 y z v 2 O 2 y 2 z 2 G G 2
61 Exhaustive generation Each simple cubic pregraph primitive on up to n vertices with n < n vertices of degree 3 and n 1 > 0 vertices of degree 1 has a canonical vertex of degree 1 (and this vertex is reducible).
62 Translation from G 1,3 to L, S and LS G 1,3 (n) to L(n): there is always a unique pregraph in L(n). G 1,3 ( 2n + 2) to S(n): if there are n vertices of degree 3, then there is a unique pregraph in S(n). G 1,3 ( 2n + 2) to LS(n): if there are at least n vertices and at most n vertices with degree 3, then there exist pregraphs in LS(n) corresponding to this pregraph primitive. n V 3 (G) vertices of degree 1 correspond to vertices with loops, rest corresponds to semi-edges
63 Homomorphism principle For a group Γ acting on a set M, let R Γ (M) be a set of orbit representatives. For m M let Γ m denote the stabiliser group. Given a group Γ acting on two sets M, M and a surjective mapping φ : M M so that φ(γm) = γ(φ(m)) m M, γ Γ, then m R Γ (M )R Γm (φ 1 m ) is a set R Γ (M) of orbit representatives for the action of Γ on M.
64 Homomorphism principle An isomorphism of 2 cubic pregraphs induces an isomorphism of the cubic pregraph primitives. Isomorphic cubic pregraphs come from the same cubic pregraph primitive. An isomorphism of 2 cubic pregraphs induces a nontrivial automorphism of the cubic pregraph primitive.
65 Homomorphism principle Compute orbits of (n V 3 (G) )-element subsets of the set of all vertices of degree 1. For each orbit choose a representative. For each representative, turn all vertices in that set into loops and the other vertices of degree 1 into semi-edges.
66 Homomorphism principle If the cubic pregraph primitive has a trivial automorphism group, then each subset corresponds to a distinct cubic pregraph. If the automorphism group acts trivially on the set of vertices of degree 1, then each subset corresponds to a distinct cubic pregraph. In other cases some work needs to be done, but the group is often smaller.
67 Results and timings n C L S M LS LM SM LSM
68 Results and timings n C L S M LS LM SM LSM s 0.0s 0.0s 0.0s 0.1s 0.0s 0.1s 0.1s s 0.0s 0.1s 0.0s 0.2s 0.0s 0.3s 0.4s s 0.0s 0.6s 0.0s 0.8s 0.0s 1.3s 1.8s s 0.0s 2.2s 0.0s 3.5s 0.0s 5.4s 7.4s s 0.0s 9.1s 0.1s 14.9s 0.2s 22.6s 32.2s s 0.0s 37.3s 0.0s 64.1s 0.0s 97.2s 144.5s s 0.3s 158.3s 0.5s 290.1s 2.5s 427.1s 669.5s s 0.0s 695.9s 0.0s s 0.0s s s s 3.0s s 5.1s s 31.0s s s s 0.0s s 0.0s s 0.0s s s s 39.0s s 67.9s s 441.9s s s s 0.0s s 0.0s s 0.0s s s s 577.2s s s s s s s s 0.0s s 0.0s 0.0s s s s s
69 Results and timings n L S M LS LM SM LSM /s /s /s /s /s /s /s /s /s /s /s /s /s /s /s /s /s /s /s /s /s /s
70 Connection loops and multi-edges
71 Subclasses
72 3-edge-colourable pregraphs Cubic pregraphs with loops are never 3-edge-colourable. Other cubic pregraphs are 3-edge-colourable if and only if the corresponding cubic pregraph primitive is 3-edge-colourable.
73 3-edge-colourable pregraphs G is not 3-edge-colourable O 1 (G) is not 3-edge-colourable. G is 3-edge-colourable O 2 (G) is 3-edge-colourable. G is 3-edge-colourable O 3 (G) is 3-edge-colourable. G: O 4 (G) is not 3-edge-colourable.
74 3-edge-colourable pregraphs 3-edge-colourability is compatible with the construction operations. Parent of 3-edge-colourable graph is 3-edge-colourable. Never perform operation O 4. Check colourability after performing operation O 1.
75 3-edge-colourable pregraphs n Cc Sc Mc SMc
76 3-edge-colourable pregraphs n Cc Sc Mc SMc s 0.0s 0.0s 0.1s s 0.2s 0.0s 0.3s s 0.6s 0.0s 1.2s s 2.4s 0.0s 4.9s s 9.3s 0.0s 20.6s s 39.2s 0.0s 88.3s s 164.1s 0.3s 395.7s s 740.1s 0.0s s s s 3.4s s s s 0.0s s s s 48.3s s s s 0.0s s s s 791.7s s s s 0.0s s s
77 3-edge-colourable pregraphs n Sc Mc SMc /s /s /s /s /s /s /s /s /s /s
78 Bipartite pregraphs Cubic pregraphs with loops are never bipartite. Other cubic pregraphs are bipartite if and only if the corresponding cubic pregraph primitive is bipartite.
79 Bipartite pregraphs G is bipartite and d(v, w) is even O 1 (G) is bipartite. G is bipartite O 2 (G) is bipartite. G is bipartite O 3 (G) is bipartite. G: O 4 (G) is not bipartite.
80 Bipartite pregraphs Being bipartite is compatible with the construction operations. Parent of bipartite graph is bipartite. Never perform operation O 4. Only perform operation O 1 for pairs of vertices in the same partition.
81 Bipartite pregraphs n CB SB MB SMB
82 Bipartite pregraphs n CB SB MB SMB s 0.0s 0.0s 0.1s s 0.1s 0.0s 0.3s s 0.3s 0.0s 1.1s s 1.2s 0.0s 3.8s s 3.8s 0.0s 13.6s s 12.8s 0.0s 50.4s s 44.6s 0.0s 186.7s s 156.4s 0.1s 709.4s s 562.2s 0.0s s s s 0.8s s s s 0.0s s s s 5.9s s s s 0.0s s s s 50.2s s
83 Bipartite pregraphs n SB MB SMB /s /s /s /s /s /s /s /s /s /s
84 Quotients of a 4-cycle
85 C q 4 -markable cubic pregraphs Cubic pregraphs admitting a 2-factor composed of quotients of C 4. Underlying graphs for Delaney-Dress graphs.
86 C q 4 -markable cubic pregraphs Being C q 4 -markable is not compatible with the construction operations. A linear time filtering algorithm was developed.
87 Timings and results n Cq Sq Mq SMq
88 Timings and results n Cq Sq Mq SMq s 0.0s 0.0s 0.1s s 0.2s 0.0s 0.3s s 0.6s 0.0s 1.3s s 2.4s 0.0s 5.2s s 9.5s 0.0s 22.0s s 39.5s 0.0s 94.8s s 168.7s 0.3s 420.5s s 743.4s 0.0s s s s 3.8s s s s 0.0s s s s 54.0s s
89 Timings and results n Sq Mq SMq /s 95.2/s /s 39.6/s /s 229.7/s 23.8/s /s 10.1/s /s 58.2/s 5.8/s
90 What s going wrong? n 3-edge-colourable C q 4 -markable ratio % % % % % % % % % % % % % % % % % % % %
91 Generating C q 4 -markable pregraphs Specific generation algorithm for C q 4 -markable pregraphs. Has nothing to do with generation algorithm for pregraphs. Uses subgraphs induced by similar quotients as a unit.
92 Timings and results n C q 4 -markable pregraphs time ddgraphs time pregraphs s 0.0s s 0.0s s 0.0s s 0.0s s 0.0s s 0.0s s 0.0s s 0.0s s 0.0s s 0.1s s 0.3s s 1.3s s 5.2s s 22.0s s 94.8s s 420.5s s s s s s s s s s s s s s s s s s s
93 Timings and results n rate /s /s /s /s /s /s /s /s /s /s /s /s /s /s /s /s
94 Generating Delaney-Dress graphs Since the quotients are the units, we already have some colour information available. Assigning the remaining colours can be done using the homomorphism principle.
95 Generating Delaney-Dress graphs n Delaney-Dress graphs time rate s /s s /s s /s s /s s /s s /s s /s s /s s /s s /s m /s m /s m /s h /s h /s h /s h /s days /s days /s
96 Thank you for your attention
Fast Generation of Cubic Graphs
 Fast Generation of Cubic Graphs Gunnar Brinkmann and Jan Goedgebeur Gunnar.Brinkmann@UGent.be Jan.Goedgebeur@UGent.be Cubic graphs are graphs where every vertex has degree 3 (3 edges meet in every vertex).
Fast Generation of Cubic Graphs Gunnar Brinkmann and Jan Goedgebeur Gunnar.Brinkmann@UGent.be Jan.Goedgebeur@UGent.be Cubic graphs are graphs where every vertex has degree 3 (3 edges meet in every vertex).
Discovering 5-Valent Semi-Symmetric Graphs
 Discovering 5-Valent Semi-Symmetric Graphs Berkeley Churchill NSF REU in Mathematics Northern Arizona University Flagstaff, AZ 86011 July 27, 2011 Groups and Graphs Graphs are taken to be simple (no loops,
Discovering 5-Valent Semi-Symmetric Graphs Berkeley Churchill NSF REU in Mathematics Northern Arizona University Flagstaff, AZ 86011 July 27, 2011 Groups and Graphs Graphs are taken to be simple (no loops,
Graph Theory: Introduction
 Graph Theory: Introduction Pallab Dasgupta, Professor, Dept. of Computer Sc. and Engineering, IIT Kharagpur pallab@cse.iitkgp.ernet.in Resources Copies of slides available at: http://www.facweb.iitkgp.ernet.in/~pallab
Graph Theory: Introduction Pallab Dasgupta, Professor, Dept. of Computer Sc. and Engineering, IIT Kharagpur pallab@cse.iitkgp.ernet.in Resources Copies of slides available at: http://www.facweb.iitkgp.ernet.in/~pallab
Public Defence. Jan Goedgebeur
 Generation Algorithms for Mathematical and Chemical Problems Public Defence Combinatorial Algorithms and Algorithmic Graph Theory Department of Applied Mathematics, Computer Science and Statistics Ghent
Generation Algorithms for Mathematical and Chemical Problems Public Defence Combinatorial Algorithms and Algorithmic Graph Theory Department of Applied Mathematics, Computer Science and Statistics Ghent
Abstract. Figure 1. No. of nodes No. of SC graphs
 CATALOGING SELF-COMPLEMENTARY GRAPHS OF ORDER THIRTEEN Myles F. McNally and Robert R. Molina Department of Mathematics and Computer Science Alma College Abstract A self-complementary graph G of odd order
CATALOGING SELF-COMPLEMENTARY GRAPHS OF ORDER THIRTEEN Myles F. McNally and Robert R. Molina Department of Mathematics and Computer Science Alma College Abstract A self-complementary graph G of odd order
Combinatorial and computational group-theoretic methods in the study of graphs and maps with maximal symmetry Banff (November 2008)
 Combinatorial and computational group-theoretic methods in the study of graphs and maps with maximal symmetry Banff (November 2008) Marston Conder University of Auckland mconder@aucklandacnz Outline of
Combinatorial and computational group-theoretic methods in the study of graphs and maps with maximal symmetry Banff (November 2008) Marston Conder University of Auckland mconder@aucklandacnz Outline of
Construction of planar triangulations with minimum degree 5
 Construction of planar triangulations with minimum degree 5 G. Brinkmann Fakultät für Mathematik Universität Bielefeld D 33501 Bielefeld, Germany gunnar@mathematik.uni-bielefeld.de Brendan D. McKay Department
Construction of planar triangulations with minimum degree 5 G. Brinkmann Fakultät für Mathematik Universität Bielefeld D 33501 Bielefeld, Germany gunnar@mathematik.uni-bielefeld.de Brendan D. McKay Department
The Graphs of Triangulations of Polygons
 The Graphs of Triangulations of Polygons Matthew O Meara Research Experience for Undergraduates Summer 006 Basic Considerations Let Γ(n) be the graph with vertices being the labeled planar triangulation
The Graphs of Triangulations of Polygons Matthew O Meara Research Experience for Undergraduates Summer 006 Basic Considerations Let Γ(n) be the graph with vertices being the labeled planar triangulation
Graph Theory S 1 I 2 I 1 S 2 I 1 I 2
 Graph Theory S I I S S I I S Graphs Definition A graph G is a pair consisting of a vertex set V (G), and an edge set E(G) ( ) V (G). x and y are the endpoints of edge e = {x, y}. They are called adjacent
Graph Theory S I I S S I I S Graphs Definition A graph G is a pair consisting of a vertex set V (G), and an edge set E(G) ( ) V (G). x and y are the endpoints of edge e = {x, y}. They are called adjacent
Discrete Mathematics SECOND EDITION OXFORD UNIVERSITY PRESS. Norman L. Biggs. Professor of Mathematics London School of Economics University of London
 Discrete Mathematics SECOND EDITION Norman L. Biggs Professor of Mathematics London School of Economics University of London OXFORD UNIVERSITY PRESS Contents PART I FOUNDATIONS Statements and proofs. 1
Discrete Mathematics SECOND EDITION Norman L. Biggs Professor of Mathematics London School of Economics University of London OXFORD UNIVERSITY PRESS Contents PART I FOUNDATIONS Statements and proofs. 1
INTRODUCTION TO GRAPH THEORY. 1. Definitions
 INTRODUCTION TO GRAPH THEORY D. JAKOBSON 1. Definitions A graph G consists of vertices {v 1, v 2,..., v n } and edges {e 1, e 2,..., e m } connecting pairs of vertices. An edge e = (uv) is incident with
INTRODUCTION TO GRAPH THEORY D. JAKOBSON 1. Definitions A graph G consists of vertices {v 1, v 2,..., v n } and edges {e 1, e 2,..., e m } connecting pairs of vertices. An edge e = (uv) is incident with
ON THE STRUCTURE OF SELF-COMPLEMENTARY GRAPHS ROBERT MOLINA DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE ALMA COLLEGE ABSTRACT
 ON THE STRUCTURE OF SELF-COMPLEMENTARY GRAPHS ROBERT MOLINA DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE ALMA COLLEGE ABSTRACT A graph G is self complementary if it is isomorphic to its complement G.
ON THE STRUCTURE OF SELF-COMPLEMENTARY GRAPHS ROBERT MOLINA DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE ALMA COLLEGE ABSTRACT A graph G is self complementary if it is isomorphic to its complement G.
Endomorphisms and synchronization, 2: Graphs and transformation monoids. Peter J. Cameron
 Endomorphisms and synchronization, 2: Graphs and transformation monoids Peter J. Cameron BIRS, November 2014 Relations and algebras From algebras to relations Given a relational structure R, there are
Endomorphisms and synchronization, 2: Graphs and transformation monoids Peter J. Cameron BIRS, November 2014 Relations and algebras From algebras to relations Given a relational structure R, there are
Endomorphisms and synchronization, 2: Graphs and transformation monoids
 Endomorphisms and synchronization, 2: Graphs and transformation monoids Peter J. Cameron BIRS, November 2014 Relations and algebras Given a relational structure R, there are several similar ways to produce
Endomorphisms and synchronization, 2: Graphs and transformation monoids Peter J. Cameron BIRS, November 2014 Relations and algebras Given a relational structure R, there are several similar ways to produce
GENERALIZED CPR-GRAPHS AND APPLICATIONS
 Volume 5, Number 2, Pages 76 105 ISSN 1715-0868 GENERALIZED CPR-GRAPHS AND APPLICATIONS DANIEL PELLICER AND ASIA IVIĆ WEISS Abstract. We give conditions for oriented labeled graphs that must be satisfied
Volume 5, Number 2, Pages 76 105 ISSN 1715-0868 GENERALIZED CPR-GRAPHS AND APPLICATIONS DANIEL PELLICER AND ASIA IVIĆ WEISS Abstract. We give conditions for oriented labeled graphs that must be satisfied
Introduction to Graph Theory
 Introduction to Graph Theory Tandy Warnow January 20, 2017 Graphs Tandy Warnow Graphs A graph G = (V, E) is an object that contains a vertex set V and an edge set E. We also write V (G) to denote the vertex
Introduction to Graph Theory Tandy Warnow January 20, 2017 Graphs Tandy Warnow Graphs A graph G = (V, E) is an object that contains a vertex set V and an edge set E. We also write V (G) to denote the vertex
Graphs. Introduction To Graphs: Exercises. Definitions:
 Graphs Eng.Jehad Aldahdooh Introduction To Graphs: Definitions: A graph G = (V, E) consists of V, a nonempty set of vertices (or nodes) and E, a set of edges. Each edge has either one or two vertices associated
Graphs Eng.Jehad Aldahdooh Introduction To Graphs: Definitions: A graph G = (V, E) consists of V, a nonempty set of vertices (or nodes) and E, a set of edges. Each edge has either one or two vertices associated
HC IN (2, 4k, 3)-CAYLEY GRAPHS
 HAMILTON CYCLES IN (2, 4k, 3)-CAYLEY GRAPHS University of Primorska November, 2008 Joint work with Henry Glover and Dragan Marušič Definitions An automorphism of a graph X = (V, E) is an isomorphism of
HAMILTON CYCLES IN (2, 4k, 3)-CAYLEY GRAPHS University of Primorska November, 2008 Joint work with Henry Glover and Dragan Marušič Definitions An automorphism of a graph X = (V, E) is an isomorphism of
Missouri State University REU, 2013
 G. Hinkle 1 C. Robichaux 2 3 1 Department of Mathematics Rice University 2 Department of Mathematics Louisiana State University 3 Department of Mathematics Missouri State University Missouri State University
G. Hinkle 1 C. Robichaux 2 3 1 Department of Mathematics Rice University 2 Department of Mathematics Louisiana State University 3 Department of Mathematics Missouri State University Missouri State University
Graphs. Pseudograph: multiple edges and loops allowed
 Graphs G = (V, E) V - set of vertices, E - set of edges Undirected graphs Simple graph: V - nonempty set of vertices, E - set of unordered pairs of distinct vertices (no multiple edges or loops) Multigraph:
Graphs G = (V, E) V - set of vertices, E - set of edges Undirected graphs Simple graph: V - nonempty set of vertices, E - set of unordered pairs of distinct vertices (no multiple edges or loops) Multigraph:
Line Graphs and Circulants
 Line Graphs and Circulants Jason Brown and Richard Hoshino Department of Mathematics and Statistics Dalhousie University Halifax, Nova Scotia, Canada B3H 3J5 Abstract The line graph of G, denoted L(G),
Line Graphs and Circulants Jason Brown and Richard Hoshino Department of Mathematics and Statistics Dalhousie University Halifax, Nova Scotia, Canada B3H 3J5 Abstract The line graph of G, denoted L(G),
Medial symmetry type graphs
 Medial symmetry type graphs Isabel Hubard Instituto de Matemáticas Universidad Nacional Autónoma de México México hubard@matem.unam.mx María del Río Francos Alen Orbanić Tomaž Pisanski Faculty of Mathematics,
Medial symmetry type graphs Isabel Hubard Instituto de Matemáticas Universidad Nacional Autónoma de México México hubard@matem.unam.mx María del Río Francos Alen Orbanić Tomaž Pisanski Faculty of Mathematics,
CS 311 Discrete Math for Computer Science Dr. William C. Bulko. Graphs
 CS 311 Discrete Math for Computer Science Dr. William C. Bulko Graphs 2014 Definitions Definition: A graph G = (V,E) consists of a nonempty set V of vertices (or nodes) and a set E of edges. Each edge
CS 311 Discrete Math for Computer Science Dr. William C. Bulko Graphs 2014 Definitions Definition: A graph G = (V,E) consists of a nonempty set V of vertices (or nodes) and a set E of edges. Each edge
On Universal Cycles of Labeled Graphs
 On Universal Cycles of Labeled Graphs Greg Brockman Harvard University Cambridge, MA 02138 United States brockman@hcs.harvard.edu Bill Kay University of South Carolina Columbia, SC 29208 United States
On Universal Cycles of Labeled Graphs Greg Brockman Harvard University Cambridge, MA 02138 United States brockman@hcs.harvard.edu Bill Kay University of South Carolina Columbia, SC 29208 United States
Lecture 4: Bipartite graphs and planarity
 Lecture 4: Bipartite graphs and planarity Anders Johansson 2011-10-22 lör Outline Bipartite graphs A graph G is bipartite with bipartition V1, V2 if V = V1 V2 and all edges ij E has one end in V1 and V2.
Lecture 4: Bipartite graphs and planarity Anders Johansson 2011-10-22 lör Outline Bipartite graphs A graph G is bipartite with bipartition V1, V2 if V = V1 V2 and all edges ij E has one end in V1 and V2.
Biquasiprimitive oriented graphs of valency four
 Biquasiprimitive oriented graphs of valency four Nemanja Poznanović and Cheryl E. Praeger Abstract In this short note we describe a recently initiated research programme aiming to use a normal quotient
Biquasiprimitive oriented graphs of valency four Nemanja Poznanović and Cheryl E. Praeger Abstract In this short note we describe a recently initiated research programme aiming to use a normal quotient
Two-graphs revisited. Peter J. Cameron University of St Andrews Modern Trends in Algebraic Graph Theory Villanova, June 2014
 Two-graphs revisited Peter J. Cameron University of St Andrews Modern Trends in Algebraic Graph Theory Villanova, June 2014 History The icosahedron has six diagonals, any two making the same angle (arccos(1/
Two-graphs revisited Peter J. Cameron University of St Andrews Modern Trends in Algebraic Graph Theory Villanova, June 2014 History The icosahedron has six diagonals, any two making the same angle (arccos(1/
Introduction III. Graphs. Motivations I. Introduction IV
 Introduction I Graphs Computer Science & Engineering 235: Discrete Mathematics Christopher M. Bourke cbourke@cse.unl.edu Graph theory was introduced in the 18th century by Leonhard Euler via the Königsberg
Introduction I Graphs Computer Science & Engineering 235: Discrete Mathematics Christopher M. Bourke cbourke@cse.unl.edu Graph theory was introduced in the 18th century by Leonhard Euler via the Königsberg
Graph and Digraph Glossary
 1 of 15 31.1.2004 14:45 Graph and Digraph Glossary A B C D E F G H I-J K L M N O P-Q R S T U V W-Z Acyclic Graph A graph is acyclic if it contains no cycles. Adjacency Matrix A 0-1 square matrix whose
1 of 15 31.1.2004 14:45 Graph and Digraph Glossary A B C D E F G H I-J K L M N O P-Q R S T U V W-Z Acyclic Graph A graph is acyclic if it contains no cycles. Adjacency Matrix A 0-1 square matrix whose
Trees. 3. (Minimally Connected) G is connected and deleting any of its edges gives rise to a disconnected graph.
 Trees 1 Introduction Trees are very special kind of (undirected) graphs. Formally speaking, a tree is a connected graph that is acyclic. 1 This definition has some drawbacks: given a graph it is not trivial
Trees 1 Introduction Trees are very special kind of (undirected) graphs. Formally speaking, a tree is a connected graph that is acyclic. 1 This definition has some drawbacks: given a graph it is not trivial
Induced Subgraph Saturated Graphs
 Theory and Applications of Graphs Volume 3 Issue Article 1 016 Induced Subgraph Saturated Graphs Craig M. Tennenhouse University of New England, ctennenhouse@une.edu Follow this and additional works at:
Theory and Applications of Graphs Volume 3 Issue Article 1 016 Induced Subgraph Saturated Graphs Craig M. Tennenhouse University of New England, ctennenhouse@une.edu Follow this and additional works at:
4. (a) Draw the Petersen graph. (b) Use Kuratowski s teorem to prove that the Petersen graph is non-planar.
 UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Graph Theory Frist, KandMa, IT 010 10 1 Problem sheet 4 Exam questions Solve a subset of, say, four questions to the problem session on friday.
UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Graph Theory Frist, KandMa, IT 010 10 1 Problem sheet 4 Exam questions Solve a subset of, say, four questions to the problem session on friday.
Groups and Graphs Lecture I: Cayley graphs
 Groups and Graphs Lecture I: Cayley graphs Vietri, 6-10 giugno 2016 Groups and Graphs Lecture I: Cayley graphs Vietri, 6-10 giugno 2016 1 / 17 graphs A GRAPH is a pair Γ = (V, E) where V - set of vertices
Groups and Graphs Lecture I: Cayley graphs Vietri, 6-10 giugno 2016 Groups and Graphs Lecture I: Cayley graphs Vietri, 6-10 giugno 2016 1 / 17 graphs A GRAPH is a pair Γ = (V, E) where V - set of vertices
The normal quotient philosophy. for edge-transitive graphs. Cheryl E Praeger. University of Western Australia
 The normal quotient philosophy for edge-transitive graphs Cheryl E Praeger University of Western Australia 1 Edge-transitive graphs Graph Γ = (V, E): V = vertex set E = edge set { unordered pairs from
The normal quotient philosophy for edge-transitive graphs Cheryl E Praeger University of Western Australia 1 Edge-transitive graphs Graph Γ = (V, E): V = vertex set E = edge set { unordered pairs from
Discharging and reducible configurations
 Discharging and reducible configurations Zdeněk Dvořák March 24, 2018 Suppose we want to show that graphs from some hereditary class G are k- colorable. Clearly, we can restrict our attention to graphs
Discharging and reducible configurations Zdeněk Dvořák March 24, 2018 Suppose we want to show that graphs from some hereditary class G are k- colorable. Clearly, we can restrict our attention to graphs
Graph theory - solutions to problem set 1
 Graph theory - solutions to problem set 1 1. (a) Is C n a subgraph of K n? Exercises (b) For what values of n and m is K n,n a subgraph of K m? (c) For what n is C n a subgraph of K n,n? (a) Yes! (you
Graph theory - solutions to problem set 1 1. (a) Is C n a subgraph of K n? Exercises (b) For what values of n and m is K n,n a subgraph of K m? (c) For what n is C n a subgraph of K n,n? (a) Yes! (you
A THREE AND FIVE COLOR THEOREM
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 52, October 1975 A THREE AND FIVE COLOR THEOREM FRANK R. BERNHART1 ABSTRACT. Let / be a face of a plane graph G. The Three and Five Color Theorem
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 52, October 1975 A THREE AND FIVE COLOR THEOREM FRANK R. BERNHART1 ABSTRACT. Let / be a face of a plane graph G. The Three and Five Color Theorem
Equipartite polytopes and graphs
 Equipartite polytopes and graphs Branko Grünbaum Tomáš Kaiser Daniel Král Moshe Rosenfeld Abstract A graph G of even order is weakly equipartite if for any partition of its vertex set into subsets V 1
Equipartite polytopes and graphs Branko Grünbaum Tomáš Kaiser Daniel Král Moshe Rosenfeld Abstract A graph G of even order is weakly equipartite if for any partition of its vertex set into subsets V 1
Graphs: Introduction. Ali Shokoufandeh, Department of Computer Science, Drexel University
 Graphs: Introduction Ali Shokoufandeh, Department of Computer Science, Drexel University Overview of this talk Introduction: Notations and Definitions Graphs and Modeling Algorithmic Graph Theory and Combinatorial
Graphs: Introduction Ali Shokoufandeh, Department of Computer Science, Drexel University Overview of this talk Introduction: Notations and Definitions Graphs and Modeling Algorithmic Graph Theory and Combinatorial
arxiv: v2 [cs.ds] 30 Jan 2018
![arxiv: v2 [cs.ds] 30 Jan 2018 arxiv: v2 [cs.ds] 30 Jan 2018](/thumbs/83/87511369.jpg) The complexity of tropical graph homomorphisms Florent Foucaud Ararat Harutyunyan Pavol Hell Sylvain Legay annis Manoussakis Reza Naserasr January 31, 2018 Note to readers. A shorter version of this article
The complexity of tropical graph homomorphisms Florent Foucaud Ararat Harutyunyan Pavol Hell Sylvain Legay annis Manoussakis Reza Naserasr January 31, 2018 Note to readers. A shorter version of this article
CHAPTER - 1 INTRODUCTION
 CHAPTER - 1 INTRODUCTION INTRODUCTION This thesis comprises of six chapters and is concerned with the construction of new classes of cordial graphs, even and odd graceful graphs, even and odd mean graphs,
CHAPTER - 1 INTRODUCTION INTRODUCTION This thesis comprises of six chapters and is concerned with the construction of new classes of cordial graphs, even and odd graceful graphs, even and odd mean graphs,
A graph is finite if its vertex set and edge set are finite. We call a graph with just one vertex trivial and all other graphs nontrivial.
 2301-670 Graph theory 1.1 What is a graph? 1 st semester 2550 1 1.1. What is a graph? 1.1.2. Definition. A graph G is a triple (V(G), E(G), ψ G ) consisting of V(G) of vertices, a set E(G), disjoint from
2301-670 Graph theory 1.1 What is a graph? 1 st semester 2550 1 1.1. What is a graph? 1.1.2. Definition. A graph G is a triple (V(G), E(G), ψ G ) consisting of V(G) of vertices, a set E(G), disjoint from
Isomorphism of Graphs Which are k-separable*
 Reprinted from INFORMATION AND CONTROL All Rights Reserved by Academic Press, New York and Vol. 56. Nos. 1-2, 1983 Printed in Belgium Isomorphism of Graphs Which are k-separable* GARY L. MILLER Department
Reprinted from INFORMATION AND CONTROL All Rights Reserved by Academic Press, New York and Vol. 56. Nos. 1-2, 1983 Printed in Belgium Isomorphism of Graphs Which are k-separable* GARY L. MILLER Department
Unlabeled equivalence for matroids representable over finite fields
 Unlabeled equivalence for matroids representable over finite fields November 16, 2012 S. R. Kingan Department of Mathematics Brooklyn College, City University of New York 2900 Bedford Avenue Brooklyn,
Unlabeled equivalence for matroids representable over finite fields November 16, 2012 S. R. Kingan Department of Mathematics Brooklyn College, City University of New York 2900 Bedford Avenue Brooklyn,
Equipartite polytopes and graphs
 Equipartite polytopes and graphs Branko Grünbaum Tomáš Kaiser Daniel Král Moshe Rosenfeld Abstract A graph G of even order is weakly equipartite if for any partition of its vertex set into subsets V 1
Equipartite polytopes and graphs Branko Grünbaum Tomáš Kaiser Daniel Král Moshe Rosenfeld Abstract A graph G of even order is weakly equipartite if for any partition of its vertex set into subsets V 1
Bounds for the m-eternal Domination Number of a Graph
 Bounds for the m-eternal Domination Number of a Graph Michael A. Henning Department of Pure and Applied Mathematics University of Johannesburg South Africa mahenning@uj.ac.za Gary MacGillivray Department
Bounds for the m-eternal Domination Number of a Graph Michael A. Henning Department of Pure and Applied Mathematics University of Johannesburg South Africa mahenning@uj.ac.za Gary MacGillivray Department
Characterizing Graphs (3) Characterizing Graphs (1) Characterizing Graphs (2) Characterizing Graphs (4)
 S-72.2420/T-79.5203 Basic Concepts 1 S-72.2420/T-79.5203 Basic Concepts 3 Characterizing Graphs (1) Characterizing Graphs (3) Characterizing a class G by a condition P means proving the equivalence G G
S-72.2420/T-79.5203 Basic Concepts 1 S-72.2420/T-79.5203 Basic Concepts 3 Characterizing Graphs (1) Characterizing Graphs (3) Characterizing a class G by a condition P means proving the equivalence G G
Figure 1: The Gray Graph with an identied Hamilton cycle as in [1]. 2 Structural properties and alternative denitions The Gray graph G is a cubic, bip
![Figure 1: The Gray Graph with an identied Hamilton cycle as in [1]. 2 Structural properties and alternative denitions The Gray graph G is a cubic, bip Figure 1: The Gray Graph with an identied Hamilton cycle as in [1]. 2 Structural properties and alternative denitions The Gray graph G is a cubic, bip](/thumbs/93/113946993.jpg) THE GRAY GRAPH REVISITED Dragan Marusic 1 Tomaz Pisanski 2 IMFM, Oddelek za matematiko IMFM, Oddelek za matematiko Univerza v Ljubljani Jadranska 19, 1000 Ljubljana Slovenija dragan.marusic@uni-lj.si Univerza
THE GRAY GRAPH REVISITED Dragan Marusic 1 Tomaz Pisanski 2 IMFM, Oddelek za matematiko IMFM, Oddelek za matematiko Univerza v Ljubljani Jadranska 19, 1000 Ljubljana Slovenija dragan.marusic@uni-lj.si Univerza
Monotone Paths in Geometric Triangulations
 Monotone Paths in Geometric Triangulations Adrian Dumitrescu Ritankar Mandal Csaba D. Tóth November 19, 2017 Abstract (I) We prove that the (maximum) number of monotone paths in a geometric triangulation
Monotone Paths in Geometric Triangulations Adrian Dumitrescu Ritankar Mandal Csaba D. Tóth November 19, 2017 Abstract (I) We prove that the (maximum) number of monotone paths in a geometric triangulation
Lecture 1: Examples, connectedness, paths and cycles
 Lecture 1: Examples, connectedness, paths and cycles Anders Johansson 2011-10-22 lör Outline The course plan Examples and applications of graphs Relations The definition of graphs as relations Connectedness,
Lecture 1: Examples, connectedness, paths and cycles Anders Johansson 2011-10-22 lör Outline The course plan Examples and applications of graphs Relations The definition of graphs as relations Connectedness,
Assignment 1 Introduction to Graph Theory CO342
 Assignment 1 Introduction to Graph Theory CO342 This assignment will be marked out of a total of thirty points, and is due on Thursday 18th May at 10am in class. Throughout the assignment, the graphs are
Assignment 1 Introduction to Graph Theory CO342 This assignment will be marked out of a total of thirty points, and is due on Thursday 18th May at 10am in class. Throughout the assignment, the graphs are
On the automorphism group of the m-coloured random graph
 On the automorphism group of the m-coloured random graph Peter J. Cameron and Sam Tarzi School of Mathematical Sciences Queen Mary, University of London Mile End Road London E1 4NS, UK p.j.cameron@qmul.ac.uk
On the automorphism group of the m-coloured random graph Peter J. Cameron and Sam Tarzi School of Mathematical Sciences Queen Mary, University of London Mile End Road London E1 4NS, UK p.j.cameron@qmul.ac.uk
Basics of Graph Theory
 Basics of Graph Theory 1 Basic notions A simple graph G = (V, E) consists of V, a nonempty set of vertices, and E, a set of unordered pairs of distinct elements of V called edges. Simple graphs have their
Basics of Graph Theory 1 Basic notions A simple graph G = (V, E) consists of V, a nonempty set of vertices, and E, a set of unordered pairs of distinct elements of V called edges. Simple graphs have their
MT5821 Advanced Combinatorics
 MT5821 Advanced Combinatorics 4 Graph colouring and symmetry There are two colourings of a 4-cycle with two colours (red and blue): one pair of opposite vertices should be red, the other pair blue. There
MT5821 Advanced Combinatorics 4 Graph colouring and symmetry There are two colourings of a 4-cycle with two colours (red and blue): one pair of opposite vertices should be red, the other pair blue. There
Math 776 Graph Theory Lecture Note 1 Basic concepts
 Math 776 Graph Theory Lecture Note 1 Basic concepts Lectured by Lincoln Lu Transcribed by Lincoln Lu Graph theory was founded by the great Swiss mathematician Leonhard Euler (1707-178) after he solved
Math 776 Graph Theory Lecture Note 1 Basic concepts Lectured by Lincoln Lu Transcribed by Lincoln Lu Graph theory was founded by the great Swiss mathematician Leonhard Euler (1707-178) after he solved
Lecture 3: Recap. Administrivia. Graph theory: Historical Motivation. COMP9020 Lecture 4 Session 2, 2017 Graphs and Trees
 Administrivia Lecture 3: Recap Assignment 1 due 23:59 tomorrow. Quiz 4 up tonight, due 15:00 Thursday 31 August. Equivalence relations: (S), (R), (T) Total orders: (AS), (R), (T), (L) Partial orders: (AS),
Administrivia Lecture 3: Recap Assignment 1 due 23:59 tomorrow. Quiz 4 up tonight, due 15:00 Thursday 31 August. Equivalence relations: (S), (R), (T) Total orders: (AS), (R), (T), (L) Partial orders: (AS),
Algorithms for group actions: homomorphism principle and orderly generation applied to graphs
 Algorithms for group actions: homomorphism principle and orderly generation applied to graphs Thomas Grüner, Reinhard Laue, and Markus Meringer Universität Bayreuth, Lehrstuhl II für Mathematik D-95440
Algorithms for group actions: homomorphism principle and orderly generation applied to graphs Thomas Grüner, Reinhard Laue, and Markus Meringer Universität Bayreuth, Lehrstuhl II für Mathematik D-95440
Product constructions for transitive decompositions of graphs
 116 Product constructions for transitive decompositions of graphs Geoffrey Pearce Abstract A decomposition of a graph is a partition of the edge set, giving a set of subgraphs. A transitive decomposition
116 Product constructions for transitive decompositions of graphs Geoffrey Pearce Abstract A decomposition of a graph is a partition of the edge set, giving a set of subgraphs. A transitive decomposition
Structures with lots of symmetry
 Structures with lots of symmetry (one of the things Bob likes to do when not doing semigroup theory) Robert Gray Centro de Álgebra da Universidade de Lisboa NBSAN Manchester, Summer 2011 Why? An advertisement
Structures with lots of symmetry (one of the things Bob likes to do when not doing semigroup theory) Robert Gray Centro de Álgebra da Universidade de Lisboa NBSAN Manchester, Summer 2011 Why? An advertisement
Discrete Math: Selected Homework Problems
 Discrete Math: Selected Homework Problems 2006 2.1 Prove: if d is a common divisor of a and b and d is also a linear combination of a and b then d is a greatest common divisor of a and b. (5 3.1 Prove:
Discrete Math: Selected Homework Problems 2006 2.1 Prove: if d is a common divisor of a and b and d is also a linear combination of a and b then d is a greatest common divisor of a and b. (5 3.1 Prove:
Homomorphisms of Signed Graphs
 Homomorphisms of Signed Graphs Reza Naserasr a, Edita Rollová b, Eric Sopena c a CNRS, LRI, UMR8623, Univ. Paris-Sud 11, F-91405 Orsay Cedex, France b Department of Computer Science, Faculty of Mathematics,
Homomorphisms of Signed Graphs Reza Naserasr a, Edita Rollová b, Eric Sopena c a CNRS, LRI, UMR8623, Univ. Paris-Sud 11, F-91405 Orsay Cedex, France b Department of Computer Science, Faculty of Mathematics,
On graph decompositions modulo k
 On graph decompositions modulo k A.D. Scott Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, 16 Mill Lane, Cambridge, CB2 1SB, England. Abstract. We prove that, for
On graph decompositions modulo k A.D. Scott Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, 16 Mill Lane, Cambridge, CB2 1SB, England. Abstract. We prove that, for
PACKING DIGRAPHS WITH DIRECTED CLOSED TRAILS
 PACKING DIGRAPHS WITH DIRECTED CLOSED TRAILS PAUL BALISTER Abstract It has been shown [Balister, 2001] that if n is odd and m 1,, m t are integers with m i 3 and t i=1 m i = E(K n) then K n can be decomposed
PACKING DIGRAPHS WITH DIRECTED CLOSED TRAILS PAUL BALISTER Abstract It has been shown [Balister, 2001] that if n is odd and m 1,, m t are integers with m i 3 and t i=1 m i = E(K n) then K n can be decomposed
On vertex types of graphs
 On vertex types of graphs arxiv:1705.09540v1 [math.co] 26 May 2017 Pu Qiao, Xingzhi Zhan Department of Mathematics, East China Normal University, Shanghai 200241, China Abstract The vertices of a graph
On vertex types of graphs arxiv:1705.09540v1 [math.co] 26 May 2017 Pu Qiao, Xingzhi Zhan Department of Mathematics, East China Normal University, Shanghai 200241, China Abstract The vertices of a graph
Combinatorics Summary Sheet for Exam 1 Material 2019
 Combinatorics Summary Sheet for Exam 1 Material 2019 1 Graphs Graph An ordered three-tuple (V, E, F ) where V is a set representing the vertices, E is a set representing the edges, and F is a function
Combinatorics Summary Sheet for Exam 1 Material 2019 1 Graphs Graph An ordered three-tuple (V, E, F ) where V is a set representing the vertices, E is a set representing the edges, and F is a function
Computer Algebra Investigation of Known Primitive Triangle-Free Strongly Regular Graphs
 Computer Algebra Investigation of Known Primitive Triangle-Free Strongly Regular Graphs Matan Ziv-Av (Jointly with Mikhail Klin) Ben-Gurion University of the Negev SCSS 2013 RISC, JKU July 5, 2013 Ziv-Av
Computer Algebra Investigation of Known Primitive Triangle-Free Strongly Regular Graphs Matan Ziv-Av (Jointly with Mikhail Klin) Ben-Gurion University of the Negev SCSS 2013 RISC, JKU July 5, 2013 Ziv-Av
Coloring Squared Rectangles
 Coloring Squared Rectangles Mark Bun August 28, 2010 Abstract We investigate the 3-colorability of rectangles dissected into squares. Our primary result is a polynomial-time algorithm for deciding whether
Coloring Squared Rectangles Mark Bun August 28, 2010 Abstract We investigate the 3-colorability of rectangles dissected into squares. Our primary result is a polynomial-time algorithm for deciding whether
The Structure of Bull-Free Perfect Graphs
 The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
Lecture Notes on Graph Theory
 Lecture Notes on Graph Theory Vadim Lozin 1 Introductory concepts A graph G = (V, E) consists of two finite sets V and E. The elements of V are called the vertices and the elements of E the edges of G.
Lecture Notes on Graph Theory Vadim Lozin 1 Introductory concepts A graph G = (V, E) consists of two finite sets V and E. The elements of V are called the vertices and the elements of E the edges of G.
Spanning tree congestion critical graphs
 Spanning tree congestion critical graphs Daniel Tanner August 24, 2007 Abstract The linear or cyclic cutwidth of a graph G is the minimum congestion when G is embedded into either a path or a cycle respectively.
Spanning tree congestion critical graphs Daniel Tanner August 24, 2007 Abstract The linear or cyclic cutwidth of a graph G is the minimum congestion when G is embedded into either a path or a cycle respectively.
Spanning trees and orientations of graphs
 Journal of Combinatorics Volume 1, Number 2, 101 111, 2010 Spanning trees and orientations of graphs Carsten Thomassen A conjecture of Merino and Welsh says that the number of spanning trees τ(g) of a
Journal of Combinatorics Volume 1, Number 2, 101 111, 2010 Spanning trees and orientations of graphs Carsten Thomassen A conjecture of Merino and Welsh says that the number of spanning trees τ(g) of a
A GRAPH FROM THE VIEWPOINT OF ALGEBRAIC TOPOLOGY
 A GRAPH FROM THE VIEWPOINT OF ALGEBRAIC TOPOLOGY KARL L. STRATOS Abstract. The conventional method of describing a graph as a pair (V, E), where V and E repectively denote the sets of vertices and edges,
A GRAPH FROM THE VIEWPOINT OF ALGEBRAIC TOPOLOGY KARL L. STRATOS Abstract. The conventional method of describing a graph as a pair (V, E), where V and E repectively denote the sets of vertices and edges,
Graphic TSP in cubic graphs
 Graphic TSP in cubic graphs arxiv:1608.07568v2 [cs.dm] 30 Aug 2016 Zdeněk Dvořák Daniel Král Bojan Mohar Abstract We prove that every simple 2-connected cubic n-vertex graph contains a spanning closed
Graphic TSP in cubic graphs arxiv:1608.07568v2 [cs.dm] 30 Aug 2016 Zdeněk Dvořák Daniel Král Bojan Mohar Abstract We prove that every simple 2-connected cubic n-vertex graph contains a spanning closed
BIL694-Lecture 1: Introduction to Graphs
 BIL694-Lecture 1: Introduction to Graphs Lecturer: Lale Özkahya Resources for the presentation: http://www.math.ucsd.edu/ gptesler/184a/calendar.html http://www.inf.ed.ac.uk/teaching/courses/dmmr/ Outline
BIL694-Lecture 1: Introduction to Graphs Lecturer: Lale Özkahya Resources for the presentation: http://www.math.ucsd.edu/ gptesler/184a/calendar.html http://www.inf.ed.ac.uk/teaching/courses/dmmr/ Outline
DEFINITION OF GRAPH GRAPH THEORY GRAPHS ACCORDING TO THEIR VERTICES AND EDGES EXAMPLE GRAPHS ACCORDING TO THEIR VERTICES AND EDGES
 DEFINITION OF GRAPH GRAPH THEORY Prepared by Engr. JP Timola Reference: Discrete Math by Kenneth H. Rosen A graph G = (V,E) consists of V, a nonempty set of vertices (or nodes) and E, a set of edges. Each
DEFINITION OF GRAPH GRAPH THEORY Prepared by Engr. JP Timola Reference: Discrete Math by Kenneth H. Rosen A graph G = (V,E) consists of V, a nonempty set of vertices (or nodes) and E, a set of edges. Each
Primitive groups, graph endomorphisms and synchronization
 Primitive groups, graph endomorphisms and synchronization João Araújo Universidade Aberta, R. Escola Politécnica, 147 1269-001 Lisboa, Portugal & CAUL/CEMAT, Universidade de Lisboa 1649-003 Lisboa, Portugal
Primitive groups, graph endomorphisms and synchronization João Araújo Universidade Aberta, R. Escola Politécnica, 147 1269-001 Lisboa, Portugal & CAUL/CEMAT, Universidade de Lisboa 1649-003 Lisboa, Portugal
Answers to specimen paper questions. Most of the answers below go into rather more detail than is really needed. Please let me know of any mistakes.
 Answers to specimen paper questions Most of the answers below go into rather more detail than is really needed. Please let me know of any mistakes. Question 1. (a) The degree of a vertex x is the number
Answers to specimen paper questions Most of the answers below go into rather more detail than is really needed. Please let me know of any mistakes. Question 1. (a) The degree of a vertex x is the number
Complexity Results on Graphs with Few Cliques
 Discrete Mathematics and Theoretical Computer Science DMTCS vol. 9, 2007, 127 136 Complexity Results on Graphs with Few Cliques Bill Rosgen 1 and Lorna Stewart 2 1 Institute for Quantum Computing and School
Discrete Mathematics and Theoretical Computer Science DMTCS vol. 9, 2007, 127 136 Complexity Results on Graphs with Few Cliques Bill Rosgen 1 and Lorna Stewart 2 1 Institute for Quantum Computing and School
MAS341 Graph Theory 2015 exam solutions
 MAS4 Graph Theory 0 exam solutions Question (i)(a) Draw a graph with a vertex for each row and column of the framework; connect a row vertex to a column vertex if there is a brace where the row and column
MAS4 Graph Theory 0 exam solutions Question (i)(a) Draw a graph with a vertex for each row and column of the framework; connect a row vertex to a column vertex if there is a brace where the row and column
motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs { }
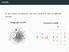 motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs G M { } 2 subgraph motifs 3 motifs Find interesting patterns in a network. 4 motifs Find
motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs G M { } 2 subgraph motifs 3 motifs Find interesting patterns in a network. 4 motifs Find
K 4 C 5. Figure 4.5: Some well known family of graphs
 08 CHAPTER. TOPICS IN CLASSICAL GRAPH THEORY K, K K K, K K, K K, K C C C C 6 6 P P P P P. Graph Operations Figure.: Some well known family of graphs A graph Y = (V,E ) is said to be a subgraph of a graph
08 CHAPTER. TOPICS IN CLASSICAL GRAPH THEORY K, K K K, K K, K K, K C C C C 6 6 P P P P P. Graph Operations Figure.: Some well known family of graphs A graph Y = (V,E ) is said to be a subgraph of a graph
The Largest Pure Partial Planes of Order 6 Have Size 25
 The Largest Pure Partial Planes of Order 6 Have Size 5 Yibo Gao arxiv:1611.00084v1 [math.co] 31 Oct 016 Abstract In this paper, we prove that the largest pure partial plane of order 6 has size 5. At the
The Largest Pure Partial Planes of Order 6 Have Size 5 Yibo Gao arxiv:1611.00084v1 [math.co] 31 Oct 016 Abstract In this paper, we prove that the largest pure partial plane of order 6 has size 5. At the
Key Graph Theory Theorems
 Key Graph Theory Theorems Rajesh Kumar MATH 239 Intro to Combinatorics August 19, 2008 3.3 Binary Trees 3.3.1 Problem (p.82) Determine the number, t n, of binary trees with n edges. The number of binary
Key Graph Theory Theorems Rajesh Kumar MATH 239 Intro to Combinatorics August 19, 2008 3.3 Binary Trees 3.3.1 Problem (p.82) Determine the number, t n, of binary trees with n edges. The number of binary
The canonical augmentation method
 The canonical augmentation method Derrick Stolee 1 University of Nebraska Lincoln s-dstolee1@math.unl.edu http://www.math.unl.edu/ s-dstolee1/ May 13, 2011 1 Supported by NSF grants CCF-0916525 and DMS-0914815.
The canonical augmentation method Derrick Stolee 1 University of Nebraska Lincoln s-dstolee1@math.unl.edu http://www.math.unl.edu/ s-dstolee1/ May 13, 2011 1 Supported by NSF grants CCF-0916525 and DMS-0914815.
Regular polytopes with few flags
 Regular polytopes with few flags Marston Conder University of Auckland mconder@aucklandacnz Introduction: Rotary and regular maps A map M is a 2-cell embedding of a connected graph or multigraph (graph
Regular polytopes with few flags Marston Conder University of Auckland mconder@aucklandacnz Introduction: Rotary and regular maps A map M is a 2-cell embedding of a connected graph or multigraph (graph
V :non-empty vertex ornode set E V V :edge set G (V, E) :directed graph on V, or digraph on V
 -93-11. Graph Theory Example: V :non-empty vertex ornode set E V V :edge set G (V, E) :directed graph on V, or digraph on V b e f V={a, b, c, d, e, f, g} a c d f E={(a,b), (b,c), (c,a),... } Note: (a,
-93-11. Graph Theory Example: V :non-empty vertex ornode set E V V :edge set G (V, E) :directed graph on V, or digraph on V b e f V={a, b, c, d, e, f, g} a c d f E={(a,b), (b,c), (c,a),... } Note: (a,
COVERING SPACES, GRAPHS, AND GROUPS
 COVERING SPACES, GRAPHS, AND GROUPS CARSON COLLINS Abstract. We introduce the theory of covering spaces, with emphasis on explaining the Galois correspondence of covering spaces and the deck transformation
COVERING SPACES, GRAPHS, AND GROUPS CARSON COLLINS Abstract. We introduce the theory of covering spaces, with emphasis on explaining the Galois correspondence of covering spaces and the deck transformation
Abstract. A graph G is perfect if for every induced subgraph H of G, the chromatic number of H is equal to the size of the largest clique of H.
 Abstract We discuss a class of graphs called perfect graphs. After defining them and getting intuition with a few simple examples (and one less simple example), we present a proof of the Weak Perfect Graph
Abstract We discuss a class of graphs called perfect graphs. After defining them and getting intuition with a few simple examples (and one less simple example), we present a proof of the Weak Perfect Graph
Math 170- Graph Theory Notes
 1 Math 170- Graph Theory Notes Michael Levet December 3, 2018 Notation: Let n be a positive integer. Denote [n] to be the set {1, 2,..., n}. So for example, [3] = {1, 2, 3}. To quote Bud Brown, Graph theory
1 Math 170- Graph Theory Notes Michael Levet December 3, 2018 Notation: Let n be a positive integer. Denote [n] to be the set {1, 2,..., n}. So for example, [3] = {1, 2, 3}. To quote Bud Brown, Graph theory
11.1. Definitions. 11. Domination in Graphs
 11. Domination in Graphs Some definitions Minimal dominating sets Bounds for the domination number. The independent domination number Other domination parameters. 11.1. Definitions A vertex v in a graph
11. Domination in Graphs Some definitions Minimal dominating sets Bounds for the domination number. The independent domination number Other domination parameters. 11.1. Definitions A vertex v in a graph
Compositions of series-parallel graphs. Brian Kell
 Compositions of series-parallel graphs Brian Kell March 29, 2006 Abstract A composition of a graph is a partition of the vertex set such that the subgraph induced by each part is connected. In this paper
Compositions of series-parallel graphs Brian Kell March 29, 2006 Abstract A composition of a graph is a partition of the vertex set such that the subgraph induced by each part is connected. In this paper
6c Lecture 3 & 4: April 8 & 10, 2014
 6c Lecture 3 & 4: April 8 & 10, 2014 3.1 Graphs and trees We begin by recalling some basic definitions from graph theory. Definition 3.1. A (undirected, simple) graph consists of a set of vertices V and
6c Lecture 3 & 4: April 8 & 10, 2014 3.1 Graphs and trees We begin by recalling some basic definitions from graph theory. Definition 3.1. A (undirected, simple) graph consists of a set of vertices V and
Non-Hamiltonian and Non-Traceable Regular 3-Connected Planar Graphs
 Introduction Quartic Quintic Conclusion Non-Hamiltonian and Non-Traceable Regular 3-Connected Planar Graphs Nico Van Cleemput Carol T. Zamfirescu Combinatorial Algorithms and Algorithmic Graph Theory Department
Introduction Quartic Quintic Conclusion Non-Hamiltonian and Non-Traceable Regular 3-Connected Planar Graphs Nico Van Cleemput Carol T. Zamfirescu Combinatorial Algorithms and Algorithmic Graph Theory Department
Connected-homogeneous graphs
 Connected-homogeneous graphs Robert Gray BIRS Workshop on Infinite Graphs October 2007 1 / 14 Homogeneous graphs Definition A graph Γ is called homogeneous if any isomorphism between finite induced subgraphs
Connected-homogeneous graphs Robert Gray BIRS Workshop on Infinite Graphs October 2007 1 / 14 Homogeneous graphs Definition A graph Γ is called homogeneous if any isomorphism between finite induced subgraphs
Binary Relations McGraw-Hill Education
 Binary Relations A binary relation R from a set A to a set B is a subset of A X B Example: Let A = {0,1,2} and B = {a,b} {(0, a), (0, b), (1,a), (2, b)} is a relation from A to B. We can also represent
Binary Relations A binary relation R from a set A to a set B is a subset of A X B Example: Let A = {0,1,2} and B = {a,b} {(0, a), (0, b), (1,a), (2, b)} is a relation from A to B. We can also represent
Base size and separation number
 Base size and separation number Peter J. Cameron CSG notes, April 2005 Brief history The concept of a base for a permutation group was introduced by Sims in the 1960s in connection with computational group
Base size and separation number Peter J. Cameron CSG notes, April 2005 Brief history The concept of a base for a permutation group was introduced by Sims in the 1960s in connection with computational group
Adjacent: Two distinct vertices u, v are adjacent if there is an edge with ends u, v. In this case we let uv denote such an edge.
 1 Graph Basics What is a graph? Graph: a graph G consists of a set of vertices, denoted V (G), a set of edges, denoted E(G), and a relation called incidence so that each edge is incident with either one
1 Graph Basics What is a graph? Graph: a graph G consists of a set of vertices, denoted V (G), a set of edges, denoted E(G), and a relation called incidence so that each edge is incident with either one
Graphs associated to CAT(0) cube complexes
 Graphs associated to CAT(0) cube complexes Mark Hagen McGill University Cornell Topology Seminar, 15 November 2011 Outline Background on CAT(0) cube complexes The contact graph: a combinatorial invariant
Graphs associated to CAT(0) cube complexes Mark Hagen McGill University Cornell Topology Seminar, 15 November 2011 Outline Background on CAT(0) cube complexes The contact graph: a combinatorial invariant
v V Question: How many edges are there in a graph with 10 vertices each of degree 6?
 ECS20 Handout Graphs and Trees March 4, 2015 (updated 3/9) Notion of a graph 1. A graph G = (V,E) consists of V, a nonempty set of vertices (or nodes) and E, a set of pairs of elements of V called edges.
ECS20 Handout Graphs and Trees March 4, 2015 (updated 3/9) Notion of a graph 1. A graph G = (V,E) consists of V, a nonempty set of vertices (or nodes) and E, a set of pairs of elements of V called edges.
A few families of non-schurian association schemes 1
 A few families of non-schurian association schemes 1 Štefan Gyürki Slovak University of Technology in Bratislava, Slovakia Ben-Gurion University of the Negev, Beer Sheva, Israel CSD6, Portorož 2012 1 Joint
A few families of non-schurian association schemes 1 Štefan Gyürki Slovak University of Technology in Bratislava, Slovakia Ben-Gurion University of the Negev, Beer Sheva, Israel CSD6, Portorož 2012 1 Joint
