Projections and Hardware Rendering. Brian Curless CSE 557 Fall 2014
|
|
|
- Godfrey Shepherd
- 5 years ago
- Views:
Transcription
1 Projections and Hardware Rendering Brian Curless CSE 557 Fall
2 Reading Required: Shirley, Ch. 7, Sec. 8.2, Ch. 18 Further reading: Foley, et al, Chapter 5.6 and Chapter 6 David F. Rogers and J. Alan Adams, Mathematical Elements for Computer Graphics, 2 nd Ed., McGraw-Hill, New York, 1990, Chapter 2. I. E. Sutherland, R. F. Sproull, and R. A. Schumacker, A characterization of ten hidden surface algorithms, ACM Computing Surveys 6(1): 1-55, March
3 Going back to the pinhole camera Recall that the Trace project uses, by default, the pinhole camera model. If we just consider finding out which surface point is visible at each image pixel, then we are ray casting. For each pixel center P ij Send ray from eye point (COP), C, through P ij into scene. Intersect ray with each object. Select nearest intersection. 3
4 Warping space A very different approach is to take the imaging setup: then warp all of space so that all the rays are parallel (and distant objects are smaller than closer objects): and then just draw everything onto the image plane, keeping track of what is in front: 4
5 3D Geometry Pipeline Graphics hardware follows the warping space approach. Before being turned into pixels, a piece of geometry goes through a number of transformations... 5
6 3D Geometry Pipeline (cont d) 6
7 Projections Projections transform points in n-space to m-space, where m<n. In 3-D, we map points from 3-space to the projection plane (PP) (a.k.a., image plane) along projectors (a.k.a., viewing rays) emanating from the center of projection (COP): There are two basic types of projections: Perspective distance from COP to PP finite Parallel distance from COP to PP infinite 7
8 Parallel projections For parallel projections, we specify a direction of projection (DOP) instead of a COP. There are two types of parallel projections: Orthographic projection DOP perpendicular to PP Oblique projection DOP not perpendicular to PP We can write orthographic projection onto the z=0 plane with a simple matrix. x x ' y y ' z Normally, we do not drop the z value right away. Why not? 8
9 Z-buffer The Z-buffer or depth buffer algorithm [Catmull, 1974] can be used to determine which surface point is visible at each pixel. Here is pseudocode for the Z-buffer hidden surface algorithm: for each pixel (i,j) do Z-buffer [i,j] FAR Framebuffer[i,j] <background color> end for for each triangle A do for each pixel in A do Compute depth z of A at (i,j) if z > Z-buffer [i,j] then Z-buffer [i,j] z Framebuffer[i,j] color of A end if end for end for Q: What should FAR be set to? 9
10 Rasterization The process of filling in the pixels inside of a polygon is called rasterization. During rasterization, the z value can be computed incrementally (fast!). Curious fact: Described as the brute-force image space algorithm by [SSS] Mentioned only in Appendix B of [SSS] as a point of comparison for huge memories, but written off as totally impractical. Today, Z-buffers are commonly implemented in hardware. 10
11 Properties of parallel projection Properties of parallel projection: Not realistic looking Good for exact measurements Are actually a kind of affine transformation Parallel lines remain parallel Ratios are preserved Angles not (in general) preserved Most often used in CAD, architectural drawings, etc., where taking exact measurement is important 11
12 Derivation of perspective projection Consider the projection of a point onto the projection plane: By similar triangles, we can compute how much the x and y coordinates are scaled: 12
13 Homogeneous coordinates revisited Remember how we said that affine transformations work with the last coordinate always set to one. What happens if the coordinate is not one? We divide all the coordinates by w: x x/ w y y/ w z z/ w w 1 If w = 1, then nothing changes. Sometimes we call this division step the perspective divide. 13
14 Homogeneous coordinates and perspective projection Now we can re-write the perspective projection as a matrix equation: x x' x y y' y z w' 0 0 1/ d 0 z/ d 1 After division by w, we get: d x x ' z d y' y z 1 1 Again, projection implies dropping the z coordinate to give a 2D image, but we usually keep it around a little while longer. 14
15 Projective normalization After applying the perspective transformation and dividing by w, we are free to do a simple parallel projection to get the 2D image. What does this imply about the shape of things after the perspective transformation + divide? 15
16 Viewing angle An alternative to specifying the distance from COP to PP is to specify a viewing angle: Given the height of the image h and, what is d? What happens to d as increases (while h is constant)? 16
17 Zoom and dolly 17
18 Vanishing points What happens to two parallel lines that are not parallel to the projection plane? Think of train tracks receding into the horizon... The equation for a line is: px vx p y v y lptv t pz vz 1 0 After perspective transformation we get: x' px tvx y' py tv y w' ( pz tvz)/ d 18
19 Vanishing points (cont'd) Dividing by w: px tvx d pz tv z x ' py tvy y' d pz tvz w ' 1 Letting t go to infinity: We get a point! What happens to the line l = q + tv? Each set of parallel lines intersect at a vanishing point on the PP. Q: How many vanishing points are there? 19
20 Clipping and the viewing frustum The center of projection and the portion of the projection plane that map to the final image form an infinite pyramid. The sides of the pyramid are clipping planes. Frequently, additional clipping planes are inserted to restrict the range of depths. These clipping planes are called the near and far or the hither and yon clipping planes. All of the clipping planes bound the the viewing frustum. 20
21 Properties of perspective projections The perspective projection is an example of a projective transformation. Here are some properties of projective transformations: Lines map to lines Parallel lines do not necessarily remain parallel Ratios are not preserved One of the advantages of perspective projection is that size varies inversely with distance looks realistic. A disadvantage is that we can't judge distances as exactly as we can with parallel projections. 21
22 Rasterization with color Recall that the z-buffer works by interpolating z-values across a triangle that has been projected into image space, a process called rasterization. During rasterization, colors can be smeared across a triangle as well: 22
23 Gouraud interpolation Recall from the shading lecture, rendering with per triangle normals leads to faceted appearance. An improvement is to compute per-vertex normals and use graphics hardware to do Gouraud interpolation: 1. Compute normals at the vertices. 2. Shade only the vertices. 3. Interpolate the resulting vertex colors. 23
24 Gouraud interpolation artifacts Gouraud interpolation has significant limitations. 1. If the polygonal approximation is too coarse, we can miss specular highlights. 2. We will encounter Mach banding (derivative discontinuity enhanced by human eye). This is what graphics hardware does by default. A substantial improvement is to do 24
25 Phong interpolation To get an even smoother result with fewer artifacts, we can perform Phong interpolation. Here s how it works: 1. Compute normals at the vertices. 2. Interpolate normals and normalize. 3. Shade using the interpolated normals. 25
26 Default pipeline: Gouraud interpolation Vertex processor Primitive assembler Default vertex processing: L determine lighting direction V determine viewing direction Nnormalize( n e ) cblinn-phong shade with LV,, N, kd, ks, ns attach c blinn-phong to vertex as varying v i project v to image i, i, vi v v triangle Rasterizer Fragment processor Default fragment processing: p color c blinn-phong 26
27 Programmable pipeline: Phong-interpolated normals! Vertex processor Vertex shader: attach n e to vertex as varying attach v e to vertex as varying v i project v to image Primitive assembler v, v, v i i i triangle Rasterizer Fragment processor Fragment shader: L determine lighting direction V determine viewing direction p N normalize( n e ) color shade with LV,, Nk,, k, n p p p d s s 27
28 Texture mapping and the z-buffer Texture-mapping can also be handled in z-buffer algorithms. Method: Scan conversion is done in screen space, as usual Each pixel is colored according to the texture Texture coordinates are found by Gouraud-style interpolation Note: Mapping is more complicated to handle perspective correctly! 28
29 Shading in OpenGL The OpenGL lighting model allows you to associate different lighting colors according to material properties they will influence. Thus, our original shading equation: I=k +k I + e a La 1 a+b r +cr NL NH I B k +k n 2 L,j j d j s j + j j j j j j s becomes: I=k +k I + e a La 1 a+b r +cr 2 j j j j j j ki + B ki ( NL ) +ki ( NH ) n a La,j j d Ld, j j s Ls,j j + s where you can have a global ambient light with intensity I La in addition to having an ambient light intensity I La,j associated with each individual light, as well as separate diffuse and specular intensities, I Ld,j and I Ls,j, repectively. 29
30 Materials in OpenGL The OpenGL code to specify the surface shading properties is fairly straightforward. For example: GLfloat ke[] = { 0.1, 0.15, 0.05, 1.0 }; GLfloat ka[] = { 0.1, 0.15, 0.1, 1.0 }; GLfloat kd[] = { 0.3, 0.3, 0.2, 1.0 }; GLfloat ks[] = { 0.2, 0.2, 0.2, 1.0 }; GLfloat ns[] = { 50.0 }; glmaterialfv(gl_front, GL_EMISSION, ke); glmaterialfv(gl_front, GL_AMBIENT, ka); glmaterialfv(gl_front, GL_DIFFUSE, kd); glmaterialfv(gl_front, GL_SPECULAR, ks); glmaterialfv(gl_front, GL_SHININESS, ns); Notes: The GL_FRONT parameter tells OpenGL that we are specifiying the materials for the front of the surface. Only the alpha value of the diffuse color is used for blending. It s usually set to 1. 30
31 Shading in OpenGL, cont d In OpenGL this equation, for one light source (the 0 th ) is specified something like: GLfloat La[] = { 0.2, 0.2, 0.2, 1.0 }; GLfloat La0[] = { 0.1, 0.1, 0.1, 1.0 }; GLfloat Ld0[] = { 1.0, 1.0, 1.0, 1.0 }; GLfloat Ls0[] = { 1.0, 1.0, 1.0, 1.0 }; GLfloat pos0[] = { 1.0, 1.0, 1.0, 0.0 }; GLfloat a0[] = { 1.0 }; GLfloat b0[] = { 0.5 }; GLfloat c0[] = { 0.25 }; GLfloat S0[] = { -1.0, -1.0, 0.0 }; GLfloat beta0[] = { 45 }; GLfloat e0[] = { 2 }; gllightmodelfv(gl_light_model_ambient, La); gllightfv(gl_light0, GL_AMBIENT, La0); gllightfv(gl_light0, GL_DIFFUSE, Ld0); gllightfv(gl_light0, GL_SPECULAR, Ls0); gllightfv(gl_light0, GL_POSITION, pos0); gllightfv(gl_light0, GL_CONSTANT_ATTENUATION, a0); gllightfv(gl_light0, GL_LINEAR_ATTENUATION, b0); gllightfv(gl_light0, GL_QUADRATIC_ATTENUATION, c0); gllightfv(gl_light0, GL_SPOT_DIRECTION, S0); gllightf(gl_light0, GL_SPOT_CUTOFF, beta0); gllightf(gl_light0, GL_SPOT_EXPONENT, e0); 31
32 Shading in OpenGL, cont d Notes: You can have as many as GL_MAX_LIGHTS lights in a scene. This number is system-dependent. For directional lights, you specify a light direction, not position, and the attenuation and spotlight terms are ignored. The directions of directional lights and spotlights are specified in the coordinate systems of the lights, not the surface points as we ve been doing in lecture. 32
Reading. 18. Projections and Z-buffers. Required: Watt, Section , 6.3, 6.6 (esp. intro and subsections 1, 4, and 8 10), Further reading:
 Reading Required: Watt, Section 5.2.2 5.2.4, 6.3, 6.6 (esp. intro and subsections 1, 4, and 8 10), Further reading: 18. Projections and Z-buffers Foley, et al, Chapter 5.6 and Chapter 6 David F. Rogers
Reading Required: Watt, Section 5.2.2 5.2.4, 6.3, 6.6 (esp. intro and subsections 1, 4, and 8 10), Further reading: 18. Projections and Z-buffers Foley, et al, Chapter 5.6 and Chapter 6 David F. Rogers
Projections. Brian Curless CSE 457 Spring Reading. Shrinking the pinhole. The pinhole camera. Required:
 Reading Required: Projections Brian Curless CSE 457 Spring 2013 Angel, 5.1-5.6 Further reading: Fole, et al, Chapter 5.6 and Chapter 6 David F. Rogers and J. Alan Adams, Mathematical Elements for Computer
Reading Required: Projections Brian Curless CSE 457 Spring 2013 Angel, 5.1-5.6 Further reading: Fole, et al, Chapter 5.6 and Chapter 6 David F. Rogers and J. Alan Adams, Mathematical Elements for Computer
Shading. CSE 457 Winter 2015
 Shading CSE 457 Winter 2015 Reading Required: Angel chapter 5. Optional: OpenGL red book, chapter 5. 2 Basic 3D graphics With affine matrices, we can now transform virtual 3D objects in their local coordinate
Shading CSE 457 Winter 2015 Reading Required: Angel chapter 5. Optional: OpenGL red book, chapter 5. 2 Basic 3D graphics With affine matrices, we can now transform virtual 3D objects in their local coordinate
Shading. Brian Curless CSE 457 Spring 2015
 Shading Brian Curless CSE 457 Spring 2015 1 Reading Required: Angel chapter 5. Optional: OpenGL red book, chapter 5. 2 Basic 3D graphics With affine matrices, we can now transform virtual 3D objects in
Shading Brian Curless CSE 457 Spring 2015 1 Reading Required: Angel chapter 5. Optional: OpenGL red book, chapter 5. 2 Basic 3D graphics With affine matrices, we can now transform virtual 3D objects in
Reading. Shading. Introduction. An abundance of photons. Required: Angel , Optional: OpenGL red book, chapter 5.
 Reading Required: Angel 6.1-6.5, 6.7-6.8 Optional: Shading OpenGL red book, chapter 5. 1 2 Introduction So far, we ve talked exclusively about geometry. What is the shape of an obect? How do I place it
Reading Required: Angel 6.1-6.5, 6.7-6.8 Optional: Shading OpenGL red book, chapter 5. 1 2 Introduction So far, we ve talked exclusively about geometry. What is the shape of an obect? How do I place it
Reading. Shading. An abundance of photons. Introduction. Required: Angel , 6.5, Optional: Angel 6.4 OpenGL red book, chapter 5.
 Reading Required: Angel 6.1-6.3, 6.5, 6.7-6.8 Optional: Shading Angel 6.4 OpenGL red book, chapter 5. 1 2 Introduction An abundance of photons So far, we ve talked exclusively about geometry. Properly
Reading Required: Angel 6.1-6.3, 6.5, 6.7-6.8 Optional: Shading Angel 6.4 OpenGL red book, chapter 5. 1 2 Introduction An abundance of photons So far, we ve talked exclusively about geometry. Properly
Shading. Brian Curless CSE 457 Spring 2017
 Shading Brian Curless CSE 457 Spring 2017 1 Reading Optional: Angel and Shreiner: chapter 5. Marschner and Shirley: chapter 10, chapter 17. Further reading: OpenGL red book, chapter 5. 2 Basic 3D graphics
Shading Brian Curless CSE 457 Spring 2017 1 Reading Optional: Angel and Shreiner: chapter 5. Marschner and Shirley: chapter 10, chapter 17. Further reading: OpenGL red book, chapter 5. 2 Basic 3D graphics
Pipeline Operations. CS 4620 Lecture Steve Marschner. Cornell CS4620 Spring 2018 Lecture 11
 Pipeline Operations CS 4620 Lecture 11 1 Pipeline you are here APPLICATION COMMAND STREAM 3D transformations; shading VERTEX PROCESSING TRANSFORMED GEOMETRY conversion of primitives to pixels RASTERIZATION
Pipeline Operations CS 4620 Lecture 11 1 Pipeline you are here APPLICATION COMMAND STREAM 3D transformations; shading VERTEX PROCESSING TRANSFORMED GEOMETRY conversion of primitives to pixels RASTERIZATION
Pipeline Operations. CS 4620 Lecture 10
 Pipeline Operations CS 4620 Lecture 10 2008 Steve Marschner 1 Hidden surface elimination Goal is to figure out which color to make the pixels based on what s in front of what. Hidden surface elimination
Pipeline Operations CS 4620 Lecture 10 2008 Steve Marschner 1 Hidden surface elimination Goal is to figure out which color to make the pixels based on what s in front of what. Hidden surface elimination
Pipeline Operations. CS 4620 Lecture 14
 Pipeline Operations CS 4620 Lecture 14 2014 Steve Marschner 1 Pipeline you are here APPLICATION COMMAND STREAM 3D transformations; shading VERTEX PROCESSING TRANSFORMED GEOMETRY conversion of primitives
Pipeline Operations CS 4620 Lecture 14 2014 Steve Marschner 1 Pipeline you are here APPLICATION COMMAND STREAM 3D transformations; shading VERTEX PROCESSING TRANSFORMED GEOMETRY conversion of primitives
CEng 477 Introduction to Computer Graphics Fall
 Illumination Models and Surface-Rendering Methods CEng 477 Introduction to Computer Graphics Fall 2007 2008 Illumination Models and Surface Rendering Methods In order to achieve realism in computer generated
Illumination Models and Surface-Rendering Methods CEng 477 Introduction to Computer Graphics Fall 2007 2008 Illumination Models and Surface Rendering Methods In order to achieve realism in computer generated
CSE 167: Lecture #8: Lighting. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2011
 CSE 167: Introduction to Computer Graphics Lecture #8: Lighting Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2011 Announcements Homework project #4 due Friday, October 28 Introduction:
CSE 167: Introduction to Computer Graphics Lecture #8: Lighting Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2011 Announcements Homework project #4 due Friday, October 28 Introduction:
Shading and Illumination
 Shading and Illumination OpenGL Shading Without Shading With Shading Physics Bidirectional Reflectance Distribution Function (BRDF) f r (ω i,ω ) = dl(ω ) L(ω i )cosθ i dω i = dl(ω ) L(ω i )( ω i n)dω
Shading and Illumination OpenGL Shading Without Shading With Shading Physics Bidirectional Reflectance Distribution Function (BRDF) f r (ω i,ω ) = dl(ω ) L(ω i )cosθ i dω i = dl(ω ) L(ω i )( ω i n)dω
Overview. Shading. Shading. Why we need shading. Shading Light-material interactions Phong model Shading polygons Shading in OpenGL
 Overview Shading Shading Light-material interactions Phong model Shading polygons Shading in OpenGL Why we need shading Suppose we build a model of a sphere using many polygons and color it with glcolor.
Overview Shading Shading Light-material interactions Phong model Shading polygons Shading in OpenGL Why we need shading Suppose we build a model of a sphere using many polygons and color it with glcolor.
Lecture 4 Advanced Computer Graphics (CS & SE )
 Lecture 4 Advanced Computer Graphics (CS & SE 233.420) Topics Covered Animation Matrices Viewing Lighting Animating Interactive Programs Consider planet.c Want to animate rotating the Earth around the
Lecture 4 Advanced Computer Graphics (CS & SE 233.420) Topics Covered Animation Matrices Viewing Lighting Animating Interactive Programs Consider planet.c Want to animate rotating the Earth around the
INF3320 Computer Graphics and Discrete Geometry
 INF3320 Computer Graphics and Discrete Geometry Visual appearance Christopher Dyken and Martin Reimers 23.09.2009 Page 1 Visual appearance Real Time Rendering: Chapter 5 Light Sources and materials Shading
INF3320 Computer Graphics and Discrete Geometry Visual appearance Christopher Dyken and Martin Reimers 23.09.2009 Page 1 Visual appearance Real Time Rendering: Chapter 5 Light Sources and materials Shading
3D Polygon Rendering. Many applications use rendering of 3D polygons with direct illumination
 Rendering Pipeline 3D Polygon Rendering Many applications use rendering of 3D polygons with direct illumination 3D Polygon Rendering What steps are necessary to utilize spatial coherence while drawing
Rendering Pipeline 3D Polygon Rendering Many applications use rendering of 3D polygons with direct illumination 3D Polygon Rendering What steps are necessary to utilize spatial coherence while drawing
Three-Dimensional Graphics V. Guoying Zhao 1 / 55
 Computer Graphics Three-Dimensional Graphics V Guoying Zhao 1 / 55 Shading Guoying Zhao 2 / 55 Objectives Learn to shade objects so their images appear three-dimensional Introduce the types of light-material
Computer Graphics Three-Dimensional Graphics V Guoying Zhao 1 / 55 Shading Guoying Zhao 2 / 55 Objectives Learn to shade objects so their images appear three-dimensional Introduce the types of light-material
Illumination and Shading
 CT4510: Computer Graphics Illumination and Shading BOCHANG MOON Photorealism The ultimate goal of rendering is to produce photo realistic images. i.e., rendered images should be indistinguishable from
CT4510: Computer Graphics Illumination and Shading BOCHANG MOON Photorealism The ultimate goal of rendering is to produce photo realistic images. i.e., rendered images should be indistinguishable from
Computer Graphics I Lecture 11
 15-462 Computer Graphics I Lecture 11 Midterm Review Assignment 3 Movie Midterm Review Midterm Preview February 26, 2002 Frank Pfenning Carnegie Mellon University http://www.cs.cmu.edu/~fp/courses/graphics/
15-462 Computer Graphics I Lecture 11 Midterm Review Assignment 3 Movie Midterm Review Midterm Preview February 26, 2002 Frank Pfenning Carnegie Mellon University http://www.cs.cmu.edu/~fp/courses/graphics/
Models and Architectures
 Models and Architectures Objectives Learn the basic design of a graphics system Introduce graphics pipeline architecture Examine software components for an interactive graphics system 1 Image Formation
Models and Architectures Objectives Learn the basic design of a graphics system Introduce graphics pipeline architecture Examine software components for an interactive graphics system 1 Image Formation
CS Surface Rendering
 CS10101001 Surface Rendering Junqiao Zhao 赵君峤 Department of Computer Science and Technology College of Electronics and Information Engineering Tongji University Surface rendering How do we choose a color
CS10101001 Surface Rendering Junqiao Zhao 赵君峤 Department of Computer Science and Technology College of Electronics and Information Engineering Tongji University Surface rendering How do we choose a color
Illumination and Shading
 Illumination and Shading Illumination (Lighting)! Model the interaction of light with surface points to determine their final color and brightness! The illumination can be computed either at vertices or
Illumination and Shading Illumination (Lighting)! Model the interaction of light with surface points to determine their final color and brightness! The illumination can be computed either at vertices or
Illumination Model. The governing principles for computing the. Apply the lighting model at a set of points across the entire surface.
 Illumination and Shading Illumination (Lighting) Model the interaction of light with surface points to determine their final color and brightness OpenGL computes illumination at vertices illumination Shading
Illumination and Shading Illumination (Lighting) Model the interaction of light with surface points to determine their final color and brightness OpenGL computes illumination at vertices illumination Shading
Illumination and Shading
 Illumination and Shading Illumination (Lighting) Model the interaction of light with surface points to determine their final color and brightness OpenGL computes illumination at vertices illumination Shading
Illumination and Shading Illumination (Lighting) Model the interaction of light with surface points to determine their final color and brightness OpenGL computes illumination at vertices illumination Shading
Homework #2. Shading, Projections, Texture Mapping, Ray Tracing, and Bezier Curves
 Computer Graphics Instructor: Brian Curless CSEP 557 Autumn 2016 Homework #2 Shading, Projections, Texture Mapping, Ray Tracing, and Bezier Curves Assigned: Wednesday, Nov 16 th Due: Wednesday, Nov 30
Computer Graphics Instructor: Brian Curless CSEP 557 Autumn 2016 Homework #2 Shading, Projections, Texture Mapping, Ray Tracing, and Bezier Curves Assigned: Wednesday, Nov 16 th Due: Wednesday, Nov 30
Why we need shading?
 Why we need shading? Suppose we build a model of a sphere using many polygons and color it with glcolor. We get something like But we want Light-material interactions cause each point to have a different
Why we need shading? Suppose we build a model of a sphere using many polygons and color it with glcolor. We get something like But we want Light-material interactions cause each point to have a different
CSE 167: Introduction to Computer Graphics Lecture #6: Lights. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2014
 CSE 167: Introduction to Computer Graphics Lecture #6: Lights Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2014 Announcements Project 2 due Friday, Oct. 24 th Midterm Exam
CSE 167: Introduction to Computer Graphics Lecture #6: Lights Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2014 Announcements Project 2 due Friday, Oct. 24 th Midterm Exam
Lecture 17: Shading in OpenGL. CITS3003 Graphics & Animation
 Lecture 17: Shading in OpenGL CITS3003 Graphics & Animation E. Angel and D. Shreiner: Interactive Computer Graphics 6E Addison-Wesley 2012 Objectives Introduce the OpenGL shading methods - per vertex shading
Lecture 17: Shading in OpenGL CITS3003 Graphics & Animation E. Angel and D. Shreiner: Interactive Computer Graphics 6E Addison-Wesley 2012 Objectives Introduce the OpenGL shading methods - per vertex shading
CS 4731: Computer Graphics Lecture 16: Phong Illumination and Shading. Emmanuel Agu
 CS 4731: Computer Graphics Lecture 16: Phong Illumination and Shading Emmanuel Agu Recall: Setting Light Property Define colors and position a light GLfloat light_ambient[] = {0.0, 0.0, 0.0, 1.0}; GLfloat
CS 4731: Computer Graphics Lecture 16: Phong Illumination and Shading Emmanuel Agu Recall: Setting Light Property Define colors and position a light GLfloat light_ambient[] = {0.0, 0.0, 0.0, 1.0}; GLfloat
Ambient reflection. Jacobs University Visualization and Computer Graphics Lab : Graphics and Visualization 407
 Ambient reflection Phong reflection is a local illumination model. It only considers the reflection of light that directly comes from the light source. It does not compute secondary reflection of light
Ambient reflection Phong reflection is a local illumination model. It only considers the reflection of light that directly comes from the light source. It does not compute secondary reflection of light
Shading in OpenGL. Outline. Defining and Maintaining Normals. Normalization. Enabling Lighting and Lights. Outline
 CSCI 420 Computer Graphics Lecture 10 Shading in OpenGL Normal Vectors in OpenGL Polygonal Shading Light Source in OpenGL Material Properties in OpenGL Approximating a Sphere [Angel Ch. 6.5-6.9] Jernej
CSCI 420 Computer Graphics Lecture 10 Shading in OpenGL Normal Vectors in OpenGL Polygonal Shading Light Source in OpenGL Material Properties in OpenGL Approximating a Sphere [Angel Ch. 6.5-6.9] Jernej
CS4620/5620: Lecture 14 Pipeline
 CS4620/5620: Lecture 14 Pipeline 1 Rasterizing triangles Summary 1! evaluation of linear functions on pixel grid 2! functions defined by parameter values at vertices 3! using extra parameters to determine
CS4620/5620: Lecture 14 Pipeline 1 Rasterizing triangles Summary 1! evaluation of linear functions on pixel grid 2! functions defined by parameter values at vertices 3! using extra parameters to determine
Orthogonal Projection Matrices. Angel and Shreiner: Interactive Computer Graphics 7E Addison-Wesley 2015
 Orthogonal Projection Matrices 1 Objectives Derive the projection matrices used for standard orthogonal projections Introduce oblique projections Introduce projection normalization 2 Normalization Rather
Orthogonal Projection Matrices 1 Objectives Derive the projection matrices used for standard orthogonal projections Introduce oblique projections Introduce projection normalization 2 Normalization Rather
Light Sources. Spotlight model
 lecture 12 Light Sources sunlight (parallel) Sunny day model : "point source at infinity" - lighting - materials: diffuse, specular, ambient spotlight - shading: Flat vs. Gouraud vs Phong light bulb ambient
lecture 12 Light Sources sunlight (parallel) Sunny day model : "point source at infinity" - lighting - materials: diffuse, specular, ambient spotlight - shading: Flat vs. Gouraud vs Phong light bulb ambient
Computer Graphics. Shadows
 Computer Graphics Lecture 10 Shadows Taku Komura Today Shadows Overview Projective shadows Shadow texture Shadow volume Shadow map Soft shadows Why Shadows? Shadows tell us about the relative locations
Computer Graphics Lecture 10 Shadows Taku Komura Today Shadows Overview Projective shadows Shadow texture Shadow volume Shadow map Soft shadows Why Shadows? Shadows tell us about the relative locations
Today s class. Simple shadows Shading Lighting in OpenGL. Informationsteknologi. Wednesday, November 21, 2007 Computer Graphics - Class 10 1
 Today s class Simple shadows Shading Lighting in OpenGL Wednesday, November 21, 27 Computer Graphics - Class 1 1 Simple shadows Simple shadows can be gotten by using projection matrices Consider a light
Today s class Simple shadows Shading Lighting in OpenGL Wednesday, November 21, 27 Computer Graphics - Class 1 1 Simple shadows Simple shadows can be gotten by using projection matrices Consider a light
5.2 Shading in OpenGL
 Fall 2017 CSCI 420: Computer Graphics 5.2 Shading in OpenGL Hao Li http://cs420.hao-li.com 1 Outline Normal Vectors in OpenGL Polygonal Shading Light Sources in OpenGL Material Properties in OpenGL Example:
Fall 2017 CSCI 420: Computer Graphics 5.2 Shading in OpenGL Hao Li http://cs420.hao-li.com 1 Outline Normal Vectors in OpenGL Polygonal Shading Light Sources in OpenGL Material Properties in OpenGL Example:
Homework #2. Shading, Ray Tracing, and Texture Mapping
 Computer Graphics Prof. Brian Curless CSE 457 Spring 2000 Homework #2 Shading, Ray Tracing, and Texture Mapping Prepared by: Doug Johnson, Maya Widyasari, and Brian Curless Assigned: Monday, May 8, 2000
Computer Graphics Prof. Brian Curless CSE 457 Spring 2000 Homework #2 Shading, Ray Tracing, and Texture Mapping Prepared by: Doug Johnson, Maya Widyasari, and Brian Curless Assigned: Monday, May 8, 2000
Introduction to Computer Graphics with WebGL
 Introduction to Computer Graphics with WebGL Ed Angel Professor Emeritus of Computer Science Founding Director, Arts, Research, Technology and Science Laboratory University of New Mexico Models and Architectures
Introduction to Computer Graphics with WebGL Ed Angel Professor Emeritus of Computer Science Founding Director, Arts, Research, Technology and Science Laboratory University of New Mexico Models and Architectures
Lighting/Shading III. Week 7, Wed Mar 3
 University of British Columbia CPSC 314 Computer Graphics Jan-Apr 2010 Tamara Munzner Lighting/Shading III Week 7, Wed Mar 3 http://www.ugrad.cs.ubc.ca/~cs314/vjan2010 reminders News don't need to tell
University of British Columbia CPSC 314 Computer Graphics Jan-Apr 2010 Tamara Munzner Lighting/Shading III Week 7, Wed Mar 3 http://www.ugrad.cs.ubc.ca/~cs314/vjan2010 reminders News don't need to tell
CS 130 Final. Fall 2015
 CS 130 Final Fall 2015 Name Student ID Signature You may not ask any questions during the test. If you believe that there is something wrong with a question, write down what you think the question is trying
CS 130 Final Fall 2015 Name Student ID Signature You may not ask any questions during the test. If you believe that there is something wrong with a question, write down what you think the question is trying
CSE528 Computer Graphics: Theory, Algorithms, and Applications
 CSE528 Computer Graphics: Theory, Algorithms, and Applications Hong Qin Stony Brook University (SUNY at Stony Brook) Stony Brook, New York 11794-2424 Tel: (631)632-845; Fax: (631)632-8334 qin@cs.stonybrook.edu
CSE528 Computer Graphics: Theory, Algorithms, and Applications Hong Qin Stony Brook University (SUNY at Stony Brook) Stony Brook, New York 11794-2424 Tel: (631)632-845; Fax: (631)632-8334 qin@cs.stonybrook.edu
Shading. Reading. Pinhole camera. Basic 3D graphics. Brian Curless CSE 557 Fall Required: Shirley, Chapter 10
 Reading Required: Shirley, Chapter 10 Shading Brian Curless CSE 557 Fall 2014 1 2 Basic 3D graphics With affine matrices, we can now transform virtual 3D objects in their local coordinate systems into
Reading Required: Shirley, Chapter 10 Shading Brian Curless CSE 557 Fall 2014 1 2 Basic 3D graphics With affine matrices, we can now transform virtual 3D objects in their local coordinate systems into
Computer Graphics. Illumination and Shading
 () Illumination and Shading Dr. Ayman Eldeib Lighting So given a 3-D triangle and a 3-D viewpoint, we can set the right pixels But what color should those pixels be? If we re attempting to create a realistic
() Illumination and Shading Dr. Ayman Eldeib Lighting So given a 3-D triangle and a 3-D viewpoint, we can set the right pixels But what color should those pixels be? If we re attempting to create a realistic
CSE328 Fundamentals of Computer Graphics
 CSE328 Fundamentals of Computer Graphics Hong Qin State University of New York at Stony Brook (Stony Brook University) Stony Brook, New York 794--44 Tel: (63)632-845; Fax: (63)632-8334 qin@cs.sunysb.edu
CSE328 Fundamentals of Computer Graphics Hong Qin State University of New York at Stony Brook (Stony Brook University) Stony Brook, New York 794--44 Tel: (63)632-845; Fax: (63)632-8334 qin@cs.sunysb.edu
Ray Tracing. Brian Curless CSEP 557 Fall 2016
 Ray Tracing Brian Curless CSEP 557 Fall 2016 1 Reading Required: Shirley, section 10.1-10.7 (online handout) Triangle intersection (online handout) Further reading: Shirley errata on syllabus page, needed
Ray Tracing Brian Curless CSEP 557 Fall 2016 1 Reading Required: Shirley, section 10.1-10.7 (online handout) Triangle intersection (online handout) Further reading: Shirley errata on syllabus page, needed
CHAPTER 1 Graphics Systems and Models 3
 ?????? 1 CHAPTER 1 Graphics Systems and Models 3 1.1 Applications of Computer Graphics 4 1.1.1 Display of Information............. 4 1.1.2 Design.................... 5 1.1.3 Simulation and Animation...........
?????? 1 CHAPTER 1 Graphics Systems and Models 3 1.1 Applications of Computer Graphics 4 1.1.1 Display of Information............. 4 1.1.2 Design.................... 5 1.1.3 Simulation and Animation...........
CSE 167: Introduction to Computer Graphics Lecture #7: Lights. Jürgen P. Schulze, Ph.D. University of California, San Diego Spring Quarter 2015
 CSE 167: Introduction to Computer Graphics Lecture #7: Lights Jürgen P. Schulze, Ph.D. University of California, San Diego Spring Quarter 2015 Announcements Thursday in-class: Midterm Can include material
CSE 167: Introduction to Computer Graphics Lecture #7: Lights Jürgen P. Schulze, Ph.D. University of California, San Diego Spring Quarter 2015 Announcements Thursday in-class: Midterm Can include material
Illumination & Shading: Part 1
 Illumination & Shading: Part 1 Light Sources Empirical Illumination Shading Local vs Global Illumination Lecture 10 Comp 236 Spring 2005 Computer Graphics Jargon: Illumination Models Illumination - the
Illumination & Shading: Part 1 Light Sources Empirical Illumination Shading Local vs Global Illumination Lecture 10 Comp 236 Spring 2005 Computer Graphics Jargon: Illumination Models Illumination - the
Virtual Reality for Human Computer Interaction
 Virtual Reality for Human Computer Interaction Appearance: Lighting Representation of Light and Color Representation of Light and Color Do we need to represent all I! to represent a color C(I)? Representation
Virtual Reality for Human Computer Interaction Appearance: Lighting Representation of Light and Color Representation of Light and Color Do we need to represent all I! to represent a color C(I)? Representation
Models and Architectures. Ed Angel Professor of Computer Science, Electrical and Computer Engineering, and Media Arts University of New Mexico
 Models and Architectures Ed Angel Professor of Computer Science, Electrical and Computer Engineering, and Media Arts University of New Mexico 1 Objectives Learn the basic design of a graphics system Introduce
Models and Architectures Ed Angel Professor of Computer Science, Electrical and Computer Engineering, and Media Arts University of New Mexico 1 Objectives Learn the basic design of a graphics system Introduce
Shadow Algorithms. CSE 781 Winter Han-Wei Shen
 Shadow Algorithms CSE 781 Winter 2010 Han-Wei Shen Why Shadows? Makes 3D Graphics more believable Provides additional cues for the shapes and relative positions of objects in 3D What is shadow? Shadow:
Shadow Algorithms CSE 781 Winter 2010 Han-Wei Shen Why Shadows? Makes 3D Graphics more believable Provides additional cues for the shapes and relative positions of objects in 3D What is shadow? Shadow:
Objectives Shading in OpenGL. Front and Back Faces. OpenGL shading. Introduce the OpenGL shading methods. Discuss polygonal shading
 Objectives Shading in OpenGL Introduce the OpenGL shading methods - per vertex shading vs per fragment shading - Where to carry out Discuss polygonal shading - Flat - Smooth - Gouraud CITS3003 Graphics
Objectives Shading in OpenGL Introduce the OpenGL shading methods - per vertex shading vs per fragment shading - Where to carry out Discuss polygonal shading - Flat - Smooth - Gouraud CITS3003 Graphics
Lighting. CSC 7443: Scientific Information Visualization
 Lighting Why Lighting? What light source is used and how the object response to the light makes difference Ocean looks bright bluish green in sunny day but dim gray green in cloudy day Lighting gives you
Lighting Why Lighting? What light source is used and how the object response to the light makes difference Ocean looks bright bluish green in sunny day but dim gray green in cloudy day Lighting gives you
graphics pipeline computer graphics graphics pipeline 2009 fabio pellacini 1
 graphics pipeline computer graphics graphics pipeline 2009 fabio pellacini 1 graphics pipeline sequence of operations to generate an image using object-order processing primitives processed one-at-a-time
graphics pipeline computer graphics graphics pipeline 2009 fabio pellacini 1 graphics pipeline sequence of operations to generate an image using object-order processing primitives processed one-at-a-time
Institutionen för systemteknik
 Code: Day: Lokal: M7002E 19 March E1026 Institutionen för systemteknik Examination in: M7002E, Computer Graphics and Virtual Environments Number of sections: 7 Max. score: 100 (normally 60 is required
Code: Day: Lokal: M7002E 19 March E1026 Institutionen för systemteknik Examination in: M7002E, Computer Graphics and Virtual Environments Number of sections: 7 Max. score: 100 (normally 60 is required
Shading , Fall 2004 Nancy Pollard Mark Tomczak
 15-462, Fall 2004 Nancy Pollard Mark Tomczak Shading Shading Concepts Shading Equations Lambertian, Gouraud shading Phong Illumination Model Non-photorealistic rendering [Shirly, Ch. 8] Announcements Written
15-462, Fall 2004 Nancy Pollard Mark Tomczak Shading Shading Concepts Shading Equations Lambertian, Gouraud shading Phong Illumination Model Non-photorealistic rendering [Shirly, Ch. 8] Announcements Written
Illumination and Shading
 Illumination and Shading Computer Graphics COMP 770 (236) Spring 2007 Instructor: Brandon Lloyd 2/14/07 1 From last time Texture mapping overview notation wrapping Perspective-correct interpolation Texture
Illumination and Shading Computer Graphics COMP 770 (236) Spring 2007 Instructor: Brandon Lloyd 2/14/07 1 From last time Texture mapping overview notation wrapping Perspective-correct interpolation Texture
graphics pipeline computer graphics graphics pipeline 2009 fabio pellacini 1
 graphics pipeline computer graphics graphics pipeline 2009 fabio pellacini 1 graphics pipeline sequence of operations to generate an image using object-order processing primitives processed one-at-a-time
graphics pipeline computer graphics graphics pipeline 2009 fabio pellacini 1 graphics pipeline sequence of operations to generate an image using object-order processing primitives processed one-at-a-time
Methodology for Lecture. Importance of Lighting. Outline. Shading Models. Brief primer on Color. Foundations of Computer Graphics (Spring 2010)
 Foundations of Computer Graphics (Spring 2010) CS 184, Lecture 11: OpenGL 3 http://inst.eecs.berkeley.edu/~cs184 Methodology for Lecture Lecture deals with lighting (teapot shaded as in HW1) Some Nate
Foundations of Computer Graphics (Spring 2010) CS 184, Lecture 11: OpenGL 3 http://inst.eecs.berkeley.edu/~cs184 Methodology for Lecture Lecture deals with lighting (teapot shaded as in HW1) Some Nate
Shading. Brian Curless CSE 557 Autumn 2017
 Shading Brian Curless CSE 557 Autumn 2017 1 Reading Optional: Angel and Shreiner: chapter 5. Marschner and Shirley: chapter 10, chapter 17. Further reading: OpenGL red book, chapter 5. 2 Basic 3D graphics
Shading Brian Curless CSE 557 Autumn 2017 1 Reading Optional: Angel and Shreiner: chapter 5. Marschner and Shirley: chapter 10, chapter 17. Further reading: OpenGL red book, chapter 5. 2 Basic 3D graphics
CS451Real-time Rendering Pipeline
 1 CS451Real-time Rendering Pipeline JYH-MING LIEN DEPARTMENT OF COMPUTER SCIENCE GEORGE MASON UNIVERSITY Based on Tomas Akenine-Möller s lecture note You say that you render a 3D 2 scene, but what does
1 CS451Real-time Rendering Pipeline JYH-MING LIEN DEPARTMENT OF COMPUTER SCIENCE GEORGE MASON UNIVERSITY Based on Tomas Akenine-Möller s lecture note You say that you render a 3D 2 scene, but what does
Deferred Rendering Due: Wednesday November 15 at 10pm
 CMSC 23700 Autumn 2017 Introduction to Computer Graphics Project 4 November 2, 2017 Deferred Rendering Due: Wednesday November 15 at 10pm 1 Summary This assignment uses the same application architecture
CMSC 23700 Autumn 2017 Introduction to Computer Graphics Project 4 November 2, 2017 Deferred Rendering Due: Wednesday November 15 at 10pm 1 Summary This assignment uses the same application architecture
Rendering. Converting a 3D scene to a 2D image. Camera. Light. Rendering. View Plane
 Rendering Pipeline Rendering Converting a 3D scene to a 2D image Rendering Light Camera 3D Model View Plane Rendering Converting a 3D scene to a 2D image Basic rendering tasks: Modeling: creating the world
Rendering Pipeline Rendering Converting a 3D scene to a 2D image Rendering Light Camera 3D Model View Plane Rendering Converting a 3D scene to a 2D image Basic rendering tasks: Modeling: creating the world
The Traditional Graphics Pipeline
 Last Time? The Traditional Graphics Pipeline Participating Media Measuring BRDFs 3D Digitizing & Scattering BSSRDFs Monte Carlo Simulation Dipole Approximation Today Ray Casting / Tracing Advantages? Ray
Last Time? The Traditional Graphics Pipeline Participating Media Measuring BRDFs 3D Digitizing & Scattering BSSRDFs Monte Carlo Simulation Dipole Approximation Today Ray Casting / Tracing Advantages? Ray
Introduction Rasterization Z-buffering Shading. Graphics 2012/2013, 4th quarter. Lecture 09: graphics pipeline (rasterization and shading)
 Lecture 9 Graphics pipeline (rasterization and shading) Graphics pipeline - part 1 (recap) Perspective projection by matrix multiplication: x pixel y pixel z canonical 1 x = M vpm per M cam y z 1 This
Lecture 9 Graphics pipeline (rasterization and shading) Graphics pipeline - part 1 (recap) Perspective projection by matrix multiplication: x pixel y pixel z canonical 1 x = M vpm per M cam y z 1 This
OpenGl Pipeline. triangles, lines, points, images. Per-vertex ops. Primitive assembly. Texturing. Rasterization. Per-fragment ops.
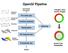 OpenGl Pipeline Individual Vertices Transformed Vertices Commands Processor Per-vertex ops Primitive assembly triangles, lines, points, images Primitives Fragments Rasterization Texturing Per-fragment
OpenGl Pipeline Individual Vertices Transformed Vertices Commands Processor Per-vertex ops Primitive assembly triangles, lines, points, images Primitives Fragments Rasterization Texturing Per-fragment
Texture Mapping. Brian Curless CSE 457 Spring 2016
 Texture Mapping Brian Curless CSE 457 Spring 2016 1 Reading Required Angel, 7.4-7.10 Recommended Paul S. Heckbert. Survey of texture mapping. IEEE Computer Graphics and Applications 6(11): 56--67, November
Texture Mapping Brian Curless CSE 457 Spring 2016 1 Reading Required Angel, 7.4-7.10 Recommended Paul S. Heckbert. Survey of texture mapping. IEEE Computer Graphics and Applications 6(11): 56--67, November
CS 130 Exam I. Fall 2015
 S 3 Exam I Fall 25 Name Student ID Signature You may not ask any questions during the test. If you believe that there is something wrong with a question, write down what you think the question is trying
S 3 Exam I Fall 25 Name Student ID Signature You may not ask any questions during the test. If you believe that there is something wrong with a question, write down what you think the question is trying
The Traditional Graphics Pipeline
 Last Time? The Traditional Graphics Pipeline Reading for Today A Practical Model for Subsurface Light Transport, Jensen, Marschner, Levoy, & Hanrahan, SIGGRAPH 2001 Participating Media Measuring BRDFs
Last Time? The Traditional Graphics Pipeline Reading for Today A Practical Model for Subsurface Light Transport, Jensen, Marschner, Levoy, & Hanrahan, SIGGRAPH 2001 Participating Media Measuring BRDFs
CS 464 Review. Review of Computer Graphics for Final Exam
 CS 464 Review Review of Computer Graphics for Final Exam Goal: Draw 3D Scenes on Display Device 3D Scene Abstract Model Framebuffer Matrix of Screen Pixels In Computer Graphics: If it looks right then
CS 464 Review Review of Computer Graphics for Final Exam Goal: Draw 3D Scenes on Display Device 3D Scene Abstract Model Framebuffer Matrix of Screen Pixels In Computer Graphics: If it looks right then
CS 381 Computer Graphics, Fall 2008 Midterm Exam Solutions. The Midterm Exam was given in class on Thursday, October 23, 2008.
 CS 381 Computer Graphics, Fall 2008 Midterm Exam Solutions The Midterm Exam was given in class on Thursday, October 23, 2008. 1. [4 pts] Drawing Where? Your instructor says that objects should always be
CS 381 Computer Graphics, Fall 2008 Midterm Exam Solutions The Midterm Exam was given in class on Thursday, October 23, 2008. 1. [4 pts] Drawing Where? Your instructor says that objects should always be
LIGHTING AND SHADING
 DH2323 DGI15 INTRODUCTION TO COMPUTER GRAPHICS AND INTERACTION LIGHTING AND SHADING Christopher Peters HPCViz, KTH Royal Institute of Technology, Sweden chpeters@kth.se http://kth.academia.edu/christopheredwardpeters
DH2323 DGI15 INTRODUCTION TO COMPUTER GRAPHICS AND INTERACTION LIGHTING AND SHADING Christopher Peters HPCViz, KTH Royal Institute of Technology, Sweden chpeters@kth.se http://kth.academia.edu/christopheredwardpeters
Shading. Reading. Pinhole camera. Basic 3D graphics. Brian Curless CSE 457 Spring Required: Angel chapter 5.
 Reading Required: Angel chapter 5. Shading Optional: OpenGL red book, chapter 5. Brian Curle CSE 457 Spring 2015 1 2 Baic 3D graphic With affine matrice, we can now tranform virtual 3D object in their
Reading Required: Angel chapter 5. Shading Optional: OpenGL red book, chapter 5. Brian Curle CSE 457 Spring 2015 1 2 Baic 3D graphic With affine matrice, we can now tranform virtual 3D object in their
Illumination and Shading ECE 567
 Illumination and Shading ECE 567 Overview Lighting Models Ambient light Diffuse light Specular light Shading Models Flat shading Gouraud shading Phong shading OpenGL 2 Introduction To add realism to drawings
Illumination and Shading ECE 567 Overview Lighting Models Ambient light Diffuse light Specular light Shading Models Flat shading Gouraud shading Phong shading OpenGL 2 Introduction To add realism to drawings
Lets assume each object has a defined colour. Hence our illumination model is looks unrealistic.
 Shading Models There are two main types of rendering that we cover, polygon rendering ray tracing Polygon rendering is used to apply illumination models to polygons, whereas ray tracing applies to arbitrary
Shading Models There are two main types of rendering that we cover, polygon rendering ray tracing Polygon rendering is used to apply illumination models to polygons, whereas ray tracing applies to arbitrary
Today. Rendering pipeline. Rendering pipeline. Object vs. Image order. Rendering engine Rendering engine (jtrt) Computergrafik. Rendering pipeline
 Computergrafik Today Rendering pipeline s View volumes, clipping Viewport Matthias Zwicker Universität Bern Herbst 2008 Rendering pipeline Rendering pipeline Hardware & software that draws 3D scenes on
Computergrafik Today Rendering pipeline s View volumes, clipping Viewport Matthias Zwicker Universität Bern Herbst 2008 Rendering pipeline Rendering pipeline Hardware & software that draws 3D scenes on
The Traditional Graphics Pipeline
 Final Projects Proposals due Thursday 4/8 Proposed project summary At least 3 related papers (read & summarized) Description of series of test cases Timeline & initial task assignment The Traditional Graphics
Final Projects Proposals due Thursday 4/8 Proposed project summary At least 3 related papers (read & summarized) Description of series of test cases Timeline & initial task assignment The Traditional Graphics
Computer Graphics. Illumination and Shading
 Rendering Pipeline modelling of geometry transformation into world coordinates placement of cameras and light sources transformation into camera coordinates backface culling projection clipping w.r.t.
Rendering Pipeline modelling of geometry transformation into world coordinates placement of cameras and light sources transformation into camera coordinates backface culling projection clipping w.r.t.
Texture Mapping. Brian Curless CSE 457 Spring 2015
 Texture Mapping Brian Curless CSE 457 Spring 2015 1 Reading Required Angel, 7.4-7.10 Recommended Paul S. Heckbert. Survey of texture mapping. IEEE Computer Graphics and Applications 6(11): 56--67, November
Texture Mapping Brian Curless CSE 457 Spring 2015 1 Reading Required Angel, 7.4-7.10 Recommended Paul S. Heckbert. Survey of texture mapping. IEEE Computer Graphics and Applications 6(11): 56--67, November
CS Computer Graphics: Illumination and Shading I
 CS 543 - Computer Graphics: Illumination and Shading I by Robert W. Lindeman gogo@wpi.edu (with help from Emmanuel Agu ;-) Illumination and Shading Problem: Model light/surface point interactions to determine
CS 543 - Computer Graphics: Illumination and Shading I by Robert W. Lindeman gogo@wpi.edu (with help from Emmanuel Agu ;-) Illumination and Shading Problem: Model light/surface point interactions to determine
CS Computer Graphics: Illumination and Shading I
 CS 543 - Computer Graphics: Illumination and Shading I by Robert W. Lindeman gogo@wpi.edu (with help from Emmanuel Agu ;-) Illumination and Shading Problem: Model light/surface point interactions to determine
CS 543 - Computer Graphics: Illumination and Shading I by Robert W. Lindeman gogo@wpi.edu (with help from Emmanuel Agu ;-) Illumination and Shading Problem: Model light/surface point interactions to determine
CS230 : Computer Graphics Lecture 4. Tamar Shinar Computer Science & Engineering UC Riverside
 CS230 : Computer Graphics Lecture 4 Tamar Shinar Computer Science & Engineering UC Riverside Shadows Shadows for each pixel do compute viewing ray if ( ray hits an object with t in [0, inf] ) then compute
CS230 : Computer Graphics Lecture 4 Tamar Shinar Computer Science & Engineering UC Riverside Shadows Shadows for each pixel do compute viewing ray if ( ray hits an object with t in [0, inf] ) then compute
Computer Vision Systems. Viewing Systems Projections Illuminations Rendering Culling and Clipping Implementations
 Computer Vision Systems Viewing Systems Projections Illuminations Rendering Culling and Clipping Implementations Viewing Systems Viewing Transformation Projective Transformation 2D Computer Graphics Devices
Computer Vision Systems Viewing Systems Projections Illuminations Rendering Culling and Clipping Implementations Viewing Systems Viewing Transformation Projective Transformation 2D Computer Graphics Devices
CS452/552; EE465/505. Intro to Lighting
 CS452/552; EE465/505 Intro to Lighting 2-10 15 Outline! Projection Normalization! Introduction to Lighting (and Shading) Read: Angel Chapter 5., sections 5.4-5.7 Parallel Projections Chapter 6, sections
CS452/552; EE465/505 Intro to Lighting 2-10 15 Outline! Projection Normalization! Introduction to Lighting (and Shading) Read: Angel Chapter 5., sections 5.4-5.7 Parallel Projections Chapter 6, sections
Rasterization Overview
 Rendering Overview The process of generating an image given a virtual camera objects light sources Various techniques rasterization (topic of this course) raytracing (topic of the course Advanced Computer
Rendering Overview The process of generating an image given a virtual camera objects light sources Various techniques rasterization (topic of this course) raytracing (topic of the course Advanced Computer
Texture Mapping. Reading. Implementing texture mapping. Texture mapping. Daniel Leventhal Adapted from Brian Curless CSE 457 Autumn 2011.
 Reading Recommended Texture Mapping Daniel Leventhal Adapted from Brian Curless CSE 457 Autumn 2011 Angel, 8.6, 8.7, 8.9, 8.10, 9.13-9.13.2 Paul S. Heckbert. Survey of texture mapping. IEEE Computer Graphics
Reading Recommended Texture Mapping Daniel Leventhal Adapted from Brian Curless CSE 457 Autumn 2011 Angel, 8.6, 8.7, 8.9, 8.10, 9.13-9.13.2 Paul S. Heckbert. Survey of texture mapping. IEEE Computer Graphics
CPSC / Illumination and Shading
 CPSC 599.64 / 601.64 Rendering Pipeline usually in one step modelling of geometry transformation into world coordinate system placement of cameras and light sources transformation into camera coordinate
CPSC 599.64 / 601.64 Rendering Pipeline usually in one step modelling of geometry transformation into world coordinate system placement of cameras and light sources transformation into camera coordinate
API for creating a display window and using keyboard/mouse interations. See RayWindow.cpp to see how these are used for Assignment3
 OpenGL Introduction Introduction OpenGL OpenGL is an API for computer graphics. Hardware-independent Windowing or getting input is not included in the API Low-level Only knows about triangles (kind of,
OpenGL Introduction Introduction OpenGL OpenGL is an API for computer graphics. Hardware-independent Windowing or getting input is not included in the API Low-level Only knows about triangles (kind of,
C P S C 314 S H A D E R S, O P E N G L, & J S RENDERING PIPELINE. Mikhail Bessmeltsev
 C P S C 314 S H A D E R S, O P E N G L, & J S RENDERING PIPELINE UGRAD.CS.UBC.C A/~CS314 Mikhail Bessmeltsev 1 WHAT IS RENDERING? Generating image from a 3D scene 2 WHAT IS RENDERING? Generating image
C P S C 314 S H A D E R S, O P E N G L, & J S RENDERING PIPELINE UGRAD.CS.UBC.C A/~CS314 Mikhail Bessmeltsev 1 WHAT IS RENDERING? Generating image from a 3D scene 2 WHAT IS RENDERING? Generating image
CS 4204 Computer Graphics
 CS 4204 Computer Graphics 3D Viewing and Projection Yong Cao Virginia Tech Objective We will develop methods to camera through scenes. We will develop mathematical tools to handle perspective projection.
CS 4204 Computer Graphics 3D Viewing and Projection Yong Cao Virginia Tech Objective We will develop methods to camera through scenes. We will develop mathematical tools to handle perspective projection.
9. Illumination and Shading
 9. Illumination and Shading Approaches for visual realism: - Remove hidden surfaces - Shade visible surfaces and reproduce shadows - Reproduce surface properties Texture Degree of transparency Roughness,
9. Illumination and Shading Approaches for visual realism: - Remove hidden surfaces - Shade visible surfaces and reproduce shadows - Reproduce surface properties Texture Degree of transparency Roughness,
Local Illumination physics. Law of reflection and Snell s law of refraction
 Local Illumination physics Law of reflection and Snell s law of refraction What are we trying to model? Surface Proof of Lambert s cosine law n db da Computing R All vectors unit length!! The effect
Local Illumination physics Law of reflection and Snell s law of refraction What are we trying to model? Surface Proof of Lambert s cosine law n db da Computing R All vectors unit length!! The effect
Graphics and Visualization
 International University Bremen Spring Semester 2006 Recap Hierarchical Modeling Perspective vs Parallel Projection Representing solid objects Displaying Wireframe models is easy from a computational
International University Bremen Spring Semester 2006 Recap Hierarchical Modeling Perspective vs Parallel Projection Representing solid objects Displaying Wireframe models is easy from a computational
Lecture 4. Viewing, Projection and Viewport Transformations
 Notes on Assignment Notes on Assignment Hw2 is dependent on hw1 so hw1 and hw2 will be graded together i.e. You have time to finish both by next monday 11:59p Email list issues - please cc: elif@cs.nyu.edu
Notes on Assignment Notes on Assignment Hw2 is dependent on hw1 so hw1 and hw2 will be graded together i.e. You have time to finish both by next monday 11:59p Email list issues - please cc: elif@cs.nyu.edu
Blue colour text questions Black colour text sample answers Red colour text further explanation or references for the sample answers
 Blue colour text questions Black colour text sample answers Red colour text further explanation or references for the sample answers Question 1. a) (5 marks) Explain the OpenGL synthetic camera model,
Blue colour text questions Black colour text sample answers Red colour text further explanation or references for the sample answers Question 1. a) (5 marks) Explain the OpenGL synthetic camera model,
Local Illumination. CMPT 361 Introduction to Computer Graphics Torsten Möller. Machiraju/Zhang/Möller
 Local Illumination CMPT 361 Introduction to Computer Graphics Torsten Möller Graphics Pipeline Hardware Modelling Transform Visibility Illumination + Shading Perception, Interaction Color Texture/ Realism
Local Illumination CMPT 361 Introduction to Computer Graphics Torsten Möller Graphics Pipeline Hardware Modelling Transform Visibility Illumination + Shading Perception, Interaction Color Texture/ Realism
Homework #2. Hidden Surfaces, Projections, Shading and Texture, Ray Tracing, and Parametric Curves
 Computer Graphics Instructor: Brian Curless CSE 457 Spring 2013 Homework #2 Hidden Surfaces, Projections, Shading and Texture, Ray Tracing, and Parametric Curves Assigned: Sunday, May 12 th Due: Thursday,
Computer Graphics Instructor: Brian Curless CSE 457 Spring 2013 Homework #2 Hidden Surfaces, Projections, Shading and Texture, Ray Tracing, and Parametric Curves Assigned: Sunday, May 12 th Due: Thursday,
Graphics Hardware and Display Devices
 Graphics Hardware and Display Devices CSE328 Lectures Graphics/Visualization Hardware Many graphics/visualization algorithms can be implemented efficiently and inexpensively in hardware Facilitates interactive
Graphics Hardware and Display Devices CSE328 Lectures Graphics/Visualization Hardware Many graphics/visualization algorithms can be implemented efficiently and inexpensively in hardware Facilitates interactive
