Generating All Solutions of Minesweeper Problem Using Degree Constrained Subgraph Model
|
|
|
- Bennett Fletcher
- 5 years ago
- Views:
Transcription
1 356 Int'l Conf. Par. and Dist. Proc. Tech. and Appl. PDPTA'16 Generating All Solutions of Minesweeper Problem Using Degree Constrained Subgraph Model Hirofumi Suzuki, Sun Hao, and Shin-ichi Minato Graduate School of Information Science and Technology, Hokkaido University Abstract Minesweeper is one of the most popular puzzle game. Several kinds of decision or counting problems on Minesweeper have been studied. In this paper, we consider the problem to generate all possible solutions for a given Minesweeper board, and propose a new formulation of the problem using a graph structure, called degree constrained subgraph model. We show experimental results of our efficient graph enumeration techniques for various sizes of Minesweeper boards. Keywords: minesweeper, generating, graph model, degree constrained subgraph 1. Introduction Minesweeper is one of the most popular puzzle game, which is frequently bundled with operating systems and GUIs, including Windows, X11, KDE, GNOME, etc. The objective of this game is to find all hidden mines in covered cells with the some helps of hints. There are several problems related to Minesweeper, the Minesweeper consistency problem [1], the Minesweeper counting problem [2], and the Minesweeper constrained counting problem [3]. Minesweeper on graph structures are also studied in [3]. These problems ask us whether or not the input Minesweeper board has any solutions, valid assignments of mines. Those problems was studied as one of decision problems or counting problems. However, the objective of Minesweeper is considered as to really assign some mines to uncovered cells with some constraints. From this viewpoint, we consider a new problem which contains the above problems. This problem requires all solutions of the input Minesweeper board. Solving this problem is useful for finding the best solution with some costed mines, revealing that there is no mine, and calculating the probability of mine placement at each cell. For finding one solution of the minesweeper, we may use some simple backtracking.search algorithms, however, it is hard to generate all the solutions because of the combinatorial explosion in terms of computation time and space. Recently, Zero-suppressed Binary Decision Diagram (ZDD) [4] is known as a compact representation for manipulating a set of combinations. ZDDs are useful for generating all the solutions for a Minesweeper board. In this method, it is a naive way to use a combinatorial model that one logic variable (combinatorial item) is assigned to each cell, to represent whether a mine exists at the cell or not. In this paper, we propose yet another formulation using a graph structure, called degree constrained subgraph model, and show an efficient method using ZDD-based graph enumeration technique [5]. We experimentally compared performance of the methods based on our graph model and the naive combinatorial model. The result showed that our formulation is effective for the problem. In section 2, we explain the rules of Minesweeper in detail, and introduce some problems related to Minesweeper. In section 3, we explain the naive combinatorial model using ZDD for finding all valid assignments of mines. In section 4, we show the proposal formulation using degree constrained subgraph model, and explain the method based on graph enumeration technique. In section 5, we show the experimental results. In section 6, we explain the calculation method for mine probability. 2. Problems on Minesweeper Minesweeper consists of a grid of cells. All cells at the initial board is covered (see Fig.1). At each move, the player may uncovers a cell. There are three types of uncovered cells, mine cells, hint cells, and free cells. A mine cell contains a mine, a hint cell has information about number of mine cells surrounding it (called count), and a free cell contains nothing. In this paper, we consider the free cells as the hint cells whose counts are 0, and draw mine as a black circle ( ). The goal of the game is to uncover all free cells (see Fig.2). If mine cell was uncovered, the game becomes over and the player loses (see Fig.3). Fig. 1: The initial board. The Minesweeper consistency problem (or simply the Minesweeper problem) is a decision problem, whether or not a given Minesweeper grid has a valid assignment of mines (see Fig.4 and Fig.5). The consistency problem was proved
2 Int'l Conf. Par. and Dist. Proc. Tech. and Appl. PDPTA' Fig. 2: A winning state. Fig. 3: A lost state. Fig. 6: Minesweeper on graph. to be NP-complete [1], even if each cell in the grid has only one mine surrounding it [6]. Counting number of valid assignments to the given Minesweeper grid is also defined as a problem, the Minesweeper counting problem (called #Minesweeper in [2]). In setting of Fig.4, the solution for the counting problem is 66. The counting problem was proved to be #P-complete [2]. In [3], Minesweeper constrained counting problem is defined. The input of the constrained counting problem also includes the total number of mines. Fig. 4: This setting has valid assignment. Fig. 5: An example of assignment for Fig.4. Althought the grid is used for the board in general Minesweeper, we can use a graph structure instead of the board. Each vertex of graph corresponds to a hint cell or a free cell, or a covered cell (see Fig.6). If vertex is a hint cell, it has a count of the number of mines in adjacent vertices, otherwise may have a mine. Then, the Minesweeper on grid boards is considered as the Minesweeper on grid graphs (see Fig.7). Minesweeper on graph structure was studied in [3], and polynomial algorithm is provided for the consistency, counting problem for Minesweeper on trees and on graphs of bounded treewidth. We consider a new problem for Minesweeper, the required output is all valid assignments of mines for given Minesweeper board. We refer to the problem as Minesweeper generation problem. The Minesweeper gener- Fig. 7: Graph based on grid board of Fig.4. ation problem is including both the consistency problem and the counting problem. In the Minesweeper generation problem, the input is a Minesweeper board MB(m, n, C, A). There is m covered cells numbered from 1 to m, and n hint cells numbered from 1 to n. Note that the covered cell is ignored if hint cell of surrounding it is nothing. C has n integers c 1,c 2,...,c n, and c i is count written in i-th hint cell (c i 0). A has n sets of integers A 1,A 2,...,A n, and A i has all numbers of covered cells surrounding i-th hint cell (A i {1, 2,...,m}). 3. Naive Combinatorial Model Using ZDD Combination of covered cells correspond to assignment of mines, namely, mines are assigned to all covered cells included in the combination. Hence set of all valid combinations of cells represents solution to Minesweeper generation problem. Zero-suppressed Binary Decision Diagram (ZDD) [4] is compact data structure for manipulating sets of combinations, and has many application to combinatorial problems [4] [7]. We explain a method for solving the Minesweeper generation problem based on naive combinatorial model using ZDD. 3.1 Zero-suppressed Binary Decision Diagram ZDD is a compact representation of binary decision tree (see Fig.8 and Fig.9). The tree has a root node and two terminal nodes, a 0-terminal and a 1-terminal. A path which connects the root to the 1-terminal node corresponds to a combination in the set. Each internal node of the tree has a label of an item and two edges, one is 0-edge, the other is 1-edge. The 0-edge represents that the item is not included in the combination, the 1-edge is opposite. In general, the order of appearances of items is fixed.
3 358 Int'l Conf. Par. and Dist. Proc. Tech. and Appl. PDPTA'16 Fig. 8: An example of binary decision tree that represents set of combinations {{a, c}, {b, c}, {b}, {c}}. 0-edge is dotted, and 1-edge is solid. Fig. 9: ZDD for Fig.8. ZDDs are based on the following reduction rules. Deletion rule: delete all redundant nodes whose 1-edge point to the 0-terminal (see Fig.10). Sharing rule: share all equivalent subgraphs (see Fig.11). To make ZDDs compact and canonical for representing sets of combinations, we should apply these reduction rules as much as possible without minding order. Fig. 10: Deletion rule. Fig. 11: Sharing rule. A conventional ZDD package supports various operations for manipulating sets of combinations. The ZDD package maintains a compact data structure in handling those operations. Here we show some operations, which used for generating the solutions of the Minesweeper generation problem. In the following, P and Q indicate an instance of sets of combinations represented by a ZDD, respectively. P Q P Q P Q the union set of P and Q result is {c c P or c Q} 3.2 Using ZDD Operation the intersection set of P and Q result is {c c P and c Q} the direct product set of P and Q result is {p q p P and q Q} For representing solutions of Minesweeper using ZDDs, we consider each covered cell as an item. We define U as the set of all items, x i U denote the item of i-th covered cell. A subset X U, combination of covered cells, corresponds to an assignment of mines. We also defile M valid 2 U as the set of combinations that each of them represents valid assignment for a given Minesweeper board. Then, our objective is to generate M valid as output. We define M i 2 U as the set of all the assignments satisfying the i-th hint. Then, a valid assignment must be commonly included in all M i (i =1, 2,...,n). Hence the set of all the valid assignments M valid is represented by: M valid = n i=1m i. Thus, our method constructs the n ZDDs each of which represent M i for all i, and calculate the intersection of those ZDDs. For calculating M i, we define the set S(X, k) as all combinations of any k items in the item set X U. For example, X = {a, b, c} and k =2, then S(X, k) = {{a, b}, {a, c}, {b, c}}. Using notation of set S(X, k), M i is represented by following, where X i = {x j j A i } is the set of all covered cells surrounding i-th hint cell. M i = S(X i,c i ) 2 (U\Xi) We can construct a ZDD which represents M i effectively, using memorised recursion technique (see algorithm 1). In algorithm 1, recursive(i, X, c, m) generates a ZDD ret which represents S(X, c) 2 ({x i,...,x m }\X). If x i X, we can divide the set of combinations represented by ret into two disjoint subsets, one has x i in each combination: ({{x i }} S(X \{x i },c 1)) 2 ({xi,...,xm}\x), and the other has no x i in each combination: S(X \{x i },c) 2 ({x i,...,x m }\X), otherwise ret equals ZDD which represents (({{x i }} S(X, c)) S(X, c)) 2 ({x i,...,x m }\X).
4 Int'l Conf. Par. and Dist. Proc. Tech. and Appl. PDPTA' As a result, we get the algorithm for calculating M valid (see Algorithm 2). In the following, we define Z(x) as ZDD which represents {{x}}, set of combinations consisting of only {x}. Algorithm 1 recursive(i, X, c, m) 1: if i = m then 2: if c =0then 3: return ZDD consisting of only 1-terminal 4: end if 5: return ZDD consisting of only 0-terminal 6: end if 7: if memo table has a ZDD at (i, c) then 8: return ZDD memorised at (i, c) 9: end if 10: ret null 11: if x i X then 12: z1 recursive(i +1,X \{x i },c 1,m) 13: z0 recursive(i +1,X \{x i },c,m) 14: ret (Z(x i ) z1) z0 15: else 16: z recursive(i +1,X,c,m) 17: ret (Z(x i ) z) z 18: end if 19: memorise ret at (i, c) 20: return ret Algorithm 2 The method for Minesweeper generation problem based on naive combinatorial model using ZDD Input: MB(m, n, C, A), and U Output: ZDD which represents all valid assignments of MB 1: for i =1to n do 2: X i {x j U j A i } 3: initialize memo table for algorithm 1 4: Z i recursive(1,x i,c i,m) 5: end for 6: Z valid n i=1 Z i 7: return Z valid This algorithm is based on the naive combinatorial model. An advantage of this model is the simple notation and compact processing with ZDD. However, the algorithm repeats algebraic operations as many as the number of hints, and thus the computation time may become large. As an improvement, we propose yet another formulation in the following section. 4. Graph Model for Minesweeper We propose a formulation for the problem to find a valid assignment of mines for the input Minesweeper board. In this formulaion, we use graph structure, called degree constrained subgraph model. Then, we show that generating all solutions of the formulated problem is equivalent to generating all valid assignments for the Minesweeper board. For solving the formulated problem, we can use ZDD-based graph enumeration technique. 4.1 Notations and Definitions for Degree Constrained Subgraph Model In undirected graph G =(V,E), we define d v as degree of vertex v, number of edges connected with v. We also define d v as degree of v V in subgraph G =(V,E E). We define the degree constraint for vertex v as follows. dc v N {0} dc v denotes the set of valid degrees of v in subgraph. For given graph G and degree constraints dc v for all v V, degree constrained subgraph is a subgraph G satisfying the following constraints (see Fig.12). d v dc v for all v Fig. 12: An example of degree constrained subgraph. 4.2 Formulation For a given Minesweeper board MB(m, n, C, A), we construct a graph (named MG). We define B as a set of the vertices for covered cells, and b i B means the vertex for the i-th covered cell. We also define H as set of vertices for hint cells. h j H means the vertex of the j-th hint cell. In the following, we call the vertex of covered cell covered vertex, and call the vertex of hint cell hint vertex. The graph has the set of edges E which connect vertices of adjacent cells, namely, e = {b i,h j } E if i A j. Then, MG =(B H, E) is a bipartite graph consisting of the covered vertices and the hint vertices. To make the correspondence between a mine assignment and a subgraph of MG, we set degree constraints on MG. If we assign a mine to the i-th covered vertices, b i should connect with all the adjacent hint vertices in the subgraph of MG, otherwise be independent. Then, we get the following degree constraints. dc bi = {0,d bi } i {1, 2,...,m} (1)
5 360 Int'l Conf. Par. and Dist. Proc. Tech. and Appl. PDPTA'16 For converting from a subgraph G of MG under the degree constraints (1) to an assignment of mines, we assign a mine to the i-th covered cell if d b i 0. In addition, since our objective is to find a valid assignment of mines, hint vertex h i should connect with c i adjacent covered vertices in the subgraph of MG. Then, we get the following degree constraints. dc hj = {c j } j {1, 2,...,n} (2) As a result, we also get the following theorem. Theorem 1 There is a one-to-one correspondence between the subgraphs of MG under degree constraints (1) (2) and the valid assignments for MB. Proof. MG has an edge e = {b i,h j } if and only if the i-th covered cell adjacent to the j-th hint cell. We define MG dc as the set of all the degree constrained subgraphs of MG. We also define MB dc as the set of assignments converted from G MG dc, and also define MB valid as the set of all the valid assignments. We should show MB dc = MB valid. First, we show MB dc MB valid.ing MG dc,any covered vertex with a non-zero degree connects to all the adjacent hint vertices. Since each hint vertices must satisfy the degree constraint, for all j, the j-th hint cell has c j mine cells surrounding it. Thus, all assignments in MB dc is valid, and we get MB dc MB valid. Next, we show MB dc MB valid. We consider an induced subgraph of MG based on a valid assignment in MB valid, and we call the subgraph MG ind. MG ind has the subset of covered vertices B B and all the hint vertices H, and B consists of the covered vertices that there is a mine in corresponding cell, then MG ind has the set of edges E = {e e E and b e and b B }. Thus, in G ind, the degree of b B is d b and the degree of b / B is 0, then all covered vertices satisfy the degree constraints. In addition, since the assignment is valid and each hint vertex connects all adjacent covered vertexes whose degree is not zero, the degree of h j H is equivalent to c j. Thus, all the hint vertices also satisfy the degree constraints. Hence MG ind MG dc, and we get MB dc MB valid. Thus, the theorem follows. 4.3 Using Graph Enumeration Technique By the theorem 1, the Minesweeper generation problem is solved by generating all solutions of the formulated problem. Here we can use an efficient ZDD-based graph enumeration technique shown in [5], frontier-based search method. The frontier-based search generates a ZDD which represents all the subgraphs as the combinations of edges, satisfying various topological constraints, for example paths, cycles, trees, forests, and the degree constraints (see Fig.13). Frontier-based search begin construction of ZDD with only the root node, and advance the search by top-down Fig. 13: An example of frontier-based search. manner which depends on the order of edges; after deciding order of the edges, in i-th step, all the bottom nodes branch off, and make two child nodes, one correspond to the case of using i-th edge, and the other correspond to the case of not using i-th edge. In addition, frontier-based search prune some unnecessary nodes, and merge some equal nodes. These processes are realized by the supporting infomation of the search which is called mate (we leave the details to reference [5]). The coventional enumeration algorithms output all solutions one by one, and thus it is hard to generate all the solutions because of the combinatorial explosion in terms of computation time and space. In contrast, the frontierbased search method output a large number of solutions as a compact ZDD to avoid combinatorial explosion in many cases, and the computation time and space depends on the size of ZDD. 5. Computational Experiments We experimentally compared the performance of the method using degree constrained model and the method using the naive combinatorial model (which based on ZDD operations). Especially, we use not only grid based Minesweeper board but also graph based Minesweeper board, to compare them under various situations. The program was coded in C++, and compiled using g++. The experiments were done on the PC with Intel Core i7-3930k 3.2GHz CPU and 64GB memory. The instance boards were randomly generated boards. Some of them are based on grid, and the others are based on randomly generated graph which has 300 vertices and 900 edges (relatively sparse). We set three types of ratio of mine cells, 10%, 20%, and 30%, and set nine types of ratio of visible hints, 10%, 20%,..., and 90%. Tables 1 and 3 summarize the computation time.zdd indicates the method based on naive combinatorial model using ZDD, and dc indicates the method based on graph enumeration technique using degree constrained subgraph model. In addition, tables 2 and 4 summarize the number of valid assignments in each instance. The computation time of the latter includes time
6 Int'l Conf. Par. and Dist. Proc. Tech. and Appl. PDPTA' of constructing graph and degree constraints. The best time is written in bold letters. The computation time results for grid based boards are shown in table 1, and table 2 shows the number of valid assignments in each instance. The number of valid assignments is over in quite of half instances. However, dc shows the best time inmost instances, and it is 100 times faster thanzdd in some instances. Thus, our formulation is efficient for the Minesweeper generation problem with board based on grid. But in instance consisting of 30% mine cells and 40% visible hits, dc is inefficient in comparison with zdd. It is thought that the reason depends on the complexity of the graph generated by the board; it is supposed that the degree constraints is easily complicated by the state of the connection of the vertexes. Table 1: Computation time (in second) for grid based board mine 10% 20% 30% hint zdd dc zdd dc zdd dc 10% % % % % % % % % Table 2: Number of valid assignments for grid based board hint\mine 10% 20% 30% 10% % % % % % % % % The computation time results for graph based boards are shown in table 3, and table 4 shows the number of valid assignments in each instance. dc shows the best time in all instances, and it is 100 times faster than zdd in some instances. The computation time of zdd is not stable compared with grid instances. It is thought that this result is caused by dispersion of the degree in the original graph, which affect number of adjacent cells. In contrast, number of adjacent cells of each cell in grid is approximately constant. On the other hand, the computation time of dc is stable. Thus, our formulation is also efficient for the Minesweeper generation problem with board based on sparse graph. Table 3: Computation time (in second) for graph ( V = 300, E = 900) based board mine 10% 20% 30% hint zdd dc zdd dc zdd dc 10% % % % % % % % % Table 4: Number of valid assignments for graph based board hint\mine 10% 20% 30% 10% % % % % % % % % Analysis of Mine Probability Calculating the probability of mine placement on each cell is useful for considering a strategy of playing Minesweeper. We can easily calculate it after generating a ZDD of all the solutions. We define C as the number of all valid assignments, and also define C i as the number of valid assignments whose i- th covered cell is mine. Then, following formula calculates the mine probability for i-th cell (we call R i ). R i = C i (3) C We can calculate the cardinality of a set of combinations in a linear time for the ZDD size, and we may use various algebraic operations for extracting a set of combinations which satisfies some additional constraints. The items in a ZDD generated by frontier-based search corresponds to the edges in the input graph. If the i-th covered cell has a mine in some assignments, the subgraphs of those assignments are sure to use all edges which connect b i. Then, we get following algorithm 3 for calculating (3). 7. Conclusion In this paper, we considered the Minesweeper generation problem to generate all possible solutions for a given Minesweeper board, and proposed a formulation of the problem using degree constrained subgraph model. For solving the problem, we used ZDD-based graph enumeration techniques. Experimental results showed that our formulation is effective for many instances of the Minesweeper boards.
7 362 Int'l Conf. Par. and Dist. Proc. Tech. and Appl. PDPTA'16 Algorithm 3 The method for calculating mine probability of the i-th cell. Input: MG =(B H, E), Z all (ZDD of all valid assignments), i Output: mine probability of i-th cell 1: L cardinality of Z all 2: e e E which satisfies b i e 3: Z i Z all (Z(e ) 2 (E\{e }) ) 4: C i cardinality of Z i 5: return Ci C As a future work, we can also consider an online problem for Minesweeper, where the hints are given one by one. Solving this online problem is close to actual play of the Minesweeper, and an efficient online method is desired. Acknowledgment For implementing frontier-based search, we coded the program based on the software library TdZdd (in [8]). Our work is partly supported by JSPS KAKENHI Scientific Research(S) - Number 15H References [1] R. Kaye, Minesweeper is NP-complete, ser. The Mathematical Intelligencer. Springer-Verlag, 2000, vol. 22, pp [2] P. Nakov and Z. Wei, MINESWEEPER, #MINESWEEPER, [3] S. Golan, Minesweeper on graphs, ser. Applied Mathematics and Computation, 2011, vol. 217, pp [4] S. Minato, Zero-suppressed BDDs for set manipulation in combinatorial problems, Proc. of 30th ACM/IEEE Design Automation Conf. (DAC 1993), pp , [5] J. Kawahara, T. Inoue, H. Iwashita, and S. Minato, Frontier-based search for enumerating all constrained subgraphs with compressed representation, Hokkaido University Graduate School of Infomation Science and Technology, Tech. Rep., Sept [6] J. D. Fix and B. McPhail, Offline 1-minesweeper is np-complete, [7] O. Coudert, Solving graph optimization problems with zbdds, in European Design and Test Conference, Mar. 1997, pp [8] H. Iwashita and S. Minato, Efficient top-down zdd construction techniques using recursive specifications, Hokkaido University Graduate School of Infomation Science and Technology, Tech. Rep., Dec
Algorithm and Complexity of Disjointed Connected Dominating Set Problem on Trees
 Algorithm and Complexity of Disjointed Connected Dominating Set Problem on Trees Wei Wang joint with Zishen Yang, Xianliang Liu School of Mathematics and Statistics, Xi an Jiaotong University Dec 20, 2016
Algorithm and Complexity of Disjointed Connected Dominating Set Problem on Trees Wei Wang joint with Zishen Yang, Xianliang Liu School of Mathematics and Statistics, Xi an Jiaotong University Dec 20, 2016
6. Lecture notes on matroid intersection
 Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans May 2, 2017 6. Lecture notes on matroid intersection One nice feature about matroids is that a simple greedy algorithm
Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans May 2, 2017 6. Lecture notes on matroid intersection One nice feature about matroids is that a simple greedy algorithm
5. Lecture notes on matroid intersection
 Massachusetts Institute of Technology Handout 14 18.433: Combinatorial Optimization April 1st, 2009 Michel X. Goemans 5. Lecture notes on matroid intersection One nice feature about matroids is that a
Massachusetts Institute of Technology Handout 14 18.433: Combinatorial Optimization April 1st, 2009 Michel X. Goemans 5. Lecture notes on matroid intersection One nice feature about matroids is that a
Fast Compilation of s-t Paths on a Graph for Counting and Enumeration
 Proceedings of Machine Learning Research vol 73:129-140, 2017 AMBN 2017 Fast Compilation of s-t Paths on a Graph for Counting and Enumeration Teruji Sugaya sugaya@ist.hokudai.ac.jp Graduate School of Information
Proceedings of Machine Learning Research vol 73:129-140, 2017 AMBN 2017 Fast Compilation of s-t Paths on a Graph for Counting and Enumeration Teruji Sugaya sugaya@ist.hokudai.ac.jp Graduate School of Information
Lecture 6: Graph Properties
 Lecture 6: Graph Properties Rajat Mittal IIT Kanpur In this section, we will look at some of the combinatorial properties of graphs. Initially we will discuss independent sets. The bulk of the content
Lecture 6: Graph Properties Rajat Mittal IIT Kanpur In this section, we will look at some of the combinatorial properties of graphs. Initially we will discuss independent sets. The bulk of the content
Exact Computation of Influence Spread by Binary Decision Diagrams
 Exact Computation of Influence Spread by Binary Decision Diagrams Takanori Maehara 1), Hirofumi Suzuki 2), Masakazu Ishihata 2) 1) Riken Center for Advanced Intelligence Project 2) Hokkaido University
Exact Computation of Influence Spread by Binary Decision Diagrams Takanori Maehara 1), Hirofumi Suzuki 2), Masakazu Ishihata 2) 1) Riken Center for Advanced Intelligence Project 2) Hokkaido University
Binary Decision Diagrams
 Logic and roof Hilary 2016 James Worrell Binary Decision Diagrams A propositional formula is determined up to logical equivalence by its truth table. If the formula has n variables then its truth table
Logic and roof Hilary 2016 James Worrell Binary Decision Diagrams A propositional formula is determined up to logical equivalence by its truth table. If the formula has n variables then its truth table
HW Graph Theory Name (andrewid) - X. 1: Draw K 7 on a torus with no edge crossings.
 1: Draw K 7 on a torus with no edge crossings. A quick calculation reveals that an embedding of K 7 on the torus is a -cell embedding. At that point, it is hard to go wrong if you start drawing C 3 faces,
1: Draw K 7 on a torus with no edge crossings. A quick calculation reveals that an embedding of K 7 on the torus is a -cell embedding. At that point, it is hard to go wrong if you start drawing C 3 faces,
2. Lecture notes on non-bipartite matching
 Massachusetts Institute of Technology 18.433: Combinatorial Optimization Michel X. Goemans February 15th, 013. Lecture notes on non-bipartite matching Given a graph G = (V, E), we are interested in finding
Massachusetts Institute of Technology 18.433: Combinatorial Optimization Michel X. Goemans February 15th, 013. Lecture notes on non-bipartite matching Given a graph G = (V, E), we are interested in finding
Math 170- Graph Theory Notes
 1 Math 170- Graph Theory Notes Michael Levet December 3, 2018 Notation: Let n be a positive integer. Denote [n] to be the set {1, 2,..., n}. So for example, [3] = {1, 2, 3}. To quote Bud Brown, Graph theory
1 Math 170- Graph Theory Notes Michael Levet December 3, 2018 Notation: Let n be a positive integer. Denote [n] to be the set {1, 2,..., n}. So for example, [3] = {1, 2, 3}. To quote Bud Brown, Graph theory
Distinctive Frequent Itemset Mining from Time Segmented Databases Using ZDD-Based Symbolic Processing. Shin-ichi Minato and Takeaki Uno
 TCS Technical Report TCS -TR-A-09-37 Distinctive Frequent Itemset Mining from Time Segmented Databases Using ZDD-Based Symbolic Processing by Shin-ichi Minato and Takeaki Uno Division of Computer Science
TCS Technical Report TCS -TR-A-09-37 Distinctive Frequent Itemset Mining from Time Segmented Databases Using ZDD-Based Symbolic Processing by Shin-ichi Minato and Takeaki Uno Division of Computer Science
1 Maximum Independent Set
 CS 408 Embeddings and MIS Abhiram Ranade In this lecture we will see another application of graph embedding. We will see that certain problems (e.g. maximum independent set, MIS) can be solved fast for
CS 408 Embeddings and MIS Abhiram Ranade In this lecture we will see another application of graph embedding. We will see that certain problems (e.g. maximum independent set, MIS) can be solved fast for
Approximation Algorithms for Geometric Intersection Graphs
 Approximation Algorithms for Geometric Intersection Graphs Subhas C. Nandy (nandysc@isical.ac.in) Advanced Computing and Microelectronics Unit Indian Statistical Institute Kolkata 700108, India. Outline
Approximation Algorithms for Geometric Intersection Graphs Subhas C. Nandy (nandysc@isical.ac.in) Advanced Computing and Microelectronics Unit Indian Statistical Institute Kolkata 700108, India. Outline
An Efficient Algorithm for Enumerating Eulerian Paths. Muhammad Kholilurrohman and Shin-ichi Minato
 TCS Technical Report TCS-TR-A-14-77 An Efficient Algorithm for Enumerating Eulerian Paths by Muhammad Kholilurrohman and Shin-ichi Minato Division of Computer Science Report Series A October 3, 014 Hokkaido
TCS Technical Report TCS-TR-A-14-77 An Efficient Algorithm for Enumerating Eulerian Paths by Muhammad Kholilurrohman and Shin-ichi Minato Division of Computer Science Report Series A October 3, 014 Hokkaido
Matching Algorithms. Proof. If a bipartite graph has a perfect matching, then it is easy to see that the right hand side is a necessary condition.
 18.433 Combinatorial Optimization Matching Algorithms September 9,14,16 Lecturer: Santosh Vempala Given a graph G = (V, E), a matching M is a set of edges with the property that no two of the edges have
18.433 Combinatorial Optimization Matching Algorithms September 9,14,16 Lecturer: Santosh Vempala Given a graph G = (V, E), a matching M is a set of edges with the property that no two of the edges have
6c Lecture 3 & 4: April 8 & 10, 2014
 6c Lecture 3 & 4: April 8 & 10, 2014 3.1 Graphs and trees We begin by recalling some basic definitions from graph theory. Definition 3.1. A (undirected, simple) graph consists of a set of vertices V and
6c Lecture 3 & 4: April 8 & 10, 2014 3.1 Graphs and trees We begin by recalling some basic definitions from graph theory. Definition 3.1. A (undirected, simple) graph consists of a set of vertices V and
PLANAR GRAPH BIPARTIZATION IN LINEAR TIME
 PLANAR GRAPH BIPARTIZATION IN LINEAR TIME SAMUEL FIORINI, NADIA HARDY, BRUCE REED, AND ADRIAN VETTA Abstract. For each constant k, we present a linear time algorithm that, given a planar graph G, either
PLANAR GRAPH BIPARTIZATION IN LINEAR TIME SAMUEL FIORINI, NADIA HARDY, BRUCE REED, AND ADRIAN VETTA Abstract. For each constant k, we present a linear time algorithm that, given a planar graph G, either
ENUMERATION OF REGION PARTITIONING FOR EVACUATION PLANNING BASED ON ZDD
 ENUMERATION OF REGION PARTITIONING FOR EVACUATION PLANNING BASED ON ZDD Atsushi Takizawa 1, Yasufumi Takechi 2, Akio Ohta 2, Naoki Katoh 2, Takeru Inoue 3, Takashi Horiyama 4, Jun Kawahara 5, Shin-ichi
ENUMERATION OF REGION PARTITIONING FOR EVACUATION PLANNING BASED ON ZDD Atsushi Takizawa 1, Yasufumi Takechi 2, Akio Ohta 2, Naoki Katoh 2, Takeru Inoue 3, Takashi Horiyama 4, Jun Kawahara 5, Shin-ichi
An Algorithm for k-pairwise Cluster-fault-tolerant Disjoint Paths in a Burnt Pancake Graph
 2015 International Conference on Computational Science and Computational Intelligence An Algorithm for k-pairwise Cluster-fault-tolerant Disjoint Paths in a Burnt Pancake Graph Masato Tokuda, Yuki Hirai,
2015 International Conference on Computational Science and Computational Intelligence An Algorithm for k-pairwise Cluster-fault-tolerant Disjoint Paths in a Burnt Pancake Graph Masato Tokuda, Yuki Hirai,
CME 305: Discrete Mathematics and Algorithms Instructor: Reza Zadeh HW#3 Due at the beginning of class Thursday 02/26/15
 CME 305: Discrete Mathematics and Algorithms Instructor: Reza Zadeh (rezab@stanford.edu) HW#3 Due at the beginning of class Thursday 02/26/15 1. Consider a model of a nonbipartite undirected graph in which
CME 305: Discrete Mathematics and Algorithms Instructor: Reza Zadeh (rezab@stanford.edu) HW#3 Due at the beginning of class Thursday 02/26/15 1. Consider a model of a nonbipartite undirected graph in which
Unit 4: Formal Verification
 Course contents Unit 4: Formal Verification Logic synthesis basics Binary-decision diagram (BDD) Verification Logic optimization Technology mapping Readings Chapter 11 Unit 4 1 Logic Synthesis & Verification
Course contents Unit 4: Formal Verification Logic synthesis basics Binary-decision diagram (BDD) Verification Logic optimization Technology mapping Readings Chapter 11 Unit 4 1 Logic Synthesis & Verification
Parameterized graph separation problems
 Parameterized graph separation problems Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary, dmarx@cs.bme.hu Abstract.
Parameterized graph separation problems Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary, dmarx@cs.bme.hu Abstract.
CS473-Algorithms I. Lecture 13-A. Graphs. Cevdet Aykanat - Bilkent University Computer Engineering Department
 CS473-Algorithms I Lecture 3-A Graphs Graphs A directed graph (or digraph) G is a pair (V, E), where V is a finite set, and E is a binary relation on V The set V: Vertex set of G The set E: Edge set of
CS473-Algorithms I Lecture 3-A Graphs Graphs A directed graph (or digraph) G is a pair (V, E), where V is a finite set, and E is a binary relation on V The set V: Vertex set of G The set E: Edge set of
COMP260 Spring 2014 Notes: February 4th
 COMP260 Spring 2014 Notes: February 4th Andrew Winslow In these notes, all graphs are undirected. We consider matching, covering, and packing in bipartite graphs, general graphs, and hypergraphs. We also
COMP260 Spring 2014 Notes: February 4th Andrew Winslow In these notes, all graphs are undirected. We consider matching, covering, and packing in bipartite graphs, general graphs, and hypergraphs. We also
Treewidth and graph minors
 Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Core Membership Computation for Succinct Representations of Coalitional Games
 Core Membership Computation for Succinct Representations of Coalitional Games Xi Alice Gao May 11, 2009 Abstract In this paper, I compare and contrast two formal results on the computational complexity
Core Membership Computation for Succinct Representations of Coalitional Games Xi Alice Gao May 11, 2009 Abstract In this paper, I compare and contrast two formal results on the computational complexity
EXTENDING SPACE SYNTAX WITH EFFICIENT ENUMERATION
 #176 Algorithms and Hypergraphs ATSUSHI TAKIZAWA Graduate School of Engineering, Osaka City University takizawa@arch.eng.osaka-cu.ac.jp ABSTRACT In this research, we perform building scale analysis, and
#176 Algorithms and Hypergraphs ATSUSHI TAKIZAWA Graduate School of Engineering, Osaka City University takizawa@arch.eng.osaka-cu.ac.jp ABSTRACT In this research, we perform building scale analysis, and
Chapter 9 Graph Algorithms
 Introduction graph theory useful in practice represent many real-life problems can be if not careful with data structures Chapter 9 Graph s 2 Definitions Definitions an undirected graph is a finite set
Introduction graph theory useful in practice represent many real-life problems can be if not careful with data structures Chapter 9 Graph s 2 Definitions Definitions an undirected graph is a finite set
arxiv:cs/ v1 [cs.ds] 20 Feb 2003
![arxiv:cs/ v1 [cs.ds] 20 Feb 2003 arxiv:cs/ v1 [cs.ds] 20 Feb 2003](/thumbs/82/85921811.jpg) The Traveling Salesman Problem for Cubic Graphs David Eppstein School of Information & Computer Science University of California, Irvine Irvine, CA 92697-3425, USA eppstein@ics.uci.edu arxiv:cs/0302030v1
The Traveling Salesman Problem for Cubic Graphs David Eppstein School of Information & Computer Science University of California, Irvine Irvine, CA 92697-3425, USA eppstein@ics.uci.edu arxiv:cs/0302030v1
Solutions to Midterm 2 - Monday, July 11th, 2009
 Solutions to Midterm - Monday, July 11th, 009 CPSC30, Summer009. Instructor: Dr. Lior Malka. (liorma@cs.ubc.ca) 1. Dynamic programming. Let A be a set of n integers A 1,..., A n such that 1 A i n for each
Solutions to Midterm - Monday, July 11th, 009 CPSC30, Summer009. Instructor: Dr. Lior Malka. (liorma@cs.ubc.ca) 1. Dynamic programming. Let A be a set of n integers A 1,..., A n such that 1 A i n for each
11/22/2016. Chapter 9 Graph Algorithms. Introduction. Definitions. Definitions. Definitions. Definitions
 Introduction Chapter 9 Graph Algorithms graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 2 Definitions an undirected graph G = (V, E) is
Introduction Chapter 9 Graph Algorithms graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 2 Definitions an undirected graph G = (V, E) is
Chapter 9 Graph Algorithms
 Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 3 Definitions an undirected graph G = (V, E)
Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 3 Definitions an undirected graph G = (V, E)
Theorem 2.9: nearest addition algorithm
 There are severe limits on our ability to compute near-optimal tours It is NP-complete to decide whether a given undirected =(,)has a Hamiltonian cycle An approximation algorithm for the TSP can be used
There are severe limits on our ability to compute near-optimal tours It is NP-complete to decide whether a given undirected =(,)has a Hamiltonian cycle An approximation algorithm for the TSP can be used
A Reduction of Conway s Thrackle Conjecture
 A Reduction of Conway s Thrackle Conjecture Wei Li, Karen Daniels, and Konstantin Rybnikov Department of Computer Science and Department of Mathematical Sciences University of Massachusetts, Lowell 01854
A Reduction of Conway s Thrackle Conjecture Wei Li, Karen Daniels, and Konstantin Rybnikov Department of Computer Science and Department of Mathematical Sciences University of Massachusetts, Lowell 01854
Learning Characteristic Structured Patterns in Rooted Planar Maps
 Learning Characteristic Structured Patterns in Rooted Planar Maps Satoshi Kawamoto Yusuke Suzuki Takayoshi Shoudai Abstract Exting the concept of ordered graphs, we propose a new data structure to express
Learning Characteristic Structured Patterns in Rooted Planar Maps Satoshi Kawamoto Yusuke Suzuki Takayoshi Shoudai Abstract Exting the concept of ordered graphs, we propose a new data structure to express
Paths, Flowers and Vertex Cover
 Paths, Flowers and Vertex Cover Venkatesh Raman M. S. Ramanujan Saket Saurabh Abstract It is well known that in a bipartite (and more generally in a König) graph, the size of the minimum vertex cover is
Paths, Flowers and Vertex Cover Venkatesh Raman M. S. Ramanujan Saket Saurabh Abstract It is well known that in a bipartite (and more generally in a König) graph, the size of the minimum vertex cover is
A Nim game played on graphs II
 Theoretical Computer Science 304 (2003) 401 419 www.elsevier.com/locate/tcs A Nim game played on graphs II Masahiko Fukuyama Graduate School of Mathematical Sciences, University of Tokyo, 3-8-1 Komaba,
Theoretical Computer Science 304 (2003) 401 419 www.elsevier.com/locate/tcs A Nim game played on graphs II Masahiko Fukuyama Graduate School of Mathematical Sciences, University of Tokyo, 3-8-1 Komaba,
Chapter 9 Graph Algorithms
 Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be if not careful with data structures 3 Definitions an undirected graph G = (V, E) is a
Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be if not careful with data structures 3 Definitions an undirected graph G = (V, E) is a
2 The Fractional Chromatic Gap
 C 1 11 2 The Fractional Chromatic Gap As previously noted, for any finite graph. This result follows from the strong duality of linear programs. Since there is no such duality result for infinite linear
C 1 11 2 The Fractional Chromatic Gap As previously noted, for any finite graph. This result follows from the strong duality of linear programs. Since there is no such duality result for infinite linear
CME 305: Discrete Mathematics and Algorithms Instructor: Reza Zadeh HW#3 Due at the beginning of class Thursday 03/02/17
 CME 305: Discrete Mathematics and Algorithms Instructor: Reza Zadeh (rezab@stanford.edu) HW#3 Due at the beginning of class Thursday 03/02/17 1. Consider a model of a nonbipartite undirected graph in which
CME 305: Discrete Mathematics and Algorithms Instructor: Reza Zadeh (rezab@stanford.edu) HW#3 Due at the beginning of class Thursday 03/02/17 1. Consider a model of a nonbipartite undirected graph in which
An Eternal Domination Problem in Grids
 Theory and Applications of Graphs Volume Issue 1 Article 2 2017 An Eternal Domination Problem in Grids William Klostermeyer University of North Florida, klostermeyer@hotmail.com Margaret-Ellen Messinger
Theory and Applications of Graphs Volume Issue 1 Article 2 2017 An Eternal Domination Problem in Grids William Klostermeyer University of North Florida, klostermeyer@hotmail.com Margaret-Ellen Messinger
1 The Traveling Salesperson Problem (TSP)
 CS 598CSC: Approximation Algorithms Lecture date: January 23, 2009 Instructor: Chandra Chekuri Scribe: Sungjin Im In the previous lecture, we had a quick overview of several basic aspects of approximation
CS 598CSC: Approximation Algorithms Lecture date: January 23, 2009 Instructor: Chandra Chekuri Scribe: Sungjin Im In the previous lecture, we had a quick overview of several basic aspects of approximation
Coloring Fuzzy Circular Interval Graphs
 Coloring Fuzzy Circular Interval Graphs Friedrich Eisenbrand 1 Martin Niemeier 2 SB IMA DISOPT EPFL Lausanne, Switzerland Abstract Computing the weighted coloring number of graphs is a classical topic
Coloring Fuzzy Circular Interval Graphs Friedrich Eisenbrand 1 Martin Niemeier 2 SB IMA DISOPT EPFL Lausanne, Switzerland Abstract Computing the weighted coloring number of graphs is a classical topic
8.1 Polynomial-Time Reductions
 8.1 Polynomial-Time Reductions Classify Problems According to Computational Requirements Q. Which problems will we be able to solve in practice? A working definition. Those with polynomial-time algorithms.
8.1 Polynomial-Time Reductions Classify Problems According to Computational Requirements Q. Which problems will we be able to solve in practice? A working definition. Those with polynomial-time algorithms.
Improved upper and lower bounds on the feedback vertex numbers of grids and butterflies
 Improved upper and lower bounds on the feedback vertex numbers of grids and butterflies Florent R. Madelaine and Iain A. Stewart Department of Computer Science, Durham University, Science Labs, South Road,
Improved upper and lower bounds on the feedback vertex numbers of grids and butterflies Florent R. Madelaine and Iain A. Stewart Department of Computer Science, Durham University, Science Labs, South Road,
Interleaving Schemes on Circulant Graphs with Two Offsets
 Interleaving Schemes on Circulant raphs with Two Offsets Aleksandrs Slivkins Department of Computer Science Cornell University Ithaca, NY 14853 slivkins@cs.cornell.edu Jehoshua Bruck Department of Electrical
Interleaving Schemes on Circulant raphs with Two Offsets Aleksandrs Slivkins Department of Computer Science Cornell University Ithaca, NY 14853 slivkins@cs.cornell.edu Jehoshua Bruck Department of Electrical
arxiv: v1 [cs.ds] 23 Jul 2014
![arxiv: v1 [cs.ds] 23 Jul 2014 arxiv: v1 [cs.ds] 23 Jul 2014](/thumbs/90/104116258.jpg) Efficient Enumeration of Induced Subtrees in a K-Degenerate Graph Kunihiro Wasa 1, Hiroki Arimura 1, and Takeaki Uno 2 arxiv:1407.6140v1 [cs.ds] 23 Jul 2014 1 Hokkaido University, Graduate School of Information
Efficient Enumeration of Induced Subtrees in a K-Degenerate Graph Kunihiro Wasa 1, Hiroki Arimura 1, and Takeaki Uno 2 arxiv:1407.6140v1 [cs.ds] 23 Jul 2014 1 Hokkaido University, Graduate School of Information
8 Matroid Intersection
 8 Matroid Intersection 8.1 Definition and examples 8.2 Matroid Intersection Algorithm 8.1 Definitions Given two matroids M 1 = (X, I 1 ) and M 2 = (X, I 2 ) on the same set X, their intersection is M 1
8 Matroid Intersection 8.1 Definition and examples 8.2 Matroid Intersection Algorithm 8.1 Definitions Given two matroids M 1 = (X, I 1 ) and M 2 = (X, I 2 ) on the same set X, their intersection is M 1
The 3-Steiner Root Problem
 The 3-Steiner Root Problem Maw-Shang Chang 1 and Ming-Tat Ko 2 1 Department of Computer Science and Information Engineering National Chung Cheng University, Chiayi 621, Taiwan, R.O.C. mschang@cs.ccu.edu.tw
The 3-Steiner Root Problem Maw-Shang Chang 1 and Ming-Tat Ko 2 1 Department of Computer Science and Information Engineering National Chung Cheng University, Chiayi 621, Taiwan, R.O.C. mschang@cs.ccu.edu.tw
Acyclic Colorings of Graph Subdivisions
 Acyclic Colorings of Graph Subdivisions Debajyoti Mondal, Rahnuma Islam Nishat, Sue Whitesides, and Md. Saidur Rahman 3 Department of Computer Science, University of Manitoba Department of Computer Science,
Acyclic Colorings of Graph Subdivisions Debajyoti Mondal, Rahnuma Islam Nishat, Sue Whitesides, and Md. Saidur Rahman 3 Department of Computer Science, University of Manitoba Department of Computer Science,
Algorithmic complexity of two defence budget problems
 21st International Congress on Modelling and Simulation, Gold Coast, Australia, 29 Nov to 4 Dec 2015 www.mssanz.org.au/modsim2015 Algorithmic complexity of two defence budget problems R. Taylor a a Defence
21st International Congress on Modelling and Simulation, Gold Coast, Australia, 29 Nov to 4 Dec 2015 www.mssanz.org.au/modsim2015 Algorithmic complexity of two defence budget problems R. Taylor a a Defence
Lecture 4: Primal Dual Matching Algorithm and Non-Bipartite Matching. 1 Primal/Dual Algorithm for weighted matchings in Bipartite Graphs
 CMPUT 675: Topics in Algorithms and Combinatorial Optimization (Fall 009) Lecture 4: Primal Dual Matching Algorithm and Non-Bipartite Matching Lecturer: Mohammad R. Salavatipour Date: Sept 15 and 17, 009
CMPUT 675: Topics in Algorithms and Combinatorial Optimization (Fall 009) Lecture 4: Primal Dual Matching Algorithm and Non-Bipartite Matching Lecturer: Mohammad R. Salavatipour Date: Sept 15 and 17, 009
Computational Discrete Mathematics
 Computational Discrete Mathematics Combinatorics and Graph Theory with Mathematica SRIRAM PEMMARAJU The University of Iowa STEVEN SKIENA SUNY at Stony Brook CAMBRIDGE UNIVERSITY PRESS Table of Contents
Computational Discrete Mathematics Combinatorics and Graph Theory with Mathematica SRIRAM PEMMARAJU The University of Iowa STEVEN SKIENA SUNY at Stony Brook CAMBRIDGE UNIVERSITY PRESS Table of Contents
An exact algorithm for max-cut in sparse graphs
 An exact algorithm for max-cut in sparse graphs F. Della Croce a M. J. Kaminski b, V. Th. Paschos c a D.A.I., Politecnico di Torino, Italy b RUTCOR, Rutgers University c LAMSADE, CNRS UMR 7024 and Université
An exact algorithm for max-cut in sparse graphs F. Della Croce a M. J. Kaminski b, V. Th. Paschos c a D.A.I., Politecnico di Torino, Italy b RUTCOR, Rutgers University c LAMSADE, CNRS UMR 7024 and Université
5.1 Min-Max Theorem for General Matching
 CSC5160: Combinatorial Optimization and Approximation Algorithms Topic: General Matching Date: 4/01/008 Lecturer: Lap Chi Lau Scribe: Jennifer X.M. WU In this lecture, we discuss matchings in general graph.
CSC5160: Combinatorial Optimization and Approximation Algorithms Topic: General Matching Date: 4/01/008 Lecturer: Lap Chi Lau Scribe: Jennifer X.M. WU In this lecture, we discuss matchings in general graph.
A Genus Bound for Digital Image Boundaries
 A Genus Bound for Digital Image Boundaries Lowell Abrams and Donniell E. Fishkind March 9, 2005 Abstract Shattuck and Leahy [4] conjectured and Abrams, Fishkind, and Priebe [1],[2] proved that the boundary
A Genus Bound for Digital Image Boundaries Lowell Abrams and Donniell E. Fishkind March 9, 2005 Abstract Shattuck and Leahy [4] conjectured and Abrams, Fishkind, and Priebe [1],[2] proved that the boundary
Efficient Enumeration Algorithm for Dominating Sets in Bounded Degenerate Graphs
 Efficient Enumeration Algorithm for Dominating Sets in Bounded Degenerate Graphs Kazuhiro Kurita 1, Kunihiro Wasa 2, Hiroki Arimura 1, and Takeaki Uno 2 1 IST, Hokkaido University, Sapporo, Japan 2 National
Efficient Enumeration Algorithm for Dominating Sets in Bounded Degenerate Graphs Kazuhiro Kurita 1, Kunihiro Wasa 2, Hiroki Arimura 1, and Takeaki Uno 2 1 IST, Hokkaido University, Sapporo, Japan 2 National
Solving the Large Scale Next Release Problem with a Backbone Based Multilevel Algorithm
 IEEE TRANSACTIONS ON JOURNAL NAME, MANUSCRIPT ID 1 Solving the Large Scale Next Release Problem with a Backbone Based Multilevel Algorithm Jifeng Xuan, He Jiang, Member, IEEE, Zhilei Ren, and Zhongxuan
IEEE TRANSACTIONS ON JOURNAL NAME, MANUSCRIPT ID 1 Solving the Large Scale Next Release Problem with a Backbone Based Multilevel Algorithm Jifeng Xuan, He Jiang, Member, IEEE, Zhilei Ren, and Zhongxuan
Seeing Around Corners: Fast Orthogonal Connector Routing
 Seeing round Corners: Fast Orthogonal Connector Routing Kim Marriott 1, Peter J. Stuckey 2, and Michael Wybrow 1 1 Caulfield School of Information Technology, Monash University, Caulfield, Victoria 3145,
Seeing round Corners: Fast Orthogonal Connector Routing Kim Marriott 1, Peter J. Stuckey 2, and Michael Wybrow 1 1 Caulfield School of Information Technology, Monash University, Caulfield, Victoria 3145,
Lecture notes on: Maximum matching in bipartite and non-bipartite graphs (Draft)
 Lecture notes on: Maximum matching in bipartite and non-bipartite graphs (Draft) Lecturer: Uri Zwick June 5, 2013 1 The maximum matching problem Let G = (V, E) be an undirected graph. A set M E is a matching
Lecture notes on: Maximum matching in bipartite and non-bipartite graphs (Draft) Lecturer: Uri Zwick June 5, 2013 1 The maximum matching problem Let G = (V, E) be an undirected graph. A set M E is a matching
A CSP Search Algorithm with Reduced Branching Factor
 A CSP Search Algorithm with Reduced Branching Factor Igor Razgon and Amnon Meisels Department of Computer Science, Ben-Gurion University of the Negev, Beer-Sheva, 84-105, Israel {irazgon,am}@cs.bgu.ac.il
A CSP Search Algorithm with Reduced Branching Factor Igor Razgon and Amnon Meisels Department of Computer Science, Ben-Gurion University of the Negev, Beer-Sheva, 84-105, Israel {irazgon,am}@cs.bgu.ac.il
Parameterized coloring problems on chordal graphs
 Parameterized coloring problems on chordal graphs Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary dmarx@cs.bme.hu
Parameterized coloring problems on chordal graphs Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary dmarx@cs.bme.hu
Steiner Trees and Forests
 Massachusetts Institute of Technology Lecturer: Adriana Lopez 18.434: Seminar in Theoretical Computer Science March 7, 2006 Steiner Trees and Forests 1 Steiner Tree Problem Given an undirected graph G
Massachusetts Institute of Technology Lecturer: Adriana Lopez 18.434: Seminar in Theoretical Computer Science March 7, 2006 Steiner Trees and Forests 1 Steiner Tree Problem Given an undirected graph G
Section 8.2 Graph Terminology. Undirected Graphs. Definition: Two vertices u, v in V are adjacent or neighbors if there is an edge e between u and v.
 Section 8.2 Graph Terminology Undirected Graphs Definition: Two vertices u, v in V are adjacent or neighbors if there is an edge e between u and v. The edge e connects u and v. The vertices u and v are
Section 8.2 Graph Terminology Undirected Graphs Definition: Two vertices u, v in V are adjacent or neighbors if there is an edge e between u and v. The edge e connects u and v. The vertices u and v are
These notes present some properties of chordal graphs, a set of undirected graphs that are important for undirected graphical models.
 Undirected Graphical Models: Chordal Graphs, Decomposable Graphs, Junction Trees, and Factorizations Peter Bartlett. October 2003. These notes present some properties of chordal graphs, a set of undirected
Undirected Graphical Models: Chordal Graphs, Decomposable Graphs, Junction Trees, and Factorizations Peter Bartlett. October 2003. These notes present some properties of chordal graphs, a set of undirected
A simple algorithm for 4-coloring 3-colorable planar graphs
 A simple algorithm for 4-coloring 3-colorable planar graphs Ken-ichi Kawarabayashi 1 National Institute of Informatics, 2-1-2 Hitotsubashi, Chiyoda-ku, Tokyo 101-8430, Japan Kenta Ozeki 2 Department of
A simple algorithm for 4-coloring 3-colorable planar graphs Ken-ichi Kawarabayashi 1 National Institute of Informatics, 2-1-2 Hitotsubashi, Chiyoda-ku, Tokyo 101-8430, Japan Kenta Ozeki 2 Department of
motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs { }
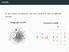 motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs G M { } 2 subgraph motifs 3 motifs Find interesting patterns in a network. 4 motifs Find
motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs G M { } 2 subgraph motifs 3 motifs Find interesting patterns in a network. 4 motifs Find
Dualization of Boolean functions Using Ternary Decision Diagrams
 Dualization of Boolean functions Using Ternary Decision Diagrams Takahisa Toda ERATO MINATO Discrete Structure Manipulation System Project, Japan Science and Technology Agency, at Hokkaido University,
Dualization of Boolean functions Using Ternary Decision Diagrams Takahisa Toda ERATO MINATO Discrete Structure Manipulation System Project, Japan Science and Technology Agency, at Hokkaido University,
Feedback Arc Set in Bipartite Tournaments is NP-Complete
 Feedback Arc Set in Bipartite Tournaments is NP-Complete Jiong Guo 1 Falk Hüffner 1 Hannes Moser 2 Institut für Informatik, Friedrich-Schiller-Universität Jena, Ernst-Abbe-Platz 2, D-07743 Jena, Germany
Feedback Arc Set in Bipartite Tournaments is NP-Complete Jiong Guo 1 Falk Hüffner 1 Hannes Moser 2 Institut für Informatik, Friedrich-Schiller-Universität Jena, Ernst-Abbe-Platz 2, D-07743 Jena, Germany
Slides for Faculty Oxford University Press All rights reserved.
 Oxford University Press 2013 Slides for Faculty Assistance Preliminaries Author: Vivek Kulkarni vivek_kulkarni@yahoo.com Outline Following topics are covered in the slides: Basic concepts, namely, symbols,
Oxford University Press 2013 Slides for Faculty Assistance Preliminaries Author: Vivek Kulkarni vivek_kulkarni@yahoo.com Outline Following topics are covered in the slides: Basic concepts, namely, symbols,
Disjoint Sets and the Union/Find Problem
 Disjoint Sets and the Union/Find Problem Equivalence Relations A binary relation R on a set S is a subset of the Cartesian product S S. If (a, b) R we write arb and say a relates to b. Relations can have
Disjoint Sets and the Union/Find Problem Equivalence Relations A binary relation R on a set S is a subset of the Cartesian product S S. If (a, b) R we write arb and say a relates to b. Relations can have
Compiling Bayesian Networks by Symbolic Probability Calculation Based on Zero-suppressed BDDs
 Compiling Bayesian Networks by Symbolic Probability Calculation Based on Zero-suppressed BDDs Shin-ichi Minato Div. of Computer Science Hokkaido University Sapporo 6 814, Japan Ken Satoh National Institute
Compiling Bayesian Networks by Symbolic Probability Calculation Based on Zero-suppressed BDDs Shin-ichi Minato Div. of Computer Science Hokkaido University Sapporo 6 814, Japan Ken Satoh National Institute
A new analysis technique for the Sprouts Game
 A new analysis technique for the Sprouts Game RICCARDO FOCARDI Università Ca Foscari di Venezia, Italy FLAMINIA L. LUCCIO Università di Trieste, Italy Abstract Sprouts is a two players game that was first
A new analysis technique for the Sprouts Game RICCARDO FOCARDI Università Ca Foscari di Venezia, Italy FLAMINIA L. LUCCIO Università di Trieste, Italy Abstract Sprouts is a two players game that was first
A new edge selection heuristic for computing the Tutte polynomial of an undirected graph.
 FPSAC 2012, Nagoya, Japan DMTCS proc. (subm.), by the authors, 1 12 A new edge selection heuristic for computing the Tutte polynomial of an undirected graph. Michael Monagan 1 1 Department of Mathematics,
FPSAC 2012, Nagoya, Japan DMTCS proc. (subm.), by the authors, 1 12 A new edge selection heuristic for computing the Tutte polynomial of an undirected graph. Michael Monagan 1 1 Department of Mathematics,
Graphs: Introduction. Ali Shokoufandeh, Department of Computer Science, Drexel University
 Graphs: Introduction Ali Shokoufandeh, Department of Computer Science, Drexel University Overview of this talk Introduction: Notations and Definitions Graphs and Modeling Algorithmic Graph Theory and Combinatorial
Graphs: Introduction Ali Shokoufandeh, Department of Computer Science, Drexel University Overview of this talk Introduction: Notations and Definitions Graphs and Modeling Algorithmic Graph Theory and Combinatorial
Testing Bipartiteness of Geometric Intersection Graphs David Eppstein
 Testing Bipartiteness of Geometric Intersection Graphs David Eppstein Univ. of California, Irvine School of Information and Computer Science Intersection Graphs Given arrangement of geometric objects,
Testing Bipartiteness of Geometric Intersection Graphs David Eppstein Univ. of California, Irvine School of Information and Computer Science Intersection Graphs Given arrangement of geometric objects,
On Sequential Topogenic Graphs
 Int. J. Contemp. Math. Sciences, Vol. 5, 2010, no. 36, 1799-1805 On Sequential Topogenic Graphs Bindhu K. Thomas, K. A. Germina and Jisha Elizabath Joy Research Center & PG Department of Mathematics Mary
Int. J. Contemp. Math. Sciences, Vol. 5, 2010, no. 36, 1799-1805 On Sequential Topogenic Graphs Bindhu K. Thomas, K. A. Germina and Jisha Elizabath Joy Research Center & PG Department of Mathematics Mary
CPSC 217 Assignment 3
 CPSC 217 Assignment 3 Due: Monday November 23, 2015 at 12:00 noon Weight: 7% Sample Solution Length: 135 lines, including some comments (not including the provided code) Individual Work: All assignments
CPSC 217 Assignment 3 Due: Monday November 23, 2015 at 12:00 noon Weight: 7% Sample Solution Length: 135 lines, including some comments (not including the provided code) Individual Work: All assignments
Hamiltonian cycles in bipartite quadrangulations on the torus
 Hamiltonian cycles in bipartite quadrangulations on the torus Atsuhiro Nakamoto and Kenta Ozeki Abstract In this paper, we shall prove that every bipartite quadrangulation G on the torus admits a simple
Hamiltonian cycles in bipartite quadrangulations on the torus Atsuhiro Nakamoto and Kenta Ozeki Abstract In this paper, we shall prove that every bipartite quadrangulation G on the torus admits a simple
Finding a winning strategy in variations of Kayles
 Finding a winning strategy in variations of Kayles Simon Prins ICA-3582809 Utrecht University, The Netherlands July 15, 2015 Abstract Kayles is a two player game played on a graph. The game can be dened
Finding a winning strategy in variations of Kayles Simon Prins ICA-3582809 Utrecht University, The Netherlands July 15, 2015 Abstract Kayles is a two player game played on a graph. The game can be dened
Hardness of Subgraph and Supergraph Problems in c-tournaments
 Hardness of Subgraph and Supergraph Problems in c-tournaments Kanthi K Sarpatwar 1 and N.S. Narayanaswamy 1 Department of Computer Science and Engineering, IIT madras, Chennai 600036, India kanthik@gmail.com,swamy@cse.iitm.ac.in
Hardness of Subgraph and Supergraph Problems in c-tournaments Kanthi K Sarpatwar 1 and N.S. Narayanaswamy 1 Department of Computer Science and Engineering, IIT madras, Chennai 600036, India kanthik@gmail.com,swamy@cse.iitm.ac.in
Vertex Deletion games with Parity rules
 Vertex Deletion games with Parity rules Richard J. Nowakowski 1 Department of Mathematics, Dalhousie University, Halifax, Nova Scotia, Canada rjn@mathstat.dal.ca Paul Ottaway Department of Mathematics,
Vertex Deletion games with Parity rules Richard J. Nowakowski 1 Department of Mathematics, Dalhousie University, Halifax, Nova Scotia, Canada rjn@mathstat.dal.ca Paul Ottaway Department of Mathematics,
Graph Algorithms Using Depth First Search
 Graph Algorithms Using Depth First Search Analysis of Algorithms Week 8, Lecture 1 Prepared by John Reif, Ph.D. Distinguished Professor of Computer Science Duke University Graph Algorithms Using Depth
Graph Algorithms Using Depth First Search Analysis of Algorithms Week 8, Lecture 1 Prepared by John Reif, Ph.D. Distinguished Professor of Computer Science Duke University Graph Algorithms Using Depth
Paths, Flowers and Vertex Cover
 Paths, Flowers and Vertex Cover Venkatesh Raman, M.S. Ramanujan, and Saket Saurabh Presenting: Hen Sender 1 Introduction 2 Abstract. It is well known that in a bipartite (and more generally in a Konig)
Paths, Flowers and Vertex Cover Venkatesh Raman, M.S. Ramanujan, and Saket Saurabh Presenting: Hen Sender 1 Introduction 2 Abstract. It is well known that in a bipartite (and more generally in a Konig)
Non-Enumerative Path Delay Fault Diagnosis
 Non-Enumerative Path Delay Fault Diagnosis Saravanan Padmanaban Spyros Tragoudas Department of Electrical and Computer Engineering Southern Illinois University Carbondale, IL 6901 Abstract The first non-enumerative
Non-Enumerative Path Delay Fault Diagnosis Saravanan Padmanaban Spyros Tragoudas Department of Electrical and Computer Engineering Southern Illinois University Carbondale, IL 6901 Abstract The first non-enumerative
On Structural Parameterizations of the Matching Cut Problem
 On Structural Parameterizations of the Matching Cut Problem N. R. Aravind, Subrahmanyam Kalyanasundaram, and Anjeneya Swami Kare Department of Computer Science and Engineering, IIT Hyderabad, Hyderabad,
On Structural Parameterizations of the Matching Cut Problem N. R. Aravind, Subrahmanyam Kalyanasundaram, and Anjeneya Swami Kare Department of Computer Science and Engineering, IIT Hyderabad, Hyderabad,
arxiv: v1 [cs.dm] 21 Dec 2015
![arxiv: v1 [cs.dm] 21 Dec 2015 arxiv: v1 [cs.dm] 21 Dec 2015](/thumbs/84/90806310.jpg) The Maximum Cardinality Cut Problem is Polynomial in Proper Interval Graphs Arman Boyacı 1, Tinaz Ekim 1, and Mordechai Shalom 1 Department of Industrial Engineering, Boğaziçi University, Istanbul, Turkey
The Maximum Cardinality Cut Problem is Polynomial in Proper Interval Graphs Arman Boyacı 1, Tinaz Ekim 1, and Mordechai Shalom 1 Department of Industrial Engineering, Boğaziçi University, Istanbul, Turkey
1. Lecture notes on bipartite matching
 Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans February 5, 2017 1. Lecture notes on bipartite matching Matching problems are among the fundamental problems in
Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans February 5, 2017 1. Lecture notes on bipartite matching Matching problems are among the fundamental problems in
Chordal deletion is fixed-parameter tractable
 Chordal deletion is fixed-parameter tractable Dániel Marx Institut für Informatik, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. dmarx@informatik.hu-berlin.de Abstract. It
Chordal deletion is fixed-parameter tractable Dániel Marx Institut für Informatik, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. dmarx@informatik.hu-berlin.de Abstract. It
Polynomial-Time Approximation Algorithms
 6.854 Advanced Algorithms Lecture 20: 10/27/2006 Lecturer: David Karger Scribes: Matt Doherty, John Nham, Sergiy Sidenko, David Schultz Polynomial-Time Approximation Algorithms NP-hard problems are a vast
6.854 Advanced Algorithms Lecture 20: 10/27/2006 Lecturer: David Karger Scribes: Matt Doherty, John Nham, Sergiy Sidenko, David Schultz Polynomial-Time Approximation Algorithms NP-hard problems are a vast
751 Problem Set I JWR. Due Sep 28, 2004
 751 Problem Set I JWR Due Sep 28, 2004 Exercise 1. For any space X define an equivalence relation by x y iff here is a path γ : I X with γ(0) = x and γ(1) = y. The equivalence classes are called the path
751 Problem Set I JWR Due Sep 28, 2004 Exercise 1. For any space X define an equivalence relation by x y iff here is a path γ : I X with γ(0) = x and γ(1) = y. The equivalence classes are called the path
CS 441 Discrete Mathematics for CS Lecture 26. Graphs. CS 441 Discrete mathematics for CS. Final exam
 CS 441 Discrete Mathematics for CS Lecture 26 Graphs Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Final exam Saturday, April 26, 2014 at 10:00-11:50am The same classroom as lectures The exam
CS 441 Discrete Mathematics for CS Lecture 26 Graphs Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Final exam Saturday, April 26, 2014 at 10:00-11:50am The same classroom as lectures The exam
On the Relationships between Zero Forcing Numbers and Certain Graph Coverings
 On the Relationships between Zero Forcing Numbers and Certain Graph Coverings Fatemeh Alinaghipour Taklimi, Shaun Fallat 1,, Karen Meagher 2 Department of Mathematics and Statistics, University of Regina,
On the Relationships between Zero Forcing Numbers and Certain Graph Coverings Fatemeh Alinaghipour Taklimi, Shaun Fallat 1,, Karen Meagher 2 Department of Mathematics and Statistics, University of Regina,
A Relational View of Subgraph Isomorphism
 A Relational View of Subgraph Isomorphism J. Cortadella and G. Valiente Department of Software, Technical University of Catalonia, Barcelona, Spain Abstract. This paper presents a novel approach to the
A Relational View of Subgraph Isomorphism J. Cortadella and G. Valiente Department of Software, Technical University of Catalonia, Barcelona, Spain Abstract. This paper presents a novel approach to the
Exam problems for the course Combinatorial Optimization I (DM208)
 Exam problems for the course Combinatorial Optimization I (DM208) Jørgen Bang-Jensen Department of Mathematics and Computer Science University of Southern Denmark The problems are available form the course
Exam problems for the course Combinatorial Optimization I (DM208) Jørgen Bang-Jensen Department of Mathematics and Computer Science University of Southern Denmark The problems are available form the course
The self-minor conjecture for infinite trees
 The self-minor conjecture for infinite trees Julian Pott Abstract We prove Seymour s self-minor conjecture for infinite trees. 1. Introduction P. D. Seymour conjectured that every infinite graph is a proper
The self-minor conjecture for infinite trees Julian Pott Abstract We prove Seymour s self-minor conjecture for infinite trees. 1. Introduction P. D. Seymour conjectured that every infinite graph is a proper
Introduction to Algorithms Third Edition
 Thomas H. Cormen Charles E. Leiserson Ronald L. Rivest Clifford Stein Introduction to Algorithms Third Edition The MIT Press Cambridge, Massachusetts London, England Preface xiü I Foundations Introduction
Thomas H. Cormen Charles E. Leiserson Ronald L. Rivest Clifford Stein Introduction to Algorithms Third Edition The MIT Press Cambridge, Massachusetts London, England Preface xiü I Foundations Introduction
KEYWORD search is a well known method for extracting
 IEEE TRANSACTIONS ON KNOWLEDGE AND DATA ENGINEERING, VOL. 26, NO. 7, JULY 2014 1657 Efficient Duplication Free and Minimal Keyword Search in Graphs Mehdi Kargar, Student Member, IEEE, Aijun An, Member,
IEEE TRANSACTIONS ON KNOWLEDGE AND DATA ENGINEERING, VOL. 26, NO. 7, JULY 2014 1657 Efficient Duplication Free and Minimal Keyword Search in Graphs Mehdi Kargar, Student Member, IEEE, Aijun An, Member,
A motion planning method for mobile robot considering rotational motion in area coverage task
 Asia Pacific Conference on Robot IoT System Development and Platform 018 (APRIS018) A motion planning method for mobile robot considering rotational motion in area coverage task Yano Taiki 1,a) Takase
Asia Pacific Conference on Robot IoT System Development and Platform 018 (APRIS018) A motion planning method for mobile robot considering rotational motion in area coverage task Yano Taiki 1,a) Takase
Computing optimal total vertex covers for trees
 Computing optimal total vertex covers for trees Pak Ching Li Department of Computer Science University of Manitoba Winnipeg, Manitoba Canada R3T 2N2 Abstract. Let G = (V, E) be a simple, undirected, connected
Computing optimal total vertex covers for trees Pak Ching Li Department of Computer Science University of Manitoba Winnipeg, Manitoba Canada R3T 2N2 Abstract. Let G = (V, E) be a simple, undirected, connected
