c-dominating Sets for Families of Graphs
|
|
|
- Paul Houston
- 6 years ago
- Views:
Transcription
1 c-domiatig Sets for Families of Graphs Kelsie Syder Mathematics Uiversity of Mary Washigto April 6, 011 1
2 Abstract The topic of domiatio i graphs has a rich history, begiig with chess ethusiasts i the 1850s determiig how may quees are ecessary to domiate a etire chessboard ad cotiuig to curret problems ivolvig computer commuicatio etworks, social etwork theory, ad other similar problems. We defie a domiatig set of a graph G to be a set of vertices of G such that every vertex of G is either i the set or adjacet to a vertex i the set. The domiatio umber for a graph G is the size of a miimum domiatig set. Determiig the domiatio umber of graphs ca prove highly useful i solvig may types of problems, ad recet studies of domiatig sets reflect this. We focus o describig various families of graphs i terms of bouds o the domiatio umber. Although the computatio of domiatig sets for arbitrary graphs is a NP-complete problem, it is possible to compute certai bouds o the domiatio umber for certai families of graphs. We examie families of graphs, specifically the family of grids, ad determie the bouds o domiatio umber for these families. We compare the domiatio umbers for the various classes of grids with other commo families of graphs.
3 1 Itroductio to Domiatio Our work focuses o the cocept of domiatio i graphs, a topic that has bee studied extesively i recet decades. We begi with a overview of the relevat defiitios alog with a series of examples. First, we review a few graph theory basics that are relevat throughout our work. More o the basics of graph theory ca be foud i [3], for istace. We defie a graph G = (V, E) as a pair of sets, with V the oempty set of vertices of G, ad E the set of edges betwee distict vertices of G. The cardiality of V, deoted V, represets the umber of vertices i G, while vertices u ad v are adjacet if the edge uv is i E. Throughout our work we cosider oly udirected simple graphs G = (V, E), that is, graphs with o directio o the edges ad at most oe edge betwee each pair of vertices. We defie the eighborhood of a vertex v (also called the closed eighborhood of v), as the set of vertices cosistig of v ad each vertex adjacet to v: N[v] = {v} {x V : vx E}. The degree of a vertex v, writte d(v), is defied as the umber of edges icidet with v. We deote the miimum degree of G with δ(g). Also, we defie d(u, v) as the distace betwee two vertices u ad v i V. A subset S of V is a domiatig set if every vertex v V is domiated by some elemet of S, that is, every v V is either a elemet of S or is adjacet to a elemet of S. The domiatio umber, γ(g) is the miimum cardiality of a domiatig set S of V. Fially, the graph G is c-domiated if for 0 < c 1, γ(g) c V. We use the cocept of c- domiatio throughout our work to describe the domiatio umbers for the graphs from various families of graphs. 1.1 Applicatios of Domiatio i Graphs The study of domiatio i graphs has historical roots as early as the 1850s whe Europea chess ethusiasts studied the problem of domiatig quees, as described i []. These ethusiasts worked to determie the miimum umber of quees ecessary so that every square o a stadard 8 8 chessboard is either occupied by a quee or ca be directly attacked by a quee, that is, every square is domiated by a quee. It was determied that a miimum of five quees are eeded, ad this problem ca be modeled by fidig a domiatig set of five quees. The mathematical study of domiatig sets bega i earest i the 1960s, ad sice that time, domiatig sets have bee used for may differet applicatios. Oe of the families of graphs we examie i detail is the family of graphs resemblig grids, which we defie i more detail i Sectio. A practical applicatio demostratig the importace of domiatio umbers i these grids utilizes grids to model city blocks. We let the vertices of the grid represet street corers ad the edges represet streets betwee corers. The, for example, cosider the problem of determiig how may police officers should be statioed across the city o street corers so that every corer is visible to at least oe officer. We assume that each officer ca view the corer o which they are statioed ad each corer that is o more tha oe street block away. The domiatio umber of the grid represetig the city would provide the miimum umber of police officers ecessary so that each corer is visible to at least oe officer. Fidig a miimum domiatig set would provide a descriptio of the street corers where officers should be statioed i order to accomplish this. Clearly may
4 other factors would eed to be cosidered if a city were tryig to solve such a problem, but domiatig sets could serve as a importat tool for decisio makers. Domiatig sets ca be used to model may other problems, icludig may relatig to computer commuicatio etworks, social etwork theory, lad surveyig, ad other similar issues. Determiig the domiatio umber for graphs ad fidig miimum domiatig sets could thus prove very useful. However, fidig the domiatio umber of a geeral graph G is a NP-complete problem []. Our work focuses o examiig certai families of graphs ad fidig the exact domiatio umbers for the graphs from these families. 1. Domiatio i Commo Families of Graphs We start by cosiderig a few examples of domiatio i commo families of graphs. Throughout our work, we focus o families of graphs with relatively small bouds o the domiatio umber. For example, cosider the family of complete graphs. A complete graph K o vertices is a graph i which each vertex is adjacet to every other vertex, that is, for every vertex v V, d(v) = 1. We see by ispectio that for all complete graphs, γ(k ) = 1, sice each vertex v V domiates itself ad its 1 eighbors. Thus the set D = {v} domiates the etire graph. Hece, we see that for a complete graph K, γ(k ) = 1 V = 1, ad so we say K is 1 -domiated. I Figure 1, we see a complete graph o 6 vertices with a domiatio umber of 1. I this figure, as well as the remaiig figures throughout our work, we use grey vertices to represet the vertices i the domiatig set D. u K 6 W 5 K,3 v Figure 1: Miimum domiatig sets for the graphs K 6, W 5 ad K,3 Aother family of graphs with a costat domiatio umber of 1 is the family of wheel graphs. A wheel graph W is a graph with vertices that cotais a cycle of legth 1 ad a cetral vertex v that is ot i the cycle but that is adjacet to every vertex i the cycle. Sice v is adjacet to every other vertex i W, it is clear that v domiates the etire graph. Thus, for all, γ(w ) = 1 V = 1, ad so W is also 1 -domiated. We see the wheel graph W 5 i Figure 1. Next, cosider the family of complete bipartite graphs, that is, graphs i which the vertices ca be partitioed ito two disjoit subsets U ad V, so that each edge coects a vertex from U to V, ad every vertex i U is adjacet to every vertex i V. For all complete bipartite graphs K,m with, m (where U cotais vertices ad V cotais m vertices), we see by ispectio that γ(k,m ) =, sice ay vertex u U domiates each of its m eighbors i V ad ay vertex v V domiates its eighbors i U. We have
5 the that K,m is -domiated, sice γ(k +m,m) = V =. For example, cosider the +m complete bipartite graph K,3 i Figure 1. We see that i these three families of graphs, the domiatio umber is costat i relatio to. I cotrast, for a geeral graph G with miimum degree 1 o vertices, it has bee prove that G is 1 -domiated [6], so that the boud o the domiatio umber of G icreases liearly with. For the families of graphs that we examie throughout the remaider of our work, the domiatio umber will also icrease with, though we will prove that the boud o the domiatio umber is sigificatly less tha the geeral boud for graphs with miimum degree Domiatio i Graphs with Miimum Degree Two The domiatio umber for graphs with miimum degree two has bee explored by William McCuaig ad Bruce Shepherd ad prove i [5]. The result provides a boud o the domiatio umber of such graphs with oly seve exceptios (details o the exceptioal graphs ca be foud i the origial paper [5]). Theorem 1.1. (McGuaig ad Shepard [5]) If G = (V, E) is a coected graph with miimum degree greater tha or equal to (δ(g) ) ad G is ot a graph of type B of exceptioal graphs, the γ(g) V. 5 Thus with this result, we see that if a graph G is coected ad cotais o vertices of degree 1, ad is ot oe of the seve bad graphs i B, the boud o domiatio umber is V. 5 Domiatio i Grids We cosider the family of grid graphs, a family of graphs with miimum degree but which has bouds o domiatio umber lower tha the geeral boud give i Theorem Defiitio of Grids For the remaider of our work, we look at the class of grid graphs, ad we determie bouds o the domiatio umber based o the size of the grid. Such graphs resemble two-dimesioal grids ad ca be used to model thigs as importat as city blocks, ad therefore could be used i applied problems related to city cogestio ad/or traversal of streets. I formal terms, a two-dimesioal grid graph is a m graph G(m ) that is the graph Cartesia product of two paths of legth m ad, respectively. Rather tha explaiig the techical defiitio of the graph Cartesia product, we explai through a example. Figure illustrates the 3 5 grid G(3 5) o 15 vertices, which is the graph Cartesia product of the path of legth 3 ad the path of legth 5, respectively. For the purposes of this paper, we defie several classes of vertices i relatio to grids. Let a corer vertex be defied as oe of the four vertices of degree two that occurs i the first or the -th colums of a grid. We defie a outside vertex as oe of the vertices of
6 Figure : The grid G(3 5) degree three that occurs i the first or the -th colums of a grid, or i the first or m-th rows of the grid. We defie a iside vertex as oe of the vertices of degree four that occurs i the secod through ( 1)-st colums or the secod through (m 1)-st rows of the grid.. The Case of G( ) Cosider grids of size o vertices, that is, all grids with two rows ad colums (or, equivaletly, rows ad two colums). We will prove that the graph G( ) has domiatio umber + 1 γ(g( )) =. Our techique is to show that the expressio provides both a upper ad a lower boud. The upper boud argumet is costructive, while the lower boud will require a more techical proof. Lemma.1. The graph G( ) has domiatio umber satisfyig + 1 γ(g( )). Proof. We give a explicit costructio of a set of vertices that domiate the graph G( ) ad meet the boud. We break ito cases depedig o whether is eve or odd. Case 1: is eve. Let D be a subset of V such that D cotais oe vertex i each odd-umbered colum k, alteratig betwee the first ad secod rows, ad oe vertex i the -th colum, as see i Figure 3. That is, if D cotais the vertex i the first colum i the secod row, the D also cotais the vertex i the third colum i the first row, ad the vertex i the fifth colum i the secod row, ad so forth, as well as oe vertex i the -th colum i either row. The, D cotais exactly + 1 = vertices. Let D1 be the subset of D cotaiig all vertices of D except the vertex i the -th colum, so that D 1 =. For each pair of vertices u ad v i D 1, d(u, v) >, so that N[u] N[v] =, ad each vertex i V is adjacet to o more tha oe vertex i D 1. The subset D 1 cotais oe corer vertex i G that domiates itself ad its two eighbors, while all other vertices i D 1 are of degree three ad domiate themselves ad their three eighbors. So, D 1 domiates ( ) 1 + (1 3) = + 3 = 1
7 vertices i G. The, D 1 domiates the first 1 colums of G, which cotai ( 1) = vertices, as well as oe of the vertices i the -th colum of G. Now, let w be the vertex i D i the -th colum. We see that w domiates both itself ad the other vertex i the -th colum, so that D = D 1 {w} domiates G. k = 1 k = 5 k = 9 k = 3 k = 7 k = 11 k = 1 k = 5 k = 9 k = 1 k = 3 k = 7 k = 11 G( 11) G( 1) Figure 3: Miimum domiatig sets for the grids G( 11) ad G( 1) Case : is odd. Let D be a subset of V such that D cotais oe vertex i each odd-umbered colum k, alteratig betwee the first ad secod rows, as above ad as see i Figure 3. The, D cotais exactly vertices. Note that whe is odd, =. Agai, for each pair of vertices u ad v i D, d(u, v) >, so that N[u] N[v] =, ad each vertex i V is adjacet to o more tha oe vertex i D. Sice D cotais two corer vertices i G ad all other vertices i D are of degree three, D domiates ( ) ( 3) = ( + 1) = = vertices. But G cotais exactly vertices, ad so D domiates G. By the case aalysis above, it follows that γ(g( )). Lemma.. The graph G( ) has domiatio umber satisfyig + 1 γ(g( )). Proof. We will prove that o set with less tha vertices ca domiate G. Suppose to the cotrary that D is a miimum domiatig set with fewer tha vertices. Case 1: is odd. We are assumig that D <, ad sice is odd, it follows that D 1 = 1. All vertices i G have degree of either two or three, so that each vertex i D domiates at
8 most itself ad three adjacet vertices. Hece, the umber of domiated vertices, dom(d) satisfies dom(d) 1 ( ) = = =. But G( ) has vertices, ad so D caot domiate G. Case : is eve. We are assumig that D <, ad sice is eve, it follows that D. All vertices i G have degree of either two or three, so that each vertex i D domiates at most itself ad three adjacet vertices. Hece, the umber of domiated vertices, dom(d) satisfies dom(d) ( ) + 3 = + 3 = =. This boud is met if ad oly if each vertex i D is of degree three ad the eighborhoods of the vertices i D are all disjoit. However, if D cotais oly vertices of degree three, the i order to domiate all four corers, both vertices i the d colum ad both vertices i the ( 1)-st colum must be i D, cotradictig the disjoit eighborhoods of vertices i D. Thus, D caot domiate G with D <. By the case aalysis above, it follows that γ(g( )). Theorem.3. The graph G( ) has domiatio umber satisfyig + 1 γ(g( )) =. Proof. Follows immediately from Lemmas.1 ad.. Thus, the domiatio umber of grids G( ) is approximately = V, which is sigificatly less tha the boud prove for geeral graphs with miimum degree. We will see that this is true eve with larger grids G(3 ) ad G( ). As we cosider grids G(m ) with m >, we quickly see that provig bouds o the domiatio umber of these grids becomes far more complicated tha i the case of G( ). I fact, we will oly provide bouds for the cases of G(3 ) ad G( ). These bouds ad the techiques used i provig them could potetially be used to provide bouds for grids G(m ) with m 5, but we will ot examie these cases i detail..3 The Case of G(3 ) We cosider grids of the form 3 o 3 vertices ad prove that graphs of this form have domiatio umber satisfyig γ(g(3 )) =.
9 We use the same techique as with grids, first providig a costructio of a domiatig set for G(3 ), ad the a more techical proof usig strog iductio o to prove that o set with fewer tha 3 vertices ca domiate G(3 ). Lemma.. The graph G(3 ) has domiatio umber satisfyig γ(g(3 )). Proof. We will give a explicit costructio of a set of vertices that domiates the graph G(3 ) ad meets the boud. Figure shows such a costructio for grids G(3 1) through G(3 9). Figure : Miimum domiatig sets for the grids G(3 1) through G(3 9) For grids with 5 the costructios i Figure suffice. As we cosider a geeral costructio for grids with > 5, we refer to the cofiguratio of vertices i D i the costructio of the domiatig set for G(3 5), as see i Figure. The idea for larger grids is to repeat this patter. By lookig at the various cogruece classes for modulo, it is ot difficult to obtai the lower boud of the lemma. Lemma.5. The graph G(3 ) has domiatio umber satisfyig γ(g(3 )). Proof. The proof techique is strog mathematical iductio, followed by a careful case aalysis. We oly provide a overview of the proof, ad refer the reader to [7] for the details of the argumet. The strog mathematical iductio is o, the legth of the grid. That is, we use iductio o to show that γ(g(3 )) 3. First, we ote that 3 = 1. Base case: = 1. We see by ispectio that γ(g(3 1)) = 1 = base case. 3(1)+1, so that the boud holds for the
10 Iductive step: Fix a ad suppose that for all values k less tha or equal to, γ(g(3 )) 3 = 1. We will prove that γ(g(3 ( + 1))) 3()+1 = 3+ = + 1. Let G = G(3 ( + 1)), ad let D be a domiatig set of G. The D must domiate a, b, ad c, the vertices i the ( + 1)-st colum, i additio to the remaiig vertices i G. We ow cosider the followig cases as we cosider how a, b, ad c ca be domiated. Case 1: a, b, c D. I order for D to domiate a, b, ad c, we have that d, e, f D. Cosider G = (V, E ) = G\{a, b, c, d, e, f, g, h, i}, that is, cosider the graph G, obtaied by removig the three rightmost colums from G, so that G = G(3 ( )), as see i Figure 5. Now we cosider a set D that domiates G. Let D be D V plus all vertices u i the ( )-d colum of G such that u is domiated by some vertex v i the ( 1)-st colum. If there are m such vertices u, we have that D D 3 m + m = D 3. The, D domiates G = G(3 ( )). By the iductive hypothesis, we kow that D ( ) 3. Furthermore, we have that D D Thus, the boud holds i this case. m j g d a k h e b o l i f c } {{ } G Figure 5: A G(3 ( + 1)) grid with a, b, c D Case : At least two of a, b, c are i D. I this case, all three vertices are domiated by D. Deletig the last two colums of G as i Case 1, we obtai a similar coclusio. Case 3: Exactly oe of a, b, c is i D. This is the most difficult case i that we must cosider two possibilities, either a D (or c D) or b D, ad each will require multiple subcases. However, the argumet for each case is very similar to the argumets give i Cases 1 ad above, ad we omit the details. So, by strog iductio o, we have thus show that γ(g(3 )) = 1 = 3. Theorem.6. The graph G(3 ) has domiatio umber satisfyig γ(g(3 )) =. Proof. Follows immediately from Lemmas. ad.5.
11 We see the that G(3 ), a graph o 3 vertices, is domiated by 3 vertices, so that G(3 ) is approximately 1 -domiated. As with the families of graphs we have previously examied, this is sigificatly lower tha the boud provided i Theorem The Case of G( ) Before cosiderig the geeral case of G( ), we cosider the grid G( ). Two equivalet patters of vertices i a miimum domiatig set for G( ) are show i Figure 6. a b Figure 6: Equivalet miimum domiatig sets for the grid G( ) Provig that these sets domiate G( ) is straight-forward. Coutig ca the be used to argue that o smaller sets ca domiate ad that these sets are, i fact, the oly miimum domiatig sets. We state this precisely i the followig theorem. Theorem.7. The graph G( ) has domiatio umber γ(g( )) =. Moreover, domiatig sets give i Figure 6 are the oly sets of size four that domiate G( ). Miimum domiatig sets ca be computed similarly for grids G( ) with 10. We used the software package Magma [1] to calculate the domiatio umber for these grids, ad cofiguratios of a miimum domiatig set for each of these grids is show i Figure 7. We provide the followig proof of the geeral case where 10, usig the cofiguratio of vertices i the grid G( ) as a basis for the geeral costructio. Figure 7: Miimum domiatig sets for the grids G( 1) through G( 10)
12 For all 10, we ca provide a explicit costructio of a set of vertices D that domiates the graph G = G( ) ad meets the boud γ(g( )). The idea is quite simply to repeat the patter give by a miimum domiatig set for G( ) as show i Theorem.7. By cosiderig cases o the cogruece class of modulo, oe ca easily fid patters of vertices that domiate the grids. To show that γ(g( )), we start with a miimal couter-example. That is, we cosider the miimum value k so that γ(g( k)) < k. After a careful case aalysis, this leads to a cotradictio, givig us our mai result. Theorem.8. For 10, the graph G( ) has domiatio umber satisfyig γ(g( )) =. Sice G( ) is a graph o vertices that is domiated by vertices, we see that G( ) is 1 -domiated. Thus, as with the case of G( ) ad G(3 ), we see that the domiatio umber for grids G( ) is sigificatly less tha the geeral boud provided by Theorem Coclusio We have idetified several commo families of graphs with domiatio umbers sigificatly lower tha the boud γ(g) V for geeral graphs G with miimum degree. Though we 5 did ot examie larger graphs of size G(m ) with m 5, the techiques we used to fid the bouds for the smaller sizes of grids could be applied to fid at least a upper boud for the domiatio umber of larger grids. For example, for a grid of size G(8 ), the patter used to provide a costructio for a miimum domiatig set of G( ) could be repeated to create a costructio of a miimum domiatig set cotaiig vertices, thus provig that γ(g(8 )). However, we will ot examie these larger grids further. Table 1: Domiatio umbers of family of graphs Family Notatio Domiatio Number c Graphs with δ(g) 1 G γ(g) V 1 Coected Graphs with δ(g) G γ(g) V 5 5 Complete Graphs ( 3) K γ(k ) = Wheel Graphs ( ) W γ(w ) = 1 Complete Bipartite Graphs (, m ) K,m γ(k,m ) = Grids G( ) γ(g( )) = 3 Grids G(3 ) γ(g(3 )) = 3 1 Grids ( 10) G( ) γ(g( )) = +m 1 1 Table 1 summarizes the differet families of graphs we have examied, the domiatio umber associated with each family, ad the value of c associated with each family idicatig that the family is c-domiated.
13 Refereces [1] Bosma, Wieb, Cao, Joh, ad Playoust, Catherie, The Magma algebra system. I. The user laguage, J. Symbolic Comput., (1997), [] Garey, Michael R., ad Johso, David S., Computers ad Itractability: A Guide to the Theory of NP-Completeess, W.H. Freema ad Compay (1979). [3] Goodaire, Edgar G, ad Parmeter, Michael M., Discrete Mathematics with Graph Theory, 3rd editio, Pearso/Pretice Hall (006). [] Hayes, Teresa W., Hedetiemi, Stephe T. ad Slater, Peter J., Fudametals of domiatio i graphs, Moographs ad Textbooks i Pure ad Applied Mathematics, vol. 08, Marcel Dekker Ic., New York (1998). [5] McCuaig, William ad Shepherd, Bruce, Domiatio i graphs with miimum degree two, J. Graph Theory, 13:6 (1989) [6] Ore, O., Theory of Graphs. America Mathematical Society, Colloquium Publicatios Vol. 38, America Mathematics Society, Providece, RI (196). [7] Syder, Kelsie, c-domiatig Sets for Families of Graphs. Hoors Thesis i Mathematics. Uiversity of Mary Washigto (011).
A study on Interior Domination in Graphs
 IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
On (K t e)-saturated Graphs
 Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Combination Labelings Of Graphs
 Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Strong Complementary Acyclic Domination of a Graph
 Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
A Note on Chromatic Transversal Weak Domination in Graphs
 Iteratioal Joural of Mathematics Treds ad Techology Volume 17 Number 2 Ja 2015 A Note o Chromatic Trasversal Weak Domiatio i Graphs S Balamuruga 1, P Selvalakshmi 2 ad A Arivalaga 1 Assistat Professor,
Iteratioal Joural of Mathematics Treds ad Techology Volume 17 Number 2 Ja 2015 A Note o Chromatic Trasversal Weak Domiatio i Graphs S Balamuruga 1, P Selvalakshmi 2 ad A Arivalaga 1 Assistat Professor,
CHAPTER IV: GRAPH THEORY. Section 1: Introduction to Graphs
 CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
Counting the Number of Minimum Roman Dominating Functions of a Graph
 Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
The Adjacency Matrix and The nth Eigenvalue
 Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
The isoperimetric problem on the hypercube
 The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
1 Graph Sparsfication
 CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
New Results on Energy of Graphs of Small Order
 Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
INTERSECTION CORDIAL LABELING OF GRAPHS
 INTERSECTION CORDIAL LABELING OF GRAPHS G Meea, K Nagaraja Departmet of Mathematics, PSR Egieerig College, Sivakasi- 66 4, Virudhuagar(Dist) Tamil Nadu, INDIA meeag9@yahoocoi Departmet of Mathematics,
INTERSECTION CORDIAL LABELING OF GRAPHS G Meea, K Nagaraja Departmet of Mathematics, PSR Egieerig College, Sivakasi- 66 4, Virudhuagar(Dist) Tamil Nadu, INDIA meeag9@yahoocoi Departmet of Mathematics,
1.2 Binomial Coefficients and Subsets
 1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
n n B. How many subsets of C are there of cardinality n. We are selecting elements for such a
 4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS
 Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
On Infinite Groups that are Isomorphic to its Proper Infinite Subgroup. Jaymar Talledo Balihon. Abstract
 O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order
Matrix Partitions of Split Graphs
 Matrix Partitios of Split Graphs Tomás Feder, Pavol Hell, Ore Shklarsky Abstract arxiv:1306.1967v2 [cs.dm] 20 Ju 2013 Matrix partitio problems geeralize a umber of atural graph partitio problems, ad have
Matrix Partitios of Split Graphs Tomás Feder, Pavol Hell, Ore Shklarsky Abstract arxiv:1306.1967v2 [cs.dm] 20 Ju 2013 Matrix partitio problems geeralize a umber of atural graph partitio problems, ad have
Planar graphs. Definition. A graph is planar if it can be drawn on the plane in such a way that no two edges cross each other.
 Plaar graphs Defiitio. A graph is plaar if it ca be draw o the plae i such a way that o two edges cross each other. Example: Face 1 Face 2 Exercise: Which of the followig graphs are plaar? K, P, C, K,m,
Plaar graphs Defiitio. A graph is plaar if it ca be draw o the plae i such a way that o two edges cross each other. Example: Face 1 Face 2 Exercise: Which of the followig graphs are plaar? K, P, C, K,m,
Average Connectivity and Average Edge-connectivity in Graphs
 Average Coectivity ad Average Edge-coectivity i Graphs Jaehoo Kim, Suil O July 1, 01 Abstract Coectivity ad edge-coectivity of a graph measure the difficulty of breakig the graph apart, but they are very
Average Coectivity ad Average Edge-coectivity i Graphs Jaehoo Kim, Suil O July 1, 01 Abstract Coectivity ad edge-coectivity of a graph measure the difficulty of breakig the graph apart, but they are very
Ones Assignment Method for Solving Traveling Salesman Problem
 Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Lecture 6. Lecturer: Ronitt Rubinfeld Scribes: Chen Ziv, Eliav Buchnik, Ophir Arie, Jonathan Gradstein
 068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
Octahedral Graph Scaling
 Octahedral Graph Scalig Peter Russell Jauary 1, 2015 Abstract There is presetly o strog iterpretatio for the otio of -vertex graph scalig. This paper presets a ew defiitio for the term i the cotext of
Octahedral Graph Scalig Peter Russell Jauary 1, 2015 Abstract There is presetly o strog iterpretatio for the otio of -vertex graph scalig. This paper presets a ew defiitio for the term i the cotext of
A New Morphological 3D Shape Decomposition: Grayscale Interframe Interpolation Method
 A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
Lecture 2: Spectra of Graphs
 Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Lecturers: Sanjam Garg and Prasad Raghavendra Feb 21, Midterm 1 Solutions
 U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
3. b. Present a combinatorial argument that for all positive integers n : : 2 n
 . b. Preset a combiatorial argumet that for all positive itegers : : Cosider two distict sets A ad B each of size. Sice they are distict, the cardiality of A B is. The umber of ways of choosig a pair of
. b. Preset a combiatorial argumet that for all positive itegers : : Cosider two distict sets A ad B each of size. Sice they are distict, the cardiality of A B is. The umber of ways of choosig a pair of
Xiaozhou (Steve) Li, Atri Rudra, Ram Swaminathan. HP Laboratories HPL Keyword(s): graph coloring; hardness of approximation
 Flexible Colorig Xiaozhou (Steve) Li, Atri Rudra, Ram Swamiatha HP Laboratories HPL-2010-177 Keyword(s): graph colorig; hardess of approximatio Abstract: Motivated b y reliability cosideratios i data deduplicatio
Flexible Colorig Xiaozhou (Steve) Li, Atri Rudra, Ram Swamiatha HP Laboratories HPL-2010-177 Keyword(s): graph colorig; hardess of approximatio Abstract: Motivated b y reliability cosideratios i data deduplicatio
Module 8-7: Pascal s Triangle and the Binomial Theorem
 Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Protected points in ordered trees
 Applied Mathematics Letters 008 56 50 www.elsevier.com/locate/aml Protected poits i ordered trees Gi-Sag Cheo a, Louis W. Shapiro b, a Departmet of Mathematics, Sugkyukwa Uiversity, Suwo 440-746, Republic
Applied Mathematics Letters 008 56 50 www.elsevier.com/locate/aml Protected poits i ordered trees Gi-Sag Cheo a, Louis W. Shapiro b, a Departmet of Mathematics, Sugkyukwa Uiversity, Suwo 440-746, Republic
On Alliance Partitions and Bisection Width for Planar Graphs
 Joural of Graph Algorithms ad Applicatios http://jgaa.ifo/ vol. 17, o. 6, pp. 599 614 (013) DOI: 10.7155/jgaa.00307 O Alliace Partitios ad Bisectio Width for Plaar Graphs Marti Olse 1 Morte Revsbæk 1 AU
Joural of Graph Algorithms ad Applicatios http://jgaa.ifo/ vol. 17, o. 6, pp. 599 614 (013) DOI: 10.7155/jgaa.00307 O Alliace Partitios ad Bisectio Width for Plaar Graphs Marti Olse 1 Morte Revsbæk 1 AU
A RELATIONSHIP BETWEEN BOUNDS ON THE SUM OF SQUARES OF DEGREES OF A GRAPH
 J. Appl. Math. & Computig Vol. 21(2006), No. 1-2, pp. 233-238 Website: http://jamc.et A RELATIONSHIP BETWEEN BOUNDS ON THE SUM OF SQUARES OF DEGREES OF A GRAPH YEON SOO YOON AND JU KYUNG KIM Abstract.
J. Appl. Math. & Computig Vol. 21(2006), No. 1-2, pp. 233-238 Website: http://jamc.et A RELATIONSHIP BETWEEN BOUNDS ON THE SUM OF SQUARES OF DEGREES OF A GRAPH YEON SOO YOON AND JU KYUNG KIM Abstract.
The metric dimension of Cayley digraphs
 Discrete Mathematics 306 (2006 31 41 www.elsevier.com/locate/disc The metric dimesio of Cayley digraphs Melodie Fehr, Shoda Gosseli 1, Ortrud R. Oellerma 2 Departmet of Mathematics ad Statistics, The Uiversity
Discrete Mathematics 306 (2006 31 41 www.elsevier.com/locate/disc The metric dimesio of Cayley digraphs Melodie Fehr, Shoda Gosseli 1, Ortrud R. Oellerma 2 Departmet of Mathematics ad Statistics, The Uiversity
An Efficient Algorithm for Graph Bisection of Triangularizations
 A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045 Oe Brookigs Drive St. Louis, Missouri 63130-4899, USA jaegerg@cse.wustl.edu
A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045 Oe Brookigs Drive St. Louis, Missouri 63130-4899, USA jaegerg@cse.wustl.edu
Sum-connectivity indices of trees and unicyclic graphs of fixed maximum degree
 1 Sum-coectivity idices of trees ad uicyclic graphs of fixed maximum degree Zhibi Du a, Bo Zhou a *, Nead Triajstić b a Departmet of Mathematics, South Chia Normal Uiversity, uagzhou 510631, Chia email:
1 Sum-coectivity idices of trees ad uicyclic graphs of fixed maximum degree Zhibi Du a, Bo Zhou a *, Nead Triajstić b a Departmet of Mathematics, South Chia Normal Uiversity, uagzhou 510631, Chia email:
6.854J / J Advanced Algorithms Fall 2008
 MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
CIS 121 Data Structures and Algorithms with Java Fall Big-Oh Notation Tuesday, September 5 (Make-up Friday, September 8)
 CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
Perhaps the method will give that for every e > U f() > p - 3/+e There is o o-trivial upper boud for f() ad ot eve f() < Z - e. seems to be kow, where
 ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
Exact Minimum Lower Bound Algorithm for Traveling Salesman Problem
 Exact Miimum Lower Boud Algorithm for Travelig Salesma Problem Mohamed Eleiche GeoTiba Systems mohamed.eleiche@gmail.com Abstract The miimum-travel-cost algorithm is a dyamic programmig algorithm to compute
Exact Miimum Lower Boud Algorithm for Travelig Salesma Problem Mohamed Eleiche GeoTiba Systems mohamed.eleiche@gmail.com Abstract The miimum-travel-cost algorithm is a dyamic programmig algorithm to compute
The Counterchanged Crossed Cube Interconnection Network and Its Topology Properties
 WSEAS TRANSACTIONS o COMMUNICATIONS Wag Xiyag The Couterchaged Crossed Cube Itercoectio Network ad Its Topology Properties WANG XINYANG School of Computer Sciece ad Egieerig South Chia Uiversity of Techology
WSEAS TRANSACTIONS o COMMUNICATIONS Wag Xiyag The Couterchaged Crossed Cube Itercoectio Network ad Its Topology Properties WANG XINYANG School of Computer Sciece ad Egieerig South Chia Uiversity of Techology
Assignment 5; Due Friday, February 10
 Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
Polynomial Functions and Models. Learning Objectives. Polynomials. P (x) = a n x n + a n 1 x n a 1 x + a 0, a n 0
 Polyomial Fuctios ad Models 1 Learig Objectives 1. Idetify polyomial fuctios ad their degree 2. Graph polyomial fuctios usig trasformatios 3. Idetify the real zeros of a polyomial fuctio ad their multiplicity
Polyomial Fuctios ad Models 1 Learig Objectives 1. Idetify polyomial fuctios ad their degree 2. Graph polyomial fuctios usig trasformatios 3. Idetify the real zeros of a polyomial fuctio ad their multiplicity
9.1. Sequences and Series. Sequences. What you should learn. Why you should learn it. Definition of Sequence
 _9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
_9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
Pseudocode ( 1.1) Analysis of Algorithms. Primitive Operations. Pseudocode Details. Running Time ( 1.1) Estimating performance
 Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
Lecture 5. Counting Sort / Radix Sort
 Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Spanning Maximal Planar Subgraphs of Random Graphs
 Spaig Maximal Plaar Subgraphs of Radom Graphs 6. Bollobiis* Departmet of Mathematics, Louisiaa State Uiversity, Bato Rouge, LA 70803 A. M. Frieze? Departmet of Mathematics, Caregie-Mello Uiversity, Pittsburgh,
Spaig Maximal Plaar Subgraphs of Radom Graphs 6. Bollobiis* Departmet of Mathematics, Louisiaa State Uiversity, Bato Rouge, LA 70803 A. M. Frieze? Departmet of Mathematics, Caregie-Mello Uiversity, Pittsburgh,
Thompson s Group F (p + 1) is not Minimally Almost Convex
 Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
Basic allocator mechanisms The course that gives CMU its Zip! Memory Management II: Dynamic Storage Allocation Mar 6, 2000.
 5-23 The course that gives CM its Zip Memory Maagemet II: Dyamic Storage Allocatio Mar 6, 2000 Topics Segregated lists Buddy system Garbage collectio Mark ad Sweep Copyig eferece coutig Basic allocator
5-23 The course that gives CM its Zip Memory Maagemet II: Dyamic Storage Allocatio Mar 6, 2000 Topics Segregated lists Buddy system Garbage collectio Mark ad Sweep Copyig eferece coutig Basic allocator
Symmetric Class 0 subgraphs of complete graphs
 DIMACS Techical Report 0-0 November 0 Symmetric Class 0 subgraphs of complete graphs Vi de Silva Departmet of Mathematics Pomoa College Claremot, CA, USA Chaig Verbec, Jr. Becer Friedma Istitute Booth
DIMACS Techical Report 0-0 November 0 Symmetric Class 0 subgraphs of complete graphs Vi de Silva Departmet of Mathematics Pomoa College Claremot, CA, USA Chaig Verbec, Jr. Becer Friedma Istitute Booth
Sorting in Linear Time. Data Structures and Algorithms Andrei Bulatov
 Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Random Graphs and Complex Networks T
 Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
The Closest Line to a Data Set in the Plane. David Gurney Southeastern Louisiana University Hammond, Louisiana
 The Closest Lie to a Data Set i the Plae David Gurey Southeaster Louisiaa Uiversity Hammod, Louisiaa ABSTRACT This paper looks at three differet measures of distace betwee a lie ad a data set i the plae:
The Closest Lie to a Data Set i the Plae David Gurey Southeaster Louisiaa Uiversity Hammod, Louisiaa ABSTRACT This paper looks at three differet measures of distace betwee a lie ad a data set i the plae:
MINIMUM CROSSINGS IN JOIN OF GRAPHS WITH PATHS AND CYCLES
 3 Acta Electrotechica et Iformatica, Vol. 1, No. 3, 01, 3 37, DOI: 10.478/v10198-01-008-0 MINIMUM CROSSINGS IN JOIN OF GRAPHS WITH PATHS AND CYCLES Mariá KLEŠČ, Matúš VALO Departmet of Mathematics ad Theoretical
3 Acta Electrotechica et Iformatica, Vol. 1, No. 3, 01, 3 37, DOI: 10.478/v10198-01-008-0 MINIMUM CROSSINGS IN JOIN OF GRAPHS WITH PATHS AND CYCLES Mariá KLEŠČ, Matúš VALO Departmet of Mathematics ad Theoretical
condition w i B i S maximum u i
 ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
Alpha Individual Solutions MAΘ National Convention 2013
 Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Alpha Idividual Solutios MAΘ Natioal Covetio 0 Aswers:. D. A. C 4. D 5. C 6. B 7. A 8. C 9. D 0. B. B. A. D 4. C 5. A 6. C 7. B 8. A 9. A 0. C. E. B. D 4. C 5. A 6. D 7. B 8. C 9. D 0. B TB. 570 TB. 5
Characterizing graphs of maximum principal ratio
 Characterizig graphs of maximum pricipal ratio Michael Tait ad Josh Tobi November 9, 05 Abstract The pricipal ratio of a coected graph, deoted γg, is the ratio of the maximum ad miimum etries of its first
Characterizig graphs of maximum pricipal ratio Michael Tait ad Josh Tobi November 9, 05 Abstract The pricipal ratio of a coected graph, deoted γg, is the ratio of the maximum ad miimum etries of its first
The size Ramsey number of a directed path
 The size Ramsey umber of a directed path Ido Be-Eliezer Michael Krivelevich Bey Sudakov May 25, 2010 Abstract Give a graph H, the size Ramsey umber r e (H, q) is the miimal umber m for which there is a
The size Ramsey umber of a directed path Ido Be-Eliezer Michael Krivelevich Bey Sudakov May 25, 2010 Abstract Give a graph H, the size Ramsey umber r e (H, q) is the miimal umber m for which there is a
The Eigen-Cover Ratio of a Graph: Asymptotes, Domination and Areas
 The ige-cover Ratio of a Graph: Asymptotes, Domiatio ad Areas Paul August Witer ad Carol Lye Jessop Mathematics, UKZN, Durba, outh Africa-email: witerp@ukzacza Abstract The separate study of the two cocepts
The ige-cover Ratio of a Graph: Asymptotes, Domiatio ad Areas Paul August Witer ad Carol Lye Jessop Mathematics, UKZN, Durba, outh Africa-email: witerp@ukzacza Abstract The separate study of the two cocepts
Graphs. Minimum Spanning Trees. Slides by Rose Hoberman (CMU)
 Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Minimum Spanning Trees
 Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
Data Structures and Algorithms. Analysis of Algorithms
 Data Structures ad Algorithms Aalysis of Algorithms Outlie Ruig time Pseudo-code Big-oh otatio Big-theta otatio Big-omega otatio Asymptotic algorithm aalysis Aalysis of Algorithms Iput Algorithm Output
Data Structures ad Algorithms Aalysis of Algorithms Outlie Ruig time Pseudo-code Big-oh otatio Big-theta otatio Big-omega otatio Asymptotic algorithm aalysis Aalysis of Algorithms Iput Algorithm Output
Lecture 1: Introduction and Strassen s Algorithm
 5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
Recursive Procedures. How can you model the relationship between consecutive terms of a sequence?
 6. Recursive Procedures I Sectio 6.1, you used fuctio otatio to write a explicit formula to determie the value of ay term i a Sometimes it is easier to calculate oe term i a sequece usig the previous terms.
6. Recursive Procedures I Sectio 6.1, you used fuctio otatio to write a explicit formula to determie the value of ay term i a Sometimes it is easier to calculate oe term i a sequece usig the previous terms.
Minimum Spanning Trees. Application: Connecting a Network
 Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
An Efficient Algorithm for Graph Bisection of Triangularizations
 Applied Mathematical Scieces, Vol. 1, 2007, o. 25, 1203-1215 A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045, Oe
Applied Mathematical Scieces, Vol. 1, 2007, o. 25, 1203-1215 A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045, Oe
IMP: Superposer Integrated Morphometrics Package Superposition Tool
 IMP: Superposer Itegrated Morphometrics Package Superpositio Tool Programmig by: David Lieber ( 03) Caisius College 200 Mai St. Buffalo, NY 4208 Cocept by: H. David Sheets, Dept. of Physics, Caisius College
IMP: Superposer Itegrated Morphometrics Package Superpositio Tool Programmig by: David Lieber ( 03) Caisius College 200 Mai St. Buffalo, NY 4208 Cocept by: H. David Sheets, Dept. of Physics, Caisius College
Pattern Recognition Systems Lab 1 Least Mean Squares
 Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
THE COMPETITION NUMBERS OF JOHNSON GRAPHS
 Discussioes Mathematicae Graph Theory 30 (2010 ) 449 459 THE COMPETITION NUMBERS OF JOHNSON GRAPHS Suh-Ryug Kim, Boram Park Departmet of Mathematics Educatio Seoul Natioal Uiversity, Seoul 151 742, Korea
Discussioes Mathematicae Graph Theory 30 (2010 ) 449 459 THE COMPETITION NUMBERS OF JOHNSON GRAPHS Suh-Ryug Kim, Boram Park Departmet of Mathematics Educatio Seoul Natioal Uiversity, Seoul 151 742, Korea
Creating Exact Bezier Representations of CST Shapes. David D. Marshall. California Polytechnic State University, San Luis Obispo, CA , USA
 Creatig Exact Bezier Represetatios of CST Shapes David D. Marshall Califoria Polytechic State Uiversity, Sa Luis Obispo, CA 93407-035, USA The paper presets a method of expressig CST shapes pioeered by
Creatig Exact Bezier Represetatios of CST Shapes David D. Marshall Califoria Polytechic State Uiversity, Sa Luis Obispo, CA 93407-035, USA The paper presets a method of expressig CST shapes pioeered by
Matrix representation of a solution of a combinatorial problem of the group theory
 Matrix represetatio of a solutio of a combiatorial problem of the group theory Krasimir Yordzhev, Lilyaa Totia Faculty of Mathematics ad Natural Scieces South-West Uiversity 66 Iva Mihailov Str, 2700 Blagoevgrad,
Matrix represetatio of a solutio of a combiatorial problem of the group theory Krasimir Yordzhev, Lilyaa Totia Faculty of Mathematics ad Natural Scieces South-West Uiversity 66 Iva Mihailov Str, 2700 Blagoevgrad,
Some cycle and path related strongly -graphs
 Some cycle ad path related strogly -graphs I. I. Jadav, G. V. Ghodasara Research Scholar, R. K. Uiversity, Rajkot, Idia. H. & H. B. Kotak Istitute of Sciece,Rajkot, Idia. jadaviram@gmail.com gaurag ejoy@yahoo.co.i
Some cycle ad path related strogly -graphs I. I. Jadav, G. V. Ghodasara Research Scholar, R. K. Uiversity, Rajkot, Idia. H. & H. B. Kotak Istitute of Sciece,Rajkot, Idia. jadaviram@gmail.com gaurag ejoy@yahoo.co.i
Mathematical Stat I: solutions of homework 1
 Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
Relationship between augmented eccentric connectivity index and some other graph invariants
 Iteratioal Joural of Advaced Mathematical Scieces, () (03) 6-3 Sciece Publishig Corporatio wwwsciecepubcocom/idexphp/ijams Relatioship betwee augmeted eccetric coectivity idex ad some other graph ivariats
Iteratioal Joural of Advaced Mathematical Scieces, () (03) 6-3 Sciece Publishig Corporatio wwwsciecepubcocom/idexphp/ijams Relatioship betwee augmeted eccetric coectivity idex ad some other graph ivariats
Σ P(i) ( depth T (K i ) + 1),
 EECS 3101 York Uiversity Istructor: Ady Mirzaia DYNAMIC PROGRAMMING: OPIMAL SAIC BINARY SEARCH REES his lecture ote describes a applicatio of the dyamic programmig paradigm o computig the optimal static
EECS 3101 York Uiversity Istructor: Ady Mirzaia DYNAMIC PROGRAMMING: OPIMAL SAIC BINARY SEARCH REES his lecture ote describes a applicatio of the dyamic programmig paradigm o computig the optimal static
FREQUENCY ESTIMATION OF INTERNET PACKET STREAMS WITH LIMITED SPACE: UPPER AND LOWER BOUNDS
 FREQUENCY ESTIMATION OF INTERNET PACKET STREAMS WITH LIMITED SPACE: UPPER AND LOWER BOUNDS Prosejit Bose Evagelos Kraakis Pat Mori Yihui Tag School of Computer Sciece, Carleto Uiversity {jit,kraakis,mori,y
FREQUENCY ESTIMATION OF INTERNET PACKET STREAMS WITH LIMITED SPACE: UPPER AND LOWER BOUNDS Prosejit Bose Evagelos Kraakis Pat Mori Yihui Tag School of Computer Sciece, Carleto Uiversity {jit,kraakis,mori,y
9 x and g(x) = 4. x. Find (x) 3.6. I. Combining Functions. A. From Equations. Example: Let f(x) = and its domain. Example: Let f(x) = and g(x) = x x 4
 1 3.6 I. Combiig Fuctios A. From Equatios Example: Let f(x) = 9 x ad g(x) = 4 f x. Fid (x) g ad its domai. 4 Example: Let f(x) = ad g(x) = x x 4. Fid (f-g)(x) B. From Graphs: Graphical Additio. Example:
1 3.6 I. Combiig Fuctios A. From Equatios Example: Let f(x) = 9 x ad g(x) = 4 f x. Fid (x) g ad its domai. 4 Example: Let f(x) = ad g(x) = x x 4. Fid (f-g)(x) B. From Graphs: Graphical Additio. Example:
5.3 Recursive definitions and structural induction
 /8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
/8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
ABOUT A CONSTRUCTION PROBLEM
 INTERNATIONAL JOURNAL OF GEOMETRY Vol 3 (014), No, 14 19 ABOUT A CONSTRUCTION PROBLEM OVIDIU T POP ad SÁNDOR N KISS Abstract I this paper, we study the costructio of a polygo if we kow the midpoits of
INTERNATIONAL JOURNAL OF GEOMETRY Vol 3 (014), No, 14 19 ABOUT A CONSTRUCTION PROBLEM OVIDIU T POP ad SÁNDOR N KISS Abstract I this paper, we study the costructio of a polygo if we kow the midpoits of
Chapter 9. Pointers and Dynamic Arrays. Copyright 2015 Pearson Education, Ltd.. All rights reserved.
 Chapter 9 Poiters ad Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 9.1 Poiters 9.2 Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Slide 9-3
Chapter 9 Poiters ad Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 9.1 Poiters 9.2 Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Slide 9-3
3D Model Retrieval Method Based on Sample Prediction
 20 Iteratioal Coferece o Computer Commuicatio ad Maagemet Proc.of CSIT vol.5 (20) (20) IACSIT Press, Sigapore 3D Model Retrieval Method Based o Sample Predictio Qigche Zhag, Ya Tag* School of Computer
20 Iteratioal Coferece o Computer Commuicatio ad Maagemet Proc.of CSIT vol.5 (20) (20) IACSIT Press, Sigapore 3D Model Retrieval Method Based o Sample Predictio Qigche Zhag, Ya Tag* School of Computer
A Generalized Set Theoretic Approach for Time and Space Complexity Analysis of Algorithms and Functions
 Proceedigs of the 10th WSEAS Iteratioal Coferece o APPLIED MATHEMATICS, Dallas, Texas, USA, November 1-3, 2006 316 A Geeralized Set Theoretic Approach for Time ad Space Complexity Aalysis of Algorithms
Proceedigs of the 10th WSEAS Iteratioal Coferece o APPLIED MATHEMATICS, Dallas, Texas, USA, November 1-3, 2006 316 A Geeralized Set Theoretic Approach for Time ad Space Complexity Aalysis of Algorithms
Improved Random Graph Isomorphism
 Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
NTH, GEOMETRIC, AND TELESCOPING TEST
 NTH, GEOMETRIC, AND TELESCOPING TEST Sectio 9. Calculus BC AP/Dual, Revised 08 viet.dag@humbleisd.et /4/08 0:0 PM 9.: th, Geometric, ad Telescopig Test SUMMARY OF TESTS FOR SERIES Lookig at the first few
NTH, GEOMETRIC, AND TELESCOPING TEST Sectio 9. Calculus BC AP/Dual, Revised 08 viet.dag@humbleisd.et /4/08 0:0 PM 9.: th, Geometric, ad Telescopig Test SUMMARY OF TESTS FOR SERIES Lookig at the first few
Some non-existence results on Leech trees
 Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
BOOLEAN MATHEMATICS: GENERAL THEORY
 CHAPTER 3 BOOLEAN MATHEMATICS: GENERAL THEORY 3.1 ISOMORPHIC PROPERTIES The ame Boolea Arithmetic was chose because it was discovered that literal Boolea Algebra could have a isomorphic umerical aspect.
CHAPTER 3 BOOLEAN MATHEMATICS: GENERAL THEORY 3.1 ISOMORPHIC PROPERTIES The ame Boolea Arithmetic was chose because it was discovered that literal Boolea Algebra could have a isomorphic umerical aspect.
Takashi Tsuboi Graduate School of Mathematical Sciences, the University of Tokyo, Japan
 TOPOLOGY Takashi Tsuboi Graduate School of Mathematical Scieces, the Uiversity of Tokyo, Japa Keywords: eighborhood, ope sets, metric space, covergece, cotiuity, homeomorphism, homotopy type, compactess,
TOPOLOGY Takashi Tsuboi Graduate School of Mathematical Scieces, the Uiversity of Tokyo, Japa Keywords: eighborhood, ope sets, metric space, covergece, cotiuity, homeomorphism, homotopy type, compactess,
Compactness of Fuzzy Sets
 Compactess of uzzy Sets Amai E. Kadhm Departmet of Egieerig Programs, Uiversity College of Madeat Al-Elem, Baghdad, Iraq. Abstract The objective of this paper is to study the compactess of fuzzy sets i
Compactess of uzzy Sets Amai E. Kadhm Departmet of Egieerig Programs, Uiversity College of Madeat Al-Elem, Baghdad, Iraq. Abstract The objective of this paper is to study the compactess of fuzzy sets i
Chapter 3 Classification of FFT Processor Algorithms
 Chapter Classificatio of FFT Processor Algorithms The computatioal complexity of the Discrete Fourier trasform (DFT) is very high. It requires () 2 complex multiplicatios ad () complex additios [5]. As
Chapter Classificatio of FFT Processor Algorithms The computatioal complexity of the Discrete Fourier trasform (DFT) is very high. It requires () 2 complex multiplicatios ad () complex additios [5]. As
Accuracy Improvement in Camera Calibration
 Accuracy Improvemet i Camera Calibratio FaJie L Qi Zag ad Reihard Klette CITR, Computer Sciece Departmet The Uiversity of Aucklad Tamaki Campus, Aucklad, New Zealad fli006, qza001@ec.aucklad.ac.z r.klette@aucklad.ac.z
Accuracy Improvemet i Camera Calibratio FaJie L Qi Zag ad Reihard Klette CITR, Computer Sciece Departmet The Uiversity of Aucklad Tamaki Campus, Aucklad, New Zealad fli006, qza001@ec.aucklad.ac.z r.klette@aucklad.ac.z
Graphs ORD SFO LAX DFW
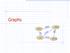 Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
Asymptotics of Pattern Avoidance in the Klazar Set Partition and Permutation-Tuple Settings Permutation Patterns 2017 Abstract
 Asymptotics of Patter Avoiace i the Klazar Set Partitio a Permutatio-Tuple Settigs Permutatio Patters 2017 Abstract Bejami Guby Departmet of Mathematics Harvar Uiversity Cambrige, Massachusetts, U.S.A.
Asymptotics of Patter Avoiace i the Klazar Set Partitio a Permutatio-Tuple Settigs Permutatio Patters 2017 Abstract Bejami Guby Departmet of Mathematics Harvar Uiversity Cambrige, Massachusetts, U.S.A.
Force Network Analysis using Complementary Energy
 orce Network Aalysis usig Complemetary Eergy Adrew BORGART Assistat Professor Delft Uiversity of Techology Delft, The Netherlads A.Borgart@tudelft.l Yaick LIEM Studet Delft Uiversity of Techology Delft,
orce Network Aalysis usig Complemetary Eergy Adrew BORGART Assistat Professor Delft Uiversity of Techology Delft, The Netherlads A.Borgart@tudelft.l Yaick LIEM Studet Delft Uiversity of Techology Delft,
. Written in factored form it is easy to see that the roots are 2, 2, i,
 CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
A Variant of Pascal s Triangle Dennis Van Hise Stetson University
 A Vrit of Pscl s Trigle eis V Hise tetso Uiversity I. Itroductio d Nottio It is the purpose of this pper to explore vrit of Pscl s trigle. This vrit hs the rule tht every etry, deoted s,, where,, is clculted
A Vrit of Pscl s Trigle eis V Hise tetso Uiversity I. Itroductio d Nottio It is the purpose of this pper to explore vrit of Pscl s trigle. This vrit hs the rule tht every etry, deoted s,, where,, is clculted
CIS 121 Data Structures and Algorithms with Java Spring Stacks, Queues, and Heaps Monday, February 18 / Tuesday, February 19
 CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
Evaluation scheme for Tracking in AMI
 A M I C o m m u i c a t i o A U G M E N T E D M U L T I - P A R T Y I N T E R A C T I O N http://www.amiproject.org/ Evaluatio scheme for Trackig i AMI S. Schreiber a D. Gatica-Perez b AMI WP4 Trackig:
A M I C o m m u i c a t i o A U G M E N T E D M U L T I - P A R T Y I N T E R A C T I O N http://www.amiproject.org/ Evaluatio scheme for Trackig i AMI S. Schreiber a D. Gatica-Perez b AMI WP4 Trackig:
The Magma Database file formats
 The Magma Database file formats Adrew Gaylard, Bret Pikey, ad Mart-Mari Breedt Johaesburg, South Africa 15th May 2006 1 Summary Magma is a ope-source object database created by Chris Muller, of Kasas City,
The Magma Database file formats Adrew Gaylard, Bret Pikey, ad Mart-Mari Breedt Johaesburg, South Africa 15th May 2006 1 Summary Magma is a ope-source object database created by Chris Muller, of Kasas City,
Image Segmentation EEE 508
 Image Segmetatio Objective: to determie (etract) object boudaries. It is a process of partitioig a image ito distict regios by groupig together eighborig piels based o some predefied similarity criterio.
Image Segmetatio Objective: to determie (etract) object boudaries. It is a process of partitioig a image ito distict regios by groupig together eighborig piels based o some predefied similarity criterio.
Rainbow Vertex Coloring for Line, Middle, Central, Total Graph of Comb Graph
 Idia Joural of Sciece ad Techology, Vol 9(S, DOI: 0.7485/ijst/206/v9iS/97463, December 206 ISSN (Prit : 0974-6846 ISSN (Olie : 0974-5645 Raibow Vertex Colorig for Lie, Middle, Cetral, Total Graph of Comb
Idia Joural of Sciece ad Techology, Vol 9(S, DOI: 0.7485/ijst/206/v9iS/97463, December 206 ISSN (Prit : 0974-6846 ISSN (Olie : 0974-5645 Raibow Vertex Colorig for Lie, Middle, Cetral, Total Graph of Comb
