Intro to Modeling Modeling in 3D
|
|
|
- Victoria Osborne
- 6 years ago
- Views:
Transcription
1 Intro to Modeling Modeling in 3D Polygon sets can approximate more complex shapes as discretized surfaces 2 1
2 2 3 Curve surfaces in 3D Sphere, ellipsoids, etc Curved Surfaces Modeling in 3D ) ( r z y x 4 Solid Models in 3D Sphere, ellipsoids, etc Modeling in 3D ) ( r z y x
3 Modeling in 3D Solid Models in 3D Boolean solids 5 Polygons Multi-sided planar element composed of edges and vertices. Vertices (singular vertex) are represented by points Edges connect vertices as line segments (x2,y2) E1 (x1,y1) E3 E2 (x3,y3) 6 3
4 Polygons Simple polygons - no edges cross Non-simple - some edges cross Simple Non-simple 7 Polygons Convex Polygon - a polygon that has no included angles larger than 180 degrees Concave Polygon - has at least one included angle greater than 180 degrees Convex Concave 8 4
5 Polygons Test for convexity- any line segment drawn between two points inside a polygon must remain inside the polygon if the poly is convex Convex Concave 9 Polygons A concave polygon can be broken up into two or more convex polygons OpenGL assumes all polygons are simple and convex 10 5
6 Rasterizing Polygons Assume that all polygons lie on the image plane (2D), then rasterization is to fill in pixels lying within a closed polygon and to do so efficiently To do this, algorithm needs to determine if a pixel is inside or outside a polygon How do we do this?? 11 Rasterizing Polygons Scan Line Approaches: - Inside test: Point P is inside a polygon iff a scanline intersects polygon edges an odd numberof times moving from P in either direction (inside) 12 6
7 Rasterizing Polygons Inside test special cases: - Horizontal edges can be ignored -Use Min-max test when scanline passes thru vertex Min-max: count twice if slope changes sign count once otherwise 13 Rasterizing Polygons Inside test: To fill polygons, one scanline at a time determine which pixels are inside and set "on" 14 7
8 Rasterizing Polygons Faster is to fill polygons, one scanline at a time determine which pixels intersect and sort by edge Scanline fill algorithm For each scanline: Find intersections Sort intersections Fill in pixels between pairs of intersections But, intersection calculations are expensive 15 Rasterizing Polygons Faster still, use edge coherence - Many edges that intersect scanline s intersect scanline s+1 Compute scanline intersection: y = mx + b and y s = s, then s = mx s + b or x s = (s-b)/m Compute difference in next scanline for intersection y s+1 = s+1, s+1 = mx s+1 + b or x s+1 = (s +1 - b)/m and, x s+1 = x s + 1/m <= USE THIS TO UPDATE Edge tables allow us to define in efficient, easy manner 16 8
9 Modeling in 3D 17 Defining 3D Polygons 3D Polygons live in 3D 18 9
10 Defining 3D Polygons 3D Polygons are truncated planes in 3-space E1 (x1,y1,z1) (x2,y2,z2) E2 E3 (x3,y3,z3) Express given the vertex and edge coordinates Start with the generic form of a plane Ax + By + Cz + D = 0 19 Defining 3D Polygons Vertices and edges are ordered, CW or CCW, usually counter clockwise Therefore, edges are directed line segments and may be treated as vectors (x2,y2,z2) E2 E1 E3 (x3,y3,z3) (x1,y1,z1) 20 10
11 Defining 3D Polygons Every plane has a vector n normal (perpendicular, orthogonal) to it From two vectors that line on the plane, we can use the cross product to find the normal, n = u v v P u 21 Vector Operations Apply the right hand rule Cross product results in a vector 22 11
12 Vector Operations Dot product can be used to define angles: For example, assume w & v are unit length v and = cos -1 ( w v ) projection w v w Also generalizes for non-normal vectors (see text) 23 Defining 3D Polygons In our plane equation: Ax + By + Cz + D = 0, [A,B,C] T = the normal of the plane From the edges find two vectors Use the cross product to find the normal, giving us A, B, C Then, to find D, plug in any vertex into the equation and solve for D 24 12
13 Defining 3D Polygons Once we know our plane equation: Ax + By + Cz + D = 0, we still need to manage the truncation which leads to the polygon itself Functionally, we will need to do this to know if a point lies in a polygon or not, for example 25 Defining 3D Polygons To do this, we can project the 3d polygon into 2d and see if the point is in the 2d z using the inside test (xi,yi,zi) y x (xi,yi ) 26 13
14 Defining 3D Polygons Project 3d to 2d based on largest of A,B,C z (xi,yi,zi) y This example: Z (or C) is principal component of N, normal so project on to xy-plane x (xi,yi ) 27 Z-buffer For 3D with multiple polygons, must deal with visibility image plane Project vertices into image plane and with projected vertex include depth in additional depth- or Z-buffer 28 14
15 Z-buffer Scan convert each projected polygon: For each polygon in scene project verticies for each pixel inside poly calculate z if z < closest draw into frame buffer update z buffer 29 Curves and Surfaces 15
16 Curves Curves are one dimensional entities where the function is nonlinear Curves 31 Representations for curves Parametric representation x = x(u), y = y(u) or simply p(u) where p = x y - More robust and general than other forms - Gives better control over curves and surfaces Notation: p(u) = c 0 + c 1 u + c 2 u 2 where each c is a vector, c i = c ix c iy 32 16
17 Representations for curves Example, quadric parametric curve: p(u) = c 0 + c 1 u + c 2 u 2 Like curve: x = 3u 2 y = 2u + 3 for u = [-1,1] c 0 = 0 c 1 = 0 c 2 = Note, more coefficients than a quadratic 33 Representations for curves Parametric curve, p(u) can as easily represent a curve in 3D (x,y,z) Simply: x = f x (u) y = fy(u) z = f z (u) Quadric coefs become: c ox c oy c oz c 1x c 1y c 1z c 0 = c 1 = c 2 = c 2x c 2y c 2z 34 17
18 Parametric Cubic (pc) curves Extension of quadrics to cubics Represented as: p(u) = c 0 + c 1 u + c 2 u 2 + c 3 u 3 Also called Hermite curves after the 17th century mathematician 35 Parametric Cubic (pc) curves Algebraic form: p(u) = c 0 + c 1 u + c 2 u 2 + c 3 u 3 (Note,unless otherwise specified u goes from 0,1) Not very intuitive, 12 values of c Instead want a better specify the curve More intuitive: control by start point p(0) and ending point p(1) and their derivatives 36 18
19 Parametric Cubic (pc) curves From: p(u) = c 0 + c 1 u + c 2 u 2 + c 3 u 3 Build a geometric form in order to specify a curves by their end points and tangents p(1) p (0) p (1) p(0) 37 Parametric Cubic curves This leads to the Geometric Form: p(u) = F 1 (u)p(0) + F 2 (u)p(1) + F 3 (u)p (0) + F 4 (u)p (1) where: F 1 (u) = 2u 3 3u 2 +1 F 2 (u) = -2u 3 + 3u 2 F 3 (u) = u 3 2u 2 + u F 4 (u) = u 3 u
20 F curves: Hermite curves basis 39 Joining Multiple Segments use p = [p 0 p 1 p 2 p 3 ] T use p = [p 3 p 4 p 5 p 6 ] T Get continuity at join points but not continuity of derivatives C0, C1, C2 continuity 40 20
21 Bezier Curves Family of curves developed in the 1970's by Bezier, a engineer for Renault, car manufacturer Bezier's curves are only guaranteed to pass through the end points, but other control points controlled the derivative at the end points Specifically, the tangent was controlled by the next control point in, the 2nd derivative by the second control point in, and the nth derivative by the nth and so on Bezier Curves 42 21
22 Bezier Curves The general form of the Bezier curve is: n p(u) = p i f i (u) 0 < u < 1 i=0 Vertices p control the curve and blending functions, f i (u), that satisfy the "derivative" condition Bernstein polynomials were a family of functions that were chosen by Bezier to satisfy his needs, these are not the only functions that could be used though 43 Convex Hull Property The properties of the Bernstein polynomials ensure that all Bezier curves lie in the convex hull of their control points Hence, even though we do not reach all the input data, we cannot be too far away Bezier curve p 1 p 2 convex hull p 0 p
23 Bernstein Polynomials The blending functions are a special case of the Bernstein polynomials d! k d k bkd ( u) u (1 u) k!( d k)! These polynomials give the blending polynomials for any degree Bezier form - All zeros at 0 and 1 - For any degree they all sum to 1 - They are all between 0 and 1 inside (0,1) 45 Bezier Curves p(u) = (1-u) 2 p 0 + 2u(1-u)p 1 + u 2 p 2 p1 p2 p
24 n = 3 n = 5 n = 4 n = 6 47 Bezier Curves Bezier curves have intuitive control, are nicely formed, convex hull of all points 48 24
25 B Splines One problem with the curves we have looked at is that changing a single control point affects the whole curve (this is called global propogation,) Also, depends on # of control pts B-Splines offer an alternative, to only affect the local region if a single control point is modified (i.e. local propogation) 49 B Splines B-splines are also called Basis Splines They have a form similar to Bezier, B- splines are defined as: n p(u) = p i f i,k (u) i=0 0 < u < n k where n +1 is the number of control points and k controls the degree of the blending (or basis) functions 50 25
26 B Splines B-splines' blending functions are defined recursively: and f i,1 (u) = 1 if t i < u < t i +1 = 0 otherwise f i,m (u) = m goes from 2 to k (u - t i ) f i,m-1 (u) (u - t i + m ) f i+1,m-1 (u) _ t i+m-1 -t i t i+m -t i+1 t i 's are knot points relating u to control points, p i 51 B Splines Knot points,t i 's, follow along like this: t i = 0 if i < k t i = i - k + 1 if k < i < n t i = n- k + 2 if i > n 52 26
27 B Splines For 6 control pts & k = 1, n= 5 and 0 < u < 6 We get the degenerate case: p(u) = p 0 0 < u < 1 p(u) = p 1 1 < u < 2 p(u) = p 2 2 < u < 3 p(u) = p 3 3 < u < 4 p(u) = p 4 4 < u < 5 p(u) = p 5 5 < u < 6 53 B Splines 54 27
28 B Splines For 6 control pts & k = 2, n= 5 and 0 < u < 5 We get a linear average of neighbors: p(u) = (1 - u)p 0 + u p 1 0 < u < 1 p(u) = (2 - u)p 1 + (u - 1)p 2 1 < u < 2 p(u) = (3 - u)p 2 + (u - 2)p 3 2 < u < 3 p(u) = (4 - u)p 3 + (u - 3)p 4 3 < u < 4 p(u) = (5 - u)p 4 + (u - 4)p 5 4 < u < 5 55 B Splines 56 28
29 B Splines For 6 control pts & k = 3, n= 5 and 0 < u < 4 We get: for 0 < u < 1 p 1 (u) = (1 - u) 2 p 0 +.5u(4-3u) p u 2 p 2 for 1 < u < 2 p 2 (u) =.5(2 - u) 2 p 1 +.5(-2u 2 + 6u - 3) p 2 +.5(u - 1) 2 p 3 for 2 < u < 3 p 3 (u) =.5(3 - u) 2 p 2 +.5(-2u u - 11) p 3 +.5(u - 2) 2 p 4 for 3 < u < 4 p 4 (u) =.5(4 - u) 2 p 3 +.5(-3u u - 32) p 4 + (u - 3) 2 p 5 57 B Splines Note, influence grows with degree k = 2 k = 3 k =
30 B Splines Thus, local influence of control points on curve as: 59 Cubic B-spline p(u) = u T M S p = b(u) T p MS
31 Rendering Curves How do we draw the curve, given p(u)? void evaluatecurve(u,pixelx,pixely) p(1) tangent p (0) p (1) tangent p(0) 61 Rendering Curves Polyline approximation p(1) p(0) piecewise linear discrete approximation 62 31
32 Curves vs. Surfaces Curves are one dimensional entities where the function is nonlinear Surfaces are formed from twodimensional functions - Linear functions give planes and polygons y Curves z x Surfaces 63 Curves vs. Surfaces Parametric curve, p(u) can as easily represent a curve in 3D (x,y,z) x = f x (u) y = fy(u) z = f z (u) u = 1 u =
33 Parametric surface is very similar: p(u,v) Curves vs. Surfaces Simply: x = f(u, v) y = f(u, v) z = f(u, v) (Just, more difficult to comprehend in a 2D representation, we must go behind the image plane) 65 Parametric Surfaces Surfaces require 2 parameters x=x(u,v) y=y(u,v) z=z(u,v) p(u,v) = [x(u,v), y(u,v), z(u,v)] T z Want same properties as curves: - Smoothness - Differentiability - Ease of evaluation y p(0,v) p(u,0) p(u,1) x p(1,v) 66 33
34 34 67 Bezier Patches p v b u b v u p ij j i j i ) ( ) ( ), ( Patch lies in convex hull 68 B-Spline Patches v u p v b u b v u p T S S T ij j i j i M P M ) ( ) ( ), ( defined region
35 Splitting a Cubic Bezier p 0, p 1,p 2,p 3 determine a cubic Bezier polynomial and its convex hull Consider left half l(u) and right half r(u) 69 l(u) and r(u) Since l(u) and r(u) are Bezier curves, we should be able to find two sets of control points {l 0, l 1, l 2, l 3 } and {r 0, r 1, r 2, r 3 } that determine them 70 35
36 Efficient Form l 0 = p 0 r 3 = p 3 l 1 = ½(p 0 + p 1 ) r 1 = ½(p 2 + p 3 ) l 2 = ½(l 1 + ½( p 1 + p 2 )) r 1 = ½(r 2 + ½( p 1 + p 2 )) l 3 = r 0 = ½(l 2 + r 1 ) Requires only shifts and adds! 71 Surfaces Can apply the recursive method to surfaces if we recall that for a Bezier patch curves of constant u (or v) are Bezier curves in u (or v) First subdivide in u - Process creates new points - Some of the original points are discarded original and discarded original and kept new 72 36
37 Second Subdivision 16 final points for 1 of 4 patches created 73 Normals We can differentiate with respect to u and v to obtain the normal at any point p p( u, v) u x( u, v) / u y( u, v) / u z( u, v) / u p( u, v) v x( u, v) / v y( u, v) / v z( u, v) / v n p( u, v) p( u, v) u v 74 37
38 Utah Teapot Most famous data set in computer graphics Widely available as a list of 306 3D vertices and the indices that define 32 Bezier patches 75 38
Rendering Curves and Surfaces. Ed Angel Professor of Computer Science, Electrical and Computer Engineering, and Media Arts University of New Mexico
 Rendering Curves and Surfaces Ed Angel Professor of Computer Science, Electrical and Computer Engineering, and Media Arts University of New Mexico Objectives Introduce methods to draw curves - Approximate
Rendering Curves and Surfaces Ed Angel Professor of Computer Science, Electrical and Computer Engineering, and Media Arts University of New Mexico Objectives Introduce methods to draw curves - Approximate
3D Modeling Parametric Curves & Surfaces. Shandong University Spring 2013
 3D Modeling Parametric Curves & Surfaces Shandong University Spring 2013 3D Object Representations Raw data Point cloud Range image Polygon soup Surfaces Mesh Subdivision Parametric Implicit Solids Voxels
3D Modeling Parametric Curves & Surfaces Shandong University Spring 2013 3D Object Representations Raw data Point cloud Range image Polygon soup Surfaces Mesh Subdivision Parametric Implicit Solids Voxels
Curves and Surfaces Computer Graphics I Lecture 9
 15-462 Computer Graphics I Lecture 9 Curves and Surfaces Parametric Representations Cubic Polynomial Forms Hermite Curves Bezier Curves and Surfaces [Angel 10.1-10.6] February 19, 2002 Frank Pfenning Carnegie
15-462 Computer Graphics I Lecture 9 Curves and Surfaces Parametric Representations Cubic Polynomial Forms Hermite Curves Bezier Curves and Surfaces [Angel 10.1-10.6] February 19, 2002 Frank Pfenning Carnegie
Until now we have worked with flat entities such as lines and flat polygons. Fit well with graphics hardware Mathematically simple
 Curves and surfaces Escaping Flatland Until now we have worked with flat entities such as lines and flat polygons Fit well with graphics hardware Mathematically simple But the world is not composed of
Curves and surfaces Escaping Flatland Until now we have worked with flat entities such as lines and flat polygons Fit well with graphics hardware Mathematically simple But the world is not composed of
Computer Graphics. Curves and Surfaces. Hermite/Bezier Curves, (B-)Splines, and NURBS. By Ulf Assarsson
 Computer Graphics Curves and Surfaces Hermite/Bezier Curves, (B-)Splines, and NURBS By Ulf Assarsson Most of the material is originally made by Edward Angel and is adapted to this course by Ulf Assarsson.
Computer Graphics Curves and Surfaces Hermite/Bezier Curves, (B-)Splines, and NURBS By Ulf Assarsson Most of the material is originally made by Edward Angel and is adapted to this course by Ulf Assarsson.
3D Modeling Parametric Curves & Surfaces
 3D Modeling Parametric Curves & Surfaces Shandong University Spring 2012 3D Object Representations Raw data Point cloud Range image Polygon soup Solids Voxels BSP tree CSG Sweep Surfaces Mesh Subdivision
3D Modeling Parametric Curves & Surfaces Shandong University Spring 2012 3D Object Representations Raw data Point cloud Range image Polygon soup Solids Voxels BSP tree CSG Sweep Surfaces Mesh Subdivision
Curves and Surfaces Computer Graphics I Lecture 10
 15-462 Computer Graphics I Lecture 10 Curves and Surfaces Parametric Representations Cubic Polynomial Forms Hermite Curves Bezier Curves and Surfaces [Angel 10.1-10.6] September 30, 2003 Doug James Carnegie
15-462 Computer Graphics I Lecture 10 Curves and Surfaces Parametric Representations Cubic Polynomial Forms Hermite Curves Bezier Curves and Surfaces [Angel 10.1-10.6] September 30, 2003 Doug James Carnegie
OUTLINE. Quadratic Bezier Curves Cubic Bezier Curves
 BEZIER CURVES 1 OUTLINE Introduce types of curves and surfaces Introduce the types of curves Interpolating Hermite Bezier B-spline Quadratic Bezier Curves Cubic Bezier Curves 2 ESCAPING FLATLAND Until
BEZIER CURVES 1 OUTLINE Introduce types of curves and surfaces Introduce the types of curves Interpolating Hermite Bezier B-spline Quadratic Bezier Curves Cubic Bezier Curves 2 ESCAPING FLATLAND Until
Bezier Curves, B-Splines, NURBS
 Bezier Curves, B-Splines, NURBS Example Application: Font Design and Display Curved objects are everywhere There is always need for: mathematical fidelity high precision artistic freedom and flexibility
Bezier Curves, B-Splines, NURBS Example Application: Font Design and Display Curved objects are everywhere There is always need for: mathematical fidelity high precision artistic freedom and flexibility
Curves and Surface I. Angel Ch.10
 Curves and Surface I Angel Ch.10 Representation of Curves and Surfaces Piece-wise linear representation is inefficient - line segments to approximate curve - polygon mesh to approximate surfaces - can
Curves and Surface I Angel Ch.10 Representation of Curves and Surfaces Piece-wise linear representation is inefficient - line segments to approximate curve - polygon mesh to approximate surfaces - can
Fall CSCI 420: Computer Graphics. 4.2 Splines. Hao Li.
 Fall 2014 CSCI 420: Computer Graphics 4.2 Splines Hao Li http://cs420.hao-li.com 1 Roller coaster Next programming assignment involves creating a 3D roller coaster animation We must model the 3D curve
Fall 2014 CSCI 420: Computer Graphics 4.2 Splines Hao Li http://cs420.hao-li.com 1 Roller coaster Next programming assignment involves creating a 3D roller coaster animation We must model the 3D curve
Surface and Solid Geometry. 3D Polygons
 Surface and Solid Geometry D olygons Once we know our plane equation: Ax + By + Cz + D = 0, we still need to manage the truncation which leads to the polygon itself Functionally, we will need to do this
Surface and Solid Geometry D olygons Once we know our plane equation: Ax + By + Cz + D = 0, we still need to manage the truncation which leads to the polygon itself Functionally, we will need to do this
Splines. Parameterization of a Curve. Curve Representations. Roller coaster. What Do We Need From Curves in Computer Graphics? Modeling Complex Shapes
 CSCI 420 Computer Graphics Lecture 8 Splines Jernej Barbic University of Southern California Hermite Splines Bezier Splines Catmull-Rom Splines Other Cubic Splines [Angel Ch 12.4-12.12] Roller coaster
CSCI 420 Computer Graphics Lecture 8 Splines Jernej Barbic University of Southern California Hermite Splines Bezier Splines Catmull-Rom Splines Other Cubic Splines [Angel Ch 12.4-12.12] Roller coaster
Curves and Surfaces 1
 Curves and Surfaces 1 Representation of Curves & Surfaces Polygon Meshes Parametric Cubic Curves Parametric Bi-Cubic Surfaces Quadric Surfaces Specialized Modeling Techniques 2 The Teapot 3 Representing
Curves and Surfaces 1 Representation of Curves & Surfaces Polygon Meshes Parametric Cubic Curves Parametric Bi-Cubic Surfaces Quadric Surfaces Specialized Modeling Techniques 2 The Teapot 3 Representing
Information Coding / Computer Graphics, ISY, LiTH. Splines
 28(69) Splines Originally a drafting tool to create a smooth curve In computer graphics: a curve built from sections, each described by a 2nd or 3rd degree polynomial. Very common in non-real-time graphics,
28(69) Splines Originally a drafting tool to create a smooth curve In computer graphics: a curve built from sections, each described by a 2nd or 3rd degree polynomial. Very common in non-real-time graphics,
CS130 : Computer Graphics Curves (cont.) Tamar Shinar Computer Science & Engineering UC Riverside
 CS130 : Computer Graphics Curves (cont.) Tamar Shinar Computer Science & Engineering UC Riverside Blending Functions Blending functions are more convenient basis than monomial basis canonical form (monomial
CS130 : Computer Graphics Curves (cont.) Tamar Shinar Computer Science & Engineering UC Riverside Blending Functions Blending functions are more convenient basis than monomial basis canonical form (monomial
Intro to Curves Week 1, Lecture 2
 CS 536 Computer Graphics Intro to Curves Week 1, Lecture 2 David Breen, William Regli and Maxim Peysakhov Department of Computer Science Drexel University Outline Math review Introduction to 2D curves
CS 536 Computer Graphics Intro to Curves Week 1, Lecture 2 David Breen, William Regli and Maxim Peysakhov Department of Computer Science Drexel University Outline Math review Introduction to 2D curves
CS 536 Computer Graphics Intro to Curves Week 1, Lecture 2
 CS 536 Computer Graphics Intro to Curves Week 1, Lecture 2 David Breen, William Regli and Maxim Peysakhov Department of Computer Science Drexel University 1 Outline Math review Introduction to 2D curves
CS 536 Computer Graphics Intro to Curves Week 1, Lecture 2 David Breen, William Regli and Maxim Peysakhov Department of Computer Science Drexel University 1 Outline Math review Introduction to 2D curves
An introduction to interpolation and splines
 An introduction to interpolation and splines Kenneth H. Carpenter, EECE KSU November 22, 1999 revised November 20, 2001, April 24, 2002, April 14, 2004 1 Introduction Suppose one wishes to draw a curve
An introduction to interpolation and splines Kenneth H. Carpenter, EECE KSU November 22, 1999 revised November 20, 2001, April 24, 2002, April 14, 2004 1 Introduction Suppose one wishes to draw a curve
Design considerations
 Curves Design considerations local control of shape design each segment independently smoothness and continuity ability to evaluate derivatives stability small change in input leads to small change in
Curves Design considerations local control of shape design each segment independently smoothness and continuity ability to evaluate derivatives stability small change in input leads to small change in
Intro to Curves Week 4, Lecture 7
 CS 430/536 Computer Graphics I Intro to Curves Week 4, Lecture 7 David Breen, William Regli and Maxim Peysakhov Geometric and Intelligent Computing Laboratory Department of Computer Science Drexel University
CS 430/536 Computer Graphics I Intro to Curves Week 4, Lecture 7 David Breen, William Regli and Maxim Peysakhov Geometric and Intelligent Computing Laboratory Department of Computer Science Drexel University
Central issues in modelling
 Central issues in modelling Construct families of curves, surfaces and volumes that can represent common objects usefully; are easy to interact with; interaction includes: manual modelling; fitting to
Central issues in modelling Construct families of curves, surfaces and volumes that can represent common objects usefully; are easy to interact with; interaction includes: manual modelling; fitting to
Parametric Curves. University of Texas at Austin CS384G - Computer Graphics
 Parametric Curves University of Texas at Austin CS384G - Computer Graphics Fall 2010 Don Fussell Parametric Representations 3 basic representation strategies: Explicit: y = mx + b Implicit: ax + by + c
Parametric Curves University of Texas at Austin CS384G - Computer Graphics Fall 2010 Don Fussell Parametric Representations 3 basic representation strategies: Explicit: y = mx + b Implicit: ax + by + c
Parametric Curves. University of Texas at Austin CS384G - Computer Graphics Fall 2010 Don Fussell
 Parametric Curves University of Texas at Austin CS384G - Computer Graphics Fall 2010 Don Fussell Parametric Representations 3 basic representation strategies: Explicit: y = mx + b Implicit: ax + by + c
Parametric Curves University of Texas at Austin CS384G - Computer Graphics Fall 2010 Don Fussell Parametric Representations 3 basic representation strategies: Explicit: y = mx + b Implicit: ax + by + c
Computer Graphics Curves and Surfaces. Matthias Teschner
 Computer Graphics Curves and Surfaces Matthias Teschner Outline Introduction Polynomial curves Bézier curves Matrix notation Curve subdivision Differential curve properties Piecewise polynomial curves
Computer Graphics Curves and Surfaces Matthias Teschner Outline Introduction Polynomial curves Bézier curves Matrix notation Curve subdivision Differential curve properties Piecewise polynomial curves
Geometric Modeling of Curves
 Curves Locus of a point moving with one degree of freedom Locus of a one-dimensional parameter family of point Mathematically defined using: Explicit equations Implicit equations Parametric equations (Hermite,
Curves Locus of a point moving with one degree of freedom Locus of a one-dimensional parameter family of point Mathematically defined using: Explicit equations Implicit equations Parametric equations (Hermite,
CS-184: Computer Graphics
 CS-184: Computer Graphics Lecture #12: Curves and Surfaces Prof. James O Brien University of California, Berkeley V2007-F-12-1.0 Today General curve and surface representations Splines and other polynomial
CS-184: Computer Graphics Lecture #12: Curves and Surfaces Prof. James O Brien University of California, Berkeley V2007-F-12-1.0 Today General curve and surface representations Splines and other polynomial
CS770/870 Spring 2017 Ray Tracing Implementation
 Useful ector Information S770/870 Spring 07 Ray Tracing Implementation Related material:angel 6e: h.3 Ray-Object intersections Spheres Plane/Polygon Box/Slab/Polyhedron Quadric surfaces Other implicit/explicit
Useful ector Information S770/870 Spring 07 Ray Tracing Implementation Related material:angel 6e: h.3 Ray-Object intersections Spheres Plane/Polygon Box/Slab/Polyhedron Quadric surfaces Other implicit/explicit
08 - Designing Approximating Curves
 08 - Designing Approximating Curves Acknowledgement: Olga Sorkine-Hornung, Alexander Sorkine-Hornung, Ilya Baran Last time Interpolating curves Monomials Lagrange Hermite Different control types Polynomials
08 - Designing Approximating Curves Acknowledgement: Olga Sorkine-Hornung, Alexander Sorkine-Hornung, Ilya Baran Last time Interpolating curves Monomials Lagrange Hermite Different control types Polynomials
Need for Parametric Equations
 Curves and Surfaces Curves and Surfaces Need for Parametric Equations Affine Combinations Bernstein Polynomials Bezier Curves and Surfaces Continuity when joining curves B Spline Curves and Surfaces Need
Curves and Surfaces Curves and Surfaces Need for Parametric Equations Affine Combinations Bernstein Polynomials Bezier Curves and Surfaces Continuity when joining curves B Spline Curves and Surfaces Need
Dgp _ lecture 2. Curves
 Dgp _ lecture 2 Curves Questions? This lecture will be asking questions about curves, their Relationship to surfaces, and how they are used and controlled. Topics of discussion will be: Free form Curves
Dgp _ lecture 2 Curves Questions? This lecture will be asking questions about curves, their Relationship to surfaces, and how they are used and controlled. Topics of discussion will be: Free form Curves
Introduction to Computer Graphics
 Introduction to Computer Graphics 2016 Spring National Cheng Kung University Instructors: Min-Chun Hu 胡敏君 Shih-Chin Weng 翁士欽 ( 西基電腦動畫 ) Data Representation Curves and Surfaces Limitations of Polygons Inherently
Introduction to Computer Graphics 2016 Spring National Cheng Kung University Instructors: Min-Chun Hu 胡敏君 Shih-Chin Weng 翁士欽 ( 西基電腦動畫 ) Data Representation Curves and Surfaces Limitations of Polygons Inherently
CHAPTER 1 Graphics Systems and Models 3
 ?????? 1 CHAPTER 1 Graphics Systems and Models 3 1.1 Applications of Computer Graphics 4 1.1.1 Display of Information............. 4 1.1.2 Design.................... 5 1.1.3 Simulation and Animation...........
?????? 1 CHAPTER 1 Graphics Systems and Models 3 1.1 Applications of Computer Graphics 4 1.1.1 Display of Information............. 4 1.1.2 Design.................... 5 1.1.3 Simulation and Animation...........
CEng 477 Introduction to Computer Graphics Fall 2007
 Visible Surface Detection CEng 477 Introduction to Computer Graphics Fall 2007 Visible Surface Detection Visible surface detection or hidden surface removal. Realistic scenes: closer objects occludes the
Visible Surface Detection CEng 477 Introduction to Computer Graphics Fall 2007 Visible Surface Detection Visible surface detection or hidden surface removal. Realistic scenes: closer objects occludes the
Sung-Eui Yoon ( 윤성의 )
 CS480: Computer Graphics Curves and Surfaces Sung-Eui Yoon ( 윤성의 ) Course URL: http://jupiter.kaist.ac.kr/~sungeui/cg Today s Topics Surface representations Smooth curves Subdivision 2 Smooth Curves and
CS480: Computer Graphics Curves and Surfaces Sung-Eui Yoon ( 윤성의 ) Course URL: http://jupiter.kaist.ac.kr/~sungeui/cg Today s Topics Surface representations Smooth curves Subdivision 2 Smooth Curves and
Computergrafik. Matthias Zwicker Universität Bern Herbst 2016
 Computergrafik Matthias Zwicker Universität Bern Herbst 2016 Today Curves NURBS Surfaces Parametric surfaces Bilinear patch Bicubic Bézier patch Advanced surface modeling 2 Piecewise Bézier curves Each
Computergrafik Matthias Zwicker Universität Bern Herbst 2016 Today Curves NURBS Surfaces Parametric surfaces Bilinear patch Bicubic Bézier patch Advanced surface modeling 2 Piecewise Bézier curves Each
Review of Tuesday. ECS 175 Chapter 3: Object Representation
 Review of Tuesday We have learnt how to rasterize lines and fill polygons Colors (and other attributes) are specified at vertices Interpolation required to fill polygon with attributes 26 Review of Tuesday
Review of Tuesday We have learnt how to rasterize lines and fill polygons Colors (and other attributes) are specified at vertices Interpolation required to fill polygon with attributes 26 Review of Tuesday
Polygon Meshes and Implicit Surfaces
 CSCI 420 Computer Graphics Lecture 9 Polygon Meshes and Implicit Surfaces Polygon Meshes Implicit Surfaces Constructive Solid Geometry [Angel Ch. 10] Jernej Barbic University of Southern California 1 Modeling
CSCI 420 Computer Graphics Lecture 9 Polygon Meshes and Implicit Surfaces Polygon Meshes Implicit Surfaces Constructive Solid Geometry [Angel Ch. 10] Jernej Barbic University of Southern California 1 Modeling
Polygon Meshes and Implicit Surfaces
 CSCI 420 Computer Graphics Lecture 9 and Constructive Solid Geometry [Angel Ch. 10] Jernej Barbic University of Southern California Modeling Complex Shapes An equation for a sphere is possible, but how
CSCI 420 Computer Graphics Lecture 9 and Constructive Solid Geometry [Angel Ch. 10] Jernej Barbic University of Southern California Modeling Complex Shapes An equation for a sphere is possible, but how
(Spline, Bezier, B-Spline)
 (Spline, Bezier, B-Spline) Spline Drafting terminology Spline is a flexible strip that is easily flexed to pass through a series of design points (control points) to produce a smooth curve. Spline curve
(Spline, Bezier, B-Spline) Spline Drafting terminology Spline is a flexible strip that is easily flexed to pass through a series of design points (control points) to produce a smooth curve. Spline curve
11/1/13. Polygon Meshes and Implicit Surfaces. Shape Representations. Polygon Models in OpenGL. Modeling Complex Shapes
 CSCI 420 Computer Graphics Lecture 7 and Constructive Solid Geometry [Angel Ch. 12.1-12.3] Jernej Barbic University of Southern California Modeling Complex Shapes An equation for a sphere is possible,
CSCI 420 Computer Graphics Lecture 7 and Constructive Solid Geometry [Angel Ch. 12.1-12.3] Jernej Barbic University of Southern California Modeling Complex Shapes An equation for a sphere is possible,
Rendering. Basic Math Review. Rasterizing Lines and Polygons Hidden Surface Remove Multi-pass Rendering with Accumulation Buffers.
 Rendering Rasterizing Lines and Polygons Hidden Surface Remove Multi-pass Rendering with Accumulation Buffers Basic Math Review Slope-Intercept Formula For Lines Given a third point on the line: P = (X,Y)
Rendering Rasterizing Lines and Polygons Hidden Surface Remove Multi-pass Rendering with Accumulation Buffers Basic Math Review Slope-Intercept Formula For Lines Given a third point on the line: P = (X,Y)
CS337 INTRODUCTION TO COMPUTER GRAPHICS. Describing Shapes. Constructing Objects in Computer Graphics. Bin Sheng Representing Shape 9/20/16 1/15
 Describing Shapes Constructing Objects in Computer Graphics 1/15 2D Object Definition (1/3) Lines and polylines: Polylines: lines drawn between ordered points A closed polyline is a polygon, a simple polygon
Describing Shapes Constructing Objects in Computer Graphics 1/15 2D Object Definition (1/3) Lines and polylines: Polylines: lines drawn between ordered points A closed polyline is a polygon, a simple polygon
Computergrafik. Matthias Zwicker. Herbst 2010
 Computergrafik Matthias Zwicker Universität Bern Herbst 2010 Today Curves NURBS Surfaces Parametric surfaces Bilinear patch Bicubic Bézier patch Advanced surface modeling Piecewise Bézier curves Each segment
Computergrafik Matthias Zwicker Universität Bern Herbst 2010 Today Curves NURBS Surfaces Parametric surfaces Bilinear patch Bicubic Bézier patch Advanced surface modeling Piecewise Bézier curves Each segment
CS123 INTRODUCTION TO COMPUTER GRAPHICS. Describing Shapes. Constructing Objects in Computer Graphics 1/15
 Describing Shapes Constructing Objects in Computer Graphics 1/15 2D Object Definition (1/3) Lines and polylines: Polylines: lines drawn between ordered points A closed polyline is a polygon, a simple polygon
Describing Shapes Constructing Objects in Computer Graphics 1/15 2D Object Definition (1/3) Lines and polylines: Polylines: lines drawn between ordered points A closed polyline is a polygon, a simple polygon
Lecture IV Bézier Curves
 Lecture IV Bézier Curves Why Curves? Why Curves? Why Curves? Why Curves? Why Curves? Linear (flat) Curved Easier More pieces Looks ugly Complicated Fewer pieces Looks smooth What is a curve? Intuitively:
Lecture IV Bézier Curves Why Curves? Why Curves? Why Curves? Why Curves? Why Curves? Linear (flat) Curved Easier More pieces Looks ugly Complicated Fewer pieces Looks smooth What is a curve? Intuitively:
LECTURE #6. Geometric Modelling for Engineering Applications. Geometric modeling for engineering applications
 LECTURE #6 Geometric modeling for engineering applications Geometric Modelling for Engineering Applications Introduction to modeling Geometric modeling Curve representation Hermite curve Bezier curve B-spline
LECTURE #6 Geometric modeling for engineering applications Geometric Modelling for Engineering Applications Introduction to modeling Geometric modeling Curve representation Hermite curve Bezier curve B-spline
Know it. Control points. B Spline surfaces. Implicit surfaces
 Know it 15 B Spline Cur 14 13 12 11 Parametric curves Catmull clark subdivision Parametric surfaces Interpolating curves 10 9 8 7 6 5 4 3 2 Control points B Spline surfaces Implicit surfaces Bezier surfaces
Know it 15 B Spline Cur 14 13 12 11 Parametric curves Catmull clark subdivision Parametric surfaces Interpolating curves 10 9 8 7 6 5 4 3 2 Control points B Spline surfaces Implicit surfaces Bezier surfaces
CS 325 Computer Graphics
 CS 325 Computer Graphics 02 / 06 / 2012 Instructor: Michael Eckmann Today s Topics Questions? Comments? Antialiasing Polygons Interior points Fill areas tiling halftoning dithering Antialiasing Aliasing
CS 325 Computer Graphics 02 / 06 / 2012 Instructor: Michael Eckmann Today s Topics Questions? Comments? Antialiasing Polygons Interior points Fill areas tiling halftoning dithering Antialiasing Aliasing
CSCI 4620/8626. Coordinate Reference Frames
 CSCI 4620/8626 Computer Graphics Graphics Output Primitives Last update: 2014-02-03 Coordinate Reference Frames To describe a picture, the world-coordinate reference frame (2D or 3D) must be selected.
CSCI 4620/8626 Computer Graphics Graphics Output Primitives Last update: 2014-02-03 Coordinate Reference Frames To describe a picture, the world-coordinate reference frame (2D or 3D) must be selected.
CS-184: Computer Graphics. Today
 CS-84: Computer Graphics Lecture #5: Curves and Surfaces Prof. James O Brien University of California, Berkeley V25F-5-. Today General curve and surface representations Splines and other polynomial bases
CS-84: Computer Graphics Lecture #5: Curves and Surfaces Prof. James O Brien University of California, Berkeley V25F-5-. Today General curve and surface representations Splines and other polynomial bases
The goal is the definition of points with numbers and primitives with equations or functions. The definition of points with numbers requires a
 The goal is the definition of points with numbers and primitives with equations or functions. The definition of points with numbers requires a coordinate system and then the measuring of the point with
The goal is the definition of points with numbers and primitives with equations or functions. The definition of points with numbers requires a coordinate system and then the measuring of the point with
ECE 600, Dr. Farag, Summer 09
 ECE 6 Summer29 Course Supplements. Lecture 4 Curves and Surfaces Aly A. Farag University of Louisville Acknowledgements: Help with these slides were provided by Shireen Elhabian A smile is a curve that
ECE 6 Summer29 Course Supplements. Lecture 4 Curves and Surfaces Aly A. Farag University of Louisville Acknowledgements: Help with these slides were provided by Shireen Elhabian A smile is a curve that
GL9: Engineering Communications. GL9: CAD techniques. Curves Surfaces Solids Techniques
 436-105 Engineering Communications GL9:1 GL9: CAD techniques Curves Surfaces Solids Techniques Parametric curves GL9:2 x = a 1 + b 1 u + c 1 u 2 + d 1 u 3 + y = a 2 + b 2 u + c 2 u 2 + d 2 u 3 + z = a
436-105 Engineering Communications GL9:1 GL9: CAD techniques Curves Surfaces Solids Techniques Parametric curves GL9:2 x = a 1 + b 1 u + c 1 u 2 + d 1 u 3 + y = a 2 + b 2 u + c 2 u 2 + d 2 u 3 + z = a
Curves and Surfaces. Computer Graphics COMP 770 (236) Spring Instructor: Brandon Lloyd
 Curves and Surfaces Computer Graphics COMP 770 (236) Spring 2007 Instructor: Brandon Lloyd 4/11/2007 Final projects Surface representations Smooth curves Subdivision Todays Topics 2 Final Project Requirements
Curves and Surfaces Computer Graphics COMP 770 (236) Spring 2007 Instructor: Brandon Lloyd 4/11/2007 Final projects Surface representations Smooth curves Subdivision Todays Topics 2 Final Project Requirements
CSE 167: Introduction to Computer Graphics Lecture 12: Bézier Curves. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2013
 CSE 167: Introduction to Computer Graphics Lecture 12: Bézier Curves Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2013 Announcements Homework assignment 5 due tomorrow, Nov
CSE 167: Introduction to Computer Graphics Lecture 12: Bézier Curves Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2013 Announcements Homework assignment 5 due tomorrow, Nov
Lecture 9: Introduction to Spline Curves
 Lecture 9: Introduction to Spline Curves Splines are used in graphics to represent smooth curves and surfaces. They use a small set of control points (knots) and a function that generates a curve through
Lecture 9: Introduction to Spline Curves Splines are used in graphics to represent smooth curves and surfaces. They use a small set of control points (knots) and a function that generates a curve through
3.2 THREE DIMENSIONAL OBJECT REPRESENTATIONS
 3.1 THREE DIMENSIONAL CONCEPTS We can rotate an object about an axis with any spatial orientation in threedimensional space. Two-dimensional rotations, on the other hand, are always around an axis that
3.1 THREE DIMENSIONAL CONCEPTS We can rotate an object about an axis with any spatial orientation in threedimensional space. Two-dimensional rotations, on the other hand, are always around an axis that
Curves. Computer Graphics CSE 167 Lecture 11
 Curves Computer Graphics CSE 167 Lecture 11 CSE 167: Computer graphics Polynomial Curves Polynomial functions Bézier Curves Drawing Bézier curves Piecewise Bézier curves Based on slides courtesy of Jurgen
Curves Computer Graphics CSE 167 Lecture 11 CSE 167: Computer graphics Polynomial Curves Polynomial functions Bézier Curves Drawing Bézier curves Piecewise Bézier curves Based on slides courtesy of Jurgen
The Graphics Pipeline. Interactive Computer Graphics. The Graphics Pipeline. The Graphics Pipeline. The Graphics Pipeline: Clipping
 Interactive Computer Graphics The Graphics Pipeline: The Graphics Pipeline Input: - geometric model - illumination model - camera model - viewport Some slides adopted from F. Durand and B. Cutler, MIT
Interactive Computer Graphics The Graphics Pipeline: The Graphics Pipeline Input: - geometric model - illumination model - camera model - viewport Some slides adopted from F. Durand and B. Cutler, MIT
Geometric Queries for Ray Tracing
 CSCI 420 Computer Graphics Lecture 16 Geometric Queries for Ray Tracing Ray-Surface Intersection Barycentric Coordinates [Angel Ch. 11] Jernej Barbic University of Southern California 1 Ray-Surface Intersections
CSCI 420 Computer Graphics Lecture 16 Geometric Queries for Ray Tracing Ray-Surface Intersection Barycentric Coordinates [Angel Ch. 11] Jernej Barbic University of Southern California 1 Ray-Surface Intersections
Curves and Surfaces. Shireen Elhabian and Aly A. Farag University of Louisville
 Curves and Surfaces Shireen Elhabian and Aly A. Farag University of Louisville February 21 A smile is a curve that sets everything straight Phyllis Diller (American comedienne and actress, born 1917) Outline
Curves and Surfaces Shireen Elhabian and Aly A. Farag University of Louisville February 21 A smile is a curve that sets everything straight Phyllis Diller (American comedienne and actress, born 1917) Outline
Curves D.A. Forsyth, with slides from John Hart
 Curves D.A. Forsyth, with slides from John Hart Central issues in modelling Construct families of curves, surfaces and volumes that can represent common objects usefully; are easy to interact with; interaction
Curves D.A. Forsyth, with slides from John Hart Central issues in modelling Construct families of curves, surfaces and volumes that can represent common objects usefully; are easy to interact with; interaction
2D rendering takes a photo of the 2D scene with a virtual camera that selects an axis aligned rectangle from the scene. The photograph is placed into
 2D rendering takes a photo of the 2D scene with a virtual camera that selects an axis aligned rectangle from the scene. The photograph is placed into the viewport of the current application window. A pixel
2D rendering takes a photo of the 2D scene with a virtual camera that selects an axis aligned rectangle from the scene. The photograph is placed into the viewport of the current application window. A pixel
Ray Tracing Basics I. Computer Graphics as Virtual Photography. camera (captures light) real scene. photo. Photographic print. Photography: processing
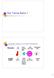 Ray Tracing Basics I Computer Graphics as Virtual Photography Photography: real scene camera (captures light) photo processing Photographic print processing Computer Graphics: 3D models camera model (focuses
Ray Tracing Basics I Computer Graphics as Virtual Photography Photography: real scene camera (captures light) photo processing Photographic print processing Computer Graphics: 3D models camera model (focuses
COMPUTER AIDED ENGINEERING DESIGN (BFF2612)
 COMPUTER AIDED ENGINEERING DESIGN (BFF2612) BASIC MATHEMATICAL CONCEPTS IN CAED by Dr. Mohd Nizar Mhd Razali Faculty of Manufacturing Engineering mnizar@ump.edu.my COORDINATE SYSTEM y+ y+ z+ z+ x+ RIGHT
COMPUTER AIDED ENGINEERING DESIGN (BFF2612) BASIC MATHEMATICAL CONCEPTS IN CAED by Dr. Mohd Nizar Mhd Razali Faculty of Manufacturing Engineering mnizar@ump.edu.my COORDINATE SYSTEM y+ y+ z+ z+ x+ RIGHT
For each question, indicate whether the statement is true or false by circling T or F, respectively.
 True/False For each question, indicate whether the statement is true or false by circling T or F, respectively. 1. (T/F) Rasterization occurs before vertex transformation in the graphics pipeline. 2. (T/F)
True/False For each question, indicate whether the statement is true or false by circling T or F, respectively. 1. (T/F) Rasterization occurs before vertex transformation in the graphics pipeline. 2. (T/F)
9. Three Dimensional Object Representations
 9. Three Dimensional Object Representations Methods: Polygon and Quadric surfaces: For simple Euclidean objects Spline surfaces and construction: For curved surfaces Procedural methods: Eg. Fractals, Particle
9. Three Dimensional Object Representations Methods: Polygon and Quadric surfaces: For simple Euclidean objects Spline surfaces and construction: For curved surfaces Procedural methods: Eg. Fractals, Particle
CSE 167: Introduction to Computer Graphics Lecture #11: Bezier Curves. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2016
 CSE 167: Introduction to Computer Graphics Lecture #11: Bezier Curves Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2016 Announcements Project 3 due tomorrow Midterm 2 next
CSE 167: Introduction to Computer Graphics Lecture #11: Bezier Curves Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2016 Announcements Project 3 due tomorrow Midterm 2 next
Curve and Surface Basics
 Curve and Surface Basics Implicit and parametric forms Power basis form Bezier curves Rational Bezier Curves Tensor Product Surfaces ME525x NURBS Curve and Surface Modeling Page 1 Implicit and Parametric
Curve and Surface Basics Implicit and parametric forms Power basis form Bezier curves Rational Bezier Curves Tensor Product Surfaces ME525x NURBS Curve and Surface Modeling Page 1 Implicit and Parametric
End-Term Examination
 Paper Code: MCA-108 Paper ID : 44108 Second Semester [MCA] MAY-JUNE 2006 Q. 1 Describe the following in brief :- (3 x 5 = 15) (a) QUADRATIC SURFACES (b) RGB Color Models. (c) BSP Tree (d) Solid Modeling
Paper Code: MCA-108 Paper ID : 44108 Second Semester [MCA] MAY-JUNE 2006 Q. 1 Describe the following in brief :- (3 x 5 = 15) (a) QUADRATIC SURFACES (b) RGB Color Models. (c) BSP Tree (d) Solid Modeling
GEOMETRIC TOOLS FOR COMPUTER GRAPHICS
 GEOMETRIC TOOLS FOR COMPUTER GRAPHICS PHILIP J. SCHNEIDER DAVID H. EBERLY MORGAN KAUFMANN PUBLISHERS A N I M P R I N T O F E L S E V I E R S C I E N C E A M S T E R D A M B O S T O N L O N D O N N E W
GEOMETRIC TOOLS FOR COMPUTER GRAPHICS PHILIP J. SCHNEIDER DAVID H. EBERLY MORGAN KAUFMANN PUBLISHERS A N I M P R I N T O F E L S E V I E R S C I E N C E A M S T E R D A M B O S T O N L O N D O N N E W
Interactive Graphics Using Parametric Equations (Day 2)
 Interactive Graphics Using Parametric Equations (Day 2) Dr. Niels Lobo Computer Science Bezier Curves Google bezier curves`` Casselman's Bezier curves Andysspline Bezier Curves Bezier Photo: Automotive
Interactive Graphics Using Parametric Equations (Day 2) Dr. Niels Lobo Computer Science Bezier Curves Google bezier curves`` Casselman's Bezier curves Andysspline Bezier Curves Bezier Photo: Automotive
Werner Purgathofer
 Einführung in Visual Computing 186.822 Visible Surface Detection Werner Purgathofer Visibility in the Rendering Pipeline scene objects in object space object capture/creation ti modeling viewing projection
Einführung in Visual Computing 186.822 Visible Surface Detection Werner Purgathofer Visibility in the Rendering Pipeline scene objects in object space object capture/creation ti modeling viewing projection
Surface Modeling. Polygon Tables. Types: Generating models: Polygon Surfaces. Polygon surfaces Curved surfaces Volumes. Interactive Procedural
 Surface Modeling Types: Polygon surfaces Curved surfaces Volumes Generating models: Interactive Procedural Polygon Tables We specify a polygon surface with a set of vertex coordinates and associated attribute
Surface Modeling Types: Polygon surfaces Curved surfaces Volumes Generating models: Interactive Procedural Polygon Tables We specify a polygon surface with a set of vertex coordinates and associated attribute
3D Modeling: Surfaces
 CS 430/536 Computer Graphics I 3D Modeling: Surfaces Week 8, Lecture 16 David Breen, William Regli and Maxim Peysakhov Geometric and Intelligent Computing Laboratory Department of Computer Science Drexel
CS 430/536 Computer Graphics I 3D Modeling: Surfaces Week 8, Lecture 16 David Breen, William Regli and Maxim Peysakhov Geometric and Intelligent Computing Laboratory Department of Computer Science Drexel
Computer Graphics I Lecture 11
 15-462 Computer Graphics I Lecture 11 Midterm Review Assignment 3 Movie Midterm Review Midterm Preview February 26, 2002 Frank Pfenning Carnegie Mellon University http://www.cs.cmu.edu/~fp/courses/graphics/
15-462 Computer Graphics I Lecture 11 Midterm Review Assignment 3 Movie Midterm Review Midterm Preview February 26, 2002 Frank Pfenning Carnegie Mellon University http://www.cs.cmu.edu/~fp/courses/graphics/
Page 1. Area-Subdivision Algorithms z-buffer Algorithm List Priority Algorithms BSP (Binary Space Partitioning Tree) Scan-line Algorithms
 Visible Surface Determination Visibility Culling Area-Subdivision Algorithms z-buffer Algorithm List Priority Algorithms BSP (Binary Space Partitioning Tree) Scan-line Algorithms Divide-and-conquer strategy:
Visible Surface Determination Visibility Culling Area-Subdivision Algorithms z-buffer Algorithm List Priority Algorithms BSP (Binary Space Partitioning Tree) Scan-line Algorithms Divide-and-conquer strategy:
CSE528 Computer Graphics: Theory, Algorithms, and Applications
 CSE528 Computer Graphics: Theory, Algorithms, and Applications Hong Qin State University of New York at Stony Brook (Stony Brook University) Stony Brook, New York 11794--4400 Tel: (631)632-8450; Fax: (631)632-8334
CSE528 Computer Graphics: Theory, Algorithms, and Applications Hong Qin State University of New York at Stony Brook (Stony Brook University) Stony Brook, New York 11794--4400 Tel: (631)632-8450; Fax: (631)632-8334
Appendix E Calculating Normal Vectors
 OpenGL Programming Guide (Addison-Wesley Publishing Company) Appendix E Calculating Normal Vectors This appendix describes how to calculate normal vectors for surfaces. You need to define normals to use
OpenGL Programming Guide (Addison-Wesley Publishing Company) Appendix E Calculating Normal Vectors This appendix describes how to calculate normal vectors for surfaces. You need to define normals to use
From curves to surfaces. Parametric surfaces and solid modeling. Extrusions. Surfaces of revolution. So far have discussed spline curves in 2D
 From curves to surfaces Parametric surfaces and solid modeling CS 465 Lecture 12 2007 Doug James & Steve Marschner 1 So far have discussed spline curves in 2D it turns out that this already provides of
From curves to surfaces Parametric surfaces and solid modeling CS 465 Lecture 12 2007 Doug James & Steve Marschner 1 So far have discussed spline curves in 2D it turns out that this already provides of
Topic #1: Rasterization (Scan Conversion)
 Topic #1: Rasterization (Scan Conversion) We will generally model objects with geometric primitives points, lines, and polygons For display, we need to convert them to pixels for points it s obvious but
Topic #1: Rasterization (Scan Conversion) We will generally model objects with geometric primitives points, lines, and polygons For display, we need to convert them to pixels for points it s obvious but
Computer Graphics II
 Computer Graphics II Autumn 2017-2018 Outline Visible Surface Determination Methods (contd.) 1 Visible Surface Determination Methods (contd.) Outline Visible Surface Determination Methods (contd.) 1 Visible
Computer Graphics II Autumn 2017-2018 Outline Visible Surface Determination Methods (contd.) 1 Visible Surface Determination Methods (contd.) Outline Visible Surface Determination Methods (contd.) 1 Visible
The Free-form Surface Modelling System
 1. Introduction The Free-form Surface Modelling System Smooth curves and surfaces must be generated in many computer graphics applications. Many real-world objects are inherently smooth (fig.1), and much
1. Introduction The Free-form Surface Modelling System Smooth curves and surfaces must be generated in many computer graphics applications. Many real-world objects are inherently smooth (fig.1), and much
9. Visible-Surface Detection Methods
 9. Visible-Surface Detection Methods More information about Modelling and Perspective Viewing: Before going to visible surface detection, we first review and discuss the followings: 1. Modelling Transformation:
9. Visible-Surface Detection Methods More information about Modelling and Perspective Viewing: Before going to visible surface detection, we first review and discuss the followings: 1. Modelling Transformation:
Computer Graphics CS 543 Lecture 13a Curves, Tesselation/Geometry Shaders & Level of Detail
 Computer Graphics CS 54 Lecture 1a Curves, Tesselation/Geometry Shaders & Level of Detail Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) So Far Dealt with straight lines
Computer Graphics CS 54 Lecture 1a Curves, Tesselation/Geometry Shaders & Level of Detail Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) So Far Dealt with straight lines
Introduction to Geometry. Computer Graphics CMU /15-662
 Introduction to Geometry Computer Graphics CMU 15-462/15-662 Assignment 2: 3D Modeling You will be able to create your own models (This mesh was created in Scotty3D in about 5 minutes... you can do much
Introduction to Geometry Computer Graphics CMU 15-462/15-662 Assignment 2: 3D Modeling You will be able to create your own models (This mesh was created in Scotty3D in about 5 minutes... you can do much
Introduction to Computer Graphics. Farhana Bandukwala, PhD Lecture 11: Surfaces
 Introduction to Computer Graphics Farhana Bandukwala, PhD Lecture 11: Surfaces Outline Linear approximation Parametric bicubic surfaces Subdividin surfaces Drawin surfaces Implicit Representation f(x,y,z)0
Introduction to Computer Graphics Farhana Bandukwala, PhD Lecture 11: Surfaces Outline Linear approximation Parametric bicubic surfaces Subdividin surfaces Drawin surfaces Implicit Representation f(x,y,z)0
Write C++/Java program to draw line using DDA and Bresenham s algorithm. Inherit pixel class and Use function overloading.
 Group A Assignment No A1. Write C++/Java program to draw line using DDA and Bresenham s algorithm. Inherit pixel class and Use function overloading. Aim: To draw line using DDA and Bresenham s algorithm
Group A Assignment No A1. Write C++/Java program to draw line using DDA and Bresenham s algorithm. Inherit pixel class and Use function overloading. Aim: To draw line using DDA and Bresenham s algorithm
Rational Bezier Curves
 Rational Bezier Curves Use of homogeneous coordinates Rational spline curve: define a curve in one higher dimension space, project it down on the homogenizing variable Mathematical formulation: n P(u)
Rational Bezier Curves Use of homogeneous coordinates Rational spline curve: define a curve in one higher dimension space, project it down on the homogenizing variable Mathematical formulation: n P(u)
Splines. Connecting the Dots
 Splines or: Connecting the Dots Jens Ogniewski Information Coding Group Linköping University Before we start... Some parts won t be part of the exam Basically all that is not described in the book. More
Splines or: Connecting the Dots Jens Ogniewski Information Coding Group Linköping University Before we start... Some parts won t be part of the exam Basically all that is not described in the book. More
Lecture 25: Bezier Subdivision. And he took unto him all these, and divided them in the midst, and laid each piece one against another: Genesis 15:10
 Lecture 25: Bezier Subdivision And he took unto him all these, and divided them in the midst, and laid each piece one against another: Genesis 15:10 1. Divide and Conquer If we are going to build useful
Lecture 25: Bezier Subdivision And he took unto him all these, and divided them in the midst, and laid each piece one against another: Genesis 15:10 1. Divide and Conquer If we are going to build useful
Further Graphics. Bezier Curves and Surfaces. Alex Benton, University of Cambridge Supported in part by Google UK, Ltd
 Further Graphics Bezier Curves and Surfaces Alex Benton, University of Cambridge alex@bentonian.com 1 Supported in part by Google UK, Ltd CAD, CAM, and a new motivation: shiny things Expensive products
Further Graphics Bezier Curves and Surfaces Alex Benton, University of Cambridge alex@bentonian.com 1 Supported in part by Google UK, Ltd CAD, CAM, and a new motivation: shiny things Expensive products
INF3320 Computer Graphics and Discrete Geometry
 INF3320 Computer Graphics and Discrete Geometry More smooth Curves and Surfaces Christopher Dyken, Michael Floater and Martin Reimers 10.11.2010 Page 1 More smooth Curves and Surfaces Akenine-Möller, Haines
INF3320 Computer Graphics and Discrete Geometry More smooth Curves and Surfaces Christopher Dyken, Michael Floater and Martin Reimers 10.11.2010 Page 1 More smooth Curves and Surfaces Akenine-Möller, Haines
Interactive Graphics. Lecture 9: Introduction to Spline Curves. Interactive Graphics Lecture 9: Slide 1
 Interactive Graphics Lecture 9: Introduction to Spline Curves Interactive Graphics Lecture 9: Slide 1 Interactive Graphics Lecture 13: Slide 2 Splines The word spline comes from the ship building trade
Interactive Graphics Lecture 9: Introduction to Spline Curves Interactive Graphics Lecture 9: Slide 1 Interactive Graphics Lecture 13: Slide 2 Splines The word spline comes from the ship building trade
8.1 Geometric Queries for Ray Tracing
 Fall 2017 CSCI 420: Computer Graphics 8.1 Geometric Queries for Ray Tracing Hao Li http://cs420.hao-li.com 1 Outline Ray-Surface Intersections Special cases: sphere, polygon Barycentric coordinates 2 Outline
Fall 2017 CSCI 420: Computer Graphics 8.1 Geometric Queries for Ray Tracing Hao Li http://cs420.hao-li.com 1 Outline Ray-Surface Intersections Special cases: sphere, polygon Barycentric coordinates 2 Outline
CSE 167: Introduction to Computer Graphics Lecture #13: Curves. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2017
 CSE 167: Introduction to Computer Graphics Lecture #13: Curves Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2017 Announcements Project 4 due Monday Nov 27 at 2pm Next Tuesday:
CSE 167: Introduction to Computer Graphics Lecture #13: Curves Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2017 Announcements Project 4 due Monday Nov 27 at 2pm Next Tuesday:
CSE328 Fundamentals of Computer Graphics: Concepts, Theory, Algorithms, and Applications
 CSE328 Fundamentals of Computer Graphics: Concepts, Theory, Algorithms, and Applications Hong Qin Stony Brook University (SUNY at Stony Brook) Stony Brook, New York 11794-4400 Tel: (631)632-8450; Fax:
CSE328 Fundamentals of Computer Graphics: Concepts, Theory, Algorithms, and Applications Hong Qin Stony Brook University (SUNY at Stony Brook) Stony Brook, New York 11794-4400 Tel: (631)632-8450; Fax:
Interactive Computer Graphics A TOP-DOWN APPROACH WITH SHADER-BASED OPENGL
 International Edition Interactive Computer Graphics A TOP-DOWN APPROACH WITH SHADER-BASED OPENGL Sixth Edition Edward Angel Dave Shreiner Interactive Computer Graphics: A Top-Down Approach with Shader-Based
International Edition Interactive Computer Graphics A TOP-DOWN APPROACH WITH SHADER-BASED OPENGL Sixth Edition Edward Angel Dave Shreiner Interactive Computer Graphics: A Top-Down Approach with Shader-Based
Visible Surface Detection Methods
 Visible urface Detection Methods Visible-urface Detection identifying visible parts of a scene (also hidden- elimination) type of algorithm depends on: complexity of scene type of objects available equipment
Visible urface Detection Methods Visible-urface Detection identifying visible parts of a scene (also hidden- elimination) type of algorithm depends on: complexity of scene type of objects available equipment
