Clipping & Culling. Lecture 11 Spring Trivial Rejection Outcode Clipping Plane-at-a-time Clipping Backface Culling
|
|
|
- Ariel Turner
- 6 years ago
- Views:
Transcription
1 Clipping & Culling Trivial Rejection Outcode Clipping Plane-at-a-time Clipping Backface Culling Lecture 11 Spring 2015
2 What is Clipping? Clipping is a procedure for spatially partitioning geometric primitives, according to their containment within some region. Clipping can be used to: Distinguish whether geometric primitives are inside or outside of a viewing frustum Distinguish whether geometric primitives are inside or outside of a picking frustum Detecting intersections between primitives 2
3 What is Clipping? Clipping is a procedure for subdividing geometric primitives. This view of clipping admits several other potential applications. Binning geometric primitives into spatial data structures. Computing analytical shadows. Computing intersections between primitives 3
4 Clipping is an important optimization Why do we Clip? Clipping is a visibility preprocess. In real-world scenes clipping can remove a substantial percentage of the environment from consideration. Assures that only potentially visible primitives are rasterized. What advantage does this have over twodimensional clipping. Are there cases where you have to clip? 4
5 Where do we Clip? There are at least 3 different stages in the rendering pipeline where we do various forms of clipping. In the trivial rejection stage we remove objects that can not be seen. The clipping stage removes objects and parts of objects that fall outside of the viewing frustum. And, when rasterizing, clipping is used to remove parts of objects outside of the view port. xmin = (int) (v[sort[xflag][0]].x); xmax = (int) (v[sort[xflag][1]].x + 1); ymin = (int) (v[sort[yflag][1]].y); ymax = (int) (v[sort[yflag][0]].y + 1); /* clip triangle's bounding box to raster */ xmin = (xmin < 0)? 0 : xmin; xmax = (xmax >= width)? width - 1 : xmax; ymin = (ymin < 0)? 0 : ymin; ymax = (ymax >= height)? height - 1 : ymax; 5
6 Trivial Rejection Clipping One of the keys to all clipping algorithms is the notion of half-space partitioning. We ve seen this before when we discussed how edge equations partition the image plane into two regions, one negative the other nonnegative. The same notion extends to 3-dimensions, but partitioning elements are planes rather than lines. The equation of a plane in 3D is given as: x y z 1 n n n 0 d x A vector dotted with a point. The vector is the plane s normal. The points of the plane are a fixed distance, d, from the origin, after projection onto the normal. y z 6
7 Here is a simple Example: Trivial Rejection Clipping If we orient a plane so that it passes through our viewing position and our look-at direction is aligned with its normal. Then we can easily partition objects into three classes, those behind our viewing frustum, those in front, and those that are partially in both half-spaces. 7
8 Outcode Clipping (a.k.a. Cohen-Sutherland Clipping) The extension of plane partitioning to multiple planes, gives a simple form of clipping called Cohen-Sutherland Clipping. This is a rough approach to clipping in that it only classifies each of it's input primitives, rather than forces them to conform to the viewing window. A simple 2-D example is shown on the right. This technique classifies each vertex of a primitive, by generating an outcode. An outcode identifies the appropriate half space location of each vertex relative to all of the clipping planes. Outcodes are usually stored as bit vectors. By comparing the bit vectors from all of the vertices associated with a primitive we can develop conclusions about the whole primitive. 8
9 Outcode Clipping of Lines First, let's consider line segments. if (outcode1 == '0000' && outcode2 == 0000) then line segment is inside else if ((outcode1 & outcode2) == 0000) then line segment potentially crosses clip region else line is entirely outside of clip region endif endif Notice that the test cannot conclusively state whether the segment crosses the clip region. This might cause some segments that are located entirely outside of the clipping volume to be subsequently processed. Is there a way to modify this test so that it can eliminate these false positives? 9
10 Outcode Clipping of Triangles For triangles we need only modify the tests so that all vertices are considered: if (outcode1 == '0000' && outcode2 == '0000' && outcode3 == '0000') then triangle is inside else if ((outcode1 & outcode2 & outcode3) == '0000') then line segment potentially crosses clip region else line is entirely outside of clip region endif endif This form of clipping is not limited to triangles or convex polygons. It is simple to implement. But, it won t handle all of our problems... 10
11 Dealing with Crossing Cases The hard part of clipping is handling objects and primitives that straddle clipping planes. In some cases we can ignore these problems because the combination of screen-space clipping and outcode clipping will handle most cases. However, there is one case in general that cannot be handled this way. This is the case when parts of a primitive lies both in front of and behind the viewpoint. This complication is caused by our projection stage. It has the nasty habit of mapping objects behind the viewpoint to positions in front of it. 11
12 One-Plane-at-a-Time Clipping (a.k.a. Sutherland-Hodgeman Clipping) The Sutherland-Hodgeman triangle clipping algorithm uses a divide-and-conquer strategy. It first solves the simple problem of clipping a triangle against a single plane. There are four possible relationships that a triangle can have relative to a clipping plane as shown in the figures on the right. Each of the clipping planes are applied in succession to every triangle. There is minimal storage requirements for this algorithm, and it is well suited to pipelining. As a result it is often used in hardware implementations. 12
13 Plane-at-a-Time Clipping The results of Sutherland-Hodgeman clipping can get complicated very quickly once multiple clip-planes are considered. However, the algorithm is still very simple. Each clip plane is treated independently, and each triangle is treated by on of the four cases mentioned previously. It is straightforward to extend this algorithm to 3D. 13
14 Advantages: Recap of Plane-at-a-time Clipping Elegant (few special cases) Robust (handles boundary and edge conditions well) Well suited to hardware Canonical clipping makes fixed-point implementations manageable Disadvantages: Hard to fix into O-O paradigm (Reentrant, objects spawn new short-lived objects) Only works for convex clipping volumes Often generates more than the minimum number of triangles needed Requires a divide per clipped edge 14
15 Alternatives to Plane-at-a-time Over the years there have been several improvements to plane-at-a-time clipping. Clipping against concave volumes (Wieler-Atherton clipping) Can clip arbitrary polygons against arbitrary polygons Maintains more state than plane-at-a-time clipping Handle all planes at once (Nicholle-Lee-Nicholle clipping) It waits before generating triangles to reduce the number of clip sections generated. Tracks polygon through the 27 sub-regions relative to the clip volume Might need to generate a "corner vertex" 15
16 Back-Face Culling Back-face culling addresses a special case of occlusion called convex self-occlusion. Basically, if an object is closed (having a well defined inside and outside) then some parts of the outer surface must be blocked by other parts of the same surface. We'll be more precise with our definitions in a minute. On such surfaces we need only consider the normals of surface elements to determine if they are visible. 16
17 Idea: Compare the normal of each face with the viewing direction Given n, the outward-pointing normal of F foreach face F of object if (n. v > 0) throw away the face Does it work? Removing Back-Faces 17
18 Fixing the Problem We can t do view direction clipping just anywhere! Downside: Projection comes fairly late in the pipeline. It would be nice to cull objects sooner. Upside: Computing the dot product is simpler. You need only look at the sign of the plane s z component. 18
19 Culling Technique #2 Detect a change in screen-space orientation. If all face vertices are ordered in a consistent way, back-facing primitives can be found by detecting a reversal in this order. One choice is a counterclockwise ordering when viewed from outside of the manifold. This is consistent with computing face normals (Why?). If, after projection, we ever see a clockwise face, it must be back facing. This approach will work for all cases, but it comes even later in the pipe, at triangle setup. We already do this calculation in our triangle rasterizer. It is equivalent to determining a triangle with negative area. 19
20 Culling Plane-Test Here is a culling test that will work anywhere in the pipeline. Remove faces that have the eye in their negative half-space. This requires computing a plane equation for each face considered. x y z 1 n n n 0 d 0 x y z We will still need to compute the normal (How?). But, we don t have to normalize it. (How do we go about computing a value for d?) 20
21 Culling Plane-Test Once we have the plane equation, we substitute the coordinate of the viewing point (the eye coordinate in our viewing matrix). If it is negative, then the surface is backfacing. Example: 21
22 Back Face Culling in OpenGL Back Face Culling is available as a mode setting in OpenGL. very flexible (can cull fronts as well as backs) it can double your performance! depends on consistent models public void backfacecull(bool turnon) { if (turnon) { glfrontface(gl_ccw); // define the orientation of front faces glenable(gl_cull_face); // enable Culling glcullface(gl_back); // tell which faces to cull } else { gldisable(gl_cull_face); // disable Culling } } 22
23 I think that I shall never see A Binary Space Partition (BSP) tree is a simple spatial data structure: 1. Select a partitioning plane/face. 2. Partition the remaining planes/faces according to the side of the partitioning plane that they fall on (+ or -). 3. Repeat with each of the two new sets. Partitioning facets: Partitioning requires testing all facets in the active set to find if they 1) lie entirely on the positive side of the partition plane, 2) lie entirely on the negative side, or 3) if they cross it. In the 3 rd case of a crossing face we clip the offending face into two halves (using our plane-at-a-time clipping algorithm). Lecture 13
24 Computing Visibility with BSP trees Starting at the root of the tree. 1. Classify viewpoint as being in the positive or negative halfspace of our plane 2. Call this routine with the negative child (if it exists) 3. Draw the current partitioning plane 4. Call this routine with the positive child (if it exists) Intuitively, at each partition, we first draw the stuff further away than the current plane, then we draw the current plane, and then we draw the closer stuff. BSP traversal is called a "hidden surface elimination" algorithm, but it doesn t really "eliminate" anything; it simply orders the drawing of primitive in a back-to-front order. Lecture 13
25 BSP Tree Example Computing visibility or depth-sorting with BSP trees is both simple and fast. It resolves visibility at the primitive level. Visibility computation is independent of screen size Requires considerable preprocessing of the scene primitives Primitives must be easy to subdivide along planes Supports Constructive Solid Geometry (CSG) modeling Lecture 13
What is Clipping? Why do we Clip? Lecture 9 Comp 236 Spring Clipping is an important optimization
 Clipping, Culling, Picking & Selection Trivial Rejection Outcode Clipping Plane-at-a-time Clipping Backface Culling Picking Selection Programming Assignment #2 Lecture 9 Comp 236 Spring 2005 What is Clipping?
Clipping, Culling, Picking & Selection Trivial Rejection Outcode Clipping Plane-at-a-time Clipping Backface Culling Picking Selection Programming Assignment #2 Lecture 9 Comp 236 Spring 2005 What is Clipping?
Computing Visibility. Backface Culling for General Visibility. One More Trick with Planes. BSP Trees Ray Casting Depth Buffering Quiz
 Computing Visibility BSP Trees Ray Casting Depth Buffering Quiz Power of Plane Equations We ve gotten a lot of mileage out of one simple equation. Basis for D outcode-clipping Basis for plane-at-a-time
Computing Visibility BSP Trees Ray Casting Depth Buffering Quiz Power of Plane Equations We ve gotten a lot of mileage out of one simple equation. Basis for D outcode-clipping Basis for plane-at-a-time
Sung-Eui Yoon ( 윤성의 )
 CS380: Computer Graphics Clipping and Culling Sung-Eui Yoon ( 윤성의 ) Course URL: http://sglab.kaist.ac.kr/~sungeui/cg/ Class Objectives Understand clipping and culling Understand view-frustum, back-face
CS380: Computer Graphics Clipping and Culling Sung-Eui Yoon ( 윤성의 ) Course URL: http://sglab.kaist.ac.kr/~sungeui/cg/ Class Objectives Understand clipping and culling Understand view-frustum, back-face
VISIBILITY & CULLING. Don t draw what you can t see. Thomas Larsson, Afshin Ameri DVA338, Spring 2018, MDH
 VISIBILITY & CULLING Don t draw what you can t see. Thomas Larsson, Afshin Ameri DVA338, Spring 2018, MDH Visibility Visibility Given a set of 3D objects, which surfaces are visible from a specific point
VISIBILITY & CULLING Don t draw what you can t see. Thomas Larsson, Afshin Ameri DVA338, Spring 2018, MDH Visibility Visibility Given a set of 3D objects, which surfaces are visible from a specific point
Culling. Computer Graphics CSE 167 Lecture 12
 Culling Computer Graphics CSE 167 Lecture 12 CSE 167: Computer graphics Culling Definition: selecting from a large quantity In computer graphics: selecting primitives (or batches of primitives) that are
Culling Computer Graphics CSE 167 Lecture 12 CSE 167: Computer graphics Culling Definition: selecting from a large quantity In computer graphics: selecting primitives (or batches of primitives) that are
3D Rendering Pipeline (for direct illumination)
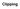 Clipping 3D Rendering Pipeline (for direct illumination) 3D Primitives 3D Modeling Coordinates Modeling Transformation Lighting 3D Camera Coordinates Projection Transformation Clipping 2D Screen Coordinates
Clipping 3D Rendering Pipeline (for direct illumination) 3D Primitives 3D Modeling Coordinates Modeling Transformation Lighting 3D Camera Coordinates Projection Transformation Clipping 2D Screen Coordinates
CSE 167: Introduction to Computer Graphics Lecture #4: Vertex Transformation
 CSE 167: Introduction to Computer Graphics Lecture #4: Vertex Transformation Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2013 Announcements Project 2 due Friday, October 11
CSE 167: Introduction to Computer Graphics Lecture #4: Vertex Transformation Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2013 Announcements Project 2 due Friday, October 11
Computer Graphics. Bing-Yu Chen National Taiwan University The University of Tokyo
 Computer Graphics Bing-Yu Chen National Taiwan University The University of Tokyo Hidden-Surface Removal Back-Face Culling The Depth-Sort Algorithm Binary Space-Partitioning Trees The z-buffer Algorithm
Computer Graphics Bing-Yu Chen National Taiwan University The University of Tokyo Hidden-Surface Removal Back-Face Culling The Depth-Sort Algorithm Binary Space-Partitioning Trees The z-buffer Algorithm
Motivation. Culling Don t draw what you can t see! What can t we see? Low-level Culling
 Motivation Culling Don t draw what you can t see! Thomas Larsson Mälardalen University April 7, 2016 Image correctness Rendering speed One day we will have enough processing power!? Goals of real-time
Motivation Culling Don t draw what you can t see! Thomas Larsson Mälardalen University April 7, 2016 Image correctness Rendering speed One day we will have enough processing power!? Goals of real-time
CSE 167: Lecture #5: Rasterization. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2012
 CSE 167: Introduction to Computer Graphics Lecture #5: Rasterization Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2012 Announcements Homework project #2 due this Friday, October
CSE 167: Introduction to Computer Graphics Lecture #5: Rasterization Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2012 Announcements Homework project #2 due this Friday, October
CSE 167: Introduction to Computer Graphics Lecture #11: Visibility Culling
 CSE 167: Introduction to Computer Graphics Lecture #11: Visibility Culling Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2017 Announcements Project 3 due Monday Nov 13 th at
CSE 167: Introduction to Computer Graphics Lecture #11: Visibility Culling Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2017 Announcements Project 3 due Monday Nov 13 th at
Computer Graphics. Bing-Yu Chen National Taiwan University
 Computer Graphics Bing-Yu Chen National Taiwan University Visible-Surface Determination Back-Face Culling The Depth-Sort Algorithm Binary Space-Partitioning Trees The z-buffer Algorithm Scan-Line Algorithm
Computer Graphics Bing-Yu Chen National Taiwan University Visible-Surface Determination Back-Face Culling The Depth-Sort Algorithm Binary Space-Partitioning Trees The z-buffer Algorithm Scan-Line Algorithm
S U N G - E U I YO O N, K A I S T R E N D E R I N G F R E E LY A VA I L A B L E O N T H E I N T E R N E T
 S U N G - E U I YO O N, K A I S T R E N D E R I N G F R E E LY A VA I L A B L E O N T H E I N T E R N E T Copyright 2018 Sung-eui Yoon, KAIST freely available on the internet http://sglab.kaist.ac.kr/~sungeui/render
S U N G - E U I YO O N, K A I S T R E N D E R I N G F R E E LY A VA I L A B L E O N T H E I N T E R N E T Copyright 2018 Sung-eui Yoon, KAIST freely available on the internet http://sglab.kaist.ac.kr/~sungeui/render
Overview. Pipeline implementation I. Overview. Required Tasks. Preliminaries Clipping. Hidden Surface removal
 Overview Pipeline implementation I Preliminaries Clipping Line clipping Hidden Surface removal Overview At end of the geometric pipeline, vertices have been assembled into primitives Must clip out primitives
Overview Pipeline implementation I Preliminaries Clipping Line clipping Hidden Surface removal Overview At end of the geometric pipeline, vertices have been assembled into primitives Must clip out primitives
CSE 167: Introduction to Computer Graphics Lecture #9: Visibility. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2018
 CSE 167: Introduction to Computer Graphics Lecture #9: Visibility Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2018 Announcements Midterm Scores are on TritonEd Exams to be
CSE 167: Introduction to Computer Graphics Lecture #9: Visibility Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2018 Announcements Midterm Scores are on TritonEd Exams to be
Hidden surface removal. Computer Graphics
 Lecture Hidden Surface Removal and Rasterization Taku Komura Hidden surface removal Drawing polygonal faces on screen consumes CPU cycles Illumination We cannot see every surface in scene We don t want
Lecture Hidden Surface Removal and Rasterization Taku Komura Hidden surface removal Drawing polygonal faces on screen consumes CPU cycles Illumination We cannot see every surface in scene We don t want
CSE 167: Introduction to Computer Graphics Lecture #10: View Frustum Culling
 CSE 167: Introduction to Computer Graphics Lecture #10: View Frustum Culling Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2015 Announcements Project 4 due tomorrow Project
CSE 167: Introduction to Computer Graphics Lecture #10: View Frustum Culling Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2015 Announcements Project 4 due tomorrow Project
Lecture 25 of 41. Spatial Sorting: Binary Space Partitioning Quadtrees & Octrees
 Spatial Sorting: Binary Space Partitioning Quadtrees & Octrees William H. Hsu Department of Computing and Information Sciences, KSU KSOL course pages: http://bit.ly/hgvxlh / http://bit.ly/evizre Public
Spatial Sorting: Binary Space Partitioning Quadtrees & Octrees William H. Hsu Department of Computing and Information Sciences, KSU KSOL course pages: http://bit.ly/hgvxlh / http://bit.ly/evizre Public
MIT EECS 6.837, Teller and Durand 1
 MIT EECS 6.837, Teller and Durand 1 Clipping MIT EECS 6.837 Frédo Durand and Seth Teller Some slides and images courtesy of Leonard McMillan MIT EECS 6.837, Teller and Durand 2 Administrative Assignment
MIT EECS 6.837, Teller and Durand 1 Clipping MIT EECS 6.837 Frédo Durand and Seth Teller Some slides and images courtesy of Leonard McMillan MIT EECS 6.837, Teller and Durand 2 Administrative Assignment
The Traditional Graphics Pipeline
 Last Time? The Traditional Graphics Pipeline Participating Media Measuring BRDFs 3D Digitizing & Scattering BSSRDFs Monte Carlo Simulation Dipole Approximation Today Ray Casting / Tracing Advantages? Ray
Last Time? The Traditional Graphics Pipeline Participating Media Measuring BRDFs 3D Digitizing & Scattering BSSRDFs Monte Carlo Simulation Dipole Approximation Today Ray Casting / Tracing Advantages? Ray
Class of Algorithms. Visible Surface Determination. Back Face Culling Test. Back Face Culling: Object Space v. Back Face Culling: Object Space.
 Utah School of Computing Spring 13 Class of Algorithms Lecture Set Visible Surface Determination CS56 Computer Graphics From Rich Riesenfeld Spring 13 Object (Model) Space Algorithms Work in the model
Utah School of Computing Spring 13 Class of Algorithms Lecture Set Visible Surface Determination CS56 Computer Graphics From Rich Riesenfeld Spring 13 Object (Model) Space Algorithms Work in the model
Spatial Data Structures and Speed-Up Techniques. Tomas Akenine-Möller Department of Computer Engineering Chalmers University of Technology
 Spatial Data Structures and Speed-Up Techniques Tomas Akenine-Möller Department of Computer Engineering Chalmers University of Technology Spatial data structures What is it? Data structure that organizes
Spatial Data Structures and Speed-Up Techniques Tomas Akenine-Möller Department of Computer Engineering Chalmers University of Technology Spatial data structures What is it? Data structure that organizes
Clipping and Scan Conversion
 15-462 Computer Graphics I Lecture 14 Clipping and Scan Conversion Line Clipping Polygon Clipping Clipping in Three Dimensions Scan Conversion (Rasterization) [Angel 7.3-7.6, 7.8-7.9] March 19, 2002 Frank
15-462 Computer Graphics I Lecture 14 Clipping and Scan Conversion Line Clipping Polygon Clipping Clipping in Three Dimensions Scan Conversion (Rasterization) [Angel 7.3-7.6, 7.8-7.9] March 19, 2002 Frank
Page 1. Area-Subdivision Algorithms z-buffer Algorithm List Priority Algorithms BSP (Binary Space Partitioning Tree) Scan-line Algorithms
 Visible Surface Determination Visibility Culling Area-Subdivision Algorithms z-buffer Algorithm List Priority Algorithms BSP (Binary Space Partitioning Tree) Scan-line Algorithms Divide-and-conquer strategy:
Visible Surface Determination Visibility Culling Area-Subdivision Algorithms z-buffer Algorithm List Priority Algorithms BSP (Binary Space Partitioning Tree) Scan-line Algorithms Divide-and-conquer strategy:
Computer Graphics. - Clipping - Philipp Slusallek & Stefan Lemme
 Computer Graphics - Clipping - Philipp Slusallek & Stefan Lemme Clipping Motivation Projected primitive might fall (partially) outside of the visible display window E.g. if standing inside a building Eliminate
Computer Graphics - Clipping - Philipp Slusallek & Stefan Lemme Clipping Motivation Projected primitive might fall (partially) outside of the visible display window E.g. if standing inside a building Eliminate
CSE328 Fundamentals of Computer Graphics: Concepts, Theory, Algorithms, and Applications
 CSE328 Fundamentals of Computer Graphics: Concepts, Theory, Algorithms, and Applications Hong Qin Stony Brook University (SUNY at Stony Brook) Stony Brook, New York 11794-4400 Tel: (631)632-8450; Fax:
CSE328 Fundamentals of Computer Graphics: Concepts, Theory, Algorithms, and Applications Hong Qin Stony Brook University (SUNY at Stony Brook) Stony Brook, New York 11794-4400 Tel: (631)632-8450; Fax:
Computer Graphics (CS 543) Lecture 9 (Part 2): Clipping. Prof Emmanuel Agu. Computer Science Dept. Worcester Polytechnic Institute (WPI)
 Computer Graphics (CS 543) Lecture 9 (Part 2): Clipping Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) OpenGL Stages After projection, several stages before objects drawn
Computer Graphics (CS 543) Lecture 9 (Part 2): Clipping Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) OpenGL Stages After projection, several stages before objects drawn
FROM VERTICES TO FRAGMENTS. Lecture 5 Comp3080 Computer Graphics HKBU
 FROM VERTICES TO FRAGMENTS Lecture 5 Comp3080 Computer Graphics HKBU OBJECTIVES Introduce basic implementation strategies Clipping Scan conversion OCTOBER 9, 2011 2 OVERVIEW At end of the geometric pipeline,
FROM VERTICES TO FRAGMENTS Lecture 5 Comp3080 Computer Graphics HKBU OBJECTIVES Introduce basic implementation strategies Clipping Scan conversion OCTOBER 9, 2011 2 OVERVIEW At end of the geometric pipeline,
Computer Graphics. Lecture 9 Hidden Surface Removal. Taku Komura
 Computer Graphics Lecture 9 Hidden Surface Removal Taku Komura 1 Why Hidden Surface Removal? A correct rendering requires correct visibility calculations When multiple opaque polygons cover the same screen
Computer Graphics Lecture 9 Hidden Surface Removal Taku Komura 1 Why Hidden Surface Removal? A correct rendering requires correct visibility calculations When multiple opaque polygons cover the same screen
CSE528 Computer Graphics: Theory, Algorithms, and Applications
 CSE528 Computer Graphics: Theory, Algorithms, and Applications Hong Qin Stony Brook University (SUNY at Stony Brook) Stony Brook, New York 11794-2424 Tel: (631)632-845; Fax: (631)632-8334 qin@cs.stonybrook.edu
CSE528 Computer Graphics: Theory, Algorithms, and Applications Hong Qin Stony Brook University (SUNY at Stony Brook) Stony Brook, New York 11794-2424 Tel: (631)632-845; Fax: (631)632-8334 qin@cs.stonybrook.edu
The Traditional Graphics Pipeline
 Last Time? The Traditional Graphics Pipeline Reading for Today A Practical Model for Subsurface Light Transport, Jensen, Marschner, Levoy, & Hanrahan, SIGGRAPH 2001 Participating Media Measuring BRDFs
Last Time? The Traditional Graphics Pipeline Reading for Today A Practical Model for Subsurface Light Transport, Jensen, Marschner, Levoy, & Hanrahan, SIGGRAPH 2001 Participating Media Measuring BRDFs
Visibility: Z Buffering
 University of British Columbia CPSC 414 Computer Graphics Visibility: Z Buffering Week 1, Mon 3 Nov 23 Tamara Munzner 1 Poll how far are people on project 2? preferences for Plan A: status quo P2 stays
University of British Columbia CPSC 414 Computer Graphics Visibility: Z Buffering Week 1, Mon 3 Nov 23 Tamara Munzner 1 Poll how far are people on project 2? preferences for Plan A: status quo P2 stays
CSE328 Fundamentals of Computer Graphics
 CSE328 Fundamentals of Computer Graphics Hong Qin State University of New York at Stony Brook (Stony Brook University) Stony Brook, New York 794--44 Tel: (63)632-845; Fax: (63)632-8334 qin@cs.sunysb.edu
CSE328 Fundamentals of Computer Graphics Hong Qin State University of New York at Stony Brook (Stony Brook University) Stony Brook, New York 794--44 Tel: (63)632-845; Fax: (63)632-8334 qin@cs.sunysb.edu
CS452/552; EE465/505. Clipping & Scan Conversion
 CS452/552; EE465/505 Clipping & Scan Conversion 3-31 15 Outline! From Geometry to Pixels: Overview Clipping (continued) Scan conversion Read: Angel, Chapter 8, 8.1-8.9 Project#1 due: this week Lab4 due:
CS452/552; EE465/505 Clipping & Scan Conversion 3-31 15 Outline! From Geometry to Pixels: Overview Clipping (continued) Scan conversion Read: Angel, Chapter 8, 8.1-8.9 Project#1 due: this week Lab4 due:
Clipping and Intersection
 Clipping and Intersection Clipping: Remove points, line segments, polygons outside a region of interest. Need to discard everything that s outside of our window. Point clipping: Remove points outside window.
Clipping and Intersection Clipping: Remove points, line segments, polygons outside a region of interest. Need to discard everything that s outside of our window. Point clipping: Remove points outside window.
The Traditional Graphics Pipeline
 Final Projects Proposals due Thursday 4/8 Proposed project summary At least 3 related papers (read & summarized) Description of series of test cases Timeline & initial task assignment The Traditional Graphics
Final Projects Proposals due Thursday 4/8 Proposed project summary At least 3 related papers (read & summarized) Description of series of test cases Timeline & initial task assignment The Traditional Graphics
CSE528 Computer Graphics: Theory, Algorithms, and Applications
 CSE528 Computer Graphics: Theory, Algorithms, and Applications Hong Qin State University of New York at Stony Brook (Stony Brook University) Stony Brook, New York 11794--4400 Tel: (631)632-8450; Fax: (631)632-8334
CSE528 Computer Graphics: Theory, Algorithms, and Applications Hong Qin State University of New York at Stony Brook (Stony Brook University) Stony Brook, New York 11794--4400 Tel: (631)632-8450; Fax: (631)632-8334
CS602 MCQ,s for midterm paper with reference solved by Shahid
 #1 Rotating a point requires The coordinates for the point The rotation angles Both of above Page No 175 None of above #2 In Trimetric the direction of projection makes unequal angle with the three principal
#1 Rotating a point requires The coordinates for the point The rotation angles Both of above Page No 175 None of above #2 In Trimetric the direction of projection makes unequal angle with the three principal
Hidden Surface Removal
 Outline Introduction Hidden Surface Removal Hidden Surface Removal Simone Gasparini gasparini@elet.polimi.it Back face culling Depth sort Z-buffer Introduction Graphics pipeline Introduction Modeling Geom
Outline Introduction Hidden Surface Removal Hidden Surface Removal Simone Gasparini gasparini@elet.polimi.it Back face culling Depth sort Z-buffer Introduction Graphics pipeline Introduction Modeling Geom
CS123 INTRODUCTION TO COMPUTER GRAPHICS. Clipping. Concepts, Algorithms for line clipping. 1 of 16. Andries van Dam. Clipping - 10/12/17
 Clipping Concepts, Algorithms for line clipping 1 of 16 Line Clipping in 2D Clipping endpoints If x min x x max and y min y y max, the point is inside the clip rectangle. Endpoint analysis for lines: if
Clipping Concepts, Algorithms for line clipping 1 of 16 Line Clipping in 2D Clipping endpoints If x min x x max and y min y y max, the point is inside the clip rectangle. Endpoint analysis for lines: if
Computer Graphics: 7-Polygon Rasterization, Clipping
 Computer Graphics: 7-Polygon Rasterization, Clipping Prof. Dr. Charles A. Wüthrich, Fakultät Medien, Medieninformatik Bauhaus-Universität Weimar caw AT medien.uni-weimar.de Filling polygons (and drawing
Computer Graphics: 7-Polygon Rasterization, Clipping Prof. Dr. Charles A. Wüthrich, Fakultät Medien, Medieninformatik Bauhaus-Universität Weimar caw AT medien.uni-weimar.de Filling polygons (and drawing
Hidden Surfaces II. Week 9, Mon Mar 15
 University of British Columbia CPSC 314 Computer Graphics Jan-Apr 2010 Tamara Munzner Hidden Surfaces II Week 9, Mon Mar 15 http://www.ugrad.cs.ubc.ca/~cs314/vjan2010 ews yes, I'm granting the request
University of British Columbia CPSC 314 Computer Graphics Jan-Apr 2010 Tamara Munzner Hidden Surfaces II Week 9, Mon Mar 15 http://www.ugrad.cs.ubc.ca/~cs314/vjan2010 ews yes, I'm granting the request
From Vertices To Fragments-1
 From Vertices To Fragments-1 1 Objectives Clipping Line-segment clipping polygon clipping 2 Overview At end of the geometric pipeline, vertices have been assembled into primitives Must clip out primitives
From Vertices To Fragments-1 1 Objectives Clipping Line-segment clipping polygon clipping 2 Overview At end of the geometric pipeline, vertices have been assembled into primitives Must clip out primitives
Visibility and Occlusion Culling
 Visibility and Occlusion Culling CS535 Fall 2014 Daniel G. Aliaga Department of Computer Science Purdue University [some slides based on those of Benjamin Mora] Why? To avoid processing geometry that does
Visibility and Occlusion Culling CS535 Fall 2014 Daniel G. Aliaga Department of Computer Science Purdue University [some slides based on those of Benjamin Mora] Why? To avoid processing geometry that does
Today. CS-184: Computer Graphics. Lecture #10: Clipping and Hidden Surfaces. Clipping. Hidden Surface Removal
 Today CS-184: Computer Graphics Lecture #10: Clipping and Hidden Surfaces!! Prof. James O Brien University of California, Berkeley! V2015-S-10-1.0 Clipping Clipping to view volume Clipping arbitrary polygons
Today CS-184: Computer Graphics Lecture #10: Clipping and Hidden Surfaces!! Prof. James O Brien University of California, Berkeley! V2015-S-10-1.0 Clipping Clipping to view volume Clipping arbitrary polygons
Hidden Surface Elimination: BSP trees
 Hidden Surface Elimination: BSP trees Outline Binary space partition (BSP) trees Polygon-aligned 1 BSP Trees Basic idea: Preprocess geometric primitives in scene to build a spatial data structure such
Hidden Surface Elimination: BSP trees Outline Binary space partition (BSP) trees Polygon-aligned 1 BSP Trees Basic idea: Preprocess geometric primitives in scene to build a spatial data structure such
Triangle Rasterization
 Triangle Rasterization Computer Graphics COMP 770 (236) Spring 2007 Instructor: Brandon Lloyd 2/07/07 1 From last time Lines and planes Culling View frustum culling Back-face culling Occlusion culling
Triangle Rasterization Computer Graphics COMP 770 (236) Spring 2007 Instructor: Brandon Lloyd 2/07/07 1 From last time Lines and planes Culling View frustum culling Back-face culling Occlusion culling
Last class. A vertex (w x, w y, w z, w) - clipping is in the - windowing and viewport normalized view volume if: - scan conversion/ rasterization
 Lecture 6 Last class Last lecture (clip coordinates): A vertex (w x, w y, w z, w) - clipping is in the - windowing and viewport normalized view volume if: - scan conversion/ rasterization normalized view
Lecture 6 Last class Last lecture (clip coordinates): A vertex (w x, w y, w z, w) - clipping is in the - windowing and viewport normalized view volume if: - scan conversion/ rasterization normalized view
2D rendering takes a photo of the 2D scene with a virtual camera that selects an axis aligned rectangle from the scene. The photograph is placed into
 2D rendering takes a photo of the 2D scene with a virtual camera that selects an axis aligned rectangle from the scene. The photograph is placed into the viewport of the current application window. A pixel
2D rendering takes a photo of the 2D scene with a virtual camera that selects an axis aligned rectangle from the scene. The photograph is placed into the viewport of the current application window. A pixel
Computer Graphics Geometry and Transform
 ! Computer Graphics 2014! 5. Geometry and Transform Hongxin Zhang State Key Lab of CAD&CG, Zhejiang University 2014-10-11! Today outline Triangle rasterization Basic vector algebra ~ geometry! Antialiasing
! Computer Graphics 2014! 5. Geometry and Transform Hongxin Zhang State Key Lab of CAD&CG, Zhejiang University 2014-10-11! Today outline Triangle rasterization Basic vector algebra ~ geometry! Antialiasing
Clipping. Angel and Shreiner: Interactive Computer Graphics 7E Addison-Wesley 2015
 Clipping 1 Objectives Clipping lines First of implementation algorithms Clipping polygons (next lecture) Focus on pipeline plus a few classic algorithms 2 Clipping 2D against clipping window 3D against
Clipping 1 Objectives Clipping lines First of implementation algorithms Clipping polygons (next lecture) Focus on pipeline plus a few classic algorithms 2 Clipping 2D against clipping window 3D against
INFOGR Computer Graphics. J. Bikker - April-July Lecture 11: Visibility. Welcome!
 INFOGR Computer Graphics J. Bikker - April-July 2016 - Lecture 11: Visibility Welcome! Smallest Ray Tracers: Executable 5692598 & 5683777: RTMini_minimal.exe 2803 bytes 5741858: ASM_CPU_Min_Exe 994 bytes
INFOGR Computer Graphics J. Bikker - April-July 2016 - Lecture 11: Visibility Welcome! Smallest Ray Tracers: Executable 5692598 & 5683777: RTMini_minimal.exe 2803 bytes 5741858: ASM_CPU_Min_Exe 994 bytes
Determination (Penentuan Permukaan Tampak)
 Visible Surface Determination (Penentuan Permukaan Tampak) Visible Surface Determination 1/26 Outline Definisi VSD Tiga Kelas Algoritma VSD Kelas : Conservative Spatial Subdivison Bounding Volume Back
Visible Surface Determination (Penentuan Permukaan Tampak) Visible Surface Determination 1/26 Outline Definisi VSD Tiga Kelas Algoritma VSD Kelas : Conservative Spatial Subdivison Bounding Volume Back
Visible-Surface Detection Methods. Chapter? Intro. to Computer Graphics Spring 2008, Y. G. Shin
 Visible-Surface Detection Methods Chapter? Intro. to Computer Graphics Spring 2008, Y. G. Shin The Visibility Problem [Problem Statement] GIVEN: a set of 3-D surfaces, a projection from 3-D to 2-D screen,
Visible-Surface Detection Methods Chapter? Intro. to Computer Graphics Spring 2008, Y. G. Shin The Visibility Problem [Problem Statement] GIVEN: a set of 3-D surfaces, a projection from 3-D to 2-D screen,
3D Polygon Rendering. Many applications use rendering of 3D polygons with direct illumination
 Rendering Pipeline 3D Polygon Rendering Many applications use rendering of 3D polygons with direct illumination 3D Polygon Rendering What steps are necessary to utilize spatial coherence while drawing
Rendering Pipeline 3D Polygon Rendering Many applications use rendering of 3D polygons with direct illumination 3D Polygon Rendering What steps are necessary to utilize spatial coherence while drawing
Graphics and Interaction Rendering pipeline & object modelling
 433-324 Graphics and Interaction Rendering pipeline & object modelling Department of Computer Science and Software Engineering The Lecture outline Introduction to Modelling Polygonal geometry The rendering
433-324 Graphics and Interaction Rendering pipeline & object modelling Department of Computer Science and Software Engineering The Lecture outline Introduction to Modelling Polygonal geometry The rendering
Performance OpenGL Programming (for whatever reason)
 Performance OpenGL Programming (for whatever reason) Mike Bailey Oregon State University Performance Bottlenecks In general there are four places a graphics system can become bottlenecked: 1. The computer
Performance OpenGL Programming (for whatever reason) Mike Bailey Oregon State University Performance Bottlenecks In general there are four places a graphics system can become bottlenecked: 1. The computer
Clipping Points Consider a clip window which is rectangular in shape. P(x, y) is a point to be displayed.
 Usually only a specified region of a picture needs to be displayed. This region is called the clip window. An algorithm which displays only those primitives (or part of the primitives) which lie inside
Usually only a specified region of a picture needs to be displayed. This region is called the clip window. An algorithm which displays only those primitives (or part of the primitives) which lie inside
Visible Surface Detection. (Chapt. 15 in FVD, Chapt. 13 in Hearn & Baker)
 Visible Surface Detection (Chapt. 15 in FVD, Chapt. 13 in Hearn & Baker) 1 Given a set of 3D objects and a viewing specifications, determine which lines or surfaces of the objects should be visible. A
Visible Surface Detection (Chapt. 15 in FVD, Chapt. 13 in Hearn & Baker) 1 Given a set of 3D objects and a viewing specifications, determine which lines or surfaces of the objects should be visible. A
Advanced 3D-Data Structures
 Advanced 3D-Data Structures Eduard Gröller, Martin Haidacher Institute of Computer Graphics and Algorithms Vienna University of Technology Motivation For different data sources and applications different
Advanced 3D-Data Structures Eduard Gröller, Martin Haidacher Institute of Computer Graphics and Algorithms Vienna University of Technology Motivation For different data sources and applications different
Midterm Exam Fundamentals of Computer Graphics (COMP 557) Thurs. Feb. 19, 2015 Professor Michael Langer
 Midterm Exam Fundamentals of Computer Graphics (COMP 557) Thurs. Feb. 19, 2015 Professor Michael Langer The exam consists of 10 questions. There are 2 points per question for a total of 20 points. You
Midterm Exam Fundamentals of Computer Graphics (COMP 557) Thurs. Feb. 19, 2015 Professor Michael Langer The exam consists of 10 questions. There are 2 points per question for a total of 20 points. You
Chapter 8: Implementation- Clipping and Rasterization
 Chapter 8: Implementation- Clipping and Rasterization Clipping Fundamentals Cohen-Sutherland Parametric Polygons Circles and Curves Text Basic Concepts: The purpose of clipping is to remove objects or
Chapter 8: Implementation- Clipping and Rasterization Clipping Fundamentals Cohen-Sutherland Parametric Polygons Circles and Curves Text Basic Concepts: The purpose of clipping is to remove objects or
Two-Dimensional Viewing. Chapter 6
 Two-Dimensional Viewing Chapter 6 Viewing Pipeline Two-Dimensional Viewing Two dimensional viewing transformation From world coordinate scene description to device (screen) coordinates Normalization and
Two-Dimensional Viewing Chapter 6 Viewing Pipeline Two-Dimensional Viewing Two dimensional viewing transformation From world coordinate scene description to device (screen) coordinates Normalization and
CS184 : Foundations of Computer Graphics Professor David Forsyth Final Examination
 CS184 : Foundations of Computer Graphics Professor David Forsyth Final Examination (Total: 100 marks) Figure 1: A perspective view of a polyhedron on an infinite plane. Cameras and Perspective Rendering
CS184 : Foundations of Computer Graphics Professor David Forsyth Final Examination (Total: 100 marks) Figure 1: A perspective view of a polyhedron on an infinite plane. Cameras and Perspective Rendering
9. Visible-Surface Detection Methods
 9. Visible-Surface Detection Methods More information about Modelling and Perspective Viewing: Before going to visible surface detection, we first review and discuss the followings: 1. Modelling Transformation:
9. Visible-Surface Detection Methods More information about Modelling and Perspective Viewing: Before going to visible surface detection, we first review and discuss the followings: 1. Modelling Transformation:
Examples. Clipping. The Rendering Pipeline. View Frustum. Normalization. How it is done. Types of operations. Removing what is not seen on the screen
 Computer Graphics, Lecture 0 November 7, 006 Eamples Clipping Types of operations Accept Reject Clip Removing what is not seen on the screen The Rendering Pipeline The Graphics pipeline includes one stage
Computer Graphics, Lecture 0 November 7, 006 Eamples Clipping Types of operations Accept Reject Clip Removing what is not seen on the screen The Rendering Pipeline The Graphics pipeline includes one stage
Realtime 3D Computer Graphics Virtual Reality
 Realtime 3D Computer Graphics Virtual Reality From Vertices to Fragments Overview Overall goal recapitulation: Input: World description, e.g., set of vertices and states for objects, attributes, camera,
Realtime 3D Computer Graphics Virtual Reality From Vertices to Fragments Overview Overall goal recapitulation: Input: World description, e.g., set of vertices and states for objects, attributes, camera,
CS559: Computer Graphics. Lecture 12: Antialiasing & Visibility Li Zhang Spring 2008
 CS559: Computer Graphics Lecture 12: Antialiasing & Visibility Li Zhang Spring 2008 Antialising Today Hidden Surface Removal Reading: Shirley ch 3.7 8 OpenGL ch 1 Last time A 2 (x 0 y 0 ) (x 1 y 1 ) P
CS559: Computer Graphics Lecture 12: Antialiasing & Visibility Li Zhang Spring 2008 Antialising Today Hidden Surface Removal Reading: Shirley ch 3.7 8 OpenGL ch 1 Last time A 2 (x 0 y 0 ) (x 1 y 1 ) P
CS184 : Foundations of Computer Graphics Professor David Forsyth Final Examination (Total: 100 marks)
 CS184 : Foundations of Computer Graphics Professor David Forsyth Final Examination (Total: 100 marks) Cameras and Perspective Figure 1: A perspective view of a polyhedron on an infinite plane. Rendering
CS184 : Foundations of Computer Graphics Professor David Forsyth Final Examination (Total: 100 marks) Cameras and Perspective Figure 1: A perspective view of a polyhedron on an infinite plane. Rendering
Real-Time Rendering (Echtzeitgraphik) Dr. Michael Wimmer
 Real-Time Rendering (Echtzeitgraphik) Dr. Michael Wimmer wimmer@cg.tuwien.ac.at Visibility Overview Basics about visibility Basics about occlusion culling View-frustum culling / backface culling Occlusion
Real-Time Rendering (Echtzeitgraphik) Dr. Michael Wimmer wimmer@cg.tuwien.ac.at Visibility Overview Basics about visibility Basics about occlusion culling View-frustum culling / backface culling Occlusion
Two basic types: image-precision and object-precision. Image-precision For each pixel, determine which object is visable Requires np operations
 walters@buffalo.edu CSE 480/580 Lecture 21 Slide 1 Visible-Surface Determination (Hidden Surface Removal) Computationaly expensive Two basic types: image-precision and object-precision For n objects and
walters@buffalo.edu CSE 480/580 Lecture 21 Slide 1 Visible-Surface Determination (Hidden Surface Removal) Computationaly expensive Two basic types: image-precision and object-precision For n objects and
COMPUTATIONAL GEOMETRY
 Thursday, September 20, 2007 (Ming C. Lin) Review on Computational Geometry & Collision Detection for Convex Polytopes COMPUTATIONAL GEOMETRY (Refer to O'Rourke's and Dutch textbook ) 1. Extreme Points
Thursday, September 20, 2007 (Ming C. Lin) Review on Computational Geometry & Collision Detection for Convex Polytopes COMPUTATIONAL GEOMETRY (Refer to O'Rourke's and Dutch textbook ) 1. Extreme Points
Illumination Models III: Ray Tracing (View Dependent Global Illumination)
 Illumination Models III: Ray Tracing (View Dependent Global Illumination) The University of Texas at Austin 1 Basic Definitions Ray Tracing/Casting: Setting: eyepoint, virtual screen (an array of virtual
Illumination Models III: Ray Tracing (View Dependent Global Illumination) The University of Texas at Austin 1 Basic Definitions Ray Tracing/Casting: Setting: eyepoint, virtual screen (an array of virtual
8. Hidden Surface Elimination
 8. Hidden Surface Elimination Identification and Removal of parts of picture that are not visible from a chosen viewing position. 1 8. Hidden Surface Elimination Basic idea: Overwriting Paint things in
8. Hidden Surface Elimination Identification and Removal of parts of picture that are not visible from a chosen viewing position. 1 8. Hidden Surface Elimination Basic idea: Overwriting Paint things in
Computer Science 474 Spring 2010 Viewing Transformation
 Viewing Transformation Previous readings have described how to transform objects from one position and orientation to another. One application for such transformations is to create complex models from
Viewing Transformation Previous readings have described how to transform objects from one position and orientation to another. One application for such transformations is to create complex models from
Spatial Data Structures and Speed-Up Techniques. Ulf Assarsson Department of Computer Science and Engineering Chalmers University of Technology
 Spatial Data Structures and Speed-Up Techniques Ulf Assarsson Department of Computer Science and Engineering Chalmers University of Technology Exercises l Create a function (by writing code on paper) that
Spatial Data Structures and Speed-Up Techniques Ulf Assarsson Department of Computer Science and Engineering Chalmers University of Technology Exercises l Create a function (by writing code on paper) that
CS488. Visible-Surface Determination. Luc RENAMBOT
 CS488 Visible-Surface Determination Luc RENAMBOT 1 Visible-Surface Determination So far in the class we have dealt mostly with simple wireframe drawings of the models The main reason for this is so that
CS488 Visible-Surface Determination Luc RENAMBOT 1 Visible-Surface Determination So far in the class we have dealt mostly with simple wireframe drawings of the models The main reason for this is so that
The Graphics Pipeline. Interactive Computer Graphics. The Graphics Pipeline. The Graphics Pipeline. The Graphics Pipeline: Clipping
 Interactive Computer Graphics The Graphics Pipeline: The Graphics Pipeline Input: - geometric model - illumination model - camera model - viewport Some slides adopted from F. Durand and B. Cutler, MIT
Interactive Computer Graphics The Graphics Pipeline: The Graphics Pipeline Input: - geometric model - illumination model - camera model - viewport Some slides adopted from F. Durand and B. Cutler, MIT
INTRODUCTION TO COMPUTER GRAPHICS. It looks like a matrix Sort of. Viewing III. Projection in Practice. Bin Sheng 10/11/ / 52
 cs337 It looks like a matrix Sort of Viewing III Projection in Practice / 52 cs337 Arbitrary 3D views Now that we have familiarity with terms we can say that these view volumes/frusta can be specified
cs337 It looks like a matrix Sort of Viewing III Projection in Practice / 52 cs337 Arbitrary 3D views Now that we have familiarity with terms we can say that these view volumes/frusta can be specified
EECE 478. Learning Objectives. Learning Objectives. Rasterization & Scenes. Rasterization. Compositing
 EECE 478 Rasterization & Scenes Rasterization Learning Objectives Be able to describe the complete graphics pipeline. Describe the process of rasterization for triangles and lines. Compositing Manipulate
EECE 478 Rasterization & Scenes Rasterization Learning Objectives Be able to describe the complete graphics pipeline. Describe the process of rasterization for triangles and lines. Compositing Manipulate
Renderer Implementation: Basics and Clipping. Overview. Preliminaries. David Carr Virtual Environments, Fundamentals Spring 2005
 INSTITUTIONEN FÖR SYSTEMTEKNIK LULEÅ TEKNISKA UNIVERSITET Renderer Implementation: Basics and Clipping David Carr Virtual Environments, Fundamentals Spring 2005 Feb-28-05 SMM009, Basics and Clipping 1
INSTITUTIONEN FÖR SYSTEMTEKNIK LULEÅ TEKNISKA UNIVERSITET Renderer Implementation: Basics and Clipping David Carr Virtual Environments, Fundamentals Spring 2005 Feb-28-05 SMM009, Basics and Clipping 1
CS 563 Advanced Topics in Computer Graphics Culling and Acceleration Techniques Part 1 by Mark Vessella
 CS 563 Advanced Topics in Computer Graphics Culling and Acceleration Techniques Part 1 by Mark Vessella Introduction Acceleration Techniques Spatial Data Structures Culling Outline for the Night Bounding
CS 563 Advanced Topics in Computer Graphics Culling and Acceleration Techniques Part 1 by Mark Vessella Introduction Acceleration Techniques Spatial Data Structures Culling Outline for the Night Bounding
CS 130 Exam I. Fall 2015
 S 3 Exam I Fall 25 Name Student ID Signature You may not ask any questions during the test. If you believe that there is something wrong with a question, write down what you think the question is trying
S 3 Exam I Fall 25 Name Student ID Signature You may not ask any questions during the test. If you believe that there is something wrong with a question, write down what you think the question is trying
CSE 167: Introduction to Computer Graphics Lecture #5: Projection. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2017
 CSE 167: Introduction to Computer Graphics Lecture #5: Projection Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2017 Announcements Friday: homework 1 due at 2pm Upload to TritonEd
CSE 167: Introduction to Computer Graphics Lecture #5: Projection Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2017 Announcements Friday: homework 1 due at 2pm Upload to TritonEd
Cs602-computer graphics MCQS MIDTERM EXAMINATION SOLVED BY ~ LIBRIANSMINE ~
 Cs602-computer graphics MCQS MIDTERM EXAMINATION SOLVED BY ~ LIBRIANSMINE ~ Question # 1 of 10 ( Start time: 08:04:29 PM ) Total Marks: 1 Sutherland-Hodgeman clipping algorithm clips any polygon against
Cs602-computer graphics MCQS MIDTERM EXAMINATION SOLVED BY ~ LIBRIANSMINE ~ Question # 1 of 10 ( Start time: 08:04:29 PM ) Total Marks: 1 Sutherland-Hodgeman clipping algorithm clips any polygon against
Ray Tracing Basics I. Computer Graphics as Virtual Photography. camera (captures light) real scene. photo. Photographic print. Photography: processing
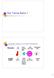 Ray Tracing Basics I Computer Graphics as Virtual Photography Photography: real scene camera (captures light) photo processing Photographic print processing Computer Graphics: 3D models camera model (focuses
Ray Tracing Basics I Computer Graphics as Virtual Photography Photography: real scene camera (captures light) photo processing Photographic print processing Computer Graphics: 3D models camera model (focuses
graphics pipeline computer graphics graphics pipeline 2009 fabio pellacini 1
 graphics pipeline computer graphics graphics pipeline 2009 fabio pellacini 1 graphics pipeline sequence of operations to generate an image using object-order processing primitives processed one-at-a-time
graphics pipeline computer graphics graphics pipeline 2009 fabio pellacini 1 graphics pipeline sequence of operations to generate an image using object-order processing primitives processed one-at-a-time
Ray tracing. Computer Graphics COMP 770 (236) Spring Instructor: Brandon Lloyd 3/19/07 1
 Ray tracing Computer Graphics COMP 770 (236) Spring 2007 Instructor: Brandon Lloyd 3/19/07 1 From last time Hidden surface removal Painter s algorithm Clipping algorithms Area subdivision BSP trees Z-Buffer
Ray tracing Computer Graphics COMP 770 (236) Spring 2007 Instructor: Brandon Lloyd 3/19/07 1 From last time Hidden surface removal Painter s algorithm Clipping algorithms Area subdivision BSP trees Z-Buffer
graphics pipeline computer graphics graphics pipeline 2009 fabio pellacini 1
 graphics pipeline computer graphics graphics pipeline 2009 fabio pellacini 1 graphics pipeline sequence of operations to generate an image using object-order processing primitives processed one-at-a-time
graphics pipeline computer graphics graphics pipeline 2009 fabio pellacini 1 graphics pipeline sequence of operations to generate an image using object-order processing primitives processed one-at-a-time
Spatial Data Structures
 15-462 Computer Graphics I Lecture 17 Spatial Data Structures Hierarchical Bounding Volumes Regular Grids Octrees BSP Trees Constructive Solid Geometry (CSG) March 28, 2002 [Angel 8.9] Frank Pfenning Carnegie
15-462 Computer Graphics I Lecture 17 Spatial Data Structures Hierarchical Bounding Volumes Regular Grids Octrees BSP Trees Constructive Solid Geometry (CSG) March 28, 2002 [Angel 8.9] Frank Pfenning Carnegie
Shadows in the graphics pipeline
 Shadows in the graphics pipeline Steve Marschner Cornell University CS 569 Spring 2008, 19 February There are a number of visual cues that help let the viewer know about the 3D relationships between objects
Shadows in the graphics pipeline Steve Marschner Cornell University CS 569 Spring 2008, 19 February There are a number of visual cues that help let the viewer know about the 3D relationships between objects
Spatial Data Structures
 CSCI 420 Computer Graphics Lecture 17 Spatial Data Structures Jernej Barbic University of Southern California Hierarchical Bounding Volumes Regular Grids Octrees BSP Trees [Angel Ch. 8] 1 Ray Tracing Acceleration
CSCI 420 Computer Graphics Lecture 17 Spatial Data Structures Jernej Barbic University of Southern California Hierarchical Bounding Volumes Regular Grids Octrees BSP Trees [Angel Ch. 8] 1 Ray Tracing Acceleration
CS 498 VR. Lecture 18-4/4/18. go.illinois.edu/vrlect18
 CS 498 VR Lecture 18-4/4/18 go.illinois.edu/vrlect18 Review and Supplement for last lecture 1. What is aliasing? What is Screen Door Effect? 2. How image-order rendering works? 3. If there are several
CS 498 VR Lecture 18-4/4/18 go.illinois.edu/vrlect18 Review and Supplement for last lecture 1. What is aliasing? What is Screen Door Effect? 2. How image-order rendering works? 3. If there are several
Identifying those parts of a scene that are visible from a chosen viewing position, and only process (scan convert) those parts
 Visible Surface Detection Identifying those parts of a scene that are visible from a chosen viewing position, and only process (scan convert) those parts Two approaches: 1. Object space methods 2. Image
Visible Surface Detection Identifying those parts of a scene that are visible from a chosen viewing position, and only process (scan convert) those parts Two approaches: 1. Object space methods 2. Image
Viewing Transformation. Clipping. 2-D Viewing Transformation
 Viewing Transformation Clipping 2-D Viewing Transformation 2-D Viewing Transformation Convert from Window Coordinates to Viewport Coordinates (xw, yw) --> (xv, yv) Maps a world coordinate window to a screen
Viewing Transformation Clipping 2-D Viewing Transformation 2-D Viewing Transformation Convert from Window Coordinates to Viewport Coordinates (xw, yw) --> (xv, yv) Maps a world coordinate window to a screen
Rendering. Converting a 3D scene to a 2D image. Camera. Light. Rendering. View Plane
 Rendering Pipeline Rendering Converting a 3D scene to a 2D image Rendering Light Camera 3D Model View Plane Rendering Converting a 3D scene to a 2D image Basic rendering tasks: Modeling: creating the world
Rendering Pipeline Rendering Converting a 3D scene to a 2D image Rendering Light Camera 3D Model View Plane Rendering Converting a 3D scene to a 2D image Basic rendering tasks: Modeling: creating the world
CSCI 4620/8626. Computer Graphics Clipping Algorithms (Chapter 8-5 )
 CSCI 4620/8626 Computer Graphics Clipping Algorithms (Chapter 8-5 ) Last update: 2016-03-15 Clipping Algorithms A clipping algorithm is any procedure that eliminates those portions of a picture outside
CSCI 4620/8626 Computer Graphics Clipping Algorithms (Chapter 8-5 ) Last update: 2016-03-15 Clipping Algorithms A clipping algorithm is any procedure that eliminates those portions of a picture outside
Set the Viewport. Set the Viewport Clipping. Set the Viewport. Set the Viewport. Set the Viewport. Resizing the Viewport W = H
 To draw an undistorted version of the data in a viewport, you need to ensure the viewport and the window have the same aspect ratio. i.e. W H window window W = H viewport viewport Computer Graphics CSC470
To draw an undistorted version of the data in a viewport, you need to ensure the viewport and the window have the same aspect ratio. i.e. W H window window W = H viewport viewport Computer Graphics CSC470
Drawing in 3D (viewing, projection, and the rest of the pipeline)
 Drawing in 3D (viewing, projection, and the rest of the pipeline) CS559 Spring 2016 Lecture 6 February 11, 2016 The first 4 Key Ideas 1. Work in convenient coordinate systems. Use transformations to get
Drawing in 3D (viewing, projection, and the rest of the pipeline) CS559 Spring 2016 Lecture 6 February 11, 2016 The first 4 Key Ideas 1. Work in convenient coordinate systems. Use transformations to get
CS602 Midterm Subjective Solved with Reference By WELL WISHER (Aqua Leo)
 CS602 Midterm Subjective Solved with Reference By WELL WISHER (Aqua Leo) www.vucybarien.com Question No: 1 What are the two focusing methods in CRT? Explain briefly. Page no : 26 1. Electrostatic focusing
CS602 Midterm Subjective Solved with Reference By WELL WISHER (Aqua Leo) www.vucybarien.com Question No: 1 What are the two focusing methods in CRT? Explain briefly. Page no : 26 1. Electrostatic focusing
