These notes are in two parts: this part has topics 1-3 above.
|
|
|
- Pauline Simpson
- 6 years ago
- Views:
Transcription
1 IEEM 0: Linear Programming and Its Applications Outline of this series of lectures:. How can we model a problem so that it can be solved to give the required solution 2. Motivation: eamples of typical linear problems in IE 3. Story by pictures: a graphical interpretation of Linear Programs (LP) 4. Solving LP using the Simple Method 4.. How to put the LP in standard form for Simple method 4.2. How to use a computer program to solve an LP 5. Some theoretical basics of Simple: the beauty of conveity These notes are in two parts: this part has topics -3 above. Modeling of Problems As we mentioned in our introduction, our interest is always to either find methods to improve a product, or a process. It is natural to ask: how much should we improve it? Obviously, we would like to improve it as much as possible, under the give constraints of time, cost, etc. In other words, we are always seeking for the maimum improvement. Thus we will often be faced with a situation that we are given some resources to do a certain task, and some constraints (e.g. time constraint such as deadlines). It is possible that there are several ways to do the task, but some ways are better than others. So how do we guarantee that the way we select is the best? It all depends, of course, on the model that we construct. This is tricky for one thing, we are often not very clear about how to define best solution ; and even when we do, the same problem may be modelled in different ways, and it could be easier to solve one model than another. An eample of the first kind of difficulty is seen in the planning of many governments: they want to minimize their epenses, but they also want to maimise employment, even if that means hiring many people to work on public sector projects; yet these two goals often conflict each other over the period of the planning horizon. In any case, we shall ignore such multi-objective problems in this course: even when there is a single, well-defined objective, there are many interesting problems. We look at some eamples to learn how problems can be modelled. In particular, we
2 shall only look at problems whose models will turn out to be linear (I will define this soon). There are many other IE problems that are non-linear; we shall meet them later on the course. Eample (The Product Mi Problem): A fertilizer factory manufactures two types of fertilizers, Type A is high in phosphorus and Type B is low in phosphorus. Each has three key ingredients: urea, rock phosphate and potash. These ingredients are also produced or mined by the company at other sites. Table gives the information about the fertilizers. Item Tons Required/ ton of Fertilizer Type A Type B Maimum amount available per day Urea Potash 200 Rock Phosphate Net profit per ton 5 0 Assuming that the company can sell all the fertilizer it can produce, how much of each type should it make, and how much of each raw material will it need per day? Model: If we know how much of each type we make per day, then it is easy to compute the raw material requirements. Step. The decision variables Let us denote the daily production of Type A by tons, and of Type B by y tons. These variables (whose values we must determine) are called the decision variables. Identifying the decision variables, what type of values they can have, is the first key step in modelling a problem. Here, and y are real numbers, which must be positive. 2
3 Step 2. The objective function We would like to maimize our profit. Based on table, our profit per day = 5 + 0y Thus the objective function is to maimize the value of the function, z = 5 + 0y Step 3. The constraints Looking at the objective function, it is clear that if we keep increasing the value of, y, or both, then our profit also keeps increasing. However, we cannot produce arbitrarily large amount of fertilizer, because our raw material supplies are limited. These, therefore, are constraints on our solution. Since the supply of each raw material is limited, we need one constraint equation for each, as follows: Urea: 2 + y Potash: + y Rock Phosphate: Step 4. Complete the formulation The problem is therefore completely specified as follows: maimize z(, y) = 5 + 0y subject to 2 + y + y y So we have managed to convert words into algebra; but how do we solve this problem? Later, we shall see how such formulations can be solved. For now, let us just concentrate on two interesting aspects. First, we call this formulation a linear system. This is because the objective function, as well as each constraint is a linear function in the variables and y (that is to say, there is no term containing, say, 2, y 2, y, y 2, etc.) Secondly, the constraints are not equations, but inequalities. What does that mean? It means that it may not be necessary for us to use all the raw material we can obtain, in order to maimize our profit (why is that?). 3
4 We define some useful terms before continuing. Note that the way that we write our constraints, the company may produce nothing, i.e. = 0 and y = 0 (verify that substituting = 0 and y = 0 in the constraint inequalities does not violate any of them). The profit in this case = 0. Likewise, =, y = also does not violate any constraint, and gives a profit, z = 25. In fact, we can find many pairs of values of (, y) that don t violate any constraint, each with a different value of profit. Each such pair of values of the decision variables is called a feasible solution. On the other hand, = 600, y = 500 is not a feasible solution, since it violates the constraint on the consumption of urea [ = 700, which is larger than 500]. Thus = 600, y = 500 is infeasible. Among all the feasible solutions, there is one (or many) that will correspond to the maimum value of the profit. We don t know the best combination yet, but if we denote one such best solution as (*, y*), then this value will be called an optimum value. Later, we shall see how to get the optimum value for this and other similar problem formulations. For now, let s look at some more eamples. Eample (The Blending Problem): Here is an etended form of the product mi problem. It is also very common in many industries, e.g. food processing companies making canned soups, animal food, chemical plants, paint manufacture, pharmaceutical companies making drugs, perfume manufacturing and so on. Our eample is from the petroleum industry. In a petroleum refinery, crude oil is separated into many different oils (based on how volatile they are). Several of these oils can be mied in different proportions to make petrol that is sold from petrol stations. Each oil has a property called octane rating (a number like 60, 80, 90, 99, etc.) Higher octane rating is more desirable for cars if you visit the petrol station, you will see 2 or 3 grades of petrol sold at different prices; the main difference is in the octane rating. An interesting property of petrol is that the octane rating (OcR) of a miture of oils is just the proportional rating of the constituents of the miture. In other words, if we mi 2 L of Oil (OcR = 60) with 3 L of Oil 2 (OcR = 80), then the OcR of the resulting miture is given by ( )/(2+3) = 72. The refinery has four types of oils that can be used to produce petrol; they sell three different types of petrol at gas stations, whose prices are based on the minimum OcR of each type. The data for the manufacture cost of each type of oil and the amounts available per day are given in the tables below. 4
5 Raw oil OcR Available amount (barrels/day) Price/barrel Sale price Petrol Type Min OcR Selling Price Demand (barrels/day) (Premium) (Super) No limit 3 (Regular) Note that the oils can be sold in raw from, or they can be blended to make petrol, and the petrol can then be sold. The objective is to find the compositions of the three types of petrol to maimize the profits. Step. The decision variables: At first glance, it seems we need to decide how many barrels of each type of petrol we need to produce, so we would need four variables, say, w,, y, z. However, notice that the petrol is only rated in terms of its minimum OcR, in other words, it could be possible to blend some etra high grade oil into a low grade petrol (e.g. making regular petrol with OcR > 85), yielding higher profits than selling the oil directly. Thus, what we really need is to figure out how much of each type of oil is blended into each type of petrol. Thus we need 43 = 2 variables, for which it is easier to adopt a subscripted notation: ij = barrels/day of oil of type i used in making petrol of type j (i = to 4, j = to 3) Thus the total amount of Premium petrol made per day = It s OcR = ( )/ ( ), which must eceed 95. Thus: ( )/ ( ) LQRWKHUZRUGV ( ) 5
6 Note that: (a) this is a linear constraint; (b) ( ) is always positive (or zero), since each ij is positive or zero; thus, if ( ) > 0, we can multiply either side of the inequality by it without changing the sign of the inequality; on the other hand, if we make 0 barrels of Premium petrol, then the linear form of the constraint is still true. Step 2. The objective function We want to maimize our profits. From the data, it is clear that any leftover oil should be sold in raw form, since that will provide some profit. Therefore, our total cost is fied, and equals Thus, to maimize profits, it is sufficient to maimise the revenue from sales. There are two types of revenues; petrol and raw oil. The revenue for petrol e.g. Premium type, is given by: 45.5( ); similarly, the revenue from sale of, e.g. raw oil type is given by: ( ( )). Following this, the objective function can be written as: Maimize: 45.5( ) ( ) ( ) (4000 ( )) (5050 ( )) (700 ( )) (4300 ( )) The first line gives the money we make by selling each type of petrol, the second and third lines give the money we make from selling the raw oils of the four types. Step 3. The constraints There are several types of constraints: (a) The OcR constraints: ( ) ( ) ( ) (b) Can t use more oil than we have:
7 (c) The demand constraints: (d) Allowed values of variables ij IRU, DQGM Steps 2 and 3 above show the complete formulation of the blending problem. As you may guess, even if we had some hope of solving our product mi problem by hand, our blending problem is already too large to try and solve using paper and pencil. Yet the two problem formulations look very similar in nature (they both have a linear objective function, and a set of linear constraints); the difference is that some constraints in the blending problem are ZKLOHRWKHUVDUHµ KRZHYHUWKLVLVQRWDSUREOHPIRUZHFDQ always multiple both sides of a FRQVWUDLQWE\-, to turn it into a FRQVWUDLQW>ZK\"@ You can see that a common method to solve problems of this form would be nice. Let us look at one last eample of a similar nature, before we begin to eplore how to solve these problems. Eample: Transportation problem Steel plant uses coal and iron ore to produce steel. There are three steel plants in a country, which receive iron ore from two different mines. The cost of transporting the ore between any mine and plant is as shown in the table below. The table also shows the maimum production at each mine, and the requirement of each plant. transportation cost per ton mine capacity/day plant plant 2 plant 3 Mine Mine daily ore requirement at each plant: The problem is to find how much ore must be shipped from each mine to each plant daily, so that the costs are minimized. 7
8 Step. The decision variables We need to figure out how much ore is sent from mine i to plant j, so let us denote: ij = amount of ore (tons) shipped from mine i to plant j per day. Step 2: The objective function Again, this is fairly straightforward. We need to minimize the transportation costs: Minimize: Step 3: The constraints There are three types of constraints: (a) ore shipment from each mine should not eceed its daily production capacity, (b) demand of each plant must be met, and (c) no decision variables can be negative. These are easily written as: >FDSDFLW\RIPLQH@ >FDSDFLW\RIPLQH@ + 2 >GHPDQGDWSODQW@ >GHPDQGDWSODQW@ >GHPDQGDWSODQW@ ij IRUDOOL DQGM Notes:. In this case, we can easily see that the total mine output = = 00, which is eactly equal to the total demand = = 00. Thus all the ore that is produced must be shipped, and so we can just replace the inequalities in the capacity and demand constraints by = signs. 2. The problem is a simple one to formulate; it has some historical importance in the field of linear programming, though. The first time these problems were solved in a systematic method (these methods were initial forms of the Simple method to be later discovered by Dantzig) by Kantorovitch in USSR in the 930 s, and later by Koopmans in 940 s: contributions for which they were awarded the Noble prize in Economics. 8
9 Graphical illustration of the LP formulations Let us first refresh some high-school geometry: Point in a D space: = c, where c is a real number on the line representing the D space. Line in 2D: a + by = c The equation above represents a line using algebra; the figure below represents a line geometrically. The figure also shows what happens to the line when we change the value of c. y 3 2+3y = 3 2+3y = y = 9 2+3y = 6 (0,0) Plane in 3D: a + by + cz = d Once again, the algebra equation can be represented by geometric figures; the images show how the plane moves as the value of the constant, d, changes (keeping the values of a, b, and c constant). Note also that while the plane is embedded in 3D space, we have managed to represent it on a 2D paper (or computer screen) by drawing its projected view ; since our childhood, humans adapt to the task of imagining 3D objects by just looking at their 2D projected views.) Also, for different values of a, b, and c, we get planes with different orientation. 9
10 z Plane: + y + z = 0 z Plane: + y + z = 2 Plane + y + z = y y Hyper-plane in nd: a + a a n n = c Now it becomes difficult to draw even projected images of such hyper-planes planes in 4D or higher dimension. We will not try to imagine such figures, and rather rely upon algebra to handle them. [Note: you may have learnt in high school that it was the brilliant French mathematician Descartes who first made the connection between algebra and geometry, by immersing the geometry into what we now call, to honour him, the Cartesian coordinate space. In the study of LP, we shall see the beauty of this correspondence the low dimension eamples can be solved geometrically to understand the meaning of things in the algebra model; this helps us to formulate the method; then, for problems with large number of variables, i.e. problems in high dimensions, we use the same method in its algebraic form]. Half spaces: Notice that a line, a + by = c, divides the plane into two halves; in one half are all points with coordinates ( u, y u ) such that a u + by u > c; similarly, for each point ( d, y d ) in the lower half, the coordinates satisfy a d + by d < c. Likewise, every plane divides the 3D space into two halves, with the coordinates of points in each half satisfying the same type of relationship. The 2D case is shown in the figure below. 0
11 y y > 6 2+3y < 6 (0,0) y = 6 Let us therefore return to the 2D case, and re-visit our product mi problem. The formulation is repeated below. maimize z(, y) = 5 + 0y subject to 2 + y + y y What is a feasible solution to this problem? Any point on the XY plane whose coordinates satisfy each of the 5 constraints. Notice that since each constraint is a linear equation, it can be represented by a halfplane. Thus if we want to satisfy two constraints simultaneously, then all we need to do is to find the set of points in the XY plane that are in the half plane of each of the constraints. If we look at the half-plane as a set of points, then we look at it as the intersection of the two sets. Etending this idea, satisfying n-constraints requires us to take the intersection of n half-planes. In the figure below, we draw the set of points related to each constraint. The set of points satisfying all the constraints is marked by hatched lines.
12 y 500 = Feasible set y = 0 (0,0) = y = y = 200 Thus any point inside the hatched region is a feasible solution. There are infinite such points. Which one will yield the best value for our objective function? Let us arbitrarily try the point (0, 0). At this point, the value of the objective function z = 5 + 0y = = 0; graphically, this means that the line 5 + 0y = 0 will pass through the point (0, 0), as shown in the figure below. 2
13 y 500 = Feasible set y = 0 (0,0) = y = 0 2+y = y = 200 Now note that our objective function is of the form a + by = c; we learnt earlier that if we keep sliding this line to the right-hand side, we progressively increase the value of c. Since our objective is to maimize 5 + 0y, let us try the line 5 + 0y = 5000, as shown in the figure below. 3
14 y 500 = y = y = Feasible set y = 0 (0,0) = y = y = 200 We can see that there are still some grey hatched points to the right-side of this new line. In other words, if we pick one of the points to the right of the new line, but still in the grey region, it must lie on some line with the equation 5 + 0y = d, where d > In other words, we can find a better solution still! So we keep sliding the line to the right (i.e. increasing the value of the objective function), until it only just touches some point in the feasible set. Moving it any further right will cause it to go entirely through the infeasible region. The value of c corresponding to this line (shown in the figure below) is the maimum value we can get for our objective function. The point where this line touches our feasible set is called the optimum point. You can verify that this is the point (300, 900) in our case. It is at the intersection of two lines that denote two of our constraints, namely: 2 + y DQG[ + y The conclusion is that our fertilizer company should produce 300 tons of Type A, and 900 tons of Type B fertilizer. Now let us verify the constraint equations for this mi: (i) = 500 >2.@ (ii) = 200 >2.@ (iii) 300 [OK] (iv, v) 300 DQG >2.@ 4
15 Notice in particular constraint (iii), which limits the maimum amount of Rock Phosphate we can use per day to 500 units. In the optimum mi, we only require 300 units. We say that there is 200 units of slack in this constraint. We shall meet this concept of slack again, later on, since it plays an important role in the algebraic method of solving the linear program. y 500 = y = Optimum point (300, 900) 500 Feasible set y = 0 (0,0) = y = y = 3,500 + y = 200 Main reference: Operations Research, K. G. Murty, Prentice Hall. 5
4 Linear Programming (LP) E. Amaldi -- Foundations of Operations Research -- Politecnico di Milano 1
 4 Linear Programming (LP) E. Amaldi -- Foundations of Operations Research -- Politecnico di Milano 1 Definition: A Linear Programming (LP) problem is an optimization problem: where min f () s.t. X n the
4 Linear Programming (LP) E. Amaldi -- Foundations of Operations Research -- Politecnico di Milano 1 Definition: A Linear Programming (LP) problem is an optimization problem: where min f () s.t. X n the
Linear Mathematical Programming (LP)
 Linear Mathematical Programming (LP) A MP is LP if : The objective function is linear where The set is defined by linear equality or inequality constraints c f T ) = ( ],..., [ n T c c c = = n b A where
Linear Mathematical Programming (LP) A MP is LP if : The objective function is linear where The set is defined by linear equality or inequality constraints c f T ) = ( ],..., [ n T c c c = = n b A where
Chapter 15 Introduction to Linear Programming
 Chapter 15 Introduction to Linear Programming An Introduction to Optimization Spring, 2015 Wei-Ta Chu 1 Brief History of Linear Programming The goal of linear programming is to determine the values of
Chapter 15 Introduction to Linear Programming An Introduction to Optimization Spring, 2015 Wei-Ta Chu 1 Brief History of Linear Programming The goal of linear programming is to determine the values of
Some Advanced Topics in Linear Programming
 Some Advanced Topics in Linear Programming Matthew J. Saltzman July 2, 995 Connections with Algebra and Geometry In this section, we will explore how some of the ideas in linear programming, duality theory,
Some Advanced Topics in Linear Programming Matthew J. Saltzman July 2, 995 Connections with Algebra and Geometry In this section, we will explore how some of the ideas in linear programming, duality theory,
UNIT 3 LINEAR PROGRAMMING GRAPHICAL METHOD
 UNIT 3 LINEAR PROGRAMMING GRAPHICAL METHOD Objectives After studying this unit, you should be able to : Formulate management problem as a linear programming problem in suitable cases identify the characteristics
UNIT 3 LINEAR PROGRAMMING GRAPHICAL METHOD Objectives After studying this unit, you should be able to : Formulate management problem as a linear programming problem in suitable cases identify the characteristics
Linear Programming. Meaning of Linear Programming. Basic Terminology
 Linear Programming Linear Programming (LP) is a versatile technique for assigning a fixed amount of resources among competing factors, in such a way that some objective is optimized and other defined conditions
Linear Programming Linear Programming (LP) is a versatile technique for assigning a fixed amount of resources among competing factors, in such a way that some objective is optimized and other defined conditions
Simulation. Lecture O1 Optimization: Linear Programming. Saeed Bastani April 2016
 Simulation Lecture O Optimization: Linear Programming Saeed Bastani April 06 Outline of the course Linear Programming ( lecture) Integer Programming ( lecture) Heuristics and Metaheursitics (3 lectures)
Simulation Lecture O Optimization: Linear Programming Saeed Bastani April 06 Outline of the course Linear Programming ( lecture) Integer Programming ( lecture) Heuristics and Metaheursitics (3 lectures)
Linear Programming: Introduction
 CSC 373 - Algorithm Design, Analysis, and Complexity Summer 2016 Lalla Mouatadid Linear Programming: Introduction A bit of a historical background about linear programming, that I stole from Jeff Erickson
CSC 373 - Algorithm Design, Analysis, and Complexity Summer 2016 Lalla Mouatadid Linear Programming: Introduction A bit of a historical background about linear programming, that I stole from Jeff Erickson
OPERATIONS RESEARCH. Linear Programming Problem
 OPERATIONS RESEARCH Chapter 1 Linear Programming Problem Prof. Bibhas C. Giri Department of Mathematics Jadavpur University Kolkata, India Email: bcgiri.jumath@gmail.com 1.0 Introduction Linear programming
OPERATIONS RESEARCH Chapter 1 Linear Programming Problem Prof. Bibhas C. Giri Department of Mathematics Jadavpur University Kolkata, India Email: bcgiri.jumath@gmail.com 1.0 Introduction Linear programming
CHAPTER 3 LINEAR PROGRAMMING: SIMPLEX METHOD
 CHAPTER 3 LINEAR PROGRAMMING: SIMPLEX METHOD Linear programming is optimization problem where the objective function is linear and all equality and inequality constraints are linear. This problem was first
CHAPTER 3 LINEAR PROGRAMMING: SIMPLEX METHOD Linear programming is optimization problem where the objective function is linear and all equality and inequality constraints are linear. This problem was first
3.1. 3x 4y = 12 3(0) 4y = 12. 3x 4y = 12 3x 4(0) = y = x 0 = 12. 4y = 12 y = 3. 3x = 12 x = 4. The Rectangular Coordinate System
 3. The Rectangular Coordinate System Interpret a line graph. Objectives Interpret a line graph. Plot ordered pairs. 3 Find ordered pairs that satisfy a given equation. 4 Graph lines. 5 Find x- and y-intercepts.
3. The Rectangular Coordinate System Interpret a line graph. Objectives Interpret a line graph. Plot ordered pairs. 3 Find ordered pairs that satisfy a given equation. 4 Graph lines. 5 Find x- and y-intercepts.
Intro to Linear Programming. The problem that we desire to address in this course is loosely stated below.
 . Introduction Intro to Linear Programming The problem that we desire to address in this course is loosely stated below. Given a number of generators make price-quantity offers to sell (each provides their
. Introduction Intro to Linear Programming The problem that we desire to address in this course is loosely stated below. Given a number of generators make price-quantity offers to sell (each provides their
BCN Decision and Risk Analysis. Syed M. Ahmed, Ph.D.
 Linear Programming Module Outline Introduction The Linear Programming Model Examples of Linear Programming Problems Developing Linear Programming Models Graphical Solution to LP Problems The Simplex Method
Linear Programming Module Outline Introduction The Linear Programming Model Examples of Linear Programming Problems Developing Linear Programming Models Graphical Solution to LP Problems The Simplex Method
Chapter 4 Linear Programming
 Chapter Objectives Check off these skills when you feel that you have mastered them. From its associated chart, write the constraints of a linear programming problem as linear inequalities. List two implied
Chapter Objectives Check off these skills when you feel that you have mastered them. From its associated chart, write the constraints of a linear programming problem as linear inequalities. List two implied
Chapter 7. Linear Programming Models: Graphical and Computer Methods
 Chapter 7 Linear Programming Models: Graphical and Computer Methods To accompany Quantitative Analysis for Management, Eleventh Edition, by Render, Stair, and Hanna Power Point slides created by Brian
Chapter 7 Linear Programming Models: Graphical and Computer Methods To accompany Quantitative Analysis for Management, Eleventh Edition, by Render, Stair, and Hanna Power Point slides created by Brian
Linear Programming & Graphic Solution. Dr. Monther Tarawneh
 Linear Programming & Graphic Solution Dr. Monther Tarawneh In this Lecture This topic concentrates on model formulation and computations in linear programming (LP). To illustrate the use of LP, real world
Linear Programming & Graphic Solution Dr. Monther Tarawneh In this Lecture This topic concentrates on model formulation and computations in linear programming (LP). To illustrate the use of LP, real world
CS 372: Computational Geometry Lecture 10 Linear Programming in Fixed Dimension
 CS 372: Computational Geometry Lecture 10 Linear Programming in Fixed Dimension Antoine Vigneron King Abdullah University of Science and Technology November 7, 2012 Antoine Vigneron (KAUST) CS 372 Lecture
CS 372: Computational Geometry Lecture 10 Linear Programming in Fixed Dimension Antoine Vigneron King Abdullah University of Science and Technology November 7, 2012 Antoine Vigneron (KAUST) CS 372 Lecture
Quantitative Technique
 Quantitative Technique Subject Course Code Number : MMAS 521 : Optimization Techniques for Managerial Decisions Instructor : Dr. Umesh Rajopadhyaya Credit Hours : 2 Main Objective : The objective of the
Quantitative Technique Subject Course Code Number : MMAS 521 : Optimization Techniques for Managerial Decisions Instructor : Dr. Umesh Rajopadhyaya Credit Hours : 2 Main Objective : The objective of the
Econ 172A - Slides from Lecture 2
 Econ 205 Sobel Econ 172A - Slides from Lecture 2 Joel Sobel September 28, 2010 Announcements 1. Sections this evening (Peterson 110, 8-9 or 9-10). 2. Podcasts available when I remember to use microphone.
Econ 205 Sobel Econ 172A - Slides from Lecture 2 Joel Sobel September 28, 2010 Announcements 1. Sections this evening (Peterson 110, 8-9 or 9-10). 2. Podcasts available when I remember to use microphone.
A Real Life Application of Linear Programming
 Dagon University Research Journal 2012, Vol. 4 A Real Life Application of Linear Programming Win Win Myo * Abstract Linear programming is heavily used in microeconomics and company management, such as
Dagon University Research Journal 2012, Vol. 4 A Real Life Application of Linear Programming Win Win Myo * Abstract Linear programming is heavily used in microeconomics and company management, such as
UNIT 2 LINEAR PROGRAMMING PROBLEMS
 UNIT 2 LINEAR PROGRAMMING PROBLEMS Structure 2.1 Introduction Objectives 2.2 Linear Programming Problem (LPP) 2.3 Mathematical Formulation of LPP 2.4 Graphical Solution of Linear Programming Problems 2.5
UNIT 2 LINEAR PROGRAMMING PROBLEMS Structure 2.1 Introduction Objectives 2.2 Linear Programming Problem (LPP) 2.3 Mathematical Formulation of LPP 2.4 Graphical Solution of Linear Programming Problems 2.5
Appendix F: Systems of Inequalities
 A0 Appendi F Sstems of Inequalities Appendi F: Sstems of Inequalities F. Solving Sstems of Inequalities The Graph of an Inequalit The statements < and are inequalities in two variables. An ordered pair
A0 Appendi F Sstems of Inequalities Appendi F: Sstems of Inequalities F. Solving Sstems of Inequalities The Graph of an Inequalit The statements < and are inequalities in two variables. An ordered pair
February 10, 2005
 15.053 February 10, 2005 The Geometry of Linear Programs the geometry of LPs illustrated on DTC Announcement: please turn in homework solutions now with a cover sheet 1 Goal of this Lecture 3 mathematical
15.053 February 10, 2005 The Geometry of Linear Programs the geometry of LPs illustrated on DTC Announcement: please turn in homework solutions now with a cover sheet 1 Goal of this Lecture 3 mathematical
Linear Programming in Small Dimensions
 Linear Programming in Small Dimensions Lekcija 7 sergio.cabello@fmf.uni-lj.si FMF Univerza v Ljubljani Edited from slides by Antoine Vigneron Outline linear programming, motivation and definition one dimensional
Linear Programming in Small Dimensions Lekcija 7 sergio.cabello@fmf.uni-lj.si FMF Univerza v Ljubljani Edited from slides by Antoine Vigneron Outline linear programming, motivation and definition one dimensional
Introduction to Linear Programing Problems
 Paper: Linear Programming and Theory of Games Lesson: Introduction to Linear Programing Problems Lesson Developers: DR. MANOJ KUMAR VARSHNEY, College/Department: Department of Statistics, Hindu College,
Paper: Linear Programming and Theory of Games Lesson: Introduction to Linear Programing Problems Lesson Developers: DR. MANOJ KUMAR VARSHNEY, College/Department: Department of Statistics, Hindu College,
4 LINEAR PROGRAMMING (LP) E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 4 LINEAR PROGRAMMING (LP) E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Mathematical programming (optimization) problem: min f (x) s.t. x X R n set of feasible solutions with linear objective function
4 LINEAR PROGRAMMING (LP) E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Mathematical programming (optimization) problem: min f (x) s.t. x X R n set of feasible solutions with linear objective function
LINEAR PROGRAMMING INTRODUCTION 12.1 LINEAR PROGRAMMING. Three Classical Linear Programming Problems (L.P.P.)
 LINEAR PROGRAMMING 12 INTRODUCTION ou are familiar with linear equations and linear inequations in one and two variables. They can be solved algebraically or graphically (by drawing a line diagram in case
LINEAR PROGRAMMING 12 INTRODUCTION ou are familiar with linear equations and linear inequations in one and two variables. They can be solved algebraically or graphically (by drawing a line diagram in case
Linear Programming and its Applications
 Linear Programming and its Applications Outline for Today What is linear programming (LP)? Examples Formal definition Geometric intuition Why is LP useful? A first look at LP algorithms Duality Linear
Linear Programming and its Applications Outline for Today What is linear programming (LP)? Examples Formal definition Geometric intuition Why is LP useful? A first look at LP algorithms Duality Linear
UNIT 6 MODELLING DECISION PROBLEMS (LP)
 UNIT 6 MODELLING DECISION This unit: PROBLEMS (LP) Introduces the linear programming (LP) technique to solve decision problems 1 INTRODUCTION TO LINEAR PROGRAMMING A Linear Programming model seeks to maximize
UNIT 6 MODELLING DECISION This unit: PROBLEMS (LP) Introduces the linear programming (LP) technique to solve decision problems 1 INTRODUCTION TO LINEAR PROGRAMMING A Linear Programming model seeks to maximize
Mathematics for Business and Economics - I. Chapter7 Linear Inequality Systems and Linear Programming (Lecture11)
 Mathematics for Business and Economics - I Chapter7 Linear Inequality Systems and Linear Programming (Lecture11) A linear inequality in two variables is an inequality that can be written in the form Ax
Mathematics for Business and Economics - I Chapter7 Linear Inequality Systems and Linear Programming (Lecture11) A linear inequality in two variables is an inequality that can be written in the form Ax
Chapter 4. Linear Programming
 Chapter 4 Linear Programming For All Practical Purposes: Effective Teaching Occasionally during the semester remind students about your office hours. Some students can perceive that they are bothering
Chapter 4 Linear Programming For All Practical Purposes: Effective Teaching Occasionally during the semester remind students about your office hours. Some students can perceive that they are bothering
Math 7 Notes - Unit 4 Pattern & Functions
 Math 7 Notes - Unit 4 Pattern & Functions Syllabus Objective: (.) The student will create tables, charts, and graphs to etend a pattern in order to describe a linear rule, including integer values. Syllabus
Math 7 Notes - Unit 4 Pattern & Functions Syllabus Objective: (.) The student will create tables, charts, and graphs to etend a pattern in order to describe a linear rule, including integer values. Syllabus
OPTIMIZATION: Linear Programming
 May 21, 2013 OPTIMIZATION: Linear Programming Linear programming (OPTIMIZATION) is the process of taking various linear inequalities (constraints) related to some situation, and finding the "best" value
May 21, 2013 OPTIMIZATION: Linear Programming Linear programming (OPTIMIZATION) is the process of taking various linear inequalities (constraints) related to some situation, and finding the "best" value
LINEAR PROGRAMMING (LP), GRAPHICAL PRESENTATION GASPAR ASAMPANA
 LINEAR PROGRAMMING (LP), GRAPHICAL PRESENTATION GASPAR ASAMPANA INTRODUCTION Linear Programming a is combination of a linear objective function and set of linear constraints. The linear constraints express
LINEAR PROGRAMMING (LP), GRAPHICAL PRESENTATION GASPAR ASAMPANA INTRODUCTION Linear Programming a is combination of a linear objective function and set of linear constraints. The linear constraints express
Design and Analysis of Algorithms (V)
 Design and Analysis of Algorithms (V) An Introduction to Linear Programming Guoqiang Li School of Software, Shanghai Jiao Tong University Homework Assignment 2 is announced! (deadline Apr. 10) Linear Programming
Design and Analysis of Algorithms (V) An Introduction to Linear Programming Guoqiang Li School of Software, Shanghai Jiao Tong University Homework Assignment 2 is announced! (deadline Apr. 10) Linear Programming
Transportation Planning: The maximum flow problem
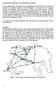 Transportation lanning: The maximum flow problem In many applications, and especially in the planning of Transportation and Logistics of materials, one important problem is that of finding how much material
Transportation lanning: The maximum flow problem In many applications, and especially in the planning of Transportation and Logistics of materials, one important problem is that of finding how much material
Matrix Representations
 CONDENSED LESSON 6. Matri Representations In this lesson, ou Represent closed sstems with transition diagrams and transition matrices Use matrices to organize information Sandra works at a da-care center.
CONDENSED LESSON 6. Matri Representations In this lesson, ou Represent closed sstems with transition diagrams and transition matrices Use matrices to organize information Sandra works at a da-care center.
1. List the Intercepts of the Inequality and then sketch the graph using the Math 125 method of shading
 Math 125 Final Exam Practice 1. List the Intercepts of the Inequality and then sketch the graph using the Math 125 method of shading 18x10y 90 2. USING ALGEBA(meaning no calculators), find the solution
Math 125 Final Exam Practice 1. List the Intercepts of the Inequality and then sketch the graph using the Math 125 method of shading 18x10y 90 2. USING ALGEBA(meaning no calculators), find the solution
CS 473: Algorithms. Ruta Mehta. Spring University of Illinois, Urbana-Champaign. Ruta (UIUC) CS473 1 Spring / 50
 CS 473: Algorithms Ruta Mehta University of Illinois, Urbana-Champaign Spring 2018 Ruta (UIUC) CS473 1 Spring 2018 1 / 50 CS 473: Algorithms, Spring 2018 Introduction to Linear Programming Lecture 18 March
CS 473: Algorithms Ruta Mehta University of Illinois, Urbana-Champaign Spring 2018 Ruta (UIUC) CS473 1 Spring 2018 1 / 50 CS 473: Algorithms, Spring 2018 Introduction to Linear Programming Lecture 18 March
Tuesday, April 10. The Network Simplex Method for Solving the Minimum Cost Flow Problem
 . Tuesday, April The Network Simplex Method for Solving the Minimum Cost Flow Problem Quotes of the day I think that I shall never see A poem lovely as a tree. -- Joyce Kilmer Knowing trees, I understand
. Tuesday, April The Network Simplex Method for Solving the Minimum Cost Flow Problem Quotes of the day I think that I shall never see A poem lovely as a tree. -- Joyce Kilmer Knowing trees, I understand
Chapter 1. Linear Equations and Straight Lines. 2 of 71. Copyright 2014, 2010, 2007 Pearson Education, Inc.
 Chapter 1 Linear Equations and Straight Lines 2 of 71 Outline 1.1 Coordinate Systems and Graphs 1.4 The Slope of a Straight Line 1.3 The Intersection Point of a Pair of Lines 1.2 Linear Inequalities 1.5
Chapter 1 Linear Equations and Straight Lines 2 of 71 Outline 1.1 Coordinate Systems and Graphs 1.4 The Slope of a Straight Line 1.3 The Intersection Point of a Pair of Lines 1.2 Linear Inequalities 1.5
LINEAR PROGRAMMING. Straight line graphs LESSON
 LINEAR PROGRAMMING Traditionall we appl our knowledge of Linear Programming to help us solve real world problems (which is referred to as modelling). Linear Programming is often linked to the field of
LINEAR PROGRAMMING Traditionall we appl our knowledge of Linear Programming to help us solve real world problems (which is referred to as modelling). Linear Programming is often linked to the field of
Fundamentals of Operations Research. Prof. G. Srinivasan. Department of Management Studies. Indian Institute of Technology Madras.
 Fundamentals of Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology Madras Lecture No # 06 Simplex Algorithm Initialization and Iteration (Refer Slide
Fundamentals of Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology Madras Lecture No # 06 Simplex Algorithm Initialization and Iteration (Refer Slide
Linear Programming has been used to:
 Linear Programming Linear programming became important during World War II: used to solve logistics problems for the military. Linear Programming (LP) was the first widely used form of optimization in
Linear Programming Linear programming became important during World War II: used to solve logistics problems for the military. Linear Programming (LP) was the first widely used form of optimization in
Lesson 1: Graphing Linear Inequalities in Two Variables Chapter 6.1
 MATH 11 FOUNDATIONS Lesson 1: Graphing Linear Inequalities in Two Variables Chapter 6.1 Name: Date: A mathematical inequality must contain one of the following: Examples of linear inequalities in a single
MATH 11 FOUNDATIONS Lesson 1: Graphing Linear Inequalities in Two Variables Chapter 6.1 Name: Date: A mathematical inequality must contain one of the following: Examples of linear inequalities in a single
CLEMSON ALGEBRA PROJECT UNIT 4: INEQUALITIES IN TWO VARIABLES
 CLEMSON ALGEBRA PROJECT UNIT 4: INEQUALITIES IN TWO VARIABLES PROBLEM 1: GIFT GIVING Gift-giving season is approaching and you wish to purchase gifts for four relatives and si friends. The amount you spend
CLEMSON ALGEBRA PROJECT UNIT 4: INEQUALITIES IN TWO VARIABLES PROBLEM 1: GIFT GIVING Gift-giving season is approaching and you wish to purchase gifts for four relatives and si friends. The amount you spend
Lesson 08 Linear Programming
 Lesson 08 Linear Programming A mathematical approach to determine optimal (maximum or minimum) solutions to problems which involve restrictions on the variables involved. 08 - Linear Programming Applications
Lesson 08 Linear Programming A mathematical approach to determine optimal (maximum or minimum) solutions to problems which involve restrictions on the variables involved. 08 - Linear Programming Applications
Chapter 3: Towards the Simplex Method for Efficient Solution of Linear Programs
 Chapter 3: Towards the Simplex Method for Efficient Solution of Linear Programs The simplex method, invented by George Dantzig in 1947, is the basic workhorse for solving linear programs, even today. While
Chapter 3: Towards the Simplex Method for Efficient Solution of Linear Programs The simplex method, invented by George Dantzig in 1947, is the basic workhorse for solving linear programs, even today. While
16.410/413 Principles of Autonomy and Decision Making
 16.410/413 Principles of Autonomy and Decision Making Lecture 16: Mathematical Programming I Emilio Frazzoli Aeronautics and Astronautics Massachusetts Institute of Technology November 8, 2010 E. Frazzoli
16.410/413 Principles of Autonomy and Decision Making Lecture 16: Mathematical Programming I Emilio Frazzoli Aeronautics and Astronautics Massachusetts Institute of Technology November 8, 2010 E. Frazzoli
I will illustrate the concepts using the example below.
 Linear Programming Notes More Tutorials at www.littledumbdoctor.com Linear Programming Notes I will illustrate the concepts using the example below. A farmer plants two crops, oats and corn, on 100 acres.
Linear Programming Notes More Tutorials at www.littledumbdoctor.com Linear Programming Notes I will illustrate the concepts using the example below. A farmer plants two crops, oats and corn, on 100 acres.
Lecture 4: Linear Programming
 COMP36111: Advanced Algorithms I Lecture 4: Linear Programming Ian Pratt-Hartmann Room KB2.38: email: ipratt@cs.man.ac.uk 2017 18 Outline The Linear Programming Problem Geometrical analysis The Simplex
COMP36111: Advanced Algorithms I Lecture 4: Linear Programming Ian Pratt-Hartmann Room KB2.38: email: ipratt@cs.man.ac.uk 2017 18 Outline The Linear Programming Problem Geometrical analysis The Simplex
1.1 What is Microeconomics?
 1.1 What is Microeconomics? Economics is the study of allocating limited resources to satisfy unlimited wants. Such a tension implies tradeoffs among competing goals. The analysis can be carried out at
1.1 What is Microeconomics? Economics is the study of allocating limited resources to satisfy unlimited wants. Such a tension implies tradeoffs among competing goals. The analysis can be carried out at
II. Linear Programming
 II. Linear Programming A Quick Example Suppose we own and manage a small manufacturing facility that produced television sets. - What would be our organization s immediate goal? - On what would our relative
II. Linear Programming A Quick Example Suppose we own and manage a small manufacturing facility that produced television sets. - What would be our organization s immediate goal? - On what would our relative
MA30SA Applied Math Unit D - Linear Programming Revd:
 1 Introduction to Linear Programming MA30SA Applied Math Unit D - Linear Programming Revd: 120051212 1. Linear programming is a very important skill. It is a brilliant method for establishing optimum solutions
1 Introduction to Linear Programming MA30SA Applied Math Unit D - Linear Programming Revd: 120051212 1. Linear programming is a very important skill. It is a brilliant method for establishing optimum solutions
a) Alternative Optima, b) Infeasible(or non existing) solution, c) unbounded solution.
 Unit 1 Lesson 5. : Special cases of LPP Learning Outcomes Special cases of linear programming problems Alternative Optima Infeasible Solution Unboundedness In the previous lecture we have discussed some
Unit 1 Lesson 5. : Special cases of LPP Learning Outcomes Special cases of linear programming problems Alternative Optima Infeasible Solution Unboundedness In the previous lecture we have discussed some
Modelling of LP-problems (2WO09)
 Modelling of LP-problems (2WO09) assignor: Judith Keijsper room: HG 9.31 email: J.C.M.Keijsper@tue.nl course info : http://www.win.tue.nl/ jkeijspe Technische Universiteit Eindhoven meeting 1 J.Keijsper
Modelling of LP-problems (2WO09) assignor: Judith Keijsper room: HG 9.31 email: J.C.M.Keijsper@tue.nl course info : http://www.win.tue.nl/ jkeijspe Technische Universiteit Eindhoven meeting 1 J.Keijsper
Chapter 5. Transforming Shapes
 Chapter 5 Transforming Shapes It is difficult to walk through daily life without being able to see geometric transformations in your surroundings. Notice how the leaves of plants, for example, are almost
Chapter 5 Transforming Shapes It is difficult to walk through daily life without being able to see geometric transformations in your surroundings. Notice how the leaves of plants, for example, are almost
Linear Programming. ICM Unit 3 Day 1 Part 1
 Linear Programming ICM Unit 3 Day 1 Part 1 Arrival: Tools of the Trade Pencils Grab a couple to SHARE with your partner. Graph Paper Two pieces per student for today. Ruler One per student. Get out a NEW
Linear Programming ICM Unit 3 Day 1 Part 1 Arrival: Tools of the Trade Pencils Grab a couple to SHARE with your partner. Graph Paper Two pieces per student for today. Ruler One per student. Get out a NEW
Controlling Air Pollution. A quick review. Reclaiming Solid Wastes. Chapter 4 The Simplex Method. Solving the Bake Sale problem. How to move?
 ESE Operations Research 9// Controlling Air Pollution Technology can be use fully () or fractional thereof A quick review ESE Operations Research Reclaiming Solid Wastes Chapter The Simple Method ESE Operations
ESE Operations Research 9// Controlling Air Pollution Technology can be use fully () or fractional thereof A quick review ESE Operations Research Reclaiming Solid Wastes Chapter The Simple Method ESE Operations
LINEAR PROGRAMMING. Chapter Introduction
 504 MATHEMATICS Chapter 12 LINEAR PROGRAMMING The mathematical experience of the student is incomplete if he never had the opportunity to solve a problem invented by himself. G. POLYA 12.1 Introduction
504 MATHEMATICS Chapter 12 LINEAR PROGRAMMING The mathematical experience of the student is incomplete if he never had the opportunity to solve a problem invented by himself. G. POLYA 12.1 Introduction
Outline. CS38 Introduction to Algorithms. Linear programming 5/21/2014. Linear programming. Lecture 15 May 20, 2014
 5/2/24 Outline CS38 Introduction to Algorithms Lecture 5 May 2, 24 Linear programming simplex algorithm LP duality ellipsoid algorithm * slides from Kevin Wayne May 2, 24 CS38 Lecture 5 May 2, 24 CS38
5/2/24 Outline CS38 Introduction to Algorithms Lecture 5 May 2, 24 Linear programming simplex algorithm LP duality ellipsoid algorithm * slides from Kevin Wayne May 2, 24 CS38 Lecture 5 May 2, 24 CS38
Resource Allocation (p. 254)
 Linear Optimization 4.2 120 Resource Allocation (p. 254) Determine the linear program corresponding to the following problem. A farmer has set aside 18 acres of land to be used entirely for plots of grapes,
Linear Optimization 4.2 120 Resource Allocation (p. 254) Determine the linear program corresponding to the following problem. A farmer has set aside 18 acres of land to be used entirely for plots of grapes,
Linear Programming: Model Formulation and Graphical Solution
 Linear Programming: Model Formulation and Graphical Solution Chapter 2 2-1 Chapter Topics Model Formulation A Maximization Model Example Graphical Solutions of Linear Programming Models A Minimization
Linear Programming: Model Formulation and Graphical Solution Chapter 2 2-1 Chapter Topics Model Formulation A Maximization Model Example Graphical Solutions of Linear Programming Models A Minimization
Linear Programming. Linear Programming. Linear Programming. Example: Profit Maximization (1/4) Iris Hui-Ru Jiang Fall Linear programming
 Linear Programming 3 describes a broad class of optimization tasks in which both the optimization criterion and the constraints are linear functions. Linear Programming consists of three parts: A set of
Linear Programming 3 describes a broad class of optimization tasks in which both the optimization criterion and the constraints are linear functions. Linear Programming consists of three parts: A set of
PROCESS MANAGEMENT. Selected Exact Managerial Methods. Study supports
 PROCESS MANAGEMENT Selected Exact Managerial Methods Study supports Darja Noskievičová FMME VŠB-TUO Ostrava 2016 Language review: Mark Landry Title:, Selected Exact Managerial Methods Author: Prof. Ing.
PROCESS MANAGEMENT Selected Exact Managerial Methods Study supports Darja Noskievičová FMME VŠB-TUO Ostrava 2016 Language review: Mark Landry Title:, Selected Exact Managerial Methods Author: Prof. Ing.
AMATH 383 Lecture Notes Linear Programming
 AMATH 8 Lecture Notes Linear Programming Jakob Kotas (jkotas@uw.edu) University of Washington February 4, 014 Based on lecture notes for IND E 51 by Zelda Zabinsky, available from http://courses.washington.edu/inde51/notesindex.htm.
AMATH 8 Lecture Notes Linear Programming Jakob Kotas (jkotas@uw.edu) University of Washington February 4, 014 Based on lecture notes for IND E 51 by Zelda Zabinsky, available from http://courses.washington.edu/inde51/notesindex.htm.
This lesson combines vertical translations and dilations in several quadratic and inverse variation modeling applications.
 Learning Objectives Combined Vertical Transformations Algebra ; Pre-Calculus Time required: 90 min. This lesson combines vertical translations and dilations in several quadratic and inverse variation modeling
Learning Objectives Combined Vertical Transformations Algebra ; Pre-Calculus Time required: 90 min. This lesson combines vertical translations and dilations in several quadratic and inverse variation modeling
OPTIMUM DESIGN. Dr. / Ahmed Nagib Elmekawy. Lecture 3
 OPTIMUM DESIGN Dr. / Ahmed Nagib Elmekawy Lecture 3 1 Graphical Solution 1. Sketch coordinate system 2. Plot constraints 3. Determine feasible region 4. Plot f(x) contours 5. Find opt solution x* & opt
OPTIMUM DESIGN Dr. / Ahmed Nagib Elmekawy Lecture 3 1 Graphical Solution 1. Sketch coordinate system 2. Plot constraints 3. Determine feasible region 4. Plot f(x) contours 5. Find opt solution x* & opt
5-8. Systems of Linear Inequalities. Vocabulary. Lesson. Mental Math
 Lesson 5-8 Systems of Linear Inequalities Vocabulary feasible set, feasible region BIG IDEA The solution to a system of linear inequalities in two variables is either the empty set, the interior of a polygon,
Lesson 5-8 Systems of Linear Inequalities Vocabulary feasible set, feasible region BIG IDEA The solution to a system of linear inequalities in two variables is either the empty set, the interior of a polygon,
Review for Mastery Using Graphs and Tables to Solve Linear Systems
 3-1 Using Graphs and Tables to Solve Linear Systems A linear system of equations is a set of two or more linear equations. To solve a linear system, find all the ordered pairs (x, y) that make both equations
3-1 Using Graphs and Tables to Solve Linear Systems A linear system of equations is a set of two or more linear equations. To solve a linear system, find all the ordered pairs (x, y) that make both equations
Linear programming II João Carlos Lourenço
 Decision Support Models Linear programming II João Carlos Lourenço joao.lourenco@ist.utl.pt Academic year 2012/2013 Readings: Hillier, F.S., Lieberman, G.J., 2010. Introduction to Operations Research,
Decision Support Models Linear programming II João Carlos Lourenço joao.lourenco@ist.utl.pt Academic year 2012/2013 Readings: Hillier, F.S., Lieberman, G.J., 2010. Introduction to Operations Research,
Linear Programming: Model Formulation and Graphical Solution
 Linear Programming: Model Formulation and Graphical Solution Chapter 2 Chapter Topics Model Formulation A Maximization Model Example Graphical Solutions of Linear Programming Models A Minimization Model
Linear Programming: Model Formulation and Graphical Solution Chapter 2 Chapter Topics Model Formulation A Maximization Model Example Graphical Solutions of Linear Programming Models A Minimization Model
Linear Programming. Formulation and Graphical Solution
 Linear Programming Formulation and Graphical Solution A Two Variable Model Simple LP with two decision variables Two dimensional model is hardly useful in the real world systems which normally encompass
Linear Programming Formulation and Graphical Solution A Two Variable Model Simple LP with two decision variables Two dimensional model is hardly useful in the real world systems which normally encompass
Graphing Linear Functions - Review 1. = 6 2. = = = Sketch the graph of each line
 FOM 11 Graphing Linear Functions - Review Sketch the graph of each line 1. =. = +1 3. 3 =1. +7= 5. a) Graph the linear function that goes through (, 3) and is perpendicular to = 11 b) What is the equation
FOM 11 Graphing Linear Functions - Review Sketch the graph of each line 1. =. = +1 3. 3 =1. +7= 5. a) Graph the linear function that goes through (, 3) and is perpendicular to = 11 b) What is the equation
Section 3.1 Graphing Using the Rectangular Coordinate System
 Objectives Section 3.1 Graphing Using the Rectangular Coordinate System n Construct a rectangular coordinate system n Plot ordered pairs and determine the coordinates of a point n Graph paired data n Read
Objectives Section 3.1 Graphing Using the Rectangular Coordinate System n Construct a rectangular coordinate system n Plot ordered pairs and determine the coordinates of a point n Graph paired data n Read
LINEAR PROGRAMMING. Chapter Overview
 Chapter 12 LINEAR PROGRAMMING 12.1 Overview 12.1.1 An Optimisation Problem A problem which seeks to maximise or minimise a function is called an optimisation problem. An optimisation problem may involve
Chapter 12 LINEAR PROGRAMMING 12.1 Overview 12.1.1 An Optimisation Problem A problem which seeks to maximise or minimise a function is called an optimisation problem. An optimisation problem may involve
Chapter II. Linear Programming
 1 Chapter II Linear Programming 1. Introduction 2. Simplex Method 3. Duality Theory 4. Optimality Conditions 5. Applications (QP & SLP) 6. Sensitivity Analysis 7. Interior Point Methods 1 INTRODUCTION
1 Chapter II Linear Programming 1. Introduction 2. Simplex Method 3. Duality Theory 4. Optimality Conditions 5. Applications (QP & SLP) 6. Sensitivity Analysis 7. Interior Point Methods 1 INTRODUCTION
We are IntechOpen, the world s leading publisher of Open Access books Built by scientists, for scientists. International authors and editors
 We are IntechOpen, the world s leading publisher of Open Access books Built by scientists, for scientists 3,500 108,000 1.7 M Open access books available International authors and editors Downloads Our
We are IntechOpen, the world s leading publisher of Open Access books Built by scientists, for scientists 3,500 108,000 1.7 M Open access books available International authors and editors Downloads Our
15-451/651: Design & Analysis of Algorithms October 11, 2018 Lecture #13: Linear Programming I last changed: October 9, 2018
 15-451/651: Design & Analysis of Algorithms October 11, 2018 Lecture #13: Linear Programming I last changed: October 9, 2018 In this lecture, we describe a very general problem called linear programming
15-451/651: Design & Analysis of Algorithms October 11, 2018 Lecture #13: Linear Programming I last changed: October 9, 2018 In this lecture, we describe a very general problem called linear programming
Section 2.1 Graphs. The Coordinate Plane
 Section 2.1 Graphs The Coordinate Plane Just as points on a line can be identified with real numbers to form the coordinate line, points in a plane can be identified with ordered pairs of numbers to form
Section 2.1 Graphs The Coordinate Plane Just as points on a line can be identified with real numbers to form the coordinate line, points in a plane can be identified with ordered pairs of numbers to form
Introduction to Linear Programming. Algorithmic and Geometric Foundations of Optimization
 Introduction to Linear Programming Algorithmic and Geometric Foundations of Optimization Optimization and Linear Programming Mathematical programming is a class of methods for solving problems which ask
Introduction to Linear Programming Algorithmic and Geometric Foundations of Optimization Optimization and Linear Programming Mathematical programming is a class of methods for solving problems which ask
Introduction to Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras
 Introduction to Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Module 03 Simplex Algorithm Lecture - 03 Tabular form (Minimization) In this
Introduction to Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Module 03 Simplex Algorithm Lecture - 03 Tabular form (Minimization) In this
LESSON 3.1 INTRODUCTION TO GRAPHING
 LESSON 3.1 INTRODUCTION TO GRAPHING LESSON 3.1 INTRODUCTION TO GRAPHING 137 OVERVIEW Here s what ou ll learn in this lesson: Plotting Points a. The -plane b. The -ais and -ais c. The origin d. Ordered
LESSON 3.1 INTRODUCTION TO GRAPHING LESSON 3.1 INTRODUCTION TO GRAPHING 137 OVERVIEW Here s what ou ll learn in this lesson: Plotting Points a. The -plane b. The -ais and -ais c. The origin d. Ordered
CCNY Math Review Chapter 2: Functions
 CCN Math Review Chapter : Functions Section.1: Functions.1.1: How functions are used.1.: Methods for defining functions.1.3: The graph of a function.1.: Domain and range.1.5: Relations, functions, and
CCN Math Review Chapter : Functions Section.1: Functions.1.1: How functions are used.1.: Methods for defining functions.1.3: The graph of a function.1.: Domain and range.1.5: Relations, functions, and
Supplemental Problems MAT (Prepared by Prof. Urmi Ghosh-Dastidar)
 Supplemental Problems MAT 3770 (Prepared by Prof. Urmi Ghosh-Dastidar) 1. Use Lagrange Multiplier methods to find the stationary values of z: (a) z = y, subject to + y = (b) z = (y+4), subject to + y =
Supplemental Problems MAT 3770 (Prepared by Prof. Urmi Ghosh-Dastidar) 1. Use Lagrange Multiplier methods to find the stationary values of z: (a) z = y, subject to + y = (b) z = (y+4), subject to + y =
LP-Modelling. dr.ir. C.A.J. Hurkens Technische Universiteit Eindhoven. January 30, 2008
 LP-Modelling dr.ir. C.A.J. Hurkens Technische Universiteit Eindhoven January 30, 2008 1 Linear and Integer Programming After a brief check with the backgrounds of the participants it seems that the following
LP-Modelling dr.ir. C.A.J. Hurkens Technische Universiteit Eindhoven January 30, 2008 1 Linear and Integer Programming After a brief check with the backgrounds of the participants it seems that the following
An introduction to pplex and the Simplex Method
 An introduction to pplex and the Simplex Method Joanna Bauer Marc Bezem Andreas Halle November 16, 2012 Abstract Linear programs occur frequently in various important disciplines, such as economics, management,
An introduction to pplex and the Simplex Method Joanna Bauer Marc Bezem Andreas Halle November 16, 2012 Abstract Linear programs occur frequently in various important disciplines, such as economics, management,
A point is pictured by a dot. While a dot must have some size, the point it represents has no size. Points are named by capital letters..
 Chapter 1 Points, Lines & Planes s we begin any new topic, we have to familiarize ourselves with the language and notation to be successful. My guess that you might already be pretty familiar with many
Chapter 1 Points, Lines & Planes s we begin any new topic, we have to familiarize ourselves with the language and notation to be successful. My guess that you might already be pretty familiar with many
Here are some guidelines for solving a linear programming problem in two variables in which an objective function is to be maximized or minimized.
 Appendi F. Linear Programming F F. Linear Programming Linear Programming: A Graphical Approach Man applications in business and economics involve a process called optimization, in which ou are asked to
Appendi F. Linear Programming F F. Linear Programming Linear Programming: A Graphical Approach Man applications in business and economics involve a process called optimization, in which ou are asked to
Chapter 10: Network Flow Programming
 Chapter 10: Network Flow Programming Linear programming, that amazingly useful technique, is about to resurface: many network problems are actually just special forms of linear programs! This includes,
Chapter 10: Network Flow Programming Linear programming, that amazingly useful technique, is about to resurface: many network problems are actually just special forms of linear programs! This includes,
LINEAR PROGRAMMING - V.
 LINEAR PROGRAMMING Vassilis Kostoglou E-mail: vkostogl@it.teithe.gr URL: www.it.teithe.gr/~vkostogl/en LINEAR PROGRAMMING - V. Kostoglou 1 The problem of limited resources Every business activity requires
LINEAR PROGRAMMING Vassilis Kostoglou E-mail: vkostogl@it.teithe.gr URL: www.it.teithe.gr/~vkostogl/en LINEAR PROGRAMMING - V. Kostoglou 1 The problem of limited resources Every business activity requires
Discrete Optimization. Lecture Notes 2
 Discrete Optimization. Lecture Notes 2 Disjunctive Constraints Defining variables and formulating linear constraints can be straightforward or more sophisticated, depending on the problem structure. The
Discrete Optimization. Lecture Notes 2 Disjunctive Constraints Defining variables and formulating linear constraints can be straightforward or more sophisticated, depending on the problem structure. The
Algebra 2 Notes Systems of Equations and Inequalities Unit 03b. Optimization with Linear Programming
 Optimization with Linear Programming Big Idea Linear programming is one of the most practical uses of mathematics in the real world. The inequalities of the system represent the constraints in the problem
Optimization with Linear Programming Big Idea Linear programming is one of the most practical uses of mathematics in the real world. The inequalities of the system represent the constraints in the problem
INTEGER AND MIXED- INTEGER OPTIMIZATION
 34 INTEGER AND MIXED- INTEGER OPTIMIZATION Conceptually, it s the same as linear optimization: Continue formulating everything using linear functions: Minimize/Maximize a linear function Subject to linear
34 INTEGER AND MIXED- INTEGER OPTIMIZATION Conceptually, it s the same as linear optimization: Continue formulating everything using linear functions: Minimize/Maximize a linear function Subject to linear
GRAPHING LINEAR INEQUALITIES AND FEASIBLE REGIONS
 SECTION 3.1: GRAPHING LINEAR INEQUALITIES AND FEASIBLE REGIONS We start with a reminder of the smart way to graph a Linear Equation for the typical example we see in this course, namely using BOTH X- and
SECTION 3.1: GRAPHING LINEAR INEQUALITIES AND FEASIBLE REGIONS We start with a reminder of the smart way to graph a Linear Equation for the typical example we see in this course, namely using BOTH X- and
AP Calculus. Extreme Values: Graphically. Slide 1 / 163 Slide 2 / 163. Slide 4 / 163. Slide 3 / 163. Slide 5 / 163. Slide 6 / 163
 Slide 1 / 163 Slide 2 / 163 AP Calculus Analyzing Functions Using Derivatives 2015-11-04 www.njctl.org Slide 3 / 163 Table of Contents click on the topic to go to that section Slide 4 / 163 Extreme Values
Slide 1 / 163 Slide 2 / 163 AP Calculus Analyzing Functions Using Derivatives 2015-11-04 www.njctl.org Slide 3 / 163 Table of Contents click on the topic to go to that section Slide 4 / 163 Extreme Values
Advanced Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras
 Advanced Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture 16 Cutting Plane Algorithm We shall continue the discussion on integer programming,
Advanced Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture 16 Cutting Plane Algorithm We shall continue the discussion on integer programming,
Unit.9 Integer Programming
 Unit.9 Integer Programming Xiaoxi Li EMS & IAS, Wuhan University Dec. 22-29, 2016 (revised) Operations Research (Li, X.) Unit.9 Integer Programming Dec. 22-29, 2016 (revised) 1 / 58 Organization of this
Unit.9 Integer Programming Xiaoxi Li EMS & IAS, Wuhan University Dec. 22-29, 2016 (revised) Operations Research (Li, X.) Unit.9 Integer Programming Dec. 22-29, 2016 (revised) 1 / 58 Organization of this
7.5. Systems of Inequalities. The Graph of an Inequality. What you should learn. Why you should learn it
 0_0705.qd /5/05 9:5 AM Page 5 Section 7.5 7.5 Sstems of Inequalities 5 Sstems of Inequalities What ou should learn Sketch the graphs of inequalities in two variables. Solve sstems of inequalities. Use
0_0705.qd /5/05 9:5 AM Page 5 Section 7.5 7.5 Sstems of Inequalities 5 Sstems of Inequalities What ou should learn Sketch the graphs of inequalities in two variables. Solve sstems of inequalities. Use
Appendix 3: PREPARATION & INTERPRETATION OF GRAPHS
 Appendi 3: PREPARATION & INTERPRETATION OF GRAPHS All of you should have had some eperience in plotting graphs. Some of you may have done this in the distant past. Some may have done it only in math courses
Appendi 3: PREPARATION & INTERPRETATION OF GRAPHS All of you should have had some eperience in plotting graphs. Some of you may have done this in the distant past. Some may have done it only in math courses
