Discrete Schemes for Gaussian Curvature and Their Convergence

Transcription

1 Dscrete Schemes for Gaussan Curvature and Ther Convergence Zhqang Xu Guolang Xu Insttute of Computatonal Math. and Sc. and Eng. Computng, Academy of Mathematcs and System Scences, Chnese Academy of Scences, Bejng, Chna Abstract In ths paper, several dscrete schemes for Gaussan curvature are surveyed. The convergence property of a modfed dscrete scheme for the Gaussan curvature s proved. Furthermore, a new dscrete scheme for Gaussan curvature s proposed. We show that ths new scheme converges at the regular vertex wth valence not less than 5. By constructng a counterexample, we also show that t s mpossble for buldng a dscrete scheme for Gaussan curvature whch converges over the regular vertex wth valence 4. Fnally, asymptotc errors of several dscrete schemes for Gaussan curvature are compared. AMS Subject Classfcatons: Prmary 68U07, 68U05, 65S05, 53A40. Keywords: Dscrete Gaussan curvature, dscrete mean curvature, geometrc modelng. 1 Introducton Some applcatons from computer vson, computer graphcs, geometrc modelng and computer aded desgn requre estmatng ntrnsc geometrc nvarants. It s well known that Gaussan curvature s one of the most essental geometrc nvarants for surfaces. However, n the classcal dfferental geometry, ths nvarant s well defned only for C 2 smooth surfaces. In modern computer-related The frst author s Supported by the NSFC grant The second author s supported by NSFC grant and Natonal Key Basc Research Project of Chna (2004CB318000). Emal:xuzq@lsec.cc.ac.cn Emal: xuguo@lsec.cc.ac.cn 1

2 geometry felds, one usually uses dscrete trangle meshes, whch are only C 0 contnues, representng smooth surfaces approxmately. Hence, the problem of estmatng accurately Gaussan curvature for trangle meshes s rased naturally. In the past years, a wealth of dfferent estmators have been proposed n the vast lterature of appled geometry. These methods for estmatng Gaussan curvature can be dvded nto two classes. The frst class s based on the local fttng or nterpolaton technque[2, 4, 5, 6, 17], whle the second class s to dscretze mathematcal formulatons whch present the nformaton about the Gaussan curvature[1, 3, 6, 10, 13, 15]. In ths paper, our focus s on the methods n the second class. Let M be a trangulaton of smooth surface S n R 3. For a vertex p of M, suppose {p } n =1 s the set of the one-rng neghbor vertces of p and the set {p pp +1 } ( = 1,, n) of n Eucldean trangles forms a pecewse lnear approxmaton of S around p. We let γ denote the angle p pp +1 and let the angular defect at p be 2π γ. Moreover, we use the followng conventons throughout the paper p n+1 = p 1 and p 0 = p n. A popular dscrete scheme for computng Gaussan curvature s n the form of 2π P γ,where G s a geometry quantty. In general, G one selects G as A(p)/3 and obtan the followng approxmaton K (1) := 3(2π γ ), (1) A(p) where A(p) s the sum of the areas of trangles p pp +1. In [1], another scheme s gven, where S p := K (2) := 2π γ S p (2) 1 [ 4 sn γ η η +1 cos γ 2 ] (η 2 + η+1) 2 2

3 s called the module of the mesh at p. In [13], the dscrete approxmaton K (1) s modfed as K (3) 2π := γ 1 2 area(p pp +1 ) 1 8 cot(γ, (3) )d 2 where d s the length of edges p p +1. There are several dfferent ponts of vew for explanng the reason why the angular defect s closely related to the Gaussan curvature wth ncludng the vewponts of Gaussan-Bonnet theorem, Gaussan map and Legendre s formula(see the next secton for detals). Asymptotc analyses for the dscrete schemes have been gven n [1, 6, 15]. In [6], the authors show that for the non-unform data, the dscrete scheme K (1) does not convergent to true Gaussan curvature always. In [1], Borrell et al. prove that the angular defect s asymptotcally equvalent to a homogeneous polynomal of degree two n the prncple curvatures and show that f p s a regular vertex wth valence sx, then the scheme K (2) converges to the exact Gaussan curvature n a lnear rate. Moreover, Borrell et al. show that 4 s the only value of the valence such that the angular defect depends upon the prncpal drectons. In [15], G. Xu proves that the dscrete scheme K (1) has quadratc convergence rate f the mesh satsfes the so-called parallelogram crteron. The convergence condtons presented n all these papers requre the valence of the vertex beng 6. Therefore, one hopes to construct a dscrete scheme whch converges over any dscrete mesh. But n [18], Z. Xu et al. show that t s mpossble to construct a dscrete scheme whch s convergent for any dscrete mesh. Hence, we have to content wth the dscrete schemes whch converge under some condtons. Accordng to the past experence[1, 7, 18], we regard a dscrete scheme desrable f t has the followng propertes 1. It converges at regular vertex, at least for suffcently large va- 3

4 lence; 2. It converges at the umblcal pont,.e. the ponts satsfyng k m = k M where k m and k M are two prncpal curvatures. As stated before, the prevous dscrete scheme only converges at the regular vertex wth valence 6. In [1], a method for computng the Gaussan curvature at the regular vertex wth valence unequal to 4 s descrbed. But the method requres two meshes wth valences n 1 and n 2 (n 1 4, n 2 4, n 1 n 2 ). In ths paper, we wll construct a dscrete scheme whch converges at the regular vertex wth valence not less than 5, and also at the umblcal ponts wth any valence. Moreover, the dscrete scheme requres only a sngle mesh. Hence, the new dscrete scheme s more desrable. Furthermore, we show that t s mpossble to construct a dscrete scheme whch s convergent at the regular vertex wth valence 4. Therefore, for the regular vertex, the convergent problem remanng open s the case of vertex wth valence 3. The rest of the paper s organzed as follows. Secton 2 descrbes some notatons and defntons and Secton 3 shows three dfferent vewponts for expressng the relaton between the angular defect and Gaussan curvature. In Secton 4, we study the convergence property of the modfed dscrete Gaussan curvature scheme. We present n Secton 5 a new dscrete scheme and prove that the scheme has good convergence property. In Secton 6, for the regular vertex wth valence 4, we show that t s mpossble to buld a dscrete scheme whch s convergent towards the real Gaussan curvature. Some numercal results are gven n Secton 7. 4

5 2 Prelmnares Ô Õ Æ «Õ ½ Ô ½ Ô Fg.1. Notatons. In ths secton, we ntroduce some notatons and defntons used throughout the paper(see Fg. 1). Let S be a gven smooth surface and p be a pont over S. Suppose the set {p pp +1 }, = 1,, n of n Eucldean trangles form a pecewse lnear approxmaton of S around p. The vector from p to p s denoted as pp. The normal vector and tangent plane of S at the pont p s denoted as n and Π, respectvely. We denote the projecton of p onto Π as q, and defne the plane contanng n, p and p as Π. Then we let κ denote the curvature of the plane curve S Π. The dstances from p to p and q are denoted as η and l, respectvely. The angles p pp +1 and q pq +1 are denoted as γ and β, respectvely. The two prncpal curvatures are denoted as k m and k M. Let η = max η. The followng results are presented n [1, 15, 7]: where w R. l η = 1 + O(η), β = γ + O(η 2 ), (4) w pp = w κ η O(η 3 ), (5) 5

6 Now we gve the defnton of the regular vertex usng the notatons above. Defnton 1 Let p be a pont of a smooth surface S and let p, = 1,, n be ts one rng neghbors. The pont p s called a regular vertex f t satsfes the followng condtons (1) the β = 2π, n (2) the η s all take the same value η. 3 Angular Defect and Gaussan Curvature In ths secton, we summarze three dfferent vewponts for expressng the relaton between angular defect and Gaussan curvature. These vewponts have been descrbed n dfferent lterature([6, 13, 15]). We collect them there. Throughout the secton, we use K (1) (p) to denote the dscrete Gaussan curvature, whch s obtaned usng K (1). 3.1 Gaussan-Bonnet theorem vewpont Let D be a regon of surface S, whose boundary conssts of pecewse smooth curves Γ j s. Then the local Gaussan-Bonnet theorem s as follows K(p)dA + k g (Γ j )ds + α j = 2π, D j Γ j j where K(p) s the Gaussan curvature at p, k g (Γ j ) s the geodesc curvature of the boundary curve Γ j and α j s the exteror angle at the jth corner pont p j of the boundary. If all the Γ j s are the geodesc curves, the above formula reduces to K(p)dA = 2π α j. (6) D j 6

7 Let M be a trangulaton of surface S. For vertex p of valence n, each trangle p pp +1 can be parttoned nto three equal parts, one correspondng to each of ts vertces. We let D be the unon of the part correspondng to p of trangles p pp +1. Note that γ = j α j. Assumng K(p) s a constant on D, and usng (6), we have K(p) can be approxmated by K (1) (p). 3.2 Sphercal mage vewpont We Now ntroduce another defnton of Gaussan curvature. Let D be a small patch of area A ncludng pont p on the surface S. There wll be a correspondng patch of area I on the Gaussan map. Gaussan curvature at p s the lmt of rato lm A 0 I A. Let us consder a dscrete verson of the defnton. The Gaussan map mage,.e. the sphercal mage, of the trangle p pp +1 s (p p the pont ) (p p +1 ) (p p ) (p p +1. Jon these pont by great crcle formng ) a sphercal polygon on the unt sphere. The area of ths sphercal polygon s 2π γ. Same as the above, each trangle s parttoned nto three parts, one correspondng to each vertex. Then the Gaussan curvature can be approxmated by K (1) (p). 3.3 Geodesc trangles vewpont Let T = ABC be a geodesc trangle on the surface S wth angles α, β, γ and geodesc edge lengths a, b, c. Let A B C be a correspondng Eucldean trangle wth edge lengths a, b, c and angles α, β, γ. Legendre presents the followng formulaton α α = area(t ) K(A) 3 + o(a 2 + b 2 + c 2 ), where area(t ) s the area of the geodesc trangle ABC, K(A) s the Gaussan curvature at A. 7

8 Usng Legendre s formulaton for each trangles wth p as a vertex, we arrve at the estmatng formula K (1) (p) agan. 4 Convergence of Angular Defect Schemes In [15], G. Xu gves an analyss about the scheme K (1) and proves that the scheme converges at the vertex satsfyng so-called parallelogram crteron. A numercal test shows that the scheme does not converge over the regular vertex wth valence unequal to 6 and umblcal ponts. In [1], V. Borrell et. al. gve an elegant analyss about the angular defect. Borrell et al. show that f the vertex p s regular, then the angular defct s asymptotcally equvalent to a homogeneous polynomal of degree two n the prncpal curvatures wth closed forms coeffcents. Moreover, they present another angular scheme K (2). In the followng, we show that K (2) and K (3) are equvalent, whch means these two schemes obtan the same value for the same trangle mesh. Theorem 1 For any vertex p of trangle meshes, K (2) K (3). Proof: To prove K (2) K (3), we only need to show S p 1 2 Note that area(p pp +1 ) 1 cot(γ )d 2. 8 d 2 = η 2 + η η η +1 cos γ and area(p pp +1 ) = 1 2 η η +1 sn γ. 8

9 We have 1 area(p pp 2 +1 ) 1 cot(γ )d 2 8 = [ 1 4 η η +1 sn γ 1 ] cos γ (η 2 + η+1 2 2η η +1 cos γ ) 8 sn γ = 1 [ η η +1 cos γ ] (η 2 + η 2 4 sn γ 2 +1) = S p. Hence, the dscrete schemes K (2) and K (3) are equvalent. Moreover, we have Theorem 2 For umblcal vertces, the modfed scheme K (3), and hence K (2), converges to the real Gaussan curvature as the edge lengths η tend to zero f all γ and sup η nf η are bounded (meanng that there exst two postve constants γ mn, γ max such that γ mn γ γ max ; there exst two postve constants η 1, η 2 such that η 1 sup η nf η η 2.). Proof: Snce K (2) K (3), we only need to prove K (2) converges to the real Gaussan curvature over the umblcal ponts. Accordng to Theorem 4 n [1], there exsts a postve constant C such that lm sup 2π γ η 0 K S p nc [ (km k m ) 2 + km 2 k 2 sn γ m ] 2, mn where K s the Gaussan curvature at p. For umblcal ponts, we have k M = k m. Hence, lm 2π γ η 0 K S p = 0, and the theorem holds. In [15], the author proves that the dscrete scheme K (1) quadratc convergence rate under the parallelogram crteron. the followng theorem, we shall show that the dscrete scheme K (3) has also quadratc convergence rate under the same crteron, has In 9

10 Theorem 3 Let p be a vertex of M wth valence sx, and let p j, j = 1,, 6 be ts neghbor vertces. Suppose p and p j, j = 1,, 6 are on a suffcently smooth parametrc surface F(ξ 1, ξ 2 ) R 3, and there exst u, u j R 2 such that Then p = F(u), p j = F(u j ) and u j = u j 1 + u j+1 u, j = 1,, 6. 2π γ 1 A(p, r) cot(γ (r))d 2 (r) = K(p) + O(r2 ), where, K(p) s the real Gaussan curvature at p, A(p, r) := area[p (r)pp +1 (r)], p (r) := F(u (r)), and u (r) = u + r(u u), = 1,, 6. Proof: Let A(p, r) = a 0 r 2 + a 1 r 3 + O(r 4 ) (7) and A(p, r) 2 1 cot(γ (r))d 2 (r) = b 0 r 2 + b 1 r 3 + O(r 4 ) 8 be the Taylor expansons wth respect to r. Accordng to Theorem 4.1 n [15], 3(2π γ ) A(p, r) = K(p) + O(r 2 ). Hence, to prove the theorem, we only need to show b 0 = a 0 /3, b 1 = 0. Wthout loss of generalty, we may assume u = [0, 0] T, u 1 = [1, 0] T. Then there exsts a constant a 0 and an angle θ such that u 2 = [a cos θ, a sn θ] T. Hence,u 3 = [a cos θ 1, a sn θ] T, u j+3 = u j, j = 1, 2, 3. Let u j = s j d j = s j [g j, l j ] T, j = 1,, 6, 10

11 where s j = u j, d j = 1. Then s 1 = 1, s 2 = a, s 3 = a 2 2ac + 1, s 4 = s 1, s 5 = s 2, s 6 = s 3, g 1 = 1, g 2 = c, g 3 = (ac 1)/s 3, g 4 = g 1, g 5 = g 2, g 6 = g 3, l 1 = 0, l 2 = t, l 3 = at/s 3, l 4 = l 1, l 5 = l 2, l 6 = l 3, where (c, t) := (cos θ, sn θ). Note that A(p, r) = j=1 p j (r) p 2 p j+1 (r) p 2 p j (r) p, p j+1 (r) p 2, (8) p j (r) p, p j+1 (r) p cot γ j (r) = pj (r) p 2 p j+1 (r) p 2 p j (r) p, p j+1 (r) p, 2 d 2 j(r) = p j (r) p 2 + p j+1 (r) p 2 2 p j (r) p, p j+1 (r) p. (9) (10) Let F k d j denote the kth order drectonal dervatve of F n the drecton d j. Then usng Taylor expanson wth respect to r, we have p j (r) p j 2 = s 2 jr 2 F dj, F dj + s 3 jr 3 F dj, F 2 d j s4 jr 4 F 2 d j, F 2 d j s4 jr 4 F dj, F 3 d j s5 jr 5 F 2 d j, F 3 d j s5 jr 5 F dj, F 4 d j + O(r 6 ),(11) p j (r) p, p j+1 (r) p = s j s j+1 r 2 F dj, F dj s js 2 j+1r 3 F dj, F 2 d j s2 js j+1 r 3 F dj+1, F 2 d j s2 js 2 j+r 4 F 2 d j+1, F 2 d j s js 3 j+r 4 F dj, F 3 d j s3 js j+1 r 4 F dj+1, F dj s2 js 3 j+1r 5 F 2 d j, F 3 d j s2 j+1s 3 jr 5 F 2 d j, F 3 d j s4 j+1s j r 5 F dj, F 4 d j s j+1s 4 jr 5 F 4 d j, F dj+1 + O(r 6 ). (12) 11

12 To compute all the nner products n the two equatons above, we let t = F(ξ 1, ξ 2 ) ξ, t j = 2 F(ξ 1, ξ 2 ) ξ ξ j, t jk = for, j, k, l = 1, 2. Let 3 F ξ ξ j ξ k, t jkl = 4 F ξ ξ j ξ k ξ l g j = t T t j, g jk = t T t jk, e jkl = t T t jkl, e jklm = t T t jklm, f jklm = t T jt klm. Snce F k d j can be wrtten as the lnear combnatorcs of t, t j, t jk and t jkl, all the nner products n (11) and (12) can be expressed as lnear combnatons of g j, g jk, g jkl, e jkl, e jklm and f jklm. Substtutng (11) and (12) nto (8), (9) and (10), and then substtutng (8), (9) and (10) nto the expresson 1A(p, r) cot(γ (r))d 2 (r), and usng Maple to conduct all the symbolc calculaton, we have b 0 = a 0 /3 = a 2 t 2 (g 11 g 22 g12), 2 b 1 = 0. The theorem s proved. Remark 1 The calculaton of b 0, b 1 nvolves a huge number of terms. It s almost mpossble to fnsh the dervaton by hand. Maple completes all the computaton n 26 seconds on a PC equpped wth a 3.0GHZ Intel(R) CPU. The Maple code that conducts all dervaton of the theorem s avalable n xuzq/ maple.html. The nterested readers are encouraged to perform the computaton. Remark 2 It should be ponted out that there s another dscrete scheme K (4) := 2π γ, A M (p) where A M (p) s the area of Vorono regon. Snce area(p pp +1 ) could be approxmated by 3A M (p) under some condtons, for example the condtons of Theorem 3, K (4) s easly derved from K (1). 12

13 5 A New Dscrete Scheme of the Gaussan Curvature and Its Convergence In ths secton, we ntroduce a new dscrete Gaussan curvature scheme whch converges for the umblcal ponts and regular vertces wth valence greater than 4. We frstly dscuss some propertes about the dscrete mean curvature. Usng the notatons n Fg. 1, we let H (1) := 2 (cot α + cot δ ) pp (cot α + cot δ )η 2, (13) whch denotes a dscrete scheme for the mean curvature at vertex p. Moreover, the real mean curvature and the real Gaussan curvature at p are denoted as H and K respectvely. Then, we have Lemma 1 At the regular vertex p, or the umblcal ponts, the dscrete scheme H (1) converges lnearly to the mean curvature H as η = η 0. Proof: Frstly, we consder the convergence property at the regular vertex. Snce p s a regular vertex, cot α +cot δ cot α j +cot δ j = 1 + O(η 2 ), for any dfferent and j. It follows from equaton (5), we have (cot α + cot δ ) pp = (cot α + cot δ )η 2 k + O(η 3 ). 2 Hence, H (1) = (cot α + cot δ )η 2 (cot α κ + cot δ )η 2 +O(η) = 1 κ +O(η) = H+O(η). n Secondly, we study the convergence propertes at the umblcal ponts. Over the umblcal ponts, k = k j = H for any and j. Hence, H (1) := 2 (cot α + cot δ ) pp (cot α + cot δ )η 2 = (cot α + cot δ )η 2 k + O(η 3 ) (cot α = H + O(η). + cot δ )η 2 13

14 Combnng the two results above, the theorem holds. Now, we turn to the dscrete scheme for Gaussan curvature. Let ϕ := j=1 γ j and where K (5) := 2π γ 2(S p A)(H (1) ) 2 2A S p, A := 1 ( η η +1 (1 cos 2ϕ cos 2ϕ +1 ) 4 sn γ 2 cos γ (η 2 sn 2 ϕ + η+1 2 sn 2 ϕ +1 )), 4 S p := [ 1 η η +1 cos(γ ] ) (η 2 + η 2 4 sn(γ ) 2 +1). Then, we have Theorem 4 For the regular vertces wth valence not less than 5, or the umblcal ponts, K (5) converges towards the Gaussan curvature K as η 0. Proof: We frstly consder the regular vertex case. We set θ(n) := 2π n. Snce p s a regular vertex, γ = θ(n) + O(η 2 ) for any accordng to (4). After a bref calculaton, we have A = A + O(η 4 ), S p = S p + O(η 4 ), where Hence, A = 1 16 sn θ(n) [2n n cos 2θ(n) n cos θ(n)]η2, S p = 2π γ 2(S p A)(H (1) ) 2 2A S p Note that ηmax η mn have 2π n 4 sn θ(n) [1 cos θ(n)]η2. = 2π γ 2(S p A )(H (1) ) 2 +O(η 2 ). 2A S p = 1 + O(η). Accordng to Theorem 3 n [1], we γ = A K + B (k 2 M + k 2 m) + o(η 2 ), 14

15 where, B = 1 16 sn θ(n) [n + n 2 cos 2θ(n) 3n 2 cos θ(n)]η2. Note that S p = A + 2B and A K + B (k 2 M + k 2 m) = A K + B [(k M + k m ) 2 2k M k m ] = A K + 4B H 2 2B K = (A 2B )K + 4B H 2. Hence, 2π γ = (A 2B )K+4B H 2 +o(η 2 ). S A = O(η 2 ), B = O(η 2 ) and when n 3, A 2B 0. Accordng to Lemma 1, H (1) converges to the real mean curvature. Hence, we have, when n 5, K = 2π n =1 γ 4B H 2 + o(1) A 2B = 2π γ 2(S p A )(H (1) ) 2 2A S P + o(1) = K (5) + o(1). Therefor, K (5) converges to the Gaussan curvature. Now, let us consder the umblcal pont case. ponts, each drectonal s the prncpal drecton. Lemma 4 n [1], For umblcal Accordng to 2π γ = (AK + (S p A)k 2 m) + o(η 2 ) holds over the umblcal ponts. Snce k 2 m = H 2 = K, we have 2π γ = (AK + (S p A)k 2 m) + o(η 2 ) = (AK + 2(S p A)H 2 (S p A)K) + o(η 2 ). Hence, K = 2π γ 2(S p A)(H (1) ) 2 2A S p The theorem holds. + o(1) = K (5) + o(1). Remark 3 Theorem 4 shows the new scheme K (5) converge over the regular vertex wth valence greater than 4. As shown before, the 15

16 prevous schemes only converge over the regular vertex wth valence 6, and hence the new scheme has better convergence propertes over the avalable scheme. Remark 4 In [7], the authors prove also that the dscrete scheme H (1) converges to the real mean curvature at the regular vertex. But the defnton of the regular vertex n [7] s dfferent wth our. Remark 5 Accordng to the conclusons above, the Gaussan curvature and mean curvature can be approxmated over the regular vertex wth valence greater than 4. Usng the formulaton k m = H H 2 G, k M = H + H 2 G, one can approxmate the prncpal curvature over the regular vertex wth valence greater than 4. 6 A Counterexample for the Regular Vertex wth Valence 4 In [18], we have constructed a trangle mesh and shown that t s mpossble for constructng a dscrete Gaussan curvature scheme whch converges for that mesh. But the vertex n the mesh s not regular. In ths secton, we shall show that t s also mpossble for buldng a dscrete Gaussan curvature scheme whch converges over the regular vertex wth valence 4. Suppose the xy plane s trangulated around (0, 0) by choosng 4 ponts q 1 = (r 1, 0), q 2 = (0, r 2 ), q 3 = ( r 3, 0) and q 4 = (0, r 4 ), where r 1 s gven and (r 1 2 r = + r4 1 ), = 2, 3, 4. 2 For a bvarate functon f(x, y), the graph of f(x, y),.e. F(x, y) = (x, y, f(x, y)) T, can be regarded as a parametrc surface. Let p 0 = F(0, 0) and p = F(q ), = 1, 2, 3, 4. The set of trangles p p 0 p +1 16

17 forms a trangular mesh approxmaton of F at p 0. The trangle mesh s denoted as M f. When f(x, y) s n the form of x 2 +cxy +y 2 where c R, t s easy to prove that p 0 := (0, 0, 0, ) T s a regular vertex wth valence 4. Moreover, p 1 = (r 1, 0, r1) 2 T, p 2 = (0, r 2, r2) 2 T, p 3 = ( r 3, 0, r3) 2 T, p 4 = (0, r 4, r4) 2 T. Now we show that t s mpossble to construct a dscrete scheme for Gaussan curvature whch converges over the vertex p 0 (See Fg. 2). We assume that the dscrete scheme for Gaussan curvature nvolvng one-rng neghbor vertces of p 0, whch s denoted as H(M f, p 0 ; p 1, p 2, p 3, p 4 ), s convergent for the regular vertex wth valence 4 over trangle mesh surface M f, where f(x, y) s n the form of x 2 + cxy + y 2. It s easy to calculate that the Gaussan curvature of F(x, y, z) at p 0 s 4 c 2. By the convergence property of H(M f, p 0 ; p 1, p 2, p 3, p 4 ) we have lm r1 0 H(M f, p 0 ; p 1, p 2, p 3, p 4 ) = 4 c 2. Note that the trangle mesh M f s ndependent of c,.e. for all the functon f(x, y) whch s n the form of x 2 + cxy + y 2, the trangle mesh M f s the same wth each other. Hence,lm r1 0 H(M f, p 0 ; p 1, p 2, p 3, p 4 ) s ndependent of c. A contradcton occurs. Hence, the assumpton of H(M f, p 0 ; p 1, p 2, p 3, p 4 ) beng convergent for the trangle mesh M f does not hold. Fg.2. A sequence of regular vertex wth valence n = 4 for the functon f(x, y) = x 2 + xy + y 2. At the regular vertex, t s mpossble to construct a dscrete Gaussan curvature scheme whch converges to the correct value. 17

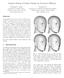
18 Remark 6 The counterexample n ths secton justfes the concluson n [1], whch says that 4 s the only value of valence such that 2π γ depends upon the prncpal drectons. Remark 7 An open problem s to fnd a dscrete scheme for Gaussan curvature whch converges at the regular vertex wth valence 3. 7 Numercal Experments The am of ths secton s to exhbt the numercal behavors of the dscrete schemes mentoned above. For a real vector a = (a 20, a 11, a 02 ), we defne a bvarate functon f a (x, y) := a 20 x 2 + a 11 xy + a 02 y 2, and regard the graph of the functon f a (x, y) as a parametrc surface F a (x, y) = [x, y, f a (x, y)] T R 3. The Gaussan curvature of F a (x, y) at the orgn s 4a 20 a 02 a The doman around (0, 0) s trangulated locally by choosng n ponts: q k = l k (cos θ k, sn θ k ), θ k = 2(k 1)π/n, k = 1,, n. Let p k = F a (q k ) and p 0 = (0, 0, f a (0, 0)) T. Hence, the set of trangles {p k p 0 p k+1 } forms a pecewse lnear approxmaton of F a around p 0. We select (lk l4 k 1 f a(cos 2 θ k, sn θ k )) l k =, k 2 (14) 2fa(cos 2 θ k, sn θ k ) so that p 0 s a regular vertex, In Fg.3, four regular vertces wth valence 6,10,15 and 35 for x 2 xy 1.5y 2 are dsplayed. 18

19 Fg. 3. The regular vertex wth valence n = 6, 10, 15, 35 for the functon x 2 xy 1.5y 2. The dscrete scheme K (5) converges at the regular vertces. We let K () (p 0 : F a ) denote the approxmated Gaussan curvatures of F a at p 0, whch s obtaned by usng the dscrete scheme K (). Suppose A s a set consstng of M randomly chosen vectors a. Then, we let ε () (n) = K () (p 0 : F a ) (4a 20 a 02 a 2 11) /M. a A In fact, ε () (n) measures the error of the dscrete scheme K () at the regular vertex wth valence n. The convergence property and the convergence rate are checked by takng l 1 = 1/8, 1/16, 1/32,. (l k, k 2 can be obtaned by (14).) Snce p s regular, each edge has the same length η. Table 1 shows the asymptotc maxmal error ε () (n) for M = Here, the vertex valences n are taken to be 4, 5,, 8. Table 1. The asymptotc maxmal error ε () (n). n ε (1) (n) ε (2) (n) ε (4) (n) ε (5) (n) e e e e e e e e + 01η e + 01η e + 01η e + 01η e + 01η e e e e 01η e e e e + 01η Moreover, we test also the senstvty of the dscrete schemes to the nose by addng ±1% unform perturbaton along the normal drecton at the regular vertex. Table 2 shows the testng results. 19

20 Table 2. The asymptotc maxmal error ε () (n) after addng ±1% unform nose along the normal drecton. n ε (1) (η; n) ε (2) (η; n) ε (4) (η; n) ε (5) (η; n) e e e e e e e e + 02η e + 01η e + 01η η e + 01η e e e e + 01η e e e e + 01η We compute the Gaussan curvature over a randomly trangulated unt sphere by the dscrete schemes to test ther convergent property at the umblcal ponts. Fg. 4 shows the random trangulaton for the unt sphere. Denote the vertces n the random trangulaton as p, = 1,, N where N s the number of the vertces n the random trangulaton. We let K (j) (p ) denote the approxmate Gaussan curvature at the vertex p whch s calculated by K (j). Smlarly to the above, we use ε (j) = N =1 K(j) (p :) 1) /N to measure the error of dscrete scheme K (j) and use η to denote the average length of the edges. Table 3 lsts ε (j) for dfferent N. Table 3. The asymptotc error ε () over a sphere wth very rregular connectvty. N η ε (1) (η; n) ε (2) (η; n) ε (4) (η; n) ε (5) (η; n) e e e e e e e e e e e e e e e e e e e e 03 Fg. 4. Our test random trangulatons. From left to rght, the number of vertces s 60,300,1000,2000,5000 respectvely. 20

21 From these numercal results, we can draw the followng conclusons: 1. For the regular vertces wth the valence greater than 4, or the umblcal ponts, the dscrete scheme K (5) converges to the real Gaussan curvature. Ths agrees wth the theoretcal result. 2. All the dscrete schemes K (1), K (2), K (4) and K (5) are not senstve to the nose. 3. At the regular vertces and the umblcal ponts, the dfference between K (2) and K (4) s very small. References [1] V.Borrell, F.Cazals and J.-M. Morvan: On the angular defect of trangulatons and the pontwse approxmaton of curvatures, Computer Aded Geometrc Desgn 20(2003), [2] F.Cazals, M.Pouget, Estmatng dfferental quanttes usng polynomal fttng of osculattng jets. Computer Aded Geometrc Desgn 22, (2005). [3] Calladne, C.R.: Gaussan curvature and shell structures, n: J.A. Gregory, ed., The mathematcs of surfaces, Clarendon Press, Oxford, (1986). [4] Douros, I., Buxton, B.F.: Three-dmensonal surface curvature estmaton usng quadrc surface patches, In Scannng 2002 Proceedngs, Pars, 2002 [5] Martn, R.: Estmaton of prncpal curvatures from range data. Internat. J. Shape Modelng 4,99-111(1998). [6] D.S. Meek, D.J. Walton: On surface normal and Gaussan curvature approxmatons gven data sampled from a smooth surface, Computer Aded Geometrc Desgn, 17, (2000). 21

22 [7] T. Langer, A. G. Belyaev and H.P. Sedel: Analyss and desgn of dscrete normals and curvatures,techncal Report,Max- Planck-Insttut für Informatk,2005. [8] M. Desbrun, M.Meyer, P.Schröder and A.H.Barr: Implct farng of rregular meshes usng dffuson and curvature flow, SIGGRAPH99, (1999). [9] G H. Lu, Y.S. Wong, Y.F.Zhang, H. T Loh: Adaptve farng of dgtzed pont data wth dscrete curvature, Computer Aded Desgn, 34, (2002). [10] Meyer. M, Desbrun, M.,Schroder, P.,Barr,A.: Dscrete dfferental-geometry operator for trangulated 2-manfolds, n:proc. VsMath 02, Berln, Germany,2002. [11] G. Taubn, A sgnal processng approach to far surface desgn, n SIGGRAPH 95 Proceedngs (1995). [12] C. Wollmann, Estmaton of prncpal curvatures of approxmated surfaces, Computer Aded Geometrc Desgn,17, (2000). [13] Jean-Lous Maltret, Marc Danel, Dscrete curvatures and applcatons : a survey, preprnt, [14] U. F. Mayer, Numercal solutons for the surface dffuson flow n three space dmensons. Computatonal and Appled Mathematcs(to appear),2001. [15] Guolang Xu, Convergence analyss of a dscretzaton scheme for Gaussan curvature over trangular surfaces, Computer Aded Geometryc Desgn, 23, (2006). 22

23 [16] Guolang Xu, Convergenc of dscrete Laplace-Beltram operator over surfaces, Computers and Mathematcs wth Applcatons, 48, (2004). [17] Guolang Xu, Descrete Laplace-Betram operators and ther convergence, Computer Aded Geometrc Desgn 21, (2004). [18] Zhqang Xu, Guolang Xu and Jaguang Sun,Convergence analyss of dscrete dfferental geometry operators over surfaces, IMA Conference on the Mathematcs of Surfaces, (2005). 23