Morphological Image Processing
|
|
|
- Wesley Tyler
- 6 years ago
- Views:
Transcription
1 Morphological Image Processing Ranga Rodrigo October 9, 29 Outline Contents Preliminaries 2 Dilation and Erosion 3 2. Dilation Erosion Opening and Closing 5 4 Labeling Connected Components Morphological image processing tools help us to extract image components that are useful in the representation and description of region shape, such as boundaries, skeletons, and convex hull. There are morphological techniques for pre- and postprocessing, such as morphological filtering, thinning, and pruning. Preliminaries Let Z be a set of integers. The sampling process used to produce the digital image may be viewed as a partitioning in the x y -plane in to a grid, with coordinates of the center of each grid being a pair of elements from the Cartesian product Z 2. In the terminology of set theory the function f (x, y ) is said to be a digital image if (x, y ) are integers from Z 2 and f is a mapping that assigns an intensity value in the set of real numbers, R, to each distinct pair of coordinates (x, y ). If the elements of R also are integers, a digital image then becomes a two-dimensional function, whose coordinates and the amplitude values are integers. Let A be a set in Z 2, the elements of which are pixel coordinates (x, y ). If w = (x, y ) is an element of A, then we write w A. Similarly, if w is not an element of A, we write w / A. A set of B pixels satisfying a particular condition is written as B = {w condition}.
2 A B A B A B (a) (b) A B (c) A B A B A (d) A (e) A B Figure : Set operations. For example, the set of all pixel coordinates that do not belong to A, denoted by A, is given by A = {w w / A}. This set is called the complement of A. The union of two sets, denoted by C = A B is the set of all elements that belong to wither A or B, or both. Similarly, the intersection of two sets A and B is the set of elements that belong to both sets, denoted by C = A B. The difference of sets A and B, denoted by A B, is the set of all elements that belong to A but not to B: A B = {w w A, w / B}. Figure illustrates these set operations. In addition to the basic operations, morphological operations often require two operations that are specific to sets whose elements are pixel coordinates. The reflection of set B, denoted by ˆB, is defined as ˆB = {w w = b, forb B}. The translation of set A by z = (z x, z y ), denoted by (A) z, is defined as (A) z = {c c = a + z, fora A}. A binary image can be viewed as a bivariate function of x and y. Morphological theory views a binary image as a set of it foreground (-valued) pixels, the elements of which are in Z 2. Set operations such as union and intersection can be applied directly to binary image sets. For example, if A and B are binary images, then C = A B is also a binary image, where a pixel in C is a foreground pixel if either or both of the corresponding pixels in A and B are foreground pixels. Table shows Matlab s logical operations that perform set operations on binary images. 2
3 y x (A) z (a) Translation ˆB (b) Reflection Figure 2: Translation and reflection. Dot identifies the origin. Table : Set operations for binary images in Matlab. Set operation MATLAB expression Name A B A & B AND A B A B OR A ~ A NOT A B A &~ B DIFFERENCE 2 Dilation and Erosion The operations of dilation and erosion are fundamental to morphological image processing. Many of the algorithms are based on these operations. 2. Dilation Dilation is an operation that grows or thickens objects in a binary image. The specific manner and the extent of this thickening is controlled by a shape referred to as a structuring element. Dilation is a process that translates the origin of the structuring element throughout the domain of the image and checks to see whether it overlaps with -valued pixels. The output image is at each location of the origin of the structuring element if the structuring element overlaps at least one -valued pixel in the input image. Mathematically, dilation is defined in terms of set operations. The dilation of A by B, denoted by A B, is defined as A B = z ( ˆB) z A, where is the empty set and B is the structuring element. In words, the dilation of A by B is the set consisting of all the structuring element origin locations where the reflected and translated B overlaps at least some portion of A. Dilation is commutative, i.e., A B = B A. It is a convention in image processing to let the first operand of A B be the image and the second operand be the structuring element, which is usually much smaller than the image. The Matlab image processing toolbox function imdilate performs dilation. The syntax is C = i m d i l a t e ( A, B) where A and C are binary images and B is a matrix of s and s that specify the structuring element. 3
4 Example. Write a Matlab program to dilate the image A with the structuring element B shown below. Structuring Element Decomposition Dilation is associative. That is A (B C ) = (A B) C. Suppose that structuring element B can be represented as a dilation of two structuring elements B and B 2 : B = B B 2. Then, A B = A (B B 2 ) = (A B ) B 2. In other words, dilating A with B is the same as first dilating A with B, and then dilating the result with B 2. We say that B can be decomposed into the structuring elements B and B 2. The associative property is important because the time required to compute dilation is proportional to the number of nonzero pixels in the structuring element. Consider for example, dilation with a 5 5 array of s:. This structuring element can be decomposed into a five-element row of s and a file-element column of s: The number of elements in the original structuring element is 25, but the total number of elements in the row-column decomposition is only. This means that dilation with the row structuring element first, followed by dilation with the column structuring element can be performed approximately 2.5 times faster that dilation with the 5 5 array of s.. 4
5 The strel Function Matlab image processing toolbox function strel constructs structuring elements with a variety of shapes and sizes. Its basic syntax is B = s t r e l ( shape, parameters ) This returns a special quantity called an strel object. The function imdilate is able to use the decomposed from of the structuring element. Example: B = s t r e l ( diamond, 5) creates a flat diamond sharped structuring element such that the distance from the structuring element s origin to the extreme points of the diamond is 5. There are other shapes such as disk, line, rectangle, etc. The following code shows how to use the structuring element generated by the strel function is used to carry out dilation. A = imread ( image. t i f ) ; B = s t r e l ( diamond, 5) C = i m d i l a t e ( A, B ) ; imshow (C) 2.2 Erosion Erosion shrinks or thins in a binary image. As in dilation, the manner and extent of shrinking is controlled by the structuring element. The output of erosion has a value at each location of the origin of the structuring element, such that the structuring element overlaps only -valued pixels of the input image. The mathematical definition of erosion is similar to that of dilation. The erosion of A by B, denoted by A B, is defined as A B = z (B) z A. In other words, erosion of A by B is the set of structuring element origin locations where the translated B has no overlap with the background of A. The Matlab image processing toolbox function imerode performs erosion. The syntax is C = imerode ( A, B) where A and C are binary images and B is a matrix of s and s that specify the structuring element. 3 Opening and Closing In practical image processing applications, dilation and erosion are used most often in various combinations. We can apply a series of dilation and erosion operations to an image, either using the same structuring element or, sometimes, a different one. Two such common operations are opening and closing. 5
6 Morphological Opening The morphological opening of A by B, denoted by A B, is simply erosion of A by B followed by the dilation of the result by B: A B = (A B) B. An alternative mathematical formulation of opening is A B = {(B) z (B) z A} where { } denotes the union of all sets inside braces, and the notation C D means that C is a subset of D. This formulation has a simple geometric interpretation: A B is the union of all translations of B that fit entirely within A. Morphological opening removes completely regions of an object that cannot 6
7 contain the structuring element, smoothes the object contours, breaks thin connections, and removes the protrusions. Morphological Closing The morphological closing of A by B, denoted by A B, is a dilation followed by an erosion: A B = (A B) B. Geometrically, A B is the complement of the union of all translations of B the do not overlap A. Like opening, morphological closing tends to smooth the contours of objects. Unlike opening, however, it generally joins narrow breaks, filling long thin gulfs, and fills holes smaller than the structuring element. 7
8 Matlab Functions for Opening and Closing Opening and closing are implemented in the toolbox with functions imopen and imclose. The following carries out opening: C = imopen ( A, B) Closing is carried out as follows: C = imclose ( A, B) In these code snippets, A is a binary image, and B is matrix of s and s that specifies the structuring element. A strel object, SE can be used instead of B. Example 2. Write a Matlab program to carry out morphological opening on an image using a square structuring element. 8
9 Example 3. Write a Matlab program to carry out morphological closing on an image using a square structuring element. Combining a closing and opening can be quite effective in removing noise. 9
10 Function bwmorph Image processing toolbox function bwmorph implements a variety of useful operations based on combinations of dilations, erosions, and lookup table operations. g = bwmorph( f, operation, n ) where f is an input binary image, operation is a string specifying the desired operation, and n is a positive integer specifying the number of times the operation is to be repeated. The operation can be open, close, dilate, erode, thin, skel, and several others. Thinning, (thin) means reducing binary objects or shapes in an image to strokes that are a single pixel wide. Skeletonisation (skel) is another way to reduce binary image objects to a set of thin strokes that retain the important information about the shapes of the original objects. Example 4. Write a Matlab program to carry out skeletonisation.
11 y w y y w y x x h h x x (a) 4-neighborhood (b) 8-neighborhood Figure 3: Neighborhoods. 4 Labeling Connected Components Using connected component analysis we can extract individual objects or connected components in an image. In order to do this, we must define connectedness A pixel p at coordinates (x, y ) has two horizontal and two vertical neighbors whose coordinates are This set is known as 4-neighbors of p, denoted by N 4 (p). In a similar manner we can define N 8 (p) as well. Figure 3 shows this. Two pixels p and q are said to be 4-adjacent if q N 4 (p). Similarly, two pixels p and q are said to be 4-adjacent if q N 8 (p). A path between pixels p and p n is a sequence of pixels p, p 2,..., p n such that p k is adjacent to p k +, for k < n. A path can be 4-connected or 8-connected depending on the definition of adjacency used. Two foreground pixels p and q are said to be 4-connected is there exists a 4- connected path between them, containing entirely foreground pixels. Similarly, two foreground pixels p and q are said to be 8-connected is there exists a 8-connected path between them, containing entirely foreground pixels. Example 5. Identify if the pixels p and q are 4-connected or 8-connected.
12 Connected Components For any foreground pixel p, the set of all foreground pixels connected to it is called the connected component containing p. The nature of the connected component depends on the definition of adjacency we choose between 4- and 8-adjacency. IPT Function bwlabel Matlab Image Processing Toolbox Function bwlabel computes all the connected components in a binary image. [ L, num] = bwlabel ( f, conn ) where f is a binary image and conn specifies the desired connectivity (either 4 or 8). Output L is called the label matrix, and num (optional) gives the total number of connected components found. 2
Introduction. Computer Vision & Digital Image Processing. Preview. Basic Concepts from Set Theory
 Introduction Computer Vision & Digital Image Processing Morphological Image Processing I Morphology a branch of biology concerned with the form and structure of plants and animals Mathematical morphology
Introduction Computer Vision & Digital Image Processing Morphological Image Processing I Morphology a branch of biology concerned with the form and structure of plants and animals Mathematical morphology
What will we learn? What is mathematical morphology? What is mathematical morphology? Fundamental concepts and operations
 What will we learn? What is mathematical morphology and how is it used in image processing? Lecture Slides ME 4060 Machine Vision and Vision-based Control Chapter 13 Morphological image processing By Dr.
What will we learn? What is mathematical morphology and how is it used in image processing? Lecture Slides ME 4060 Machine Vision and Vision-based Control Chapter 13 Morphological image processing By Dr.
Morphological Image Processing
 Morphological Image Processing Morphology Identification, analysis, and description of the structure of the smallest unit of words Theory and technique for the analysis and processing of geometric structures
Morphological Image Processing Morphology Identification, analysis, and description of the structure of the smallest unit of words Theory and technique for the analysis and processing of geometric structures
Mathematical Morphology and Distance Transforms. Robin Strand
 Mathematical Morphology and Distance Transforms Robin Strand robin.strand@it.uu.se Morphology Form and structure Mathematical framework used for: Pre-processing Noise filtering, shape simplification,...
Mathematical Morphology and Distance Transforms Robin Strand robin.strand@it.uu.se Morphology Form and structure Mathematical framework used for: Pre-processing Noise filtering, shape simplification,...
Morphological Image Processing
 Morphological Image Processing Binary image processing In binary images, we conventionally take background as black (0) and foreground objects as white (1 or 255) Morphology Figure 4.1 objects on a conveyor
Morphological Image Processing Binary image processing In binary images, we conventionally take background as black (0) and foreground objects as white (1 or 255) Morphology Figure 4.1 objects on a conveyor
Morphological Image Processing
 Morphological Image Processing Introduction Morphology: a branch of biology that deals with the form and structure of animals and plants Morphological image processing is used to extract image components
Morphological Image Processing Introduction Morphology: a branch of biology that deals with the form and structure of animals and plants Morphological image processing is used to extract image components
Biomedical Image Analysis. Mathematical Morphology
 Biomedical Image Analysis Mathematical Morphology Contents: Foundation of Mathematical Morphology Structuring Elements Applications BMIA 15 V. Roth & P. Cattin 265 Foundations of Mathematical Morphology
Biomedical Image Analysis Mathematical Morphology Contents: Foundation of Mathematical Morphology Structuring Elements Applications BMIA 15 V. Roth & P. Cattin 265 Foundations of Mathematical Morphology
morphology on binary images
 morphology on binary images Ole-Johan Skrede 10.05.2017 INF2310 - Digital Image Processing Department of Informatics The Faculty of Mathematics and Natural Sciences University of Oslo After original slides
morphology on binary images Ole-Johan Skrede 10.05.2017 INF2310 - Digital Image Processing Department of Informatics The Faculty of Mathematics and Natural Sciences University of Oslo After original slides
International Journal of Advance Engineering and Research Development. Applications of Set Theory in Digital Image Processing
 Scientific Journal of Impact Factor (SJIF): 4.72 International Journal of Advance Engineering and Research Development Volume 4, Issue 11, November -2017 Applications of Set Theory in Digital Image Processing
Scientific Journal of Impact Factor (SJIF): 4.72 International Journal of Advance Engineering and Research Development Volume 4, Issue 11, November -2017 Applications of Set Theory in Digital Image Processing
EECS490: Digital Image Processing. Lecture #17
 Lecture #17 Morphology & set operations on images Structuring elements Erosion and dilation Opening and closing Morphological image processing, boundary extraction, region filling Connectivity: convex
Lecture #17 Morphology & set operations on images Structuring elements Erosion and dilation Opening and closing Morphological image processing, boundary extraction, region filling Connectivity: convex
09/11/2017. Morphological image processing. Morphological image processing. Morphological image processing. Morphological image processing (binary)
 Towards image analysis Goal: Describe the contents of an image, distinguishing meaningful information from irrelevant one. Perform suitable transformations of images so as to make explicit particular shape
Towards image analysis Goal: Describe the contents of an image, distinguishing meaningful information from irrelevant one. Perform suitable transformations of images so as to make explicit particular shape
Morphological Image Processing
 Digital Image Processing Lecture # 10 Morphological Image Processing Autumn 2012 Agenda Extraction of Connected Component Convex Hull Thinning Thickening Skeletonization Pruning Gray-scale Morphology Digital
Digital Image Processing Lecture # 10 Morphological Image Processing Autumn 2012 Agenda Extraction of Connected Component Convex Hull Thinning Thickening Skeletonization Pruning Gray-scale Morphology Digital
Lecture 7: Morphological Image Processing
 I2200: Digital Image processing Lecture 7: Morphological Image Processing Prof. YingLi Tian Oct. 25, 2017 Department of Electrical Engineering The City College of New York The City University of New York
I2200: Digital Image processing Lecture 7: Morphological Image Processing Prof. YingLi Tian Oct. 25, 2017 Department of Electrical Engineering The City College of New York The City University of New York
[ ] Review. Edges and Binary Images. Edge detection. Derivative of Gaussian filter. Image gradient. Tuesday, Sept 16
![[ ] Review. Edges and Binary Images. Edge detection. Derivative of Gaussian filter. Image gradient. Tuesday, Sept 16 [ ] Review. Edges and Binary Images. Edge detection. Derivative of Gaussian filter. Image gradient. Tuesday, Sept 16](/thumbs/89/98496315.jpg) Review Edges and Binary Images Tuesday, Sept 6 Thought question: how could we compute a temporal gradient from video data? What filter is likely to have produced this image output? original filtered output
Review Edges and Binary Images Tuesday, Sept 6 Thought question: how could we compute a temporal gradient from video data? What filter is likely to have produced this image output? original filtered output
Morphological Image Processing
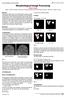 Morphological Image Processing Megha Goyal Dept. of ECE, Doaba Institute of Engineering and Technology, Kharar, Mohali, Punjab, India Abstract The purpose of this paper is to provide readers with an in-depth
Morphological Image Processing Megha Goyal Dept. of ECE, Doaba Institute of Engineering and Technology, Kharar, Mohali, Punjab, India Abstract The purpose of this paper is to provide readers with an in-depth
Lab 2. Hanz Cuevas Velásquez, Bob Fisher Advanced Vision School of Informatics, University of Edinburgh Week 3, 2018
 Lab 2 Hanz Cuevas Velásquez, Bob Fisher Advanced Vision School of Informatics, University of Edinburgh Week 3, 2018 This lab will focus on learning simple image transformations and the Canny edge detector.
Lab 2 Hanz Cuevas Velásquez, Bob Fisher Advanced Vision School of Informatics, University of Edinburgh Week 3, 2018 This lab will focus on learning simple image transformations and the Canny edge detector.
EE 584 MACHINE VISION
 EE 584 MACHINE VISION Binary Images Analysis Geometrical & Topological Properties Connectedness Binary Algorithms Morphology Binary Images Binary (two-valued; black/white) images gives better efficiency
EE 584 MACHINE VISION Binary Images Analysis Geometrical & Topological Properties Connectedness Binary Algorithms Morphology Binary Images Binary (two-valued; black/white) images gives better efficiency
Morphological Image Algorithms
 Morphological Image Algorithms Examples 1 Example 1 Use thresholding and morphological operations to segment coins from background Matlab s eight.tif image 2 clear all close all I = imread('eight.tif');
Morphological Image Algorithms Examples 1 Example 1 Use thresholding and morphological operations to segment coins from background Matlab s eight.tif image 2 clear all close all I = imread('eight.tif');
Image Analysis. Morphological Image Analysis
 Image Analysis Morphological Image Analysis Christophoros Nikou cnikou@cs.uoi.gr Images taken from: R. Gonzalez and R. Woods. Digital Image Processing, Prentice Hall, 2008 University of Ioannina - Department
Image Analysis Morphological Image Analysis Christophoros Nikou cnikou@cs.uoi.gr Images taken from: R. Gonzalez and R. Woods. Digital Image Processing, Prentice Hall, 2008 University of Ioannina - Department
Topic 6 Representation and Description
 Topic 6 Representation and Description Background Segmentation divides the image into regions Each region should be represented and described in a form suitable for further processing/decision-making Representation
Topic 6 Representation and Description Background Segmentation divides the image into regions Each region should be represented and described in a form suitable for further processing/decision-making Representation
EE795: Computer Vision and Intelligent Systems
 EE795: Computer Vision and Intelligent Systems Spring 2012 TTh 17:30-18:45 WRI C225 Lecture 04 130131 http://www.ee.unlv.edu/~b1morris/ecg795/ 2 Outline Review Histogram Equalization Image Filtering Linear
EE795: Computer Vision and Intelligent Systems Spring 2012 TTh 17:30-18:45 WRI C225 Lecture 04 130131 http://www.ee.unlv.edu/~b1morris/ecg795/ 2 Outline Review Histogram Equalization Image Filtering Linear
Bioimage Informatics
 Bioimage Informatics Lecture 14, Spring 2012 Bioimage Data Analysis (IV) Image Segmentation (part 3) Lecture 14 March 07, 2012 1 Outline Review: intensity thresholding based image segmentation Morphological
Bioimage Informatics Lecture 14, Spring 2012 Bioimage Data Analysis (IV) Image Segmentation (part 3) Lecture 14 March 07, 2012 1 Outline Review: intensity thresholding based image segmentation Morphological
From Pixels to Blobs
 From Pixels to Blobs 15-463: Rendering and Image Processing Alexei Efros Today Blobs Need for blobs Extracting blobs Image Segmentation Working with binary images Mathematical Morphology Blob properties
From Pixels to Blobs 15-463: Rendering and Image Processing Alexei Efros Today Blobs Need for blobs Extracting blobs Image Segmentation Working with binary images Mathematical Morphology Blob properties
Mathematical morphology (1)
 Chapter 9 Mathematical morphology () 9. Introduction Morphology, or morphology for short, is a branch of image processing which is particularly useful for analyzing shapes in images. We shall develop basic
Chapter 9 Mathematical morphology () 9. Introduction Morphology, or morphology for short, is a branch of image processing which is particularly useful for analyzing shapes in images. We shall develop basic
10.5 Morphological Reconstruction
 518 Chapter 10 Morphological Image Processing See Sections 11.4.2 and 11.4.3 for additional applications of morphological reconstruction. This definition of reconstruction is based on dilation. It is possible
518 Chapter 10 Morphological Image Processing See Sections 11.4.2 and 11.4.3 for additional applications of morphological reconstruction. This definition of reconstruction is based on dilation. It is possible
Morphological Image Processing
 Morphological Image Processing Binary dilation and erosion" Set-theoretic interpretation" Opening, closing, morphological edge detectors" Hit-miss filter" Morphological filters for gray-level images" Cascading
Morphological Image Processing Binary dilation and erosion" Set-theoretic interpretation" Opening, closing, morphological edge detectors" Hit-miss filter" Morphological filters for gray-level images" Cascading
Filters. Advanced and Special Topics: Filters. Filters
 Filters Advanced and Special Topics: Filters Dr. Edmund Lam Department of Electrical and Electronic Engineering The University of Hong Kong ELEC4245: Digital Image Processing (Second Semester, 2016 17)
Filters Advanced and Special Topics: Filters Dr. Edmund Lam Department of Electrical and Electronic Engineering The University of Hong Kong ELEC4245: Digital Image Processing (Second Semester, 2016 17)
Chapter 9 Morphological Image Processing
 Morphological Image Processing Question What is Mathematical Morphology? An (imprecise) Mathematical Answer A mathematical tool for investigating geometric structure in binary and grayscale images. Shape
Morphological Image Processing Question What is Mathematical Morphology? An (imprecise) Mathematical Answer A mathematical tool for investigating geometric structure in binary and grayscale images. Shape
Edges and Binary Images
 CS 699: Intro to Computer Vision Edges and Binary Images Prof. Adriana Kovashka University of Pittsburgh September 5, 205 Plan for today Edge detection Binary image analysis Homework Due on 9/22, :59pm
CS 699: Intro to Computer Vision Edges and Binary Images Prof. Adriana Kovashka University of Pittsburgh September 5, 205 Plan for today Edge detection Binary image analysis Homework Due on 9/22, :59pm
Mathematical morphology... M.1 Introduction... M.1 Dilation... M.3 Erosion... M.3 Closing... M.4 Opening... M.5 Summary... M.6
 Chapter M Misc. Contents Mathematical morphology.............................................. M.1 Introduction................................................... M.1 Dilation.....................................................
Chapter M Misc. Contents Mathematical morphology.............................................. M.1 Introduction................................................... M.1 Dilation.....................................................
CITS 4402 Computer Vision
 CITS 4402 Computer Vision A/Prof Ajmal Mian Adj/A/Prof Mehdi Ravanbakhsh, CEO at Mapizy (www.mapizy.com) and InFarm (www.infarm.io) Lecture 02 Binary Image Analysis Objectives Revision of image formation
CITS 4402 Computer Vision A/Prof Ajmal Mian Adj/A/Prof Mehdi Ravanbakhsh, CEO at Mapizy (www.mapizy.com) and InFarm (www.infarm.io) Lecture 02 Binary Image Analysis Objectives Revision of image formation
Chapter 11 Representation & Description
 Chain Codes Chain codes are used to represent a boundary by a connected sequence of straight-line segments of specified length and direction. The direction of each segment is coded by using a numbering
Chain Codes Chain codes are used to represent a boundary by a connected sequence of straight-line segments of specified length and direction. The direction of each segment is coded by using a numbering
Machine vision. Summary # 5: Morphological operations
 1 Machine vision Summary # 5: Mphological operations MORPHOLOGICAL OPERATIONS A real image has continuous intensity. It is quantized to obtain a digital image with a given number of gray levels. Different
1 Machine vision Summary # 5: Mphological operations MORPHOLOGICAL OPERATIONS A real image has continuous intensity. It is quantized to obtain a digital image with a given number of gray levels. Different
Elaborazione delle Immagini Informazione multimediale - Immagini. Raffaella Lanzarotti
 Elaborazione delle Immagini Informazione multimediale - Immagini Raffaella Lanzarotti MATHEMATICAL MORPHOLOGY 2 Definitions Morphology: branch of biology studying shape and structure of plants and animals
Elaborazione delle Immagini Informazione multimediale - Immagini Raffaella Lanzarotti MATHEMATICAL MORPHOLOGY 2 Definitions Morphology: branch of biology studying shape and structure of plants and animals
Digital Image Processing
 Digital Image Processing Lecture # 4 Digital Image Fundamentals - II ALI JAVED Lecturer SOFTWARE ENGINEERING DEPARTMENT U.E.T TAXILA Email:: ali.javed@uettaxila.edu.pk Office Room #:: 7 Presentation Outline
Digital Image Processing Lecture # 4 Digital Image Fundamentals - II ALI JAVED Lecturer SOFTWARE ENGINEERING DEPARTMENT U.E.T TAXILA Email:: ali.javed@uettaxila.edu.pk Office Room #:: 7 Presentation Outline
Previously. Edge detection. Today. Thresholding. Gradients -> edges 2/1/2011. Edges and Binary Image Analysis
 2//20 Previously Edges and Binary Image Analysis Mon, Jan 3 Prof. Kristen Grauman UT-Austin Filters allow local image neighborhood to influence our description and features Smoothing to reduce noise Derivatives
2//20 Previously Edges and Binary Image Analysis Mon, Jan 3 Prof. Kristen Grauman UT-Austin Filters allow local image neighborhood to influence our description and features Smoothing to reduce noise Derivatives
Morphological Image Processing GUI using MATLAB
 Trends Journal of Sciences Research (2015) 2(3):90-94 http://www.tjsr.org Morphological Image Processing GUI using MATLAB INTRODUCTION A digital image is a representation of twodimensional images as a
Trends Journal of Sciences Research (2015) 2(3):90-94 http://www.tjsr.org Morphological Image Processing GUI using MATLAB INTRODUCTION A digital image is a representation of twodimensional images as a
C E N T E R A T H O U S T O N S C H O O L of H E A L T H I N F O R M A T I O N S C I E N C E S. Image Operations II
 T H E U N I V E R S I T Y of T E X A S H E A L T H S C I E N C E C E N T E R A T H O U S T O N S C H O O L of H E A L T H I N F O R M A T I O N S C I E N C E S Image Operations II For students of HI 5323
T H E U N I V E R S I T Y of T E X A S H E A L T H S C I E N C E C E N T E R A T H O U S T O N S C H O O L of H E A L T H I N F O R M A T I O N S C I E N C E S Image Operations II For students of HI 5323
Digital Image Processing Fundamentals
 Ioannis Pitas Digital Image Processing Fundamentals Chapter 7 Shape Description Answers to the Chapter Questions Thessaloniki 1998 Chapter 7: Shape description 7.1 Introduction 1. Why is invariance to
Ioannis Pitas Digital Image Processing Fundamentals Chapter 7 Shape Description Answers to the Chapter Questions Thessaloniki 1998 Chapter 7: Shape description 7.1 Introduction 1. Why is invariance to
CS443: Digital Imaging and Multimedia Binary Image Analysis. Spring 2008 Ahmed Elgammal Dept. of Computer Science Rutgers University
 CS443: Digital Imaging and Multimedia Binary Image Analysis Spring 2008 Ahmed Elgammal Dept. of Computer Science Rutgers University Outlines A Simple Machine Vision System Image segmentation by thresholding
CS443: Digital Imaging and Multimedia Binary Image Analysis Spring 2008 Ahmed Elgammal Dept. of Computer Science Rutgers University Outlines A Simple Machine Vision System Image segmentation by thresholding
Edges and Binary Image Analysis. Thurs Jan 26 Kristen Grauman UT Austin. Today. Edge detection and matching
 /25/207 Edges and Binary Image Analysis Thurs Jan 26 Kristen Grauman UT Austin Today Edge detection and matching process the image gradient to find curves/contours comparing contours Binary image analysis
/25/207 Edges and Binary Image Analysis Thurs Jan 26 Kristen Grauman UT Austin Today Edge detection and matching process the image gradient to find curves/contours comparing contours Binary image analysis
Processing of binary images
 Binary Image Processing Tuesday, 14/02/2017 ntonis rgyros e-mail: argyros@csd.uoc.gr 1 Today From gray level to binary images Processing of binary images Mathematical morphology 2 Computer Vision, Spring
Binary Image Processing Tuesday, 14/02/2017 ntonis rgyros e-mail: argyros@csd.uoc.gr 1 Today From gray level to binary images Processing of binary images Mathematical morphology 2 Computer Vision, Spring
ECEN 447 Digital Image Processing
 ECEN 447 Digital Image Processing Lecture 7: Mathematical Morphology Ulisses Braga-Neto ECE Department Texas A&M University Basics of Mathematical Morphology Mathematical Morphology (MM) is a discipline
ECEN 447 Digital Image Processing Lecture 7: Mathematical Morphology Ulisses Braga-Neto ECE Department Texas A&M University Basics of Mathematical Morphology Mathematical Morphology (MM) is a discipline
Edges and Binary Image Analysis April 12 th, 2018
 4/2/208 Edges and Binary Image Analysis April 2 th, 208 Yong Jae Lee UC Davis Previously Filters allow local image neighborhood to influence our description and features Smoothing to reduce noise Derivatives
4/2/208 Edges and Binary Image Analysis April 2 th, 208 Yong Jae Lee UC Davis Previously Filters allow local image neighborhood to influence our description and features Smoothing to reduce noise Derivatives
11/10/2011 small set, B, to probe the image under study for each SE, define origo & pixels in SE
 Mathematical Morphology Sonka 13.1-13.6 Ida-Maria Sintorn ida@cb.uu.se Today s lecture SE, morphological transformations inary MM Gray-level MM Applications Geodesic transformations Morphology-form and
Mathematical Morphology Sonka 13.1-13.6 Ida-Maria Sintorn ida@cb.uu.se Today s lecture SE, morphological transformations inary MM Gray-level MM Applications Geodesic transformations Morphology-form and
Image Processing. Bilkent University. CS554 Computer Vision Pinar Duygulu
 Image Processing CS 554 Computer Vision Pinar Duygulu Bilkent University Today Image Formation Point and Blob Processing Binary Image Processing Readings: Gonzalez & Woods, Ch. 3 Slides are adapted from
Image Processing CS 554 Computer Vision Pinar Duygulu Bilkent University Today Image Formation Point and Blob Processing Binary Image Processing Readings: Gonzalez & Woods, Ch. 3 Slides are adapted from
11. Gray-Scale Morphology. Computer Engineering, i Sejong University. Dongil Han
 Computer Vision 11. Gray-Scale Morphology Computer Engineering, i Sejong University i Dongil Han Introduction Methematical morphology represents image objects as sets in a Euclidean space by Serra [1982],
Computer Vision 11. Gray-Scale Morphology Computer Engineering, i Sejong University i Dongil Han Introduction Methematical morphology represents image objects as sets in a Euclidean space by Serra [1982],
Chapter 3. Image Processing Methods. (c) 2008 Prof. Dr. Michael M. Richter, Universität Kaiserslautern
 Chapter 3 Image Processing Methods The Role of Image Processing Methods (1) An image is an nxn matrix of gray or color values An image processing method is algorithm transforming such matrices or assigning
Chapter 3 Image Processing Methods The Role of Image Processing Methods (1) An image is an nxn matrix of gray or color values An image processing method is algorithm transforming such matrices or assigning
Digital Image Processing COSC 6380/4393
 Digital Image Processing COSC 6380/4393 Lecture 6 Sept 6 th, 2017 Pranav Mantini Slides from Dr. Shishir K Shah and Frank (Qingzhong) Liu Today Review Logical Operations on Binary Images Blob Coloring
Digital Image Processing COSC 6380/4393 Lecture 6 Sept 6 th, 2017 Pranav Mantini Slides from Dr. Shishir K Shah and Frank (Qingzhong) Liu Today Review Logical Operations on Binary Images Blob Coloring
CS 5540 Spring 2013 Assignment 3, v1.0 Due: Apr. 24th 11:59PM
 1 Introduction In this programming project, we are going to do a simple image segmentation task. Given a grayscale image with a bright object against a dark background and we are going to do a binary decision
1 Introduction In this programming project, we are going to do a simple image segmentation task. Given a grayscale image with a bright object against a dark background and we are going to do a binary decision
Babu Madhav Institute of Information Technology Years Integrated M.Sc.(IT)(Semester - 7)
 5 Years Integrated M.Sc.(IT)(Semester - 7) 060010707 Digital Image Processing UNIT 1 Introduction to Image Processing Q: 1 Answer in short. 1. What is digital image? 1. Define pixel or picture element?
5 Years Integrated M.Sc.(IT)(Semester - 7) 060010707 Digital Image Processing UNIT 1 Introduction to Image Processing Q: 1 Answer in short. 1. What is digital image? 1. Define pixel or picture element?
Morphological Compound Operations-Opening and CLosing
 Morphological Compound Operations-Opening and CLosing COMPSCI 375 S1 T 2006, A/P Georgy Gimel farb Revised COMPSCI 373 S1C -2010, Patrice Delmas AP Georgy Gimel'farb 1 Set-theoretic Binary Operations Many
Morphological Compound Operations-Opening and CLosing COMPSCI 375 S1 T 2006, A/P Georgy Gimel farb Revised COMPSCI 373 S1C -2010, Patrice Delmas AP Georgy Gimel'farb 1 Set-theoretic Binary Operations Many
Relational Database: The Relational Data Model; Operations on Database Relations
 Relational Database: The Relational Data Model; Operations on Database Relations Greg Plaxton Theory in Programming Practice, Spring 2005 Department of Computer Science University of Texas at Austin Overview
Relational Database: The Relational Data Model; Operations on Database Relations Greg Plaxton Theory in Programming Practice, Spring 2005 Department of Computer Science University of Texas at Austin Overview
Digital Image Fundamentals II
 Digital Image Fundamentals II 1. Image modeling and representations 2. Pixels and Pixel relations 3. Arithmetic operations of images 4. Image geometry operation 5. Image processing with Matlab - Image
Digital Image Fundamentals II 1. Image modeling and representations 2. Pixels and Pixel relations 3. Arithmetic operations of images 4. Image geometry operation 5. Image processing with Matlab - Image
Digital Image Processing
 Digital Image Processing Third Edition Rafael C. Gonzalez University of Tennessee Richard E. Woods MedData Interactive PEARSON Prentice Hall Pearson Education International Contents Preface xv Acknowledgments
Digital Image Processing Third Edition Rafael C. Gonzalez University of Tennessee Richard E. Woods MedData Interactive PEARSON Prentice Hall Pearson Education International Contents Preface xv Acknowledgments
Image Processing (IP) Through Erosion and Dilation Methods
 Image Processing (IP) Through Erosion and Dilation Methods Prof. sagar B Tambe 1, Prof. Deepak Kulhare 2, M. D. Nirmal 3, Prof. Gopal Prajapati 4 1 MITCOE Pune 2 H.O.D. Computer Dept., 3 Student, CIIT,
Image Processing (IP) Through Erosion and Dilation Methods Prof. sagar B Tambe 1, Prof. Deepak Kulhare 2, M. D. Nirmal 3, Prof. Gopal Prajapati 4 1 MITCOE Pune 2 H.O.D. Computer Dept., 3 Student, CIIT,
Lecture 18 Representation and description I. 2. Boundary descriptors
 Lecture 18 Representation and description I 1. Boundary representation 2. Boundary descriptors What is representation What is representation After segmentation, we obtain binary image with interested regions
Lecture 18 Representation and description I 1. Boundary representation 2. Boundary descriptors What is representation What is representation After segmentation, we obtain binary image with interested regions
Morphological track 1
 Morphological track 1 Shapes Painting of living beings on cave walls at Lascaux [about 1500 th BC] L homme qui marche by Alberto Giacometti, 1948, NOUVELLES IMAGES Editor (1976) Les lutteurs by Honoré
Morphological track 1 Shapes Painting of living beings on cave walls at Lascaux [about 1500 th BC] L homme qui marche by Alberto Giacometti, 1948, NOUVELLES IMAGES Editor (1976) Les lutteurs by Honoré
Albert M. Vossepoel. Center for Image Processing
 Albert M. Vossepoel www.ph.tn.tudelft.nl/~albert scene image formation sensor pre-processing image enhancement image restoration texture filtering segmentation user analysis classification CBP course:
Albert M. Vossepoel www.ph.tn.tudelft.nl/~albert scene image formation sensor pre-processing image enhancement image restoration texture filtering segmentation user analysis classification CBP course:
Table 1. Different types of Defects on Tiles
 DETECTION OF SURFACE DEFECTS ON CERAMIC TILES BASED ON MORPHOLOGICAL TECHNIQUES ABSTRACT Grasha Jacob 1, R. Shenbagavalli 2, S. Karthika 3 1 Associate Professor, 2 Assistant Professor, 3 Research Scholar
DETECTION OF SURFACE DEFECTS ON CERAMIC TILES BASED ON MORPHOLOGICAL TECHNIQUES ABSTRACT Grasha Jacob 1, R. Shenbagavalli 2, S. Karthika 3 1 Associate Professor, 2 Assistant Professor, 3 Research Scholar
Detection of Edges Using Mathematical Morphological Operators
 OPEN TRANSACTIONS ON INFORMATION PROCESSING Volume 1, Number 1, MAY 2014 OPEN TRANSACTIONS ON INFORMATION PROCESSING Detection of Edges Using Mathematical Morphological Operators Suman Rani*, Deepti Bansal,
OPEN TRANSACTIONS ON INFORMATION PROCESSING Volume 1, Number 1, MAY 2014 OPEN TRANSACTIONS ON INFORMATION PROCESSING Detection of Edges Using Mathematical Morphological Operators Suman Rani*, Deepti Bansal,
Finger Print Analysis and Matching Daniel Novák
 Finger Print Analysis and Matching Daniel Novák 1.11, 2016, Prague Acknowledgments: Chris Miles,Tamer Uz, Andrzej Drygajlo Handbook of Fingerprint Recognition, Chapter III Sections 1-6 Outline - Introduction
Finger Print Analysis and Matching Daniel Novák 1.11, 2016, Prague Acknowledgments: Chris Miles,Tamer Uz, Andrzej Drygajlo Handbook of Fingerprint Recognition, Chapter III Sections 1-6 Outline - Introduction
Two Image-Template Operations for Binary Image Processing. Hongchi Shi. Department of Computer Engineering and Computer Science
 Two Image-Template Operations for Binary Image Processing Hongchi Shi Department of Computer Engineering and Computer Science Engineering Building West, Room 331 University of Missouri - Columbia Columbia,
Two Image-Template Operations for Binary Image Processing Hongchi Shi Department of Computer Engineering and Computer Science Engineering Building West, Room 331 University of Missouri - Columbia Columbia,
Interpolation is a basic tool used extensively in tasks such as zooming, shrinking, rotating, and geometric corrections.
 Image Interpolation 48 Interpolation is a basic tool used extensively in tasks such as zooming, shrinking, rotating, and geometric corrections. Fundamentally, interpolation is the process of using known
Image Interpolation 48 Interpolation is a basic tool used extensively in tasks such as zooming, shrinking, rotating, and geometric corrections. Fundamentally, interpolation is the process of using known
Image Segmentation. Figure 1: Input image. Step.2. Use Morphological Opening to Estimate the Background
 Image Segmentation Image segmentation is the process of dividing an image into multiple parts. This is typically used to identify objects or other relevant information in digital images. There are many
Image Segmentation Image segmentation is the process of dividing an image into multiple parts. This is typically used to identify objects or other relevant information in digital images. There are many
Chapter 4 Concepts from Geometry
 Chapter 4 Concepts from Geometry An Introduction to Optimization Spring, 2014 Wei-Ta Chu 1 Line Segments The line segment between two points and in R n is the set of points on the straight line joining
Chapter 4 Concepts from Geometry An Introduction to Optimization Spring, 2014 Wei-Ta Chu 1 Line Segments The line segment between two points and in R n is the set of points on the straight line joining
Colorado School of Mines. Computer Vision. Professor William Hoff Dept of Electrical Engineering &Computer Science.
 Professor William Hoff Dept of Electrical Engineering &Computer Science http://inside.mines.edu/~whoff/ 1 Binary Image Processing 2 Binary means 0 or 1 values only Also called logical type (true/false)
Professor William Hoff Dept of Electrical Engineering &Computer Science http://inside.mines.edu/~whoff/ 1 Binary Image Processing 2 Binary means 0 or 1 values only Also called logical type (true/false)
[Ch 6] Set Theory. 1. Basic Concepts and Definitions. 400 lecture note #4. 1) Basics
![[Ch 6] Set Theory. 1. Basic Concepts and Definitions. 400 lecture note #4. 1) Basics [Ch 6] Set Theory. 1. Basic Concepts and Definitions. 400 lecture note #4. 1) Basics](/thumbs/82/86066673.jpg) 400 lecture note #4 [Ch 6] Set Theory 1. Basic Concepts and Definitions 1) Basics Element: ; A is a set consisting of elements x which is in a/another set S such that P(x) is true. Empty set: notated {
400 lecture note #4 [Ch 6] Set Theory 1. Basic Concepts and Definitions 1) Basics Element: ; A is a set consisting of elements x which is in a/another set S such that P(x) is true. Empty set: notated {
Morphology-form and structure. Who am I? structuring element (SE) Today s lecture. Morphological Transformation. Mathematical Morphology
 Mathematical Morphology Morphology-form and structure Sonka 13.1-13.6 Ida-Maria Sintorn Ida.sintorn@cb.uu.se mathematical framework used for: pre-processing - noise filtering, shape simplification,...
Mathematical Morphology Morphology-form and structure Sonka 13.1-13.6 Ida-Maria Sintorn Ida.sintorn@cb.uu.se mathematical framework used for: pre-processing - noise filtering, shape simplification,...
Interactive Math Glossary Terms and Definitions
 Terms and Definitions Absolute Value the magnitude of a number, or the distance from 0 on a real number line Addend any number or quantity being added addend + addend = sum Additive Property of Area the
Terms and Definitions Absolute Value the magnitude of a number, or the distance from 0 on a real number line Addend any number or quantity being added addend + addend = sum Additive Property of Area the
Digital Image Processing Chapter 11: Image Description and Representation
 Digital Image Processing Chapter 11: Image Description and Representation Image Representation and Description? Objective: To represent and describe information embedded in an image in other forms that
Digital Image Processing Chapter 11: Image Description and Representation Image Representation and Description? Objective: To represent and describe information embedded in an image in other forms that
EC-433 Digital Image Processing
 EC-433 Digital Image Processing Lecture 4 Digital Image Fundamentals Dr. Arslan Shaukat Acknowledgement: Lecture slides material from Dr. Rehan Hafiz, Gonzalez and Woods Interpolation Required in image
EC-433 Digital Image Processing Lecture 4 Digital Image Fundamentals Dr. Arslan Shaukat Acknowledgement: Lecture slides material from Dr. Rehan Hafiz, Gonzalez and Woods Interpolation Required in image
Fuzzy Soft Mathematical Morphology
 Fuzzy Soft Mathematical Morphology. Gasteratos, I. ndreadis and Ph. Tsalides Laboratory of Electronics Section of Electronics and Information Systems Technology Department of Electrical and Computer Engineering
Fuzzy Soft Mathematical Morphology. Gasteratos, I. ndreadis and Ph. Tsalides Laboratory of Electronics Section of Electronics and Information Systems Technology Department of Electrical and Computer Engineering
Sets MAT231. Fall Transition to Higher Mathematics. MAT231 (Transition to Higher Math) Sets Fall / 31
 Sets MAT231 Transition to Higher Mathematics Fall 2014 MAT231 (Transition to Higher Math) Sets Fall 2014 1 / 31 Outline 1 Sets Introduction Cartesian Products Subsets Power Sets Union, Intersection, Difference
Sets MAT231 Transition to Higher Mathematics Fall 2014 MAT231 (Transition to Higher Math) Sets Fall 2014 1 / 31 Outline 1 Sets Introduction Cartesian Products Subsets Power Sets Union, Intersection, Difference
INF Exercise for Thursday
 INF 4300 - Exercise for Thursday 24.09.2014 Exercise 1. Problem 10.2 in Gonzales&Woods Exercise 2. Problem 10.38 in Gonzales&Woods Exercise 3. Problem 10.39 in Gonzales&Woods Exercise 4. Problem 10.43
INF 4300 - Exercise for Thursday 24.09.2014 Exercise 1. Problem 10.2 in Gonzales&Woods Exercise 2. Problem 10.38 in Gonzales&Woods Exercise 3. Problem 10.39 in Gonzales&Woods Exercise 4. Problem 10.43
Binary Image Processing. Introduction to Computer Vision CSE 152 Lecture 5
 Binary Image Processing CSE 152 Lecture 5 Announcements Homework 2 is due Apr 25, 11:59 PM Reading: Szeliski, Chapter 3 Image processing, Section 3.3 More neighborhood operators Binary System Summary 1.
Binary Image Processing CSE 152 Lecture 5 Announcements Homework 2 is due Apr 25, 11:59 PM Reading: Szeliski, Chapter 3 Image processing, Section 3.3 More neighborhood operators Binary System Summary 1.
SPEED OPTIMIZATION OF CT-BASED MICROSTRUCTURE DETERMINATION USING MATRIX DECOMPOSITION
 SPEED OPTIMIZATION OF CT-BASED MICROSTRUCTURE DETERMINATION USING MATRIX DECOMPOSITION Simon Kranzer, Gernot Standfest, Karl Entacher School of Information Technologies and Systems-Management Salzburg
SPEED OPTIMIZATION OF CT-BASED MICROSTRUCTURE DETERMINATION USING MATRIX DECOMPOSITION Simon Kranzer, Gernot Standfest, Karl Entacher School of Information Technologies and Systems-Management Salzburg
Binary Shape Characterization using Morphological Boundary Class Distribution Functions
 Binary Shape Characterization using Morphological Boundary Class Distribution Functions Marcin Iwanowski Institute of Control and Industrial Electronics, Warsaw University of Technology, ul.koszykowa 75,
Binary Shape Characterization using Morphological Boundary Class Distribution Functions Marcin Iwanowski Institute of Control and Industrial Electronics, Warsaw University of Technology, ul.koszykowa 75,
Image segmentation. Stefano Ferrari. Università degli Studi di Milano Methods for Image Processing. academic year
 Image segmentation Stefano Ferrari Università degli Studi di Milano stefano.ferrari@unimi.it Methods for Image Processing academic year 2017 2018 Segmentation by thresholding Thresholding is the simplest
Image segmentation Stefano Ferrari Università degli Studi di Milano stefano.ferrari@unimi.it Methods for Image Processing academic year 2017 2018 Segmentation by thresholding Thresholding is the simplest
CS534 Introduction to Computer Vision Binary Image Analysis. Ahmed Elgammal Dept. of Computer Science Rutgers University
 CS534 Introduction to Computer Vision Binary Image Analysis Ahmed Elgammal Dept. of Computer Science Rutgers University Outlines A Simple Machine Vision System Image segmentation by thresholding Digital
CS534 Introduction to Computer Vision Binary Image Analysis Ahmed Elgammal Dept. of Computer Science Rutgers University Outlines A Simple Machine Vision System Image segmentation by thresholding Digital
Binary Image Analysis. Binary Image Analysis. What kinds of operations? Results of analysis. Useful Operations. Example: red blood cell image
 inary Image Analysis inary Image Analysis inary image analysis consists of a set of image analysis operations that are used to produce or process binary images, usually images of s and s. represents the
inary Image Analysis inary Image Analysis inary image analysis consists of a set of image analysis operations that are used to produce or process binary images, usually images of s and s. represents the
Introduction to Medical Imaging (5XSA0)
 1 Introduction to Medical Imaging (5XSA0) Visual feature extraction Color and texture analysis Sveta Zinger ( s.zinger@tue.nl ) Introduction (1) Features What are features? Feature a piece of information
1 Introduction to Medical Imaging (5XSA0) Visual feature extraction Color and texture analysis Sveta Zinger ( s.zinger@tue.nl ) Introduction (1) Features What are features? Feature a piece of information
ECG782: Multidimensional Digital Signal Processing
 Professor Brendan Morris, SEB 3216, brendan.morris@unlv.edu ECG782: Multidimensional Digital Signal Processing Spring 2014 TTh 14:30-15:45 CBC C313 Lecture 03 Image Processing Basics 13/01/28 http://www.ee.unlv.edu/~b1morris/ecg782/
Professor Brendan Morris, SEB 3216, brendan.morris@unlv.edu ECG782: Multidimensional Digital Signal Processing Spring 2014 TTh 14:30-15:45 CBC C313 Lecture 03 Image Processing Basics 13/01/28 http://www.ee.unlv.edu/~b1morris/ecg782/
ECG782: Multidimensional Digital Signal Processing
 Professor Brendan Morris, SEB 3216, brendan.morris@unlv.edu ECG782: Multidimensional Digital Signal Processing Spatial Domain Filtering http://www.ee.unlv.edu/~b1morris/ecg782/ 2 Outline Background Intensity
Professor Brendan Morris, SEB 3216, brendan.morris@unlv.edu ECG782: Multidimensional Digital Signal Processing Spatial Domain Filtering http://www.ee.unlv.edu/~b1morris/ecg782/ 2 Outline Background Intensity
Lecture 3: Basic Morphological Image Processing
 Lecture 3: Basic Morphological Image Processing Harvey Rhody Chester F. Carlson Center for Imaging Science Rochester Institute of Technology rhody@cis.rit.edu September 13, 2005 Abstract Morphological
Lecture 3: Basic Morphological Image Processing Harvey Rhody Chester F. Carlson Center for Imaging Science Rochester Institute of Technology rhody@cis.rit.edu September 13, 2005 Abstract Morphological
Curriki Geometry Glossary
 Curriki Geometry Glossary The following terms are used throughout the Curriki Geometry projects and represent the core vocabulary and concepts that students should know to meet Common Core State Standards.
Curriki Geometry Glossary The following terms are used throughout the Curriki Geometry projects and represent the core vocabulary and concepts that students should know to meet Common Core State Standards.
Approximation Algorithms for Geometric Intersection Graphs
 Approximation Algorithms for Geometric Intersection Graphs Subhas C. Nandy (nandysc@isical.ac.in) Advanced Computing and Microelectronics Unit Indian Statistical Institute Kolkata 700108, India. Outline
Approximation Algorithms for Geometric Intersection Graphs Subhas C. Nandy (nandysc@isical.ac.in) Advanced Computing and Microelectronics Unit Indian Statistical Institute Kolkata 700108, India. Outline
Gesture based PTZ camera control
 Gesture based PTZ camera control Report submitted in May 2014 to the department of Computer Science and Engineering of National Institute of Technology Rourkela in partial fulfillment of the requirements
Gesture based PTZ camera control Report submitted in May 2014 to the department of Computer Science and Engineering of National Institute of Technology Rourkela in partial fulfillment of the requirements
CSci 4968 and 6270 Computational Vision, Fall Semester, 2011 Lectures 2&3, Image Processing. Corners, boundaries, homogeneous regions, textures?
 1 Introduction CSci 4968 and 6270 Computational Vision, Fall Semester, 2011 Lectures 2&3, Image Processing How Do We Start Working with Images? Corners, boundaries, homogeneous regions, textures? How do
1 Introduction CSci 4968 and 6270 Computational Vision, Fall Semester, 2011 Lectures 2&3, Image Processing How Do We Start Working with Images? Corners, boundaries, homogeneous regions, textures? How do
Hierarchical Representation of 2-D Shapes using Convex Polygons: a Contour-Based Approach
 Hierarchical Representation of 2-D Shapes using Convex Polygons: a Contour-Based Approach O. El Badawy, M. S. Kamel Pattern Analysis and Machine Intelligence Laboratory, Department of Systems Design Engineering,
Hierarchical Representation of 2-D Shapes using Convex Polygons: a Contour-Based Approach O. El Badawy, M. S. Kamel Pattern Analysis and Machine Intelligence Laboratory, Department of Systems Design Engineering,
Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 24 Solid Modelling
 Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 24 Solid Modelling Welcome to the lectures on computer graphics. We have
Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 24 Solid Modelling Welcome to the lectures on computer graphics. We have
Practical Image and Video Processing Using MATLAB
 Practical Image and Video Processing Using MATLAB Chapter 18 Feature extraction and representation What will we learn? What is feature extraction and why is it a critical step in most computer vision and
Practical Image and Video Processing Using MATLAB Chapter 18 Feature extraction and representation What will we learn? What is feature extraction and why is it a critical step in most computer vision and
1.1 - Introduction to Sets
 1.1 - Introduction to Sets Math 166-502 Blake Boudreaux Department of Mathematics Texas A&M University January 18, 2018 Blake Boudreaux (Texas A&M University) 1.1 - Introduction to Sets January 18, 2018
1.1 - Introduction to Sets Math 166-502 Blake Boudreaux Department of Mathematics Texas A&M University January 18, 2018 Blake Boudreaux (Texas A&M University) 1.1 - Introduction to Sets January 18, 2018
2 Review of Set Theory
 2 Review of Set Theory Example 2.1. Let Ω = {1, 2, 3, 4, 5, 6} 2.2. Venn diagram is very useful in set theory. It is often used to portray relationships between sets. Many identities can be read out simply
2 Review of Set Theory Example 2.1. Let Ω = {1, 2, 3, 4, 5, 6} 2.2. Venn diagram is very useful in set theory. It is often used to portray relationships between sets. Many identities can be read out simply
Fast Distance Transform Computation using Dual Scan Line Propagation
 Fast Distance Transform Computation using Dual Scan Line Propagation Fatih Porikli Tekin Kocak Mitsubishi Electric Research Laboratories, Cambridge, USA ABSTRACT We present two fast algorithms that approximate
Fast Distance Transform Computation using Dual Scan Line Propagation Fatih Porikli Tekin Kocak Mitsubishi Electric Research Laboratories, Cambridge, USA ABSTRACT We present two fast algorithms that approximate
Grade 5. Massachusetts Curriculum Framework for Mathematics 48
 Grade 5 Introduction In grade 5, instructional time should focus on four critical areas: (1) developing fluency with addition and subtraction of fractions, and developing understanding of the multiplication
Grade 5 Introduction In grade 5, instructional time should focus on four critical areas: (1) developing fluency with addition and subtraction of fractions, and developing understanding of the multiplication
Image representation. 1. Introduction
 Image representation Introduction Representation schemes Chain codes Polygonal approximations The skeleton of a region Boundary descriptors Some simple descriptors Shape numbers Fourier descriptors Moments
Image representation Introduction Representation schemes Chain codes Polygonal approximations The skeleton of a region Boundary descriptors Some simple descriptors Shape numbers Fourier descriptors Moments
Figure 8-7: Cameraman.tif Before and After Remapping, and Widening its Dynamic Range
 Image Enhancement Figure 8-7: Cameraman.tif Before and After Remapping, and Widening its Dynamic Range Notice that this operation results in much of the image being washed out. This is because all values
Image Enhancement Figure 8-7: Cameraman.tif Before and After Remapping, and Widening its Dynamic Range Notice that this operation results in much of the image being washed out. This is because all values
 1 of 7 7/15/2009 3:40 PM Virtual Laboratories > 1. Foundations > 1 2 3 4 5 6 7 8 9 1. Sets Poincaré's quote, on the title page of this chapter could not be more wrong (what was he thinking?). Set theory
1 of 7 7/15/2009 3:40 PM Virtual Laboratories > 1. Foundations > 1 2 3 4 5 6 7 8 9 1. Sets Poincaré's quote, on the title page of this chapter could not be more wrong (what was he thinking?). Set theory
CLASSIFICATION OF BOUNDARY AND REGION SHAPES USING HU-MOMENT INVARIANTS
 CLASSIFICATION OF BOUNDARY AND REGION SHAPES USING HU-MOMENT INVARIANTS B.Vanajakshi Department of Electronics & Communications Engg. Assoc.prof. Sri Viveka Institute of Technology Vijayawada, India E-mail:
CLASSIFICATION OF BOUNDARY AND REGION SHAPES USING HU-MOMENT INVARIANTS B.Vanajakshi Department of Electronics & Communications Engg. Assoc.prof. Sri Viveka Institute of Technology Vijayawada, India E-mail:
