The statement implies that any three intersection points of two distinct planes lie on a line.
|
|
|
- Arthur Whitehead
- 6 years ago
- Views:
Transcription
1 Math 3181 Dr. Franz Rothe February 23, 2015 All3181\3181_spr15ts1.tex 1 Solution of Test Name: Problem 1.1. The second part of Hilbert s Proposition 1 states: Any two different planes have either no point in common, or they have one line and no further points in common. Encircle the correct commentaries about this statement, and scratch through the false assertions. Almost all axioms of incidence are used in the proof of this statement. The only exception is axiom (I.3). The statement implies that any three intersection points of two distinct planes lie on a line. The statement excludes the existence of any parallel planes. The statement implies neither existence nor uniqueness of a parallel plane, to a given plane through a given point. The statement implies that a third plane which intersects one of two parallel planes, intersects the other one, too. Remark. In order to prove Any two different planes have either no point in common, or they have one line and no further points in common. one needs axioms (I.1)(I.2)(I.5)(I.6)(I.7). Almost all axioms of incidence are used in the proof of the above statement. The exceptions are axioms (I.3)(I.4)(I.8). 1
2 Problem 1.2 (The four-point incidence geometries). Find all non isomorphic incidence geometries with four points. For each one of them provide a drawing; tell how many lines there exist; tell which parallel property (elliptic, Euclidean, hyperbolic, or neither) does hold. Figure 1: There are two four-point incidence geometries. Answer. There exist two non-isomorphic four-point geometries. (a) Six lines with each one two points. It has the Euclidean parallel property, and is the smallest affine plane. (b) There are four lines, one of which has three points. property. It has the elliptic parallel Definition 1 (Hand-shake model). A hand shake model is an incidence geometry for which every line has exactly two points. Definition 2 (Straight fan). A straight fan is an incidence geometry with all but one point lying on one line. Problem 1.3. How many lines does the hand-shake incidence geometry with n points have. How many lines does the straight fan with n points have. Answer. The hand-shake incidence geometry with n points has (n 1)n (n 1) + (n 2) = 2 lines. We see this as follows. We can connect the first point to the other (n 1) points. Disregarding this point, we connect the second point to (n 2) different points, and so on. The last line to be drawn is between the (n 1)-th and the n-th point. The straight fan with n points has n lines. There is one long line with n 1 points, and only one point P does not lie on this line. There are n 1 lines with two points each of which connects P to a different point on the long line. 2
3 Problem 1.4. Match the figures on page 3 with the following descriptions: a handshake model (f) a model with eight lines (c) a straight fan (d) the smallest affine plane (e) the smallest projective plane (b) the number of lines is one more than the number of points (a) Figure 2: Six examples for incidence planes. 3
4 Figure 3: Two intersecting segments. Problem 1.5. We assume A B C and A X Y, and that not all five points lie on a line. Prove that the segments BY and CX intersect each other. Provide a drawing. (i) Why does the segment BY intersect the line CX? (ii) Why does the segment CX intersect the line BY? (iii) Why are these two intersection points equal? Why do the segments BY and CX intersect each other? Answer. (i) We use Pasch s axiom for triangle ABY and line CX. This line intersects side AY, but not side AC. Hence line CX intersects the side BY. (ii) We use Pasch s axiom for triangle ACX and line BY. This line intersects side AC, but not side AX. Hence line BY intersects the side CX. (iii) The two lines CX and BY are distinct, otherwise all points A, B, C, X, Y would lie on a line. Hence lines CX and BY have unique intersection point. By items (i) and (ii), this point is the intersection of the segments BY and CX. 4
5 Problem 1.6. Give exact definitions of the terms segment, ray, triangle in terms of the order relation. Clarify the obvious questions. Give illustrations. Why does one assign a definite order to the vertices and sides of a triangle? Answer. Definition 3 (Segment). Let A and B be two distinct points. The segment AB is the set consisting of the points A and B and all points lying between A and B. The points A and B are called the endpoints of the segment, the points between A and B are called the interior points, and the remaining points on the line AB are called the exterior points of the segment. Definition 4 (Ray). Given two distinct points A and B, the ray AB is the set consisting of the points A and B, the points inside the segment AB, and all points P on the line AB such that the given point B lies between A and P. The point A is called the vertex of the ray. The axiom of order II.2 tells that the ray AB contains points not lying in the segment AB. Definition 5 (Triangle). We define a triangle to be union of the three segments AB, BC and CA. The three points A, B and C are assumed not to lie on a line. These three points are the vertices, and the segments BC, AC, and AB are the sides of the triangle. For a segment or ray, it is assumed that the two endpoints A and B are different. For a triangle ABC, it is assumed that the three vertices do not lie on a line. For the correct statement of the Theorems about congruence, similarity of two triangles, as well as for the Theorem of Desargues, and for the purpose of fixing an orientation, we assign a definite order to the vertices and sides of the relevant triangles. 5
6 Problem 1.7. Give exact definitions of the terms angle, interior and exterior of an angle. Clarify the obvious questions. Give illustrations. Definition 6 (Angle). An angle BAC is the union of two rays AB and AC with common vertex A not lying on one line. The point A is called the vertex of the angle. The rays AB and AC are called the sides of the angle. Figure 4: Interior and exterior of an angle Definition 7 (Interior and exterior domain of an angle). The interior of an angle lying in a plane A is the intersection of two corresponding half planes bordered by the sides of the angle, and containing points on the other side of the angle, respectively. The exterior of an angle is the union of two opposite half planes -bordered by the sides of the angle, and not containing the points neither in the interior nor on the legs of the angle. Half planes, interior and exterior of an angle all do not include the lines or rays on their boundary. Thus the interior of BAD is the intersection of the half plane of AB in which D lies, and the half plane of AD in which B lies. The exterior of BAD is the union of the half plane of AB opposite to D, and the half plane of AD opposite to B. Problem 1.8. Prove the Four-point Theorem directly from the Three-point Theorem and the Plane separation Theorem Answer. Given are four different points on a line l. By the Three-point Theorem, one of them, which we name C lies between two others. We draw a line m through C different from l and use plane separation. In one half-plane of l lie two of the remaining points, in the other half-plane only the last remaining point, which we call D. Of the two points in the same half plane, one which we name B lies between C and the other one, finally named A. This statement follows from the three-point theorem. We have thus obtained the order relations A B C, A C D, B C D To confirm the fourth order relation, we draw a third line n through B different from l, and use plane separation once more. Point C and D lie in the same half-plane of n whereas A lies in the opposite half-plane from C. Hence A and D lie in opposite half-planes, confirming the order relation A B D. 6
7 Problem 1.9. Show that the interior domain of a triangle is nonempty. Which are the two theorems used in this reasoning. (i) Why do the points D and E exist? (ii) Why does point E lie in the interior of the triangle? Figure 5: Why is the interior of a triangle nonempty. Answer. Twice, we use Hilberts proposition 3, saying that the interior of a segment is nonempty. There exists a point D in the segment AB, and a point E in the segment CD. Finally, we use the plane separation theorem to confirm that point E lies in this interior of the triangle ABC. Indeed, points C and E lie on the same side of line AB, Points E, D, A lie on the same side of line BC, and finally points E, D, B lie on the same side of line AC. 7
8 Problem Given is a triangle and a line through an interior point of the triangle. We suppose that the line does not intersect a vertex the triangle. Show that the line intersects two sides of the triangle. Put the appropriate names into the figure on page 8. Figure 6: A line through an interior point of a triangle. Answer. Let the line l go the point P in the interior of triangle ABC. We suppose that the line does not go through any vertex of the triangle. We draw the ray AP. Because point P lies in the interior of angle BAC, the Crossbar theorem shows that the ray AP intersects the opposite side BC at some point, say Q. We now apply Pasch s axiom to the triangle ABQ and the line l. This line intersects side AQ at point P. Hence it intersects a second side, either BQ BC or AB, say at point D. In both cases, the line l intersects one side of the given triangle ABC. By Pasch s axiom it intersects a second side, say at point E. By Bernays lemma, the line l intersects exactly two sides of the given triangle. 8
Definition 1 (Hand-shake model). A hand shake model is an incidence geometry for which every line has exactly two points.
 Math 3181 Dr. Franz Rothe Name: All3181\3181_spr13t1.tex 1 Solution of Test I Definition 1 (Hand-shake model). A hand shake model is an incidence geometry for which every line has exactly two points. Definition
Math 3181 Dr. Franz Rothe Name: All3181\3181_spr13t1.tex 1 Solution of Test I Definition 1 (Hand-shake model). A hand shake model is an incidence geometry for which every line has exactly two points. Definition
2 Solution of Homework
 Math 3181 Name: Dr. Franz Rothe February 6, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Solution of Homework
Math 3181 Name: Dr. Franz Rothe February 6, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Solution of Homework
Definition 2 (Projective plane). A projective plane is a class of points, and a class of lines satisfying the axioms:
 Math 3181 Name: Dr. Franz Rothe January 30, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Homework 1 Definition
Math 3181 Name: Dr. Franz Rothe January 30, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Homework 1 Definition
Provide a drawing. Mark any line with three points in blue color.
 Math 3181 Name: Dr. Franz Rothe August 18, 2014 All3181\3181_fall14h1.tex Homework has to be turned in this handout. For extra space, use the back pages, or blank pages between. The homework can be done
Math 3181 Name: Dr. Franz Rothe August 18, 2014 All3181\3181_fall14h1.tex Homework has to be turned in this handout. For extra space, use the back pages, or blank pages between. The homework can be done
Problem 3.1 (Building up geometry). For an axiomatically built-up geometry, six groups of axioms needed:
 Math 3181 Dr. Franz Rothe September 29, 2016 All3181\3181_fall16h3.tex Names: Homework has to be turned in this handout. For extra space, use the back pages, or put blank pages between. The homework can
Math 3181 Dr. Franz Rothe September 29, 2016 All3181\3181_fall16h3.tex Names: Homework has to be turned in this handout. For extra space, use the back pages, or put blank pages between. The homework can
2 Solution of Homework II
 Math 3181 Dr. Franz Rothe Name: All3181\3181_spr13h2.tex 2 Solution of Homework II 10 Problem 2.1. Prove the Four-point Theorem directly from the Three-point Theorem and the Plane separation Theorem. Answer.
Math 3181 Dr. Franz Rothe Name: All3181\3181_spr13h2.tex 2 Solution of Homework II 10 Problem 2.1. Prove the Four-point Theorem directly from the Three-point Theorem and the Plane separation Theorem. Answer.
the projective completion of the affine plane with four points
 Math 3181 Dr. Franz Rothe November 23, 20 1 Test Name: 50 Problem 1.1. Here are once more: a highly symmetric illustration for the Fano plane based on an equilateral triangle the projective completion
Math 3181 Dr. Franz Rothe November 23, 20 1 Test Name: 50 Problem 1.1. Here are once more: a highly symmetric illustration for the Fano plane based on an equilateral triangle the projective completion
Problem 2.1. Complete the following proof of Euclid III.20, referring to the figure on page 1.
 Math 3181 Dr. Franz Rothe October 30, 2015 All3181\3181_fall15t2.tex 2 Solution of Test Name: Figure 1: Central and circumference angle of a circular arc, both obtained as differences Problem 2.1. Complete
Math 3181 Dr. Franz Rothe October 30, 2015 All3181\3181_fall15t2.tex 2 Solution of Test Name: Figure 1: Central and circumference angle of a circular arc, both obtained as differences Problem 2.1. Complete
3 Solution of Homework
 Math 3181 Name: Dr. Franz Rothe February 25, 2014 All3181\3181_spr14h3.tex Homework has to be turned in this handout. The homework can be done in groups up to three due March 11/12 3 Solution of Homework
Math 3181 Name: Dr. Franz Rothe February 25, 2014 All3181\3181_spr14h3.tex Homework has to be turned in this handout. The homework can be done in groups up to three due March 11/12 3 Solution of Homework
Betweenness and the Crossbar Theorem. Lemma: Let A, B, and C be distinct points. If A*B*C, then neither A*C*B nor B*A*C.
 Betweenness and the Crossbar Theorem Lemma: Let A, B, and C be distinct points. If A*B*C, then neither A*C*B nor B*A*C. Suppose that both A*B*C and A*C*B. Thus AB+BC =AC, and AC +CB = AB. From this we
Betweenness and the Crossbar Theorem Lemma: Let A, B, and C be distinct points. If A*B*C, then neither A*C*B nor B*A*C. Suppose that both A*B*C and A*C*B. Thus AB+BC =AC, and AC +CB = AB. From this we
Honors 213. Third Hour Exam. Name
 Honors 213 Third Hour Exam Name Monday, March 27, 2000 100 points Page 1 Please note: Because of multiple exams given Monday, this exam will be returned by Thursday, March 30. 1. (5 pts.) Define what it
Honors 213 Third Hour Exam Name Monday, March 27, 2000 100 points Page 1 Please note: Because of multiple exams given Monday, this exam will be returned by Thursday, March 30. 1. (5 pts.) Define what it
Mth 97 Winter 2013 Sections 4.3 and 4.4
 Section 4.3 Problem Solving Using Triangle Congruence Isosceles Triangles Theorem 4.5 In an isosceles triangle, the angles opposite the congruent sides are congruent. A Given: ABC with AB AC Prove: B C
Section 4.3 Problem Solving Using Triangle Congruence Isosceles Triangles Theorem 4.5 In an isosceles triangle, the angles opposite the congruent sides are congruent. A Given: ABC with AB AC Prove: B C
A Communications Network???
 A Communications Network??? A Communications Network What are the desirable properties of the switching box? 1. Every two users must be connected at a switch. 2. Every switch must "look alike". 3. The
A Communications Network??? A Communications Network What are the desirable properties of the switching box? 1. Every two users must be connected at a switch. 2. Every switch must "look alike". 3. The
Definition (Axiomatic System). An axiomatic system (a set of axioms and their logical consequences) consists of:
 Course Overview Contents 1 AxiomaticSystems.............................. 1 2 Undefined Terms............................... 2 3 Incidence................................... 2 4 Distance....................................
Course Overview Contents 1 AxiomaticSystems.............................. 1 2 Undefined Terms............................... 2 3 Incidence................................... 2 4 Distance....................................
Synthetic Geometry. 1.1 Foundations 1.2 The axioms of projective geometry
 Synthetic Geometry 1.1 Foundations 1.2 The axioms of projective geometry Foundations Def: A geometry is a pair G = (Ω, I), where Ω is a set and I a relation on Ω that is symmetric and reflexive, i.e. 1.
Synthetic Geometry 1.1 Foundations 1.2 The axioms of projective geometry Foundations Def: A geometry is a pair G = (Ω, I), where Ω is a set and I a relation on Ω that is symmetric and reflexive, i.e. 1.
An Approach to Geometry (stolen in part from Moise and Downs: Geometry)
 An Approach to Geometry (stolen in part from Moise and Downs: Geometry) Undefined terms: point, line, plane The rules, axioms, theorems, etc. of elementary algebra are assumed as prior knowledge, and apply
An Approach to Geometry (stolen in part from Moise and Downs: Geometry) Undefined terms: point, line, plane The rules, axioms, theorems, etc. of elementary algebra are assumed as prior knowledge, and apply
Solutions to the Test. Problem 1. 1) Who is the author of the first comprehensive text on geometry? When and where was it written?
 Solutions to the Test Problem 1. 1) Who is the author of the first comprehensive text on geometry? When and where was it written? Answer: The first comprehensive text on geometry is called The Elements
Solutions to the Test Problem 1. 1) Who is the author of the first comprehensive text on geometry? When and where was it written? Answer: The first comprehensive text on geometry is called The Elements
8 Standard Euclidean Triangle Geometry
 8 Standard Euclidean Triangle Geometry 8.1 The circum-center Figure 8.1: In hyperbolic geometry, the perpendicular bisectors can be parallel as shown but this figure is impossible in Euclidean geometry.
8 Standard Euclidean Triangle Geometry 8.1 The circum-center Figure 8.1: In hyperbolic geometry, the perpendicular bisectors can be parallel as shown but this figure is impossible in Euclidean geometry.
1. A statement is a set of words and/or symbols that collectively make a claim that can be classified as true or false.
 Chapter 1 Line and Angle Relationships 1.1 Sets, Statements and Reasoning Definitions 1. A statement is a set of words and/or symbols that collectively make a claim that can be classified as true or false.
Chapter 1 Line and Angle Relationships 1.1 Sets, Statements and Reasoning Definitions 1. A statement is a set of words and/or symbols that collectively make a claim that can be classified as true or false.
FIGURES FOR SOLUTIONS TO SELECTED EXERCISES. V : Introduction to non Euclidean geometry
 FIGURES FOR SOLUTIONS TO SELECTED EXERCISES V : Introduction to non Euclidean geometry V.1 : Facts from spherical geometry V.1.1. The objective is to show that the minor arc m does not contain a pair of
FIGURES FOR SOLUTIONS TO SELECTED EXERCISES V : Introduction to non Euclidean geometry V.1 : Facts from spherical geometry V.1.1. The objective is to show that the minor arc m does not contain a pair of
Geometry Definitions, Postulates, and Theorems. Chapter 3: Parallel and Perpendicular Lines. Section 3.1: Identify Pairs of Lines and Angles.
 Geometry Definitions, Postulates, and Theorems Chapter : Parallel and Perpendicular Lines Section.1: Identify Pairs of Lines and Angles Standards: Prepare for 7.0 Students prove and use theorems involving
Geometry Definitions, Postulates, and Theorems Chapter : Parallel and Perpendicular Lines Section.1: Identify Pairs of Lines and Angles Standards: Prepare for 7.0 Students prove and use theorems involving
2 Partial Solution of Homework
 Math 3181 Dr. Franz Rothe Name: All3181\3181_fall12h2.tex Use the back pages for extra space, attach blank pages if necessary You may submit the solution in groups up to four students due September 21
Math 3181 Dr. Franz Rothe Name: All3181\3181_fall12h2.tex Use the back pages for extra space, attach blank pages if necessary You may submit the solution in groups up to four students due September 21
Inversive Plane Geometry
 Inversive Plane Geometry An inversive plane is a geometry with three undefined notions: points, circles, and an incidence relation between points and circles, satisfying the following three axioms: (I.1)
Inversive Plane Geometry An inversive plane is a geometry with three undefined notions: points, circles, and an incidence relation between points and circles, satisfying the following three axioms: (I.1)
Transformations and Isometries
 Transformations and Isometries Definition: A transformation in absolute geometry is a function f that associates with each point P in the plane some other point P in the plane such that (1) f is one-to-one
Transformations and Isometries Definition: A transformation in absolute geometry is a function f that associates with each point P in the plane some other point P in the plane such that (1) f is one-to-one
Some Comments on Leaving Certificate Geometry Work in Progress
 Some Comments on Leaving Certificate Geometry Work in Progress D. R. Wilkins April 23, 2016 i Axioms for Leaving Certificate Geometry In 1932, George D. Birkhoff published a paper entitled A set of postulates
Some Comments on Leaving Certificate Geometry Work in Progress D. R. Wilkins April 23, 2016 i Axioms for Leaving Certificate Geometry In 1932, George D. Birkhoff published a paper entitled A set of postulates
Math 308, Section 101 Solutions to Study Questions for Final Exam (Thursday, December 16, 2004)
 NEUTRAL GEOMETRY Math 308, Section 0 Solutions to Study Questions for Final Exam (Thursday, December 6, 00) I. Given a triangle AEF, let M be the midpoint of the segment EF. Choose a point D on the ray
NEUTRAL GEOMETRY Math 308, Section 0 Solutions to Study Questions for Final Exam (Thursday, December 6, 00) I. Given a triangle AEF, let M be the midpoint of the segment EF. Choose a point D on the ray
5. THE ISOPERIMETRIC PROBLEM
 Math 501 - Differential Geometry Herman Gluck March 1, 2012 5. THE ISOPERIMETRIC PROBLEM Theorem. Let C be a simple closed curve in the plane with length L and bounding a region of area A. Then L 2 4 A,
Math 501 - Differential Geometry Herman Gluck March 1, 2012 5. THE ISOPERIMETRIC PROBLEM Theorem. Let C be a simple closed curve in the plane with length L and bounding a region of area A. Then L 2 4 A,
Acute Triangulations of Polygons
 Europ. J. Combinatorics (2002) 23, 45 55 doi:10.1006/eujc.2001.0531 Available online at http://www.idealibrary.com on Acute Triangulations of Polygons H. MAEHARA We prove that every n-gon can be triangulated
Europ. J. Combinatorics (2002) 23, 45 55 doi:10.1006/eujc.2001.0531 Available online at http://www.idealibrary.com on Acute Triangulations of Polygons H. MAEHARA We prove that every n-gon can be triangulated
Plane Geometry: Reflection Across a Line Does It! at the Marin Math Circle 1
 Plane Geometry: Reflection Across a Line Does It! at the Marin Math Circle 1 by Zvezdelina Stankova Berkeley Math Circle Director September 29 and October 13, 2010 Note: We shall work on the problems below
Plane Geometry: Reflection Across a Line Does It! at the Marin Math Circle 1 by Zvezdelina Stankova Berkeley Math Circle Director September 29 and October 13, 2010 Note: We shall work on the problems below
If three points A (h, 0), P (a, b) and B (0, k) lie on a line, show that: a b 1.
 ASSIGNMENT ON STRAIGHT LINES LEVEL 1 (CBSE/NCERT/STATE BOARDS) 1 Find the angle between the lines joining the points (0, 0), (2, 3) and the points (2, 2), (3, 5). 2 What is the value of y so that the line
ASSIGNMENT ON STRAIGHT LINES LEVEL 1 (CBSE/NCERT/STATE BOARDS) 1 Find the angle between the lines joining the points (0, 0), (2, 3) and the points (2, 2), (3, 5). 2 What is the value of y so that the line
Downloaded from
 Lines and Angles 1.If two supplementary angles are in the ratio 2:7, then the angles are (A) 40, 140 (B) 85, 95 (C) 40, 50 (D) 60, 120. 2.Supplementary angle of 103.5 is (A) 70.5 (B) 76.5 (C) 70 (D)
Lines and Angles 1.If two supplementary angles are in the ratio 2:7, then the angles are (A) 40, 140 (B) 85, 95 (C) 40, 50 (D) 60, 120. 2.Supplementary angle of 103.5 is (A) 70.5 (B) 76.5 (C) 70 (D)
1 Solution of Homework
 Math 3181 Dr. Franz Rothe February 2, 2012 All3181\4080_spr12h1.tex Name: Use the back pages for extra space due date: February 10 1 Solution of Homework Figure 1: A neutral construction of the tangents
Math 3181 Dr. Franz Rothe February 2, 2012 All3181\4080_spr12h1.tex Name: Use the back pages for extra space due date: February 10 1 Solution of Homework Figure 1: A neutral construction of the tangents
The angle measure at for example the vertex A is denoted by m A, or m BAC.
 MT 200 ourse notes on Geometry 5 2. Triangles and congruence of triangles 2.1. asic measurements. Three distinct lines, a, b and c, no two of which are parallel, form a triangle. That is, they divide the
MT 200 ourse notes on Geometry 5 2. Triangles and congruence of triangles 2.1. asic measurements. Three distinct lines, a, b and c, no two of which are parallel, form a triangle. That is, they divide the
no triangle can have more than one right angle or obtuse angle.
 Congruence Theorems in Action Isosceles Triangle Theorems.3 Learning Goals In this lesson, you will: Prove the Isosceles Triangle Base Theorem. Prove the Isosceles Triangle Vertex Angle Theorem. Prove
Congruence Theorems in Action Isosceles Triangle Theorems.3 Learning Goals In this lesson, you will: Prove the Isosceles Triangle Base Theorem. Prove the Isosceles Triangle Vertex Angle Theorem. Prove
Unit 6: Connecting Algebra and Geometry Through Coordinates
 Unit 6: Connecting Algebra and Geometry Through Coordinates The focus of this unit is to have students analyze and prove geometric properties by applying algebraic concepts and skills on a coordinate plane.
Unit 6: Connecting Algebra and Geometry Through Coordinates The focus of this unit is to have students analyze and prove geometric properties by applying algebraic concepts and skills on a coordinate plane.
1 Solution of Homework I
 Math 3181 Dr. Franz Rothe Name: All3181\3181_spr13h1.tex 1 Solution of Homework I 10 Problem 1.1. As far as two-dimensional geometry is concerned, Hilbert s Proposition 1 reduces to one simple statement:
Math 3181 Dr. Franz Rothe Name: All3181\3181_spr13h1.tex 1 Solution of Homework I 10 Problem 1.1. As far as two-dimensional geometry is concerned, Hilbert s Proposition 1 reduces to one simple statement:
EUCLID S GEOMETRY. Raymond Hoobler. January 27, 2008
 EUCLID S GEOMETRY Raymond Hoobler January 27, 2008 Euclid rst codi ed the procedures and results of geometry, and he did such a good job that even today it is hard to improve on his presentation. He lived
EUCLID S GEOMETRY Raymond Hoobler January 27, 2008 Euclid rst codi ed the procedures and results of geometry, and he did such a good job that even today it is hard to improve on his presentation. He lived
Unit 2A: Angle Pairs and Transversal Notes
 Unit 2A: Angle Pairs and Transversal Notes Day 1: Special angle pairs Day 2: Angle pairs formed by transversal through two nonparallel lines Day 3: Angle pairs formed by transversal through parallel lines
Unit 2A: Angle Pairs and Transversal Notes Day 1: Special angle pairs Day 2: Angle pairs formed by transversal through two nonparallel lines Day 3: Angle pairs formed by transversal through parallel lines
GEOMETRY POSTULATES AND THEOREMS. Postulate 1: Through any two points, there is exactly one line.
 GEOMETRY POSTULATES AND THEOREMS Postulate 1: Through any two points, there is exactly one line. Postulate 2: The measure of any line segment is a unique positive number. The measure (or length) of AB
GEOMETRY POSTULATES AND THEOREMS Postulate 1: Through any two points, there is exactly one line. Postulate 2: The measure of any line segment is a unique positive number. The measure (or length) of AB
Exercises for Chapter Three You know you've got to exercise your brain just like your muscles. Will Rogers ( )
 Exercises for Chapter Three You know you've got to exercise your brain just like your muscles. Will Rogers (1879 1935) Investigation Exercise 3.1. (a) Construct a tessellation. (Directions for construction.)
Exercises for Chapter Three You know you've got to exercise your brain just like your muscles. Will Rogers (1879 1935) Investigation Exercise 3.1. (a) Construct a tessellation. (Directions for construction.)
Definitions. You can represent a point by a dot and name it by a capital letter.
 Definitions Name Block Term Definition Notes Sketch Notation Point A location in space that is represented by a dot and has no dimension You can represent a point by a dot and name it by a capital letter.
Definitions Name Block Term Definition Notes Sketch Notation Point A location in space that is represented by a dot and has no dimension You can represent a point by a dot and name it by a capital letter.
Hyperbolic Geometry. Chaper Hyperbolic Geometry
 Hyperbolic Geometry Chaper 6.1-6.6 Hyperbolic Geometry Theorems Unique to Hyperbolic Geometry Now we assume Hyperbolic Parallel Postulate (HPP - p21) With the HPP we get for free all the negations of the
Hyperbolic Geometry Chaper 6.1-6.6 Hyperbolic Geometry Theorems Unique to Hyperbolic Geometry Now we assume Hyperbolic Parallel Postulate (HPP - p21) With the HPP we get for free all the negations of the
And Now From a New Angle Special Angles and Postulates LEARNING GOALS
 And Now From a New Angle Special Angles and Postulates LEARNING GOALS KEY TERMS. In this lesson, you will: Calculate the complement and supplement of an angle. Classify adjacent angles, linear pairs, and
And Now From a New Angle Special Angles and Postulates LEARNING GOALS KEY TERMS. In this lesson, you will: Calculate the complement and supplement of an angle. Classify adjacent angles, linear pairs, and
Transactions in Euclidean Geometry
 Transactions in Euclidean Geometry Volume 207F Issue # 4 Table of Contents Title Author Square Construction Katherine Bertacini, Rachelle Feldmann, & Kaelyn Koontz Squares and Rectangles Rachelle Feldmann
Transactions in Euclidean Geometry Volume 207F Issue # 4 Table of Contents Title Author Square Construction Katherine Bertacini, Rachelle Feldmann, & Kaelyn Koontz Squares and Rectangles Rachelle Feldmann
On the Minimum Number of Convex Quadrilaterals in Point Sets of Given Numbers of Points
 On the Minimum Number of Convex Quadrilaterals in Point Sets of Given Numbers of Points Hu Yuzhong Chen Luping Zhu Hui Ling Xiaofeng (Supervisor) Abstract Consider the following problem. Given n, k N,
On the Minimum Number of Convex Quadrilaterals in Point Sets of Given Numbers of Points Hu Yuzhong Chen Luping Zhu Hui Ling Xiaofeng (Supervisor) Abstract Consider the following problem. Given n, k N,
Interpretations and Models. Chapter Axiomatic Systems and Incidence Geometry
 Interpretations and Models Chapter 2.1-2.4 - Axiomatic Systems and Incidence Geometry Axiomatic Systems in Mathematics The gold standard for rigor in an area of mathematics Not fully achieved in most areas
Interpretations and Models Chapter 2.1-2.4 - Axiomatic Systems and Incidence Geometry Axiomatic Systems in Mathematics The gold standard for rigor in an area of mathematics Not fully achieved in most areas
Vocabulary Point- Line- Plane- Ray- Line segment- Congruent-
 * Geometry Overview Vocabulary Point- an exact location. It is usually represented as a dot, but it has no size at all. Line- a straight path that extends without end in opposite directions. Plane- a flat
* Geometry Overview Vocabulary Point- an exact location. It is usually represented as a dot, but it has no size at all. Line- a straight path that extends without end in opposite directions. Plane- a flat
(1) Page #1 24 all. (2) Page #7-21 odd, all. (3) Page #8 20 Even, Page 35 # (4) Page #1 8 all #13 23 odd
 Geometry/Trigonometry Unit 1: Parallel Lines Notes Name: Date: Period: # (1) Page 25-26 #1 24 all (2) Page 33-34 #7-21 odd, 23 28 all (3) Page 33-34 #8 20 Even, Page 35 #40 44 (4) Page 60 61 #1 8 all #13
Geometry/Trigonometry Unit 1: Parallel Lines Notes Name: Date: Period: # (1) Page 25-26 #1 24 all (2) Page 33-34 #7-21 odd, 23 28 all (3) Page 33-34 #8 20 Even, Page 35 #40 44 (4) Page 60 61 #1 8 all #13
Planarity: dual graphs
 : dual graphs Math 104, Graph Theory March 28, 2013 : dual graphs Duality Definition Given a plane graph G, the dual graph G is the plane graph whose vtcs are the faces of G. The correspondence between
: dual graphs Math 104, Graph Theory March 28, 2013 : dual graphs Duality Definition Given a plane graph G, the dual graph G is the plane graph whose vtcs are the faces of G. The correspondence between
Geometry Notes Chapter 4: Triangles
 Geometry Notes Chapter 4: Triangles Name Date Assignment Questions I have Day 1 Section 4.1: Triangle Sum, Exterior Angles, and Classifying Triangles Day 2 Assign: Finish Ch. 3 Review Sheet, WS 4.1 Section
Geometry Notes Chapter 4: Triangles Name Date Assignment Questions I have Day 1 Section 4.1: Triangle Sum, Exterior Angles, and Classifying Triangles Day 2 Assign: Finish Ch. 3 Review Sheet, WS 4.1 Section
Topics in geometry Exam 1 Solutions 7/8/4
 Topics in geometry Exam 1 Solutions 7/8/4 Question 1 Consider the following axioms for a geometry: There are exactly five points. There are exactly five lines. Each point lies on exactly three lines. Each
Topics in geometry Exam 1 Solutions 7/8/4 Question 1 Consider the following axioms for a geometry: There are exactly five points. There are exactly five lines. Each point lies on exactly three lines. Each
Warm-Up. Find the domain and range:
 Warm-Up Find the domain and range: Geometry Vocabulary & Notation Point Name: Use only the capital letter, without any symbol. Line Name: Use any two points on the line with a line symbol above. AB Line
Warm-Up Find the domain and range: Geometry Vocabulary & Notation Point Name: Use only the capital letter, without any symbol. Line Name: Use any two points on the line with a line symbol above. AB Line
POTENTIAL REASONS: Definition of Congruence:
 Sec 1.6 CC Geometry Triangle Proofs Name: POTENTIAL REASONS: Definition of Congruence: Having the exact same size and shape and there by having the exact same measures. Definition of Midpoint: The point
Sec 1.6 CC Geometry Triangle Proofs Name: POTENTIAL REASONS: Definition of Congruence: Having the exact same size and shape and there by having the exact same measures. Definition of Midpoint: The point
Elementary Planar Geometry
 Elementary Planar Geometry What is a geometric solid? It is the part of space occupied by a physical object. A geometric solid is separated from the surrounding space by a surface. A part of the surface
Elementary Planar Geometry What is a geometric solid? It is the part of space occupied by a physical object. A geometric solid is separated from the surrounding space by a surface. A part of the surface
Segment Addition Postulate: If B is BETWEEN A and C, then AB + BC = AC. If AB + BC = AC, then B is BETWEEN A and C.
 Ruler Postulate: The points on a line can be matched one to one with the REAL numbers. The REAL number that corresponds to a point is the COORDINATE of the point. The DISTANCE between points A and B, written
Ruler Postulate: The points on a line can be matched one to one with the REAL numbers. The REAL number that corresponds to a point is the COORDINATE of the point. The DISTANCE between points A and B, written
Euclid. Father of Geometry Euclidean Geometry Euclid s Elements
 Euclid Father of Geometry Euclidean Geometry Euclid s Elements Point Description Indicates a location and has no size. How to Name it You can represent a point by a dot and name it by a capital letter.
Euclid Father of Geometry Euclidean Geometry Euclid s Elements Point Description Indicates a location and has no size. How to Name it You can represent a point by a dot and name it by a capital letter.
NAME DATE PER. GEOMETRY FALL SEMESTER REVIEW FIRST SIX WEEKS PART 1. A REVIEW OF ALGEBRA Find the correct answer for each of the following.
 NAME ATE PER. GEOMETRY FALL SEMESTER REVIEW FIRST SIX WEEKS PART 1. A REVIEW OF ALGEBRA Find the correct answer for each of the following. 1. m = Solve for m : m 7 = -13 + m FIRST SIX-WEEKS REVIEW 2. x
NAME ATE PER. GEOMETRY FALL SEMESTER REVIEW FIRST SIX WEEKS PART 1. A REVIEW OF ALGEBRA Find the correct answer for each of the following. 1. m = Solve for m : m 7 = -13 + m FIRST SIX-WEEKS REVIEW 2. x
Mathematics For Class IX Lines and Angles
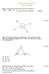 Mathematics For Class IX Lines and Angles (Q.1) In Fig, lines PQ and RS intersect each other at point O. If, find angle POR and angle ROQ (1 Marks) (Q.2) An exterior angle of a triangle is 110 and one
Mathematics For Class IX Lines and Angles (Q.1) In Fig, lines PQ and RS intersect each other at point O. If, find angle POR and angle ROQ (1 Marks) (Q.2) An exterior angle of a triangle is 110 and one
Maintaining Mathematical Proficiency
 Chapter 3 Maintaining Mathematical Proficiency Find the slope of the line.. y. y 3. ( 3, 3) y (, ) (, ) x x (, ) x (, ) ( 3, 3)... (, ) y (0, 0) 8 8 x x 8 8 y (, ) (, ) y (, ) (, 0) x Write an equation
Chapter 3 Maintaining Mathematical Proficiency Find the slope of the line.. y. y 3. ( 3, 3) y (, ) (, ) x x (, ) x (, ) ( 3, 3)... (, ) y (0, 0) 8 8 x x 8 8 y (, ) (, ) y (, ) (, 0) x Write an equation
Polygon Triangulation
 Polygon Triangulation Definition Simple Polygons 1. A polygon is the region of a plane bounded by a finite collection of line segments forming a simple closed curve. 2. Simple closed curve means a certain
Polygon Triangulation Definition Simple Polygons 1. A polygon is the region of a plane bounded by a finite collection of line segments forming a simple closed curve. 2. Simple closed curve means a certain
5200/7200 Fall 2007 Concurrence theorems for triangles
 5200/7200 Fall 2007 Concurrence theorems for triangles There are two basic concurrence theorems for triangles that hold in neutral geometry, that of medians and of angle bisectors, but it seems hard to
5200/7200 Fall 2007 Concurrence theorems for triangles There are two basic concurrence theorems for triangles that hold in neutral geometry, that of medians and of angle bisectors, but it seems hard to
Geometry - Chapter 1 - Corrective #1
 Class: Date: Geometry - Chapter 1 - Corrective #1 Short Answer 1. Sketch a figure that shows two coplanar lines that do not intersect, but one of the lines is the intersection of two planes. 2. Name two
Class: Date: Geometry - Chapter 1 - Corrective #1 Short Answer 1. Sketch a figure that shows two coplanar lines that do not intersect, but one of the lines is the intersection of two planes. 2. Name two
Math 102A Hw 3 P a (2 points)
 Math 102 Hw 3 P.93 12 a (2 points) If any pair of these lines are equal, the conclusion is immediate, so assume that we have three distinct lines such that l m and m n. Suppose, on the contrary, that l
Math 102 Hw 3 P.93 12 a (2 points) If any pair of these lines are equal, the conclusion is immediate, so assume that we have three distinct lines such that l m and m n. Suppose, on the contrary, that l
Geometry Unit 6 Properties of Quadrilaterals Classifying Polygons Review
 Geometry Unit 6 Properties of Quadrilaterals Classifying Polygons Review Polygon a closed plane figure with at least 3 sides that are segments -the sides do not intersect except at the vertices N-gon -
Geometry Unit 6 Properties of Quadrilaterals Classifying Polygons Review Polygon a closed plane figure with at least 3 sides that are segments -the sides do not intersect except at the vertices N-gon -
Math-2. Lesson 5-3 Two Column Proofs
 Math-2 Lesson 5-3 Two Column Proofs Vocabulary Adjacent Angles have a common side and share a common vertex Vertex. B C D A Common Side A Two-Column Proof is a logical argument written so that the 1st
Math-2 Lesson 5-3 Two Column Proofs Vocabulary Adjacent Angles have a common side and share a common vertex Vertex. B C D A Common Side A Two-Column Proof is a logical argument written so that the 1st
Type of Triangle Definition Drawing. Name the triangles below, and list the # of congruent sides and angles:
 Name: Triangles Test Type of Triangle Definition Drawing Right Obtuse Acute Scalene Isosceles Equilateral Number of congruent angles = Congruent sides are of the congruent angles Name the triangles below,
Name: Triangles Test Type of Triangle Definition Drawing Right Obtuse Acute Scalene Isosceles Equilateral Number of congruent angles = Congruent sides are of the congruent angles Name the triangles below,
Euclid s Axioms. 1 There is exactly one line that contains any two points.
 11.1 Basic Notions Euclid s Axioms 1 There is exactly one line that contains any two points. Euclid s Axioms 1 There is exactly one line that contains any two points. 2 If two points line in a plane then
11.1 Basic Notions Euclid s Axioms 1 There is exactly one line that contains any two points. Euclid s Axioms 1 There is exactly one line that contains any two points. 2 If two points line in a plane then
Assignments in Mathematics Class IX (Term I) 5. InTroduCTIon To EuClId s GEoMETry. l Euclid s five postulates are : ANIL TUTORIALS
 Assignments in Mathematics Class IX (Term I) 5. InTroduCTIon To EuClId s GEoMETry IMporTAnT TErMs, definitions And results l In geometry, we take a point, a line and a plane as undefined terms. l An axiom
Assignments in Mathematics Class IX (Term I) 5. InTroduCTIon To EuClId s GEoMETry IMporTAnT TErMs, definitions And results l In geometry, we take a point, a line and a plane as undefined terms. l An axiom
Mth 97 Fall 2013 Chapter 4
 4.1 Reasoning and Proof in Geometry Direct reasoning or reasoning is used to draw a conclusion from a series of statements. Conditional statements, if p, then q, play a central role in deductive reasoning.
4.1 Reasoning and Proof in Geometry Direct reasoning or reasoning is used to draw a conclusion from a series of statements. Conditional statements, if p, then q, play a central role in deductive reasoning.
EXTREME POINTS AND AFFINE EQUIVALENCE
 EXTREME POINTS AND AFFINE EQUIVALENCE The purpose of this note is to use the notions of extreme points and affine transformations which are studied in the file affine-convex.pdf to prove that certain standard
EXTREME POINTS AND AFFINE EQUIVALENCE The purpose of this note is to use the notions of extreme points and affine transformations which are studied in the file affine-convex.pdf to prove that certain standard
Proving Triangles and Quadrilaterals Satisfy Transformational Definitions
 Proving Triangles and Quadrilaterals Satisfy Transformational Definitions 1. Definition of Isosceles Triangle: A triangle with one line of symmetry. a. If a triangle has two equal sides, it is isosceles.
Proving Triangles and Quadrilaterals Satisfy Transformational Definitions 1. Definition of Isosceles Triangle: A triangle with one line of symmetry. a. If a triangle has two equal sides, it is isosceles.
GEOMETRY R Unit 2: Angles and Parallel Lines
 GEOMETRY R Unit 2: Angles and Parallel Lines Day Classwork Homework Friday 9/15 Unit 1 Test Monday 9/18 Tuesday 9/19 Angle Relationships HW 2.1 Angle Relationships with Transversals HW 2.2 Wednesday 9/20
GEOMETRY R Unit 2: Angles and Parallel Lines Day Classwork Homework Friday 9/15 Unit 1 Test Monday 9/18 Tuesday 9/19 Angle Relationships HW 2.1 Angle Relationships with Transversals HW 2.2 Wednesday 9/20
Preparing High School Geometry Teachers to Teach the Common Core
 Preparing High School Geometry Teachers to Teach the Common Core NCTM Regional Meeting Atlantic City, NJ October 22, 2014 Timothy Craine, Central Connecticut State University crainet@ccsu.edu Edward DePeau,
Preparing High School Geometry Teachers to Teach the Common Core NCTM Regional Meeting Atlantic City, NJ October 22, 2014 Timothy Craine, Central Connecticut State University crainet@ccsu.edu Edward DePeau,
Grade IX. Mathematics Geometry Notes. #GrowWithGreen
 Grade IX Mathematics Geometry Notes #GrowWithGreen The distance of a point from the y - axis is called its x -coordinate, or abscissa, and the distance of the point from the x -axis is called its y-coordinate,
Grade IX Mathematics Geometry Notes #GrowWithGreen The distance of a point from the y - axis is called its x -coordinate, or abscissa, and the distance of the point from the x -axis is called its y-coordinate,
1 Some Solution of Homework
 Math 3116 Dr. Franz Rothe May 30, 2012 08SUM\3116_2012h1.tex Name: Use the back pages for extra space 1 Some Solution of Homework Proposition 1 (Counting labeled trees). There are n n 2 different labeled
Math 3116 Dr. Franz Rothe May 30, 2012 08SUM\3116_2012h1.tex Name: Use the back pages for extra space 1 Some Solution of Homework Proposition 1 (Counting labeled trees). There are n n 2 different labeled
Pebble Sets in Convex Polygons
 2 1 Pebble Sets in Convex Polygons Kevin Iga, Randall Maddox June 15, 2005 Abstract Lukács and András posed the problem of showing the existence of a set of n 2 points in the interior of a convex n-gon
2 1 Pebble Sets in Convex Polygons Kevin Iga, Randall Maddox June 15, 2005 Abstract Lukács and András posed the problem of showing the existence of a set of n 2 points in the interior of a convex n-gon
 1 www.gradestack.com/ssc Dear readers, ADVANCE MATHS - GEOMETRY DIGEST Geometry is a very important topic in numerical ability section of SSC Exams. You can expect 14-15 questions from Geometry in SSC
1 www.gradestack.com/ssc Dear readers, ADVANCE MATHS - GEOMETRY DIGEST Geometry is a very important topic in numerical ability section of SSC Exams. You can expect 14-15 questions from Geometry in SSC
Transformations Part If then, the identity transformation.
 Transformations Part 2 Definition: Given rays with common endpoint O, we define the rotation with center O and angle as follows: 1. If then, the identity transformation. 2. If A, O, and B are noncollinear,
Transformations Part 2 Definition: Given rays with common endpoint O, we define the rotation with center O and angle as follows: 1. If then, the identity transformation. 2. If A, O, and B are noncollinear,
Unit 1 Lesson 13 Proving Theorems involving parallel and perp lines WITH ANSWERS!.notebook. Proofs involving Parallel lines
 Unit 1 Lesson 13 Proofs involving Parallel lines We will need to recall the different postulates and Theorems involving Parallel lines... Can you name the following types of angles from the diagram below???
Unit 1 Lesson 13 Proofs involving Parallel lines We will need to recall the different postulates and Theorems involving Parallel lines... Can you name the following types of angles from the diagram below???
1 I am given. (Label the triangle with letters and mark congruent parts based on definitions.)
 Name (print first and last) Per Date: 12/13 due 12/15 5.2 Congruence Geometry Regents 2013-2014 Ms. Lomac SLO: I can use SAS to prove the isosceles triangle theorem. (1) Prove: If a triangle is isosceles
Name (print first and last) Per Date: 12/13 due 12/15 5.2 Congruence Geometry Regents 2013-2014 Ms. Lomac SLO: I can use SAS to prove the isosceles triangle theorem. (1) Prove: If a triangle is isosceles
.(3, 2) Co-ordinate Geometry Co-ordinates. Every point has two co-ordinates. Plot the following points on the plane. A (4, 1) D (2, 5) G (6, 3)
 Co-ordinate Geometry Co-ordinates Every point has two co-ordinates. (3, 2) x co-ordinate y co-ordinate Plot the following points on the plane..(3, 2) A (4, 1) D (2, 5) G (6, 3) B (3, 3) E ( 4, 4) H (6,
Co-ordinate Geometry Co-ordinates Every point has two co-ordinates. (3, 2) x co-ordinate y co-ordinate Plot the following points on the plane..(3, 2) A (4, 1) D (2, 5) G (6, 3) B (3, 3) E ( 4, 4) H (6,
I can position figures in the coordinate plane for use in coordinate proofs. I can prove geometric concepts by using coordinate proof.
 Page 1 of 14 Attendance Problems. 1. Find the midpoint between (0, x) and (y, z).. One leg of a right triangle has length 1, and the hypotenuse has length 13. What is the length of the other leg? 3. Find
Page 1 of 14 Attendance Problems. 1. Find the midpoint between (0, x) and (y, z).. One leg of a right triangle has length 1, and the hypotenuse has length 13. What is the length of the other leg? 3. Find
Hawraa Abbas Almurieb. Axiomatic Systems
 2 Axiomatic Systems 2.1. Introduction to Axiomatic Systems We need undefined terms for any axiomatic system to build the axioms upon them. Which are basic worlds or things for the system. 2.1.1 Definitions
2 Axiomatic Systems 2.1. Introduction to Axiomatic Systems We need undefined terms for any axiomatic system to build the axioms upon them. Which are basic worlds or things for the system. 2.1.1 Definitions
Geometry. Parallel Lines.
 1 Geometry Parallel Lines 2015 10 21 www.njctl.org 2 Table of Contents Lines: Intersecting, Parallel & Skew Lines & Transversals Parallel Lines & Proofs Properties of Parallel Lines Constructing Parallel
1 Geometry Parallel Lines 2015 10 21 www.njctl.org 2 Table of Contents Lines: Intersecting, Parallel & Skew Lines & Transversals Parallel Lines & Proofs Properties of Parallel Lines Constructing Parallel
Geometry Practice. 1. Angles located next to one another sharing a common side are called angles.
 Geometry Practice Name 1. Angles located next to one another sharing a common side are called angles. 2. Planes that meet to form right angles are called planes. 3. Lines that cross are called lines. 4.
Geometry Practice Name 1. Angles located next to one another sharing a common side are called angles. 2. Planes that meet to form right angles are called planes. 3. Lines that cross are called lines. 4.
Grade 5 Geometry. Answer the questions. For more such worksheets visit
 ID : ae-5-geometry [1] Grade 5 Geometry For more such worksheets visit www.edugain.com Answer the questions (1) A 4-sided flat shape with straight sides where the opposite sides are parallel is called
ID : ae-5-geometry [1] Grade 5 Geometry For more such worksheets visit www.edugain.com Answer the questions (1) A 4-sided flat shape with straight sides where the opposite sides are parallel is called
Geometry Reasons for Proofs Chapter 1
 Geometry Reasons for Proofs Chapter 1 Lesson 1.1 Defined Terms: Undefined Terms: Point: Line: Plane: Space: Postulate 1: Postulate : terms that are explained using undefined and/or other defined terms
Geometry Reasons for Proofs Chapter 1 Lesson 1.1 Defined Terms: Undefined Terms: Point: Line: Plane: Space: Postulate 1: Postulate : terms that are explained using undefined and/or other defined terms
Chapter. Triangles. Copyright Cengage Learning. All rights reserved.
 Chapter 3 Triangles Copyright Cengage Learning. All rights reserved. 3.3 Isosceles Triangles Copyright Cengage Learning. All rights reserved. In an isosceles triangle, the two sides of equal length are
Chapter 3 Triangles Copyright Cengage Learning. All rights reserved. 3.3 Isosceles Triangles Copyright Cengage Learning. All rights reserved. In an isosceles triangle, the two sides of equal length are
Naming Angles. One complete rotation measures 360º. Half a rotation would then measure 180º. A quarter rotation would measure 90º.
 Naming Angles What s the secret for doing well in geometry? Knowing all the angles. An angle can be seen as a rotation of a line about a fixed point. In other words, if I were mark a point on a paper,
Naming Angles What s the secret for doing well in geometry? Knowing all the angles. An angle can be seen as a rotation of a line about a fixed point. In other words, if I were mark a point on a paper,
Objective- the students will be able to use undefined terms and definitions to work with points, lines and planes. Undefined Terms
 Unit 1 asics of Geometry Objective- the students will be able to use undefined terms and definitions to work with points, lines and planes. Undefined Terms 1. Point has no dimension, geometrically looks
Unit 1 asics of Geometry Objective- the students will be able to use undefined terms and definitions to work with points, lines and planes. Undefined Terms 1. Point has no dimension, geometrically looks
DEFINITIONS. Perpendicular Two lines are called perpendicular if they form a right angle.
 DEFINITIONS Degree A degree is the 1 th part of a straight angle. 180 Right Angle A 90 angle is called a right angle. Perpendicular Two lines are called perpendicular if they form a right angle. Congruent
DEFINITIONS Degree A degree is the 1 th part of a straight angle. 180 Right Angle A 90 angle is called a right angle. Perpendicular Two lines are called perpendicular if they form a right angle. Congruent
Situation 1: Congruent Triangles vs. Similar Triangles
 Situation 1: Congruent Triangles vs. Similar Triangles Prepared at the University of Georgia EMAT 6500 Date last revised: July 24 th, 2013 Nicolina Scarpelli Prompt: A teacher in a high school Analytic
Situation 1: Congruent Triangles vs. Similar Triangles Prepared at the University of Georgia EMAT 6500 Date last revised: July 24 th, 2013 Nicolina Scarpelli Prompt: A teacher in a high school Analytic
Lesson 3.6 Overlapping Triangles
 Lesson 3.6 Overlapping Triangles Getting Ready: Each division in the given triangle is 1 unit long. Hence, the side of the largest triangle is 4- unit long. Figure 3.6.1. Something to think about How many
Lesson 3.6 Overlapping Triangles Getting Ready: Each division in the given triangle is 1 unit long. Hence, the side of the largest triangle is 4- unit long. Figure 3.6.1. Something to think about How many
CIRCLE. Circle is a collection of all points in a plane which are equidistant from a fixed point.
 CIRCLE Circle is a collection of all points in a plane which are equidistant from a fixed point. The fixed point is called as the centre and the constant distance is called as the radius. Parts of a Circle
CIRCLE Circle is a collection of all points in a plane which are equidistant from a fixed point. The fixed point is called as the centre and the constant distance is called as the radius. Parts of a Circle
GEOMETRY BASIC GEOMETRICAL IDEAS. 3) A point has no dimensions (length, breadth or thickness).
 CLASS 6 - GEOMETRY BASIC GEOMETRICAL IDEAS Geo means Earth and metron means Measurement. POINT 1) The most basic shape in geometry is the Point. 2) A point determines a location. 3) A point has no dimensions
CLASS 6 - GEOMETRY BASIC GEOMETRICAL IDEAS Geo means Earth and metron means Measurement. POINT 1) The most basic shape in geometry is the Point. 2) A point determines a location. 3) A point has no dimensions
MAKE GEOMETRIC CONSTRUCTIONS
 MAKE GEOMETRIC CONSTRUCTIONS KEY IDEAS 1. To copy a segment, follow the steps given: Given: AB Construct: PQ congruent to AB 1. Use a straightedge to draw a line, l. 2. Choose a point on line l and label
MAKE GEOMETRIC CONSTRUCTIONS KEY IDEAS 1. To copy a segment, follow the steps given: Given: AB Construct: PQ congruent to AB 1. Use a straightedge to draw a line, l. 2. Choose a point on line l and label
On the number of distinct directions of planes determined by n points in R 3
 On the number of distinct directions of planes determined by n points in R 3 Rom Pinchasi August 27, 2007 Abstract We show that any set of n points in R 3, that is not contained in a plane, determines
On the number of distinct directions of planes determined by n points in R 3 Rom Pinchasi August 27, 2007 Abstract We show that any set of n points in R 3, that is not contained in a plane, determines
MAT 3271: Selected Solutions to the Assignment 6
 Chapter 2: Major Exercises MAT 3271: Selected Solutions to the Assignment 6 1. Since a projective plan is a model of incidence geometry, Incidence Axioms 1-3 and Propositions 2.1-2.5 (which follow logically
Chapter 2: Major Exercises MAT 3271: Selected Solutions to the Assignment 6 1. Since a projective plan is a model of incidence geometry, Incidence Axioms 1-3 and Propositions 2.1-2.5 (which follow logically
7. The Gauss-Bonnet theorem
 7. The Gauss-Bonnet theorem 7.1 Hyperbolic polygons In Euclidean geometry, an n-sided polygon is a subset of the Euclidean plane bounded by n straight lines. Thus the edges of a Euclidean polygon are formed
7. The Gauss-Bonnet theorem 7.1 Hyperbolic polygons In Euclidean geometry, an n-sided polygon is a subset of the Euclidean plane bounded by n straight lines. Thus the edges of a Euclidean polygon are formed
No triangle can be decomposed into seven congruent triangles
 No triangle can be decomposed into seven congruent triangles Michael Beeson November 27, 2008 Abstract We investigate the problem of cutting a triangle into N congruent triangles. While this can be done
No triangle can be decomposed into seven congruent triangles Michael Beeson November 27, 2008 Abstract We investigate the problem of cutting a triangle into N congruent triangles. While this can be done
