ECEN 447 Digital Image Processing
|
|
|
- Vincent Dennis
- 6 years ago
- Views:
Transcription
1 ECEN 447 Digital Image Processing Lecture 7: Mathematical Morphology Ulisses Braga-Neto ECE Department Texas A&M University
2 Basics of Mathematical Morphology Mathematical Morphology (MM) is a discipline whose roots can be traced to the Ecole de Mines de Paris in the 1960's. It was basically created by the mathematician Georges Matheron and further developed and popularized by his colleague Jean Serra and others. Unlike image processing based on linear shift-invariant operators, MM is based on nonlinear operators. In Biology, morphology means the study of shape. MM may be said to be the study of shapes from a mathematical perspective. For that reason, it depends heavily on concepts from set theory. An attractive feature of MM is that all its numerous operators and algorithms are based on the composition of a small number of building blocks, called dilation, erosion, opening, and closing.
3 Brief Review of Set Theory Set inclusion: given two sets A and B, we have A B if Set intersection: given a family of sets A i, i I Note that the sets A i, i I are said to be disjoint if
4 Brief Review of Set Theory - II Set union: given a family of sets A i, i I Note that so that
5 Brief Review of Set Theory - III Set Difference: given two sets A and B Note that and
6 Brief Review of Set Theory - IV Set complement: given a universal set E and a set A E Clearly and De Morgan's Law: given sets A i, i I
7 Binary Images and Sets Assume a universal set E = Z 2 (for discrete images) or E = R 2 (for continuous images). For higher-dimensional "images", one has E = Z d or E=R d with d>2. Any given set A E corresponds to a binary image I A : E {0,1} : the binary image I A is sometimes called an indicator function. The converse is also true: any binary image f: E {0,1} corresponds to a set A f E : this is called the image foreground, while its complement A f c is the image background.
8 Logic and Order Operations The equivalence between sets and binary images leads to the realization that set operations are actually logic and order operations. Set intersection corresponds to AND and to minimum Set union corresponds to OR and to maximum Set complementation corresponds to negation
9 Translation and Reflection Since E = Z 2 or E = R 2 have an Abelian group structure for addition, one can define translation and reflection of a set. The translation of a set B E to point x E is The reflection of B E is B is symmetric if Both translation and reflection are affected by the position of B with respect to the origin o E.
10 Structuring Element The basic operations in MM are defined in terms of a small set, called the structuring element (S.E.). The S.E. may be seen as a template used to probe an image. Both the shape and size of the S.E. affect the result of the operation. S.E.s are usually (but not always) symmetric and contain the origin. Examples (note the position of the origin, marked by a black dot): 3x3 "cross" 3x3 "box" 5x1 "line" 5x5 "cross"
11 Erosion It can be said that the most basic MM operator is the erosion. Given an image A E and a S.E. B E, the erosion of A by B is therefore, the erosion is equal to the points where one may "place" the S.E. such that it "fits" in the image. Alternatively, it can be shown that Provided that the origin o is contained in B, erosion has the effect of shrinking the image, that is,
12 Example
13 Erosion as Morphological Filter The term "filter" has a precise meaning in MM, according to which erosion is not a filter. However, erosion is a (nonlinear) filter in the general sense of the word, as seen in the following example. original image erosion by small box erosion by medium-sized box erosion by large box
14 Properties of Erosion translation-invariant increasing distributive over intersection origin is neutral element scaling property
15 Dilation The "inverse" operation to erosion is dilation (but not a true inverse). Given an image A E and a S.E. B E, the dilation of A by B is therefore, the dilation is equal to the points where if one "places" the (reflected) S.E., it "hits" the image. Obviously, If B is symmetric, one does not need to worry about reflecting B. Alternatively, it can be shown that From this, and recalling that union is equivalent to maximum, it can be seen that dilation is a mask-based maximum filter (similar to the median filter). Similarly, erosion is a mask-based minimum filter.
16 Dilation - II Provided that the origin is contained in B, dilation has the effect of expanding the image, that is, Dilation is commutative, that is, From this and the definition on the previous page, we have that is, dilation corresponds to sliding the "mask" B over all points of the original image and taking the union. This process is sometimes called morphological convolution.
17 Example
18 Dilation as Morphological Filter Once again, strictly speaking, dilation is not a "morphological filter," (more on MM filters shortly), but in a general sense, dilation performs nonliner filtering. For example: original image with broken characters dilation by 3x3 cross
19 Properties of Dilation translation-invariant increasing commutative distributive over union origin is neutral element "impulse response" associative scaling property
20 Duality of Erosion and Dilation Erosion and dilation are not the exact inverses of each other, but for each given fixed S.E., they form pairs of dual operations. One form of such duality is called complementation duality. Given a fixed S.E. B E, we obtain, using De Morgan's Law: Similarly, we can show Assuming symmetric B for simplicity, we can see that dilating an image is equivalent to eroding its background (and then taking the complement), and eroding an image is equivalent to dilating its background (and then taking the complement).
21 Opening Dilation is not the inverse of erosion; that is, if one composes them, one does not get identity. What does one get? There are two answers, depending on the order of composition. One of the things one gets is called opening. Given an image A E and a S.E. B E, the opening of A by B is Using the previous definitions of erosion and dilation, it can be easily shown that
22 Opening - II Opening therefore is equal to sliding the S.E. (the "mask" B) and unionizing its translates at all points where it "fits" in the image (this is similar, but different than erosion). Opening can be described thus as "rolling a ball from the inside."
23 Closing Composition of erosion and dilation the other way is called closing. Given an image A E and a S.E. B E, the closing of A by B is Closing can be described as "rolling a ball from the outside."
24 Opening and Closing as MM Filters In addition to rounding convex corners, opening eliminates narrow "isthmuses" and "capes," and small "islands." In addition to rounding concave corners, closing fills up narrow "channels" and "inlets," and small "lakes."
25 Properties of Opening translation-invariant increasing idempotent anti-extensive invariant to origin of S.E. any singleton is a neutral element
26 Properties of Closing translation-invariant increasing idempotent extensive invariant to origin of S.E. any singleton is a neutral element
27 Duality of Opening and Closing Similarly to erosion and dilation, opening and closing are dual by complementation. Given a fixed S.E. B E, we obtain, by repeated application of the previous duality result for dilation and erosion Similarly, we can show Assuming symmetric B for simplicity, we can see that opening an image is equivalent to closing its background (and then taking the complement), and closing an image is equivalent to opening its background (and then taking the complement).
28 Granulometries Given a S.E. B E, a set A E is said to be B-open if that is, A is invariant to opening by B. It can be shown that this is true if and only if for some X. It is also clear that is B-open, by idempotence. The scaling property for openings is For an integer k 1, define the scaled S.E. kb: It is clear that if r k, then kb is rb-open (why?).
29 Granulometries - II The family is called a granulometry. The term comes from the mineralogy field, where it corresponds to the classification of grainy material by means of sieving. Applying the granulometry of openings corresponds to sieving with varying sieve mesh size, because, from the scaling property, for r k, The first property says that more and more of the image is removed as k increases (i.e., a granulometry forms a pyramid representation). The second property means that applying sieves of different mesh size is the same as applying just the sieve of the largest size. The analogous development for families of closings of increasing size leads to the concept of anti-granulometries.
30 Granulometry Example Printed circuit board (PCB) inspection
31 Counter-Example The definition of scaled replicas kb of the S.E. is fundamental to guarantee the scaling property. Consider this example: (Adapted from H, Heijmans, "Morphological Image Operators," Academic Press, 1994) Note that but. This illustrates the fact that more than inclusion of B 1 into B 2 is required; one needs that B 2 be B 1 -open.
32 Pattern Spectrum Given a granulometry, the pattern spectrum is where the area of a continuous set has the usual meaning, while the area of a discrete set is just its cardinality, i.e., its number of pixels, and where. The pattern spectrum thus measures the size of the details that are removed at step k of the granulometry. This has an analogy to the Fourier transform; rather than measuring the content at a given frequency, the PS measures the content at a given size. The pattern spectrum can also be defined for anti-granulometries (closings). Sometimes the two are combined, and the PS is defined for negative k (closing of size k) and positive k (opening of size k).
33 Pattern Spectrum Example (From P.A.Maragos, "Pattern Spectrum and Multiscale Shape Representation," IEEE Transactions on Pattern Analysis and Machine Intelligence, PAMI-11, pp ,1989)
34 General Openings and Closings Any operator that is increasing, idempotent, and anti-extensive is said to be an opening. Similarly, any operator that is increasing, idempotent, and extensive is said to be a closing. Sometimes these operators are referred to as algebraic openings and algebraic closings. The opening and closing introduced earlier are sometimes called structural opening and structural closing. They are examples of translation-invariant algebraic openings and closings, respectively. An important example of algebraic opening is the area opening. This operator removes all connected components of area less than a given threshold S. Similarly, the area closing fills up all holes of area less than a given threshold S.
35 Example of Area Opening Automatic test scoring binarized image of bubble answer sheet area opening with S=500 extracts filled-in bubbles
36 Morphological Filters Even more generally, any operator that is increasing and idempotent is said to be a morphological filter, or simply a filter (when no confusion is possible). Algebraic openings form the class of anti-extensive filters, whereas algebraic closings form the class of extensive filters. Our familiar openings and closings, as well area openings and area closings, are morphological filters. According to this definition, erosions and dilations are not filters (they lack the idempotence property).
37 Alternating Sequential Filters It is possible to compose opening and closing, obtaining open-close and close-open filters and Further composing gives close-open-close and open-close-open filters and Further composition does not yield new operators, because Open-close, close-open, close-open-close and open-close-open filters, as well as their composition using different structuring elements, are called alternating sequential filters.
38 Example of Alternating Sequential Filter
39 Hit-or-Miss Transform Given an image A E and two S.E.s B 1,B 2 E, the hit-or-miss transform of of A by B 1,B 2 is therefore, the hit-or-miss transform is equal to the points where one may "place" the first S.E. such that it "fits" in the image foreground and at the same time place the second S.E. such that it fits in the image background. The hit-or-miss transform is another MM operation that can be defined in terms of simpler operations (in this case, erosion): This is clearly translation-invariant, and it is also true that
40 Example The hit-or-miss transform can be used for shape detection. Example: detection of lower-left corners in an object. (Adapted from H, Heijmans, "Morphological Image Operators," Academic Press, 1994)
41 Geodesic Dilation Given an image A E, a marker M E and a S.E. B E, the geodesic dilation of size 1 of M by B conditioned on A is the intersection limits the dilation of M to the interior of A (which is therefore sometimes called the mask). Note that we omit the S.E. B from the operator symbol, but it is always implicit in what follows. The geodesic dilation of size n can be defined recursively as where.
42 Geodesic Dilation - Example
43 Geodesic Erosion The dual of geodesic dilation is called geodesic erosion. Given an image A E, a marker M E and a S.E. B E, the geodesic erosion of size 1 of M by B conditioned on A is the union limits the erosion of M to the exterior of A (as before, A is called the mask but now it limits the operation "from below"). The geodesic erosion of size n can be defined recursively as where.
44 Geodesic Erosion - Example
45 Morphological Reconstruction Geodesic operations lead to the concept of morphological reconstruction, a powerful tool in MM. Here, the S.E. itself ceases to be the main focus of interest, but rather it is the connectivity implied by the S.E. which is important. Given an image A E, a marker M E and a S.E. B E, the reconstruction (by dilation) of M by B conditioned on A is In practice, for finite images, the limit corresponds to iteration of the geodesic dilation until stability, that is, where.
46 Morphological Reconstruction - Example
47 Connected Component Extraction Reconstruction performs connected component extraction. The S.E. determines the connectivity. S.E. = 3x3 cross 4-connectivity. S.E. = 3x3 box 8-connectivity.
48 Dual Reconstruction Given an image A E, a marker M E and a S.E. B E, the dual reconstruction (by erosion) of M by B conditioned on A is As before, for finite images, the limit corresponds to iteration of the geodesic erosion until stability, that is, where. The dual reconstruction is indeed the dual of reconstruction: with the same implicit S.E. B (assuming symmetric B, otherwise there is a reflection involved).
49 Close-Holes Filter Reconstruction can be used to fill up all holes in an image, where a "hole" is any connected component of the background that is not connected to the image border. Let the marker image be given by then is an image equal to A with all holes closed. This is really a dual reconstruction operation.
50 Border-Clearing Filter Similarly, if the marker image is now given by then is an image equal to A with all components touching the border removed. Example: Text processing. original image close-holes border-clearing
51 Opening by Reconstruction Given an image A E and a S.E. C E, the opening by reconstruction of A by C (for a given connectivity) is This is simply reconstruction where the marker is obtained by a structural opening of the original image by the S.E. C. We deliberately use the letter "C" to make clear this is distinct from the underlying S.E. B that gives the connectivity. Example: Text processing. The aim is to extract characters containing long vertical strokes. To obain this, C must be a vertical line S.E. original image opening by C opening by reconstruction
52 Opening by Reconstruction - II The opening by reconstruction has exactly the same properties of the structural opening: it is increasing, idempotent, anti-extensive, insensitive to origin of S.E. C, and any singleton is a neutral element. The family is a granulometry by reconstruction. It has all the properties of a regular granulometry, including, for r k, The S.E. B is often, but not necessarily, the same S.E. used for the connectivity. One may also define a pattern spectrum just as before. The dual operator is the closing by reconstruction: This operator has exactly the same properties of the strucutral closing. It can also be used to define anti-granulometries.
53 Granulometry by Reconstruction Example Printed circuit board (PCB) inspection
54 Boundary Extraction Given an image A E and a symmetric S.E. B E, boundary extraction can be accomplished in MM in several ways: Interior boundary: example of interior boundary Exterior boundary: Centered boundary:
55 Boundary Extraction - Example interior boundary
56 Skeleton A skeleton is a reduced representation that contain the major structural features of a binary image. It should be possible to invert the process and recover the image from its skeleton. For continuous shapes, the skeleton corresponds to the medial axis.
57 Discrete Skeleton A simple MM algorithm for computing the skeleton of a discrete image is based on sucessive erosions and opening. Consider the skeleton subsets: Note: using the following property of erosion we can write so that the skeleton subsets are found by means of using succesive erosions and an opening at each step.
58 Discrete Skeleton - II The discrete morphological skeleton of A is given by In practice, the skeleton subsets become empty after a certain number of steps, so the above set union operation is finite. It can be shown that the image can be recovered by As before, this is in actuality a finite union operation.
59 Discrete Skeleton - Example
60 Grayscale Morphology There are several approaches to extend MM to grayscale images. Umbra approach: if an image is thought of as a surface, the volume under the image is a set, called the "umbra." One can apply binary MM operations to this and then reconstruct a grayscale image. Threshold decomposition approach: any image can be decomposed in a series of binary images by thresholding. One can apply binary MM operations to these and then reconstruct a grayscale image. Algebraic approach: one can use the equivalence between set operations and general order operations (e.g., union and intersection are equivalent to max and min, respectively). The latter can be applied to grayscale images. This is the approach we will follow.
61 Grayscale Images Similarly as before, we assume an image domain E = Z d (for discrete images) or E = R d (for continuous images). For higher-dimensional "images", one has E = Z d or E = R d with d>2. A grayscale image is a function f: E {0,1,...,N-1} where N is the number of grayvalues. For example, for an 8-bit image, N = 256.
62 Image Inclusion "Inclusion" of two grayscale images is defined by the pointwise order relation:
63 Image Infimum "Intersection" corresponds to the infimum, which is given by the pointwise minimum:
64 Image Supremum "Union" corresponds to the supremum, which is given by the pointwise maximum:
65 Image Difference and Negation "Set difference" is defined by pointwise subtraction: "Set complement" is defined by pointwise negation:
66 Grayscale Erosion Given an image f: E {0,1,...,N-1} and a S.E. B E, the flat erosion of f by B is therefore, the grayscale flat erosion is a min filter. It can still be seen as fitting the S.E., this time the fitting occurs "under" the image. Provided that the origin o is contained in B, erosion has the effect of darkening the image, that is,
67 Grayscale Dilation Given an image f: E {0,1,...,N-1} and a S.E. B E, the flat dilation of f by B is therefore, the grayscale flat dilation is a max filter. It can still be seen as the loci of points where the (reflected) S.E. "hits" the image. Provided that the origin is contained in B, dilation has the effect of brightening the image, that is,
68 Example original image erosion by disk of radius 2 dilation by disk of radius 2
69 Properties of Grayscale Erosion translation-invariant increasing distributive over infimum origin is neutral element scaling property
70 Properties of Grayscale Dilation translation-invariant increasing distributive over supremum associative origin is neutral element scaling property
71 Duality of Grayscale Erosion and Dilation Just as in the binary case, grayscale erosion and dilation are not the exact inverses of each other, but for each given fixed S.E., they form pairs of dual operations. As we saw before, one form of such duality is called complementation duality. Given a fixed S.E. B E, it can be shown that and Assuming symmetric B for simplicity, we can see that dilating an image is equivalent to eroding its negative (complement) and then taking the complement, and eroding an image is equivalent to dilating its negative, and then taking the complement.
72 Grayscale Morphological Gradient Coresponding to boundary extraction in binary MM, we have the morphological gradient in grayscale MM.
73 Nonflat Grayscale Morphology It is also possible to define erosion and dilation between grayscale images (that is, the S.E. itself is a grayscale image). Given two images f, g: E {0,1,...,N-1}, the nonflat erosion and nonflat dilation of f by g are given by A Nonflat S.E. is usually an image with a small domain of definition. Nonflat MM operators are not commonly used in image processing.
74 Grayscale Opening and Closing Given an image f: E {0,1,...,N-1} and a S.E. B E, the flat opening and flat closing of f by B is obtained just as in the binary case: Opening and closing still have the interpretation of "stamping" the S.E., "under" the image and "above" the image, respectively.
75 Example original image opening by disk of radius 3 closing by disk of radius 5
76 Properties of Grayscale Opening translation-invariant increasing idempotent anti-extensive invariant to origin of S.E. any singleton is a neutral element
77 Properties of Grayscale Closing translation-invariant increasing idempotent extensive invariant to origin of S.E. any singleton is a neutral element
78 Duality of Grayscale Opening and Closing Just as in the binary case, opening and closing are dual by complementation. Given a fixed S.E. B E, it can be shown that and Assuming symmetric B for simplicity, we can see that opening an image is equivalent to closing its negative (and then taking the complement), and closing an image is equivalent to opening its negative (and then taking the complement).
79 Grayscale Alternating Sequential Filters Just as in the binary case, is is possible to define grayscale ASFs for image smoothing. original image open-close by disk radius 2 open-close by disk radius 3 open-close by disk radius 5
80 Top-Hat and Bottom-Hat The top-hat and bottom-hat operations are defined respectively as and A useful application of these operations is background removal. original image bad segmentation result opening by disk of radius 40 good segmentation result top-hat image
81 Textural Segmentation Another interesting application of opening and closings is in the segmentation of textures. original image closing by medium-size disk opening by large-size disk morphological gradient superimposed on image
82 Grayscale Granulometries The definition of B-open and the scaling property apply without change to grayscale opening. The family is called a grayscale granulometry. As in the binary case, the scaling property implies that, for r k, The analogous development for families of grayscale closings of increasing size leads to the concept of grayscale anti-granulometries. The concept of grayscale pattern spectrum can be defined as before. The "area" of the image is usually taken to be the volume under the image, considered as a surface.
83 Grayscale Granulometry Example original image = open-close by pattern spectrum
84 Grayscale Geodesic Dilation and Erosion Given a mask g: E {0,1,...,N-1}, a marker f: E {0,1,...,N-1}, and a S.E. B E, the grayscale geodesic dilation and grayscale geodesic erosion of size 1 of f by B conditioned on g are given by We omit the S.E. B from the operator symbol, but it is always implicit. The grayscale geodesic dilation and erosion of size n can be defined recursively as where and.
85 Grayscale Reconstruction Grayscale geodesic operations lead to grayscale reconstruction, a powerful and useful operation in a variety of imaging applications. As in binary case, the connectivity implied by the S.E. is the focus. Given a mask g: E {0,1,...,N-1}, a marker f: E {0,1,...,N-1}, and a S.E. B E, the grayscale reconstruction (by dilation) of f by B conditioned on g is given by In practice, for finite images, the limit corresponds to iteration of the geodesic dilation until stability, that is, where.
86 Grayscale Dual Reconstruction Given a mask g: E {0,1,...,N-1}, a marker f: E {0,1,...,N-1}, and a S.E. B E, the grayscale dual reconstruction (by erosion) of f by B conditioned on g is As before, for finite images, the limit corresponds to iteration of the geodesic erosion until stability, that is, where. The dual reconstruction is the dual of reconstruction: with same S.E. B (assuming symmetric B, else there is a reflection).
87 Grayscale Opening/Closing by Reconstruction Given an image f: E {0,1,...,N-1} and a S.E. C E, the grayscale opening by reconstruction of A by C (for a given connectivity) is We deliberately use the letter "C" to make clear this is distinct from the underlying S.E. B that gives the connectivity. The grayscale opening by reconstruction has exactly the same properties of the structural grayscale opening. The family is a granulometry by reconstruction. The dual operator is the closing by reconstruction: This operator has exactly the same properties of the structural grayscale closing. It can also be used to define anti-granulometries.
88 Example original image opening by rec with horiz line top-hat by rec (*) opening by rec with small horiz line dilation with small horiz line (**) minimum of (**) with (*) reconstruction with minimum as marker and (**) as mask
09/11/2017. Morphological image processing. Morphological image processing. Morphological image processing. Morphological image processing (binary)
 Towards image analysis Goal: Describe the contents of an image, distinguishing meaningful information from irrelevant one. Perform suitable transformations of images so as to make explicit particular shape
Towards image analysis Goal: Describe the contents of an image, distinguishing meaningful information from irrelevant one. Perform suitable transformations of images so as to make explicit particular shape
Morphological Image Processing
 Morphological Image Processing Binary image processing In binary images, we conventionally take background as black (0) and foreground objects as white (1 or 255) Morphology Figure 4.1 objects on a conveyor
Morphological Image Processing Binary image processing In binary images, we conventionally take background as black (0) and foreground objects as white (1 or 255) Morphology Figure 4.1 objects on a conveyor
Biomedical Image Analysis. Mathematical Morphology
 Biomedical Image Analysis Mathematical Morphology Contents: Foundation of Mathematical Morphology Structuring Elements Applications BMIA 15 V. Roth & P. Cattin 265 Foundations of Mathematical Morphology
Biomedical Image Analysis Mathematical Morphology Contents: Foundation of Mathematical Morphology Structuring Elements Applications BMIA 15 V. Roth & P. Cattin 265 Foundations of Mathematical Morphology
Morphological Image Processing
 Morphological Image Processing Morphology Identification, analysis, and description of the structure of the smallest unit of words Theory and technique for the analysis and processing of geometric structures
Morphological Image Processing Morphology Identification, analysis, and description of the structure of the smallest unit of words Theory and technique for the analysis and processing of geometric structures
Chapter 9 Morphological Image Processing
 Morphological Image Processing Question What is Mathematical Morphology? An (imprecise) Mathematical Answer A mathematical tool for investigating geometric structure in binary and grayscale images. Shape
Morphological Image Processing Question What is Mathematical Morphology? An (imprecise) Mathematical Answer A mathematical tool for investigating geometric structure in binary and grayscale images. Shape
morphology on binary images
 morphology on binary images Ole-Johan Skrede 10.05.2017 INF2310 - Digital Image Processing Department of Informatics The Faculty of Mathematics and Natural Sciences University of Oslo After original slides
morphology on binary images Ole-Johan Skrede 10.05.2017 INF2310 - Digital Image Processing Department of Informatics The Faculty of Mathematics and Natural Sciences University of Oslo After original slides
11/10/2011 small set, B, to probe the image under study for each SE, define origo & pixels in SE
 Mathematical Morphology Sonka 13.1-13.6 Ida-Maria Sintorn ida@cb.uu.se Today s lecture SE, morphological transformations inary MM Gray-level MM Applications Geodesic transformations Morphology-form and
Mathematical Morphology Sonka 13.1-13.6 Ida-Maria Sintorn ida@cb.uu.se Today s lecture SE, morphological transformations inary MM Gray-level MM Applications Geodesic transformations Morphology-form and
Morphological Image Processing
 Morphological Image Processing Binary dilation and erosion" Set-theoretic interpretation" Opening, closing, morphological edge detectors" Hit-miss filter" Morphological filters for gray-level images" Cascading
Morphological Image Processing Binary dilation and erosion" Set-theoretic interpretation" Opening, closing, morphological edge detectors" Hit-miss filter" Morphological filters for gray-level images" Cascading
Mathematical Morphology and Distance Transforms. Robin Strand
 Mathematical Morphology and Distance Transforms Robin Strand robin.strand@it.uu.se Morphology Form and structure Mathematical framework used for: Pre-processing Noise filtering, shape simplification,...
Mathematical Morphology and Distance Transforms Robin Strand robin.strand@it.uu.se Morphology Form and structure Mathematical framework used for: Pre-processing Noise filtering, shape simplification,...
Lecture 7: Morphological Image Processing
 I2200: Digital Image processing Lecture 7: Morphological Image Processing Prof. YingLi Tian Oct. 25, 2017 Department of Electrical Engineering The City College of New York The City University of New York
I2200: Digital Image processing Lecture 7: Morphological Image Processing Prof. YingLi Tian Oct. 25, 2017 Department of Electrical Engineering The City College of New York The City University of New York
Image Analysis. Morphological Image Analysis
 Image Analysis Morphological Image Analysis Christophoros Nikou cnikou@cs.uoi.gr Images taken from: R. Gonzalez and R. Woods. Digital Image Processing, Prentice Hall, 2008 University of Ioannina - Department
Image Analysis Morphological Image Analysis Christophoros Nikou cnikou@cs.uoi.gr Images taken from: R. Gonzalez and R. Woods. Digital Image Processing, Prentice Hall, 2008 University of Ioannina - Department
Morphological Image Processing
 Morphological Image Processing Introduction Morphology: a branch of biology that deals with the form and structure of animals and plants Morphological image processing is used to extract image components
Morphological Image Processing Introduction Morphology: a branch of biology that deals with the form and structure of animals and plants Morphological image processing is used to extract image components
Erosion, dilation and related operators
 Erosion, dilation and related operators Mariusz Jankowski Department of Electrical Engineering University of Southern Maine Portland, Maine, USA mjankowski@usm.maine.edu This paper will present implementation
Erosion, dilation and related operators Mariusz Jankowski Department of Electrical Engineering University of Southern Maine Portland, Maine, USA mjankowski@usm.maine.edu This paper will present implementation
Morphological Image Processing
 Morphological Image Processing Ranga Rodrigo October 9, 29 Outline Contents Preliminaries 2 Dilation and Erosion 3 2. Dilation.............................................. 3 2.2 Erosion..............................................
Morphological Image Processing Ranga Rodrigo October 9, 29 Outline Contents Preliminaries 2 Dilation and Erosion 3 2. Dilation.............................................. 3 2.2 Erosion..............................................
Topic 6 Representation and Description
 Topic 6 Representation and Description Background Segmentation divides the image into regions Each region should be represented and described in a form suitable for further processing/decision-making Representation
Topic 6 Representation and Description Background Segmentation divides the image into regions Each region should be represented and described in a form suitable for further processing/decision-making Representation
Machine vision. Summary # 5: Morphological operations
 1 Machine vision Summary # 5: Mphological operations MORPHOLOGICAL OPERATIONS A real image has continuous intensity. It is quantized to obtain a digital image with a given number of gray levels. Different
1 Machine vision Summary # 5: Mphological operations MORPHOLOGICAL OPERATIONS A real image has continuous intensity. It is quantized to obtain a digital image with a given number of gray levels. Different
Introduction. Computer Vision & Digital Image Processing. Preview. Basic Concepts from Set Theory
 Introduction Computer Vision & Digital Image Processing Morphological Image Processing I Morphology a branch of biology concerned with the form and structure of plants and animals Mathematical morphology
Introduction Computer Vision & Digital Image Processing Morphological Image Processing I Morphology a branch of biology concerned with the form and structure of plants and animals Mathematical morphology
11. Gray-Scale Morphology. Computer Engineering, i Sejong University. Dongil Han
 Computer Vision 11. Gray-Scale Morphology Computer Engineering, i Sejong University i Dongil Han Introduction Methematical morphology represents image objects as sets in a Euclidean space by Serra [1982],
Computer Vision 11. Gray-Scale Morphology Computer Engineering, i Sejong University i Dongil Han Introduction Methematical morphology represents image objects as sets in a Euclidean space by Serra [1982],
EE795: Computer Vision and Intelligent Systems
 EE795: Computer Vision and Intelligent Systems Spring 2012 TTh 17:30-18:45 WRI C225 Lecture 04 130131 http://www.ee.unlv.edu/~b1morris/ecg795/ 2 Outline Review Histogram Equalization Image Filtering Linear
EE795: Computer Vision and Intelligent Systems Spring 2012 TTh 17:30-18:45 WRI C225 Lecture 04 130131 http://www.ee.unlv.edu/~b1morris/ecg795/ 2 Outline Review Histogram Equalization Image Filtering Linear
Morphology-form and structure. Who am I? structuring element (SE) Today s lecture. Morphological Transformation. Mathematical Morphology
 Mathematical Morphology Morphology-form and structure Sonka 13.1-13.6 Ida-Maria Sintorn Ida.sintorn@cb.uu.se mathematical framework used for: pre-processing - noise filtering, shape simplification,...
Mathematical Morphology Morphology-form and structure Sonka 13.1-13.6 Ida-Maria Sintorn Ida.sintorn@cb.uu.se mathematical framework used for: pre-processing - noise filtering, shape simplification,...
What will we learn? What is mathematical morphology? What is mathematical morphology? Fundamental concepts and operations
 What will we learn? What is mathematical morphology and how is it used in image processing? Lecture Slides ME 4060 Machine Vision and Vision-based Control Chapter 13 Morphological image processing By Dr.
What will we learn? What is mathematical morphology and how is it used in image processing? Lecture Slides ME 4060 Machine Vision and Vision-based Control Chapter 13 Morphological image processing By Dr.
EECS490: Digital Image Processing. Lecture #17
 Lecture #17 Morphology & set operations on images Structuring elements Erosion and dilation Opening and closing Morphological image processing, boundary extraction, region filling Connectivity: convex
Lecture #17 Morphology & set operations on images Structuring elements Erosion and dilation Opening and closing Morphological image processing, boundary extraction, region filling Connectivity: convex
Digital Image Processing COSC 6380/4393
 Digital Image Processing COSC 6380/4393 Lecture 6 Sept 6 th, 2017 Pranav Mantini Slides from Dr. Shishir K Shah and Frank (Qingzhong) Liu Today Review Logical Operations on Binary Images Blob Coloring
Digital Image Processing COSC 6380/4393 Lecture 6 Sept 6 th, 2017 Pranav Mantini Slides from Dr. Shishir K Shah and Frank (Qingzhong) Liu Today Review Logical Operations on Binary Images Blob Coloring
Research Article Image Segmentation Using Gray-Scale Morphology and Marker-Controlled Watershed Transformation
 Discrete Dynamics in Nature and Society Volume 2008, Article ID 384346, 8 pages doi:10.1155/2008/384346 Research Article Image Segmentation Using Gray-Scale Morphology and Marker-Controlled Watershed Transformation
Discrete Dynamics in Nature and Society Volume 2008, Article ID 384346, 8 pages doi:10.1155/2008/384346 Research Article Image Segmentation Using Gray-Scale Morphology and Marker-Controlled Watershed Transformation
EE 584 MACHINE VISION
 EE 584 MACHINE VISION Binary Images Analysis Geometrical & Topological Properties Connectedness Binary Algorithms Morphology Binary Images Binary (two-valued; black/white) images gives better efficiency
EE 584 MACHINE VISION Binary Images Analysis Geometrical & Topological Properties Connectedness Binary Algorithms Morphology Binary Images Binary (two-valued; black/white) images gives better efficiency
CSC Discrete Math I, Spring Sets
 CSC 125 - Discrete Math I, Spring 2017 Sets Sets A set is well-defined, unordered collection of objects The objects in a set are called the elements, or members, of the set A set is said to contain its
CSC 125 - Discrete Math I, Spring 2017 Sets Sets A set is well-defined, unordered collection of objects The objects in a set are called the elements, or members, of the set A set is said to contain its
Mathematical morphology... M.1 Introduction... M.1 Dilation... M.3 Erosion... M.3 Closing... M.4 Opening... M.5 Summary... M.6
 Chapter M Misc. Contents Mathematical morphology.............................................. M.1 Introduction................................................... M.1 Dilation.....................................................
Chapter M Misc. Contents Mathematical morphology.............................................. M.1 Introduction................................................... M.1 Dilation.....................................................
Mathematical Morphology a non exhaustive overview. Adrien Bousseau
 a non exhaustive overview Adrien Bousseau Shape oriented operations, that simplify image data, preserving their essential shape characteristics and eliminating irrelevancies [Haralick87] 2 Overview Basic
a non exhaustive overview Adrien Bousseau Shape oriented operations, that simplify image data, preserving their essential shape characteristics and eliminating irrelevancies [Haralick87] 2 Overview Basic
Fundamentals of Digital Image Processing
 \L\.6 Gw.i Fundamentals of Digital Image Processing A Practical Approach with Examples in Matlab Chris Solomon School of Physical Sciences, University of Kent, Canterbury, UK Toby Breckon School of Engineering,
\L\.6 Gw.i Fundamentals of Digital Image Processing A Practical Approach with Examples in Matlab Chris Solomon School of Physical Sciences, University of Kent, Canterbury, UK Toby Breckon School of Engineering,
Fuzzy Soft Mathematical Morphology
 Fuzzy Soft Mathematical Morphology. Gasteratos, I. ndreadis and Ph. Tsalides Laboratory of Electronics Section of Electronics and Information Systems Technology Department of Electrical and Computer Engineering
Fuzzy Soft Mathematical Morphology. Gasteratos, I. ndreadis and Ph. Tsalides Laboratory of Electronics Section of Electronics and Information Systems Technology Department of Electrical and Computer Engineering
Digital Image Processing Fundamentals
 Ioannis Pitas Digital Image Processing Fundamentals Chapter 7 Shape Description Answers to the Chapter Questions Thessaloniki 1998 Chapter 7: Shape description 7.1 Introduction 1. Why is invariance to
Ioannis Pitas Digital Image Processing Fundamentals Chapter 7 Shape Description Answers to the Chapter Questions Thessaloniki 1998 Chapter 7: Shape description 7.1 Introduction 1. Why is invariance to
2 Review of Set Theory
 2 Review of Set Theory Example 2.1. Let Ω = {1, 2, 3, 4, 5, 6} 2.2. Venn diagram is very useful in set theory. It is often used to portray relationships between sets. Many identities can be read out simply
2 Review of Set Theory Example 2.1. Let Ω = {1, 2, 3, 4, 5, 6} 2.2. Venn diagram is very useful in set theory. It is often used to portray relationships between sets. Many identities can be read out simply
C E N T E R A T H O U S T O N S C H O O L of H E A L T H I N F O R M A T I O N S C I E N C E S. Image Operations II
 T H E U N I V E R S I T Y of T E X A S H E A L T H S C I E N C E C E N T E R A T H O U S T O N S C H O O L of H E A L T H I N F O R M A T I O N S C I E N C E S Image Operations II For students of HI 5323
T H E U N I V E R S I T Y of T E X A S H E A L T H S C I E N C E C E N T E R A T H O U S T O N S C H O O L of H E A L T H I N F O R M A T I O N S C I E N C E S Image Operations II For students of HI 5323
University of Groningen. Morphological design of Discrete-Time Cellular Neural Networks Brugge, Mark Harm ter
 University of Groningen Morphological design of Discrete-Time Cellular Neural Networks Brugge, Mark Harm ter IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you
University of Groningen Morphological design of Discrete-Time Cellular Neural Networks Brugge, Mark Harm ter IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you
Morphological Image Processing
 Digital Image Processing Lecture # 10 Morphological Image Processing Autumn 2012 Agenda Extraction of Connected Component Convex Hull Thinning Thickening Skeletonization Pruning Gray-scale Morphology Digital
Digital Image Processing Lecture # 10 Morphological Image Processing Autumn 2012 Agenda Extraction of Connected Component Convex Hull Thinning Thickening Skeletonization Pruning Gray-scale Morphology Digital
International Journal of Advance Engineering and Research Development. Applications of Set Theory in Digital Image Processing
 Scientific Journal of Impact Factor (SJIF): 4.72 International Journal of Advance Engineering and Research Development Volume 4, Issue 11, November -2017 Applications of Set Theory in Digital Image Processing
Scientific Journal of Impact Factor (SJIF): 4.72 International Journal of Advance Engineering and Research Development Volume 4, Issue 11, November -2017 Applications of Set Theory in Digital Image Processing
Binary Shape Characterization using Morphological Boundary Class Distribution Functions
 Binary Shape Characterization using Morphological Boundary Class Distribution Functions Marcin Iwanowski Institute of Control and Industrial Electronics, Warsaw University of Technology, ul.koszykowa 75,
Binary Shape Characterization using Morphological Boundary Class Distribution Functions Marcin Iwanowski Institute of Control and Industrial Electronics, Warsaw University of Technology, ul.koszykowa 75,
The Geodesic Integral on Medial Graphs
 The Geodesic Integral on Medial Graphs Kolya Malkin August 013 We define the geodesic integral defined on paths in the duals of medial graphs on surfaces and use it to study lens elimination and connection
The Geodesic Integral on Medial Graphs Kolya Malkin August 013 We define the geodesic integral defined on paths in the duals of medial graphs on surfaces and use it to study lens elimination and connection
Mathematical morphology (1)
 Chapter 9 Mathematical morphology () 9. Introduction Morphology, or morphology for short, is a branch of image processing which is particularly useful for analyzing shapes in images. We shall develop basic
Chapter 9 Mathematical morphology () 9. Introduction Morphology, or morphology for short, is a branch of image processing which is particularly useful for analyzing shapes in images. We shall develop basic
EECS490: Digital Image Processing. Lecture #19
 Lecture #19 Shading and texture analysis using morphology Gray scale reconstruction Basic image segmentation: edges v. regions Point and line locators, edge types and noise Edge operators: LoG, DoG, Canny
Lecture #19 Shading and texture analysis using morphology Gray scale reconstruction Basic image segmentation: edges v. regions Point and line locators, edge types and noise Edge operators: LoG, DoG, Canny
Image Processing. Bilkent University. CS554 Computer Vision Pinar Duygulu
 Image Processing CS 554 Computer Vision Pinar Duygulu Bilkent University Today Image Formation Point and Blob Processing Binary Image Processing Readings: Gonzalez & Woods, Ch. 3 Slides are adapted from
Image Processing CS 554 Computer Vision Pinar Duygulu Bilkent University Today Image Formation Point and Blob Processing Binary Image Processing Readings: Gonzalez & Woods, Ch. 3 Slides are adapted from
Digital Image Processing
 Digital Image Processing Third Edition Rafael C. Gonzalez University of Tennessee Richard E. Woods MedData Interactive PEARSON Prentice Hall Pearson Education International Contents Preface xv Acknowledgments
Digital Image Processing Third Edition Rafael C. Gonzalez University of Tennessee Richard E. Woods MedData Interactive PEARSON Prentice Hall Pearson Education International Contents Preface xv Acknowledgments
Morphological Image Processing GUI using MATLAB
 Trends Journal of Sciences Research (2015) 2(3):90-94 http://www.tjsr.org Morphological Image Processing GUI using MATLAB INTRODUCTION A digital image is a representation of twodimensional images as a
Trends Journal of Sciences Research (2015) 2(3):90-94 http://www.tjsr.org Morphological Image Processing GUI using MATLAB INTRODUCTION A digital image is a representation of twodimensional images as a
CITS 4402 Computer Vision
 CITS 4402 Computer Vision A/Prof Ajmal Mian Adj/A/Prof Mehdi Ravanbakhsh, CEO at Mapizy (www.mapizy.com) and InFarm (www.infarm.io) Lecture 02 Binary Image Analysis Objectives Revision of image formation
CITS 4402 Computer Vision A/Prof Ajmal Mian Adj/A/Prof Mehdi Ravanbakhsh, CEO at Mapizy (www.mapizy.com) and InFarm (www.infarm.io) Lecture 02 Binary Image Analysis Objectives Revision of image formation
Morphological Image Processing
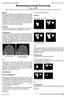 Morphological Image Processing Megha Goyal Dept. of ECE, Doaba Institute of Engineering and Technology, Kharar, Mohali, Punjab, India Abstract The purpose of this paper is to provide readers with an in-depth
Morphological Image Processing Megha Goyal Dept. of ECE, Doaba Institute of Engineering and Technology, Kharar, Mohali, Punjab, India Abstract The purpose of this paper is to provide readers with an in-depth
2.2 Set Operations. Introduction DEFINITION 1. EXAMPLE 1 The union of the sets {1, 3, 5} and {1, 2, 3} is the set {1, 2, 3, 5}; that is, EXAMPLE 2
 2.2 Set Operations 127 2.2 Set Operations Introduction Two, or more, sets can be combined in many different ways. For instance, starting with the set of mathematics majors at your school and the set of
2.2 Set Operations 127 2.2 Set Operations Introduction Two, or more, sets can be combined in many different ways. For instance, starting with the set of mathematics majors at your school and the set of
ECG782: Multidimensional Digital Signal Processing
 Professor Brendan Morris, SEB 3216, brendan.morris@unlv.edu ECG782: Multidimensional Digital Signal Processing Spring 2014 TTh 14:30-15:45 CBC C313 Lecture 03 Image Processing Basics 13/01/28 http://www.ee.unlv.edu/~b1morris/ecg782/
Professor Brendan Morris, SEB 3216, brendan.morris@unlv.edu ECG782: Multidimensional Digital Signal Processing Spring 2014 TTh 14:30-15:45 CBC C313 Lecture 03 Image Processing Basics 13/01/28 http://www.ee.unlv.edu/~b1morris/ecg782/
Detection of Edges Using Mathematical Morphological Operators
 OPEN TRANSACTIONS ON INFORMATION PROCESSING Volume 1, Number 1, MAY 2014 OPEN TRANSACTIONS ON INFORMATION PROCESSING Detection of Edges Using Mathematical Morphological Operators Suman Rani*, Deepti Bansal,
OPEN TRANSACTIONS ON INFORMATION PROCESSING Volume 1, Number 1, MAY 2014 OPEN TRANSACTIONS ON INFORMATION PROCESSING Detection of Edges Using Mathematical Morphological Operators Suman Rani*, Deepti Bansal,
CLASSIFICATION OF BOUNDARY AND REGION SHAPES USING HU-MOMENT INVARIANTS
 CLASSIFICATION OF BOUNDARY AND REGION SHAPES USING HU-MOMENT INVARIANTS B.Vanajakshi Department of Electronics & Communications Engg. Assoc.prof. Sri Viveka Institute of Technology Vijayawada, India E-mail:
CLASSIFICATION OF BOUNDARY AND REGION SHAPES USING HU-MOMENT INVARIANTS B.Vanajakshi Department of Electronics & Communications Engg. Assoc.prof. Sri Viveka Institute of Technology Vijayawada, India E-mail:
66 III Complexes. R p (r) }.
 66 III Complexes III.4 Alpha Complexes In this section, we use a radius constraint to introduce a family of subcomplexes of the Delaunay complex. These complexes are similar to the Čech complexes but differ
66 III Complexes III.4 Alpha Complexes In this section, we use a radius constraint to introduce a family of subcomplexes of the Delaunay complex. These complexes are similar to the Čech complexes but differ
Filters. Advanced and Special Topics: Filters. Filters
 Filters Advanced and Special Topics: Filters Dr. Edmund Lam Department of Electrical and Electronic Engineering The University of Hong Kong ELEC4245: Digital Image Processing (Second Semester, 2016 17)
Filters Advanced and Special Topics: Filters Dr. Edmund Lam Department of Electrical and Electronic Engineering The University of Hong Kong ELEC4245: Digital Image Processing (Second Semester, 2016 17)
Intensity Transformations and Spatial Filtering
 77 Chapter 3 Intensity Transformations and Spatial Filtering Spatial domain refers to the image plane itself, and image processing methods in this category are based on direct manipulation of pixels in
77 Chapter 3 Intensity Transformations and Spatial Filtering Spatial domain refers to the image plane itself, and image processing methods in this category are based on direct manipulation of pixels in
Elaborazione delle Immagini Informazione multimediale - Immagini. Raffaella Lanzarotti
 Elaborazione delle Immagini Informazione multimediale - Immagini Raffaella Lanzarotti MATHEMATICAL MORPHOLOGY 2 Definitions Morphology: branch of biology studying shape and structure of plants and animals
Elaborazione delle Immagini Informazione multimediale - Immagini Raffaella Lanzarotti MATHEMATICAL MORPHOLOGY 2 Definitions Morphology: branch of biology studying shape and structure of plants and animals
4. Simplicial Complexes and Simplicial Homology
 MATH41071/MATH61071 Algebraic topology Autumn Semester 2017 2018 4. Simplicial Complexes and Simplicial Homology Geometric simplicial complexes 4.1 Definition. A finite subset { v 0, v 1,..., v r } R n
MATH41071/MATH61071 Algebraic topology Autumn Semester 2017 2018 4. Simplicial Complexes and Simplicial Homology Geometric simplicial complexes 4.1 Definition. A finite subset { v 0, v 1,..., v r } R n
CS443: Digital Imaging and Multimedia Binary Image Analysis. Spring 2008 Ahmed Elgammal Dept. of Computer Science Rutgers University
 CS443: Digital Imaging and Multimedia Binary Image Analysis Spring 2008 Ahmed Elgammal Dept. of Computer Science Rutgers University Outlines A Simple Machine Vision System Image segmentation by thresholding
CS443: Digital Imaging and Multimedia Binary Image Analysis Spring 2008 Ahmed Elgammal Dept. of Computer Science Rutgers University Outlines A Simple Machine Vision System Image segmentation by thresholding
EECS490: Digital Image Processing. Lecture #23
 Lecture #23 Motion segmentation & motion tracking Boundary tracking Chain codes Minimum perimeter polygons Signatures Motion Segmentation P k Accumulative Difference Image Positive ADI Negative ADI (ADI)
Lecture #23 Motion segmentation & motion tracking Boundary tracking Chain codes Minimum perimeter polygons Signatures Motion Segmentation P k Accumulative Difference Image Positive ADI Negative ADI (ADI)
Hierarchical Representation of 2-D Shapes using Convex Polygons: a Contour-Based Approach
 Hierarchical Representation of 2-D Shapes using Convex Polygons: a Contour-Based Approach O. El Badawy, M. S. Kamel Pattern Analysis and Machine Intelligence Laboratory, Department of Systems Design Engineering,
Hierarchical Representation of 2-D Shapes using Convex Polygons: a Contour-Based Approach O. El Badawy, M. S. Kamel Pattern Analysis and Machine Intelligence Laboratory, Department of Systems Design Engineering,
Morphological Compound Operations-Opening and CLosing
 Morphological Compound Operations-Opening and CLosing COMPSCI 375 S1 T 2006, A/P Georgy Gimel farb Revised COMPSCI 373 S1C -2010, Patrice Delmas AP Georgy Gimel'farb 1 Set-theoretic Binary Operations Many
Morphological Compound Operations-Opening and CLosing COMPSCI 375 S1 T 2006, A/P Georgy Gimel farb Revised COMPSCI 373 S1C -2010, Patrice Delmas AP Georgy Gimel'farb 1 Set-theoretic Binary Operations Many
[ ] Review. Edges and Binary Images. Edge detection. Derivative of Gaussian filter. Image gradient. Tuesday, Sept 16
![[ ] Review. Edges and Binary Images. Edge detection. Derivative of Gaussian filter. Image gradient. Tuesday, Sept 16 [ ] Review. Edges and Binary Images. Edge detection. Derivative of Gaussian filter. Image gradient. Tuesday, Sept 16](/thumbs/89/98496315.jpg) Review Edges and Binary Images Tuesday, Sept 6 Thought question: how could we compute a temporal gradient from video data? What filter is likely to have produced this image output? original filtered output
Review Edges and Binary Images Tuesday, Sept 6 Thought question: how could we compute a temporal gradient from video data? What filter is likely to have produced this image output? original filtered output
COMPUTER AND ROBOT VISION
 VOLUME COMPUTER AND ROBOT VISION Robert M. Haralick University of Washington Linda G. Shapiro University of Washington A^ ADDISON-WESLEY PUBLISHING COMPANY Reading, Massachusetts Menlo Park, California
VOLUME COMPUTER AND ROBOT VISION Robert M. Haralick University of Washington Linda G. Shapiro University of Washington A^ ADDISON-WESLEY PUBLISHING COMPANY Reading, Massachusetts Menlo Park, California
Processing of binary images
 Binary Image Processing Tuesday, 14/02/2017 ntonis rgyros e-mail: argyros@csd.uoc.gr 1 Today From gray level to binary images Processing of binary images Mathematical morphology 2 Computer Vision, Spring
Binary Image Processing Tuesday, 14/02/2017 ntonis rgyros e-mail: argyros@csd.uoc.gr 1 Today From gray level to binary images Processing of binary images Mathematical morphology 2 Computer Vision, Spring
Biometrics Technology: Image Processing & Pattern Recognition (by Dr. Dickson Tong)
 Biometrics Technology: Image Processing & Pattern Recognition (by Dr. Dickson Tong) References: [1] http://homepages.inf.ed.ac.uk/rbf/hipr2/index.htm [2] http://www.cs.wisc.edu/~dyer/cs540/notes/vision.html
Biometrics Technology: Image Processing & Pattern Recognition (by Dr. Dickson Tong) References: [1] http://homepages.inf.ed.ac.uk/rbf/hipr2/index.htm [2] http://www.cs.wisc.edu/~dyer/cs540/notes/vision.html
Interactive Math Glossary Terms and Definitions
 Terms and Definitions Absolute Value the magnitude of a number, or the distance from 0 on a real number line Addend any number or quantity being added addend + addend = sum Additive Property of Area the
Terms and Definitions Absolute Value the magnitude of a number, or the distance from 0 on a real number line Addend any number or quantity being added addend + addend = sum Additive Property of Area the
Connectivity Preserving Digitization of Blurred Binary Images in 2D and 3D
 Connectivity Preserving Digitization of Blurred Binary Images in 2D and 3D Peer Stelldinger a Ullrich Köthe a a Cognitive Systems Group, University of Hamburg, Vogt-Köln-Str. 30, D-22527 Hamburg, Germany
Connectivity Preserving Digitization of Blurred Binary Images in 2D and 3D Peer Stelldinger a Ullrich Köthe a a Cognitive Systems Group, University of Hamburg, Vogt-Köln-Str. 30, D-22527 Hamburg, Germany
[Ch 6] Set Theory. 1. Basic Concepts and Definitions. 400 lecture note #4. 1) Basics
![[Ch 6] Set Theory. 1. Basic Concepts and Definitions. 400 lecture note #4. 1) Basics [Ch 6] Set Theory. 1. Basic Concepts and Definitions. 400 lecture note #4. 1) Basics](/thumbs/82/86066673.jpg) 400 lecture note #4 [Ch 6] Set Theory 1. Basic Concepts and Definitions 1) Basics Element: ; A is a set consisting of elements x which is in a/another set S such that P(x) is true. Empty set: notated {
400 lecture note #4 [Ch 6] Set Theory 1. Basic Concepts and Definitions 1) Basics Element: ; A is a set consisting of elements x which is in a/another set S such that P(x) is true. Empty set: notated {
1.1 - Introduction to Sets
 1.1 - Introduction to Sets Math 166-502 Blake Boudreaux Department of Mathematics Texas A&M University January 18, 2018 Blake Boudreaux (Texas A&M University) 1.1 - Introduction to Sets January 18, 2018
1.1 - Introduction to Sets Math 166-502 Blake Boudreaux Department of Mathematics Texas A&M University January 18, 2018 Blake Boudreaux (Texas A&M University) 1.1 - Introduction to Sets January 18, 2018
COMP combinational logic 1 Jan. 18, 2016
 In lectures 1 and 2, we looked at representations of numbers. For the case of integers, we saw that we could perform addition of two numbers using a binary representation and using the same algorithm that
In lectures 1 and 2, we looked at representations of numbers. For the case of integers, we saw that we could perform addition of two numbers using a binary representation and using the same algorithm that
Chapter IX : SKIZ and Watershed
 J. Serra Ecole des Mines de Paris ( 2000 ) Course on Math. Morphology IX. 1 Chapter IX : SKIZ and Watershed Distance function Euclidean and Geodesic SKIZ Watersheds Definition and properties Algorithms
J. Serra Ecole des Mines de Paris ( 2000 ) Course on Math. Morphology IX. 1 Chapter IX : SKIZ and Watershed Distance function Euclidean and Geodesic SKIZ Watersheds Definition and properties Algorithms
Digital Image Processing. Prof. P. K. Biswas. Department of Electronic & Electrical Communication Engineering
 Digital Image Processing Prof. P. K. Biswas Department of Electronic & Electrical Communication Engineering Indian Institute of Technology, Kharagpur Lecture - 21 Image Enhancement Frequency Domain Processing
Digital Image Processing Prof. P. K. Biswas Department of Electronic & Electrical Communication Engineering Indian Institute of Technology, Kharagpur Lecture - 21 Image Enhancement Frequency Domain Processing
MA651 Topology. Lecture 4. Topological spaces 2
 MA651 Topology. Lecture 4. Topological spaces 2 This text is based on the following books: Linear Algebra and Analysis by Marc Zamansky Topology by James Dugundgji Fundamental concepts of topology by Peter
MA651 Topology. Lecture 4. Topological spaces 2 This text is based on the following books: Linear Algebra and Analysis by Marc Zamansky Topology by James Dugundgji Fundamental concepts of topology by Peter
Application of mathematical morphology to problems related to Image Segmentation
 Application of mathematical morphology to problems related to Image Segmentation Bala S Divakaruni and Sree T. Sunkara Department of Computer Science, Northern Illinois University DeKalb IL 60115 mrdivakaruni
Application of mathematical morphology to problems related to Image Segmentation Bala S Divakaruni and Sree T. Sunkara Department of Computer Science, Northern Illinois University DeKalb IL 60115 mrdivakaruni
Spatial Enhancement Definition
 Spatial Enhancement Nickolas Faust The Electro- Optics, Environment, and Materials Laboratory Georgia Tech Research Institute Georgia Institute of Technology Definition Spectral enhancement relies on changing
Spatial Enhancement Nickolas Faust The Electro- Optics, Environment, and Materials Laboratory Georgia Tech Research Institute Georgia Institute of Technology Definition Spectral enhancement relies on changing
(Refer Slide Time 00:17) Welcome to the course on Digital Image Processing. (Refer Slide Time 00:22)
 Digital Image Processing Prof. P. K. Biswas Department of Electronics and Electrical Communications Engineering Indian Institute of Technology, Kharagpur Module Number 01 Lecture Number 02 Application
Digital Image Processing Prof. P. K. Biswas Department of Electronics and Electrical Communications Engineering Indian Institute of Technology, Kharagpur Module Number 01 Lecture Number 02 Application
Image Processing: Final Exam November 10, :30 10:30
 Image Processing: Final Exam November 10, 2017-8:30 10:30 Student name: Student number: Put your name and student number on all of the papers you hand in (if you take out the staple). There are always
Image Processing: Final Exam November 10, 2017-8:30 10:30 Student name: Student number: Put your name and student number on all of the papers you hand in (if you take out the staple). There are always
Babu Madhav Institute of Information Technology Years Integrated M.Sc.(IT)(Semester - 7)
 5 Years Integrated M.Sc.(IT)(Semester - 7) 060010707 Digital Image Processing UNIT 1 Introduction to Image Processing Q: 1 Answer in short. 1. What is digital image? 1. Define pixel or picture element?
5 Years Integrated M.Sc.(IT)(Semester - 7) 060010707 Digital Image Processing UNIT 1 Introduction to Image Processing Q: 1 Answer in short. 1. What is digital image? 1. Define pixel or picture element?
Image Processing (IP) Through Erosion and Dilation Methods
 Image Processing (IP) Through Erosion and Dilation Methods Prof. sagar B Tambe 1, Prof. Deepak Kulhare 2, M. D. Nirmal 3, Prof. Gopal Prajapati 4 1 MITCOE Pune 2 H.O.D. Computer Dept., 3 Student, CIIT,
Image Processing (IP) Through Erosion and Dilation Methods Prof. sagar B Tambe 1, Prof. Deepak Kulhare 2, M. D. Nirmal 3, Prof. Gopal Prajapati 4 1 MITCOE Pune 2 H.O.D. Computer Dept., 3 Student, CIIT,
Taibah University College of Computer Science & Engineering Course Title: Discrete Mathematics Code: CS 103. Chapter 2. Sets
 Taibah University College of Computer Science & Engineering Course Title: Discrete Mathematics Code: CS 103 Chapter 2 Sets Slides are adopted from Discrete Mathematics and It's Applications Kenneth H.
Taibah University College of Computer Science & Engineering Course Title: Discrete Mathematics Code: CS 103 Chapter 2 Sets Slides are adopted from Discrete Mathematics and It's Applications Kenneth H.
A Case Study on Mathematical Morphology Segmentation for MRI Brain Image
 A Case Study on Mathematical Morphology Segmentation for MRI Brain Image Senthilkumaran N, Kirubakaran C Department of Computer Science and Application, Gandhigram Rural Institute, Deemed University, Gandhigram,
A Case Study on Mathematical Morphology Segmentation for MRI Brain Image Senthilkumaran N, Kirubakaran C Department of Computer Science and Application, Gandhigram Rural Institute, Deemed University, Gandhigram,
10.5 Morphological Reconstruction
 518 Chapter 10 Morphological Image Processing See Sections 11.4.2 and 11.4.3 for additional applications of morphological reconstruction. This definition of reconstruction is based on dilation. It is possible
518 Chapter 10 Morphological Image Processing See Sections 11.4.2 and 11.4.3 for additional applications of morphological reconstruction. This definition of reconstruction is based on dilation. It is possible
Binary Image Processing. Introduction to Computer Vision CSE 152 Lecture 5
 Binary Image Processing CSE 152 Lecture 5 Announcements Homework 2 is due Apr 25, 11:59 PM Reading: Szeliski, Chapter 3 Image processing, Section 3.3 More neighborhood operators Binary System Summary 1.
Binary Image Processing CSE 152 Lecture 5 Announcements Homework 2 is due Apr 25, 11:59 PM Reading: Szeliski, Chapter 3 Image processing, Section 3.3 More neighborhood operators Binary System Summary 1.
Albert M. Vossepoel. Center for Image Processing
 Albert M. Vossepoel www.ph.tn.tudelft.nl/~albert scene image formation sensor pre-processing image enhancement image restoration texture filtering segmentation user analysis classification CBP course:
Albert M. Vossepoel www.ph.tn.tudelft.nl/~albert scene image formation sensor pre-processing image enhancement image restoration texture filtering segmentation user analysis classification CBP course:
Image Sampling and Quantisation
 Image Sampling and Quantisation Introduction to Signal and Image Processing Prof. Dr. Philippe Cattin MIAC, University of Basel 1 of 46 22.02.2016 09:17 Contents Contents 1 Motivation 2 Sampling Introduction
Image Sampling and Quantisation Introduction to Signal and Image Processing Prof. Dr. Philippe Cattin MIAC, University of Basel 1 of 46 22.02.2016 09:17 Contents Contents 1 Motivation 2 Sampling Introduction
On Soft Topological Linear Spaces
 Republic of Iraq Ministry of Higher Education and Scientific Research University of AL-Qadisiyah College of Computer Science and Formation Technology Department of Mathematics On Soft Topological Linear
Republic of Iraq Ministry of Higher Education and Scientific Research University of AL-Qadisiyah College of Computer Science and Formation Technology Department of Mathematics On Soft Topological Linear
Digital image processing
 Digital image processing Morphological image analysis. Binary morphology operations Introduction The morphological transformations extract or modify the structure of the particles in an image. Such transformations
Digital image processing Morphological image analysis. Binary morphology operations Introduction The morphological transformations extract or modify the structure of the particles in an image. Such transformations
Slides for Faculty Oxford University Press All rights reserved.
 Oxford University Press 2013 Slides for Faculty Assistance Preliminaries Author: Vivek Kulkarni vivek_kulkarni@yahoo.com Outline Following topics are covered in the slides: Basic concepts, namely, symbols,
Oxford University Press 2013 Slides for Faculty Assistance Preliminaries Author: Vivek Kulkarni vivek_kulkarni@yahoo.com Outline Following topics are covered in the slides: Basic concepts, namely, symbols,
A set with only one member is called a SINGLETON. A set with no members is called the EMPTY SET or 2 N
 Mathematical Preliminaries Read pages 529-540 1. Set Theory 1.1 What is a set? A set is a collection of entities of any kind. It can be finite or infinite. A = {a, b, c} N = {1, 2, 3, } An entity is an
Mathematical Preliminaries Read pages 529-540 1. Set Theory 1.1 What is a set? A set is a collection of entities of any kind. It can be finite or infinite. A = {a, b, c} N = {1, 2, 3, } An entity is an
ECG782: Multidimensional Digital Signal Processing
 Professor Brendan Morris, SEB 3216, brendan.morris@unlv.edu ECG782: Multidimensional Digital Signal Processing Spatial Domain Filtering http://www.ee.unlv.edu/~b1morris/ecg782/ 2 Outline Background Intensity
Professor Brendan Morris, SEB 3216, brendan.morris@unlv.edu ECG782: Multidimensional Digital Signal Processing Spatial Domain Filtering http://www.ee.unlv.edu/~b1morris/ecg782/ 2 Outline Background Intensity
SETS. Sets are of two sorts: finite infinite A system of sets is a set, whose elements are again sets.
 SETS A set is a file of objects which have at least one property in common. The objects of the set are called elements. Sets are notated with capital letters K, Z, N, etc., the elements are a, b, c, d,
SETS A set is a file of objects which have at least one property in common. The objects of the set are called elements. Sets are notated with capital letters K, Z, N, etc., the elements are a, b, c, d,
Image Sampling & Quantisation
 Image Sampling & Quantisation Biomedical Image Analysis Prof. Dr. Philippe Cattin MIAC, University of Basel Contents 1 Motivation 2 Sampling Introduction and Motivation Sampling Example Quantisation Example
Image Sampling & Quantisation Biomedical Image Analysis Prof. Dr. Philippe Cattin MIAC, University of Basel Contents 1 Motivation 2 Sampling Introduction and Motivation Sampling Example Quantisation Example
Manifolds. Chapter X. 44. Locally Euclidean Spaces
 Chapter X Manifolds 44. Locally Euclidean Spaces 44 1. Definition of Locally Euclidean Space Let n be a non-negative integer. A topological space X is called a locally Euclidean space of dimension n if
Chapter X Manifolds 44. Locally Euclidean Spaces 44 1. Definition of Locally Euclidean Space Let n be a non-negative integer. A topological space X is called a locally Euclidean space of dimension n if
Topology Homework 3. Section Section 3.3. Samuel Otten
 Topology Homework 3 Section 3.1 - Section 3.3 Samuel Otten 3.1 (1) Proposition. The intersection of finitely many open sets is open and the union of finitely many closed sets is closed. Proof. Note that
Topology Homework 3 Section 3.1 - Section 3.3 Samuel Otten 3.1 (1) Proposition. The intersection of finitely many open sets is open and the union of finitely many closed sets is closed. Proof. Note that
Topology Correction for Brain Atlas Segmentation using a Multiscale Algorithm
 Topology Correction for Brain Atlas Segmentation using a Multiscale Algorithm Lin Chen and Gudrun Wagenknecht Central Institute for Electronics, Research Center Jülich, Jülich, Germany Email: l.chen@fz-juelich.de
Topology Correction for Brain Atlas Segmentation using a Multiscale Algorithm Lin Chen and Gudrun Wagenknecht Central Institute for Electronics, Research Center Jülich, Jülich, Germany Email: l.chen@fz-juelich.de
= [ U 1 \ U 2 = B \ [ B \ B.
 5. Mon, Sept. 8 At the end of class on Friday, we introduced the notion of a topology, and I asked you to think about how many possible topologies there are on a 3-element set. The answer is... 29. The
5. Mon, Sept. 8 At the end of class on Friday, we introduced the notion of a topology, and I asked you to think about how many possible topologies there are on a 3-element set. The answer is... 29. The
Lecture 8 Object Descriptors
 Lecture 8 Object Descriptors Azadeh Fakhrzadeh Centre for Image Analysis Swedish University of Agricultural Sciences Uppsala University 2 Reading instructions Chapter 11.1 11.4 in G-W Azadeh Fakhrzadeh
Lecture 8 Object Descriptors Azadeh Fakhrzadeh Centre for Image Analysis Swedish University of Agricultural Sciences Uppsala University 2 Reading instructions Chapter 11.1 11.4 in G-W Azadeh Fakhrzadeh
EXAM SOLUTIONS. Image Processing and Computer Vision Course 2D1421 Monday, 13 th of March 2006,
 School of Computer Science and Communication, KTH Danica Kragic EXAM SOLUTIONS Image Processing and Computer Vision Course 2D1421 Monday, 13 th of March 2006, 14.00 19.00 Grade table 0-25 U 26-35 3 36-45
School of Computer Science and Communication, KTH Danica Kragic EXAM SOLUTIONS Image Processing and Computer Vision Course 2D1421 Monday, 13 th of March 2006, 14.00 19.00 Grade table 0-25 U 26-35 3 36-45
Solids as point set. Solid models. Solid representation schemes (cont d) Solid representation schemes. Solid representation schemes (cont d)
 Solid models Solid models developed to address limitations of wireframe modeling. Attempt was to create systems which create only complete representations. Modelers would support direct creation of 3D
Solid models Solid models developed to address limitations of wireframe modeling. Attempt was to create systems which create only complete representations. Modelers would support direct creation of 3D
Lecture : Topological Space
 Example of Lecture : Dr. Department of Mathematics Lovely Professional University Punjab, India October 18, 2014 Outline Example of 1 2 3 Example of 4 5 6 Example of I Topological spaces and continuous
Example of Lecture : Dr. Department of Mathematics Lovely Professional University Punjab, India October 18, 2014 Outline Example of 1 2 3 Example of 4 5 6 Example of I Topological spaces and continuous
Asynchronous Cellular Operations on Gray Images Extracting Topographic Shape Features and Their Relations
 Asynchronous Cellular Operations on Gray Images Extracting Topographic Shape Features and Their Relations Igor Polkovnikov Yes San Francisco LLC, ipolk@virtuar.com, www.virtuar.com/ia/ March 19, 2013 Abstract
Asynchronous Cellular Operations on Gray Images Extracting Topographic Shape Features and Their Relations Igor Polkovnikov Yes San Francisco LLC, ipolk@virtuar.com, www.virtuar.com/ia/ March 19, 2013 Abstract
Lecture 3: Basic Morphological Image Processing
 Lecture 3: Basic Morphological Image Processing Harvey Rhody Chester F. Carlson Center for Imaging Science Rochester Institute of Technology rhody@cis.rit.edu September 13, 2005 Abstract Morphological
Lecture 3: Basic Morphological Image Processing Harvey Rhody Chester F. Carlson Center for Imaging Science Rochester Institute of Technology rhody@cis.rit.edu September 13, 2005 Abstract Morphological
Introduction II. Sets. Terminology III. Definition. Definition. Definition. Example
 Sets Slides by Christopher M. ourke Instructor: erthe Y. Choueiry Spring 2006 Computer Science & Engineering 235 Introduction to Discrete Mathematics Sections 1.6 1.7 of Rosen cse235@cse.unl.edu Introduction
Sets Slides by Christopher M. ourke Instructor: erthe Y. Choueiry Spring 2006 Computer Science & Engineering 235 Introduction to Discrete Mathematics Sections 1.6 1.7 of Rosen cse235@cse.unl.edu Introduction
