THE PROBLEM THE PROBLEM (1) THE PROBLEM (2) THE MINIMUM ENERGY BROADCAST PROBLEM THE MINIMUM SPANNING TREE
|
|
|
- Loreen Carter
- 6 years ago
- Views:
Transcription
1 THE MINIMUM ENERGY BROADCAST PROBLEM I.E. THE MINIMUM SPANNING TREE PROBLEM Prof. Tiziaa Calamoeri Network Algorithms A.y. 05/ THE PROBLEM THE PROBLEM () THE PROBLEM () What does it meas sufficietly close?! A wireless ad-hoc etwork cosists of a set S of (fixed) radio statios joit by wireless coectios.! We assume that statios are located o the Euclidea plae (oly partially realistic hp).! Nodes have omidirectioal ateas: each trasmissio is listeed by all the eighborhood (atural broadcast)!! Two statios commuicate either directly (sigle-hop) -if they are sufficietly close- or through itermediate odes (multi-hop).! A trasmissio rage is assiged to every statio: a rage assigmet r : S R determies a directed commuicatio graph G=(S,E), where edge (i, j) E iff dist(i, j) r(i) (dist(i, j)= euclidea distace betwee i ad j).! I other words, (i, j) E iff j belogs to the disk cetered at i ad havig radius r(i). 3
2 THE PROBLEM (3)! For reasos coected with eergy savig, each statio ca dyamically modulate its ow trasmissio power.! I fact, the trasmissio radius of a statio depeds o the eergy power supplied to the statio.! The geeral aim is to save eergy as much as possible. THE PROBLEM ()! I particular, the power P s required by a statio s to trasmit data to aother statio t must satisfy: P s dist(s,t) α where is the distace-power gradiet. Usually (it depeds o the evorimet) I the empty space =.! Hece, i order to have a commuicatio from s to t, the power P s must be proportioal to dist(s,t) 5 THE PROBLEM (5)! Statios of a ad hoc etwork cooperate i order to provide specific etwork coectivity properties by adaptig their trasmissio rages ad, at the same time, they try to save eergy.! THE PROBLEM ()! Accordig to the required property, differet problems are proposed.! For example:! The trasmissio graph is required to be strogly coected. I such a case, the problem is NP-hard ad there is a -approximate alg. i dim. [Kirousis, Kraakis, Krizac, Pelc 0]; there exists a r> s.t. the problem is ot r-approximable.! The trasmissio graph is required to have diameter at most h. Not trivial approximate results are ot kow.! Give a source ode s, the trasmissio graph is required to iclude a spaig tree rooted at s.
3 THE PROBLEM () I this latter case:! A Broadcast Rage Assigmet (for short Broadcast) is a rage assigmet that yields a commuicatio graph G cotaiig a directed spaig tree rooted at a give source statio s.! A fudametal problem i the desig of ad-hoc wireless etworks is the Miimum-Eergy Broadcast problem (for short Mi Broadcast), that cosists i fidig a broadcast of miimal overall eergy. THE PROBLEM () Th. Mi Broadcast is ot approximable withi ay costat factor. Proof. Recall the MiSetCover problem: give a collectio C of subsets of a fiite set S, fid a subset C of C with mi cardiality, s.t. each elemet i S belogs to at least oe elemet of C. Example: S={,,3,,5} C={{,}, {,,3}, {3}, {3,,5}} C ={{,,3},{3,,5}} 0 THE PROBLEM () Proof (ctd). Note. MiSetCover is ot approximable withi c log for some costat c>0, where = S. Give a istace x of MiSetCover it is possible to costruct a istace y of MiBroadcast s.t. there exists a solutio for x of cardiality k iff there exists a solutio for y of cost k+. So, if MiBroadcast is approximable withig a costat the eve MiSetCover is. Cotradictio. THE PROBLEM (0) Proof (ctd). Reductio: x=(s,c) istace of MiSetCover with: S={s, s,, s } ad C={C, C,, C m }. We costruct y=(g,w,s) of MiBroadcast. Nodes of G: {s} U {V C } U {V S } Edges of G:{(s, v ic ), i m}u{(v ic, v js ), i m, s.t. s j i C i } s v C v i C v m C v j S s.t. s j is i C i V C V S
4 THE PROBLEM () THE PROBLEM () Proof (ctd). Fially, defie w(e)= for ay edge e. Let C be a solutio for x. A sol. for y assigs to s ad to all odes of V C i C. The resultig trasmissio graph cotais a spaig tree rooted at s because each elemet i S is cotaied i at least oe elemet of C. The cost of such a sol. is C +. Proof (ctd). Coversely, assume that r is a feasible sol. for y, (w.l.o.g. r(v) is either 0 or if v is i V C : other values would be meaigless) ad r(v)=0 if v is i V S. We derive a sol. C for x selectig all subsets C i s.t. r(v ic )=. It holds that C =cost(r)-. " 3 THE PROBLEM (5) Note We proved that Mi Broadcast is ot approximable withi a costat factor, but we have dealt with the geeral problem. There are some special cases (e.g. the Euclidea bidimesioal oe) that are particularly iterestig ad that behave better! I the followig, we restrict to the special case of Euclidea plae 5 THE PROBLEM ()! Collaboratig i order to miimize the overall eergy is crucial: S S 3 S! S eeds to commuicate with S! let =! Cost of S!S = dist(s, S )! Cost of S!S 3!S = dist(s, S 3 ) +dist(s 3, S )! Whe agle S S 3 S is obtuse: dist(s, S ) > dist(s, S 3 ) +dist(s 3, S )
5 THE PROBLEM () THE PROBLEM ()! I the Euclidea case, a rage assigmet r ca be represeted by the correspodet family D = {D,..., D l } of disks, ad the overall eergy is defied as: cost(d) = where r i is the radius of D i. l i= r i α! Cosider the complete ad weighted graph G ( ) where the weight of each arc e=(u,v) is dist(u,v).! The broadcast problem is strictly related with the miimum spaig tree o G ( ), i view of some importat properties THE PROBLEM () The set of coectios used to perform a broadcast from s: caot geerate a cycle, because odes do ot eed to be iformed twice tree miimizes the overall eergy log arcs waste more eergy tha short oes. THE PROBLEM (0)! Nevertheless, the Miimum Broadcast problem is ot the same as the Mi Spaig Tree problem: The eergy wasted by each ode u is max (u,v) T { dist(u,v) } α (i.e. ot all the arcs appear with their cotributio) Leaves waste o eergy 0
6 THE PROBLEM ()! The Miimum Broadcast problem is NP-hard i its geeral versio ad it is either approximable withi (- ) where is the maximum degree of T ad is a arbitrary costat! Nothig is kow about the hardess of the geometric versio. THE PROBLEM ()! A approx algorithm is based o the computatio of the MST:! compute the MST of the complete graph iduced by S,! Assig a directio to arcs (from s to the leaves)! Assig to each ode i a radius equal to the legth of the logest arc outgoig from i! Easy to implemet # deep aalysis of the approx ratio.! [Clemeti+al. 0] the first costat approx ratio (about 0)! [Ambüehl 05] the best (tight) kow approx ratio () MINIMUM SPANNING TREE ()! Obs. : If the weights are positive, the a MST is i fact a miimum-cost subgraph coectig all odes.! Proof: A subgraph cotaiig cycles ecessarily has a higher total weight. " 3 THE MINIMUM SPANNING TREE PROBLEM (RECUP)! Obs. : There may be several miimum spaig trees of the same weight havig a miimum umber of edges.! I particular, if all the edge weights of a give graph are the same, the every spaig tree of that graph is miimum.
7 MINIMUM SPANNING TREE ()! Obs. 3: If each edge has a distict weight, the there is a uique MST.! This is true i may realistic situatios, where it's ulikely that ay two coectios have exactly the same cost! Proof: Assume by cotradictio that MST T is ot uique. So, there is aother MST with equal weight, say T. 5 MINIMUM SPANNING TREE (3) (proof ctd)! Let e be a edge that is i T but ot i T. As T is a MST, {e } U T cotais a cycle C ad there is at least oe edge e i T that is ot i T ad lies o C.! If the weight of e is less tha that of e : replacig e with e i T yields tree {e } U T \ {e } which has a smaller weight compared to T. Cotradictio, as we assumed T is a MST but it is ot.! If the weight of e is larger tha that of e : a similar argumet ivolvig tree {e } U T \ {e } also leads to a cotradictio.! We coclude that the assumptio that there is a further MST was false. " MINIMUM SPANNING TREE ()! Obs. : For ay cycle C i the graph, if the weight of a edge e of C is larger tha the weights of all other edges of C, the this edge caot belog to a MST.! Proof: Assumig the cotrary, i.e. that e belogs to a MST T, the deletig e will break T ito two subtrees with the two edpoits of e i differet subtrees. The remaider of C recoects the subtrees, i particular there is a edge f of C with edpoits i differet subtrees, i.e., it recoects the subtrees ito a tree T with weight less tha that of T, because the weight of f is less tha the weight of e. " MINIMUM SPANNING TREE (5)! Obs. 5: If the edge of a graph with the miimum cost e is uique, the this edge is icluded i ay MST.! Proof: If e was ot icluded i the MST, removig ay of the (larger cost) edges i the cycle formed after addig e to the MST, would yield a spaig tree of smaller weight. "
8 MINIMUM SPANNING TREE () MINIMUM SPANNING TREE ()! Obs. : For ay cut C i the graph, if the weight of a edge e of C is strictly smaller tha the weights of all other edges of C, the this edge belogs to all MSTs of the graph.! Proof: If e was ot icluded i the MST, addig e to the MST produces a cycle. Removig ay of the (larger cost) edges of the cut i the cycle, would yield a spaig tree of smaller weight. "! By similar argumets, if more tha oe edge is of miimum weight across a cut, the each such edge is cotaied i a miimum spaig tree. Three classical algorithms:! Kruskal [ 5]! Prim [ 5]! Boruvka [ ] 30 MINIMUM SPANNING TREE () MINIMUM SPANNING TREE ()! The three algorithms are all greedy algorithms ad based o the same structure:! Give a set of arcs A cotaiig some MST arcs, e is a safe arc w.r.t. A if A U {e} cotais oly MST arcs, too.! A=empty set While A is ot a MST fid a safe arc e w.r.t. A A=A U e difficult issue 3! A=empty set while A is ot a MST fid a safe arc e w.r.t. A A=A U e wheever:! A is acyclic! graph G A =(V, A) is a forest whose each coected compoet is either a ode or a tree! Each safe arc coects differet coected compoets of G A! the while loop is ru - times 3
9 KRUSKAL ALGORITHM ()! A=empty set While GA is ot a MST fid a safe arc e w.r.t. A A=A U {e} KRUSKAL ALGORITHM () Amog those coectig two differet coected compoets i GA, choose the oe with miimum weight 0 Implemetatio usig:! Nodes i a mi-priority queue w.r.t. key(v)=mi weight of a arc coectig v to a ode of the mai coected compoet; if it does ot exist! If the priority queue is a heap # Complexity: O(m log )! If the priority queue is a Fiboacci heap # Complexity: O(m+ log ) 35 [Ahuja, Magati & Orli 3] 0 33 A=empty set While GA is ot a MST fid a safe arc e w.r.t. A A=A U {e}! 0 [Johso 5, Cherito & Tarja ] Amog those coectig the mai coected compoet with a isolated ode, choose the oe with miimum weight Implemetatio usig:! Data structure Uio-Fid! The set of the arcs of G is sorted w.r.t. their weight! Time Complexity: O(m log ) PRIM ALGORITHM () PRIM ALGORITHM ()
10 BORUVKA ALGORITHM () (purpose: a efficiet electrical coverage of Moravia) Hipothesis: each arc has a distict weight! A=empty set While A is ot a MST for each coected compoet C i of G A fid a safe arc e i w.r.t. C i A=A U {e i } Amog those coectig C i to aother compoet, the oe with miimum weight Trick: hadle may arcs (exactly log of the # of coected compoets) durig the same loop 3 Impossible to itroduce cycles, thaks to the hipothesis! Complexity: O(m log ) BORUVKA ALGORITHM () OTHER ALGORITHMS () OTHER ALGORITHMS ()! [Friedma & Willard ] Liear time algorithm, but it assumes the edges are already sorted w.r.t. their weight. Not used i practice, as the asymptotic otatio hides a huge costat.! [Matsui 5] Liear time algorithm for plaar graphs (possible lesso)! [Frederickso 5, Eppstei ] Give a graph ad its MST, it is eve iterestig to fid a ew MST after that the origial graph has bee slightly modified. It ca be performed i average time O(log )! Oly O(+m) time is ecessary to verify whether a give spaig tree is miimum. 3 0
11 ANOTHER APPLICATION A telecommuicatio compay wats to lay cable to a ew eighborhood.! It is costraied to bury the cable oly alog certai paths (e.g. alog roads).! Model as a (ot geometrical) graph:!!!! odes: represet poits edges: represet those paths (edge) weight: cost of addig cable o that path. AGAIN ON MINIMUM ENERGY BROADCAST Note. some of those paths might be more expesive, because they are loger, or require the cable to be buried deeper Note. there is o requiremet for edge legths to obey ormal rules of geometry such as the triagle iequality.! A miimum spaig tree for that graph would be a subset of those paths that has o cycles but still coects to every house with the lowest total cost, thus would represet the least expesive path for layig the cable. HEURISTICS () I [Wieselthier, Nguye, Ephremides, 00]: three heuristics all based o the greedy techique:! SPT (spaig path tree): it rus Dijkstra algorithm to get the miimum path tree, the it directs the edges of the tree from the root to the leaves.! BAIP (Broadcast Average Icremetal Power): it is a modificatio of the Dijkstra algorithm based o the odes (i.e. a ew ode is added to the tree o the basis of its miimum average cost).! MST (mi spaig tree): it rus Prim algorithm to get a MST, the it directs the edges of the tree from the 3 root to the leaves. HEURISTICS () GREEDY IS NOT ALWAYS GOOD Greedy is ot always good [Wa, Caliescu, Li, Frieder 0]:! SPT: it rus Dijkstra algorithm to get the miimum path tree, the it directs the edges of the tree from the root to the leaves p3 p q3 ε ε q o q p qm pm (let =)! SPT outputs a tree with total eergy: +/(- )! If the root trasmits with radius the eergy is! Whe $0 SPT is far / from the optimal solutio.
12 HEURISTICS (3) GREEDY IS NOT ALWAYS GOOD HEURISTICS () GREEDY IS NOT ALWAYS GOOD! BAIP (Broadcast Average Icremetal Power): it is a modificatio of the Dijkstra algorithm based o the odes: a ew ode is added to the tree o the basis of the mi average cost=eergy icreasig/# of added odes! It has bee desiged to solve the problems of SPT 5 (let =): 3 ε! The mi trasmissio power of the source to reach k receivig odes is k =k ad thus the average power efficiecy is k/k=! O the other had, the mi trasmissio power of the source to reach all receivig odes is ( - ) =- ad thus the average power efficiecy is (- )/=- / HEURISTICS (5) GREEDY IS NOT ALWAYS GOOD! BAIP will let the source to trasmit at power - to reach all odes i a sigle step.! However, the opt. routig is a path cosistig of all odes from left to right. Its mi power is: ( i i ) + ( ε ) < ( i i ) = i= i= 3 ε ( i + i ) (( i i )( i + i )) ( i i ) = = ( i + i ) i= ( i + i ) i= (i (i )) = = =+ ( i + i ) ( i + i ) ( i + i ) i= i= i= HEURISTICS () 3 GREEDY IS NOT ALWAYS GOOD (computatio of the performace ratio of BAIP ctd) + + i= i + (i ) + i i ) i + (i ) i= + i + (i ) =+ + i 3 (i ) i= Substitutig i=j+: + j + j = j = Thus the approx ratio of BAIP is at least: ε (ε 0) l( ) + 5 l( ) + 5 = l + o() i= i= ε j + l( ) + 5 (l( ) +) =
13 HEURISTICS () GREEDY IS NOT ALWAYS GOOD MST: it rus Prim algorithm to get a MST, the it directs the edges of the tree from the root to the leaves p p 5 +ε +ε p 3 +ε +ε o +ε p p! Path op p is the uique MST, ad its total eergy is.! O the other had, the opt. routig is the star cetered at o, whose eergy is (+ ).! The approx. ratio coverges to, as goes to 0. HEURISTICS ()! We have just show a lower boud o the approximatio ratio of MST.! This ratio is a costat ad a upper boud is.! The proof ivolves complicated geometric argumets, ad therefore we oly sketch some of them:! 50 p HEURISTICS ()! Ay pair of edges do ot cross each other The blue edge is ecessarily shorter tha at least oe of the two crossig edges HEURISTICS (0) (properties of the geometric MST ctd)! The agles betwee ay two edges icidet to a commo ode is at least π/3 The blue edge is ecessarily shorter tha at least oe of the two orage edges 5 5
14 HEURISTICS () (properties of the geometric MST - ctd)! The lue determied by each edge does ot cotai ay other odes. The lue through poits p ad p is the itersectio of the two ope disks of radius dist(p,p ) cetered at p ad p, respectively, hece a iteral ode would create a cycle 53 HEURISTICS () (properties of the geometric MST ctd)! Let p p be ay edge. The the two edpoits of ay other edge are either both outside the ope disk D(p, dist(p, p )) or both outside the ope disk D(p, dist(p, p )) The red edges are added before tha the blue edge because they are shorter. The blue edge would create a cycle. 5 HEURISTICS (3) HEURISTICS ()! Obs. The proof i [Wa, Caliescu, Li, Frieder 0] cotais a small flaw that ca be solved, arrivig to a approximatio ratio of,5 [Klasig, Navarra, Papadopoulos, Perees 0]! Idipedetly, a approximatio ratio of 0 has bee stated i [Clemeti, Crescezi, Pea, Rossi, Vocca 0]! For realistic istaces, experimets suggest that the tight approximatio ratio is ot but [Flammii, Navarra, Perees 0] -> possible lesso! Approx. ratio improved to, [Flammii, Klasig, Navarra, Perees 0]! Approx. ratio improved to,33 [Navarra 05]! Optimal boud [Ambüehl 05] 55 5
Graphs. Minimum Spanning Trees. Slides by Rose Hoberman (CMU)
 Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Graphs Miimum Spaig Trees Slides by Rose Hoberma (CMU) Problem: Layig Telephoe Wire Cetral office 2 Wirig: Naïve Approach Cetral office Expesive! 3 Wirig: Better Approach Cetral office Miimize the total
Minimum Spanning Trees
 Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 0 Miimum Spaig Trees 0 Goodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig a Network Suppose
Minimum Spanning Trees. Application: Connecting a Network
 Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
Miimum Spaig Tree // : Presetatio for use with the textbook, lgorithm esig ad pplicatios, by M. T. oodrich ad R. Tamassia, Wiley, Miimum Spaig Trees oodrich ad Tamassia Miimum Spaig Trees pplicatio: oectig
Lecturers: Sanjam Garg and Prasad Raghavendra Feb 21, Midterm 1 Solutions
 U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
U.C. Berkeley CS170 : Algorithms Midterm 1 Solutios Lecturers: Sajam Garg ad Prasad Raghavedra Feb 1, 017 Midterm 1 Solutios 1. (4 poits) For the directed graph below, fid all the strogly coected compoets
1 Graph Sparsfication
 CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
Greedy Algorithms. Interval Scheduling. Greedy Algorithms. Interval scheduling. Greedy Algorithms. Interval Scheduling
 Greedy Algorithms Greedy Algorithms Witer Paul Beame Hard to defie exactly but ca give geeral properties Solutio is built i small steps Decisios o how to build the solutio are made to maximize some criterio
Greedy Algorithms Greedy Algorithms Witer Paul Beame Hard to defie exactly but ca give geeral properties Solutio is built i small steps Decisios o how to build the solutio are made to maximize some criterio
Computational Geometry
 Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
Computatioal Geometry Chapter 4 Liear programmig Duality Smallest eclosig disk O the Ageda Liear Programmig Slides courtesy of Craig Gotsma 4. 4. Liear Programmig - Example Defie: (amout amout cosumed
6.854J / J Advanced Algorithms Fall 2008
 MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
Lecture 6. Lecturer: Ronitt Rubinfeld Scribes: Chen Ziv, Eliav Buchnik, Ophir Arie, Jonathan Gradstein
 068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
The isoperimetric problem on the hypercube
 The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
Minimum Spanning Trees
 Miimum Spaig Trees Miimum Spaig Trees Spaig subgraph Subgraph of a graph G cotaiig all the vertices of G Spaig tree Spaig subgraph that is itself a (free) tree Miimum spaig tree (MST) Spaig tree of a weighted
Miimum Spaig Trees Miimum Spaig Trees Spaig subgraph Subgraph of a graph G cotaiig all the vertices of G Spaig tree Spaig subgraph that is itself a (free) tree Miimum spaig tree (MST) Spaig tree of a weighted
15-859E: Advanced Algorithms CMU, Spring 2015 Lecture #2: Randomized MST and MST Verification January 14, 2015
 15-859E: Advaced Algorithms CMU, Sprig 2015 Lecture #2: Radomized MST ad MST Verificatio Jauary 14, 2015 Lecturer: Aupam Gupta Scribe: Yu Zhao 1 Prelimiaries I this lecture we are talkig about two cotets:
15-859E: Advaced Algorithms CMU, Sprig 2015 Lecture #2: Radomized MST ad MST Verificatio Jauary 14, 2015 Lecturer: Aupam Gupta Scribe: Yu Zhao 1 Prelimiaries I this lecture we are talkig about two cotets:
n n B. How many subsets of C are there of cardinality n. We are selecting elements for such a
 4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
Ones Assignment Method for Solving Traveling Salesman Problem
 Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Combination Labelings Of Graphs
 Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
condition w i B i S maximum u i
 ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
On (K t e)-saturated Graphs
 Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Xiaozhou (Steve) Li, Atri Rudra, Ram Swaminathan. HP Laboratories HPL Keyword(s): graph coloring; hardness of approximation
 Flexible Colorig Xiaozhou (Steve) Li, Atri Rudra, Ram Swamiatha HP Laboratories HPL-2010-177 Keyword(s): graph colorig; hardess of approximatio Abstract: Motivated b y reliability cosideratios i data deduplicatio
Flexible Colorig Xiaozhou (Steve) Li, Atri Rudra, Ram Swamiatha HP Laboratories HPL-2010-177 Keyword(s): graph colorig; hardess of approximatio Abstract: Motivated b y reliability cosideratios i data deduplicatio
Lecture Notes 6 Introduction to algorithm analysis CSS 501 Data Structures and Object-Oriented Programming
 Lecture Notes 6 Itroductio to algorithm aalysis CSS 501 Data Structures ad Object-Orieted Programmig Readig for this lecture: Carrao, Chapter 10 To be covered i this lecture: Itroductio to algorithm aalysis
Lecture Notes 6 Itroductio to algorithm aalysis CSS 501 Data Structures ad Object-Orieted Programmig Readig for this lecture: Carrao, Chapter 10 To be covered i this lecture: Itroductio to algorithm aalysis
Heaps. Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015
 Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 201 Heaps 201 Goodrich ad Tamassia xkcd. http://xkcd.com/83/. Tree. Used with permissio uder
Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 201 Heaps 201 Goodrich ad Tamassia xkcd. http://xkcd.com/83/. Tree. Used with permissio uder
c-dominating Sets for Families of Graphs
 c-domiatig Sets for Families of Graphs Kelsie Syder Mathematics Uiversity of Mary Washigto April 6, 011 1 Abstract The topic of domiatio i graphs has a rich history, begiig with chess ethusiasts i the
c-domiatig Sets for Families of Graphs Kelsie Syder Mathematics Uiversity of Mary Washigto April 6, 011 1 Abstract The topic of domiatio i graphs has a rich history, begiig with chess ethusiasts i the
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
CIS 121 Data Structures and Algorithms with Java Fall Big-Oh Notation Tuesday, September 5 (Make-up Friday, September 8)
 CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
CIS 11 Data Structures ad Algorithms with Java Fall 017 Big-Oh Notatio Tuesday, September 5 (Make-up Friday, September 8) Learig Goals Review Big-Oh ad lear big/small omega/theta otatios Practice solvig
Algorithms for Disk Covering Problems with the Most Points
 Algorithms for Disk Coverig Problems with the Most Poits Bi Xiao Departmet of Computig Hog Kog Polytechic Uiversity Hug Hom, Kowloo, Hog Kog csbxiao@comp.polyu.edu.hk Qigfeg Zhuge, Yi He, Zili Shao, Edwi
Algorithms for Disk Coverig Problems with the Most Poits Bi Xiao Departmet of Computig Hog Kog Polytechic Uiversity Hug Hom, Kowloo, Hog Kog csbxiao@comp.polyu.edu.hk Qigfeg Zhuge, Yi He, Zili Shao, Edwi
arxiv: v2 [cs.ds] 24 Mar 2018
![arxiv: v2 [cs.ds] 24 Mar 2018 arxiv: v2 [cs.ds] 24 Mar 2018](/thumbs/81/83887444.jpg) Similar Elemets ad Metric Labelig o Complete Graphs arxiv:1803.08037v [cs.ds] 4 Mar 018 Pedro F. Felzeszwalb Brow Uiversity Providece, RI, USA pff@brow.edu March 8, 018 We cosider a problem that ivolves
Similar Elemets ad Metric Labelig o Complete Graphs arxiv:1803.08037v [cs.ds] 4 Mar 018 Pedro F. Felzeszwalb Brow Uiversity Providece, RI, USA pff@brow.edu March 8, 018 We cosider a problem that ivolves
1.2 Binomial Coefficients and Subsets
 1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
New Results on Energy of Graphs of Small Order
 Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Improved Random Graph Isomorphism
 Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
Perhaps the method will give that for every e > U f() > p - 3/+e There is o o-trivial upper boud for f() ad ot eve f() < Z - e. seems to be kow, where
 ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
The Closest Line to a Data Set in the Plane. David Gurney Southeastern Louisiana University Hammond, Louisiana
 The Closest Lie to a Data Set i the Plae David Gurey Southeaster Louisiaa Uiversity Hammod, Louisiaa ABSTRACT This paper looks at three differet measures of distace betwee a lie ad a data set i the plae:
The Closest Lie to a Data Set i the Plae David Gurey Southeaster Louisiaa Uiversity Hammod, Louisiaa ABSTRACT This paper looks at three differet measures of distace betwee a lie ad a data set i the plae:
CIS 121 Data Structures and Algorithms with Java Spring Stacks, Queues, and Heaps Monday, February 18 / Tuesday, February 19
 CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
Strong Complementary Acyclic Domination of a Graph
 Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
Lecture 5. Counting Sort / Radix Sort
 Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Fundamentals of Media Processing. Shin'ichi Satoh Kazuya Kodama Hiroshi Mo Duy-Dinh Le
 Fudametals of Media Processig Shi'ichi Satoh Kazuya Kodama Hiroshi Mo Duy-Dih Le Today's topics Noparametric Methods Parze Widow k-nearest Neighbor Estimatio Clusterig Techiques k-meas Agglomerative Hierarchical
Fudametals of Media Processig Shi'ichi Satoh Kazuya Kodama Hiroshi Mo Duy-Dih Le Today's topics Noparametric Methods Parze Widow k-nearest Neighbor Estimatio Clusterig Techiques k-meas Agglomerative Hierarchical
Lecture 2: Spectra of Graphs
 Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
. Written in factored form it is easy to see that the roots are 2, 2, i,
 CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
Lecture 28: Data Link Layer
 Automatic Repeat Request (ARQ) 2. Go ack N ARQ Although the Stop ad Wait ARQ is very simple, you ca easily show that it has very the low efficiecy. The low efficiecy comes from the fact that the trasmittig
Automatic Repeat Request (ARQ) 2. Go ack N ARQ Although the Stop ad Wait ARQ is very simple, you ca easily show that it has very the low efficiecy. The low efficiecy comes from the fact that the trasmittig
Some non-existence results on Leech trees
 Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
The Adjacency Matrix and The nth Eigenvalue
 Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
Spectral Graph Theory Lecture 3 The Adjacecy Matrix ad The th Eigevalue Daiel A. Spielma September 5, 2012 3.1 About these otes These otes are ot ecessarily a accurate represetatio of what happeed i class.
Force Network Analysis using Complementary Energy
 orce Network Aalysis usig Complemetary Eergy Adrew BORGART Assistat Professor Delft Uiversity of Techology Delft, The Netherlads A.Borgart@tudelft.l Yaick LIEM Studet Delft Uiversity of Techology Delft,
orce Network Aalysis usig Complemetary Eergy Adrew BORGART Assistat Professor Delft Uiversity of Techology Delft, The Netherlads A.Borgart@tudelft.l Yaick LIEM Studet Delft Uiversity of Techology Delft,
A SOFTWARE MODEL FOR THE MULTILAYER PERCEPTRON
 A SOFTWARE MODEL FOR THE MULTILAYER PERCEPTRON Roberto Lopez ad Eugeio Oñate Iteratioal Ceter for Numerical Methods i Egieerig (CIMNE) Edificio C1, Gra Capitá s/, 08034 Barceloa, Spai ABSTRACT I this work
A SOFTWARE MODEL FOR THE MULTILAYER PERCEPTRON Roberto Lopez ad Eugeio Oñate Iteratioal Ceter for Numerical Methods i Egieerig (CIMNE) Edificio C1, Gra Capitá s/, 08034 Barceloa, Spai ABSTRACT I this work
Module 8-7: Pascal s Triangle and the Binomial Theorem
 Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
CIS 121 Data Structures and Algorithms with Java Spring Stacks and Queues Monday, February 12 / Tuesday, February 13
 CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
Exact Minimum Lower Bound Algorithm for Traveling Salesman Problem
 Exact Miimum Lower Boud Algorithm for Travelig Salesma Problem Mohamed Eleiche GeoTiba Systems mohamed.eleiche@gmail.com Abstract The miimum-travel-cost algorithm is a dyamic programmig algorithm to compute
Exact Miimum Lower Boud Algorithm for Travelig Salesma Problem Mohamed Eleiche GeoTiba Systems mohamed.eleiche@gmail.com Abstract The miimum-travel-cost algorithm is a dyamic programmig algorithm to compute
Announcements. Reading. Project #4 is on the web. Homework #1. Midterm #2. Chapter 4 ( ) Note policy about project #3 missing components
 Aoucemets Readig Chapter 4 (4.1-4.2) Project #4 is o the web ote policy about project #3 missig compoets Homework #1 Due 11/6/01 Chapter 6: 4, 12, 24, 37 Midterm #2 11/8/01 i class 1 Project #4 otes IPv6Iit,
Aoucemets Readig Chapter 4 (4.1-4.2) Project #4 is o the web ote policy about project #3 missig compoets Homework #1 Due 11/6/01 Chapter 6: 4, 12, 24, 37 Midterm #2 11/8/01 i class 1 Project #4 otes IPv6Iit,
prerequisites: 6.046, 6.041/2, ability to do proofs Randomized algorithms: make random choices during run. Main benefits:
 Itro Admiistrivia. Sigup sheet. prerequisites: 6.046, 6.041/2, ability to do proofs homework weekly (first ext week) collaboratio idepedet homeworks gradig requiremet term project books. questio: scribig?
Itro Admiistrivia. Sigup sheet. prerequisites: 6.046, 6.041/2, ability to do proofs homework weekly (first ext week) collaboratio idepedet homeworks gradig requiremet term project books. questio: scribig?
CS 683: Advanced Design and Analysis of Algorithms
 CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
CS 683: Advaced Desig ad Aalysis of Algorithms Lecture 6, February 1, 2008 Lecturer: Joh Hopcroft Scribes: Shaomei Wu, Etha Feldma February 7, 2008 1 Threshold for k CNF Satisfiability I the previous lecture,
A Note on Chromatic Transversal Weak Domination in Graphs
 Iteratioal Joural of Mathematics Treds ad Techology Volume 17 Number 2 Ja 2015 A Note o Chromatic Trasversal Weak Domiatio i Graphs S Balamuruga 1, P Selvalakshmi 2 ad A Arivalaga 1 Assistat Professor,
Iteratioal Joural of Mathematics Treds ad Techology Volume 17 Number 2 Ja 2015 A Note o Chromatic Trasversal Weak Domiatio i Graphs S Balamuruga 1, P Selvalakshmi 2 ad A Arivalaga 1 Assistat Professor,
Chapter 3 Classification of FFT Processor Algorithms
 Chapter Classificatio of FFT Processor Algorithms The computatioal complexity of the Discrete Fourier trasform (DFT) is very high. It requires () 2 complex multiplicatios ad () complex additios [5]. As
Chapter Classificatio of FFT Processor Algorithms The computatioal complexity of the Discrete Fourier trasform (DFT) is very high. It requires () 2 complex multiplicatios ad () complex additios [5]. As
Copyright 2016 Ramez Elmasri and Shamkant B. Navathe
 Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe CHAPTER 19 Query Optimizatio Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe Itroductio Query optimizatio Coducted by a query optimizer i a DBMS Goal:
Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe CHAPTER 19 Query Optimizatio Copyright 2016 Ramez Elmasri ad Shamkat B. Navathe Itroductio Query optimizatio Coducted by a query optimizer i a DBMS Goal:
Pattern Recognition Systems Lab 1 Least Mean Squares
 Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
Pseudocode ( 1.1) Analysis of Algorithms. Primitive Operations. Pseudocode Details. Running Time ( 1.1) Estimating performance
 Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
Image Segmentation EEE 508
 Image Segmetatio Objective: to determie (etract) object boudaries. It is a process of partitioig a image ito distict regios by groupig together eighborig piels based o some predefied similarity criterio.
Image Segmetatio Objective: to determie (etract) object boudaries. It is a process of partitioig a image ito distict regios by groupig together eighborig piels based o some predefied similarity criterio.
Assignment 5; Due Friday, February 10
 Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
Characterizing graphs of maximum principal ratio
 Characterizig graphs of maximum pricipal ratio Michael Tait ad Josh Tobi November 9, 05 Abstract The pricipal ratio of a coected graph, deoted γg, is the ratio of the maximum ad miimum etries of its first
Characterizig graphs of maximum pricipal ratio Michael Tait ad Josh Tobi November 9, 05 Abstract The pricipal ratio of a coected graph, deoted γg, is the ratio of the maximum ad miimum etries of its first
15-850: Advanced Algorithms CMU, Spring 2017 Lecture #2: Randomized MST and Directed MSTs January 27, 2017
 15-850: Advaced Algorithms CMU, Sprig 2017 Lecture #2: Radomized MST ad Directed MSTs Jauary 27, 2017 Lecturer: Aupam Gupta Scribe: Yu Zhao, Xiyu Wu 1 Prelimiaries I this lecture we itroduce the Karger-Klai-Tarja
15-850: Advaced Algorithms CMU, Sprig 2017 Lecture #2: Radomized MST ad Directed MSTs Jauary 27, 2017 Lecturer: Aupam Gupta Scribe: Yu Zhao, Xiyu Wu 1 Prelimiaries I this lecture we itroduce the Karger-Klai-Tarja
Basic allocator mechanisms The course that gives CMU its Zip! Memory Management II: Dynamic Storage Allocation Mar 6, 2000.
 5-23 The course that gives CM its Zip Memory Maagemet II: Dyamic Storage Allocatio Mar 6, 2000 Topics Segregated lists Buddy system Garbage collectio Mark ad Sweep Copyig eferece coutig Basic allocator
5-23 The course that gives CM its Zip Memory Maagemet II: Dyamic Storage Allocatio Mar 6, 2000 Topics Segregated lists Buddy system Garbage collectio Mark ad Sweep Copyig eferece coutig Basic allocator
Running Time. Analysis of Algorithms. Experimental Studies. Limitations of Experiments
 Ruig Time Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Most algorithms trasform iput objects ito output objects. The
Ruig Time Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Most algorithms trasform iput objects ito output objects. The
Counting the Number of Minimum Roman Dominating Functions of a Graph
 Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
Data Structures and Algorithms. Analysis of Algorithms
 Data Structures ad Algorithms Aalysis of Algorithms Outlie Ruig time Pseudo-code Big-oh otatio Big-theta otatio Big-omega otatio Asymptotic algorithm aalysis Aalysis of Algorithms Iput Algorithm Output
Data Structures ad Algorithms Aalysis of Algorithms Outlie Ruig time Pseudo-code Big-oh otatio Big-theta otatio Big-omega otatio Asymptotic algorithm aalysis Aalysis of Algorithms Iput Algorithm Output
A New Morphological 3D Shape Decomposition: Grayscale Interframe Interpolation Method
 A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
Evaluation scheme for Tracking in AMI
 A M I C o m m u i c a t i o A U G M E N T E D M U L T I - P A R T Y I N T E R A C T I O N http://www.amiproject.org/ Evaluatio scheme for Trackig i AMI S. Schreiber a D. Gatica-Perez b AMI WP4 Trackig:
A M I C o m m u i c a t i o A U G M E N T E D M U L T I - P A R T Y I N T E R A C T I O N http://www.amiproject.org/ Evaluatio scheme for Trackig i AMI S. Schreiber a D. Gatica-Perez b AMI WP4 Trackig:
Efficient Synthesis of Networks On Chip
 Efficiet Sythesis of Networks O Chip Alessadro Pito Luca P. Carloi Alberto L. Sagiovai-Vicetelli EECS Departmet, Uiversity of Califoria at Berkeley, Berkeley, CA 947-77 Abstract We propose a efficiet heuristic
Efficiet Sythesis of Networks O Chip Alessadro Pito Luca P. Carloi Alberto L. Sagiovai-Vicetelli EECS Departmet, Uiversity of Califoria at Berkeley, Berkeley, CA 947-77 Abstract We propose a efficiet heuristic
On Alliance Partitions and Bisection Width for Planar Graphs
 Joural of Graph Algorithms ad Applicatios http://jgaa.ifo/ vol. 17, o. 6, pp. 599 614 (013) DOI: 10.7155/jgaa.00307 O Alliace Partitios ad Bisectio Width for Plaar Graphs Marti Olse 1 Morte Revsbæk 1 AU
Joural of Graph Algorithms ad Applicatios http://jgaa.ifo/ vol. 17, o. 6, pp. 599 614 (013) DOI: 10.7155/jgaa.00307 O Alliace Partitios ad Bisectio Width for Plaar Graphs Marti Olse 1 Morte Revsbæk 1 AU
Random Graphs and Complex Networks T
 Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
Radom Graphs ad Complex Networks T-79.7003 Charalampos E. Tsourakakis Aalto Uiversity Lecture 3 7 September 013 Aoucemet Homework 1 is out, due i two weeks from ow. Exercises: Probabilistic iequalities
Graphs ORD SFO LAX DFW
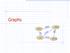 Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
Graphs SFO 337 1843 802 ORD LAX 1233 DFW Graphs A graph is a pair (V, E), where V is a set of odes, called vertices E is a collectio of pairs of vertices, called edges Vertices ad edges are positios ad
Graphs. Shortest Path and Topological Sort
 Graphs Shortest Path ad Topological Sort Example Relatioal Networks School Friedship Network (from Moody 2001) Yeast Metabolic Network (from https://www.d.edu/~etworks/cell/) Terrorist Network (by Valdis
Graphs Shortest Path ad Topological Sort Example Relatioal Networks School Friedship Network (from Moody 2001) Yeast Metabolic Network (from https://www.d.edu/~etworks/cell/) Terrorist Network (by Valdis
3. b. Present a combinatorial argument that for all positive integers n : : 2 n
 . b. Preset a combiatorial argumet that for all positive itegers : : Cosider two distict sets A ad B each of size. Sice they are distict, the cardiality of A B is. The umber of ways of choosig a pair of
. b. Preset a combiatorial argumet that for all positive itegers : : Cosider two distict sets A ad B each of size. Sice they are distict, the cardiality of A B is. The umber of ways of choosig a pair of
2. ALGORITHM ANALYSIS
 2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times 2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times Lecture slides by Kevi Waye Copyright 2005 Pearso-Addiso
2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times 2. ALGORITHM ANALYSIS computatioal tractability survey of commo ruig times Lecture slides by Kevi Waye Copyright 2005 Pearso-Addiso
Running Time ( 3.1) Analysis of Algorithms. Experimental Studies. Limitations of Experiments
 Ruig Time ( 3.1) Aalysis of Algorithms Iput Algorithm Output A algorithm is a step- by- step procedure for solvig a problem i a fiite amout of time. Most algorithms trasform iput objects ito output objects.
Ruig Time ( 3.1) Aalysis of Algorithms Iput Algorithm Output A algorithm is a step- by- step procedure for solvig a problem i a fiite amout of time. Most algorithms trasform iput objects ito output objects.
Analysis of Algorithms
 Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Ruig Time Most algorithms trasform iput objects ito output objects. The
Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Ruig Time Most algorithms trasform iput objects ito output objects. The
MINIMUM CROSSINGS IN JOIN OF GRAPHS WITH PATHS AND CYCLES
 3 Acta Electrotechica et Iformatica, Vol. 1, No. 3, 01, 3 37, DOI: 10.478/v10198-01-008-0 MINIMUM CROSSINGS IN JOIN OF GRAPHS WITH PATHS AND CYCLES Mariá KLEŠČ, Matúš VALO Departmet of Mathematics ad Theoretical
3 Acta Electrotechica et Iformatica, Vol. 1, No. 3, 01, 3 37, DOI: 10.478/v10198-01-008-0 MINIMUM CROSSINGS IN JOIN OF GRAPHS WITH PATHS AND CYCLES Mariá KLEŠČ, Matúš VALO Departmet of Mathematics ad Theoretical
1. SWITCHING FUNDAMENTALS
 . SWITCING FUNDMENTLS Switchig is the provisio of a o-demad coectio betwee two ed poits. Two distict switchig techiques are employed i commuicatio etwors-- circuit switchig ad pacet switchig. Circuit switchig
. SWITCING FUNDMENTLS Switchig is the provisio of a o-demad coectio betwee two ed poits. Two distict switchig techiques are employed i commuicatio etwors-- circuit switchig ad pacet switchig. Circuit switchig
Chapter 11. Friends, Overloaded Operators, and Arrays in Classes. Copyright 2014 Pearson Addison-Wesley. All rights reserved.
 Chapter 11 Frieds, Overloaded Operators, ad Arrays i Classes Copyright 2014 Pearso Addiso-Wesley. All rights reserved. Overview 11.1 Fried Fuctios 11.2 Overloadig Operators 11.3 Arrays ad Classes 11.4
Chapter 11 Frieds, Overloaded Operators, ad Arrays i Classes Copyright 2014 Pearso Addiso-Wesley. All rights reserved. Overview 11.1 Fried Fuctios 11.2 Overloadig Operators 11.3 Arrays ad Classes 11.4
Numerical Methods Lecture 6 - Curve Fitting Techniques
 Numerical Methods Lecture 6 - Curve Fittig Techiques Topics motivatio iterpolatio liear regressio higher order polyomial form expoetial form Curve fittig - motivatio For root fidig, we used a give fuctio
Numerical Methods Lecture 6 - Curve Fittig Techiques Topics motivatio iterpolatio liear regressio higher order polyomial form expoetial form Curve fittig - motivatio For root fidig, we used a give fuctio
An Efficient Algorithm for Graph Bisection of Triangularizations
 A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045 Oe Brookigs Drive St. Louis, Missouri 63130-4899, USA jaegerg@cse.wustl.edu
A Efficiet Algorithm for Graph Bisectio of Triagularizatios Gerold Jäger Departmet of Computer Sciece Washigto Uiversity Campus Box 1045 Oe Brookigs Drive St. Louis, Missouri 63130-4899, USA jaegerg@cse.wustl.edu
A study on Interior Domination in Graphs
 IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
9.1. Sequences and Series. Sequences. What you should learn. Why you should learn it. Definition of Sequence
 _9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
_9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
A Generalized Set Theoretic Approach for Time and Space Complexity Analysis of Algorithms and Functions
 Proceedigs of the 10th WSEAS Iteratioal Coferece o APPLIED MATHEMATICS, Dallas, Texas, USA, November 1-3, 2006 316 A Geeralized Set Theoretic Approach for Time ad Space Complexity Aalysis of Algorithms
Proceedigs of the 10th WSEAS Iteratioal Coferece o APPLIED MATHEMATICS, Dallas, Texas, USA, November 1-3, 2006 316 A Geeralized Set Theoretic Approach for Time ad Space Complexity Aalysis of Algorithms
Administrative UNSUPERVISED LEARNING. Unsupervised learning. Supervised learning 11/25/13. Final project. No office hours today
 Admiistrative Fial project No office hours today UNSUPERVISED LEARNING David Kauchak CS 451 Fall 2013 Supervised learig Usupervised learig label label 1 label 3 model/ predictor label 4 label 5 Supervised
Admiistrative Fial project No office hours today UNSUPERVISED LEARNING David Kauchak CS 451 Fall 2013 Supervised learig Usupervised learig label label 1 label 3 model/ predictor label 4 label 5 Supervised
MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS
 Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
A Note on Least-norm Solution of Global WireWarping
 A Note o Least-orm Solutio of Global WireWarpig Charlie C. L. Wag Departmet of Mechaical ad Automatio Egieerig The Chiese Uiversity of Hog Kog Shati, N.T., Hog Kog E-mail: cwag@mae.cuhk.edu.hk Abstract
A Note o Least-orm Solutio of Global WireWarpig Charlie C. L. Wag Departmet of Mechaical ad Automatio Egieerig The Chiese Uiversity of Hog Kog Shati, N.T., Hog Kog E-mail: cwag@mae.cuhk.edu.hk Abstract
Design and Analysis of Algorithms Notes
 Desig ad Aalysis of Algorithms Notes Notes by Wist Course taught by Dr. K Amer Course started: Jauary 4, 013 Course eded: December 13, 01 Curret geeratio: December 18, 013 Listigs 1 Array sum pseudocode.................................
Desig ad Aalysis of Algorithms Notes Notes by Wist Course taught by Dr. K Amer Course started: Jauary 4, 013 Course eded: December 13, 01 Curret geeratio: December 18, 013 Listigs 1 Array sum pseudocode.................................
Throughput-Delay Scaling in Wireless Networks with Constant-Size Packets
 Throughput-Delay Scalig i Wireless Networks with Costat-Size Packets Abbas El Gamal, James Mamme, Balaji Prabhakar, Devavrat Shah Departmets of EE ad CS Staford Uiversity, CA 94305 Email: {abbas, jmamme,
Throughput-Delay Scalig i Wireless Networks with Costat-Size Packets Abbas El Gamal, James Mamme, Balaji Prabhakar, Devavrat Shah Departmets of EE ad CS Staford Uiversity, CA 94305 Email: {abbas, jmamme,
Using the Keyboard. Using the Wireless Keyboard. > Using the Keyboard
 1 A wireless keyboard is supplied with your computer. The wireless keyboard uses a stadard key arragemet with additioal keys that perform specific fuctios. Usig the Wireless Keyboard Two AA alkalie batteries
1 A wireless keyboard is supplied with your computer. The wireless keyboard uses a stadard key arragemet with additioal keys that perform specific fuctios. Usig the Wireless Keyboard Two AA alkalie batteries
CSCI 5090/7090- Machine Learning. Spring Mehdi Allahyari Georgia Southern University
 CSCI 5090/7090- Machie Learig Sprig 018 Mehdi Allahyari Georgia Souther Uiversity Clusterig (slides borrowed from Tom Mitchell, Maria Floria Balca, Ali Borji, Ke Che) 1 Clusterig, Iformal Goals Goal: Automatically
CSCI 5090/7090- Machie Learig Sprig 018 Mehdi Allahyari Georgia Souther Uiversity Clusterig (slides borrowed from Tom Mitchell, Maria Floria Balca, Ali Borji, Ke Che) 1 Clusterig, Iformal Goals Goal: Automatically
Thompson s Group F (p + 1) is not Minimally Almost Convex
 Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
Sorting in Linear Time. Data Structures and Algorithms Andrei Bulatov
 Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Introduction to OSPF. ISP Training Workshops
 Itroductio to OSPF ISP Traiig Workshops 1 OSPF p Ope Shortest Path First p Lik state or SPF techology p Developed by OSPF workig group of IETF (RFC 1247) p OSPFv2 stadard described i RFC2328 p Desiged
Itroductio to OSPF ISP Traiig Workshops 1 OSPF p Ope Shortest Path First p Lik state or SPF techology p Developed by OSPF workig group of IETF (RFC 1247) p OSPFv2 stadard described i RFC2328 p Desiged
Lecture 18. Optimization in n dimensions
 Lecture 8 Optimizatio i dimesios Itroductio We ow cosider the problem of miimizig a sigle scalar fuctio of variables, f x, where x=[ x, x,, x ]T. The D case ca be visualized as fidig the lowest poit of
Lecture 8 Optimizatio i dimesios Itroductio We ow cosider the problem of miimizig a sigle scalar fuctio of variables, f x, where x=[ x, x,, x ]T. The D case ca be visualized as fidig the lowest poit of
How do we evaluate algorithms?
 F2 Readig referece: chapter 2 + slides Algorithm complexity Big O ad big Ω To calculate ruig time Aalysis of recursive Algorithms Next time: Litterature: slides mostly The first Algorithm desig methods:
F2 Readig referece: chapter 2 + slides Algorithm complexity Big O ad big Ω To calculate ruig time Aalysis of recursive Algorithms Next time: Litterature: slides mostly The first Algorithm desig methods:
Introduction. Nature-Inspired Computing. Terminology. Problem Types. Constraint Satisfaction Problems - CSP. Free Optimization Problem - FOP
 Nature-Ispired Computig Hadlig Costraits Dr. Şima Uyar September 2006 Itroductio may practical problems are costraied ot all combiatios of variable values represet valid solutios feasible solutios ifeasible
Nature-Ispired Computig Hadlig Costraits Dr. Şima Uyar September 2006 Itroductio may practical problems are costraied ot all combiatios of variable values represet valid solutios feasible solutios ifeasible
Improvement of the Orthogonal Code Convolution Capabilities Using FPGA Implementation
 Improvemet of the Orthogoal Code Covolutio Capabilities Usig FPGA Implemetatio Naima Kaabouch, Member, IEEE, Apara Dhirde, Member, IEEE, Saleh Faruque, Member, IEEE Departmet of Electrical Egieerig, Uiversity
Improvemet of the Orthogoal Code Covolutio Capabilities Usig FPGA Implemetatio Naima Kaabouch, Member, IEEE, Apara Dhirde, Member, IEEE, Saleh Faruque, Member, IEEE Departmet of Electrical Egieerig, Uiversity
Average Connectivity and Average Edge-connectivity in Graphs
 Average Coectivity ad Average Edge-coectivity i Graphs Jaehoo Kim, Suil O July 1, 01 Abstract Coectivity ad edge-coectivity of a graph measure the difficulty of breakig the graph apart, but they are very
Average Coectivity ad Average Edge-coectivity i Graphs Jaehoo Kim, Suil O July 1, 01 Abstract Coectivity ad edge-coectivity of a graph measure the difficulty of breakig the graph apart, but they are very
Symmetric Class 0 subgraphs of complete graphs
 DIMACS Techical Report 0-0 November 0 Symmetric Class 0 subgraphs of complete graphs Vi de Silva Departmet of Mathematics Pomoa College Claremot, CA, USA Chaig Verbec, Jr. Becer Friedma Istitute Booth
DIMACS Techical Report 0-0 November 0 Symmetric Class 0 subgraphs of complete graphs Vi de Silva Departmet of Mathematics Pomoa College Claremot, CA, USA Chaig Verbec, Jr. Becer Friedma Istitute Booth
COMP 558 lecture 6 Sept. 27, 2010
 Radiometry We have discussed how light travels i straight lies through space. We would like to be able to talk about how bright differet light rays are. Imagie a thi cylidrical tube ad cosider the amout
Radiometry We have discussed how light travels i straight lies through space. We would like to be able to talk about how bright differet light rays are. Imagie a thi cylidrical tube ad cosider the amout
Optimum Solution of Quadratic Programming Problem: By Wolfe s Modified Simplex Method
 Volume VI, Issue III, March 7 ISSN 78-5 Optimum Solutio of Quadratic Programmig Problem: By Wolfe s Modified Simple Method Kalpaa Lokhade, P. G. Khot & N. W. Khobragade, Departmet of Mathematics, MJP Educatioal
Volume VI, Issue III, March 7 ISSN 78-5 Optimum Solutio of Quadratic Programmig Problem: By Wolfe s Modified Simple Method Kalpaa Lokhade, P. G. Khot & N. W. Khobragade, Departmet of Mathematics, MJP Educatioal
Spanning Maximal Planar Subgraphs of Random Graphs
 Spaig Maximal Plaar Subgraphs of Radom Graphs 6. Bollobiis* Departmet of Mathematics, Louisiaa State Uiversity, Bato Rouge, LA 70803 A. M. Frieze? Departmet of Mathematics, Caregie-Mello Uiversity, Pittsburgh,
Spaig Maximal Plaar Subgraphs of Radom Graphs 6. Bollobiis* Departmet of Mathematics, Louisiaa State Uiversity, Bato Rouge, LA 70803 A. M. Frieze? Departmet of Mathematics, Caregie-Mello Uiversity, Pittsburgh,
Ch 9.3 Geometric Sequences and Series Lessons
 Ch 9.3 Geometric Sequeces ad Series Lessos SKILLS OBJECTIVES Recogize a geometric sequece. Fid the geeral, th term of a geometric sequece. Evaluate a fiite geometric series. Evaluate a ifiite geometric
Ch 9.3 Geometric Sequeces ad Series Lessos SKILLS OBJECTIVES Recogize a geometric sequece. Fid the geeral, th term of a geometric sequece. Evaluate a fiite geometric series. Evaluate a ifiite geometric
