Parallel Systems Course: Chapter VIII. Sorting Algorithms. Kumar Chapter 9. Jan Lemeire ETRO Dept. Fall Parallel Sorting
|
|
|
- Beatrix Parsons
- 5 years ago
- Views:
Transcription
1 Parallel Systems Course: Chapter VIII Sorting Algorithms Kumar Chapter 9 Jan Lemeire ETRO Dept. Fall 2017
2 Overview 1. Parallel sort distributed memory 2. Parallel sort shared memory 3. Sorting Networks A. Odd-even B. Bitonic 4. Parallel sort - GPU Jan Lemeire Pag. 2 / 72
3 Sorting: Overview One of the most commonly used and well-studied kernels. Sorting can be comparison-based or non-comparisonbased. Non-comparison: determine rank (index) in list of element E.g. Radix sort: put elements in buckets We focus here on comparison-based sorting algorithms. The fundamental operation of comparison-based sorting is compare-exchange. The lower bound on any comparison-based sort of n numbers is Θ(nlog n), the quicksort performance. Jan Lemeire Pag. 3 / 72
4 Overview 1. Parallel sort distributed memory 2. Parallel sort shared memory 3. Sorting Networks A. Odd-even B. Bitonic 4. Parallel sort - GPU Jan Lemeire Pag. 4 / 72
5 Mission Sort array asap by exploiting parallel system with distributed memory Idea: based on quicksort leads to most-optimal parallel algorithm? Jan Lemeire Pag. 5 / 72
6 Quicksort Quicksort is one of the most common sorting algorithms for sequential computers because of its simplicity, low overhead, and optimal average complexity. Quicksort selects one of the entries in the sequence to be the pivot and divides the sequence into two - one with all elements less than the pivot and other greater. The process is recursively applied to each of the sublists. Jan Lemeire Pag. 6 / 72
7 The sequential quicksort algorithm. Jan Lemeire Pag. 7 / 72
8 Quicksort Example of the quicksort algorithm sorting a sequence of size n = 8. Jan Lemeire Pag. 8 / 72
9 Quicksort The performance of quicksort depends critically on the quality of the pivot. In the best case, the pivot divides the list in such a way that the larger of the two lists does not have more than αn elements (for some constant α). In this case, the complexity of quicksort is O(nlog n). Jan Lemeire Pag. 9 / 72
10 v1. Parallel Quicksort Lets start with recursive decomposition - the list is partitioned serially and each of the subproblems is handled by a different processor. The time for this algorithm is lower-bounded by Ω(n)! Since the partitioning is done on single processor Can we parallelize the partitioning step - in particular, if we can use n processors to partition a list of length n around a pivot in O(1) time, we have a winner. Then we obtain a runtime of O(log n)!! This is difficult to do on real machines, though. Jan Lemeire Pag. 10 / 72
11 Parallel Quicksort Jan Lemeire Pag. 11 / 72
12 Execution Profile Jan Lemeire Pag. 12 / 72
13 Can we resolve the load imbalances? Make sure that each processor has the same number of elements locally. Merge results Merge sort! Actually better than quicksort Disadvantage: not in place (need copy of matrix) Use quicksort for local sort Jan Lemeire Pag. 13 / 72
14 v2. based on merge sort Similar communication overhead, but without load imbalances! Jan Lemeire Pag. 14 / 72
15 v3. Can we overcome the limited parallelism in the beginning? A simple message passing formulation is based on the recursive halving of the machine. Assume that each processor in the lower half of a p processor ensemble is paired with a corresponding processor in the upper half. A designated processor selects and broadcasts the pivot. Each processor splits its local list into two lists, one less (L i ), and other greater (U i ) than the pivot. A processor in the low half of the machine sends its list U i to the paired processor in the other half. The paired processor sends its list L i. Jan Lemeire Pag. 15 / 72
16 Halving process in parallel Jan Lemeire Pag. 16 / 72
17 Sorting: Parallel Compare Exchange Operation A parallel compare-exchange operation. Processes P i and P j send their elements to each other. Process P i keeps min{a i,a j }, and P j keeps max{a i, a j }. Jan Lemeire Pag. 17 / 72
18 Extending to n/p elements What is the parallel counterpart to a sequential comparator? If each processor has one element, the compare exchange operation can be done in t s + t w time (startup latency and per-word time). If we have more than one element per processor, we call this operation a compare split. Assume each of two processors have n/p elements. After the compare-split operation, the smaller n/p elements are at processor P i and the larger n/p elements at P j, where i < j. The time for a compare-split operation is (t s + t w n/p), assuming that the two partial lists were initially sorted. Jan Lemeire Pag. 18 / 72
19 A compare-split operation. Each process sends its block of size n/p to the other process. Each process merges the received block with its own block and retains only the appropriate half of the merged block. In this example, process P i retains the smaller elements and process P i retains the larger elements. There are alternatives! With more communication, however Jan Lemeire Pag. 19 / 72
20 After this step: all elements < pivot in the low half of the machine all elements > pivot in the high half. The above process is recursed until each processor has its own local list, which is sorted locally. The time for a single reorganization is Θ(log p) for broadcasting the pivot element, Θ(n/p) for splitting the locally assigned portion of the array, Θ(n/p) for exchange and local reorganization. Note that this time is identical to that of the corresponding shared address space formulation. However, it is important to remember that the reorganization of elements is a bandwidth sensitive operation. Jan Lemeire Pag. 20 / 72
21 Overview 1. Parallel sort distributed memory 2. Parallel sort shared memory 3. Sorting Networks A. Odd-even B. Bitonic 4. Parallel sort - GPU Jan Lemeire Pag. 21 / 72
22 Parallelizing Quicksort: Shared Address Space Formulation A list of size n equally divided across p processors. A pivot is selected by one of the processors and made known to all processors. Each processor partitions its list into two, say L i and U i, based on the selected pivot. All of the L i lists are merged and all of the U i lists are merged separately. The set of processors is partitioned into two (in proportion of the size of lists L and U). The process is recursively applied to each of the lists. Jan Lemeire Pag. 22 / 72
23 Jan Lemeire Pag. 23 / 72
24 Parallelizing Quicksort: Shared Address Space Formulation Remaining problem: global reorganization (merging) of local lists to form L and U. The problem is one of determining the right location for each element in the merged list. Each processor computes the number of elements locally less than and greater than pivot. It computes two sum-scans (also called prefix sum) to determine the starting location for its elements in the merged L and U lists. Once it knows the starting locations, it can write its elements safely. Jan Lemeire Pag. 24 / 72
25 Scan operation PPP 27 Parallel prefix sum: every node got sum of previous nodes + itself Jan Lemeire Pag. 25 / 72
26 Efficient global rearrangement of the array. Jan Lemeire Pag. 26 / 72
27 Parallelizing Quicksort: Shared Address Space Formulation The parallel time depends on the split and merge time, and the quality of the pivot. The latter is an issue independent of parallelism, so we focus on the first aspect, assuming ideal pivot selection. One iteration has four steps: (i) determine and broadcast the pivot; (ii) locally rearrange the array assigned to each process; (iii) determine the locations in the globally rearranged array that the local elements will go to; and (iv) perform the global rearrangement. The first step takes time Θ(log p), the second, Θ(n/p), the third, Θ(log p), and the fourth, Θ(n/p). The overall complexity of splitting an n-element array is Θ(n/p) + Θ(log p). Jan Lemeire Pag. 27 / 72
28 Parallelizing Quicksort: Shared Address Space Formulation The process recurses until there are p lists, at which point, the lists are sorted locally. Therefore, the total parallel time is: Useful work Overhead (neglectable for large n) (the same as sequential algorithm) Jan Lemeire Pag. 28 / 72
29 Alternative: PRAM Formulation We assume a CRCW (concurrent read, concurrent write) PRAM with concurrent writes resulting in an arbitrary write succeeding (!!). The formulation works by creating pools of processors. Every processor is assigned to the same pool initially and has one element. Each processor attempts to write its element to a common location (for the pool). Each processor tries to read back the location. If the value read back is greater than the processor's value, it assigns itself to the `left' pool, else, it assigns itself to the `right' pool. Each pool performs this operation recursively, in lockstep. Note that the algorithm generates a tree of pivots. The depth of the tree is the expected parallel runtime. The average value is O(log n). Jan Lemeire Pag. 29 / 72
30 Parallel Quicksort: PRAM Formulation Each thread has 1 value, which will be arranged in a sorted tree while(true){ write value to pool barrier read pivot from pool if (pivot == value) break else if (pivot < value) pool = pool->left else pool = pool->right } Performed by all threads in lock-step GPU: Within warps OK, otherwise barrier Jan Lemeire Pag. 30 / 72
31 Parallel Quicksort: PRAM Formulation A binary tree generated by the execution of the quicksort algorithm. Each level of the tree represents a different arraypartitioning iteration. If pivot selection is optimal, then the height of the tree is Θ(log n), which is also the number of iterations. Which is almost the ideal speedup! Overhead = pivot selection. Jan Lemeire Pag. 31 / 72
32 The execution of the PRAM algorithm on the array shown in (a). Jan Lemeire Pag. 32 / 72
33 Overview 1. Parallel sort distributed memory 2. Parallel sort shared memory 3. Sorting Networks A. Odd-even B. Bitonic 4. Parallel sort - GPU Jan Lemeire Pag. 33 / 72
34 Mission Digital circuit that transforms an unsorted list (input) into a sorted list (output) Idea: parallel processing! By putting components in parallel (width)!! So: runtime is determined by depth Goal: minimal depth Jan Lemeire Pag. 34 / 72
35 Sorting Networks A typical sorting network. Every sorting network is made up of a series of columns, and each column contains a number of comparators connected in parallel. Jan Lemeire Pag. 35 / 72
36 Sorting Networks Networks of comparators designed specifically for sorting (time < Θ(nlog n) ). Specific-designed parallel system. A comparator is a device with two inputs x and y and two outputs x' and y'. For an increasing comparator, x' = min{x,y} and y' = max{x,y}; and vice-versa for a decreasing comparator. We denote an increasing comparator by and a decreasing comparator by Ө. The speed of the network is proportional to its depth. Jan Lemeire Pag. 36 / 72
37 Basic component: Comparators A schematic representation of comparators: (a) an increasing comparator, and (b) a decreasing comparator. Jan Lemeire Pag. 37 / 72
38 KUMAR p. 416 Best algorithm to hardwire? Can we sort n elements in time O(log n)? = quicksort performance Quicksort not possible: communication paths are not fixed Best: using O(n.log n) comparators, but with a quite large constant (many thousands) Not practical Bitonic sort and odd-even sort: sort n elements in time O(log 2 n) Jan Lemeire Pag. 38 / 72
39 Overview 1. Parallel sort distributed memory 2. Parallel sort shared memory 3. Sorting Networks A. Odd-even B. Bitonic 4. Parallel sort - GPU Jan Lemeire Pag. 39 / 72
40 Bubble Sort and its Variants The sequential bubble sort algorithm compares and exchanges adjacent elements in the sequence to be sorted: Sequential bubble sort algorithm. Jan Lemeire Pag. 40 / 72
41 Bubble Sort and its Variants The complexity of bubble sort is Θ(n 2 ). Bubble sort is difficult to parallelize since the algorithm has no concurrency. A simple variant, though, uncovers the concurrency. Complexity is lower than quicksort, but parallelization is more efficient Jan Lemeire Pag. 41 / 72
42 Odd-Even Transposition Sequential odd-even transposition sort algorithm. Jan Lemeire Pag. 42 / 72
43 Sorting n = 8 elements, using the odd-even transposition sort algorithm. During each phase, n = 8 elements are compared. Jan Lemeire Pag. 43 / 72
44 Odd-Even Transposition After n phases of odd-even exchanges, the sequence is sorted. Each phase of the algorithm (either odd or even) requires Θ(n) comparisons. Serial complexity is Θ(n 2 ). Parallel version can be implemented by 1 network which is used iteratively! Conclusion: very simple, but not the fastest Jan Lemeire Pag. 44 / 72
45 Implementation with 1 network Use wraparound links to iterate over both stages Jan Lemeire Pag. 45 / 72
46 Parallel Odd-Even Transposition Consider the one item per processor case. There are n iterations, in each iteration, each processor does one compare-exchange. The parallel run time of this formulation is Θ(n). This is cost optimal with respect to the base serial algorithm but not to the optimal one (Θ(n log n) ). Jan Lemeire Pag. 46 / 72
47 Parallel formulation of odd-even transposition. Jan Lemeire Pag. 47 / 72
48 Parallel Odd-Even Transposition Consider a block of n/p elements per processor. The first step is a local sort. In each subsequent step of p steps, the compare exchange operation is replaced by the compare split operation (n/p comparisons). The parallel run time of the formulation is Jan Lemeire Pag. 48 / 72
49 Overview 1. Parallel sort distributed memory 2. Parallel sort shared memory 3. Sorting Networks A. Odd-even B. Bitonic 4. Parallel sort - GPU Jan Lemeire Pag. 49 / 72
50 Sorting Networks: Bitonic Sort Also in PPP118 A bitonic sorting network sorts n elements in Θ(log 2 n) time. A bitonic sequence has two tones - increasing and decreasing, or vice versa.. 1,2,4,7,6,0 is a bitonic sequence, because it first increases and then decreases. Not important here: Any cyclic rotation of a two-tone sequence is also considered bitonic. 8,9,2,1,0,4 is another bitonic sequence, because it is a cyclic shift of 0,4,8,9,2,1. The kernel of the network is the rearrangement of a bitonic sequence into a sorted sequence. Jan Lemeire Pag. 50 / 72
51 Sorting Networks: Bitonic Sort Let s = a 0,a 1,,a n-1 be a bitonic sequence such that a 0 a 1 a n/2-1 and a n/2 a n/2+1 a n-1. Consider the following subsequences of s: s 1 = min{a 0,a n/2 },min{a 1,a n/2+1 },,min{a n/2-1,a n-1 } s 2 = max{a 0,a n/2 },max{a 1,a n/2+1 },,max{a n/2-1,a n-1 } (1) s 1 and s 2 are both bitonic and each element of s 1 is less than every element in s 2. We can apply the procedure recursively on s 1 and s 2 to get the sorted sequence. Jan Lemeire Pag. 51 / 72
52 Bitonic sort s basic merge component Basic operation: change a bitonic array into a sorted array. For 16 elements this can be done in 4 steps. Merging a 16-element bitonic sequence through a series of log 16 bitonic splits. The complete network will be based on this component. Jan Lemeire Pag. 52 / 72
53 We can easily build a sorting network to implement this bitonic merge algorithm. Such a network is called a bitonic merging network. The network contains log n columns. Each column contains n/2 comparators and performs one step of the bitonic merge. We denote a bitonic merging network with n inputs by BM[n]. Replacing the comparators by Ө comparators results in a decreasing output sequence; such a network is denoted by ӨBM[n]. Jan Lemeire Pag. 53 / 72
54 A bitonic merging network for n = 16. The input wires are numbered 0,1,, n - 1, and the binary representation of these numbers is shown. Each column of comparators is drawn separately; the entire figure represents a BM[16] bitonic merging network. The network takes a bitonic sequence and outputs it in sorted order. Jan Lemeire Pag. 54 / 72
55 Sorting Networks: Bitonic Sort How do we sort an unsorted sequence using a bitonic merge? We must first build a single bitonic sequence from the given sequence. A sequence of length 2 is a bitonic sequence. A bitonic sequence of length 4 can be built by sorting the first two elements using BM[2] and next two, using ӨBM[2]. This process can be repeated to generate larger bitonic sequences. Jan Lemeire Pag. 55 / 72
56 A schematic representation of a network that converts an input sequence into a bitonic sequence. In this example, BM[k] and ӨBM[k] denote bitonic merging networks of input size k that use and Ө comparators, respectively. The last merging network ( BM[16]) sorts the input. In this example, n = 16. Jan Lemeire Pag. 56 / 72
57 The comparator network that transforms an input sequence of 16 unordered numbers into a bitonic sequence. Jan Lemeire Pag. 57 / 72
58 Sorting Networks: Bitonic Sort The depth of the network is Θ(log 2 n) log n = (1+ log n). log n /2 Each stage of the network contains n/2 comparators. A serial implementation of the network would have complexity Θ(nlog 2 n). Jan Lemeire Pag. 58 / 72
59 Mapping Bitonic Sort to Hypercubes Map on a general-purpose parallel computer. Consider the case of one item per processor. The question becomes one of how the wires in the bitonic network should be mapped to the hypercube interconnect. Note from our earlier examples that the compareexchange operation is performed between two wires only if their labels differ in exactly one bit! a direct mapping of wires to processors; all communication is nearest neighbor! Jan Lemeire Pag. 59 / 72
60 Communication during the last stage of bitonic sort. Each wire is mapped to a hypercube process; each connection represents a compare-exchange between processes. Jan Lemeire Pag. 60 / 72
61 Mapping Bitonic Sort to Hypercubes Communication characteristics of bitonic sort on a hypercube. During each stage of the algorithm, processes communicate along the dimensions shown. Jan Lemeire Pag. 61 / 72
62 Mapping Bitonic Sort to Hypercubes Parallel formulation of bitonic sort on a hypercube with n = 2 d processes. Jan Lemeire Pag. 62 / 72
63 Mapping Bitonic Sort to Hypercubes During each step of the algorithm, every process performs a compare-exchange operation (single nearest neighbor communication of one word). Since each step takes Θ(1) time, the parallel time is T p = Θ(log 2 n) (2) This algorithm is cost optimal w.r.t. its serial counterpart, but not w.r.t. the best sorting algorithm (Θ(n log n) ). Jan Lemeire Pag. 63 / 72
64 Mapping Bitonic Sort to Meshes The connectivity of a mesh is lower than that of a hypercube, so we must expect some overhead in this mapping. Consider the row-major shuffled mapping of wires to processors. Jan Lemeire Pag. 64 / 72
65 Mapping Bitonic Sort to Meshes Different ways of mapping the input wires of the bitonic sorting network to a mesh of processes: (a) row-major mapping, (b) row-major snakelike mapping, and (c) row-major shuffled mapping. Jan Lemeire Pag. 65 / 72
66 Mapping Bitonic Sort to Meshes The last stage of the bitonic sort algorithm for n = 16 on a mesh, using the row-major shuffled mapping. During each step, process pairs compare-exchange their elements. Arrows indicate the pairs of processes that perform compare-exchange operations. Jan Lemeire Pag. 66 / 72
67 Mapping Bitonic Sort to Meshes In the row-major shuffled mapping, wires that differ at the i th least-significant bit are mapped onto mesh processes that are 2 (i-1)/2 communication links away. The total amount of communication performed by each process is: log n i ( j 1)/ n, or ( n) i 1 j 1 The total computation performed by each process is Θ(log 2 n). The parallel runtime is: This is optimal for the mesh, but not cost optimal. Jan Lemeire Pag. 67 / 72
68 Block of Elements Per Processor Each process is assigned a block of n/p elements. The first step is a local sort of the local block. Each subsequent compare-exchange operation is replaced by a compare-split operation. We can effectively view the bitonic network as having (1 + log p)(log p)/2 steps => Θ(log 2 p). Jan Lemeire Pag. 68 / 72
69 Block of Elements Per Processor: Hypercube Initially the processes sort their n/p elements (using merge sort) in time Θ((n/p)log(n/p)) and then perform Θ(log 2 p) compare-split steps. The parallel run time of this formulation is Jan Lemeire Pag. 69 / 72
70 Block of Elements Per Processor: Mesh The parallel runtime in this case is given by: Jan Lemeire Pag. 70 / 72
71 Overview 1. Parallel sort distributed memory 2. Parallel sort shared memory 3. Sorting Networks A. Odd-even B. Bitonic 4. Parallel sort - GPU Jan Lemeire Pag. 71 / 72
72 Which algorithms on GPU? Quicksort: shared-memory formulation? Mergesort? PRAM formulation Odd-even transposition Bitonic sort Jan Lemeire Pag. 72 / 72
Parallel Systems Course: Chapter VIII. Sorting Algorithms. Kumar Chapter 9. Jan Lemeire ETRO Dept. November Parallel Sorting
 Parallel Systems Course: Chapter VIII Sorting Algorithms Kumar Chapter 9 Jan Lemeire ETRO Dept. November 2014 Overview 1. Parallel sort distributed memory 2. Parallel sort shared memory 3. Sorting Networks
Parallel Systems Course: Chapter VIII Sorting Algorithms Kumar Chapter 9 Jan Lemeire ETRO Dept. November 2014 Overview 1. Parallel sort distributed memory 2. Parallel sort shared memory 3. Sorting Networks
Sorting Algorithms. Ananth Grama, Anshul Gupta, George Karypis, and Vipin Kumar
 Sorting Algorithms Ananth Grama, Anshul Gupta, George Karypis, and Vipin Kumar To accompany the text ``Introduction to Parallel Computing'', Addison Wesley, 2003. Topic Overview Issues in Sorting on Parallel
Sorting Algorithms Ananth Grama, Anshul Gupta, George Karypis, and Vipin Kumar To accompany the text ``Introduction to Parallel Computing'', Addison Wesley, 2003. Topic Overview Issues in Sorting on Parallel
Lecture 8 Parallel Algorithms II
 Lecture 8 Parallel Algorithms II Dr. Wilson Rivera ICOM 6025: High Performance Computing Electrical and Computer Engineering Department University of Puerto Rico Original slides from Introduction to Parallel
Lecture 8 Parallel Algorithms II Dr. Wilson Rivera ICOM 6025: High Performance Computing Electrical and Computer Engineering Department University of Puerto Rico Original slides from Introduction to Parallel
CSC 447: Parallel Programming for Multi- Core and Cluster Systems
 CSC 447: Parallel Programming for Multi- Core and Cluster Systems Parallel Sorting Algorithms Instructor: Haidar M. Harmanani Spring 2016 Topic Overview Issues in Sorting on Parallel Computers Sorting
CSC 447: Parallel Programming for Multi- Core and Cluster Systems Parallel Sorting Algorithms Instructor: Haidar M. Harmanani Spring 2016 Topic Overview Issues in Sorting on Parallel Computers Sorting
CSC630/CSC730 Parallel & Distributed Computing
 CSC630/CSC730 Parallel & Distributed Computing Parallel Sorting Chapter 9 1 Contents General issues Sorting network Bitonic sort Bubble sort and its variants Odd-even transposition Quicksort Other Sorting
CSC630/CSC730 Parallel & Distributed Computing Parallel Sorting Chapter 9 1 Contents General issues Sorting network Bitonic sort Bubble sort and its variants Odd-even transposition Quicksort Other Sorting
Sorting Algorithms. Slides used during lecture of 8/11/2013 (D. Roose) Adapted from slides by
 Sorting Algorithms Slides used during lecture of 8/11/2013 (D. Roose) Adapted from slides by Ananth Grama, Anshul Gupta, George Karypis, and Vipin Kumar To accompany the text ``Introduction to Parallel
Sorting Algorithms Slides used during lecture of 8/11/2013 (D. Roose) Adapted from slides by Ananth Grama, Anshul Gupta, George Karypis, and Vipin Kumar To accompany the text ``Introduction to Parallel
Lecture 3: Sorting 1
 Lecture 3: Sorting 1 Sorting Arranging an unordered collection of elements into monotonically increasing (or decreasing) order. S = a sequence of n elements in arbitrary order After sorting:
Lecture 3: Sorting 1 Sorting Arranging an unordered collection of elements into monotonically increasing (or decreasing) order. S = a sequence of n elements in arbitrary order After sorting:
Sorting (Chapter 9) Alexandre David B2-206
 Sorting (Chapter 9) Alexandre David B2-206 1 Sorting Problem Arrange an unordered collection of elements into monotonically increasing (or decreasing) order. Let S = . Sort S into S =
Sorting (Chapter 9) Alexandre David B2-206 1 Sorting Problem Arrange an unordered collection of elements into monotonically increasing (or decreasing) order. Let S = . Sort S into S =
Introduction to Parallel Computing
 Introduction to Parallel Computing George Karypis Sorting Outline Background Sorting Networks Quicksort Bucket-Sort & Sample-Sort Background Input Specification Each processor has n/p elements A ordering
Introduction to Parallel Computing George Karypis Sorting Outline Background Sorting Networks Quicksort Bucket-Sort & Sample-Sort Background Input Specification Each processor has n/p elements A ordering
Sorting (Chapter 9) Alexandre David B2-206
 Sorting (Chapter 9) Alexandre David B2-206 Sorting Problem Arrange an unordered collection of elements into monotonically increasing (or decreasing) order. Let S = . Sort S into S =
Sorting (Chapter 9) Alexandre David B2-206 Sorting Problem Arrange an unordered collection of elements into monotonically increasing (or decreasing) order. Let S = . Sort S into S =
CS475 Parallel Programming
 CS475 Parallel Programming Sorting Wim Bohm, Colorado State University Except as otherwise noted, the content of this presentation is licensed under the Creative Commons Attribution 2.5 license. Sorting
CS475 Parallel Programming Sorting Wim Bohm, Colorado State University Except as otherwise noted, the content of this presentation is licensed under the Creative Commons Attribution 2.5 license. Sorting
John Mellor-Crummey Department of Computer Science Rice University
 Parallel Sorting John Mellor-Crummey Department of Computer Science Rice University johnmc@rice.edu COMP 422/534 Lecture 23 6 April 2017 Topics for Today Introduction Sorting networks and Batcher s bitonic
Parallel Sorting John Mellor-Crummey Department of Computer Science Rice University johnmc@rice.edu COMP 422/534 Lecture 23 6 April 2017 Topics for Today Introduction Sorting networks and Batcher s bitonic
Algorithms and Applications
 Algorithms and Applications 1 Areas done in textbook: Sorting Algorithms Numerical Algorithms Image Processing Searching and Optimization 2 Chapter 10 Sorting Algorithms - rearranging a list of numbers
Algorithms and Applications 1 Areas done in textbook: Sorting Algorithms Numerical Algorithms Image Processing Searching and Optimization 2 Chapter 10 Sorting Algorithms - rearranging a list of numbers
Parallel Sorting Algorithms
 Parallel Sorting Algorithms Ricardo Rocha and Fernando Silva Computer Science Department Faculty of Sciences University of Porto Parallel Computing 2016/2017 (Slides based on the book Parallel Programming:
Parallel Sorting Algorithms Ricardo Rocha and Fernando Silva Computer Science Department Faculty of Sciences University of Porto Parallel Computing 2016/2017 (Slides based on the book Parallel Programming:
Contents. Preface xvii Acknowledgments. CHAPTER 1 Introduction to Parallel Computing 1. CHAPTER 2 Parallel Programming Platforms 11
 Preface xvii Acknowledgments xix CHAPTER 1 Introduction to Parallel Computing 1 1.1 Motivating Parallelism 2 1.1.1 The Computational Power Argument from Transistors to FLOPS 2 1.1.2 The Memory/Disk Speed
Preface xvii Acknowledgments xix CHAPTER 1 Introduction to Parallel Computing 1 1.1 Motivating Parallelism 2 1.1.1 The Computational Power Argument from Transistors to FLOPS 2 1.1.2 The Memory/Disk Speed
Sorting Algorithms. - rearranging a list of numbers into increasing (or decreasing) order. Potential Speedup
 Sorting Algorithms - rearranging a list of numbers into increasing (or decreasing) order. Potential Speedup The worst-case time complexity of mergesort and the average time complexity of quicksort are
Sorting Algorithms - rearranging a list of numbers into increasing (or decreasing) order. Potential Speedup The worst-case time complexity of mergesort and the average time complexity of quicksort are
Parallel Sorting. Sathish Vadhiyar
 Parallel Sorting Sathish Vadhiyar Parallel Sorting Problem The input sequence of size N is distributed across P processors The output is such that elements in each processor P i is sorted elements in P
Parallel Sorting Sathish Vadhiyar Parallel Sorting Problem The input sequence of size N is distributed across P processors The output is such that elements in each processor P i is sorted elements in P
Information Coding / Computer Graphics, ISY, LiTH
 Sorting on GPUs Revisiting some algorithms from lecture 6: Some not-so-good sorting approaches Bitonic sort QuickSort Concurrent kernels and recursion Adapt to parallel algorithms Many sorting algorithms
Sorting on GPUs Revisiting some algorithms from lecture 6: Some not-so-good sorting approaches Bitonic sort QuickSort Concurrent kernels and recursion Adapt to parallel algorithms Many sorting algorithms
Dense Matrix Algorithms
 Dense Matrix Algorithms Ananth Grama, Anshul Gupta, George Karypis, and Vipin Kumar To accompany the text Introduction to Parallel Computing, Addison Wesley, 2003. Topic Overview Matrix-Vector Multiplication
Dense Matrix Algorithms Ananth Grama, Anshul Gupta, George Karypis, and Vipin Kumar To accompany the text Introduction to Parallel Computing, Addison Wesley, 2003. Topic Overview Matrix-Vector Multiplication
Sorting and Selection
 Sorting and Selection Introduction Divide and Conquer Merge-Sort Quick-Sort Radix-Sort Bucket-Sort 10-1 Introduction Assuming we have a sequence S storing a list of keyelement entries. The key of the element
Sorting and Selection Introduction Divide and Conquer Merge-Sort Quick-Sort Radix-Sort Bucket-Sort 10-1 Introduction Assuming we have a sequence S storing a list of keyelement entries. The key of the element
Parallel Sorting Algorithms
 CSC 391/691: GPU Programming Fall 015 Parallel Sorting Algorithms Copyright 015 Samuel S. Cho Sorting Algorithms Review Bubble Sort: O(n ) Insertion Sort: O(n ) Quick Sort: O(n log n) Heap Sort: O(n log
CSC 391/691: GPU Programming Fall 015 Parallel Sorting Algorithms Copyright 015 Samuel S. Cho Sorting Algorithms Review Bubble Sort: O(n ) Insertion Sort: O(n ) Quick Sort: O(n log n) Heap Sort: O(n log
DIVIDE AND CONQUER ALGORITHMS ANALYSIS WITH RECURRENCE EQUATIONS
 CHAPTER 11 SORTING ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY M. AMATO AND
CHAPTER 11 SORTING ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY M. AMATO AND
SAMPLE OF THE STUDY MATERIAL PART OF CHAPTER 6. Sorting Algorithms
 SAMPLE OF THE STUDY MATERIAL PART OF CHAPTER 6 6.0 Introduction Sorting algorithms used in computer science are often classified by: Computational complexity (worst, average and best behavior) of element
SAMPLE OF THE STUDY MATERIAL PART OF CHAPTER 6 6.0 Introduction Sorting algorithms used in computer science are often classified by: Computational complexity (worst, average and best behavior) of element
CSL 860: Modern Parallel
 CSL 860: Modern Parallel Computation PARALLEL SORTING BitonicMerge and Sort Bitonicsequence: {a 0, a 1,, a n-1 }: A sequence with a monotonically increasing part and a monotonically decreasing part For
CSL 860: Modern Parallel Computation PARALLEL SORTING BitonicMerge and Sort Bitonicsequence: {a 0, a 1,, a n-1 }: A sequence with a monotonically increasing part and a monotonically decreasing part For
Unit 6 Chapter 15 EXAMPLES OF COMPLEXITY CALCULATION
 DESIGN AND ANALYSIS OF ALGORITHMS Unit 6 Chapter 15 EXAMPLES OF COMPLEXITY CALCULATION http://milanvachhani.blogspot.in EXAMPLES FROM THE SORTING WORLD Sorting provides a good set of examples for analyzing
DESIGN AND ANALYSIS OF ALGORITHMS Unit 6 Chapter 15 EXAMPLES OF COMPLEXITY CALCULATION http://milanvachhani.blogspot.in EXAMPLES FROM THE SORTING WORLD Sorting provides a good set of examples for analyzing
CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics
 CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics 1 Sorting 1.1 Problem Statement You are given a sequence of n numbers < a 1, a 2,..., a n >. You need to
CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics 1 Sorting 1.1 Problem Statement You are given a sequence of n numbers < a 1, a 2,..., a n >. You need to
Lecture 4: Graph Algorithms
 Lecture 4: Graph Algorithms Definitions Undirected graph: G =(V, E) V finite set of vertices, E finite set of edges any edge e = (u,v) is an unordered pair Directed graph: edges are ordered pairs If e
Lecture 4: Graph Algorithms Definitions Undirected graph: G =(V, E) V finite set of vertices, E finite set of edges any edge e = (u,v) is an unordered pair Directed graph: edges are ordered pairs If e
SORTING AND SELECTION
 2 < > 1 4 8 6 = 9 CHAPTER 12 SORTING AND SELECTION ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN JAVA, GOODRICH, TAMASSIA AND GOLDWASSER (WILEY 2016)
2 < > 1 4 8 6 = 9 CHAPTER 12 SORTING AND SELECTION ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN JAVA, GOODRICH, TAMASSIA AND GOLDWASSER (WILEY 2016)
Sorting Goodrich, Tamassia Sorting 1
 Sorting Put array A of n numbers in increasing order. A core algorithm with many applications. Simple algorithms are O(n 2 ). Optimal algorithms are O(n log n). We will see O(n) for restricted input in
Sorting Put array A of n numbers in increasing order. A core algorithm with many applications. Simple algorithms are O(n 2 ). Optimal algorithms are O(n log n). We will see O(n) for restricted input in
EE/CSCI 451 Midterm 1
 EE/CSCI 451 Midterm 1 Spring 2018 Instructor: Xuehai Qian Friday: 02/26/2018 Problem # Topic Points Score 1 Definitions 20 2 Memory System Performance 10 3 Cache Performance 10 4 Shared Memory Programming
EE/CSCI 451 Midterm 1 Spring 2018 Instructor: Xuehai Qian Friday: 02/26/2018 Problem # Topic Points Score 1 Definitions 20 2 Memory System Performance 10 3 Cache Performance 10 4 Shared Memory Programming
CS61BL. Lecture 5: Graphs Sorting
 CS61BL Lecture 5: Graphs Sorting Graphs Graphs Edge Vertex Graphs (Undirected) Graphs (Directed) Graphs (Multigraph) Graphs (Acyclic) Graphs (Cyclic) Graphs (Connected) Graphs (Disconnected) Graphs (Unweighted)
CS61BL Lecture 5: Graphs Sorting Graphs Graphs Edge Vertex Graphs (Undirected) Graphs (Directed) Graphs (Multigraph) Graphs (Acyclic) Graphs (Cyclic) Graphs (Connected) Graphs (Disconnected) Graphs (Unweighted)
SORTING, SETS, AND SELECTION
 CHAPTER 11 SORTING, SETS, AND SELECTION ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM
CHAPTER 11 SORTING, SETS, AND SELECTION ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM
Basic Communication Operations (Chapter 4)
 Basic Communication Operations (Chapter 4) Vivek Sarkar Department of Computer Science Rice University vsarkar@cs.rice.edu COMP 422 Lecture 17 13 March 2008 Review of Midterm Exam Outline MPI Example Program:
Basic Communication Operations (Chapter 4) Vivek Sarkar Department of Computer Science Rice University vsarkar@cs.rice.edu COMP 422 Lecture 17 13 March 2008 Review of Midterm Exam Outline MPI Example Program:
O(n): printing a list of n items to the screen, looking at each item once.
 UNIT IV Sorting: O notation efficiency of sorting bubble sort quick sort selection sort heap sort insertion sort shell sort merge sort radix sort. O NOTATION BIG OH (O) NOTATION Big oh : the function f(n)=o(g(n))
UNIT IV Sorting: O notation efficiency of sorting bubble sort quick sort selection sort heap sort insertion sort shell sort merge sort radix sort. O NOTATION BIG OH (O) NOTATION Big oh : the function f(n)=o(g(n))
Sorting Algorithms. + Analysis of the Sorting Algorithms
 Sorting Algorithms + Analysis of the Sorting Algorithms Insertion Sort What if first k elements of array are already sorted? 4, 7, 12, 5, 19, 16 We can shift the tail of the sorted elements list down and
Sorting Algorithms + Analysis of the Sorting Algorithms Insertion Sort What if first k elements of array are already sorted? 4, 7, 12, 5, 19, 16 We can shift the tail of the sorted elements list down and
High Performance Computing Programming Paradigms and Scalability Part 6: Examples of Parallel Algorithms
 High Performance Computing Programming Paradigms and Scalability Part 6: Examples of Parallel Algorithms PD Dr. rer. nat. habil. Ralf-Peter Mundani Computation in Engineering (CiE) Scientific Computing
High Performance Computing Programming Paradigms and Scalability Part 6: Examples of Parallel Algorithms PD Dr. rer. nat. habil. Ralf-Peter Mundani Computation in Engineering (CiE) Scientific Computing
Lesson 1 4. Prefix Sum Definitions. Scans. Parallel Scans. A Naive Parallel Scans
 Lesson 1 4 Prefix Sum Definitions Prefix sum given an array...the prefix sum is the sum of all the elements in the array from the beginning to the position, including the value at the position. The sequential
Lesson 1 4 Prefix Sum Definitions Prefix sum given an array...the prefix sum is the sum of all the elements in the array from the beginning to the position, including the value at the position. The sequential
COMP 352 FALL Tutorial 10
 1 COMP 352 FALL 2016 Tutorial 10 SESSION OUTLINE Divide-and-Conquer Method Sort Algorithm Properties Quick Overview on Sorting Algorithms Merge Sort Quick Sort Bucket Sort Radix Sort Problem Solving 2
1 COMP 352 FALL 2016 Tutorial 10 SESSION OUTLINE Divide-and-Conquer Method Sort Algorithm Properties Quick Overview on Sorting Algorithms Merge Sort Quick Sort Bucket Sort Radix Sort Problem Solving 2
Network Algorithms. Distributed Sorting
 Network Algorithms Distributed Sorting Stefan Schmid @ T-Labs, 2 Sorting Distributed Sorting Graph with n nodes {v,,v n } and n values. Goal: node vi should store i-th smallest value. v 6 v 2 2 v 3 7 v
Network Algorithms Distributed Sorting Stefan Schmid @ T-Labs, 2 Sorting Distributed Sorting Graph with n nodes {v,,v n } and n values. Goal: node vi should store i-th smallest value. v 6 v 2 2 v 3 7 v
CSC Design and Analysis of Algorithms
 CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conquer Algorithm Design Technique Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide a problem instance into two
CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conquer Algorithm Design Technique Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide a problem instance into two
Data Partitioning. Figure 1-31: Communication Topologies. Regular Partitions
 Data In single-program multiple-data (SPMD) parallel programs, global data is partitioned, with a portion of the data assigned to each processing node. Issues relevant to choosing a partitioning strategy
Data In single-program multiple-data (SPMD) parallel programs, global data is partitioned, with a portion of the data assigned to each processing node. Issues relevant to choosing a partitioning strategy
CSC Design and Analysis of Algorithms. Lecture 6. Divide and Conquer Algorithm Design Technique. Divide-and-Conquer
 CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conquer Algorithm Design Technique Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide a problem instance into two
CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conquer Algorithm Design Technique Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide a problem instance into two
CPS222 Lecture: Parallel Algorithms Last Revised 4/20/2015. Objectives
 CPS222 Lecture: Parallel Algorithms Last Revised 4/20/2015 Objectives 1. To introduce fundamental concepts of parallel algorithms, including speedup and cost. 2. To introduce some simple parallel algorithms.
CPS222 Lecture: Parallel Algorithms Last Revised 4/20/2015 Objectives 1. To introduce fundamental concepts of parallel algorithms, including speedup and cost. 2. To introduce some simple parallel algorithms.
Lecture 16: Sorting. CS178: Programming Parallel and Distributed Systems. April 2, 2001 Steven P. Reiss
 Lecture 16: Sorting CS178: Programming Parallel and Distributed Systems April 2, 2001 Steven P. Reiss I. Overview A. Before break we started talking about parallel computing and MPI 1. Basic idea of a
Lecture 16: Sorting CS178: Programming Parallel and Distributed Systems April 2, 2001 Steven P. Reiss I. Overview A. Before break we started talking about parallel computing and MPI 1. Basic idea of a
I/O Model. Cache-Oblivious Algorithms : Algorithms in the Real World. Advantages of Cache-Oblivious Algorithms 4/9/13
 I/O Model 15-853: Algorithms in the Real World Locality II: Cache-oblivious algorithms Matrix multiplication Distribution sort Static searching Abstracts a single level of the memory hierarchy Fast memory
I/O Model 15-853: Algorithms in the Real World Locality II: Cache-oblivious algorithms Matrix multiplication Distribution sort Static searching Abstracts a single level of the memory hierarchy Fast memory
08 A: Sorting III. CS1102S: Data Structures and Algorithms. Martin Henz. March 10, Generated on Tuesday 9 th March, 2010, 09:58
 08 A: Sorting III CS1102S: Data Structures and Algorithms Martin Henz March 10, 2010 Generated on Tuesday 9 th March, 2010, 09:58 CS1102S: Data Structures and Algorithms 08 A: Sorting III 1 1 Recap: Sorting
08 A: Sorting III CS1102S: Data Structures and Algorithms Martin Henz March 10, 2010 Generated on Tuesday 9 th March, 2010, 09:58 CS1102S: Data Structures and Algorithms 08 A: Sorting III 1 1 Recap: Sorting
Quick-Sort fi fi fi 7 9. Quick-Sort Goodrich, Tamassia
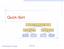 Quick-Sort 7 4 9 6 2 fi 2 4 6 7 9 4 2 fi 2 4 7 9 fi 7 9 2 fi 2 9 fi 9 Quick-Sort 1 Quick-Sort ( 10.2 text book) Quick-sort is a randomized sorting algorithm based on the divide-and-conquer paradigm: x
Quick-Sort 7 4 9 6 2 fi 2 4 6 7 9 4 2 fi 2 4 7 9 fi 7 9 2 fi 2 9 fi 9 Quick-Sort 1 Quick-Sort ( 10.2 text book) Quick-sort is a randomized sorting algorithm based on the divide-and-conquer paradigm: x
Sorting Pearson Education, Inc. All rights reserved.
 1 19 Sorting 2 19.1 Introduction (Cont.) Sorting data Place data in order Typically ascending or descending Based on one or more sort keys Algorithms Insertion sort Selection sort Merge sort More efficient,
1 19 Sorting 2 19.1 Introduction (Cont.) Sorting data Place data in order Typically ascending or descending Based on one or more sort keys Algorithms Insertion sort Selection sort Merge sort More efficient,
Lecture 19 Sorting Goodrich, Tamassia
 Lecture 19 Sorting 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 2004 Goodrich, Tamassia Outline Review 3 simple sorting algorithms: 1. selection Sort (in previous course) 2. insertion Sort (in previous
Lecture 19 Sorting 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 2004 Goodrich, Tamassia Outline Review 3 simple sorting algorithms: 1. selection Sort (in previous course) 2. insertion Sort (in previous
Quick-Sort. Quick-Sort 1
 Quick-Sort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 Quick-Sort 1 Outline and Reading Quick-sort ( 4.3) Algorithm Partition step Quick-sort tree Execution example Analysis of quick-sort (4.3.1) In-place
Quick-Sort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 Quick-Sort 1 Outline and Reading Quick-sort ( 4.3) Algorithm Partition step Quick-sort tree Execution example Analysis of quick-sort (4.3.1) In-place
Sorting. Data structures and Algorithms
 Sorting Data structures and Algorithms Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++ Goodrich, Tamassia and Mount (Wiley, 2004) Outline Bubble
Sorting Data structures and Algorithms Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++ Goodrich, Tamassia and Mount (Wiley, 2004) Outline Bubble
The Limits of Sorting Divide-and-Conquer Comparison Sorts II
 The Limits of Sorting Divide-and-Conquer Comparison Sorts II CS 311 Data Structures and Algorithms Lecture Slides Monday, October 12, 2009 Glenn G. Chappell Department of Computer Science University of
The Limits of Sorting Divide-and-Conquer Comparison Sorts II CS 311 Data Structures and Algorithms Lecture Slides Monday, October 12, 2009 Glenn G. Chappell Department of Computer Science University of
Parallel Graph Algorithms
 Parallel Graph Algorithms Design and Analysis of Parallel Algorithms 5DV050/VT3 Part I Introduction Overview Graphs definitions & representations Minimal Spanning Tree (MST) Prim s algorithm Single Source
Parallel Graph Algorithms Design and Analysis of Parallel Algorithms 5DV050/VT3 Part I Introduction Overview Graphs definitions & representations Minimal Spanning Tree (MST) Prim s algorithm Single Source
With regards to bitonic sorts, everything boils down to doing bitonic sorts efficiently.
 Lesson 2 5 Distributed Memory Sorting Bitonic Sort The pseudo code for generating a bitonic sequence: 1. create two bitonic subsequences 2. Make one an increasing sequence 3. Make one into a decreasing
Lesson 2 5 Distributed Memory Sorting Bitonic Sort The pseudo code for generating a bitonic sequence: 1. create two bitonic subsequences 2. Make one an increasing sequence 3. Make one into a decreasing
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 6 - Jan. 15, 2018 CLRS 7.1, 7-4, 9.1, 9.3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures 1 / 12 Quick-sort
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 6 - Jan. 15, 2018 CLRS 7.1, 7-4, 9.1, 9.3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures 1 / 12 Quick-sort
Fundamentals of. Parallel Computing. Sanjay Razdan. Alpha Science International Ltd. Oxford, U.K.
 Fundamentals of Parallel Computing Sanjay Razdan Alpha Science International Ltd. Oxford, U.K. CONTENTS Preface Acknowledgements vii ix 1. Introduction to Parallel Computing 1.1-1.37 1.1 Parallel Computing
Fundamentals of Parallel Computing Sanjay Razdan Alpha Science International Ltd. Oxford, U.K. CONTENTS Preface Acknowledgements vii ix 1. Introduction to Parallel Computing 1.1-1.37 1.1 Parallel Computing
17/05/2018. Outline. Outline. Divide and Conquer. Control Abstraction for Divide &Conquer. Outline. Module 2: Divide and Conquer
 Module 2: Divide and Conquer Divide and Conquer Control Abstraction for Divide &Conquer 1 Recurrence equation for Divide and Conquer: If the size of problem p is n and the sizes of the k sub problems are
Module 2: Divide and Conquer Divide and Conquer Control Abstraction for Divide &Conquer 1 Recurrence equation for Divide and Conquer: If the size of problem p is n and the sizes of the k sub problems are
Lecture 9: Group Communication Operations. Shantanu Dutt ECE Dept. UIC
 Lecture 9: Group Communication Operations Shantanu Dutt ECE Dept. UIC Acknowledgement Adapted from Chapter 4 slides of the text, by A. Grama w/ a few changes, augmentations and corrections Topic Overview
Lecture 9: Group Communication Operations Shantanu Dutt ECE Dept. UIC Acknowledgement Adapted from Chapter 4 slides of the text, by A. Grama w/ a few changes, augmentations and corrections Topic Overview
UNIT-2. Problem of size n. Sub-problem 1 size n/2. Sub-problem 2 size n/2. Solution to the original problem
 Divide-and-conquer method: Divide-and-conquer is probably the best known general algorithm design technique. The principle behind the Divide-and-conquer algorithm design technique is that it is easier
Divide-and-conquer method: Divide-and-conquer is probably the best known general algorithm design technique. The principle behind the Divide-and-conquer algorithm design technique is that it is easier
1 (15 points) LexicoSort
 CS161 Homework 2 Due: 22 April 2016, 12 noon Submit on Gradescope Handed out: 15 April 2016 Instructions: Please answer the following questions to the best of your ability. If you are asked to show your
CS161 Homework 2 Due: 22 April 2016, 12 noon Submit on Gradescope Handed out: 15 April 2016 Instructions: Please answer the following questions to the best of your ability. If you are asked to show your
Problem. Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all. 1 i j n.
![Problem. Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all. 1 i j n. Problem. Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all. 1 i j n.](/thumbs/84/89326706.jpg) Problem 5. Sorting Simple Sorting, Quicksort, Mergesort Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all 1 i j n. 98 99 Selection Sort
Problem 5. Sorting Simple Sorting, Quicksort, Mergesort Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all 1 i j n. 98 99 Selection Sort
Lecture 8: Mergesort / Quicksort Steven Skiena
 Lecture 8: Mergesort / Quicksort Steven Skiena Department of Computer Science State University of New York Stony Brook, NY 11794 4400 http://www.cs.stonybrook.edu/ skiena Problem of the Day Give an efficient
Lecture 8: Mergesort / Quicksort Steven Skiena Department of Computer Science State University of New York Stony Brook, NY 11794 4400 http://www.cs.stonybrook.edu/ skiena Problem of the Day Give an efficient
Parallel Convex Hull using MPI. CSE633 Fall 2012 Alex Vertlieb
 Parallel Convex Hull using MPI CSE633 Fall 2012 Alex Vertlieb What is a Convex Polygon? Convex Not Convex If you can draw a straight line from one point in the polygon to another and have the line exit
Parallel Convex Hull using MPI CSE633 Fall 2012 Alex Vertlieb What is a Convex Polygon? Convex Not Convex If you can draw a straight line from one point in the polygon to another and have the line exit
Merge Sort
 Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 Divide-and-Conuer Divide-and conuer is a general algorithm design paradigm: n Divide: divide the input data S in two disjoint subsets S 1 and
Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 Divide-and-Conuer Divide-and conuer is a general algorithm design paradigm: n Divide: divide the input data S in two disjoint subsets S 1 and
arxiv: v1 [cs.dc] 24 Feb 2010
![arxiv: v1 [cs.dc] 24 Feb 2010 arxiv: v1 [cs.dc] 24 Feb 2010](/thumbs/95/126041962.jpg) Deterministic Sample Sort For GPUs arxiv:1002.4464v1 [cs.dc] 24 Feb 2010 Frank Dehne School of Computer Science Carleton University Ottawa, Canada K1S 5B6 frank@dehne.net http://www.dehne.net February
Deterministic Sample Sort For GPUs arxiv:1002.4464v1 [cs.dc] 24 Feb 2010 Frank Dehne School of Computer Science Carleton University Ottawa, Canada K1S 5B6 frank@dehne.net http://www.dehne.net February
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Quick-Sort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 2015 Goodrich and Tamassia
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Quick-Sort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 2015 Goodrich and Tamassia
Module 3: Sorting and Randomized Algorithms. Selection vs. Sorting. Crucial Subroutines. CS Data Structures and Data Management
 Module 3: Sorting and Randomized Algorithms CS 240 - Data Structures and Data Management Sajed Haque Veronika Irvine Taylor Smith Based on lecture notes by many previous cs240 instructors David R. Cheriton
Module 3: Sorting and Randomized Algorithms CS 240 - Data Structures and Data Management Sajed Haque Veronika Irvine Taylor Smith Based on lecture notes by many previous cs240 instructors David R. Cheriton
Examination Questions Midterm 2
 CS1102s Data Structures and Algorithms 12/3/2010 Examination Questions Midterm 2 This examination question booklet has 6 pages, including this cover page, and contains 12 questions. You have 30 minutes
CS1102s Data Structures and Algorithms 12/3/2010 Examination Questions Midterm 2 This examination question booklet has 6 pages, including this cover page, and contains 12 questions. You have 30 minutes
Unit-2 Divide and conquer 2016
 2 Divide and conquer Overview, Structure of divide-and-conquer algorithms, binary search, quick sort, Strassen multiplication. 13% 05 Divide-and- conquer The Divide and Conquer Paradigm, is a method of
2 Divide and conquer Overview, Structure of divide-and-conquer algorithms, binary search, quick sort, Strassen multiplication. 13% 05 Divide-and- conquer The Divide and Conquer Paradigm, is a method of
Module 3: Sorting and Randomized Algorithms
 Module 3: Sorting and Randomized Algorithms CS 240 - Data Structures and Data Management Sajed Haque Veronika Irvine Taylor Smith Based on lecture notes by many previous cs240 instructors David R. Cheriton
Module 3: Sorting and Randomized Algorithms CS 240 - Data Structures and Data Management Sajed Haque Veronika Irvine Taylor Smith Based on lecture notes by many previous cs240 instructors David R. Cheriton
CS125 : Introduction to Computer Science. Lecture Notes #40 Advanced Sorting Analysis. c 2005, 2004 Jason Zych
 CS125 : Introduction to Computer Science Lecture Notes #40 Advanced Sorting Analysis c 2005, 2004 Jason Zych 1 Lecture 40 : Advanced Sorting Analysis Mergesort can be described in this manner: Analyzing
CS125 : Introduction to Computer Science Lecture Notes #40 Advanced Sorting Analysis c 2005, 2004 Jason Zych 1 Lecture 40 : Advanced Sorting Analysis Mergesort can be described in this manner: Analyzing
QuickSort
 QuickSort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 1 QuickSort QuickSort on an input sequence S with n elements consists of three steps: n n n Divide: partition S into two sequences S 1 and S 2 of about
QuickSort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 1 QuickSort QuickSort on an input sequence S with n elements consists of three steps: n n n Divide: partition S into two sequences S 1 and S 2 of about
Parallel Algorithms for (PRAM) Computers & Some Parallel Algorithms. Reference : Horowitz, Sahni and Rajasekaran, Computer Algorithms
 Parallel Algorithms for (PRAM) Computers & Some Parallel Algorithms Reference : Horowitz, Sahni and Rajasekaran, Computer Algorithms Part 2 1 3 Maximum Selection Problem : Given n numbers, x 1, x 2,, x
Parallel Algorithms for (PRAM) Computers & Some Parallel Algorithms Reference : Horowitz, Sahni and Rajasekaran, Computer Algorithms Part 2 1 3 Maximum Selection Problem : Given n numbers, x 1, x 2,, x
CSE Introduction to Parallel Processing. Chapter 5. PRAM and Basic Algorithms
 Dr Izadi CSE-40533 Introduction to Parallel Processing Chapter 5 PRAM and Basic Algorithms Define PRAM and its various submodels Show PRAM to be a natural extension of the sequential computer (RAM) Develop
Dr Izadi CSE-40533 Introduction to Parallel Processing Chapter 5 PRAM and Basic Algorithms Define PRAM and its various submodels Show PRAM to be a natural extension of the sequential computer (RAM) Develop
Dr. Amotz Bar-Noy s Compendium of Algorithms Problems. Problems, Hints, and Solutions
 Dr. Amotz Bar-Noy s Compendium of Algorithms Problems Problems, Hints, and Solutions Chapter 1 Searching and Sorting Problems 1 1.1 Array with One Missing 1.1.1 Problem Let A = A[1],..., A[n] be an array
Dr. Amotz Bar-Noy s Compendium of Algorithms Problems Problems, Hints, and Solutions Chapter 1 Searching and Sorting Problems 1 1.1 Array with One Missing 1.1.1 Problem Let A = A[1],..., A[n] be an array
CS256 Applied Theory of Computation
 CS256 Applied Theory of Computation Parallel Computation II John E Savage Overview Mesh-based architectures Hypercubes Embedding meshes in hypercubes Normal algorithms on hypercubes Summing and broadcasting
CS256 Applied Theory of Computation Parallel Computation II John E Savage Overview Mesh-based architectures Hypercubes Embedding meshes in hypercubes Normal algorithms on hypercubes Summing and broadcasting
Partitioning. Partition the problem into parts such that each part can be solved separately. 1/22
 Partitioning Partition the problem into parts such that each part can be solved separately. 1/22 Partitioning Partition the problem into parts such that each part can be solved separately. At the end the
Partitioning Partition the problem into parts such that each part can be solved separately. 1/22 Partitioning Partition the problem into parts such that each part can be solved separately. At the end the
Elementary maths for GMT. Algorithm analysis Part II
 Elementary maths for GMT Algorithm analysis Part II Algorithms, Big-Oh and Big-Omega An algorithm has a O( ) and Ω( ) running time By default, we mean the worst case running time A worst case O running
Elementary maths for GMT Algorithm analysis Part II Algorithms, Big-Oh and Big-Omega An algorithm has a O( ) and Ω( ) running time By default, we mean the worst case running time A worst case O running
Parallel quicksort algorithms with isoefficiency analysis. Parallel quicksort algorithmswith isoefficiency analysis p. 1
 Parallel quicksort algorithms with isoefficiency analysis Parallel quicksort algorithmswith isoefficiency analysis p. 1 Overview Sequential quicksort algorithm Three parallel quicksort algorithms Isoefficiency
Parallel quicksort algorithms with isoefficiency analysis Parallel quicksort algorithmswith isoefficiency analysis p. 1 Overview Sequential quicksort algorithm Three parallel quicksort algorithms Isoefficiency
CSC Design and Analysis of Algorithms. Lecture 6. Divide and Conquer Algorithm Design Technique. Divide-and-Conquer
 CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conuer Algorithm Design Techniue Divide-and-Conuer The most-well known algorithm design strategy: 1. Divide a problem instance into two
CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conuer Algorithm Design Techniue Divide-and-Conuer The most-well known algorithm design strategy: 1. Divide a problem instance into two
II (Sorting and) Order Statistics
 II (Sorting and) Order Statistics Heapsort Quicksort Sorting in Linear Time Medians and Order Statistics 8 Sorting in Linear Time The sorting algorithms introduced thus far are comparison sorts Any comparison
II (Sorting and) Order Statistics Heapsort Quicksort Sorting in Linear Time Medians and Order Statistics 8 Sorting in Linear Time The sorting algorithms introduced thus far are comparison sorts Any comparison
Data Structures and Algorithms
 Data Structures and Algorithms Session 24. Earth Day, 2009 Instructor: Bert Huang http://www.cs.columbia.edu/~bert/courses/3137 Announcements Homework 6 due before last class: May 4th Final Review May
Data Structures and Algorithms Session 24. Earth Day, 2009 Instructor: Bert Huang http://www.cs.columbia.edu/~bert/courses/3137 Announcements Homework 6 due before last class: May 4th Final Review May
Parallel Computing: Parallel Algorithm Design Examples Jin, Hai
 Parallel Computing: Parallel Algorithm Design Examples Jin, Hai School of Computer Science and Technology Huazhong University of Science and Technology ! Given associative operator!! a 0! a 1! a 2!! a
Parallel Computing: Parallel Algorithm Design Examples Jin, Hai School of Computer Science and Technology Huazhong University of Science and Technology ! Given associative operator!! a 0! a 1! a 2!! a
Parallel Processing IMP Questions
 Winter 14 Summer 14 Winter 13 Summer 13 180702 Parallel Processing IMP Questions Sr Chapter Questions Total 1 3 2 9 3 10 4 9 5 7 What is Data Decomposition? Explain Data Decomposition with proper example.
Winter 14 Summer 14 Winter 13 Summer 13 180702 Parallel Processing IMP Questions Sr Chapter Questions Total 1 3 2 9 3 10 4 9 5 7 What is Data Decomposition? Explain Data Decomposition with proper example.
Introduction to Parallel & Distributed Computing Parallel Graph Algorithms
 Introduction to Parallel & Distributed Computing Parallel Graph Algorithms Lecture 16, Spring 2014 Instructor: 罗国杰 gluo@pku.edu.cn In This Lecture Parallel formulations of some important and fundamental
Introduction to Parallel & Distributed Computing Parallel Graph Algorithms Lecture 16, Spring 2014 Instructor: 罗国杰 gluo@pku.edu.cn In This Lecture Parallel formulations of some important and fundamental
CSE 373: Data Structures and Algorithms
 CSE 373: Data Structures and Algorithms Lecture 19: Comparison Sorting Algorithms Instructor: Lilian de Greef Quarter: Summer 2017 Today Intro to sorting Comparison sorting Insertion Sort Selection Sort
CSE 373: Data Structures and Algorithms Lecture 19: Comparison Sorting Algorithms Instructor: Lilian de Greef Quarter: Summer 2017 Today Intro to sorting Comparison sorting Insertion Sort Selection Sort
Chapter 4. Divide-and-Conquer. Copyright 2007 Pearson Addison-Wesley. All rights reserved.
 Chapter 4 Divide-and-Conquer Copyright 2007 Pearson Addison-Wesley. All rights reserved. Divide-and-Conquer The most-well known algorithm design strategy: 2. Divide instance of problem into two or more
Chapter 4 Divide-and-Conquer Copyright 2007 Pearson Addison-Wesley. All rights reserved. Divide-and-Conquer The most-well known algorithm design strategy: 2. Divide instance of problem into two or more
Divide-and-Conquer. Dr. Yingwu Zhu
 Divide-and-Conquer Dr. Yingwu Zhu Divide-and-Conquer The most-well known algorithm design technique: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances independently
Divide-and-Conquer Dr. Yingwu Zhu Divide-and-Conquer The most-well known algorithm design technique: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances independently
Sorting. Sorting in Arrays. SelectionSort. SelectionSort. Binary search works great, but how do we create a sorted array in the first place?
 Sorting Binary search works great, but how do we create a sorted array in the first place? Sorting in Arrays Sorting algorithms: Selection sort: O(n 2 ) time Merge sort: O(nlog 2 (n)) time Quicksort: O(n
Sorting Binary search works great, but how do we create a sorted array in the first place? Sorting in Arrays Sorting algorithms: Selection sort: O(n 2 ) time Merge sort: O(nlog 2 (n)) time Quicksort: O(n
Chapter 7 Sorting. Terminology. Selection Sort
 Chapter 7 Sorting Terminology Internal done totally in main memory. External uses auxiliary storage (disk). Stable retains original order if keys are the same. Oblivious performs the same amount of work
Chapter 7 Sorting Terminology Internal done totally in main memory. External uses auxiliary storage (disk). Stable retains original order if keys are the same. Oblivious performs the same amount of work
Module 3: Sorting and Randomized Algorithms
 Module 3: Sorting and Randomized Algorithms CS 240 - Data Structures and Data Management Reza Dorrigiv, Daniel Roche School of Computer Science, University of Waterloo Winter 2010 Reza Dorrigiv, Daniel
Module 3: Sorting and Randomized Algorithms CS 240 - Data Structures and Data Management Reza Dorrigiv, Daniel Roche School of Computer Science, University of Waterloo Winter 2010 Reza Dorrigiv, Daniel
Basic Communication Ops
 CS 575 Parallel Processing Lecture 5: Ch 4 (GGKK) Sanjay Rajopadhye Colorado State University Basic Communication Ops n PRAM, final thoughts n Quiz 3 n Collective Communication n Broadcast & Reduction
CS 575 Parallel Processing Lecture 5: Ch 4 (GGKK) Sanjay Rajopadhye Colorado State University Basic Communication Ops n PRAM, final thoughts n Quiz 3 n Collective Communication n Broadcast & Reduction
School of Computer and Information Science
 School of Computer and Information Science CIS Research Placement Report Multiple threads in floating-point sort operations Name: Quang Do Date: 8/6/2012 Supervisor: Grant Wigley Abstract Despite the vast
School of Computer and Information Science CIS Research Placement Report Multiple threads in floating-point sort operations Name: Quang Do Date: 8/6/2012 Supervisor: Grant Wigley Abstract Despite the vast
Introduction to Parallel Computing Errata
 Introduction to Parallel Computing Errata John C. Kirk 27 November, 2004 Overview Book: Introduction to Parallel Computing, Second Edition, first printing (hardback) ISBN: 0-201-64865-2 Official book website:
Introduction to Parallel Computing Errata John C. Kirk 27 November, 2004 Overview Book: Introduction to Parallel Computing, Second Edition, first printing (hardback) ISBN: 0-201-64865-2 Official book website:
COMMUNICATION IN HYPERCUBES
 PARALLEL AND DISTRIBUTED ALGORITHMS BY DEBDEEP MUKHOPADHYAY AND ABHISHEK SOMANI http://cse.iitkgp.ac.in/~debdeep/courses_iitkgp/palgo/index.htm COMMUNICATION IN HYPERCUBES 2 1 OVERVIEW Parallel Sum (Reduction)
PARALLEL AND DISTRIBUTED ALGORITHMS BY DEBDEEP MUKHOPADHYAY AND ABHISHEK SOMANI http://cse.iitkgp.ac.in/~debdeep/courses_iitkgp/palgo/index.htm COMMUNICATION IN HYPERCUBES 2 1 OVERVIEW Parallel Sum (Reduction)
Sorting Shabsi Walfish NYU - Fundamental Algorithms Summer 2006
 Sorting The Sorting Problem Input is a sequence of n items (a 1, a 2,, a n ) The mapping we want is determined by a comparison operation, denoted by Output is a sequence (b 1, b 2,, b n ) such that: {
Sorting The Sorting Problem Input is a sequence of n items (a 1, a 2,, a n ) The mapping we want is determined by a comparison operation, denoted by Output is a sequence (b 1, b 2,, b n ) such that: {
Parallel Graph Algorithms
 Parallel Graph Algorithms Design and Analysis of Parallel Algorithms 5DV050 Spring 202 Part I Introduction Overview Graphsdenitions, properties, representation Minimal spanning tree Prim's algorithm Shortest
Parallel Graph Algorithms Design and Analysis of Parallel Algorithms 5DV050 Spring 202 Part I Introduction Overview Graphsdenitions, properties, representation Minimal spanning tree Prim's algorithm Shortest
Complexity and Advanced Algorithms Monsoon Parallel Algorithms Lecture 2
 Complexity and Advanced Algorithms Monsoon 2011 Parallel Algorithms Lecture 2 Trivia ISRO has a new supercomputer rated at 220 Tflops Can be extended to Pflops. Consumes only 150 KW of power. LINPACK is
Complexity and Advanced Algorithms Monsoon 2011 Parallel Algorithms Lecture 2 Trivia ISRO has a new supercomputer rated at 220 Tflops Can be extended to Pflops. Consumes only 150 KW of power. LINPACK is
Student Number: CSE191 Midterm II Spring Plagiarism will earn you an F in the course and a recommendation of expulsion from the university.
 Plagiarism will earn you an F in the course and a recommendation of expulsion from the university. (1 pt each) For Questions 1-5, when asked for a running time or the result of a summation, you must choose
Plagiarism will earn you an F in the course and a recommendation of expulsion from the university. (1 pt each) For Questions 1-5, when asked for a running time or the result of a summation, you must choose
CS 137 Part 8. Merge Sort, Quick Sort, Binary Search. November 20th, 2017
 CS 137 Part 8 Merge Sort, Quick Sort, Binary Search November 20th, 2017 This Week We re going to see two more complicated sorting algorithms that will be our first introduction to O(n log n) sorting algorithms.
CS 137 Part 8 Merge Sort, Quick Sort, Binary Search November 20th, 2017 This Week We re going to see two more complicated sorting algorithms that will be our first introduction to O(n log n) sorting algorithms.
