Hermite Splines in Lie Groups as Products of Geodesics
|
|
|
- Dulcie Ray
- 5 years ago
- Views:
Transcription
1 Hermte Splnes n Le Groups as Products of Geodescs Ethan Eade Updated May 28, Introducton 1.1 Goal Ths document defnes a curve n the Le group G parametrzed by tme and by structural parameters n the assocated Le algebra g, and shows how to compute ts dfferentals by all parameters. The curve s expressed prmarly n the form S n : R g n G (1) S n (t) exp (a n p n ) exp (a n 1 p n 1 )... exp (a 1 p 1 ) (2) Havng establshed notaton and some useful denttes, we show how to compute dfferentals of the product of exponentals, and then descrbe how to acheve boundary condtons on the curve s values and dervatves by choosng a and p approprately. The result s a form sutable for expressng an ndvdual segment of a Hermte splne n the group, complete wth all the structural dfferentals useful for fttng the splne to data. Channg such segments wth shared boundary condtons on neghbors yelds a C 2 trajectory n the group, permttng parametrc regresson aganst observatons nvolvng the value, frst, and second tme dervatves of the trajectory. The formulaton s vald for any Le group, but as a motvatng example, consder usng such a splne to model a rgd body trajectory n SE (3), and adjustng the splne parameters to maxmze the lkelhood of nosy observatons from a gyroscope and accelerometer on the body. 1.2 Notaton Elements of the Le group G are denoted wth upper-case letters, whle elements of the assocated Le algebra g are denoted wth lower-case letters. The dentty matrx s wrtten I. The adjont representaton n the group s wrtten Ad [], whle the adjont representaton n the algebra s wrtten ad []. The exponental map s wrtten exp. It maps elements of g to G, and elements of ad [g] to Ad [G]. Its nverse s the logarthm log. Corrected left-hand-sdes of equatons from S to S. 1
2 2 Identtes Ths secton enumerates denttes useful n the rest of the document, and can be skpped f the reader s famlar wth representatons of Le groups and ther propertes. Throughout ths secton, let x, y g and X, Y G. 2.1 Basc propertes of Ad [],ad [], and exp () The adjont operator n g s ant-commutatve: The exponental map and the adjont representaton commute: ad [x] y ad [y] x (3) The adjont transforms rght tangent vectors to left tangent vectors: exp (ad [x]) Ad [exp (x)] (4) The adjont s a group homomorphsm: X exp (y) exp (Ad [X] y) X (5) Ad [X Y] Ad [X] Ad [Y] (6) 2.2 Ad [X] ad [y] ad [Ad [X] y] Ad [X] Usng the above, we can show that the adjont n the group can transform the adjont n the algebra from rght to left as well. Consder t R. Frst send all factors to the adjont representaton: X exp (t y) exp (Ad [X] t y) X (7) Ad [X] Ad [exp (t y)] Ad [exp (Ad [X] t y)] Ad [X] (8) Next re-order the applcaton of the exponental map and the adjont operator: Ad [X] exp (ad [t y]) exp (ad [Ad [X] t y]) Ad [X] (9) Then use the lnearty of the adjont operator n the algebra: Fnally, dfferentate by t at t 0: Ad [X] exp (t ad [y]) exp (t ad [Ad [X] y]) Ad [X] (10) Ad [X] ad [y] ad [Ad [X] y] Ad [X] (11) 2
3 2.3 Dfferentals n G and the adjont We defne dfferentals n the group n terms of left updates, so that the dfferental s a lnear mappng from the parameter(s) of nterest α to the algebra g: X (α) α ( log (X (α + δ) X (α) 1)) Dfferentals by left updates are then smple. Consder a lnear operator on the algebra,l: Ths makes dfferentals of products straghtforward: δ0 (12) (exp (L ɛ) X) ɛ ɛ0 L (13) (X Y) Y (X Y) X Ad [X] (14) I (15) We can also dfferentate transformatons of algebra vectors by the adjont: (Ad [exp (δ) X] y) (Ad [exp (δ)] Ad [X] y) δ0 (16) (exp (ad [δ]) Ad [X] y) (17) (ad [δ] Ad [X] y) (18) ad [Ad [X] y] δ (19) ad [Ad [X] y] (20) 3 S (t) and ts Tme Dervatves 3.1 Functon of tme We defne the product recursvely: a : R R (21) p g (22) S : R g G (23) S (t) exp (a (t) p ) S 1 (t) (24) S 1 (t) exp (a 1 (t) p 1 ) (25) S n (t) s then evaluated by left-multplyng each exponental term from 1 to n. 3
4 3.2 Frst dervatve by tme Consder the exponental factor A (t) exp (a (t) p ): A (t + ɛ) exp ((a (t) + ɛ a (ɛ (t) + O 2)) ) p (26) exp ((ɛ a (ɛ (t) + O 2)) ) p exp (a (t) p ) (27) exp ((ɛ a (ɛ (t) + O 2)) ) p A (t) (28) A (t) A (t + ɛ) ɛ0 (29) ɛ a (t) p (30) The frst tme dervatve S n (t) of S n (t) s then straghtforward to express recursvely usng the product and chan rules: S (t) A (t) S 1 (t) (31) S (t) A (t) S 1 (t) + Ad [A (t)] S 1 (t) (32) a (t) p + Ad [A (t)] S 1 (t) (33) 3.3 Second dervatve by tme The second dervatve s the partal dervatve by t of Eq.33: S (t) S (t) t a (t) p + Ad [A (t)] S 1 (t) ad [ Ad [A (t)] S 1 (t) ] A (34) (t) (35) a (t) p + Ad [A (t)] S 1 (t) + ad [ A (t)] Ad [A (t)] S 1 (t) (36) 4 Structural Dfferentals for Regresson In order to perform regresson of the model aganst observatons, we ll need dfferentals of S, S, and S by the parameters {p }. To ths end, we ll requre the dfferental of the exponental map, descrbed n detal n another document ( Dfferental of the Exponental Map ): D exp [x] exp (x) x log (exp (x + δ) exp ( x)) (37) For many Le groups of nterest, D exp [x] can be computed n closed form. For convenence, we label the dfferental of the exponental factor A of S by ts argument: The tme parameter t s omtted n most of the equatons below to avod clutter. D D exp [a (t) p ] (38) 4
5 4.1 Structural dfferentals of S (t) Eq.24 s dfferentated usng the chan rule and Eq.14: S A p p (39) D exp [a p ] a (40) D a (41) S p j { Ad [A ] S 1 p j j < 0 j > (42) 4.2 Structural dfferentals of S (t) Eq.33 s dfferentated usng the product rule and Eq.20: S ( A ) ad [ Ad [A p p ] S 1] A p a I ad [ Ad [A ] S 1] A p S S 1 Ad [A ] p j < j p j 0 j > 4.3 Structural dfferentals of S (t) Eq.36 s dfferentated usng the product rule and Eq.20: S p a I ad [ Ad [A ] S 1] S p j a I ( ad [ Ad [A ] S A ad [ A [ p ] ad Ad [A ] S 1] A p ( [ ] [ 1] + ad A ad Ad [A ] S 1]) A p S 1 Ad [A ] p + ad [ A S j ] Ad [A 1 ] p j j < 0 j > a ad [ Ad [A ] S 1 ] (43) ) a ad [ Ad [A ] S 1 ] (44) (45) 4.4 Effcent computaton of structural dfferentals Drectly applyng the recursve defntons above requres O ( n 2) tme to compute structural dfferentals S n, S n, and S n. By reorderng the recurson from left to rght and accumulatng products and sums, these dfferentals can all be computed n O (n) tme: 5
6 Note that Eq. 50 makes use of the dentty gven n Eq.11. L n I (46) l n 0 (47) S n S Ad [L p ] (48) p S n ( S ) Ad [L p ] (49) p S n ( S ) ( S ) Ad [L p ] + ad [l p ] n (50) p L 1 L A (51) l 1 l + Ad [L ] A (52) 5 Constructng a Splne Segment wth Boundary Condtons By choosng a and p approprately, we can construct a C curve segment B (t) wth specfed boundary values and dervatves (sometmes called a Hermte splne). Such segments can then be concatenated to form a C 2 splne n the group by matchng the boundary condtons (value, frst, and second tme dervatves) between neghborng segments. The tme nterval n each segment s, wthout loss of generalty, assumed to be the unt nterval [0, 1]. Any other nterval can be remapped to ths by an affne transformaton (as can the dfferentals). The desred boundary condtons of the segment are specfed as group elements for the functon values at the boundares, and algebra elements for the tme dervatves: B (0) B 0 G (53) B (1) B 1 G (54) B (0) d 0 g (55) B (1) d 1 g (56) B (0) h 0 g (57) B (1) h 1 g (58) 5.1 Segment defnton In order to have enough degrees of freedom to acheve the boundary condtons, the Hermte splne segment s defned as a product of sx terms, one of whch s constant over tme: B (t) S 5 (t) B 0 (59) We choose the {a } to be quntc polynomals wth values and dervatves at 0 and 1 that make satsfyng the boundary condtons of B (t) trval. 6
7 a 5 (t) 1 2 t5 t t3 (60) a 4 (t) 1 2 t t4 3 2 t t2 (61) a 3 (t) 3t 5 + 7t 4 4t 3 (62) a 2 (t) 3t 5 + 8t 4 6t 3 + t (63) a 1 (t) 6t 5 15t t 3 (64) or equvalently: a 1 (t) a 2 (t) a 3 (t) a 4 (t) a 5 (t) t t 2 t 3 t 4 t 5 (65) These polynomals are constructed to satsfy the followng boundary condtons: a 5 (0) a 4 (0) a 3 (0) a 2 (0) a 1 (0) 0 (66) a 5 (1) a 4 (1) a 3 (1) a 2 (1) 0 (67) a 1 (1) 1 (68) a 2 (0) 1 (69) a 5 (0) a 4 (0) a 3 (0) a 1 (0) 0 (70) a 5 (1) a 4 (1) a 2 (1) a 1 (1) 0 (71) a 3 (1) 1 (72) a 5 (0) a 3 (0) a 2 (0) a (0) 0 (73) a 4 (1) a 3 (1) a 1 a 4 (0) 1 (74) 2 (1) a 1 (1) 0 (75) a 5 (1) 1 (76) Thus each polynomal selects for the value, frst tme dervatve, or second tme dervatve at one of the boundares. The parameters of S 5 (t) are then straghtforward to assgn: p 5 h 1 (77) p 4 h 0 (78) p 3 d 1 (79) p 2 d 0 (80) p 1 log B 1 B0 1 (81) By Eq.66 all of the factors of S 5 (0) are the dentty, so we satsfy the frst boundary condton trvally: B (0) B 0 (82) 7
8 By Eq.67 and 68 the second boundary condton s satsfed: Smlar nspecton of S 5 are satsfed. B (1) S 5 (1) B 0 (83) B 1 B0 1 B 0 (84) B 1 (85) (t) and S 5 (t) shows that all four of the boundary condtons on the dervatves {d 0, d 1, h 0, h 1 } 5.2 Tme dervatves of B (t) Because the B 0 factor s constant over tme, the tme dervatves of B (t) are taken drectly from those of S 5 (t), descrbed n detal above: B (t) S 5 (t) (86) B (t) S 5 (t) (87) 5.3 Structural dfferentals of B (t) The dfferentals of B (t) by the boundary parameters {B 0, B 1, d 0, d 1, h 0, h 1 } follow from the dfferentals of S 5 (t) by p, along wth the chan rule. Frst we make explct the parametrc perturbatons of B 0 and B 1 : B 0 exp (ɛ 0 ) B 0 (88) B 1 exp (ɛ 1 ) B 1 (89) p 1 log B 1 B 0 1 (90) ( ) log exp (ɛ 1 ) B 1 B0 1 exp ( ɛ 0 ) (91) B (t) exp (a 5 (t) p 5 ) exp (a 4 (t) p 4 ) exp (a 3 (t) p 3 ) exp (a 2 (t) p 2 ) exp (a 1 (t) p 1 ) B 0 (92) Note that changes to the ntal value parameter B 0 (va ɛ 0 ) affect B(t) both drectly and through the resultng modfcaton of p 1, whle changes to B 1 (va ɛ 1 ) affect B(t) only through the modfcaton of p 1. To dfferentate p 1 by ts arguments, we employ the property that the dfferental of the nverse s the nverse of the dfferental (see document Dfferental of the Exponental Map ) : p 1 p 1 ɛ 0 ( D exp [p B 1 ɛ 1 ] ) 1 1 p 1 p 1 ɛ 0 ( D exp [p B 0 ɛ 1 ] ) [ ] 1 Ad B 1 B0 1 0 (93) (94) Fnally, the structural dfferentals of B (t) follow by the chan rule: 8
9 B (t) S5 (t) p1 + Ad [S 5 (t)] (95) C 0 p 1 B 0 B (t) S5 (t) p1 (96) C 1 p 1 B 1 B (t) S 5 (t) (97) d 0 p 2 B (t) S 5 (t) d 1 p 3 (98) B (t) S 5 (t) h 0 p 4 (99) B (t) S 5 (t) h 1 p 5 (100) 9
2x x l. Module 3: Element Properties Lecture 4: Lagrange and Serendipity Elements
 Module 3: Element Propertes Lecture : Lagrange and Serendpty Elements 5 In last lecture note, the nterpolaton functons are derved on the bass of assumed polynomal from Pascal s trangle for the fled varable.
Module 3: Element Propertes Lecture : Lagrange and Serendpty Elements 5 In last lecture note, the nterpolaton functons are derved on the bass of assumed polynomal from Pascal s trangle for the fled varable.
Analysis of Continuous Beams in General
 Analyss of Contnuous Beams n General Contnuous beams consdered here are prsmatc, rgdly connected to each beam segment and supported at varous ponts along the beam. onts are selected at ponts of support,
Analyss of Contnuous Beams n General Contnuous beams consdered here are prsmatc, rgdly connected to each beam segment and supported at varous ponts along the beam. onts are selected at ponts of support,
S1 Note. Basis functions.
 S1 Note. Bass functons. Contents Types of bass functons...1 The Fourer bass...2 B-splne bass...3 Power and type I error rates wth dfferent numbers of bass functons...4 Table S1. Smulaton results of type
S1 Note. Bass functons. Contents Types of bass functons...1 The Fourer bass...2 B-splne bass...3 Power and type I error rates wth dfferent numbers of bass functons...4 Table S1. Smulaton results of type
Math Homotopy Theory Additional notes
 Math 527 - Homotopy Theory Addtonal notes Martn Frankland February 4, 2013 The category Top s not Cartesan closed. problem. In these notes, we explan how to remedy that 1 Compactly generated spaces Ths
Math 527 - Homotopy Theory Addtonal notes Martn Frankland February 4, 2013 The category Top s not Cartesan closed. problem. In these notes, we explan how to remedy that 1 Compactly generated spaces Ths
NAG Fortran Library Chapter Introduction. G10 Smoothing in Statistics
 Introducton G10 NAG Fortran Lbrary Chapter Introducton G10 Smoothng n Statstcs Contents 1 Scope of the Chapter... 2 2 Background to the Problems... 2 2.1 Smoothng Methods... 2 2.2 Smoothng Splnes and Regresson
Introducton G10 NAG Fortran Lbrary Chapter Introducton G10 Smoothng n Statstcs Contents 1 Scope of the Chapter... 2 2 Background to the Problems... 2 2.1 Smoothng Methods... 2 2.2 Smoothng Splnes and Regresson
y and the total sum of
 Lnear regresson Testng for non-lnearty In analytcal chemstry, lnear regresson s commonly used n the constructon of calbraton functons requred for analytcal technques such as gas chromatography, atomc absorpton
Lnear regresson Testng for non-lnearty In analytcal chemstry, lnear regresson s commonly used n the constructon of calbraton functons requred for analytcal technques such as gas chromatography, atomc absorpton
Learning the Kernel Parameters in Kernel Minimum Distance Classifier
 Learnng the Kernel Parameters n Kernel Mnmum Dstance Classfer Daoqang Zhang 1,, Songcan Chen and Zh-Hua Zhou 1* 1 Natonal Laboratory for Novel Software Technology Nanjng Unversty, Nanjng 193, Chna Department
Learnng the Kernel Parameters n Kernel Mnmum Dstance Classfer Daoqang Zhang 1,, Songcan Chen and Zh-Hua Zhou 1* 1 Natonal Laboratory for Novel Software Technology Nanjng Unversty, Nanjng 193, Chna Department
6.854 Advanced Algorithms Petar Maymounkov Problem Set 11 (November 23, 2005) With: Benjamin Rossman, Oren Weimann, and Pouya Kheradpour
 6.854 Advanced Algorthms Petar Maymounkov Problem Set 11 (November 23, 2005) Wth: Benjamn Rossman, Oren Wemann, and Pouya Kheradpour Problem 1. We reduce vertex cover to MAX-SAT wth weghts, such that the
6.854 Advanced Algorthms Petar Maymounkov Problem Set 11 (November 23, 2005) Wth: Benjamn Rossman, Oren Wemann, and Pouya Kheradpour Problem 1. We reduce vertex cover to MAX-SAT wth weghts, such that the
For instance, ; the five basic number-sets are increasingly more n A B & B A A = B (1)
 Secton 1.2 Subsets and the Boolean operatons on sets If every element of the set A s an element of the set B, we say that A s a subset of B, or that A s contaned n B, or that B contans A, and we wrte A
Secton 1.2 Subsets and the Boolean operatons on sets If every element of the set A s an element of the set B, we say that A s a subset of B, or that A s contaned n B, or that B contans A, and we wrte A
Harmonic Coordinates for Character Articulation PIXAR
 Harmonc Coordnates for Character Artculaton PIXAR Pushkar Josh Mark Meyer Tony DeRose Bran Green Tom Sanock We have a complex source mesh nsde of a smpler cage mesh We want vertex deformatons appled to
Harmonc Coordnates for Character Artculaton PIXAR Pushkar Josh Mark Meyer Tony DeRose Bran Green Tom Sanock We have a complex source mesh nsde of a smpler cage mesh We want vertex deformatons appled to
Problem Set 3 Solutions
 Introducton to Algorthms October 4, 2002 Massachusetts Insttute of Technology 6046J/18410J Professors Erk Demane and Shaf Goldwasser Handout 14 Problem Set 3 Solutons (Exercses were not to be turned n,
Introducton to Algorthms October 4, 2002 Massachusetts Insttute of Technology 6046J/18410J Professors Erk Demane and Shaf Goldwasser Handout 14 Problem Set 3 Solutons (Exercses were not to be turned n,
Lecture 5: Multilayer Perceptrons
 Lecture 5: Multlayer Perceptrons Roger Grosse 1 Introducton So far, we ve only talked about lnear models: lnear regresson and lnear bnary classfers. We noted that there are functons that can t be represented
Lecture 5: Multlayer Perceptrons Roger Grosse 1 Introducton So far, we ve only talked about lnear models: lnear regresson and lnear bnary classfers. We noted that there are functons that can t be represented
Machine Learning: Algorithms and Applications
 14/05/1 Machne Learnng: Algorthms and Applcatons Florano Zn Free Unversty of Bozen-Bolzano Faculty of Computer Scence Academc Year 011-01 Lecture 10: 14 May 01 Unsupervsed Learnng cont Sldes courtesy of
14/05/1 Machne Learnng: Algorthms and Applcatons Florano Zn Free Unversty of Bozen-Bolzano Faculty of Computer Scence Academc Year 011-01 Lecture 10: 14 May 01 Unsupervsed Learnng cont Sldes courtesy of
Outline. Type of Machine Learning. Examples of Application. Unsupervised Learning
 Outlne Artfcal Intellgence and ts applcatons Lecture 8 Unsupervsed Learnng Professor Danel Yeung danyeung@eee.org Dr. Patrck Chan patrckchan@eee.org South Chna Unversty of Technology, Chna Introducton
Outlne Artfcal Intellgence and ts applcatons Lecture 8 Unsupervsed Learnng Professor Danel Yeung danyeung@eee.org Dr. Patrck Chan patrckchan@eee.org South Chna Unversty of Technology, Chna Introducton
Smoothing Spline ANOVA for variable screening
 Smoothng Splne ANOVA for varable screenng a useful tool for metamodels tranng and mult-objectve optmzaton L. Rcco, E. Rgon, A. Turco Outlne RSM Introducton Possble couplng Test case MOO MOO wth Game Theory
Smoothng Splne ANOVA for varable screenng a useful tool for metamodels tranng and mult-objectve optmzaton L. Rcco, E. Rgon, A. Turco Outlne RSM Introducton Possble couplng Test case MOO MOO wth Game Theory
Compiler Design. Spring Register Allocation. Sample Exercises and Solutions. Prof. Pedro C. Diniz
 Compler Desgn Sprng 2014 Regster Allocaton Sample Exercses and Solutons Prof. Pedro C. Dnz USC / Informaton Scences Insttute 4676 Admralty Way, Sute 1001 Marna del Rey, Calforna 90292 pedro@s.edu Regster
Compler Desgn Sprng 2014 Regster Allocaton Sample Exercses and Solutons Prof. Pedro C. Dnz USC / Informaton Scences Insttute 4676 Admralty Way, Sute 1001 Marna del Rey, Calforna 90292 pedro@s.edu Regster
Interpolation of the Irregular Curve Network of Ship Hull Form Using Subdivision Surfaces
 7 Interpolaton of the Irregular Curve Network of Shp Hull Form Usng Subdvson Surfaces Kyu-Yeul Lee, Doo-Yeoun Cho and Tae-Wan Km Seoul Natonal Unversty, kylee@snu.ac.kr,whendus@snu.ac.kr,taewan}@snu.ac.kr
7 Interpolaton of the Irregular Curve Network of Shp Hull Form Usng Subdvson Surfaces Kyu-Yeul Lee, Doo-Yeoun Cho and Tae-Wan Km Seoul Natonal Unversty, kylee@snu.ac.kr,whendus@snu.ac.kr,taewan}@snu.ac.kr
12/2/2009. Announcements. Parametric / Non-parametric. Case-Based Reasoning. Nearest-Neighbor on Images. Nearest-Neighbor Classification
 Introducton to Artfcal Intellgence V22.0472-001 Fall 2009 Lecture 24: Nearest-Neghbors & Support Vector Machnes Rob Fergus Dept of Computer Scence, Courant Insttute, NYU Sldes from Danel Yeung, John DeNero
Introducton to Artfcal Intellgence V22.0472-001 Fall 2009 Lecture 24: Nearest-Neghbors & Support Vector Machnes Rob Fergus Dept of Computer Scence, Courant Insttute, NYU Sldes from Danel Yeung, John DeNero
Type-2 Fuzzy Non-uniform Rational B-spline Model with Type-2 Fuzzy Data
 Malaysan Journal of Mathematcal Scences 11(S) Aprl : 35 46 (2017) Specal Issue: The 2nd Internatonal Conference and Workshop on Mathematcal Analyss (ICWOMA 2016) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES
Malaysan Journal of Mathematcal Scences 11(S) Aprl : 35 46 (2017) Specal Issue: The 2nd Internatonal Conference and Workshop on Mathematcal Analyss (ICWOMA 2016) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES
An Application of the Dulmage-Mendelsohn Decomposition to Sparse Null Space Bases of Full Row Rank Matrices
 Internatonal Mathematcal Forum, Vol 7, 2012, no 52, 2549-2554 An Applcaton of the Dulmage-Mendelsohn Decomposton to Sparse Null Space Bases of Full Row Rank Matrces Mostafa Khorramzadeh Department of Mathematcal
Internatonal Mathematcal Forum, Vol 7, 2012, no 52, 2549-2554 An Applcaton of the Dulmage-Mendelsohn Decomposton to Sparse Null Space Bases of Full Row Rank Matrces Mostafa Khorramzadeh Department of Mathematcal
 Chapter 6 Programmng the fnte element method Inow turn to the man subject of ths book: The mplementaton of the fnte element algorthm n computer programs. In order to make my dscusson as straghtforward
Chapter 6 Programmng the fnte element method Inow turn to the man subject of ths book: The mplementaton of the fnte element algorthm n computer programs. In order to make my dscusson as straghtforward
APPLICATION OF MULTIVARIATE LOSS FUNCTION FOR ASSESSMENT OF THE QUALITY OF TECHNOLOGICAL PROCESS MANAGEMENT
 3. - 5. 5., Brno, Czech Republc, EU APPLICATION OF MULTIVARIATE LOSS FUNCTION FOR ASSESSMENT OF THE QUALITY OF TECHNOLOGICAL PROCESS MANAGEMENT Abstract Josef TOŠENOVSKÝ ) Lenka MONSPORTOVÁ ) Flp TOŠENOVSKÝ
3. - 5. 5., Brno, Czech Republc, EU APPLICATION OF MULTIVARIATE LOSS FUNCTION FOR ASSESSMENT OF THE QUALITY OF TECHNOLOGICAL PROCESS MANAGEMENT Abstract Josef TOŠENOVSKÝ ) Lenka MONSPORTOVÁ ) Flp TOŠENOVSKÝ
Support Vector Machines
 /9/207 MIST.6060 Busness Intellgence and Data Mnng What are Support Vector Machnes? Support Vector Machnes Support Vector Machnes (SVMs) are supervsed learnng technques that analyze data and recognze patterns.
/9/207 MIST.6060 Busness Intellgence and Data Mnng What are Support Vector Machnes? Support Vector Machnes Support Vector Machnes (SVMs) are supervsed learnng technques that analyze data and recognze patterns.
Unsupervised Learning
 Pattern Recognton Lecture 8 Outlne Introducton Unsupervsed Learnng Parametrc VS Non-Parametrc Approach Mxture of Denstes Maxmum-Lkelhood Estmates Clusterng Prof. Danel Yeung School of Computer Scence and
Pattern Recognton Lecture 8 Outlne Introducton Unsupervsed Learnng Parametrc VS Non-Parametrc Approach Mxture of Denstes Maxmum-Lkelhood Estmates Clusterng Prof. Danel Yeung School of Computer Scence and
Reading. 14. Subdivision curves. Recommended:
 eadng ecommended: Stollntz, Deose, and Salesn. Wavelets for Computer Graphcs: heory and Applcatons, 996, secton 6.-6., A.5. 4. Subdvson curves Note: there s an error n Stollntz, et al., secton A.5. Equaton
eadng ecommended: Stollntz, Deose, and Salesn. Wavelets for Computer Graphcs: heory and Applcatons, 996, secton 6.-6., A.5. 4. Subdvson curves Note: there s an error n Stollntz, et al., secton A.5. Equaton
Mathematics 256 a course in differential equations for engineering students
 Mathematcs 56 a course n dfferental equatons for engneerng students Chapter 5. More effcent methods of numercal soluton Euler s method s qute neffcent. Because the error s essentally proportonal to the
Mathematcs 56 a course n dfferental equatons for engneerng students Chapter 5. More effcent methods of numercal soluton Euler s method s qute neffcent. Because the error s essentally proportonal to the
Kent State University CS 4/ Design and Analysis of Algorithms. Dept. of Math & Computer Science LECT-16. Dynamic Programming
 CS 4/560 Desgn and Analyss of Algorthms Kent State Unversty Dept. of Math & Computer Scence LECT-6 Dynamc Programmng 2 Dynamc Programmng Dynamc Programmng, lke the dvde-and-conquer method, solves problems
CS 4/560 Desgn and Analyss of Algorthms Kent State Unversty Dept. of Math & Computer Scence LECT-6 Dynamc Programmng 2 Dynamc Programmng Dynamc Programmng, lke the dvde-and-conquer method, solves problems
Wishing you all a Total Quality New Year!
 Total Qualty Management and Sx Sgma Post Graduate Program 214-15 Sesson 4 Vnay Kumar Kalakband Assstant Professor Operatons & Systems Area 1 Wshng you all a Total Qualty New Year! Hope you acheve Sx sgma
Total Qualty Management and Sx Sgma Post Graduate Program 214-15 Sesson 4 Vnay Kumar Kalakband Assstant Professor Operatons & Systems Area 1 Wshng you all a Total Qualty New Year! Hope you acheve Sx sgma
A Newton-Type Method for Constrained Least-Squares Data-Fitting with Easy-to-Control Rational Curves
 A Newton-Type Method for Constraned Least-Squares Data-Fttng wth Easy-to-Control Ratonal Curves G. Cascola a, L. Roman b, a Department of Mathematcs, Unversty of Bologna, P.zza d Porta San Donato 5, 4017
A Newton-Type Method for Constraned Least-Squares Data-Fttng wth Easy-to-Control Ratonal Curves G. Cascola a, L. Roman b, a Department of Mathematcs, Unversty of Bologna, P.zza d Porta San Donato 5, 4017
Radial Basis Functions
 Radal Bass Functons Mesh Reconstructon Input: pont cloud Output: water-tght manfold mesh Explct Connectvty estmaton Implct Sgned dstance functon estmaton Image from: Reconstructon and Representaton of
Radal Bass Functons Mesh Reconstructon Input: pont cloud Output: water-tght manfold mesh Explct Connectvty estmaton Implct Sgned dstance functon estmaton Image from: Reconstructon and Representaton of
Sum of Linear and Fractional Multiobjective Programming Problem under Fuzzy Rules Constraints
 Australan Journal of Basc and Appled Scences, 2(4): 1204-1208, 2008 ISSN 1991-8178 Sum of Lnear and Fractonal Multobjectve Programmng Problem under Fuzzy Rules Constrants 1 2 Sanjay Jan and Kalash Lachhwan
Australan Journal of Basc and Appled Scences, 2(4): 1204-1208, 2008 ISSN 1991-8178 Sum of Lnear and Fractonal Multobjectve Programmng Problem under Fuzzy Rules Constrants 1 2 Sanjay Jan and Kalash Lachhwan
Exercises (Part 4) Introduction to R UCLA/CCPR. John Fox, February 2005
 Exercses (Part 4) Introducton to R UCLA/CCPR John Fox, February 2005 1. A challengng problem: Iterated weghted least squares (IWLS) s a standard method of fttng generalzed lnear models to data. As descrbed
Exercses (Part 4) Introducton to R UCLA/CCPR John Fox, February 2005 1. A challengng problem: Iterated weghted least squares (IWLS) s a standard method of fttng generalzed lnear models to data. As descrbed
Multi-stable Perception. Necker Cube
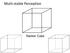 Mult-stable Percepton Necker Cube Spnnng dancer lluson, Nobuuk Kaahara Fttng and Algnment Computer Vson Szelsk 6.1 James Has Acknowledgment: Man sldes from Derek Hoem, Lana Lazebnk, and Grauman&Lebe 2008
Mult-stable Percepton Necker Cube Spnnng dancer lluson, Nobuuk Kaahara Fttng and Algnment Computer Vson Szelsk 6.1 James Has Acknowledgment: Man sldes from Derek Hoem, Lana Lazebnk, and Grauman&Lebe 2008
A Unified, Integral Construction For Coordinates Over Closed Curves
 A Unfed, Integral Constructon For Coordnates Over Closed Curves Schaefer S., Ju T. and Warren J. Abstract We propose a smple generalzaton of Shephard s nterpolaton to pecewse smooth, convex closed curves
A Unfed, Integral Constructon For Coordnates Over Closed Curves Schaefer S., Ju T. and Warren J. Abstract We propose a smple generalzaton of Shephard s nterpolaton to pecewse smooth, convex closed curves
Concurrent models of computation for embedded software
 Concurrent models of computaton for embedded software and hardware! Researcher overvew what t looks lke semantcs what t means and how t relates desgnng an actor language actor propertes and how to represent
Concurrent models of computaton for embedded software and hardware! Researcher overvew what t looks lke semantcs what t means and how t relates desgnng an actor language actor propertes and how to represent
Proper Choice of Data Used for the Estimation of Datum Transformation Parameters
 Proper Choce of Data Used for the Estmaton of Datum Transformaton Parameters Hakan S. KUTOGLU, Turkey Key words: Coordnate systems; transformaton; estmaton, relablty. SUMMARY Advances n technologes and
Proper Choce of Data Used for the Estmaton of Datum Transformaton Parameters Hakan S. KUTOGLU, Turkey Key words: Coordnate systems; transformaton; estmaton, relablty. SUMMARY Advances n technologes and
Parallel Numerics. 1 Preconditioning & Iterative Solvers (From 2016)
 Technsche Unverstät München WSe 6/7 Insttut für Informatk Prof. Dr. Thomas Huckle Dpl.-Math. Benjamn Uekermann Parallel Numercs Exercse : Prevous Exam Questons Precondtonng & Iteratve Solvers (From 6)
Technsche Unverstät München WSe 6/7 Insttut für Informatk Prof. Dr. Thomas Huckle Dpl.-Math. Benjamn Uekermann Parallel Numercs Exercse : Prevous Exam Questons Precondtonng & Iteratve Solvers (From 6)
LECTURE : MANIFOLD LEARNING
 LECTURE : MANIFOLD LEARNING Rta Osadchy Some sldes are due to L.Saul, V. C. Raykar, N. Verma Topcs PCA MDS IsoMap LLE EgenMaps Done! Dmensonalty Reducton Data representaton Inputs are real-valued vectors
LECTURE : MANIFOLD LEARNING Rta Osadchy Some sldes are due to L.Saul, V. C. Raykar, N. Verma Topcs PCA MDS IsoMap LLE EgenMaps Done! Dmensonalty Reducton Data representaton Inputs are real-valued vectors
Array transposition in CUDA shared memory
 Array transposton n CUDA shared memory Mke Gles February 19, 2014 Abstract Ths short note s nspred by some code wrtten by Jeremy Appleyard for the transposton of data through shared memory. I had some
Array transposton n CUDA shared memory Mke Gles February 19, 2014 Abstract Ths short note s nspred by some code wrtten by Jeremy Appleyard for the transposton of data through shared memory. I had some
Adaptive Transfer Learning
 Adaptve Transfer Learnng Bn Cao, Snno Jaln Pan, Yu Zhang, Dt-Yan Yeung, Qang Yang Hong Kong Unversty of Scence and Technology Clear Water Bay, Kowloon, Hong Kong {caobn,snnopan,zhangyu,dyyeung,qyang}@cse.ust.hk
Adaptve Transfer Learnng Bn Cao, Snno Jaln Pan, Yu Zhang, Dt-Yan Yeung, Qang Yang Hong Kong Unversty of Scence and Technology Clear Water Bay, Kowloon, Hong Kong {caobn,snnopan,zhangyu,dyyeung,qyang}@cse.ust.hk
A Geometric Approach for Multi-Degree Spline
 L X, Huang ZJ, Lu Z. A geometrc approach for mult-degree splne. JOURNAL OF COMPUTER SCIENCE AND TECHNOLOGY 27(4): 84 850 July 202. DOI 0.007/s390-02-268-2 A Geometrc Approach for Mult-Degree Splne Xn L
L X, Huang ZJ, Lu Z. A geometrc approach for mult-degree splne. JOURNAL OF COMPUTER SCIENCE AND TECHNOLOGY 27(4): 84 850 July 202. DOI 0.007/s390-02-268-2 A Geometrc Approach for Mult-Degree Splne Xn L
ON SOME ENTERTAINING APPLICATIONS OF THE CONCEPT OF SET IN COMPUTER SCIENCE COURSE
 Yordzhev K., Kostadnova H. Інформаційні технології в освіті ON SOME ENTERTAINING APPLICATIONS OF THE CONCEPT OF SET IN COMPUTER SCIENCE COURSE Yordzhev K., Kostadnova H. Some aspects of programmng educaton
Yordzhev K., Kostadnova H. Інформаційні технології в освіті ON SOME ENTERTAINING APPLICATIONS OF THE CONCEPT OF SET IN COMPUTER SCIENCE COURSE Yordzhev K., Kostadnova H. Some aspects of programmng educaton
1 Linear and Nonlinear Subdivision Schemes in Geometric Modeling
 1 Lnear and Nonlnear Subdvson Schemes n Geometrc Modelng Nra dyn School of Mathematcal Scences Tel Avv Unversty Tel Avv, Israel e-mal: nradyn@post.tau.ac.l Abstract Subdvson schemes are effcent computatonal
1 Lnear and Nonlnear Subdvson Schemes n Geometrc Modelng Nra dyn School of Mathematcal Scences Tel Avv Unversty Tel Avv, Israel e-mal: nradyn@post.tau.ac.l Abstract Subdvson schemes are effcent computatonal
Assignment # 2. Farrukh Jabeen Algorithms 510 Assignment #2 Due Date: June 15, 2009.
 Farrukh Jabeen Algorthms 51 Assgnment #2 Due Date: June 15, 29. Assgnment # 2 Chapter 3 Dscrete Fourer Transforms Implement the FFT for the DFT. Descrbed n sectons 3.1 and 3.2. Delverables: 1. Concse descrpton
Farrukh Jabeen Algorthms 51 Assgnment #2 Due Date: June 15, 29. Assgnment # 2 Chapter 3 Dscrete Fourer Transforms Implement the FFT for the DFT. Descrbed n sectons 3.1 and 3.2. Delverables: 1. Concse descrpton
NOVEL CONSTRUCTION OF SHORT LENGTH LDPC CODES FOR SIMPLE DECODING
 Journal of Theoretcal and Appled Informaton Technology 27 JATIT. All rghts reserved. www.jatt.org NOVEL CONSTRUCTION OF SHORT LENGTH LDPC CODES FOR SIMPLE DECODING Fatma A. Newagy, Yasmne A. Fahmy, and
Journal of Theoretcal and Appled Informaton Technology 27 JATIT. All rghts reserved. www.jatt.org NOVEL CONSTRUCTION OF SHORT LENGTH LDPC CODES FOR SIMPLE DECODING Fatma A. Newagy, Yasmne A. Fahmy, and
Numerical Solution of Deformation Equations. in Homotopy Analysis Method
 Appled Mathematcal Scences, Vol. 6, 2012, no. 8, 357 367 Nmercal Solton of Deformaton Eqatons n Homotopy Analyss Method J. Izadan and M. MohammadzadeAttar Department of Mathematcs, Faclty of Scences, Mashhad
Appled Mathematcal Scences, Vol. 6, 2012, no. 8, 357 367 Nmercal Solton of Deformaton Eqatons n Homotopy Analyss Method J. Izadan and M. MohammadzadeAttar Department of Mathematcs, Faclty of Scences, Mashhad
CMPS 10 Introduction to Computer Science Lecture Notes
 CPS 0 Introducton to Computer Scence Lecture Notes Chapter : Algorthm Desgn How should we present algorthms? Natural languages lke Englsh, Spansh, or French whch are rch n nterpretaton and meanng are not
CPS 0 Introducton to Computer Scence Lecture Notes Chapter : Algorthm Desgn How should we present algorthms? Natural languages lke Englsh, Spansh, or French whch are rch n nterpretaton and meanng are not
ROBOT KINEMATICS. ME Robotics ME Robotics
 ROBOT KINEMATICS Purpose: The purpose of ths chapter s to ntroduce you to robot knematcs, and the concepts related to both open and closed knematcs chans. Forward knematcs s dstngushed from nverse knematcs.
ROBOT KINEMATICS Purpose: The purpose of ths chapter s to ntroduce you to robot knematcs, and the concepts related to both open and closed knematcs chans. Forward knematcs s dstngushed from nverse knematcs.
Active Contours/Snakes
 Actve Contours/Snakes Erkut Erdem Acknowledgement: The sldes are adapted from the sldes prepared by K. Grauman of Unversty of Texas at Austn Fttng: Edges vs. boundares Edges useful sgnal to ndcate occludng
Actve Contours/Snakes Erkut Erdem Acknowledgement: The sldes are adapted from the sldes prepared by K. Grauman of Unversty of Texas at Austn Fttng: Edges vs. boundares Edges useful sgnal to ndcate occludng
On Some Entertaining Applications of the Concept of Set in Computer Science Course
 On Some Entertanng Applcatons of the Concept of Set n Computer Scence Course Krasmr Yordzhev *, Hrstna Kostadnova ** * Assocate Professor Krasmr Yordzhev, Ph.D., Faculty of Mathematcs and Natural Scences,
On Some Entertanng Applcatons of the Concept of Set n Computer Scence Course Krasmr Yordzhev *, Hrstna Kostadnova ** * Assocate Professor Krasmr Yordzhev, Ph.D., Faculty of Mathematcs and Natural Scences,
Inverse-Polar Ray Projection for Recovering Projective Transformations
 nverse-polar Ray Projecton for Recoverng Projectve Transformatons Yun Zhang The Center for Advanced Computer Studes Unversty of Lousana at Lafayette yxz646@lousana.edu Henry Chu The Center for Advanced
nverse-polar Ray Projecton for Recoverng Projectve Transformatons Yun Zhang The Center for Advanced Computer Studes Unversty of Lousana at Lafayette yxz646@lousana.edu Henry Chu The Center for Advanced
Polyhedral Compilation Foundations
 Polyhedral Complaton Foundatons Lous-Noël Pouchet pouchet@cse.oho-state.edu Dept. of Computer Scence and Engneerng, the Oho State Unversty Feb 8, 200 888., Class # Introducton: Polyhedral Complaton Foundatons
Polyhedral Complaton Foundatons Lous-Noël Pouchet pouchet@cse.oho-state.edu Dept. of Computer Scence and Engneerng, the Oho State Unversty Feb 8, 200 888., Class # Introducton: Polyhedral Complaton Foundatons
Support Vector Machines
 Support Vector Machnes Decson surface s a hyperplane (lne n 2D) n feature space (smlar to the Perceptron) Arguably, the most mportant recent dscovery n machne learnng In a nutshell: map the data to a predetermned
Support Vector Machnes Decson surface s a hyperplane (lne n 2D) n feature space (smlar to the Perceptron) Arguably, the most mportant recent dscovery n machne learnng In a nutshell: map the data to a predetermned
A Binarization Algorithm specialized on Document Images and Photos
 A Bnarzaton Algorthm specalzed on Document mages and Photos Ergna Kavalleratou Dept. of nformaton and Communcaton Systems Engneerng Unversty of the Aegean kavalleratou@aegean.gr Abstract n ths paper, a
A Bnarzaton Algorthm specalzed on Document mages and Photos Ergna Kavalleratou Dept. of nformaton and Communcaton Systems Engneerng Unversty of the Aegean kavalleratou@aegean.gr Abstract n ths paper, a
5 The Primal-Dual Method
 5 The Prmal-Dual Method Orgnally desgned as a method for solvng lnear programs, where t reduces weghted optmzaton problems to smpler combnatoral ones, the prmal-dual method (PDM) has receved much attenton
5 The Prmal-Dual Method Orgnally desgned as a method for solvng lnear programs, where t reduces weghted optmzaton problems to smpler combnatoral ones, the prmal-dual method (PDM) has receved much attenton
Machine Learning. Support Vector Machines. (contains material adapted from talks by Constantin F. Aliferis & Ioannis Tsamardinos, and Martin Law)
 Machne Learnng Support Vector Machnes (contans materal adapted from talks by Constantn F. Alfers & Ioanns Tsamardnos, and Martn Law) Bryan Pardo, Machne Learnng: EECS 349 Fall 2014 Support Vector Machnes
Machne Learnng Support Vector Machnes (contans materal adapted from talks by Constantn F. Alfers & Ioanns Tsamardnos, and Martn Law) Bryan Pardo, Machne Learnng: EECS 349 Fall 2014 Support Vector Machnes
High-Boost Mesh Filtering for 3-D Shape Enhancement
 Hgh-Boost Mesh Flterng for 3-D Shape Enhancement Hrokazu Yagou Λ Alexander Belyaev y Damng We z Λ y z ; ; Shape Modelng Laboratory, Unversty of Azu, Azu-Wakamatsu 965-8580 Japan y Computer Graphcs Group,
Hgh-Boost Mesh Flterng for 3-D Shape Enhancement Hrokazu Yagou Λ Alexander Belyaev y Damng We z Λ y z ; ; Shape Modelng Laboratory, Unversty of Azu, Azu-Wakamatsu 965-8580 Japan y Computer Graphcs Group,
Rational Interpolants with Tension Parameters
 Ratonal Interpolants wt Tenson Parameters Gulo Cascola and Luca Roman Abstract. In ts paper we present a NURBS verson of te ratonal nterpolatng splne wt tenson ntroduced n [2], and we extend our proposal
Ratonal Interpolants wt Tenson Parameters Gulo Cascola and Luca Roman Abstract. In ts paper we present a NURBS verson of te ratonal nterpolatng splne wt tenson ntroduced n [2], and we extend our proposal
Course Introduction. Algorithm 8/31/2017. COSC 320 Advanced Data Structures and Algorithms. COSC 320 Advanced Data Structures and Algorithms
 Course Introducton Course Topcs Exams, abs, Proects A quc loo at a few algorthms 1 Advanced Data Structures and Algorthms Descrpton: We are gong to dscuss algorthm complexty analyss, algorthm desgn technques
Course Introducton Course Topcs Exams, abs, Proects A quc loo at a few algorthms 1 Advanced Data Structures and Algorthms Descrpton: We are gong to dscuss algorthm complexty analyss, algorthm desgn technques
Mercer Kernels for Object Recognition with Local Features
 TR004-50, October 004, Department of Computer Scence, Dartmouth College Mercer Kernels for Object Recognton wth Local Features Swe Lyu Department of Computer Scence Dartmouth College Hanover NH 03755 A
TR004-50, October 004, Department of Computer Scence, Dartmouth College Mercer Kernels for Object Recognton wth Local Features Swe Lyu Department of Computer Scence Dartmouth College Hanover NH 03755 A
A B-Snake Model Using Statistical and Geometric Information - Applications to Medical Images
 A B-Snake Model Usng Statstcal and Geometrc Informaton - Applcatons to Medcal Images Yue Wang, Eam Khwang Teoh and Dnggang Shen 2 School of Electrcal and Electronc Engneerng, Nanyang Technologcal Unversty
A B-Snake Model Usng Statstcal and Geometrc Informaton - Applcatons to Medcal Images Yue Wang, Eam Khwang Teoh and Dnggang Shen 2 School of Electrcal and Electronc Engneerng, Nanyang Technologcal Unversty
CHAPTER 2 DECOMPOSITION OF GRAPHS
 CHAPTER DECOMPOSITION OF GRAPHS. INTRODUCTION A graph H s called a Supersubdvson of a graph G f H s obtaned from G by replacng every edge uv of G by a bpartte graph,m (m may vary for each edge by dentfyng
CHAPTER DECOMPOSITION OF GRAPHS. INTRODUCTION A graph H s called a Supersubdvson of a graph G f H s obtaned from G by replacng every edge uv of G by a bpartte graph,m (m may vary for each edge by dentfyng
Feature Reduction and Selection
 Feature Reducton and Selecton Dr. Shuang LIANG School of Software Engneerng TongJ Unversty Fall, 2012 Today s Topcs Introducton Problems of Dmensonalty Feature Reducton Statstc methods Prncpal Components
Feature Reducton and Selecton Dr. Shuang LIANG School of Software Engneerng TongJ Unversty Fall, 2012 Today s Topcs Introducton Problems of Dmensonalty Feature Reducton Statstc methods Prncpal Components
Research Article Quasi-Bézier Curves with Shape Parameters
 Hndaw Publshng Corporaton Appled Mathematcs Volume 3, Artcle ID 739, 9 pages http://dxdoorg/55/3/739 Research Artcle Quas-Bézer Curves wth Shape Parameters Jun Chen Faculty of Scence, Nngbo Unversty of
Hndaw Publshng Corporaton Appled Mathematcs Volume 3, Artcle ID 739, 9 pages http://dxdoorg/55/3/739 Research Artcle Quas-Bézer Curves wth Shape Parameters Jun Chen Faculty of Scence, Nngbo Unversty of
Lecture #15 Lecture Notes
 Lecture #15 Lecture Notes The ocean water column s very much a 3-D spatal entt and we need to represent that structure n an economcal way to deal wth t n calculatons. We wll dscuss one way to do so, emprcal
Lecture #15 Lecture Notes The ocean water column s very much a 3-D spatal entt and we need to represent that structure n an economcal way to deal wth t n calculatons. We wll dscuss one way to do so, emprcal
Outline. Self-Organizing Maps (SOM) US Hebbian Learning, Cntd. The learning rule is Hebbian like:
 Self-Organzng Maps (SOM) Turgay İBRİKÇİ, PhD. Outlne Introducton Structures of SOM SOM Archtecture Neghborhoods SOM Algorthm Examples Summary 1 2 Unsupervsed Hebban Learnng US Hebban Learnng, Cntd 3 A
Self-Organzng Maps (SOM) Turgay İBRİKÇİ, PhD. Outlne Introducton Structures of SOM SOM Archtecture Neghborhoods SOM Algorthm Examples Summary 1 2 Unsupervsed Hebban Learnng US Hebban Learnng, Cntd 3 A
S.P.H. : A SOLUTION TO AVOID USING EROSION CRITERION?
 S.P.H. : A SOLUTION TO AVOID USING EROSION CRITERION? Célne GALLET ENSICA 1 place Emle Bloun 31056 TOULOUSE CEDEX e-mal :cgallet@ensca.fr Jean Luc LACOME DYNALIS Immeuble AEROPOLE - Bat 1 5, Avenue Albert
S.P.H. : A SOLUTION TO AVOID USING EROSION CRITERION? Célne GALLET ENSICA 1 place Emle Bloun 31056 TOULOUSE CEDEX e-mal :cgallet@ensca.fr Jean Luc LACOME DYNALIS Immeuble AEROPOLE - Bat 1 5, Avenue Albert
UNIT 2 : INEQUALITIES AND CONVEX SETS
 UNT 2 : NEQUALTES AND CONVEX SETS ' Structure 2. ntroducton Objectves, nequaltes and ther Graphs Convex Sets and ther Geometry Noton of Convex Sets Extreme Ponts of Convex Set Hyper Planes and Half Spaces
UNT 2 : NEQUALTES AND CONVEX SETS ' Structure 2. ntroducton Objectves, nequaltes and ther Graphs Convex Sets and ther Geometry Noton of Convex Sets Extreme Ponts of Convex Set Hyper Planes and Half Spaces
Image Representation & Visualization Basic Imaging Algorithms Shape Representation and Analysis. outline
 mage Vsualzaton mage Vsualzaton mage Representaton & Vsualzaton Basc magng Algorthms Shape Representaton and Analyss outlne mage Representaton & Vsualzaton Basc magng Algorthms Shape Representaton and
mage Vsualzaton mage Vsualzaton mage Representaton & Vsualzaton Basc magng Algorthms Shape Representaton and Analyss outlne mage Representaton & Vsualzaton Basc magng Algorthms Shape Representaton and
Discrete Schemes for Gaussian Curvature and Their Convergence
 Dscrete Schemes for Gaussan Curvature and Ther Convergence Zhqang Xu Guolang Xu Insttute of Computatonal Math. and Sc. and Eng. Computng, Academy of Mathematcs and System Scences, Chnese Academy of Scences,
Dscrete Schemes for Gaussan Curvature and Ther Convergence Zhqang Xu Guolang Xu Insttute of Computatonal Math. and Sc. and Eng. Computng, Academy of Mathematcs and System Scences, Chnese Academy of Scences,
Lecture 5: Probability Distributions. Random Variables
 Lecture 5: Probablty Dstrbutons Random Varables Probablty Dstrbutons Dscrete Random Varables Contnuous Random Varables and ther Dstrbutons Dscrete Jont Dstrbutons Contnuous Jont Dstrbutons Independent
Lecture 5: Probablty Dstrbutons Random Varables Probablty Dstrbutons Dscrete Random Varables Contnuous Random Varables and ther Dstrbutons Dscrete Jont Dstrbutons Contnuous Jont Dstrbutons Independent
A New Approach For the Ranking of Fuzzy Sets With Different Heights
 New pproach For the ankng of Fuzzy Sets Wth Dfferent Heghts Pushpnder Sngh School of Mathematcs Computer pplcatons Thapar Unversty, Patala-7 00 Inda pushpndersnl@gmalcom STCT ankng of fuzzy sets plays
New pproach For the ankng of Fuzzy Sets Wth Dfferent Heghts Pushpnder Sngh School of Mathematcs Computer pplcatons Thapar Unversty, Patala-7 00 Inda pushpndersnl@gmalcom STCT ankng of fuzzy sets plays
The Greedy Method. Outline and Reading. Change Money Problem. Greedy Algorithms. Applications of the Greedy Strategy. The Greedy Method Technique
 //00 :0 AM Outlne and Readng The Greedy Method The Greedy Method Technque (secton.) Fractonal Knapsack Problem (secton..) Task Schedulng (secton..) Mnmum Spannng Trees (secton.) Change Money Problem Greedy
//00 :0 AM Outlne and Readng The Greedy Method The Greedy Method Technque (secton.) Fractonal Knapsack Problem (secton..) Task Schedulng (secton..) Mnmum Spannng Trees (secton.) Change Money Problem Greedy
Intro. Iterators. 1. Access
 Intro Ths mornng I d lke to talk a lttle bt about s and s. We wll start out wth smlartes and dfferences, then we wll see how to draw them n envronment dagrams, and we wll fnsh wth some examples. Happy
Intro Ths mornng I d lke to talk a lttle bt about s and s. We wll start out wth smlartes and dfferences, then we wll see how to draw them n envronment dagrams, and we wll fnsh wth some examples. Happy
2D Raster Graphics. Integer grid Sequential (left-right, top-down) scan. Computer Graphics
 2D Graphcs 2D Raster Graphcs Integer grd Sequental (left-rght, top-down scan j Lne drawng A ver mportant operaton used frequentl, block dagrams, bar charts, engneerng drawng, archtecture plans, etc. curves
2D Graphcs 2D Raster Graphcs Integer grd Sequental (left-rght, top-down scan j Lne drawng A ver mportant operaton used frequentl, block dagrams, bar charts, engneerng drawng, archtecture plans, etc. curves
Explicit Formulas and Efficient Algorithm for Moment Computation of Coupled RC Trees with Lumped and Distributed Elements
 Explct Formulas and Effcent Algorthm for Moment Computaton of Coupled RC Trees wth Lumped and Dstrbuted Elements Qngan Yu and Ernest S.Kuh Electroncs Research Lab. Unv. of Calforna at Berkeley Berkeley
Explct Formulas and Effcent Algorthm for Moment Computaton of Coupled RC Trees wth Lumped and Dstrbuted Elements Qngan Yu and Ernest S.Kuh Electroncs Research Lab. Unv. of Calforna at Berkeley Berkeley
Biostatistics 615/815
 The E-M Algorthm Bostatstcs 615/815 Lecture 17 Last Lecture: The Smplex Method General method for optmzaton Makes few assumptons about functon Crawls towards mnmum Some recommendatons Multple startng ponts
The E-M Algorthm Bostatstcs 615/815 Lecture 17 Last Lecture: The Smplex Method General method for optmzaton Makes few assumptons about functon Crawls towards mnmum Some recommendatons Multple startng ponts
Computers and Mathematics with Applications. Discrete schemes for Gaussian curvature and their convergence
 Computers and Mathematcs wth Applcatons 57 (009) 87 95 Contents lsts avalable at ScenceDrect Computers and Mathematcs wth Applcatons journal homepage: www.elsever.com/locate/camwa Dscrete schemes for Gaussan
Computers and Mathematcs wth Applcatons 57 (009) 87 95 Contents lsts avalable at ScenceDrect Computers and Mathematcs wth Applcatons journal homepage: www.elsever.com/locate/camwa Dscrete schemes for Gaussan
Related-Mode Attacks on CTR Encryption Mode
 Internatonal Journal of Network Securty, Vol.4, No.3, PP.282 287, May 2007 282 Related-Mode Attacks on CTR Encrypton Mode Dayn Wang, Dongda Ln, and Wenlng Wu (Correspondng author: Dayn Wang) Key Laboratory
Internatonal Journal of Network Securty, Vol.4, No.3, PP.282 287, May 2007 282 Related-Mode Attacks on CTR Encrypton Mode Dayn Wang, Dongda Ln, and Wenlng Wu (Correspondng author: Dayn Wang) Key Laboratory
Overview. Basic Setup [9] Motivation and Tasks. Modularization 2008/2/20 IMPROVED COVERAGE CONTROL USING ONLY LOCAL INFORMATION
![Overview. Basic Setup [9] Motivation and Tasks. Modularization 2008/2/20 IMPROVED COVERAGE CONTROL USING ONLY LOCAL INFORMATION Overview. Basic Setup [9] Motivation and Tasks. Modularization 2008/2/20 IMPROVED COVERAGE CONTROL USING ONLY LOCAL INFORMATION](/thumbs/89/100766536.jpg) Overvew 2 IMPROVED COVERAGE CONTROL USING ONLY LOCAL INFORMATION Introducton Mult- Smulator MASIM Theoretcal Work and Smulaton Results Concluson Jay Wagenpfel, Adran Trachte Motvaton and Tasks Basc Setup
Overvew 2 IMPROVED COVERAGE CONTROL USING ONLY LOCAL INFORMATION Introducton Mult- Smulator MASIM Theoretcal Work and Smulaton Results Concluson Jay Wagenpfel, Adran Trachte Motvaton and Tasks Basc Setup
Joint Probabilistic Curve Clustering and Alignment
 Jont Probablstc Curve Clusterng and Algnment Scott Gaffney and Padhrac Smyth School of Informaton and Computer Scence Unversty of Calforna, Irvne, CA 9697-345 {sgaffney,smyth}@cs.uc.edu Abstract Clusterng
Jont Probablstc Curve Clusterng and Algnment Scott Gaffney and Padhrac Smyth School of Informaton and Computer Scence Unversty of Calforna, Irvne, CA 9697-345 {sgaffney,smyth}@cs.uc.edu Abstract Clusterng
Outline. Midterm Review. Declaring Variables. Main Variable Data Types. Symbolic Constants. Arithmetic Operators. Midterm Review March 24, 2014
 Mdterm Revew March 4, 4 Mdterm Revew Larry Caretto Mechancal Engneerng 9 Numercal Analyss of Engneerng Systems March 4, 4 Outlne VBA and MATLAB codng Varable types Control structures (Loopng and Choce)
Mdterm Revew March 4, 4 Mdterm Revew Larry Caretto Mechancal Engneerng 9 Numercal Analyss of Engneerng Systems March 4, 4 Outlne VBA and MATLAB codng Varable types Control structures (Loopng and Choce)
NURBS Curve Shape Modification and Fairness Evaluation
 NURBS Curve Shape Modfcaton and Farness Evaluaton TETSUZO KURAGANO AND AKIRA YAMAGUCHI Graduate School of Informaton Scence, Mese Unverst 2-590 Nagabuch, Ome-Ct, Toko, 98-8655, JAPAN kuragano@e.mese-u.ac.jp
NURBS Curve Shape Modfcaton and Farness Evaluaton TETSUZO KURAGANO AND AKIRA YAMAGUCHI Graduate School of Informaton Scence, Mese Unverst 2-590 Nagabuch, Ome-Ct, Toko, 98-8655, JAPAN kuragano@e.mese-u.ac.jp
Adaptive Fairing of Surface Meshes by Geometric Diffusion
 Adaptve Farng of Surface Meshes by Geometrc Dffuson Chandrajt L. Bajaj Department of Computer Scences, Unversty of Texas, Austn, TX 78712 Emal: bajaj@cs.utexas.edu Guolang Xu State Key Lab. of Scentfc
Adaptve Farng of Surface Meshes by Geometrc Dffuson Chandrajt L. Bajaj Department of Computer Scences, Unversty of Texas, Austn, TX 78712 Emal: bajaj@cs.utexas.edu Guolang Xu State Key Lab. of Scentfc
LS-TaSC Version 2.1. Willem Roux Livermore Software Technology Corporation, Livermore, CA, USA. Abstract
 12 th Internatonal LS-DYNA Users Conference Optmzaton(1) LS-TaSC Verson 2.1 Wllem Roux Lvermore Software Technology Corporaton, Lvermore, CA, USA Abstract Ths paper gves an overvew of LS-TaSC verson 2.1,
12 th Internatonal LS-DYNA Users Conference Optmzaton(1) LS-TaSC Verson 2.1 Wllem Roux Lvermore Software Technology Corporaton, Lvermore, CA, USA Abstract Ths paper gves an overvew of LS-TaSC verson 2.1,
Topology Design using LS-TaSC Version 2 and LS-DYNA
 Topology Desgn usng LS-TaSC Verson 2 and LS-DYNA Wllem Roux Lvermore Software Technology Corporaton, Lvermore, CA, USA Abstract Ths paper gves an overvew of LS-TaSC verson 2, a topology optmzaton tool
Topology Desgn usng LS-TaSC Verson 2 and LS-DYNA Wllem Roux Lvermore Software Technology Corporaton, Lvermore, CA, USA Abstract Ths paper gves an overvew of LS-TaSC verson 2, a topology optmzaton tool
A new paradigm of fuzzy control point in space curve
 MATEMATIKA, 2016, Volume 32, Number 2, 153 159 c Penerbt UTM Press All rghts reserved A new paradgm of fuzzy control pont n space curve 1 Abd Fatah Wahab, 2 Mohd Sallehuddn Husan and 3 Mohammad Izat Emr
MATEMATIKA, 2016, Volume 32, Number 2, 153 159 c Penerbt UTM Press All rghts reserved A new paradgm of fuzzy control pont n space curve 1 Abd Fatah Wahab, 2 Mohd Sallehuddn Husan and 3 Mohammad Izat Emr
Cubic Spline Interpolation for. Petroleum Engineering Data
 Appled Mathematcal Scences, Vol. 8, 014, no. 10, 5083-5098 HIKARI Ltd, www.m-hkar.com http://dx.do.org/10.1988/ams.014.4484 Cubc Splne Interpolaton for Petroleum Engneerng Data * Samsul Arffn Abdul Karm
Appled Mathematcal Scences, Vol. 8, 014, no. 10, 5083-5098 HIKARI Ltd, www.m-hkar.com http://dx.do.org/10.1988/ams.014.4484 Cubc Splne Interpolaton for Petroleum Engneerng Data * Samsul Arffn Abdul Karm
Steps for Computing the Dissimilarity, Entropy, Herfindahl-Hirschman and. Accessibility (Gravity with Competition) Indices
 Steps for Computng the Dssmlarty, Entropy, Herfndahl-Hrschman and Accessblty (Gravty wth Competton) Indces I. Dssmlarty Index Measurement: The followng formula can be used to measure the evenness between
Steps for Computng the Dssmlarty, Entropy, Herfndahl-Hrschman and Accessblty (Gravty wth Competton) Indces I. Dssmlarty Index Measurement: The followng formula can be used to measure the evenness between
LOOP ANALYSIS. The second systematic technique to determine all currents and voltages in a circuit
 LOOP ANALYSS The second systematic technique to determine all currents and voltages in a circuit T S DUAL TO NODE ANALYSS - T FRST DETERMNES ALL CURRENTS N A CRCUT AND THEN T USES OHM S LAW TO COMPUTE
LOOP ANALYSS The second systematic technique to determine all currents and voltages in a circuit T S DUAL TO NODE ANALYSS - T FRST DETERMNES ALL CURRENTS N A CRCUT AND THEN T USES OHM S LAW TO COMPUTE
NUMERICAL SOLVING OPTIMAL CONTROL PROBLEMS BY THE METHOD OF VARIATIONS
 ARPN Journal of Engneerng and Appled Scences 006-017 Asan Research Publshng Network (ARPN). All rghts reserved. NUMERICAL SOLVING OPTIMAL CONTROL PROBLEMS BY THE METHOD OF VARIATIONS Igor Grgoryev, Svetlana
ARPN Journal of Engneerng and Appled Scences 006-017 Asan Research Publshng Network (ARPN). All rghts reserved. NUMERICAL SOLVING OPTIMAL CONTROL PROBLEMS BY THE METHOD OF VARIATIONS Igor Grgoryev, Svetlana
Accounting for the Use of Different Length Scale Factors in x, y and z Directions
 1 Accountng for the Use of Dfferent Length Scale Factors n x, y and z Drectons Taha Soch (taha.soch@kcl.ac.uk) Imagng Scences & Bomedcal Engneerng, Kng s College London, The Rayne Insttute, St Thomas Hosptal,
1 Accountng for the Use of Dfferent Length Scale Factors n x, y and z Drectons Taha Soch (taha.soch@kcl.ac.uk) Imagng Scences & Bomedcal Engneerng, Kng s College London, The Rayne Insttute, St Thomas Hosptal,
Shape Preserving Positive and Convex Data Visualization using Rational Bi-cubic Functions
 Shape Preservng Postve and Conve Data Vsualzaton usng Ratonal B-cubc unctons Muhammad Sarfraz Malk Zawwar Hussan 3 Tahra Sumbal Shakh Department of Informaton Scence Adala Campus Kuwat Unverst Kuwat E-mal:
Shape Preservng Postve and Conve Data Vsualzaton usng Ratonal B-cubc unctons Muhammad Sarfraz Malk Zawwar Hussan 3 Tahra Sumbal Shakh Department of Informaton Scence Adala Campus Kuwat Unverst Kuwat E-mal:
KFUPM. SE301: Numerical Methods Topic 8 Ordinary Differential Equations (ODEs) Lecture (Term 101) Section 04. Read
 SE3: Numercal Metods Topc 8 Ordnar Dfferental Equatons ODEs Lecture 8-36 KFUPM Term Secton 4 Read 5.-5.4 6-7- C ISE3_Topc8L Outlne of Topc 8 Lesson : Introducton to ODEs Lesson : Talor seres metods Lesson
SE3: Numercal Metods Topc 8 Ordnar Dfferental Equatons ODEs Lecture 8-36 KFUPM Term Secton 4 Read 5.-5.4 6-7- C ISE3_Topc8L Outlne of Topc 8 Lesson : Introducton to ODEs Lesson : Talor seres metods Lesson
Programming in Fortran 90 : 2017/2018
 Programmng n Fortran 90 : 2017/2018 Programmng n Fortran 90 : 2017/2018 Exercse 1 : Evaluaton of functon dependng on nput Wrte a program who evaluate the functon f (x,y) for any two user specfed values
Programmng n Fortran 90 : 2017/2018 Programmng n Fortran 90 : 2017/2018 Exercse 1 : Evaluaton of functon dependng on nput Wrte a program who evaluate the functon f (x,y) for any two user specfed values
An efficient iterative source routing algorithm
 An effcent teratve source routng algorthm Gang Cheng Ye Tan Nrwan Ansar Advanced Networng Lab Department of Electrcal Computer Engneerng New Jersey Insttute of Technology Newar NJ 7 {gc yt Ansar}@ntedu
An effcent teratve source routng algorthm Gang Cheng Ye Tan Nrwan Ansar Advanced Networng Lab Department of Electrcal Computer Engneerng New Jersey Insttute of Technology Newar NJ 7 {gc yt Ansar}@ntedu
Module 6: FEM for Plates and Shells Lecture 6: Finite Element Analysis of Shell
 Module 6: FEM for Plates and Shells Lecture 6: Fnte Element Analyss of Shell 3 6.6. Introducton A shell s a curved surface, whch by vrtue of ther shape can wthstand both membrane and bendng forces. A shell
Module 6: FEM for Plates and Shells Lecture 6: Fnte Element Analyss of Shell 3 6.6. Introducton A shell s a curved surface, whch by vrtue of ther shape can wthstand both membrane and bendng forces. A shell
CSE 326: Data Structures Quicksort Comparison Sorting Bound
 CSE 326: Data Structures Qucksort Comparson Sortng Bound Steve Setz Wnter 2009 Qucksort Qucksort uses a dvde and conquer strategy, but does not requre the O(N) extra space that MergeSort does. Here s the
CSE 326: Data Structures Qucksort Comparson Sortng Bound Steve Setz Wnter 2009 Qucksort Qucksort uses a dvde and conquer strategy, but does not requre the O(N) extra space that MergeSort does. Here s the
CS 534: Computer Vision Model Fitting
 CS 534: Computer Vson Model Fttng Sprng 004 Ahmed Elgammal Dept of Computer Scence CS 534 Model Fttng - 1 Outlnes Model fttng s mportant Least-squares fttng Maxmum lkelhood estmaton MAP estmaton Robust
CS 534: Computer Vson Model Fttng Sprng 004 Ahmed Elgammal Dept of Computer Scence CS 534 Model Fttng - 1 Outlnes Model fttng s mportant Least-squares fttng Maxmum lkelhood estmaton MAP estmaton Robust
Kiran Joy, International Journal of Advanced Engineering Technology E-ISSN
 Kran oy, nternatonal ournal of Advanced Engneerng Technology E-SS 0976-3945 nt Adv Engg Tech/Vol. V/ssue /Aprl-une,04/9-95 Research Paper DETERMATO O RADATVE VEW ACTOR WTOUT COSDERG TE SADOWG EECT Kran
Kran oy, nternatonal ournal of Advanced Engneerng Technology E-SS 0976-3945 nt Adv Engg Tech/Vol. V/ssue /Aprl-une,04/9-95 Research Paper DETERMATO O RADATVE VEW ACTOR WTOUT COSDERG TE SADOWG EECT Kran
