Fuzzy Soft Mathematical Morphology
|
|
|
- Grace Lawrence
- 5 years ago
- Views:
Transcription
1 Fuzzy Soft Mathematical Morphology. Gasteratos, I. ndreadis and Ph. Tsalides Laboratory of Electronics Section of Electronics and Information Systems Technology Department of Electrical and Computer Engineering Democritus University of Thrace GR Xanthi, Greece ioannis@orfeas.ee.duth.gr bstract : new framework which extends the concepts of soft mathematical morphology into fuzzy sets is presented in this paper. Images can be considered as arrays of fuzzy singletons on the Cartesian grid. Based on this notion the definitions for the basic fuzzy soft morphological operations are derived. Compatibility with binary soft mathematical morphology as well as the algebraic properties of fuzzy soft operations are studied. Explanation of the defined operations is also provided through several examples and experimental results. Indexing terms : computer vision, mathematical morphology, fuzzy sets.
2 . Introduction Mathematical morphology was firstly introduced by Matheron [] and Serra [, 3] as a methodology for image processing. In this early form, mathematical morphology handles binary images as sets and probes them with a structuring element. The latter is a set, normally smaller than the image on which it is translated. By translating the structuring element over an image, and by applying basic set operations, such as intersection or union, the basic morphological operations are obtained. Grey-scale mathematical morphology is a natural extension of binary mathematical morphology into grey-scale images. The operations of intersection and union used in binary mathematical morphology are replaced by minimum and maximum operations, respectively. review of grey-scale mathematical morphology, with particular emphasis on algorithms and applications is presented in [4]. The two basic morphological operations are erosion and dilation, from which all the other morphological transforms can be composed. Morphological transforms can decompose complex shapes into more meaningful representations and separate them from undesirable parts [5]. Mathematical morphology has provided solutions to many computer vision problems, such as noise suppression, feature extraction, edge detection etc. [6]. Sinha and Dougherty [7] have introduced fuzzy mathematical morphology. In this approach the images are not treated as crisp binary sets, but as fuzzy sets. The set union and intersection have been replaced by fuzzy bold union and bold intersection, respectively, in order to formulate fuzzy erosion and dilation, respectively. This attempt to adapt mathematical morphology into fuzzy set theory is not unique. Several other attempts have been developed independently by researchers, and they are all described/discussed in [8].
3 nother approach to mathematical morphology is soft mathematical morphology introduced by Koskinen et al. [9]. In this approach weighted order statistics are used instead of the minima or maxima. The weights depend on the structuring element, which is divided into two parts : the core, the pixels that participate with weights greater than one, and the soft boundary, the pixels that participate with weights equal to one. It has been shown that soft morphological operations are less sensitive to additive noise and to small variations in object shape [0-]. In this paper a new framework which extends the concepts of soft mathematical morphology into fuzzy sets is presented. The definitions of the basic fuzzy soft morphological operations are given and their properties are also studied. It is shown that fuzzy soft morphological operations are dual, translation invariant and increasing, whilst they do not distribute over basic set operations, such as intersection and union. Furthermore, it is shown that fuzzy soft opening and closing are neither idempotent nor anti-extensive and extensive, respectively. The paper is organised as follows. In section fuzzy sets are reviewed. Binary and grey-scale mathematical morphology are summarised in section 3. In section 4 binary and grey-scale soft mathematical morphology are presented. Fuzzy mathematical morphology is reviewed in section 5. In section 6 the new definitions of fuzzy soft mathematical morphology are presented and their algebraic properties are studied. Examples and experimental results illustrating the new definitions are presented in section 7. Concluding remarks are made in section 8.. Fuzzy Sets Fundamentals Membership, in the N-dimensional Euclidean space E N, of a crisp set, may be defined in terms of the characteristic function µ : E N {0,} [3]: 3
4 ( ) µ x = 0 if if x x () Likewise, membership of a fuzzy set is characterised by its membership function µ : E N [0,]. The value µ (x) of the membership function at point x of the N-dimensional Euclidean space denotes the degree that point x belongs to set. The basic set operations, i.e. intersection, union, complement and difference, in terms of the characteristic functions (for crisp sets), or the membership functions (for fuzzy sets), are defined as follows: [ ] µ ( x ) min µ ( x ), µ ( x) () B = B [ ] µ ( x ) max µ ( x ), µ ( x) (3) B = B µ C ( x ) = µ ( x) (4) [ ] µ \ B( x ) = min µ ( x ), µ B( x) (5) Finally, the subset relation is : [ ] [ ] B µ ( x ) = min µ, µ B µ B( x ) = max µ, µ B (6) Let Z be the Cartesian grid and G={0, /L, /L,... L/L} the set of L+ normalised grey-levels. normalised image is defined as a mapping : Z G. Bearing the above definition in mind, an image can be considered as an array of fuzzy singletons, each with a membership function equal to the normalised grey-level value of the image at that point [4, 5]. fuzzy singleton is a fuzzy set whose support is a single point. 4
5 3. Standard Morphology [5, 6] In this paper binary and grey-scale mathematical morphology are referred to as standard mathematical morphology. This distinction is made frequently in the literature, in order to be discriminated by their extensions, such as soft mathematical morphology and fuzzy mathematical morphology. 3. Binary morphology Binary erosion and dilation are defined according to eqn.(7) and eqn.(8), respectively : È? = I ( ) x (7) x B? = U ( ) x (8) x B where, B are sets of Z ; () x is the translation of by x, and -B is the reflection of B. These are defined as follows : ( ) = { c Z c = a + x for some a x } (9) { x b x = -b} B = for some B, (0) Set is the image under process and set B is the structuring element. The definitions of binary opening and closing are : o B = ( È B) B and () B = ( B) È B () respectively. 5
6 3. Grey-scale morphology In terms of grey-scale morphology erosion and dilation are : ( f È g)( x) = min{ f ( x + y) g( y)} y G and (3) ( f g)( x) = max { f ( x - y) + g( y)} respectively. y G F ( x y) (4) where x, y Z are the spatial coordinates, f :F g :G Z is the integer value grey-scale image, Z is the grey-scale structuring element and F, G Z, are the domains of the grey-scale image and grey-scale structuring element, respectively. 4. Soft Mathematical Morphology [9, 0] In soft morphological operations the maximum or the minimum operations, used in standard morphology, are replaced by weighted order statistics. Furthermore, the structuring element B is divided into two subsets: the core B and the soft boundary B =B\B. 4. Grey-scale soft mathematical morphology In soft morphological erosion and in soft morphological dilation of an image f the pixels of f are combined with the pixels of the structuring element as in traditional morphology; the results which are related with the soft boundary of the structuring element and the results which are related with the core of the structuring element (repeated k times) are put in an ascending or a descending order list. The kth element of this list is the result of soft morphological erosion or dilation. Let {k f(x)} denote the repetition of f(x) 6
7 for k times, i.e.{k f (x )}={ f (x ), f (x ),... f (x )} (k times). Soft morphological erosion of a grey-scale image f by a soft grey-scale structuring element [ß, a, k ] is []: [ ]( ) th smallest of ( ) ( ) ({ ( )} { ( ) ( )}) f È ß,a,k x = k k f y a x + y f z ß x + z ( x+ y) K ( x + z) K (5) Soft morphological dilation of f by [ß, a, k ] is : [ ]( ) th largest of ( ) ( ) ({ ( )} { ( ) ( )}) f ß,a, k x = k k f y + a x y f z + ß x z ( x-y) K ( x z) K where x, y, z Z, are the spatial coordinates, f:f a:k ß:K Z is the grey-scale image, Z is the core of the grey-scale structuring element, Z is the soft boundary of the grey-scale structuring element, F, K, K Z are the domains of the grey-scale image, the core of the grey-scale structuring element and the soft boundary of the grey-scale structuring element, respectively, and element. K =K\K, where K Z is the domain of the grey-scale structuring (6) 4. Binary soft mathematical morphology The basic definitions of the binary soft erosion and dilation, are respectively [] : ( È [?,?, k ])( x ) = 0 ( k [ ( ) ] [ ( ) x x ]) kcard[ B ] + Card[ B ] k + if Card B + Card B otherwise (7) 7
8 = 0 ( [?,?, k ])( x ) ( k [ ( ) x ] [ ( ) x ]) if Card B + Card B k otherwise (8) where, Card[X] denotes the cardinality of set X. 5. Fuzzy Mathematical Morphology In the past several attempts have been made to apply fuzzy set theory to mathematical morphology. These attempts have resulted in different approaches and definitions. These are reviewed in [8], where a general framework is proposed. This framework leads to an infinity of fuzzy mathematical morphologies, which are constructed in families with specific properties. In this paper the approach described by Sinha and Dougherty [7] has been used. This is a special case of the framework presented in [8]. In this approach, fuzzy mathematical morphology is examined in terms of fuzzy fitting. The fuzziness is introduced by the degree to which the structuring element fits into the image. The operations of erosion and dilation of a fuzzy image by a fuzzy structuring element having a bounded support, are defined in terms of their membership functions as follows : [ [ B ]] µ È B( x ) = min min, + µ ( x + y ) µ ( y) y B = min, min [ + µ ( x + y ) µ B( y) ] y B and (9) [ [ 0 B ] ] µ ( x ) = max max, µ ( x - y ) + µ ( y) = B y B = max 0, max [ µ ( x - y ) + µ B( y) ] y B (0) where x, y Z are the spatial coordinates and 8
9 µ, µ B are the membership functions of the image and the structuring element, respectively. It is obvious from eqns. (9) and (0) that the result of both fuzzy erosion and dilation have membership functions whose values are restricted to the interval [0,]. 6. Fuzzy Soft Mathematical Morphology 6. Definitions Fuzzy soft mathematical morphology operations are defined taking into consideration that in soft mathematical morphology the structuring element is divided into two subsets, i.e. the core and the soft boundary, from which the core 'weights' more than the soft boundary in the formation of the final result. lso, depending on k, the kth order statistic provides the result of the operation. lso, fuzzy soft morphological operation should preserve the notion of fuzzy fitting [7]. Thus, the definitions for fuzzy soft erosion and fuzzy soft dilation are derived in this paper for the first time as far as we know, as follows : { ( B ) } µ x k k µ x + y µ y È [ ( ) min[, th smallest of ( ( ) ( ) + B B,, k ] y B z B () and { µ x +z µ B z + } ( ) ( ) )] { ( B )} µ ( x) max[ 0, k th larg est of( k µ ( x - y ) + µ ( y) [ B, B, k ] y B z B { µ x - z + µ B z } ( ) ( ) )] () where x, y, z Z, are the spatial coordinates and µ, µ B, µ B are the membership functions of the image, the core of the structuring element and the soft boundary of the structuring element. 9
10 and B dditionally, for the fuzzy structuring element B Z : B = B B B =. It is obvious that for k= eqns. () and () are reformed to eqns. (9) and (0) respectively, i.e. simple fuzzy morphology. Example : In this example the adopted coordinate system is (row, column). The arrows denote the origin of the coordinate system and direction. Let us consider the image and the structuring element B. The core in B is separated from the soft boundary by a bold line. Fuzzy soft erosion and fuzzy soft dilation are computed for cases k= and k=. If k>card[b], where B is the soft boundary of the structuring element, the soft morphological operations are affected only by the core B, i.e. using B as the structuring element. Therefore, in this case the nature of soft morphological operations is not preserved [0, ]. For this reason the k min Card B /, Card B is adopted in fuzzy soft { } constraint ( ) ( ) mathematical morphology, as well as in soft mathematical morphology. In this example only the cases of k= and k= are considered, in order to comply with this constraint B B Case : k= The fuzzy soft erosion of the image is calculated as follows : 0
11 ? [ ] [ ] ( ),, [ ] ( 0) [ ], min,min , , , ] = 0. 4 µ? 0, 0 = µ È [ B B ( 0, 0) = min,min , , = 0. 3 µ? =... µ 5, = min,min , = 0. [ ] ( ) [ ] Therefore, the eroded image is : The values of the eroded image at points (0, ) and (, ) are higher than the rest values of the image. This agrees with the notion of fuzzy fitting, since only at these points the structuring element fits better than the rest points of the image. Fuzzy erosion quantifies the degree of structuring element fitting. The larger the number of pixels of the structuring element, the more difficult the fitting. Furthermore, fuzzy soft erosion shrinks the image. If fuzzy image is considered as a noisy version of a binary image [7], then the object of interest consists of points (0, ), (0, ), (0, 3), (0, 4), (, ), (, ), (, 3), (, 4), (, ), (, ) and (, 3) and the rest is the background. By eroding the image with a 4-pixel horizontal structuring element it would be expected that the eroded image would comprise points (0, ) and (,). This is exactly what it has been obtained. Similarly, the dilation of the image is calculated as follows : µ D ( 0, 0) = µ [ B, B, 0 0 [ 0 [ ] ] 0 8 µ D ( 0) = [ ](, ) = max,max. +., +. =., max 0,max [ , , ] ] = µ 5, = max 0,max , , = 0. D [ ] ( ) [ ]
12 Therefore, the dilated image is : s it can be seen, fuzzy soft dilation expands the image. In other words the dilated image includes the points of the original image and also points (0, 0), (0, 5), (, 0), (, 5), and (, 0). Case : k= The erosion of the image is calculated as follows : µ? ( 0, 0) = µ È [ (0, 0 ) = min B B [, nd smallest[ 0. 3, 0. 3,.,., ] ] = 0. 3,, ] [ ] ( ) nd smallest[ ] µ 0, = min, 0. 4,.,., 0. 9, 0. 9, 0. 9 = ? [ ] ( ) nd smallest[ ] µ 5, = min, 0. 4, 0., 0. = 0.? The eroded image for k= is : In this case the values of the eroded image at points (0, ), (0, ), (0, 3), (, ), (, ) and (, 3) are higher than the rest values of the image. This is in agreement with the notion of fuzzy soft fitting. t these points the repeated k times "high value" pixels, which are combined with the core of the structuring
13 element, plus the pixels which are combined with the soft boundary of the structuring element, are greater than or equal to the kcard[b]+card[b]- k+. Similarly the dilation of the image is calculated : µ D ( 0, 0) = µ (0, 0 ) = max B B [ 0, nd l arg est[ 0., 0., 0. 8] ] = 0.,, ] [ ] ( ) nd l est[ ] µ 0, = max 0, arg 0., 0., 0. 9, 0. 9, 0. 6 = D [ ] ( ) nd l est[ ] µ 5, = max 0, arg 0. 0, 0., 0., 0. 0, 0. 0 = 0. D [ Therefore, the dilated image for k= is : Here again fuzzy soft dilation expands the image, but more softly, than when k=. This means that certain points which were previously belonging (k=) to the image ((0, 0),(, 0), (, 0) and (, 4)), now these belong (k=) to the background. The greater the k, the less the effect of the dilation. Finally, fuzzy soft opening and closing are defined, as : µ o [ B B k x µ ( È [ B B k ) [ B B k x,, ]( ),, ],, ]( ) (3) and µ [ B B k x µ ( [ B B k ) È [ B B k x,, ]( ),, ],, ]( ) (4) respectively. 6. Compatibility with soft mathematical morphology 3
14 Lets us consider Example. By thresholding image and structuring element B (using a threshold equal to 0.5), the following binary image and binary structuring element are obtained : B By applying soft binary erosion and soft binary dilation to image with structuring element B the following images are obtained for k= and k= : k= : k= : It is obvious that these results are identical to those of Example, when the same threshold value is used. This was expected, since binary soft morphology quantifies the soft fitting in a crisp way, whereas fuzzy soft erosion quantifies the soft fitting in a fuzzy way. The same results are obtained using a threshold equal to However, when fuzzy soft morphology and thresholding with a threshold equal to 0.6 on the one hand and thresholding with the same threshold and soft morphology on the other 4
15 hand are applied, different results will be obtained. This means that the operations, generally, do not commute. 6.3 lgebraic properties in fuzzy soft mathematical morphology The following algebraic properties for fuzzy soft erosion and dilation, as well as for fuzzy soft opening and closing operations are studied : Duality Theorem Fuzzy soft erosion and dilation are dual operations i.e.: µ k x µ ( ) x C C [ B B =,, ]( ) È ( ) (5) [ B, B, k ] Proof: µ C ( x ) = µ ( x) ( k ) È [ È [ B, B, ] B, B, k ] { ( B )} = min[, k th smallest of( k µ ( x + y ) µ ( y) + y B z B { µ ( x + z ) µ B ( z) + } )] ( B ) { } = max[, [ k th smallest of( k µ ( x + y ) µ ( y) + y B z B { µ ( x + z) µ z B ( ) + } )]] 5
16 { ( ( B ) )} = max[ 0, k th larg est of( k µ ( x + y ) µ ( y) + y B z B { ( µ x + z µ B z + ) } ( B ) ( ) ( ) )]] { } = max[ 0, k th l arg est of( k -µ ( x + y ) + µ ( y) y B z B {-µ ( x +z ) + µ B ( z) })]] ( C B ) { } = max[ 0, k th l arg est of( k µ ( x + y ) + µ ( y) y B z B = µ ( x) [-B, B, k ] { µ C x + z + µ z B } ( ) ( ) )]] Eqn. (4) and identities [6] : k th larg est of( p, q) = k th smallest of( -p, - q) and k th larg est of( p, q) + r = k th l arg est of( p+r, q+r) have been used, to prove the duality theorem. Opening and closing are also dual operations i.e.: µ C ( ) x µ C x [ ( ) = B B k [ B B k,, ] o,, ]( ) (6) Proof: µ C x µ C ( ) ( ) x ( ) = [ B B k [ B B k È [ ( ) B B k,, ] [,, ],, ]] = µ C ( x ) ( [ B, B, k ]) [ B, B, k ] = µ C ( ) x È[- B B k [ ( ),, ] B, B, k ] = µ C ( x) o [ B, B, k ] Translation Invariance Fuzzy soft erosion and dilation are translation invariant, i.e. : µ x = µ x (7) ( ) k ( k u È [ ( ) B B È [ ( ) B B ),, ],, ] u 6
17 where u Z. Proof: ( B B k ) µ È [ ( x ) = µ x + u,, ] È [ ( ) B, B, k ] u { ( u B )} = min[, k th smallest of( k µ ( x + + y ) µ ( y) + y B z B { µ x + u + z µ B z + } { ( ( ) B u )} { µ ( ) ( x + z ) µ B ( z) + })] = min[, k th smallest of( k µ ( x + y ) µ ( y) + = ( ) È [ u y B z B µ ( x ) B, B, k ] ( ) ( ) )] u Similarly, or by the duality theorem (eqn. (5)) it can be proven that fuzzy soft dilation is also invariant under translation. Increasing Both fuzzy soft erosion and dilation are increasing operations, i.e. : µ B B k x < µ B B k x È [,, ]( ) ',, ]( ) È [ µ? < µ? ' µ B B k x < µ B B k x [,, ]( ) ' [,, ]( ) (8) where and?, are two images with membership functions µ? and µ?, respectively and µ? < µ? in the whole Z grid. Proof: 7
18 ( ) < ' ( ) ( ) < '( ) µ? x + y µ? x + y µ? < µ? ' µ? x +z µ? x +z ( ) ( ) < ( ) ( ) ' ( ) ( ) < ' ( ) ( ) µ? x + y µ B y + µ? x + y µ B y + µ? x + z µ B z + µ? x + z µ B z + { ( B ) } min[, k th smallest of( k µ ( x + y ) µ ( y) + y B z B { µ ( x + z ) µ B ( z) + } )] ( ' B ) { } < min[, k th smallest of( k µ ( x + y ) µ ( y) + y B z B µ ( x ) < µ ( x) È [ È [ B, B, k ] ' B, B, k ] { µ ' x +z µ B z + } ( ) ( ) )] Similarly, or by the duality theorem it is proven that fuzzy soft dilation is also an increasing operation. Distributivity Fuzzy soft erosion is not distributive over intersection, as it is in standard morphology; i.e. in general : µ ( x ) µ ( x ) (9) ( ) È [ B, B, k ] ( È [ B, B, k ] ) ( È [ B, B, k ]) n illustrative example follows : Example : Consider image and structuring element B. Suppose that image is the intersection of two images and. 8
19 B = The fuzzy soft erosion for k= of,, and the intersection of the eroded and the eroded are, respectively: [B, B, ] [B, B, ] [B, B, ] [B, B, ] [B, B, ] From the above example it is clear that µ ( ) È [ B B k x,, ] ( ) µ ( È [ B B k ) ( B B k ) x È [ ( ), and thus fuzzy soft erosion generally,, ],, ] does not distribute over intersection. Similarly, or by the duality theorem it can be proven that fuzzy soft dilation does in general not distribute over union : µ ( ) [ B B k x µ ( B B k ) ( B B k ) x,, ]( ) [,, ] [,, ] ( ) (30) nti-extensivity - Extensivity Fuzzy soft opening is not anti-extensive. If it were anti-extensive, then : µ ( x )??? k µ ( o[,, ]? x ), x Z. However, in the following example it is ß shown that x Z, so that : µ ( x ) o[ B, B, k ] > µ ( x ). Similarly, it is shown that, in general, fuzzy soft closing is not extensive too : x Z, so that : µ ( x ) [ B, B, k ] < µ ( x ). 9
20 Example 3 : Consider the image and the structuring element B, for k= B B B In the above example µ ( o[ B, B, k ] 0, ) =. 0 > µ (, ). 0 = 0, which means that fuzzy soft opening is not anti-extensive. lso, µ [ B, B, k ](0, 3) = 0. < µ (0, 3) = 0,. which means that fuzzy soft closing is not extensive too. Idempotency Fuzzy soft opening and closing have been defined as fuzzy soft erosion followed by fuzzy soft dilation and fuzzy soft dilation followed by fuzzy soft erosion, respectively. However, in algebra an application is said to be an opening if it is anti-extensive, increasing and idempotent []. It is straightforward that fuzzy soft opening is increasing, since both fuzzy soft erosion and dilation are increasing. It has been shown that fuzzy soft opening is not anti-extensive (Example 3). lso, in general, fuzzy soft opening is not idempotent : µ o [ B B k x µ ( o [ B B k ) o [ B B k x,, ]( ),, ],, ]( ) (3) This is illustrated by the following example : 0
21 Example 4 : Consider the image and the structuring element B, for k= B ( B) ( B) B From the above example it is obvious that fuzzy soft opening is not idempotent. By duality theorem (eqn. (6)) it can be proven that, in general, fuzzy soft closing is not idempotent too : µ [ B B k x µ ( [ B B k ) [ B B k x,, ]( ),, ],, ]( ) (3) 7. Experimental Results Illustration of the basic fuzzy soft morphological operations defined in this paper are given through -dimensional (-d) and -dimensional (-d) images. Figure depicts fuzzy soft morphological erosion and dilation in -d space. More specifically, Figure a shows the initial -d image and Figure b shows the structuring element. The core of the structuring element is the shaded area and the rest area of the structuring element is the soft boundary. Figures c and d are the images for k= of fuzzy soft erosion and fuzzy soft dilation, respectively. Figures e and f are the images for k= of fuzzy soft erosion and fuzzy soft dilation, respectively. In the latter four
22 Figures the original image is represented by a dotted line and the results by a continuous line. By comparing Figure c with Figure e and Figure d with Figure f it becomes clear that the action of the structuring element is more effective when k=, i.e. the results of both fuzzy soft erosion and dilation are more visible in case of k=, than in case of k=. Figure shows the result of fuzzy soft morphological erosion and dilation in a -d image. Figure 3a shows the initial image. Figure b shows the structuring element. The core of the structuring element is separated from the soft boundary by the bold line. Experiments have been performed using a commercial frame grabber. The image in Figure b has been considered as an array of fuzzy singletons [4]. The results of fuzzy soft erosion (k=) after the first and the second interaction are presented in Figures c and d, respectively. The white area is reduced after each interaction. The white area of the eroded image (Figure c) is the area of the initial image, where the structuring element fits better. Similarly, in Figures e and f are presented the results of fuzzy soft erosion (k=3) after the first and the second interaction. Comparing Figures c and e it is made clear that the greater the k the less visible the results of fuzzy soft erosion. Figures g and h present the results of fuzzy soft dilation (k=) after the first and the second interaction, respectively. In the case of fuzzy soft dilation the white area increases. Similarly in Figures i and j are presented the results of fuzzy soft dilation (k=3) after the first and the second interaction. gain the greater the k the less visible the results of fuzzy soft dilation. 8. Conclusions new approach to soft morphology has been presented in this paper. The proposed approach is based on fuzzy set theory. The definitions for the basic fuzzy soft morphological operations have been extracted and their
23 algebraic properties have been studied. Fuzzy soft morphological operations inherit properties and restrictions of both soft morphology and fuzzy morphology. More specifically, it has been shown that fuzzy soft morphological operations are dual, translation invariant and increasing, whilst they do not distribute over basic set operations, such as intersection and union and they are not extensive, anti-extensive and idempotent. The definitions and the algebraic properties have been illustrated through examples and experimental results. 3
24 REFERENCES MTHERON, G. : Random sets and integral geometry (Wiley, New York, 975). SERR, J. : Image analysis and mathematical morphology : Vol.I (cademic Press, London, 98). 3 SERR, J. : Introduction to mathematical morphology, Comp. Vision Graph. Imag. Proc., 986, 35, (3), pp STERNBERG, R. : Grayscale morphology, Computer Vision, Graphics and Image Processing, 986, 35, (3), pp HRLICK, R. M., STERNBERG, R., and ZHUNG, X. : Image analysis using mathematical morphology, IEEE Trans. Pattern nalysis and Machine Intelligence, 987, PMI-9, (4), pp GONZLEZ, R. C. and WOODS, R. E.: Digital image processing (ddison-wesley, New York, 99). 7 SHINH, D., and DOUGHERTY, E. R. : Fuzzy mathematical morphology, Journal Visual Commun. Imag. Repres., 99, 3, (3), pp BLOCH, I., and MITRE, H. : Fuzzy mathematical morphologies: a comparative study, Pattern Recognition, 995, 8, (9), pp KOSKINEN, L., STOL, J., and NEUVO, Y. : Soft morphological filters, Proc. SPIE Symp. Image lgebra and Morphological Image Proc., 99, 568, pp KUOSMNEN, P., and STOL, J. : Soft morphological filtering, Journal Mathematical Imag. Vision, 995, 5, (3), pp.3-6. PU, C. C. and SHIH, F. Y.: Threshold decomposition of grey-scale soft morphology into binary soft morphology, Graphical Models and Image Processing, 995, 57, pp
25 SHIH, F. Y., and PU, C. C. : nalysis of the properties of soft morphological filtering using threshold decomposition, IEEE Trans. Signal Proc., 995, 43, (), pp ZDEH, L.. : Fuzzy sets, Inform. Control, 965, 8, pp GOETCHRIN, V. : From binary to grey tone image processing using fuzzy logic concepts, Pattern Recognition, 980,, (), pp BEZDEK, J. C. and PL, S. K., (editors) : Fuzzy models for pattern recognition, (IEEE Press, New York, 99). 6 DVID, H.. : Order statistics, (Wiley, New York, 98) nd edn. 5
26 FIGURE CPTIONS Figure : (a) Initial -d fuzzy set, (b) structuring element, (c) fuzzy soft erosion (k=), (d) fuzzy soft dilation (k=), (e) fuzzy soft erosion (k=) and (f) fuzzy soft dilation (k=). Figure : (a) The initial image, (b) structuring element, (c) fuzzy soft erosion (k=) after the first interaction, (d) fuzzy soft erosion (k=) after the second interaction, (e) fuzzy soft erosion (k=3) after the first interaction, (f) fuzzy soft erosion (k=3) after the second interaction, (g) fuzzy soft dilation (k=) after the first interaction, (h) fuzzy soft dilation (k=) after the second interaction, (i) fuzzy soft dilation (k=3) after the first interaction and (j) fuzzy soft dilation (k=3) after the second interaction. 6
27 Membership values Spatial coordinates Figure a Membership values Spatial coordinates Figure b 7
28 Membership values Spatial coordinates Figure c Membership values Spatial coordinates Figure d 8
29 Membership values Spatial coordinates Figure e Membership values Spatial coordinates Figure f 9
30 Figure a Figure b Figure c Figure d Figure e Figure f 30
31 Figure g Figure h Figure i Figure j 3
Improvement of the Majority Gate Algorithm for Grey Scale Dilation/Erosion
 Improvement of the Majority Gate Algorithm for Grey Scale Dilation/Erosion A Gasteratos, I Andreadis and Ph Tsalides Laboratory of Electronics Section of Electronics and Information Systems Technology
Improvement of the Majority Gate Algorithm for Grey Scale Dilation/Erosion A Gasteratos, I Andreadis and Ph Tsalides Laboratory of Electronics Section of Electronics and Information Systems Technology
Extension and VLSI Implementation of the Majority-Gate Algorithm for Gray-Scale Morphological Operations
 Extension and VLSI Implementation of the Majority-Gate Algorithm for Gray-Scale Morphological Operations A Gasteratos, I Andreadis and Ph Tsalides Laboratory of Electronics Section of Electronics and Information
Extension and VLSI Implementation of the Majority-Gate Algorithm for Gray-Scale Morphological Operations A Gasteratos, I Andreadis and Ph Tsalides Laboratory of Electronics Section of Electronics and Information
Morphological Image Processing
 Morphological Image Processing Ranga Rodrigo October 9, 29 Outline Contents Preliminaries 2 Dilation and Erosion 3 2. Dilation.............................................. 3 2.2 Erosion..............................................
Morphological Image Processing Ranga Rodrigo October 9, 29 Outline Contents Preliminaries 2 Dilation and Erosion 3 2. Dilation.............................................. 3 2.2 Erosion..............................................
ECEN 447 Digital Image Processing
 ECEN 447 Digital Image Processing Lecture 7: Mathematical Morphology Ulisses Braga-Neto ECE Department Texas A&M University Basics of Mathematical Morphology Mathematical Morphology (MM) is a discipline
ECEN 447 Digital Image Processing Lecture 7: Mathematical Morphology Ulisses Braga-Neto ECE Department Texas A&M University Basics of Mathematical Morphology Mathematical Morphology (MM) is a discipline
Morphological Image Processing
 Morphological Image Processing Morphology Identification, analysis, and description of the structure of the smallest unit of words Theory and technique for the analysis and processing of geometric structures
Morphological Image Processing Morphology Identification, analysis, and description of the structure of the smallest unit of words Theory and technique for the analysis and processing of geometric structures
Morphological Image Processing
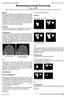
 Morphological Image Processing Binary image processing In binary images, we conventionally take background as black (0) and foreground objects as white (1 or 255) Morphology Figure 4.1 objects on a conveyor
Morphological Image Processing Binary image processing In binary images, we conventionally take background as black (0) and foreground objects as white (1 or 255) Morphology Figure 4.1 objects on a conveyor
09/11/2017. Morphological image processing. Morphological image processing. Morphological image processing. Morphological image processing (binary)
 Towards image analysis Goal: Describe the contents of an image, distinguishing meaningful information from irrelevant one. Perform suitable transformations of images so as to make explicit particular shape
Towards image analysis Goal: Describe the contents of an image, distinguishing meaningful information from irrelevant one. Perform suitable transformations of images so as to make explicit particular shape
Introduction. Computer Vision & Digital Image Processing. Preview. Basic Concepts from Set Theory
 Introduction Computer Vision & Digital Image Processing Morphological Image Processing I Morphology a branch of biology concerned with the form and structure of plants and animals Mathematical morphology
Introduction Computer Vision & Digital Image Processing Morphological Image Processing I Morphology a branch of biology concerned with the form and structure of plants and animals Mathematical morphology
Biomedical Image Analysis. Mathematical Morphology
 Biomedical Image Analysis Mathematical Morphology Contents: Foundation of Mathematical Morphology Structuring Elements Applications BMIA 15 V. Roth & P. Cattin 265 Foundations of Mathematical Morphology
Biomedical Image Analysis Mathematical Morphology Contents: Foundation of Mathematical Morphology Structuring Elements Applications BMIA 15 V. Roth & P. Cattin 265 Foundations of Mathematical Morphology
Chapter 9 Morphological Image Processing
 Morphological Image Processing Question What is Mathematical Morphology? An (imprecise) Mathematical Answer A mathematical tool for investigating geometric structure in binary and grayscale images. Shape
Morphological Image Processing Question What is Mathematical Morphology? An (imprecise) Mathematical Answer A mathematical tool for investigating geometric structure in binary and grayscale images. Shape
morphology on binary images
 morphology on binary images Ole-Johan Skrede 10.05.2017 INF2310 - Digital Image Processing Department of Informatics The Faculty of Mathematics and Natural Sciences University of Oslo After original slides
morphology on binary images Ole-Johan Skrede 10.05.2017 INF2310 - Digital Image Processing Department of Informatics The Faculty of Mathematics and Natural Sciences University of Oslo After original slides
Image Enhancement Using Fuzzy Morphology
 Image Enhancement Using Fuzzy Morphology Dillip Ranjan Nayak, Assistant Professor, Department of CSE, GCEK Bhwanipatna, Odissa, India Ashutosh Bhoi, Lecturer, Department of CSE, GCEK Bhawanipatna, Odissa,
Image Enhancement Using Fuzzy Morphology Dillip Ranjan Nayak, Assistant Professor, Department of CSE, GCEK Bhwanipatna, Odissa, India Ashutosh Bhoi, Lecturer, Department of CSE, GCEK Bhawanipatna, Odissa,
MA651 Topology. Lecture 4. Topological spaces 2
 MA651 Topology. Lecture 4. Topological spaces 2 This text is based on the following books: Linear Algebra and Analysis by Marc Zamansky Topology by James Dugundgji Fundamental concepts of topology by Peter
MA651 Topology. Lecture 4. Topological spaces 2 This text is based on the following books: Linear Algebra and Analysis by Marc Zamansky Topology by James Dugundgji Fundamental concepts of topology by Peter
Processing of binary images
 Binary Image Processing Tuesday, 14/02/2017 ntonis rgyros e-mail: argyros@csd.uoc.gr 1 Today From gray level to binary images Processing of binary images Mathematical morphology 2 Computer Vision, Spring
Binary Image Processing Tuesday, 14/02/2017 ntonis rgyros e-mail: argyros@csd.uoc.gr 1 Today From gray level to binary images Processing of binary images Mathematical morphology 2 Computer Vision, Spring
Mathematical Morphology and Distance Transforms. Robin Strand
 Mathematical Morphology and Distance Transforms Robin Strand robin.strand@it.uu.se Morphology Form and structure Mathematical framework used for: Pre-processing Noise filtering, shape simplification,...
Mathematical Morphology and Distance Transforms Robin Strand robin.strand@it.uu.se Morphology Form and structure Mathematical framework used for: Pre-processing Noise filtering, shape simplification,...
2 Review of Set Theory
 2 Review of Set Theory Example 2.1. Let Ω = {1, 2, 3, 4, 5, 6} 2.2. Venn diagram is very useful in set theory. It is often used to portray relationships between sets. Many identities can be read out simply
2 Review of Set Theory Example 2.1. Let Ω = {1, 2, 3, 4, 5, 6} 2.2. Venn diagram is very useful in set theory. It is often used to portray relationships between sets. Many identities can be read out simply
CS 5540 Spring 2013 Assignment 3, v1.0 Due: Apr. 24th 11:59PM
 1 Introduction In this programming project, we are going to do a simple image segmentation task. Given a grayscale image with a bright object against a dark background and we are going to do a binary decision
1 Introduction In this programming project, we are going to do a simple image segmentation task. Given a grayscale image with a bright object against a dark background and we are going to do a binary decision
CSC Discrete Math I, Spring Sets
 CSC 125 - Discrete Math I, Spring 2017 Sets Sets A set is well-defined, unordered collection of objects The objects in a set are called the elements, or members, of the set A set is said to contain its
CSC 125 - Discrete Math I, Spring 2017 Sets Sets A set is well-defined, unordered collection of objects The objects in a set are called the elements, or members, of the set A set is said to contain its
Two Image-Template Operations for Binary Image Processing. Hongchi Shi. Department of Computer Engineering and Computer Science
 Two Image-Template Operations for Binary Image Processing Hongchi Shi Department of Computer Engineering and Computer Science Engineering Building West, Room 331 University of Missouri - Columbia Columbia,
Two Image-Template Operations for Binary Image Processing Hongchi Shi Department of Computer Engineering and Computer Science Engineering Building West, Room 331 University of Missouri - Columbia Columbia,
EE 584 MACHINE VISION
 EE 584 MACHINE VISION Binary Images Analysis Geometrical & Topological Properties Connectedness Binary Algorithms Morphology Binary Images Binary (two-valued; black/white) images gives better efficiency
EE 584 MACHINE VISION Binary Images Analysis Geometrical & Topological Properties Connectedness Binary Algorithms Morphology Binary Images Binary (two-valued; black/white) images gives better efficiency
A New Algorithm for Weighted Order Statistics Operations
 A ew Algorithm for Weighted Order Statistics Operations A. Gasteratos and I. Andreadis Laboratory of Electronics Section of Electronics and Information Systems Technology Department of Electrical and Computer
A ew Algorithm for Weighted Order Statistics Operations A. Gasteratos and I. Andreadis Laboratory of Electronics Section of Electronics and Information Systems Technology Department of Electrical and Computer
[Ch 6] Set Theory. 1. Basic Concepts and Definitions. 400 lecture note #4. 1) Basics
![[Ch 6] Set Theory. 1. Basic Concepts and Definitions. 400 lecture note #4. 1) Basics [Ch 6] Set Theory. 1. Basic Concepts and Definitions. 400 lecture note #4. 1) Basics](/thumbs/82/86066673.jpg) 400 lecture note #4 [Ch 6] Set Theory 1. Basic Concepts and Definitions 1) Basics Element: ; A is a set consisting of elements x which is in a/another set S such that P(x) is true. Empty set: notated {
400 lecture note #4 [Ch 6] Set Theory 1. Basic Concepts and Definitions 1) Basics Element: ; A is a set consisting of elements x which is in a/another set S such that P(x) is true. Empty set: notated {
Research Article Image Segmentation Using Gray-Scale Morphology and Marker-Controlled Watershed Transformation
 Discrete Dynamics in Nature and Society Volume 2008, Article ID 384346, 8 pages doi:10.1155/2008/384346 Research Article Image Segmentation Using Gray-Scale Morphology and Marker-Controlled Watershed Transformation
Discrete Dynamics in Nature and Society Volume 2008, Article ID 384346, 8 pages doi:10.1155/2008/384346 Research Article Image Segmentation Using Gray-Scale Morphology and Marker-Controlled Watershed Transformation
ROUGH MEMBERSHIP FUNCTIONS: A TOOL FOR REASONING WITH UNCERTAINTY
 ALGEBRAIC METHODS IN LOGIC AND IN COMPUTER SCIENCE BANACH CENTER PUBLICATIONS, VOLUME 28 INSTITUTE OF MATHEMATICS POLISH ACADEMY OF SCIENCES WARSZAWA 1993 ROUGH MEMBERSHIP FUNCTIONS: A TOOL FOR REASONING
ALGEBRAIC METHODS IN LOGIC AND IN COMPUTER SCIENCE BANACH CENTER PUBLICATIONS, VOLUME 28 INSTITUTE OF MATHEMATICS POLISH ACADEMY OF SCIENCES WARSZAWA 1993 ROUGH MEMBERSHIP FUNCTIONS: A TOOL FOR REASONING
Discrete Mathematics Lecture 4. Harper Langston New York University
 Discrete Mathematics Lecture 4 Harper Langston New York University Sequences Sequence is a set of (usually infinite number of) ordered elements: a 1, a 2,, a n, Each individual element a k is called a
Discrete Mathematics Lecture 4 Harper Langston New York University Sequences Sequence is a set of (usually infinite number of) ordered elements: a 1, a 2,, a n, Each individual element a k is called a
Topic 6 Representation and Description
 Topic 6 Representation and Description Background Segmentation divides the image into regions Each region should be represented and described in a form suitable for further processing/decision-making Representation
Topic 6 Representation and Description Background Segmentation divides the image into regions Each region should be represented and described in a form suitable for further processing/decision-making Representation
Mathematical morphology (1)
 Chapter 9 Mathematical morphology () 9. Introduction Morphology, or morphology for short, is a branch of image processing which is particularly useful for analyzing shapes in images. We shall develop basic
Chapter 9 Mathematical morphology () 9. Introduction Morphology, or morphology for short, is a branch of image processing which is particularly useful for analyzing shapes in images. We shall develop basic
Binary Shape Characterization using Morphological Boundary Class Distribution Functions
 Binary Shape Characterization using Morphological Boundary Class Distribution Functions Marcin Iwanowski Institute of Control and Industrial Electronics, Warsaw University of Technology, ul.koszykowa 75,
Binary Shape Characterization using Morphological Boundary Class Distribution Functions Marcin Iwanowski Institute of Control and Industrial Electronics, Warsaw University of Technology, ul.koszykowa 75,
Slides for Faculty Oxford University Press All rights reserved.
 Oxford University Press 2013 Slides for Faculty Assistance Preliminaries Author: Vivek Kulkarni vivek_kulkarni@yahoo.com Outline Following topics are covered in the slides: Basic concepts, namely, symbols,
Oxford University Press 2013 Slides for Faculty Assistance Preliminaries Author: Vivek Kulkarni vivek_kulkarni@yahoo.com Outline Following topics are covered in the slides: Basic concepts, namely, symbols,
 1 of 7 7/15/2009 3:40 PM Virtual Laboratories > 1. Foundations > 1 2 3 4 5 6 7 8 9 1. Sets Poincaré's quote, on the title page of this chapter could not be more wrong (what was he thinking?). Set theory
1 of 7 7/15/2009 3:40 PM Virtual Laboratories > 1. Foundations > 1 2 3 4 5 6 7 8 9 1. Sets Poincaré's quote, on the title page of this chapter could not be more wrong (what was he thinking?). Set theory
Fabric Defect Detection Based on Computer Vision
 Fabric Defect Detection Based on Computer Vision Jing Sun and Zhiyu Zhou College of Information and Electronics, Zhejiang Sci-Tech University, Hangzhou, China {jings531,zhouzhiyu1993}@163.com Abstract.
Fabric Defect Detection Based on Computer Vision Jing Sun and Zhiyu Zhou College of Information and Electronics, Zhejiang Sci-Tech University, Hangzhou, China {jings531,zhouzhiyu1993}@163.com Abstract.
Mathematical morphology... M.1 Introduction... M.1 Dilation... M.3 Erosion... M.3 Closing... M.4 Opening... M.5 Summary... M.6
 Chapter M Misc. Contents Mathematical morphology.............................................. M.1 Introduction................................................... M.1 Dilation.....................................................
Chapter M Misc. Contents Mathematical morphology.............................................. M.1 Introduction................................................... M.1 Dilation.....................................................
Looming Motion Segmentation in Vehicle Tracking System using Wavelet Transforms
 Looming Motion Segmentation in Vehicle Tracking System using Wavelet Transforms K. SUBRAMANIAM, S. SHUKLA, S.S. DLAY and F.C. RIND Department of Electrical and Electronic Engineering University of Newcastle-Upon-Tyne
Looming Motion Segmentation in Vehicle Tracking System using Wavelet Transforms K. SUBRAMANIAM, S. SHUKLA, S.S. DLAY and F.C. RIND Department of Electrical and Electronic Engineering University of Newcastle-Upon-Tyne
Erosion, dilation and related operators
 Erosion, dilation and related operators Mariusz Jankowski Department of Electrical Engineering University of Southern Maine Portland, Maine, USA mjankowski@usm.maine.edu This paper will present implementation
Erosion, dilation and related operators Mariusz Jankowski Department of Electrical Engineering University of Southern Maine Portland, Maine, USA mjankowski@usm.maine.edu This paper will present implementation
2.2 Set Operations. Introduction DEFINITION 1. EXAMPLE 1 The union of the sets {1, 3, 5} and {1, 2, 3} is the set {1, 2, 3, 5}; that is, EXAMPLE 2
 2.2 Set Operations 127 2.2 Set Operations Introduction Two, or more, sets can be combined in many different ways. For instance, starting with the set of mathematics majors at your school and the set of
2.2 Set Operations 127 2.2 Set Operations Introduction Two, or more, sets can be combined in many different ways. For instance, starting with the set of mathematics majors at your school and the set of
A MORPHOLOGY-BASED FILTER STRUCTURE FOR EDGE-ENHANCING SMOOTHING
 Proceedings of the 1994 IEEE International Conference on Image Processing (ICIP-94), pp. 530-534. (Austin, Texas, 13-16 November 1994.) A MORPHOLOGY-BASED FILTER STRUCTURE FOR EDGE-ENHANCING SMOOTHING
Proceedings of the 1994 IEEE International Conference on Image Processing (ICIP-94), pp. 530-534. (Austin, Texas, 13-16 November 1994.) A MORPHOLOGY-BASED FILTER STRUCTURE FOR EDGE-ENHANCING SMOOTHING
Review of Sets. Review. Philippe B. Laval. Current Semester. Kennesaw State University. Philippe B. Laval (KSU) Sets Current Semester 1 / 16
 Review of Sets Review Philippe B. Laval Kennesaw State University Current Semester Philippe B. Laval (KSU) Sets Current Semester 1 / 16 Outline 1 Introduction 2 Definitions, Notations and Examples 3 Special
Review of Sets Review Philippe B. Laval Kennesaw State University Current Semester Philippe B. Laval (KSU) Sets Current Semester 1 / 16 Outline 1 Introduction 2 Definitions, Notations and Examples 3 Special
Morphological Image Processing
 Morphological Image Processing Binary dilation and erosion" Set-theoretic interpretation" Opening, closing, morphological edge detectors" Hit-miss filter" Morphological filters for gray-level images" Cascading
Morphological Image Processing Binary dilation and erosion" Set-theoretic interpretation" Opening, closing, morphological edge detectors" Hit-miss filter" Morphological filters for gray-level images" Cascading
Motion Detection Algorithm
 Volume 1, No. 12, February 2013 ISSN 2278-1080 The International Journal of Computer Science & Applications (TIJCSA) RESEARCH PAPER Available Online at http://www.journalofcomputerscience.com/ Motion Detection
Volume 1, No. 12, February 2013 ISSN 2278-1080 The International Journal of Computer Science & Applications (TIJCSA) RESEARCH PAPER Available Online at http://www.journalofcomputerscience.com/ Motion Detection
Application of mathematical morphology to problems related to Image Segmentation
 Application of mathematical morphology to problems related to Image Segmentation Bala S Divakaruni and Sree T. Sunkara Department of Computer Science, Northern Illinois University DeKalb IL 60115 mrdivakaruni
Application of mathematical morphology to problems related to Image Segmentation Bala S Divakaruni and Sree T. Sunkara Department of Computer Science, Northern Illinois University DeKalb IL 60115 mrdivakaruni
RESTORATION OF ARCHIVE FILM MATERIAL USING MULTI-DIMENSIONAL SOFT MORPHOLOGICAL FILTERS
 RESTORATION OF ARCHIVE FILM MATERIAL USING MULTI-DIMENSIONAL SOFT MORPHOLOGICAL FILTERS Neal R. Harvey Los Alamos National Laboratory, Los Alamos, NM, USA Stephen Marshall University of Strathclyde, Glasgow,
RESTORATION OF ARCHIVE FILM MATERIAL USING MULTI-DIMENSIONAL SOFT MORPHOLOGICAL FILTERS Neal R. Harvey Los Alamos National Laboratory, Los Alamos, NM, USA Stephen Marshall University of Strathclyde, Glasgow,
Lecture 15: The subspace topology, Closed sets
 Lecture 15: The subspace topology, Closed sets 1 The Subspace Topology Definition 1.1. Let (X, T) be a topological space with topology T. subset of X, the collection If Y is a T Y = {Y U U T} is a topology
Lecture 15: The subspace topology, Closed sets 1 The Subspace Topology Definition 1.1. Let (X, T) be a topological space with topology T. subset of X, the collection If Y is a T Y = {Y U U T} is a topology
Connectivity Preserving Digitization of Blurred Binary Images in 2D and 3D
 Connectivity Preserving Digitization of Blurred Binary Images in 2D and 3D Peer Stelldinger a Ullrich Köthe a a Cognitive Systems Group, University of Hamburg, Vogt-Köln-Str. 30, D-22527 Hamburg, Germany
Connectivity Preserving Digitization of Blurred Binary Images in 2D and 3D Peer Stelldinger a Ullrich Köthe a a Cognitive Systems Group, University of Hamburg, Vogt-Köln-Str. 30, D-22527 Hamburg, Germany
FUZZY BOOLEAN ALGEBRAS AND LUKASIEWICZ LOGIC. Angel Garrido
 Acta Universitatis Apulensis ISSN: 1582-5329 No. 22/2010 pp. 101-111 FUZZY BOOLEAN ALGEBRAS AND LUKASIEWICZ LOGIC Angel Garrido Abstract. In this paper, we analyze the more adequate tools to solve many
Acta Universitatis Apulensis ISSN: 1582-5329 No. 22/2010 pp. 101-111 FUZZY BOOLEAN ALGEBRAS AND LUKASIEWICZ LOGIC Angel Garrido Abstract. In this paper, we analyze the more adequate tools to solve many
Morphological Image Processing
 Morphological Image Processing Megha Goyal Dept. of ECE, Doaba Institute of Engineering and Technology, Kharar, Mohali, Punjab, India Abstract The purpose of this paper is to provide readers with an in-depth
Morphological Image Processing Megha Goyal Dept. of ECE, Doaba Institute of Engineering and Technology, Kharar, Mohali, Punjab, India Abstract The purpose of this paper is to provide readers with an in-depth
On Soft Topological Linear Spaces
 Republic of Iraq Ministry of Higher Education and Scientific Research University of AL-Qadisiyah College of Computer Science and Formation Technology Department of Mathematics On Soft Topological Linear
Republic of Iraq Ministry of Higher Education and Scientific Research University of AL-Qadisiyah College of Computer Science and Formation Technology Department of Mathematics On Soft Topological Linear
CITS 4402 Computer Vision
 CITS 4402 Computer Vision A/Prof Ajmal Mian Adj/A/Prof Mehdi Ravanbakhsh, CEO at Mapizy (www.mapizy.com) and InFarm (www.infarm.io) Lecture 02 Binary Image Analysis Objectives Revision of image formation
CITS 4402 Computer Vision A/Prof Ajmal Mian Adj/A/Prof Mehdi Ravanbakhsh, CEO at Mapizy (www.mapizy.com) and InFarm (www.infarm.io) Lecture 02 Binary Image Analysis Objectives Revision of image formation
What will we learn? What is mathematical morphology? What is mathematical morphology? Fundamental concepts and operations
 What will we learn? What is mathematical morphology and how is it used in image processing? Lecture Slides ME 4060 Machine Vision and Vision-based Control Chapter 13 Morphological image processing By Dr.
What will we learn? What is mathematical morphology and how is it used in image processing? Lecture Slides ME 4060 Machine Vision and Vision-based Control Chapter 13 Morphological image processing By Dr.
CLASSIFICATION OF BOUNDARY AND REGION SHAPES USING HU-MOMENT INVARIANTS
 CLASSIFICATION OF BOUNDARY AND REGION SHAPES USING HU-MOMENT INVARIANTS B.Vanajakshi Department of Electronics & Communications Engg. Assoc.prof. Sri Viveka Institute of Technology Vijayawada, India E-mail:
CLASSIFICATION OF BOUNDARY AND REGION SHAPES USING HU-MOMENT INVARIANTS B.Vanajakshi Department of Electronics & Communications Engg. Assoc.prof. Sri Viveka Institute of Technology Vijayawada, India E-mail:
A GRAPH FROM THE VIEWPOINT OF ALGEBRAIC TOPOLOGY
 A GRAPH FROM THE VIEWPOINT OF ALGEBRAIC TOPOLOGY KARL L. STRATOS Abstract. The conventional method of describing a graph as a pair (V, E), where V and E repectively denote the sets of vertices and edges,
A GRAPH FROM THE VIEWPOINT OF ALGEBRAIC TOPOLOGY KARL L. STRATOS Abstract. The conventional method of describing a graph as a pair (V, E), where V and E repectively denote the sets of vertices and edges,
Taibah University College of Computer Science & Engineering Course Title: Discrete Mathematics Code: CS 103. Chapter 2. Sets
 Taibah University College of Computer Science & Engineering Course Title: Discrete Mathematics Code: CS 103 Chapter 2 Sets Slides are adopted from Discrete Mathematics and It's Applications Kenneth H.
Taibah University College of Computer Science & Engineering Course Title: Discrete Mathematics Code: CS 103 Chapter 2 Sets Slides are adopted from Discrete Mathematics and It's Applications Kenneth H.
Unlabeled equivalence for matroids representable over finite fields
 Unlabeled equivalence for matroids representable over finite fields November 16, 2012 S. R. Kingan Department of Mathematics Brooklyn College, City University of New York 2900 Bedford Avenue Brooklyn,
Unlabeled equivalence for matroids representable over finite fields November 16, 2012 S. R. Kingan Department of Mathematics Brooklyn College, City University of New York 2900 Bedford Avenue Brooklyn,
FUZZY INFERENCE SYSTEMS
 CHAPTER-IV FUZZY INFERENCE SYSTEMS Fuzzy inference is the process of formulating the mapping from a given input to an output using fuzzy logic. The mapping then provides a basis from which decisions can
CHAPTER-IV FUZZY INFERENCE SYSTEMS Fuzzy inference is the process of formulating the mapping from a given input to an output using fuzzy logic. The mapping then provides a basis from which decisions can
INTRODUCTION TO THE HOMOLOGY GROUPS OF COMPLEXES
 INTRODUCTION TO THE HOMOLOGY GROUPS OF COMPLEXES RACHEL CARANDANG Abstract. This paper provides an overview of the homology groups of a 2- dimensional complex. It then demonstrates a proof of the Invariance
INTRODUCTION TO THE HOMOLOGY GROUPS OF COMPLEXES RACHEL CARANDANG Abstract. This paper provides an overview of the homology groups of a 2- dimensional complex. It then demonstrates a proof of the Invariance
An Introduction to Projection Fuzzy Associative Memories in Complete Inf-Semilattices
 Trabalho apresentado no XXXVII CNMAC, S.J. dos Campos - SP, 2017. Proceeding Series of the Brazilian Society of Computational and Applied Mathematics An Introduction to Projection Fuzzy Associative Memories
Trabalho apresentado no XXXVII CNMAC, S.J. dos Campos - SP, 2017. Proceeding Series of the Brazilian Society of Computational and Applied Mathematics An Introduction to Projection Fuzzy Associative Memories
Chapter 2 The Operation of Fuzzy Set
 Chapter 2 The Operation of Fuzzy Set Standard operations of Fuzzy Set! Complement set! Union Ma[, ]! Intersection Min[, ]! difference between characteristics of crisp fuzzy set operator n law of contradiction
Chapter 2 The Operation of Fuzzy Set Standard operations of Fuzzy Set! Complement set! Union Ma[, ]! Intersection Min[, ]! difference between characteristics of crisp fuzzy set operator n law of contradiction
Chapter IX : SKIZ and Watershed
 J. Serra Ecole des Mines de Paris ( 2000 ) Course on Math. Morphology IX. 1 Chapter IX : SKIZ and Watershed Distance function Euclidean and Geodesic SKIZ Watersheds Definition and properties Algorithms
J. Serra Ecole des Mines de Paris ( 2000 ) Course on Math. Morphology IX. 1 Chapter IX : SKIZ and Watershed Distance function Euclidean and Geodesic SKIZ Watersheds Definition and properties Algorithms
Image Enhancement: To improve the quality of images
 Image Enhancement: To improve the quality of images Examples: Noise reduction (to improve SNR or subjective quality) Change contrast, brightness, color etc. Image smoothing Image sharpening Modify image
Image Enhancement: To improve the quality of images Examples: Noise reduction (to improve SNR or subjective quality) Change contrast, brightness, color etc. Image smoothing Image sharpening Modify image
6. Concluding Remarks
 [8] K. J. Supowit, The relative neighborhood graph with an application to minimum spanning trees, Tech. Rept., Department of Computer Science, University of Illinois, Urbana-Champaign, August 1980, also
[8] K. J. Supowit, The relative neighborhood graph with an application to minimum spanning trees, Tech. Rept., Department of Computer Science, University of Illinois, Urbana-Champaign, August 1980, also
Complexity Theory. Compiled By : Hari Prasad Pokhrel Page 1 of 20. ioenotes.edu.np
 Chapter 1: Introduction Introduction Purpose of the Theory of Computation: Develop formal mathematical models of computation that reflect real-world computers. Nowadays, the Theory of Computation can be
Chapter 1: Introduction Introduction Purpose of the Theory of Computation: Develop formal mathematical models of computation that reflect real-world computers. Nowadays, the Theory of Computation can be
On the Relationships between Zero Forcing Numbers and Certain Graph Coverings
 On the Relationships between Zero Forcing Numbers and Certain Graph Coverings Fatemeh Alinaghipour Taklimi, Shaun Fallat 1,, Karen Meagher 2 Department of Mathematics and Statistics, University of Regina,
On the Relationships between Zero Forcing Numbers and Certain Graph Coverings Fatemeh Alinaghipour Taklimi, Shaun Fallat 1,, Karen Meagher 2 Department of Mathematics and Statistics, University of Regina,
Rigidity, connectivity and graph decompositions
 First Prev Next Last Rigidity, connectivity and graph decompositions Brigitte Servatius Herman Servatius Worcester Polytechnic Institute Page 1 of 100 First Prev Next Last Page 2 of 100 We say that a framework
First Prev Next Last Rigidity, connectivity and graph decompositions Brigitte Servatius Herman Servatius Worcester Polytechnic Institute Page 1 of 100 First Prev Next Last Page 2 of 100 We say that a framework
FUDMA Journal of Sciences (FJS) Maiden Edition Vol. 1 No. 1, November, 2017, pp ON ISOMORPHIC SOFT LATTICES AND SOFT SUBLATTICES
 FUDMA Journal of Sciences (FJS) Maiden Edition Vol 1 No 1 November 2017 pp 28-34 ON ISOMORPHIC SOFT LATTICES AND SOFT SUBLATTICES * A O Yusuf 1 A M Ibrahim 2 1 Department of Mathematical Sciences Information
FUDMA Journal of Sciences (FJS) Maiden Edition Vol 1 No 1 November 2017 pp 28-34 ON ISOMORPHIC SOFT LATTICES AND SOFT SUBLATTICES * A O Yusuf 1 A M Ibrahim 2 1 Department of Mathematical Sciences Information
Lecture 7: Morphological Image Processing
 I2200: Digital Image processing Lecture 7: Morphological Image Processing Prof. YingLi Tian Oct. 25, 2017 Department of Electrical Engineering The City College of New York The City University of New York
I2200: Digital Image processing Lecture 7: Morphological Image Processing Prof. YingLi Tian Oct. 25, 2017 Department of Electrical Engineering The City College of New York The City University of New York
MORPHOLOGICAL BOUNDARY BASED SHAPE REPRESENTATION SCHEMES ON MOMENT INVARIANTS FOR CLASSIFICATION OF TEXTURES
 International Journal of Computer Science and Communication Vol. 3, No. 1, January-June 2012, pp. 125-130 MORPHOLOGICAL BOUNDARY BASED SHAPE REPRESENTATION SCHEMES ON MOMENT INVARIANTS FOR CLASSIFICATION
International Journal of Computer Science and Communication Vol. 3, No. 1, January-June 2012, pp. 125-130 MORPHOLOGICAL BOUNDARY BASED SHAPE REPRESENTATION SCHEMES ON MOMENT INVARIANTS FOR CLASSIFICATION
Granular Computing: A Paradigm in Information Processing Saroj K. Meher Center for Soft Computing Research Indian Statistical Institute, Kolkata
 Granular Computing: A Paradigm in Information Processing Saroj K. Meher Center for Soft Computing Research Indian Statistical Institute, Kolkata Granular computing (GrC): Outline Introduction Definitions
Granular Computing: A Paradigm in Information Processing Saroj K. Meher Center for Soft Computing Research Indian Statistical Institute, Kolkata Granular computing (GrC): Outline Introduction Definitions
MATA GUJRI MAHILA MAHAVIDYALAYA (AUTO), JABALPUR DEPARTMENT OF MATHEMATICS M.Sc. (MATHEMATICS) THIRD SEMESTER
 MATA GUJRI MAHILA MAHAVIDYALAYA (AUTO), JABALPUR DEPARTMENT OF MATHEMATICS 2017-18 M.Sc. (MATHEMATICS) THIRD SEMESTER Name of the Papers Theory Min. C.C.E. Min. Practical Min. Total (MM) Pass. Pass. Pass
MATA GUJRI MAHILA MAHAVIDYALAYA (AUTO), JABALPUR DEPARTMENT OF MATHEMATICS 2017-18 M.Sc. (MATHEMATICS) THIRD SEMESTER Name of the Papers Theory Min. C.C.E. Min. Practical Min. Total (MM) Pass. Pass. Pass
AN EFFICIENT ALGORITHM FOR 3D BINARY MORPHOLOGICAL TRANSFORMATIONS WITH 3D STRUCTURING ELEMENTS OF ARBITRARY SIZE AND SHAPE
 AN EFFICIENT ALGORITHM FOR 3D BINARY MORPHOLOGICAL TRANSFORMATIONS WITH 3D STRUCTURING ELEMENTS OF ARBITRARY SIZE AND SHAPE Nikos Nikopoulos and Ioannis Pitas Department of Informatics, University of Thessaloniki
AN EFFICIENT ALGORITHM FOR 3D BINARY MORPHOLOGICAL TRANSFORMATIONS WITH 3D STRUCTURING ELEMENTS OF ARBITRARY SIZE AND SHAPE Nikos Nikopoulos and Ioannis Pitas Department of Informatics, University of Thessaloniki
EE795: Computer Vision and Intelligent Systems
 EE795: Computer Vision and Intelligent Systems Spring 2012 TTh 17:30-18:45 WRI C225 Lecture 04 130131 http://www.ee.unlv.edu/~b1morris/ecg795/ 2 Outline Review Histogram Equalization Image Filtering Linear
EE795: Computer Vision and Intelligent Systems Spring 2012 TTh 17:30-18:45 WRI C225 Lecture 04 130131 http://www.ee.unlv.edu/~b1morris/ecg795/ 2 Outline Review Histogram Equalization Image Filtering Linear
Product constructions for transitive decompositions of graphs
 116 Product constructions for transitive decompositions of graphs Geoffrey Pearce Abstract A decomposition of a graph is a partition of the edge set, giving a set of subgraphs. A transitive decomposition
116 Product constructions for transitive decompositions of graphs Geoffrey Pearce Abstract A decomposition of a graph is a partition of the edge set, giving a set of subgraphs. A transitive decomposition
DEVELOPMENT OF A MATHEMATICAL MORPHOLOGY TOOL FOR EDUCATION PURPOSE
 12 TH INTERNATIONAL CONFERENCE ON GEOMETRY AND GRAPHICS 2006 ISGG 6-10 AUGUST, 2006, SALVADOR, BRAZIL DEVELOPMENT OF A MATHEMATICAL MORPHOLOGY TOOL FOR EDUCATION PURPOSE César C. NUÑEZ and Aura CONCI Federal
12 TH INTERNATIONAL CONFERENCE ON GEOMETRY AND GRAPHICS 2006 ISGG 6-10 AUGUST, 2006, SALVADOR, BRAZIL DEVELOPMENT OF A MATHEMATICAL MORPHOLOGY TOOL FOR EDUCATION PURPOSE César C. NUÑEZ and Aura CONCI Federal
Machine vision. Summary # 5: Morphological operations
 1 Machine vision Summary # 5: Mphological operations MORPHOLOGICAL OPERATIONS A real image has continuous intensity. It is quantized to obtain a digital image with a given number of gray levels. Different
1 Machine vision Summary # 5: Mphological operations MORPHOLOGICAL OPERATIONS A real image has continuous intensity. It is quantized to obtain a digital image with a given number of gray levels. Different
IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 15, NO. 11, NOVEMBER
 IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 15, NO. 11, NOVEMBER 2006 3579 Spatially Variant Morphological Restoration and Skeleton Representation Nidhal Bouaynaya, Student Member, IEEE, Mohammed Charif-Chefchaouni,
IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 15, NO. 11, NOVEMBER 2006 3579 Spatially Variant Morphological Restoration and Skeleton Representation Nidhal Bouaynaya, Student Member, IEEE, Mohammed Charif-Chefchaouni,
SYLLABUS. M.Sc. III rd SEMESTER Department of Mathematics Mata Gujri Mahila Mahavidyalaya,(Auto), Jabalpur
 SYLLABUS M.Sc. III rd SEMESTER 2018-19 Department of Mathematics Mata Gujri Mahila Mahavidyalaya,(Auto), Jabalpur MATA GUJRI MAHILA MAHAVIDYALAYA (AUTO), JABALPUR M.Sc. (MATHEMATICS) THIRD SEMESTER Name
SYLLABUS M.Sc. III rd SEMESTER 2018-19 Department of Mathematics Mata Gujri Mahila Mahavidyalaya,(Auto), Jabalpur MATA GUJRI MAHILA MAHAVIDYALAYA (AUTO), JABALPUR M.Sc. (MATHEMATICS) THIRD SEMESTER Name
Disjunctive and Conjunctive Normal Forms in Fuzzy Logic
 Disjunctive and Conjunctive Normal Forms in Fuzzy Logic K. Maes, B. De Baets and J. Fodor 2 Department of Applied Mathematics, Biometrics and Process Control Ghent University, Coupure links 653, B-9 Gent,
Disjunctive and Conjunctive Normal Forms in Fuzzy Logic K. Maes, B. De Baets and J. Fodor 2 Department of Applied Mathematics, Biometrics and Process Control Ghent University, Coupure links 653, B-9 Gent,
Hybrid filters for medical image reconstruction
 Vol. 6(9), pp. 177-182, October, 2013 DOI: 10.5897/AJMCSR11.124 ISSN 2006-9731 2013 Academic Journals http://www.academicjournals.org/ajmcsr African Journal of Mathematics and Computer Science Research
Vol. 6(9), pp. 177-182, October, 2013 DOI: 10.5897/AJMCSR11.124 ISSN 2006-9731 2013 Academic Journals http://www.academicjournals.org/ajmcsr African Journal of Mathematics and Computer Science Research
DILATION AND EROSION OF GRAY IMAGES WITH SPHERICAL MASKS
 DILATION AND EROSION OF GRAY IMAGES WITH SPHERICAL MASKS J. Kukal 1,2, D. Majerová 1, A. Procházka 2 1 CTU in Prague 2 ICT Prague Abstract Any morphological operation with binary or gray image is a time
DILATION AND EROSION OF GRAY IMAGES WITH SPHERICAL MASKS J. Kukal 1,2, D. Majerová 1, A. Procházka 2 1 CTU in Prague 2 ICT Prague Abstract Any morphological operation with binary or gray image is a time
Introduction II. Sets. Terminology III. Definition. Definition. Definition. Example
 Sets Slides by Christopher M. ourke Instructor: erthe Y. Choueiry Spring 2006 Computer Science & Engineering 235 Introduction to Discrete Mathematics Sections 1.6 1.7 of Rosen cse235@cse.unl.edu Introduction
Sets Slides by Christopher M. ourke Instructor: erthe Y. Choueiry Spring 2006 Computer Science & Engineering 235 Introduction to Discrete Mathematics Sections 1.6 1.7 of Rosen cse235@cse.unl.edu Introduction
The minimum spanning tree and duality in graphs
 The minimum spanning tree and duality in graphs Wim Pijls Econometric Institute Report EI 2013-14 April 19, 2013 Abstract Several algorithms for the minimum spanning tree are known. The Blue-red algorithm
The minimum spanning tree and duality in graphs Wim Pijls Econometric Institute Report EI 2013-14 April 19, 2013 Abstract Several algorithms for the minimum spanning tree are known. The Blue-red algorithm
Digital Image Processing COSC 6380/4393
 Digital Image Processing COSC 6380/4393 Lecture 6 Sept 6 th, 2017 Pranav Mantini Slides from Dr. Shishir K Shah and Frank (Qingzhong) Liu Today Review Logical Operations on Binary Images Blob Coloring
Digital Image Processing COSC 6380/4393 Lecture 6 Sept 6 th, 2017 Pranav Mantini Slides from Dr. Shishir K Shah and Frank (Qingzhong) Liu Today Review Logical Operations on Binary Images Blob Coloring
Fast Distance Transform Computation using Dual Scan Line Propagation
 Fast Distance Transform Computation using Dual Scan Line Propagation Fatih Porikli Tekin Kocak Mitsubishi Electric Research Laboratories, Cambridge, USA ABSTRACT We present two fast algorithms that approximate
Fast Distance Transform Computation using Dual Scan Line Propagation Fatih Porikli Tekin Kocak Mitsubishi Electric Research Laboratories, Cambridge, USA ABSTRACT We present two fast algorithms that approximate
REDUNDANCY OF MULTISET TOPOLOGICAL SPACES
 Iranian Journal of Fuzzy Systems Vol. 14, No. 4, (2017) pp. 163-168 163 REDUNDANCY OF MULTISET TOPOLOGICAL SPACES A. GHAREEB Abstract. In this paper, we show the redundancies of multiset topological spaces.
Iranian Journal of Fuzzy Systems Vol. 14, No. 4, (2017) pp. 163-168 163 REDUNDANCY OF MULTISET TOPOLOGICAL SPACES A. GHAREEB Abstract. In this paper, we show the redundancies of multiset topological spaces.
Digital straight lines in the Khalimsky plane
 Digital straight lines in the Khalimsky plane Erik Melin Uppsala University, Department of Mathematics Box 480, SE-751 06 Uppsala, Sweden melin@math.uu.se http://www.math.uu.se/~melin September 2003 Abstract
Digital straight lines in the Khalimsky plane Erik Melin Uppsala University, Department of Mathematics Box 480, SE-751 06 Uppsala, Sweden melin@math.uu.se http://www.math.uu.se/~melin September 2003 Abstract
Irregular Interval Valued Fuzzy Graphs
 nnals of Pure and pplied Mathematics Vol 3, No, 03, 56-66 ISSN: 79-087X (P), 79-0888(online) Published on 0 May 03 wwwresearchmathsciorg nnals of Irregular Interval Valued Fuzzy Graphs Madhumangal Pal
nnals of Pure and pplied Mathematics Vol 3, No, 03, 56-66 ISSN: 79-087X (P), 79-0888(online) Published on 0 May 03 wwwresearchmathsciorg nnals of Irregular Interval Valued Fuzzy Graphs Madhumangal Pal
Morphological Compound Operations-Opening and CLosing
 Morphological Compound Operations-Opening and CLosing COMPSCI 375 S1 T 2006, A/P Georgy Gimel farb Revised COMPSCI 373 S1C -2010, Patrice Delmas AP Georgy Gimel'farb 1 Set-theoretic Binary Operations Many
Morphological Compound Operations-Opening and CLosing COMPSCI 375 S1 T 2006, A/P Georgy Gimel farb Revised COMPSCI 373 S1C -2010, Patrice Delmas AP Georgy Gimel'farb 1 Set-theoretic Binary Operations Many
Image Processing (IP) Through Erosion and Dilation Methods
 Image Processing (IP) Through Erosion and Dilation Methods Prof. sagar B Tambe 1, Prof. Deepak Kulhare 2, M. D. Nirmal 3, Prof. Gopal Prajapati 4 1 MITCOE Pune 2 H.O.D. Computer Dept., 3 Student, CIIT,
Image Processing (IP) Through Erosion and Dilation Methods Prof. sagar B Tambe 1, Prof. Deepak Kulhare 2, M. D. Nirmal 3, Prof. Gopal Prajapati 4 1 MITCOE Pune 2 H.O.D. Computer Dept., 3 Student, CIIT,
The Fibonacci hypercube
 AUSTRALASIAN JOURNAL OF COMBINATORICS Volume 40 (2008), Pages 187 196 The Fibonacci hypercube Fred J. Rispoli Department of Mathematics and Computer Science Dowling College, Oakdale, NY 11769 U.S.A. Steven
AUSTRALASIAN JOURNAL OF COMBINATORICS Volume 40 (2008), Pages 187 196 The Fibonacci hypercube Fred J. Rispoli Department of Mathematics and Computer Science Dowling College, Oakdale, NY 11769 U.S.A. Steven
Information Granulation and Approximation in a Decision-theoretic Model of Rough Sets
 Information Granulation and Approximation in a Decision-theoretic Model of Rough Sets Y.Y. Yao Department of Computer Science University of Regina Regina, Saskatchewan Canada S4S 0A2 E-mail: yyao@cs.uregina.ca
Information Granulation and Approximation in a Decision-theoretic Model of Rough Sets Y.Y. Yao Department of Computer Science University of Regina Regina, Saskatchewan Canada S4S 0A2 E-mail: yyao@cs.uregina.ca
γ 2 γ 3 γ 1 R 2 (b) a bounded Yin set (a) an unbounded Yin set
 γ 1 γ 3 γ γ 3 γ γ 1 R (a) an unbounded Yin set (b) a bounded Yin set Fig..1: Jordan curve representation of a connected Yin set M R. A shaded region represents M and the dashed curves its boundary M that
γ 1 γ 3 γ γ 3 γ γ 1 R (a) an unbounded Yin set (b) a bounded Yin set Fig..1: Jordan curve representation of a connected Yin set M R. A shaded region represents M and the dashed curves its boundary M that
TEXTURE SEGMENTATION USING AREA MORPHOLOGY LOCAL GRANULOMETRIES
 TEXTURE SEGMENTATION USING AREA MORPHOLOGY LOCAL GRANULOMETRIES Neil D Fletcher and Adrian N Evans Department of Electronic and Electrical Engineering University of Bath, BA2 7AY, UK N.D.Fletcher@bath.ac.uk
TEXTURE SEGMENTATION USING AREA MORPHOLOGY LOCAL GRANULOMETRIES Neil D Fletcher and Adrian N Evans Department of Electronic and Electrical Engineering University of Bath, BA2 7AY, UK N.D.Fletcher@bath.ac.uk
MRI Brain Image Segmentation Using an AM-FM Model
 MRI Brain Image Segmentation Using an AM-FM Model Marios S. Pattichis', Helen Petropoulos2, and William M. Brooks2 1 Department of Electrical and Computer Engineering, The University of New Mexico, Albuquerque,
MRI Brain Image Segmentation Using an AM-FM Model Marios S. Pattichis', Helen Petropoulos2, and William M. Brooks2 1 Department of Electrical and Computer Engineering, The University of New Mexico, Albuquerque,
Introduction to Fuzzy Logic. IJCAI2018 Tutorial
 Introduction to Fuzzy Logic IJCAI2018 Tutorial 1 Crisp set vs. Fuzzy set A traditional crisp set A fuzzy set 2 Crisp set vs. Fuzzy set 3 Crisp Logic Example I Crisp logic is concerned with absolutes-true
Introduction to Fuzzy Logic IJCAI2018 Tutorial 1 Crisp set vs. Fuzzy set A traditional crisp set A fuzzy set 2 Crisp set vs. Fuzzy set 3 Crisp Logic Example I Crisp logic is concerned with absolutes-true
2. Sets. 2.1&2.2: Sets and Subsets. Combining Sets. c Dr Oksana Shatalov, Fall
 c Dr Oksana Shatalov, Fall 2014 1 2. Sets 2.1&2.2: Sets and Subsets. Combining Sets. Set Terminology and Notation DEFINITIONS: Set is well-defined collection of objects. Elements are objects or members
c Dr Oksana Shatalov, Fall 2014 1 2. Sets 2.1&2.2: Sets and Subsets. Combining Sets. Set Terminology and Notation DEFINITIONS: Set is well-defined collection of objects. Elements are objects or members
Chapter 4 Fuzzy Logic
 4.1 Introduction Chapter 4 Fuzzy Logic The human brain interprets the sensory information provided by organs. Fuzzy set theory focus on processing the information. Numerical computation can be performed
4.1 Introduction Chapter 4 Fuzzy Logic The human brain interprets the sensory information provided by organs. Fuzzy set theory focus on processing the information. Numerical computation can be performed
Digital Image Processing
 Digital Image Processing Lecture # 4 Digital Image Fundamentals - II ALI JAVED Lecturer SOFTWARE ENGINEERING DEPARTMENT U.E.T TAXILA Email:: ali.javed@uettaxila.edu.pk Office Room #:: 7 Presentation Outline
Digital Image Processing Lecture # 4 Digital Image Fundamentals - II ALI JAVED Lecturer SOFTWARE ENGINEERING DEPARTMENT U.E.T TAXILA Email:: ali.javed@uettaxila.edu.pk Office Room #:: 7 Presentation Outline
International Journal of Advance Engineering and Research Development. Applications of Set Theory in Digital Image Processing
 Scientific Journal of Impact Factor (SJIF): 4.72 International Journal of Advance Engineering and Research Development Volume 4, Issue 11, November -2017 Applications of Set Theory in Digital Image Processing
Scientific Journal of Impact Factor (SJIF): 4.72 International Journal of Advance Engineering and Research Development Volume 4, Issue 11, November -2017 Applications of Set Theory in Digital Image Processing
Topology notes. Basic Definitions and Properties.
 Topology notes. Basic Definitions and Properties. Intuitively, a topological space consists of a set of points and a collection of special sets called open sets that provide information on how these points
Topology notes. Basic Definitions and Properties. Intuitively, a topological space consists of a set of points and a collection of special sets called open sets that provide information on how these points
Genus Ranges of 4-Regular Rigid Vertex Graphs
 Genus Ranges of 4-Regular Rigid Vertex Graphs Dorothy Buck Department of Mathematics Imperial College London London, England, UK d.buck@imperial.ac.uk Nataša Jonoska Egor Dolzhenko Molecular and Computational
Genus Ranges of 4-Regular Rigid Vertex Graphs Dorothy Buck Department of Mathematics Imperial College London London, England, UK d.buck@imperial.ac.uk Nataša Jonoska Egor Dolzhenko Molecular and Computational
Efficient Object Extraction Using Fuzzy Cardinality Based Thresholding and Hopfield Network
 Efficient Object Extraction Using Fuzzy Cardinality Based Thresholding and Hopfield Network S. Bhattacharyya U. Maulik S. Bandyopadhyay Dept. of Information Technology Dept. of Comp. Sc. and Tech. Machine
Efficient Object Extraction Using Fuzzy Cardinality Based Thresholding and Hopfield Network S. Bhattacharyya U. Maulik S. Bandyopadhyay Dept. of Information Technology Dept. of Comp. Sc. and Tech. Machine
University of Groningen. Morphological design of Discrete-Time Cellular Neural Networks Brugge, Mark Harm ter
 University of Groningen Morphological design of Discrete-Time Cellular Neural Networks Brugge, Mark Harm ter IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you
University of Groningen Morphological design of Discrete-Time Cellular Neural Networks Brugge, Mark Harm ter IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you
