Shading. Brian Curless CSE 457 Spring 2015
|
|
|
- Mercy Cole
- 5 years ago
- Views:
Transcription
1 Shading Brian Curless CSE 457 Spring
2 Reading Required: Angel chapter 5. Optional: OpenGL red book, chapter 5. 2
3 Basic 3D graphics With affine matrices, we can now transform virtual 3D objects in their local coordinate systems into a global (world) coordinate system: M 1 M 2 To synthesize an image of the scene, we also need to add light sources and a viewer/camera: 3
4 Pinhole camera To create an image of a virtual scene, we need to define a camera, and we need to model lighting and shading. For the camera, we use a pinhole camera. [Angel, 2011] The image is rendered onto an image plane (usually in front of the camera). Viewing rays emanate from the center of projection (COP) at the center of the pinhole. The image of an object point P is at the intersection of the viewing ray through P and the image plane. But is P visible? This the problem of hidden surface removal (a.k.a., visible surface determination). We ll consider this problem later. 4
5 Shading Next, we ll need a model to describe how light interacts with surfaces. Such a model is called a shading model. Other names: Lighting model Light reflection model Local illumination model Reflectance model BRDF 5
6 An abundance of photons Given the camera and shading model, properly determining the right color at each pixel is extremely hard. Look around the room. Each light source has different characteristics. Trillions of photons are pouring out every second. These photons can: interact with molecules and particles in the air ( participating media ) strike a surface and be absorbed be reflected (scattered) cause fluorescence or phosphorescence. interact in a wavelength-dependent manner generally bounce around and around 6
7 Our problem We re going to build up to a approximations of reality called the Phong and Blinn-Phong illumination models. They have the following characteristics: not physically correct gives a first-order approximation to physical light reflection very fast widely used In addition, we will assume local illumination, i.e., light goes: light source -> surface -> viewer. No interreflections, no shadows. 7
8 Setup Given: a point P on a surface visible through pixel p The normal N at P The lighting direction, L, and (color) intensity, I L, at P The viewing direction, V, at P The shading coefficients at P Compute the color, I, of pixel p. Assume that the direction vectors are normalized: N L V 1 8
9 Iteration zero The simplest thing you can do is Assign each polygon a single color: where I=k e I is the resulting intensity k e is the emissivity or intrinsic shade associated with the object This has some special-purpose uses, but not really good for drawing a scene. [Note: k e is omitted in Angel.] 9
10 Iteration one Let s make the color at least dependent on the overall quantity of light available in the scene: I k k I e a La k a is the ambient reflection coefficient. really the reflectance of ambient light ambient light is assumed to be equal in all directions I La is the ambient light intensity. Physically, what is ambient light? [Note: Angel uses L a instead of I La.] 10
11 Wavelength dependence Really, k e, k a, and I La are functions over all wavelengths. Ideally, we would do the calculation on these functions. For the ambient shading equation, we would start with: I ( ) =k ( ) I ( ) a La then we would find good RGB values to represent the spectrum I (). Traditionally, though, k a and I La are represented as RGB triples, and the computation is performed on each color channel separately: I I =k I R R R a La G G G =k a ILa B B B a La I =k I 11
12 Diffuse reflection Let s examine the ambient shading model: objects have different colors we can control the overall light intensity what happens when we turn off the lights? what happens as the light intensity increases? what happens if we change the color of the lights? So far, objects are uniformly lit. not the way things really appear in reality, light sources are localized in position or direction Diffuse, or Lambertian reflection will allow reflected intensity to vary with the direction of the light. 12
13 Diffuse reflectors Diffuse reflection occurs from dull, matte surfaces, like latex paint, or chalk. These diffuse or Lambertian reflectors reradiate light equally in all directions. Picture a rough surface with lots of tiny microfacets. 13
14 Diffuse reflectors or picture a surface with little pigment particles embedded beneath the surface (neglect reflection at the surface for the moment): The microfacets and pigments distribute light rays in all directions. Embedded pigments are responsible for the coloration of diffusely reflected light in plastics and paints. Note: the figures above are intuitive, but not strictly (physically) correct. 14
15 Diffuse reflectors, cont. The reflected intensity from a diffuse surface does not depend on the direction of the viewer. The incoming light, though, does depend on the direction of the light source: 15
16 Iteration two The incoming energy is proportional to the diffuse reflection equations:, giving I=k +k I +k I e a La d L B =k +k I +k I B( ) e a La d L where: k d is the diffuse reflection coefficient I L is the (color) intensity of the light source N is the normal to the surface (unit vector) L is the direction to the light source (unit vector) B prevents contribution of light from below the surface: [Note: Angel uses L d 1 if NL 0 B= 0 if NL 0 instead of I L and f instead of B.] 16
17 Specular reflection Specular reflection accounts for the highlight that you see on some objects. It is particularly important for smooth, shiny surfaces, such as: metal polished stone plastics apples skin Properties: Specular reflection depends on the viewing direction V. For non-metals, the color is determined solely by the color of the light. For metals, the color may be altered (e.g., brass) 17
18 Specular reflection derivation For a perfect mirror reflector, light is reflected about N, so I L if V R I 0 otherwise For a near-perfect reflector, you might expect the highlight to fall off quickly with increasing angle. Also known as: rough specular reflection directional diffuse reflection glossy reflection 18
19 Phong specular reflection cos n s φ ns = ns = φ One way to get this effect is to take (R V), raised to a power n s. As n s gets larger, the dropoff becomes {more,less} gradual gives a {larger,smaller} highlight simulates a {more,less} mirror-like surface Phong specular reflection is proportional to: where (x ) + max(0, x ). n specular ~ B R V s I ( ) 19
20 Blinn-Phong specular reflection A common alternative for specular reflection is the Blinn-Phong model (sometimes called the modified Phong model.) We compute the vector halfway between L and V as: Analogous to Phong specular reflection, we can compute the specular contribution in terms of (N H), raised to a power n s : n specular ~ B NH s I ( ) where, again, (x ) + max(0, x ). 20
21 Iteration three The next update to the Blinn-Phong shading model is then: I=k +k I +k I B( NL ) +k I B( NH) e a La d L s L ns k e+kai La+ ILB k d( NL ) +ks( NH) ns where: k s is the specular reflection coefficient n s is the specular exponent or shininess H is the unit halfway vector between L and V, where V is the viewing direction. [Note: Angel uses a instead of n s, and maintains a separate L d and L s, instead of a single I L. This choice reflects the flexibility available in OpenGL.] 21
22 Directional lights The simplest form of lights supported by renderers are ambient, directional, and point. Spotlights are also supported often as a special form of point light. We ve seen ambient light sources, which are not really geometric. Directional light sources have a single direction and intensity associated with them. Using affine notation, what is the homogeneous coordinate for a directional light? 22
23 Point lights The direction of a point light sources is determined by the vector from the light position to the surface point. E-P L= E-P r =E-P Physics tells us the intensity must drop off inversely with the square of the distance: 1 f atten r 2 Sometimes, this distance-squared dropoff is considered too harsh. A common alternative is: 1 f atten 2 a+br +cr with user-supplied constants for a, b, and c. Using affine notation, what is the homogeneous coordinate for a point light? 23
24 Spotlights We can also apply a directional attenuation of a point light source, giving a spotlight effect. A common choice for the spotlight intensity is: where L is the direction to the point light. S is the center direction of the spotlight. is the angle between L and S is the cutoff angle for the spotlight e is the angular falloff coefficient LS f = 2 spot abrcr 0 otherwise 1 Note: cos ( LS ) LS cos. e 24
25 Iteration four Since light is additive, we can handle multiple lights by taking the sum over every light. Our equation is now: I=k +k I + e L a La S e j j j j 2 j a+b j jrj +cjrj NL NH I B k +k L,j j d j s j n s This is the Blinn-Phong illumination model (for spotlights). Which quantities are spatial vectors? Which are RGB triples? Which are scalars? 25
26 Shading in OpenGL The OpenGL lighting model allows you to associate different lighting colors according to material properties they will influence. Thus, our original shading equation (for point lights): I=k +k I + e a La 1 a+b r +cr NL NH I B k +k 2 L, j j d j s j + j j j j j j n s becomes: I=k +k I + e a La 1 a+b r +cr 2 j j j j j j ki + B ki ( NL ) +ki ( NH ) n a La, j j d Ld, j j s Ls, j j + s where you can have a global ambient light with intensity I La in addition to having an ambient light intensity I La, j associated with each individual light, as well as separate diffuse and specular intensities, I Ld, j and I Ls, j, repectively. 26
27 Materials in OpenGL The OpenGL code to specify the surface shading properties is fairly straightforward. For example: GLfloat ke[] = { 0.1, 0.15, 0.05, 1.0 }; GLfloat ka[] = { 0.1, 0.15, 0.1, 1.0 }; GLfloat kd[] = { 0.3, 0.3, 0.2, 1.0 }; GLfloat ks[] = { 0.2, 0.2, 0.2, 1.0 }; GLfloat ns[] = { 50.0 }; glmaterialfv(gl_front, GL_EMISSION, ke); glmaterialfv(gl_front, GL_AMBIENT, ka); glmaterialfv(gl_front, GL_DIFFUSE, kd); glmaterialfv(gl_front, GL_SPECULAR, ks); glmaterialfv(gl_front, GL_SHININESS, ns); Notes: The GL_FRONT parameter tells OpenGL that we are specifiying the materials for the front of the surface. Only the alpha value of the diffuse color is used for blending. It s usually set to 1. 27
28 Shading in OpenGL, cont d In OpenGL this equation, for one light source (the 0 th ) is specified something like: GLfloat La[] = { 0.2, 0.2, 0.2, 1.0 }; GLfloat La0[] = { 0.1, 0.1, 0.1, 1.0 }; GLfloat Ld0[] = { 1.0, 1.0, 1.0, 1.0 }; GLfloat Ls0[] = { 1.0, 1.0, 1.0, 1.0 }; GLfloat pos0[] = { 1.0, 1.0, 1.0, 0.0 }; GLfloat a0[] = { 1.0 }; GLfloat b0[] = { 0.5 }; GLfloat c0[] = { 0.25 }; GLfloat S0[] = { -1.0, -1.0, 0.0 }; GLfloat beta0[] = { 45 }; GLfloat e0[] = { 2 }; gllightmodelfv(gl_light_model_ambient, La); gllightfv(gl_light0, GL_AMBIENT, La0); gllightfv(gl_light0, GL_DIFFUSE, Ld0); gllightfv(gl_light0, GL_SPECULAR, Ls0); gllightfv(gl_light0, GL_POSITION, pos0); gllightfv(gl_light0, GL_CONSTANT_ATTENUATION, a0); gllightfv(gl_light0, GL_LINEAR_ATTENUATION, b0); gllightfv(gl_light0, GL_QUADRATIC_ATTENUATION, c0); gllightfv(gl_light0, GL_SPOT_DIRECTION, S0); gllightf(gl_light0, GL_SPOT_CUTOFF, beta0); gllightf(gl_light0, GL_SPOT_EXPONENT, e0); 28
29 Shading in OpenGL, cont d Notes: You can have as many as GL_MAX_LIGHTS lights in a scene. This number is system-dependent. For directional lights, you specify a light direction, not position, and the attenuation and spotlight terms are ignored. The directions of directional lights and spotlights are specified in the coordinate systems of the lights, not the surface points as we ve been doing in lecture. 29
30 3D Geometry in the Graphics Hardware Pipeline Graphics hardware applies transformations to bring the objects and lighting into the camera s coordinate system: The geometry is assumed to be made of triangles, and the vertices are projected onto the image plane. 30
31 Rasterization After projecting the vertices, graphics hardware smears vertex properties across the interior of the triangle in a process called rasterization. Smearing the z-values and using a Z-buffer will enable the graphics hardware to determine if a point inside a triangle is visible. (More on this in another lecture.) If we have stored colors at the vertices, then we can smear these as well. 31
32 Shading the interiors of triangles We will be computing colors using the Blinn-Phong lighting model. Let s assume (as graphics hardware does) that we are working with triangles. How should we shade the interiors of triangles? 32
33 Shading with per-face normals Assume each face has a constant normal: For a distant viewer and a distant light source and constant material properties over the surface, how will the color of each triangle vary? 33
34 Faceted shading (cont d) [Williams and Siegel 1990] 34
35 Gouraud interpolation To get a smoother result that is easily performed in hardware, we can do Gouraud interpolation. Here s how it works: 1. Compute normals at the vertices. 2. Shade only the vertices. 3. Interpolate the resulting vertex colors. 35
36 Facted shading vs. Gouraud interpolation [Williams and Siegel 1990] 36
37 Gouraud interpolation artifacts Gouraud interpolation has significant limitations. 1. If the polygonal approximation is too coarse, we can miss specular highlights. 2. We will encounter Mach banding (derivative discontinuity enhanced by human eye). This is what graphics hardware does by default. A substantial improvement is to do 37
38 Phong interpolation To get an even smoother result with fewer artifacts, we can perform Phong interpolation. Here s how it works: 1. Compute normals at the vertices. 2. Interpolate normals and normalize. 3. Shade using the interpolated normals. 38
39 Gouraud vs. Phong interpolation [Williams and Siegel 1990] 39
40 Old pipeline: Gouraud interpolation Vertex processor Primitive assembler Default vertex processing: L determine lighting direction V determine viewing direction Nnormalize( n e ) cblinn-phong shade with LV,, N, kd, ks, ns attach c blinn-phong to vertex as varying v i project v to image i, i, vi v v triangle Rasterizer Fragment processor Default fragment processing: p color c blinn-phong 40
41 Programmable pipeline: Phong-interpolated normals! Vertex processor Vertex shader: attach n e to vertex as varying attach v e to vertex as varying v i project v to image Primitive assembler v, v, v i i i triangle Rasterizer Fragment processor Fragment shader: p L determine lighting direction (using v e ) V v p e p N normalize( n e ) color shade with LV,, Nk,, k, n d s s 41
42 Choosing Blinn-Phong shading parameters Experiment with different parameter settings. To get you started, here are a few suggestions: Try n s in the range [0,100] Try k a + k d + k s < 1 Use a small k a (~0.1) n s k d k s Metal large Small, color of metal Large, color of metal Plastic medium Medium, color of plastic Medium, white Planet 0 varying 0 42
43 BRDF The diffuse+specular parts of the Blinn-Phong illumination model are a mapping from light to viewing directions: L V I= I LB k d( NL ) +ksn L V I f ( LV, ) The mapping function f r is often written in terms of incoming (light) directions in and outgoing (viewing) directions out : f (, ) or f ( ) r L in r out This function is called the Bi-directional Reflectance Distribution Function (BRDF). r in n s out Here s a plot with in held constant: f (, ) r in out in BRDF s can be quite sophisticated 43
44 More sophisticated BRDF s [Cook and Torrance, 1982] Anisotropic BRDFs [Westin, Arvo, Torrance 1992] Artistics BRDFs [Gooch] 44
45 More sophisticated BRDF s (cont d) Hair illuminated from different angles [Marschner et al., 2003] Wool cloth and silk cloth [Irawan and Marschner, 2012] 45
46 BSSRDFs for subsurface scattering [Jensen et al. 2001] 46
47 Summary You should understand the equation for the Blinn- Phong lighting model described in the Iteration Four slide: What is the physical meaning of each variable? How are the terms computed? What effect does each term contribute to the image? What does varying the parameters do? You should also understand the differences between faceted, Gouraud, and Phong interpolated shading. 47
Shading. Reading. Pinhole camera. Basic 3D graphics. Brian Curless CSE 557 Fall Required: Shirley, Chapter 10
 Reading Required: Shirley, Chapter 10 Shading Brian Curless CSE 557 Fall 2014 1 2 Basic 3D graphics With affine matrices, we can now transform virtual 3D objects in their local coordinate systems into
Reading Required: Shirley, Chapter 10 Shading Brian Curless CSE 557 Fall 2014 1 2 Basic 3D graphics With affine matrices, we can now transform virtual 3D objects in their local coordinate systems into
Shading. Brian Curless CSE 457 Spring 2017
 Shading Brian Curless CSE 457 Spring 2017 1 Reading Optional: Angel and Shreiner: chapter 5. Marschner and Shirley: chapter 10, chapter 17. Further reading: OpenGL red book, chapter 5. 2 Basic 3D graphics
Shading Brian Curless CSE 457 Spring 2017 1 Reading Optional: Angel and Shreiner: chapter 5. Marschner and Shirley: chapter 10, chapter 17. Further reading: OpenGL red book, chapter 5. 2 Basic 3D graphics
Reading. Shading. An abundance of photons. Introduction. Required: Angel , 6.5, Optional: Angel 6.4 OpenGL red book, chapter 5.
 Reading Required: Angel 6.1-6.3, 6.5, 6.7-6.8 Optional: Shading Angel 6.4 OpenGL red book, chapter 5. 1 2 Introduction An abundance of photons So far, we ve talked exclusively about geometry. Properly
Reading Required: Angel 6.1-6.3, 6.5, 6.7-6.8 Optional: Shading Angel 6.4 OpenGL red book, chapter 5. 1 2 Introduction An abundance of photons So far, we ve talked exclusively about geometry. Properly
Shading. Brian Curless CSE 557 Autumn 2017
 Shading Brian Curless CSE 557 Autumn 2017 1 Reading Optional: Angel and Shreiner: chapter 5. Marschner and Shirley: chapter 10, chapter 17. Further reading: OpenGL red book, chapter 5. 2 Basic 3D graphics
Shading Brian Curless CSE 557 Autumn 2017 1 Reading Optional: Angel and Shreiner: chapter 5. Marschner and Shirley: chapter 10, chapter 17. Further reading: OpenGL red book, chapter 5. 2 Basic 3D graphics
Shading. CSE 457 Winter 2015
 Shading CSE 457 Winter 2015 Reading Required: Angel chapter 5. Optional: OpenGL red book, chapter 5. 2 Basic 3D graphics With affine matrices, we can now transform virtual 3D objects in their local coordinate
Shading CSE 457 Winter 2015 Reading Required: Angel chapter 5. Optional: OpenGL red book, chapter 5. 2 Basic 3D graphics With affine matrices, we can now transform virtual 3D objects in their local coordinate
Reading. Shading. Introduction. An abundance of photons. Required: Angel , Optional: OpenGL red book, chapter 5.
 Reading Required: Angel 6.1-6.5, 6.7-6.8 Optional: Shading OpenGL red book, chapter 5. 1 2 Introduction So far, we ve talked exclusively about geometry. What is the shape of an obect? How do I place it
Reading Required: Angel 6.1-6.5, 6.7-6.8 Optional: Shading OpenGL red book, chapter 5. 1 2 Introduction So far, we ve talked exclusively about geometry. What is the shape of an obect? How do I place it
Introduction. Lighting model Light reflection model Local illumination model Reflectance model BRDF
 Shading Introduction Affine transformations help us to place objects into a scene. Before creating images of these objects, we ll look at models for how light interacts with their surfaces. Such a model
Shading Introduction Affine transformations help us to place objects into a scene. Before creating images of these objects, we ll look at models for how light interacts with their surfaces. Such a model
w Foley, Section16.1 Reading
 Shading w Foley, Section16.1 Reading Introduction So far, we ve talked exclusively about geometry. w What is the shape of an object? w How do I place it in a virtual 3D space? w How do I know which pixels
Shading w Foley, Section16.1 Reading Introduction So far, we ve talked exclusively about geometry. w What is the shape of an object? w How do I place it in a virtual 3D space? w How do I know which pixels
Projections and Hardware Rendering. Brian Curless CSE 557 Fall 2014
 Projections and Hardware Rendering Brian Curless CSE 557 Fall 2014 1 Reading Required: Shirley, Ch. 7, Sec. 8.2, Ch. 18 Further reading: Foley, et al, Chapter 5.6 and Chapter 6 David F. Rogers and J. Alan
Projections and Hardware Rendering Brian Curless CSE 557 Fall 2014 1 Reading Required: Shirley, Ch. 7, Sec. 8.2, Ch. 18 Further reading: Foley, et al, Chapter 5.6 and Chapter 6 David F. Rogers and J. Alan
Overview. Shading. Shading. Why we need shading. Shading Light-material interactions Phong model Shading polygons Shading in OpenGL
 Overview Shading Shading Light-material interactions Phong model Shading polygons Shading in OpenGL Why we need shading Suppose we build a model of a sphere using many polygons and color it with glcolor.
Overview Shading Shading Light-material interactions Phong model Shading polygons Shading in OpenGL Why we need shading Suppose we build a model of a sphere using many polygons and color it with glcolor.
Computer Graphics. Illumination and Shading
 () Illumination and Shading Dr. Ayman Eldeib Lighting So given a 3-D triangle and a 3-D viewpoint, we can set the right pixels But what color should those pixels be? If we re attempting to create a realistic
() Illumination and Shading Dr. Ayman Eldeib Lighting So given a 3-D triangle and a 3-D viewpoint, we can set the right pixels But what color should those pixels be? If we re attempting to create a realistic
Shading. Reading. Pinhole camera. Basic 3D graphics. Brian Curless CSE 457 Spring Required: Angel chapter 5.
 Reading Required: Angel chapter 5. Shading Optional: OpenGL red book, chapter 5. Brian Curle CSE 457 Spring 2015 1 2 Baic 3D graphic With affine matrice, we can now tranform virtual 3D object in their
Reading Required: Angel chapter 5. Shading Optional: OpenGL red book, chapter 5. Brian Curle CSE 457 Spring 2015 1 2 Baic 3D graphic With affine matrice, we can now tranform virtual 3D object in their
Today. Global illumination. Shading. Interactive applications. Rendering pipeline. Computergrafik. Shading Introduction Local shading models
 Computergrafik Thomas Buchberger, Matthias Zwicker Universität Bern Herbst 2008 Today Introduction Local shading models Light sources strategies Compute interaction of light with surfaces Requires simulation
Computergrafik Thomas Buchberger, Matthias Zwicker Universität Bern Herbst 2008 Today Introduction Local shading models Light sources strategies Compute interaction of light with surfaces Requires simulation
Illumination & Shading: Part 1
 Illumination & Shading: Part 1 Light Sources Empirical Illumination Shading Local vs Global Illumination Lecture 10 Comp 236 Spring 2005 Computer Graphics Jargon: Illumination Models Illumination - the
Illumination & Shading: Part 1 Light Sources Empirical Illumination Shading Local vs Global Illumination Lecture 10 Comp 236 Spring 2005 Computer Graphics Jargon: Illumination Models Illumination - the
CEng 477 Introduction to Computer Graphics Fall
 Illumination Models and Surface-Rendering Methods CEng 477 Introduction to Computer Graphics Fall 2007 2008 Illumination Models and Surface Rendering Methods In order to achieve realism in computer generated
Illumination Models and Surface-Rendering Methods CEng 477 Introduction to Computer Graphics Fall 2007 2008 Illumination Models and Surface Rendering Methods In order to achieve realism in computer generated
Shading and Illumination
 Shading and Illumination OpenGL Shading Without Shading With Shading Physics Bidirectional Reflectance Distribution Function (BRDF) f r (ω i,ω ) = dl(ω ) L(ω i )cosθ i dω i = dl(ω ) L(ω i )( ω i n)dω
Shading and Illumination OpenGL Shading Without Shading With Shading Physics Bidirectional Reflectance Distribution Function (BRDF) f r (ω i,ω ) = dl(ω ) L(ω i )cosθ i dω i = dl(ω ) L(ω i )( ω i n)dω
Today. Global illumination. Shading. Interactive applications. Rendering pipeline. Computergrafik. Shading Introduction Local shading models
 Computergrafik Matthias Zwicker Universität Bern Herbst 2009 Today Introduction Local shading models Light sources strategies Compute interaction of light with surfaces Requires simulation of physics Global
Computergrafik Matthias Zwicker Universität Bern Herbst 2009 Today Introduction Local shading models Light sources strategies Compute interaction of light with surfaces Requires simulation of physics Global
Why we need shading?
 Why we need shading? Suppose we build a model of a sphere using many polygons and color it with glcolor. We get something like But we want Light-material interactions cause each point to have a different
Why we need shading? Suppose we build a model of a sphere using many polygons and color it with glcolor. We get something like But we want Light-material interactions cause each point to have a different
OpenGl Pipeline. triangles, lines, points, images. Per-vertex ops. Primitive assembly. Texturing. Rasterization. Per-fragment ops.
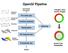 OpenGl Pipeline Individual Vertices Transformed Vertices Commands Processor Per-vertex ops Primitive assembly triangles, lines, points, images Primitives Fragments Rasterization Texturing Per-fragment
OpenGl Pipeline Individual Vertices Transformed Vertices Commands Processor Per-vertex ops Primitive assembly triangles, lines, points, images Primitives Fragments Rasterization Texturing Per-fragment
Three-Dimensional Graphics V. Guoying Zhao 1 / 55
 Computer Graphics Three-Dimensional Graphics V Guoying Zhao 1 / 55 Shading Guoying Zhao 2 / 55 Objectives Learn to shade objects so their images appear three-dimensional Introduce the types of light-material
Computer Graphics Three-Dimensional Graphics V Guoying Zhao 1 / 55 Shading Guoying Zhao 2 / 55 Objectives Learn to shade objects so their images appear three-dimensional Introduce the types of light-material
Light Sources. Spotlight model
 lecture 12 Light Sources sunlight (parallel) Sunny day model : "point source at infinity" - lighting - materials: diffuse, specular, ambient spotlight - shading: Flat vs. Gouraud vs Phong light bulb ambient
lecture 12 Light Sources sunlight (parallel) Sunny day model : "point source at infinity" - lighting - materials: diffuse, specular, ambient spotlight - shading: Flat vs. Gouraud vs Phong light bulb ambient
INF3320 Computer Graphics and Discrete Geometry
 INF3320 Computer Graphics and Discrete Geometry Visual appearance Christopher Dyken and Martin Reimers 23.09.2009 Page 1 Visual appearance Real Time Rendering: Chapter 5 Light Sources and materials Shading
INF3320 Computer Graphics and Discrete Geometry Visual appearance Christopher Dyken and Martin Reimers 23.09.2009 Page 1 Visual appearance Real Time Rendering: Chapter 5 Light Sources and materials Shading
CPSC 314 LIGHTING AND SHADING
 CPSC 314 LIGHTING AND SHADING UGRAD.CS.UBC.CA/~CS314 slide credits: Mikhail Bessmeltsev et al 1 THE RENDERING PIPELINE Vertices and attributes Vertex Shader Modelview transform Per-vertex attributes Vertex
CPSC 314 LIGHTING AND SHADING UGRAD.CS.UBC.CA/~CS314 slide credits: Mikhail Bessmeltsev et al 1 THE RENDERING PIPELINE Vertices and attributes Vertex Shader Modelview transform Per-vertex attributes Vertex
CS5620 Intro to Computer Graphics
 So Far wireframe hidden surfaces Next step 1 2 Light! Need to understand: How lighting works Types of lights Types of surfaces How shading works Shading algorithms What s Missing? Lighting vs. Shading
So Far wireframe hidden surfaces Next step 1 2 Light! Need to understand: How lighting works Types of lights Types of surfaces How shading works Shading algorithms What s Missing? Lighting vs. Shading
Illumination and Shading
 CT4510: Computer Graphics Illumination and Shading BOCHANG MOON Photorealism The ultimate goal of rendering is to produce photo realistic images. i.e., rendered images should be indistinguishable from
CT4510: Computer Graphics Illumination and Shading BOCHANG MOON Photorealism The ultimate goal of rendering is to produce photo realistic images. i.e., rendered images should be indistinguishable from
CMSC427 Shading Intro. Credit: slides from Dr. Zwicker
 CMSC427 Shading Intro Credit: slides from Dr. Zwicker 2 Today Shading Introduction Radiometry & BRDFs Local shading models Light sources Shading strategies Shading Compute interaction of light with surfaces
CMSC427 Shading Intro Credit: slides from Dr. Zwicker 2 Today Shading Introduction Radiometry & BRDFs Local shading models Light sources Shading strategies Shading Compute interaction of light with surfaces
Illumination and Shading ECE 567
 Illumination and Shading ECE 567 Overview Lighting Models Ambient light Diffuse light Specular light Shading Models Flat shading Gouraud shading Phong shading OpenGL 2 Introduction To add realism to drawings
Illumination and Shading ECE 567 Overview Lighting Models Ambient light Diffuse light Specular light Shading Models Flat shading Gouraud shading Phong shading OpenGL 2 Introduction To add realism to drawings
Comp 410/510 Computer Graphics. Spring Shading
 Comp 410/510 Computer Graphics Spring 2017 Shading Why we need shading Suppose we build a model of a sphere using many polygons and then color it using a fixed color. We get something like But we rather
Comp 410/510 Computer Graphics Spring 2017 Shading Why we need shading Suppose we build a model of a sphere using many polygons and then color it using a fixed color. We get something like But we rather
Shading. Reading. Pinhole camera. Basic 3D graphics. Brian Curless CSE 457 Spring 2017
 Reading Optional: Angel and Shreiner: chapter 5. Marchner and Shirley: chapter 0, chapter 7. Shading Further reading: OpenGL red book, chapter 5. Brian Curle CSE 457 Spring 207 2 Baic 3D graphic With affine
Reading Optional: Angel and Shreiner: chapter 5. Marchner and Shirley: chapter 0, chapter 7. Shading Further reading: OpenGL red book, chapter 5. Brian Curle CSE 457 Spring 207 2 Baic 3D graphic With affine
Ambient reflection. Jacobs University Visualization and Computer Graphics Lab : Graphics and Visualization 407
 Ambient reflection Phong reflection is a local illumination model. It only considers the reflection of light that directly comes from the light source. It does not compute secondary reflection of light
Ambient reflection Phong reflection is a local illumination model. It only considers the reflection of light that directly comes from the light source. It does not compute secondary reflection of light
CSE 167: Introduction to Computer Graphics Lecture #6: Lights. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2016
 CSE 167: Introduction to Computer Graphics Lecture #6: Lights Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2016 Announcements Thursday in class: midterm #1 Closed book Material
CSE 167: Introduction to Computer Graphics Lecture #6: Lights Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2016 Announcements Thursday in class: midterm #1 Closed book Material
Sung-Eui Yoon ( 윤성의 )
 CS380: Computer Graphics Illumination and Shading Sung-Eui Yoon ( 윤성의 ) Course URL: http://sglab.kaist.ac.kr/~sungeui/cg/ Course Objectives (Ch. 10) Know how to consider lights during rendering models
CS380: Computer Graphics Illumination and Shading Sung-Eui Yoon ( 윤성의 ) Course URL: http://sglab.kaist.ac.kr/~sungeui/cg/ Course Objectives (Ch. 10) Know how to consider lights during rendering models
Virtual Reality for Human Computer Interaction
 Virtual Reality for Human Computer Interaction Appearance: Lighting Representation of Light and Color Representation of Light and Color Do we need to represent all I! to represent a color C(I)? Representation
Virtual Reality for Human Computer Interaction Appearance: Lighting Representation of Light and Color Representation of Light and Color Do we need to represent all I! to represent a color C(I)? Representation
Illumination and Shading
 Illumination and Shading Computer Graphics COMP 770 (236) Spring 2007 Instructor: Brandon Lloyd 2/14/07 1 From last time Texture mapping overview notation wrapping Perspective-correct interpolation Texture
Illumination and Shading Computer Graphics COMP 770 (236) Spring 2007 Instructor: Brandon Lloyd 2/14/07 1 From last time Texture mapping overview notation wrapping Perspective-correct interpolation Texture
Virtual Reality for Human Computer Interaction
 Virtual Reality for Human Computer Interaction Appearance: Lighting Representation of Light and Color Do we need to represent all I! to represent a color C(I)? No we can approximate using a three-color
Virtual Reality for Human Computer Interaction Appearance: Lighting Representation of Light and Color Do we need to represent all I! to represent a color C(I)? No we can approximate using a three-color
Computer Graphics (CS 543) Lecture 7b: Intro to lighting, Shading and Materials + Phong Lighting Model
 Computer Graphics (CS 543) Lecture 7b: Intro to lighting, Shading and Materials + Phong Lighting Model Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) Why do we need Lighting
Computer Graphics (CS 543) Lecture 7b: Intro to lighting, Shading and Materials + Phong Lighting Model Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) Why do we need Lighting
Illumination & Shading
 Illumination & Shading Goals Introduce the types of light-material interactions Build a simple reflection model---the Phong model--- that can be used with real time graphics hardware Why we need Illumination
Illumination & Shading Goals Introduce the types of light-material interactions Build a simple reflection model---the Phong model--- that can be used with real time graphics hardware Why we need Illumination
Methodology for Lecture. Importance of Lighting. Outline. Shading Models. Brief primer on Color. Foundations of Computer Graphics (Spring 2010)
 Foundations of Computer Graphics (Spring 2010) CS 184, Lecture 11: OpenGL 3 http://inst.eecs.berkeley.edu/~cs184 Methodology for Lecture Lecture deals with lighting (teapot shaded as in HW1) Some Nate
Foundations of Computer Graphics (Spring 2010) CS 184, Lecture 11: OpenGL 3 http://inst.eecs.berkeley.edu/~cs184 Methodology for Lecture Lecture deals with lighting (teapot shaded as in HW1) Some Nate
Shading , Fall 2004 Nancy Pollard Mark Tomczak
 15-462, Fall 2004 Nancy Pollard Mark Tomczak Shading Shading Concepts Shading Equations Lambertian, Gouraud shading Phong Illumination Model Non-photorealistic rendering [Shirly, Ch. 8] Announcements Written
15-462, Fall 2004 Nancy Pollard Mark Tomczak Shading Shading Concepts Shading Equations Lambertian, Gouraud shading Phong Illumination Model Non-photorealistic rendering [Shirly, Ch. 8] Announcements Written
Illumination Models & Shading
 Illumination Models & Shading Lighting vs. Shading Lighting Interaction between materials and light sources Physics Shading Determining the color of a pixel Computer Graphics ZBuffer(Scene) PutColor(x,y,Col(P));
Illumination Models & Shading Lighting vs. Shading Lighting Interaction between materials and light sources Physics Shading Determining the color of a pixel Computer Graphics ZBuffer(Scene) PutColor(x,y,Col(P));
Shading I Computer Graphics I, Fall 2008
 Shading I 1 Objectives Learn to shade objects ==> images appear threedimensional Introduce types of light-material interactions Build simple reflection model Phong model Can be used with real time graphics
Shading I 1 Objectives Learn to shade objects ==> images appear threedimensional Introduce types of light-material interactions Build simple reflection model Phong model Can be used with real time graphics
Topic 9: Lighting & Reflection models 9/10/2016. Spot the differences. Terminology. Two Components of Illumination. Ambient Light Source
 Topic 9: Lighting & Reflection models Lighting & reflection The Phong reflection model diffuse component ambient component specular component Spot the differences Terminology Illumination The transport
Topic 9: Lighting & Reflection models Lighting & reflection The Phong reflection model diffuse component ambient component specular component Spot the differences Terminology Illumination The transport
Computer Graphics (CS 4731) Lecture 16: Lighting, Shading and Materials (Part 1)
 Computer Graphics (CS 4731) Lecture 16: Lighting, Shading and Materials (Part 1) Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) Why do we need Lighting & shading? Sphere
Computer Graphics (CS 4731) Lecture 16: Lighting, Shading and Materials (Part 1) Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI) Why do we need Lighting & shading? Sphere
Lecture 15: Shading-I. CITS3003 Graphics & Animation
 Lecture 15: Shading-I CITS3003 Graphics & Animation E. Angel and D. Shreiner: Interactive Computer Graphics 6E Addison-Wesley 2012 Objectives Learn that with appropriate shading so objects appear as threedimensional
Lecture 15: Shading-I CITS3003 Graphics & Animation E. Angel and D. Shreiner: Interactive Computer Graphics 6E Addison-Wesley 2012 Objectives Learn that with appropriate shading so objects appear as threedimensional
CS Surface Rendering
 CS10101001 Surface Rendering Junqiao Zhao 赵君峤 Department of Computer Science and Technology College of Electronics and Information Engineering Tongji University Surface rendering How do we choose a color
CS10101001 Surface Rendering Junqiao Zhao 赵君峤 Department of Computer Science and Technology College of Electronics and Information Engineering Tongji University Surface rendering How do we choose a color
CSE 167: Lecture #8: Lighting. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2011
 CSE 167: Introduction to Computer Graphics Lecture #8: Lighting Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2011 Announcements Homework project #4 due Friday, October 28 Introduction:
CSE 167: Introduction to Computer Graphics Lecture #8: Lighting Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2011 Announcements Homework project #4 due Friday, October 28 Introduction:
Lighting/Shading III. Week 7, Wed Mar 3
 University of British Columbia CPSC 314 Computer Graphics Jan-Apr 2010 Tamara Munzner Lighting/Shading III Week 7, Wed Mar 3 http://www.ugrad.cs.ubc.ca/~cs314/vjan2010 reminders News don't need to tell
University of British Columbia CPSC 314 Computer Graphics Jan-Apr 2010 Tamara Munzner Lighting/Shading III Week 7, Wed Mar 3 http://www.ugrad.cs.ubc.ca/~cs314/vjan2010 reminders News don't need to tell
ECS 175 COMPUTER GRAPHICS. Ken Joy.! Winter 2014
 ECS 175 COMPUTER GRAPHICS Ken Joy Winter 2014 Shading To be able to model shading, we simplify Uniform Media no scattering of light Opaque Objects No Interreflection Point Light Sources RGB Color (eliminating
ECS 175 COMPUTER GRAPHICS Ken Joy Winter 2014 Shading To be able to model shading, we simplify Uniform Media no scattering of light Opaque Objects No Interreflection Point Light Sources RGB Color (eliminating
Topic 9: Lighting & Reflection models. Lighting & reflection The Phong reflection model diffuse component ambient component specular component
 Topic 9: Lighting & Reflection models Lighting & reflection The Phong reflection model diffuse component ambient component specular component Spot the differences Terminology Illumination The transport
Topic 9: Lighting & Reflection models Lighting & reflection The Phong reflection model diffuse component ambient component specular component Spot the differences Terminology Illumination The transport
Computer Graphics. Illumination and Shading
 Rendering Pipeline modelling of geometry transformation into world coordinates placement of cameras and light sources transformation into camera coordinates backface culling projection clipping w.r.t.
Rendering Pipeline modelling of geometry transformation into world coordinates placement of cameras and light sources transformation into camera coordinates backface culling projection clipping w.r.t.
Introduction to Computer Graphics 7. Shading
 Introduction to Computer Graphics 7. Shading National Chiao Tung Univ, Taiwan By: I-Chen Lin, Assistant Professor Textbook: Hearn and Baker, Computer Graphics, 3rd Ed., Prentice Hall Ref: E.Angel, Interactive
Introduction to Computer Graphics 7. Shading National Chiao Tung Univ, Taiwan By: I-Chen Lin, Assistant Professor Textbook: Hearn and Baker, Computer Graphics, 3rd Ed., Prentice Hall Ref: E.Angel, Interactive
University of British Columbia CPSC 314 Computer Graphics Sep-Dec Tamara Munzner (guest lecturing) Lighting/Shading
 University of British Columbia CPSC 314 Computer Graphics Sep-Dec 2010 Tamara Munzner (guest lecturing) Lighting/Shading Lighting 2 Rendering Pipeline Geometry Database Model/View Transform. Lighting Perspective
University of British Columbia CPSC 314 Computer Graphics Sep-Dec 2010 Tamara Munzner (guest lecturing) Lighting/Shading Lighting 2 Rendering Pipeline Geometry Database Model/View Transform. Lighting Perspective
Computer Graphics. Shading. Based on slides by Dianna Xu, Bryn Mawr College
 Computer Graphics Shading Based on slides by Dianna Xu, Bryn Mawr College Image Synthesis and Shading Perception of 3D Objects Displays almost always 2 dimensional. Depth cues needed to restore the third
Computer Graphics Shading Based on slides by Dianna Xu, Bryn Mawr College Image Synthesis and Shading Perception of 3D Objects Displays almost always 2 dimensional. Depth cues needed to restore the third
CPSC / Illumination and Shading
 CPSC 599.64 / 601.64 Rendering Pipeline usually in one step modelling of geometry transformation into world coordinate system placement of cameras and light sources transformation into camera coordinate
CPSC 599.64 / 601.64 Rendering Pipeline usually in one step modelling of geometry transformation into world coordinate system placement of cameras and light sources transformation into camera coordinate
Illumination and Shading
 Illumination and Shading Illumination (Lighting)! Model the interaction of light with surface points to determine their final color and brightness! The illumination can be computed either at vertices or
Illumination and Shading Illumination (Lighting)! Model the interaction of light with surface points to determine their final color and brightness! The illumination can be computed either at vertices or
Orthogonal Projection Matrices. Angel and Shreiner: Interactive Computer Graphics 7E Addison-Wesley 2015
 Orthogonal Projection Matrices 1 Objectives Derive the projection matrices used for standard orthogonal projections Introduce oblique projections Introduce projection normalization 2 Normalization Rather
Orthogonal Projection Matrices 1 Objectives Derive the projection matrices used for standard orthogonal projections Introduce oblique projections Introduce projection normalization 2 Normalization Rather
C O M P U T E R G R A P H I C S. Computer Graphics. Three-Dimensional Graphics V. Guoying Zhao 1 / 65
 Computer Graphics Three-Dimensional Graphics V Guoying Zhao 1 / 65 Shading Guoying Zhao 2 / 65 Objectives Learn to shade objects so their images appear three-dimensional Introduce the types of light-material
Computer Graphics Three-Dimensional Graphics V Guoying Zhao 1 / 65 Shading Guoying Zhao 2 / 65 Objectives Learn to shade objects so their images appear three-dimensional Introduce the types of light-material
WHY WE NEED SHADING. Suppose we build a model of a sphere using many polygons and color it with glcolor. We get something like.
 LIGHTING 1 OUTLINE Learn to light/shade objects so their images appear three-dimensional Introduce the types of light-material interactions Build a simple reflection model---the Phong model--- that can
LIGHTING 1 OUTLINE Learn to light/shade objects so their images appear three-dimensional Introduce the types of light-material interactions Build a simple reflection model---the Phong model--- that can
Illumination. Illumination CMSC 435/634
 Illumination CMSC 435/634 Illumination Interpolation Illumination Illumination Interpolation Illumination Illumination Effect of light on objects Mostly look just at intensity Apply to each color channel
Illumination CMSC 435/634 Illumination Interpolation Illumination Illumination Interpolation Illumination Illumination Effect of light on objects Mostly look just at intensity Apply to each color channel
OpenGL Lighting Computer Graphics Spring Frank Palermo
 OpenGL Lighting 15-462 Computer Graphics Spring 2009 Frank Palermo OpenGL is just a bunch of hacks. -Adrien Treuille What Adrien Means... What Adrien means is that OpenGL was designed to produce reasonable-looking
OpenGL Lighting 15-462 Computer Graphics Spring 2009 Frank Palermo OpenGL is just a bunch of hacks. -Adrien Treuille What Adrien Means... What Adrien means is that OpenGL was designed to produce reasonable-looking
Lighting and Shading Computer Graphics I Lecture 7. Light Sources Phong Illumination Model Normal Vectors [Angel, Ch
 15-462 Computer Graphics I Lecture 7 Lighting and Shading February 12, 2002 Frank Pfenning Carnegie Mellon University http://www.cs.cmu.edu/~fp/courses/graphics/ Light Sources Phong Illumination Model
15-462 Computer Graphics I Lecture 7 Lighting and Shading February 12, 2002 Frank Pfenning Carnegie Mellon University http://www.cs.cmu.edu/~fp/courses/graphics/ Light Sources Phong Illumination Model
CSE 167: Lecture #7: Color and Shading. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2011
 CSE 167: Introduction to Computer Graphics Lecture #7: Color and Shading Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2011 Announcements Homework project #3 due this Friday,
CSE 167: Introduction to Computer Graphics Lecture #7: Color and Shading Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2011 Announcements Homework project #3 due this Friday,
Lighting. CSC 7443: Scientific Information Visualization
 Lighting Why Lighting? What light source is used and how the object response to the light makes difference Ocean looks bright bluish green in sunny day but dim gray green in cloudy day Lighting gives you
Lighting Why Lighting? What light source is used and how the object response to the light makes difference Ocean looks bright bluish green in sunny day but dim gray green in cloudy day Lighting gives you
CS452/552; EE465/505. Intro to Lighting
 CS452/552; EE465/505 Intro to Lighting 2-10 15 Outline! Projection Normalization! Introduction to Lighting (and Shading) Read: Angel Chapter 5., sections 5.4-5.7 Parallel Projections Chapter 6, sections
CS452/552; EE465/505 Intro to Lighting 2-10 15 Outline! Projection Normalization! Introduction to Lighting (and Shading) Read: Angel Chapter 5., sections 5.4-5.7 Parallel Projections Chapter 6, sections
Simple Lighting/Illumination Models
 Simple Lighting/Illumination Models Scene rendered using direct lighting only Photograph Scene rendered using a physically-based global illumination model with manual tuning of colors (Frederic Drago and
Simple Lighting/Illumination Models Scene rendered using direct lighting only Photograph Scene rendered using a physically-based global illumination model with manual tuning of colors (Frederic Drago and
CS 5625 Lec 2: Shading Models
 CS 5625 Lec 2: Shading Models Kavita Bala Spring 2013 Shading Models Chapter 7 Next few weeks Textures Graphics Pipeline Light Emission To compute images What are the light sources? Light Propagation Fog/Clear?
CS 5625 Lec 2: Shading Models Kavita Bala Spring 2013 Shading Models Chapter 7 Next few weeks Textures Graphics Pipeline Light Emission To compute images What are the light sources? Light Propagation Fog/Clear?
Illumination & Shading
 Illumination & Shading Light Sources Empirical Illumination Shading Lecture 15 CISC440/640 Spring 2015 Illumination Models Computer Graphics Jargon: Illumination - the transport luminous flux from light
Illumination & Shading Light Sources Empirical Illumination Shading Lecture 15 CISC440/640 Spring 2015 Illumination Models Computer Graphics Jargon: Illumination - the transport luminous flux from light
Light Transport Baoquan Chen 2017
 Light Transport 1 Physics of Light and Color It s all electromagnetic (EM) radiation Different colors correspond to radiation of different wavelengths Intensity of each wavelength specified by amplitude
Light Transport 1 Physics of Light and Color It s all electromagnetic (EM) radiation Different colors correspond to radiation of different wavelengths Intensity of each wavelength specified by amplitude
Lecture 4 Advanced Computer Graphics (CS & SE )
 Lecture 4 Advanced Computer Graphics (CS & SE 233.420) Topics Covered Animation Matrices Viewing Lighting Animating Interactive Programs Consider planet.c Want to animate rotating the Earth around the
Lecture 4 Advanced Computer Graphics (CS & SE 233.420) Topics Covered Animation Matrices Viewing Lighting Animating Interactive Programs Consider planet.c Want to animate rotating the Earth around the
Today s class. Simple shadows Shading Lighting in OpenGL. Informationsteknologi. Wednesday, November 21, 2007 Computer Graphics - Class 10 1
 Today s class Simple shadows Shading Lighting in OpenGL Wednesday, November 21, 27 Computer Graphics - Class 1 1 Simple shadows Simple shadows can be gotten by using projection matrices Consider a light
Today s class Simple shadows Shading Lighting in OpenGL Wednesday, November 21, 27 Computer Graphics - Class 1 1 Simple shadows Simple shadows can be gotten by using projection matrices Consider a light
CSE 167: Introduction to Computer Graphics Lecture #7: Lights. Jürgen P. Schulze, Ph.D. University of California, San Diego Spring Quarter 2015
 CSE 167: Introduction to Computer Graphics Lecture #7: Lights Jürgen P. Schulze, Ph.D. University of California, San Diego Spring Quarter 2015 Announcements Thursday in-class: Midterm Can include material
CSE 167: Introduction to Computer Graphics Lecture #7: Lights Jürgen P. Schulze, Ph.D. University of California, San Diego Spring Quarter 2015 Announcements Thursday in-class: Midterm Can include material
Homework #2. Shading, Ray Tracing, and Texture Mapping
 Computer Graphics Prof. Brian Curless CSE 457 Spring 2000 Homework #2 Shading, Ray Tracing, and Texture Mapping Prepared by: Doug Johnson, Maya Widyasari, and Brian Curless Assigned: Monday, May 8, 2000
Computer Graphics Prof. Brian Curless CSE 457 Spring 2000 Homework #2 Shading, Ray Tracing, and Texture Mapping Prepared by: Doug Johnson, Maya Widyasari, and Brian Curless Assigned: Monday, May 8, 2000
Pipeline Operations. CS 4620 Lecture 10
 Pipeline Operations CS 4620 Lecture 10 2008 Steve Marschner 1 Hidden surface elimination Goal is to figure out which color to make the pixels based on what s in front of what. Hidden surface elimination
Pipeline Operations CS 4620 Lecture 10 2008 Steve Marschner 1 Hidden surface elimination Goal is to figure out which color to make the pixels based on what s in front of what. Hidden surface elimination
CS Computer Graphics: Illumination and Shading I
 CS 543 - Computer Graphics: Illumination and Shading I by Robert W. Lindeman gogo@wpi.edu (with help from Emmanuel Agu ;-) Illumination and Shading Problem: Model light/surface point interactions to determine
CS 543 - Computer Graphics: Illumination and Shading I by Robert W. Lindeman gogo@wpi.edu (with help from Emmanuel Agu ;-) Illumination and Shading Problem: Model light/surface point interactions to determine
CS Computer Graphics: Illumination and Shading I
 CS 543 - Computer Graphics: Illumination and Shading I by Robert W. Lindeman gogo@wpi.edu (with help from Emmanuel Agu ;-) Illumination and Shading Problem: Model light/surface point interactions to determine
CS 543 - Computer Graphics: Illumination and Shading I by Robert W. Lindeman gogo@wpi.edu (with help from Emmanuel Agu ;-) Illumination and Shading Problem: Model light/surface point interactions to determine
Shading. Why we need shading. Scattering. Shading. Objectives
 Shading Why we need shading Objectives Learn to shade objects so their images appear three-dimensional Suppose we build a model of a sphere using many polygons and color it with glcolor. We get something
Shading Why we need shading Objectives Learn to shade objects so their images appear three-dimensional Suppose we build a model of a sphere using many polygons and color it with glcolor. We get something
Lecture 17: Shading in OpenGL. CITS3003 Graphics & Animation
 Lecture 17: Shading in OpenGL CITS3003 Graphics & Animation E. Angel and D. Shreiner: Interactive Computer Graphics 6E Addison-Wesley 2012 Objectives Introduce the OpenGL shading methods - per vertex shading
Lecture 17: Shading in OpenGL CITS3003 Graphics & Animation E. Angel and D. Shreiner: Interactive Computer Graphics 6E Addison-Wesley 2012 Objectives Introduce the OpenGL shading methods - per vertex shading
CS130 : Computer Graphics Lecture 8: Lighting and Shading. Tamar Shinar Computer Science & Engineering UC Riverside
 CS130 : Computer Graphics Lecture 8: Lighting and Shading Tamar Shinar Computer Science & Engineering UC Riverside Why we need shading Suppose we build a model of a sphere using many polygons and color
CS130 : Computer Graphics Lecture 8: Lighting and Shading Tamar Shinar Computer Science & Engineering UC Riverside Why we need shading Suppose we build a model of a sphere using many polygons and color
Illumination Model. The governing principles for computing the. Apply the lighting model at a set of points across the entire surface.
 Illumination and Shading Illumination (Lighting) Model the interaction of light with surface points to determine their final color and brightness OpenGL computes illumination at vertices illumination Shading
Illumination and Shading Illumination (Lighting) Model the interaction of light with surface points to determine their final color and brightness OpenGL computes illumination at vertices illumination Shading
Illumination and Shading
 Illumination and Shading Illumination (Lighting) Model the interaction of light with surface points to determine their final color and brightness OpenGL computes illumination at vertices illumination Shading
Illumination and Shading Illumination (Lighting) Model the interaction of light with surface points to determine their final color and brightness OpenGL computes illumination at vertices illumination Shading
LIGHTING AND SHADING
 DH2323 DGI15 INTRODUCTION TO COMPUTER GRAPHICS AND INTERACTION LIGHTING AND SHADING Christopher Peters HPCViz, KTH Royal Institute of Technology, Sweden chpeters@kth.se http://kth.academia.edu/christopheredwardpeters
DH2323 DGI15 INTRODUCTION TO COMPUTER GRAPHICS AND INTERACTION LIGHTING AND SHADING Christopher Peters HPCViz, KTH Royal Institute of Technology, Sweden chpeters@kth.se http://kth.academia.edu/christopheredwardpeters
Introduction Rasterization Z-buffering Shading. Graphics 2012/2013, 4th quarter. Lecture 09: graphics pipeline (rasterization and shading)
 Lecture 9 Graphics pipeline (rasterization and shading) Graphics pipeline - part 1 (recap) Perspective projection by matrix multiplication: x pixel y pixel z canonical 1 x = M vpm per M cam y z 1 This
Lecture 9 Graphics pipeline (rasterization and shading) Graphics pipeline - part 1 (recap) Perspective projection by matrix multiplication: x pixel y pixel z canonical 1 x = M vpm per M cam y z 1 This
CS 4600 Fall Utah School of Computing
 Lighting CS 4600 Fall 2015 Utah School of Computing Objectives Learn to shade objects so their images appear three-dimensional Introduce the types of light-material interactions Build a simple reflection
Lighting CS 4600 Fall 2015 Utah School of Computing Objectives Learn to shade objects so their images appear three-dimensional Introduce the types of light-material interactions Build a simple reflection
Illumination in Computer Graphics
 Illumination in Computer Graphics Ann McNamara Illumination in Computer Graphics Definition of light sources. Analysis of interaction between light and objects in a scene. Rendering images that are faithful
Illumination in Computer Graphics Ann McNamara Illumination in Computer Graphics Definition of light sources. Analysis of interaction between light and objects in a scene. Rendering images that are faithful
Pipeline Operations. CS 4620 Lecture 14
 Pipeline Operations CS 4620 Lecture 14 2014 Steve Marschner 1 Pipeline you are here APPLICATION COMMAND STREAM 3D transformations; shading VERTEX PROCESSING TRANSFORMED GEOMETRY conversion of primitives
Pipeline Operations CS 4620 Lecture 14 2014 Steve Marschner 1 Pipeline you are here APPLICATION COMMAND STREAM 3D transformations; shading VERTEX PROCESSING TRANSFORMED GEOMETRY conversion of primitives
Lighting affects appearance
 Lighting affects appearance 1 Source emits photons Light And then some reach the eye/camera. Photons travel in a straight line When they hit an object they: bounce off in a new direction or are absorbed
Lighting affects appearance 1 Source emits photons Light And then some reach the eye/camera. Photons travel in a straight line When they hit an object they: bounce off in a new direction or are absorbed
Complex Shading Algorithms
 Complex Shading Algorithms CPSC 414 Overview So far Rendering Pipeline including recent developments Today Shading algorithms based on the Rendering Pipeline Arbitrary reflection models (BRDFs) Bump mapping
Complex Shading Algorithms CPSC 414 Overview So far Rendering Pipeline including recent developments Today Shading algorithms based on the Rendering Pipeline Arbitrary reflection models (BRDFs) Bump mapping
Illumination & Shading I
 CS 543: Computer Graphics Illumination & Shading I Robert W. Lindeman Associate Professor Interactive Media & Game Development Department of Computer Science Worcester Polytechnic Institute gogo@wpi.edu
CS 543: Computer Graphics Illumination & Shading I Robert W. Lindeman Associate Professor Interactive Media & Game Development Department of Computer Science Worcester Polytechnic Institute gogo@wpi.edu
CS 148, Summer 2012 Introduction to Computer Graphics and Imaging
 http://www.ann.jussieu.fr/~frey/papers/scivi/cook%20r.l.,%20a%20reflectance%20model%20for%20computer%20graphics.pdf CS 148, Summer 2012 Introduction to Computer Graphics and Imaging f(~v 2 ) A 3 A 1 f(~v
http://www.ann.jussieu.fr/~frey/papers/scivi/cook%20r.l.,%20a%20reflectance%20model%20for%20computer%20graphics.pdf CS 148, Summer 2012 Introduction to Computer Graphics and Imaging f(~v 2 ) A 3 A 1 f(~v
Graphics and Visualization
 International University Bremen Spring Semester 2006 Recap Hierarchical Modeling Perspective vs Parallel Projection Representing solid objects Displaying Wireframe models is easy from a computational
International University Bremen Spring Semester 2006 Recap Hierarchical Modeling Perspective vs Parallel Projection Representing solid objects Displaying Wireframe models is easy from a computational
CSE 167: Lecture #8: GLSL. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2012
 CSE 167: Introduction to Computer Graphics Lecture #8: GLSL Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2012 Announcements Homework project #4 due Friday, November 2 nd Introduction:
CSE 167: Introduction to Computer Graphics Lecture #8: GLSL Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2012 Announcements Homework project #4 due Friday, November 2 nd Introduction:
CSE 167: Introduction to Computer Graphics Lecture #6: Lights. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2014
 CSE 167: Introduction to Computer Graphics Lecture #6: Lights Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2014 Announcements Project 2 due Friday, Oct. 24 th Midterm Exam
CSE 167: Introduction to Computer Graphics Lecture #6: Lights Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2014 Announcements Project 2 due Friday, Oct. 24 th Midterm Exam
Local Illumination. CMPT 361 Introduction to Computer Graphics Torsten Möller. Machiraju/Zhang/Möller
 Local Illumination CMPT 361 Introduction to Computer Graphics Torsten Möller Graphics Pipeline Hardware Modelling Transform Visibility Illumination + Shading Perception, Interaction Color Texture/ Realism
Local Illumination CMPT 361 Introduction to Computer Graphics Torsten Möller Graphics Pipeline Hardware Modelling Transform Visibility Illumination + Shading Perception, Interaction Color Texture/ Realism
Ligh%ng and Shading. Ligh%ng and Shading. q Is this a plate or a ball? q What color should I set for each pixel?
 Ligh%ng and Shading Ligh%ng and Shading Is this a plate or a ball? What color should I set for each pixel? 1 Physical Reality As light hits the surface: Part is absorbed Part is reflected Visible light
Ligh%ng and Shading Ligh%ng and Shading Is this a plate or a ball? What color should I set for each pixel? 1 Physical Reality As light hits the surface: Part is absorbed Part is reflected Visible light
Objectives. Introduce Phong model Introduce modified Phong model Consider computation of required vectors Discuss polygonal shading.
 Shading II 1 Objectives Introduce Phong model Introduce modified Phong model Consider computation of required vectors Discuss polygonal shading Flat Smooth Gouraud 2 Phong Lighting Model A simple model
Shading II 1 Objectives Introduce Phong model Introduce modified Phong model Consider computation of required vectors Discuss polygonal shading Flat Smooth Gouraud 2 Phong Lighting Model A simple model
surface: reflectance transparency, opacity, translucency orientation illumination: location intensity wavelength point-source, diffuse source
 walters@buffalo.edu CSE 480/580 Lecture 18 Slide 1 Illumination and Shading Light reflected from nonluminous objects depends on: surface: reflectance transparency, opacity, translucency orientation illumination:
walters@buffalo.edu CSE 480/580 Lecture 18 Slide 1 Illumination and Shading Light reflected from nonluminous objects depends on: surface: reflectance transparency, opacity, translucency orientation illumination:
Pipeline Operations. CS 4620 Lecture Steve Marschner. Cornell CS4620 Spring 2018 Lecture 11
 Pipeline Operations CS 4620 Lecture 11 1 Pipeline you are here APPLICATION COMMAND STREAM 3D transformations; shading VERTEX PROCESSING TRANSFORMED GEOMETRY conversion of primitives to pixels RASTERIZATION
Pipeline Operations CS 4620 Lecture 11 1 Pipeline you are here APPLICATION COMMAND STREAM 3D transformations; shading VERTEX PROCESSING TRANSFORMED GEOMETRY conversion of primitives to pixels RASTERIZATION
Introduction to Visualization and Computer Graphics
 Introduction to Visualization and Computer Graphics DH2320, Fall 2015 Prof. Dr. Tino Weinkauf Introduction to Visualization and Computer Graphics Visibility Shading 3D Rendering Geometric Model Color Perspective
Introduction to Visualization and Computer Graphics DH2320, Fall 2015 Prof. Dr. Tino Weinkauf Introduction to Visualization and Computer Graphics Visibility Shading 3D Rendering Geometric Model Color Perspective
Objectives Shading in OpenGL. Front and Back Faces. OpenGL shading. Introduce the OpenGL shading methods. Discuss polygonal shading
 Objectives Shading in OpenGL Introduce the OpenGL shading methods - per vertex shading vs per fragment shading - Where to carry out Discuss polygonal shading - Flat - Smooth - Gouraud CITS3003 Graphics
Objectives Shading in OpenGL Introduce the OpenGL shading methods - per vertex shading vs per fragment shading - Where to carry out Discuss polygonal shading - Flat - Smooth - Gouraud CITS3003 Graphics
Lighting affects appearance
 Lighting affects appearance 1 Source emits photons Light And then some reach the eye/camera. Photons travel in a straight line When they hit an object they: bounce off in a new direction or are absorbed
Lighting affects appearance 1 Source emits photons Light And then some reach the eye/camera. Photons travel in a straight line When they hit an object they: bounce off in a new direction or are absorbed
