A Unified, Integral Construction For Coordinates Over Closed Curves

Transcription

1 A Unfed, Integral Constructon For Coordnates Over Closed Curves Schaefer S., Ju T. and Warren J. Abstract We propose a smple generalzaton of Shephard s nterpolaton to pecewse smooth, convex closed curves that yelds a famly of boundary nterpolants wth lnear precson. Two nstances of ths famly reduce to prevously known nterpolants: one based on a generalzaton of Wachspress coordnates to smooth curves and the other an ntegral verson of mean value coordnates for smooth curves. A thrd nstance of ths famly yelds a prevously unknown generalzaton of dscrete harmonc coordnates to smooth curves. For closed, pecewse lnear curves, we prove that our nterpolant reproduces a general famly of barycentrc coordnates consdered by Floater, Hormann and Kós that ncludes Wachspress coordnates, mean value coordnates and dscrete harmonc coordnates. Key words: barycentrc coordnates, Shepard s nterpolant, boundary value Introducton Constructng a functon that nterpolates known values at a set of data stes s a common problem n mathematcs. Gven a set of values f j specfed at a set of ponts p j, the problem reduces to constructng a functon ˆf[v] such that ˆf[p j ] = f j. Perhaps the smplest known soluton to ths problem s Shepard s method []. Ths nterpolant has the form j w j f j ˆf[v] = () j w j where the weght w j = v p j. The resultng functon ˆf[v] satsfes the nterpolaton condtons snce w j as v p j. The fnal dvson by j w j ensures that the resultng nterpolant reproduces constant functons;.e.; f the f j = for all j, ˆf[v] = for all v. Preprnt submtted to Elsever Scence 4 August 2006

2 In computer graphcs, a common varant of ths nterpolaton problem s to specfy the data f not at a fnte set of sample ponts, but along an entre closed curve P. For example, gven a set of specfed colors at the vertces of a closed polygon, we extend those colors to the nteror of the polygon usng a functon that nterpolates the specfed colors at the vertces and s pecewse lnear along the edges of the polygon. More precsely, gven a parameterzaton p[x] for the closed curve P and a data value f[x] assocated wth each pont p[x] on P, we wsh to construct a functon ˆf[v] that nterpolates f along P (.e.; ˆf[p[x]] = f[x] for all x) and behaves reasonably on the nteror of P. Interestngly, generalzng Shephard s method to boundary nterpolaton s qute straghtforward. We smply replace the dscrete sums of equaton by ther correspondng ntegrals, ˆf[v] = f[x] p[x] v dp/ dp. (2) p[x] v Agan, ˆf nterpolates f on P. In partcular, ˆf[v] f[x] as v p[x] snce approaches nfnty. As n the dscrete case, ths nterpolant reproduces p[x] v constant functons. Buldng coordnates usng nterpolants: Another mportant use of nterpolants arses n applcatons such as mesh parameterzaton [2 6] and deformaton [7 ] where expressng a pont v as a weghted combnaton of the ponts p j s crtcal. These weghts are often referred to as the coordnates of v wth respect to the p j. One common technque for buldng coordnates s to construct an nterpolant that reproduces not only constant functons, but also reproduces lnear functons. A dscrete nterpolant ˆf[v] has lnear precson f settng the data values f j to be the data stes p j yelds the dentty functon ˆv = v. In ths case, the j weghts w j satsfy v = w jp j and thus form coordnates for v wth respect to j w j the p j. Unfortunately, Shepard s method s not sutable for constructng coordnates: the nterpolant ˆf[v] of equaton does not reproduce lnear functons. In partcular, f we set w j =, the weght sum j w jp j v p j does not reproduce j w j the pont v. Drven by the need for coordnates, there has been a large amount of research on boundary nterpolants that possess lnear precson. Such methods have the property that f f[x] = p[x] for all x, ˆf[v] = v for all v n P. The earlest work on ths boundary nterpolaton problem s due to Wachspress [2]. The resultng Wachspress coordnates (defned for convex polygons) have been the subject of numerous papers that generalze these coordnates to hgher dmensons and smooth convex shapes [3 5]. More recently, Floater [6] proposed an 2

3 alternatve set of coordnates for any closed polygon known as mean value coordnates. Agan, subsequent work has generalzed these coordnates to hgher dmensons and smooth shapes [7,]. Fnally, a thrd class of coordnates, dscrete harmonc coordnates, have been used n several applcatons [8,9]. These coordnates arse from solvng a smple varatonal problem nvolvng the harmonc functonal over a convex polygon P. In the case where P s a closed polygon, Floater et al. [20] have observed that all three of these coordnate constructons are nstances of a more general famly of 2D coordnates for closed polygons. Interestngly, Belyaev [2] showed that barycentrc coordnates are related to nverse problems n dfferental and convex geometry. In that paper (submtted n parallel wth ours), Belyaev generates a smlar extenson of Wachspress and harmonc coordnates to smooth shapes and studes the ablty of these coordnates to approxmate harmonc functons. Contrbutons: In ths paper, we propose a smple modfcaton to the contnuous verson of Shephard s method (gven n equaton 2) that yelds a famly of boundary nterpolants wth lnear precson. For smooth boundary curves, the nterpolant s equvalent to the ntegral verson of Wachspress coordnates for smooth convex curves [4] when k = 0 and reproduces the mean value nterpolant proposed n [] when k =. For k = 2, the nterpolant yelds a prevously unknown nterpolant that generalzes dscrete harmonc coordnates to smooth curves. For pecewse lnear curves, the ntegral verson of ths nterpolant reduces to a dscrete sum. Based on the choce of a parameter k, ths dscrete method can reproduce ether Wachspress coordnates (k = 0), mean value coordnates (k = ) or dscrete harmonc coordnates (k = 2). For arbtrary k, the ntegral verson reduces to the famly of dscrete coordnates descrbed n [20]. 2 A boundary nterpolant for closed curves The followng secton gves a smple modfcaton to the contnuous verson of Shephard s method for closed shapes (gven n equaton 2) that has lnear precson. Whle the exposton n ths secton s entrely 2D, the ntegral constructon extends to hgher dmensons wthout dffculty. 2. The modfed nterpolant Gven a closed curve P wth a parameterzaton p[x] and an assocated scalar functon f[x], we desre a functon ˆf[v] such that ˆf nterpolates f (.e.; ˆf[p[x]] = 3

4 f[x]) and ˆf reproduces lnear functons. Our modfcaton to the contnuous form of Shephard s method s to perform the ntegrals of equaton 2 wth respect to a curve P v nstead of the orgnal boundary curve P, ˆf[v] = f[x] p[x] v d P v / p[x] v d P v. (3) Ths auxlary curve P v depends on both the boundary curve P and the pont of evaluaton v. For a gven v, we smply normalze each ntegrand by the length of the dfferental d P v on P v as the parameter x vares over P. Snce p[x] v approaches nfnty as p[x] v, the modfed nterpolant ˆf[v] converges to f[x] as v p[x]. On the other hand, only certan specal choces for P v cause the modfed nterpolant to have lnear precson. If we substtute f[x] = p[x] and ˆf[v] = v nto equaton 3, we observe the nterpolant has lnear precson f and only f the auxlary curve d P v satsfes p[x] v p[x] v d P v = 0. (4) In the next subsecton, we construct a famly of auxlary curves P v for whch ths ntegral s exactly zero. 2.2 A constructon for the auxlary curve In ths subsecton, we gve a general constructon for a class of auxlary curves P v that satsfy equaton 4. Gven the closed boundary curve P and a pont v, we construct the auxlary curve P v n two steps.. We translate P such that v s shfted to the orgn and radally scale the shfted curve by where a a v [x] v[x] s any non-negatve scalar functon. Ths new curve P v has a parameterzaton gven by p v [x] = p[x] v. a v [x] 2. We construct the auxlary curve P v by takng the polar dual of P v [5]. Ths curve has a parameterzaton of the form p v [x] = d[p v [x]] 4

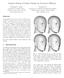
5 Fg.. Dual of an ellpse wth respect to the pont shown. The top row shows P v for k = 0,, 2 (see secton 3). The bottom row shows the dual of the shape above. where the operator d computes the followng: d[p[x]] = p[x] p[x] p[x]. (5) For curves, p[x] s the outward normal vector to the curve p[x] whose length s equal to that of the tangent vector p [x]. (In m dmensons, we defne p[x] to the be outward normal vector formed by takng cross product of the m tangent vectors p[x] x.) Gven that we have smply changed the ntegral n equaton 2 to be wth respect to the dual shape, we call our modfed nterpolant the Dual Shepard s nterpolant or DS nterpolant for short. Fgure llustrates the case when the closed curve P s an ellpse wth parameterzaton p[x] = (2 cos[x], sn[x]) and the sample pont v has coordnates (, 0). The three curves n the upper part of the fgure are P v where the radal scalng functon a v [x] s chosen to be p[x] v k wth k = 0,, 2, respectvely. The lower three curves are the polar duals P v of ther correspondng upper curve P v. Observe that for k = 2, the radally scaled curve P v s not convex and as a result the polar dual P v has a self ntersecton. Each nflecton pont of P v corresponds to a cusp on P v. Equaton 5 gves an explct formula for computng the dual. Note that the dual curve also satsfes the followng propertes: d[p[x]] p[x] =, (6) d[p[x]] p[x] = 0. x (7) The dual d[p[x]] as defned n equaton 5 trvally satsfes these propertes 5

6 snce p[x] p[x] x = 0. The functon d[p[x]] s unquely characterzed by these equatons as long as the the vectors p[x] and p[x] x form a lnearly ndependent bass,.e; p[x] p[x] 0. Geometrcally, ths condton corresponds to requrng that the tangent space to p[x] not pass through the orgn. (If the tangent space does pass through the orgn at some parameter value x 0, d[p[x]] goes to nfnty as x x 0.) Ths observaton leads to the followng theorem. Theorem: Gven a curve p[x] whose tangent lne does not pass through the orgn, the dual of the dual of p[x] s p[x]; that s, d[d[p[x]]] = p[x]. Proof: We frst replace p[x] by d[p[x]] n equatons 6 and 7. If d[d[p[x]] and p[x] are dentcal, replacng d[d[p[x]] by p[x] n these two new equatons should also yeld equalty; that s, p[x] d[p[x]] =, p[x] d[p[x]] x = 0. The frst equaton follows drectly from equaton 6. The second equaton s verfed by dfferentatng equaton 6. 0 = x (d[p[x]] p[x]) = d[p[x]] x p[x] + d[p[x]] p[x] x Fnally, we apply equaton 7 to yeld d[p[x]] x p[x] = 0. QED 2.3 A proof of lnear precson We next show that the DS nterpolant has lnear precson. The key ngredent s to show that equaton 4 reduces to an nstance of the dvergence theorem appled to P v. For the rest of the paper, we defne p v [x] to be the parameterzaton of P v computed va d[p v [x]]. Theorem: If the radally scaled curve P v s convex, the ntegral of expresson 4 (wth respect d P v ) s dentcally zero. 6

7 Proof: If p v [x] s an outward normal to P v at p v [x], the ntegral of the untzed verson of ths normal s exactly zero by the dvergence theorem [22],.e.; p v [x] p v [x] d P v = 0 Snce teratng the dual operator d s the dentty, the vectors p v [x] and p v [x] are also related va the formula p v [x] = d[d[p v [x]]] = d[ p v [x]] = p v [x] p v [x] p v [x]. (8) where p v [x] p v [x] s a scalar. If P v s convex, the polar dual Pv s also convex and ths scalar expresson s always non-negatve. Therefore, the vectors p[x] v, p v [x] and p v [x] are all scalar multples of each other. Thus, the untzed versons of these vectors are all equal, p[x] v p[x] v = p v[x] p v [x] = p v[x] p v [x]. (9) Drect substtuton of the left-hand sde of ths expresson nto the ntegral yelds the theorem. QED When P v s convex, p v [x] p v [x] s always non-negatve. However, when P v s not convex, p v [x] p v [x] may change sgns. These sgn changes correspond to cusps on P v where the wndng of P v reverses wth respect to the orgn. (See the lower rght curve n fgure.) In ths stuaton, the DS nterpolant of equaton 3 stll has lnear precson as long as d P v s treated as a sgned quantty where sgn of d P v corresponds to the sgn of p v [x] p v [x]. Snce ths modfcaton entals extra complexty, we next consder an equvalent form of the DS nterpolant that s easer to evaluate. 2.4 A dx form of the DS nterpolant The ntegrals of equatons 3 and 4 were taken wth respect to d P v. To facltate evaluaton of these ntegrals, we can rewrte the nterpolant usng ntegrals taken wth respect to dx. In partcular, we can replace the functon p[x] v 7

8 n equaton 3 by a generc weght functon w v [x] and construct an equvalent form of nterpolant n terms of ntegrals taken wth respect to dx, ˆf[v] = wv [x]f[x]dx wv [x]dx. To construct the desred weght functon, we note that from equaton 8 p[x] v a v [x] = p v [x] p v [x] p v [x]. Now, the dfferental dx and d P v are related by the Jacoban of the parameterzaton p v [x] for P v. However, by constructon, the Jacoban s exactly the length of the normal vector p v [x]. Thus, p v [x] dx = d P v. Combnng these two expressons yelds d P v p[x] v = p v[x] p v [x] dx. a v [x] Substtutng ths expresson nto equaton 3 yelds the desred form weght functon. w v [x] = p v[x] p v [x] a v [x] (0) Note the DS nterpolant may be undefned f v les on the tangent space of P v for some x = x 0. In ths case, p v [x 0 ] p v [x 0 ] = 0 and p v [x 0 ] p v [x 0 ] s unbounded. Also, f P v folds back on tself, t s possble that d P p[x] v v = 0 leadng to an undefned nterpolant. In the case of the mean value nterpolant (see Sectons 3 and 4), the DS nterpolant s well-defned for all closed, nonntersectng shapes. The nvarance of these coordnates under dfferent types of transformatons depends on the nvarance of the weght functon a v [x]. For example, n Sectons 3 and 4, each of these coordnates are nvarant under smlarty transformatons (translaton, rotaton and unform scalng). However, when a v [x] =, Wachspress coordnates have the added beneft of full affne nvarance. 8

9 3 Equvalence to prevous smooth nterpolants Our DS nterpolant reproduces two known nterpolants for partcularly smple choces of a v [x]. In partcular, we consder radal scalng functons of the form a v [x] = p[x] v k. For k = 0, our nterpolant reproduces a smooth nterpolant frst proposed n [4] that generalzes the dscrete nterpolant assocated wth Wachspress coordnates. For k =, our nterpolant reproduces the mean value nterpolant frst proposed n []. Fnally, for k = 2, we show that our nterpolant has an nterpretaton n terms of mnmzng a certan class of ruled surfaces wth respect to the harmonc functonal and produces a contnuous analog of dscrete harmonc coordnates. 3. Mean value nterpolaton In the process of extendng mean value coordnates to 3D trangular meshes, Ju et al. [] ntroduced the concept of mean value nterpolaton. Gven a closed smooth curve P wth a parameterzaton p[x] and assocated data values f[x], mean value nterpolaton computes ˆf[v] as the rato of two ntegrals, ˆf[v] = f[x] p[x] v ds v/ p[x] v ds v where S v s the unt crcle centered at v. In terms of our constructon, when k =, the radally scaled curve P v s exactly the unt crcle centered at orgn. Lkewse, the polar dual Pv s the unt crcle centered at the orgn (see fgure mddle). Snce S v and P v are smply translates of each other, the dfferentals ds v and d P v are dentcal and the two nterpolants agree. 3.2 Wachspress nterpolaton For k = 0, our DS nterpolant reduces to a contnuous nterpolant frst ntroduced n Warren et al. [4]. Ths nterpolant was developed n the context of extendng Wachspress coordnates for convex polygons to smooth convex curves. For a closed shape P n m dmensons, Wachspress nterpolaton has 9

10 the form ˆf[v] = wv [x]f[x]dp wv [x]dp () κ[x] (n[x] (p[x] v)) m where w v [x] = wth κ[x] beng the Gaussan curvature of P at p[x] and n[x] beng the outward unt normal to P at p[x]. As we now show, the choce of k = 0 (and thus a v [x] = ) for our modfed Shephard s nterpolant exactly reproduces Wachspress nterpolaton. Theorem: Let a v [x] =. The DS nterpolant of equaton 3 s equvalent to the Wachspress nterpolant of equaton. Proof: Note that the nterpolant of equaton can be wrtten n dx form wth a weght functon κ[x] p v [x] (n[x] (p[x] v)) m. Our task s show that ths weght functon s equvalent to the dx weght functon of equaton 0. Followng DoCarmo [23], Gaussan curvature at pont p[x] s the lmt of the rato of the area of a patch on the Gauss sphere (the sphere defned by n[x]) to the area of a correspondng surface patch on P as the patch sze approaches zero. Mathematcally, the Gaussan curvature κ[x] satsfes κ[x] = n[x] p[x] n[x] n[x] =. p v [x] The second equalty s true because n[x] s the unt normal to the sphere. Recallng that p v [x] s exactly by constructon, we note that p v [x] p v [x] = n[x] n[x] (p[x] v) ( ) n[x] n[x] (p[x] v) n[x] = n[x] (p[x] v) n[x] n[x] (n[x] (p[x] v)) m. Here, the second equalty holds by observng that the mddle expresson s a determnant wth each row havng a factor of n[x] (p[x] v). Extractng the m factors of ths quantty from the determnant and smplfyng yelds the expresson on the rght-hand sde. 0

11 To complete the proof, we combne the defnton of κ[x] wth ths equaton and elmnate the common expresson of n[x] n[x]. Ths combnaton yelds κ[x] p v [x] (n[x] (p[x] v)) m = p v[x] p v [x]. whch s exactly the weght functon assocated wth the dx form of our nterpolant gven n secton 2.4. QED 3.3 Harmonc nterpolaton For k = 0 and k =, our DS nterpolant reproduces known smooth nterpolants that themselves were developed as generalzatons of known dscrete nterpolants for closed polygons. For k = 2, we know of no equvalent smooth nterpolant. However, the correspondng dscrete nterpolant for k = 2 s based on dscrete harmonc coordnates [8]. These coordnates are referred to as harmonc snce the value of ther assocated nterpolant can be defned as the result of mnmzng a harmonc functonal. Gven a convex polygon P, lnear boundary data f on the edges of P and an nteror pont v, consder a pecewse lnear functon form by radally trangulatng the nteror of P from v and that nterpolates f on the edges of P. The value of the harmonc nterpolant s now the heght value of ths pecewse lnear surface at v that mnmzes the ntegral of the harmonc functonal of ths pecewse lnear functon taken over P. In ths subsecton, we observe that our DS nterpolant has a smlar nterpretaton n terms of harmonc mnmzaton. Gven a smooth closed p[x], an assocated scalar functon f[x] and an nteror pont v, consder a ruled surface formed by connectng the boundary curve (p[x], f[x]) to the nteror pont (v, f ) where f s an arbtrary heght at v. We can parameterze ths surface va (p[x, t], f[x, t]) where p[x, t] = p[x]( t) + vt, f[x, t] = f[x]( t) + f t. Gven ths parameterzaton, we defne the value of the (smooth) harmonc nterpolant ˆf[v] as f[x, t] ˆf[v] = mn ( ) 2 f[x, t] + ( ) 2 dv dv 2. (2) f v v 2 P

12 Fg. 2. Examples of nterpolants created for an ellpse wth a heght functon v 2 v2 2 specfed on the boundary. The nterpolants correspond to k = 0 on the top row and k =, 2 on the bottom row. We hypothesze that our DS nterpolant reproduces the harmonc nterpolant of equaton 2 for k = 2. To support ths hypothess, we make two crucal observatons. Frst, the ruled surface (p[x, t], f[x, t]) n our defnton of the harmonc nterpolant reduces to the graph of the pecewse lnear functon used n the tradtonal constructon of dscrete harmonc coordnates when P s a closed polygon. Second, as, we shall show n the next secton, our DS nterpolant (wth k = 2) reproduces dscrete harmonc coordnates for closed polygons. Furthermore, we have numercally verfed that our coordnates satsfy equaton 2 for our ellptcal test case n fgure 2. Fgure 2 shows three examples of the DS nterpolant appled to our ellpse from fgure. The upper left fgure shows a 3D vew of the space curve (p[x], f[x]) where the scalar functon f[x] s 4 cos[x] 2 sn[x] 2. The remanng three fgures shows a graph generated by applyng DS nterpolaton to nteror of the ellpse. In the case of Wachspress nterpolaton and harmonc nterpolaton, the nterpolant was computed by evaluatng the ntegral of equaton 2 n closed form usng Mathematca for a undetermned pont v and evaluatng the resultng expresson for grd of values of v. 4 Equvalence to prevous dscrete nterpolants In ths secton we nvestgate the behavor of the DS nterpolant when the curve P as well as the assocated functon f are pecewse lnear. Let P be a 2D polygon wth vertces {p 0, p,..., p n = p 0 } and functon values {f 0, f,..., f n = f 0 }. Furthermore, assocated wth each pont parameter values {x 0, x,..., x n = x 0 } such that p[x] = (x x)p +(x x )p x x for x x x f[x] = (x x)f +(x x )f x x for x x x. (3) 2

13 p v x [ ] p v x [ + ] p v x ] [ p v x [ + ] p v x ] [ p v x [ ] l r p v [ x ] p [ x ] p v [ x ] r v + l + r r l l + p [ x ] v + O O (a ) (b ) Fg. 3. Convex (a) and concave (b) vertces of P v (dark) and ther correspondng peces on P v (gray and dashed). The vertces l and r of P v correspond to the two dstnct normals to P v at p v [x ]. Our goal s to reduce our nterpolant to the dscrete form ˆf[v] = w f w where the weghts w depend on v. In partcular, we show that our ntegral constructon reproduces a famly of barycentrc coordnates frst descrbed n Floater et al. [20]. 4. Structure of the dual We frst consder the structure of the dual Pv for pecewse lnear shapes. To construct the polar dual of a shape wth normal dscontnutes, we treat a pont on the curve that exhbts ths dscontnuty as an nfnte collecton of ponts at the same locaton but wth smoothly varyng normals. Let p v [x ] and p v [x + ] be the normal vectors of p v [x ] on ts left and rght curve segments (see fgure 3). Interestngly, by representng p v [x ] as an nfnte collecton of ponts wth normals varyng contnuously from p v [x ] to p v [x + ], the polar dual of p v [x ] forms a straght lne segment wth end ponts at p v [x ] l = p v [x ] p v [x ] p v [x + ] r = p v [x + ] p v [x ] 3

14 Fg. 4. Examples of duals of a ellptcal hexagon wth respect to the pont shown. The top row shows P v for k = 0,, 2. The bottom row shows the dual of the shape above. When p v [x ] forms a concave corner, the locaton of l and r wth respect to p may be reversed as shown n fgure 3 (b). Fgure 4 shows a dscrete verson of the ellpse from fgure sampled at ntervals of π. The top row llustrates 3 P v for dfferent values of k whle the bottom row shows the correspondng dual Pv. When k 0, P v s curved as s the dual Pv. Notce that when P v s not convex, Pv may fold back and self-ntersect as shown n the bottom-rght corner. Now we can descrbe the structure of the polar dual Pv n relaton to the polygon P. As shown n fgure 3 (a), P v s composed of two types of segments: curved segments between {r, l } correspondng to each edge {p, p } and straght segments {l, r } correspondng to each vertex p. In order to parameterze P v, we let l and r correspond to parameters x and x +, that s, l = p v [x ] and r = p v [x + ]. Usng ths structure of the dual and equaton 3, we can rewrte the numerator of equaton 3 n the form x x + f ( t) + f t d p[x] v P v + x + x f p[x] v d P v (4) where t = x x+. x x+ 4

15 p [ x ] = p v v p [ x p v p [ x p v v ] = v + ] = + = l r = + r l O Fg. 5. The dual for Wachspress coordnates s a pecewse lnear shape where l = r. The dscrete weght for these coordnates s proportonal to the area of the shaded wedge on the dual. We then use ths pecewse defnton of the nterpolant ˆf[v] to rewrte the ntegral equaton as a dscrete sum ˆf[v] = w f where w = α + β + γ and w α = x + x + t p[x] v d P v β = x x + t p[x] v d P v γ = x + x d P p[x] v v. 4.2 Equvalence to Wachspress To gve more ntuton about the shape of the auxlary curve P v, we frst look at the specal case when a v [x] s the dentty functon and p v [x] = p[x] v. Notce that the normal vectors p v [x ] and p v [x + ] now become the outward unt normals of the edges {p, p } and {p, p + }. Furthermore, by applyng the defnton of the dual from equaton 5 to ths pecewse lnear shape, we fnd that r = l. As a result, the polar dual Pv conssts solely of straght segments {l, r } as shown n fgures 4(left) and 5. Snce x + = x +, α = β = 0. γ s also easy to calculate because = p[x] v p v over {x, x + }. Therefore, γ = l r p, whch s proportonal to the area of the v shaded wedge n fgure 5. Ths relaton to the area of the dual s exactly the same as the dscrete defnton of Wachspress coordnates gven by Ju et al. [5]. 5

16 p p p A A p + p p + B θ θ v v (a ) (b ) Fg. 6. The areas of trangles formed by the vertces of P and v for Floater s famly of barycentrc coordnates. 4.3 Equvalence to Floater s famly of coordnates Floater et al. [20] consders a general famly of barycentrc coordnates for 2D polygons wth weghts w of the form w = c A + c + A c B A A where A s the sgned area of the trangle {v, p, p + }, B s the sgned area of the trangle {v, p, p + } and c s an arbtrary scalar assocated wth the vertex p as shown n fgure 6. Furthermore, the authors show that gven any set of weghts w that are barycentrc coordnates, there exsts choces of c such that w = w. In other words, ths famly of coordnates can reproduce all possble dscrete barycentrc coordnates. In partcular, f c = p v k, these coordnates reproduce Wachspress coordnates when k = 0, mean value coordnates when k = and dscrete harmonc coordnates when k = 2. Theorem: The DS nterpolant of equaton 3 reproduces Floater s famly of coordnates f a v [x ] = c. Proof: We begn by usng the propertes of the dual to relate vertces of P v to the vertces P usng α, β, γ. To do so, we overload the operator to apply to vectors as well as functons. If z s a vector n 2D from the orgn, we defne z to be the vector z rotated counter-clockwse by π 2 radans. Consder the quantty α (p v) + β + (p + v). Based on the defnton of α and β + n terms of ntegrals (as well as equaton 3), ths quantty s exactly α (p v) + β + (p + v) = x + x + p[x] v p[x] v d P v. 6

17 p v p v + p v r r l + l + p v l r l ( p ) v O O (a ) (b ) r ( p + ) v p p v v p + Fg. 7. The dual P v n relaton to P. l and r are the correspondng vectors rotated counter-clockwse by π 2 radans. Now, as shown n secton 2.3, the rght-hand sde of ths expresson s exactly the ntegral of the outward unt normal of P v restrcted to the nterval [x +, x +] (.e; the dotted curve from r to l + n fgure 7(a)). If we apply the dvergence theorem to the shaded wedge n fgure 7(a), ths ntegral tself s exactly equal to dfference of the vectors l + and r. So, n summary, we have derved an equaton relatng the vector p v to the vectors l and r. α (p v) + β + (p + v) = l + r. (5) Usng a smlar argument, we can show that γ (p v) = r l. We can solve for α n closed form by dottng both sdes of equaton 5 wth (p + v) and dvdng the result by (p v) (p + v) = 2A, α = l + (p + v) r (p + v) = a v[x + ] r (p + v), (p v) (p + v) 2A where A s defned as n fgure 6. The second equalty s due to the dentty l + (p + v) = l + (p + v) = p v [x + +] (p v [x + ]a v [x + ]) = a v [x + ]. Smlarly, we can solve for β and γ. β = a v[x ] l (p v) 2A γ = (r l ) (p v) p v 2 7

18 Fg. 8. Examples of nterpolants created for a dscrete pecewse lnear ellptcal hexagon wth heght values specfed at the vertces. The nterpolants correspond to k = 0 on the top row and k =, 2 on the bottom row. To fnd the weght w = α + β + γ we use the above equaltes and apply trgonometrc denttes to obtan α + β + γ = a v[x ] + a v[x + ] a v[x ](cos[θ ] sn[θ ] + cos[θ ] sn[θ ]) 2A 2A p v 2 sn[θ ] sn[θ ] = a v[x ] + a v[x + ] a v[x ]B 2A 2A 2A A Snce we chose a v [x ] = c, ths completes the proof of equvalence to Floater s famly of coordnates. QED Fgure 8 shows three examples of DS nterpolant appled to the ellptcal hexagon of fgure 2. 5 Concluson and future work The man usefulness of the Dual Shephard nterpolant proposed here s that t gves a smple conceptual framework for understandng a range of nterpolants developed for generatng 2D coordnates. Ths nterpolant readly generalzes to hgher dmensons and, n future work, we ntend to nvestgate the usefulness of ths nterpolant n constructng coordnates for closed 3D shapes. For example, we may be able to develop coordnates for closed, pecewse polynomal curves and surfaces. In ths case, we beleve that computng closed form solutons to the ntegral of equaton 3 should be possble. Such an extenson would allow curved shapes to be used as control meshes for defnng deformatons (as done n [] for trangular meshes). 8

19 References [] D. Shepard, A two-dmensonal nterpolaton functon for rregularly-spaced data, n: Proceedngs of the rd ACM natonal conference, ACM Press, 968, pp [2] K. Hormann, G. Grener, MIPS - An Effcent Global Parametrzaton Method, n: Curves and Surfaces Proceedngs (Sant Malo, France), 2000, pp [3] M. Desbrun, M. Meyer, P. Allez, Intrnsc Parameterzatons of Surface Meshes, Computer Graphcs Forum 2 (3) (2002) [4] A. Khodakovsky, N. Ltke, P. Schröder, Globally smooth parameterzatons wth low dstorton, ACM Trans. Graph. 22 (3) (2003) [5] J. Schrener, A. Asrvatham, E. Praun, H. Hoppe, Inter-surface mappng, ACM Trans. Graph. 23 (3) (2004) [6] M. S. Floater, K. Hormann, Surface parameterzaton: a tutoral and survey, n: N. A. Dodgson, M. S. Floater, M. A. Sabn (Eds.), Advances n Multresoluton for Geometrc Modellng, Mathematcs and Vsualzaton, Sprnger, Berln, Hedelberg, 2005, pp [7] T. W. Sederberg, S. R. Parry, Free-form deformaton of sold geometrc models, n: SIGGRAPH 86: Proceedngs of the 3th annual conference on Computer graphcs and nteractve technques, ACM Press, 986, pp [8] S. Coqullart, Extended free-form deformaton: a sculpturng tool for 3d geometrc modelng, n: SIGGRAPH 90: Proceedngs of the 7th annual conference on Computer graphcs and nteractve technques, ACM Press, 990, pp [9] R. MacCracken, K. I. Joy, Free-form deformatons wth lattces of arbtrary topology, n: SIGGRAPH 96: Proceedngs of the 23rd annual conference on Computer graphcs and nteractve technques, ACM Press, 996, pp [0] K. G. Kobayash, K. Ootsubo, t-ffd: free-form deformaton by usng trangular mesh, n: SM 03: Proceedngs of the eghth ACM symposum on Sold modelng and applcatons, ACM Press, 2003, pp [] T. Ju, S. Schaefer, J. Warren, Mean Value Coordnates for Closed Trangular Meshes, n: ACM Trans. on Graphcs (SIGGRAPH Proceedngs), 2005, pp [2] E. Wachspress, A Ratonal Fnte Element Bass, Manuscrpt. [3] J. Warren, Barycentrc Coordnates for Convex Polytopes, Advances n Computatonal Mathematcs 6 (996) [4] J. Warren, S. Schaefer, A. Hran, M. Desbrun, Barycentrc coordnates for convex sets, To appear n Advances n Computatonal and Appled Mathematcs. 9

20 [5] T. Ju, S. Schaefer, J. Warren, M. Desbrun, A Geometrc Constructon of Coordnates for Convex Polyhedra usng Polar Duals, n: ACM/EG Symposum on Geometry Processng, 2005, pp [6] M. Floater, Mean value coordnates, Computer Aded Geometrc Desgn 20 (2003) [7] M. S. Floater, G. Kós, M. Remers, Mean value coordnates n 3d, Computer Aded Geometrc Desgn 22 (2005) [8] U. Pnkall, K. Polther, Computng dscrete mnmal surfaces and ther conjugates, Expermental Mathematcs 2 () (993) [9] M. Eck, T. DeRose, T. Duchamp, H. Hoppe, M. Lounsbery, W. Stuetzle, Multresoluton analyss of arbtrary meshes, n: Proceedngs of SIGGRAPH 95, 995, pp [20] M. Floater, K. Hormann, G. Kós, A general constructon of barycentrc coordnates over convex polygons, To appear n Advances n Computatonal Mathematcs. [2] A. Belyaev, On transfnte barycentrc coordnates, n: ACM/EG Symposum on Geometry Processng, 2006, pp [22] W. Flemng, Functons of Several Varables, Sprnger-Verlag, 977. [23] M. DoCarmo, Dfferental geometry of curves and surfaces, Prentce-Hall,