Active Learning Support Vector Machines to Classify Imbalanced Reservoir Simulation Data
|
|
|
- Daniel Horn
- 5 years ago
- Views:
Transcription
1 WCCI 2010 IEEE World Congress on Computational Intelligence July, 18-23, CCIB, Barcelona, Spain IJCNN Active Learning Support Vector Machines to Classify Imbalanced Reservoir Simulation Data Tina Yu, Member, IEEE Abstract Reservoir modeling is an on-going activity during the production life of a reservoir. One challenge to constructing accurate reservoir models is the time required to carry out a large number of computer simulations. To address this issue, we have constructed surrogate models (proxies) for the computer simulator to reduce the simulation time. The quality of the proxies, however, relies on the quality of the computer simulation data. Frequently, the majority of the simulation outputs match poorly to the production data collected from the field. In other words, most of the data describe the characteristics of what the reservoir is not (negative samples), rather than what the reservoir is (positive samples). Applying machine learning methods to train a simulator proxy based on these data faces the challenge of imbalanced training data. This work applies active learning support vector machines to incrementally select a subset of informative simulation data to train a classifier as the simulator proxy. We compare the results with the results produced by the standard support vector machines combined with other imbalanced training data handling techniques. Based on the support vectors in the trained classifiers, we analyze high impact parameters that separating good-matching reservoir models from bad-matching models. I. INTRODUCTION Petroleum reservoirs are normally large and geologically complex. In order to make management decisions that maximize oil recovery, reservoir models are constructed with as many details as possible. Two types of data that are commonly used in reservoir modeling are geophysical data and production data. Geophysical data, such as seismic and wire-line logs, describe earth properties, e.g. porosity, of the reservoir. In contrast, production data, such as water saturation and pressure information, relate to the fluid flow dynamics of the reservoir. Both data types are required to be honored so that the resulting models are as close to reality as possible. Based on these models, managers make business decisions that attempt to minimize risk and maximize profits. The integration of production data into a reservoir model is usually accomplished through computer simulation. Normally, multiple simulations are conducted to identify reservoir models that generate fluid flows matching the historical production data. This process is called history matching. History matching is a challenging task for the following reasons: Computer simulation is very time consuming. On average, each run takes 2 to 10 hours to complete. This is an inverse problem where more than one reservoir model can produce flow outputs that give acceptable match to the production data. Tina Yu is with the Department of Computer Science, Memorial University of Newfoundland, Canada (phone: ; fax: ; tinayu@cs.mun.ca). As a result, only a small number of computer simulation runs are conducted and the history matching results are associated with uncertainty. To address this issue, we have constructed approximate models (proxies) for the computer simulator, based on the computer simulation data. Unlike the full reservoir simulator, which gives the flow of fluids of a reservoir, this proxy only labels a reservoir model as good or bad, based on whether or not its flow outputs match well with the production data. In other words, this proxy acts as a classifier to separate good models from bad models in the reservoir descriptor parameter space. Using this cheap proxy as a surrogate of the full-simulator, we can examine a large number of reservoir models in the parameter space in a short period of time. Collectively, the identified good-matching reservoir models provide us with comprehensive information about the reservoir with a high degree of certainty. The quality of a proxy, however, relies on the quality of computer simulation data. Frequently, the majority of the simulation outputs match poorly to the historical production data. In other words, most of the data describe the characteristics of what the reservoir is not (negative samples), rather than what the reservoir is (positive samples). Applying machine learning methods to train a simulator proxy based on these data faces the challenge of imbalanced training data. This work applies active learning support vector machines (SVMs) to incrementally select a subset of informative simulation data to train a classifier as the simulator proxy. We compare the results with the results produced by the standard support vector machines combined with other imbalanced training data handling techniques. Based on the support vectors in the trained classifiers, we analyze high impact parameters that separating good-matching reservoir models from bad-matching models. The paper is organized as follows. Section II explains SVM, active learning SVM and other techniques used in this work to address the issue of learning using imbalanced data. In Section III, the reservoir field and the computer simulation data are described. We explain the performance measurements in Section IV. In Section V, the data preprocessing and the experimental setup are detailed. We present the results and give our analysis in Section VI. Finally, Section VII concludes the paper and outlines our future work. II. METHODOLOGY In this section, we first briefly describe the basic concept of two-class SVM classification [13], [3]. Extension of SVM /10/$26.00 c2010 IEEE 568
2 Fig. 1. 5(%67)* +, -./01231?*!"#$%&#'()$*+, -./01234* +, -./0123&?* 8* 9:##;%<*=$><;%9* Hyper-plane and the maximum margin. and other techniques we used to handle imbalanced training data will be explained in the subsections. For a binary SVM classification task, the training data are mapped into a higher dimensional feature space using a kernel function, such that a hyper-plane separating the two classes of data can be found. The hyper-plane consists of data x that satisfies w T φ(x)+b = 0, where w is the weight vector, x is the training data, φ is the kernel function and b is the bias (see Figure 1). While there are more than one hyper-planes that can separate the two classes of data, a SVM learner finds the one that has the maximal margin or the distance between the data that are closest to the hyper-plane (see Figure 1). Using the Lagrangian formation, w = n i=1 α iy i φ(x i ) gives the largest margin. The optimal separating hyper-plane is: w T φ(x)+b (1) n = α i y i φ(x i ) T φ(x)+b (2) = i=1 n α i y i K(x, x i )+b (3) i=1 where n is the number of training data, y i is the label value of data i, K is the kernel matrix, and α i is the Lagrange multipliers, where α i 0 and α i y i =0. Each training data x i is associated with a Lagrange multiplier α i. The larger the α i is, the more important that data is to the classification decision. Those data that lie close to the hyper-plane decision boundaries have nonzero α i and are called support vectors. These support vectors form the classifier that will be used to predict the class of new data. When dealing with real-world data, which are normally noisy and uncertain, the hyper-plane margins can be relaxed by using a slack variable ξ. This approach is called soft margin [7]. Thus, a hyper-plane becomes: w T φ(x i )+b +1 ξ i, y i =+1 w T φ(x i )+b 1 ξ i, y i = 1 x i 0 i An error occurs when the corresponding ξ i for a data x i exceeds 1 (see Figure 1). Under this setup, the optimal hyperplane is not just with the maximal margin but also with the minimal total error. A SVM learner finds the optimal hyperplanes by maximizing the following objective function: w 2 + C n i=1 ξ i where C is a regularization parameter that controls the trade-off between the two objectives. The larger the C is, the more penalty is assigned to the errors. Smaller C values relax this penalty and produce better results with noisy data [7]. Solving this multi-objective problem leads to the optimal hyper-plane that is the same as before (Equation 3). The only difference is that the Lagrange multiplier is constrained by C, i.e. 0 α i C. That is, the influence of an individual Lagrange multiplier α i has on the prediction decision is limited to C. A. Asymmetric Soft Margins When the training data set is imbalanced, we can assign different cost C + and C to each of the two classes. The object function to optimize the hyper-plane thus becomes: w 2 + C + n i=1 ξ i + C n i=1 ξ i This approach was introduced by [14] to control the trade-off between false positives and false negatives. The idea was that by introducing different cost for positive and negative data, a bias of larger Lagrange multiplier α i is given to the class where the cost of misclassification is heavier. This, in turn, introduces a decision boundary which is much more distant from the critical class than from the other. According to [11], the distance of a test data point from the boundary is related to its probability of mis-classificaiton. Test points that are farther away from the hyper-plane are less likely to be misclassified. In our study, we will assign C + a smaller value than the value of C to encourage the SVM learner to find a hyperplane that classifies more positive samples correctly. B. Active Learning SVM SVM is a passive learning method if the training data are pre-selected for the learner to find the optimal separating hyper-plane. In an active learning framework, the learner actively seeks the training data, one after another, based on its needs. In other words, the learner can query/select informative new data to help train a better hyper-plane. Various research has explored this active learning framework in SVMs. For example, Campbell, Cristianini and Smola[4] used the strategy that starts by requesting the labels of a random subset of instances and subsequently iteratively requesting the label of that data point which is closest to the current hyper-plane in their active learning SVM system. In terms of termination criterion, they trained until either the margin band is empty or until a stopping point specified by the user has been met. Their experimental results showed that their SVM learner processed a smaller number of training 569
3 data to find the hyper-plane that performed as well or better (in terms of classification accuracy) than that found by the SVM using the random selection strategy. This indicates that the samples their method selected are more informative than the randomly selected samples. Schohn and Cohn also independently devised a similar selection method in their active learning SVM [10]. Tong and Koller [12] worked on the kind of training set that has some data labeled and some not. Active learning SVMs were used to select an unlabeled data sample, label it and then add it to the training set for the SVM learner to find a better separating hyper-plane. They devised 3 selection schemes: Simple Margin: select the data that is closest to the hyper-plane, which is the same as that used in [4] [10]. MaxMin Margin: for each unlabeled data x, compute the margin m + and m of the hyper-planes obtained when the data is labeled as +1 and -1 respectively; then select the unlabeled data whose min(m +,m ) is the greatest. Ratio Margin: compute m + and m as that in the MaxMin Margin method. However, select the data for which min( m m, m+ + m ) is the largest. They reported that all 3 strategies performed better than the random selection strategy in that their strategies selected a smaller number of data for the SVM learner to find the optimal hyper-plane. Moreover, the MaxMin and Ratio margin strategies gave more stable performance on different data sets than the Simple margin strategy did. However, MaxMin and Ratio margins took longer to compute, hence lead to a longer SVM training time. LASVM is an active learning SVM system developed by Bordes, Ertekin, Weston and Bottou [2] with the aim to speed up the SVM training time for applications which have a very large volume of data. The selection methods they used include: Gradient Selection: randomly select 50 data that have not been processed. Among them, the one that is most mis-classified, according to the current hyper-plane decision, is selected. Active Selection: randomly select 50 data that have not be processed. Among them, the one that is closet to the current hyper-plane decision boundaries is selected. Autoactive Selection: This replaces the sampling size of 50 in the Active Selection with a more flexible size. It continues to sample the unprocessed data until 5 of the samples are within the distance of 1+δ/2 (δ is the gradient of the most τ-violating pair in the current support vector set) to the hyper-plane decision boundaries or the maximum number of 100 samples is reached. Among them, the one that is closet to the current hyper-plane decision boundaries is selected. Among the data sets they tested, Active and Autoactive selections performed well consistently. These two methods selected a smaller number of training data for LASVM to find an equivalent or better hyper-plane as that found by a standard SVM system (LIBSVM). The trained SVMs also contained a smaller number of support vectors than the SVM trained by LIBSVM. In contrast, Gradient selection only performed well when the data set was not noisy. This is understandable as a misclassified data, according to the current hyper-plane decision, might be actually classified correctly, since the data is noisy. Selecting those kind of misclassified data to add into the training set is less likely to help train an improved hyper-plane. LASVM differs from the three previous mentioned active learning SVMs in the following two ways: The selection is based on a small number of random samples, instead of the entire unprocessed samples. Once a new data sample is selected and added into the training set, the current hyper-plane is updated, instead of being completely retrained. They also compared the performance of the hyper-planes learned under the selection based on a small sample size (50) or a large sample size (all), and with the hyper-plane retrained or updated at each iteration. They reported that if the data set size is large, all setups produced SVMs that had a similar prediction accuracy. But when the data set size is small, the SVMs trained by selection within a small sample size of 50 or with hyper-plane updated (instead of retrained) after a new data point was added to the training set had a small accuracy loss. In [8], Ertekin, Huang, Bottou and Giles applied LASVM to imbalanced data to improve the SVM prediction on minority class data. They used the Active selection method to select new data from a pool of 50 random samples. They also implemented the termination criterion of [4] by comparing the newly selected data with the support vectors in its distance to the hyper-plane. If the new data (which is the closest to the hyper-plane among the 50 random samples) is not closer to the hyper-plane than any of the current support vectors, this indicates that there is no data points within the margin band and the learning process stopped. They tested their version of LASVM on a number of imbalanced data sets. They also applied a standard SVM system (LIBSVM) combined with other techniques that handle imbalanced data, such as asymmetric soft margins and SMOTE (explained in the next subsection). They reported that all techniques produced SVMs that gave similar prediction performance. However, their LASVM processed a smaller number of data and the produced hyper-plane contained a smaller number of support vectors. In our work, we will design experimental setups (detailed in Section V) similar to theirs and run the same version of LASVM on our data set. C. SMOTE SMOTE stands for Synthetic Minority Oversampling Technique, which was developed to improve the prediction accuracy of classifiers trained under imbalanced data [6]. For each minority sample, the algorithm first finds its k-nearest minority neighbors. Among these neighbors, j of them are 570
4 randomly selected. Each of the j neighbors is paired with the original sample to create one synthetic data point using the following three steps: Take the difference between the feature vectors of the original sample and sample j; Multiply this difference vector by a random number between 0 and 1; Add this vector to the feature vector of the original sample; The value k and j are parameters which can be varied depending on the amount of over-sampling needed. For example, if 200% of the minority class data are needed, the j is 2. The value of k is set as 5 in their examples. For the imbalanced data sets they tested, SMOTE worked better (measured by the AUC of the trained classifiers, which will be explained in Section IV) than the undersampling of the majority class method in most of the tested data sets. They explained that the reason why SMOTE technique helped a learning method to produce a better classifier was because it caused the classifier to build larger decision regions that contain nearby minority class points. In contrast, the duplication of minority data method led to smaller and more specific decision regions. We will include this oversampling technique to create a more balanced data set for SVM training in our study. Fig. 2. 3D structural view of the field. III. RESERVOIR SIMULATION DATA The simulation data were based on a large reservoir that has been in production for a long time. Due to the long production history, the data collected from the field were not consistent and the quality was not reliable. Although we do not know for sure what causes the production measurements to be inaccurate, we could speculate on newer technology but more likely it is just poor measurement taken from time to time. This reservoir is overlain by a significant gas cap. Figure 2 shows the gas oil contact (GOC), which is the surface separating the gas cap from the underneath oil, and the water oil contact (WOC), which is the surface that separates oil from the water below, of the reservoir. The space between GOC and WOC surfaces is the oil volume to be recovered. The field also has 4 geological faults, illustrated in Figure 3, which affect the oil flow patterns. Those faults have to be considered in the computer flow simulation. As a mature field with most of its oil recovered, the reservoir had residual pore space which can be used for storage. One proposed plan was using the pore space to store the gas produced (as a side product) from the neighboring oil fields. In this particular case, the gas produced had no economical value and re-injecting it back into the field was one environmental-friendly method to dispose the gas. In order to evaluate the feasibility of the plan, the cumulative volume of gas that can be injected (stored) in year 2031 needed to be evaluated. This evaluation would assist managers in making decisions such as how much gas to transport from the neighboring oil fields and the frequency of the transportation. Fig. 3. Reservoir compartmentalization. The cumulative volume of the gas that can be injected in the field is essentially the cumulative volume of the oil that will be produced from the field, since this is the amount of space that will become available for gas storage. To answer that question, a production forecast study of this field in the year of 2031 was conducted. Prior to carrying out the production forecast, the reservoir model has to be updated through the history matching process. We consulted a field engineer to select 10 reservoir parameters and their value ranges to conduct computer simulation. These parameters, as shown in Table I, are unitless except WOC and GOC, which have feet as their unit. Critical Gas Saturation (SGC) is the gas saturation values for each phase (water and oil) and has a value between 0 and 1. Skin (SKIN), which is the rock formation damage caused by the drilling of new gas injector wells, has a value between 0 and 30. The other 6 parameters are multipliers whose values are in log10 scale. During computer simulation, the 10 parameter values are used to define reservoir properties in each grid of the 3-D model in two different ways. The values of the 4 regular parameters are used to replace the default values in the original 3-D reservoir model while the 6 multipliers are applied to the default values in the original model. Computer simulations are then performed on the updated 3-D reservoir model to generate flow outputs. Based on the uniform design method, values of the 10 parameters were decided to conduct 600 computer simulation 571
5 TABLE I RESERVOIR PARAMETERS VALUES FOR COMPUTER SIMULATION. Parameters Min Max Water Oil Contact (WOC) 7339 feet 7339 feet Gas Oil Contact (GOC) 6572 feet 6572 feet Fault Transmissibility Multiplier (TRANS) 0 1 Global K h Multiplier (XYPERM) 1 20 Global K v Multiplier (ZPERM) Fairway Y-Perm Multiplier (YPERM) Fairway K v Multipilier2 (ZPERM2) Critical Gas Saturation (SGC) Vertical Communication Multiplier (ZTRANS) 0 5 Skin at new Gas Injection (SKIN) 0 30 runs. Among them, 593 were successful in that the runs continued until year The other 7 runs failed for various reasons, such as power failures, and terminated before the runs reached year During the computer simulation, various flow data were generated. Among them, only field water production rate (FWPR) and field gas production rate (FGPR) of 30 production years were used for history matching. The other flow data were ignored because we do not trust the quality of their corresponding production data collected from the field. FWPR and FGPR collected from the field were compared to the computer simulation outputs at each run. The error E, defined as the mismatch between the two, is the sum of squared errors calculated as follows: 30 E = (FWPR obs i FWPR sim i ) 2 i=1 +(FGPR obs i FGPR sim i ) 2 Here, obs indicates production data while sim indicates computer simulation outputs. The largest E that can be accepted as good match is 1.2. Additionally, if a model has E smaller than 1.2 but has any of its FWPR or FGPR simulation outputs match badly to the corresponding production data (difference is greater than 1), the production data were deemed to be unreliable and the entire simulation record is disregarded. Based on this criterion, 12 data were removed. We then conducted an outlier study on the remaining simulation data by examining the consistency of inputs and outputs patterns [15]. There were 7 data points falling outside the patterns and were removed from the data set. The final set contained 564 simulation data. Among them, 63 were labeled as good models while 501 were labeled as bad models. In the rest of the paper, we will call the data labeled as good models positive samples and the data labeled as bad models negative samples. IV. PERFORMANCE MEASURES In binary classification problems, to which this work belongs, performance measures based on classification accuracy are meaningless, since a classifier can simply predict all data as the majority class to obtain a reasonably good accuracy. Yet, this classifier is practically useless in identifying the TABLE II CONFUSION MATRIX. Predicted Predicted negative positive Actual TN: the number of FP: the number of negative positive data negative data correctly classified incorrectly classified Actual FN: the number of TP: the number of positive positive data positive data incorrectly classified correctly classified minority class data, which is more important in most cases. In our case, if the simulator proxy can not identify good reservoir models, this proxy can not be used to substitute the computer simulator. There are several performance measures developed to evaluate classifiers trained under imbalanced data. We adopted several of them to provide a more subjective view of the quality of the trained classifiers. Most of these measures are calculated from the values in a confusion matrix (Table II). Precision gives the percentage of data that is predicted as positive is indeed positive. Recall gives the percentage of the positive data that is correctly predicted as positive. Precision and recall often have an inverse relationship, where the increase of one may reduce the other. Usually, these two measures are used in combination. For example, F-score is the weighted harmonic mean of precision and recall. Precision = TP/(TP + FP). Recall = TP/(TP + FN). Fscore = 2 Precision Recall/(Precision + Recall). AUC = area under ROC curve. Receiver Operating Characteristic (ROC) displays the relationship between sensitivity (TP/(TP+FN)) and specificity (TN/(TN + FP)) of all possible thresholds for a binary classifier, applied to previous unseen testing data. In other words, ROC is a plot of the TP rate against the FP rate as the decision threshold is changed. The area under a ROC (AUC) is the numerical measure of a classifier s prediction ability to separate the positive and negative data. Since AUC evaluates a classifier across the entire range of decision thresholds, it gives a good indication of the classifier s performance under the situation where the data distribution is imbalanced [9]. The larger the AUC of a classifier is, the better its performance is. V. EXPERIMENTAL SETUP We first normalized the data to have values between 0 and 1. The resulting 564 data were then split into training (2/3) and testing (1/3) sets. We used the 451 training data (50 were positive and 401 were negative samples) to conduct 5- fold cross-validation to identify SVM parameter values that gave the best AUC. The selected parameter values were then used to train the final SVM model using the 451 data. The quality of the final SVM model was evaluated based on its prediction on the 113 testing data (13 were positive and 100 were negative samples). 572
6 TABLE III PARAMETERS DECIDED BY CROSS-VALIDATION. SETUP (a) (b) (c) (d) (e) (f) γ C C + C We used two public domain SVM tools to conduct our experiments: LIBSVM [5] and LASVM [2]. LIBSVM is a state-of-the-art SVM solver while LASVM is an active learning SVM system. We conducted six sets of experiments: (a) LIBSVM baseline (b) LIBSVM with asymmetric soft margins (c) LIBSVM on SMOTE data (d) LIBSVM with asymmetric soft margins on SMOTE data (e) LASVM (f) LASVM with asymmetric soft margins. All these experiments used the radial basis function (RBF) kernel K(u, v) = e γ(u v) (u v) to conduct SVM training. The values of other SVM parameters (see Table III) were decided by 5- fold cross-validation. We applied the SMOTE process to the 50 positive training data to generate 400 synthetic data, 8 for each positive sample. This led to a total of 450 positive and 401 negative samples in the final training set. For setups 5 and 6, LASVM started with an initial training set of 10 data, 5 were positive and 5 were negative samples, which were randomly selected from the entire training data set. We carried out the 6 sets of experiments and applied the learned SVMs on the 113 testing data. The results are given in Table IV. Note that in addition to the performance measurements discussed in Section IV, we also provide classification accuracy (acc) for reference. VI. RESULTS AND ANALYSIS As shown in Table IV, the LIBSVM baseline, setup (a), gave the worst performance, in terms of F-score and AUC. The other 5 setups, which included one or two of the imbalanced data handling techniques discussed previously, trained SVMs that gave similar performance. Among them, LIBSVM combined with asymmetric soft margins and the SMOTE technique, setup (d), gave the best F-score and AUC. This is similar to that reported in [1] where the SVM trained under asymmetric soft margins and SMOTE data gave better performance than the SVM trained under either of the two techniques alone. However, the AUC and F-score differences between setups (b), (c) and (d) are marginal. LASVM, setup (e) and (f), did not work better than LIBSVM combined with the SMOTE technique, setup (c) and (d). This result is similar to that reported in [2] where in small data sets, which our data set belongs to, LASVM does not provide performance advantage over other techniques. However, it selected a smaller number of data samples (see Table V) to train a SVM with a smaller number of support vectors (see Table VI) than that based on SMOTE data. A similar result was also reported in [8]. It has been suggested that the performance gain of the TABLE IV PERFORMANCE EVALUATION ON 113 TESTING DATA. SETUP (a) (b) (c) (d) (e) (f) TP TN FP FN Acc 87.61% 86.73% 83.19% 84.07% 87.61% 87.61% Pre 44.44% 45.45% 38.46% 40% 46.67% 47.37% Rec 30.77% 76.92% 76.92% 76.92% 53.85% 69.23% F-s 36.36% 57.14% 51.28% 56.63% 50% 56.25% AUC 80.07% 89.93% 92.08% 92.23% 86.46% 90.15% TABLE V NUMBER OF DATA PROCESSED. SETUP (a) (b) (c) (d) (e) (f) positive samples negative samples total samples active learning SVM on imbalanced data, compared to the standard SVM (setup (a)), is due to its ability to supply the learner a more balanced training data set [8]. This is shown to be untrue in our case. The ratio of the positive and negative samples selected by LASVM (setup (e) and (f)) is the same as that of the entire training set: 1:8. This indicates that the active learning method is choosing more informative samples to overcome the learning bias created by the majority class data. Tong and Koller also observed a similar data selection ratio as ours in their active learning SVM system [12]. LIBSVM combined with the SMOTE technique (setup (c) and (d)) produced classifiers with the best AUC. This indicates that there is a certain smoothness in the inputs space. The SVM learner was able to use the gradient information to find the optimal hyper-plane. A. Model Interpretation In data mining, one of the objectives is to understand the knowledge extracted in the learned model and apply that knowledge to the domain system. Unfortunately, SVM is a black-box model, which is not easy to interpret. However, since the model is essentially the critical samples (support vectors) for classification, we can examine the support vectors, particularly their relationship to the entire training set in the input space, to gain some insights of the reservoir characteristics. To be conservative in our interpretation, we only use the support vectors selected by all 6 SVM learning systems to conduct our analysis. The number of such kind of support vectors is 32. Figure 4 gives the mean and standard deviation of the 10 reservoir parameter values calculated from the 32 support TABLE VI NUMBER OF SUPPORT VECTORS. SETUP (a) (b) (c) (d) (e) (f) positive SVs negative SVs total SVs
7 WOC- GOC TRANS XYPERM ZPERM YPERM ZPERM2 SGC ZTRANS SKIN Parameter Name sv_avg sv_stdev train_avg train_stdev 0.3 WOC- GOC TRANS XYPERM ZPERM YPERM ZPERM2 SGC ZTRANS SKIN Parameter Name good- matching models bad- matching models Fig. 4. Reservoir parameter values mean and standard deviation. Fig. 5. Support vector parameter mean values. vectors and from the entire training set. For WOC and GOC, we report the mean and standard deviation of the oil column (WOC-GOC) instead, as our previous study [15] has identified that oil column is an important feature to distinguish a good-matching reservoir model from a badmatching reservoir model. Note that all parameter values have been normalized to have values between 0 and 1. Selected by the uniform design method, the parameter values of the training data are consistent with mean around 0.5 and standard deviation around 0.3. The parameter values of the support vectors, however, are more diverse. Among them, WOC-GOC and YERM have the mean values that are higher than the means of the training data. Similarly, TRANS and SGC have their mean values that are lower than the means of the training data. This indicates that these 5 reservoir parameters are important features separating a good-matching reservoir model from a bad-matching reservoir model. This result is consistent with that found in our previous study on the same reservoir [15]. Note that we ignore SKIN parameter as it is related to the future drilling of new injector wells. We analyze the 32 support vectors farther by dividing them into two groups: good-matching reservoir models and bad-matching reservoir models. Figure 5 gives the parameter mean values of the two groups. As shown, the same 5 parameters have their good-matching model mean and badmatching model mean close to each other, indicating they are similar in behavior. In other words, these 5 reservoir parameters have values in the support vector group that are similar to each other but are different from that in the nonsupport-vector group. This supports our analysis that they are important reservoir features to classify a good-matching reservoir model from a bad-matching model. Note that we ignore XYPERM as its mean in the support vector group is similar to the mean in the training data, hence can not be considered as an important feature for classification. YPERM Oil Column (WOC- GOC) positive sv negative sv positive samples negative samples Fig. 6. Oil Column (WOC-GOC) vs. YPERM cross-plot. Figure 6 gives the cross-plot between WOC-GOC and YPERM for the training data and the support vectors. It shows that good-matching models have oil column height (WOC-GOC) between 750 and 825. Also, their YPERM is higher than We will validate these reservoir characteristics by studying more good-matching reservoir models interpolated by the trained SVM classifier proxy in our future work. Figure 7 gives the cross-plot between TRANS and SGC for the training data and the support vectors. As shown, goodmatching reservoir models have their TRANS and SGC cross the entire value ranges. We therefore can not conclude their value ranges in this reservoir. We will conduct more analysis on these two reservoir characteristics by studying more goodmatching reservoir models interpolated by the trained SVM classifier proxy in our future work. 574
8 Critical Gas Saturation (SGC) Fault Transmissibility Multiplier (TRANS) positive samples negative samples positive sv negative sv Fig. 7. TRANS vs. SGC cross-plot. VII. CONCLUSION Reservoir modeling and simulation play an important role in the management of petroleum energy exploration and production. Although the surrogate model approach has great potentials to provide more accurate reservoir models, hence help management making more reliable decisions, its effectiveness is dependent upon the construction of high quality proxies. One challenge that makes quality proxies unattainable is the inadequacy of the computer simulation data, which frequently only provide partial views of the reservoir characteristics. One typical case is the majority of the simulation data describe the characteristics of what the reservoir is not (negative samples), rather than what the reservoir is (positive samples). Such kind of data set is difficult for most machine learning methods to produce a proxy model that can separate reservoir models that match historical production data well from those that don t. This work addresses this problem by applying an active learning SVM system to construct a classifier as the proxy model. The result of our investigation is very encouraging. During the training process, the active learning method intelligently selected informative data, one after another to help the SVM learner improving the hyper-plane. The resulting model is a classifier that performs well on the testing data, based on the AUC measure. This indicates that the technique is suitable in handling imbalanced reservoir simulation data produced by computers. Other investigated techniques also worked well. This gives us multiple tools to use in the future depending on the size and quality of the data set. Additionally, the SMOTE technique, which relies on the smoothness in the input space, helped the SVM learner to build a quality classifier. This suggests that this technique can be effective on other type of data, as long as the smoothness holds in the input space. We will test this method on other type of data in conjunction with other machine learning methods to produce models represented in different forms. We also examined the support vectors in the trained classifiers to analyze parameters that have high impact on reservoir classification. Our analysis shows that oil column (WOC-GOC), YPERM, TRANS and SGC have values in the support vector group that are similar to each other but are different from that in the non-support-vector group. This indicates that they are important characteristics separating good-matching reservoir models from bad-matching reservoir models. This result is consistent with what we have found in our previous study on this reservoir. In terms of these 5 critical parameters value ranges in this reservoir, the oil column is approximately between 750 and 825 feet and the Y-perm multiplier is greater than 1.07, based on the provided good-matching reservoir model data. The fault transmissiility multiplier (TRANS) and the critical gas saturation (SGC) values, however, can not be derived from these good-matching reservoir model data. In our future work, we will examine more good-matching reservoir models interpolated by the trained SVM classifier proxy. With a larger number of good-matching models, the reservoir characteristics related to these 5 critical parameters will be estimated more accurately. REFERENCES [1] R. Akhani, S. Kwek, and N. Japkowicz. Applying support vector machines to imbalanced datasets. In Proceedings of European Conference in Machine Learning, pages 39 50, [2] A. Bordes, S. Ertekin, J. Weston, and L. Bottou. Fast kernel classifiers with online and active learning. Journal of Machine learning Research, 6: , [3] C. J. C. Burges. A tutorial on support vector machines for pattern recognition. Data Mining and Knowledge Discovery 2, 2: , November [4] C. Campbell, N. Cristianini, and A. Smola. Query learning with large margin classifiers. In Proceedings of the Seventeenth International Conference on Machine Learning, pages , [5] C.-C. Chang and C.-J. Lin. LIBSVM: a library for support vector machines, [6] N. V. Chawla, K. W. Bowyer, L. O. Hall, and W. P. Kegelmeyer. Smote: Synthetic minority over sampling technique. Journal of Artificial Intelligence Research, 16: , [7] C. Cortes and V. Vapnik. Support vector networks. Machine Learning, 20: , [8] S. Ertekin, J. Huang, L. Bottou, and C. L. Giles. Learning on the border: Active learning in imbalanced data classification. In Proceedings of International Conference on Information and Knowledge Management, pages , [9] F. Provost and T. Fawcett. Robust classification for imprecise environments. Machine Learning, 42(3): , [10] G. Schohn and D. Cohn. Less is more: Active learning with support vector machines. In P. Langley, editor, Proceedings of the Seventeenth International Conference in Machine Learning, pages , [11] J. Shawe-Taylor. Classification accuracy based on observed margin. Algorithmica, 22(1/2): , [12] S. Tong and D. Koller. Support vector machine active learning with applications to text classification. Journal of Machine Learning Research, pages 45 66, [13] V. N. Vapnik. The Nature of Statistical Learning. Springer-Verlag, New York, [14] K. Veropoulos, C. Campbell, and N. Cristianini. Controlling the sensitivity of support vector machines. In Proceedings of International Joint Conference on AI, pages 55 60, [15] T. Yu, D. Wilkinson, and A. Castellini. Constructing reservoir flow simulator proxies using genetic programming for history matching and production forecast uncertainty analysis. Journal of Artificial Evolution and Application, Article ID , 13 pages,
Support Vector Machines (a brief introduction) Adrian Bevan.
 Support Vector Machines (a brief introduction) Adrian Bevan email: a.j.bevan@qmul.ac.uk Outline! Overview:! Introduce the problem and review the various aspects that underpin the SVM concept.! Hard margin
Support Vector Machines (a brief introduction) Adrian Bevan email: a.j.bevan@qmul.ac.uk Outline! Overview:! Introduce the problem and review the various aspects that underpin the SVM concept.! Hard margin
CLASS IMBALANCE LEARNING METHODS FOR SUPPORT VECTOR MACHINES
 CHAPTER 6 CLASS IMBALANCE LEARNING METHODS FOR SUPPORT VECTOR MACHINES Rukshan Batuwita and Vasile Palade Singapore-MIT Alliance for Research and Technology Centre; University of Oxford. Abstract Support
CHAPTER 6 CLASS IMBALANCE LEARNING METHODS FOR SUPPORT VECTOR MACHINES Rukshan Batuwita and Vasile Palade Singapore-MIT Alliance for Research and Technology Centre; University of Oxford. Abstract Support
CS145: INTRODUCTION TO DATA MINING
 CS145: INTRODUCTION TO DATA MINING 08: Classification Evaluation and Practical Issues Instructor: Yizhou Sun yzsun@cs.ucla.edu October 24, 2017 Learnt Prediction and Classification Methods Vector Data
CS145: INTRODUCTION TO DATA MINING 08: Classification Evaluation and Practical Issues Instructor: Yizhou Sun yzsun@cs.ucla.edu October 24, 2017 Learnt Prediction and Classification Methods Vector Data
A novel supervised learning algorithm and its use for Spam Detection in Social Bookmarking Systems
 A novel supervised learning algorithm and its use for Spam Detection in Social Bookmarking Systems Anestis Gkanogiannis and Theodore Kalamboukis Department of Informatics Athens University of Economics
A novel supervised learning algorithm and its use for Spam Detection in Social Bookmarking Systems Anestis Gkanogiannis and Theodore Kalamboukis Department of Informatics Athens University of Economics
An Intelligent Clustering Algorithm for High Dimensional and Highly Overlapped Photo-Thermal Infrared Imaging Data
 An Intelligent Clustering Algorithm for High Dimensional and Highly Overlapped Photo-Thermal Infrared Imaging Data Nian Zhang and Lara Thompson Department of Electrical and Computer Engineering, University
An Intelligent Clustering Algorithm for High Dimensional and Highly Overlapped Photo-Thermal Infrared Imaging Data Nian Zhang and Lara Thompson Department of Electrical and Computer Engineering, University
Data Mining: Concepts and Techniques. Chapter 9 Classification: Support Vector Machines. Support Vector Machines (SVMs)
 Data Mining: Concepts and Techniques Chapter 9 Classification: Support Vector Machines 1 Support Vector Machines (SVMs) SVMs are a set of related supervised learning methods used for classification Based
Data Mining: Concepts and Techniques Chapter 9 Classification: Support Vector Machines 1 Support Vector Machines (SVMs) SVMs are a set of related supervised learning methods used for classification Based
All lecture slides will be available at CSC2515_Winter15.html
 CSC2515 Fall 2015 Introduc3on to Machine Learning Lecture 9: Support Vector Machines All lecture slides will be available at http://www.cs.toronto.edu/~urtasun/courses/csc2515/ CSC2515_Winter15.html Many
CSC2515 Fall 2015 Introduc3on to Machine Learning Lecture 9: Support Vector Machines All lecture slides will be available at http://www.cs.toronto.edu/~urtasun/courses/csc2515/ CSC2515_Winter15.html Many
Evaluating Classifiers
 Evaluating Classifiers Reading for this topic: T. Fawcett, An introduction to ROC analysis, Sections 1-4, 7 (linked from class website) Evaluating Classifiers What we want: Classifier that best predicts
Evaluating Classifiers Reading for this topic: T. Fawcett, An introduction to ROC analysis, Sections 1-4, 7 (linked from class website) Evaluating Classifiers What we want: Classifier that best predicts
Machine Learning for NLP
 Machine Learning for NLP Support Vector Machines Aurélie Herbelot 2018 Centre for Mind/Brain Sciences University of Trento 1 Support Vector Machines: introduction 2 Support Vector Machines (SVMs) SVMs
Machine Learning for NLP Support Vector Machines Aurélie Herbelot 2018 Centre for Mind/Brain Sciences University of Trento 1 Support Vector Machines: introduction 2 Support Vector Machines (SVMs) SVMs
Kernel Methods & Support Vector Machines
 & Support Vector Machines & Support Vector Machines Arvind Visvanathan CSCE 970 Pattern Recognition 1 & Support Vector Machines Question? Draw a single line to separate two classes? 2 & Support Vector
& Support Vector Machines & Support Vector Machines Arvind Visvanathan CSCE 970 Pattern Recognition 1 & Support Vector Machines Question? Draw a single line to separate two classes? 2 & Support Vector
Using Real-valued Meta Classifiers to Integrate and Contextualize Binding Site Predictions
 Using Real-valued Meta Classifiers to Integrate and Contextualize Binding Site Predictions Offer Sharabi, Yi Sun, Mark Robinson, Rod Adams, Rene te Boekhorst, Alistair G. Rust, Neil Davey University of
Using Real-valued Meta Classifiers to Integrate and Contextualize Binding Site Predictions Offer Sharabi, Yi Sun, Mark Robinson, Rod Adams, Rene te Boekhorst, Alistair G. Rust, Neil Davey University of
Second Order SMO Improves SVM Online and Active Learning
 Second Order SMO Improves SVM Online and Active Learning Tobias Glasmachers and Christian Igel Institut für Neuroinformatik, Ruhr-Universität Bochum 4478 Bochum, Germany Abstract Iterative learning algorithms
Second Order SMO Improves SVM Online and Active Learning Tobias Glasmachers and Christian Igel Institut für Neuroinformatik, Ruhr-Universität Bochum 4478 Bochum, Germany Abstract Iterative learning algorithms
A Feature Selection Method to Handle Imbalanced Data in Text Classification
 A Feature Selection Method to Handle Imbalanced Data in Text Classification Fengxiang Chang 1*, Jun Guo 1, Weiran Xu 1, Kejun Yao 2 1 School of Information and Communication Engineering Beijing University
A Feature Selection Method to Handle Imbalanced Data in Text Classification Fengxiang Chang 1*, Jun Guo 1, Weiran Xu 1, Kejun Yao 2 1 School of Information and Communication Engineering Beijing University
SUPPORT VECTOR MACHINES
 SUPPORT VECTOR MACHINES Today Reading AIMA 8.9 (SVMs) Goals Finish Backpropagation Support vector machines Backpropagation. Begin with randomly initialized weights 2. Apply the neural network to each training
SUPPORT VECTOR MACHINES Today Reading AIMA 8.9 (SVMs) Goals Finish Backpropagation Support vector machines Backpropagation. Begin with randomly initialized weights 2. Apply the neural network to each training
The Effects of Outliers on Support Vector Machines
 The Effects of Outliers on Support Vector Machines Josh Hoak jrhoak@gmail.com Portland State University Abstract. Many techniques have been developed for mitigating the effects of outliers on the results
The Effects of Outliers on Support Vector Machines Josh Hoak jrhoak@gmail.com Portland State University Abstract. Many techniques have been developed for mitigating the effects of outliers on the results
.. Spring 2017 CSC 566 Advanced Data Mining Alexander Dekhtyar..
 .. Spring 2017 CSC 566 Advanced Data Mining Alexander Dekhtyar.. Machine Learning: Support Vector Machines: Linear Kernel Support Vector Machines Extending Perceptron Classifiers. There are two ways to
.. Spring 2017 CSC 566 Advanced Data Mining Alexander Dekhtyar.. Machine Learning: Support Vector Machines: Linear Kernel Support Vector Machines Extending Perceptron Classifiers. There are two ways to
Boosting Support Vector Machines for Imbalanced Data Sets
 Boosting Support Vector Machines for Imbalanced Data Sets Benjamin X. Wang and Nathalie Japkowicz School of information Technology and Engineering, University of Ottawa, 800 King Edward Ave., P.O.Box 450
Boosting Support Vector Machines for Imbalanced Data Sets Benjamin X. Wang and Nathalie Japkowicz School of information Technology and Engineering, University of Ottawa, 800 King Edward Ave., P.O.Box 450
Evaluating Classifiers
 Evaluating Classifiers Reading for this topic: T. Fawcett, An introduction to ROC analysis, Sections 1-4, 7 (linked from class website) Evaluating Classifiers What we want: Classifier that best predicts
Evaluating Classifiers Reading for this topic: T. Fawcett, An introduction to ROC analysis, Sections 1-4, 7 (linked from class website) Evaluating Classifiers What we want: Classifier that best predicts
A New Fuzzy Membership Computation Method for Fuzzy Support Vector Machines
 A New Fuzzy Membership Computation Method for Fuzzy Support Vector Machines Trung Le, Dat Tran, Wanli Ma and Dharmendra Sharma Faculty of Information Sciences and Engineering University of Canberra, Australia
A New Fuzzy Membership Computation Method for Fuzzy Support Vector Machines Trung Le, Dat Tran, Wanli Ma and Dharmendra Sharma Faculty of Information Sciences and Engineering University of Canberra, Australia
SUPPORT VECTOR MACHINES
 SUPPORT VECTOR MACHINES Today Reading AIMA 18.9 Goals (Naïve Bayes classifiers) Support vector machines 1 Support Vector Machines (SVMs) SVMs are probably the most popular off-the-shelf classifier! Software
SUPPORT VECTOR MACHINES Today Reading AIMA 18.9 Goals (Naïve Bayes classifiers) Support vector machines 1 Support Vector Machines (SVMs) SVMs are probably the most popular off-the-shelf classifier! Software
Evaluation Measures. Sebastian Pölsterl. April 28, Computer Aided Medical Procedures Technische Universität München
 Evaluation Measures Sebastian Pölsterl Computer Aided Medical Procedures Technische Universität München April 28, 2015 Outline 1 Classification 1. Confusion Matrix 2. Receiver operating characteristics
Evaluation Measures Sebastian Pölsterl Computer Aided Medical Procedures Technische Universität München April 28, 2015 Outline 1 Classification 1. Confusion Matrix 2. Receiver operating characteristics
Information Management course
 Università degli Studi di Milano Master Degree in Computer Science Information Management course Teacher: Alberto Ceselli Lecture 20: 10/12/2015 Data Mining: Concepts and Techniques (3 rd ed.) Chapter
Università degli Studi di Milano Master Degree in Computer Science Information Management course Teacher: Alberto Ceselli Lecture 20: 10/12/2015 Data Mining: Concepts and Techniques (3 rd ed.) Chapter
Non-Bayesian Classifiers Part II: Linear Discriminants and Support Vector Machines
 Non-Bayesian Classifiers Part II: Linear Discriminants and Support Vector Machines Selim Aksoy Department of Computer Engineering Bilkent University saksoy@cs.bilkent.edu.tr CS 551, Spring 2007 c 2007,
Non-Bayesian Classifiers Part II: Linear Discriminants and Support Vector Machines Selim Aksoy Department of Computer Engineering Bilkent University saksoy@cs.bilkent.edu.tr CS 551, Spring 2007 c 2007,
12 Classification using Support Vector Machines
 160 Bioinformatics I, WS 14/15, D. Huson, January 28, 2015 12 Classification using Support Vector Machines This lecture is based on the following sources, which are all recommended reading: F. Markowetz.
160 Bioinformatics I, WS 14/15, D. Huson, January 28, 2015 12 Classification using Support Vector Machines This lecture is based on the following sources, which are all recommended reading: F. Markowetz.
Combination of PCA with SMOTE Resampling to Boost the Prediction Rate in Lung Cancer Dataset
 International Journal of Computer Applications (0975 8887) Combination of PCA with SMOTE Resampling to Boost the Prediction Rate in Lung Cancer Dataset Mehdi Naseriparsa Islamic Azad University Tehran
International Journal of Computer Applications (0975 8887) Combination of PCA with SMOTE Resampling to Boost the Prediction Rate in Lung Cancer Dataset Mehdi Naseriparsa Islamic Azad University Tehran
Support Vector Machines
 Support Vector Machines RBF-networks Support Vector Machines Good Decision Boundary Optimization Problem Soft margin Hyperplane Non-linear Decision Boundary Kernel-Trick Approximation Accurancy Overtraining
Support Vector Machines RBF-networks Support Vector Machines Good Decision Boundary Optimization Problem Soft margin Hyperplane Non-linear Decision Boundary Kernel-Trick Approximation Accurancy Overtraining
Metrics for Performance Evaluation How to evaluate the performance of a model? Methods for Performance Evaluation How to obtain reliable estimates?
 Model Evaluation Metrics for Performance Evaluation How to evaluate the performance of a model? Methods for Performance Evaluation How to obtain reliable estimates? Methods for Model Comparison How to
Model Evaluation Metrics for Performance Evaluation How to evaluate the performance of a model? Methods for Performance Evaluation How to obtain reliable estimates? Methods for Model Comparison How to
Opinion Mining by Transformation-Based Domain Adaptation
 Opinion Mining by Transformation-Based Domain Adaptation Róbert Ormándi, István Hegedűs, and Richárd Farkas University of Szeged, Hungary {ormandi,ihegedus,rfarkas}@inf.u-szeged.hu Abstract. Here we propose
Opinion Mining by Transformation-Based Domain Adaptation Róbert Ormándi, István Hegedűs, and Richárd Farkas University of Szeged, Hungary {ormandi,ihegedus,rfarkas}@inf.u-szeged.hu Abstract. Here we propose
Introduction to Machine Learning
 Introduction to Machine Learning Maximum Margin Methods Varun Chandola Computer Science & Engineering State University of New York at Buffalo Buffalo, NY, USA chandola@buffalo.edu Chandola@UB CSE 474/574
Introduction to Machine Learning Maximum Margin Methods Varun Chandola Computer Science & Engineering State University of New York at Buffalo Buffalo, NY, USA chandola@buffalo.edu Chandola@UB CSE 474/574
Support Vector Machine with Restarting Genetic Algorithm for Classifying Imbalanced Data
 Support Vector Machine with Restarting Genetic Algorithm for Classifying Imbalanced Data Keerachart Suksut, Kittisak Kerdprasop, and Nittaya Kerdprasop Abstract Algorithms for data classification are normally
Support Vector Machine with Restarting Genetic Algorithm for Classifying Imbalanced Data Keerachart Suksut, Kittisak Kerdprasop, and Nittaya Kerdprasop Abstract Algorithms for data classification are normally
Support vector machines
 Support vector machines When the data is linearly separable, which of the many possible solutions should we prefer? SVM criterion: maximize the margin, or distance between the hyperplane and the closest
Support vector machines When the data is linearly separable, which of the many possible solutions should we prefer? SVM criterion: maximize the margin, or distance between the hyperplane and the closest
Lecture 9: Support Vector Machines
 Lecture 9: Support Vector Machines William Webber (william@williamwebber.com) COMP90042, 2014, Semester 1, Lecture 8 What we ll learn in this lecture Support Vector Machines (SVMs) a highly robust and
Lecture 9: Support Vector Machines William Webber (william@williamwebber.com) COMP90042, 2014, Semester 1, Lecture 8 What we ll learn in this lecture Support Vector Machines (SVMs) a highly robust and
Binarization of Color Character Strings in Scene Images Using K-means Clustering and Support Vector Machines
 2011 International Conference on Document Analysis and Recognition Binarization of Color Character Strings in Scene Images Using K-means Clustering and Support Vector Machines Toru Wakahara Kohei Kita
2011 International Conference on Document Analysis and Recognition Binarization of Color Character Strings in Scene Images Using K-means Clustering and Support Vector Machines Toru Wakahara Kohei Kita
Fraud Detection using Machine Learning
 Fraud Detection using Machine Learning Aditya Oza - aditya19@stanford.edu Abstract Recent research has shown that machine learning techniques have been applied very effectively to the problem of payments
Fraud Detection using Machine Learning Aditya Oza - aditya19@stanford.edu Abstract Recent research has shown that machine learning techniques have been applied very effectively to the problem of payments
PARALLEL SELECTIVE SAMPLING USING RELEVANCE VECTOR MACHINE FOR IMBALANCE DATA M. Athitya Kumaraguru 1, Viji Vinod 2, N.
 Volume 117 No. 20 2017, 873-879 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu ijpam.eu PARALLEL SELECTIVE SAMPLING USING RELEVANCE VECTOR MACHINE FOR IMBALANCE
Volume 117 No. 20 2017, 873-879 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu ijpam.eu PARALLEL SELECTIVE SAMPLING USING RELEVANCE VECTOR MACHINE FOR IMBALANCE
CS249: ADVANCED DATA MINING
 CS249: ADVANCED DATA MINING Classification Evaluation and Practical Issues Instructor: Yizhou Sun yzsun@cs.ucla.edu April 24, 2017 Homework 2 out Announcements Due May 3 rd (11:59pm) Course project proposal
CS249: ADVANCED DATA MINING Classification Evaluation and Practical Issues Instructor: Yizhou Sun yzsun@cs.ucla.edu April 24, 2017 Homework 2 out Announcements Due May 3 rd (11:59pm) Course project proposal
K- Nearest Neighbors(KNN) And Predictive Accuracy
 Contact: mailto: Ammar@cu.edu.eg Drammarcu@gmail.com K- Nearest Neighbors(KNN) And Predictive Accuracy Dr. Ammar Mohammed Associate Professor of Computer Science ISSR, Cairo University PhD of CS ( Uni.
Contact: mailto: Ammar@cu.edu.eg Drammarcu@gmail.com K- Nearest Neighbors(KNN) And Predictive Accuracy Dr. Ammar Mohammed Associate Professor of Computer Science ISSR, Cairo University PhD of CS ( Uni.
DM6 Support Vector Machines
 DM6 Support Vector Machines Outline Large margin linear classifier Linear separable Nonlinear separable Creating nonlinear classifiers: kernel trick Discussion on SVM Conclusion SVM: LARGE MARGIN LINEAR
DM6 Support Vector Machines Outline Large margin linear classifier Linear separable Nonlinear separable Creating nonlinear classifiers: kernel trick Discussion on SVM Conclusion SVM: LARGE MARGIN LINEAR
Lecture Linear Support Vector Machines
 Lecture 8 In this lecture we return to the task of classification. As seen earlier, examples include spam filters, letter recognition, or text classification. In this lecture we introduce a popular method
Lecture 8 In this lecture we return to the task of classification. As seen earlier, examples include spam filters, letter recognition, or text classification. In this lecture we introduce a popular method
A Comparative Study of SVM Kernel Functions Based on Polynomial Coefficients and V-Transform Coefficients
 www.ijecs.in International Journal Of Engineering And Computer Science ISSN:2319-7242 Volume 6 Issue 3 March 2017, Page No. 20765-20769 Index Copernicus value (2015): 58.10 DOI: 18535/ijecs/v6i3.65 A Comparative
www.ijecs.in International Journal Of Engineering And Computer Science ISSN:2319-7242 Volume 6 Issue 3 March 2017, Page No. 20765-20769 Index Copernicus value (2015): 58.10 DOI: 18535/ijecs/v6i3.65 A Comparative
Lab 2: Support vector machines
 Artificial neural networks, advanced course, 2D1433 Lab 2: Support vector machines Martin Rehn For the course given in 2006 All files referenced below may be found in the following directory: /info/annfk06/labs/lab2
Artificial neural networks, advanced course, 2D1433 Lab 2: Support vector machines Martin Rehn For the course given in 2006 All files referenced below may be found in the following directory: /info/annfk06/labs/lab2
A Short SVM (Support Vector Machine) Tutorial
 A Short SVM (Support Vector Machine) Tutorial j.p.lewis CGIT Lab / IMSC U. Southern California version 0.zz dec 004 This tutorial assumes you are familiar with linear algebra and equality-constrained optimization/lagrange
A Short SVM (Support Vector Machine) Tutorial j.p.lewis CGIT Lab / IMSC U. Southern California version 0.zz dec 004 This tutorial assumes you are familiar with linear algebra and equality-constrained optimization/lagrange
Rule extraction from support vector machines
 Rule extraction from support vector machines Haydemar Núñez 1,3 Cecilio Angulo 1,2 Andreu Català 1,2 1 Dept. of Systems Engineering, Polytechnical University of Catalonia Avda. Victor Balaguer s/n E-08800
Rule extraction from support vector machines Haydemar Núñez 1,3 Cecilio Angulo 1,2 Andreu Català 1,2 1 Dept. of Systems Engineering, Polytechnical University of Catalonia Avda. Victor Balaguer s/n E-08800
Data Analysis 3. Support Vector Machines. Jan Platoš October 30, 2017
 Data Analysis 3 Support Vector Machines Jan Platoš October 30, 2017 Department of Computer Science Faculty of Electrical Engineering and Computer Science VŠB - Technical University of Ostrava Table of
Data Analysis 3 Support Vector Machines Jan Platoš October 30, 2017 Department of Computer Science Faculty of Electrical Engineering and Computer Science VŠB - Technical University of Ostrava Table of
ECG782: Multidimensional Digital Signal Processing
 ECG782: Multidimensional Digital Signal Processing Object Recognition http://www.ee.unlv.edu/~b1morris/ecg782/ 2 Outline Knowledge Representation Statistical Pattern Recognition Neural Networks Boosting
ECG782: Multidimensional Digital Signal Processing Object Recognition http://www.ee.unlv.edu/~b1morris/ecg782/ 2 Outline Knowledge Representation Statistical Pattern Recognition Neural Networks Boosting
Support Vector Machines
 Support Vector Machines . Importance of SVM SVM is a discriminative method that brings together:. computational learning theory. previously known methods in linear discriminant functions 3. optimization
Support Vector Machines . Importance of SVM SVM is a discriminative method that brings together:. computational learning theory. previously known methods in linear discriminant functions 3. optimization
Bagging and Boosting Algorithms for Support Vector Machine Classifiers
 Bagging and Boosting Algorithms for Support Vector Machine Classifiers Noritaka SHIGEI and Hiromi MIYAJIMA Dept. of Electrical and Electronics Engineering, Kagoshima University 1-21-40, Korimoto, Kagoshima
Bagging and Boosting Algorithms for Support Vector Machine Classifiers Noritaka SHIGEI and Hiromi MIYAJIMA Dept. of Electrical and Electronics Engineering, Kagoshima University 1-21-40, Korimoto, Kagoshima
CS6375: Machine Learning Gautam Kunapuli. Mid-Term Review
 Gautam Kunapuli Machine Learning Data is identically and independently distributed Goal is to learn a function that maps to Data is generated using an unknown function Learn a hypothesis that minimizes
Gautam Kunapuli Machine Learning Data is identically and independently distributed Goal is to learn a function that maps to Data is generated using an unknown function Learn a hypothesis that minimizes
Well Analysis: Program psvm_welllogs
 Proximal Support Vector Machine Classification on Well Logs Overview Support vector machine (SVM) is a recent supervised machine learning technique that is widely used in text detection, image recognition
Proximal Support Vector Machine Classification on Well Logs Overview Support vector machine (SVM) is a recent supervised machine learning technique that is widely used in text detection, image recognition
Efficient Tuning of SVM Hyperparameters Using Radius/Margin Bound and Iterative Algorithms
 IEEE TRANSACTIONS ON NEURAL NETWORKS, VOL. 13, NO. 5, SEPTEMBER 2002 1225 Efficient Tuning of SVM Hyperparameters Using Radius/Margin Bound and Iterative Algorithms S. Sathiya Keerthi Abstract This paper
IEEE TRANSACTIONS ON NEURAL NETWORKS, VOL. 13, NO. 5, SEPTEMBER 2002 1225 Efficient Tuning of SVM Hyperparameters Using Radius/Margin Bound and Iterative Algorithms S. Sathiya Keerthi Abstract This paper
A Practical Guide to Support Vector Classification
 A Practical Guide to Support Vector Classification Chih-Wei Hsu, Chih-Chung Chang, and Chih-Jen Lin Department of Computer Science and Information Engineering National Taiwan University Taipei 106, Taiwan
A Practical Guide to Support Vector Classification Chih-Wei Hsu, Chih-Chung Chang, and Chih-Jen Lin Department of Computer Science and Information Engineering National Taiwan University Taipei 106, Taiwan
Title: A Batch Mode Active Learning Technique Based on Multiple Uncertainty for SVM Classifier
 2011 IEEE. Personal use of this material is permitted. Permission from IEEE must be obtained for all other uses, in any current or future media, including reprinting/republishing this material for advertising
2011 IEEE. Personal use of this material is permitted. Permission from IEEE must be obtained for all other uses, in any current or future media, including reprinting/republishing this material for advertising
Support Vector Machines.
 Support Vector Machines srihari@buffalo.edu SVM Discussion Overview 1. Overview of SVMs 2. Margin Geometry 3. SVM Optimization 4. Overlapping Distributions 5. Relationship to Logistic Regression 6. Dealing
Support Vector Machines srihari@buffalo.edu SVM Discussion Overview 1. Overview of SVMs 2. Margin Geometry 3. SVM Optimization 4. Overlapping Distributions 5. Relationship to Logistic Regression 6. Dealing
Data-driven Kernels for Support Vector Machines
 Data-driven Kernels for Support Vector Machines by Xin Yao A research paper presented to the University of Waterloo in partial fulfillment of the requirement for the degree of Master of Mathematics in
Data-driven Kernels for Support Vector Machines by Xin Yao A research paper presented to the University of Waterloo in partial fulfillment of the requirement for the degree of Master of Mathematics in
Support Vector Machines
 Support Vector Machines RBF-networks Support Vector Machines Good Decision Boundary Optimization Problem Soft margin Hyperplane Non-linear Decision Boundary Kernel-Trick Approximation Accurancy Overtraining
Support Vector Machines RBF-networks Support Vector Machines Good Decision Boundary Optimization Problem Soft margin Hyperplane Non-linear Decision Boundary Kernel-Trick Approximation Accurancy Overtraining
Kernel Methods and Visualization for Interval Data Mining
 Kernel Methods and Visualization for Interval Data Mining Thanh-Nghi Do 1 and François Poulet 2 1 College of Information Technology, Can Tho University, 1 Ly Tu Trong Street, Can Tho, VietNam (e-mail:
Kernel Methods and Visualization for Interval Data Mining Thanh-Nghi Do 1 and François Poulet 2 1 College of Information Technology, Can Tho University, 1 Ly Tu Trong Street, Can Tho, VietNam (e-mail:
Introduction to Support Vector Machines
 Introduction to Support Vector Machines CS 536: Machine Learning Littman (Wu, TA) Administration Slides borrowed from Martin Law (from the web). 1 Outline History of support vector machines (SVM) Two classes,
Introduction to Support Vector Machines CS 536: Machine Learning Littman (Wu, TA) Administration Slides borrowed from Martin Law (from the web). 1 Outline History of support vector machines (SVM) Two classes,
Constrained Classification of Large Imbalanced Data
 Constrained Classification of Large Imbalanced Data Martin Hlosta, R. Stríž, J. Zendulka, T. Hruška Brno University of Technology, Faculty of Information Technology Božetěchova 2, 612 66 Brno ihlosta@fit.vutbr.cz
Constrained Classification of Large Imbalanced Data Martin Hlosta, R. Stríž, J. Zendulka, T. Hruška Brno University of Technology, Faculty of Information Technology Božetěchova 2, 612 66 Brno ihlosta@fit.vutbr.cz
Lina Guzman, DIRECTV
 Paper 3483-2015 Data sampling improvement by developing SMOTE technique in SAS Lina Guzman, DIRECTV ABSTRACT A common problem when developing classification models is the imbalance of classes in the classification
Paper 3483-2015 Data sampling improvement by developing SMOTE technique in SAS Lina Guzman, DIRECTV ABSTRACT A common problem when developing classification models is the imbalance of classes in the classification
CS4491/CS 7265 BIG DATA ANALYTICS
 CS4491/CS 7265 BIG DATA ANALYTICS EVALUATION * Some contents are adapted from Dr. Hung Huang and Dr. Chengkai Li at UT Arlington Dr. Mingon Kang Computer Science, Kennesaw State University Evaluation for
CS4491/CS 7265 BIG DATA ANALYTICS EVALUATION * Some contents are adapted from Dr. Hung Huang and Dr. Chengkai Li at UT Arlington Dr. Mingon Kang Computer Science, Kennesaw State University Evaluation for
Evaluation Metrics. (Classifiers) CS229 Section Anand Avati
 Evaluation Metrics (Classifiers) CS Section Anand Avati Topics Why? Binary classifiers Metrics Rank view Thresholding Confusion Matrix Point metrics: Accuracy, Precision, Recall / Sensitivity, Specificity,
Evaluation Metrics (Classifiers) CS Section Anand Avati Topics Why? Binary classifiers Metrics Rank view Thresholding Confusion Matrix Point metrics: Accuracy, Precision, Recall / Sensitivity, Specificity,
Robust PDF Table Locator
 Robust PDF Table Locator December 17, 2016 1 Introduction Data scientists rely on an abundance of tabular data stored in easy-to-machine-read formats like.csv files. Unfortunately, most government records
Robust PDF Table Locator December 17, 2016 1 Introduction Data scientists rely on an abundance of tabular data stored in easy-to-machine-read formats like.csv files. Unfortunately, most government records
Predict Employees Computer Access Needs in Company
 Predict Employees Computer Access Needs in Company Xin Zhou & Wenqi Xiang Email: xzhou15,wenqi@stanford.edu 1.Department of Computer Science 2.Department of Electrical Engineering 1 Abstract When an employee
Predict Employees Computer Access Needs in Company Xin Zhou & Wenqi Xiang Email: xzhou15,wenqi@stanford.edu 1.Department of Computer Science 2.Department of Electrical Engineering 1 Abstract When an employee
Kernels + K-Means Introduction to Machine Learning. Matt Gormley Lecture 29 April 25, 2018
 10-601 Introduction to Machine Learning Machine Learning Department School of Computer Science Carnegie Mellon University Kernels + K-Means Matt Gormley Lecture 29 April 25, 2018 1 Reminders Homework 8:
10-601 Introduction to Machine Learning Machine Learning Department School of Computer Science Carnegie Mellon University Kernels + K-Means Matt Gormley Lecture 29 April 25, 2018 1 Reminders Homework 8:
Best First and Greedy Search Based CFS and Naïve Bayes Algorithms for Hepatitis Diagnosis
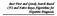 Best First and Greedy Search Based CFS and Naïve Bayes Algorithms for Hepatitis Diagnosis CHAPTER 3 BEST FIRST AND GREEDY SEARCH BASED CFS AND NAÏVE BAYES ALGORITHMS FOR HEPATITIS DIAGNOSIS 3.1 Introduction
Best First and Greedy Search Based CFS and Naïve Bayes Algorithms for Hepatitis Diagnosis CHAPTER 3 BEST FIRST AND GREEDY SEARCH BASED CFS AND NAÏVE BAYES ALGORITHMS FOR HEPATITIS DIAGNOSIS 3.1 Introduction
Coevolution of Simulator Proxies and Sampling Strategies for Petroleum Reservoir Modeling
 Coevolution of Simulator Proxies and Sampling Strategies for Petroleum Reservoir Modeling Tina Yu Memorial University of Newfoundland, Canada Dave Wilkinson Chevron Energy Technology Company, USA Outline
Coevolution of Simulator Proxies and Sampling Strategies for Petroleum Reservoir Modeling Tina Yu Memorial University of Newfoundland, Canada Dave Wilkinson Chevron Energy Technology Company, USA Outline
Statistics 202: Statistical Aspects of Data Mining
 Statistics 202: Statistical Aspects of Data Mining Professor Rajan Patel Lecture 9 = More of Chapter 5 Agenda: 1) Lecture over more of Chapter 5 1 Introduction to Data Mining by Tan, Steinbach, Kumar Chapter
Statistics 202: Statistical Aspects of Data Mining Professor Rajan Patel Lecture 9 = More of Chapter 5 Agenda: 1) Lecture over more of Chapter 5 1 Introduction to Data Mining by Tan, Steinbach, Kumar Chapter
Classification Lecture Notes cse352. Neural Networks. Professor Anita Wasilewska
 Classification Lecture Notes cse352 Neural Networks Professor Anita Wasilewska Neural Networks Classification Introduction INPUT: classification data, i.e. it contains an classification (class) attribute
Classification Lecture Notes cse352 Neural Networks Professor Anita Wasilewska Neural Networks Classification Introduction INPUT: classification data, i.e. it contains an classification (class) attribute
Safe-Level-SMOTE: Safe-Level-Synthetic Minority Over-Sampling TEchnique for Handling the Class Imbalanced Problem
 Safe-Level-SMOTE: Safe-Level-Synthetic Minority Over-Sampling TEchnique for Handling the Class Imbalanced Problem Chumphol Bunkhumpornpat, Krung Sinapiromsaran, and Chidchanok Lursinsap Department of Mathematics,
Safe-Level-SMOTE: Safe-Level-Synthetic Minority Over-Sampling TEchnique for Handling the Class Imbalanced Problem Chumphol Bunkhumpornpat, Krung Sinapiromsaran, and Chidchanok Lursinsap Department of Mathematics,
An Effective Performance of Feature Selection with Classification of Data Mining Using SVM Algorithm
 Proceedings of the National Conference on Recent Trends in Mathematical Computing NCRTMC 13 427 An Effective Performance of Feature Selection with Classification of Data Mining Using SVM Algorithm A.Veeraswamy
Proceedings of the National Conference on Recent Trends in Mathematical Computing NCRTMC 13 427 An Effective Performance of Feature Selection with Classification of Data Mining Using SVM Algorithm A.Veeraswamy
Chapter 22 Information Gain, Correlation and Support Vector Machines
 Chapter 22 Information Gain, Correlation and Support Vector Machines Danny Roobaert, Grigoris Karakoulas, and Nitesh V. Chawla Customer Behavior Analytics Retail Risk Management Canadian Imperial Bank
Chapter 22 Information Gain, Correlation and Support Vector Machines Danny Roobaert, Grigoris Karakoulas, and Nitesh V. Chawla Customer Behavior Analytics Retail Risk Management Canadian Imperial Bank
CS570: Introduction to Data Mining
 CS570: Introduction to Data Mining Classification Advanced Reading: Chapter 8 & 9 Han, Chapters 4 & 5 Tan Anca Doloc-Mihu, Ph.D. Slides courtesy of Li Xiong, Ph.D., 2011 Han, Kamber & Pei. Data Mining.
CS570: Introduction to Data Mining Classification Advanced Reading: Chapter 8 & 9 Han, Chapters 4 & 5 Tan Anca Doloc-Mihu, Ph.D. Slides courtesy of Li Xiong, Ph.D., 2011 Han, Kamber & Pei. Data Mining.
A Two-phase Distributed Training Algorithm for Linear SVM in WSN
 Proceedings of the World Congress on Electrical Engineering and Computer Systems and Science (EECSS 015) Barcelona, Spain July 13-14, 015 Paper o. 30 A wo-phase Distributed raining Algorithm for Linear
Proceedings of the World Congress on Electrical Engineering and Computer Systems and Science (EECSS 015) Barcelona, Spain July 13-14, 015 Paper o. 30 A wo-phase Distributed raining Algorithm for Linear
Support Vector Machines
 Support Vector Machines Chapter 9 Chapter 9 1 / 50 1 91 Maximal margin classifier 2 92 Support vector classifiers 3 93 Support vector machines 4 94 SVMs with more than two classes 5 95 Relationshiop to
Support Vector Machines Chapter 9 Chapter 9 1 / 50 1 91 Maximal margin classifier 2 92 Support vector classifiers 3 93 Support vector machines 4 94 SVMs with more than two classes 5 95 Relationshiop to
Combine Vector Quantization and Support Vector Machine for Imbalanced Datasets
 Combine Vector Quantization and Support Vector Machine for Imbalanced Datasets Ting Yu, John Debenham, Tony Jan and Simeon Simoff Institute for Information and Communication Technologies Faculty of Information
Combine Vector Quantization and Support Vector Machine for Imbalanced Datasets Ting Yu, John Debenham, Tony Jan and Simeon Simoff Institute for Information and Communication Technologies Faculty of Information
Data Mining Classification: Alternative Techniques. Imbalanced Class Problem
 Data Mining Classification: Alternative Techniques Imbalanced Class Problem Introduction to Data Mining, 2 nd Edition by Tan, Steinbach, Karpatne, Kumar Class Imbalance Problem Lots of classification problems
Data Mining Classification: Alternative Techniques Imbalanced Class Problem Introduction to Data Mining, 2 nd Edition by Tan, Steinbach, Karpatne, Kumar Class Imbalance Problem Lots of classification problems
Weka ( )
 Weka ( http://www.cs.waikato.ac.nz/ml/weka/ ) The phases in which classifier s design can be divided are reflected in WEKA s Explorer structure: Data pre-processing (filtering) and representation Supervised
Weka ( http://www.cs.waikato.ac.nz/ml/weka/ ) The phases in which classifier s design can be divided are reflected in WEKA s Explorer structure: Data pre-processing (filtering) and representation Supervised
Louis Fourrier Fabien Gaie Thomas Rolf
 CS 229 Stay Alert! The Ford Challenge Louis Fourrier Fabien Gaie Thomas Rolf Louis Fourrier Fabien Gaie Thomas Rolf 1. Problem description a. Goal Our final project is a recent Kaggle competition submitted
CS 229 Stay Alert! The Ford Challenge Louis Fourrier Fabien Gaie Thomas Rolf Louis Fourrier Fabien Gaie Thomas Rolf 1. Problem description a. Goal Our final project is a recent Kaggle competition submitted
Use of Multi-category Proximal SVM for Data Set Reduction
 Use of Multi-category Proximal SVM for Data Set Reduction S.V.N Vishwanathan and M Narasimha Murty Department of Computer Science and Automation, Indian Institute of Science, Bangalore 560 012, India Abstract.
Use of Multi-category Proximal SVM for Data Set Reduction S.V.N Vishwanathan and M Narasimha Murty Department of Computer Science and Automation, Indian Institute of Science, Bangalore 560 012, India Abstract.
Overview Citation. ML Introduction. Overview Schedule. ML Intro Dataset. Introduction to Semi-Supervised Learning Review 10/4/2010
 INFORMATICS SEMINAR SEPT. 27 & OCT. 4, 2010 Introduction to Semi-Supervised Learning Review 2 Overview Citation X. Zhu and A.B. Goldberg, Introduction to Semi- Supervised Learning, Morgan & Claypool Publishers,
INFORMATICS SEMINAR SEPT. 27 & OCT. 4, 2010 Introduction to Semi-Supervised Learning Review 2 Overview Citation X. Zhu and A.B. Goldberg, Introduction to Semi- Supervised Learning, Morgan & Claypool Publishers,
INF4820, Algorithms for AI and NLP: Evaluating Classifiers Clustering
 INF4820, Algorithms for AI and NLP: Evaluating Classifiers Clustering Erik Velldal University of Oslo Sept. 18, 2012 Topics for today 2 Classification Recap Evaluating classifiers Accuracy, precision,
INF4820, Algorithms for AI and NLP: Evaluating Classifiers Clustering Erik Velldal University of Oslo Sept. 18, 2012 Topics for today 2 Classification Recap Evaluating classifiers Accuracy, precision,
Kernel Combination Versus Classifier Combination
 Kernel Combination Versus Classifier Combination Wan-Jui Lee 1, Sergey Verzakov 2, and Robert P.W. Duin 2 1 EE Department, National Sun Yat-Sen University, Kaohsiung, Taiwan wrlee@water.ee.nsysu.edu.tw
Kernel Combination Versus Classifier Combination Wan-Jui Lee 1, Sergey Verzakov 2, and Robert P.W. Duin 2 1 EE Department, National Sun Yat-Sen University, Kaohsiung, Taiwan wrlee@water.ee.nsysu.edu.tw
Application of Support Vector Machine Algorithm in Spam Filtering
 Application of Support Vector Machine Algorithm in E-Mail Spam Filtering Julia Bluszcz, Daria Fitisova, Alexander Hamann, Alexey Trifonov, Advisor: Patrick Jähnichen Abstract The problem of spam classification
Application of Support Vector Machine Algorithm in E-Mail Spam Filtering Julia Bluszcz, Daria Fitisova, Alexander Hamann, Alexey Trifonov, Advisor: Patrick Jähnichen Abstract The problem of spam classification
Contents Machine Learning concepts 4 Learning Algorithm 4 Predictive Model (Model) 4 Model, Classification 4 Model, Regression 4 Representation
 Contents Machine Learning concepts 4 Learning Algorithm 4 Predictive Model (Model) 4 Model, Classification 4 Model, Regression 4 Representation Learning 4 Supervised Learning 4 Unsupervised Learning 4
Contents Machine Learning concepts 4 Learning Algorithm 4 Predictive Model (Model) 4 Model, Classification 4 Model, Regression 4 Representation Learning 4 Supervised Learning 4 Unsupervised Learning 4
Network Traffic Measurements and Analysis
 DEIB - Politecnico di Milano Fall, 2017 Sources Hastie, Tibshirani, Friedman: The Elements of Statistical Learning James, Witten, Hastie, Tibshirani: An Introduction to Statistical Learning Andrew Ng:
DEIB - Politecnico di Milano Fall, 2017 Sources Hastie, Tibshirani, Friedman: The Elements of Statistical Learning James, Witten, Hastie, Tibshirani: An Introduction to Statistical Learning Andrew Ng:
Lecture #11: The Perceptron
 Lecture #11: The Perceptron Mat Kallada STAT2450 - Introduction to Data Mining Outline for Today Welcome back! Assignment 3 The Perceptron Learning Method Perceptron Learning Rule Assignment 3 Will be
Lecture #11: The Perceptron Mat Kallada STAT2450 - Introduction to Data Mining Outline for Today Welcome back! Assignment 3 The Perceptron Learning Method Perceptron Learning Rule Assignment 3 Will be
Tutorials Case studies
 1. Subject Three curves for the evaluation of supervised learning methods. Evaluation of classifiers is an important step of the supervised learning process. We want to measure the performance of the classifier.
1. Subject Three curves for the evaluation of supervised learning methods. Evaluation of classifiers is an important step of the supervised learning process. We want to measure the performance of the classifier.
Classification. Instructor: Wei Ding
 Classification Part II Instructor: Wei Ding Tan,Steinbach, Kumar Introduction to Data Mining 4/18/004 1 Practical Issues of Classification Underfitting and Overfitting Missing Values Costs of Classification
Classification Part II Instructor: Wei Ding Tan,Steinbach, Kumar Introduction to Data Mining 4/18/004 1 Practical Issues of Classification Underfitting and Overfitting Missing Values Costs of Classification
Classification by Support Vector Machines
 Classification by Support Vector Machines Florian Markowetz Max-Planck-Institute for Molecular Genetics Computational Molecular Biology Berlin Practical DNA Microarray Analysis 2003 1 Overview I II III
Classification by Support Vector Machines Florian Markowetz Max-Planck-Institute for Molecular Genetics Computational Molecular Biology Berlin Practical DNA Microarray Analysis 2003 1 Overview I II III
Cluster analysis of 3D seismic data for oil and gas exploration
 Data Mining VII: Data, Text and Web Mining and their Business Applications 63 Cluster analysis of 3D seismic data for oil and gas exploration D. R. S. Moraes, R. P. Espíndola, A. G. Evsukoff & N. F. F.
Data Mining VII: Data, Text and Web Mining and their Business Applications 63 Cluster analysis of 3D seismic data for oil and gas exploration D. R. S. Moraes, R. P. Espíndola, A. G. Evsukoff & N. F. F.
SoftDoubleMinOver: A Simple Procedure for Maximum Margin Classification
 SoftDoubleMinOver: A Simple Procedure for Maximum Margin Classification Thomas Martinetz, Kai Labusch, and Daniel Schneegaß Institute for Neuro- and Bioinformatics University of Lübeck D-23538 Lübeck,
SoftDoubleMinOver: A Simple Procedure for Maximum Margin Classification Thomas Martinetz, Kai Labusch, and Daniel Schneegaß Institute for Neuro- and Bioinformatics University of Lübeck D-23538 Lübeck,
Module 4. Non-linear machine learning econometrics: Support Vector Machine
 Module 4. Non-linear machine learning econometrics: Support Vector Machine THE CONTRACTOR IS ACTING UNDER A FRAMEWORK CONTRACT CONCLUDED WITH THE COMMISSION Introduction When the assumption of linearity
Module 4. Non-linear machine learning econometrics: Support Vector Machine THE CONTRACTOR IS ACTING UNDER A FRAMEWORK CONTRACT CONCLUDED WITH THE COMMISSION Introduction When the assumption of linearity
Large synthetic data sets to compare different data mining methods
 Large synthetic data sets to compare different data mining methods Victoria Ivanova, Yaroslav Nalivajko Superviser: David Pfander, IPVS ivanova.informatics@gmail.com yaroslav.nalivayko@gmail.com June 3,
Large synthetic data sets to compare different data mining methods Victoria Ivanova, Yaroslav Nalivajko Superviser: David Pfander, IPVS ivanova.informatics@gmail.com yaroslav.nalivayko@gmail.com June 3,
Combine the PA Algorithm with a Proximal Classifier
 Combine the Passive and Aggressive Algorithm with a Proximal Classifier Yuh-Jye Lee Joint work with Y.-C. Tseng Dept. of Computer Science & Information Engineering TaiwanTech. Dept. of Statistics@NCKU
Combine the Passive and Aggressive Algorithm with a Proximal Classifier Yuh-Jye Lee Joint work with Y.-C. Tseng Dept. of Computer Science & Information Engineering TaiwanTech. Dept. of Statistics@NCKU
LARGE MARGIN CLASSIFIERS
 Admin Assignment 5 LARGE MARGIN CLASSIFIERS David Kauchak CS 451 Fall 2013 Midterm Download from course web page when you re ready to take it 2 hours to complete Must hand-in (or e-mail in) by 11:59pm
Admin Assignment 5 LARGE MARGIN CLASSIFIERS David Kauchak CS 451 Fall 2013 Midterm Download from course web page when you re ready to take it 2 hours to complete Must hand-in (or e-mail in) by 11:59pm
Choosing the kernel parameters for SVMs by the inter-cluster distance in the feature space Authors: Kuo-Ping Wu, Sheng-De Wang Published 2008
 Choosing the kernel parameters for SVMs by the inter-cluster distance in the feature space Authors: Kuo-Ping Wu, Sheng-De Wang Published 2008 Presented by: Nandini Deka UH Mathematics Spring 2014 Workshop
Choosing the kernel parameters for SVMs by the inter-cluster distance in the feature space Authors: Kuo-Ping Wu, Sheng-De Wang Published 2008 Presented by: Nandini Deka UH Mathematics Spring 2014 Workshop
SUPPORT VECTOR MACHINE ACTIVE LEARNING
 SUPPORT VECTOR MACHINE ACTIVE LEARNING CS 101.2 Caltech, 03 Feb 2009 Paper by S. Tong, D. Koller Presented by Krzysztof Chalupka OUTLINE SVM intro Geometric interpretation Primal and dual form Convexity,
SUPPORT VECTOR MACHINE ACTIVE LEARNING CS 101.2 Caltech, 03 Feb 2009 Paper by S. Tong, D. Koller Presented by Krzysztof Chalupka OUTLINE SVM intro Geometric interpretation Primal and dual form Convexity,
HOG-based Pedestriant Detector Training
 HOG-based Pedestriant Detector Training evs embedded Vision Systems Srl c/o Computer Science Park, Strada Le Grazie, 15 Verona- Italy http: // www. embeddedvisionsystems. it Abstract This paper describes
HOG-based Pedestriant Detector Training evs embedded Vision Systems Srl c/o Computer Science Park, Strada Le Grazie, 15 Verona- Italy http: // www. embeddedvisionsystems. it Abstract This paper describes
Software Documentation of the Potential Support Vector Machine
 Software Documentation of the Potential Support Vector Machine Tilman Knebel and Sepp Hochreiter Department of Electrical Engineering and Computer Science Technische Universität Berlin 10587 Berlin, Germany
Software Documentation of the Potential Support Vector Machine Tilman Knebel and Sepp Hochreiter Department of Electrical Engineering and Computer Science Technische Universität Berlin 10587 Berlin, Germany
Lecture 6 K- Nearest Neighbors(KNN) And Predictive Accuracy
 Lecture 6 K- Nearest Neighbors(KNN) And Predictive Accuracy Machine Learning Dr.Ammar Mohammed Nearest Neighbors Set of Stored Cases Atr1... AtrN Class A Store the training samples Use training samples
Lecture 6 K- Nearest Neighbors(KNN) And Predictive Accuracy Machine Learning Dr.Ammar Mohammed Nearest Neighbors Set of Stored Cases Atr1... AtrN Class A Store the training samples Use training samples
