Very simple computational domains can be discretized using boundary-fitted structured meshes (also called grids)
|
|
|
- Phyllis Hampton
- 5 years ago
- Views:
Transcription
1 Structured meshes Very smple computatonal domans can be dscretzed usng boundary-ftted structured meshes (also called grds) The grd lnes of a Cartesan mesh are parallel to one another
2 Structured meshes A general structured mesh s logcally equvalent to a unform Cartesan grd (there exsts a one-to-one mappng) There are d famles of grd lnes n R d, d = 1, 2, 3 Members of the same famly do not cross each other and cross each member of the other famles just once The grd lnes of each famly can be numbered consecutvely The poston of each grd pont (or mesh cell) s unquely dentfed by a set of d ndces n R d, e.g., (x, y j ) R 2, (x, y j, z k ) R 3
3 Structured meshes Each nternal grd pont has 4 nearest neghbors n 2D, 6 n 3D One of the ndces of each par of neghbor ponts dffers by ±1 Ths neghbor connectvty smplfes programmng, provdes fast data access and leads to effcent numercal algorthms The matrces of lnear algebrac systems are banded and fast solvers (both drect and teratve) are readly avalable for such systems
4 Structured meshes The generaton of a structured mesh may be dffcult or mpossble for computatonal domans of complex geometrcal shape Local mesh refnement n one subdoman produces unnecessarly small spacng n other parts of the doman Long thn cells may adversely affect convergence of teratve solvers or result n volatons of dscrete maxmum prncples
5 Block-structured meshes Two (or more) level subdvson of the computatonal doman Decomposton nto relatvely large overlappng or nonoverlappng subdomans (blocks, macroelements) on the coarse level Dscretzaton of these blocks usng structured meshes
6 Block-structured meshes Block-structured meshes wth overlappng blocks are sometmes called composte or Chmera meshes Mesh generaton for complex domans and flow problems wth movng objects or nterfaces becomes relatvely easy
7 Block-structured meshes More flexblty than wth sngle-block structured meshes Mesh spacng may be chosen ndvdually for each block Local refnement n one block does not affect other blocks Solvers for structured grds can be appled blockwse Programmng s more dffcult than for structured meshes Interpolaton and/or conservaton errors at block nterfaces
8 Unstructured meshes No restrctons on the number of neghbor elements or nodes Automatc mesh generaton for complex domans (trangles or quadrlaterals n 2D, tetrahedra or hexaedra n 3D)
9 Unstructured meshes Hghest flexblty w.r.t. mesh generaton and adaptaton (refnement, coarsenng, redstrbuton of mesh ponts) The coordnates of each mesh pont and numbers of nodes belongng to each element must be stored and retreved Hgh mplementaton effort, rregular sparsty pattern of coeffcent matrces, slow data access due to ndrect addressng Computatonal cost s sgnfcantly hgher than that for a structured grd wth the same number of mesh ponts/elements
10 Choce of the mesh Summary of pros and cons structured unstructured complex geometres + local mesh refnement + automatc mesh generaton + cost of mesh generaton + programmng effort + effcency of data access + effcency of algorthms +
11 Fnte approxmatons Followng the choce of the computatonal mesh, a dscretzaton method for the equatons of the mathematcal model s selected Partal dervatves or ntegrals are commonly approxmated by lnear combnatons of dscrete functon values The choce of the dscretzaton method depends on the mesh structured meshes: fnte dfferences or fnte volumes unstructured meshes: fnte volumes or fnte elements
12 Fnte dfferences Conservaton law u + f = q n Ω (0, T ) t Dscrete unknowns u (t) u(x, t), Approxmaton of dervatves ( ) u u +1 u 1, 2 x = 1,..., N ( 2 ) u u +1 2u + u 1 2 ( x) 2
13 Fnte dfferences Ths s the smplest and oldest dscretzaton technque Dervaton from the PDE form of the governng equaton The dscrete unknowns are soluton values at the grd ponts The approxmaton of partal dervatves n terms of these values yelds one algebrac equaton per grd pont The use of a (block-)structured mesh s usually requred
14 Fnte volumes Integral conservaton law d u dx + f nds = q dx dt V S V Dscrete soluton values u (t) = 1 V V u(x, t) dx u(x, t) V n Vj xj V n x n Vj
15 Fnte volumes Dervaton from the ntegral form of a conservaton law The dscrete unknowns are cell averages or soluton values at the centers of control volumes (mesh cells or dual mesh cells) Volume and surface ntegrals that appear n the conservaton law are approxmated usng numercal quadrature rules Functon values at the quadrature ponts are obtaned usng nterpolaton technques (polynomal fttng) The computatonal mesh can be structured or unstructured
16 Fnte elements Varatonal problem ( w u ) w f wq dx + wf nds = 0 t Γ Ω Dscrete soluton values u h (x, t) = j u j (t)ϕ j (x), u (t) u(x, t) Bass and test functons ϕ (x ) = 1, ϕ (x j ) = 0, j
17 Fnte elements Dervaton from a varatonal form of a PDE model The coeffcents of the bass functons ϕ typcally represent approxmate functon values at nterpolaton ponts Insde each cell, the approxmate soluton u h s a polynomal Substtuton of u h u nto the varatonal formulaton wth w {ϕ } yelds one algebrac equaton per mesh node The computatonal mesh can be structured or unstructured
18 Tme dscretzaton Dscrete tme levels 0 = t 0 < t 1 < < t M = T, t n = n t Approxmaton of the tme dervatve u t un+1 u n, u n u (t n ), u 0 = u 0 (x ) t Lnear algebrac systems Au n+1 = b(u n ), n = 0, 1,..., M 1
19 Lnear solvers Explct methods: A s a dagonal matrx; the equatons of the lnear system are decoupled and can be solved n a segregated manner Implct methods: A s a sparse matrx; the equatons of the lnear system are coupled and must be solved usng numercal methods Iteratve solvers that explot sparsty (and structure, f any) of the coeffcent matrx are usually more effcent than drect methods
20 Choce of numercal tools There are many possbltes to dscretze a gven problem usng fnte dfference, fnte volume or fnte element methods The choce of approxmatons nfluences the accuracy of numercal solutons, programmng effort, and computatonal cost A compromse between smplcty, ease of mplementaton, accuracy and computatonal effcency has to be made Numercal algorthms must be stable to produce reasonable results
21 Desgn crtera Consstency: local dscretzaton errors should be proportonal to postve powers of the mesh sze h and tme step t Stablty: roundng and teraton errors that appear n the process of numercal soluton should not be magnfed Convergence: numercal solutons should become exact n the lmt of vanshng mesh szes and tme steps
22 Desgn crtera Conservaton: numercal solutons should satsfy a dscrete form of the ntegral conservaton law (local or global) Boundedness: dscrete maxmum prncples should hold f the exact soluton satsfes a maxmum prncple Accuracy: at least second-order convergence for smooth data
23 Fnte dfferences n 1D Let u : [a, b] R be a dfferentable functon of x A unform mesh s generated usng a subdvson of the doman Ω = (a, b) nto N subntervals of equal length x x = a + x, x = b a N The dscrete unknowns are gven by u u(x ), = 0, 1,..., N
24 Frst dervatve The frst dervatve of u(x) at the mesh pont x s defned by u (x u(x + x) u(x ) ) = lm x 0 x u(x ) u(x x) = lm x 0 x u(x + x) u(x x) = lm x 0 2 x and can be approxmated usng a fnte (but small) spacng x
25 Fnte dfferences The frst dervatve of u(x) at x can be approxmated by forward dfference backward dfference central dfference ( ) u u +1 u x ( ) u u u 1 x ( ) u u +1 u 1 2 x The qualty of these approxmatons depends on u and x
26 Geometrc nterpretaton The frst dervatve of u at the mesh pont x s the slope of the tangent to the curve u(x) at that mesh pont It can be approxmated by the slope of a straght lne passng through two nearby ponts on the curve Ù ÒØÖ Ð ÓÖÛ Ö Û Ö Ü Ü Ü Ø Ü ½ Ü Ü ½ Ü
27 Dervaton from Taylor seres The Taylor seres expanson of u about x s gven by u(x) = ( ) u u(x ) + (x x ) + (x x ) 2 ( 2 ) u (x x ) 3 ( 3 ) u (x x ) n ( n ) u n! n +... Usng ths expanson at the neghbor ponts, we fnd that u(x ±1 ) = u(x ) ± x ( u ) + ( x)2 2 ( 2 u ± ) ( x)3 2 6 ( 3 u 3 ) +...
28 Truncaton errors Forward dfference ( ) u = u +1 u x Backward dfference ( ) u = u u 1 x Central dfference ( ) u x 2 + x 2 = u +1 u 1 2 x ( 2 ) u 2 ( x)2 6 ( 2 ) u 2 ( x)2 6 ( x)2 6 ( 3 ) u ( 3 ) u ( 3 ) u
29 Truncaton errors The local truncaton error ɛ of a fnte dfference approxmaton s the neglected remander of the Taylor seres ɛ = α p+1 ( x) p + α p+2 ( x) p The term proportonal to ( x) p s the leadng truncaton error whch determnes the order of consstency ɛ = O( x) p The order of a numercal approxmaton ndcates how fast the error s reduced when the mesh s refned It does not, however, provde any nformaton about the accuracy of the approxmaton on a gven mesh
30 Second dervatve Taylor seres expanson about x u(x +1 ) = u(x )+ x u(x 1 ) = u(x ) x ( ) u + ( x)2 2 ) ( u + ( x)2 2 ( 2 ) u 2 + ( x)3 6 ) ( 2 u 2 ( x)3 6 ( 3 ) u ) ( 3 u Central dfference approxmaton ( 2 ) u 2 = u +1 2u + u 1 ( x) 2 + O( x) 2
31 Second dervatve Approxmaton n terms of frst-order dvded dfferences 2 u 2 = ( ) ( u 2 ) ( u ) u +1/2 2 ( ) u x 1/2 Central dfference approxmaton at the ponts x ±1/2 ( 2 ) u 2 u +1 u x u u 1 x x = u +1 2u + u 1 ( x) 2
32 Dffusve fluxes Approxmaton n terms of frst-order dvded dfferences ( f x, u ) = a(x) u ( ) f f +1/2 f 1/2 x Central dfference approxmaton at the ponts x ±1/2 ( ) f a +1/2 u+1 u x a 1/2 u u 1 x x = a +1/2u +1 (a +1/2 + a 1/2 )u + a 1/2 u 1 ( x) 2
33 One-sded approxmatons No left or rght neghbors at the boundary ponts x 0 = a, x N = b Ü ¼ Ü ½ Ü ¾ Frst-order forward dfference ( ) u = u 1 u 0 + O( x) 0 x How can we construct hgher-order one-sded approxmatons?
34 Polynomal fttng Taylor expanson about the boundary pont x = 0 ( ) ( u u(x) = u(0) + x + x2 2 ) ( u x3 3 ) u Approxmaton by a polynomal and dfferentaton u(x) a + bx + cx 2, u 0 = a u 1 = a + b x + c( x) 2 u 2 = a + 2b x + 4c( x) 2 u b + 2cx, ( ) u b 0 c( x) 2 = u 1 u 0 b x b = 3u0+4u1 u2 2 x
35 Error analyss Consder a one-sded dfference approxmaton of the form ( ) u αu + βu +1 + γu +2, α, β, γ R x To prove consstency and derve the local truncaton error, substtute the Taylor seres expansons u +1 = u + x ( ( u ) + ( x)2 2 u 2 + ) ( x)3 2 6 u +2 = u + 2 x ( u ) + (2 x)2 2 ( ) 2 u 2 + (2 x) 3 6 ( 3 u 3 ) +... ( 3 u 3 ) +...
36 Error analyss Substtuton of the Taylor seres expansons yelds αu + βu +1 + γu +2 x = α + β + γ u + (β + 2γ) x + x (β + 4γ) 2 The approxmaton s second-order accurate f ( ) u ( 2 ) u 2 + O( x) 2 α + β + γ = 0, β + 2γ = 1, β + 4γ = 0 It follows that ( u ) = 3u+4u+1 u+2 2 x + O( x) 2
37 Error analyss Consder a one-sded dfference approxmaton of the form ( 2 ) u 2 αu + βu +1 + γu +2 ( x) 2, α, β, γ R To prove consstency and derve the local truncaton error, substtute the Taylor seres expansons u +1 = u + x ( ( u ) + ( x)2 2 u 2 + ) ( x)3 2 6 u +2 = u + 2 x ( u ) + (2 x)2 2 ( 2 u + ) (2 x)3 2 6 ( 3 u 3 ) +... ( 3 u 3 ) +...
38 Error analyss Substtuton of the Taylor seres expansons yelds αu + βu +1 + γu +2 ( x) 2 = α + β + γ ( x) 2 u + β + 2γ ( ) u x + β + 4γ ( 2 ) u O( x) The approxmaton s frst-order accurate f α + β + γ = 0, β + 2γ = 0, β + 4γ = 2 It follows that ( 2 u = ) u 2u+1+u+2 2 ( x) + O( x) 2
39 Hgher-order approxmatons Thrd-order forward dfference / 1st dervatve ( ) u = u u +1 3u 2u 1 6 x + O( x) 3 Thrd-order backward dfference / 1st dervatve ( ) u = 2u u 6u 1 + u 2 + O( x) 3 6 x
40 Hgher-order approxmatons Fourth-order central dfference / 1st dervatve ( ) u = u u +1 8u 1 + u 2 + O( x) 4 12 x Fourth-order central dfference / 2nd dervatve ( 2 ) u 2 = u u +1 30u + 16u 1 u 2 12( x) 2 + O( x) 4
41 Propertes To acheve hgher order accuracy, we need more grd ponts One-sded hgh-order approxmatons must be used at boundary ponts; the mplementaton becomes more nvolved The larger number of unknowns per equaton requres more memory and ncreases the cost of solvng lnear systems Desred accuracy can be attaned on coarser meshes Second-order approxmatons are usually optmal for CFD
42 Posson equaton n 1D Drchlet problem { 2 u 2 = f n Ω = (0, 1) u(0) = 0, u(1) = 0 Physcal nterpretaton: u(x) s the dsplacement of a suspenson brdge, f(x) s the load at pont x Ω Maxmum prncple: f(x) 0, x u(x) 0, x Dscretzaton: x = x, where x = 1 N u u(x ), f = f(x )
43 Posson equaton n 1D Approxmaton by central dfferences { u 1 2u+u+1 ( x) = f 2, = 1,..., N 1 u 0 = u N = 0 (boundary condtons) Lnear algebrac system = 1 = 2 = 3 = N 1 u0 2u1+u2 ( x) 2 = f 1 u1 2u2+u3 ( x) 2 = f 2 u2 2u3+u4 ( x) = f u N 2 2u N 1 +u N ( x) 2 = f N 1
44 Posson equaton n 1D The matrx form of the lnear system s gven by Au = f, A R (N 1) (N 1), u, f R N 1 where A s trdagonal, symmetrc postve-defnte 2 1 A = ( x) The dscrete problem s well-posed (the soluton u = A 1 f exsts and s unque snce the matrx A s nvertble) There are effcent drect solvers for trdagonal matrces
45 Thomas algorthm Trdagonal matrx algorthm (TDMA) a x 1 + b x + c x +1 = d, = 1,..., n a 1 = 0, c n = 0 Matrx form of the lnear system b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3... a n b n x 1 x 2 x 3 x n = d 1 d 2 d 3 d n
46 Thomas algorthm Fast Gaussan elmnaton for trdagonal systems: Forward sweep for k = 2,..., n do c b k = b k a k 1 k b k 1 d d k = d k a k 1 k b k 1 end k-loop Backward sweep x n = dn b n for k = n 1,..., 1 do x k = d k c k x k+1 b k end k-loop Computatonal cost: just O(n) arthmetc operatons nstead of O(n 3 )
An Accurate Evaluation of Integrals in Convex and Non convex Polygonal Domain by Twelve Node Quadrilateral Finite Element Method
 Internatonal Journal of Computatonal and Appled Mathematcs. ISSN 89-4966 Volume, Number (07), pp. 33-4 Research Inda Publcatons http://www.rpublcaton.com An Accurate Evaluaton of Integrals n Convex and
Internatonal Journal of Computatonal and Appled Mathematcs. ISSN 89-4966 Volume, Number (07), pp. 33-4 Research Inda Publcatons http://www.rpublcaton.com An Accurate Evaluaton of Integrals n Convex and
Mathematics 256 a course in differential equations for engineering students
 Mathematcs 56 a course n dfferental equatons for engneerng students Chapter 5. More effcent methods of numercal soluton Euler s method s qute neffcent. Because the error s essentally proportonal to the
Mathematcs 56 a course n dfferental equatons for engneerng students Chapter 5. More effcent methods of numercal soluton Euler s method s qute neffcent. Because the error s essentally proportonal to the
Outline. Midterm Review. Declaring Variables. Main Variable Data Types. Symbolic Constants. Arithmetic Operators. Midterm Review March 24, 2014
 Mdterm Revew March 4, 4 Mdterm Revew Larry Caretto Mechancal Engneerng 9 Numercal Analyss of Engneerng Systems March 4, 4 Outlne VBA and MATLAB codng Varable types Control structures (Loopng and Choce)
Mdterm Revew March 4, 4 Mdterm Revew Larry Caretto Mechancal Engneerng 9 Numercal Analyss of Engneerng Systems March 4, 4 Outlne VBA and MATLAB codng Varable types Control structures (Loopng and Choce)
2x x l. Module 3: Element Properties Lecture 4: Lagrange and Serendipity Elements
 Module 3: Element Propertes Lecture : Lagrange and Serendpty Elements 5 In last lecture note, the nterpolaton functons are derved on the bass of assumed polynomal from Pascal s trangle for the fled varable.
Module 3: Element Propertes Lecture : Lagrange and Serendpty Elements 5 In last lecture note, the nterpolaton functons are derved on the bass of assumed polynomal from Pascal s trangle for the fled varable.
S1 Note. Basis functions.
 S1 Note. Bass functons. Contents Types of bass functons...1 The Fourer bass...2 B-splne bass...3 Power and type I error rates wth dfferent numbers of bass functons...4 Table S1. Smulaton results of type
S1 Note. Bass functons. Contents Types of bass functons...1 The Fourer bass...2 B-splne bass...3 Power and type I error rates wth dfferent numbers of bass functons...4 Table S1. Smulaton results of type
Parallel matrix-vector multiplication
 Appendx A Parallel matrx-vector multplcaton The reduced transton matrx of the three-dmensonal cage model for gel electrophoress, descrbed n secton 3.2, becomes excessvely large for polymer lengths more
Appendx A Parallel matrx-vector multplcaton The reduced transton matrx of the three-dmensonal cage model for gel electrophoress, descrbed n secton 3.2, becomes excessvely large for polymer lengths more
Multiblock method for database generation in finite element programs
 Proc. of the 9th WSEAS Int. Conf. on Mathematcal Methods and Computatonal Technques n Electrcal Engneerng, Arcachon, October 13-15, 2007 53 Multblock method for database generaton n fnte element programs
Proc. of the 9th WSEAS Int. Conf. on Mathematcal Methods and Computatonal Technques n Electrcal Engneerng, Arcachon, October 13-15, 2007 53 Multblock method for database generaton n fnte element programs
Radial Basis Functions
 Radal Bass Functons Mesh Reconstructon Input: pont cloud Output: water-tght manfold mesh Explct Connectvty estmaton Implct Sgned dstance functon estmaton Image from: Reconstructon and Representaton of
Radal Bass Functons Mesh Reconstructon Input: pont cloud Output: water-tght manfold mesh Explct Connectvty estmaton Implct Sgned dstance functon estmaton Image from: Reconstructon and Representaton of
Structured Grid Generation Via Constraint on Displacement of Internal Nodes
 Internatonal Journal of Basc & Appled Scences IJBAS-IJENS Vol: 11 No: 4 79 Structured Grd Generaton Va Constrant on Dsplacement of Internal Nodes Al Ashrafzadeh, Razeh Jalalabad Abstract Structured grd
Internatonal Journal of Basc & Appled Scences IJBAS-IJENS Vol: 11 No: 4 79 Structured Grd Generaton Va Constrant on Dsplacement of Internal Nodes Al Ashrafzadeh, Razeh Jalalabad Abstract Structured grd
Hermite Splines in Lie Groups as Products of Geodesics
 Hermte Splnes n Le Groups as Products of Geodescs Ethan Eade Updated May 28, 2017 1 Introducton 1.1 Goal Ths document defnes a curve n the Le group G parametrzed by tme and by structural parameters n the
Hermte Splnes n Le Groups as Products of Geodescs Ethan Eade Updated May 28, 2017 1 Introducton 1.1 Goal Ths document defnes a curve n the Le group G parametrzed by tme and by structural parameters n the
Image Representation & Visualization Basic Imaging Algorithms Shape Representation and Analysis. outline
 mage Vsualzaton mage Vsualzaton mage Representaton & Vsualzaton Basc magng Algorthms Shape Representaton and Analyss outlne mage Representaton & Vsualzaton Basc magng Algorthms Shape Representaton and
mage Vsualzaton mage Vsualzaton mage Representaton & Vsualzaton Basc magng Algorthms Shape Representaton and Analyss outlne mage Representaton & Vsualzaton Basc magng Algorthms Shape Representaton and
 Chapter 6 Programmng the fnte element method Inow turn to the man subject of ths book: The mplementaton of the fnte element algorthm n computer programs. In order to make my dscusson as straghtforward
Chapter 6 Programmng the fnte element method Inow turn to the man subject of ths book: The mplementaton of the fnte element algorthm n computer programs. In order to make my dscusson as straghtforward
An Application of the Dulmage-Mendelsohn Decomposition to Sparse Null Space Bases of Full Row Rank Matrices
 Internatonal Mathematcal Forum, Vol 7, 2012, no 52, 2549-2554 An Applcaton of the Dulmage-Mendelsohn Decomposton to Sparse Null Space Bases of Full Row Rank Matrces Mostafa Khorramzadeh Department of Mathematcal
Internatonal Mathematcal Forum, Vol 7, 2012, no 52, 2549-2554 An Applcaton of the Dulmage-Mendelsohn Decomposton to Sparse Null Space Bases of Full Row Rank Matrces Mostafa Khorramzadeh Department of Mathematcal
6.854 Advanced Algorithms Petar Maymounkov Problem Set 11 (November 23, 2005) With: Benjamin Rossman, Oren Weimann, and Pouya Kheradpour
 6.854 Advanced Algorthms Petar Maymounkov Problem Set 11 (November 23, 2005) Wth: Benjamn Rossman, Oren Wemann, and Pouya Kheradpour Problem 1. We reduce vertex cover to MAX-SAT wth weghts, such that the
6.854 Advanced Algorthms Petar Maymounkov Problem Set 11 (November 23, 2005) Wth: Benjamn Rossman, Oren Wemann, and Pouya Kheradpour Problem 1. We reduce vertex cover to MAX-SAT wth weghts, such that the
Wavefront Reconstructor
 A Dstrbuted Smplex B-Splne Based Wavefront Reconstructor Coen de Vsser and Mchel Verhaegen 14-12-201212 2012 Delft Unversty of Technology Contents Introducton Wavefront reconstructon usng Smplex B-Splnes
A Dstrbuted Smplex B-Splne Based Wavefront Reconstructor Coen de Vsser and Mchel Verhaegen 14-12-201212 2012 Delft Unversty of Technology Contents Introducton Wavefront reconstructon usng Smplex B-Splnes
A 2D pre-processor for finite element programs based on a knowledge-based system
 5th WSEAS / IASME Internatonal Conference on ENGINEERING EDUCATION (EE'08), Heraklon, Greece, July 22-24, 2008 A 2D pre-processor for fnte element programs based on a knowledge-based system DANIELA CÂRSTEA
5th WSEAS / IASME Internatonal Conference on ENGINEERING EDUCATION (EE'08), Heraklon, Greece, July 22-24, 2008 A 2D pre-processor for fnte element programs based on a knowledge-based system DANIELA CÂRSTEA
Quality Improvement Algorithm for Tetrahedral Mesh Based on Optimal Delaunay Triangulation
 Intellgent Informaton Management, 013, 5, 191-195 Publshed Onlne November 013 (http://www.scrp.org/journal/m) http://dx.do.org/10.36/m.013.5601 Qualty Improvement Algorthm for Tetrahedral Mesh Based on
Intellgent Informaton Management, 013, 5, 191-195 Publshed Onlne November 013 (http://www.scrp.org/journal/m) http://dx.do.org/10.36/m.013.5601 Qualty Improvement Algorthm for Tetrahedral Mesh Based on
Using Radial Basis Functions to Solve Geodesics Equations for Body Measurements *
 7659, England, UK Journal of Informaton and Computng Scence Vol. 2, No. 2, 2007, pp. 119-126 Usng Radal Bass Functons to Solve Geodescs Equatons for Body Measurements * R. Ng 1+, G.T.Y. Pong 2 and M. Wong
7659, England, UK Journal of Informaton and Computng Scence Vol. 2, No. 2, 2007, pp. 119-126 Usng Radal Bass Functons to Solve Geodescs Equatons for Body Measurements * R. Ng 1+, G.T.Y. Pong 2 and M. Wong
RECENT research on structured mesh flow solver for aerodynamic problems shows that for practical levels of
 A Hgh-Order Accurate Unstructured GMRES Algorthm for Invscd Compressble Flows A. ejat * and C. Ollver-Gooch Department of Mechancal Engneerng, The Unversty of Brtsh Columba, 054-650 Appled Scence Lane,
A Hgh-Order Accurate Unstructured GMRES Algorthm for Invscd Compressble Flows A. ejat * and C. Ollver-Gooch Department of Mechancal Engneerng, The Unversty of Brtsh Columba, 054-650 Appled Scence Lane,
The Greedy Method. Outline and Reading. Change Money Problem. Greedy Algorithms. Applications of the Greedy Strategy. The Greedy Method Technique
 //00 :0 AM Outlne and Readng The Greedy Method The Greedy Method Technque (secton.) Fractonal Knapsack Problem (secton..) Task Schedulng (secton..) Mnmum Spannng Trees (secton.) Change Money Problem Greedy
//00 :0 AM Outlne and Readng The Greedy Method The Greedy Method Technque (secton.) Fractonal Knapsack Problem (secton..) Task Schedulng (secton..) Mnmum Spannng Trees (secton.) Change Money Problem Greedy
Parallel Numerics. 1 Preconditioning & Iterative Solvers (From 2016)
 Technsche Unverstät München WSe 6/7 Insttut für Informatk Prof. Dr. Thomas Huckle Dpl.-Math. Benjamn Uekermann Parallel Numercs Exercse : Prevous Exam Questons Precondtonng & Iteratve Solvers (From 6)
Technsche Unverstät München WSe 6/7 Insttut für Informatk Prof. Dr. Thomas Huckle Dpl.-Math. Benjamn Uekermann Parallel Numercs Exercse : Prevous Exam Questons Precondtonng & Iteratve Solvers (From 6)
Exercises (Part 4) Introduction to R UCLA/CCPR. John Fox, February 2005
 Exercses (Part 4) Introducton to R UCLA/CCPR John Fox, February 2005 1. A challengng problem: Iterated weghted least squares (IWLS) s a standard method of fttng generalzed lnear models to data. As descrbed
Exercses (Part 4) Introducton to R UCLA/CCPR John Fox, February 2005 1. A challengng problem: Iterated weghted least squares (IWLS) s a standard method of fttng generalzed lnear models to data. As descrbed
Universität Stuttgart Direkte numerische Simulation von Strömungslärm in komplexen Geometrien
 Unverstät Stuttgart Drekte numersche Smulaton von Strömungslärm n komplexen Geometren Claus-Deter Munz Gregor Gassner, Floran Hndenlang, Andreas Brkefeld, Andrea Beck, Marc Staudenmaer, Thomas Bolemann,
Unverstät Stuttgart Drekte numersche Smulaton von Strömungslärm n komplexen Geometren Claus-Deter Munz Gregor Gassner, Floran Hndenlang, Andreas Brkefeld, Andrea Beck, Marc Staudenmaer, Thomas Bolemann,
TECHNICAL TRANSACTIONS 7/2017 CZASOPISMO TECHNICZNE 7/2017 MECHANICS
 TECHCAL TRASACTOS 7/207 CZASOPSMO TECHCZE 7/207 MECHACS DO: 0.4467/2353737XCT.7.5.6656 Artur Krowa (rowa@mech.p.edu.pl) nsttute of Computer Scence, Faculty of Mechancal Engneerng, Cracow Unversty of Technology
TECHCAL TRASACTOS 7/207 CZASOPSMO TECHCZE 7/207 MECHACS DO: 0.4467/2353737XCT.7.5.6656 Artur Krowa (rowa@mech.p.edu.pl) nsttute of Computer Scence, Faculty of Mechancal Engneerng, Cracow Unversty of Technology
Adaptive Fairing of Surface Meshes by Geometric Diffusion
 Adaptve Farng of Surface Meshes by Geometrc Dffuson Chandrajt L. Bajaj Department of Computer Scences, Unversty of Texas, Austn, TX 78712 Emal: bajaj@cs.utexas.edu Guolang Xu State Key Lab. of Scentfc
Adaptve Farng of Surface Meshes by Geometrc Dffuson Chandrajt L. Bajaj Department of Computer Scences, Unversty of Texas, Austn, TX 78712 Emal: bajaj@cs.utexas.edu Guolang Xu State Key Lab. of Scentfc
Parallelism for Nested Loops with Non-uniform and Flow Dependences
 Parallelsm for Nested Loops wth Non-unform and Flow Dependences Sam-Jn Jeong Dept. of Informaton & Communcaton Engneerng, Cheonan Unversty, 5, Anseo-dong, Cheonan, Chungnam, 330-80, Korea. seong@cheonan.ac.kr
Parallelsm for Nested Loops wth Non-unform and Flow Dependences Sam-Jn Jeong Dept. of Informaton & Communcaton Engneerng, Cheonan Unversty, 5, Anseo-dong, Cheonan, Chungnam, 330-80, Korea. seong@cheonan.ac.kr
LECTURE : MANIFOLD LEARNING
 LECTURE : MANIFOLD LEARNING Rta Osadchy Some sldes are due to L.Saul, V. C. Raykar, N. Verma Topcs PCA MDS IsoMap LLE EgenMaps Done! Dmensonalty Reducton Data representaton Inputs are real-valued vectors
LECTURE : MANIFOLD LEARNING Rta Osadchy Some sldes are due to L.Saul, V. C. Raykar, N. Verma Topcs PCA MDS IsoMap LLE EgenMaps Done! Dmensonalty Reducton Data representaton Inputs are real-valued vectors
AMath 483/583 Lecture 21 May 13, Notes: Notes: Jacobi iteration. Notes: Jacobi with OpenMP coarse grain
 AMath 483/583 Lecture 21 May 13, 2011 Today: OpenMP and MPI versons of Jacob teraton Gauss-Sedel and SOR teratve methods Next week: More MPI Debuggng and totalvew GPU computng Read: Class notes and references
AMath 483/583 Lecture 21 May 13, 2011 Today: OpenMP and MPI versons of Jacob teraton Gauss-Sedel and SOR teratve methods Next week: More MPI Debuggng and totalvew GPU computng Read: Class notes and references
Reading. 14. Subdivision curves. Recommended:
 eadng ecommended: Stollntz, Deose, and Salesn. Wavelets for Computer Graphcs: heory and Applcatons, 996, secton 6.-6., A.5. 4. Subdvson curves Note: there s an error n Stollntz, et al., secton A.5. Equaton
eadng ecommended: Stollntz, Deose, and Salesn. Wavelets for Computer Graphcs: heory and Applcatons, 996, secton 6.-6., A.5. 4. Subdvson curves Note: there s an error n Stollntz, et al., secton A.5. Equaton
Programming in Fortran 90 : 2017/2018
 Programmng n Fortran 90 : 2017/2018 Programmng n Fortran 90 : 2017/2018 Exercse 1 : Evaluaton of functon dependng on nput Wrte a program who evaluate the functon f (x,y) for any two user specfed values
Programmng n Fortran 90 : 2017/2018 Programmng n Fortran 90 : 2017/2018 Exercse 1 : Evaluaton of functon dependng on nput Wrte a program who evaluate the functon f (x,y) for any two user specfed values
Electrical analysis of light-weight, triangular weave reflector antennas
 Electrcal analyss of lght-weght, trangular weave reflector antennas Knud Pontoppdan TICRA Laederstraede 34 DK-121 Copenhagen K Denmark Emal: kp@tcra.com INTRODUCTION The new lght-weght reflector antenna
Electrcal analyss of lght-weght, trangular weave reflector antennas Knud Pontoppdan TICRA Laederstraede 34 DK-121 Copenhagen K Denmark Emal: kp@tcra.com INTRODUCTION The new lght-weght reflector antenna
Review of approximation techniques
 CHAPTER 2 Revew of appromaton technques 2. Introducton Optmzaton problems n engneerng desgn are characterzed by the followng assocated features: the objectve functon and constrants are mplct functons evaluated
CHAPTER 2 Revew of appromaton technques 2. Introducton Optmzaton problems n engneerng desgn are characterzed by the followng assocated features: the objectve functon and constrants are mplct functons evaluated
A MOVING MESH APPROACH FOR SIMULATION BUDGET ALLOCATION ON CONTINUOUS DOMAINS
 Proceedngs of the Wnter Smulaton Conference M E Kuhl, N M Steger, F B Armstrong, and J A Jones, eds A MOVING MESH APPROACH FOR SIMULATION BUDGET ALLOCATION ON CONTINUOUS DOMAINS Mark W Brantley Chun-Hung
Proceedngs of the Wnter Smulaton Conference M E Kuhl, N M Steger, F B Armstrong, and J A Jones, eds A MOVING MESH APPROACH FOR SIMULATION BUDGET ALLOCATION ON CONTINUOUS DOMAINS Mark W Brantley Chun-Hung
NUMERICAL SOLVING OPTIMAL CONTROL PROBLEMS BY THE METHOD OF VARIATIONS
 ARPN Journal of Engneerng and Appled Scences 006-017 Asan Research Publshng Network (ARPN). All rghts reserved. NUMERICAL SOLVING OPTIMAL CONTROL PROBLEMS BY THE METHOD OF VARIATIONS Igor Grgoryev, Svetlana
ARPN Journal of Engneerng and Appled Scences 006-017 Asan Research Publshng Network (ARPN). All rghts reserved. NUMERICAL SOLVING OPTIMAL CONTROL PROBLEMS BY THE METHOD OF VARIATIONS Igor Grgoryev, Svetlana
NUMERICAL ANALYSIS OF A COUPLED FINITE-INFINITE ELEMENT METHOD FOR EXTERIOR HELMHOLTZ PROBLEMS
 Journal of Computatonal Acoustcs, Vol. 14, No. 1 (2006) 21 43 c IMACS NUMERICAL ANALYSIS OF A COUPLED FINITE-INFINITE ELEMENT METHOD FOR EXTERIOR HELMHOLTZ PROBLEMS JEAN-CHRISTOPHE AUTRIQUE LMS Internatonal,
Journal of Computatonal Acoustcs, Vol. 14, No. 1 (2006) 21 43 c IMACS NUMERICAL ANALYSIS OF A COUPLED FINITE-INFINITE ELEMENT METHOD FOR EXTERIOR HELMHOLTZ PROBLEMS JEAN-CHRISTOPHE AUTRIQUE LMS Internatonal,
Preconditioning Parallel Sparse Iterative Solvers for Circuit Simulation
 Precondtonng Parallel Sparse Iteratve Solvers for Crcut Smulaton A. Basermann, U. Jaekel, and K. Hachya 1 Introducton One mportant mathematcal problem n smulaton of large electrcal crcuts s the soluton
Precondtonng Parallel Sparse Iteratve Solvers for Crcut Smulaton A. Basermann, U. Jaekel, and K. Hachya 1 Introducton One mportant mathematcal problem n smulaton of large electrcal crcuts s the soluton
Keywords: Additive Correction Multigrid (ACM), Agglomeration scheme, Multigrid cycles, Element- based Finite Volume Method, Unstructured grids.
 Suse Crstne Keller suse@snmec.ufsc.br Jonas Cordazzo jonas@snmec.ufsc.br THE ADDITIVE CORRECTIO MULTIGRID METHOD FOR USTRUCTURED GRIDS Pedro H. Hnckel phhnckel@snmec.ufsc.br Clovs R. Malska malska@snmec.ufsc.br
Suse Crstne Keller suse@snmec.ufsc.br Jonas Cordazzo jonas@snmec.ufsc.br THE ADDITIVE CORRECTIO MULTIGRID METHOD FOR USTRUCTURED GRIDS Pedro H. Hnckel phhnckel@snmec.ufsc.br Clovs R. Malska malska@snmec.ufsc.br
Harmonic Coordinates for Character Articulation PIXAR
 Harmonc Coordnates for Character Artculaton PIXAR Pushkar Josh Mark Meyer Tony DeRose Bran Green Tom Sanock We have a complex source mesh nsde of a smpler cage mesh We want vertex deformatons appled to
Harmonc Coordnates for Character Artculaton PIXAR Pushkar Josh Mark Meyer Tony DeRose Bran Green Tom Sanock We have a complex source mesh nsde of a smpler cage mesh We want vertex deformatons appled to
Simulation Based Analysis of FAST TCP using OMNET++
 Smulaton Based Analyss of FAST TCP usng OMNET++ Umar ul Hassan 04030038@lums.edu.pk Md Term Report CS678 Topcs n Internet Research Sprng, 2006 Introducton Internet traffc s doublng roughly every 3 months
Smulaton Based Analyss of FAST TCP usng OMNET++ Umar ul Hassan 04030038@lums.edu.pk Md Term Report CS678 Topcs n Internet Research Sprng, 2006 Introducton Internet traffc s doublng roughly every 3 months
Fair Triangle Mesh Generation with Discrete Elastica
 Far Trangle Mesh Generaton wth Dscrete Elastca Shn Yoshzawa, and Alexander G. Belyaev, Computer Graphcs Group, Max-Planck-Insttut für Informatk, 66123 Saarbrücken, Germany Phone: [+49](681)9325-414 Fax:
Far Trangle Mesh Generaton wth Dscrete Elastca Shn Yoshzawa, and Alexander G. Belyaev, Computer Graphcs Group, Max-Planck-Insttut für Informatk, 66123 Saarbrücken, Germany Phone: [+49](681)9325-414 Fax:
Support Vector Machines
 Support Vector Machnes Decson surface s a hyperplane (lne n 2D) n feature space (smlar to the Perceptron) Arguably, the most mportant recent dscovery n machne learnng In a nutshell: map the data to a predetermned
Support Vector Machnes Decson surface s a hyperplane (lne n 2D) n feature space (smlar to the Perceptron) Arguably, the most mportant recent dscovery n machne learnng In a nutshell: map the data to a predetermned
Smoothing Spline ANOVA for variable screening
 Smoothng Splne ANOVA for varable screenng a useful tool for metamodels tranng and mult-objectve optmzaton L. Rcco, E. Rgon, A. Turco Outlne RSM Introducton Possble couplng Test case MOO MOO wth Game Theory
Smoothng Splne ANOVA for varable screenng a useful tool for metamodels tranng and mult-objectve optmzaton L. Rcco, E. Rgon, A. Turco Outlne RSM Introducton Possble couplng Test case MOO MOO wth Game Theory
arxiv: v3 [cs.na] 18 Mar 2015
![arxiv: v3 [cs.na] 18 Mar 2015 arxiv: v3 [cs.na] 18 Mar 2015](/thumbs/90/101415471.jpg) A Fast Block Low-Rank Dense Solver wth Applcatons to Fnte-Element Matrces AmrHossen Amnfar a,1,, Svaram Ambkasaran b,, Erc Darve c,1 a 496 Lomta Mall, Room 14, Stanford, CA, 9435 b Warren Weaver Hall,
A Fast Block Low-Rank Dense Solver wth Applcatons to Fnte-Element Matrces AmrHossen Amnfar a,1,, Svaram Ambkasaran b,, Erc Darve c,1 a 496 Lomta Mall, Room 14, Stanford, CA, 9435 b Warren Weaver Hall,
Design for Reliability: Case Studies in Manufacturing Process Synthesis
 Desgn for Relablty: Case Studes n Manufacturng Process Synthess Y. Lawrence Yao*, and Chao Lu Department of Mechancal Engneerng, Columba Unversty, Mudd Bldg., MC 473, New York, NY 7, USA * Correspondng
Desgn for Relablty: Case Studes n Manufacturng Process Synthess Y. Lawrence Yao*, and Chao Lu Department of Mechancal Engneerng, Columba Unversty, Mudd Bldg., MC 473, New York, NY 7, USA * Correspondng
An Improved Isogeometric Analysis Using the Lagrange Multiplier Method
 An Improved Isogeometrc Analyss Usng the Lagrange Mltpler Method N. Valzadeh 1, S. Sh. Ghorash 2, S. Mohammad 3, S. Shojaee 1, H. Ghasemzadeh 2 1 Department of Cvl Engneerng, Unversty of Kerman, Kerman,
An Improved Isogeometrc Analyss Usng the Lagrange Mltpler Method N. Valzadeh 1, S. Sh. Ghorash 2, S. Mohammad 3, S. Shojaee 1, H. Ghasemzadeh 2 1 Department of Cvl Engneerng, Unversty of Kerman, Kerman,
Accounting for the Use of Different Length Scale Factors in x, y and z Directions
 1 Accountng for the Use of Dfferent Length Scale Factors n x, y and z Drectons Taha Soch (taha.soch@kcl.ac.uk) Imagng Scences & Bomedcal Engneerng, Kng s College London, The Rayne Insttute, St Thomas Hosptal,
1 Accountng for the Use of Dfferent Length Scale Factors n x, y and z Drectons Taha Soch (taha.soch@kcl.ac.uk) Imagng Scences & Bomedcal Engneerng, Kng s College London, The Rayne Insttute, St Thomas Hosptal,
A gradient smoothing method (GSM) for fluid dynamics problems
 INTERNATIONAL JOURNAL FOR NUMERICAL METHODS IN FLUIDS Int. J. Numer. Meth. Fluds 2008; 58:1101 1133 Publshed onlne 27 March 2008 n Wley InterScence (www.nterscence.wley.com)..1788 A gradent smoothng method
INTERNATIONAL JOURNAL FOR NUMERICAL METHODS IN FLUIDS Int. J. Numer. Meth. Fluds 2008; 58:1101 1133 Publshed onlne 27 March 2008 n Wley InterScence (www.nterscence.wley.com)..1788 A gradent smoothng method
High resolution 3D Tau-p transform by matching pursuit Weiping Cao* and Warren S. Ross, Shearwater GeoServices
 Hgh resoluton 3D Tau-p transform by matchng pursut Wepng Cao* and Warren S. Ross, Shearwater GeoServces Summary The 3D Tau-p transform s of vtal sgnfcance for processng sesmc data acqured wth modern wde
Hgh resoluton 3D Tau-p transform by matchng pursut Wepng Cao* and Warren S. Ross, Shearwater GeoServces Summary The 3D Tau-p transform s of vtal sgnfcance for processng sesmc data acqured wth modern wde
(e.g., []). In such cases, both the grd generaton process and the soluton of the resultng lnear systems can be computatonally expensve. The lack of re
![(e.g., []). In such cases, both the grd generaton process and the soluton of the resultng lnear systems can be computatonally expensve. The lack of re (e.g., []). In such cases, both the grd generaton process and the soluton of the resultng lnear systems can be computatonally expensve. The lack of re](/thumbs/83/88573484.jpg) A Free-Space Adaptve FMM-ased PDE Solver n Three Dmensons H. Langston L. Greengard D. orn October, Abstract We present a kernel-ndependent, adaptve fast multpole method (FMM) of arbtrary order accuracy
A Free-Space Adaptve FMM-ased PDE Solver n Three Dmensons H. Langston L. Greengard D. orn October, Abstract We present a kernel-ndependent, adaptve fast multpole method (FMM) of arbtrary order accuracy
SLAM Summer School 2006 Practical 2: SLAM using Monocular Vision
 SLAM Summer School 2006 Practcal 2: SLAM usng Monocular Vson Javer Cvera, Unversty of Zaragoza Andrew J. Davson, Imperal College London J.M.M Montel, Unversty of Zaragoza. josemar@unzar.es, jcvera@unzar.es,
SLAM Summer School 2006 Practcal 2: SLAM usng Monocular Vson Javer Cvera, Unversty of Zaragoza Andrew J. Davson, Imperal College London J.M.M Montel, Unversty of Zaragoza. josemar@unzar.es, jcvera@unzar.es,
NAG Fortran Library Chapter Introduction. G10 Smoothing in Statistics
 Introducton G10 NAG Fortran Lbrary Chapter Introducton G10 Smoothng n Statstcs Contents 1 Scope of the Chapter... 2 2 Background to the Problems... 2 2.1 Smoothng Methods... 2 2.2 Smoothng Splnes and Regresson
Introducton G10 NAG Fortran Lbrary Chapter Introducton G10 Smoothng n Statstcs Contents 1 Scope of the Chapter... 2 2 Background to the Problems... 2 2.1 Smoothng Methods... 2 2.2 Smoothng Splnes and Regresson
In the planar case, one possibility to create a high quality. curve that interpolates a given set of points is to use a clothoid spline,
 Dscrete Farng of Curves and Surfaces Based on Lnear Curvature Dstrbuton R. Schneder and L. Kobbelt Abstract. In the planar case, one possblty to create a hgh qualty curve that nterpolates a gven set of
Dscrete Farng of Curves and Surfaces Based on Lnear Curvature Dstrbuton R. Schneder and L. Kobbelt Abstract. In the planar case, one possblty to create a hgh qualty curve that nterpolates a gven set of
AP PHYSICS B 2008 SCORING GUIDELINES
 AP PHYSICS B 2008 SCORING GUIDELINES General Notes About 2008 AP Physcs Scorng Gudelnes 1. The solutons contan the most common method of solvng the free-response questons and the allocaton of ponts for
AP PHYSICS B 2008 SCORING GUIDELINES General Notes About 2008 AP Physcs Scorng Gudelnes 1. The solutons contan the most common method of solvng the free-response questons and the allocaton of ponts for
Multi-stable Perception. Necker Cube
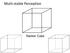 Mult-stable Percepton Necker Cube Spnnng dancer lluson, Nobuuk Kaahara Fttng and Algnment Computer Vson Szelsk 6.1 James Has Acknowledgment: Man sldes from Derek Hoem, Lana Lazebnk, and Grauman&Lebe 2008
Mult-stable Percepton Necker Cube Spnnng dancer lluson, Nobuuk Kaahara Fttng and Algnment Computer Vson Szelsk 6.1 James Has Acknowledgment: Man sldes from Derek Hoem, Lana Lazebnk, and Grauman&Lebe 2008
The Codesign Challenge
 ECE 4530 Codesgn Challenge Fall 2007 Hardware/Software Codesgn The Codesgn Challenge Objectves In the codesgn challenge, your task s to accelerate a gven software reference mplementaton as fast as possble.
ECE 4530 Codesgn Challenge Fall 2007 Hardware/Software Codesgn The Codesgn Challenge Objectves In the codesgn challenge, your task s to accelerate a gven software reference mplementaton as fast as possble.
Positive Semi-definite Programming Localization in Wireless Sensor Networks
 Postve Sem-defnte Programmng Localzaton n Wreless Sensor etworks Shengdong Xe 1,, Jn Wang, Aqun Hu 1, Yunl Gu, Jang Xu, 1 School of Informaton Scence and Engneerng, Southeast Unversty, 10096, anjng Computer
Postve Sem-defnte Programmng Localzaton n Wreless Sensor etworks Shengdong Xe 1,, Jn Wang, Aqun Hu 1, Yunl Gu, Jang Xu, 1 School of Informaton Scence and Engneerng, Southeast Unversty, 10096, anjng Computer
Barycentric Coordinates. From: Mean Value Coordinates for Closed Triangular Meshes by Ju et al.
 Barycentrc Coordnates From: Mean Value Coordnates for Closed Trangular Meshes by Ju et al. Motvaton Data nterpolaton from the vertces of a boundary polygon to ts nteror Boundary value problems Shadng Space
Barycentrc Coordnates From: Mean Value Coordnates for Closed Trangular Meshes by Ju et al. Motvaton Data nterpolaton from the vertces of a boundary polygon to ts nteror Boundary value problems Shadng Space
Assignment # 2. Farrukh Jabeen Algorithms 510 Assignment #2 Due Date: June 15, 2009.
 Farrukh Jabeen Algorthms 51 Assgnment #2 Due Date: June 15, 29. Assgnment # 2 Chapter 3 Dscrete Fourer Transforms Implement the FFT for the DFT. Descrbed n sectons 3.1 and 3.2. Delverables: 1. Concse descrpton
Farrukh Jabeen Algorthms 51 Assgnment #2 Due Date: June 15, 29. Assgnment # 2 Chapter 3 Dscrete Fourer Transforms Implement the FFT for the DFT. Descrbed n sectons 3.1 and 3.2. Delverables: 1. Concse descrpton
NORMALE. A modied structured central scheme for. 2D hyperbolic conservation laws. Theodoros KATSAOUNIS. Doron LEVY
 E COLE NORMALE SUPERIEURE A moded structured central scheme for 2D hyperbolc conservaton laws Theodoros KATSAOUNIS Doron LEVY LMENS - 98-30 Département de Mathématques et Informatque CNRS URA 762 A moded
E COLE NORMALE SUPERIEURE A moded structured central scheme for 2D hyperbolc conservaton laws Theodoros KATSAOUNIS Doron LEVY LMENS - 98-30 Département de Mathématques et Informatque CNRS URA 762 A moded
GSLM Operations Research II Fall 13/14
 GSLM 58 Operatons Research II Fall /4 6. Separable Programmng Consder a general NLP mn f(x) s.t. g j (x) b j j =. m. Defnton 6.. The NLP s a separable program f ts objectve functon and all constrants are
GSLM 58 Operatons Research II Fall /4 6. Separable Programmng Consder a general NLP mn f(x) s.t. g j (x) b j j =. m. Defnton 6.. The NLP s a separable program f ts objectve functon and all constrants are
An accelerated value/policy iteration scheme for the solution of DP equations
 An accelerated value/polcy teraton scheme for the soluton of DP equatons Alessandro Alla 1, Maurzo Falcone 2, and Dante Kalse 3 1 SAPIENZA - Unversty of Rome, Ple. Aldo Moro 2, Rome, Italy alla@mat.unroma1.t
An accelerated value/polcy teraton scheme for the soluton of DP equatons Alessandro Alla 1, Maurzo Falcone 2, and Dante Kalse 3 1 SAPIENZA - Unversty of Rome, Ple. Aldo Moro 2, Rome, Italy alla@mat.unroma1.t
Active Contours/Snakes
 Actve Contours/Snakes Erkut Erdem Acknowledgement: The sldes are adapted from the sldes prepared by K. Grauman of Unversty of Texas at Austn Fttng: Edges vs. boundares Edges useful sgnal to ndcate occludng
Actve Contours/Snakes Erkut Erdem Acknowledgement: The sldes are adapted from the sldes prepared by K. Grauman of Unversty of Texas at Austn Fttng: Edges vs. boundares Edges useful sgnal to ndcate occludng
Compiler Design. Spring Register Allocation. Sample Exercises and Solutions. Prof. Pedro C. Diniz
 Compler Desgn Sprng 2014 Regster Allocaton Sample Exercses and Solutons Prof. Pedro C. Dnz USC / Informaton Scences Insttute 4676 Admralty Way, Sute 1001 Marna del Rey, Calforna 90292 pedro@s.edu Regster
Compler Desgn Sprng 2014 Regster Allocaton Sample Exercses and Solutons Prof. Pedro C. Dnz USC / Informaton Scences Insttute 4676 Admralty Way, Sute 1001 Marna del Rey, Calforna 90292 pedro@s.edu Regster
An Iterative Solution Approach to Process Plant Layout using Mixed Integer Optimisation
 17 th European Symposum on Computer Aded Process Engneerng ESCAPE17 V. Plesu and P.S. Agach (Edtors) 2007 Elsever B.V. All rghts reserved. 1 An Iteratve Soluton Approach to Process Plant Layout usng Mxed
17 th European Symposum on Computer Aded Process Engneerng ESCAPE17 V. Plesu and P.S. Agach (Edtors) 2007 Elsever B.V. All rghts reserved. 1 An Iteratve Soluton Approach to Process Plant Layout usng Mxed
Improvement of Spatial Resolution Using BlockMatching Based Motion Estimation and Frame. Integration
 Improvement of Spatal Resoluton Usng BlockMatchng Based Moton Estmaton and Frame Integraton Danya Suga and Takayuk Hamamoto Graduate School of Engneerng, Tokyo Unversty of Scence, 6-3-1, Nuku, Katsuska-ku,
Improvement of Spatal Resoluton Usng BlockMatchng Based Moton Estmaton and Frame Integraton Danya Suga and Takayuk Hamamoto Graduate School of Engneerng, Tokyo Unversty of Scence, 6-3-1, Nuku, Katsuska-ku,
G 2 Surface Modeling Using Minimal Mean-Curvature-Variation Flow
 G 2 Surface Modelng Usng Mnmal Mean-Curvature-Varaton Flow Guolang Xu 1 Qn Zhang 2 1,2 LSEC, Insttute of Computatonal Mathematcs, Academy of Mathematcs and System Scences, Chnese Academy of Scences, Bejng
G 2 Surface Modelng Usng Mnmal Mean-Curvature-Varaton Flow Guolang Xu 1 Qn Zhang 2 1,2 LSEC, Insttute of Computatonal Mathematcs, Academy of Mathematcs and System Scences, Chnese Academy of Scences, Bejng
SENSITIVITY ANALYSIS WITH UNSTRUCTURED FREE MESH GENERATORS IN 2-D AND 3-D SHAPE OPTIMIZATION.
 SENSITIVITY ANALYSIS WITH UNSTRUCTURED FREE MESH GENERATORS IN 2-D AND 3-D SHAPE OPTIMIZATION. P. Duysnx, W.H. Zhang, C. Fleury. Aerospace Laboratory, LTAS, Unversty of Lège B-4000 LIEGE, BELGIUM. ABSTRACT.
SENSITIVITY ANALYSIS WITH UNSTRUCTURED FREE MESH GENERATORS IN 2-D AND 3-D SHAPE OPTIMIZATION. P. Duysnx, W.H. Zhang, C. Fleury. Aerospace Laboratory, LTAS, Unversty of Lège B-4000 LIEGE, BELGIUM. ABSTRACT.
A HIGH-ORDER SPECTRAL (FINITE) VOLUME METHOD FOR CONSERVATION LAWS ON UNSTRUCTURED GRIDS
 AIAA-00-058 A HIGH-ORDER SPECTRAL (FIITE) VOLUME METHOD FOR COSERVATIO LAWS O USTRUCTURED GRIDS Z.J. Wang Department of Mechancal Engneerng Mchgan State Unversty, East Lansng, MI 88 Yen Lu * MS T7B-, ASA
AIAA-00-058 A HIGH-ORDER SPECTRAL (FIITE) VOLUME METHOD FOR COSERVATIO LAWS O USTRUCTURED GRIDS Z.J. Wang Department of Mechancal Engneerng Mchgan State Unversty, East Lansng, MI 88 Yen Lu * MS T7B-, ASA
12/2/2009. Announcements. Parametric / Non-parametric. Case-Based Reasoning. Nearest-Neighbor on Images. Nearest-Neighbor Classification
 Introducton to Artfcal Intellgence V22.0472-001 Fall 2009 Lecture 24: Nearest-Neghbors & Support Vector Machnes Rob Fergus Dept of Computer Scence, Courant Insttute, NYU Sldes from Danel Yeung, John DeNero
Introducton to Artfcal Intellgence V22.0472-001 Fall 2009 Lecture 24: Nearest-Neghbors & Support Vector Machnes Rob Fergus Dept of Computer Scence, Courant Insttute, NYU Sldes from Danel Yeung, John DeNero
Support Vector Machines. CS534 - Machine Learning
 Support Vector Machnes CS534 - Machne Learnng Perceptron Revsted: Lnear Separators Bnar classfcaton can be veed as the task of separatng classes n feature space: b > 0 b 0 b < 0 f() sgn( b) Lnear Separators
Support Vector Machnes CS534 - Machne Learnng Perceptron Revsted: Lnear Separators Bnar classfcaton can be veed as the task of separatng classes n feature space: b > 0 b 0 b < 0 f() sgn( b) Lnear Separators
Course Introduction. Algorithm 8/31/2017. COSC 320 Advanced Data Structures and Algorithms. COSC 320 Advanced Data Structures and Algorithms
 Course Introducton Course Topcs Exams, abs, Proects A quc loo at a few algorthms 1 Advanced Data Structures and Algorthms Descrpton: We are gong to dscuss algorthm complexty analyss, algorthm desgn technques
Course Introducton Course Topcs Exams, abs, Proects A quc loo at a few algorthms 1 Advanced Data Structures and Algorthms Descrpton: We are gong to dscuss algorthm complexty analyss, algorthm desgn technques
Wishing you all a Total Quality New Year!
 Total Qualty Management and Sx Sgma Post Graduate Program 214-15 Sesson 4 Vnay Kumar Kalakband Assstant Professor Operatons & Systems Area 1 Wshng you all a Total Qualty New Year! Hope you acheve Sx sgma
Total Qualty Management and Sx Sgma Post Graduate Program 214-15 Sesson 4 Vnay Kumar Kalakband Assstant Professor Operatons & Systems Area 1 Wshng you all a Total Qualty New Year! Hope you acheve Sx sgma
Computer Animation and Visualisation. Lecture 4. Rigging / Skinning
 Computer Anmaton and Vsualsaton Lecture 4. Rggng / Sknnng Taku Komura Overvew Sknnng / Rggng Background knowledge Lnear Blendng How to decde weghts? Example-based Method Anatomcal models Sknnng Assume
Computer Anmaton and Vsualsaton Lecture 4. Rggng / Sknnng Taku Komura Overvew Sknnng / Rggng Background knowledge Lnear Blendng How to decde weghts? Example-based Method Anatomcal models Sknnng Assume
Kinematics of pantograph masts
 Abstract Spacecraft Mechansms Group, ISRO Satellte Centre, Arport Road, Bangalore 560 07, Emal:bpn@sac.ernet.n Flght Dynamcs Dvson, ISRO Satellte Centre, Arport Road, Bangalore 560 07 Emal:pandyan@sac.ernet.n
Abstract Spacecraft Mechansms Group, ISRO Satellte Centre, Arport Road, Bangalore 560 07, Emal:bpn@sac.ernet.n Flght Dynamcs Dvson, ISRO Satellte Centre, Arport Road, Bangalore 560 07 Emal:pandyan@sac.ernet.n
S.P.H. : A SOLUTION TO AVOID USING EROSION CRITERION?
 S.P.H. : A SOLUTION TO AVOID USING EROSION CRITERION? Célne GALLET ENSICA 1 place Emle Bloun 31056 TOULOUSE CEDEX e-mal :cgallet@ensca.fr Jean Luc LACOME DYNALIS Immeuble AEROPOLE - Bat 1 5, Avenue Albert
S.P.H. : A SOLUTION TO AVOID USING EROSION CRITERION? Célne GALLET ENSICA 1 place Emle Bloun 31056 TOULOUSE CEDEX e-mal :cgallet@ensca.fr Jean Luc LACOME DYNALIS Immeuble AEROPOLE - Bat 1 5, Avenue Albert
Solitary and Traveling Wave Solutions to a Model. of Long Range Diffusion Involving Flux with. Stability Analysis
 Internatonal Mathematcal Forum, Vol. 6,, no. 7, 8 Soltary and Travelng Wave Solutons to a Model of Long Range ffuson Involvng Flux wth Stablty Analyss Manar A. Al-Qudah Math epartment, Rabgh Faculty of
Internatonal Mathematcal Forum, Vol. 6,, no. 7, 8 Soltary and Travelng Wave Solutons to a Model of Long Range ffuson Involvng Flux wth Stablty Analyss Manar A. Al-Qudah Math epartment, Rabgh Faculty of
A COMPARISON OF TWO METHODS FOR FITTING HIGH DIMENSIONAL RESPONSE SURFACES
 Mam, Florda, U.S.A., Aprl 6-8, 7 A COMPARISON OF TWO METHODS FOR FITTING HIGH DIMENSIONAL RESPONSE SURFACES Marcelo J. Colaço Department of Mechancal and Materals Eng. Mltary Insttute of Engneerng Ro de
Mam, Florda, U.S.A., Aprl 6-8, 7 A COMPARISON OF TWO METHODS FOR FITTING HIGH DIMENSIONAL RESPONSE SURFACES Marcelo J. Colaço Department of Mechancal and Materals Eng. Mltary Insttute of Engneerng Ro de
Differential formulation of discontinuous Galerkin and related methods for compressible Euler and Navier-Stokes equations
 Graduate Theses and Dssertatons Graduate College 2011 Dfferental formulaton of dscontnuous Galerkn and related methods for compressble Euler and Naver-Stokes equatons Hayang Gao Iowa State Unversty Follow
Graduate Theses and Dssertatons Graduate College 2011 Dfferental formulaton of dscontnuous Galerkn and related methods for compressble Euler and Naver-Stokes equatons Hayang Gao Iowa State Unversty Follow
c 2009 Society for Industrial and Applied Mathematics
 SIAM J. MATRIX ANAL. APPL. Vol. 31, No. 3, pp. 1382 1411 c 2009 Socety for Industral and Appled Mathematcs SUPERFAST MULTIFRONTAL METHOD FOR LARGE STRUCTURED LINEAR SYSTEMS OF EQUATIONS JIANLIN XIA, SHIVKUMAR
SIAM J. MATRIX ANAL. APPL. Vol. 31, No. 3, pp. 1382 1411 c 2009 Socety for Industral and Appled Mathematcs SUPERFAST MULTIFRONTAL METHOD FOR LARGE STRUCTURED LINEAR SYSTEMS OF EQUATIONS JIANLIN XIA, SHIVKUMAR
Determining the Optimal Bandwidth Based on Multi-criterion Fusion
 Proceedngs of 01 4th Internatonal Conference on Machne Learnng and Computng IPCSIT vol. 5 (01) (01) IACSIT Press, Sngapore Determnng the Optmal Bandwdth Based on Mult-crteron Fuson Ha-L Lang 1+, Xan-Mn
Proceedngs of 01 4th Internatonal Conference on Machne Learnng and Computng IPCSIT vol. 5 (01) (01) IACSIT Press, Sngapore Determnng the Optmal Bandwdth Based on Mult-crteron Fuson Ha-L Lang 1+, Xan-Mn
Discontinuous Galerkin methods for flow and transport problems in porous media
 T COMMUNICATIONS IN NUMERICA METHODS IN ENGINEERING Commun. Numer. Meth. Engng 2; :1 6 [Verson: 2/3/22 v1.] Dscontnuous Galerkn methods for flow and transport problems n porous meda Béatrve Rvère and Mary
T COMMUNICATIONS IN NUMERICA METHODS IN ENGINEERING Commun. Numer. Meth. Engng 2; :1 6 [Verson: 2/3/22 v1.] Dscontnuous Galerkn methods for flow and transport problems n porous meda Béatrve Rvère and Mary
Analysis of 3D Cracks in an Arbitrary Geometry with Weld Residual Stress
 Analyss of 3D Cracks n an Arbtrary Geometry wth Weld Resdual Stress Greg Thorwald, Ph.D. Ted L. Anderson, Ph.D. Structural Relablty Technology, Boulder, CO Abstract Materals contanng flaws lke nclusons
Analyss of 3D Cracks n an Arbtrary Geometry wth Weld Resdual Stress Greg Thorwald, Ph.D. Ted L. Anderson, Ph.D. Structural Relablty Technology, Boulder, CO Abstract Materals contanng flaws lke nclusons
Research Article Quasi-Bézier Curves with Shape Parameters
 Hndaw Publshng Corporaton Appled Mathematcs Volume 3, Artcle ID 739, 9 pages http://dxdoorg/55/3/739 Research Artcle Quas-Bézer Curves wth Shape Parameters Jun Chen Faculty of Scence, Nngbo Unversty of
Hndaw Publshng Corporaton Appled Mathematcs Volume 3, Artcle ID 739, 9 pages http://dxdoorg/55/3/739 Research Artcle Quas-Bézer Curves wth Shape Parameters Jun Chen Faculty of Scence, Nngbo Unversty of
Lecture #15 Lecture Notes
 Lecture #15 Lecture Notes The ocean water column s very much a 3-D spatal entt and we need to represent that structure n an economcal way to deal wth t n calculatons. We wll dscuss one way to do so, emprcal
Lecture #15 Lecture Notes The ocean water column s very much a 3-D spatal entt and we need to represent that structure n an economcal way to deal wth t n calculatons. We wll dscuss one way to do so, emprcal
Unsupervised Learning and Clustering
 Unsupervsed Learnng and Clusterng Why consder unlabeled samples?. Collectng and labelng large set of samples s costly Gettng recorded speech s free, labelng s tme consumng 2. Classfer could be desgned
Unsupervsed Learnng and Clusterng Why consder unlabeled samples?. Collectng and labelng large set of samples s costly Gettng recorded speech s free, labelng s tme consumng 2. Classfer could be desgned
Structure from Motion
 Structure from Moton Structure from Moton For now, statc scene and movng camera Equvalentl, rgdl movng scene and statc camera Lmtng case of stereo wth man cameras Lmtng case of multvew camera calbraton
Structure from Moton Structure from Moton For now, statc scene and movng camera Equvalentl, rgdl movng scene and statc camera Lmtng case of stereo wth man cameras Lmtng case of multvew camera calbraton
c 2014 Xiaojia(Shelly) Zhang
 c 2014 Xaoja(Shelly) Zhang MACRO-ELEMENT APPROACH FOR TOPOLOGY OPTIMIZATION OF TRUSSES USING A GROUND STRUCTURE METHOD BY XIAOJIA(SHELLY) ZHANG THESIS Submtted n partal fulfllment of the requrements for
c 2014 Xaoja(Shelly) Zhang MACRO-ELEMENT APPROACH FOR TOPOLOGY OPTIMIZATION OF TRUSSES USING A GROUND STRUCTURE METHOD BY XIAOJIA(SHELLY) ZHANG THESIS Submtted n partal fulfllment of the requrements for
Range images. Range image registration. Examples of sampling patterns. Range images and range surfaces
 Range mages For many structured lght scanners, the range data forms a hghly regular pattern known as a range mage. he samplng pattern s determned by the specfc scanner. Range mage regstraton 1 Examples
Range mages For many structured lght scanners, the range data forms a hghly regular pattern known as a range mage. he samplng pattern s determned by the specfc scanner. Range mage regstraton 1 Examples
Domain decomposition in shallow-water modelling for practical flow applications
 Doman decomposton n shallow-water modellng for practcal flow applcatons Mart Borsboom 1, Menno Genseberger 1, Bas van t Hof 2, and Edwn Spee 1 1 Introducton For the smulaton of flows n rvers, lakes, and
Doman decomposton n shallow-water modellng for practcal flow applcatons Mart Borsboom 1, Menno Genseberger 1, Bas van t Hof 2, and Edwn Spee 1 1 Introducton For the smulaton of flows n rvers, lakes, and
On the Efficiency of Swap-Based Clustering
 On the Effcency of Swap-Based Clusterng Pas Fränt and Oll Vrmaok Department of Computer Scence, Unversty of Joensuu, Fnland {frant, ovrma}@cs.oensuu.f Abstract. Random swap-based clusterng s very smple
On the Effcency of Swap-Based Clusterng Pas Fränt and Oll Vrmaok Department of Computer Scence, Unversty of Joensuu, Fnland {frant, ovrma}@cs.oensuu.f Abstract. Random swap-based clusterng s very smple
Solutions to Programming Assignment Five Interpolation and Numerical Differentiation
 College of Engneerng and Coputer Scence Mechancal Engneerng Departent Mechancal Engneerng 309 Nuercal Analyss of Engneerng Systes Sprng 04 Nuber: 537 Instructor: Larry Caretto Solutons to Prograng Assgnent
College of Engneerng and Coputer Scence Mechancal Engneerng Departent Mechancal Engneerng 309 Nuercal Analyss of Engneerng Systes Sprng 04 Nuber: 537 Instructor: Larry Caretto Solutons to Prograng Assgnent
Scan Conversion & Shading
 Scan Converson & Shadng Thomas Funkhouser Prnceton Unversty C0S 426, Fall 1999 3D Renderng Ppelne (for drect llumnaton) 3D Prmtves 3D Modelng Coordnates Modelng Transformaton 3D World Coordnates Lghtng
Scan Converson & Shadng Thomas Funkhouser Prnceton Unversty C0S 426, Fall 1999 3D Renderng Ppelne (for drect llumnaton) 3D Prmtves 3D Modelng Coordnates Modelng Transformaton 3D World Coordnates Lghtng
LU Decomposition Method Jamie Trahan, Autar Kaw, Kevin Martin University of South Florida United States of America
 nbm_sle_sm_ludecomp.nb 1 LU Decomposton Method Jame Trahan, Autar Kaw, Kevn Martn Unverst of South Florda Unted States of Amerca aw@eng.usf.edu nbm_sle_sm_ludecomp.nb 2 Introducton When solvng multple
nbm_sle_sm_ludecomp.nb 1 LU Decomposton Method Jame Trahan, Autar Kaw, Kevn Martn Unverst of South Florda Unted States of Amerca aw@eng.usf.edu nbm_sle_sm_ludecomp.nb 2 Introducton When solvng multple
Time Integration Schemes in Dynamic Problems
 Internatonal Workshop of Advanced Manufacturng and Automaton (IWAMA 016) Tme Integraton Schemes n Dynamc Problems Effect of Dampng on Numercal Stablty and Accuracy Ashsh Aeran and Hrpa G. Lemu Dept. Mechancal
Internatonal Workshop of Advanced Manufacturng and Automaton (IWAMA 016) Tme Integraton Schemes n Dynamc Problems Effect of Dampng on Numercal Stablty and Accuracy Ashsh Aeran and Hrpa G. Lemu Dept. Mechancal
SPH and ALE formulations for sloshing tank analysis
 Int. Jnl. of Multphyscs Volume 9 Number 3 2015 209 SPH and ALE formulatons for sloshng tank analyss Jngxao Xu 1, Jason Wang 1 and Mhamed Soul*, 2 1 LSTC, Lvermore Software Technology Corp. Lvermore CA
Int. Jnl. of Multphyscs Volume 9 Number 3 2015 209 SPH and ALE formulatons for sloshng tank analyss Jngxao Xu 1, Jason Wang 1 and Mhamed Soul*, 2 1 LSTC, Lvermore Software Technology Corp. Lvermore CA
Performance Evaluation of Information Retrieval Systems
 Why System Evaluaton? Performance Evaluaton of Informaton Retreval Systems Many sldes n ths secton are adapted from Prof. Joydeep Ghosh (UT ECE) who n turn adapted them from Prof. Dk Lee (Unv. of Scence
Why System Evaluaton? Performance Evaluaton of Informaton Retreval Systems Many sldes n ths secton are adapted from Prof. Joydeep Ghosh (UT ECE) who n turn adapted them from Prof. Dk Lee (Unv. of Scence
Introduction to Geometrical Optics - a 2D ray tracing Excel model for spherical mirrors - Part 2
 Introducton to Geometrcal Optcs - a D ra tracng Ecel model for sphercal mrrors - Part b George ungu - Ths s a tutoral eplanng the creaton of an eact D ra tracng model for both sphercal concave and sphercal
Introducton to Geometrcal Optcs - a D ra tracng Ecel model for sphercal mrrors - Part b George ungu - Ths s a tutoral eplanng the creaton of an eact D ra tracng model for both sphercal concave and sphercal
Measuring Integration in the Network Structure: Some Suggestions on the Connectivity Index
 Measurng Integraton n the Network Structure: Some Suggestons on the Connectvty Inde 1. Measures of Connectvty The connectvty can be dvded nto two levels, one s domestc connectvty, n the case of the physcal
Measurng Integraton n the Network Structure: Some Suggestons on the Connectvty Inde 1. Measures of Connectvty The connectvty can be dvded nto two levels, one s domestc connectvty, n the case of the physcal
A Five-Point Subdivision Scheme with Two Parameters and a Four-Point Shape-Preserving Scheme
 Mathematcal and Computatonal Applcatons Artcle A Fve-Pont Subdvson Scheme wth Two Parameters and a Four-Pont Shape-Preservng Scheme Jeqng Tan,2, Bo Wang, * and Jun Sh School of Mathematcs, Hefe Unversty
Mathematcal and Computatonal Applcatons Artcle A Fve-Pont Subdvson Scheme wth Two Parameters and a Four-Pont Shape-Preservng Scheme Jeqng Tan,2, Bo Wang, * and Jun Sh School of Mathematcs, Hefe Unversty
Categories and Subject Descriptors B.7.2 [Integrated Circuits]: Design Aids Verification. General Terms Algorithms
![Categories and Subject Descriptors B.7.2 [Integrated Circuits]: Design Aids Verification. General Terms Algorithms Categories and Subject Descriptors B.7.2 [Integrated Circuits]: Design Aids Verification. General Terms Algorithms](/thumbs/79/79370883.jpg) 3. Fndng Determnstc Soluton from Underdetermned Equaton: Large-Scale Performance Modelng by Least Angle Regresson Xn L ECE Department, Carnege Mellon Unversty Forbs Avenue, Pttsburgh, PA 3 xnl@ece.cmu.edu
3. Fndng Determnstc Soluton from Underdetermned Equaton: Large-Scale Performance Modelng by Least Angle Regresson Xn L ECE Department, Carnege Mellon Unversty Forbs Avenue, Pttsburgh, PA 3 xnl@ece.cmu.edu
