Interpretations and Models. Chapter Axiomatic Systems and Incidence Geometry
|
|
|
- Margery Curtis
- 5 years ago
- Views:
Transcription
1 Interpretations and Models Chapter Axiomatic Systems and Incidence Geometry
2 Axiomatic Systems in Mathematics The gold standard for rigor in an area of mathematics Not fully achieved in most areas of mathematics Russel and Whitehead tried in early 20th century to axiomatize all of mathematics Goedel proved a complete axiomatization is not possible Geometry is the area in which the axiomatic approach was most successful A study of geometry using the axiomatic approach is called synthetic geometry Axiomatic systems are now really a branch of mathematical logic rather than mathematics in general Axiomatic systems are a natural component of computer science and computational representation of knowledge
3 Components of Axiomatic Systems Undefined terms Definitions of defined terms Axioms We use axiom and postulate interchangeably Axioms give meaning to undefined terms Axioms are fundamental assumptions without proof Everything else is logically deduced from the axioms The only properties of definitions that can be used are those spelled out in the axioms Theorems (lemmas and corollaries too) Theorem and proposition mean the same thing Theorems must be deduced by valid rules of reasoning Only axioms and previously proved theorems can be used
4 Interpretations An interpretation gives specific meaning to undefined terms Undefined terms may be interpreted in any way that is consistent with the axioms Euclidean geometry was "truth" about the physical space, so there were no alternative interpretations Non-Euclidean geometry opened up the possibility of alternative interpretations for an axiomatic system Non-Euclidean geometry also suggested that physical space may not be (as flat) as we think it is.
5 Models An interpretation is called a model for the axiomatic system if the axioms are true statements in that interpretation All theorems are logically deduced from the axioms, so all theorems are automatically true (correct) in that interpretation A model is a system of entities that behave in all ways according to the rules or laws of the axiomatic system
6 Consistency of an Axiomatic System The axioms in an axiomatic system are said to be consistent if no logical contradiction can be derived from them A contradiction is a statement that is both true and false at the same time (eg: A and (not A) ) If you can show there exists a model for an axiomatic system then it must be consistent
7 Independent Statements A statement in an axiomatic system is independent of the axioms if it is impossible to either prove or disprove the statement as a logical consequence of the axioms You can show a statement is independent of the axioms if you can give two distinct models - one in which the statement is true and the other in which the statement is false Euclid's fifth postulate was eventually determined to be independent of the other postulates We can build a Euclidean model in which the fifth postulate is true And we can build a Non-Euclidean model in which the fifth postulate is false (actually two distinct models)
8 Axioms for Incidence Geometry Undefined terms point line lie on (incident with) Axioms 1. For every pair of distinct points P and Q there exists exactly one line l such that both P and Q lie on l 2. For every line l there exist at least two points P and Q such that both P and Q lie on l 3. There exist three points that do not all lie on any one line, that is, there exists three noncollinear points Three points A, B, C are collinear if there exists one line l such that all three points A, B, and C all lie on l.
9 Theories and Models for Incidence Geometries The axiomatic system with the three undefined terms and the three axioms above is called an Incidence Geometry We also usually call a model for the axiomatic system an Incidence Geometry Note that the axiomatic system and the model are distinct mathematical systems. The axiomatic system is just a set of rules. The models are "real" things that obey those rules. An axiomatic system fully characterizes some "real" system - even if we don't know what that "real" system is. Conversely, we have a "real" universe for which physicists are seeking an axiomatization - the theory of everything!
10 The three-point plane geometry Interpret point to mean one of three symbols A, B, C interpret line to mean a set of two points interpret lie on to mean "is an element of" This is Example There are three lines: {A,B}, {A,C}, {B,C} The three-point plane is a finite geometry Show that this is a model for incidence geometry - demonstrate that all three axioms are true in this interpretation. Note that the drawing for this and other finite interpretations are misleading because the drawn "lines" are really just sets of the endpoints. The "line" part of the drawing is not part of the interpretation!
11 Other Finite Interpretations of Incidence Axioms Four-point geometry (p21) Fano's geometry (p22) Three point line (p21) - not a model Show that the first two are models and show why the third is not a model To show an interpretation is not a model you need only find one counterexample to one of the axioms The three point line does not satisfy the Incidence Axiom 3 To show that an interpretation is a model, you essentially have to prove that there are no counterexamples
12 The Cartesian plane geometry This one you know well. It is based on the real number plane which we denote R 2 Interpret point to be a pair of real numbers (x,y) Interpret line to be the collection of points whose coordinates satisfy a linear equation of the form 0 = ax + by + c where a, b, and c are real numbers and not both a and b are 0 Note that ax + by + c = 0 is y = -(a/b)x - (c/b) We could just say a line is the set of all pairs of points (x,y) in R 2 such that y=mx + b The Cartesian plane is obviously not a finite geometry
13 The sphere Interpret point to mean a point on the surface of a 2-sphere in three-dimensional space. Interpret line to be a great circle - a circle on the surface whose radius equals the radius of the sphere We denote the sphere by S 2 Note that we are only talking about the surface of the sphere when we talk about S 2 The sphere is not a model for the incidence axioms - why? There are no parallel lines in the sphere - all lines intersect The sphere is a non-finite geometry, but it is a bounded geometry!
14 The Klein disk This one is fun. We'll come back to it later in the quarter The Klein disk is a non-finite geometry, but it is a bounded geometry!
15 The parallel postulates in incidence geometry Two lines l and m are parallel if there is no point P such that P lies on both l and m, denoted m l (note: a line is not parallel to itself) Euclidean Parallel Postulate For every line l and for every point P that does not lie on l, there is exactly one line m such that P lies on m and m l Elliptic Parallel Postulate... there is no line m such that P lies on M and m l Hyperbolic Parallel Postulate... there are at least two lines m and n such that P lies on both m and n and both m and n are parallel to l
16 The parallel postulates in incidence geometry These are not necessarily new axioms for incidence geometry They are additional statements that may or may not be satisfied by a particular model for incidence geometry We may choose to add one of them to incidence geometry as a further refinement (like the 5th postulate of Euclid). Euclidean Incidence Geometry adds the Euclidean Parallel Postulate Elliptical Incidence Geometry adds the Elliptical Parallel Postulate Hyperbolic Incidence Geometry adds the Hyperbolic Parallel Postulate
17 Neutral Incidence geometry We can call the original Incidence Geometry the Neutral Incidence Geometry. We say neutral because we don't have any of the parallel postulates. Anything true in Neutral Incidence Geometry is also true in each of the other incidence geometries (Euclidean, Elliptical, Hyperbolic). Note that the three parallel postulates are mutually exclusive - for any Incidence Geometry, if one of the postulates is true, then the other two can't be true. This is how we build independent geometries!
18 Foundations of Geometry Neutral Geometry is Geometry without a parallel postulate. In Neutral Geometry parallel lines will be shown to exist. We just don't know if there are more than one! Chapter 4 - Axioms for Neutral Geometry Chapter 5 - Axioms for Euclidean Geometry - add to Neutral Geometry the Euclidean Parallel Postulate (Equivalent to Euclid's 5th). Chapter 6 - Axioms for Hyperbolic Geometry - add to Neutral Geometry the Hyperbolic Parallel Postulate which is equivalent to the negation of the Euclidean Parallel Postulate
Synthetic Geometry. 1.1 Foundations 1.2 The axioms of projective geometry
 Synthetic Geometry 1.1 Foundations 1.2 The axioms of projective geometry Foundations Def: A geometry is a pair G = (Ω, I), where Ω is a set and I a relation on Ω that is symmetric and reflexive, i.e. 1.
Synthetic Geometry 1.1 Foundations 1.2 The axioms of projective geometry Foundations Def: A geometry is a pair G = (Ω, I), where Ω is a set and I a relation on Ω that is symmetric and reflexive, i.e. 1.
Assignments in Mathematics Class IX (Term I) 5. InTroduCTIon To EuClId s GEoMETry. l Euclid s five postulates are : ANIL TUTORIALS
 Assignments in Mathematics Class IX (Term I) 5. InTroduCTIon To EuClId s GEoMETry IMporTAnT TErMs, definitions And results l In geometry, we take a point, a line and a plane as undefined terms. l An axiom
Assignments in Mathematics Class IX (Term I) 5. InTroduCTIon To EuClId s GEoMETry IMporTAnT TErMs, definitions And results l In geometry, we take a point, a line and a plane as undefined terms. l An axiom
A Communications Network???
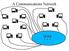 A Communications Network??? A Communications Network What are the desirable properties of the switching box? 1. Every two users must be connected at a switch. 2. Every switch must "look alike". 3. The
A Communications Network??? A Communications Network What are the desirable properties of the switching box? 1. Every two users must be connected at a switch. 2. Every switch must "look alike". 3. The
Hawraa Abbas Almurieb. Axiomatic Systems
 2 Axiomatic Systems 2.1. Introduction to Axiomatic Systems We need undefined terms for any axiomatic system to build the axioms upon them. Which are basic worlds or things for the system. 2.1.1 Definitions
2 Axiomatic Systems 2.1. Introduction to Axiomatic Systems We need undefined terms for any axiomatic system to build the axioms upon them. Which are basic worlds or things for the system. 2.1.1 Definitions
What makes geometry Euclidean or Non-Euclidean?
 What makes geometry Euclidean or Non-Euclidean? I-1. Each two distinct points determine a line I-2. Three noncollinear points determine a plane The 5 Axioms of I-3. If two points lie in a plane, then any
What makes geometry Euclidean or Non-Euclidean? I-1. Each two distinct points determine a line I-2. Three noncollinear points determine a plane The 5 Axioms of I-3. If two points lie in a plane, then any
And Now From a New Angle Special Angles and Postulates LEARNING GOALS
 And Now From a New Angle Special Angles and Postulates LEARNING GOALS KEY TERMS. In this lesson, you will: Calculate the complement and supplement of an angle. Classify adjacent angles, linear pairs, and
And Now From a New Angle Special Angles and Postulates LEARNING GOALS KEY TERMS. In this lesson, you will: Calculate the complement and supplement of an angle. Classify adjacent angles, linear pairs, and
Provide a drawing. Mark any line with three points in blue color.
 Math 3181 Name: Dr. Franz Rothe August 18, 2014 All3181\3181_fall14h1.tex Homework has to be turned in this handout. For extra space, use the back pages, or blank pages between. The homework can be done
Math 3181 Name: Dr. Franz Rothe August 18, 2014 All3181\3181_fall14h1.tex Homework has to be turned in this handout. For extra space, use the back pages, or blank pages between. The homework can be done
Problem 3.1 (Building up geometry). For an axiomatically built-up geometry, six groups of axioms needed:
 Math 3181 Dr. Franz Rothe September 29, 2016 All3181\3181_fall16h3.tex Names: Homework has to be turned in this handout. For extra space, use the back pages, or put blank pages between. The homework can
Math 3181 Dr. Franz Rothe September 29, 2016 All3181\3181_fall16h3.tex Names: Homework has to be turned in this handout. For extra space, use the back pages, or put blank pages between. The homework can
2 Solution of Homework
 Math 3181 Name: Dr. Franz Rothe February 6, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Solution of Homework
Math 3181 Name: Dr. Franz Rothe February 6, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Solution of Homework
Betweenness and the Crossbar Theorem. Lemma: Let A, B, and C be distinct points. If A*B*C, then neither A*C*B nor B*A*C.
 Betweenness and the Crossbar Theorem Lemma: Let A, B, and C be distinct points. If A*B*C, then neither A*C*B nor B*A*C. Suppose that both A*B*C and A*C*B. Thus AB+BC =AC, and AC +CB = AB. From this we
Betweenness and the Crossbar Theorem Lemma: Let A, B, and C be distinct points. If A*B*C, then neither A*C*B nor B*A*C. Suppose that both A*B*C and A*C*B. Thus AB+BC =AC, and AC +CB = AB. From this we
(1) Page #1 24 all. (2) Page #7-21 odd, all. (3) Page #8 20 Even, Page 35 # (4) Page #1 8 all #13 23 odd
 Geometry/Trigonometry Unit 1: Parallel Lines Notes Name: Date: Period: # (1) Page 25-26 #1 24 all (2) Page 33-34 #7-21 odd, 23 28 all (3) Page 33-34 #8 20 Even, Page 35 #40 44 (4) Page 60 61 #1 8 all #13
Geometry/Trigonometry Unit 1: Parallel Lines Notes Name: Date: Period: # (1) Page 25-26 #1 24 all (2) Page 33-34 #7-21 odd, 23 28 all (3) Page 33-34 #8 20 Even, Page 35 #40 44 (4) Page 60 61 #1 8 all #13
Inversive Plane Geometry
 Inversive Plane Geometry An inversive plane is a geometry with three undefined notions: points, circles, and an incidence relation between points and circles, satisfying the following three axioms: (I.1)
Inversive Plane Geometry An inversive plane is a geometry with three undefined notions: points, circles, and an incidence relation between points and circles, satisfying the following three axioms: (I.1)
Copyright 2009 Pearson Education, Inc. Chapter 9 Section 7 - Slide 1 AND
 Copyright 2009 Pearson Education, Inc. Chapter 9 Section 7 - Slide 1 AND Chapter 9 Geometry Copyright 2009 Pearson Education, Inc. Chapter 9 Section 7 - Slide 2 WHAT YOU WILL LEARN Transformational geometry,
Copyright 2009 Pearson Education, Inc. Chapter 9 Section 7 - Slide 1 AND Chapter 9 Geometry Copyright 2009 Pearson Education, Inc. Chapter 9 Section 7 - Slide 2 WHAT YOU WILL LEARN Transformational geometry,
Test 1, Spring 2013 ( Solutions): Provided by Jeff Collins and Anil Patel. 1. Axioms for a finite AFFINE plane of order n.
 Math 532, 736I: Modern Geometry Test 1, Spring 2013 ( Solutions): Provided by Jeff Collins and Anil Patel Part 1: 1. Axioms for a finite AFFINE plane of order n. AA1: There exist at least 4 points, no
Math 532, 736I: Modern Geometry Test 1, Spring 2013 ( Solutions): Provided by Jeff Collins and Anil Patel Part 1: 1. Axioms for a finite AFFINE plane of order n. AA1: There exist at least 4 points, no
Discrete Mathematics Lecture 4. Harper Langston New York University
 Discrete Mathematics Lecture 4 Harper Langston New York University Sequences Sequence is a set of (usually infinite number of) ordered elements: a 1, a 2,, a n, Each individual element a k is called a
Discrete Mathematics Lecture 4 Harper Langston New York University Sequences Sequence is a set of (usually infinite number of) ordered elements: a 1, a 2,, a n, Each individual element a k is called a
The statement implies that any three intersection points of two distinct planes lie on a line.
 Math 3181 Dr. Franz Rothe February 23, 2015 All3181\3181_spr15ts1.tex 1 Solution of Test Name: Problem 1.1. The second part of Hilbert s Proposition 1 states: Any two different planes have either no point
Math 3181 Dr. Franz Rothe February 23, 2015 All3181\3181_spr15ts1.tex 1 Solution of Test Name: Problem 1.1. The second part of Hilbert s Proposition 1 states: Any two different planes have either no point
Definition 2 (Projective plane). A projective plane is a class of points, and a class of lines satisfying the axioms:
 Math 3181 Name: Dr. Franz Rothe January 30, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Homework 1 Definition
Math 3181 Name: Dr. Franz Rothe January 30, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Homework 1 Definition
Course Number: Course Title: Geometry
 Course Number: 1206310 Course Title: Geometry RELATED GLOSSARY TERM DEFINITIONS (89) Altitude The perpendicular distance from the top of a geometric figure to its opposite side. Angle Two rays or two line
Course Number: 1206310 Course Title: Geometry RELATED GLOSSARY TERM DEFINITIONS (89) Altitude The perpendicular distance from the top of a geometric figure to its opposite side. Angle Two rays or two line
The Foundations of Geometry
 The Foundations of Geometry Gerard A. Venema Department of Mathematics and Statistics Calvin College SUB Gottingen 7 219 059 926 2006 A 7409 PEARSON Prentice Hall Upper Saddle River, New Jersey 07458 Contents
The Foundations of Geometry Gerard A. Venema Department of Mathematics and Statistics Calvin College SUB Gottingen 7 219 059 926 2006 A 7409 PEARSON Prentice Hall Upper Saddle River, New Jersey 07458 Contents
MAT 3271: Selected Solutions to the Assignment 6
 Chapter 2: Major Exercises MAT 3271: Selected Solutions to the Assignment 6 1. Since a projective plan is a model of incidence geometry, Incidence Axioms 1-3 and Propositions 2.1-2.5 (which follow logically
Chapter 2: Major Exercises MAT 3271: Selected Solutions to the Assignment 6 1. Since a projective plan is a model of incidence geometry, Incidence Axioms 1-3 and Propositions 2.1-2.5 (which follow logically
I can identify, name, and draw points, lines, segments, rays, and planes. I can apply basic facts about points, lines, and planes.
 Page 1 of 9 Are You Ready Chapter 1 Pretest & skills Attendance Problems Graph each inequality. 1. x > 3 2. 2 < x < 6 3. x > 1 or x < 0 Vocabulary undefined term point line plane collinear coplanar segment
Page 1 of 9 Are You Ready Chapter 1 Pretest & skills Attendance Problems Graph each inequality. 1. x > 3 2. 2 < x < 6 3. x > 1 or x < 0 Vocabulary undefined term point line plane collinear coplanar segment
Hyperbolic Geometry. Chaper Hyperbolic Geometry
 Hyperbolic Geometry Chaper 6.1-6.6 Hyperbolic Geometry Theorems Unique to Hyperbolic Geometry Now we assume Hyperbolic Parallel Postulate (HPP - p21) With the HPP we get for free all the negations of the
Hyperbolic Geometry Chaper 6.1-6.6 Hyperbolic Geometry Theorems Unique to Hyperbolic Geometry Now we assume Hyperbolic Parallel Postulate (HPP - p21) With the HPP we get for free all the negations of the
2-5 Postulates and Paragraph Proofs
 Determine whether each statement is always, sometimes, or never true. Explain your reasoning. 7. The intersection of three planes is a line. If three planes intersect, then their intersection may be a
Determine whether each statement is always, sometimes, or never true. Explain your reasoning. 7. The intersection of three planes is a line. If three planes intersect, then their intersection may be a
Projective geometry and the extended Euclidean plane
 Chapter 2 Projective geometry and the extended Euclidean plane Math 4520, Fall 2017 As we can see from Hilbert s treatment, a completely worked out axiom system for geometry in the plane is quite complicated.
Chapter 2 Projective geometry and the extended Euclidean plane Math 4520, Fall 2017 As we can see from Hilbert s treatment, a completely worked out axiom system for geometry in the plane is quite complicated.
FIGURES FOR SOLUTIONS TO SELECTED EXERCISES. V : Introduction to non Euclidean geometry
 FIGURES FOR SOLUTIONS TO SELECTED EXERCISES V : Introduction to non Euclidean geometry V.1 : Facts from spherical geometry V.1.1. The objective is to show that the minor arc m does not contain a pair of
FIGURES FOR SOLUTIONS TO SELECTED EXERCISES V : Introduction to non Euclidean geometry V.1 : Facts from spherical geometry V.1.1. The objective is to show that the minor arc m does not contain a pair of
Math Introduction to Advanced Mathematics
 Math 215 - Introduction to Advanced Mathematics Number Theory Fall 2017 The following introductory guide to number theory is borrowed from Drew Shulman and is used in a couple of other Math 215 classes.
Math 215 - Introduction to Advanced Mathematics Number Theory Fall 2017 The following introductory guide to number theory is borrowed from Drew Shulman and is used in a couple of other Math 215 classes.
08. Non-Euclidean Geometry 1. Euclidean Geometry
 08. Non-Euclidean Geometry 1. Euclidean Geometry The Elements. ~300 B.C. ~100 A.D. Earliest existing copy 1570 A.D. First English translation 1956 Dover Edition 13 books of propositions, based on 5 postulates.
08. Non-Euclidean Geometry 1. Euclidean Geometry The Elements. ~300 B.C. ~100 A.D. Earliest existing copy 1570 A.D. First English translation 1956 Dover Edition 13 books of propositions, based on 5 postulates.
Some Comments on Leaving Certificate Geometry Work in Progress
 Some Comments on Leaving Certificate Geometry Work in Progress D. R. Wilkins April 23, 2016 i Axioms for Leaving Certificate Geometry In 1932, George D. Birkhoff published a paper entitled A set of postulates
Some Comments on Leaving Certificate Geometry Work in Progress D. R. Wilkins April 23, 2016 i Axioms for Leaving Certificate Geometry In 1932, George D. Birkhoff published a paper entitled A set of postulates
2.1 Angles, Lines and Parallels & 2.2 Congruent Triangles and Pasch s Axiom
 2 Euclidean Geometry In the previous section we gave a sketch overview of the early parts of Euclid s Elements. While the Elements set the standard for the modern axiomatic approach to mathematics, it
2 Euclidean Geometry In the previous section we gave a sketch overview of the early parts of Euclid s Elements. While the Elements set the standard for the modern axiomatic approach to mathematics, it
CS-9645 Introduction to Computer Vision Techniques Winter 2019
 Table of Contents Projective Geometry... 1 Definitions...1 Axioms of Projective Geometry... Ideal Points...3 Geometric Interpretation... 3 Fundamental Transformations of Projective Geometry... 4 The D
Table of Contents Projective Geometry... 1 Definitions...1 Axioms of Projective Geometry... Ideal Points...3 Geometric Interpretation... 3 Fundamental Transformations of Projective Geometry... 4 The D
Slope, Distance, Midpoint
 Line segments in a coordinate plane can be analyzed by finding various characteristics of the line including slope, length, and midpoint. These values are useful in applications and coordinate proofs.
Line segments in a coordinate plane can be analyzed by finding various characteristics of the line including slope, length, and midpoint. These values are useful in applications and coordinate proofs.
1 Appendix to notes 2, on Hyperbolic geometry:
 1230, notes 3 1 Appendix to notes 2, on Hyperbolic geometry: The axioms of hyperbolic geometry are axioms 1-4 of Euclid, plus an alternative to axiom 5: Axiom 5-h: Given a line l and a point p not on l,
1230, notes 3 1 Appendix to notes 2, on Hyperbolic geometry: The axioms of hyperbolic geometry are axioms 1-4 of Euclid, plus an alternative to axiom 5: Axiom 5-h: Given a line l and a point p not on l,
Honors 213. Third Hour Exam. Name
 Honors 213 Third Hour Exam Name Monday, March 27, 2000 100 points Page 1 Please note: Because of multiple exams given Monday, this exam will be returned by Thursday, March 30. 1. (5 pts.) Define what it
Honors 213 Third Hour Exam Name Monday, March 27, 2000 100 points Page 1 Please note: Because of multiple exams given Monday, this exam will be returned by Thursday, March 30. 1. (5 pts.) Define what it
1. A model for spherical/elliptic geometry
 Math 3329-Uniform Geometries Lecture 13 Let s take an overview of what we know. 1. A model for spherical/elliptic geometry Hilbert s axiom system goes with Euclidean geometry. This is the same geometry
Math 3329-Uniform Geometries Lecture 13 Let s take an overview of what we know. 1. A model for spherical/elliptic geometry Hilbert s axiom system goes with Euclidean geometry. This is the same geometry
The Use of Repeating Patterns to Teach Hyperbolic Geometry Concepts
 The Use of Repeating Patterns to Teach Hyperbolic Geometry Concepts Douglas Dunham Department of Computer Science University of Minnesota, Duluth Duluth, MN 55812-3036, USA E-mail: ddunham@d.umn.edu Web
The Use of Repeating Patterns to Teach Hyperbolic Geometry Concepts Douglas Dunham Department of Computer Science University of Minnesota, Duluth Duluth, MN 55812-3036, USA E-mail: ddunham@d.umn.edu Web
Math 102A Hw 3 P a (2 points)
 Math 102 Hw 3 P.93 12 a (2 points) If any pair of these lines are equal, the conclusion is immediate, so assume that we have three distinct lines such that l m and m n. Suppose, on the contrary, that l
Math 102 Hw 3 P.93 12 a (2 points) If any pair of these lines are equal, the conclusion is immediate, so assume that we have three distinct lines such that l m and m n. Suppose, on the contrary, that l
1. A statement is a set of words and/or symbols that collectively make a claim that can be classified as true or false.
 Chapter 1 Line and Angle Relationships 1.1 Sets, Statements and Reasoning Definitions 1. A statement is a set of words and/or symbols that collectively make a claim that can be classified as true or false.
Chapter 1 Line and Angle Relationships 1.1 Sets, Statements and Reasoning Definitions 1. A statement is a set of words and/or symbols that collectively make a claim that can be classified as true or false.
[Ch 6] Set Theory. 1. Basic Concepts and Definitions. 400 lecture note #4. 1) Basics
![[Ch 6] Set Theory. 1. Basic Concepts and Definitions. 400 lecture note #4. 1) Basics [Ch 6] Set Theory. 1. Basic Concepts and Definitions. 400 lecture note #4. 1) Basics](/thumbs/82/86066673.jpg) 400 lecture note #4 [Ch 6] Set Theory 1. Basic Concepts and Definitions 1) Basics Element: ; A is a set consisting of elements x which is in a/another set S such that P(x) is true. Empty set: notated {
400 lecture note #4 [Ch 6] Set Theory 1. Basic Concepts and Definitions 1) Basics Element: ; A is a set consisting of elements x which is in a/another set S such that P(x) is true. Empty set: notated {
Notes on Spherical Geometry
 Notes on Spherical Geometry Abhijit Champanerkar College of Staten Island & The Graduate Center, CUNY Spring 2018 1. Vectors and planes in R 3 To review vector, dot and cross products, lines and planes
Notes on Spherical Geometry Abhijit Champanerkar College of Staten Island & The Graduate Center, CUNY Spring 2018 1. Vectors and planes in R 3 To review vector, dot and cross products, lines and planes
Situation 1: Congruent Triangles vs. Similar Triangles
 Situation 1: Congruent Triangles vs. Similar Triangles Prepared at the University of Georgia EMAT 6500 Date last revised: July 24 th, 2013 Nicolina Scarpelli Prompt: A teacher in a high school Analytic
Situation 1: Congruent Triangles vs. Similar Triangles Prepared at the University of Georgia EMAT 6500 Date last revised: July 24 th, 2013 Nicolina Scarpelli Prompt: A teacher in a high school Analytic
Definition 1 (Hand-shake model). A hand shake model is an incidence geometry for which every line has exactly two points.
 Math 3181 Dr. Franz Rothe Name: All3181\3181_spr13t1.tex 1 Solution of Test I Definition 1 (Hand-shake model). A hand shake model is an incidence geometry for which every line has exactly two points. Definition
Math 3181 Dr. Franz Rothe Name: All3181\3181_spr13t1.tex 1 Solution of Test I Definition 1 (Hand-shake model). A hand shake model is an incidence geometry for which every line has exactly two points. Definition
Grade 6 Math Circles October 16 & Non-Euclidean Geometry and the Globe
 Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
Grade 6 Math Circles October 16 & Non-Euclidean Geometry and the Globe
 Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
1 Elementary number theory
 Math 215 - Introduction to Advanced Mathematics Spring 2019 1 Elementary number theory We assume the existence of the natural numbers and the integers N = {1, 2, 3,...} Z = {..., 3, 2, 1, 0, 1, 2, 3,...},
Math 215 - Introduction to Advanced Mathematics Spring 2019 1 Elementary number theory We assume the existence of the natural numbers and the integers N = {1, 2, 3,...} Z = {..., 3, 2, 1, 0, 1, 2, 3,...},
Geometry: Foundations and Finite Geometries
 Geometry: Foundations and Finite Geometries MATH 3120, Spring 2016 1 Axiomatic Systems Consider a proof of a theorem in mathematics, say, the Pythagorean Theorem. Mathematicians cannot prove this theorem
Geometry: Foundations and Finite Geometries MATH 3120, Spring 2016 1 Axiomatic Systems Consider a proof of a theorem in mathematics, say, the Pythagorean Theorem. Mathematicians cannot prove this theorem
Definition (Axiomatic System). An axiomatic system (a set of axioms and their logical consequences) consists of:
 Course Overview Contents 1 AxiomaticSystems.............................. 1 2 Undefined Terms............................... 2 3 Incidence................................... 2 4 Distance....................................
Course Overview Contents 1 AxiomaticSystems.............................. 1 2 Undefined Terms............................... 2 3 Incidence................................... 2 4 Distance....................................
Thomas Jefferson High School for Science and Technology Program of Studies TJ Math 1
 Course Description: This course is designed for students who have successfully completed the standards for Honors Algebra I. Students will study geometric topics in depth, with a focus on building critical
Course Description: This course is designed for students who have successfully completed the standards for Honors Algebra I. Students will study geometric topics in depth, with a focus on building critical
TECHNISCHE UNIVERSITÄT BERLIN WS2005 Fachbereich 3 - Mathematik Prof. Dr. U. Pinkall / Charles Gunn Abgabe:
 TECHNISCHE UNIVERSITÄT BERLIN WS2005 Fachbereich 3 - Mathematik Prof. Dr. U. Pinkall / Charles Gunn Abgabe: 27.10.2005 1. Übung Geometrie I (Lines in P 2 (R), Separation, Desargues) 1. Aufgabe Line equations
TECHNISCHE UNIVERSITÄT BERLIN WS2005 Fachbereich 3 - Mathematik Prof. Dr. U. Pinkall / Charles Gunn Abgabe: 27.10.2005 1. Übung Geometrie I (Lines in P 2 (R), Separation, Desargues) 1. Aufgabe Line equations
Hyperbolic Geometry and the Universe. the questions of the cosmos. Advances in mathematics and physics have given insight
 Garth Butcher April 17, 2002 Hyperbolic Geometry and the Universe Throughout our history, men have pondered the universe in which we live and the nature of that universe. In the twenty first century we
Garth Butcher April 17, 2002 Hyperbolic Geometry and the Universe Throughout our history, men have pondered the universe in which we live and the nature of that universe. In the twenty first century we
8 Standard Euclidean Triangle Geometry
 8 Standard Euclidean Triangle Geometry 8.1 The circum-center Figure 8.1: In hyperbolic geometry, the perpendicular bisectors can be parallel as shown but this figure is impossible in Euclidean geometry.
8 Standard Euclidean Triangle Geometry 8.1 The circum-center Figure 8.1: In hyperbolic geometry, the perpendicular bisectors can be parallel as shown but this figure is impossible in Euclidean geometry.
<Outline> Mathematical Training Program for Laotian Teachers
 Mathematical Training Program for Laotian Teachers Euclidean Geometry Analytic Geometry Trigonometry Dr Wattana Toutip Department of Mathematics Faculty of Science Khon Kaen University February
Mathematical Training Program for Laotian Teachers Euclidean Geometry Analytic Geometry Trigonometry Dr Wattana Toutip Department of Mathematics Faculty of Science Khon Kaen University February
Objective- the students will be able to use undefined terms and definitions to work with points, lines and planes. Undefined Terms
 Unit 1 asics of Geometry Objective- the students will be able to use undefined terms and definitions to work with points, lines and planes. Undefined Terms 1. Point has no dimension, geometrically looks
Unit 1 asics of Geometry Objective- the students will be able to use undefined terms and definitions to work with points, lines and planes. Undefined Terms 1. Point has no dimension, geometrically looks
Mathematical mysteries: Strange Geometries
 1997 2009, Millennium Mathematics Project, University of Cambridge. Permission is granted to print and copy this page on paper for non commercial use. For other uses, including electronic redistribution,
1997 2009, Millennium Mathematics Project, University of Cambridge. Permission is granted to print and copy this page on paper for non commercial use. For other uses, including electronic redistribution,
Michael Greenberg. September 13, 2004
 Finite Geometries for Those with a Finite Patience for Mathematics Michael Greenberg September 13, 2004 1 Introduction 1.1 Objective When my friends ask me what I ve been studying this past summer and
Finite Geometries for Those with a Finite Patience for Mathematics Michael Greenberg September 13, 2004 1 Introduction 1.1 Objective When my friends ask me what I ve been studying this past summer and
1.1 IDENTIFY POINTS, LINES AND PLANES
 1.1 IDENTIFY POINTS, LINES AND PLANES OBJECTIVE I WILL KNOW THESE DEFINITIONS AND BE ABLE TO SKETCH THEM: POINT LINE PLANE RAY OPPOSITE RAY COLLINEAR AND COPLANAR POINTS INTERSECTIONS OF TWO LINES AND
1.1 IDENTIFY POINTS, LINES AND PLANES OBJECTIVE I WILL KNOW THESE DEFINITIONS AND BE ABLE TO SKETCH THEM: POINT LINE PLANE RAY OPPOSITE RAY COLLINEAR AND COPLANAR POINTS INTERSECTIONS OF TWO LINES AND
Geometry Semester 1 Final Exam Study Guide FCS, Mr. Garcia
 Name Date Period This is your semester 1 exam review study guide. It is designed for you to do a portion each day until the day of the exam. You may use the following formula to calculate your semester
Name Date Period This is your semester 1 exam review study guide. It is designed for you to do a portion each day until the day of the exam. You may use the following formula to calculate your semester
Finding and Extracting Computational Content in Euclid s Elements
 Finding and Extracting Computational Content in Euclid s Elements Ariel Kellison Septemeber 2017 Outline Introduction Computational Content Intro. Why Implement Results and Future Work Implementing Euclid
Finding and Extracting Computational Content in Euclid s Elements Ariel Kellison Septemeber 2017 Outline Introduction Computational Content Intro. Why Implement Results and Future Work Implementing Euclid
1stQuarterReview.nb If two parallel lines are cut by a transversal, 2. If point B is between points A and C, then AB + BC =.
 1stQuarterReview.nb 1 Geometry (H) Review: First Quarter Test Part I Fill in the blank with the appropriate word or phrase. 1. If two parallel lines are cut by a transversal,. 2. If point B is between
1stQuarterReview.nb 1 Geometry (H) Review: First Quarter Test Part I Fill in the blank with the appropriate word or phrase. 1. If two parallel lines are cut by a transversal,. 2. If point B is between
Chapter 8. Voronoi Diagrams. 8.1 Post Oce Problem
 Chapter 8 Voronoi Diagrams 8.1 Post Oce Problem Suppose there are n post oces p 1,... p n in a city. Someone who is located at a position q within the city would like to know which post oce is closest
Chapter 8 Voronoi Diagrams 8.1 Post Oce Problem Suppose there are n post oces p 1,... p n in a city. Someone who is located at a position q within the city would like to know which post oce is closest
EM225 Projective Geometry Part 2
 EM225 Projective Geometry Part 2 eview In projective geometry, we regard figures as being the same if they can be made to appear the same as in the diagram below. In projective geometry: a projective point
EM225 Projective Geometry Part 2 eview In projective geometry, we regard figures as being the same if they can be made to appear the same as in the diagram below. In projective geometry: a projective point
An Approach to Geometry (stolen in part from Moise and Downs: Geometry)
 An Approach to Geometry (stolen in part from Moise and Downs: Geometry) Undefined terms: point, line, plane The rules, axioms, theorems, etc. of elementary algebra are assumed as prior knowledge, and apply
An Approach to Geometry (stolen in part from Moise and Downs: Geometry) Undefined terms: point, line, plane The rules, axioms, theorems, etc. of elementary algebra are assumed as prior knowledge, and apply
Chapter 1 Tools of Geometry
 Chapter 1 Tools of Geometry Goals: 1) learn to draw conclusions based on patterns 2) learn the building blocks for the structure of geometry 3) learn to measure line segments and angles 4) understand the
Chapter 1 Tools of Geometry Goals: 1) learn to draw conclusions based on patterns 2) learn the building blocks for the structure of geometry 3) learn to measure line segments and angles 4) understand the
Pre AP Geometry. Mathematics Standards of Learning Curriculum Framework 2009: Pre AP Geometry
 Pre AP Geometry Mathematics Standards of Learning Curriculum Framework 2009: Pre AP Geometry 1 The content of the mathematics standards is intended to support the following five goals for students: becoming
Pre AP Geometry Mathematics Standards of Learning Curriculum Framework 2009: Pre AP Geometry 1 The content of the mathematics standards is intended to support the following five goals for students: becoming
On the Minimum Number of Convex Quadrilaterals in Point Sets of Given Numbers of Points
 On the Minimum Number of Convex Quadrilaterals in Point Sets of Given Numbers of Points Hu Yuzhong Chen Luping Zhu Hui Ling Xiaofeng (Supervisor) Abstract Consider the following problem. Given n, k N,
On the Minimum Number of Convex Quadrilaterals in Point Sets of Given Numbers of Points Hu Yuzhong Chen Luping Zhu Hui Ling Xiaofeng (Supervisor) Abstract Consider the following problem. Given n, k N,
Card Games in an Undergraduate Geometry Course. Dr. Cherith Tucker, Oklahoma Baptist University MAA MathFest, July 28, 2017
 Card Games in an Undergraduate Geometry Course Dr. Cherith Tucker, Oklahoma Baptist University MAA MathFest, July 28, 2017 Presentation Overview The Game of SET Brief Introduction to the Game of SET Incidence
Card Games in an Undergraduate Geometry Course Dr. Cherith Tucker, Oklahoma Baptist University MAA MathFest, July 28, 2017 Presentation Overview The Game of SET Brief Introduction to the Game of SET Incidence
INDEPENDENT POSTULATES FOR THE "INFORMAL" PART OF PRINCIPIA MATHEMATICA*
 9- "INFORMAL" PART OF PRINCIPIA 7 INDEPENDENT POSTULATES FOR THE "INFORMAL" PART OF PRINCIPIA MATHEMATICA* BY E. V. HUNTINGTON. Introduction. It has long been recognized that Section A of Whitehead and
9- "INFORMAL" PART OF PRINCIPIA 7 INDEPENDENT POSTULATES FOR THE "INFORMAL" PART OF PRINCIPIA MATHEMATICA* BY E. V. HUNTINGTON. Introduction. It has long been recognized that Section A of Whitehead and
The Interplay Between Hyperbolic Symmetry and History
 The Interplay Between Hyperbolic Symmetry and History Douglas Dunham Department of Computer Science University of Minnesota, Duluth Duluth, MN 55812-3036, USA E-mail: ddunham@d.umn.edu Web Site: http://www.d.umn.edu/
The Interplay Between Hyperbolic Symmetry and History Douglas Dunham Department of Computer Science University of Minnesota, Duluth Duluth, MN 55812-3036, USA E-mail: ddunham@d.umn.edu Web Site: http://www.d.umn.edu/
Basics of Geometry Unit 1 - Notes. Objective- the students will be able to use undefined terms and definitions to work with points, lines and planes.
 asics of Geometry Unit 1 - Notes Objective- the students will be able to use undefined terms and definitions to work with points, lines and planes. Undefined Terms 1. Point has no dimension, geometrically
asics of Geometry Unit 1 - Notes Objective- the students will be able to use undefined terms and definitions to work with points, lines and planes. Undefined Terms 1. Point has no dimension, geometrically
Exercises for Chapter Three You know you've got to exercise your brain just like your muscles. Will Rogers ( )
 Exercises for Chapter Three You know you've got to exercise your brain just like your muscles. Will Rogers (1879 1935) Investigation Exercise 3.1. (a) Construct a tessellation. (Directions for construction.)
Exercises for Chapter Three You know you've got to exercise your brain just like your muscles. Will Rogers (1879 1935) Investigation Exercise 3.1. (a) Construct a tessellation. (Directions for construction.)
A Quick Introduction to Non-Euclidean Geometry. A Tiling of the Poincare Plane From Geometry: Plane and Fancy, David Singer, page 61.
 A Quick Introduction to Non-Euclidean Geometry A Tiling of the Poincare Plane From Geometry: Plane and Fancy, David Singer, page 61. Dr. Robert Gardner Presented at Science Hill High School March 22, 2006
A Quick Introduction to Non-Euclidean Geometry A Tiling of the Poincare Plane From Geometry: Plane and Fancy, David Singer, page 61. Dr. Robert Gardner Presented at Science Hill High School March 22, 2006
Prentice Hall Mathematics Geometry, Foundations Series 2011
 Prentice Hall Mathematics Geometry, Foundations Series 2011 Geometry C O R R E L A T E D T O from March 2009 Geometry G.1 Points, Lines, Angles and Planes G.1.1 Find the length of line segments in one-
Prentice Hall Mathematics Geometry, Foundations Series 2011 Geometry C O R R E L A T E D T O from March 2009 Geometry G.1 Points, Lines, Angles and Planes G.1.1 Find the length of line segments in one-
euclidean geometry given a line and a point P which is not on, how many lines pass through P and are parallel to?
 euclidean geometry my goal with all of these lessons is to provide an introduction to both euclidean non-euclidean geometry. the two geometries share many features, but they also have very fundamental
euclidean geometry my goal with all of these lessons is to provide an introduction to both euclidean non-euclidean geometry. the two geometries share many features, but they also have very fundamental
Click the mouse button or press the Space Bar to display the answers.
 Click the mouse button or press the Space Bar to display the answers. 2-5 Objectives You will learn to: Identify and use basic postulates about points, lines, and planes. Write paragraph proofs. Vocabulary
Click the mouse button or press the Space Bar to display the answers. 2-5 Objectives You will learn to: Identify and use basic postulates about points, lines, and planes. Write paragraph proofs. Vocabulary
Unit 2A: Angle Pairs and Transversal Notes
 Unit 2A: Angle Pairs and Transversal Notes Day 1: Special angle pairs Day 2: Angle pairs formed by transversal through two nonparallel lines Day 3: Angle pairs formed by transversal through parallel lines
Unit 2A: Angle Pairs and Transversal Notes Day 1: Special angle pairs Day 2: Angle pairs formed by transversal through two nonparallel lines Day 3: Angle pairs formed by transversal through parallel lines
MS2013: Euclidean Geometry. Anca Mustata
 MS2013: Euclidean Geometry Anca Mustata January 10, 2012 Warning: please read this text with a pencil at hand, as you will need to draw your own pictures to illustrate some statements. Euclid s Geometry
MS2013: Euclidean Geometry Anca Mustata January 10, 2012 Warning: please read this text with a pencil at hand, as you will need to draw your own pictures to illustrate some statements. Euclid s Geometry
On the number of distinct directions of planes determined by n points in R 3
 On the number of distinct directions of planes determined by n points in R 3 Rom Pinchasi August 27, 2007 Abstract We show that any set of n points in R 3, that is not contained in a plane, determines
On the number of distinct directions of planes determined by n points in R 3 Rom Pinchasi August 27, 2007 Abstract We show that any set of n points in R 3, that is not contained in a plane, determines
of Nebraska - Lincoln
 University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-2007 Hyperbolic Geometry Christina L. Sheets University
University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-2007 Hyperbolic Geometry Christina L. Sheets University
Geometry Definitions, Postulates, and Theorems. Chapter 3: Parallel and Perpendicular Lines. Section 3.1: Identify Pairs of Lines and Angles.
 Geometry Definitions, Postulates, and Theorems Chapter : Parallel and Perpendicular Lines Section.1: Identify Pairs of Lines and Angles Standards: Prepare for 7.0 Students prove and use theorems involving
Geometry Definitions, Postulates, and Theorems Chapter : Parallel and Perpendicular Lines Section.1: Identify Pairs of Lines and Angles Standards: Prepare for 7.0 Students prove and use theorems involving
Prentice Hall CME Project Geometry 2009
 Prentice Hall CME Project Geometry 2009 Geometry C O R R E L A T E D T O from March 2009 Geometry G.1 Points, Lines, Angles and Planes G.1.1 Find the length of line segments in one- or two-dimensional
Prentice Hall CME Project Geometry 2009 Geometry C O R R E L A T E D T O from March 2009 Geometry G.1 Points, Lines, Angles and Planes G.1.1 Find the length of line segments in one- or two-dimensional
A HISTORICAL INTRODUCTION TO ELEMENTARY GEOMETRY
 i MATH 119 A HISTORICAL INTRODUCTION TO ELEMENTARY GEOMETRY Geometry is an word derived from ancient Greek meaning earth measure ( ge = earth or land ) + ( metria = measure ). Euclid wrote the Elements
i MATH 119 A HISTORICAL INTRODUCTION TO ELEMENTARY GEOMETRY Geometry is an word derived from ancient Greek meaning earth measure ( ge = earth or land ) + ( metria = measure ). Euclid wrote the Elements
Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts
 Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
Pearson Mathematics Geometry
 A Correlation of Pearson Mathematics Geometry Indiana 2017 To the INDIANA ACADEMIC STANDARDS Mathematics (2014) Geometry The following shows where all of the standards that are part of the Indiana Mathematics
A Correlation of Pearson Mathematics Geometry Indiana 2017 To the INDIANA ACADEMIC STANDARDS Mathematics (2014) Geometry The following shows where all of the standards that are part of the Indiana Mathematics
Geometry Reasons for Proofs Chapter 1
 Geometry Reasons for Proofs Chapter 1 Lesson 1.1 Defined Terms: Undefined Terms: Point: Line: Plane: Space: Postulate 1: Postulate : terms that are explained using undefined and/or other defined terms
Geometry Reasons for Proofs Chapter 1 Lesson 1.1 Defined Terms: Undefined Terms: Point: Line: Plane: Space: Postulate 1: Postulate : terms that are explained using undefined and/or other defined terms
Geometry Curriculum Map
 Geometry Curriculum Map Unit 1 st Quarter Content/Vocabulary Assessment AZ Standards Addressed Essentials of Geometry 1. What are points, lines, and planes? 1. Identify Points, Lines, and Planes 1. Observation
Geometry Curriculum Map Unit 1 st Quarter Content/Vocabulary Assessment AZ Standards Addressed Essentials of Geometry 1. What are points, lines, and planes? 1. Identify Points, Lines, and Planes 1. Observation
A point is pictured by a dot. While a dot must have some size, the point it represents has no size. Points are named by capital letters..
 Chapter 1 Points, Lines & Planes s we begin any new topic, we have to familiarize ourselves with the language and notation to be successful. My guess that you might already be pretty familiar with many
Chapter 1 Points, Lines & Planes s we begin any new topic, we have to familiarize ourselves with the language and notation to be successful. My guess that you might already be pretty familiar with many
Course Name - Strategic Math - Geometry Qtr./Mon. Content HSCE Essential Skills Assessment Vocabulary
 Sem. 1 Sept. Points & Lines G1.1.6 Recognize Euclidean geometry as an axiom system. Know the key axioms and understand the meaning of and distinguish between undefined terms, axioms, definitions, and theorems.
Sem. 1 Sept. Points & Lines G1.1.6 Recognize Euclidean geometry as an axiom system. Know the key axioms and understand the meaning of and distinguish between undefined terms, axioms, definitions, and theorems.
Planar graphs. Math Prof. Kindred - Lecture 16 Page 1
 Planar graphs Typically a drawing of a graph is simply a notational shorthand or a more visual way to capture the structure of the graph. Now we focus on the drawings themselves. Definition A drawing of
Planar graphs Typically a drawing of a graph is simply a notational shorthand or a more visual way to capture the structure of the graph. Now we focus on the drawings themselves. Definition A drawing of
Department: Course: Chapter 1
 Department: Course: 2016-2017 Term, Phrase, or Expression Simple Definition Chapter 1 Comprehension Support Point Line plane collinear coplanar A location in space. It does not have a size or shape The
Department: Course: 2016-2017 Term, Phrase, or Expression Simple Definition Chapter 1 Comprehension Support Point Line plane collinear coplanar A location in space. It does not have a size or shape The
Final Exam 1:15-3:15 pm Thursday, December 13, 2018
 Final Exam 1:15-3:15 pm Thursday, December 13, 2018 Instructions: Answer all questions in the space provided (or attach additional pages as needed). You are permitted to use pencils/pens, one cheat sheet
Final Exam 1:15-3:15 pm Thursday, December 13, 2018 Instructions: Answer all questions in the space provided (or attach additional pages as needed). You are permitted to use pencils/pens, one cheat sheet
Geometry Curriculum Guide Lunenburg County Public Schools June 2014
 Marking Period: 1 Days: 4 Reporting Category/Strand: Reasoning, Lines, and Transformations SOL G.1 The student will construct and judge the validity of a logical argument consisting of a set of premises
Marking Period: 1 Days: 4 Reporting Category/Strand: Reasoning, Lines, and Transformations SOL G.1 The student will construct and judge the validity of a logical argument consisting of a set of premises
Three applications of Euler s formula. Chapter 10
 Three applications of Euler s formula Chapter 10 A graph is planar if it can be drawn in the plane R without crossing edges (or, equivalently, on the -dimensional sphere S ). We talk of a plane graph if
Three applications of Euler s formula Chapter 10 A graph is planar if it can be drawn in the plane R without crossing edges (or, equivalently, on the -dimensional sphere S ). We talk of a plane graph if
Module 1 Session 1 HS. Critical Areas for Traditional Geometry Page 1 of 6
 Critical Areas for Traditional Geometry Page 1 of 6 There are six critical areas (units) for Traditional Geometry: Critical Area 1: Congruence, Proof, and Constructions In previous grades, students were
Critical Areas for Traditional Geometry Page 1 of 6 There are six critical areas (units) for Traditional Geometry: Critical Area 1: Congruence, Proof, and Constructions In previous grades, students were
Mathematics High School Geometry
 Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
CSC Discrete Math I, Spring Sets
 CSC 125 - Discrete Math I, Spring 2017 Sets Sets A set is well-defined, unordered collection of objects The objects in a set are called the elements, or members, of the set A set is said to contain its
CSC 125 - Discrete Math I, Spring 2017 Sets Sets A set is well-defined, unordered collection of objects The objects in a set are called the elements, or members, of the set A set is said to contain its
Little Piece of Random
 Miss C's Little Piece of Random Is this figure possible with a straight arrow and a solid board? Use the toothpick and slip of paper on your desk help you figure out the answer. Announcements Take-Home
Miss C's Little Piece of Random Is this figure possible with a straight arrow and a solid board? Use the toothpick and slip of paper on your desk help you figure out the answer. Announcements Take-Home
7. The Gauss-Bonnet theorem
 7. The Gauss-Bonnet theorem 7.1 Hyperbolic polygons In Euclidean geometry, an n-sided polygon is a subset of the Euclidean plane bounded by n straight lines. Thus the edges of a Euclidean polygon are formed
7. The Gauss-Bonnet theorem 7.1 Hyperbolic polygons In Euclidean geometry, an n-sided polygon is a subset of the Euclidean plane bounded by n straight lines. Thus the edges of a Euclidean polygon are formed
6th Bay Area Mathematical Olympiad
 6th Bay Area Mathematical Olympiad February 4, 004 Problems and Solutions 1 A tiling of the plane with polygons consists of placing the polygons in the plane so that interiors of polygons do not overlap,
6th Bay Area Mathematical Olympiad February 4, 004 Problems and Solutions 1 A tiling of the plane with polygons consists of placing the polygons in the plane so that interiors of polygons do not overlap,
Lines That Intersect Circles
 LESSON 11-1 Lines That Intersect Circles Lesson Objectives (p. 746): Vocabulary 1. Interior of a circle (p. 746): 2. Exterior of a circle (p. 746): 3. Chord (p. 746): 4. Secant (p. 746): 5. Tangent of
LESSON 11-1 Lines That Intersect Circles Lesson Objectives (p. 746): Vocabulary 1. Interior of a circle (p. 746): 2. Exterior of a circle (p. 746): 3. Chord (p. 746): 4. Secant (p. 746): 5. Tangent of
Prentice Hall Geometry 2011 Correlated to: Washington Mathematics Standards, Geometry (2008)
 Geometry G.1. Core Content: Logical arguments and proofs (Logic) Students formalize the reasoning skills they have developed in previous grades and solidify their understanding of what it means to prove
Geometry G.1. Core Content: Logical arguments and proofs (Logic) Students formalize the reasoning skills they have developed in previous grades and solidify their understanding of what it means to prove
Technische Universität München Zentrum Mathematik
 Technische Universität München Zentrum Mathematik Prof. Dr. Dr. Jürgen Richter-Gebert, Bernhard Werner Projective Geometry SS 208 https://www-m0.ma.tum.de/bin/view/lehre/ss8/pgss8/webhome Solutions for
Technische Universität München Zentrum Mathematik Prof. Dr. Dr. Jürgen Richter-Gebert, Bernhard Werner Projective Geometry SS 208 https://www-m0.ma.tum.de/bin/view/lehre/ss8/pgss8/webhome Solutions for
