Reliability Coefficients
|
|
|
- Edith Long
- 5 years ago
- Views:
Transcription
1 Reliability Coefficients Introductory notes That data used for these computations is the pre-treatment scores of all subjects. There are three items in the SIAS (5, 9 and 11) that require reverse-scoring. Those items are stored in the data frame in reverse-coded format. In other words, if a subject responded to one of those items with a score of 0, it has been coded as a 4; if the client responded with a score of 1 it has been coded as a 3, and so on. The following code computes categorical McDonald s omega using the MBESS::ci.reliability() function, classical Cronbach s alpha and the mean inter-item correlation using psych::alpha(). In general, we would expect McDonald s omega values to be higher than the alpha values, as (i) they are based on polychoric correlations, rather than Pearson correlations, and (ii) because it is well known in the psychometric literature that alpha tends to under-estimate reliability for congeneric measurement models. # Load libraries library(dplyr) Attaching package: 'dplyr' The following objects are masked from 'package:stats': filter, lag The following objects are masked from 'package:base': intersect, setdiff, setequal, union library(psych) library(mbess) Attaching package: 'MBESS' The following object is masked from 'package:psych': cor2cov library(lavaan) This is lavaan lavaan is BETA software! Please report any bugs. Attaching package: 'lavaan' 1
2 The following object is masked from 'package:mbess': cor2cov The following object is masked from 'package:psych': cor2cov # Load datafile load("dat.rda") # Setup dummy matrix for storing store reliabilty coefficients x <- matrix(na, nrow = 12, ncol = 3) rownames(x) <- c("sias20", "SIAS19", "SIAS17", "SIAS6", "SIPS-INT", "SPS", "SPS6", "SIPS-FOE", "SIPS-FAA", "SIPS-AGG", "Peters", "SIPS-Tot") colnames(x) <- c("omega", "alpha", "mean_r") # Function to compute omega, alpha, and mean inter-item correlation rel_stats <- function(data, items){ df <- data[, items] x <- c(mbess::ci.reliability(data = df, type = "categorical", interval.type = "none")$est, psych::alpha(df)[[1]][c(1,4)] %>% unlist() ) names(x) <- c("omega", "alpha", "mean_r") x } # Compute Omega, alpha and mean-inter-item correlation # Extract SIAS items at pre-treatment df <- dat %>% select(sias_0_1:sias_0_20) # Compute stats for SIAS measures x[1, ] <- rel_stats(df, 1:20) # sias20 x[2, ] <- rel_stats(df, c(1:4, 6:20)) # sias19 x[3, ] <- rel_stats(df, c(1:4, 6:8, 10, 12:20)) # sias17 x[4, ] <- rel_stats(df, c(2, 4, 6, 8, 10, 13)) # sias6 x[5, ] <- rel_stats(df, c(7, 10, 15, 16, 19)) # sips-int # Extract SPS items at pre-treatment df2 <- dat %>% select(sps_0_1:sps_0_20) 2
3 # Compute stats for SPS measures x[6, ] <- rel_stats(df2, 1:20) # sps20 x[7, ] <- rel_stats(df2, c(4, 7, 8, 15:17)) # sps6 x[8, ] <- rel_stats(df2, c(4, 6, 8, 13, 16, 17)) # sips-foe x[9, ] <- rel_stats(df2, c(12, 14, 15)) # sips-faa x[10, ] <- rel_stats(df2, c(4, 6, 8, 12:17)) # sips-agg # Peters total (SIAS6 + SPS6) df3 <- cbind(df[,c(2, 4, 6, 8, 10, 13)], df2[, c(4, 7, 8, 15:17)]) x[11, ] <- rel_stats(df3, 1:12) # SIPS total df4 <- cbind(df[,c(7, 10, 15, 16, 19)], df2[, c(4, 6, 8, 12:17)]) x[12, ] <- rel_stats(df4, 1:14) # sips total # Display coefficients round(x, 2) omega alpha mean_r SIAS SIAS SIAS SIAS SIPS-INT SPS SPS SIPS-FOE SIPS-FAA SIPS-AGG Peters SIPS-Tot Note that in the above code, separate factor models were specified for each SIPS subscale. An alternate way of computing omega for the SIPS is to define the full two- or three-factor model, and use those solutions to compute omega. library(semtools) # This is semtools All users of R (or SEM) are invited to submit functions or ideas for functions. # 3
4 Attaching package: 'semtools' The following object is masked from 'package:psych': skew # Rearrange SIPS items so that items 1-5 = interaction scale, 6-11 are foe and faa df5 <- cbind(df[,c(7, 10, 15, 16, 19)], df2[, c(4, 6, 8, 13, 16, 17, 12, 14, 15)]) names(df5) <- paste0("v", 1:14) # SIPS 3 factor model m1 <- ' INT =~ v1 + v2 + v3 + v4 + v5 FOE =~ v6 + v7 + v8 + v9 +v10 + v11 FAA =~ v12 + v13 + v14 ' # Omega = Raykov's omega, omega2 = bentler's omega, omega3 = McDonald's omega # Note that alpha is model based on polychoric correlations and thus will differ # from traditional alpha (in the above table) computed using Pearson correlations fit_m1 <- cfa(m1, data = df5, estimator = "WLSMV", std.lv = TRUE, orthogonal = FALSE, missing = "pairwise") round(semtools::reliability(fit_m1),2) INT FOE FAA total alpha omega omega omega avevar The code below compute omega for the SIPS two-factor model, where the two performance anxiety subscales (FOE and FAA) are aggregated. m2 <- ' INT =~ v1 + v2 + v3 + v4 + v5 AGG =~ v6 + v7 + v8 + v9 +v10 + v11 + v12 + v13 + v14 ' fit_m2 <- cfa(m2, data = df5, estimator = "WLSMV", std.lv = TRUE, orthogonal = FALSE, missing = "pairwise") round(semtools::reliability(fit_m2),2) INT AGG total 4
5 alpha omega omega omega avevar SIAS-6 correlation matrix The reliability coefficients for the SIAS-6 is notably lower than for the other scales. We can probe the reason for this by examining the inter-item correlations which should be quite low (the mean inter-item correlation is.27). cor(df[, c(2, 4, 6, 8, 10, 13)]) %>% round(2) sias_0_2 sias_0_4 sias_0_6 sias_0_8 sias_0_10 sias_0_13 sias_0_ NA NA sias_0_4 NA 1 NA NA NA NA sias_0_ NA NA sias_0_ NA NA sias_0_ NA NA sias_0_13 NA NA NA NA NA 1 5
Subsetting, dplyr, magrittr Author: Lloyd Low; add:
 Subsetting, dplyr, magrittr Author: Lloyd Low; Email add: wai.low@adelaide.edu.au Introduction So you have got a table with data that might be a mixed of categorical, integer, numeric, etc variables? And
Subsetting, dplyr, magrittr Author: Lloyd Low; Email add: wai.low@adelaide.edu.au Introduction So you have got a table with data that might be a mixed of categorical, integer, numeric, etc variables? And
Study Guide. Module 1. Key Terms
 Study Guide Module 1 Key Terms general linear model dummy variable multiple regression model ANOVA model ANCOVA model confounding variable squared multiple correlation adjusted squared multiple correlation
Study Guide Module 1 Key Terms general linear model dummy variable multiple regression model ANOVA model ANCOVA model confounding variable squared multiple correlation adjusted squared multiple correlation
050 0 N 03 BECABCDDDBDBCDBDBCDADDBACACBCCBAACEDEDBACBECCDDCEA
 050 0 N 03 BECABCDDDBDBCDBDBCDADDBACACBCCBAACEDEDBACBECCDDCEA 55555555555555555555555555555555555555555555555555 YYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYY 01 CAEADDBEDEDBABBBBCBDDDBAAAECEEDCDCDBACCACEECACCCEA
050 0 N 03 BECABCDDDBDBCDBDBCDADDBACACBCCBAACEDEDBACBECCDDCEA 55555555555555555555555555555555555555555555555555 YYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYY 01 CAEADDBEDEDBABBBBCBDDDBAAAECEEDCDCDBACCACEECACCCEA
050 0 N 03 BECABCDDDBDBCDBDBCDADDBACACBCCBAACEDEDBACBECCDDCEA
 050 0 N 03 BECABCDDDBDBCDBDBCDADDBACACBCCBAACEDEDBACBECCDDCEA 55555555555555555555555555555555555555555555555555 NYYNNYNNNYNYYYYYNNYNNNNNYNYYYYYNYNNNNYNNYNNNYNNNNN 01 CAEADDBEDEDBABBBBCBDDDBAAAECEEDCDCDBACCACEECACCCEA
050 0 N 03 BECABCDDDBDBCDBDBCDADDBACACBCCBAACEDEDBACBECCDDCEA 55555555555555555555555555555555555555555555555555 NYYNNYNNNYNYYYYYNNYNNNNNYNYYYYYNYNNNNYNNYNNNYNNNNN 01 CAEADDBEDEDBABBBBCBDDDBAAAECEEDCDCDBACCACEECACCCEA
Principal Leadership Reliability Measures
 Principal Leadership Reliability Measures Ben Saville, PhD, and JoAnn Alvarez March 26, 2009 This document gives information about missing data as well as cronbach alphas for the 72-item teacher s evaluation
Principal Leadership Reliability Measures Ben Saville, PhD, and JoAnn Alvarez March 26, 2009 This document gives information about missing data as well as cronbach alphas for the 72-item teacher s evaluation
Chapitre 2 : modèle linéaire généralisé
 Chapitre 2 : modèle linéaire généralisé Introduction et jeux de données Avant de commencer Faire pointer R vers votre répertoire setwd("~/dropbox/evry/m1geniomhe/cours/") source(file = "fonction_illustration_logistique.r")
Chapitre 2 : modèle linéaire généralisé Introduction et jeux de données Avant de commencer Faire pointer R vers votre répertoire setwd("~/dropbox/evry/m1geniomhe/cours/") source(file = "fonction_illustration_logistique.r")
SEM 1: Confirmatory Factor Analysis
 SEM 1: Confirmatory Factor Analysis Week 3 - Measurement invariance and ordinal data Sacha Epskamp 17-04-2018 General factor analysis framework: in which: y i = Λη i + ε i y N(0, Σ) η N(0, Ψ) ε N(0, Θ),
SEM 1: Confirmatory Factor Analysis Week 3 - Measurement invariance and ordinal data Sacha Epskamp 17-04-2018 General factor analysis framework: in which: y i = Λη i + ε i y N(0, Σ) η N(0, Ψ) ε N(0, Θ),
SEM 1: Confirmatory Factor Analysis
 SEM 1: Confirmatory Factor Analysis Week 3 - Measurement invariance and ordinal data Sacha Epskamp 18-04-2017 General factor analysis framework: in which: y i = Λη i + ε i y N(0, Σ) η N(0, Ψ) ε N(0, Θ),
SEM 1: Confirmatory Factor Analysis Week 3 - Measurement invariance and ordinal data Sacha Epskamp 18-04-2017 General factor analysis framework: in which: y i = Λη i + ε i y N(0, Σ) η N(0, Ψ) ε N(0, Θ),
How to use the SimpleCOMPASS Interface
 Greg Finak 2018-04-30 Contents 1 Purpose................................ 2 1.1 Prerequisites........................... 2 2 Using SimpleCOMPASS....................... 2 2.1 Reading tabular ICS data.....................
Greg Finak 2018-04-30 Contents 1 Purpose................................ 2 1.1 Prerequisites........................... 2 2 Using SimpleCOMPASS....................... 2 2.1 Reading tabular ICS data.....................
Reproducible Research Week4
 Page 1 of 10 Reproducible Research Week4 Assignment Madhu Lakshmikanthan July 31, 2016 This paper analyzes NOAA storm data from 1950 to November, 2011 obtained from Storm Data (https://d396qusza40orc.cloudfront.net/repdata%
Page 1 of 10 Reproducible Research Week4 Assignment Madhu Lakshmikanthan July 31, 2016 This paper analyzes NOAA storm data from 1950 to November, 2011 obtained from Storm Data (https://d396qusza40orc.cloudfront.net/repdata%
The lavaan tutorial. Yves Rosseel Department of Data Analysis Ghent University (Belgium) December 18, 2017
 The lavaan tutorial Yves Rosseel Department of Data Analysis Ghent University (Belgium) December 18, 2017 Abstract If you are new to lavaan, this is the place to start. In this tutorial, we introduce the
The lavaan tutorial Yves Rosseel Department of Data Analysis Ghent University (Belgium) December 18, 2017 Abstract If you are new to lavaan, this is the place to start. In this tutorial, we introduce the
Day 1: Working with Data
 Day 1: Working with Data Kenneth Benoit Data Mining and Statistical Learning February 9, 2015 Why focus on data types and structures? data mining and data science imply that we know how to work with data
Day 1: Working with Data Kenneth Benoit Data Mining and Statistical Learning February 9, 2015 Why focus on data types and structures? data mining and data science imply that we know how to work with data
Using R and the psych package to find ω
 Using R and the psych package to find ω William Revelle Department of Psychology Northwestern University December 19, 2017 Contents 1 Overview of this and related documents 2 1.1 omega h as an estimate
Using R and the psych package to find ω William Revelle Department of Psychology Northwestern University December 19, 2017 Contents 1 Overview of this and related documents 2 1.1 omega h as an estimate
Data Analysis and Solver Plugins for KSpread USER S MANUAL. Tomasz Maliszewski
 Data Analysis and Solver Plugins for KSpread USER S MANUAL Tomasz Maliszewski tmaliszewski@wp.pl Table of Content CHAPTER 1: INTRODUCTION... 3 1.1. ABOUT DATA ANALYSIS PLUGIN... 3 1.3. ABOUT SOLVER PLUGIN...
Data Analysis and Solver Plugins for KSpread USER S MANUAL Tomasz Maliszewski tmaliszewski@wp.pl Table of Content CHAPTER 1: INTRODUCTION... 3 1.1. ABOUT DATA ANALYSIS PLUGIN... 3 1.3. ABOUT SOLVER PLUGIN...
Introduction to Factor Analysis for Marketing
 Introduction to Factor Analysis for Marketing SKIM/Sawtooth Software Conference 2016, Rome Chris Chapman, Google. April 2016. Special thanks to Josh Lewandowski at Google for helpful feedback (errors are
Introduction to Factor Analysis for Marketing SKIM/Sawtooth Software Conference 2016, Rome Chris Chapman, Google. April 2016. Special thanks to Josh Lewandowski at Google for helpful feedback (errors are
Path Analysis using lm and lavaan
 Path Analysis using lm and lavaan Grant B. Morgan Baylor University September 10, 2014 First of all, this post is going to mirror a page on the Institute for Digital Research and Education (IDRE) site
Path Analysis using lm and lavaan Grant B. Morgan Baylor University September 10, 2014 First of all, this post is going to mirror a page on the Institute for Digital Research and Education (IDRE) site
Data visualization with ggplot2
 Data visualization with ggplot2 Visualizing data in R with the ggplot2 package Authors: Mateusz Kuzak, Diana Marek, Hedi Peterson, Dmytro Fishman Disclaimer We will be using the functions in the ggplot2
Data visualization with ggplot2 Visualizing data in R with the ggplot2 package Authors: Mateusz Kuzak, Diana Marek, Hedi Peterson, Dmytro Fishman Disclaimer We will be using the functions in the ggplot2
Instructions for uploading a file into YouTube, setting up YouTube s Creator Studio and creating closed captions.
 Instructions for uploading a file into YouTube, setting up YouTube s Creator Studio and creating closed captions. Step 1) Go to YouTube and sign into your Google account. a) Select the add video icon.
Instructions for uploading a file into YouTube, setting up YouTube s Creator Studio and creating closed captions. Step 1) Go to YouTube and sign into your Google account. a) Select the add video icon.
Package autovarcore. June 4, 2018
 Package autovarcore June 4, 2018 Type Package Title Automated Vector Autoregression Models and Networks Version 1.0-4 Date 2018-06-04 BugReports https://github.com/roqua/autovarcore/issues Maintainer Ando
Package autovarcore June 4, 2018 Type Package Title Automated Vector Autoregression Models and Networks Version 1.0-4 Date 2018-06-04 BugReports https://github.com/roqua/autovarcore/issues Maintainer Ando
Contents 1 Admin 2 Testing hypotheses tests 4 Simulation 5 Parallelization Admin
 magrittr t F F .. NA library(pacman) p_load(dplyr) x % as_tibble() ## # A tibble: 5 x 2 ## a b ## ## 1 1.. ## 2 2 1 ## 3 3 2 ##
magrittr t F F .. NA library(pacman) p_load(dplyr) x % as_tibble() ## # A tibble: 5 x 2 ## a b ## ## 1 1.. ## 2 2 1 ## 3 3 2 ##
Advanced Plotting Di Cook, Eric Hare May 14, 2015
 Advanced Plotting Di Cook, Eric Hare May 14, 2015 California Dreaming - ASA Travelling Workshop Back to the Oscars oscars
Advanced Plotting Di Cook, Eric Hare May 14, 2015 California Dreaming - ASA Travelling Workshop Back to the Oscars oscars
Main, Paxton, & Dale Data Analysis
 Main, Paxton, & Dale Data Analysis Interest/Validation setwd('/main_paxton_dale-analyses') # preliminaries rm(list=ls()) getwd() [1] "/Main_Paxton_Dale-Analyses" source('globals_functions.r') Loading required
Main, Paxton, & Dale Data Analysis Interest/Validation setwd('/main_paxton_dale-analyses') # preliminaries rm(list=ls()) getwd() [1] "/Main_Paxton_Dale-Analyses" source('globals_functions.r') Loading required
Cut Out The Cut And Paste: SAS Macros For Presenting Statistical Output ABSTRACT INTRODUCTION
 Cut Out The Cut And Paste: SAS Macros For Presenting Statistical Output Myungshin Oh, UCLA Department of Biostatistics Mel Widawski, UCLA School of Nursing ABSTRACT We, as statisticians, often spend more
Cut Out The Cut And Paste: SAS Macros For Presenting Statistical Output Myungshin Oh, UCLA Department of Biostatistics Mel Widawski, UCLA School of Nursing ABSTRACT We, as statisticians, often spend more
Contents 1 Admin 2 Testing hypotheses tests 4 Simulation 5 Parallelization Admin
 magrittr t F F dplyr lfe readr magrittr parallel parallel auto.csv y x y x y x y x # Setup ---- # Settings options(stringsasfactors = F) # Packages library(dplyr) library(lfe) library(magrittr) library(readr)
magrittr t F F dplyr lfe readr magrittr parallel parallel auto.csv y x y x y x y x # Setup ---- # Settings options(stringsasfactors = F) # Packages library(dplyr) library(lfe) library(magrittr) library(readr)
Using R to score personality scales
 Using R to score personality scales William Revelle Northwestern University February 27, 2013 Contents 1 Overview for the impatient 2 2 An example 2 2.1 Getting the data.................................
Using R to score personality scales William Revelle Northwestern University February 27, 2013 Contents 1 Overview for the impatient 2 2 An example 2 2.1 Getting the data.................................
Using R to score personality scales
 Using R to score personality scales William Revelle Northwestern University December 19, 2017 Abstract The psych package (Revelle, 2017) was developed to perform most basic psychometric functions using
Using R to score personality scales William Revelle Northwestern University December 19, 2017 Abstract The psych package (Revelle, 2017) was developed to perform most basic psychometric functions using
2006 Annual Report for the. National Athletic Trainers Association Board of Certification. Inc. CASTLE Worldwide, Inc. March, 2007
 2006 Annual Report for the National Athletic Trainers Association Board of Certification. Inc. CASTLE Worldwide, Inc. March, 2007 The National Athletic Trainers Association Board of Certification, Inc.
2006 Annual Report for the National Athletic Trainers Association Board of Certification. Inc. CASTLE Worldwide, Inc. March, 2007 The National Athletic Trainers Association Board of Certification, Inc.
Simulating Multivariate Normal Data
 Simulating Multivariate Normal Data You have a population correlation matrix and wish to simulate a set of data randomly sampled from a population with that structure. I shall present here code and examples
Simulating Multivariate Normal Data You have a population correlation matrix and wish to simulate a set of data randomly sampled from a population with that structure. I shall present here code and examples
A Worked Example of Goldberg s Bass Ackwards Method
 A Worked Example of Goldberg s Bass Ackwards Method Niels Waller Department of Psychology University of Minnesota nwaller@umn.edu May 10, 2006 This document presents a worked example for Goldberg s Bass
A Worked Example of Goldberg s Bass Ackwards Method Niels Waller Department of Psychology University of Minnesota nwaller@umn.edu May 10, 2006 This document presents a worked example for Goldberg s Bass
Introduction to R. Nishant Gopalakrishnan, Martin Morgan January, Fred Hutchinson Cancer Research Center
 Introduction to R Nishant Gopalakrishnan, Martin Morgan Fred Hutchinson Cancer Research Center 19-21 January, 2011 Getting Started Atomic Data structures Creating vectors Subsetting vectors Factors Matrices
Introduction to R Nishant Gopalakrishnan, Martin Morgan Fred Hutchinson Cancer Research Center 19-21 January, 2011 Getting Started Atomic Data structures Creating vectors Subsetting vectors Factors Matrices
New Features in qgraph Sacha Epskamp
 New Features in qgraph Sacha Epskamp Contents New features in version.4. EBICglasso refitting............................................ Gaussian graphical model fit measures..................................
New Features in qgraph Sacha Epskamp Contents New features in version.4. EBICglasso refitting............................................ Gaussian graphical model fit measures..................................
ehealth literacy and Cancer Screening: A Structural Equation Modeling
 ehealth and Cancer Screening: A Structural Equation Modeling Jung Hoon Baeg, Florida State University Hye-Jin Park, Florida State University Abstract Many people use the Internet for their health information
ehealth and Cancer Screening: A Structural Equation Modeling Jung Hoon Baeg, Florida State University Hye-Jin Park, Florida State University Abstract Many people use the Internet for their health information
CDAA No. 4 - Part Two - Multiple Regression - Initial Data Screening
 CDAA No. 4 - Part Two - Multiple Regression - Initial Data Screening Variables Entered/Removed b Variables Entered GPA in other high school, test, Math test, GPA, High school math GPA a Variables Removed
CDAA No. 4 - Part Two - Multiple Regression - Initial Data Screening Variables Entered/Removed b Variables Entered GPA in other high school, test, Math test, GPA, High school math GPA a Variables Removed
Package MultiVarMI. April 9, 2018
 Type Package Title Multiple Imputation for Multivariate Data Version 1.0 Date 2018-04-08 Author Rawan Allozi, Hakan Demirtas Maintainer Rawan Allozi Package MultiVarMI April 9, 2018 Fully
Type Package Title Multiple Imputation for Multivariate Data Version 1.0 Date 2018-04-08 Author Rawan Allozi, Hakan Demirtas Maintainer Rawan Allozi Package MultiVarMI April 9, 2018 Fully
1, if item A was preferred to item B 0, if item B was preferred to item A
 VERSION 2 BETA (PLEASE EMAIL A.A.BROWN@KENT.AC.UK IF YOU FIND ANY BUGS) MPLUS SYNTAX BUILDER FOR TESTING FORCED-CHOICE DATA WITH THE THURSTONIAN IRT MODEL USER GUIDE INTRODUCTION Brown and Maydeu-Olivares
VERSION 2 BETA (PLEASE EMAIL A.A.BROWN@KENT.AC.UK IF YOU FIND ANY BUGS) MPLUS SYNTAX BUILDER FOR TESTING FORCED-CHOICE DATA WITH THE THURSTONIAN IRT MODEL USER GUIDE INTRODUCTION Brown and Maydeu-Olivares
Using EdSurvey to Analyze NAEP Data: An Illustration of Analyzing NAEP Primer
 Using EdSurvey 1.0.6 to Analyze NAEP Data: An Illustration of Analyzing NAEP Primer Developed by Paul Bailey, Ahmad Emad, Michael Lee, Ting Zhang, Qingshu Xie, & Jiao Yu May 04, 2017 Overview of the EdSurvey
Using EdSurvey 1.0.6 to Analyze NAEP Data: An Illustration of Analyzing NAEP Primer Developed by Paul Bailey, Ahmad Emad, Michael Lee, Ting Zhang, Qingshu Xie, & Jiao Yu May 04, 2017 Overview of the EdSurvey
Package nsprcomp. August 29, 2016
 Version 0.5 Date 2014-02-03 Title Non-Negative and Sparse PCA Package nsprcomp August 29, 2016 Description This package implements two methods for performing a constrained principal component analysis
Version 0.5 Date 2014-02-03 Title Non-Negative and Sparse PCA Package nsprcomp August 29, 2016 Description This package implements two methods for performing a constrained principal component analysis
The Mplus modelling framework
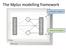 The Mplus modelling framework Continuous variables Categorical variables 1 Mplus syntax structure TITLE: a title for the analysis (not part of the syntax) DATA: (required) information about the data set
The Mplus modelling framework Continuous variables Categorical variables 1 Mplus syntax structure TITLE: a title for the analysis (not part of the syntax) DATA: (required) information about the data set
Package starank. May 11, 2018
 Type Package Title Stability Ranking Version 1.22.0 Date 2012-02-09 Author Juliane Siebourg, Niko Beerenwinkel Package starank May 11, 2018 Maintainer Juliane Siebourg Detecting
Type Package Title Stability Ranking Version 1.22.0 Date 2012-02-09 Author Juliane Siebourg, Niko Beerenwinkel Package starank May 11, 2018 Maintainer Juliane Siebourg Detecting
Package starank. August 3, 2013
 Package starank August 3, 2013 Type Package Title Stability Ranking Version 1.3.0 Date 2012-02-09 Author Juliane Siebourg, Niko Beerenwinkel Maintainer Juliane Siebourg
Package starank August 3, 2013 Type Package Title Stability Ranking Version 1.3.0 Date 2012-02-09 Author Juliane Siebourg, Niko Beerenwinkel Maintainer Juliane Siebourg
Using R for statistics and data analysis
 Introduction ti to R: Using R for statistics and data analysis BaRC Hot Topics October 2011 George Bell, Ph.D. http://iona.wi.mit.edu/bio/education/r2011/ Why use R? To perform inferential statistics (e.g.,
Introduction ti to R: Using R for statistics and data analysis BaRC Hot Topics October 2011 George Bell, Ph.D. http://iona.wi.mit.edu/bio/education/r2011/ Why use R? To perform inferential statistics (e.g.,
Introduction to Mixed Models: Multivariate Regression
 Introduction to Mixed Models: Multivariate Regression EPSY 905: Multivariate Analysis Spring 2016 Lecture #9 March 30, 2016 EPSY 905: Multivariate Regression via Path Analysis Today s Lecture Multivariate
Introduction to Mixed Models: Multivariate Regression EPSY 905: Multivariate Analysis Spring 2016 Lecture #9 March 30, 2016 EPSY 905: Multivariate Regression via Path Analysis Today s Lecture Multivariate
Unified Visualizations of Structural Equation Models
 Chapter 11 Unified Visualizations of Structural Equation Models Abstract Structural Equation Modeling (SEM) has a long history of representing models graphically as path diagrams. This chapter presents
Chapter 11 Unified Visualizations of Structural Equation Models Abstract Structural Equation Modeling (SEM) has a long history of representing models graphically as path diagrams. This chapter presents
An Introductory Guide to R
 An Introductory Guide to R By Claudia Mahler 1 Contents Installing and Operating R 2 Basics 4 Importing Data 5 Types of Data 6 Basic Operations 8 Selecting and Specifying Data 9 Matrices 11 Simple Statistics
An Introductory Guide to R By Claudia Mahler 1 Contents Installing and Operating R 2 Basics 4 Importing Data 5 Types of Data 6 Basic Operations 8 Selecting and Specifying Data 9 Matrices 11 Simple Statistics
Chong Ho Yu, Ph.D., MCSE, CNE. Paper presented at the annual meeting of the American Educational Research Association, 2001, Seattle, WA
 RUNNING HEAD: On-line assessment Developing Data Systems to Support the Analysis and Development of Large-Scale, On-line Assessment Chong Ho Yu, Ph.D., MCSE, CNE Paper presented at the annual meeting of
RUNNING HEAD: On-line assessment Developing Data Systems to Support the Analysis and Development of Large-Scale, On-line Assessment Chong Ho Yu, Ph.D., MCSE, CNE Paper presented at the annual meeting of
Standard Errors in OLS Luke Sonnet
 Standard Errors in OLS Luke Sonnet Contents Variance-Covariance of ˆβ 1 Standard Estimation (Spherical Errors) 2 Robust Estimation (Heteroskedasticity Constistent Errors) 4 Cluster Robust Estimation 7
Standard Errors in OLS Luke Sonnet Contents Variance-Covariance of ˆβ 1 Standard Estimation (Spherical Errors) 2 Robust Estimation (Heteroskedasticity Constistent Errors) 4 Cluster Robust Estimation 7
Package misclassglm. September 3, 2016
 Type Package Package misclassglm September 3, 2016 Title Computation of Generalized Linear Models with Misclassified Covariates Using Side Information Version 0.2.0 Date 2016-09-02 Author Stephan Dlugosz
Type Package Package misclassglm September 3, 2016 Title Computation of Generalized Linear Models with Misclassified Covariates Using Side Information Version 0.2.0 Date 2016-09-02 Author Stephan Dlugosz
STATISTICS (STAT) Statistics (STAT) 1
 Statistics (STAT) 1 STATISTICS (STAT) STAT 2013 Elementary Statistics (A) Prerequisites: MATH 1483 or MATH 1513, each with a grade of "C" or better; or an acceptable placement score (see placement.okstate.edu).
Statistics (STAT) 1 STATISTICS (STAT) STAT 2013 Elementary Statistics (A) Prerequisites: MATH 1483 or MATH 1513, each with a grade of "C" or better; or an acceptable placement score (see placement.okstate.edu).
NAME: BEST FIT LINES USING THE NSPIRE
 NAME: BEST FIT LINES USING THE NSPIRE For this portion of the activity, you will be using the same data sets you just completed where you visually estimated the line of best fit..) Load the data sets into
NAME: BEST FIT LINES USING THE NSPIRE For this portion of the activity, you will be using the same data sets you just completed where you visually estimated the line of best fit..) Load the data sets into
Cluster Analysis. Angela Montanari and Laura Anderlucci
 Cluster Analysis Angela Montanari and Laura Anderlucci 1 Introduction Clustering a set of n objects into k groups is usually moved by the aim of identifying internally homogenous groups according to a
Cluster Analysis Angela Montanari and Laura Anderlucci 1 Introduction Clustering a set of n objects into k groups is usually moved by the aim of identifying internally homogenous groups according to a
Supplementary Material
 Supplementary Material Figure 1S: Scree plot of the 400 dimensional data. The Figure shows the 20 largest eigenvalues of the (normalized) correlation matrix sorted in decreasing order; the insert shows
Supplementary Material Figure 1S: Scree plot of the 400 dimensional data. The Figure shows the 20 largest eigenvalues of the (normalized) correlation matrix sorted in decreasing order; the insert shows
Package fsrm. January 23, 2016
 Encoding UTF-8 Type Package Package fsrm January 23, 2016 Title Social Relations Analyses with Roles (``Family SRM'') Version 0.6.4 Date 2016-01-22 Author Felix Schönbrodt, Lara Stas, Tom Loeys Maintainer
Encoding UTF-8 Type Package Package fsrm January 23, 2016 Title Social Relations Analyses with Roles (``Family SRM'') Version 0.6.4 Date 2016-01-22 Author Felix Schönbrodt, Lara Stas, Tom Loeys Maintainer
Functions and data structures. Programming in R for Data Science Anders Stockmarr, Kasper Kristensen, Anders Nielsen
 Functions and data structures Programming in R for Data Science Anders Stockmarr, Kasper Kristensen, Anders Nielsen Objects of the game In R we have objects which are functions and objects which are data.
Functions and data structures Programming in R for Data Science Anders Stockmarr, Kasper Kristensen, Anders Nielsen Objects of the game In R we have objects which are functions and objects which are data.
Performance of Latent Growth Curve Models with Binary Variables
 Performance of Latent Growth Curve Models with Binary Variables Jason T. Newsom & Nicholas A. Smith Department of Psychology Portland State University 1 Goal Examine estimation of latent growth curve models
Performance of Latent Growth Curve Models with Binary Variables Jason T. Newsom & Nicholas A. Smith Department of Psychology Portland State University 1 Goal Examine estimation of latent growth curve models
Math CST 2003 Accuracy
 probability 1 Math CST 2003 Accuracy 0.8 Average Hitrate 0.6 Two-test Consistency 0.4 0.2 Proficiency Standard false negative false positive 2 3 4 5 6 7 Grade probability 1 ELA CST 2003 Accuracy 0.8 Average
probability 1 Math CST 2003 Accuracy 0.8 Average Hitrate 0.6 Two-test Consistency 0.4 0.2 Proficiency Standard false negative false positive 2 3 4 5 6 7 Grade probability 1 ELA CST 2003 Accuracy 0.8 Average
Online Supplementary Appendix for. Dziak, Nahum-Shani and Collins (2012), Multilevel Factorial Experiments for Developing Behavioral Interventions:
 Online Supplementary Appendix for Dziak, Nahum-Shani and Collins (2012), Multilevel Factorial Experiments for Developing Behavioral Interventions: Power, Sample Size, and Resource Considerations 1 Appendix
Online Supplementary Appendix for Dziak, Nahum-Shani and Collins (2012), Multilevel Factorial Experiments for Developing Behavioral Interventions: Power, Sample Size, and Resource Considerations 1 Appendix
Sub-setting Data. Tzu L. Phang
 Sub-setting Data Tzu L. Phang 2016-10-13 Subsetting in R Let s start with a (dummy) vectors. x
Sub-setting Data Tzu L. Phang 2016-10-13 Subsetting in R Let s start with a (dummy) vectors. x
WELCOME! Lecture 3 Thommy Perlinger
 Quantitative Methods II WELCOME! Lecture 3 Thommy Perlinger Program Lecture 3 Cleaning and transforming data Graphical examination of the data Missing Values Graphical examination of the data It is important
Quantitative Methods II WELCOME! Lecture 3 Thommy Perlinger Program Lecture 3 Cleaning and transforming data Graphical examination of the data Missing Values Graphical examination of the data It is important
DU PhD in Physical Education
 DU PhD in Physical Education Topic:- DU_J18_PHD_PE 1) Classifying a person on the basis of his attribute is an example of [Question ID = 52236] 1. Discrete variable [Option ID = 88938] 2. Random Variable
DU PhD in Physical Education Topic:- DU_J18_PHD_PE 1) Classifying a person on the basis of his attribute is an example of [Question ID = 52236] 1. Discrete variable [Option ID = 88938] 2. Random Variable
Distributed Itembased Collaborative Filtering with Apache Mahout. Sebastian Schelter twitter.com/sscdotopen. 7.
 Distributed Itembased Collaborative Filtering with Apache Mahout Sebastian Schelter ssc@apache.org twitter.com/sscdotopen 7. October 2010 Overview 1. What is Apache Mahout? 2. Introduction to Collaborative
Distributed Itembased Collaborative Filtering with Apache Mahout Sebastian Schelter ssc@apache.org twitter.com/sscdotopen 7. October 2010 Overview 1. What is Apache Mahout? 2. Introduction to Collaborative
WEEK 8: FUNCTIONS AND LOOPS. 1. Functions
 WEEK 8: FUNCTIONS AND LOOPS THOMAS ELLIOTT 1. Functions Functions allow you to define a set of instructions and then call the code in a single line. In R, functions are defined much like any other object,
WEEK 8: FUNCTIONS AND LOOPS THOMAS ELLIOTT 1. Functions Functions allow you to define a set of instructions and then call the code in a single line. In R, functions are defined much like any other object,
3. CENTRAL TENDENCY MEASURES AND OTHER CLASSICAL ITEM ANALYSES OF THE 2011 MOD-MSA: MATHEMATICS
 3. CENTRAL TENDENCY MEASURES AND OTHER CLASSICAL ITEM ANALYSES OF THE 2011 MOD-MSA: MATHEMATICS This section provides central tendency statistics and results of classical statistical item analyses for
3. CENTRAL TENDENCY MEASURES AND OTHER CLASSICAL ITEM ANALYSES OF THE 2011 MOD-MSA: MATHEMATICS This section provides central tendency statistics and results of classical statistical item analyses for
Comparison of Linear Regression with K-Nearest Neighbors
 Comparison of Linear Regression with K-Nearest Neighbors Rebecca C. Steorts, Duke University STA 325, Chapter 3.5 ISL Agenda Intro to KNN Comparison of KNN and Linear Regression K-Nearest Neighbors vs
Comparison of Linear Regression with K-Nearest Neighbors Rebecca C. Steorts, Duke University STA 325, Chapter 3.5 ISL Agenda Intro to KNN Comparison of KNN and Linear Regression K-Nearest Neighbors vs
Independent Variables
 1 Stepwise Multiple Regression Olivia Cohen Com 631, Spring 2017 Data: Film & TV Usage 2015 I. MODEL Independent Variables Demographics Item: Age Item: Income Dummied Item: Gender (Female) Digital Media
1 Stepwise Multiple Regression Olivia Cohen Com 631, Spring 2017 Data: Film & TV Usage 2015 I. MODEL Independent Variables Demographics Item: Age Item: Income Dummied Item: Gender (Female) Digital Media
Description/History Objects/Language Description Commonly Used Basic Functions. More Specific Functionality Further Resources
 R Outline Description/History Objects/Language Description Commonly Used Basic Functions Basic Stats and distributions I/O Plotting Programming More Specific Functionality Further Resources www.r-project.org
R Outline Description/History Objects/Language Description Commonly Used Basic Functions Basic Stats and distributions I/O Plotting Programming More Specific Functionality Further Resources www.r-project.org
An Introduction to Growth Curve Analysis using Structural Equation Modeling
 An Introduction to Growth Curve Analysis using Structural Equation Modeling James Jaccard New York University 1 Overview Will introduce the basics of growth curve analysis (GCA) and the fundamental questions
An Introduction to Growth Curve Analysis using Structural Equation Modeling James Jaccard New York University 1 Overview Will introduce the basics of growth curve analysis (GCA) and the fundamental questions
Package filematrix. R topics documented: February 27, Type Package
 Type Package Package filematrix February 27, 2018 Title File-Backed Matrix Class with Convenient Read and Write Access Version 1.3 Date 2018-02-26 Description Interface for working with large matrices
Type Package Package filematrix February 27, 2018 Title File-Backed Matrix Class with Convenient Read and Write Access Version 1.3 Date 2018-02-26 Description Interface for working with large matrices
Why use R? Getting started. Why not use R? Introduction to R: Log into tak. Start R R or. It s hard to use at first
 Why use R? Introduction to R: Using R for statistics ti ti and data analysis BaRC Hot Topics October 2011 George Bell, Ph.D. http://iona.wi.mit.edu/bio/education/r2011/ To perform inferential statistics
Why use R? Introduction to R: Using R for statistics ti ti and data analysis BaRC Hot Topics October 2011 George Bell, Ph.D. http://iona.wi.mit.edu/bio/education/r2011/ To perform inferential statistics
Differential Expression Analysis at PATRIC
 Differential Expression Analysis at PATRIC The following step- by- step workflow is intended to help users learn how to upload their differential gene expression data to their private workspace using Expression
Differential Expression Analysis at PATRIC The following step- by- step workflow is intended to help users learn how to upload their differential gene expression data to their private workspace using Expression
Kingsley Associates Portal User Guide
 Kingsley Associates Portal User Guide Kingsley Portal Overview The Kingsley Portal is a web-based, real time survey tracking tool Dashboard Response Rates Respondent List Reporting Online Reputation Key
Kingsley Associates Portal User Guide Kingsley Portal Overview The Kingsley Portal is a web-based, real time survey tracking tool Dashboard Response Rates Respondent List Reporting Online Reputation Key
Using the Manage Institution Users Tool
 Using the Manage Institution Users Tool Welcome to the Pearson eportfolio system. This guide contains instructions for Faculty Administrators to assign roles to participating faculty. The role assignment
Using the Manage Institution Users Tool Welcome to the Pearson eportfolio system. This guide contains instructions for Faculty Administrators to assign roles to participating faculty. The role assignment
Product Catalog. AcaStat. Software
 Product Catalog AcaStat Software AcaStat AcaStat is an inexpensive and easy-to-use data analysis tool. Easily create data files or import data from spreadsheets or delimited text files. Run crosstabulations,
Product Catalog AcaStat Software AcaStat AcaStat is an inexpensive and easy-to-use data analysis tool. Easily create data files or import data from spreadsheets or delimited text files. Run crosstabulations,
lavaan: an R package for structural equation modeling and more Version (BETA)
 lavaan: an R package for structural equation modeling and more Version 0.4-9 (BETA) Yves Rosseel Department of Data Analysis Ghent University (Belgium) June 14, 2011 Abstract The lavaan package is developed
lavaan: an R package for structural equation modeling and more Version 0.4-9 (BETA) Yves Rosseel Department of Data Analysis Ghent University (Belgium) June 14, 2011 Abstract The lavaan package is developed
Package apricom. R topics documented: November 24, 2015
 Package apricom November 24, 2015 Title Tools for the a Priori Comparison of Regression Modelling Strategies Version 1.0.0 Date 2015-11-11 Maintainer Romin Pajouheshnia Tools
Package apricom November 24, 2015 Title Tools for the a Priori Comparison of Regression Modelling Strategies Version 1.0.0 Date 2015-11-11 Maintainer Romin Pajouheshnia Tools
Count outlier detection using Cook s distance
 Count outlier detection using Cook s distance Michael Love August 9, 2014 1 Run DE analysis with and without outlier removal The following vignette produces the Supplemental Figure of the effect of replacing
Count outlier detection using Cook s distance Michael Love August 9, 2014 1 Run DE analysis with and without outlier removal The following vignette produces the Supplemental Figure of the effect of replacing
Mathematics Masters Examination
 Mathematics Masters Examination OPTION 4 March 30, 2004 COMPUTER SCIENCE 2 5 PM NOTE: Any student whose answers require clarification may be required to submit to an oral examination. Each of the fourteen
Mathematics Masters Examination OPTION 4 March 30, 2004 COMPUTER SCIENCE 2 5 PM NOTE: Any student whose answers require clarification may be required to submit to an oral examination. Each of the fourteen
Package SMAT. January 29, 2013
 Package SMAT January 29, 2013 Type Package Title Scaled Multiple-phenotype Association Test Version 0.98 Date 2013-01-26 Author Lin Li, Ph.D.; Elizabeth D. Schifano, Ph.D. Maintainer Lin Li ;
Package SMAT January 29, 2013 Type Package Title Scaled Multiple-phenotype Association Test Version 0.98 Date 2013-01-26 Author Lin Li, Ph.D.; Elizabeth D. Schifano, Ph.D. Maintainer Lin Li ;
The SQLiteDF Package
 The SQLiteDF Package August 25, 2006 Type Package Title Stores data frames & matrices in SQLite tables Version 0.1.18 Date 2006-08-18 Author Maintainer Transparently stores data frames
The SQLiteDF Package August 25, 2006 Type Package Title Stores data frames & matrices in SQLite tables Version 0.1.18 Date 2006-08-18 Author Maintainer Transparently stores data frames
Python for Data Analysis. Prof.Sushila Aghav-Palwe Assistant Professor MIT
 Python for Data Analysis Prof.Sushila Aghav-Palwe Assistant Professor MIT Four steps to apply data analytics: 1. Define your Objective What are you trying to achieve? What could the result look like? 2.
Python for Data Analysis Prof.Sushila Aghav-Palwe Assistant Professor MIT Four steps to apply data analytics: 1. Define your Objective What are you trying to achieve? What could the result look like? 2.
Programming with R. Educational Materials 2006 S. Falcon, R. Ihaka, and R. Gentleman
 Programming with R Educational Materials 2006 S. Falcon, R. Ihaka, and R. Gentleman 1 Data Structures ˆ R has a rich set of self-describing data structures. > class(z) [1] "character" > class(x) [1] "data.frame"
Programming with R Educational Materials 2006 S. Falcon, R. Ihaka, and R. Gentleman 1 Data Structures ˆ R has a rich set of self-describing data structures. > class(z) [1] "character" > class(x) [1] "data.frame"
Introduction to R. Educational Materials 2007 S. Falcon, R. Ihaka, and R. Gentleman
 Introduction to R Educational Materials 2007 S. Falcon, R. Ihaka, and R. Gentleman 1 Data Structures ˆ R has a rich set of self-describing data structures. > class(z) [1] "character" > class(x) [1] "data.frame"
Introduction to R Educational Materials 2007 S. Falcon, R. Ihaka, and R. Gentleman 1 Data Structures ˆ R has a rich set of self-describing data structures. > class(z) [1] "character" > class(x) [1] "data.frame"
Package doppelgangr. March 25, 2019
 Package doppelgangr March 25, 2019 Title Identify likely duplicate samples from genomic or meta-data Version 1.10.1 The main function is doppelgangr(), which takes as minimal input a list of ExpressionSet
Package doppelgangr March 25, 2019 Title Identify likely duplicate samples from genomic or meta-data Version 1.10.1 The main function is doppelgangr(), which takes as minimal input a list of ExpressionSet
Multivariate Capability Analysis
 Multivariate Capability Analysis Summary... 1 Data Input... 3 Analysis Summary... 4 Capability Plot... 5 Capability Indices... 6 Capability Ellipse... 7 Correlation Matrix... 8 Tests for Normality... 8
Multivariate Capability Analysis Summary... 1 Data Input... 3 Analysis Summary... 4 Capability Plot... 5 Capability Indices... 6 Capability Ellipse... 7 Correlation Matrix... 8 Tests for Normality... 8
Programming with R. Educational Materials 2006 S. Falcon, R. Ihaka, and R. Gentleman
 Programming with R Educational Materials 2006 S. Falcon, R. Ihaka, and R. Gentleman 1 Data Structures ˆ R has a rich set of self-describing data structures. > class(z) [1] "character" > class(x) [1] "data.frame"
Programming with R Educational Materials 2006 S. Falcon, R. Ihaka, and R. Gentleman 1 Data Structures ˆ R has a rich set of self-describing data structures. > class(z) [1] "character" > class(x) [1] "data.frame"
Simple_h2o Rob McCulloch April 15, 2019
 Simple_h2o Rob McCulloch April 15, 2019 Contents Start Up h2o 1 Setup up the data 2 Run a logit for comparison 3 Put the data in h2o form 4 Fit a Deep Neural Net 6 Start Up h2o To use h2o you have to imagine
Simple_h2o Rob McCulloch April 15, 2019 Contents Start Up h2o 1 Setup up the data 2 Run a logit for comparison 3 Put the data in h2o form 4 Fit a Deep Neural Net 6 Start Up h2o To use h2o you have to imagine
Package texteffect. November 27, 2017
 Version 0.1 Date 2017-11-27 Package texteffect November 27, 2017 Title Discovering Latent Treatments in Text Corpora and Estimating Their Causal Effects Author Christian Fong
Version 0.1 Date 2017-11-27 Package texteffect November 27, 2017 Title Discovering Latent Treatments in Text Corpora and Estimating Their Causal Effects Author Christian Fong
Application of Hierarchical Clustering to Find Expression Modules in Cancer
 Application of Hierarchical Clustering to Find Expression Modules in Cancer T. M. Murali August 18, 2008 Innovative Application of Hierarchical Clustering A module map showing conditional activity of expression
Application of Hierarchical Clustering to Find Expression Modules in Cancer T. M. Murali August 18, 2008 Innovative Application of Hierarchical Clustering A module map showing conditional activity of expression
Package tidystats. May 6, 2018
 Title Create a Tidy Statistics Output File Version 0.2 Package tidystats May 6, 2018 Produce a data file containing the output of statistical models and assist with a workflow aimed at writing scientific
Title Create a Tidy Statistics Output File Version 0.2 Package tidystats May 6, 2018 Produce a data file containing the output of statistical models and assist with a workflow aimed at writing scientific
Introduction to R: Using R for Statistics and Data Analysis. BaRC Hot Topics
 Introduction to R: Using R for Statistics and Data Analysis BaRC Hot Topics http://barc.wi.mit.edu/hot_topics/ Why use R? Perform inferential statistics (e.g., use a statistical test to calculate a p-value)
Introduction to R: Using R for Statistics and Data Analysis BaRC Hot Topics http://barc.wi.mit.edu/hot_topics/ Why use R? Perform inferential statistics (e.g., use a statistical test to calculate a p-value)
Florida State University Libraries
 Florida State University Libraries Electronic Theses, Treatises and Dissertations The Graduate School 2013 Use of Item Parceling in Structural Equation Modeling with Missing Data Fatih Orcan Follow this
Florida State University Libraries Electronic Theses, Treatises and Dissertations The Graduate School 2013 Use of Item Parceling in Structural Equation Modeling with Missing Data Fatih Orcan Follow this
Stat 579: Objects in R Vectors
 Stat 579: Objects in R Vectors Ranjan Maitra 2220 Snedecor Hall Department of Statistics Iowa State University. Phone: 515-294-7757 maitra@iastate.edu, 1/23 Logical Vectors I R allows manipulation of logical
Stat 579: Objects in R Vectors Ranjan Maitra 2220 Snedecor Hall Department of Statistics Iowa State University. Phone: 515-294-7757 maitra@iastate.edu, 1/23 Logical Vectors I R allows manipulation of logical
Package linkspotter. July 22, Type Package
 Type Package Package linkspotter July 22, 2018 Title Bivariate Correlations Calculation and Visualization Version 1.2.0 Date 2018-07-18 Compute and visualize using the 'visnetwork' package all the bivariate
Type Package Package linkspotter July 22, 2018 Title Bivariate Correlations Calculation and Visualization Version 1.2.0 Date 2018-07-18 Compute and visualize using the 'visnetwork' package all the bivariate
Intermediate Programming in R Session 2: Loops. Olivia Lau, PhD
 Intermediate Programming in R Session 2: Loops Olivia Lau, PhD Outline When to Use Loops Measuring and Monitoring R s Performance Different Types of Loops Fast Loops 2 When to Use Loops Loops repeat a
Intermediate Programming in R Session 2: Loops Olivia Lau, PhD Outline When to Use Loops Measuring and Monitoring R s Performance Different Types of Loops Fast Loops 2 When to Use Loops Loops repeat a
Bivariate (Simple) Regression Analysis
 Revised July 2018 Bivariate (Simple) Regression Analysis This set of notes shows how to use Stata to estimate a simple (two-variable) regression equation. It assumes that you have set Stata up on your
Revised July 2018 Bivariate (Simple) Regression Analysis This set of notes shows how to use Stata to estimate a simple (two-variable) regression equation. It assumes that you have set Stata up on your
Section 4: FWL and model fit
 Section 4: FWL and model fit Ed Rubin Contents 1 Admin 1 1.1 What you will need........................................ 1 1.2 Last week............................................. 2 1.3 This week.............................................
Section 4: FWL and model fit Ed Rubin Contents 1 Admin 1 1.1 What you will need........................................ 1 1.2 Last week............................................. 2 1.3 This week.............................................
Special review: Evaluation of the exploratory factor analysis programs provided in SPSSX and SPSS/PC+
 Bond University From the SelectedWorks of Gregory J. Boyle 1993 Special review: Evaluation of the exploratory factor analysis programs provided in SPSSX and SPSS/PC+ Gregory J. Boyle, University of Queensland
Bond University From the SelectedWorks of Gregory J. Boyle 1993 Special review: Evaluation of the exploratory factor analysis programs provided in SPSSX and SPSS/PC+ Gregory J. Boyle, University of Queensland
Introduction: EViews. Dr. Peerapat Wongchaiwat
 Introduction: EViews Dr. Peerapat Wongchaiwat wongchaiwat@hotmail.com Today s Workshop Basic grasp of how EViews manages data Creating Workfiles Importing data Running regressions Performing basic tests
Introduction: EViews Dr. Peerapat Wongchaiwat wongchaiwat@hotmail.com Today s Workshop Basic grasp of how EViews manages data Creating Workfiles Importing data Running regressions Performing basic tests
- 1 - Fig. A5.1 Missing value analysis dialog box
 WEB APPENDIX Sarstedt, M. & Mooi, E. (2019). A concise guide to market research. The process, data, and methods using SPSS (3 rd ed.). Heidelberg: Springer. Missing Value Analysis and Multiple Imputation
WEB APPENDIX Sarstedt, M. & Mooi, E. (2019). A concise guide to market research. The process, data, and methods using SPSS (3 rd ed.). Heidelberg: Springer. Missing Value Analysis and Multiple Imputation
Package endogenous. October 29, 2016
 Package endogenous October 29, 2016 Type Package Title Classical Simultaneous Equation Models Version 1.0 Date 2016-10-25 Maintainer Andrew J. Spieker Description Likelihood-based
Package endogenous October 29, 2016 Type Package Title Classical Simultaneous Equation Models Version 1.0 Date 2016-10-25 Maintainer Andrew J. Spieker Description Likelihood-based
Estimation of Item Response Models
 Estimation of Item Response Models Lecture #5 ICPSR Item Response Theory Workshop Lecture #5: 1of 39 The Big Picture of Estimation ESTIMATOR = Maximum Likelihood; Mplus Any questions? answers Lecture #5:
Estimation of Item Response Models Lecture #5 ICPSR Item Response Theory Workshop Lecture #5: 1of 39 The Big Picture of Estimation ESTIMATOR = Maximum Likelihood; Mplus Any questions? answers Lecture #5:
