Induction and Recursion
|
|
|
- Lawrence Boyd
- 5 years ago
- Views:
Transcription
1 Induction and Recursion Induction is a mathematical proof technique. When this technique is used in programming, it is called recursion. The difference is that induction applies to infinite sets and cannot be implemented, while recursion applies to finite sets and can be implemented. Induction/recursion is the fundamental mechanism for extending logical proof techniques into object domains and data structures, defining and building mathematical and programming objects, decomposing objects so that functions can be applied to the elementary units, and robust programming style and program verification. Most practical computational problems are succinctly expressed in a recursive form (for instance, tree and graph traversal, spatial decomposition, divide-and-conquer algorithms, sorting, searching, and large classes of mathematical functions). As well, recursive function theory defines what can and cannot be computed. Optimizing compilers usually convert recursion into do-loops. This is because the overhead of making multiple function calls during recursion is greater than a single do-loop. During the 1980s, programmers learned to write loops rather than recursions so that programs would run faster. This type of optimization is irrelevant today. It is far more important to enhance code readability, maintenance, and extendibility than to do an obsolete runtime optimization. Recursive programming is mathematical programming. Once learned, almost all data structures and algorithms become both simpler and more comprehendible using recursion. The essential difficulty is that programmers need to be trained to think recursively. Recursive Programming Inductive definitions build up from the base case to any degree of complexity. Recursive programs reduce any degree of complexity one step at a time until the base case is reached. A recursion must be well-founded, that is, the steps must eventually terminate at the base. In most cases, the step increment is monotonically decreasing. Recursive programs can be expressed in two forms, mathematical and accumulating. The mathematical form accumulates unevaluated operators on the outside and evaluates them after the base is reached. The accumulating form evaluates operators as they accumulate; when the base is reached, the result is returned. Accumulating functions have better performance than mathematical recursions, and easily compile into do-loops. Mathematical: if (base-case is true) then base-value else F[recursive-step] Accumulating: if (base-case is true) then accum else F[recursive-step, (accum + step)] 1
2 Mathematical Induction Induction depends on a order relation over a domain U. The idea is to demonstrate truth for the base case (the simplest member of the ordered set), and then to demonstrate the truth for an arbitrary member of the set, assuming the truth of the member next to it in the order relation. If N is an ordered set and property P istrue for 1) the minimal member of N, and 2) if P(x) then P(next(x)) then P istrue for all members x of N. Using the natural numbers, N = {1, 2,...}: If P(1) istrue, and assuming P(x) we can show that P(x+1) istrue, then P(x) istrue for all members of N. Some Inductive Definitions Base case: the value of the most elementary case Examples: zero one Phi nil false the additive identity the multiplicative identity the empty set the empty list, the empty tree the logical ground Generating rule: the transform which defines the next case, given an arbitrary case Examples: successor[n] = current[n] + 1 power-of-2[n] = 2 * current[n] summation[n] = n + current[n] last[list] = rest[list] = nil length[list] = length[rest[list]] + 1 member[x,s] = x=select[s] or member[x,rest[s]] power-set[s] = current[s] * S cardinality[s] = cardinality[rest[s]] + 1 node[btree] = left[btree] + right[btree] logic-form[lf] = current[lf] implies next[lf] parenthesis[pf] = "(" + current[pf] + ")" or current[pf] + next[pf] 2
3 R e c u r s i o n Recursion is a form of induction in which we demonstrate two truths via computation. For the boolean property P, 1) P(minimal-member) istrue 2) If P(arbitrary-member) istrue then P(arbitrary-member-one-step-closer-to-minimal-member) istrue Without algebraic processing, the second step requires an instance of the arbitrary member in order to perform computation. For example, say you are trying to find the product of N integers (the factorial function): factorial[n] =def= (if n=1 then 1 else (n * factorial[n-1])) This code requires a value of N in order to compute a value for the factorial of N. However, writing and proving the code itself requires mathematical induction. Above, the base case is when N=1. The recursive invariant, which is true for all N>1, is: factorial[n] = (n * factorial[n-1]) The recursive invariant is the general definition of the function. It states what remains the same when the value of N changes. When a function is written as a do-loop, the recursive invariant is called the loop invariant. Again, it defines what is always true each time through the loop. By verifying that a loop or a recursion maintains its invariant, it is possible to prove that code performs correctly. The accumulating version of the factorial function is factorial-acc[n, acc] =def= (if n=1 then acc else factorial-acc[n-1, n*acc]) Recursive Function Exercises Write recursive procedures (actual or pseudo-code) for the following functions. Where possible, write both the mathematical and the accumulating versions. Example: +[i,j] =def= (if j=0 then i else (+[i,j-1] + 1)) +[i,j] =def= +acc[j,i] +acc[j,acc] =def= (if j=0 then acc else +acc[j-1,acc+1]) 3
4 Integer Domain: {i,j,k,n} are positive integers. Note that the definitions below use mathematical induction; a recursive procedure must phrase the ordering relation in a descending form. i+j =def= i+0 = i i+next[j] = (i+j) + 1 i*j =def= i*0 = 0 i*next[j] = (i*j) + i i^j =def= i^0 = 1 i^next[j] = (i^j) * i sum[n] =def= sum[0] = 0 sum[i+1] = sum[i] + (i+1) fac[n] =def= fac[0] = 1 fac[i+1] = fac[i] * (i+1) fib[n] =def= fib[1] = fib[2] = 1 fib[i+2] = fib[i+1] + fib[n] Using mathematical induction, prove the following for integers: (i*i) = (i^2) (i*j) + (i*k) = i*(j+k) (2*sum[n]) = n*(n+1) (n^2) = (2*sum[n-1]) + n (3*sum[n^2]) = (2*n + 1) * sum[n] fib[n^2] = fib[n+1] * fib[n] sum[n^3] = (sum[n]^2) List Domain: {x,y} are elements, list is a list. Write these recursive functions: last[list] returns the last element of list. length[list] returns the length of list. member[x,list] Boolean, returns T iff x is a member of list. 4
5 copy[list] returns a copy of list. alternating-elements[list] returns a new list of every other element of list. reverse[list] returns a new list with the elements of list in reverse order. samelength[list1,list2] Boolean, returns T iff both lists have the same length (Do not use any integer arithmetic for this.) intersection[list1,list2] returns a new list which contains elements in both list1 and list2. list-equal[list1,list2] Boolean, returns T iff list1=list2 (elements in same order). set-equal[list1,list2] Boolean, returns T iff both list1 and list2 have the same elements, not necessarily in order. append[list1,list2] returns a new list which is list1 appended to list2. substitute[x,y,list] returns a new list with x substituted for every occurrence of y in list. Using mathematical induction, prove the following properties about list functions (harder): length[append[list1,list2]] = length[list1] + length[list2] last[list] = first[reverse[list]] samelength[list, reverse[list]] reverse[reverse[list]] = list substitute[x,y,substitute[y,x,list]] =/= list 5
6 Tree Domain: tree is an arbitrary tree. depth[tree] returns the maximum depth of tree. flatten[tree] returns a list of all nodes of tree fringe[tree] returns a list of the leaf nodes of tree Function Domain: f is a function; p is a Boolean function andlist[list] returns the Boolean AND of a list of Boolean elements map[f,list] returns a new list with the function f applied to each element of list mapchoose[p,list] returns a new list with every element from list which satisfies test p Challenge: Implement the following recursive functions over integers and trace their execution. What do you observe? (Try fm for i= {341,96,104,336,133}; try ackermann and takeuchi for small integers only.) fm[i] =def= ackermann[i,j] =def= ackermann2[i,j] =def= if i=1 then stop else if even[i] then fm[i/2] else fm[(3i+1)/2] if i=0 then j+1 else if j=0 then ackermann[i-1,j] else ackermann[i,j-1] if i=0 then j+1 else if j=0 then ackermann[i-1,1] else ackermann[i-1,ackermann[i,j-1]] 6
7 takeuchi[i,j,k] =def= if (i =< j) then k else takeuchi[takeuchi[i-1,j,k],takeuchi[j-1,k,i],takeuchi[k-1,i,j]] 7
Recursion. Tjark Weber. Functional Programming 1. Based on notes by Sven-Olof Nyström. Tjark Weber (UU) Recursion 1 / 37
 Tjark Weber Functional Programming 1 Based on notes by Sven-Olof Nyström Tjark Weber (UU) Recursion 1 / 37 Background FP I / Advanced FP FP I / Advanced FP This course (Functional Programming I) (5 hp,
Tjark Weber Functional Programming 1 Based on notes by Sven-Olof Nyström Tjark Weber (UU) Recursion 1 / 37 Background FP I / Advanced FP FP I / Advanced FP This course (Functional Programming I) (5 hp,
A Small Interpreted Language
 A Small Interpreted Language What would you need to build a small computing language based on mathematical principles? The language should be simple, Turing equivalent (i.e.: it can compute anything that
A Small Interpreted Language What would you need to build a small computing language based on mathematical principles? The language should be simple, Turing equivalent (i.e.: it can compute anything that
Module 05: Types of recursion
 Module 05: Types of recursion Topics: Review of purely structural recursion Accumulative recursion Generative recursion Readings:ThinkP 5.8-5.10, 6.5-6.7 1 Review: Structural Recursion Template for code
Module 05: Types of recursion Topics: Review of purely structural recursion Accumulative recursion Generative recursion Readings:ThinkP 5.8-5.10, 6.5-6.7 1 Review: Structural Recursion Template for code
1.3. Conditional expressions To express case distinctions like
 Introduction Much of the theory developed in the underlying course Logic II can be implemented in a proof assistant. In the present setting this is interesting, since we can then machine extract from a
Introduction Much of the theory developed in the underlying course Logic II can be implemented in a proof assistant. In the present setting this is interesting, since we can then machine extract from a
Recursion. What is Recursion? Simple Example. Repeatedly Reduce the Problem Into Smaller Problems to Solve the Big Problem
 Recursion Repeatedly Reduce the Problem Into Smaller Problems to Solve the Big Problem What is Recursion? A problem is decomposed into smaller sub-problems, one or more of which are simpler versions of
Recursion Repeatedly Reduce the Problem Into Smaller Problems to Solve the Big Problem What is Recursion? A problem is decomposed into smaller sub-problems, one or more of which are simpler versions of
recursive algorithms 1
 COMP 250 Lecture 11 recursive algorithms 1 Oct. 2, 2017 1 Example 1: Factorial (iterative)! = 1 2 3 1 factorial( n ){ // assume n >= 1 result = 1 for (k = 2; k
COMP 250 Lecture 11 recursive algorithms 1 Oct. 2, 2017 1 Example 1: Factorial (iterative)! = 1 2 3 1 factorial( n ){ // assume n >= 1 result = 1 for (k = 2; k
Recursion. Lars-Henrik Eriksson. Functional Programming 1. Based on a presentation by Tjark Weber and notes by Sven-Olof Nyström
 Lars-Henrik Eriksson Functional Programming 1 Based on a presentation by Tjark Weber and notes by Sven-Olof Nyström Tjark Weber (UU) Recursion 1 / 41 Comparison: Imperative/Functional Programming Comparison:
Lars-Henrik Eriksson Functional Programming 1 Based on a presentation by Tjark Weber and notes by Sven-Olof Nyström Tjark Weber (UU) Recursion 1 / 41 Comparison: Imperative/Functional Programming Comparison:
COMP 202 Recursion. CONTENTS: Recursion. COMP Recursion 1
 COMP 202 Recursion CONTENTS: Recursion COMP 202 - Recursion 1 Recursive Thinking A recursive definition is one which uses the word or concept being defined in the definition itself COMP 202 - Recursion
COMP 202 Recursion CONTENTS: Recursion COMP 202 - Recursion 1 Recursive Thinking A recursive definition is one which uses the word or concept being defined in the definition itself COMP 202 - Recursion
An Evolution of Mathematical Tools
 An Evolution of Mathematical Tools From Conceptualization to Formalization Here's what we do when we build a formal model (or do a computation): 0. Identify a collection of objects/events in the real world.
An Evolution of Mathematical Tools From Conceptualization to Formalization Here's what we do when we build a formal model (or do a computation): 0. Identify a collection of objects/events in the real world.
Lecture 10: Recursion vs Iteration
 cs2010: algorithms and data structures Lecture 10: Recursion vs Iteration Vasileios Koutavas School of Computer Science and Statistics Trinity College Dublin how methods execute Call stack: is a stack
cs2010: algorithms and data structures Lecture 10: Recursion vs Iteration Vasileios Koutavas School of Computer Science and Statistics Trinity College Dublin how methods execute Call stack: is a stack
Last week. Another example. More recursive examples. How about these functions? Recursive programs. CSC148 Intro. to Computer Science
 CSC48 Intro. to Computer Science Lecture 7: Recursive Functions/Structures Trees mir H. Chinaei, Summer 206 Office Hours: R 0-2 B4222 ahchinaei@cs.toronto.edu http://www.cs.toronto.edu/~ahchinaei/ Course
CSC48 Intro. to Computer Science Lecture 7: Recursive Functions/Structures Trees mir H. Chinaei, Summer 206 Office Hours: R 0-2 B4222 ahchinaei@cs.toronto.edu http://www.cs.toronto.edu/~ahchinaei/ Course
Programming Languages 3. Definition and Proof by Induction
 Programming Languages 3. Definition and Proof by Induction Shin-Cheng Mu Oct. 22, 2015 Total Functional Programming The next few lectures concerns inductive definitions and proofs of datatypes and programs.
Programming Languages 3. Definition and Proof by Induction Shin-Cheng Mu Oct. 22, 2015 Total Functional Programming The next few lectures concerns inductive definitions and proofs of datatypes and programs.
Discrete Mathematics Lecture 4. Harper Langston New York University
 Discrete Mathematics Lecture 4 Harper Langston New York University Sequences Sequence is a set of (usually infinite number of) ordered elements: a 1, a 2,, a n, Each individual element a k is called a
Discrete Mathematics Lecture 4 Harper Langston New York University Sequences Sequence is a set of (usually infinite number of) ordered elements: a 1, a 2,, a n, Each individual element a k is called a
Identify recursive algorithms Write simple recursive algorithms Understand recursive function calling
 Recursion Identify recursive algorithms Write simple recursive algorithms Understand recursive function calling With reference to the call stack Compute the result of simple recursive algorithms Understand
Recursion Identify recursive algorithms Write simple recursive algorithms Understand recursive function calling With reference to the call stack Compute the result of simple recursive algorithms Understand
PROGRAMMING IN HASKELL. CS Chapter 6 - Recursive Functions
 PROGRAMMING IN HASKELL CS-205 - Chapter 6 - Recursive Functions 0 Introduction As we have seen, many functions can naturally be defined in terms of other functions. factorial :: Int Int factorial n product
PROGRAMMING IN HASKELL CS-205 - Chapter 6 - Recursive Functions 0 Introduction As we have seen, many functions can naturally be defined in terms of other functions. factorial :: Int Int factorial n product
Reduction & Recursion Overview
 Reduction & Recursion Overview Reduction definition Reduction techniques Recursion definition Recursive thinking (Many) recursion examples Indirect recursion Runtime stack Factorial isnumericstring add
Reduction & Recursion Overview Reduction definition Reduction techniques Recursion definition Recursive thinking (Many) recursion examples Indirect recursion Runtime stack Factorial isnumericstring add
Two Approaches to Algorithms An Example (1) Iteration (2) Recursion
 2. Recursion Algorithm Two Approaches to Algorithms (1) Iteration It exploits while-loop, for-loop, repeat-until etc. Classical, conventional, and general approach (2) Recursion Self-function call It exploits
2. Recursion Algorithm Two Approaches to Algorithms (1) Iteration It exploits while-loop, for-loop, repeat-until etc. Classical, conventional, and general approach (2) Recursion Self-function call It exploits
Admin. How's the project coming? After these slides, read chapter 13 in your book. Quizzes will return
 Recursion CS 1 Admin How's the project coming? After these slides, read chapter 13 in your book Yes that is out of order, but we can read it stand alone Quizzes will return Tuesday Nov 29 th see calendar
Recursion CS 1 Admin How's the project coming? After these slides, read chapter 13 in your book Yes that is out of order, but we can read it stand alone Quizzes will return Tuesday Nov 29 th see calendar
Recursive Definitions
 Recursion Objectives Explain the underlying concepts of recursion Examine recursive methods and unravel their processing steps Explain when recursion should and should not be used Demonstrate the use of
Recursion Objectives Explain the underlying concepts of recursion Examine recursive methods and unravel their processing steps Explain when recursion should and should not be used Demonstrate the use of
CSC Discrete Math I, Spring Sets
 CSC 125 - Discrete Math I, Spring 2017 Sets Sets A set is well-defined, unordered collection of objects The objects in a set are called the elements, or members, of the set A set is said to contain its
CSC 125 - Discrete Math I, Spring 2017 Sets Sets A set is well-defined, unordered collection of objects The objects in a set are called the elements, or members, of the set A set is said to contain its
UNIT 5A Recursion: Basics. Recursion
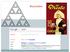
 UNIT 5A Recursion: Basics 1 Recursion A recursive operation is an operation that is defined in terms of itself. Sierpinski's Gasket http://fusionanomaly.net/recursion.jpg 2 1 Recursive Definitions Every
UNIT 5A Recursion: Basics 1 Recursion A recursive operation is an operation that is defined in terms of itself. Sierpinski's Gasket http://fusionanomaly.net/recursion.jpg 2 1 Recursive Definitions Every
Outline. Introduction. 2 Proof of Correctness. 3 Final Notes. Precondition P 1 : Inputs include
 Outline Computer Science 331 Correctness of Algorithms Mike Jacobson Department of Computer Science University of Calgary Lectures #2-4 1 What is a? Applications 2 Recursive Algorithms 3 Final Notes Additional
Outline Computer Science 331 Correctness of Algorithms Mike Jacobson Department of Computer Science University of Calgary Lectures #2-4 1 What is a? Applications 2 Recursive Algorithms 3 Final Notes Additional
Formal Methods. CITS5501 Software Testing and Quality Assurance
 Formal Methods CITS5501 Software Testing and Quality Assurance Pressman, R. Software Engineering: A Practitioner s Approach. Chapter 28. McGraw-Hill, 2005 The Science of Programming, David Gries, 1981
Formal Methods CITS5501 Software Testing and Quality Assurance Pressman, R. Software Engineering: A Practitioner s Approach. Chapter 28. McGraw-Hill, 2005 The Science of Programming, David Gries, 1981
Functional Programming. Overview. Topics. Definition n-th Fibonacci Number. Graph
 Topics Functional Programming Christian Sternagel Harald Zankl Evgeny Zuenko Department of Computer Science University of Innsbruck WS 2017/2018 abstract data types, algebraic data types, binary search
Topics Functional Programming Christian Sternagel Harald Zankl Evgeny Zuenko Department of Computer Science University of Innsbruck WS 2017/2018 abstract data types, algebraic data types, binary search
CS 310 Advanced Data Structures and Algorithms
 CS 310 Advanced Data Structures and Algorithms Recursion June 27, 2017 Tong Wang UMass Boston CS 310 June 27, 2017 1 / 20 Recursion Recursion means defining something, such as a function, in terms of itself
CS 310 Advanced Data Structures and Algorithms Recursion June 27, 2017 Tong Wang UMass Boston CS 310 June 27, 2017 1 / 20 Recursion Recursion means defining something, such as a function, in terms of itself
Announcements. Project 5 is on the street. Second part is essay questions for CoS teaming requirements.
 Announcements Project 5 is on the street. Second part is essay questions for CoS teaming requirements. The first part you do as a team The CoS essay gets individually answered and has separate submission
Announcements Project 5 is on the street. Second part is essay questions for CoS teaming requirements. The first part you do as a team The CoS essay gets individually answered and has separate submission
SEQUENCES, MATHEMATICAL INDUCTION, AND RECURSION
 CHAPTER 5 SEQUENCES, MATHEMATICAL INDUCTION, AND RECURSION Alessandro Artale UniBZ - http://www.inf.unibz.it/ artale/ SECTION 5.5 Application: Correctness of Algorithms Copyright Cengage Learning. All
CHAPTER 5 SEQUENCES, MATHEMATICAL INDUCTION, AND RECURSION Alessandro Artale UniBZ - http://www.inf.unibz.it/ artale/ SECTION 5.5 Application: Correctness of Algorithms Copyright Cengage Learning. All
COMP-202. Recursion. COMP Recursion, 2011 Jörg Kienzle and others
 COMP-202 Recursion Recursion Recursive Definitions Run-time Stacks Recursive Programming Recursion vs. Iteration Indirect Recursion Lecture Outline 2 Recursive Definitions (1) A recursive definition is
COMP-202 Recursion Recursion Recursive Definitions Run-time Stacks Recursive Programming Recursion vs. Iteration Indirect Recursion Lecture Outline 2 Recursive Definitions (1) A recursive definition is
CS116 - Module 5 - Accumulative Recursion
 CS116 - Module 5 - Accumulative Recursion Cameron Morland Winter 2018 1 Cameron Morland CS116 - Module 5 - Accumulative Recursion Types of Recursion Structural Recursion Generative Recursion Accumulative
CS116 - Module 5 - Accumulative Recursion Cameron Morland Winter 2018 1 Cameron Morland CS116 - Module 5 - Accumulative Recursion Types of Recursion Structural Recursion Generative Recursion Accumulative
Introduction to Automata Theory. BİL405 - Automata Theory and Formal Languages 1
 Introduction to Automata Theory BİL405 - Automata Theory and Formal Languages 1 Automata, Computability and Complexity Automata, Computability and Complexity are linked by the question: What are the fundamental
Introduction to Automata Theory BİL405 - Automata Theory and Formal Languages 1 Automata, Computability and Complexity Automata, Computability and Complexity are linked by the question: What are the fundamental
Algorithm Design and Recursion. Search and Sort Algorithms
 Algorithm Design and Recursion Search and Sort Algorithms Objectives To understand the basic techniques for analyzing the efficiency of algorithms. To know what searching is and understand the algorithms
Algorithm Design and Recursion Search and Sort Algorithms Objectives To understand the basic techniques for analyzing the efficiency of algorithms. To know what searching is and understand the algorithms
CS 173, Running Time Analysis, Counting, and Dynamic Programming. Tandy Warnow
 CS 173, Running Time Analysis, Counting, and Dynamic Programming Tandy Warnow CS 173 September 25, 2018 Tandy Warnow Today Topics: Results from survey Midterm Very basic counting Analyzing running times
CS 173, Running Time Analysis, Counting, and Dynamic Programming Tandy Warnow CS 173 September 25, 2018 Tandy Warnow Today Topics: Results from survey Midterm Very basic counting Analyzing running times
Recursive Data and Recursive Functions
 Structural Recursion and Induction Of all the material in this course, this lesson is probably the hardest for students to grasp at first, but it s also one of the most fundamental. Once you understand
Structural Recursion and Induction Of all the material in this course, this lesson is probably the hardest for students to grasp at first, but it s also one of the most fundamental. Once you understand
1KOd17RMoURxjn2 CSE 20 DISCRETE MATH Fall
 CSE 20 https://goo.gl/forms/1o 1KOd17RMoURxjn2 DISCRETE MATH Fall 2017 http://cseweb.ucsd.edu/classes/fa17/cse20-ab/ Today's learning goals Explain the steps in a proof by mathematical and/or structural
CSE 20 https://goo.gl/forms/1o 1KOd17RMoURxjn2 DISCRETE MATH Fall 2017 http://cseweb.ucsd.edu/classes/fa17/cse20-ab/ Today's learning goals Explain the steps in a proof by mathematical and/or structural
Verification Overview Testing Theory and Principles Testing in Practice. Verification. Miaoqing Huang University of Arkansas 1 / 80
 1 / 80 Verification Miaoqing Huang University of Arkansas Outline 1 Verification Overview 2 Testing Theory and Principles Theoretical Foundations of Testing Empirical Testing Principles 3 Testing in Practice
1 / 80 Verification Miaoqing Huang University of Arkansas Outline 1 Verification Overview 2 Testing Theory and Principles Theoretical Foundations of Testing Empirical Testing Principles 3 Testing in Practice
CS200: Recursion and induction (recap from cs161)
 CS200: Recursion and induction (recap from cs161) Prichard Ch. 6.1 & 6.3 1 2 Backtracking n Problem solving technique that involves moves: guesses at a solution. n Depth First Search: in case of failure
CS200: Recursion and induction (recap from cs161) Prichard Ch. 6.1 & 6.3 1 2 Backtracking n Problem solving technique that involves moves: guesses at a solution. n Depth First Search: in case of failure
Fundamental mathematical techniques reviewed: Mathematical induction Recursion. Typically taught in courses such as Calculus and Discrete Mathematics.
 Fundamental mathematical techniques reviewed: Mathematical induction Recursion Typically taught in courses such as Calculus and Discrete Mathematics. Techniques introduced: Divide-and-Conquer Algorithms
Fundamental mathematical techniques reviewed: Mathematical induction Recursion Typically taught in courses such as Calculus and Discrete Mathematics. Techniques introduced: Divide-and-Conquer Algorithms
P1 Engineering Computation
 1EC 2001 1 / 1 P1 Engineering Computation David Murray david.murray@eng.ox.ac.uk www.robots.ox.ac.uk/ dwm/courses/1ec Hilary 2001 1EC 2001 2 / 1 Algorithms: Design, Constructs and Correctness 1EC 2001
1EC 2001 1 / 1 P1 Engineering Computation David Murray david.murray@eng.ox.ac.uk www.robots.ox.ac.uk/ dwm/courses/1ec Hilary 2001 1EC 2001 2 / 1 Algorithms: Design, Constructs and Correctness 1EC 2001
Lecture 7 CS2110 Fall 2014 RECURSION
 Lecture 7 CS2110 Fall 2014 RECURSION Overview references to sections in text 2 Note: We ve covered everything in JavaSummary.pptx! What is recursion? 7.1-7.39 slide 1-7 Base case 7.1-7.10 slide 13 How
Lecture 7 CS2110 Fall 2014 RECURSION Overview references to sections in text 2 Note: We ve covered everything in JavaSummary.pptx! What is recursion? 7.1-7.39 slide 1-7 Base case 7.1-7.10 slide 13 How
9/16/14. Overview references to sections in text RECURSION. What does generic mean? A little about generics used in A3
 Overview references to sections in text 2 Note: We ve covered everything in JavaSummary.pptx! What is recursion 7.1-7.39 slide 1-7 Base case 7.1-7.10 slide 13 How Java stack frames work 7.8-7.10 slide
Overview references to sections in text 2 Note: We ve covered everything in JavaSummary.pptx! What is recursion 7.1-7.39 slide 1-7 Base case 7.1-7.10 slide 13 How Java stack frames work 7.8-7.10 slide
CS 206 Introduction to Computer Science II
 CS 206 Introduction to Computer Science II 03 / 05 / 2018 Instructor: Michael Eckmann Today s Topics Questions? Comments? binary search trees Finish delete method Discuss run times of various methods Michael
CS 206 Introduction to Computer Science II 03 / 05 / 2018 Instructor: Michael Eckmann Today s Topics Questions? Comments? binary search trees Finish delete method Discuss run times of various methods Michael
Figure 4.1: The evolution of a rooted tree.
 106 CHAPTER 4. INDUCTION, RECURSION AND RECURRENCES 4.6 Rooted Trees 4.6.1 The idea of a rooted tree We talked about how a tree diagram helps us visualize merge sort or other divide and conquer algorithms.
106 CHAPTER 4. INDUCTION, RECURSION AND RECURRENCES 4.6 Rooted Trees 4.6.1 The idea of a rooted tree We talked about how a tree diagram helps us visualize merge sort or other divide and conquer algorithms.
Recursive Methods and Problem Solving. Chris Kiekintveld CS 2401 (Fall 2010) Elementary Data Structures and Algorithms
 Recursive Methods and Problem Solving Chris Kiekintveld CS 2401 (Fall 2010) Elementary Data Structures and Algorithms Review: Calling Methods int x(int n) { int m = 0; n = n + m + 1; return n; int y(int
Recursive Methods and Problem Solving Chris Kiekintveld CS 2401 (Fall 2010) Elementary Data Structures and Algorithms Review: Calling Methods int x(int n) { int m = 0; n = n + m + 1; return n; int y(int
Recursion and Induction
 Recursion and Induction Paul S. Miner NASA Langley Formal Methods Group p.s.miner@nasa.gov 28 November 2007 Outline Recursive definitions in PVS Simple inductive proofs Automated proofs by induction More
Recursion and Induction Paul S. Miner NASA Langley Formal Methods Group p.s.miner@nasa.gov 28 November 2007 Outline Recursive definitions in PVS Simple inductive proofs Automated proofs by induction More
Shell CSCE 314 TAMU. Functions continued
 1 CSCE 314: Programming Languages Dr. Dylan Shell Functions continued 2 Outline Defining Functions List Comprehensions Recursion 3 A Function without Recursion Many functions can naturally be defined in
1 CSCE 314: Programming Languages Dr. Dylan Shell Functions continued 2 Outline Defining Functions List Comprehensions Recursion 3 A Function without Recursion Many functions can naturally be defined in
CS 3512, Spring Instructor: Doug Dunham. Textbook: James L. Hein, Discrete Structures, Logic, and Computability, 3rd Ed. Jones and Barlett, 2010
 CS 3512, Spring 2011 Instructor: Doug Dunham Textbook: James L. Hein, Discrete Structures, Logic, and Computability, 3rd Ed. Jones and Barlett, 2010 Prerequisites: Calc I, CS2511 Rough course outline:
CS 3512, Spring 2011 Instructor: Doug Dunham Textbook: James L. Hein, Discrete Structures, Logic, and Computability, 3rd Ed. Jones and Barlett, 2010 Prerequisites: Calc I, CS2511 Rough course outline:
CMSC 132: Object-Oriented Programming II. Recursive Algorithms. Department of Computer Science University of Maryland, College Park
 CMSC 132: Object-Oriented Programming II Recursive Algorithms Department of Computer Science University of Maryland, College Park Recursion Recursion is a strategy for solving problems A procedure that
CMSC 132: Object-Oriented Programming II Recursive Algorithms Department of Computer Science University of Maryland, College Park Recursion Recursion is a strategy for solving problems A procedure that
Handout 9: Imperative Programs and State
 06-02552 Princ. of Progr. Languages (and Extended ) The University of Birmingham Spring Semester 2016-17 School of Computer Science c Uday Reddy2016-17 Handout 9: Imperative Programs and State Imperative
06-02552 Princ. of Progr. Languages (and Extended ) The University of Birmingham Spring Semester 2016-17 School of Computer Science c Uday Reddy2016-17 Handout 9: Imperative Programs and State Imperative
Recursion Chapter 8. What is recursion? How can a function call itself? How can a function call itself?
 Recursion Chapter 8 CS 3358 Summer I 2012 Jill Seaman What is recursion? Generally, when something contains a reference to itself Math: defining a function in terms of itself Computer science: when a function
Recursion Chapter 8 CS 3358 Summer I 2012 Jill Seaman What is recursion? Generally, when something contains a reference to itself Math: defining a function in terms of itself Computer science: when a function
Recursion CSCI 136: Fundamentals of Computer Science II Keith Vertanen Copyright 2011
 Recursion CSCI 136: Fundamentals of Computer Science II Keith Vertanen Copyright 2011 Recursion A method calling itself Overview A new way of thinking about a problem Divide and conquer A powerful programming
Recursion CSCI 136: Fundamentals of Computer Science II Keith Vertanen Copyright 2011 Recursion A method calling itself Overview A new way of thinking about a problem Divide and conquer A powerful programming
Fun facts about recursion
 Outline examples of recursion principles of recursion review: recursive linked list methods binary search more examples of recursion problem solving using recursion 1 Fun facts about recursion every loop
Outline examples of recursion principles of recursion review: recursive linked list methods binary search more examples of recursion problem solving using recursion 1 Fun facts about recursion every loop
COMP-202: Foundations of Programming. Lecture 13: Recursion Sandeep Manjanna, Summer 2015
 COMP-202: Foundations of Programming Lecture 13: Recursion Sandeep Manjanna, Summer 2015 Announcements Final exams : 26 th of June (2pm to 5pm) @ MAASS 112 Assignment 4 is posted and Due on 29 th of June
COMP-202: Foundations of Programming Lecture 13: Recursion Sandeep Manjanna, Summer 2015 Announcements Final exams : 26 th of June (2pm to 5pm) @ MAASS 112 Assignment 4 is posted and Due on 29 th of June
34. Recursion. Java. Summer 2008 Instructor: Dr. Masoud Yaghini
 34. Recursion Java Summer 2008 Instructor: Dr. Masoud Yaghini Outline Introduction Example: Factorials Example: Fibonacci Numbers Recursion vs. Iteration References Introduction Introduction Recursion
34. Recursion Java Summer 2008 Instructor: Dr. Masoud Yaghini Outline Introduction Example: Factorials Example: Fibonacci Numbers Recursion vs. Iteration References Introduction Introduction Recursion
Recursion. Overview. Mathematical induction. Hello recursion. Recursion. Example applications. Goal: Compute factorial N! = 1 * 2 * 3...
 Recursion Recursion Overview A method calling itself A new way of thinking about a problem Divide and conquer A powerful programming paradigm Related to mathematical induction Example applications Factorial
Recursion Recursion Overview A method calling itself A new way of thinking about a problem Divide and conquer A powerful programming paradigm Related to mathematical induction Example applications Factorial
Chapter 3 Programming with Recursion
 Plan Chapter 3 Programming with Recursion 1. Examples... 3.2 2. Correctness... 3.5 3. Construction methodology... 3.13 4. Forms of recursion... 3.16 Sven-Olof Nyström/IT Dept/Uppsala University FP 3.1
Plan Chapter 3 Programming with Recursion 1. Examples... 3.2 2. Correctness... 3.5 3. Construction methodology... 3.13 4. Forms of recursion... 3.16 Sven-Olof Nyström/IT Dept/Uppsala University FP 3.1
Logic and Computation Lecture 20 CSU 290 Spring 2009 (Pucella) Thursday, Mar 12, 2009
 Logic and Computation Lecture 20 CSU 290 Spring 2009 (Pucella) Thursday, Mar 12, 2009 Note that I change the name of the functions slightly in these notes from what I used in class, to be consistent with
Logic and Computation Lecture 20 CSU 290 Spring 2009 (Pucella) Thursday, Mar 12, 2009 Note that I change the name of the functions slightly in these notes from what I used in class, to be consistent with
Recursion Chapter 8. What is recursion? How can a function call itself? How can a function call itself? contains a reference to itself.
 Recursion Chapter 8 CS 3358 Summer II 2013 Jill Seaman What is recursion?! Generally, when something contains a reference to itself! Math: defining a function in terms of itself! Computer science: when
Recursion Chapter 8 CS 3358 Summer II 2013 Jill Seaman What is recursion?! Generally, when something contains a reference to itself! Math: defining a function in terms of itself! Computer science: when
REGULAR GRAPHS OF GIVEN GIRTH. Contents
 REGULAR GRAPHS OF GIVEN GIRTH BROOKE ULLERY Contents 1. Introduction This paper gives an introduction to the area of graph theory dealing with properties of regular graphs of given girth. A large portion
REGULAR GRAPHS OF GIVEN GIRTH BROOKE ULLERY Contents 1. Introduction This paper gives an introduction to the area of graph theory dealing with properties of regular graphs of given girth. A large portion
Assignment 1. Stefano Guerra. October 11, The following observation follows directly from the definition of in order and pre order traversal:
 Assignment 1 Stefano Guerra October 11, 2016 1 Problem 1 Describe a recursive algorithm to reconstruct an arbitrary binary tree, given its preorder and inorder node sequences as input. First, recall that
Assignment 1 Stefano Guerra October 11, 2016 1 Problem 1 Describe a recursive algorithm to reconstruct an arbitrary binary tree, given its preorder and inorder node sequences as input. First, recall that
Verifying Safety Property of Lustre Programs: Temporal Induction
 22c181: Formal Methods in Software Engineering The University of Iowa Spring 2008 Verifying Safety Property of Lustre Programs: Temporal Induction Copyright 2008 Cesare Tinelli. These notes are copyrighted
22c181: Formal Methods in Software Engineering The University of Iowa Spring 2008 Verifying Safety Property of Lustre Programs: Temporal Induction Copyright 2008 Cesare Tinelli. These notes are copyrighted
CS 3410 Ch 7 Recursion
 CS 3410 Ch 7 Recursion Sections Pages 7.1-7.4, 7.7 93-319, 333-336 7.1 Introduction 1. A recursive method is a method that either directly or indirectly makes a call to itself. [Weiss]. It does this by
CS 3410 Ch 7 Recursion Sections Pages 7.1-7.4, 7.7 93-319, 333-336 7.1 Introduction 1. A recursive method is a method that either directly or indirectly makes a call to itself. [Weiss]. It does this by
Recursion. Fundamentals of Computer Science
 Recursion Fundamentals of Computer Science Outline Recursion A method calling itself All good recursion must come to an end A powerful tool in computer science Allows writing elegant and easy to understand
Recursion Fundamentals of Computer Science Outline Recursion A method calling itself All good recursion must come to an end A powerful tool in computer science Allows writing elegant and easy to understand
Searching Algorithms/Time Analysis
 Searching Algorithms/Time Analysis CSE21 Fall 2017, Day 8 Oct 16, 2017 https://sites.google.com/a/eng.ucsd.edu/cse21-fall-2017-miles-jones/ (MinSort) loop invariant induction Loop invariant: After the
Searching Algorithms/Time Analysis CSE21 Fall 2017, Day 8 Oct 16, 2017 https://sites.google.com/a/eng.ucsd.edu/cse21-fall-2017-miles-jones/ (MinSort) loop invariant induction Loop invariant: After the
SOFTWARE DEVELOPMENT 1. Recursion 2018W A. Ferscha (Institute of Pervasive Computing, JKU Linz)
 SOFTWARE DEVELOPMENT 1 Recursion 2018W (Institute of Pervasive Computing, JKU Linz) PRINCIPLE OF SELF-REFERENCE Recursion: Describing something in a self-similar way. An elegant, powerful and simple way
SOFTWARE DEVELOPMENT 1 Recursion 2018W (Institute of Pervasive Computing, JKU Linz) PRINCIPLE OF SELF-REFERENCE Recursion: Describing something in a self-similar way. An elegant, powerful and simple way
Chapter 12 Supplement: Recursion with Java 1.5. Mr. Dave Clausen La Cañada High School
 Chapter 12 Supplement: Recursion with Java 1.5 La Cañada High School Recursion: Definitions Recursion The process of a subprogram (method) calling itself. A clearly defined stopping state must exist. The
Chapter 12 Supplement: Recursion with Java 1.5 La Cañada High School Recursion: Definitions Recursion The process of a subprogram (method) calling itself. A clearly defined stopping state must exist. The
Artificial Intelligence Lecture 1
 Artificial Intelligence Lecture 1 istrative Matters Webpage: www.aass.oru.se/~mbl/ai Examiner: Mathias Broxvall Assistant: Lia Susana d.c. Silva Lopez Schedule 20 hours/week on this course. 4 hours lectures,
Artificial Intelligence Lecture 1 istrative Matters Webpage: www.aass.oru.se/~mbl/ai Examiner: Mathias Broxvall Assistant: Lia Susana d.c. Silva Lopez Schedule 20 hours/week on this course. 4 hours lectures,
Announcements. Recursion and why study it. Recursive programming. Recursion basic idea
 Announcements Recursion and why study it Tutoring schedule updated Do you find the sessions helpful? Midterm exam 1: Tuesday, April 11, in class Scope: will cover up to recursion Closed book but one sheet,
Announcements Recursion and why study it Tutoring schedule updated Do you find the sessions helpful? Midterm exam 1: Tuesday, April 11, in class Scope: will cover up to recursion Closed book but one sheet,
Foundations of Computer Science Spring Mathematical Preliminaries
 Foundations of Computer Science Spring 2017 Equivalence Relation, Recursive Definition, and Mathematical Induction Mathematical Preliminaries Mohammad Ashiqur Rahman Department of Computer Science College
Foundations of Computer Science Spring 2017 Equivalence Relation, Recursive Definition, and Mathematical Induction Mathematical Preliminaries Mohammad Ashiqur Rahman Department of Computer Science College
Lecture Notes 4 More C++ and recursion CSS 501 Data Structures and Object-Oriented Programming Professor Clark F. Olson
 Lecture Notes 4 More C++ and recursion CSS 501 Data Structures and Object-Oriented Programming Professor Clark F. Olson Reading for this lecture: Carrano, Chapter 2 Copy constructor, destructor, operator=
Lecture Notes 4 More C++ and recursion CSS 501 Data Structures and Object-Oriented Programming Professor Clark F. Olson Reading for this lecture: Carrano, Chapter 2 Copy constructor, destructor, operator=
More Complicated Recursion CMPSC 122
 More Complicated Recursion CMPSC 122 Now that we've gotten a taste of recursion, we'll look at several more examples of recursion that are special in their own way. I. Example with More Involved Arithmetic
More Complicated Recursion CMPSC 122 Now that we've gotten a taste of recursion, we'll look at several more examples of recursion that are special in their own way. I. Example with More Involved Arithmetic
Proving Properties of Recursive Functions and Data Structures. CS 270 Math Foundations of CS Jeremy Johnson
 Proving Properties of Recursive Functions and Data Structures CS 270 Math Foundations of CS Jeremy Johnson 1 Objective To implement and verify recursive functions for processing recursive data structures.
Proving Properties of Recursive Functions and Data Structures CS 270 Math Foundations of CS Jeremy Johnson 1 Objective To implement and verify recursive functions for processing recursive data structures.
Recursion defining an object (or function, algorithm, etc.) in terms of itself. Recursion can be used to define sequences
 Section 5.3 1 Recursion Recursion defining an object (or function, algorithm, etc.) in terms of itself. Recursion can be used to define sequences Previously sequences were defined using a specific formula,
Section 5.3 1 Recursion Recursion defining an object (or function, algorithm, etc.) in terms of itself. Recursion can be used to define sequences Previously sequences were defined using a specific formula,
Data structure and algorithm in Python
 Data structure and algorithm in Python Recursion Xiaoping Zhang School of Mathematics and Statistics, Wuhan University Table of contents 1. Illustrative Examples 2. Poor Implementation of Recursion 3.
Data structure and algorithm in Python Recursion Xiaoping Zhang School of Mathematics and Statistics, Wuhan University Table of contents 1. Illustrative Examples 2. Poor Implementation of Recursion 3.
CS 220: Discrete Structures and their Applications. Recursive objects and structural induction in zybooks
 CS 220: Discrete Structures and their Applications Recursive objects and structural induction 6.9 6.10 in zybooks Using recursion to define objects We can use recursion to define functions: The factorial
CS 220: Discrete Structures and their Applications Recursive objects and structural induction 6.9 6.10 in zybooks Using recursion to define objects We can use recursion to define functions: The factorial
CSCE 110 Dr. Amr Goneid Exercise Sheet (7): Exercises on Recursion
 CSCE 110 Dr. Amr Goneid Exercise Sheet (7): Exercises on Recursion Consider the following recursive function: int what ( int x, int y) if (x > y) return what (x-y, y); else if (y > x) return what (x, y-x);
CSCE 110 Dr. Amr Goneid Exercise Sheet (7): Exercises on Recursion Consider the following recursive function: int what ( int x, int y) if (x > y) return what (x-y, y); else if (y > x) return what (x, y-x);
SEQUENCES, MATHEMATICAL INDUCTION, AND RECURSION
 CHAPTER 5 SEQUENCES, MATHEMATICAL INDUCTION, AND RECURSION Copyright Cengage Learning. All rights reserved. SECTION 5.5 Application: Correctness of Algorithms Copyright Cengage Learning. All rights reserved.
CHAPTER 5 SEQUENCES, MATHEMATICAL INDUCTION, AND RECURSION Copyright Cengage Learning. All rights reserved. SECTION 5.5 Application: Correctness of Algorithms Copyright Cengage Learning. All rights reserved.
Programming Languages Third Edition
 Programming Languages Third Edition Chapter 12 Formal Semantics Objectives Become familiar with a sample small language for the purpose of semantic specification Understand operational semantics Understand
Programming Languages Third Edition Chapter 12 Formal Semantics Objectives Become familiar with a sample small language for the purpose of semantic specification Understand operational semantics Understand
CMPSCI 250: Introduction to Computation. Lecture #14: Induction and Recursion (Still More Induction) David Mix Barrington 14 March 2013
 CMPSCI 250: Introduction to Computation Lecture #14: Induction and Recursion (Still More Induction) David Mix Barrington 14 March 2013 Induction and Recursion Three Rules for Recursive Algorithms Proving
CMPSCI 250: Introduction to Computation Lecture #14: Induction and Recursion (Still More Induction) David Mix Barrington 14 March 2013 Induction and Recursion Three Rules for Recursive Algorithms Proving
Functions and Recursion
 Functions and Recursion Chapter 5 Prof. Mauro Gaspari: gaspari@cs.unibo.it Example import math def area(radius): temp = math.pi * radius**2 return temp # or def area(radius): return math.pi * radius**2
Functions and Recursion Chapter 5 Prof. Mauro Gaspari: gaspari@cs.unibo.it Example import math def area(radius): temp = math.pi * radius**2 return temp # or def area(radius): return math.pi * radius**2
What is a Computer Algorithm?
 What is a Computer Algorithm? A computer algorithm is a detailed step-by-step method for solving a problem by using a computer. Problem-Solving (Science and Engineering) Analysis How does it work? Breaking
What is a Computer Algorithm? A computer algorithm is a detailed step-by-step method for solving a problem by using a computer. Problem-Solving (Science and Engineering) Analysis How does it work? Breaking
Last time. Reasoning about programs. Coming up. Project Final Presentations. This Thursday, Nov 30: 4 th in-class exercise
 Last time Reasoning about programs Coming up This Thursday, Nov 30: 4 th in-class exercise sign up for group on moodle bring laptop to class Final projects: final project presentations: Tue Dec 12, in
Last time Reasoning about programs Coming up This Thursday, Nov 30: 4 th in-class exercise sign up for group on moodle bring laptop to class Final projects: final project presentations: Tue Dec 12, in
Reasoning about programs
 Reasoning about programs Last time Coming up This Thursday, Nov 30: 4 th in-class exercise sign up for group on moodle bring laptop to class Final projects: final project presentations: Tue Dec 12, in
Reasoning about programs Last time Coming up This Thursday, Nov 30: 4 th in-class exercise sign up for group on moodle bring laptop to class Final projects: final project presentations: Tue Dec 12, in
MATHEMATICAL STRUCTURES FOR COMPUTER SCIENCE
 MATHEMATICAL STRUCTURES FOR COMPUTER SCIENCE A Modern Approach to Discrete Mathematics SIXTH EDITION Judith L. Gersting University of Hawaii at Hilo W. H. Freeman and Company New York Preface Note to the
MATHEMATICAL STRUCTURES FOR COMPUTER SCIENCE A Modern Approach to Discrete Mathematics SIXTH EDITION Judith L. Gersting University of Hawaii at Hilo W. H. Freeman and Company New York Preface Note to the
Binary Search to find item in sorted array
 Binary Search to find item in sorted array January 15, 2008 QUESTION: Suppose we are given a sorted list A[1..n] (as an array), of n real numbers: A[1] A[2] A[n]. Given a real number x, decide whether
Binary Search to find item in sorted array January 15, 2008 QUESTION: Suppose we are given a sorted list A[1..n] (as an array), of n real numbers: A[1] A[2] A[n]. Given a real number x, decide whether
CITS3001. Algorithms, Agents and Artificial Intelligence. Semester 2, 2016
 CITS3001 Algorithms, Agents and Artificial Intelligence Semester 2, 2016 Tim French School of Computer Science & Software Eng. The University of Western Australia 2. Review of algorithmic concepts CLRS,
CITS3001 Algorithms, Agents and Artificial Intelligence Semester 2, 2016 Tim French School of Computer Science & Software Eng. The University of Western Australia 2. Review of algorithmic concepts CLRS,
UNIT 5A Recursion: Basics. Recursion
 UNIT 5A Recursion: Basics 1 Recursion A recursive function is one that calls itself. Infinite loop? Not necessarily. 2 1 Recursive Definitions Every recursive definition includes two parts: Base case (non
UNIT 5A Recursion: Basics 1 Recursion A recursive function is one that calls itself. Infinite loop? Not necessarily. 2 1 Recursive Definitions Every recursive definition includes two parts: Base case (non
TECH. Recurrence Equations vs. Recursive Procedures. Recursion and Induction. e.g. Fibonacci Function. The working of recursive procedure
 Recursion and Induction For advanced algorithm development, recursion is an essential design technique Recursive Procedures What is a Proof? Induction Proofs Proving Correctness of Procedures Recurrence
Recursion and Induction For advanced algorithm development, recursion is an essential design technique Recursive Procedures What is a Proof? Induction Proofs Proving Correctness of Procedures Recurrence
Functions. CS10001: Programming & Data Structures. Sudeshna Sarkar Professor, Dept. of Computer Sc. & Engg., Indian Institute of Technology Kharagpur
 Functions CS10001: Programming & Data Structures Sudeshna Sarkar Professor, Dept. of Computer Sc. & Engg., Indian Institute of Technology Kharagpur 1 Recursion A process by which a function calls itself
Functions CS10001: Programming & Data Structures Sudeshna Sarkar Professor, Dept. of Computer Sc. & Engg., Indian Institute of Technology Kharagpur 1 Recursion A process by which a function calls itself
Context-Free Languages & Grammars (CFLs & CFGs) Reading: Chapter 5
 Context-Free Languages & Grammars (CFLs & CFGs) Reading: Chapter 5 1 Not all languages are regular So what happens to the languages which are not regular? Can we still come up with a language recognizer?
Context-Free Languages & Grammars (CFLs & CFGs) Reading: Chapter 5 1 Not all languages are regular So what happens to the languages which are not regular? Can we still come up with a language recognizer?
Treewidth and graph minors
 Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
ENVIRONMENT DIAGRAMS AND RECURSION 2
 ENVIRONMENT DIAGRAMS AND RECURSION 2 COMPUTER SCIENCE 61A September 8, 2016 1 More Environment Diagrams Recall that an environment diagram keeps track of all the variables that have been defined and the
ENVIRONMENT DIAGRAMS AND RECURSION 2 COMPUTER SCIENCE 61A September 8, 2016 1 More Environment Diagrams Recall that an environment diagram keeps track of all the variables that have been defined and the
Test Bank Ver. 5.0: Data Abstraction and Problem Solving with C++: Walls and Mirrors, 5 th edition, Frank M. Carrano
 Chapter 2 Recursion: The Mirrors Multiple Choice Questions 1. In a recursive solution, the terminates the recursive processing. a) local environment b) pivot item c) base case d) recurrence relation 2.
Chapter 2 Recursion: The Mirrors Multiple Choice Questions 1. In a recursive solution, the terminates the recursive processing. a) local environment b) pivot item c) base case d) recurrence relation 2.
Inference rule for Induction
 Inference rule for Induction Let P( ) be a predicate with domain the positive integers BASE CASE INDUCTIVE STEP INDUCTIVE Step: Usually a direct proof Assume P(x) for arbitrary x (Inductive Hypothesis),
Inference rule for Induction Let P( ) be a predicate with domain the positive integers BASE CASE INDUCTIVE STEP INDUCTIVE Step: Usually a direct proof Assume P(x) for arbitrary x (Inductive Hypothesis),
CSC 505, Spring 2005 Week 6 Lectures page 1 of 9
 CSC 505, Spring 2005 Week 6 Lectures page 1 of 9 Objectives: learn general strategies for problems about order statistics learn how to find the median (or k-th largest) in linear average-case number of
CSC 505, Spring 2005 Week 6 Lectures page 1 of 9 Objectives: learn general strategies for problems about order statistics learn how to find the median (or k-th largest) in linear average-case number of
Recursion. Dr. Jürgen Eckerle FS Recursive Functions
 Recursion Dr. Jürgen Eckerle FS 2008 Recursive Functions Recursion, in mathematics and computer science, is a method of defining functions in which the function being defined is applied within its own
Recursion Dr. Jürgen Eckerle FS 2008 Recursive Functions Recursion, in mathematics and computer science, is a method of defining functions in which the function being defined is applied within its own
Environment Diagrams and Recursion Fall 2017 Discussion 2: September 6, 2017 Solutions. 1 More Environment Diagrams
 CS 61A Environment Diagrams and Recursion Fall 2017 Discussion 2: September 6, 2017 Solutions 1 More Environment Diagrams Recall that an environment diagram keeps track of all the variables that have been
CS 61A Environment Diagrams and Recursion Fall 2017 Discussion 2: September 6, 2017 Solutions 1 More Environment Diagrams Recall that an environment diagram keeps track of all the variables that have been
RECURSION. Many Slides from Ken Birman, Cornell University
 RECURSION Many Slides from Ken Birman, Cornell University Iteration Computers are well-suited for executing the same task repeatedly Programs and algorithms use iteration to perform repetitive jobs Programming
RECURSION Many Slides from Ken Birman, Cornell University Iteration Computers are well-suited for executing the same task repeatedly Programs and algorithms use iteration to perform repetitive jobs Programming
Reference Sheet for CO142.2 Discrete Mathematics II
 Reference Sheet for CO14. Discrete Mathematics II Spring 017 1 Graphs Defintions 1. Graph: set of N nodes and A arcs such that each a A is associated with an unordered pair of nodes.. Simple graph: no
Reference Sheet for CO14. Discrete Mathematics II Spring 017 1 Graphs Defintions 1. Graph: set of N nodes and A arcs such that each a A is associated with an unordered pair of nodes.. Simple graph: no
Recursive Definitions Structural Induction Recursive Algorithms
 Chapter 4 1 4.3-4.4 Recursive Definitions Structural Induction Recursive Algorithms 2 Section 4.1 3 Principle of Mathematical Induction Principle of Mathematical Induction: To prove that P(n) is true for
Chapter 4 1 4.3-4.4 Recursive Definitions Structural Induction Recursive Algorithms 2 Section 4.1 3 Principle of Mathematical Induction Principle of Mathematical Induction: To prove that P(n) is true for
Note that in this definition, n + m denotes the syntactic expression with three symbols n, +, and m, not to the number that is the sum of n and m.
 CS 6110 S18 Lecture 8 Structural Operational Semantics and IMP Today we introduce a very simple imperative language, IMP, along with two systems of rules for evaluation called small-step and big-step semantics.
CS 6110 S18 Lecture 8 Structural Operational Semantics and IMP Today we introduce a very simple imperative language, IMP, along with two systems of rules for evaluation called small-step and big-step semantics.
