Arithmetic Logic Unit
|
|
|
- Kerry Hall
- 6 years ago
- Views:
Transcription
1 Arithmetic Logic Unit A.R. Hurson Department of Computer Science Missouri University of Science & Technology A.R. Hurson 1
2 Arithmetic Logic Unit It is a functional bo designed to perform "basic" arithmetic, logic, and shift operations on the data. Implementation of the basic operations such as logic, program control, and data transfer operations are easier than arithmetic and I/O operations. Therefore, in this section we concentrate on arithmetic operations. A.R. Hurson 2
3 Arithmetic Logic Unit For a simple machine, the ALU should at least be able to perform operations such as: add increment subtract decrement A simple ALU is basically an adder and some control circuits augmented by special circuits to carry out the logic and shift operations. A.R. Hurson 3
4 Arithmetic Logic Unit An ALU can be of three types: Serial Parallel Functional (Modular) A.R. Hurson 4
5 Arithmetic Logic Unit Similar to the definition of serial and parallel adders, one can define serial and parallel ALUs. In a serial ALU during each clock pulse one bit of operand(s) participates in the operation. In a parallel ALU operation on all the bits of operand(s) is initiated simultaneously. In a simple word a parallel ALU can be looked at as a cascade of identical units forming a one dimensional array of cells. A.R. Hurson 5
6 Arithmetic Logic Unit Parallel ALU ALU operation is determined by the control signals. In a very simple form, the bit-pattern of the control signals is determined by the operation code. In a parallel ALU, one needs to determine the design of a unit and then replicate it. Control Signals B n A n B 2 A 2 B 1 A 1 C n+1 C n C 3 C 2 C 1 F n F 2 F 1 A.R. Hurson 6
7 Arithmetic Logic Unit Parallel ALU (Eample) S 2, S 1, S, and M are the control signals. A i, B i, and C i are the operand bits and carry-in, respectively. F i and C i+1 are the result bit and carry-out, respectively. A.R. Hurson 7
8 A i X i S 2 C i+1 B i S Y F Arithmetic 1 Logic i Unit Parallel ALU i (Eample) S C i Z i M A.R. Hurson 8
9 Arithmetic Logic Unit Parallel ALU (Eample) The function of each stage can be defined as: F i = X i Y i Z i C i+1 = X i Y i +(X i Y i )Z i = X i Y i +X i Z i +Y i Z i By appropriate setting of the control signals one can initiate a variety of the operations. A.R. Hurson 9
10 Arithmetic Logic Unit Parallel ALU (Eample) M = S 2 =1 S 1 =1 F S =1 M=1 S 2 =1 S 1 =1 S =1 C 1 = F A - 1 A.R. Hurson 1
11 Arithmetic Logic Unit As discussed before a parallel ALU offers a higher speed relative to a serial ALU. How can one improve the performance (speed) of ALU further? In other words; is it possible to build (design) an ALU faster than a parallel ALU? A.R. Hurson 11
12 Arithmetic Logic Unit Functional (modular) ALU In this model, ALU is a collection of independent units each tailored (specialized) for a specific operation. As a result, eecution of independent operations can be overlapped. This approach allows an additional degree of concurrency relative to a parallel ALU, since it allows several operations to be performed on data simultaneously. However, this speed improvement comes at the epense of etra overhead which is needed to detect data independent operations. A.R. Hurson 12
13 Arithmetic Logic Unit Functional (modular) ALU Adder Adder 1 2 Subtractor Multiplier A.R. Hurson 13
14 Arithmetic Logic Unit Question Is it possible to improve the performance of an ALU further? Naturally, we can improve performance (physical speed) by taking advantage of the advances in technology. How can we improve the logical speed of the ALU further? In a functional ALU, is it possible to devise algorithms which allow one to improve the performance of the basic operations? If this is a valid direction, then the question of "How to design a fast ALU?" will change to "How to design a fast adder, a fast multiplier,...?" A.R. Hurson 14
15 Arithmetic Logic Unit Arithmetic Algorithm The goal is to develop a set of algorithms which allow the eecution of basic arithmetic operations on data values presented in different formats and notations (i.e., fied point, floating point, signed numbers). In general fied point operations are easier and faster than floating point operations. Signed numbers could be in signed magnitude or signed complement format. A.R. Hurson 15
16 Arithmetic Logic Unit Comparison of 2-Unsigned Numbers (Direct Comparison) Two binary bits (a, b) are equal iff: Consequently two registers of n-bits are equal iff: = n-1 n-2... = 1 where i = A i B i i n-1 In other words ( a b ) ( a ) = 1 = b n 1 A = B = i i= = 1 A.R. Hurson 16
17 Arithmetic Logic Unit Comparison of 2-Unsigned Numbers (Direct Comparison) Similarly A >B A n-1 B n-1 + n-1 A n-2 B n n-1 n A B = 1 A <B A n-1 B n-1 + n-1 A n-2 B n n-1 n A B = 1 A.R. Hurson 17
18 Arithmetic Logic Unit Comparison of 2-Unsigned Numbers (Direct Comparison) Eample: A= B= = = A B A.R. Hurson 18
19 Arithmetic Logic Unit Comparison of 2-Unsigned Numbers (Direct Comparison) = = A B A B A B A B A B A B A B A.R. Hurson = = A B A > B = = A B A B A B A B A B A B A B A < B
20 Arithmetic Logic Unit Comparison of 2-Unsigned Numbers (Direct Subtraction) Assume E is the borrow-out of a parallel subtractor then: if A B then E = if A < B then E =1 if A = B then E = and result all s In other words, to check the relative magnitude of two unsigned numbers say, A and B. Perform A-B and then check the borrow-out. The relative magnitude of A and B is determined according to the above relationships. A.R. Hurson 2
21 Arithmetic Logic Unit Comparison of 2-Unsigned Numbers (2 s Complement Addition) Assume E is the carry-out of a parallel adder then: if A < B then E = if A B then E = 1 if A = B then E = 1 and result all s A.R. Hurson 21
22 Arithmetic Logic Unit Comparison of 2-Unsigned Numbers (2 s Complement Addition) Proof: ~ A B = A + B = A + n 2 B = 2 if A B A - B 2 n + A - B 2 n E = 1 if A < B A B < 2 n + A - B < 2 n E = if A = B A - B = 2 n + A - B = 2 n E = 1 and result all s To determine the relative magnitude of two unsigned numbers, perform A + B ~ and then check the carry-out. A.R. Hurson 22 n + A B
23 Arithmetic Logic Unit Comparison of 2-Unsigned Numbers (1 s Complement Addition) Assume E is the carry-out of a parallel adder then: if A B then E = if A = B then E= and result all 1s if A > B then E =1 To determine the relative magnitude of two unsigned numbers, perform A + B and then check the carry-out. A.R. Hurson 23
24 Arithmetic Logic Unit Comparison of 2-Unsigned Numbers (Direct Subtraction) Eample Borrow-out A - B E = 1 A < B A.R. Hurson 24
25 Arithmetic Logic Unit Comparison of 2-Unsigned Numbers (2 s Complement Addition) Eample Carry-out A B E = A < B A.R. Hurson 25
26 Arithmetic Logic Unit Comparison of 2-Unsigned Numbers (1 s Complement Addition) Eample Carry-out A B E = A < B.. A.R. Hurson 26
27 Questions Prove the aforementioned formulas for the 1 s complement addition operation. How can one determine the relative magnitude of signed numbers? A.R. Hurson 27
28 Arithmetic Logic Unit Addition Algorithm (2 s Complement Numbers) Add numbers including the sign bits. If there is a carry-out of the last digit, then disregard it. A.R. Hurson 28
29 Arithmetic Logic Unit Addition Algorithm (1 s Complement Numbers) Add numbers including the sign bits. If there is a carry-out then increment the result by 1 (wrap around the carry). A.R. Hurson 29
30 Arithmetic Logic Unit Addition Algorithm (Signed magnitude numbers) Addition (Subtraction): When the signs of numbers (say A and B) are identical (different) add the two magnitudes. Sign of the result is the same as A. When the signs of A and B are different (identical), compare the magnitudes and subtract the smaller magnitude from the larger one. Sign of the result is the same as the sign of the larger magnitude. If result zero then set the sign of the result to. A.R. Hurson 3
31 Arithmetic Logic Unit Addition Algorithm (Signed magnitude numbers) How to reduce hardware requirements of the proposed algorithm? Subtraction can be converted into addition. Magnitudes can be compared using an adder. A.R. Hurson 31
32 Arithmetic Logic Unit Addition Algorithm (Signed magnitude numbers) B s B Register End Carry Complementor Parallel Adder cc A s E A Register cc = if (addition and A s = B s ) or (subtraction and A s B s ) cc = 1 if (addition and A s B s ) or (subtraction and A s = B s ) A.R. Hurson 32
33 Arithmetic Logic Unit Addition Algorithm (Signed magnitude numbers) Eample A (+29) +B (+14) Same signs and addition E Add the magnitudes E = A = Final result (+43). A.R. Hurson 33
34 Arithmetic Logic Unit Addition Algorithm (Signed magnitude numbers) Eample A (-14) +B (-7) E Same signs and addition Add the magnitudes. 111 E = A = 1111 Final result (-21). A.R. Hurson 34
35 Arithmetic Logic Unit Addition Algorithm (Signed magnitude numbers) Eample A (-14) -B (-7) E Same signs and subtract Add 2 s complete of B to A E = 1, A>B A = 1111 Final result (-7). A.R. Hurson 35
36 Arithmetic Logic Unit Addition Algorithm (Signed magnitude numbers) Eample A (+14) -B (+2) Same signs and subtract E Add 2 s complete of B to A. 111 E =, A<B, take 2 s complement of result A = 111 Final result (-6). A.R. Hurson 36
37 Arithmetic Logic Unit Addition Algorithm (Signed magnitude numbers) Eample A (-14) -B (-14) E Same signs and subtract Add 2 s complete of B to A. 1 E = 1, and result zero A = Final result (+). A.R. Hurson 37
38 Arithmetic Logic Unit Addition Algorithm (Signed magnitude numbers) Eample A +B E Different signs and addition Take 2 s complement of B and add E = 1 and result A > B A = 111 Final result. A.R. Hurson 38
39 Arithmetic Logic Unit Addition Algorithm (Signed magnitude numbers) Eample A +B Different signs and addition Take 2 s complement of B and add. E 11 1 E = 1 and result A > B A = 1 1 Fin al r esu lt. A.R. Hurson 39
40 Arithmetic Logic Unit Addition Algorithm (Signed magnitude numbers) Eample A - B Same signs and subtraction. E Take 2 s complement of B and add. E = B > A A = 1 1 Final result, take 2 s complement of result. A.R. Hurson 4
41 Questions What is an overflow? How can we detect overflow for: Signed magnitude addition? 1 s complement addition? 2 s complement addition? A.R. Hurson 41
42 Arithmetic Logic Unit Addition Overflow Overflow occurs when two numbers of n digits each are added and the sum occupies n+1 digits. An overflow cannot occur after an addition if one number is positive and the other is negative. In general, overflow can only occur when adding numbers of the same sign or subtracting numbers of different signs. A.R. Hurson 42
43 Arithmetic Logic Unit Addition Overflow (Signed magnitude numbers) Detection of overflow in signed magnitude addition is simple. Carry-out of the magnitude bits represents an overflow: B s B Overflow Bit AVF Complementor CC Parallel-Adder A s E A If (cc = and E = 1) then AVF 1 otherwise AVF A.R. Hurson 43
44 Arithmetic Logic Unit Addition Overflow (2 s Complement Numbers) Overflow is occurred when adding numbers of the same sign results in a number of a different sign. C n B s B FA Parallel-Adder C n-1 A s Overflow occurs if C n C n-1 = 1 A.R. Hurson 44 A
45 Arithmetic Logic Unit Multiplication Algorithm Multiplication can be performed as a sequence of additions. B * Q add B, Q times Two general approaches have been adapted for multiplication. Software approach Hardware approach A.R. Hurson 45
46 Arithmetic Logic Unit Multiplication Algorithm Software approach AC ; For i = 1 to Q do; AC (AC) + (B); End; Time compleity of this algorithm is (m) where m is the magnitude of Q. A.R. Hurson 46
47 Arithmetic Logic Unit Multiplication Algorithm Software approach Time compleity of the algorithm can be improved if the number of iterations is based on the multiplier length: AC ; For i = 1 to n Do; if Q 1 = 1 then C out AC (AC) + (B); AC n...ac 2 AC 1 Q n...q 2 Q 1 C out AC n...ac 2 AC 1 Q n...q 2 ; End; A.R. Hurson 47
48 Arithmetic Logic Unit Multiplication Algorithm Hardware Approach The simplest hardware approach is based on the previous algorithm - e.g., add and shift. In each iteration the least-significant bit of multiplier (Q) is checked; If one, then B is added to the accumulator and the contents of accumulator and Q is shifted right one position. If zero, just shift accumulator and Q to the right. A.R. Hurson 48
49 Arithmetic Logic Unit Multiplication Algorithm (Signed magnitude numbers) Hardware Configuration A double register (AC and Q) holds the final result. Sign of the result is the EX-OR of the signs of multiplier and multiplicand. B s B Parallel Adder AC s Q s AC Q C out Least Significant Bit A.R. Hurson 49
50 Arithmetic Logic Unit Multiplication Algorithm (Signed magnitude numbers) Eample E B s B AC Q s Q 1 Q1=1 then EAC (AC)+(B) 1) ) Shift E(AC)(Q) to the right Q1=1 then EAC (AC)+(B) Shift E(AC)(Q) to the right Q1= shift E(AC)(Q) to the right 3) 4) Q1= shift E(AC)(Q) to the right Q1=1 then EAC (AC)+(B) 5) Shift E(AC)(Q) to the right A.R. Hurson 5 AC s Q s
51 Arithmetic Logic Unit Multiplication Algorithm (2 s Complement numbers) Pre-Post Complementation Convert negative numbers to positive numbers. Apply "add and shift" algorithm. Convert the result - if necessary. A.R. Hurson 51
52 Arithmetic Logic Unit Multiplication Algorithm (2 s Complement numbers) Etension of "add and shift" Convert the multiplier to a positive number - i.e., if multiplier is negative then multiply the multiplier and the multiplicand by -1. Apply a modified "add and shift" algorithm in which addition and shift operations are done for 2 s complement numbers. A.R. Hurson 52
53 Arithmetic Logic Unit Multiplication Algorithm (2 s Complement numbers) Booth's Algorithm Instead of checking one bit of the multiplier at a time, check two bits at a time and take proper actions according to the following table: no action, shift right. 1 add multiplicand, shift right. 1 subtract multiplicand, shift right. 11 no action, shift right. A.R. Hurson 53
54 Arithmetic Logic Unit Multiplication Algorithm (2 s Complement numbers) Booth's Algorithm It is suitable for 2 s complement numbers. On average, Booth's Algorithm is faster than "add and shift". Always, etend the multiplier by a zero on the right. A.R. Hurson 54
55 Arithmetic Logic Unit Multiplication Algorithm (2 s Complement numbers) Booth's Algorithm (Eample) Etension st 2 bits are 1 subtract (add 2 s complement) A.R. Hurson 55 B * Q Shift right 1 st 2 bits are 11 shift right 1 st 2 bits are 11 shift right 1 st 2 bits are 1 add Shift right 1 st 2 bits are shift right 1 st 2 bits are shift right 1 st 2 bits are shift right
56 Questions Why is Booth's algorithm faster than "add and shift" algorithm (in general)? Why does Booth's Algorithm work? A.R. Hurson 56
57 Arithmetic Logic Unit Division Algorithm Similar to multiplication, one can develop a software routine which performs division as a sequence of subtractions. Naturally, such an algorithm is very inefficient and slow. A.R. Hurson 57
58 Arithmetic Logic Unit Division Algorithm Similar to the pencil and paper routine, one can develop an algorithm which performs division as a sequence of Compare, Shift, and Subtract operations. One should note that division in a binary system is much simpler than the division in decimal system, since the quotient digits are either or 1. A.R. Hurson 58
59 Arithmetic Logic Unit Division Algorithm To minimize the hardware requirements for division, we should remember that: Comparison can be performed via arithmetic operation(s). Subtraction can be performed via complement-addition. In other words; division requires almost the same hardware modules as multiplication does. A.R. Hurson 59
60 Arithmetic Logic Unit Division Algorithm (Signed magnitude numbers) Division can be carried out as a sequence of n (n is the length of divisor) iterations. Dividend is a double register. One bit of the quotient is generated in each iteration. At the end of the operation, the quotient is in the 1 st half part of the double register (low-order part), and remainder is in the 2 nd half part. Sign of the quotient is the XOR of the signs of dividend and divisor. Sign of the remainder is the same as the sign of the dividend. A.R. Hurson 6
61 Arithmetic Logic Unit Division Algorithm (Divide Overflow) In the division algorithm for signed magnitude numbers, if the 1 st half part of dividend is larger than or equal to the divisor, then the quotient overflows to the remainder part. This phenomenon is called divide overflow. As a result, a wrong answer will be generated. To avoid divide overflow and also due to the fact that division is a time consuming operation, the divide overflow condition is checked at the beginning of the operation. In case of divide overflow, proper actions will be taken (in the form of say an interrupt). A.R. Hurson 61
62 Arithmetic Logic Unit Methods of Division There are several different algorithms for division: Restoring Method Non-Restoring Method Direct Comparison A.R. Hurson 62
63 Arithmetic Logic Unit Methods of Division Restoring Method: In the restoring method, the contents of the partial remainder is restored whenever it is detected that the divisor is larger than the partial remainder. A.R. Hurson 63
64 Arithmetic Logic Unit Methods of Division Non-Restoring Method: In non-restoring method, if it is detected that the divisor is larger than the partial remainder, its contents are not restored. However, in the net iteration, instead of subtracting the divisor from the partial remainder, it will be added to the partial remainder. A.R. Hurson 64
65 Arithmetic Logic Unit Methods of Division Direct Comparison: divisor is compared against partial remainder. If it is smaller than or equal to partial remainder, it will be subtracted and quotient digit is set to 1. Otherwise, just the quotient digit is set to zero. A.R. Hurson 65
66 Arithmetic Logic Unit Methods of Division Naturally, restoring and non-restoring techniques are equivalent. Consider the consecutive sequence of iterations for both restoring and non-restoring techniques (net slide). As can be seen, both schemes generate the same value as the partial remainder. However, the non-restoring technique should be faster than the restoring method since it requires fewer number of operations. A.R. Hurson 66
67 Arithmetic Logic Unit Methods of Division Restoring Non-Restoring Subtract, Restore, and Shift in the first iteration Subtract in the second Iteration (2 ( (A-B)+B) -B) =2A-B Addition in the second Iteration 2 (A-B) +B =2A-B Subtraction and shift in the first iteration A.R. Hurson 67
68 Arithmetic Logic Unit Division Algorithm (Eample) Restoring Method E Etended A Q B Sign Bit Shift left EAQ. Subtract B. E=1 Q 1. Restore A. Shift left EAQ. Subtract B. E=1 Q 1. Restore A. Shift left EAQ. Subtract B. E= Q 1 1. Shift left EAQ. Subtract B. E= Q A.R. Hurson R Q Q n
69 Arithmetic Logic Unit Division Algorithm (Eample) Non-restoring Method E A Q B R Shift left EAQ. Subtract B. E=1 Q 1. Shift left EAQ. Add B. E=1 Q 1. Shift left EAQ. Add B. E= Q 1 1. Shift left EAQ. Subtract B. E= Q 1 1. A.R. Hurson 69 Q
70 Arithmetic Logic Unit Floating Point Numbers A number N in base r can be represented in many ways. For eample, decimal number can be represented as:.2945 * * 1-1 A scientific or floating point format of a number is a unique representation in which a number is represented as the multiple of 2 parts: a power of the base (called eponent)* a fraction (called mantissa) For eample, = * 1 +2 A.R. Hurson 7
71 Arithmetic Logic Unit Floating Point Numbers Such a representation in the computer requires two registers, one to represent the eponent and one to represent the mantissa. Note that each part is a signed number which could be represented in signed magnitude or signed complement format. A floating point number is normalized if the most significant digit of the mantissa is non-zero. In most systems the eponent is represented in ecess base. This means positive eponent. Therefore, a fied value (e.g., biased value) will be added to the eponent. For eample, IBM uses ecess 64 for the power, and DEC1 uses ecess 128 to represent the power. A.R. Hurson 71
72 Arithmetic Logic Unit Floating Point Numbers Convert (-25.75) 1 to a floating point number for IBM: (-25.75) 1 = -(111.11) 2 = -( * 2 5 ) 2 = ( * 2 8 ) 2 = * 16 2 A.R. Hurson 72
73 Arithmetic Logic Unit Floating Point Addition and Subtraction Check for zeroes. Align the mantissas (smaller eponent should be equated to the larger one). Add or subtract the mantissas. Normalize the result. If ep 1 ep 2 then If ep 1 < ep 2 then ( mantissa ) ( mantissa ) ( ep ep ) r 2 fl1 fl2 = ± 1 ± 2 * * b fl ( mantissa ) ( ep ep ) 1 ep A.R. Hurson 73 r ( mantissa ) r 2 r 1 = 1 * ± b 2 ep 1 ± fl2 * b b 1 2
74 Arithmetic Logic Unit Floating Point Multiplication Check for zeros. Add the eponents. Adjust the eponent of the result. Multiply the mantissas. Normalize the result. fl * fl 2 = ( mantissa 1 ) * (mantissa) 2 * r b (ep 1 + ep 2 ) 1 A.R. Hurson 74
75 Arithmetic Logic Unit Floating Point Division Check for zeroes. Align the dividend (for divide overflow condition). Subtract the eponents. Adjust the eponent of the result. Divide the mantissas. fl 1 / fl 2 = ( mantissa 1 ) / (mantissa) 2 * r b (ep 1 - ep 2 ) A.R. Hurson 75
76 Arithmetic Logic Unit Singed magnitude number: A method to represent signed numbers. 2 s complement number: A method to represent signed numbers. 1 s complement number: A method to represent signed numbers. Addition overflow: A case where the addition result is too big to fit in the destination register. A.R. Hurson 76
77 Arithmetic Logic Unit Divide overflow: A case when the quotient result is too big to fit in the quotient register. Add-and-shift algorithm: A method to perform multiplication. Booth's algorithm: A method to perform multiplication for 2 s complement numbers. Restoring technique: A method to perform division. Non-restoring technique: A faster method than restoring technique to perform division. A.R. Hurson 77
78 Arithmetic Logic Unit Biased value: A fied and positive value added to the eponent of a floating point number. The goal is to deal with positive (unsigned) eponents. Normalized number: A floating point number is normalized if the first digit in the mantissa is a non zero digit. Aligning the mantissa: A process by which the mantissa is shifted to the right by the number of differences between two eponents. Mantissa: The fraction portion of a floating point number. A.R. Hurson 78
79 Questions: Prove that two unsigned numbers can be compared by means of 1s complement addition. How do we detect overflow for signed magnitude addition? How do we detect overflow for 2s complement addition (note I am looking for another technique than the one discussed in this unit)? Prove that the add-and-shift algorithm, as implemented in this unit, does not generate an overflow. Justify the following statement. On average, Booth s algorithm is faster than add-and-shift algorithm. A.R. Hurson 79
80 Questions: On average, Booth s algorithm is faster than add-and-shift algorithm, this means that in some cases Booth s algorithm would be slower than add-and-shift algorithm. Can you give an eample that supports this? Add-and-shift checks one bit of multiplier during each iteration, Booth s algorithm checks two bits of multiplier during each iteration and as we discussed Booth s algorithm is faster that addand-shift. Can you come up with an algorithm that multilies two numbers faster than Booth s algorithm? A.R. Hurson 8
81 Questions: In case of a floating point addition or subtraction operation, why should we always align the mantissa of the smaller number? In the case of multiplication of two floating point numbers, after adding the eponents, why should we subtract one ecess base from the result? In the case of division of two floating point numbers, after subtracting the eponents, why should we add one ecess base to the result? A.R. Hurson 81
CS 5803 Introduction to High Performance Computer Architecture: Arithmetic Logic Unit. A.R. Hurson 323 CS Building, Missouri S&T
 CS 5803 Introduction to High Performance Computer Architecture: Arithmetic Logic Unit A.R. Hurson 323 CS Building, Missouri S&T hurson@mst.edu 1 Outline Motivation Design of a simple ALU How to design
CS 5803 Introduction to High Performance Computer Architecture: Arithmetic Logic Unit A.R. Hurson 323 CS Building, Missouri S&T hurson@mst.edu 1 Outline Motivation Design of a simple ALU How to design
COMPUTER ARCHITECTURE AND ORGANIZATION. Operation Add Magnitudes Subtract Magnitudes (+A) + ( B) + (A B) (B A) + (A B)
 Computer Arithmetic Data is manipulated by using the arithmetic instructions in digital computers. Data is manipulated to produce results necessary to give solution for the computation problems. The Addition,
Computer Arithmetic Data is manipulated by using the arithmetic instructions in digital computers. Data is manipulated to produce results necessary to give solution for the computation problems. The Addition,
Divide: Paper & Pencil
 Divide: Paper & Pencil 1001 Quotient Divisor 1000 1001010 Dividend -1000 10 101 1010 1000 10 Remainder See how big a number can be subtracted, creating quotient bit on each step Binary => 1 * divisor or
Divide: Paper & Pencil 1001 Quotient Divisor 1000 1001010 Dividend -1000 10 101 1010 1000 10 Remainder See how big a number can be subtracted, creating quotient bit on each step Binary => 1 * divisor or
COMP 303 Computer Architecture Lecture 6
 COMP 303 Computer Architecture Lecture 6 MULTIPLY (unsigned) Paper and pencil example (unsigned): Multiplicand 1000 = 8 Multiplier x 1001 = 9 1000 0000 0000 1000 Product 01001000 = 72 n bits x n bits =
COMP 303 Computer Architecture Lecture 6 MULTIPLY (unsigned) Paper and pencil example (unsigned): Multiplicand 1000 = 8 Multiplier x 1001 = 9 1000 0000 0000 1000 Product 01001000 = 72 n bits x n bits =
Module 2: Computer Arithmetic
 Module 2: Computer Arithmetic 1 B O O K : C O M P U T E R O R G A N I Z A T I O N A N D D E S I G N, 3 E D, D A V I D L. P A T T E R S O N A N D J O H N L. H A N N E S S Y, M O R G A N K A U F M A N N
Module 2: Computer Arithmetic 1 B O O K : C O M P U T E R O R G A N I Z A T I O N A N D D E S I G N, 3 E D, D A V I D L. P A T T E R S O N A N D J O H N L. H A N N E S S Y, M O R G A N K A U F M A N N
(+A) + ( B) + (A B) (B A) + (A B) ( A) + (+ B) (A B) + (B A) + (A B) (+ A) (+ B) + (A - B) (B A) + (A B) ( A) ( B) (A B) + (B A) + (A B)
 COMPUTER ARITHMETIC 1. Addition and Subtraction of Unsigned Numbers The direct method of subtraction taught in elementary schools uses the borrowconcept. In this method we borrow a 1 from a higher significant
COMPUTER ARITHMETIC 1. Addition and Subtraction of Unsigned Numbers The direct method of subtraction taught in elementary schools uses the borrowconcept. In this method we borrow a 1 from a higher significant
UNIT - I: COMPUTER ARITHMETIC, REGISTER TRANSFER LANGUAGE & MICROOPERATIONS
 UNIT - I: COMPUTER ARITHMETIC, REGISTER TRANSFER LANGUAGE & MICROOPERATIONS (09 periods) Computer Arithmetic: Data Representation, Fixed Point Representation, Floating Point Representation, Addition and
UNIT - I: COMPUTER ARITHMETIC, REGISTER TRANSFER LANGUAGE & MICROOPERATIONS (09 periods) Computer Arithmetic: Data Representation, Fixed Point Representation, Floating Point Representation, Addition and
Number Systems and Computer Arithmetic
 Number Systems and Computer Arithmetic Counting to four billion two fingers at a time What do all those bits mean now? bits (011011011100010...01) instruction R-format I-format... integer data number text
Number Systems and Computer Arithmetic Counting to four billion two fingers at a time What do all those bits mean now? bits (011011011100010...01) instruction R-format I-format... integer data number text
An instruction set processor consist of two important units: Data Processing Unit (DataPath) Program Control Unit
 DataPath Design An instruction set processor consist of two important units: Data Processing Unit (DataPath) Program Control Unit Add & subtract instructions for fixed binary numbers are found in the
DataPath Design An instruction set processor consist of two important units: Data Processing Unit (DataPath) Program Control Unit Add & subtract instructions for fixed binary numbers are found in the
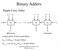
Chapter 3: part 3 Binary Subtraction
 Chapter 3: part 3 Binary Subtraction Iterative combinational circuits Binary adders Half and full adders Ripple carry and carry lookahead adders Binary subtraction Binary adder-subtractors Signed binary
Chapter 3: part 3 Binary Subtraction Iterative combinational circuits Binary adders Half and full adders Ripple carry and carry lookahead adders Binary subtraction Binary adder-subtractors Signed binary
Chapter 10 - Computer Arithmetic
 Chapter 10 - Computer Arithmetic Luis Tarrataca luis.tarrataca@gmail.com CEFET-RJ L. Tarrataca Chapter 10 - Computer Arithmetic 1 / 126 1 Motivation 2 Arithmetic and Logic Unit 3 Integer representation
Chapter 10 - Computer Arithmetic Luis Tarrataca luis.tarrataca@gmail.com CEFET-RJ L. Tarrataca Chapter 10 - Computer Arithmetic 1 / 126 1 Motivation 2 Arithmetic and Logic Unit 3 Integer representation
Organisasi Sistem Komputer
 LOGO Organisasi Sistem Komputer OSK 8 Aritmatika Komputer 1 1 PT. Elektronika FT UNY Does the calculations Arithmetic & Logic Unit Everything else in the computer is there to service this unit Handles
LOGO Organisasi Sistem Komputer OSK 8 Aritmatika Komputer 1 1 PT. Elektronika FT UNY Does the calculations Arithmetic & Logic Unit Everything else in the computer is there to service this unit Handles
Chapter 5 : Computer Arithmetic
 Chapter 5 Computer Arithmetic Integer Representation: (Fixedpoint representation): An eight bit word can be represented the numbers from zero to 255 including = 1 = 1 11111111 = 255 In general if an nbit
Chapter 5 Computer Arithmetic Integer Representation: (Fixedpoint representation): An eight bit word can be represented the numbers from zero to 255 including = 1 = 1 11111111 = 255 In general if an nbit
COMPUTER ARITHMETIC (Part 1)
 Eastern Mediterranean University School of Computing and Technology ITEC255 Computer Organization & Architecture COMPUTER ARITHMETIC (Part 1) Introduction The two principal concerns for computer arithmetic
Eastern Mediterranean University School of Computing and Technology ITEC255 Computer Organization & Architecture COMPUTER ARITHMETIC (Part 1) Introduction The two principal concerns for computer arithmetic
Chapter 5: Computer Arithmetic. In this chapter you will learn about:
 Slide 1/29 Learning Objectives In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations using binary numbers Addition (+) Subtraction (-) Multiplication
Slide 1/29 Learning Objectives In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations using binary numbers Addition (+) Subtraction (-) Multiplication
Learning Objectives. Binary over Decimal. In this chapter you will learn about:
 Ref Page Slide 1/29 Learning Objectives In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations using binary numbers Addition (+) Subtraction
Ref Page Slide 1/29 Learning Objectives In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations using binary numbers Addition (+) Subtraction
UNIT-III COMPUTER ARTHIMETIC
 UNIT-III COMPUTER ARTHIMETIC INTRODUCTION Arithmetic Instructions in digital computers manipulate data to produce results necessary for the of activity solution of computational problems. These instructions
UNIT-III COMPUTER ARTHIMETIC INTRODUCTION Arithmetic Instructions in digital computers manipulate data to produce results necessary for the of activity solution of computational problems. These instructions
VTU NOTES QUESTION PAPERS NEWS RESULTS FORUMS Arithmetic (a) The four possible cases Carry (b) Truth table x y
 Arithmetic A basic operation in all digital computers is the addition and subtraction of two numbers They are implemented, along with the basic logic functions such as AND,OR, NOT,EX- OR in the ALU subsystem
Arithmetic A basic operation in all digital computers is the addition and subtraction of two numbers They are implemented, along with the basic logic functions such as AND,OR, NOT,EX- OR in the ALU subsystem
CHW 261: Logic Design
 CHW 261: Logic Design Instructors: Prof. Hala Zayed Dr. Ahmed Shalaby http://www.bu.edu.eg/staff/halazayed14 http://bu.edu.eg/staff/ahmedshalaby14# Slide 1 Slide 2 Slide 3 Digital Fundamentals CHAPTER
CHW 261: Logic Design Instructors: Prof. Hala Zayed Dr. Ahmed Shalaby http://www.bu.edu.eg/staff/halazayed14 http://bu.edu.eg/staff/ahmedshalaby14# Slide 1 Slide 2 Slide 3 Digital Fundamentals CHAPTER
At the ith stage: Input: ci is the carry-in Output: si is the sum ci+1 carry-out to (i+1)st state
 Chapter 4 xi yi Carry in ci Sum s i Carry out c i+ At the ith stage: Input: ci is the carry-in Output: si is the sum ci+ carry-out to (i+)st state si = xi yi ci + xi yi ci + xi yi ci + xi yi ci = x i yi
Chapter 4 xi yi Carry in ci Sum s i Carry out c i+ At the ith stage: Input: ci is the carry-in Output: si is the sum ci+ carry-out to (i+)st state si = xi yi ci + xi yi ci + xi yi ci + xi yi ci = x i yi
CPE300: Digital System Architecture and Design
 CPE300: Digital System Architecture and Design Fall 2011 MW 17:30-18:45 CBC C316 Arithmetic Unit 10122011 http://www.egr.unlv.edu/~b1morris/cpe300/ 2 Outline Recap Fixed Point Arithmetic Addition/Subtraction
CPE300: Digital System Architecture and Design Fall 2011 MW 17:30-18:45 CBC C316 Arithmetic Unit 10122011 http://www.egr.unlv.edu/~b1morris/cpe300/ 2 Outline Recap Fixed Point Arithmetic Addition/Subtraction
Chapter 3: Arithmetic for Computers
 Chapter 3: Arithmetic for Computers Objectives Signed and Unsigned Numbers Addition and Subtraction Multiplication and Division Floating Point Computer Architecture CS 35101-002 2 The Binary Numbering
Chapter 3: Arithmetic for Computers Objectives Signed and Unsigned Numbers Addition and Subtraction Multiplication and Division Floating Point Computer Architecture CS 35101-002 2 The Binary Numbering
9 Multiplication and Division
 9 Multiplication and Division Multiplication is done by doing shifts and additions. Multiplying two (unsigned) numbers of n bits each results in a product of 2n bits. Example: 0110 x 0011 (6x3) At start,
9 Multiplication and Division Multiplication is done by doing shifts and additions. Multiplying two (unsigned) numbers of n bits each results in a product of 2n bits. Example: 0110 x 0011 (6x3) At start,
Advanced Computer Architecture-CS501
 Advanced Computer Architecture Lecture No. 34 Reading Material Vincent P. Heuring & Harry F. Jordan Chapter 6 Computer Systems Design and Architecture 6.1, 6.2 Summary Introduction to ALSU Radix Conversion
Advanced Computer Architecture Lecture No. 34 Reading Material Vincent P. Heuring & Harry F. Jordan Chapter 6 Computer Systems Design and Architecture 6.1, 6.2 Summary Introduction to ALSU Radix Conversion
MIPS Integer ALU Requirements
 MIPS Integer ALU Requirements Add, AddU, Sub, SubU, AddI, AddIU: 2 s complement adder/sub with overflow detection. And, Or, Andi, Ori, Xor, Xori, Nor: Logical AND, logical OR, XOR, nor. SLTI, SLTIU (set
MIPS Integer ALU Requirements Add, AddU, Sub, SubU, AddI, AddIU: 2 s complement adder/sub with overflow detection. And, Or, Andi, Ori, Xor, Xori, Nor: Logical AND, logical OR, XOR, nor. SLTI, SLTIU (set
Integer Multiplication and Division
 Integer Multiplication and Division COE 301 Computer Organization Prof. Muhamed Mudawar College of Computer Sciences and Engineering King Fahd University of Petroleum and Minerals Presentation Outline
Integer Multiplication and Division COE 301 Computer Organization Prof. Muhamed Mudawar College of Computer Sciences and Engineering King Fahd University of Petroleum and Minerals Presentation Outline
CS/COE 0447 Example Problems for Exam 2 Spring 2011
 CS/COE 0447 Example Problems for Exam 2 Spring 2011 1) Show the steps to multiply the 4-bit numbers 3 and 5 with the fast shift-add multipler. Use the table below. List the multiplicand (M) and product
CS/COE 0447 Example Problems for Exam 2 Spring 2011 1) Show the steps to multiply the 4-bit numbers 3 and 5 with the fast shift-add multipler. Use the table below. List the multiplicand (M) and product
Timing for Ripple Carry Adder
 Timing for Ripple Carry Adder 1 2 3 Look Ahead Method 5 6 7 8 9 Look-Ahead, bits wide 10 11 Multiplication Simple Gradeschool Algorithm for 32 Bits (6 Bit Result) Multiplier Multiplicand AND gates 32
Timing for Ripple Carry Adder 1 2 3 Look Ahead Method 5 6 7 8 9 Look-Ahead, bits wide 10 11 Multiplication Simple Gradeschool Algorithm for 32 Bits (6 Bit Result) Multiplier Multiplicand AND gates 32
Chapter 5: Computer Arithmetic
 Slide 1/29 Learning Objectives Computer Fundamentals: Pradeep K. Sinha & Priti Sinha In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations
Slide 1/29 Learning Objectives Computer Fundamentals: Pradeep K. Sinha & Priti Sinha In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations
ECE260: Fundamentals of Computer Engineering
 Arithmetic for Computers James Moscola Dept. of Engineering & Computer Science York College of Pennsylvania Based on Computer Organization and Design, 5th Edition by Patterson & Hennessy Arithmetic for
Arithmetic for Computers James Moscola Dept. of Engineering & Computer Science York College of Pennsylvania Based on Computer Organization and Design, 5th Edition by Patterson & Hennessy Arithmetic for
Computer Organisation CS303
 Computer Organisation CS303 Module Period Assignments 1 Day 1 to Day 6 1. Write a program to evaluate the arithmetic statement: X=(A-B + C * (D * E-F))/G + H*K a. Using a general register computer with
Computer Organisation CS303 Module Period Assignments 1 Day 1 to Day 6 1. Write a program to evaluate the arithmetic statement: X=(A-B + C * (D * E-F))/G + H*K a. Using a general register computer with
COMPUTER ORGANIZATION AND ARCHITECTURE
 COMPUTER ORGANIZATION AND ARCHITECTURE For COMPUTER SCIENCE COMPUTER ORGANIZATION. SYLLABUS AND ARCHITECTURE Machine instructions and addressing modes, ALU and data-path, CPU control design, Memory interface,
COMPUTER ORGANIZATION AND ARCHITECTURE For COMPUTER SCIENCE COMPUTER ORGANIZATION. SYLLABUS AND ARCHITECTURE Machine instructions and addressing modes, ALU and data-path, CPU control design, Memory interface,
9/6/2011. Multiplication. Binary Multipliers The key trick of multiplication is memorizing a digit-to-digit table Everything else was just adding
 9/6/2 Multiplication Binary Multipliers The key trick of multiplication is memorizing a digit-to-digit table Everything else was just adding 2 3 4 5 6 7 8 9 2 3 4 5 6 7 8 9 2 2 4 6 8 2 4 6 8 3 3 6 9 2
9/6/2 Multiplication Binary Multipliers The key trick of multiplication is memorizing a digit-to-digit table Everything else was just adding 2 3 4 5 6 7 8 9 2 3 4 5 6 7 8 9 2 2 4 6 8 2 4 6 8 3 3 6 9 2
Operations On Data CHAPTER 4. (Solutions to Odd-Numbered Problems) Review Questions
 CHAPTER 4 Operations On Data (Solutions to Odd-Numbered Problems) Review Questions 1. Arithmetic operations interpret bit patterns as numbers. Logical operations interpret each bit as a logical values
CHAPTER 4 Operations On Data (Solutions to Odd-Numbered Problems) Review Questions 1. Arithmetic operations interpret bit patterns as numbers. Logical operations interpret each bit as a logical values
EECS150 - Digital Design Lecture 13 - Combinational Logic & Arithmetic Circuits Part 3
 EECS15 - Digital Design Lecture 13 - Combinational Logic & Arithmetic Circuits Part 3 October 8, 22 John Wawrzynek Fall 22 EECS15 - Lec13-cla3 Page 1 Multiplication a 3 a 2 a 1 a Multiplicand b 3 b 2 b
EECS15 - Digital Design Lecture 13 - Combinational Logic & Arithmetic Circuits Part 3 October 8, 22 John Wawrzynek Fall 22 EECS15 - Lec13-cla3 Page 1 Multiplication a 3 a 2 a 1 a Multiplicand b 3 b 2 b
Chapter 03: Computer Arithmetic. Lesson 09: Arithmetic using floating point numbers
 Chapter 03: Computer Arithmetic Lesson 09: Arithmetic using floating point numbers Objective To understand arithmetic operations in case of floating point numbers 2 Multiplication of Floating Point Numbers
Chapter 03: Computer Arithmetic Lesson 09: Arithmetic using floating point numbers Objective To understand arithmetic operations in case of floating point numbers 2 Multiplication of Floating Point Numbers
EE260: Logic Design, Spring n Integer multiplication. n Booth s algorithm. n Integer division. n Restoring, non-restoring
 EE 260: Introduction to Digital Design Arithmetic II Yao Zheng Department of Electrical Engineering University of Hawaiʻi at Mānoa Overview n Integer multiplication n Booth s algorithm n Integer division
EE 260: Introduction to Digital Design Arithmetic II Yao Zheng Department of Electrical Engineering University of Hawaiʻi at Mānoa Overview n Integer multiplication n Booth s algorithm n Integer division
 CS6303 COMPUTER ARCHITECTURE LESSION NOTES UNIT II ARITHMETIC OPERATIONS ALU In computing an arithmetic logic unit (ALU) is a digital circuit that performs arithmetic and logical operations. The ALU is
CS6303 COMPUTER ARCHITECTURE LESSION NOTES UNIT II ARITHMETIC OPERATIONS ALU In computing an arithmetic logic unit (ALU) is a digital circuit that performs arithmetic and logical operations. The ALU is
361 div.1. Computer Architecture EECS 361 Lecture 7: ALU Design : Division
 361 div.1 Computer Architecture EECS 361 Lecture 7: ALU Design : Division Outline of Today s Lecture Introduction to Today s Lecture Divide Questions and Administrative Matters Introduction to Single cycle
361 div.1 Computer Architecture EECS 361 Lecture 7: ALU Design : Division Outline of Today s Lecture Introduction to Today s Lecture Divide Questions and Administrative Matters Introduction to Single cycle
CPS 104 Computer Organization and Programming
 CPS 104 Computer Organization and Programming Lecture 9: Integer Arithmetic. Robert Wagner CPS104 IMD.1 RW Fall 2000 Overview of Today s Lecture: Integer Multiplication and Division. Read Appendix B CPS104
CPS 104 Computer Organization and Programming Lecture 9: Integer Arithmetic. Robert Wagner CPS104 IMD.1 RW Fall 2000 Overview of Today s Lecture: Integer Multiplication and Division. Read Appendix B CPS104
More complicated than addition. Let's look at 3 versions based on grade school algorithm (multiplicand) More time and more area
 Multiplication More complicated than addition accomplished via shifting and addition More time and more area Let's look at 3 versions based on grade school algorithm 01010010 (multiplicand) x01101101 (multiplier)
Multiplication More complicated than addition accomplished via shifting and addition More time and more area Let's look at 3 versions based on grade school algorithm 01010010 (multiplicand) x01101101 (multiplier)
Computer Organization and Structure. Bing-Yu Chen National Taiwan University
 Computer Organization and Structure Bing-Yu Chen National Taiwan University Arithmetic for Computers Addition and Subtraction Gate Logic and K-Map Method Constructing a Basic ALU Arithmetic Logic Unit
Computer Organization and Structure Bing-Yu Chen National Taiwan University Arithmetic for Computers Addition and Subtraction Gate Logic and K-Map Method Constructing a Basic ALU Arithmetic Logic Unit
Chapter 4. Operations on Data
 Chapter 4 Operations on Data 1 OBJECTIVES After reading this chapter, the reader should be able to: List the three categories of operations performed on data. Perform unary and binary logic operations
Chapter 4 Operations on Data 1 OBJECTIVES After reading this chapter, the reader should be able to: List the three categories of operations performed on data. Perform unary and binary logic operations
Kinds Of Data CHAPTER 3 DATA REPRESENTATION. Numbers Are Different! Positional Number Systems. Text. Numbers. Other
 Kinds Of Data CHAPTER 3 DATA REPRESENTATION Numbers Integers Unsigned Signed Reals Fixed-Point Floating-Point Binary-Coded Decimal Text ASCII Characters Strings Other Graphics Images Video Audio Numbers
Kinds Of Data CHAPTER 3 DATA REPRESENTATION Numbers Integers Unsigned Signed Reals Fixed-Point Floating-Point Binary-Coded Decimal Text ASCII Characters Strings Other Graphics Images Video Audio Numbers
Number Systems. Both numbers are positive
 Number Systems Range of Numbers and Overflow When arithmetic operation such as Addition, Subtraction, Multiplication and Division are performed on numbers the results generated may exceed the range of
Number Systems Range of Numbers and Overflow When arithmetic operation such as Addition, Subtraction, Multiplication and Division are performed on numbers the results generated may exceed the range of
Computer Organization
 Register Transfer Logic Department of Computer Science Missouri University of Science & Technology hurson@mst.edu 1 Note, this unit will be covered in three lectures. In case you finish it earlier, then
Register Transfer Logic Department of Computer Science Missouri University of Science & Technology hurson@mst.edu 1 Note, this unit will be covered in three lectures. In case you finish it earlier, then
CS 64 Week 1 Lecture 1. Kyle Dewey
 CS 64 Week 1 Lecture 1 Kyle Dewey Overview Bitwise operation wrap-up Two s complement Addition Subtraction Multiplication (if time) Bitwise Operation Wrap-up Shift Left Move all the bits N positions to
CS 64 Week 1 Lecture 1 Kyle Dewey Overview Bitwise operation wrap-up Two s complement Addition Subtraction Multiplication (if time) Bitwise Operation Wrap-up Shift Left Move all the bits N positions to
By, Ajinkya Karande Adarsh Yoga
 By, Ajinkya Karande Adarsh Yoga Introduction Early computer designers believed saving computer time and memory were more important than programmer time. Bug in the divide algorithm used in Intel chips.
By, Ajinkya Karande Adarsh Yoga Introduction Early computer designers believed saving computer time and memory were more important than programmer time. Bug in the divide algorithm used in Intel chips.
Tailoring the 32-Bit ALU to MIPS
 Tailoring the 32-Bit ALU to MIPS MIPS ALU extensions Overflow detection: Carry into MSB XOR Carry out of MSB Branch instructions Shift instructions Slt instruction Immediate instructions ALU performance
Tailoring the 32-Bit ALU to MIPS MIPS ALU extensions Overflow detection: Carry into MSB XOR Carry out of MSB Branch instructions Shift instructions Slt instruction Immediate instructions ALU performance
Computer Architecture Set Four. Arithmetic
 Computer Architecture Set Four Arithmetic Arithmetic Where we ve been: Performance (seconds, cycles, instructions) Abstractions: Instruction Set Architecture Assembly Language and Machine Language What
Computer Architecture Set Four Arithmetic Arithmetic Where we ve been: Performance (seconds, cycles, instructions) Abstractions: Instruction Set Architecture Assembly Language and Machine Language What
carry in carry 1101 carry carry
 Chapter Binary arithmetic Arithmetic is the process of applying a mathematical operator (such as negation or addition) to one or more operands (the values being operated upon). Binary arithmetic works
Chapter Binary arithmetic Arithmetic is the process of applying a mathematical operator (such as negation or addition) to one or more operands (the values being operated upon). Binary arithmetic works
EEC 483 Computer Organization
 EEC 483 Computer Organization Chapter 3. Arithmetic for Computers Chansu Yu Table of Contents Ch.1 Introduction Ch. 2 Instruction: Machine Language Ch. 3-4 CPU Implementation Ch. 5 Cache and VM Ch. 6-7
EEC 483 Computer Organization Chapter 3. Arithmetic for Computers Chansu Yu Table of Contents Ch.1 Introduction Ch. 2 Instruction: Machine Language Ch. 3-4 CPU Implementation Ch. 5 Cache and VM Ch. 6-7
COMPUTER ORGANIZATION AND DESIGN. 5 th Edition. The Hardware/Software Interface. Chapter 3. Arithmetic for Computers Implementation
 COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Interface 5 th Edition Chapter 3 Arithmetic for Computers Implementation Today Review representations (252/352 recap) Floating point Addition: Ripple
COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Interface 5 th Edition Chapter 3 Arithmetic for Computers Implementation Today Review representations (252/352 recap) Floating point Addition: Ripple
UNIVERSITY OF MASSACHUSETTS Dept. of Electrical & Computer Engineering. Digital Computer Arithmetic ECE 666
 UNIVERSITY OF MASSACHUSETTS Dept. of Electrical & Computer Engineering Digital Computer Arithmetic ECE 666 Part 4-A Floating-Point Arithmetic Israel Koren ECE666/Koren Part.4a.1 Preliminaries - Representation
UNIVERSITY OF MASSACHUSETTS Dept. of Electrical & Computer Engineering Digital Computer Arithmetic ECE 666 Part 4-A Floating-Point Arithmetic Israel Koren ECE666/Koren Part.4a.1 Preliminaries - Representation
Week 7: Assignment Solutions
 Week 7: Assignment Solutions 1. In 6-bit 2 s complement representation, when we subtract the decimal number +6 from +3, the result (in binary) will be: a. 111101 b. 000011 c. 100011 d. 111110 Correct answer
Week 7: Assignment Solutions 1. In 6-bit 2 s complement representation, when we subtract the decimal number +6 from +3, the result (in binary) will be: a. 111101 b. 000011 c. 100011 d. 111110 Correct answer
D I G I T A L C I R C U I T S E E
 D I G I T A L C I R C U I T S E E Digital Circuits Basic Scope and Introduction This book covers theory solved examples and previous year gate question for following topics: Number system, Boolean algebra,
D I G I T A L C I R C U I T S E E Digital Circuits Basic Scope and Introduction This book covers theory solved examples and previous year gate question for following topics: Number system, Boolean algebra,
Homework 3. Assigned on 02/15 Due time: midnight on 02/21 (1 WEEK only!) B.2 B.11 B.14 (hint: use multiplexors) CSCI 402: Computer Architectures
 Homework 3 Assigned on 02/15 Due time: midnight on 02/21 (1 WEEK only!) B.2 B.11 B.14 (hint: use multiplexors) 1 CSCI 402: Computer Architectures Arithmetic for Computers (2) Fengguang Song Department
Homework 3 Assigned on 02/15 Due time: midnight on 02/21 (1 WEEK only!) B.2 B.11 B.14 (hint: use multiplexors) 1 CSCI 402: Computer Architectures Arithmetic for Computers (2) Fengguang Song Department
Computer Arithmetic Ch 8
 Computer Arithmetic Ch 8 ALU Integer Representation Integer Arithmetic Floating-Point Representation Floating-Point Arithmetic 1 Arithmetic Logical Unit (ALU) (2) (aritmeettis-looginen yksikkö) Does all
Computer Arithmetic Ch 8 ALU Integer Representation Integer Arithmetic Floating-Point Representation Floating-Point Arithmetic 1 Arithmetic Logical Unit (ALU) (2) (aritmeettis-looginen yksikkö) Does all
Computer Arithmetic Ch 8
 Computer Arithmetic Ch 8 ALU Integer Representation Integer Arithmetic Floating-Point Representation Floating-Point Arithmetic 1 Arithmetic Logical Unit (ALU) (2) Does all work in CPU (aritmeettis-looginen
Computer Arithmetic Ch 8 ALU Integer Representation Integer Arithmetic Floating-Point Representation Floating-Point Arithmetic 1 Arithmetic Logical Unit (ALU) (2) Does all work in CPU (aritmeettis-looginen
Computer Architecture and Organization: L04: Micro-operations
 Computer Architecture and Organization: L4: Micro-operations By: A. H. Abdul Hafez Abdul.hafez@hku.edu.tr, ah.abdulhafez@gmail.com, hafez@research.iiit.ac.in 1 Outlines 1. Arithmetic microoperation 2.
Computer Architecture and Organization: L4: Micro-operations By: A. H. Abdul Hafez Abdul.hafez@hku.edu.tr, ah.abdulhafez@gmail.com, hafez@research.iiit.ac.in 1 Outlines 1. Arithmetic microoperation 2.
COMPUTER ORGANIZATION AND. Edition. The Hardware/Software Interface. Chapter 3. Arithmetic for Computers
 ARM D COMPUTER ORGANIZATION AND Edition The Hardware/Software Interface Chapter 3 Arithmetic for Computers Modified and extended by R.J. Leduc - 2016 In this chapter, we will investigate: How integer arithmetic
ARM D COMPUTER ORGANIZATION AND Edition The Hardware/Software Interface Chapter 3 Arithmetic for Computers Modified and extended by R.J. Leduc - 2016 In this chapter, we will investigate: How integer arithmetic
DIGITAL ARITHMETIC: OPERATIONS AND CIRCUITS
 C H A P T E R 6 DIGITAL ARITHMETIC: OPERATIONS AND CIRCUITS OUTLINE 6- Binary Addition 6-2 Representing Signed Numbers 6-3 Addition in the 2 s- Complement System 6-4 Subtraction in the 2 s- Complement
C H A P T E R 6 DIGITAL ARITHMETIC: OPERATIONS AND CIRCUITS OUTLINE 6- Binary Addition 6-2 Representing Signed Numbers 6-3 Addition in the 2 s- Complement System 6-4 Subtraction in the 2 s- Complement
Math in MIPS. Subtracting a binary number from another binary number also bears an uncanny resemblance to the way it s done in decimal.
 Page < 1 > Math in MIPS Adding and Subtracting Numbers Adding two binary numbers together is very similar to the method used with decimal numbers, except simpler. When you add two binary numbers together,
Page < 1 > Math in MIPS Adding and Subtracting Numbers Adding two binary numbers together is very similar to the method used with decimal numbers, except simpler. When you add two binary numbers together,
Lecture 8: Addition, Multiplication & Division
 Lecture 8: Addition, Multiplication & Division Today s topics: Signed/Unsigned Addition Multiplication Division 1 Signed / Unsigned The hardware recognizes two formats: unsigned (corresponding to the C
Lecture 8: Addition, Multiplication & Division Today s topics: Signed/Unsigned Addition Multiplication Division 1 Signed / Unsigned The hardware recognizes two formats: unsigned (corresponding to the C
REGISTER TRANSFER LANGUAGE
 REGISTER TRANSFER LANGUAGE The operations executed on the data stored in the registers are called micro operations. Classifications of micro operations Register transfer micro operations Arithmetic micro
REGISTER TRANSFER LANGUAGE The operations executed on the data stored in the registers are called micro operations. Classifications of micro operations Register transfer micro operations Arithmetic micro
Floating-Point Data Representation and Manipulation 198:231 Introduction to Computer Organization Lecture 3
 Floating-Point Data Representation and Manipulation 198:231 Introduction to Computer Organization Instructor: Nicole Hynes nicole.hynes@rutgers.edu 1 Fixed Point Numbers Fixed point number: integer part
Floating-Point Data Representation and Manipulation 198:231 Introduction to Computer Organization Instructor: Nicole Hynes nicole.hynes@rutgers.edu 1 Fixed Point Numbers Fixed point number: integer part
Chapter 4 Arithmetic Functions
 Logic and Computer Design Fundamentals Chapter 4 Arithmetic Functions Charles Kime & Thomas Kaminski 2008 Pearson Education, Inc. (Hyperlinks are active in View Show mode) Overview Iterative combinational
Logic and Computer Design Fundamentals Chapter 4 Arithmetic Functions Charles Kime & Thomas Kaminski 2008 Pearson Education, Inc. (Hyperlinks are active in View Show mode) Overview Iterative combinational
Review: MIPS Organization
 1 MIPS Arithmetic Review: MIPS Organization Processor Memory src1 addr 5 src2 addr 5 dst addr 5 write data Register File registers ($zero - $ra) bits src1 data src2 data read/write addr 1 1100 2 30 words
1 MIPS Arithmetic Review: MIPS Organization Processor Memory src1 addr 5 src2 addr 5 dst addr 5 write data Register File registers ($zero - $ra) bits src1 data src2 data read/write addr 1 1100 2 30 words
Floating Point Arithmetic
 Floating Point Arithmetic CS 365 Floating-Point What can be represented in N bits? Unsigned 0 to 2 N 2s Complement -2 N-1 to 2 N-1-1 But, what about? very large numbers? 9,349,398,989,787,762,244,859,087,678
Floating Point Arithmetic CS 365 Floating-Point What can be represented in N bits? Unsigned 0 to 2 N 2s Complement -2 N-1 to 2 N-1-1 But, what about? very large numbers? 9,349,398,989,787,762,244,859,087,678
Topics. 6.1 Number Systems and Radix Conversion 6.2 Fixed-Point Arithmetic 6.3 Seminumeric Aspects of ALU Design 6.4 Floating-Point Arithmetic
 6-1 Chapter 6 Computer Arithmetic and the Arithmetic Unit Chapter 6: Computer Arithmetic and the Arithmetic Unit Topics 6.1 Number Systems and Radix Conversion 6.2 Fixed-Point Arithmetic 6.3 Seminumeric
6-1 Chapter 6 Computer Arithmetic and the Arithmetic Unit Chapter 6: Computer Arithmetic and the Arithmetic Unit Topics 6.1 Number Systems and Radix Conversion 6.2 Fixed-Point Arithmetic 6.3 Seminumeric
EC2303-COMPUTER ARCHITECTURE AND ORGANIZATION
 EC2303-COMPUTER ARCHITECTURE AND ORGANIZATION QUESTION BANK UNIT-II 1. What are the disadvantages in using a ripple carry adder? (NOV/DEC 2006) The main disadvantage using ripple carry adder is time delay.
EC2303-COMPUTER ARCHITECTURE AND ORGANIZATION QUESTION BANK UNIT-II 1. What are the disadvantages in using a ripple carry adder? (NOV/DEC 2006) The main disadvantage using ripple carry adder is time delay.
UNIT-IV COMPUTER ARITHMETIC
 UNIT-IV COMPUTER ARITHMETIC Introduction: Data is manipulated by using the arithmetic instructions in digital computers. Data is manipulated to produce results necessary to give solution for the computation
UNIT-IV COMPUTER ARITHMETIC Introduction: Data is manipulated by using the arithmetic instructions in digital computers. Data is manipulated to produce results necessary to give solution for the computation
Data Representation Type of Data Representation Integers Bits Unsigned 2 s Comp Excess 7 Excess 8
 Data Representation At its most basic level, all digital information must reduce to 0s and 1s, which can be discussed as binary, octal, or hex data. There s no practical limit on how it can be interpreted
Data Representation At its most basic level, all digital information must reduce to 0s and 1s, which can be discussed as binary, octal, or hex data. There s no practical limit on how it can be interpreted
Adding Binary Integers. Part 5. Adding Base 10 Numbers. Adding 2's Complement. Adding Binary Example = 10. Arithmetic Logic Unit
 Part 5 Adding Binary Integers Arithmetic Logic Unit = Adding Binary Integers Adding Base Numbers Computer's add binary numbers the same way that we do with decimal Columns are aligned, added, and "'s"
Part 5 Adding Binary Integers Arithmetic Logic Unit = Adding Binary Integers Adding Base Numbers Computer's add binary numbers the same way that we do with decimal Columns are aligned, added, and "'s"
1. NUMBER SYSTEMS USED IN COMPUTING: THE BINARY NUMBER SYSTEM
 1. NUMBER SYSTEMS USED IN COMPUTING: THE BINARY NUMBER SYSTEM 1.1 Introduction Given that digital logic and memory devices are based on two electrical states (on and off), it is natural to use a number
1. NUMBER SYSTEMS USED IN COMPUTING: THE BINARY NUMBER SYSTEM 1.1 Introduction Given that digital logic and memory devices are based on two electrical states (on and off), it is natural to use a number
CMPSCI 145 MIDTERM #1 Solution Key. SPRING 2017 March 3, 2017 Professor William T. Verts
 CMPSCI 145 MIDTERM #1 Solution Key NAME SPRING 2017 March 3, 2017 PROBLEM SCORE POINTS 1 10 2 10 3 15 4 15 5 20 6 12 7 8 8 10 TOTAL 100 10 Points Examine the following diagram of two systems, one involving
CMPSCI 145 MIDTERM #1 Solution Key NAME SPRING 2017 March 3, 2017 PROBLEM SCORE POINTS 1 10 2 10 3 15 4 15 5 20 6 12 7 8 8 10 TOTAL 100 10 Points Examine the following diagram of two systems, one involving
The ALU consists of combinational logic. Processes all data in the CPU. ALL von Neuman machines have an ALU loop.
 CS 320 Ch 10 Computer Arithmetic The ALU consists of combinational logic. Processes all data in the CPU. ALL von Neuman machines have an ALU loop. Signed integers are typically represented in sign-magnitude
CS 320 Ch 10 Computer Arithmetic The ALU consists of combinational logic. Processes all data in the CPU. ALL von Neuman machines have an ALU loop. Signed integers are typically represented in sign-magnitude
Principles of Computer Architecture. Chapter 3: Arithmetic
 3-1 Chapter 3 - Arithmetic Principles of Computer Architecture Miles Murdocca and Vincent Heuring Chapter 3: Arithmetic 3-2 Chapter 3 - Arithmetic 3.1 Overview Chapter Contents 3.2 Fixed Point Addition
3-1 Chapter 3 - Arithmetic Principles of Computer Architecture Miles Murdocca and Vincent Heuring Chapter 3: Arithmetic 3-2 Chapter 3 - Arithmetic 3.1 Overview Chapter Contents 3.2 Fixed Point Addition
NUMBER OPERATIONS. Mahdi Nazm Bojnordi. CS/ECE 3810: Computer Organization. Assistant Professor School of Computing University of Utah
 NUMBER OPERATIONS Mahdi Nazm Bojnordi Assistant Professor School of Computing University of Utah CS/ECE 3810: Computer Organization Overview Homework 4 is due tonight Verify your uploaded file before the
NUMBER OPERATIONS Mahdi Nazm Bojnordi Assistant Professor School of Computing University of Utah CS/ECE 3810: Computer Organization Overview Homework 4 is due tonight Verify your uploaded file before the
Floating Point. The World is Not Just Integers. Programming languages support numbers with fraction
 1 Floating Point The World is Not Just Integers Programming languages support numbers with fraction Called floating-point numbers Examples: 3.14159265 (π) 2.71828 (e) 0.000000001 or 1.0 10 9 (seconds in
1 Floating Point The World is Not Just Integers Programming languages support numbers with fraction Called floating-point numbers Examples: 3.14159265 (π) 2.71828 (e) 0.000000001 or 1.0 10 9 (seconds in
Chapter 2 Data Representations
 Computer Engineering Chapter 2 Data Representations Hiroaki Kobayashi 4/21/2008 4/21/2008 1 Agenda in Chapter 2 Translation between binary numbers and decimal numbers Data Representations for Integers
Computer Engineering Chapter 2 Data Representations Hiroaki Kobayashi 4/21/2008 4/21/2008 1 Agenda in Chapter 2 Translation between binary numbers and decimal numbers Data Representations for Integers
COMPUTER ARCHITECTURE AND ORGANIZATION Register Transfer and Micro-operations 1. Introduction A digital system is an interconnection of digital
 Register Transfer and Micro-operations 1. Introduction A digital system is an interconnection of digital hardware modules that accomplish a specific information-processing task. Digital systems vary in
Register Transfer and Micro-operations 1. Introduction A digital system is an interconnection of digital hardware modules that accomplish a specific information-processing task. Digital systems vary in
Chapter 3 Arithmetic for Computers (Part 2)
 Department of Electr rical Eng ineering, Chapter 3 Arithmetic for Computers (Part 2) 王振傑 (Chen-Chieh Wang) ccwang@mail.ee.ncku.edu.tw ncku edu Depar rtment of Electr rical Eng ineering, Feng-Chia Unive
Department of Electr rical Eng ineering, Chapter 3 Arithmetic for Computers (Part 2) 王振傑 (Chen-Chieh Wang) ccwang@mail.ee.ncku.edu.tw ncku edu Depar rtment of Electr rical Eng ineering, Feng-Chia Unive
EE878 Special Topics in VLSI. Computer Arithmetic for Digital Signal Processing
 EE878 Special Topics in VLSI Computer Arithmetic for Digital Signal Processing Part 6c High-Speed Multiplication - III Spring 2017 Koren Part.6c.1 Array Multipliers The two basic operations - generation
EE878 Special Topics in VLSI Computer Arithmetic for Digital Signal Processing Part 6c High-Speed Multiplication - III Spring 2017 Koren Part.6c.1 Array Multipliers The two basic operations - generation
Numbering systems. Dr Abu Arqoub
 Numbering systems The decimal numbering system is widely used, because the people Accustomed (معتاد) to use the hand fingers in their counting. But with the development of the computer science another
Numbering systems The decimal numbering system is widely used, because the people Accustomed (معتاد) to use the hand fingers in their counting. But with the development of the computer science another
Outline. EEL-4713 Computer Architecture Multipliers and shifters. Deriving requirements of ALU. MIPS arithmetic instructions
 Outline EEL-4713 Computer Architecture Multipliers and shifters Multiplication and shift registers Chapter 3, section 3.4 Next lecture Division, floating-point 3.5 3.6 EEL-4713 Ann Gordon-Ross.1 EEL-4713
Outline EEL-4713 Computer Architecture Multipliers and shifters Multiplication and shift registers Chapter 3, section 3.4 Next lecture Division, floating-point 3.5 3.6 EEL-4713 Ann Gordon-Ross.1 EEL-4713
Number Systems and Conversions UNIT 1 NUMBER SYSTEMS & CONVERSIONS. Number Systems (2/2) Number Systems (1/2) Iris Hui-Ru Jiang Spring 2010
 Contents Number systems and conversion Binary arithmetic Representation of negative numbers Addition of two s complement numbers Addition of one s complement numbers Binary s Readings Unit.~. UNIT NUMBER
Contents Number systems and conversion Binary arithmetic Representation of negative numbers Addition of two s complement numbers Addition of one s complement numbers Binary s Readings Unit.~. UNIT NUMBER
CS/COE0447: Computer Organization
 CS/COE0447: Computer Organization and Assembly Language Chapter 3 Sangyeun Cho Dept. of Computer Science Five classic components I am like a control tower I am like a pack of file folders I am like a conveyor
CS/COE0447: Computer Organization and Assembly Language Chapter 3 Sangyeun Cho Dept. of Computer Science Five classic components I am like a control tower I am like a pack of file folders I am like a conveyor
CS/COE0447: Computer Organization
 Five classic components CS/COE0447: Computer Organization and Assembly Language I am like a control tower I am like a pack of file folders Chapter 3 I am like a conveyor belt + service stations I exchange
Five classic components CS/COE0447: Computer Organization and Assembly Language I am like a control tower I am like a pack of file folders Chapter 3 I am like a conveyor belt + service stations I exchange
PESIT Bangalore South Campus
 INTERNAL ASSESSMENT TEST III Date : 21/11/2017 Max Marks : 40 Subject & Code : Computer Organization (15CS34) Semester : III (A & B) Name of the faculty: Mrs. Sharmila Banu Time : 11.30 am 1.00 pm Answer
INTERNAL ASSESSMENT TEST III Date : 21/11/2017 Max Marks : 40 Subject & Code : Computer Organization (15CS34) Semester : III (A & B) Name of the faculty: Mrs. Sharmila Banu Time : 11.30 am 1.00 pm Answer
Computer Architecture and Organization
 3-1 Chapter 3 - Arithmetic Computer Architecture and Organization Miles Murdocca and Vincent Heuring Chapter 3 Arithmetic 3-2 Chapter 3 - Arithmetic Chapter Contents 3.1 Fixed Point Addition and Subtraction
3-1 Chapter 3 - Arithmetic Computer Architecture and Organization Miles Murdocca and Vincent Heuring Chapter 3 Arithmetic 3-2 Chapter 3 - Arithmetic Chapter Contents 3.1 Fixed Point Addition and Subtraction
Data Representations & Arithmetic Operations
 Data Representations & Arithmetic Operations Hiroaki Kobayashi 7/13/2011 7/13/2011 Computer Science 1 Agenda Translation between binary numbers and decimal numbers Data Representations for Integers Negative
Data Representations & Arithmetic Operations Hiroaki Kobayashi 7/13/2011 7/13/2011 Computer Science 1 Agenda Translation between binary numbers and decimal numbers Data Representations for Integers Negative
Number Systems Standard positional representation of numbers: An unsigned number with whole and fraction portions is represented as:
 N Number Systems Standard positional representation of numbers: An unsigned number with whole and fraction portions is represented as: a n a a a The value of this number is given by: = a n Ka a a a a a
N Number Systems Standard positional representation of numbers: An unsigned number with whole and fraction portions is represented as: a n a a a The value of this number is given by: = a n Ka a a a a a
UNIVERSITY OF MASSACHUSETTS Dept. of Electrical & Computer Engineering. Digital Computer Arithmetic ECE 666
 UNIVERSITY OF MASSACHUSETTS Dept. of Electrical & Computer Engineering Digital Computer Arithmetic ECE 666 Part 6c High-Speed Multiplication - III Israel Koren Fall 2010 ECE666/Koren Part.6c.1 Array Multipliers
UNIVERSITY OF MASSACHUSETTS Dept. of Electrical & Computer Engineering Digital Computer Arithmetic ECE 666 Part 6c High-Speed Multiplication - III Israel Koren Fall 2010 ECE666/Koren Part.6c.1 Array Multipliers
4 Operations On Data 4.1. Foundations of Computer Science Cengage Learning
 4 Operations On Data 4.1 Foundations of Computer Science Cengage Learning Objectives After studying this chapter, the student should be able to: List the three categories of operations performed on data.
4 Operations On Data 4.1 Foundations of Computer Science Cengage Learning Objectives After studying this chapter, the student should be able to: List the three categories of operations performed on data.
Floating Point Arithmetic
 Floating Point Arithmetic Floating point numbers are frequently used in many applications. Implementation of arithmetic units such as adder, multiplier, etc for Floating point numbers are more complex
Floating Point Arithmetic Floating point numbers are frequently used in many applications. Implementation of arithmetic units such as adder, multiplier, etc for Floating point numbers are more complex
COMPUTER ORGANIZATION AND DESIGN
 COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Interface 5 th Edition Chapter 3 Arithmetic for Computers Arithmetic for Computers Operations on integers Addition and subtraction Multiplication
COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Interface 5 th Edition Chapter 3 Arithmetic for Computers Arithmetic for Computers Operations on integers Addition and subtraction Multiplication
Digital Fundamentals
 Digital Fundamentals Tenth Edition Floyd Chapter 2 2009 Pearson Education, Upper 2008 Pearson Saddle River, Education NJ 07458. All Rights Reserved Decimal Numbers The position of each digit in a weighted
Digital Fundamentals Tenth Edition Floyd Chapter 2 2009 Pearson Education, Upper 2008 Pearson Saddle River, Education NJ 07458. All Rights Reserved Decimal Numbers The position of each digit in a weighted
Binary Adders. Ripple-Carry Adder
 Ripple-Carry Adder Binary Adders x n y n x y x y c n FA c n - c 2 FA c FA c s n MSB position Longest delay (Critical-path delay): d c(n) = n d carry = 2n gate delays d s(n-) = (n-) d carry +d sum = 2n
Ripple-Carry Adder Binary Adders x n y n x y x y c n FA c n - c 2 FA c FA c s n MSB position Longest delay (Critical-path delay): d c(n) = n d carry = 2n gate delays d s(n-) = (n-) d carry +d sum = 2n
Integer Multiplication. Back to Arithmetic. Integer Multiplication. Example (Fig 4.25)
 Back to Arithmetic Before, we did Representation of integers Addition/Subtraction Logical ops Forecast Integer Multiplication Integer Division Floating-point Numbers Floating-point Addition/Multiplication
Back to Arithmetic Before, we did Representation of integers Addition/Subtraction Logical ops Forecast Integer Multiplication Integer Division Floating-point Numbers Floating-point Addition/Multiplication
