ECE608 - Chapter 8 answers
|
|
|
- Marilynn Bishop
- 6 years ago
- Views:
Transcription
1 ¼ À ÈÌ Ê ÈÊÇ Ä ÅË ½µ º½¹ ¾µ º¾¹ µ º ¹½ µ º ¹ µ º ¹ µ º ¹¾ µ ¹ µ ¹ ½
2 ECE608 - Chapter 8 answers (1) CLR If the sort runs in linear time for m input permutations, then the height h of those paths of the decision tree consisting of the m corresponding leaves and their ancestors must be linear. Hence, we can use the same argument as in the proof of Theorem 8.1 to show that this is impossible for m = n!, n! n!, or. Wehave2 h m, which gives 2 n 2 n h lg m, and so for all possible m s given here, lg m =Ω(nlg n), so h =Ω(nlg n). In particular, (i) lg( n! )=lg(n!) 1 (n lg n n lg e) 1 2 (ii) lg( n! )=lg(n!) lg n (n lg n n lg e) lg n n (iii) lg( n! 2 n )=lg(n!) n (n lg n n lg e) n (2) CLR For the preprocessing step, compute the C array as in lines 1 through 7 of Counting- Sort. Then for any query Num-in-Range(a, b), we simply return C[b] C[a 1], where C[0] = 0. The query requires O(1) time to answer. (3) CLR
3 COW SEA TAB BAR DOG TEA BAR BIG SEA MOB EAR BOX RUG TAB TAR COW ROW DOG SEA DIG MOB RUG TEA DOG BOX DIG DIG EAR TAB BIG BIG FOX BAR BAR MOB MOB EAR EAR DOG NOW TAR TAR COW ROW DIG COW ROW RUG BIG ROW NOW SEA TEA NOW BOX TAB NOW BOX FOX TAR FOX FOX RUG TEA (4) CLR Basis: If d = 1, there is only one digit, so sorting on that digit sorts the array. Inductive step: Assuming that RADIX-SORT works for d 1 digits, we will show that it works for d digits. RADIX-SORT sorts separately on each digit, starting from digit 1. Thus RADIX- SORT of d digits, which sort on digits 1,...,d is equivalent to RADIX-SORT of the low-order d 1 digits followed by a sort on digit d. By our induction hypothesis, the sort of the low-order d 1 digits works, so just before the sort on digit d, the elements are in order according to their low-order d 1 digits. The sort on digit d will order the elements by their dth digit. Consider two elements, a and b, withdth digits a d and b d respectively. 2
4 If a d <b d, the sort will put a before b, which is correct, since a<bregardless of the low-order digits. If a d >b d, the sort will put a after b, which is correct, since a>bregardless of the low-order digits. If a d = b d, the sort will leave a and b in the same order they were in, because it is stable. But that order is already correct, since the correct order of a and b is determined by the low-order d 1 digits when their dth digits are equal, and the elements are already sorted by their low-order d 1 digits. If the intermediate sort were not stable, it might rearrange elements whose dth digits were equal elements that were in the right order after the sort on their lower-order digits. (5) CLR (note: Same argument can be used with d = 3 instead of d = 2) With n input elements having values between 0 and n 2 1, we represent the numbers with a two-digit place notation using n as the base(radix). For example, when n = 1000, 0 is represented as (000, 000), 999, 999 is represented as (999, 999), and 623 is represented as (000, 623), 999 is represented as (000, 999), 1, 000 is represented as (001, 000), etc. Then, by using RADIX-SORT to sort the above inputs with d =2 and k = n, the running time is Θ(dn + dk) =Θ(2n +2k) =Θ(2n +2n) =Θ(n). (6) CLR The worst case occurs when every element falls into the same bucket. When this occurs, INSERTION-SORT in the worst case takes Θ(n 2 ). So the worst case running time is determined by the worst case running time of the sorting algorithm used. If we use MERGE-SORT instead of INSERTION-SORT, then the worst case running time is Θ(n lg n), while we still preserve the linear expected running time because E[n i lg n i ] E[n 2 i ]=Θ(1). 3
5 (7) CLR 8-3 (a) The first thing to note is that numbers with fewer digits are smaller than numbers with more digits. So the numbers first need to sorted on the basis of how many digits they have. Say that the maximum number of digits any number has is D. Thenwe first sort the numbers into D sub-arrays, such that the first sub-array consists of all numbers with one digit, the second one with two digits... and so on. The procedure SORT-BY-DIGITS given below performs this task in O(n) SORT-BY-DIGITS (A, B, C, D) 1. for i 0toD 2. do C[i] 0 3. for j 1tolength[A] 4. do C[digits[A[j]]] C[digits[A[j]]] for i 1toD 6. do C[i] C[i]+C[i 1] 7. Save a copy of the C array in O(D) time 8. for j length[a] downto1 9. do B[C[digits[A[j]]]] A[j] 10. C[digits[A[j]]]C[digits[A[j]]] SORT-BY-DIGITS takes O(n) because each of the for loops either iterates n times or D times and even if each number has 1 digit D is less than n. We assume that the contents of the array C were saved before the for-loop of line 8-9, this is acceptable as it will take O(D) time. Once this is done, we can run radix sort on each of the subarrays. There are D subarrays, let n k denote the number of elements in the k th subarray and k be the number of digits of each elements in the k th sub-array. The following procedure sorts all sub-arrays in O(n) time. SORT-SUBARRAYS (A, B, C, D) 1. for k0 tod 1 4
6 2. RADIX-SORT( B[C[k]..C[k +1]],k+1) Each invocation of RADIX-SORT takes O(n k k) time, as there are n k numbers in the k th subarray and each has k digits. The total running time is given as: D T (n) = n k k Because the sum of all n k products is the number of digits in the entire array, we have: k=1 T (n) =O(n) (b) We are given a stream of n characters, thats makes up upto n strings. The strings are to be sorted in alphabetic order, and a short string of k characters is to be ordered before a longer string that has the same first k characters. We use a counting sort to sort the words based on their first letter. Then, for each initial letter, we recursively sort the words with that first letter using the sort algorithm we are designing here, but with the first letter of each word removed. If any one of these entries is just one letter long then we do not include it in the recursion but place it at the beginning of the results (when the recursion returns, place the first letter back on the front of each word). The base case of the recursion is when the set of words to sort is empty. Analysis: Each counting sort call is O(k + 26) = O(k) whenk words are sorted. Let T (n) be the worst-case cost for sorting total length n. For each letter a, letn a be the total length of the words starting with letter a, andc a be the number of words starting with a. The sort requires a recursive call of cost T (n a c a ). Also, there is a divide and recombine cost for each subproblem of size O(c a ). Also, there is a counting sort call at cost O(Sum a c a ). These last two kinds of cost can be combined as one charge or O(Sum a c a ). TherecurrenceforthesortisthusT (n) =Sum a T (n a c a )+k(sum a c a ), for some k. 5
7 Here,weknowthatSum a n a + c a = n, because every letter is either the first letter of a distinct word or one of the remaining letters passed on, and Sum a c a 1, because there is at least one word. We show by substitution that T(n) is dn for some constant d, for all n 1. In the base case, n=1, and the cost is k(1), so we can take d k. In the recursive case, we have T (n) Sum a d(n a c a )+k(sum a c a ) Sum a d(n a ) [using d k] dn, as desired. (8) CLR 8-6 (a) There are 2n elements in total. We select n elements from the total to obtain one of the arrays, and the remaining elements must automatically belong to the second array. Sothenumberofchoicesisthesameasifwewereselectingn items from 2n items. And this is exactly ( ( ) 2n n ). (b) Lets call the two arrays a and b. And name the elements of the array a 1 ; a 2 ::: and b 1 ; b 2 :::. The decision tree for merging of the two arrays a and b will be as follows, note that once all elements from any array have been exhausted no further comparisons are required: (a 1 b 1 ) (a 2 b 1 )(a 1 b 2 ) (a 3 b 1 )(a 2 b 2 )(a 2 b 2 )(a 1 b 3 ) :::::: (a n b 1 )(a n 1 b 2 ) ::::: (a n k b k ) ::::: (a 1 b n ) :::: (a n 1 b n 1 ) :::: :::: (a n b n 1 )(a n 1 b n ) :::: :::: (a n b n )(a n b n ) :::: 6
8 We see that the left-most and right-most ends of the tree have only depth of n comparisons as they continuously use up elements from only one array. Subtrees down the middle tend to use elements from both arrays and so are deeper. The deepest path results when one element is taken from either array in strict alternation and it results in the last leaf being 2n deep from the root. Every time two elements get consecutively chosen from the same array, the depth of the tree along that path reduces by 1. Thus the number of comparisons can be expressed as 2n -(number of times elements do not get taken from alternating arrays). Because each array has n elements, the number of times you can consecutively take from the same array is bounded by n. So the total number of comparisons is 2n - O(n). (c) Imagine three elements in the final merged list C, letscallthemc i ; c i+1 and c i+2. Lets say that c i is a j i.e., the j th element from the array A. And similarily c i+1 is b k. When c i was chosen from A and B to be placed as the next element in the merging of C, it was compared to the current head of the array B and found to be smaller. This current head of B must have been bk. To prove by contradiction lets say the current head was b <k, then in the final merged list C, at least one element from B must have come between a j and bk which contradicts our assumption that they are consecutive. Similariliy if the current head of B was b >k,thenc i+1 could only be some other element from B, while b k itself must have already been added to C at some earlier step and so it contradicts the assumption that c i+1 is b k. Therefore the current head of B must have been bk when a j was added to C and hence they must have been compared. (d) We note that every time two consecutive elements in C do not belong to the same array, they must have been compared against each other. So the maximum number of comparison are obtained when C strictly alternates between elements from A and B. This would result in a comparison at every element merging except for the last one (when the other array has gone empty and there is nothing to compare). Thus the worst case number of comparisons would be 2n 1. 7
HOMEWORK 4 CS5381 Analysis of Algorithm
 HOMEWORK 4 CS5381 Analysis of Algorithm 1. QUESTION 1 Why do we want the loop index i in line 2 of BUILD-MAX-HEAP as shown below to decrease from length[a]/2 to 2 rather than increase from 1 to length[a]/2?
HOMEWORK 4 CS5381 Analysis of Algorithm 1. QUESTION 1 Why do we want the loop index i in line 2 of BUILD-MAX-HEAP as shown below to decrease from length[a]/2 to 2 rather than increase from 1 to length[a]/2?
8 SortinginLinearTime
 8 SortinginLinearTime We have now introduced several algorithms that can sort n numbers in O(n lg n) time. Merge sort and heapsort achieve this upper bound in the worst case; quicksort achieves it on average.
8 SortinginLinearTime We have now introduced several algorithms that can sort n numbers in O(n lg n) time. Merge sort and heapsort achieve this upper bound in the worst case; quicksort achieves it on average.
How many leaves on the decision tree? There are n! leaves, because every permutation appears at least once.
 Chapter 8. Sorting in Linear Time Types of Sort Algorithms The only operation that may be used to gain order information about a sequence is comparison of pairs of elements. Quick Sort -- comparison-based
Chapter 8. Sorting in Linear Time Types of Sort Algorithms The only operation that may be used to gain order information about a sequence is comparison of pairs of elements. Quick Sort -- comparison-based
Chapter 8 Sort in Linear Time
 Chapter 8 Sort in Linear Time We have so far discussed several sorting algorithms that sort a list of n numbers in O(nlog n) time. Both the space hungry merge sort and the structurely interesting heapsort
Chapter 8 Sort in Linear Time We have so far discussed several sorting algorithms that sort a list of n numbers in O(nlog n) time. Both the space hungry merge sort and the structurely interesting heapsort
Design and Analysis of Algorithms
 Design and Analysis of Algorithms CSE 5311 Lecture 8 Sorting in Linear Time Junzhou Huang, Ph.D. Department of Computer Science and Engineering CSE5311 Design and Analysis of Algorithms 1 Sorting So Far
Design and Analysis of Algorithms CSE 5311 Lecture 8 Sorting in Linear Time Junzhou Huang, Ph.D. Department of Computer Science and Engineering CSE5311 Design and Analysis of Algorithms 1 Sorting So Far
The divide-and-conquer paradigm involves three steps at each level of the recursion: Divide the problem into a number of subproblems.
 2.3 Designing algorithms There are many ways to design algorithms. Insertion sort uses an incremental approach: having sorted the subarray A[1 j - 1], we insert the single element A[j] into its proper
2.3 Designing algorithms There are many ways to design algorithms. Insertion sort uses an incremental approach: having sorted the subarray A[1 j - 1], we insert the single element A[j] into its proper
Algorithms Chapter 8 Sorting in Linear Time
 Algorithms Chapter 8 Sorting in Linear Time Assistant Professor: Ching Chi Lin 林清池助理教授 chingchi.lin@gmail.com Department of Computer Science and Engineering National Taiwan Ocean University Outline Lower
Algorithms Chapter 8 Sorting in Linear Time Assistant Professor: Ching Chi Lin 林清池助理教授 chingchi.lin@gmail.com Department of Computer Science and Engineering National Taiwan Ocean University Outline Lower
CS502 Midterm Spring 2013 (26 May-05 June)
 How would you modify QUICKSORT to sort into non-increasing order? Answer: - Click here for detail To make QUICKSORT sort in non-increasing order we must modify PARTITION. Q- We can avoid unnecessary repetitions
How would you modify QUICKSORT to sort into non-increasing order? Answer: - Click here for detail To make QUICKSORT sort in non-increasing order we must modify PARTITION. Q- We can avoid unnecessary repetitions
Lower bound for comparison-based sorting
 COMP3600/6466 Algorithms 2018 Lecture 8 1 Lower bound for comparison-based sorting Reading: Cormen et al, Section 8.1 and 8.2 Different sorting algorithms may have different running-time complexities.
COMP3600/6466 Algorithms 2018 Lecture 8 1 Lower bound for comparison-based sorting Reading: Cormen et al, Section 8.1 and 8.2 Different sorting algorithms may have different running-time complexities.
Can we do faster? What is the theoretical best we can do?
 Non-Comparison Based Sorting How fast can we sort? 2 Insertion-Sort On ( ) Merge-Sort, Quicksort (expected), Heapsort : Θ( nlg n ) Can we do faster? What is the theoretical best we can do? So far we have
Non-Comparison Based Sorting How fast can we sort? 2 Insertion-Sort On ( ) Merge-Sort, Quicksort (expected), Heapsort : Θ( nlg n ) Can we do faster? What is the theoretical best we can do? So far we have
Chapter 8 Sorting in Linear Time
 Chapter 8 Sorting in Linear Time The slides for this course are based on the course textbook: Cormen, Leiserson, Rivest, and Stein, Introduction to Algorithms, 3rd edition, The MIT Press, McGraw-Hill,
Chapter 8 Sorting in Linear Time The slides for this course are based on the course textbook: Cormen, Leiserson, Rivest, and Stein, Introduction to Algorithms, 3rd edition, The MIT Press, McGraw-Hill,
II (Sorting and) Order Statistics
 II (Sorting and) Order Statistics Heapsort Quicksort Sorting in Linear Time Medians and Order Statistics 8 Sorting in Linear Time The sorting algorithms introduced thus far are comparison sorts Any comparison
II (Sorting and) Order Statistics Heapsort Quicksort Sorting in Linear Time Medians and Order Statistics 8 Sorting in Linear Time The sorting algorithms introduced thus far are comparison sorts Any comparison
Midterm 2. Read all of the following information before starting the exam:
 Midterm 2 ECE 608 April 7, 2004, 7-9pm Name: Read all of the following information before starting the exam: NOTE: Unanswered questions are worth 30% credit, rounded down. Writing any answer loses this
Midterm 2 ECE 608 April 7, 2004, 7-9pm Name: Read all of the following information before starting the exam: NOTE: Unanswered questions are worth 30% credit, rounded down. Writing any answer loses this
Sorting. Popular algorithms: Many algorithms for sorting in parallel also exist.
 Sorting Popular algorithms: Selection sort* Insertion sort* Bubble sort* Quick sort* Comb-sort Shell-sort Heap sort* Merge sort* Counting-sort Radix-sort Bucket-sort Tim-sort Many algorithms for sorting
Sorting Popular algorithms: Selection sort* Insertion sort* Bubble sort* Quick sort* Comb-sort Shell-sort Heap sort* Merge sort* Counting-sort Radix-sort Bucket-sort Tim-sort Many algorithms for sorting
Can we do faster? What is the theoretical best we can do?
 Non-Comparison Based Sorting How fast can we sort? 2 Insertion-Sort O( n ) Merge-Sort, Quicksort (expected), Heapsort : ( n lg n ) Can we do faster? What is the theoretical best we can do? So far we have
Non-Comparison Based Sorting How fast can we sort? 2 Insertion-Sort O( n ) Merge-Sort, Quicksort (expected), Heapsort : ( n lg n ) Can we do faster? What is the theoretical best we can do? So far we have
Lecture: Analysis of Algorithms (CS )
 Lecture: Analysis of Algorithms (CS583-002) Amarda Shehu Fall 2017 Amarda Shehu Lecture: Analysis of Algorithms (CS583-002) Sorting in O(n lg n) Time: Heapsort 1 Outline of Today s Class Sorting in O(n
Lecture: Analysis of Algorithms (CS583-002) Amarda Shehu Fall 2017 Amarda Shehu Lecture: Analysis of Algorithms (CS583-002) Sorting in O(n lg n) Time: Heapsort 1 Outline of Today s Class Sorting in O(n
Comparison Based Sorting Algorithms. Algorithms and Data Structures: Lower Bounds for Sorting. Comparison Based Sorting Algorithms
 Comparison Based Sorting Algorithms Algorithms and Data Structures: Lower Bounds for Sorting Definition 1 A sorting algorithm is comparison based if comparisons A[i] < A[j], A[i] A[j], A[i] = A[j], A[i]
Comparison Based Sorting Algorithms Algorithms and Data Structures: Lower Bounds for Sorting Definition 1 A sorting algorithm is comparison based if comparisons A[i] < A[j], A[i] A[j], A[i] = A[j], A[i]
Jana Kosecka. Linear Time Sorting, Median, Order Statistics. Many slides here are based on E. Demaine, D. Luebke slides
 Jana Kosecka Linear Time Sorting, Median, Order Statistics Many slides here are based on E. Demaine, D. Luebke slides Insertion sort: Easy to code Fast on small inputs (less than ~50 elements) Fast on
Jana Kosecka Linear Time Sorting, Median, Order Statistics Many slides here are based on E. Demaine, D. Luebke slides Insertion sort: Easy to code Fast on small inputs (less than ~50 elements) Fast on
COT 6405 Introduction to Theory of Algorithms
 COT 6405 Introduction to Theory of Algorithms Topic 10. Linear Time Sorting 10/5/2016 2 How fast can we sort? The sorting algorithms we learned so far Insertion Sort, Merge Sort, Heap Sort, and Quicksort
COT 6405 Introduction to Theory of Algorithms Topic 10. Linear Time Sorting 10/5/2016 2 How fast can we sort? The sorting algorithms we learned so far Insertion Sort, Merge Sort, Heap Sort, and Quicksort
Algorithms and Data Structures: Lower Bounds for Sorting. ADS: lect 7 slide 1
 Algorithms and Data Structures: Lower Bounds for Sorting ADS: lect 7 slide 1 ADS: lect 7 slide 2 Comparison Based Sorting Algorithms Definition 1 A sorting algorithm is comparison based if comparisons
Algorithms and Data Structures: Lower Bounds for Sorting ADS: lect 7 slide 1 ADS: lect 7 slide 2 Comparison Based Sorting Algorithms Definition 1 A sorting algorithm is comparison based if comparisons
CPSC 311 Lecture Notes. Sorting and Order Statistics (Chapters 6-9)
 CPSC 311 Lecture Notes Sorting and Order Statistics (Chapters 6-9) Acknowledgement: These notes are compiled by Nancy Amato at Texas A&M University. Parts of these course notes are based on notes from
CPSC 311 Lecture Notes Sorting and Order Statistics (Chapters 6-9) Acknowledgement: These notes are compiled by Nancy Amato at Texas A&M University. Parts of these course notes are based on notes from
Other techniques for sorting exist, such as Linear Sorting which is not based on comparisons. Linear Sorting techniques include:
 Sorting in Linear Time Comparison Sorts O(nlgn), Ω(nlgn) for some input The best we can do for comparison sorts is Ω(nlgn). Other techniques for sorting exist, such as Linear Sorting which is not based
Sorting in Linear Time Comparison Sorts O(nlgn), Ω(nlgn) for some input The best we can do for comparison sorts is Ω(nlgn). Other techniques for sorting exist, such as Linear Sorting which is not based
The complexity of Sorting and sorting in linear-time. Median and Order Statistics. Chapter 8 and Chapter 9
 Subject 6 Spring 2017 The complexity of Sorting and sorting in linear-time Median and Order Statistics Chapter 8 and Chapter 9 Disclaimer: These abbreviated notes DO NOT substitute the textbook for this
Subject 6 Spring 2017 The complexity of Sorting and sorting in linear-time Median and Order Statistics Chapter 8 and Chapter 9 Disclaimer: These abbreviated notes DO NOT substitute the textbook for this
The divide and conquer strategy has three basic parts. For a given problem of size n,
 1 Divide & Conquer One strategy for designing efficient algorithms is the divide and conquer approach, which is also called, more simply, a recursive approach. The analysis of recursive algorithms often
1 Divide & Conquer One strategy for designing efficient algorithms is the divide and conquer approach, which is also called, more simply, a recursive approach. The analysis of recursive algorithms often
CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics
 CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics 1 Sorting 1.1 Problem Statement You are given a sequence of n numbers < a 1, a 2,..., a n >. You need to
CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics 1 Sorting 1.1 Problem Statement You are given a sequence of n numbers < a 1, a 2,..., a n >. You need to
Introduction to Algorithms
 Introduction to Algorithms 6.046J/18.401J/SMA5503 Lecture 5 Prof. Erik Demaine How fast can we sort? All the sorting algorithms we have seen so far are comparison sorts: only use comparisons to determine
Introduction to Algorithms 6.046J/18.401J/SMA5503 Lecture 5 Prof. Erik Demaine How fast can we sort? All the sorting algorithms we have seen so far are comparison sorts: only use comparisons to determine
Lecture 2: Getting Started
 Lecture 2: Getting Started Insertion Sort Our first algorithm is Insertion Sort Solves the sorting problem Input: A sequence of n numbers a 1, a 2,..., a n. Output: A permutation (reordering) a 1, a 2,...,
Lecture 2: Getting Started Insertion Sort Our first algorithm is Insertion Sort Solves the sorting problem Input: A sequence of n numbers a 1, a 2,..., a n. Output: A permutation (reordering) a 1, a 2,...,
Chapter 4: Sorting. Spring 2014 Sorting Fun 1
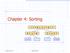 Chapter 4: Sorting 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 Spring 2014 Sorting Fun 1 What We ll Do! Quick Sort! Lower bound on runtimes for comparison based sort! Radix and Bucket sort Spring 2014
Chapter 4: Sorting 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 Spring 2014 Sorting Fun 1 What We ll Do! Quick Sort! Lower bound on runtimes for comparison based sort! Radix and Bucket sort Spring 2014
Plotting run-time graphically. Plotting run-time graphically. CS241 Algorithmics - week 1 review. Prefix Averages - Algorithm #1
 CS241 - week 1 review Special classes of algorithms: logarithmic: O(log n) linear: O(n) quadratic: O(n 2 ) polynomial: O(n k ), k 1 exponential: O(a n ), a > 1 Classifying algorithms is generally done
CS241 - week 1 review Special classes of algorithms: logarithmic: O(log n) linear: O(n) quadratic: O(n 2 ) polynomial: O(n k ), k 1 exponential: O(a n ), a > 1 Classifying algorithms is generally done
EECS 2011M: Fundamentals of Data Structures
 M: Fundamentals of Data Structures Instructor: Suprakash Datta Office : LAS 3043 Course page: http://www.eecs.yorku.ca/course/2011m Also on Moodle Note: Some slides in this lecture are adopted from James
M: Fundamentals of Data Structures Instructor: Suprakash Datta Office : LAS 3043 Course page: http://www.eecs.yorku.ca/course/2011m Also on Moodle Note: Some slides in this lecture are adopted from James
Fast Sorting and Selection. A Lower Bound for Worst Case
 Lists and Iterators 0//06 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 0 Fast Sorting and Selection USGS NEIC. Public domain government
Lists and Iterators 0//06 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 0 Fast Sorting and Selection USGS NEIC. Public domain government
Introduction to Algorithms
 Introduction to Algorithms 6.046J/18.401J Lecture 6 Prof. Piotr Indyk Today: sorting Show that Θ (n lg n) is the best possible running time for a sorting algorithm. Design an algorithm that sorts in O(n)
Introduction to Algorithms 6.046J/18.401J Lecture 6 Prof. Piotr Indyk Today: sorting Show that Θ (n lg n) is the best possible running time for a sorting algorithm. Design an algorithm that sorts in O(n)
Lecture 3. Recurrences / Heapsort
 Lecture 3. Recurrences / Heapsort T. H. Cormen, C. E. Leiserson and R. L. Rivest Introduction to Algorithms, 3rd Edition, MIT Press, 2009 Sungkyunkwan University Hyunseung Choo choo@skku.edu Copyright
Lecture 3. Recurrences / Heapsort T. H. Cormen, C. E. Leiserson and R. L. Rivest Introduction to Algorithms, 3rd Edition, MIT Press, 2009 Sungkyunkwan University Hyunseung Choo choo@skku.edu Copyright
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
O(n): printing a list of n items to the screen, looking at each item once.
 UNIT IV Sorting: O notation efficiency of sorting bubble sort quick sort selection sort heap sort insertion sort shell sort merge sort radix sort. O NOTATION BIG OH (O) NOTATION Big oh : the function f(n)=o(g(n))
UNIT IV Sorting: O notation efficiency of sorting bubble sort quick sort selection sort heap sort insertion sort shell sort merge sort radix sort. O NOTATION BIG OH (O) NOTATION Big oh : the function f(n)=o(g(n))
ECE608 - Chapter 16 answers
 ¼ À ÈÌ Ê ½ ÈÊÇ Ä ÅË ½µ ½ º½¹ ¾µ ½ º½¹ µ ½ º¾¹½ µ ½ º¾¹¾ µ ½ º¾¹ µ ½ º ¹ µ ½ º ¹ µ ½ ¹½ ½ ECE68 - Chapter 6 answers () CLR 6.-4 Let S be the set of n activities. The obvious solution of using Greedy-Activity-
¼ À ÈÌ Ê ½ ÈÊÇ Ä ÅË ½µ ½ º½¹ ¾µ ½ º½¹ µ ½ º¾¹½ µ ½ º¾¹¾ µ ½ º¾¹ µ ½ º ¹ µ ½ º ¹ µ ½ ¹½ ½ ECE68 - Chapter 6 answers () CLR 6.-4 Let S be the set of n activities. The obvious solution of using Greedy-Activity-
Lower Bound on Comparison-based Sorting
 Lower Bound on Comparison-based Sorting Different sorting algorithms may have different time complexity, how to know whether the running time of an algorithm is best possible? We know of several sorting
Lower Bound on Comparison-based Sorting Different sorting algorithms may have different time complexity, how to know whether the running time of an algorithm is best possible? We know of several sorting
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba 1 / 12 Binary Search Trees (review) Structure
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba 1 / 12 Binary Search Trees (review) Structure
Sorting. CMPS 2200 Fall Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk
 CMPS 2200 Fall 2014 Sorting Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk 11/11/14 CMPS 2200 Intro. to Algorithms 1 How fast can we sort? All the sorting algorithms
CMPS 2200 Fall 2014 Sorting Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk 11/11/14 CMPS 2200 Intro. to Algorithms 1 How fast can we sort? All the sorting algorithms
MergeSort. Algorithm : Design & Analysis [5]
![MergeSort. Algorithm : Design & Analysis [5] MergeSort. Algorithm : Design & Analysis [5]](/thumbs/72/66691138.jpg) MergeSort Algorithm : Design & Analysis [5] In the last class Insertion sort Analysis of insertion sorting algorithm Lower bound of local comparison based sorting algorithm General pattern of divide-and-conquer
MergeSort Algorithm : Design & Analysis [5] In the last class Insertion sort Analysis of insertion sorting algorithm Lower bound of local comparison based sorting algorithm General pattern of divide-and-conquer
15.4 Longest common subsequence
 15.4 Longest common subsequence Biological applications often need to compare the DNA of two (or more) different organisms A strand of DNA consists of a string of molecules called bases, where the possible
15.4 Longest common subsequence Biological applications often need to compare the DNA of two (or more) different organisms A strand of DNA consists of a string of molecules called bases, where the possible
CSC 273 Data Structures
 CSC 273 Data Structures Lecture 6 - Faster Sorting Methods Merge Sort Divides an array into halves Sorts the two halves, Then merges them into one sorted array. The algorithm for merge sort is usually
CSC 273 Data Structures Lecture 6 - Faster Sorting Methods Merge Sort Divides an array into halves Sorts the two halves, Then merges them into one sorted array. The algorithm for merge sort is usually
How fast can we sort? Sorting. Decision-tree example. Decision-tree example. CS 3343 Fall by Charles E. Leiserson; small changes by Carola
 CS 3343 Fall 2007 Sorting Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk CS 3343 Analysis of Algorithms 1 How fast can we sort? All the sorting algorithms we have seen
CS 3343 Fall 2007 Sorting Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk CS 3343 Analysis of Algorithms 1 How fast can we sort? All the sorting algorithms we have seen
Comparisons. Θ(n 2 ) Θ(n) Sorting Revisited. So far we talked about two algorithms to sort an array of numbers. What is the advantage of merge sort?
 So far we have studied: Comparisons Insertion Sort Merge Sort Worst case Θ(n 2 ) Θ(nlgn) Best case Θ(n) Θ(nlgn) Sorting Revisited So far we talked about two algorithms to sort an array of numbers What
So far we have studied: Comparisons Insertion Sort Merge Sort Worst case Θ(n 2 ) Θ(nlgn) Best case Θ(n) Θ(nlgn) Sorting Revisited So far we talked about two algorithms to sort an array of numbers What
Solutions. (a) Claim: A d-ary tree of height h has at most 1 + d +...
 Design and Analysis of Algorithms nd August, 016 Problem Sheet 1 Solutions Sushant Agarwal Solutions 1. A d-ary tree is a rooted tree in which each node has at most d children. Show that any d-ary tree
Design and Analysis of Algorithms nd August, 016 Problem Sheet 1 Solutions Sushant Agarwal Solutions 1. A d-ary tree is a rooted tree in which each node has at most d children. Show that any d-ary tree
CS 303 Design and Analysis of Algorithms
 Mid-term CS 303 Design and Analysis of Algorithms Review For Midterm Dong Xu (Based on class note of David Luebke) 12:55-1:55pm, Friday, March 19 Close book Bring your calculator 30% of your final score
Mid-term CS 303 Design and Analysis of Algorithms Review For Midterm Dong Xu (Based on class note of David Luebke) 12:55-1:55pm, Friday, March 19 Close book Bring your calculator 30% of your final score
Sorting and Selection
 Sorting and Selection Introduction Divide and Conquer Merge-Sort Quick-Sort Radix-Sort Bucket-Sort 10-1 Introduction Assuming we have a sequence S storing a list of keyelement entries. The key of the element
Sorting and Selection Introduction Divide and Conquer Merge-Sort Quick-Sort Radix-Sort Bucket-Sort 10-1 Introduction Assuming we have a sequence S storing a list of keyelement entries. The key of the element
Comparisons. Heaps. Heaps. Heaps. Sorting Revisited. Heaps. So far we talked about two algorithms to sort an array of numbers
 So far we have studied: Comparisons Tree is completely filled on all levels except possibly the lowest, which is filled from the left up to a point Insertion Sort Merge Sort Worst case Θ(n ) Θ(nlgn) Best
So far we have studied: Comparisons Tree is completely filled on all levels except possibly the lowest, which is filled from the left up to a point Insertion Sort Merge Sort Worst case Θ(n ) Θ(nlgn) Best
ECE608 - Chapter 15 answers
 ¼ À ÈÌ Ê ½ ÈÊÇ Ä ÅË ½µ ½ º¾¹¾ ¾µ ½ º¾¹ µ ½ º¾¹ µ ½ º ¹½ µ ½ º ¹¾ µ ½ º ¹ µ ½ º ¹¾ µ ½ º ¹ µ ½ º ¹ ½¼µ ½ º ¹ ½½µ ½ ¹ ½ ECE608 - Chapter 15 answers (1) CLR 15.2-2 MATRIX CHAIN MULTIPLY(A, s, i, j) 1. if
¼ À ÈÌ Ê ½ ÈÊÇ Ä ÅË ½µ ½ º¾¹¾ ¾µ ½ º¾¹ µ ½ º¾¹ µ ½ º ¹½ µ ½ º ¹¾ µ ½ º ¹ µ ½ º ¹¾ µ ½ º ¹ µ ½ º ¹ ½¼µ ½ º ¹ ½½µ ½ ¹ ½ ECE608 - Chapter 15 answers (1) CLR 15.2-2 MATRIX CHAIN MULTIPLY(A, s, i, j) 1. if
CSE 3101: Introduction to the Design and Analysis of Algorithms. Office hours: Wed 4-6 pm (CSEB 3043), or by appointment.
 CSE 3101: Introduction to the Design and Analysis of Algorithms Instructor: Suprakash Datta (datta[at]cse.yorku.ca) ext 77875 Lectures: Tues, BC 215, 7 10 PM Office hours: Wed 4-6 pm (CSEB 3043), or by
CSE 3101: Introduction to the Design and Analysis of Algorithms Instructor: Suprakash Datta (datta[at]cse.yorku.ca) ext 77875 Lectures: Tues, BC 215, 7 10 PM Office hours: Wed 4-6 pm (CSEB 3043), or by
Algorithms and Data Structures for Mathematicians
 Algorithms and Data Structures for Mathematicians Lecture 5: Sorting Peter Kostolányi kostolanyi at fmph and so on Room M-258 26 October 2017 Sorting Algorithms Covered So Far Worst-case time complexity
Algorithms and Data Structures for Mathematicians Lecture 5: Sorting Peter Kostolányi kostolanyi at fmph and so on Room M-258 26 October 2017 Sorting Algorithms Covered So Far Worst-case time complexity
Sorting Shabsi Walfish NYU - Fundamental Algorithms Summer 2006
 Sorting The Sorting Problem Input is a sequence of n items (a 1, a 2,, a n ) The mapping we want is determined by a comparison operation, denoted by Output is a sequence (b 1, b 2,, b n ) such that: {
Sorting The Sorting Problem Input is a sequence of n items (a 1, a 2,, a n ) The mapping we want is determined by a comparison operation, denoted by Output is a sequence (b 1, b 2,, b n ) such that: {
CS473 - Algorithms I
 CS473 - Algorithms I Lecture 4 The Divide-and-Conquer Design Paradigm View in slide-show mode 1 Reminder: Merge Sort Input array A sort this half sort this half Divide Conquer merge two sorted halves Combine
CS473 - Algorithms I Lecture 4 The Divide-and-Conquer Design Paradigm View in slide-show mode 1 Reminder: Merge Sort Input array A sort this half sort this half Divide Conquer merge two sorted halves Combine
Question 7.11 Show how heapsort processes the input:
 Question 7.11 Show how heapsort processes the input: 142, 543, 123, 65, 453, 879, 572, 434, 111, 242, 811, 102. Solution. Step 1 Build the heap. 1.1 Place all the data into a complete binary tree in the
Question 7.11 Show how heapsort processes the input: 142, 543, 123, 65, 453, 879, 572, 434, 111, 242, 811, 102. Solution. Step 1 Build the heap. 1.1 Place all the data into a complete binary tree in the
15.4 Longest common subsequence
 15.4 Longest common subsequence Biological applications often need to compare the DNA of two (or more) different organisms A strand of DNA consists of a string of molecules called bases, where the possible
15.4 Longest common subsequence Biological applications often need to compare the DNA of two (or more) different organisms A strand of DNA consists of a string of molecules called bases, where the possible
Problem. Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all. 1 i j n.
![Problem. Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all. 1 i j n. Problem. Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all. 1 i j n.](/thumbs/84/89326706.jpg) Problem 5. Sorting Simple Sorting, Quicksort, Mergesort Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all 1 i j n. 98 99 Selection Sort
Problem 5. Sorting Simple Sorting, Quicksort, Mergesort Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all 1 i j n. 98 99 Selection Sort
Treaps. 1 Binary Search Trees (BSTs) CSE341T/CSE549T 11/05/2014. Lecture 19
 CSE34T/CSE549T /05/04 Lecture 9 Treaps Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types
CSE34T/CSE549T /05/04 Lecture 9 Treaps Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 7 - Jan. 17, 2018 CLRS 7.1, 7-4, 9.1, 9.3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures 1 / 11 QuickSelect
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 7 - Jan. 17, 2018 CLRS 7.1, 7-4, 9.1, 9.3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures 1 / 11 QuickSelect
/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Sorting lower bound and Linear-time sorting Date: 9/19/17
 601.433/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Sorting lower bound and Linear-time sorting Date: 9/19/17 5.1 Introduction You should all know a few ways of sorting in O(n log n)
601.433/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Sorting lower bound and Linear-time sorting Date: 9/19/17 5.1 Introduction You should all know a few ways of sorting in O(n log n)
SORTING AND SELECTION
 2 < > 1 4 8 6 = 9 CHAPTER 12 SORTING AND SELECTION ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN JAVA, GOODRICH, TAMASSIA AND GOLDWASSER (WILEY 2016)
2 < > 1 4 8 6 = 9 CHAPTER 12 SORTING AND SELECTION ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN JAVA, GOODRICH, TAMASSIA AND GOLDWASSER (WILEY 2016)
Scribe: Virginia Williams, Sam Kim (2016), Mary Wootters (2017) Date: May 22, 2017
 CS6 Lecture 4 Greedy Algorithms Scribe: Virginia Williams, Sam Kim (26), Mary Wootters (27) Date: May 22, 27 Greedy Algorithms Suppose we want to solve a problem, and we re able to come up with some recursive
CS6 Lecture 4 Greedy Algorithms Scribe: Virginia Williams, Sam Kim (26), Mary Wootters (27) Date: May 22, 27 Greedy Algorithms Suppose we want to solve a problem, and we re able to come up with some recursive
Introduction to Algorithms I
 Summer School on Algorithms and Optimization Organized by: ACM Unit, ISI and IEEE CEDA. Tutorial II Date: 05.07.017 Introduction to Algorithms I (Q1) A binary tree is a rooted tree in which each node has
Summer School on Algorithms and Optimization Organized by: ACM Unit, ISI and IEEE CEDA. Tutorial II Date: 05.07.017 Introduction to Algorithms I (Q1) A binary tree is a rooted tree in which each node has
Greedy Algorithms. CLRS Chapters Introduction to greedy algorithms. Design of data-compression (Huffman) codes
 Greedy Algorithms CLRS Chapters 16.1 16.3 Introduction to greedy algorithms Activity-selection problem Design of data-compression (Huffman) codes (Minimum spanning tree problem) (Shortest-path problem)
Greedy Algorithms CLRS Chapters 16.1 16.3 Introduction to greedy algorithms Activity-selection problem Design of data-compression (Huffman) codes (Minimum spanning tree problem) (Shortest-path problem)
/463 Algorithms - Fall 2013 Solution to Assignment 3
 600.363/463 Algorithms - Fall 2013 Solution to Assignment 3 (120 points) I (30 points) (Hint: This problem is similar to parenthesization in matrix-chain multiplication, except the special treatment on
600.363/463 Algorithms - Fall 2013 Solution to Assignment 3 (120 points) I (30 points) (Hint: This problem is similar to parenthesization in matrix-chain multiplication, except the special treatment on
logn D. Θ C. Θ n 2 ( ) ( ) f n B. nlogn Ο n2 n 2 D. Ο & % ( C. Θ # ( D. Θ n ( ) Ω f ( n)
 CSE 0 Test Your name as it appears on your UTA ID Card Fall 0 Multiple Choice:. Write the letter of your answer on the line ) to the LEFT of each problem.. CIRCLED ANSWERS DO NOT COUNT.. points each. The
CSE 0 Test Your name as it appears on your UTA ID Card Fall 0 Multiple Choice:. Write the letter of your answer on the line ) to the LEFT of each problem.. CIRCLED ANSWERS DO NOT COUNT.. points each. The
Algorithms Dr. Haim Levkowitz
 91.503 Algorithms Dr. Haim Levkowitz Fall 2007 Lecture 4 Tuesday, 25 Sep 2007 Design Patterns for Optimization Problems Greedy Algorithms 1 Greedy Algorithms 2 What is Greedy Algorithm? Similar to dynamic
91.503 Algorithms Dr. Haim Levkowitz Fall 2007 Lecture 4 Tuesday, 25 Sep 2007 Design Patterns for Optimization Problems Greedy Algorithms 1 Greedy Algorithms 2 What is Greedy Algorithm? Similar to dynamic
Analysis of Algorithms - Quicksort -
 Analysis of Algorithms - Quicksort - Andreas Ermedahl MRTC (Mälardalens Real-Time Reseach Center) andreas.ermedahl@mdh.se Autumn 2003 Quicksort Proposed by C.A.R. Hoare in 962. Divide- and- conquer algorithm
Analysis of Algorithms - Quicksort - Andreas Ermedahl MRTC (Mälardalens Real-Time Reseach Center) andreas.ermedahl@mdh.se Autumn 2003 Quicksort Proposed by C.A.R. Hoare in 962. Divide- and- conquer algorithm
Module 2: Classical Algorithm Design Techniques
 Module 2: Classical Algorithm Design Techniques Dr. Natarajan Meghanathan Associate Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu Module
Module 2: Classical Algorithm Design Techniques Dr. Natarajan Meghanathan Associate Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu Module
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
08 A: Sorting III. CS1102S: Data Structures and Algorithms. Martin Henz. March 10, Generated on Tuesday 9 th March, 2010, 09:58
 08 A: Sorting III CS1102S: Data Structures and Algorithms Martin Henz March 10, 2010 Generated on Tuesday 9 th March, 2010, 09:58 CS1102S: Data Structures and Algorithms 08 A: Sorting III 1 1 Recap: Sorting
08 A: Sorting III CS1102S: Data Structures and Algorithms Martin Henz March 10, 2010 Generated on Tuesday 9 th March, 2010, 09:58 CS1102S: Data Structures and Algorithms 08 A: Sorting III 1 1 Recap: Sorting
Algorithms - Ch2 Sorting
 Algorithms - Ch2 Sorting (courtesy of Prof.Pecelli with some changes from Prof. Daniels) 1/28/2015 91.404 - Algorithms 1 Algorithm Description Algorithm Description: -Pseudocode see conventions on p. 20-22
Algorithms - Ch2 Sorting (courtesy of Prof.Pecelli with some changes from Prof. Daniels) 1/28/2015 91.404 - Algorithms 1 Algorithm Description Algorithm Description: -Pseudocode see conventions on p. 20-22
Trees (Part 1, Theoretical) CSE 2320 Algorithms and Data Structures University of Texas at Arlington
 Trees (Part 1, Theoretical) CSE 2320 Algorithms and Data Structures University of Texas at Arlington 1 Trees Trees are a natural data structure for representing specific data. Family trees. Organizational
Trees (Part 1, Theoretical) CSE 2320 Algorithms and Data Structures University of Texas at Arlington 1 Trees Trees are a natural data structure for representing specific data. Family trees. Organizational
Introduction to Algorithms
 Introduction to Algorithms An algorithm is any well-defined computational procedure that takes some value or set of values as input, and produces some value or set of values as output. 1 Why study algorithms?
Introduction to Algorithms An algorithm is any well-defined computational procedure that takes some value or set of values as input, and produces some value or set of values as output. 1 Why study algorithms?
Count Sort, Bucket Sort, Radix Sort. CSE 2320 Algorithms and Data Structures Vassilis Athitsos University of Texas at Arlington
 Count Sort, Bucket Sort, Radix Sort CSE 2320 Algorithms and Data Structures Vassilis Athitsos University of Texas at Arlington 1 Overview Lower bounds on comparison-based sorting Count sort Bucket sort
Count Sort, Bucket Sort, Radix Sort CSE 2320 Algorithms and Data Structures Vassilis Athitsos University of Texas at Arlington 1 Overview Lower bounds on comparison-based sorting Count sort Bucket sort
Wellesley College CS231 Algorithms September 25, 1996 Handout #11 COMPARISON-BASED SORTING
 Wellesley College C231 Algorithms eptember 25, 1996 Handout #11 COMPARIO-BA ORTIG Reading: CLR Chapters 7 & 8. --------------------- The Comparison-Based orting Problem Given An array A[1..n] of values.
Wellesley College C231 Algorithms eptember 25, 1996 Handout #11 COMPARIO-BA ORTIG Reading: CLR Chapters 7 & 8. --------------------- The Comparison-Based orting Problem Given An array A[1..n] of values.
Introduction. e.g., the item could be an entire block of information about a student, while the search key might be only the student's name
 Chapter 7 Sorting 2 Introduction sorting fundamental task in data management well-studied problem in computer science basic problem given an of items where each item contains a key, rearrange the items
Chapter 7 Sorting 2 Introduction sorting fundamental task in data management well-studied problem in computer science basic problem given an of items where each item contains a key, rearrange the items
I/O Model. Cache-Oblivious Algorithms : Algorithms in the Real World. Advantages of Cache-Oblivious Algorithms 4/9/13
 I/O Model 15-853: Algorithms in the Real World Locality II: Cache-oblivious algorithms Matrix multiplication Distribution sort Static searching Abstracts a single level of the memory hierarchy Fast memory
I/O Model 15-853: Algorithms in the Real World Locality II: Cache-oblivious algorithms Matrix multiplication Distribution sort Static searching Abstracts a single level of the memory hierarchy Fast memory
EE 368. Weeks 5 (Notes)
 EE 368 Weeks 5 (Notes) 1 Chapter 5: Trees Skip pages 273-281, Section 5.6 - If A is the root of a tree and B is the root of a subtree of that tree, then A is B s parent (or father or mother) and B is A
EE 368 Weeks 5 (Notes) 1 Chapter 5: Trees Skip pages 273-281, Section 5.6 - If A is the root of a tree and B is the root of a subtree of that tree, then A is B s parent (or father or mother) and B is A
COMP 352 FALL Tutorial 10
 1 COMP 352 FALL 2016 Tutorial 10 SESSION OUTLINE Divide-and-Conquer Method Sort Algorithm Properties Quick Overview on Sorting Algorithms Merge Sort Quick Sort Bucket Sort Radix Sort Problem Solving 2
1 COMP 352 FALL 2016 Tutorial 10 SESSION OUTLINE Divide-and-Conquer Method Sort Algorithm Properties Quick Overview on Sorting Algorithms Merge Sort Quick Sort Bucket Sort Radix Sort Problem Solving 2
Search Trees. Undirected graph Directed graph Tree Binary search tree
 Search Trees Undirected graph Directed graph Tree Binary search tree 1 Binary Search Tree Binary search key property: Let x be a node in a binary search tree. If y is a node in the left subtree of x, then
Search Trees Undirected graph Directed graph Tree Binary search tree 1 Binary Search Tree Binary search key property: Let x be a node in a binary search tree. If y is a node in the left subtree of x, then
CS 5321: Advanced Algorithms Sorting. Acknowledgement. Ali Ebnenasir Department of Computer Science Michigan Technological University
 CS 5321: Advanced Algorithms Sorting Ali Ebnenasir Department of Computer Science Michigan Technological University Acknowledgement Eric Torng Moon Jung Chung Charles Ofria Nishit Chapter 22 Bill 23 Martin
CS 5321: Advanced Algorithms Sorting Ali Ebnenasir Department of Computer Science Michigan Technological University Acknowledgement Eric Torng Moon Jung Chung Charles Ofria Nishit Chapter 22 Bill 23 Martin
Sample Solutions to Homework #2
 National aiwan University andout #1 epartment of lectrical ngineering November, 01 lgorithms, Fall 01 : Zhi-en in and Yen-hun iu ample olutions to omework # 1. (15) (a) ee Figure 1. 3 1 3 1 3 1 3 1 1 1
National aiwan University andout #1 epartment of lectrical ngineering November, 01 lgorithms, Fall 01 : Zhi-en in and Yen-hun iu ample olutions to omework # 1. (15) (a) ee Figure 1. 3 1 3 1 3 1 3 1 1 1
Sorting & Growth of Functions
 Sorting & Growth of Functions CSci 588: Data Structures, Algorithms and Software Design Introduction to Algorithms, Cormen et al., Chapter 3 All material not from online sources or text copyright Travis
Sorting & Growth of Functions CSci 588: Data Structures, Algorithms and Software Design Introduction to Algorithms, Cormen et al., Chapter 3 All material not from online sources or text copyright Travis
INDIAN STATISTICAL INSTITUTE
 INDIAN STATISTICAL INSTITUTE Mid Semestral Examination M. Tech (CS) - I Year, 2016-2017 (Semester - II) Design and Analysis of Algorithms Date : 21.02.2017 Maximum Marks : 60 Duration : 3.0 Hours Note:
INDIAN STATISTICAL INSTITUTE Mid Semestral Examination M. Tech (CS) - I Year, 2016-2017 (Semester - II) Design and Analysis of Algorithms Date : 21.02.2017 Maximum Marks : 60 Duration : 3.0 Hours Note:
Trees. 3. (Minimally Connected) G is connected and deleting any of its edges gives rise to a disconnected graph.
 Trees 1 Introduction Trees are very special kind of (undirected) graphs. Formally speaking, a tree is a connected graph that is acyclic. 1 This definition has some drawbacks: given a graph it is not trivial
Trees 1 Introduction Trees are very special kind of (undirected) graphs. Formally speaking, a tree is a connected graph that is acyclic. 1 This definition has some drawbacks: given a graph it is not trivial
Chapter 6 Heap and Its Application
 Chapter 6 Heap and Its Application We have already discussed two sorting algorithms: Insertion sort and Merge sort; and also witnessed both Bubble sort and Selection sort in a project. Insertion sort takes
Chapter 6 Heap and Its Application We have already discussed two sorting algorithms: Insertion sort and Merge sort; and also witnessed both Bubble sort and Selection sort in a project. Insertion sort takes
Lecture 5. Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs
 Lecture 5 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs Reading: Randomized Search Trees by Aragon & Seidel, Algorithmica 1996, http://sims.berkeley.edu/~aragon/pubs/rst96.pdf;
Lecture 5 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs Reading: Randomized Search Trees by Aragon & Seidel, Algorithmica 1996, http://sims.berkeley.edu/~aragon/pubs/rst96.pdf;
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, Merge Sort & Quick Sort
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Merge Sort & Quick Sort 1 Divide-and-Conquer Divide-and conquer is a general algorithm
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Merge Sort & Quick Sort 1 Divide-and-Conquer Divide-and conquer is a general algorithm
Lecture 5: Sorting Part A
 Lecture 5: Sorting Part A Heapsort Running time O(n lg n), like merge sort Sorts in place (as insertion sort), only constant number of array elements are stored outside the input array at any time Combines
Lecture 5: Sorting Part A Heapsort Running time O(n lg n), like merge sort Sorts in place (as insertion sort), only constant number of array elements are stored outside the input array at any time Combines
Introduction to Algorithms 6.046J/18.401J
 Introduction to Algorithms 6.046J/18.401J Menu for Today Show that Θ (n lg n) is the best possible running time for a sorting algorithm. Design an algorithm that sorts in linear time. Hint: maybe the models
Introduction to Algorithms 6.046J/18.401J Menu for Today Show that Θ (n lg n) is the best possible running time for a sorting algorithm. Design an algorithm that sorts in linear time. Hint: maybe the models
Lecture 9 March 4, 2010
 6.851: Advanced Data Structures Spring 010 Dr. André Schulz Lecture 9 March 4, 010 1 Overview Last lecture we defined the Least Common Ancestor (LCA) and Range Min Query (RMQ) problems. Recall that an
6.851: Advanced Data Structures Spring 010 Dr. André Schulz Lecture 9 March 4, 010 1 Overview Last lecture we defined the Least Common Ancestor (LCA) and Range Min Query (RMQ) problems. Recall that an
Fundamental mathematical techniques reviewed: Mathematical induction Recursion. Typically taught in courses such as Calculus and Discrete Mathematics.
 Fundamental mathematical techniques reviewed: Mathematical induction Recursion Typically taught in courses such as Calculus and Discrete Mathematics. Techniques introduced: Divide-and-Conquer Algorithms
Fundamental mathematical techniques reviewed: Mathematical induction Recursion Typically taught in courses such as Calculus and Discrete Mathematics. Techniques introduced: Divide-and-Conquer Algorithms
Module 3: Sorting and Randomized Algorithms
 Module 3: Sorting and Randomized Algorithms CS 240 - Data Structures and Data Management Reza Dorrigiv, Daniel Roche School of Computer Science, University of Waterloo Winter 2010 Reza Dorrigiv, Daniel
Module 3: Sorting and Randomized Algorithms CS 240 - Data Structures and Data Management Reza Dorrigiv, Daniel Roche School of Computer Science, University of Waterloo Winter 2010 Reza Dorrigiv, Daniel
4. Sorting and Order-Statistics
 4. Sorting and Order-Statistics 4. Sorting and Order-Statistics The sorting problem consists in the following : Input : a sequence of n elements (a 1, a 2,..., a n ). Output : a permutation (a 1, a 2,...,
4. Sorting and Order-Statistics 4. Sorting and Order-Statistics The sorting problem consists in the following : Input : a sequence of n elements (a 1, a 2,..., a n ). Output : a permutation (a 1, a 2,...,
( ) D. Θ ( ) ( ) Ο f ( n) ( ) Ω. C. T n C. Θ. B. n logn Ο
 CSE 0 Name Test Fall 0 Multiple Choice. Write your answer to the LEFT of each problem. points each. The expected time for insertion sort for n keys is in which set? (All n! input permutations are equally
CSE 0 Name Test Fall 0 Multiple Choice. Write your answer to the LEFT of each problem. points each. The expected time for insertion sort for n keys is in which set? (All n! input permutations are equally
LECTURE NOTES OF ALGORITHMS: DESIGN TECHNIQUES AND ANALYSIS
 Department of Computer Science University of Babylon LECTURE NOTES OF ALGORITHMS: DESIGN TECHNIQUES AND ANALYSIS By Faculty of Science for Women( SCIW), University of Babylon, Iraq Samaher@uobabylon.edu.iq
Department of Computer Science University of Babylon LECTURE NOTES OF ALGORITHMS: DESIGN TECHNIQUES AND ANALYSIS By Faculty of Science for Women( SCIW), University of Babylon, Iraq Samaher@uobabylon.edu.iq
Practical Session #11 Sorting in Linear Time
 Practical Session #11 Counting-Sort A sort algorithm that is not based on comparisons, and supports duplicate keys. A is an input array of length n. B is the output array of length n too. C is an auxiliary
Practical Session #11 Counting-Sort A sort algorithm that is not based on comparisons, and supports duplicate keys. A is an input array of length n. B is the output array of length n too. C is an auxiliary
Data Structures and Algorithms Week 4
 Data Structures and Algorithms Week. About sorting algorithms. Heapsort Complete binary trees Heap data structure. Quicksort a popular algorithm very fast on average Previous Week Divide and conquer Merge
Data Structures and Algorithms Week. About sorting algorithms. Heapsort Complete binary trees Heap data structure. Quicksort a popular algorithm very fast on average Previous Week Divide and conquer Merge
data structures and algorithms lecture 6
 data structures and algorithms 2017 09 21 lecture 6 overview lower bound counting sort radix sort stacks queues material question we have seen for example insertion sort: worst-case in O(n 2 ) merge sort:
data structures and algorithms 2017 09 21 lecture 6 overview lower bound counting sort radix sort stacks queues material question we have seen for example insertion sort: worst-case in O(n 2 ) merge sort:
11/8/2016. Chapter 7 Sorting. Introduction. Introduction. Sorting Algorithms. Sorting. Sorting
 Introduction Chapter 7 Sorting sorting fundamental task in data management well-studied problem in computer science basic problem given an array of items where each item contains a key, rearrange the items
Introduction Chapter 7 Sorting sorting fundamental task in data management well-studied problem in computer science basic problem given an array of items where each item contains a key, rearrange the items
