COMPUTER THE DESIGN AND ANALYSIS OF ALGO R ITH M S. John E H opm Cornell University Jeffrey D. Ulhn Princeton University. Ahd V. Ah0 Bell Laboratories
|
|
|
- Jeffery Harmon
- 6 years ago
- Views:
Transcription
1 THE DESIGN AND ANALYSIS OF COMPUTER ALGO R ITH M S Ahd V. Ah0 Bell Laboratories John E H opm Cornell University Jeffrey D. Ulhn Princeton University A W Addison-Wesley Publishing Company Reading, Massachusetts - Menlo Park, California London - Amsterdam - Don Mills, Ontario * Sydney
2 RADIX SORTING 77 The sorting problem can be formulated as follows. We are given a sequence of n elements a,, a2,..., a, drawn from a set having a linear order, which we shall usually denote 5. We are to find a permutation m of these n elements that will map the given sequence into a nondecreasing sequence ud,), adz),..., a,(n) such that a,(f) 5 a,(i+l) for 1 I i < n. Usually we shall produce the sorted sequence itself rather than the sorting permutation m. Sorting methods are classified as being internal (where the data resides in random access memory) or external (where the data is predominantly outside the random access memory). External sorting is an integral part of such applications as account processing, which usually involve far more elements than can be stored in random access memory at one time. Thus external sorting methods for data which are on secondary storage devices (such as a disk memory or a magnetic tape) have great commercial importance. Internal sorting is important in algorithm design as well as commercial applications. In those cases where sorting arises as part of another algorithm, the number of items to be sorted is usually small enough to fit in random access memory. However, we assume that the number of items to be sorted is moderately large. If one is going to sort only a handful of items, a simple strategy such as the O(n2) bubble sort (see Exercise 3.5) is far more expedient. There are numerous sorting algorithms. We make no attempt to survey all the important ones; rather we limit ourselves to methods which we have found to be of use in algorithm design. We first consider the case in which the elements to be sorted are integers or (almost equivalently) strings over a finite alphabet. Here, we see that sorting can be performed in linear time. Then we consider the problem of sorting without making use of the special properties of integers or strings, in which case we are forced to make program branches dep only on comparisons between the elements to be sorted. Under these conditions we shall see that O(n log n) comparisons are necessary, as well as sufficient, to sort a sequence of n elements. 3.2 RADIX SORTING To our study of integer sorting, let a,, a2,..., a, be a sequence of integers in the range 0 to m - 1. If m is not too large, the sequence can easily be sorted in the following manner. 1. Initialize m empty queues, one for each integer in the range 0 to m - 1. Each queue is called a bucket. 2. Scan the sequence a,, a2,..., a, from left to right, placing element ai in the ui-th queue. 3. Concatenate the queues (the contents of queue i + 1 are apped to the of queue i) to obtain the sorted sequence.
3 78 SORTINQ AND ORDER STATISTICS 3.2 Since an element can be inserted into the ith queue in constant time, the n elements can be inserted into the queues in time O(n). Concatenating the m queues requires O(m) time. If m is O(n), then the algorithm sorts n in- tegers in time O(n). We call this algorithm a bucket sort. The bucket sort can be exted to sort a sequence of tuples (i.e., lists) of integers into lexicographic order. Let 5 be a linear order on set S. The relation 5 when exted to tuples whose components are from S is a lexicographic order if (sl, s2,..., sp) 5 (Il, t2,..., r,) exactly when either: 1. there exists an integer j such that s, < r, and for all i < j, sf = tj, or 2. p I q and sf = tf for 1 c: i I p. For example, if one treats strings of letters (under the natural alphabetic ordering) as tuples, then the words in a dictionary are in lexicographic order. We first generalize the bucket sort to sequences consisting of k-tuples whose components are integers in the range 0 to m - 1. The sorting is done by making k passes over the sequence using the bucket sort on each pass. On the first pass the k-tuples are sorted according to their kth components. On the second pass the resulting sequence is sorted according to the (k- 1)st components. On the third pass the sequence resulting from the second pass is sorted according to the (k- 2)nd components, and so on. On the kth (and final) pass the sequence resulting from the (k- 1)st pass is sorted according to the first components.t The sequence is now in lexicographic order. A precise description of the algorithm is given below. Algorithm 3.1. Lexicographic sort. Input. A sequence Al, A2,..., A, where each Af is a k-tuple (ail, ai27 - * * 9 aid with ali an integer in the range 0 to m - 1. (A convenient data structure for this sequence of k-tuples is an n x k array.) Output. A sequence B 1, B2, such that Bi s Bi+l for 1 5 i < n...., B, which is a permutation of A 1, A 2,..., A, Method. In transferring a k-tuple At to some bucket, only a pointer to Ai is actually moved. Thus Ai can be added to a bucket in fixed time rather than time bounded by k. We use a queue called QUEUE to hold the current sequence of elements. An array Q of m buckets is also used, where bucket Q[i] is inted to hold those k-tuples that have the integer i in the component currently under consideration. The algorithm is shown in Fig t In many practical situations it is sufficient to bucket sort the strings only on the basis of their first components. If the number of elements that get placed into each bucket is small, then we can sort the strings in each bucket with some straightforward sorting algorithm such as bubble sort.
4 RADIX SORTING 79 - placea,,a,,...,a, in QUEUE; forj k step - 1 until 1 do for until m - 1 do make Q[1] empty; while QUEUE not empty do let Ai be the first element in QUEUE; move Ai from QUEUE to bucket Q[au] ; for I + 0 until m - I do concatenate contents of Q{1] to the of QUEUE Fig Lexicographic sort algorithm. Theorem 3.1. Algorithm 3.1 lexicographically sorts a length n sequence of k-tuples, where each component of a k-tuple is an integer between 0 and m - 1, in time O((m + n)k). Proof. The proof that Algorithm 3.1 works correctly is by induction on the number of executions of the outer loop. The induction hypothesis is that after r executions, the k-tuples in QUEUE will be lexicographically sorted according to their r rightmost components. The result is easily established once it is observed that the (r + 1)st execution sorts k-tuples by their (r + 1)st component from the right, and that if two k-tuples are placed in the same bucket, the first k-tuple precedes the second in the lexicographic order determined by the r rightmost components. One pass of the outer loop of Algorithm 3.1 requires O(m + n) time. The loop is repeated k times to give a time complexity of O((m + n)k). 0 Algorithm 3.1 has a variety of applications. It has been used in punched card sorting machines for a long time. It can also be used to sort O(n) integers in the range 0 to nk - I in time O(kn), since such an integer can be thought of as a k-tuple of digits in the range 0 to n - 1 (i.e., the representation of the integer in base n notation). Our final generalization of the bucket sort will be to tuples of varying sizes, which we shall call strings. If the longest string is of length k, we could pad out every string with a special symbol to make all strings be of length k and then use Algorithm 3.1. However, if there are only a few long strings, then this approach is unnecessarily inefficient for two reasons. First, on each pass, every string is examined, and second, every bucket Q[i] is examined even if almost all of these buckets are empty. We shall describe an algorithm that sorts a sequence of n strings of varying length, whose components are in
5 80 SORTINQ AND ORDER STATISTICS 3.2 the range 0 to m - 1, in time O(m + I,&,), where I, is the length of the ith string, and I, = ZtlIi. The algorithm is useful in the situation where m and are both O(n). The essence of the algorithm is to first arrange the strings in order of decreasing length. Let I, be the length of the longest string. Then, as in Algorithm 3.1, I, passes of the bucket sort are used. However, the first pass sorts (by rightmost component) only those strings of length I,. The second pass sorts [according to the (I,,, - 1)st component] those strings of length at least I, - 1, and so on. For example, suppose bab, abc, and a are three strings to be sorted. (We have assumed that the components of tuples are integers, but for notational convenience we shall often use letters instead. This should cause no difficulty because we can always substitute 0, 1, and 2 for a, 6, and c, if we like.) Here I,,,,, = 3, so on the first pass we would sort only the first two strings on the basis of their third components. In sorting these two strings we would put bab into the b-bucket and abc into the c-bucket. The a-bucket would remain empty. In the second pass we would sort these same two strings on the second component. Now the a-bucket and b-bucket would be occupied, but the c-bucket would remain empty. On the third and final pass we would sort all three strings on the basis of their first component. This time the a- and 6-buckets would be occupied and the c-bucket would be empty. We can see that in general on a given pass many buckets can be empty. Thus a preprocessing step that determines which buckets will be nonempty on a given pass is beneficial. The list of nonempty buckets for each pass is determined in increasing order of bucket number. This allows us to concatenate the nonempty buckets in time proportional to the number of nonempty buckets. Algorithm 3.2. Lexicographic sort of strings of varying length. A sequence of strings (tuples), Al, Az,..., A,, whose compo- Input. nents are integers in the range 0 to m - 1. Let Ii be the length of Ai = (ail, ai2,..., ail(), and let I, be the largest of the 1,'s. Output. A permutation B1, Bz,..., B, of thea,'s such that Method B, I Bz B,. 1. We by making lists, one for each I, 1 I 1 5 I, of those symbols that appear in the Ith component of one or more of the strings. We do so by first creating, for each component a,,, 1 I i 5 n, 1 I 1 s I* of each string A$, a pair (I, an). Such a pair indicates that the Ith component of some string contains the integer at,. These pairs are then sorted lex-
6 RADIX SORTING make QUEUE empty; 2. forj + 0 until m - 1 do make Qfi] empty; 3. for I + I,,, step - 1 until 1 do 4. concatenate LENGTH [I] to the ning of QUEUE ;t 5. while QUEUE not empty do let At be the first string on QUEUE; move At from QUEUE to bucket Q[atl] 8. ; for eachj on NONEMPTY [f] do 9. concatenate Q[j] to the of QUEUE; 10. make Qfi] empty t Technically, we should only concatenate to the of a queue, but concatenation to the ning should present no conceptual difficulty. The most efficient approach here would be to select At s from LENGTH[/] first at line 6, then select them from QUEUE, without ever concatenating LENGTHCI] and QUEUE at all. Fe Lexicographic sort of strings of varying length. icographically by an obvious generalization of Algorithm 3.1.$ Then, by scanning the sorted list from left to right it is easy to create, f sorted lists NONEMPTY [I], for 1 I zs I,,,, such that NONEMPTY [I] contains exactly those symbols that appear in the fth component of some string. That is, NONEMPTYCI] contains, in sorted order, all those integers j such that ail = j for some i. 2. We determine the length of each string. We then make lists LENGTH[I], for 1 I I; I, where LENGTH[/] consists of all strings of length 1. (Although we speak of moving a string, we are only moving a pointer to a string. Thus each string can be added to LENGTH[I] in a fixed number of steps.) 3. We now sort the strings by components as in Algorithm 3.1, ning with the components in position I,. However, after the ith pass $ In Algorithm 3.1, the assumption was made that components were chosen from the same alphabet. Here, the second component ranges from 0 to m - 1, while the first ranges from 1 to I,.
7 82 SORTING AND ORDER STATISTICS 3.2 QUEUE contains only those strings of length I, - i + 1 or greater, and these strings will already be sorted according to components I, - i + 1 through I,. The NONEMPTY lists computed in step 1 are used to determine which buckets are occupied at each pass of the bucket sort. This information is used to help speed up the concatenation of the buckets. This part of the algorithm is given in Pidgin ALGOL in Fig. 3.2 on p Example 3.1. Let us sort the strings a, bab, and abc using Algorithm 3.2. One possible representation for these strings is the data structure shown in Fig STRING is an array such that STRING[i] is a pointer to the rep resentation of the ith string whose length and components are stored in the array DATA. The cell in DATA pointed to by STRING[i] gives the number j of symbols in the ith string. The next j cells of DATA contain these symbols. The lists of strings used by Algorithm 3.2 are really lists of pointers such as those in the array STRING. For notational convenience, in the remainder of this example we shall write the actual strings, rather than the pointers to the strings, on lists. Bear in mind, however, that it is the pointers rather than the strings themselves that are being stored in the queues. In part 1 of Algorithm 3.2 we create the pair (1, a) from the first string, the pairs (1, b), (2, a), (3, b) from the second, and the pairs (1, a), (2, b), (3, c) from the third. The sorted list of these pairs is: (1, a) (1, a) (1, b) (2, a) (2, b) (3, b) (3, c). By scanning this sorted list from left to right we deduce that NONEMPTY [ 11 = a, b NONEMPTY[2] = a, b NONEMPTY[3] = b, c In part 2 of Algorithm 3.2 we compute 1, = 1, 1, = 3, and l3 = 3. Thus LENGTH[l] = a, LENGTH[2] is empty, and LENGTH[3] = bab, abc. We therefore part 3 by setting QUEUE = bab, abc, and sorting these strings by their third component. The fact that NONEMPTY[3] = b, c assures us that when we form the sorted list in lines 8-10 of Fig. 3.2, Q[a] need not be concatenated to the of QUEUE. We thus have QUEUE = bab, abc after the first pass of the loop of lines 3-10 in Fig In the second pass, QUEUE does not change, since LENGTHC2) is empty and the sort by second component does not change the order. In the third pass, we set QUEUE to a, bab, abc at line 4. The sort by first components gives QUEUE = a, abc, bab, which is the correct order. Note that in the third pass, Q[c] remains empty, and since c is not on NONEMPTY[l], we do not concatenate Q [c] to the of QUEUE. 0
8 RADIXSORTING 83 STRING DATA Fig. 3.3 Data structure for strings. Theorem 3.2. Algorithm 3.2 sorts its input in time O(lbhl + m), where Proof. An easy induction on the number of passes through the outer loop in Fig. 3.2 proves that after i passes, QUEUE contains those strings of length I, - i + 1 or greater, and that they are sorted according to components I, - i + 1 through I,,,. Thus the algorithm lexicographically sorts its input. For the timing result, part 1 of the algorithm uses O(lbhl) time to create the pairs and O(m + Ibtal) time to sort them. Similarly, part 2 requires no more than O(l,,d time. We must now direct our attention to part 3 and the program of Fig Let ni be the number of strings having an ith component. Let mf be the number of different symbols appearing in the ith components of the strings (i.e. mi is the length of NONEMPTY [i]). Consider a fixed value of 1 in line 3 of Fig The loop of lines 5-7 requires O(nJ time and the loop of lines 8-10 requires O(ml) time. Step 4 requires constant time, so one pass through the loop of lines 3-10 requires O(ml + nl) time. Thus the entire loop takes time. Since
9 84 SORTING AND ORDER STATISTICS 3.2 we see that lines 3-10 require time O(Ibta,). Then, as line I requires constant time and line 2 requires O(m) time, we have the desired result. 0 We offer one example where string sorting arises in the design of an algorithm. Example 3.2. Two trees are said to be isomorphic if we can map one tree into the other by permuting the order of the sons of vertices. Consider the problem of determining whether two trees T1 and Tz are isomorphic. The following algorithm works in time linearly proportional to the number of vertices. The algorithm assigns integers to the vertices of the two trees, starting with vertices at level 0 and working up towards the roots, in such a way that the trees are isomorphic if and only if their roots are assigned the same integer. The algorithm proceeds as follows. 1. Assign to all leaves of T, and T2 the integer Inductively, assume that all vertices of T1 and T2 at level i - 1 have been assigned integers. Assume L, is a list of the vertices of T, at level i - 1 sorted by nondecreasing value of the assigned integers. Assume L2 is the corresponding list for Tz.t 3. Assign to the nonleaves of T, at level i a tuple of integers by scanning the list L, from left to right and performing the following actions: For each vertex v on list L, take the integer assigned to v to be the next component of the tuple associated with the father of v. On completion of this step, each nonleaf w of T, at level i will have a tuple (i,, iz,..., ik) associated with it, where i,, i2,..., ik are the integers, in nondecreasing order, associated with the sons of w. Let S, be the sequence of tuples created for the vertices of T, on level i. 4. Repeat step 3 for Tz and let S2 be the sequence of tuples created for the vertices of Tz on level i. 5. Sort S, and S2 using Algorithm 3.2. Let S; and S;, respectively, be the sorted sequences of tuples. 6. If Sl and S; are not identical, then halt; the trees are not isomorphic. Otherwise, assign the integer 1 to those vertices of T, on level i represented by the first distinct tuple on S;, assign the integer 2 to the vertices represented by the second distinct tuple, and so on. As these integers are assigned to the vertices of T1 on level i, make a list L1 of the vertices so assigned. App to the front of L1 all leaves of T, on level i. Let L2 be the corresponding list of vertices of Tz. These two lists can now be used for the assignment of tuples to vertices at level i + 1 by returning to step 3. t You should convince yourself that level numbers can be assigned in O(n) steps by a preorder traversal of the tree.
Trees. 3. (Minimally Connected) G is connected and deleting any of its edges gives rise to a disconnected graph.
 Trees 1 Introduction Trees are very special kind of (undirected) graphs. Formally speaking, a tree is a connected graph that is acyclic. 1 This definition has some drawbacks: given a graph it is not trivial
Trees 1 Introduction Trees are very special kind of (undirected) graphs. Formally speaking, a tree is a connected graph that is acyclic. 1 This definition has some drawbacks: given a graph it is not trivial
THE DESIGN AND ANALYSIS OF COMPUTER ALGORITHMS
 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. THE DESIGN AND ANALYSIS OF COMPUTER ALGORITHMS Alfred V. Aho Bell
2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. THE DESIGN AND ANALYSIS OF COMPUTER ALGORITHMS Alfred V. Aho Bell
Fast Sorting and Selection. A Lower Bound for Worst Case
 Lists and Iterators 0//06 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 0 Fast Sorting and Selection USGS NEIC. Public domain government
Lists and Iterators 0//06 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 0 Fast Sorting and Selection USGS NEIC. Public domain government
How many leaves on the decision tree? There are n! leaves, because every permutation appears at least once.
 Chapter 8. Sorting in Linear Time Types of Sort Algorithms The only operation that may be used to gain order information about a sequence is comparison of pairs of elements. Quick Sort -- comparison-based
Chapter 8. Sorting in Linear Time Types of Sort Algorithms The only operation that may be used to gain order information about a sequence is comparison of pairs of elements. Quick Sort -- comparison-based
Verifying a Border Array in Linear Time
 Verifying a Border Array in Linear Time František Franěk Weilin Lu P. J. Ryan W. F. Smyth Yu Sun Lu Yang Algorithms Research Group Department of Computing & Software McMaster University Hamilton, Ontario
Verifying a Border Array in Linear Time František Franěk Weilin Lu P. J. Ryan W. F. Smyth Yu Sun Lu Yang Algorithms Research Group Department of Computing & Software McMaster University Hamilton, Ontario
Unit 6 Chapter 15 EXAMPLES OF COMPLEXITY CALCULATION
 DESIGN AND ANALYSIS OF ALGORITHMS Unit 6 Chapter 15 EXAMPLES OF COMPLEXITY CALCULATION http://milanvachhani.blogspot.in EXAMPLES FROM THE SORTING WORLD Sorting provides a good set of examples for analyzing
DESIGN AND ANALYSIS OF ALGORITHMS Unit 6 Chapter 15 EXAMPLES OF COMPLEXITY CALCULATION http://milanvachhani.blogspot.in EXAMPLES FROM THE SORTING WORLD Sorting provides a good set of examples for analyzing
CSE 326: Data Structures Sorting Conclusion
 CSE 36: Data Structures Sorting Conclusion James Fogarty Spring 009 Administrivia Homework Due Homework Assigned Better be working on Project 3 (code due May 7) Sorting Recap Selection Sort Bubble Sort
CSE 36: Data Structures Sorting Conclusion James Fogarty Spring 009 Administrivia Homework Due Homework Assigned Better be working on Project 3 (code due May 7) Sorting Recap Selection Sort Bubble Sort
Tree Isomorphism Algorithms.
 Tree Isomorphism Algorithms. Oleg Eterevsky vs. Arist Kojevnikov based on Tree Isomorphism Algorithms: Speed vs. Clarity Douglas M. Campbell 1 Observation 1. Since a tree isomorphism preserves root and
Tree Isomorphism Algorithms. Oleg Eterevsky vs. Arist Kojevnikov based on Tree Isomorphism Algorithms: Speed vs. Clarity Douglas M. Campbell 1 Observation 1. Since a tree isomorphism preserves root and
Introduction to Automata Theory. BİL405 - Automata Theory and Formal Languages 1
 Introduction to Automata Theory BİL405 - Automata Theory and Formal Languages 1 Automata, Computability and Complexity Automata, Computability and Complexity are linked by the question: What are the fundamental
Introduction to Automata Theory BİL405 - Automata Theory and Formal Languages 1 Automata, Computability and Complexity Automata, Computability and Complexity are linked by the question: What are the fundamental
Solution to Problem 1 of HW 2. Finding the L1 and L2 edges of the graph used in the UD problem, using a suffix array instead of a suffix tree.
 Solution to Problem 1 of HW 2. Finding the L1 and L2 edges of the graph used in the UD problem, using a suffix array instead of a suffix tree. The basic approach is the same as when using a suffix tree,
Solution to Problem 1 of HW 2. Finding the L1 and L2 edges of the graph used in the UD problem, using a suffix array instead of a suffix tree. The basic approach is the same as when using a suffix tree,
14.1 Encoding for different models of computation
 Lecture 14 Decidable languages In the previous lecture we discussed some examples of encoding schemes, through which various objects can be represented by strings over a given alphabet. We will begin this
Lecture 14 Decidable languages In the previous lecture we discussed some examples of encoding schemes, through which various objects can be represented by strings over a given alphabet. We will begin this
COMP Data Structures
 COMP 2140 - Data Structures Shahin Kamali Topic 5 - Sorting University of Manitoba Based on notes by S. Durocher. COMP 2140 - Data Structures 1 / 55 Overview Review: Insertion Sort Merge Sort Quicksort
COMP 2140 - Data Structures Shahin Kamali Topic 5 - Sorting University of Manitoba Based on notes by S. Durocher. COMP 2140 - Data Structures 1 / 55 Overview Review: Insertion Sort Merge Sort Quicksort
/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Sorting lower bound and Linear-time sorting Date: 9/19/17
 601.433/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Sorting lower bound and Linear-time sorting Date: 9/19/17 5.1 Introduction You should all know a few ways of sorting in O(n log n)
601.433/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Sorting lower bound and Linear-time sorting Date: 9/19/17 5.1 Introduction You should all know a few ways of sorting in O(n log n)
Extremal Graph Theory: Turán s Theorem
 Bridgewater State University Virtual Commons - Bridgewater State University Honors Program Theses and Projects Undergraduate Honors Program 5-9-07 Extremal Graph Theory: Turán s Theorem Vincent Vascimini
Bridgewater State University Virtual Commons - Bridgewater State University Honors Program Theses and Projects Undergraduate Honors Program 5-9-07 Extremal Graph Theory: Turán s Theorem Vincent Vascimini
Chapter 3 Trees. Theorem A graph T is a tree if, and only if, every two distinct vertices of T are joined by a unique path.
 Chapter 3 Trees Section 3. Fundamental Properties of Trees Suppose your city is planning to construct a rapid rail system. They want to construct the most economical system possible that will meet the
Chapter 3 Trees Section 3. Fundamental Properties of Trees Suppose your city is planning to construct a rapid rail system. They want to construct the most economical system possible that will meet the
Worst-case running time for RANDOMIZED-SELECT
 Worst-case running time for RANDOMIZED-SELECT is ), even to nd the minimum The algorithm has a linear expected running time, though, and because it is randomized, no particular input elicits the worst-case
Worst-case running time for RANDOMIZED-SELECT is ), even to nd the minimum The algorithm has a linear expected running time, though, and because it is randomized, no particular input elicits the worst-case
2. CONNECTIVITY Connectivity
 2. CONNECTIVITY 70 2. Connectivity 2.1. Connectivity. Definition 2.1.1. (1) A path in a graph G = (V, E) is a sequence of vertices v 0, v 1, v 2,..., v n such that {v i 1, v i } is an edge of G for i =
2. CONNECTIVITY 70 2. Connectivity 2.1. Connectivity. Definition 2.1.1. (1) A path in a graph G = (V, E) is a sequence of vertices v 0, v 1, v 2,..., v n such that {v i 1, v i } is an edge of G for i =
Lecture 5: Suffix Trees
 Longest Common Substring Problem Lecture 5: Suffix Trees Given a text T = GGAGCTTAGAACT and a string P = ATTCGCTTAGCCTA, how do we find the longest common substring between them? Here the longest common
Longest Common Substring Problem Lecture 5: Suffix Trees Given a text T = GGAGCTTAGAACT and a string P = ATTCGCTTAGCCTA, how do we find the longest common substring between them? Here the longest common
II (Sorting and) Order Statistics
 II (Sorting and) Order Statistics Heapsort Quicksort Sorting in Linear Time Medians and Order Statistics 8 Sorting in Linear Time The sorting algorithms introduced thus far are comparison sorts Any comparison
II (Sorting and) Order Statistics Heapsort Quicksort Sorting in Linear Time Medians and Order Statistics 8 Sorting in Linear Time The sorting algorithms introduced thus far are comparison sorts Any comparison
CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics
 CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics 1 Sorting 1.1 Problem Statement You are given a sequence of n numbers < a 1, a 2,..., a n >. You need to
CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics 1 Sorting 1.1 Problem Statement You are given a sequence of n numbers < a 1, a 2,..., a n >. You need to
Greedy Algorithms 1 {K(S) K(S) C} For large values of d, brute force search is not feasible because there are 2 d {1,..., d}.
 Greedy Algorithms 1 Simple Knapsack Problem Greedy Algorithms form an important class of algorithmic techniques. We illustrate the idea by applying it to a simplified version of the Knapsack Problem. Informally,
Greedy Algorithms 1 Simple Knapsack Problem Greedy Algorithms form an important class of algorithmic techniques. We illustrate the idea by applying it to a simplified version of the Knapsack Problem. Informally,
CS 337 Project 1: Minimum-Weight Binary Search Trees
 CS 337 Project 1: Minimum-Weight Binary Search Trees September 6, 2006 1 Preliminaries Let X denote a set of keys drawn from some totally ordered universe U, such as the set of all integers, or the set
CS 337 Project 1: Minimum-Weight Binary Search Trees September 6, 2006 1 Preliminaries Let X denote a set of keys drawn from some totally ordered universe U, such as the set of all integers, or the set
DATA STRUCTURES/UNIT 3
 UNIT III SORTING AND SEARCHING 9 General Background Exchange sorts Selection and Tree Sorting Insertion Sorts Merge and Radix Sorts Basic Search Techniques Tree Searching General Search Trees- Hashing.
UNIT III SORTING AND SEARCHING 9 General Background Exchange sorts Selection and Tree Sorting Insertion Sorts Merge and Radix Sorts Basic Search Techniques Tree Searching General Search Trees- Hashing.
Suffix Trees and Arrays
 Suffix Trees and Arrays Yufei Tao KAIST May 1, 2013 We will discuss the following substring matching problem: Problem (Substring Matching) Let σ be a single string of n characters. Given a query string
Suffix Trees and Arrays Yufei Tao KAIST May 1, 2013 We will discuss the following substring matching problem: Problem (Substring Matching) Let σ be a single string of n characters. Given a query string
4.1 COMPUTATIONAL THINKING AND PROBLEM-SOLVING
 4.1 COMPUTATIONAL THINKING AND PROBLEM-SOLVING 4.1.2 ALGORITHMS ALGORITHM An Algorithm is a procedure or formula for solving a problem. It is a step-by-step set of operations to be performed. It is almost
4.1 COMPUTATIONAL THINKING AND PROBLEM-SOLVING 4.1.2 ALGORITHMS ALGORITHM An Algorithm is a procedure or formula for solving a problem. It is a step-by-step set of operations to be performed. It is almost
1 ICS 161: Design and Analysis of Algorithms Lecture notes for January 23, Bucket Sorting
 1 ICS 161: Design and Analysis of Algorithms Lecture notes for January 23, 1996 2 Bucket Sorting We ve seen various algorithms for sorting in O(n log n) time and a lower bound showing that O(n log n) is
1 ICS 161: Design and Analysis of Algorithms Lecture notes for January 23, 1996 2 Bucket Sorting We ve seen various algorithms for sorting in O(n log n) time and a lower bound showing that O(n log n) is
Dynamic Programming Algorithms
 Based on the notes for the U of Toronto course CSC 364 Dynamic Programming Algorithms The setting is as follows. We wish to find a solution to a given problem which optimizes some quantity Q of interest;
Based on the notes for the U of Toronto course CSC 364 Dynamic Programming Algorithms The setting is as follows. We wish to find a solution to a given problem which optimizes some quantity Q of interest;
Data Structures in C++ Using the Standard Template Library
 Data Structures in C++ Using the Standard Template Library Timothy Budd Oregon State University ^ ADDISON-WESLEY An imprint of Addison Wesley Longman, Inc. Reading, Massachusetts Harlow, England Menlo
Data Structures in C++ Using the Standard Template Library Timothy Budd Oregon State University ^ ADDISON-WESLEY An imprint of Addison Wesley Longman, Inc. Reading, Massachusetts Harlow, England Menlo
TAFL 1 (ECS-403) Unit- V. 5.1 Turing Machine. 5.2 TM as computer of Integer Function
 TAFL 1 (ECS-403) Unit- V 5.1 Turing Machine 5.2 TM as computer of Integer Function 5.2.1 Simulating Turing Machine by Computer 5.2.2 Simulating Computer by Turing Machine 5.3 Universal Turing Machine 5.4
TAFL 1 (ECS-403) Unit- V 5.1 Turing Machine 5.2 TM as computer of Integer Function 5.2.1 Simulating Turing Machine by Computer 5.2.2 Simulating Computer by Turing Machine 5.3 Universal Turing Machine 5.4
Computing the Longest Common Substring with One Mismatch 1
 ISSN 0032-9460, Problems of Information Transmission, 2011, Vol. 47, No. 1, pp. 1??. c Pleiades Publishing, Inc., 2011. Original Russian Text c M.A. Babenko, T.A. Starikovskaya, 2011, published in Problemy
ISSN 0032-9460, Problems of Information Transmission, 2011, Vol. 47, No. 1, pp. 1??. c Pleiades Publishing, Inc., 2011. Original Russian Text c M.A. Babenko, T.A. Starikovskaya, 2011, published in Problemy
9/24/ Hash functions
 11.3 Hash functions A good hash function satis es (approximately) the assumption of SUH: each key is equally likely to hash to any of the slots, independently of the other keys We typically have no way
11.3 Hash functions A good hash function satis es (approximately) the assumption of SUH: each key is equally likely to hash to any of the slots, independently of the other keys We typically have no way
Outline. Introduction. 2 Proof of Correctness. 3 Final Notes. Precondition P 1 : Inputs include
 Outline Computer Science 331 Correctness of Algorithms Mike Jacobson Department of Computer Science University of Calgary Lectures #2-4 1 What is a? Applications 2 Recursive Algorithms 3 Final Notes Additional
Outline Computer Science 331 Correctness of Algorithms Mike Jacobson Department of Computer Science University of Calgary Lectures #2-4 1 What is a? Applications 2 Recursive Algorithms 3 Final Notes Additional
Assignment 1. Stefano Guerra. October 11, The following observation follows directly from the definition of in order and pre order traversal:
 Assignment 1 Stefano Guerra October 11, 2016 1 Problem 1 Describe a recursive algorithm to reconstruct an arbitrary binary tree, given its preorder and inorder node sequences as input. First, recall that
Assignment 1 Stefano Guerra October 11, 2016 1 Problem 1 Describe a recursive algorithm to reconstruct an arbitrary binary tree, given its preorder and inorder node sequences as input. First, recall that
CPSC 311 Lecture Notes. Sorting and Order Statistics (Chapters 6-9)
 CPSC 311 Lecture Notes Sorting and Order Statistics (Chapters 6-9) Acknowledgement: These notes are compiled by Nancy Amato at Texas A&M University. Parts of these course notes are based on notes from
CPSC 311 Lecture Notes Sorting and Order Statistics (Chapters 6-9) Acknowledgement: These notes are compiled by Nancy Amato at Texas A&M University. Parts of these course notes are based on notes from
SORTING AND SELECTION
 2 < > 1 4 8 6 = 9 CHAPTER 12 SORTING AND SELECTION ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN JAVA, GOODRICH, TAMASSIA AND GOLDWASSER (WILEY 2016)
2 < > 1 4 8 6 = 9 CHAPTER 12 SORTING AND SELECTION ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN JAVA, GOODRICH, TAMASSIA AND GOLDWASSER (WILEY 2016)
CS5371 Theory of Computation. Lecture 8: Automata Theory VI (PDA, PDA = CFG)
 CS5371 Theory of Computation Lecture 8: Automata Theory VI (PDA, PDA = CFG) Objectives Introduce Pushdown Automaton (PDA) Show that PDA = CFG In terms of descriptive power Pushdown Automaton (PDA) Roughly
CS5371 Theory of Computation Lecture 8: Automata Theory VI (PDA, PDA = CFG) Objectives Introduce Pushdown Automaton (PDA) Show that PDA = CFG In terms of descriptive power Pushdown Automaton (PDA) Roughly
Treaps. 1 Binary Search Trees (BSTs) CSE341T/CSE549T 11/05/2014. Lecture 19
 CSE34T/CSE549T /05/04 Lecture 9 Treaps Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types
CSE34T/CSE549T /05/04 Lecture 9 Treaps Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types
CS 161 Lecture 11 BFS, Dijkstra s algorithm Jessica Su (some parts copied from CLRS) 1 Review
 1 Review 1 Something I did not emphasize enough last time is that during the execution of depth-firstsearch, we construct depth-first-search trees. One graph may have multiple depth-firstsearch trees,
1 Review 1 Something I did not emphasize enough last time is that during the execution of depth-firstsearch, we construct depth-first-search trees. One graph may have multiple depth-firstsearch trees,
4 Fractional Dimension of Posets from Trees
 57 4 Fractional Dimension of Posets from Trees In this last chapter, we switch gears a little bit, and fractionalize the dimension of posets We start with a few simple definitions to develop the language
57 4 Fractional Dimension of Posets from Trees In this last chapter, we switch gears a little bit, and fractionalize the dimension of posets We start with a few simple definitions to develop the language
Complexity Theory. Compiled By : Hari Prasad Pokhrel Page 1 of 20. ioenotes.edu.np
 Chapter 1: Introduction Introduction Purpose of the Theory of Computation: Develop formal mathematical models of computation that reflect real-world computers. Nowadays, the Theory of Computation can be
Chapter 1: Introduction Introduction Purpose of the Theory of Computation: Develop formal mathematical models of computation that reflect real-world computers. Nowadays, the Theory of Computation can be
Power Set of a set and Relations
 Power Set of a set and Relations 1 Power Set (1) Definition: The power set of a set S, denoted P(S), is the set of all subsets of S. Examples Let A={a,b,c}, P(A)={,{a},{b},{c},{a,b},{b,c},{a,c},{a,b,c}}
Power Set of a set and Relations 1 Power Set (1) Definition: The power set of a set S, denoted P(S), is the set of all subsets of S. Examples Let A={a,b,c}, P(A)={,{a},{b},{c},{a,b},{b,c},{a,c},{a,b,c}}
Algorithms Exam TIN093/DIT600
 Algorithms Exam TIN093/DIT600 Course: Algorithms Course code: TIN 093 (CTH), DIT 600 (GU) Date, time: 22nd October 2016, 14:00 18:00 Building: M Responsible teacher: Peter Damaschke, Tel. 5405 Examiner:
Algorithms Exam TIN093/DIT600 Course: Algorithms Course code: TIN 093 (CTH), DIT 600 (GU) Date, time: 22nd October 2016, 14:00 18:00 Building: M Responsible teacher: Peter Damaschke, Tel. 5405 Examiner:
Lecture 23: Priority Queues, Part 2 10:00 AM, Mar 19, 2018
 CS8 Integrated Introduction to Computer Science Fisler, Nelson Lecture : Priority Queues, Part : AM, Mar 9, 8 Contents Sorting, Revisited Counting Sort Bucket Sort 4 Radix Sort 6 4. MSD Radix Sort......................................
CS8 Integrated Introduction to Computer Science Fisler, Nelson Lecture : Priority Queues, Part : AM, Mar 9, 8 Contents Sorting, Revisited Counting Sort Bucket Sort 4 Radix Sort 6 4. MSD Radix Sort......................................
CSCI2100B Data Structures Trees
 CSCI2100B Data Structures Trees Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction General Tree
CSCI2100B Data Structures Trees Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction General Tree
CS 6783 (Applied Algorithms) Lecture 5
 CS 6783 (Applied Algorithms) Lecture 5 Antonina Kolokolova January 19, 2012 1 Minimum Spanning Trees An undirected graph G is a pair (V, E); V is a set (of vertices or nodes); E is a set of (undirected)
CS 6783 (Applied Algorithms) Lecture 5 Antonina Kolokolova January 19, 2012 1 Minimum Spanning Trees An undirected graph G is a pair (V, E); V is a set (of vertices or nodes); E is a set of (undirected)
Chapter 4: Sorting. Spring 2014 Sorting Fun 1
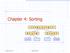 Chapter 4: Sorting 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 Spring 2014 Sorting Fun 1 What We ll Do! Quick Sort! Lower bound on runtimes for comparison based sort! Radix and Bucket sort Spring 2014
Chapter 4: Sorting 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 Spring 2014 Sorting Fun 1 What We ll Do! Quick Sort! Lower bound on runtimes for comparison based sort! Radix and Bucket sort Spring 2014
Let v be a vertex primed by v i (s). Then the number f(v) of neighbours of v which have
 Let v be a vertex primed by v i (s). Then the number f(v) of neighbours of v which have been red in the sequence up to and including v i (s) is deg(v)? s(v), and by the induction hypothesis this sequence
Let v be a vertex primed by v i (s). Then the number f(v) of neighbours of v which have been red in the sequence up to and including v i (s) is deg(v)? s(v), and by the induction hypothesis this sequence
Comparison Based Sorting Algorithms. Algorithms and Data Structures: Lower Bounds for Sorting. Comparison Based Sorting Algorithms
 Comparison Based Sorting Algorithms Algorithms and Data Structures: Lower Bounds for Sorting Definition 1 A sorting algorithm is comparison based if comparisons A[i] < A[j], A[i] A[j], A[i] = A[j], A[i]
Comparison Based Sorting Algorithms Algorithms and Data Structures: Lower Bounds for Sorting Definition 1 A sorting algorithm is comparison based if comparisons A[i] < A[j], A[i] A[j], A[i] = A[j], A[i]
Jana Kosecka. Linear Time Sorting, Median, Order Statistics. Many slides here are based on E. Demaine, D. Luebke slides
 Jana Kosecka Linear Time Sorting, Median, Order Statistics Many slides here are based on E. Demaine, D. Luebke slides Insertion sort: Easy to code Fast on small inputs (less than ~50 elements) Fast on
Jana Kosecka Linear Time Sorting, Median, Order Statistics Many slides here are based on E. Demaine, D. Luebke slides Insertion sort: Easy to code Fast on small inputs (less than ~50 elements) Fast on
Finding the Depth of a Flow Graph*
 JOURNAL OF COMPUTER AND SYSTEI~! SCIENCES 15, 300-309 (I 977) Finding the Depth of a Flow Graph* AMELIA C. FONG Department of Computer Science, University of Toronto, Toronto, Ontario, Canada AND JEFFREY
JOURNAL OF COMPUTER AND SYSTEI~! SCIENCES 15, 300-309 (I 977) Finding the Depth of a Flow Graph* AMELIA C. FONG Department of Computer Science, University of Toronto, Toronto, Ontario, Canada AND JEFFREY
Adjacent: Two distinct vertices u, v are adjacent if there is an edge with ends u, v. In this case we let uv denote such an edge.
 1 Graph Basics What is a graph? Graph: a graph G consists of a set of vertices, denoted V (G), a set of edges, denoted E(G), and a relation called incidence so that each edge is incident with either one
1 Graph Basics What is a graph? Graph: a graph G consists of a set of vertices, denoted V (G), a set of edges, denoted E(G), and a relation called incidence so that each edge is incident with either one
8 SortinginLinearTime
 8 SortinginLinearTime We have now introduced several algorithms that can sort n numbers in O(n lg n) time. Merge sort and heapsort achieve this upper bound in the worst case; quicksort achieves it on average.
8 SortinginLinearTime We have now introduced several algorithms that can sort n numbers in O(n lg n) time. Merge sort and heapsort achieve this upper bound in the worst case; quicksort achieves it on average.
Slides for Faculty Oxford University Press All rights reserved.
 Oxford University Press 2013 Slides for Faculty Assistance Preliminaries Author: Vivek Kulkarni vivek_kulkarni@yahoo.com Outline Following topics are covered in the slides: Basic concepts, namely, symbols,
Oxford University Press 2013 Slides for Faculty Assistance Preliminaries Author: Vivek Kulkarni vivek_kulkarni@yahoo.com Outline Following topics are covered in the slides: Basic concepts, namely, symbols,
Algorithms and Data Structures: Lower Bounds for Sorting. ADS: lect 7 slide 1
 Algorithms and Data Structures: Lower Bounds for Sorting ADS: lect 7 slide 1 ADS: lect 7 slide 2 Comparison Based Sorting Algorithms Definition 1 A sorting algorithm is comparison based if comparisons
Algorithms and Data Structures: Lower Bounds for Sorting ADS: lect 7 slide 1 ADS: lect 7 slide 2 Comparison Based Sorting Algorithms Definition 1 A sorting algorithm is comparison based if comparisons
2 The Fractional Chromatic Gap
 C 1 11 2 The Fractional Chromatic Gap As previously noted, for any finite graph. This result follows from the strong duality of linear programs. Since there is no such duality result for infinite linear
C 1 11 2 The Fractional Chromatic Gap As previously noted, for any finite graph. This result follows from the strong duality of linear programs. Since there is no such duality result for infinite linear
Chapter 12: Indexing and Hashing. Basic Concepts
 Chapter 12: Indexing and Hashing! Basic Concepts! Ordered Indices! B+-Tree Index Files! B-Tree Index Files! Static Hashing! Dynamic Hashing! Comparison of Ordered Indexing and Hashing! Index Definition
Chapter 12: Indexing and Hashing! Basic Concepts! Ordered Indices! B+-Tree Index Files! B-Tree Index Files! Static Hashing! Dynamic Hashing! Comparison of Ordered Indexing and Hashing! Index Definition
Sorting. Popular algorithms: Many algorithms for sorting in parallel also exist.
 Sorting Popular algorithms: Selection sort* Insertion sort* Bubble sort* Quick sort* Comb-sort Shell-sort Heap sort* Merge sort* Counting-sort Radix-sort Bucket-sort Tim-sort Many algorithms for sorting
Sorting Popular algorithms: Selection sort* Insertion sort* Bubble sort* Quick sort* Comb-sort Shell-sort Heap sort* Merge sort* Counting-sort Radix-sort Bucket-sort Tim-sort Many algorithms for sorting
III Data Structures. Dynamic sets
 III Data Structures Elementary Data Structures Hash Tables Binary Search Trees Red-Black Trees Dynamic sets Sets are fundamental to computer science Algorithms may require several different types of operations
III Data Structures Elementary Data Structures Hash Tables Binary Search Trees Red-Black Trees Dynamic sets Sets are fundamental to computer science Algorithms may require several different types of operations
1 Computing alignments in only linear space
 1 Computing alignments in only linear space One of the defects of dynamic programming for all the problems we have discussed is that the dynamic programming tables use Θ(nm) space when the input strings
1 Computing alignments in only linear space One of the defects of dynamic programming for all the problems we have discussed is that the dynamic programming tables use Θ(nm) space when the input strings
Discrete Mathematics. Kruskal, order, sorting, induction
 Discrete Mathematics wwwmifvult/~algis Kruskal, order, sorting, induction Kruskal algorithm Kruskal s Algorithm for Minimal Spanning Trees The algorithm constructs a minimal spanning tree as follows: Starting
Discrete Mathematics wwwmifvult/~algis Kruskal, order, sorting, induction Kruskal algorithm Kruskal s Algorithm for Minimal Spanning Trees The algorithm constructs a minimal spanning tree as follows: Starting
We assume uniform hashing (UH):
 We assume uniform hashing (UH): the probe sequence of each key is equally likely to be any of the! permutations of 0,1,, 1 UH generalizes the notion of SUH that produces not just a single number, but a
We assume uniform hashing (UH): the probe sequence of each key is equally likely to be any of the! permutations of 0,1,, 1 UH generalizes the notion of SUH that produces not just a single number, but a
Chapter 12: Indexing and Hashing
 Chapter 12: Indexing and Hashing Basic Concepts Ordered Indices B+-Tree Index Files B-Tree Index Files Static Hashing Dynamic Hashing Comparison of Ordered Indexing and Hashing Index Definition in SQL
Chapter 12: Indexing and Hashing Basic Concepts Ordered Indices B+-Tree Index Files B-Tree Index Files Static Hashing Dynamic Hashing Comparison of Ordered Indexing and Hashing Index Definition in SQL
CS161 - Final Exam Computer Science Department, Stanford University August 16, 2008
 CS161 - Final Exam Computer Science Department, Stanford University August 16, 2008 Name: Honor Code 1. The Honor Code is an undertaking of the students, individually and collectively: a) that they will
CS161 - Final Exam Computer Science Department, Stanford University August 16, 2008 Name: Honor Code 1. The Honor Code is an undertaking of the students, individually and collectively: a) that they will
Data Structures and Algorithms Dr. Naveen Garg Department of Computer Science and Engineering Indian Institute of Technology, Delhi.
 Data Structures and Algorithms Dr. Naveen Garg Department of Computer Science and Engineering Indian Institute of Technology, Delhi Lecture 18 Tries Today we are going to be talking about another data
Data Structures and Algorithms Dr. Naveen Garg Department of Computer Science and Engineering Indian Institute of Technology, Delhi Lecture 18 Tries Today we are going to be talking about another data
Discrete Mathematics for CS Spring 2008 David Wagner Note 13. An Introduction to Graphs
 CS 70 Discrete Mathematics for CS Spring 2008 David Wagner Note 13 An Introduction to Graphs Formulating a simple, precise specification of a computational problem is often a prerequisite to writing a
CS 70 Discrete Mathematics for CS Spring 2008 David Wagner Note 13 An Introduction to Graphs Formulating a simple, precise specification of a computational problem is often a prerequisite to writing a
DIVIDE AND CONQUER ALGORITHMS ANALYSIS WITH RECURRENCE EQUATIONS
 CHAPTER 11 SORTING ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY M. AMATO AND
CHAPTER 11 SORTING ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY M. AMATO AND
Chapter 11: Indexing and Hashing
 Chapter 11: Indexing and Hashing Basic Concepts Ordered Indices B + -Tree Index Files B-Tree Index Files Static Hashing Dynamic Hashing Comparison of Ordered Indexing and Hashing Index Definition in SQL
Chapter 11: Indexing and Hashing Basic Concepts Ordered Indices B + -Tree Index Files B-Tree Index Files Static Hashing Dynamic Hashing Comparison of Ordered Indexing and Hashing Index Definition in SQL
Heap-on-Top Priority Queues. March Abstract. We introduce the heap-on-top (hot) priority queue data structure that combines the
 Heap-on-Top Priority Queues Boris V. Cherkassky Central Economics and Mathematics Institute Krasikova St. 32 117418, Moscow, Russia cher@cemi.msk.su Andrew V. Goldberg NEC Research Institute 4 Independence
Heap-on-Top Priority Queues Boris V. Cherkassky Central Economics and Mathematics Institute Krasikova St. 32 117418, Moscow, Russia cher@cemi.msk.su Andrew V. Goldberg NEC Research Institute 4 Independence
1 (15 points) LexicoSort
 CS161 Homework 2 Due: 22 April 2016, 12 noon Submit on Gradescope Handed out: 15 April 2016 Instructions: Please answer the following questions to the best of your ability. If you are asked to show your
CS161 Homework 2 Due: 22 April 2016, 12 noon Submit on Gradescope Handed out: 15 April 2016 Instructions: Please answer the following questions to the best of your ability. If you are asked to show your
AD0A STANFORD UNIV CA DEPT OP COMPUTER SCIENCE F/6 12/1 VERIFICATION OF LINK-LEVEL PROTOCOLS,(U) JAN 81 D E KNUTH. N0R11476-C0330 UNCLASSIFIED
 AD0A099 140 STANFORD UNIV CA DEPT OP COMPUTER SCIENCE F/6 12/1 VERIFICATION OF LINK-LEVEL PROTOCOLS,(U) JAN 81 D E KNUTH. N0R11476-C0330 UNCLASSIFIED STANCS-81-84 NL Report. N STAN I [EVEV iv Verification
AD0A099 140 STANFORD UNIV CA DEPT OP COMPUTER SCIENCE F/6 12/1 VERIFICATION OF LINK-LEVEL PROTOCOLS,(U) JAN 81 D E KNUTH. N0R11476-C0330 UNCLASSIFIED STANCS-81-84 NL Report. N STAN I [EVEV iv Verification
Abstract Path Planning for Multiple Robots: An Empirical Study
 Abstract Path Planning for Multiple Robots: An Empirical Study Charles University in Prague Faculty of Mathematics and Physics Department of Theoretical Computer Science and Mathematical Logic Malostranské
Abstract Path Planning for Multiple Robots: An Empirical Study Charles University in Prague Faculty of Mathematics and Physics Department of Theoretical Computer Science and Mathematical Logic Malostranské
Fundamental Properties of Graphs
 Chapter three In many real-life situations we need to know how robust a graph that represents a certain network is, how edges or vertices can be removed without completely destroying the overall connectivity,
Chapter three In many real-life situations we need to know how robust a graph that represents a certain network is, how edges or vertices can be removed without completely destroying the overall connectivity,
Module 2: Classical Algorithm Design Techniques
 Module 2: Classical Algorithm Design Techniques Dr. Natarajan Meghanathan Associate Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu Module
Module 2: Classical Algorithm Design Techniques Dr. Natarajan Meghanathan Associate Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu Module
The complexity of Sorting and sorting in linear-time. Median and Order Statistics. Chapter 8 and Chapter 9
 Subject 6 Spring 2017 The complexity of Sorting and sorting in linear-time Median and Order Statistics Chapter 8 and Chapter 9 Disclaimer: These abbreviated notes DO NOT substitute the textbook for this
Subject 6 Spring 2017 The complexity of Sorting and sorting in linear-time Median and Order Statistics Chapter 8 and Chapter 9 Disclaimer: These abbreviated notes DO NOT substitute the textbook for this
Learning Characteristic Structured Patterns in Rooted Planar Maps
 Learning Characteristic Structured Patterns in Rooted Planar Maps Satoshi Kawamoto Yusuke Suzuki Takayoshi Shoudai Abstract Exting the concept of ordered graphs, we propose a new data structure to express
Learning Characteristic Structured Patterns in Rooted Planar Maps Satoshi Kawamoto Yusuke Suzuki Takayoshi Shoudai Abstract Exting the concept of ordered graphs, we propose a new data structure to express
ISA 562: Information Security, Theory and Practice. Lecture 1
 ISA 562: Information Security, Theory and Practice Lecture 1 1 Encryption schemes 1.1 The semantics of an encryption scheme. A symmetric key encryption scheme allows two parties that share a secret key
ISA 562: Information Security, Theory and Practice Lecture 1 1 Encryption schemes 1.1 The semantics of an encryption scheme. A symmetric key encryption scheme allows two parties that share a secret key
The Football Pool Problem for 5 Matches
 JOURNAL OF COMBINATORIAL THEORY 3, 35-325 (967) The Football Pool Problem for 5 Matches H. J. L. KAMPS AND J. H. VAN LINT Technological University, Eindhoven, The Netherlands Communicated by N. G. debruijn
JOURNAL OF COMBINATORIAL THEORY 3, 35-325 (967) The Football Pool Problem for 5 Matches H. J. L. KAMPS AND J. H. VAN LINT Technological University, Eindhoven, The Netherlands Communicated by N. G. debruijn
Integer Programming ISE 418. Lecture 7. Dr. Ted Ralphs
 Integer Programming ISE 418 Lecture 7 Dr. Ted Ralphs ISE 418 Lecture 7 1 Reading for This Lecture Nemhauser and Wolsey Sections II.3.1, II.3.6, II.4.1, II.4.2, II.5.4 Wolsey Chapter 7 CCZ Chapter 1 Constraint
Integer Programming ISE 418 Lecture 7 Dr. Ted Ralphs ISE 418 Lecture 7 1 Reading for This Lecture Nemhauser and Wolsey Sections II.3.1, II.3.6, II.4.1, II.4.2, II.5.4 Wolsey Chapter 7 CCZ Chapter 1 Constraint
We will show that the height of a RB tree on n vertices is approximately 2*log n. In class I presented a simple structural proof of this claim:
 We have seen that the insert operation on a RB takes an amount of time proportional to the number of the levels of the tree (since the additional operations required to do any rebalancing require constant
We have seen that the insert operation on a RB takes an amount of time proportional to the number of the levels of the tree (since the additional operations required to do any rebalancing require constant
( ) D. Θ ( ) ( ) Ο f ( n) ( ) Ω. C. T n C. Θ. B. n logn Ο
 CSE 0 Name Test Fall 0 Multiple Choice. Write your answer to the LEFT of each problem. points each. The expected time for insertion sort for n keys is in which set? (All n! input permutations are equally
CSE 0 Name Test Fall 0 Multiple Choice. Write your answer to the LEFT of each problem. points each. The expected time for insertion sort for n keys is in which set? (All n! input permutations are equally
9.5 Equivalence Relations
 9.5 Equivalence Relations You know from your early study of fractions that each fraction has many equivalent forms. For example, 2, 2 4, 3 6, 2, 3 6, 5 30,... are all different ways to represent the same
9.5 Equivalence Relations You know from your early study of fractions that each fraction has many equivalent forms. For example, 2, 2 4, 3 6, 2, 3 6, 5 30,... are all different ways to represent the same
Introduction to Algorithms / Algorithms I Lecturer: Michael Dinitz Topic: Shortest Paths Date: 10/13/15
 600.363 Introduction to Algorithms / 600.463 Algorithms I Lecturer: Michael Dinitz Topic: Shortest Paths Date: 10/13/15 14.1 Introduction Today we re going to talk about algorithms for computing shortest
600.363 Introduction to Algorithms / 600.463 Algorithms I Lecturer: Michael Dinitz Topic: Shortest Paths Date: 10/13/15 14.1 Introduction Today we re going to talk about algorithms for computing shortest
Machine-Independent Optimizations
 Chapter 9 Machine-Independent Optimizations High-level language constructs can introduce substantial run-time overhead if we naively translate each construct independently into machine code. This chapter
Chapter 9 Machine-Independent Optimizations High-level language constructs can introduce substantial run-time overhead if we naively translate each construct independently into machine code. This chapter
 Ordered Indices To gain fast random access to records in a file, we can use an index structure. Each index structure is associated with a particular search key. Just like index of a book, library catalog,
Ordered Indices To gain fast random access to records in a file, we can use an index structure. Each index structure is associated with a particular search key. Just like index of a book, library catalog,
Computer Science 236 Fall Nov. 11, 2010
 Computer Science 26 Fall Nov 11, 2010 St George Campus University of Toronto Assignment Due Date: 2nd December, 2010 1 (10 marks) Assume that you are given a file of arbitrary length that contains student
Computer Science 26 Fall Nov 11, 2010 St George Campus University of Toronto Assignment Due Date: 2nd December, 2010 1 (10 marks) Assume that you are given a file of arbitrary length that contains student
Pebbling on Directed Graphs
 Pebbling on Directed Graphs Gayatri Gunda E-mail: gundagay@notes.udayton.edu Dr. Aparna Higgins E-mail: Aparna.Higgins@notes.udayton.edu University of Dayton Dayton, OH 45469 Submitted January 25 th, 2004
Pebbling on Directed Graphs Gayatri Gunda E-mail: gundagay@notes.udayton.edu Dr. Aparna Higgins E-mail: Aparna.Higgins@notes.udayton.edu University of Dayton Dayton, OH 45469 Submitted January 25 th, 2004
CMSC 341 Lecture 16/17 Hashing, Parts 1 & 2
 CMSC 341 Lecture 16/17 Hashing, Parts 1 & 2 Prof. John Park Based on slides from previous iterations of this course Today s Topics Overview Uses and motivations of hash tables Major concerns with hash
CMSC 341 Lecture 16/17 Hashing, Parts 1 & 2 Prof. John Park Based on slides from previous iterations of this course Today s Topics Overview Uses and motivations of hash tables Major concerns with hash
Binary search trees. Binary search trees are data structures based on binary trees that support operations on dynamic sets.
 COMP3600/6466 Algorithms 2018 Lecture 12 1 Binary search trees Reading: Cormen et al, Sections 12.1 to 12.3 Binary search trees are data structures based on binary trees that support operations on dynamic
COMP3600/6466 Algorithms 2018 Lecture 12 1 Binary search trees Reading: Cormen et al, Sections 12.1 to 12.3 Binary search trees are data structures based on binary trees that support operations on dynamic
Lecture 1. 1 Notation
 Lecture 1 (The material on mathematical logic is covered in the textbook starting with Chapter 5; however, for the first few lectures, I will be providing some required background topics and will not be
Lecture 1 (The material on mathematical logic is covered in the textbook starting with Chapter 5; however, for the first few lectures, I will be providing some required background topics and will not be
Binary search trees 3. Binary search trees. Binary search trees 2. Reading: Cormen et al, Sections 12.1 to 12.3
 Binary search trees Reading: Cormen et al, Sections 12.1 to 12.3 Binary search trees 3 Binary search trees are data structures based on binary trees that support operations on dynamic sets. Each element
Binary search trees Reading: Cormen et al, Sections 12.1 to 12.3 Binary search trees 3 Binary search trees are data structures based on binary trees that support operations on dynamic sets. Each element
CS Sorting Terms & Definitions. Comparing Sorting Algorithms. Bubble Sort. Bubble Sort: Graphical Trace
 CS 704 Introduction to Data Structures and Software Engineering Sorting Terms & Definitions Internal sorts holds all data in RAM External sorts use Files Ascending : Low to High Descending : High to Low
CS 704 Introduction to Data Structures and Software Engineering Sorting Terms & Definitions Internal sorts holds all data in RAM External sorts use Files Ascending : Low to High Descending : High to Low
Space Efficient Linear Time Construction of
 Space Efficient Linear Time Construction of Suffix Arrays Pang Ko and Srinivas Aluru Dept. of Electrical and Computer Engineering 1 Laurence H. Baker Center for Bioinformatics and Biological Statistics
Space Efficient Linear Time Construction of Suffix Arrays Pang Ko and Srinivas Aluru Dept. of Electrical and Computer Engineering 1 Laurence H. Baker Center for Bioinformatics and Biological Statistics
Greedy Algorithms 1. For large values of d, brute force search is not feasible because there are 2 d
 Greedy Algorithms 1 Simple Knapsack Problem Greedy Algorithms form an important class of algorithmic techniques. We illustrate the idea by applying it to a simplified version of the Knapsack Problem. Informally,
Greedy Algorithms 1 Simple Knapsack Problem Greedy Algorithms form an important class of algorithmic techniques. We illustrate the idea by applying it to a simplified version of the Knapsack Problem. Informally,
Lecture 7: Primitive Recursion is Turing Computable. Michael Beeson
 Lecture 7: Primitive Recursion is Turing Computable Michael Beeson Closure under composition Let f and g be Turing computable. Let h(x) = f(g(x)). Then h is Turing computable. Similarly if h(x) = f(g 1
Lecture 7: Primitive Recursion is Turing Computable Michael Beeson Closure under composition Let f and g be Turing computable. Let h(x) = f(g(x)). Then h is Turing computable. Similarly if h(x) = f(g 1
(Refer Slide Time: 0:19)
 Theory of Computation. Professor somenath Biswas. Department of Computer Science & Engineering. Indian Institute of Technology, Kanpur. Lecture-15. Decision Problems for Regular Languages. (Refer Slide
Theory of Computation. Professor somenath Biswas. Department of Computer Science & Engineering. Indian Institute of Technology, Kanpur. Lecture-15. Decision Problems for Regular Languages. (Refer Slide
16 Greedy Algorithms
 16 Greedy Algorithms Optimization algorithms typically go through a sequence of steps, with a set of choices at each For many optimization problems, using dynamic programming to determine the best choices
16 Greedy Algorithms Optimization algorithms typically go through a sequence of steps, with a set of choices at each For many optimization problems, using dynamic programming to determine the best choices
Introduction to Algorithms I
 Summer School on Algorithms and Optimization Organized by: ACM Unit, ISI and IEEE CEDA. Tutorial II Date: 05.07.017 Introduction to Algorithms I (Q1) A binary tree is a rooted tree in which each node has
Summer School on Algorithms and Optimization Organized by: ACM Unit, ISI and IEEE CEDA. Tutorial II Date: 05.07.017 Introduction to Algorithms I (Q1) A binary tree is a rooted tree in which each node has
Bucket-Sort and Radix-Sort
 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 2014 Bucket-Sort and Radix-Sort B 0 1 2 3 4 5 6
Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 2014 Bucket-Sort and Radix-Sort B 0 1 2 3 4 5 6
SORTING LOWER BOUND & BUCKET-SORT AND RADIX-SORT
 Bucket-Sort and Radix-Sort SORTING LOWER BOUND & BUCKET-SORT AND RADIX-SORT 1, c 3, a 3, b 7, d 7, g 7, e B 0 1 2 3 4 5 6 7 8 9 Presentation for use with the textbook Data Structures and Algorithms in
Bucket-Sort and Radix-Sort SORTING LOWER BOUND & BUCKET-SORT AND RADIX-SORT 1, c 3, a 3, b 7, d 7, g 7, e B 0 1 2 3 4 5 6 7 8 9 Presentation for use with the textbook Data Structures and Algorithms in
Operations on Heap Tree The major operations required to be performed on a heap tree are Insertion, Deletion, and Merging.
 Priority Queue, Heap and Heap Sort In this time, we will study Priority queue, heap and heap sort. Heap is a data structure, which permits one to insert elements into a set and also to find the largest
Priority Queue, Heap and Heap Sort In this time, we will study Priority queue, heap and heap sort. Heap is a data structure, which permits one to insert elements into a set and also to find the largest
