Type Inference. COS 326 David Walker Princeton University
|
|
|
- Mabel Carr
- 6 years ago
- Views:
Transcription
1 Type Inference COS 326 David Walker Princeton University slides copyright 2017 David Walker permission granted to reuse these slides for non-commercial educafonal purposes
2 2 Midterm Exam Wed Oct 25, 2017 In Class (11:00-12:20) Midterm Week Be there or be square!
3 TYPE INFERENCE 3
4 Language Design for Type Inference The ML language and type system is designed to support a very strong form of type inference.
5 Language Design for Type Inference The ML language and type system is designed to support a very strong form of type inference. let rec map f l = match l with [ ] -> [ ] hd::tl -> f hd :: map f tl ML finds this type for map: map : ('a -> 'b) -> 'a list -> 'b list
6 Language Design for Type Inference The ML language and type system is designed to support a very strong form of type inference. let rec map f l = match l with [ ] -> [ ] hd::tl -> f hd :: map f tl ML finds this type for map: map : ('a -> 'b) -> 'a list -> 'b list which is really an abbreviafon for this type: map : forall 'a,'b.('a -> 'b) -> 'a list -> 'b list
7 Language Design for Type Inference map : ('a -> 'b) -> 'a list -> 'b list We call this type the principle type (scheme) for map. Any other ML-style type you can give map is an instance of this type, meaning we can obtain the other types via subs3tu3on of types for parameters from the principle type. Eg: (bool -> int) -> bool list -> int list ('a -> int) -> 'a list -> int list ('a -> 'a) -> 'a list -> 'a list
8 Language Design for Type Inference Principle types are great: the type inference engine can make a best choice for the type to give an expression the engine doesn't have to guess (and won't have to guess wrong) The fact that principle types exist is surprisingly briyle. If you change ML's type system a liyle bit in either direcfon, it can fall apart.
9 Language Design for Type Inference Suppose we take out polymorphic types and need a type for id: let id x = x Then the compiler might guess that id has one (and only one) of these types: id : bool -> bool id : int -> int
10 Language Design for Type Inference Suppose we take out polymorphic types and need a type for id: let id x = x Then the compiler might guess that id has one (and only one) of these types: id : bool -> bool id : int -> int But later on, one of the following code snippets won't type check: id true id 3 So whatever choice is made, a different one might have been beyer.
11 Language Design for Type Inference We showed that removing types from the language causes a failure of principle types. Does adding more types always make type inference easier?
12 Language Design for Type Inference We showed that removing types from the language causes a failure of principle types. Does adding more types always make type inference easier?
13 Language Design for Type Inference OCaml only has universal types on the outside: forall 'a,'b. ('a -> 'b) -> 'a list -> 'b list Consider this program: let f g = (g true, g 3) It won't type check in OCaml. We might want to give it this type: f : (forall a.a->a) -> bool * int NoFce that the universal quanffier appears under an ->
14 Language Design for Type Inference System F is a lot like OCaml, except that it allows universal quanffiers in any posifon. It could type check f. let f g = (g true, g 3) f : (forall a.a->a) -> bool * int Unfortunately, type inference in System F is undecideable..
15 Language Design for Type Inference System F is a lot like OCaml, except that it allows universal quanffiers in any posifon. It could type check f. let f g = (g true, g 3) f : (forall a.a->a) -> bool * int Unfortunately, type inference in System F is undecideable. Developed in 1972 by logician Jean Yves-Girard who was interested in the consistency of a logic of 2 nd -order arithemefc. Rediscovered as programming language by John Reynolds in 1974.
16 Language Design for Type Inference Even seemingly small changes can effect type inference. Suppose "+" operated on both floats and ints. What type for this? let f x = x + x
17 Language Design for Type Inference Even seemingly small changes can effect type inference. Suppose "+" operated on both floats and ints. What type for this? let f x = x + x f : int -> int? f : float -> float?
18 Language Design for Type Inference Even seemingly small changes can effect type inference. Suppose "+" operated on both floats and ints. What type for this? let f x = x + x f : int -> int? f : float -> float? f : 'a -> 'a?
19 Language Design for Type Inference Even seemingly small changes can effect type inference. Suppose "+" operated on both floats and ints. What type for this? let f x = x + x f : int -> int? f : float -> float? f : 'a -> 'a? No type in OCaml's type system works. In Haskell: f : Num 'a => 'a -> 'a
20 INFERRING SIMPLE TYPES 20
21 Type Schemes A type scheme contains type variables that may be filled in during type inference s ::= a int bool s -> s A term scheme is a term that contains type schemes rather than proper types. eg, for funcfons: fun (x:s) -> e let rec f (x:s) : s = e
22 The Generic Type Inference Algorithm 1) Add disfnct variables in all places type schemes are needed 22
23 The Generic Type Inference Algorithm 23 1) Add disfnct variables in all places type schemes are needed 2) Generate constraints (equafons between types) that must be safsfied in order for an expression to type check NoFce the difference between this and the type checking algorithm from last Fme. Last Fme, we tried to: eagerly deduce the concrete type when checking every expression reject programs when types didn't match. eg: f e -- f's argument type must equal e This Fme, we'll collect up equafons like: a -> b = c
24 The Generic Type Inference Algorithm 24 1) Add disfnct variables in all places type schemes are needed 2) Generate constraints (equafons between types) that must be safsfied in order for an expression to type check NoFce the difference between this and the type checking algorithm from last Fme. Last Fme, we tried to: eagerly deduce the concrete type when checking every expression reject programs when types didn't match. eg: f e -- f's argument type must equal e This Fme, we'll collect up equafons like: a -> b = c 3) Solve the equafons, generafng subsftufons of types for var's
25 Example: Inferring types for map let rec map f l = match l with [] -> [] hd::tl -> f hd :: map f tl
26 Step 1: Annotate let rec map (f:a) (l:b) : c = match l with [] -> [] hd::tl -> f hd :: map f tl
27 Step 2: Generate Constraints let rec map (f:a) (l:b) : c = match l with [] -> [] hd::tl -> f hd :: map f tl b = d list a = d -> f...
28 Step 2: Generate Constraints let rec map (f:a) (l:b) : c = match l with [] -> [] hd::tl -> f hd :: map f tl final constraints: b = b list b = b list b = b list a = a b = b list a = b -> a c = c list a = c d list = c list d list = c
29 Step 3: Solve Constraints let rec map (f:a) (l:b) : c = match l with [] -> [] hd::tl -> f hd :: map f tl final constraints: b = b list b = b list b = b list a = a b = b list a = b -> a c = c list a = c d list = c list d list = c final solufon: [b' -> c'/a] [b' list/b] [c' list/c]
30 Step 3: Solve Constraints final solufon: [b' -> c'/a] [b' list/b] [c' list/c] let rec map (f:a) (l:b) : c = match l with [] -> [] hd::tl -> f hd :: map f tl let rec map (f:b' -> c') (l:b' list) : c' list = match l with [] -> [] hd::tl -> f hd :: map f tl
31 Step 3: Solve Constraints let rec map (f:a) (l:b) : c = match l with [] -> [] hd::tl -> f hd :: map f tl renaming type variables: let rec map (f:a -> b) (l:a list) : b list = match l with [] -> [] hd::tl -> f hd :: map f tl
32 Step 4: Generate types Generate types from type schemes OpFon 1: pick an instance of the most general type when we have completed type inference on the enfre program map : (int -> int) -> int list -> int list OpFon 2: generate polymorphic types for program parts and confnue (polymorphic) type inference map : forall a,b,c. (a -> b) -> a list -> b list
33 Type Inference Details Type constraints are sets of equafons between type schemes q ::= {s11 = s12,..., sn1 = sn2} eg: {b = b list, a = b -> c}
34 Constraint GeneraFon Syntax-directed constraint generafon our algorithm crawls over abstract syntax of untyped expressions and generates a term scheme a set of constraints Algorithm defined as set of inference rules: G -- u => e : t, q constraints that must be solved context unannotated expression annotated expression type (scheme) in OCaml: gen : ctxt -> exp -> ann_exp * scheme * constraints
35 Constraint GeneraFon Simple rules: G -- x ==> x : s, { } (if G(x) = s) G -- 3 ==> 3 : int, { } (same for other ints) G -- true ==> true : bool, { } G -- false ==> false : bool, { }
36 Operators G -- u1 ==> e1 : t1, q1 G -- u2 ==> e2 : t2, q G -- u1 + u2 ==> e1 + e2 : int, q1 U q2 U {t1 = int, t2 = int} G -- u1 ==> e1 : t1, q1 G -- u2 ==> e2 : t2, q G -- u1 < u2 ==> e1 + e2 : bool, q1 U q2 U {t1 = int, t2 = int}
37 If statements G -- u1 ==> e1 : t1, q1 G -- u2 ==> e2 : t2, q2 G -- u3 ==> e3 : t3, q G -- if u1 then u2 else u3 ==> if e1 then e2 else e3 : a, q1 U q2 U q3 U {t1 = bool, a = t2, a = t3}
38 FuncFon ApplicaFon G -- u1 ==> e1 : t1, q1 G -- u2 ==> e2 : t2, q2 (for a fresh a) G -- u1 u2==> e1 e2 : a, q1 U q2 U {t1 = t2 -> a}
39 FuncFon DeclaraFon G, x : a -- u ==> e : t, q (for fresh a) G -- fun x -> e ==> fun (x : a) -> e : a -> b, q U {t = b}
40 FuncFon DeclaraFon G, f : a -> b, x : a -- u ==> e : t, q (for fresh a,b) G -- rec f(x) = u ==> rec f (x : a) : b = e : a -> b, q U {t = b}
41 Solving Constraints A solufon to a system of type constraints is a subs3tu3on S a funcfon from type variables to types assume subsftufons are defined on all type variables: S(a) = a (for almost all variables a) S(a) = s (for some type scheme s) dom(s) = set of variables s.t. S(a) a
42 Solving Constraints A solufon to a system of type constraints is a subs3tu3on S a funcfon from type variables to types assume subsftufons are defined on all type variables: S(a) = a (for almost all variables a) S(a) = s (for some type scheme s) dom(s) = set of variables s.t. S(a) a We can also apply a subsftufon S to a full type scheme s. apply: [ int/a, int->bool/b ] to: b -> a -> b returns: (int->bool) -> int -> (int->bool)
43 SubsFtuFons We can apply a subsftufon S to a full type scheme: eg: apply [ int/a, int->bool/b ] to b -> a -> b returns: (int->bool) -> int -> (int->bool)
44 SubsFtuFons When is a subsftufon S a solufon to a set of constraints? Constraints: { s1 = s2, s3 = s4, s5 = s6,... } When the subsftufon makes both sides of all equafons the same. Eg: constraints: a = b -> c c = int -> bool
45 SubsFtuFons When is a subsftufon S a solufon to a set of constraints? Constraints: { s1 = s2, s3 = s4, s5 = s6,... } When the subsftufon makes both sides of all equafons the same. Eg: constraints: a = b -> c c = int -> bool solufon: b -> (int -> bool)/a int -> bool/c b/b
46 SubsFtuFons When is a subsftufon S a solufon to a set of constraints? Constraints: { s1 = s2, s3 = s4, s5 = s6,... } When the subsftufon makes both sides of all equafons the same. Eg: constraints: a = b -> c c = int -> bool solufon: b -> (int -> bool)/a int -> bool/c b/b constraints with solufon applied: b -> (int -> bool) = b -> (int -> bool) int -> bool = int -> bool
47 SubsFtuFons When is a subsftufon S a solufon to a set of constraints? Constraints: { s1 = s2, s3 = s4, s5 = s6,... } When the subsftufon makes both sides of all equafons the same. A second solufon constraints: a = b -> c c = int -> bool solufon 1: b -> (int -> bool)/a int -> bool/c b/b solufon 2: int -> (int -> bool)/a int -> bool/c int/b
48 SubsFtuFons When is one solufon beyer than another to a set of constraints? constraints: a = b -> c c = int -> bool solufon 1: b -> (int -> bool)/a int -> bool/c b/b solufon 2: int -> (int -> bool)/a int -> bool/c int/b type b -> c with solufon applied: b -> (int -> bool) type b -> c with solufon applied: int -> (int -> bool)
49 SubsFtuFons solufon 1: b -> (int -> bool)/a int -> bool/c b/b solufon 2: int -> (int -> bool)/a int -> bool/c int/b type b -> c with solufon applied: b -> (int -> bool) type b -> c with solufon applied: int -> (int -> bool) SoluFon 1 is "more general" there is more flex. SoluFon 2 is "more concrete" We prefer solufon 1.
50 SubsFtuFons solufon 1: b -> (int -> bool)/a int -> bool/c b/b solufon 2: int -> (int -> bool)/a int -> bool/c int/b type b -> c with solufon applied: b -> (int -> bool) type b -> c with solufon applied: int -> (int -> bool) SoluFon 1 is "more general" there is more flex. SoluFon 2 is "more concrete" We prefer the more general (less concrete) solufon 1. Technically, we prefer T to S if there exists another subsftufon U and for all types t, S (t) = U (T (t))
51 SubsFtuFons solufon 1: b -> (int -> bool)/a int -> bool/c b/b solufon 2: int -> (int -> bool)/a int -> bool/c int/b type b -> c with solufon applied: b -> (int -> bool) type b -> c with solufon applied: int -> (int -> bool) There is always a best solufon, which we can a principle solu3on. The best solufon is (at least as) preferred as any other solufon.
52 Most General SoluFons S is the principal (most general) solufon of a constraint q if S = q (it is a solufon) if T = q then T <= S (it is the most general one) Lemma: If q has a solufon, then it has a most general one We care about principal solufons since they will give us the most general types for terms
53 ComposiFon of SubsFtuFons We will need to compare subsftufons: T <= S. eg: T <= S if T is more specific /"less general" than S If there is a Formally: T <= S if and only if T = U o S for some U
54 ComposiFon of SubsFtuFons ComposiFon (U o S) applies the subsftufon S and then applies the subsftufon U: (U o S)(a) = U(S(a)) We will need to compare subsftufons T <= S if T is more specific than S T <= S if T is less general than S Formally: T <= S if and only if T = U o S for some U
55 ComposiFon of SubsFtuFons Examples: example 1: any subsftufon is less general than the idenfty subsftufon I: S <= I because S = S o I example 2: S(a) = int, S(b) = c -> c T(a) = int, T(b) = int -> int we conclude: T <= S if T(a) = int, T(b) = int -> bool then T is unrelated to S (neither more nor less general)
56 Solving a Constraint S = q if S is a solufon to the constraints q S = { } S(s1) = S(s2) S = q S = {s1 = s2} U q any subsftufon is a solufon for the empty set of constraints a solufon to an equafon is a subsftufon that makes let and right sides equal
57 Examples Example 1 q = {a=int, b=a} principal solufon S:
58 Example 1 q = {a=int, b=a} principal solufon S: Examples S(a) = S(b) = int S(c) = c (for all c other than a,b)
59 Example 2 q = {a=int, b=a, b=bool} principal solufon S: Examples
60 Example 2 q = {a=int, b=a, b=bool} principal solufon S: Examples does not exist (there is no solufon to q)
61 UnificaFon UnificaFon: An algorithm that provides the principal solufon to a set of constraints (if one exists) UnificaFon systemafcally simplifies a set of constraints, yielding a subsftufon StarFng state of unificafon process: (I,q) Final state of unificafon process: (S, { })
62 UnificaFon Machine We can specify unificafon as a transifon system: (S1, q1) -> (S2, q2) Base types & simple variables: (S,{bool=bool} U q) -> (S, q) (S,{int=int} U q) -> (S, q) (S,{a=a} U q) -> (S, q)
63 FuncFons: UnificaFon Machine (S, {s11 -> s12 = s21 -> s22} U q) -> (S, {s11 = s21, s12 = s22} U q) breaks down into smaller constraints Variable definifons when a is not in FreeVars(s) (S, {a=s} U q) -> ([a=s] o S, [s/a]q) do S and then do [a=b] (S, {s=a} U q) -> ([a=s] o S, [s/a]q)
64 Occurs Check Recall this program: fun x -> x x It generates the the constraints: a -> a = a What is the solufon to {a = a -> a}?
65 Occurs Check Recall this program: fun x -> x x It generates the the constraints: a -> a = a What is the solufon to {a = a -> a}? There is none! (S, {s=a} U q) -> ([a=s] o S, [s/a]q) "when a is not in FreeVars(s)" the "occurs check"
66 Irreducible States When all the constraints have been processed, we win! (S1, q1) -> (S2, q2) -> (S3, q3)... -> (Sn, { }) But somefmes we get stuck, with an equafon like this int = bool s1 -> s2 = int s1 -> s2 = bool a = s (s contains a) or is symmetric to one of the above Stuck states arise when constraints are unsolvable & the program does not type check.
67 TerminaFon We want unificafon to terminate (to give us a type reconstrucfon algorithm) In other words, we want to show that there is no infinite sequence of states (S1,q1) -> (S2,q2) ->...
68 TerminaFon We associate an ordering with constraints q < q if and only if q contains fewer variables than q q contains the same number of variables as q but fewer type constructors (ie: fewer occurrences of int, bool, or -> ) This is a lexacographic ordering we can prove (by contradicfon) that there is no infinite decreasing sequence of constraints
69 TerminaFon Lemma: Every step reduces the size of q Proof: By cases (ie: inducfon) on the definifon of the reducfon relafon (S,{int=int} U q) -> (S, q) (S,{bool=bool} U q) -> (S, q) (S,{a=a} U q) -> (S, q) (S,{s11 -> s12= s21 -> s22} U q) -> (S, {s11 = s21, s12 = s22} U q) (a not in FV(s)) (S,{a=s} U q) -> ([a=s] o S, [s/a]q)
70 Complete SoluFons A complete solufon for (S,q) is a subsftufon T such that T <= S T = q
71 ProperFes of SoluFons Lemma 1: Every final state (S, { }) has a complete solufon. It is S: S <= S S = { }
72 ProperFes of SoluFons Lemma 2 No stuck state has a complete solufon (or any solufon at all) it is impossible for a subsftufon to make the necessary equafons equal int bool int t1 -> t2...
73 Lemma 3 If (S,q) -> (S,q ) then ProperFes of SoluFons T is complete for (S,q) iff T is complete for (S,q ) proof by? in the forward direcfon, this is the preservafon theorem for the unificafon machine!
74 Summary: UnificaFon By terminafon, (I,q) ->* (S,q ) where (S,q ) is irreducible. Moreover: If q = { } then (S,q ) is final (by definifon) S is a principal solufon for q Consider any T such that T is a solufon to q. Now nofce, S is complete for (S,q ) (by lemma 1) S is complete for (I,q) (by lemma 3) Since S is complete for (I,q), T <= S and therefore S is principal.
75 Summary: UnificaFon (cont.)... Moreover: If q is not { } (and (I,q) ->* (S,q ) where (S,q ) is irreducible) then (S,q) is stuck. Consequently, (S,q) has no complete solufon. By lemma 3, even (I,q) has no complete solufon and therefore q has no solufon at all.
76 MORE TYPE INFERENCE 76
77 let GeneralizaFon Where do we introduce polymorphic values? let x = v ==> let x : forall a1,..,an.s = v if v : s and a1,...,an are the variables of s And place x : forall a1,...,an.s in the context.
78 let GeneralizaFon Where do we introduce polymorphic values? let x = v ==> let x : forall a1,..,an.s = v if v : s and a1,...,an are the variables of s And place x : forall a1,...,an.s in the context. Where and how do we use a polymorphic value? G - x ==> x : s[b1/a1,...,bn/an), {} when G(x) = forall a1,...,an.s and b1,...,bn are fresh
79 What is the cost of type inference? In pracfce? Linear in the size of the program In theory, DEXPTIME-complete. Why? Because we can generate a program that has a type that is exponenfally large: let f1 x = x f1 : a -> a let f2 = f1 f1 f2 : (a -> a) -> (a -> a) let f3 = f2 f2 f3 : ((a -> a) -> (a -> a)) -> ((a -> a) -> (a -> a)) let f4 = f3 f3...
80 Summary: Type Inference Given a context G, and untyped term u: Find e, t, q such that G - u ==> e : t, q Find principal solufon S of q via unificafon if no solufon exists, there is no reconstrucfon Apply S to e, ie our solufon is S(e) S(e) contains schemafc type variables a,b,c, etc that may be instanfated with any type Since S is principal, S(e) characterizes all reconstrucfons. If desired, use the type checking algorithm to validate
Programming Language Concepts: Lecture 19
 Programming Language Concepts: Lecture 19 Madhavan Mukund Chennai Mathematical Institute madhavan@cmi.ac.in http://www.cmi.ac.in/~madhavan/courses/pl2009 PLC 2009, Lecture 19, 01 April 2009 Adding types
Programming Language Concepts: Lecture 19 Madhavan Mukund Chennai Mathematical Institute madhavan@cmi.ac.in http://www.cmi.ac.in/~madhavan/courses/pl2009 PLC 2009, Lecture 19, 01 April 2009 Adding types
Principles of Programming Languages
 Principles of Programming Languages h"p://www.di.unipi.it/~andrea/dida2ca/plp-16/ Prof. Andrea Corradini Department of Computer Science, Pisa Lesson 24! Type inference in ML / Haskell 1 Type Checking vs
Principles of Programming Languages h"p://www.di.unipi.it/~andrea/dida2ca/plp-16/ Prof. Andrea Corradini Department of Computer Science, Pisa Lesson 24! Type inference in ML / Haskell 1 Type Checking vs
Lecture #13: Type Inference and Unification. Typing In the Language ML. Type Inference. Doing Type Inference
 Lecture #13: Type Inference and Unification Typing In the Language ML Examples from the language ML: fun map f [] = [] map f (a :: y) = (f a) :: (map f y) fun reduce f init [] = init reduce f init (a ::
Lecture #13: Type Inference and Unification Typing In the Language ML Examples from the language ML: fun map f [] = [] map f (a :: y) = (f a) :: (map f y) fun reduce f init [] = init reduce f init (a ::
A Functional Evaluation Model
 A Functional Evaluation Model COS 326 Andrew W. Appel Princeton University slides copyright 2013-2015 David Walker and Andrew W. Appel A Functional Evaluation Model In order to be able to write a program,
A Functional Evaluation Model COS 326 Andrew W. Appel Princeton University slides copyright 2013-2015 David Walker and Andrew W. Appel A Functional Evaluation Model In order to be able to write a program,
Lecture #23: Conversion and Type Inference
 Lecture #23: Conversion and Type Inference Administrivia. Due date for Project #2 moved to midnight tonight. Midterm mean 20, median 21 (my expectation: 17.5). Last modified: Fri Oct 20 10:46:40 2006 CS164:
Lecture #23: Conversion and Type Inference Administrivia. Due date for Project #2 moved to midnight tonight. Midterm mean 20, median 21 (my expectation: 17.5). Last modified: Fri Oct 20 10:46:40 2006 CS164:
Conversion vs. Subtyping. Lecture #23: Conversion and Type Inference. Integer Conversions. Conversions: Implicit vs. Explicit. Object x = "Hello";
 Lecture #23: Conversion and Type Inference Administrivia. Due date for Project #2 moved to midnight tonight. Midterm mean 20, median 21 (my expectation: 17.5). In Java, this is legal: Object x = "Hello";
Lecture #23: Conversion and Type Inference Administrivia. Due date for Project #2 moved to midnight tonight. Midterm mean 20, median 21 (my expectation: 17.5). In Java, this is legal: Object x = "Hello";
Thinking Induc,vely. COS 326 David Walker Princeton University
 Thinking Induc,vely COS 326 David Walker Princeton University slides copyright 2017 David Walker permission granted to reuse these slides for non-commercial educa,onal purposes Administra,on 2 Assignment
Thinking Induc,vely COS 326 David Walker Princeton University slides copyright 2017 David Walker permission granted to reuse these slides for non-commercial educa,onal purposes Administra,on 2 Assignment
Polymorphic lambda calculus Princ. of Progr. Languages (and Extended ) The University of Birmingham. c Uday Reddy
 06-02552 Princ. of Progr. Languages (and Extended ) The University of Birmingham Spring Semester 2016-17 School of Computer Science c Uday Reddy2016-17 Handout 6: Polymorphic Type Systems 1. Polymorphic
06-02552 Princ. of Progr. Languages (and Extended ) The University of Birmingham Spring Semester 2016-17 School of Computer Science c Uday Reddy2016-17 Handout 6: Polymorphic Type Systems 1. Polymorphic
Introduction to OCaml
 Introduction to OCaml Jed Liu Department of Computer Science Cornell University CS 6110 Lecture 26 January 2009 Based on CS 3110 course notes and an SML tutorial by Mike George Jed Liu Introduction to
Introduction to OCaml Jed Liu Department of Computer Science Cornell University CS 6110 Lecture 26 January 2009 Based on CS 3110 course notes and an SML tutorial by Mike George Jed Liu Introduction to
COSE212: Programming Languages. Lecture 3 Functional Programming in OCaml
 COSE212: Programming Languages Lecture 3 Functional Programming in OCaml Hakjoo Oh 2017 Fall Hakjoo Oh COSE212 2017 Fall, Lecture 3 September 18, 2017 1 / 44 Why learn ML? Learning ML is a good way of
COSE212: Programming Languages Lecture 3 Functional Programming in OCaml Hakjoo Oh 2017 Fall Hakjoo Oh COSE212 2017 Fall, Lecture 3 September 18, 2017 1 / 44 Why learn ML? Learning ML is a good way of
More Untyped Lambda Calculus & Simply Typed Lambda Calculus
 Concepts in Programming Languages Recitation 6: More Untyped Lambda Calculus & Simply Typed Lambda Calculus Oded Padon & Mooly Sagiv (original slides by Kathleen Fisher, John Mitchell, Shachar Itzhaky,
Concepts in Programming Languages Recitation 6: More Untyped Lambda Calculus & Simply Typed Lambda Calculus Oded Padon & Mooly Sagiv (original slides by Kathleen Fisher, John Mitchell, Shachar Itzhaky,
CMSC 330: Organization of Programming Languages. OCaml Expressions and Functions
 CMSC 330: Organization of Programming Languages OCaml Expressions and Functions CMSC330 Spring 2018 1 Lecture Presentation Style Our focus: semantics and idioms for OCaml Semantics is what the language
CMSC 330: Organization of Programming Languages OCaml Expressions and Functions CMSC330 Spring 2018 1 Lecture Presentation Style Our focus: semantics and idioms for OCaml Semantics is what the language
Modules and Representation Invariants
 Modules and Representation Invariants COS 326 Andrew W. Appel Princeton University slides copyright 2013-2015 David Walker and Andrew W. Appel In previous classes: Reasoning about individual OCaml expressions.
Modules and Representation Invariants COS 326 Andrew W. Appel Princeton University slides copyright 2013-2015 David Walker and Andrew W. Appel In previous classes: Reasoning about individual OCaml expressions.
CS-XXX: Graduate Programming Languages. Lecture 9 Simply Typed Lambda Calculus. Dan Grossman 2012
 CS-XXX: Graduate Programming Languages Lecture 9 Simply Typed Lambda Calculus Dan Grossman 2012 Types Major new topic worthy of several lectures: Type systems Continue to use (CBV) Lambda Caluclus as our
CS-XXX: Graduate Programming Languages Lecture 9 Simply Typed Lambda Calculus Dan Grossman 2012 Types Major new topic worthy of several lectures: Type systems Continue to use (CBV) Lambda Caluclus as our
CS153: Compilers Lecture 14: Type Checking
 CS153: Compilers Lecture 14: Type Checking Stephen Chong https://www.seas.harvard.edu/courses/cs153 Announcements Project 4 out Due Thursday Oct 25 (7 days) Project 5 out Due Tuesday Nov 13 (26 days) Project
CS153: Compilers Lecture 14: Type Checking Stephen Chong https://www.seas.harvard.edu/courses/cs153 Announcements Project 4 out Due Thursday Oct 25 (7 days) Project 5 out Due Tuesday Nov 13 (26 days) Project
CS Lecture 5: Pattern Matching. Prof. Clarkson Fall Today s music: Puff, the Magic Dragon by Peter, Paul & Mary
 CS 3110 Lecture 5: Pattern Matching Prof. Clarkson Fall 2014 Today s music: Puff, the Magic Dragon by Peter, Paul & Mary Review Features so far: variables, operators, let expressions, if expressions, functions
CS 3110 Lecture 5: Pattern Matching Prof. Clarkson Fall 2014 Today s music: Puff, the Magic Dragon by Peter, Paul & Mary Review Features so far: variables, operators, let expressions, if expressions, functions
Introduction to ML. Mooly Sagiv. Cornell CS 3110 Data Structures and Functional Programming
 Introduction to ML Mooly Sagiv Cornell CS 3110 Data Structures and Functional Programming Typed Lambda Calculus Chapter 9 Benjamin Pierce Types and Programming Languages Call-by-value Operational Semantics
Introduction to ML Mooly Sagiv Cornell CS 3110 Data Structures and Functional Programming Typed Lambda Calculus Chapter 9 Benjamin Pierce Types and Programming Languages Call-by-value Operational Semantics
CSCI-GA Scripting Languages
 CSCI-GA.3033.003 Scripting Languages 12/02/2013 OCaml 1 Acknowledgement The material on these slides is based on notes provided by Dexter Kozen. 2 About OCaml A functional programming language All computation
CSCI-GA.3033.003 Scripting Languages 12/02/2013 OCaml 1 Acknowledgement The material on these slides is based on notes provided by Dexter Kozen. 2 About OCaml A functional programming language All computation
Once Upon a Polymorphic Type
 Once Upon a Polymorphic Type Keith Wansbrough Computer Laboratory University of Cambridge kw217@cl.cam.ac.uk http://www.cl.cam.ac.uk/users/kw217/ Simon Peyton Jones Microsoft Research Cambridge 20 January,
Once Upon a Polymorphic Type Keith Wansbrough Computer Laboratory University of Cambridge kw217@cl.cam.ac.uk http://www.cl.cam.ac.uk/users/kw217/ Simon Peyton Jones Microsoft Research Cambridge 20 January,
CSE505, Fall 2012, Midterm Examination October 30, 2012
 CSE505, Fall 2012, Midterm Examination October 30, 2012 Rules: The exam is closed-book, closed-notes, except for one side of one 8.5x11in piece of paper. Please stop promptly at Noon. You can rip apart
CSE505, Fall 2012, Midterm Examination October 30, 2012 Rules: The exam is closed-book, closed-notes, except for one side of one 8.5x11in piece of paper. Please stop promptly at Noon. You can rip apart
CS Lecture 6: Map and Fold. Prof. Clarkson Fall Today s music: Selections from the soundtrack to 2001: A Space Odyssey
 CS 3110 Lecture 6: Map and Fold Prof. Clarkson Fall 2014 Today s music: Selections from the soundtrack to 2001: A Space Odyssey Review Features so far: variables, operators, let expressions, if expressions,
CS 3110 Lecture 6: Map and Fold Prof. Clarkson Fall 2014 Today s music: Selections from the soundtrack to 2001: A Space Odyssey Review Features so far: variables, operators, let expressions, if expressions,
Programming Languages Fall 2014
 Programming Languages Fall 2014 Lecture 7: Simple Types and Simply-Typed Lambda Calculus Prof. Liang Huang huang@qc.cs.cuny.edu 1 Types stuck terms? how to fix it? 2 Plan First I For today, we ll go back
Programming Languages Fall 2014 Lecture 7: Simple Types and Simply-Typed Lambda Calculus Prof. Liang Huang huang@qc.cs.cuny.edu 1 Types stuck terms? how to fix it? 2 Plan First I For today, we ll go back
The Substitution Model
 The Substitution Model Prof. Clarkson Fall 2017 Today s music: Substitute by The Who Review Previously in 3110: simple interpreter for expression language abstract syntax tree (AST) evaluation based on
The Substitution Model Prof. Clarkson Fall 2017 Today s music: Substitute by The Who Review Previously in 3110: simple interpreter for expression language abstract syntax tree (AST) evaluation based on
Types, Type Inference and Unification
 Types, Type Inference and Unification Mooly Sagiv Slides by Kathleen Fisher and John Mitchell Cornell CS 6110 Summary (Functional Programming) Lambda Calculus Basic ML Advanced ML: Modules, References,
Types, Type Inference and Unification Mooly Sagiv Slides by Kathleen Fisher and John Mitchell Cornell CS 6110 Summary (Functional Programming) Lambda Calculus Basic ML Advanced ML: Modules, References,
Lambda Calculus and Type Inference
 Lambda Calculus and Type Inference Björn Lisper Dept. of Computer Science and Engineering Mälardalen University bjorn.lisper@mdh.se http://www.idt.mdh.se/ blr/ October 13, 2004 Lambda Calculus and Type
Lambda Calculus and Type Inference Björn Lisper Dept. of Computer Science and Engineering Mälardalen University bjorn.lisper@mdh.se http://www.idt.mdh.se/ blr/ October 13, 2004 Lambda Calculus and Type
CS 11 Haskell track: lecture 1
 CS 11 Haskell track: lecture 1 This week: Introduction/motivation/pep talk Basics of Haskell Prerequisite Knowledge of basic functional programming e.g. Scheme, Ocaml, Erlang CS 1, CS 4 "permission of
CS 11 Haskell track: lecture 1 This week: Introduction/motivation/pep talk Basics of Haskell Prerequisite Knowledge of basic functional programming e.g. Scheme, Ocaml, Erlang CS 1, CS 4 "permission of
l e t print_name r = p r i n t _ e n d l i n e ( Name : ^ r. name)
 Chapter 8 Row polymorphism Consider the following code: type name_home = {name : s t r i n g ; home : s t r i n g } type name_mobile = {name : s t r i n g ; mobile : s t r i n g } l e t jane = {name =
Chapter 8 Row polymorphism Consider the following code: type name_home = {name : s t r i n g ; home : s t r i n g } type name_mobile = {name : s t r i n g ; mobile : s t r i n g } l e t jane = {name =
MA/CS 109 Lecture 3. Networks, Euler paths, and speaking carefully!
 MA/CS 109 Lecture 3 Networks, Euler paths, and speaking carefully! Last Time: Last Fme we proved the statement: Theorem 1: If a network has an Euler circuit, then the degree of every node must be an even
MA/CS 109 Lecture 3 Networks, Euler paths, and speaking carefully! Last Time: Last Fme we proved the statement: Theorem 1: If a network has an Euler circuit, then the degree of every node must be an even
Two Problems. Programming Languages and Compilers (CS 421) Type Inference - Example. Type Inference - Outline. Type Inference - Example
 Two Problems Programming Languages and Compilers (CS 421) Sasa Misailovic 4110 SC, UIUC https://courses.engr.illinois.edu/cs421/fa2017/cs421a Based in part on slides by Mattox Beckman, as updated by Vikram
Two Problems Programming Languages and Compilers (CS 421) Sasa Misailovic 4110 SC, UIUC https://courses.engr.illinois.edu/cs421/fa2017/cs421a Based in part on slides by Mattox Beckman, as updated by Vikram
Type Checking and Type Inference
 Type Checking and Type Inference Principles of Programming Languages CSE 307 1 Types in Programming Languages 2 Static Type Checking 3 Polymorphic Type Inference Version: 1.8 17:20:56 2014/08/25 Compiled
Type Checking and Type Inference Principles of Programming Languages CSE 307 1 Types in Programming Languages 2 Static Type Checking 3 Polymorphic Type Inference Version: 1.8 17:20:56 2014/08/25 Compiled
CMSC330 Fall 2016 Midterm #1 2:00pm/3:30pm
 CMSC330 Fall 2016 Midterm #1 2:00pm/3:30pm Name: Discussion Time: 10am 11am 12pm 1pm 2pm 3pm TA Name (Circle): Alex Austin Ayman Brian Damien Daniel K. Daniel P. Greg Tammy Tim Vitung Will K. Instructions
CMSC330 Fall 2016 Midterm #1 2:00pm/3:30pm Name: Discussion Time: 10am 11am 12pm 1pm 2pm 3pm TA Name (Circle): Alex Austin Ayman Brian Damien Daniel K. Daniel P. Greg Tammy Tim Vitung Will K. Instructions
CSE 505: Concepts of Programming Languages
 CSE 505: Concepts of Programming Languages Dan Grossman Fall 2003 Lecture 6 Lambda Calculus Dan Grossman CSE505 Fall 2003, Lecture 6 1 Where we are Done: Modeling mutation and local control-flow Proving
CSE 505: Concepts of Programming Languages Dan Grossman Fall 2003 Lecture 6 Lambda Calculus Dan Grossman CSE505 Fall 2003, Lecture 6 1 Where we are Done: Modeling mutation and local control-flow Proving
Type Systems. Seman&cs. CMPT 379: Compilers Instructor: Anoop Sarkar. anoopsarkar.github.io/compilers-class
 Type Systems Seman&cs CMPT 379: Compilers Instructor: Anoop Sarkar anoopsarkar.github.io/compilers-class 1 Equality of types Main seman&c tasks involve liveness analysis and checking equality Equality
Type Systems Seman&cs CMPT 379: Compilers Instructor: Anoop Sarkar anoopsarkar.github.io/compilers-class 1 Equality of types Main seman&c tasks involve liveness analysis and checking equality Equality
Lambda Calculus and Type Inference
 Lambda Calculus and Type Inference Björn Lisper Dept. of Computer Science and Engineering Mälardalen University bjorn.lisper@mdh.se http://www.idt.mdh.se/ blr/ August 17, 2007 Lambda Calculus and Type
Lambda Calculus and Type Inference Björn Lisper Dept. of Computer Science and Engineering Mälardalen University bjorn.lisper@mdh.se http://www.idt.mdh.se/ blr/ August 17, 2007 Lambda Calculus and Type
Lambda Calculus. Concepts in Programming Languages Recitation 6:
 Concepts in Programming Languages Recitation 6: Lambda Calculus Oded Padon & Mooly Sagiv (original slides by Kathleen Fisher, John Mitchell, Shachar Itzhaky, S. Tanimoto ) Reference: Types and Programming
Concepts in Programming Languages Recitation 6: Lambda Calculus Oded Padon & Mooly Sagiv (original slides by Kathleen Fisher, John Mitchell, Shachar Itzhaky, S. Tanimoto ) Reference: Types and Programming
Introduction to OCaml
 Fall 2018 Introduction to OCaml Yu Zhang Course web site: http://staff.ustc.edu.cn/~yuzhang/tpl References Learn X in Y Minutes Ocaml Real World OCaml Cornell CS 3110 Spring 2018 Data Structures and Functional
Fall 2018 Introduction to OCaml Yu Zhang Course web site: http://staff.ustc.edu.cn/~yuzhang/tpl References Learn X in Y Minutes Ocaml Real World OCaml Cornell CS 3110 Spring 2018 Data Structures and Functional
02157 Functional Programming. Michael R. Ha. Lecture 2: Functions, Types and Lists. Michael R. Hansen
 Lecture 2: Functions, Types and Lists nsen 1 DTU Compute, Technical University of Denmark Lecture 2: Functions, Types and Lists MRH 13/09/2018 Outline Functions as first-class citizens Types, polymorphism
Lecture 2: Functions, Types and Lists nsen 1 DTU Compute, Technical University of Denmark Lecture 2: Functions, Types and Lists MRH 13/09/2018 Outline Functions as first-class citizens Types, polymorphism
COSE212: Programming Languages. Lecture 4 Recursive and Higher-Order Programming
 COSE212: Programming Languages Lecture 4 Recursive and Higher-Order Programming Hakjoo Oh 2016 Fall Hakjoo Oh COSE212 2016 Fall, Lecture 4 September 27, 2016 1 / 21 Recursive and Higher-Order Programming
COSE212: Programming Languages Lecture 4 Recursive and Higher-Order Programming Hakjoo Oh 2016 Fall Hakjoo Oh COSE212 2016 Fall, Lecture 4 September 27, 2016 1 / 21 Recursive and Higher-Order Programming
CMSC 330: Organization of Programming Languages
 CMSC 330: Organization of Programming Languages Operational Semantics CMSC 330 Summer 2018 1 Formal Semantics of a Prog. Lang. Mathematical description of the meaning of programs written in that language
CMSC 330: Organization of Programming Languages Operational Semantics CMSC 330 Summer 2018 1 Formal Semantics of a Prog. Lang. Mathematical description of the meaning of programs written in that language
Scope and Introduction to Functional Languages. Review and Finish Scoping. Announcements. Assignment 3 due Thu at 11:55pm. Website has SML resources
 Scope and Introduction to Functional Languages Prof. Evan Chang Meeting 7, CSCI 3155, Fall 2009 Announcements Assignment 3 due Thu at 11:55pm Submit in pairs Website has SML resources Text: Harper, Programming
Scope and Introduction to Functional Languages Prof. Evan Chang Meeting 7, CSCI 3155, Fall 2009 Announcements Assignment 3 due Thu at 11:55pm Submit in pairs Website has SML resources Text: Harper, Programming
Turing Machine Languages
 Turing Machine Languages Based on Chapters 23-24-25 of (Cohen 1997) Introduction A language L over alphabet is called recursively enumerable (r.e.) if there is a Turing Machine T that accepts every word
Turing Machine Languages Based on Chapters 23-24-25 of (Cohen 1997) Introduction A language L over alphabet is called recursively enumerable (r.e.) if there is a Turing Machine T that accepts every word
CS152: Programming Languages. Lecture 11 STLC Extensions and Related Topics. Dan Grossman Spring 2011
 CS152: Programming Languages Lecture 11 STLC Extensions and Related Topics Dan Grossman Spring 2011 Review e ::= λx. e x e e c v ::= λx. e c τ ::= int τ τ Γ ::= Γ, x : τ (λx. e) v e[v/x] e 1 e 1 e 1 e
CS152: Programming Languages Lecture 11 STLC Extensions and Related Topics Dan Grossman Spring 2011 Review e ::= λx. e x e e c v ::= λx. e c τ ::= int τ τ Γ ::= Γ, x : τ (λx. e) v e[v/x] e 1 e 1 e 1 e
Overview. Elements of Programming Languages. Another example. Consider the humble identity function
 Overview Elements of Programming Languages Lecture 8: Polymorphism and type inference James Cheney University of Edinburgh October 21, 2016 This week and next week, we will cover di erent forms of abstraction
Overview Elements of Programming Languages Lecture 8: Polymorphism and type inference James Cheney University of Edinburgh October 21, 2016 This week and next week, we will cover di erent forms of abstraction
Type Inference Systems. Type Judgments. Deriving a Type Judgment. Deriving a Judgment. Hypothetical Type Judgments CS412/CS413
 Type Inference Systems CS412/CS413 Introduction to Compilers Tim Teitelbaum Type inference systems define types for all legal programs in a language Type inference systems are to type-checking: As regular
Type Inference Systems CS412/CS413 Introduction to Compilers Tim Teitelbaum Type inference systems define types for all legal programs in a language Type inference systems are to type-checking: As regular
Let Arguments Go First
 Let Arguments Go First Ningning Xie and Bruno C. d. S. Oliveira The University of Hong Kong {nnxie,bruno}@cs.hku.hk Abstract. Bi-directional type checking has proved to be an extremely useful and versatile
Let Arguments Go First Ningning Xie and Bruno C. d. S. Oliveira The University of Hong Kong {nnxie,bruno}@cs.hku.hk Abstract. Bi-directional type checking has proved to be an extremely useful and versatile
CMSC 330: Organization of Programming Languages. Functional Programming with Lists
 CMSC 330: Organization of Programming Languages Functional Programming with Lists CMSC330 Spring 2018 1 Lists in OCaml The basic data structure in OCaml Lists can be of arbitrary length Implemented as
CMSC 330: Organization of Programming Languages Functional Programming with Lists CMSC330 Spring 2018 1 Lists in OCaml The basic data structure in OCaml Lists can be of arbitrary length Implemented as
Modules and Representa/on Invariants
 Modules and Representa/on Invariants COS 326 David Walker Princeton University slides copyright 2017 David Walker permission granted to reuse these slides for non-commercial educa/onal purposes LAST TIME
Modules and Representa/on Invariants COS 326 David Walker Princeton University slides copyright 2017 David Walker permission granted to reuse these slides for non-commercial educa/onal purposes LAST TIME
Compiler Construction
 Compiler Construction Exercises 1 Review of some Topics in Formal Languages 1. (a) Prove that two words x, y commute (i.e., satisfy xy = yx) if and only if there exists a word w such that x = w m, y =
Compiler Construction Exercises 1 Review of some Topics in Formal Languages 1. (a) Prove that two words x, y commute (i.e., satisfy xy = yx) if and only if there exists a word w such that x = w m, y =
Programming Languages
 CSE 130: Fall 2009 Programming Languages Lecture 2: A Crash Course in ML News On webpage: Suggested HW #1 PA #1 (due next Fri 10/9) Technical issues installing Ocaml - should be resolved soon! Ranjit Jhala
CSE 130: Fall 2009 Programming Languages Lecture 2: A Crash Course in ML News On webpage: Suggested HW #1 PA #1 (due next Fri 10/9) Technical issues installing Ocaml - should be resolved soon! Ranjit Jhala
Lecture Notes on Induction and Recursion
 Lecture Notes on Induction and Recursion 15-317: Constructive Logic Frank Pfenning Lecture 7 September 19, 2017 1 Introduction At this point in the course we have developed a good formal understanding
Lecture Notes on Induction and Recursion 15-317: Constructive Logic Frank Pfenning Lecture 7 September 19, 2017 1 Introduction At this point in the course we have developed a good formal understanding
CMSC330 Fall 2017 Final Exam
 CMSC330 Fall 2017 Final Exam Name (PRINT YOUR NAME IN ALL CAPS ): Discussion Time (circle one) 10am 11am 12pm 1pm 2pm 3pm Discussion TA (circle one) JT Greg Justin Michael BT Daniel David Derek Cameron
CMSC330 Fall 2017 Final Exam Name (PRINT YOUR NAME IN ALL CAPS ): Discussion Time (circle one) 10am 11am 12pm 1pm 2pm 3pm Discussion TA (circle one) JT Greg Justin Michael BT Daniel David Derek Cameron
OCaml. ML Flow. Complex types: Lists. Complex types: Lists. The PL for the discerning hacker. All elements must have same type.
 OCaml The PL for the discerning hacker. ML Flow Expressions (Syntax) Compile-time Static 1. Enter expression 2. ML infers a type Exec-time Dynamic Types 3. ML crunches expression down to a value 4. Value
OCaml The PL for the discerning hacker. ML Flow Expressions (Syntax) Compile-time Static 1. Enter expression 2. ML infers a type Exec-time Dynamic Types 3. ML crunches expression down to a value 4. Value
Dependent types and program equivalence. Stephanie Weirich, University of Pennsylvania with Limin Jia, Jianzhou Zhao, and Vilhelm Sjöberg
 Dependent types and program equivalence Stephanie Weirich, University of Pennsylvania with Limin Jia, Jianzhou Zhao, and Vilhelm Sjöberg Doing dependent types wrong without going wrong Stephanie Weirich,
Dependent types and program equivalence Stephanie Weirich, University of Pennsylvania with Limin Jia, Jianzhou Zhao, and Vilhelm Sjöberg Doing dependent types wrong without going wrong Stephanie Weirich,
Tracing Ambiguity in GADT Type Inference
 Tracing Ambiguity in GADT Type Inference ML Workshop 2012, Copenhagen Jacques Garrigue & Didier Rémy Nagoya University / INRIA Garrigue & Rémy Tracing ambiguity 1 Generalized Algebraic Datatypes Algebraic
Tracing Ambiguity in GADT Type Inference ML Workshop 2012, Copenhagen Jacques Garrigue & Didier Rémy Nagoya University / INRIA Garrigue & Rémy Tracing ambiguity 1 Generalized Algebraic Datatypes Algebraic
Arbitrary-rank polymorphism in (GHC) Haskell
 Arbitrary-rank polymorphism in (GHC) Haskell CAS 743 Stephen Forrest 20 March 2006 Damas-Milner Type System A Damas-Milner type system (also called Hindley-Milner) is a traditional type system for functional
Arbitrary-rank polymorphism in (GHC) Haskell CAS 743 Stephen Forrest 20 March 2006 Damas-Milner Type System A Damas-Milner type system (also called Hindley-Milner) is a traditional type system for functional
CS Lecture 6: Map and Fold. Prof. Clarkson Spring Today s music: Selections from the soundtrack to 2001: A Space Odyssey
 CS 3110 Lecture 6: Map and Fold Prof. Clarkson Spring 2015 Today s music: Selections from the soundtrack to 2001: A Space Odyssey Review Course so far: Syntax and semantics of (most of) OCaml Today: No
CS 3110 Lecture 6: Map and Fold Prof. Clarkson Spring 2015 Today s music: Selections from the soundtrack to 2001: A Space Odyssey Review Course so far: Syntax and semantics of (most of) OCaml Today: No
Programming Language Features. CMSC 330: Organization of Programming Languages. Turing Completeness. Turing Machine.
 CMSC 330: Organization of Programming Languages Lambda Calculus Programming Language Features Many features exist simply for convenience Multi-argument functions foo ( a, b, c ) Ø Use currying or tuples
CMSC 330: Organization of Programming Languages Lambda Calculus Programming Language Features Many features exist simply for convenience Multi-argument functions foo ( a, b, c ) Ø Use currying or tuples
CMSC 330: Organization of Programming Languages
 CMSC 330: Organization of Programming Languages Lambda Calculus CMSC 330 1 Programming Language Features Many features exist simply for convenience Multi-argument functions foo ( a, b, c ) Ø Use currying
CMSC 330: Organization of Programming Languages Lambda Calculus CMSC 330 1 Programming Language Features Many features exist simply for convenience Multi-argument functions foo ( a, b, c ) Ø Use currying
h0ps://
 2 For more insanity: h0ps://www.destroyallso7ware.com/talks/wat [Broader point: No one (few people) knows what their programs do in untyped languages.] 3 Type Checking Basics COS 326 David Walker Princeton
2 For more insanity: h0ps://www.destroyallso7ware.com/talks/wat [Broader point: No one (few people) knows what their programs do in untyped languages.] 3 Type Checking Basics COS 326 David Walker Princeton
Limitations of Algorithmic Solvability In this Chapter we investigate the power of algorithms to solve problems Some can be solved algorithmically and
 Computer Language Theory Chapter 4: Decidability 1 Limitations of Algorithmic Solvability In this Chapter we investigate the power of algorithms to solve problems Some can be solved algorithmically and
Computer Language Theory Chapter 4: Decidability 1 Limitations of Algorithmic Solvability In this Chapter we investigate the power of algorithms to solve problems Some can be solved algorithmically and
Type Systems, Type Inference, and Polymorphism
 6 Type Systems, Type Inference, and Polymorphism Programming involves a wide range of computational constructs, such as data structures, functions, objects, communication channels, and threads of control.
6 Type Systems, Type Inference, and Polymorphism Programming involves a wide range of computational constructs, such as data structures, functions, objects, communication channels, and threads of control.
Type Systems COMP 311 Rice University Houston, Texas
 Rice University Houston, Texas 1 Type Systems for Programming Language were invented by mathematicians before electronic computers were invented. What is a type? A meaningful subset of the set of the domain
Rice University Houston, Texas 1 Type Systems for Programming Language were invented by mathematicians before electronic computers were invented. What is a type? A meaningful subset of the set of the domain
According to Larry Wall (designer of PERL): a language by geniuses! for geniuses. Lecture 7: Haskell. Haskell 98. Haskell (cont) - Type-safe!
 Lecture 7: Haskell CSC 131 Fall, 2014 Kim Bruce According to Larry Wall (designer of PERL): a language by geniuses for geniuses He s wrong at least about the latter part though you might agree when we
Lecture 7: Haskell CSC 131 Fall, 2014 Kim Bruce According to Larry Wall (designer of PERL): a language by geniuses for geniuses He s wrong at least about the latter part though you might agree when we
Chapter 13: Reference. Why reference Typing Evaluation Store Typings Safety Notes
 Chapter 13: Reference Why reference Typing Evaluation Store Typings Safety Notes References Computational Effects Also known as side effects. A function or expression is said to have a side effect if,
Chapter 13: Reference Why reference Typing Evaluation Store Typings Safety Notes References Computational Effects Also known as side effects. A function or expression is said to have a side effect if,
A Functional Space Model. COS 326 David Walker Princeton University
 A Functional Space Model COS 326 David Walker Princeton University Data type representations: Last Time type tree = Leaf Node of int * tree * tree Leaf: Node(i, left, right): 0 Node 3 left right This Time
A Functional Space Model COS 326 David Walker Princeton University Data type representations: Last Time type tree = Leaf Node of int * tree * tree Leaf: Node(i, left, right): 0 Node 3 left right This Time
COMPUTABILITY THEORY AND RECURSIVELY ENUMERABLE SETS
 COMPUTABILITY THEORY AND RECURSIVELY ENUMERABLE SETS JOSHUA LENERS Abstract. An algorithm is function from ω to ω defined by a finite set of instructions to transform a given input x to the desired output
COMPUTABILITY THEORY AND RECURSIVELY ENUMERABLE SETS JOSHUA LENERS Abstract. An algorithm is function from ω to ω defined by a finite set of instructions to transform a given input x to the desired output
CS4215 Programming Language Implementation. Martin Henz
 CS4215 Programming Language Implementation Martin Henz Thursday 26 January, 2012 2 Chapter 4 The Language simpl In this chapter, we are exting the language epl in order to provide a more powerful programming
CS4215 Programming Language Implementation Martin Henz Thursday 26 January, 2012 2 Chapter 4 The Language simpl In this chapter, we are exting the language epl in order to provide a more powerful programming
Adding GADTs to OCaml the direct approach
 Adding GADTs to OCaml the direct approach Jacques Garrigue & Jacques Le Normand Nagoya University / LexiFi (Paris) https://sites.google.com/site/ocamlgadt/ Garrigue & Le Normand Adding GADTs to OCaml 1
Adding GADTs to OCaml the direct approach Jacques Garrigue & Jacques Le Normand Nagoya University / LexiFi (Paris) https://sites.google.com/site/ocamlgadt/ Garrigue & Le Normand Adding GADTs to OCaml 1
CS 421, Fall Sample Final Questions & Solutions
 S 421, Fall 2012 Sample Final Questions & Solutions You should review the questions from the sample midterm exams, the practice midterm exams, and the assignments (MPs, MLs and Ws), as well as these question.
S 421, Fall 2012 Sample Final Questions & Solutions You should review the questions from the sample midterm exams, the practice midterm exams, and the assignments (MPs, MLs and Ws), as well as these question.
Dialects of ML. CMSC 330: Organization of Programming Languages. Dialects of ML (cont.) Features of ML. Functional Languages. Features of ML (cont.
 CMSC 330: Organization of Programming Languages OCaml 1 Functional Programming Dialects of ML ML (Meta Language) Univ. of Edinburgh,1973 Part of a theorem proving system LCF The Logic of Computable Functions
CMSC 330: Organization of Programming Languages OCaml 1 Functional Programming Dialects of ML ML (Meta Language) Univ. of Edinburgh,1973 Part of a theorem proving system LCF The Logic of Computable Functions
Functors signature Order = sig functor name type elem (structname:signature) = structure definition; val le : elem*elem -> bool end; elem
 Functors The general form of a functor is functor name (structname:signature) = structure definition; This functor will create a specific version of the structure definition using the structure parameter
Functors The general form of a functor is functor name (structname:signature) = structure definition; This functor will create a specific version of the structure definition using the structure parameter
CSE 3302 Programming Languages Lecture 8: Functional Programming
 CSE 3302 Programming Languages Lecture 8: Functional Programming (based on the slides by Tim Sheard) Leonidas Fegaras University of Texas at Arlington CSE 3302 L8 Spring 2011 1 Functional Programming Languages
CSE 3302 Programming Languages Lecture 8: Functional Programming (based on the slides by Tim Sheard) Leonidas Fegaras University of Texas at Arlington CSE 3302 L8 Spring 2011 1 Functional Programming Languages
Haskell Types, Classes, and Functions, Currying, and Polymorphism
 1 CSCE 314: Programming Languages Dr. Flemming Andersen Haskell Types, Classes, and Functions, Currying, and Polymorphism 2 Types A type is a collection of related values. For example, Bool contains the
1 CSCE 314: Programming Languages Dr. Flemming Andersen Haskell Types, Classes, and Functions, Currying, and Polymorphism 2 Types A type is a collection of related values. For example, Bool contains the
Writing code that I'm not smart enough to write. A funny thing happened at Lambda Jam
 Writing code that I'm not smart enough to write A funny thing happened at Lambda Jam Background "Let s make a lambda calculator" Rúnar Bjarnason Task: write an interpreter for the lambda calculus Lambda
Writing code that I'm not smart enough to write A funny thing happened at Lambda Jam Background "Let s make a lambda calculator" Rúnar Bjarnason Task: write an interpreter for the lambda calculus Lambda
Goal. CS152: Programming Languages. Lecture 15 Parametric Polymorphism. What the Library Likes. What The Client Likes. Start simpler.
 Goal Understand what this interface means and why it matters: CS152: Programming Languages Lecture 15 Parametric Polymorphism Dan Grossman Spring 2011 type a mylist; val mt_list : a mylist val cons : a
Goal Understand what this interface means and why it matters: CS152: Programming Languages Lecture 15 Parametric Polymorphism Dan Grossman Spring 2011 type a mylist; val mt_list : a mylist val cons : a
The Substitution Model. Nate Foster Spring 2018
 The Substitution Model Nate Foster Spring 2018 Review Previously in 3110: simple interpreter for expression language abstract syntax tree (AST) evaluation based on single steps parser and lexer (in lab)
The Substitution Model Nate Foster Spring 2018 Review Previously in 3110: simple interpreter for expression language abstract syntax tree (AST) evaluation based on single steps parser and lexer (in lab)
MATH 22 MORE ABOUT FUNCTIONS. Lecture M: 10/14/2003. Form follows function. Louis Henri Sullivan
 MATH 22 Lecture M: 10/14/2003 MORE ABOUT FUNCTIONS Form follows function. Louis Henri Sullivan This frightful word, function, was born under other skies than those I have loved. Le Corbusier D ora innanzi
MATH 22 Lecture M: 10/14/2003 MORE ABOUT FUNCTIONS Form follows function. Louis Henri Sullivan This frightful word, function, was born under other skies than those I have loved. Le Corbusier D ora innanzi
Simply-Typed Lambda Calculus
 #1 Simply-Typed Lambda Calculus #2 Back to School What is operational semantics? When would you use contextual (small-step) semantics? What is denotational semantics? What is axiomatic semantics? What
#1 Simply-Typed Lambda Calculus #2 Back to School What is operational semantics? When would you use contextual (small-step) semantics? What is denotational semantics? What is axiomatic semantics? What
Programming Languages
 CSE 130: Spring 2010 Programming Languages Lecture 2: A Crash Course in ML Ranjit Jhala UC San Diego News On webpage: Suggested HW #1 PA #1 (due next Wed 4/9) Please post questions to WebCT Today: A crash
CSE 130: Spring 2010 Programming Languages Lecture 2: A Crash Course in ML Ranjit Jhala UC San Diego News On webpage: Suggested HW #1 PA #1 (due next Wed 4/9) Please post questions to WebCT Today: A crash
Programming Languages
 CSE 230: Winter 2008 Principles of Programming Languages Ocaml/HW #3 Q-A Session Push deadline = Mar 10 Session Mon 3pm? Lecture 15: Type Systems Ranjit Jhala UC San Diego Why Typed Languages? Development
CSE 230: Winter 2008 Principles of Programming Languages Ocaml/HW #3 Q-A Session Push deadline = Mar 10 Session Mon 3pm? Lecture 15: Type Systems Ranjit Jhala UC San Diego Why Typed Languages? Development
Formal Methods of Software Design, Eric Hehner, segment 24 page 1 out of 5
 Formal Methods of Software Design, Eric Hehner, segment 24 page 1 out of 5 [talking head] This lecture we study theory design and implementation. Programmers have two roles to play here. In one role, they
Formal Methods of Software Design, Eric Hehner, segment 24 page 1 out of 5 [talking head] This lecture we study theory design and implementation. Programmers have two roles to play here. In one role, they
Haskell Overview III (3A) Young Won Lim 10/4/16
 (3A) Copyright (c) 2016 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published
(3A) Copyright (c) 2016 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published
Begin at the beginning
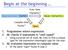 Begin at the beginning Expressions (Syntax) Exec-time Dynamic Values (Semantics) Compile-time Static Types 1. Programmer enters expression 2. ML checks if expression is well-typed Using a precise set of
Begin at the beginning Expressions (Syntax) Exec-time Dynamic Values (Semantics) Compile-time Static Types 1. Programmer enters expression 2. ML checks if expression is well-typed Using a precise set of
Lecture 2: SML Basics
 15-150 Lecture 2: SML Basics Lecture by Dan Licata January 19, 2012 I d like to start off by talking about someone named Alfred North Whitehead. With someone named Bertrand Russell, Whitehead wrote Principia
15-150 Lecture 2: SML Basics Lecture by Dan Licata January 19, 2012 I d like to start off by talking about someone named Alfred North Whitehead. With someone named Bertrand Russell, Whitehead wrote Principia
CIS 500 Software Foundations Midterm I
 CIS 500 Software Foundations Midterm I October 11, 2006 Name: Student ID: Email: Status: Section: registered for the course not registered: sitting in to improve a previous grade not registered: just taking
CIS 500 Software Foundations Midterm I October 11, 2006 Name: Student ID: Email: Status: Section: registered for the course not registered: sitting in to improve a previous grade not registered: just taking
15 212: Principles of Programming. Some Notes on Continuations
 15 212: Principles of Programming Some Notes on Continuations Michael Erdmann Spring 2011 These notes provide a brief introduction to continuations as a programming technique. Continuations have a rich
15 212: Principles of Programming Some Notes on Continuations Michael Erdmann Spring 2011 These notes provide a brief introduction to continuations as a programming technique. Continuations have a rich
15 212: Principles of Programming. Some Notes on Induction
 5 22: Principles of Programming Some Notes on Induction Michael Erdmann Spring 20 These notes provide a brief introduction to induction for proving properties of ML programs. We assume that the reader
5 22: Principles of Programming Some Notes on Induction Michael Erdmann Spring 20 These notes provide a brief introduction to induction for proving properties of ML programs. We assume that the reader
CS3110 Spring 2016 Lecture 6: Modules
 CS3110 Spring 2016 Lecture 6: Modules Modules are the O part of OCaml, influenced by objects in Java. We see the evolution: Classic ML, CambridgeML (CAML), and finally OCaml. David McQueen is writing the
CS3110 Spring 2016 Lecture 6: Modules Modules are the O part of OCaml, influenced by objects in Java. We see the evolution: Classic ML, CambridgeML (CAML), and finally OCaml. David McQueen is writing the
Lecture 3: Recursion; Structural Induction
 15-150 Lecture 3: Recursion; Structural Induction Lecture by Dan Licata January 24, 2012 Today, we are going to talk about one of the most important ideas in functional programming, structural recursion
15-150 Lecture 3: Recursion; Structural Induction Lecture by Dan Licata January 24, 2012 Today, we are going to talk about one of the most important ideas in functional programming, structural recursion
COS 320. Compiling Techniques
 Topic 5: Types COS 320 Compiling Techniques Princeton University Spring 2016 Lennart Beringer 1 Types: potential benefits (I) 2 For programmers: help to eliminate common programming mistakes, particularly
Topic 5: Types COS 320 Compiling Techniques Princeton University Spring 2016 Lennart Beringer 1 Types: potential benefits (I) 2 For programmers: help to eliminate common programming mistakes, particularly
A First Look at ML. Chapter Five Modern Programming Languages, 2nd ed. 1
 A First Look at ML Chapter Five Modern Programming Languages, 2nd ed. 1 ML Meta Language One of the more popular functional languages (which, admittedly, isn t saying much) Edinburgh, 1974, Robin Milner
A First Look at ML Chapter Five Modern Programming Languages, 2nd ed. 1 ML Meta Language One of the more popular functional languages (which, admittedly, isn t saying much) Edinburgh, 1974, Robin Milner
CS558 Programming Languages
 CS558 Programming Languages Winter 2017 Lecture 7b Andrew Tolmach Portland State University 1994-2017 Values and Types We divide the universe of values according to types A type is a set of values and
CS558 Programming Languages Winter 2017 Lecture 7b Andrew Tolmach Portland State University 1994-2017 Values and Types We divide the universe of values according to types A type is a set of values and
Agenda. CS301 Session 11. Common type constructors. Things we could add to Impcore. Discussion: midterm exam - take-home or inclass?
 Agenda CS301 Session 11 Discussion: midterm exam - take-home or inclass? Interlude: common type constructors Type soundness 1 2 Things we could add to Impcore Common type constructors Array is a type constructor,
Agenda CS301 Session 11 Discussion: midterm exam - take-home or inclass? Interlude: common type constructors Type soundness 1 2 Things we could add to Impcore Common type constructors Array is a type constructor,
Fall 2013 Midterm Exam 10/22/13. This is a closed-book, closed-notes exam. Problem Points Score. Various definitions are provided in the exam.
 Programming Languages Fall 2013 Midterm Exam 10/22/13 Time Limit: 100 Minutes Name (Print): Graduate Center I.D. This is a closed-book, closed-notes exam. Various definitions are provided in the exam.
Programming Languages Fall 2013 Midterm Exam 10/22/13 Time Limit: 100 Minutes Name (Print): Graduate Center I.D. This is a closed-book, closed-notes exam. Various definitions are provided in the exam.
Polymorphic Types in ACL2
 Polymorphic Types in ACL2 Benjamin Selfridge University of Texas at Austin Austin, TX benself@cs.utexas.edu Eric Smith Kestrel Institute Palo Alto, CA eric.smith@kestrel.edu This paper describes a tool
Polymorphic Types in ACL2 Benjamin Selfridge University of Texas at Austin Austin, TX benself@cs.utexas.edu Eric Smith Kestrel Institute Palo Alto, CA eric.smith@kestrel.edu This paper describes a tool
CSE 130, Fall 2005: Final Examination
 CSE 130, Fall 2005: Final Examination Name: ID: Instructions, etc. 1. Write your answers in the space provided. 2. Wherever it says explain, write no more than three lines as explanation. The rest will
CSE 130, Fall 2005: Final Examination Name: ID: Instructions, etc. 1. Write your answers in the space provided. 2. Wherever it says explain, write no more than three lines as explanation. The rest will
CSE 130, Fall 2006: Final Examination
 CSE 130, Fall 2006: Final Examination Name: ID: Instructions, etc. 1. Write your answers in the space provided. 2. Wherever it says explain, write no more than three lines as explanation. The rest will
CSE 130, Fall 2006: Final Examination Name: ID: Instructions, etc. 1. Write your answers in the space provided. 2. Wherever it says explain, write no more than three lines as explanation. The rest will
Introduction to ML. Mooly Sagiv. Cornell CS 3110 Data Structures and Functional Programming
 Introduction to ML Mooly Sagiv Cornell CS 3110 Data Structures and Functional Programming The ML Programming Language General purpose programming language designed by Robin Milner in 1970 Meta Language
Introduction to ML Mooly Sagiv Cornell CS 3110 Data Structures and Functional Programming The ML Programming Language General purpose programming language designed by Robin Milner in 1970 Meta Language
CSE341: Programming Languages Lecture 11 Type Inference. Dan Grossman Spring 2016
 CSE341: Programming Languages Lecture 11 Type Inference Dan Grossman Spring 2016 Type-checking (Static) type-checking can reject a program before it runs to prevent the possibility of some errors A feature
CSE341: Programming Languages Lecture 11 Type Inference Dan Grossman Spring 2016 Type-checking (Static) type-checking can reject a program before it runs to prevent the possibility of some errors A feature
Introduction to ML. Mooly Sagiv. Cornell CS 3110 Data Structures and Functional Programming
 Introduction to ML Mooly Sagiv Cornell CS 3110 Data Structures and Functional Programming The ML Programming Language General purpose programming language designed by Robin Milner in 1970 Meta Language
Introduction to ML Mooly Sagiv Cornell CS 3110 Data Structures and Functional Programming The ML Programming Language General purpose programming language designed by Robin Milner in 1970 Meta Language
