Programming Languages. Next: Building datatypes. Suppose I wanted. Next: Building datatypes 10/4/2017. Review so far. Datatypes.
|
|
|
- Jeffrey West
- 6 years ago
- Views:
Transcription
1 Review so far Programming Languages Expressions Values Datatypes Types Many kinds of expressions: 1. Simple 2. Variables 3. Functions Review so far We ve seen some base types and values: Integers, Floats, Bool, String etc. Some ways to build up types: Products (tuples), records, lists Functions Design Principle: Orthogonality Don t clutter core language with stuff Few, powerful orthogonal building techniques Put derived types, values, functions in libraries Next: Building datatypes Three key ways to build complex types/values 1. Each-of types Value of T contains value of T1 and a value of T2 2. One-of types Value of T contains value of T1 or a value of T2 3. Recursive Value of T contains (sub)-value of same type T Next: Building datatypes Three key ways to build complex types/values 1. Each-of types (T1 * T2) Value of T contains value of T1 and a value of T2 Suppose I wanted a program that processed lists of attributes Name (string) Age (integer) 2. One-of types Value of T contains value of T1 or a value of T2 3. Recursive Value of T contains (sub)-value of same type T 1
2 Suppose I wanted a program that processed lists of attributes Name (string) Age (integer) DOB (int-int-int) Address (string) Height (float) Alive (boolean) Phone (int-int) (string) Many kinds of attributes (too many to put in a record) can have multiple names, addresses, phones, s etc. Want to store them in a list. Can I? Constructing Datatypes type t = C1 of t1 C2 of t2 Cn of tn t is a new datatype. A value of type t is either: a value of type t1 placed in a box labeled C1 Or a value of type t2 placed in a box labeled C2 Or Or a value of type tn placed in a box labeled Cn Constructing Datatypes type t = C1 of t1 C2 of t2 Cn of tn t Label=C1 Label=C2 Label=Cn Value:t1 OR Value:t2 OR Value:tn All have the type t Suppose I wanted Attributes: Name (string) Age (integer) DOB (int-int-int) Address (string) Height (real) Alive (boolean) Phone (int-int) (string) type attrib = Name of string Age of int DOB of int*int*int Address of string Height of float Alive of bool Phone of int*int of string;; How to PUT values into box? How to PUT values into box? How to create values of type attrib? # let a1 = Name Bob ;; val x : attrib = Name Bob # let a2 = Height 5.83;; val a2 : attrib = Height 5.83 # let year = 1977 ;; val year : int = 1977 # let a3 = DOB (9,8,year) ;; val a3 : attrib = DOB (9,8,1977) # let a_l = [a1;a2;a3];; val a3 : attrib list = type attrib = Name of string Age of int DOB of int*int*int Address of string Height of float Alive of bool Phone of int*int of string;; 2
3 Constructing Datatypes One-of types type attrib = Name of string Age of int DOB of int*int*int Address of string Height of float Alive of bool Phone of int*int of string;; Name Bob OR Age 34 OR DOB (9,8,77) Name Bob Age 34 DOB (9,8,77) All have type attrib We ve defined a one-of type named attrib Elements are one of: string, int, int*int*int, float, bool Can create uniform attrib lists Say I want a function to print attribs datatype attrib = Name of string Age of int DOB of int*int*int Address of string Height of real Alive of bool Phone of int*int of string; How to TEST & TAKE whats in box? Is it a... string? or an int? or an int*int*int? or... How to TEST & TAKE whats in box? Look at TAG! How to tell whats in the box? match e with Name s -> printf "%s" s Age i -> printf "%d" i DOB(d,m,y) -> printf "%d/%d/%d" d m y Address s -> printf "%s" s Height h -> printf "%f" h Alive b -> printf "%b" b s Phone(a,r) -> printf "(%d)-%d" a r Pattern-match expression: check if e is of the form On match: value in box bound to pattern variable matching result expression is evaluated Simultaneously test and extract contents of box How to tell whats in the box? type attrib = Name of string Age of int DOB of int*int*int Address of string Height of float Alive of bool Phone of int*int match e with Name s ->...(*s: string *) Age i ->...(*i: int *) DOB(d,m,y)->...(*d: int,m: int,y: int*) Address a ->...(*a: string*) Height h ->...(*h: int *) Alive b ->...(*b: bool*) Phone(a,r)->...(*a: int, r: int*) Pattern-match expression: check if e is of the form On match: value in box bound to pattern variable matching result expression is evaluated Simultaneously test and extract contents of box 3
4 How to tell whats in the box How to TEST & TAKE whats in box? # match (Name Bob ) with Name s -> printf "Hello %s\n" s Age i -> printf "%d years old" i ;; Hello Bob - : unit = () None of the cases matched the tag (Name) Causes nasty Run-Time Error BEWARE!! Be sure to handle all TAGS! Beware! Handle All TAGS! Compiler to the Rescue! # match (Name Bob ) with Age i -> Printf.printf "%d" I s -> Printf.printf "%s" s ;; Exception: Match Failure!! # match (Name Bob ) with Age i -> Printf.printf "%d" I s -> Printf.printf "%s" s ;; Exception: Match Failure!! None of the cases matched the tag (Name) Causes nasty Run-Time Error None of the cases matched the tag (Name) Causes nasty Run-Time Error Compiler To The Rescue!! # let printattrib a = match a with Name s -> Printf.printf "%s" s Age i -> Printf.printf "%d" I DOB (d,m,y) -> Printf.printf "%d / %d / %d" d m y Address addr -> Printf.printf "%s" addr Height h -> Printf.printf "%f" h Alive b -> Printf.printf "%b" b e -> Printf.printf "%s" e ;; Warning P: this pattern-matching is not exhaustive.here is an example of a value that is not matched:phone (_, _) Compile-time checks for: missed cases: ML warns if you miss a case! Compiler To The Rescue!! # let printattrib a = match a with Name s -> Printf.printf "%s" s Age i -> Printf.printf "%d" I DOB (d,m,y) -> Printf.printf "%d / %d / %d" d m y... Age i -> Printf.printf "%d" i ;; Warning U: this match case is unused. Compile-time checks for: redundant cases: ML warns if a case never matches 4
5 Another Few Examples match-with is an Expression # let printattrib a = match a with Name s -> Printf.printf "%s" s Age i -> Printf.printf "%d" I DOB (d,m,y) -> Printf.printf "%d / %d / %d" d m y... Age i -> Printf.printf "%d" i ;; Warning U: this match case is unused. match e with C1 x1 -> e1 C2 x2 -> e2 Cn xn -> en See code text file Type Rule e1, e2,,en must have same type T Type of whole expression is T match-with is an Expression { T T match e with Name s -> e1 Age i -> e2 DOB (m,d,y) -> e3 Address a -> e4 Height h -> e5 Alive b -> e6 Phone (a,n) -> e7 e -> e8 Type Rule e1, e2,,en must have same type T Type of whole expression is T Benefits of match-with match e with C1 x1 -> e1 C2 x2 -> e2 Cn xn -> en type t = C1 of t1 C2 of t2 Cn of tn 1. Simultaneous test-extract-bind 2. Compile-time checks for: missed cases: ML warns if you miss a t value redundant cases: ML warns if a case never matches Next: Building datatypes Three key ways to build complex types/values 1. Each-of types t1 * t2 Value of T contains value of T1 and a value of T2 Zero of nat 2. One-of types type t = C1 of t1 C2 of t2 Value of T contains value of T1 or a value of T2 3. Recursive type Value of T contains (sub)-value of same type T 5
6 Zero of nat Zero of nat Wait a minute! Zero of what?! Wait a minute! Zero of what?! Relax. Means empty box with label Zero Zero of nat Zero of nat What are values of nat? What are values of nat? Zero Zero of nat Zero of nat What are values of nat? One nat contains another! What are values of nat? One nat contains another! Zero Zero 6
7 Zero of nat Zero of nat What are values of nat? One nat contains another! What are values of nat? One nat contains another! nat = recursive type Zero Zero Next: Building datatypes Three key ways to build complex types/values 1. Each-of types t1 * t2 Value of T contains value of T1 and a value of T2 2. One-of types type t = C1 of t1 C2 of t2 Value of T contains value of T1 or a value of T2 Next: Lets get cosy with Recursion Recursive Code Mirrors Recursive Data 3. Recursive type type t =... C of (...*t) Value of T contains (sub)-value of same type T to_int : nat -> int Next: Lets get cosy with Recursion Code Structure = Type Structure!!! Zero of nat let rec to_int n = 7
8 to_int : nat -> int to_int : nat -> int let rec to_int n = let rec to_int n = match n with -> 0 Base Expression Inductive pattern m -> 1 + to_int m Inductive Expression of_int : int -> nat Zero of nat of_int : int -> nat let rec of_int n = let rec of_int n = of_int : int -> nat of_int : int -> nat Base pattern Inductive pattern let rec of_int n = if n <= 0 then else let rec of_int n = Base pattern if n <= 0 then Zero Base Expression Inductive pattern else (of_int (n-1)) Inductive Expression 8
9 plus : nat*nat -> nat Zero of nat plus : nat*nat -> nat let rec plus n m = let rec plus n m = plus : nat*nat -> nat plus : nat*nat -> nat let rec plus n m = match m with -> Inductive pattern m -> let rec plus n m = match m with -> n Base Expression Inductive pattern m -> (plus n m ) Inductive Expression times: nat*nat -> nat Zero of nat times: nat*nat -> nat let rec times n m = let rec times n m = 9
10 times: nat*nat -> nat times: nat*nat -> nat let rec times n m = match m with -> Inductive pattern m -> let rec times n m = match m with -> Zero Base Expression Inductive pattern m -> plus n (times n m ) Inductive Expression Lists are recursive types! Next: Lets get cosy with Recursion Recursive Code Mirrors Recursive Data type int_list = Nil Cons of int * int_list Think about this! What are values of int_list? Cons(1,Cons(2,Cons(3,Nil))) Cons(2,Cons(3,Nil)) Cons(3,Nil) Nil Cons 1, Cons 2, Cons 3, Nil Lists aren t built-in! Lists are a derived type: built using elegant core! 1. Each-of 2. One-of 3. Recursive datatype int_list = Nil Cons of int * int_list :: is just a pretty way to say Cons [] is just a pretty way to say Nil Some functions on Lists : Length Base pattern let rec len l = match l with Nil -> 0 Base Expression Inductive pattern Cons(h,t) -> 1 + (len t) let rec len l = match l with Nil -> 0 Cons(_,t) -> 1 + (len t) No binding for head Inductive Expression let rec len l = match l with Cons(_,t) -> 1 + (len t) _ -> 0 Pattern-matching in order 10
11 Some functions on Lists : Append let rec append (l1,l2) = Some functions on Lists : Max let rec max xs = Find the right induction strategy Base case: pattern + expression Induction case: pattern + expression Find the right induction strategy Base case: pattern + expression Induction case: pattern + expression Well designed datatype gives strategy Well designed datatype gives strategy null, hd, tl are all functions Bad ML style: More than aesthetics! Pattern-matching better than test-extract: ML checks all cases covered ML checks no redundant cases at compile-time: fewer errors (crashes) during execution get the bugs out ASAP! Next: Lets get cosy with Recursion Recursive Code Mirrors Recursive Data Representing Trees Representing Trees Node(Node( 1, 2), 3) Node(Node( 1, 2), 3) 11
12 Representing Trees Representing Trees Node Node(Node( 1, 2), 3) Node(Node( 1, 2), 3) Representing Trees Node Node 2 3 Next: Lets get cosy with Recursion Recursive Code Mirrors Recursive Data Node(Node( 1, 2), 3) sum_leaf: tree -> int sum_leaf: tree -> int Sum up the leaf values. E.g. # let t0 = Node(Node( 1, 2), 3);; - : int = 6 let rec sum_leaf t = 12
13 sum_leaf: tree -> int sum_leaf: tree -> int Base pattern Inductive pattern Base pattern Inductive pattern let rec sum_leaf t = let rec sum_leaf t = match t with Base pattern n -> Inductive pattern Node(t1,t2)-> sum_leaf: tree -> int Base pattern Inductive pattern let rec sum_leaf t = match t with Base pattern n -> n Base Expression Inductive pattern Node(t1,t2)-> sum_leaf t1 + sum_leaf t2 Inductive Expression Recursive Code Mirrors Recursive Data Code almost writes itself! Another Example: Calculator Want an arithmetic calculator to evaluate expressions like: ( ) * ( ) Another Example: Calculator Want an arithmetic calculator to evaluate expressions like: ====> ====> ( ) * ( ) ====> Whats a ML TYPE for REPRESENTING expressions? 13
14 Another Example: Calculator Want an arithmetic calculator to evaluate expressions like: ====> ====> ( ) * ( ) ====> Whats a ML TYPE for REPRESENTING expressions? Another Example: Calculator Want an arithmetic calculator to evaluate expressions like: ====> ====> ( ) * ( ) ====> Whats a ML FUNCTION for EVALUATING expressions? type expr = Num of float Add of expr*expr Sub of expr*expr Mul of expr*expr type expr = Num of float Add of expr*expr Sub of expr*expr Mul of expr*expr Another Example: Calculator Want an arithmetic calculator to evaluate expressions like: ====> ====> ( ) * ( ) ====> Whats a ML FUNCTION for EVALUATING expressions? Another Example: Calculator Want an arithmetic calculator to evaluate expressions like: ====> ====> ( ) * ( ) ====> Whats a ML FUNCTION for EVALUATING expressions? type expr = Num of float Add of expr*expr Sub of expr*expr Mul of expr*expr let rec eval e = match e with Num f -> Add(e1,e2)-> Sub(e1,e2)-> Mul(e1,e2)-> type expr = Num of float Add of expr*expr Sub of expr*expr Mul of expr*expr let rec eval e = match e with Num f -> f Add(e1,e2)-> eval e1 +. eval e2 Sub(e1,e2)-> eval e1 -. eval e2 Mul(e1,e2)-> eval e1 *. eval e2 Random Art from Expressions PA #2 Build more funky expressions, evaluate them, to produce: 14
Programming Languages. Datatypes
 Programming Languages Datatypes Review so far Expressions Values Types Many kinds of expressions: 1. Simple 2. Variables 3. Functions Review so far We ve seen some base types and values: Integers, Floats,
Programming Languages Datatypes Review so far Expressions Values Types Many kinds of expressions: 1. Simple 2. Variables 3. Functions Review so far We ve seen some base types and values: Integers, Floats,
Programming Languages
 What about more complex data? CSE 130 : Fall 2012 Programming Languages Expressions Values Lecture 3: Datatypes Ranjit Jhala UC San Diego Types Many kinds of expressions: 1. Simple 2. Variables 3. Functions
What about more complex data? CSE 130 : Fall 2012 Programming Languages Expressions Values Lecture 3: Datatypes Ranjit Jhala UC San Diego Types Many kinds of expressions: 1. Simple 2. Variables 3. Functions
Recap: ML s Holy Trinity
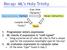 Recap: ML s Holy Trinity Expressions (Syntax) Exec-time Dynamic Values (Semantics) Compile-time Static Types 1. Programmer enters expression 2. ML checks if expression is well-typed Using a precise set
Recap: ML s Holy Trinity Expressions (Syntax) Exec-time Dynamic Values (Semantics) Compile-time Static Types 1. Programmer enters expression 2. ML checks if expression is well-typed Using a precise set
Programming Languages
 CSE 130 : Winter 2013 Programming Languages Lecture 3: Crash Course, Datatypes Ranjit Jhala UC San Diego 1 Story So Far... Simple Expressions Branches Let-Bindings... Today: Finish Crash Course Datatypes
CSE 130 : Winter 2013 Programming Languages Lecture 3: Crash Course, Datatypes Ranjit Jhala UC San Diego 1 Story So Far... Simple Expressions Branches Let-Bindings... Today: Finish Crash Course Datatypes
Recap: ML s Holy Trinity. Story So Far... CSE 130 Programming Languages. Datatypes. A function is a value! Next: functions, but remember.
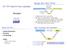 CSE 130 Programming Languages Recap: ML s Holy Trinity Expressions (Syntax) Exec-time Dynamic Values (Semantics) Datatypes Compile-time Static Types Ranjit Jhala UC San Diego 1. Programmer enters expression
CSE 130 Programming Languages Recap: ML s Holy Trinity Expressions (Syntax) Exec-time Dynamic Values (Semantics) Datatypes Compile-time Static Types Ranjit Jhala UC San Diego 1. Programmer enters expression
CSE 130 Programming Languages. Datatypes. Ranjit Jhala UC San Diego
 CSE 130 Programming Languages Datatypes Ranjit Jhala UC San Diego Recap: ML s Holy Trinity Expressions (Syntax) Exec-time Dynamic Values (Semantics) Compile-time Static Types 1. Programmer enters expression
CSE 130 Programming Languages Datatypes Ranjit Jhala UC San Diego Recap: ML s Holy Trinity Expressions (Syntax) Exec-time Dynamic Values (Semantics) Compile-time Static Types 1. Programmer enters expression
CSE 130 Programming Languages. Lecture 3: Datatypes. Ranjit Jhala UC San Diego
 CSE 130 Programming Languages Lecture 3: Datatypes Ranjit Jhala UC San Diego News? PA #2 (coming tonight) Ocaml-top issues? Pleas post questions to Piazza Recap: ML s Holy Trinity Expressions (Syntax)
CSE 130 Programming Languages Lecture 3: Datatypes Ranjit Jhala UC San Diego News? PA #2 (coming tonight) Ocaml-top issues? Pleas post questions to Piazza Recap: ML s Holy Trinity Expressions (Syntax)
News. Programming Languages. Recap. Recap: Environments. Functions. of functions: Closures. CSE 130 : Fall Lecture 5: Functions and Datatypes
 CSE 130 : Fall 2007 Programming Languages News PA deadlines shifted PA #2 now due 10/24 (next Wed) Lecture 5: Functions and Datatypes Ranjit Jhala UC San Diego Recap: Environments Phone book Variables
CSE 130 : Fall 2007 Programming Languages News PA deadlines shifted PA #2 now due 10/24 (next Wed) Lecture 5: Functions and Datatypes Ranjit Jhala UC San Diego Recap: Environments Phone book Variables
Recap from last time. Programming Languages. CSE 130 : Fall Lecture 3: Data Types. Put it together: a filter function
 CSE 130 : Fall 2011 Recap from last time Programming Languages Lecture 3: Data Types Ranjit Jhala UC San Diego 1 2 A shorthand for function binding Put it together: a filter function # let neg = fun f
CSE 130 : Fall 2011 Recap from last time Programming Languages Lecture 3: Data Types Ranjit Jhala UC San Diego 1 2 A shorthand for function binding Put it together: a filter function # let neg = fun f
Programming Languages
 CSE 130 : Winter 2009 Programming Languages News PA 2 out, and due Mon 1/26 5pm Lecture 5: Functions and Datatypes t UC San Diego Recap: Environments Phone book Variables = names Values = phone number
CSE 130 : Winter 2009 Programming Languages News PA 2 out, and due Mon 1/26 5pm Lecture 5: Functions and Datatypes t UC San Diego Recap: Environments Phone book Variables = names Values = phone number
Programming Languages
 CSE 130 : Fall 2008 Programming Languages Lecture 6: Datatypes t and Recursion Ranjit Jhala UC San Diego News PA 2 Due Fri (and PA3 up) PA3 is a bit difficult, but do it yourself, or repent in the final
CSE 130 : Fall 2008 Programming Languages Lecture 6: Datatypes t and Recursion Ranjit Jhala UC San Diego News PA 2 Due Fri (and PA3 up) PA3 is a bit difficult, but do it yourself, or repent in the final
CSE 130 [Winter 2014] Programming Languages
![CSE 130 [Winter 2014] Programming Languages CSE 130 [Winter 2014] Programming Languages](/thumbs/85/92581372.jpg) CSE 130 [Winter 2014] Programming Languages Introduction to OCaml (Continued) Ravi Chugh! Jan 14 Announcements HW #1 due Mon Jan 20 Post questions/discussion to Piazza Check Piazza for TA/Tutor lab hours
CSE 130 [Winter 2014] Programming Languages Introduction to OCaml (Continued) Ravi Chugh! Jan 14 Announcements HW #1 due Mon Jan 20 Post questions/discussion to Piazza Check Piazza for TA/Tutor lab hours
Recap. Recap. If-then-else expressions. If-then-else expressions. If-then-else expressions. If-then-else expressions
 Recap Epressions (Synta) Compile-time Static Eec-time Dynamic Types (Semantics) Recap Integers: +,-,* floats: +,-,* Booleans: =,
Recap Epressions (Synta) Compile-time Static Eec-time Dynamic Types (Semantics) Recap Integers: +,-,* floats: +,-,* Booleans: =,
sum: tree -> int sum_leaf: tree -> int sum_leaf: tree -> int Representing Trees Next: Lets get cosy with Recursion Sum up the leaf values. E.g.
 Representing Trees Node Next: Lets get cosy with Recursion 1 2 3 1 Node 2 3 Node(Node( 1, 2), 3) sum: tree -> int Next: Lets get cosy with Recursion Sum up the leaf values. E.g. # let t0 = sum Node(Node(
Representing Trees Node Next: Lets get cosy with Recursion 1 2 3 1 Node 2 3 Node(Node( 1, 2), 3) sum: tree -> int Next: Lets get cosy with Recursion Sum up the leaf values. E.g. # let t0 = sum Node(Node(
CMSC 330: Organization of Programming Languages. Functional Programming with Lists
 CMSC 330: Organization of Programming Languages Functional Programming with Lists 1 Lists in OCaml The basic data structure in OCaml Lists can be of arbitrary length Implemented as a linked data structure
CMSC 330: Organization of Programming Languages Functional Programming with Lists 1 Lists in OCaml The basic data structure in OCaml Lists can be of arbitrary length Implemented as a linked data structure
CMSC 330: Organization of Programming Languages. Functional Programming with Lists
 CMSC 330: Organization of Programming Languages Functional Programming with Lists CMSC330 Spring 2018 1 Lists in OCaml The basic data structure in OCaml Lists can be of arbitrary length Implemented as
CMSC 330: Organization of Programming Languages Functional Programming with Lists CMSC330 Spring 2018 1 Lists in OCaml The basic data structure in OCaml Lists can be of arbitrary length Implemented as
Begin at the beginning
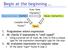 Begin at the beginning Expressions (Syntax) Exec-time Dynamic Values (Semantics) Compile-time Static Types 1. Programmer enters expression 2. ML checks if expression is well-typed Using a precise set of
Begin at the beginning Expressions (Syntax) Exec-time Dynamic Values (Semantics) Compile-time Static Types 1. Programmer enters expression 2. ML checks if expression is well-typed Using a precise set of
CS Lecture 5: Pattern Matching. Prof. Clarkson Fall Today s music: Puff, the Magic Dragon by Peter, Paul & Mary
 CS 3110 Lecture 5: Pattern Matching Prof. Clarkson Fall 2014 Today s music: Puff, the Magic Dragon by Peter, Paul & Mary Review Features so far: variables, operators, let expressions, if expressions, functions
CS 3110 Lecture 5: Pattern Matching Prof. Clarkson Fall 2014 Today s music: Puff, the Magic Dragon by Peter, Paul & Mary Review Features so far: variables, operators, let expressions, if expressions, functions
Mini-ML. CS 502 Lecture 2 8/28/08
 Mini-ML CS 502 Lecture 2 8/28/08 ML This course focuses on compilation techniques for functional languages Programs expressed in Standard ML Mini-ML (the source language) is an expressive core subset of
Mini-ML CS 502 Lecture 2 8/28/08 ML This course focuses on compilation techniques for functional languages Programs expressed in Standard ML Mini-ML (the source language) is an expressive core subset of
CSE341: Programming Languages Lecture 2 Functions, Pairs, Lists. Zach Tatlock Winter 2018
 CSE341: Programming Languages Lecture 2 Functions, Pairs, Lists Zach Tatlock Winter 2018 Function definitions Functions: the most important building block in the whole course Like Java methods, have arguments
CSE341: Programming Languages Lecture 2 Functions, Pairs, Lists Zach Tatlock Winter 2018 Function definitions Functions: the most important building block in the whole course Like Java methods, have arguments
Function definitions. CSE341: Programming Languages Lecture 2 Functions, Pairs, Lists. Example, extended. Some gotchas. Zach Tatlock Winter 2018
 Function definitions CSE341: Programming Languages Lecture 2 Functions, Pairs, Lists Zach Tatlock Winter 2018 Functions: the most important building block in the whole course Like Java methods, have arguments
Function definitions CSE341: Programming Languages Lecture 2 Functions, Pairs, Lists Zach Tatlock Winter 2018 Functions: the most important building block in the whole course Like Java methods, have arguments
Programming Languages
 CSE 130 : Spring 2011 Programming Languages Lecture 3: Crash Course Ctd, Expressions and Types Ranjit Jhala UC San Diego A shorthand for function binding # let neg = fun f -> fun x -> not (f x); # let
CSE 130 : Spring 2011 Programming Languages Lecture 3: Crash Course Ctd, Expressions and Types Ranjit Jhala UC San Diego A shorthand for function binding # let neg = fun f -> fun x -> not (f x); # let
OCaml. ML Flow. Complex types: Lists. Complex types: Lists. The PL for the discerning hacker. All elements must have same type.
 OCaml The PL for the discerning hacker. ML Flow Expressions (Syntax) Compile-time Static 1. Enter expression 2. ML infers a type Exec-time Dynamic Types 3. ML crunches expression down to a value 4. Value
OCaml The PL for the discerning hacker. ML Flow Expressions (Syntax) Compile-time Static 1. Enter expression 2. ML infers a type Exec-time Dynamic Types 3. ML crunches expression down to a value 4. Value
News. Programming Languages. Complex types: Lists. Recap: ML s Holy Trinity. CSE 130: Spring 2012
 News CSE 130: Spring 2012 Programming Languages On webpage: Suggested HW #1 PA #1 (due next Fri 4/13) Lecture 2: A Crash Course in ML Please post questions to Piazza Ranjit Jhala UC San Diego Today: A
News CSE 130: Spring 2012 Programming Languages On webpage: Suggested HW #1 PA #1 (due next Fri 4/13) Lecture 2: A Crash Course in ML Please post questions to Piazza Ranjit Jhala UC San Diego Today: A
Programming Languages
 CSE 130 : Fall 2008 Programming Languages Lecture 2: A Crash Course in ML Ranjit Jhala UC San Diego News On webpage: Suggested HW #1, sample for Quiz #1 on Thu PA #1 (due next Fri 10/10) No make-up quizzes
CSE 130 : Fall 2008 Programming Languages Lecture 2: A Crash Course in ML Ranjit Jhala UC San Diego News On webpage: Suggested HW #1, sample for Quiz #1 on Thu PA #1 (due next Fri 10/10) No make-up quizzes
Side note: Tail Recursion. Begin at the beginning. Side note: Tail Recursion. Base Types. Base Type: int. Base Type: int
 Begin at the beginning Epressions (Synta) Compile-time Static Eec-time Dynamic Types Values (Semantics) 1. Programmer enters epression 2. ML checks if epression is well-typed Using a precise set of rules,
Begin at the beginning Epressions (Synta) Compile-time Static Eec-time Dynamic Types Values (Semantics) 1. Programmer enters epression 2. ML checks if epression is well-typed Using a precise set of rules,
Tail Recursion: Factorial. Begin at the beginning. How does it execute? Tail recursion. Tail recursive factorial. Tail recursive factorial
 Begin at the beginning Epressions (Synta) Compile-time Static Eec-time Dynamic Types Values (Semantics) 1. Programmer enters epression 2. ML checks if epression is well-typed Using a precise set of rules,
Begin at the beginning Epressions (Synta) Compile-time Static Eec-time Dynamic Types Values (Semantics) 1. Programmer enters epression 2. ML checks if epression is well-typed Using a precise set of rules,
Programming Languages
 CSE 130: Spring 2010 Programming Languages Lecture 2: A Crash Course in ML Ranjit Jhala UC San Diego News On webpage: Suggested HW #1 PA #1 (due next Wed 4/9) Please post questions to WebCT Today: A crash
CSE 130: Spring 2010 Programming Languages Lecture 2: A Crash Course in ML Ranjit Jhala UC San Diego News On webpage: Suggested HW #1 PA #1 (due next Wed 4/9) Please post questions to WebCT Today: A crash
Inductive Data Types
 Inductive Data Types Lars-Henrik Eriksson Functional Programming 1 Original slides by Tjark Weber Lars-Henrik Eriksson (UU) Inductive Data Types 1 / 42 Inductive Data Types Today Today New names for old
Inductive Data Types Lars-Henrik Eriksson Functional Programming 1 Original slides by Tjark Weber Lars-Henrik Eriksson (UU) Inductive Data Types 1 / 42 Inductive Data Types Today Today New names for old
CSE341: Programming Languages Lecture 2 Functions, Pairs, Lists. Dan Grossman Fall 2011
 CSE341: Programming Languages Lecture 2 Functions, Pairs, Lists Dan Grossman Fall 2011 Review Building up SML one construct at a time via precise definitions Constructs have syntax, type-checking rules,
CSE341: Programming Languages Lecture 2 Functions, Pairs, Lists Dan Grossman Fall 2011 Review Building up SML one construct at a time via precise definitions Constructs have syntax, type-checking rules,
Programming Languages
 CSE 130: Fall 2009 Programming Languages Lecture 2: A Crash Course in ML News On webpage: Suggested HW #1 PA #1 (due next Fri 10/9) Technical issues installing Ocaml - should be resolved soon! Ranjit Jhala
CSE 130: Fall 2009 Programming Languages Lecture 2: A Crash Course in ML News On webpage: Suggested HW #1 PA #1 (due next Fri 10/9) Technical issues installing Ocaml - should be resolved soon! Ranjit Jhala
Homework 3 COSE212, Fall 2018
 Homework 3 COSE212, Fall 2018 Hakjoo Oh Due: 10/28, 24:00 Problem 1 (100pts) Let us design and implement a programming language called ML. ML is a small yet Turing-complete functional language that supports
Homework 3 COSE212, Fall 2018 Hakjoo Oh Due: 10/28, 24:00 Problem 1 (100pts) Let us design and implement a programming language called ML. ML is a small yet Turing-complete functional language that supports
CSE 130: Programming Languages. Polymorphism. Ranjit Jhala UC San Diego
 CSE 130: Programming Languages Polymorphism Ranjit Jhala UC San Diego Q: What is the value of res? let f g = let x = 0 in g 2 let x = 100 let h y = x + y let res = f h (a) 0 (b) 2 (c) 100 (d) 102 (e) 12
CSE 130: Programming Languages Polymorphism Ranjit Jhala UC San Diego Q: What is the value of res? let f g = let x = 0 in g 2 let x = 100 let h y = x + y let res = f h (a) 0 (b) 2 (c) 100 (d) 102 (e) 12
Typed Racket: Racket with Static Types
 Typed Racket: Racket with Static Types Version 5.0.2 Sam Tobin-Hochstadt November 6, 2010 Typed Racket is a family of languages, each of which enforce that programs written in the language obey a type
Typed Racket: Racket with Static Types Version 5.0.2 Sam Tobin-Hochstadt November 6, 2010 Typed Racket is a family of languages, each of which enforce that programs written in the language obey a type
Programming Languages
 CSE 130 : Fall 2008 Programming Languages Lecture 3: Epressions and Types Ranjit Jhala UC San Diego News PA 1 due (net) Fri 10/10 5pm PA 2 out today or tomorrow Office hours posted on Webpage: Held in
CSE 130 : Fall 2008 Programming Languages Lecture 3: Epressions and Types Ranjit Jhala UC San Diego News PA 1 due (net) Fri 10/10 5pm PA 2 out today or tomorrow Office hours posted on Webpage: Held in
CMSC 330: Organization of Programming Languages
 CMSC 330: Organization of Programming Languages CMSC330 Fall 2017 OCaml Data Types CMSC330 Fall 2017 1 OCaml Data So far, we ve seen the following kinds of data Basic types (int, float, char, string) Lists
CMSC 330: Organization of Programming Languages CMSC330 Fall 2017 OCaml Data Types CMSC330 Fall 2017 1 OCaml Data So far, we ve seen the following kinds of data Basic types (int, float, char, string) Lists
Informatics 1 Functional Programming Lecture 9. Algebraic Data Types. Don Sannella University of Edinburgh
 Informatics 1 Functional Programming Lecture 9 Algebraic Data Types Don Sannella University of Edinburgh Part I Algebraic types Everything is an algebraic type data Bool = False True data Season = Winter
Informatics 1 Functional Programming Lecture 9 Algebraic Data Types Don Sannella University of Edinburgh Part I Algebraic types Everything is an algebraic type data Bool = False True data Season = Winter
CSE 341, Autumn 2005, Assignment 3 ML - MiniML Interpreter
 Due: Thurs October 27, 10:00pm CSE 341, Autumn 2005, Assignment 3 ML - MiniML Interpreter Note: This is a much longer assignment than anything we ve seen up until now. You are given two weeks to complete
Due: Thurs October 27, 10:00pm CSE 341, Autumn 2005, Assignment 3 ML - MiniML Interpreter Note: This is a much longer assignment than anything we ve seen up until now. You are given two weeks to complete
Type Checking and Type Inference
 Type Checking and Type Inference Principles of Programming Languages CSE 307 1 Types in Programming Languages 2 Static Type Checking 3 Polymorphic Type Inference Version: 1.8 17:20:56 2014/08/25 Compiled
Type Checking and Type Inference Principles of Programming Languages CSE 307 1 Types in Programming Languages 2 Static Type Checking 3 Polymorphic Type Inference Version: 1.8 17:20:56 2014/08/25 Compiled
Ornaments in ML. Thomas Williams, Didier Rémy. April 18, Inria - Gallium
 Ornaments in ML Thomas Williams, Didier Rémy Inria - Gallium April 18, 2017 1 Motivation Two very similar functions let rec add m n = match m with Z n S m S (add m n) let rec append ml nl = match ml with
Ornaments in ML Thomas Williams, Didier Rémy Inria - Gallium April 18, 2017 1 Motivation Two very similar functions let rec add m n = match m with Z n S m S (add m n) let rec append ml nl = match ml with
Lists. Prof. Clarkson Fall Today s music: "Blank Space" by Taylor Swift
 Lists Prof. Clarkson Fall 2017 Today s music: "Blank Space" by Taylor Swift I could show you incredible things // Magic, madness, heaven, sin So it's gonna be forever // Or it's gonna go down in flames
Lists Prof. Clarkson Fall 2017 Today s music: "Blank Space" by Taylor Swift I could show you incredible things // Magic, madness, heaven, sin So it's gonna be forever // Or it's gonna go down in flames
Logic - CM0845 Introduction to Haskell
 Logic - CM0845 Introduction to Haskell Diego Alejandro Montoya-Zapata EAFIT University Semester 2016-1 Diego Alejandro Montoya-Zapata (EAFIT University) Logic - CM0845 Introduction to Haskell Semester
Logic - CM0845 Introduction to Haskell Diego Alejandro Montoya-Zapata EAFIT University Semester 2016-1 Diego Alejandro Montoya-Zapata (EAFIT University) Logic - CM0845 Introduction to Haskell Semester
Introduction to Functional Programming in Haskell 1 / 56
 Introduction to Functional Programming in Haskell 1 / 56 Outline Why learn functional programming? The essence of functional programming What is a function? Equational reasoning First-order vs. higher-order
Introduction to Functional Programming in Haskell 1 / 56 Outline Why learn functional programming? The essence of functional programming What is a function? Equational reasoning First-order vs. higher-order
Plan (next 4 weeks) 1. Fast forward. 2. Rewind. 3. Slow motion. Rapid introduction to what s in OCaml. Go over the pieces individually
 Plan (next 4 weeks) 1. Fast forward Rapid introduction to what s in OCaml 2. Rewind 3. Slow motion Go over the pieces individually History, Variants Meta Language Designed by Robin Milner @ Edinburgh Language
Plan (next 4 weeks) 1. Fast forward Rapid introduction to what s in OCaml 2. Rewind 3. Slow motion Go over the pieces individually History, Variants Meta Language Designed by Robin Milner @ Edinburgh Language
Programming Languages
 CSE 130: Spring 2010 Programming Languages Lecture 3: Epressions and Types Ranjit Jhala UC San Diego A Problem fun -> +1 Can functions only have a single parameter? A Solution: Simultaneous Binding Parameter
CSE 130: Spring 2010 Programming Languages Lecture 3: Epressions and Types Ranjit Jhala UC San Diego A Problem fun -> +1 Can functions only have a single parameter? A Solution: Simultaneous Binding Parameter
OCaml. History, Variants. ML s holy trinity. Interacting with ML. Base type: Integers. Base type: Strings. *Notes from Sorin Lerner at UCSD*
 OCaml 1. Introduction Rapid introduction to what s in OCaml 2. Focus on Features Individually as Needed as Semester Progresses *Notes from Sorin Lerner at UCSD* History, Variants Meta Language Designed
OCaml 1. Introduction Rapid introduction to what s in OCaml 2. Focus on Features Individually as Needed as Semester Progresses *Notes from Sorin Lerner at UCSD* History, Variants Meta Language Designed
Background. CMSC 330: Organization of Programming Languages. Useful Information on OCaml language. Dialects of ML. ML (Meta Language) Standard ML
 CMSC 330: Organization of Programming Languages Functional Programming with OCaml 1 Background ML (Meta Language) Univ. of Edinburgh, 1973 Part of a theorem proving system LCF The Logic of Computable Functions
CMSC 330: Organization of Programming Languages Functional Programming with OCaml 1 Background ML (Meta Language) Univ. of Edinburgh, 1973 Part of a theorem proving system LCF The Logic of Computable Functions
GADTs. Wouter Swierstra. Advanced functional programming - Lecture 7. Faculty of Science Information and Computing Sciences
 GADTs Advanced functional programming - Lecture 7 Wouter Swierstra 1 Today s lecture Generalized algebraic data types (GADTs) 2 A datatype data Tree a = Leaf Node (Tree a) a (Tree a) This definition introduces:
GADTs Advanced functional programming - Lecture 7 Wouter Swierstra 1 Today s lecture Generalized algebraic data types (GADTs) 2 A datatype data Tree a = Leaf Node (Tree a) a (Tree a) This definition introduces:
GADTs. Wouter Swierstra and Alejandro Serrano. Advanced functional programming - Lecture 7. [Faculty of Science Information and Computing Sciences]
![GADTs. Wouter Swierstra and Alejandro Serrano. Advanced functional programming - Lecture 7. [Faculty of Science Information and Computing Sciences] GADTs. Wouter Swierstra and Alejandro Serrano. Advanced functional programming - Lecture 7. [Faculty of Science Information and Computing Sciences]](/thumbs/78/76904283.jpg) GADTs Advanced functional programming - Lecture 7 Wouter Swierstra and Alejandro Serrano 1 Today s lecture Generalized algebraic data types (GADTs) 2 A datatype data Tree a = Leaf Node (Tree a) a (Tree
GADTs Advanced functional programming - Lecture 7 Wouter Swierstra and Alejandro Serrano 1 Today s lecture Generalized algebraic data types (GADTs) 2 A datatype data Tree a = Leaf Node (Tree a) a (Tree
Administrative Stuff
 Administrative Stuff Use the new version of PLAI from planet. It will download the first time you run a program with the 7, like this: #lang planet plai/plai:1:7 This lets you ignore passing test cases
Administrative Stuff Use the new version of PLAI from planet. It will download the first time you run a program with the 7, like this: #lang planet plai/plai:1:7 This lets you ignore passing test cases
The Typed Racket Guide
 The Typed Racket Guide Version 5.3.6 Sam Tobin-Hochstadt and Vincent St-Amour August 9, 2013 Typed Racket is a family of languages, each of which enforce
The Typed Racket Guide Version 5.3.6 Sam Tobin-Hochstadt and Vincent St-Amour August 9, 2013 Typed Racket is a family of languages, each of which enforce
GADTs. Alejandro Serrano. AFP Summer School. [Faculty of Science Information and Computing Sciences]
![GADTs. Alejandro Serrano. AFP Summer School. [Faculty of Science Information and Computing Sciences] GADTs. Alejandro Serrano. AFP Summer School. [Faculty of Science Information and Computing Sciences]](/thumbs/95/124893351.jpg) GADTs AFP Summer School Alejandro Serrano 1 Today s lecture Generalized algebraic data types (GADTs) 2 A datatype data Tree a = Leaf Node (Tree a) a (Tree a) This definition introduces: 3 A datatype data
GADTs AFP Summer School Alejandro Serrano 1 Today s lecture Generalized algebraic data types (GADTs) 2 A datatype data Tree a = Leaf Node (Tree a) a (Tree a) This definition introduces: 3 A datatype data
CMSC 330: Organization of Programming Languages. OCaml Data Types
 CMSC 330: Organization of Programming Languages OCaml Data Types CMSC330 Spring 2018 1 OCaml Data So far, we ve seen the following kinds of data Basic types (int, float, char, string) Lists Ø One kind
CMSC 330: Organization of Programming Languages OCaml Data Types CMSC330 Spring 2018 1 OCaml Data So far, we ve seen the following kinds of data Basic types (int, float, char, string) Lists Ø One kind
Functions & First Class Function Values
 Functions & First Class Function Values PLAI 1st ed Chapter 4, PLAI 2ed Chapter 5 The concept of a function is itself very close to substitution, and to our with form. Consider the following morph 1 {
Functions & First Class Function Values PLAI 1st ed Chapter 4, PLAI 2ed Chapter 5 The concept of a function is itself very close to substitution, and to our with form. Consider the following morph 1 {
Intro. Scheme Basics. scm> 5 5. scm>
 Intro Let s take some time to talk about LISP. It stands for LISt Processing a way of coding using only lists! It sounds pretty radical, and it is. There are lots of cool things to know about LISP; if
Intro Let s take some time to talk about LISP. It stands for LISt Processing a way of coding using only lists! It sounds pretty radical, and it is. There are lots of cool things to know about LISP; if
CSC324- TUTORIAL 5. Shems Saleh* *Some slides inspired by/based on Afsaneh Fazly s slides
 CSC324- TUTORIAL 5 ML Shems Saleh* *Some slides inspired by/based on Afsaneh Fazly s slides Assignment 1 2 More questions were added Questions regarding the assignment? Starting ML Who am I? Shems Saleh
CSC324- TUTORIAL 5 ML Shems Saleh* *Some slides inspired by/based on Afsaneh Fazly s slides Assignment 1 2 More questions were added Questions regarding the assignment? Starting ML Who am I? Shems Saleh
SCHEME The Scheme Interpreter. 2 Primitives COMPUTER SCIENCE 61A. October 29th, 2012
 SCHEME COMPUTER SCIENCE 6A October 29th, 202 In the next part of the course, we will be working with the Scheme programming language. In addition to learning how to write Scheme programs, we will eventually
SCHEME COMPUTER SCIENCE 6A October 29th, 202 In the next part of the course, we will be working with the Scheme programming language. In addition to learning how to write Scheme programs, we will eventually
Which of the following expressions has the type int list?
 Which of the following expressions has the type int list? 1) [3; true] 2) [1;2;3]::[1;2] 3) []::[1;2]::[] 4) (1::2)::(3::4)::[] 5) [1;2;3;4] Answer: 5 Which of the following expressions has the type (int
Which of the following expressions has the type int list? 1) [3; true] 2) [1;2;3]::[1;2] 3) []::[1;2]::[] 4) (1::2)::(3::4)::[] 5) [1;2;3;4] Answer: 5 Which of the following expressions has the type (int
Lists. Michael P. Fourman. February 2, 2010
 Lists Michael P. Fourman February 2, 2010 1 Introduction The list is a fundamental datatype in most functional languages. ML is no exception; list is a built-in ML type constructor. However, to introduce
Lists Michael P. Fourman February 2, 2010 1 Introduction The list is a fundamental datatype in most functional languages. ML is no exception; list is a built-in ML type constructor. However, to introduce
CSE 307: Principles of Programming Languages
 1 / 63 CSE 307: Principles of Programming Languages Syntax R. Sekar Topics 1. Introduction 2. Basics 3. Functions 4. Data Structures 5. Overview 6. OCAML Performance 2 / 63 3 / 63 Section 1 Introduction
1 / 63 CSE 307: Principles of Programming Languages Syntax R. Sekar Topics 1. Introduction 2. Basics 3. Functions 4. Data Structures 5. Overview 6. OCAML Performance 2 / 63 3 / 63 Section 1 Introduction
Random Testing in 321
 Random Testing in 321 1 Test Cases So Far Each test relates a particular input to a particular output. (test (bound-ids (with 'x (id 'y) (id 'x))) '(x)) (test (binding-ids (with 'x (id 'y) (id 'x))) '(x))
Random Testing in 321 1 Test Cases So Far Each test relates a particular input to a particular output. (test (bound-ids (with 'x (id 'y) (id 'x))) '(x)) (test (binding-ids (with 'x (id 'y) (id 'x))) '(x))
CSCE 314 Programming Languages
 CSCE 314 Programming Languages Haskell: Declaring Types and Classes Dr. Hyunyoung Lee 1 Outline Declaring Data Types Class and Instance Declarations 2 Defining New Types Three constructs for defining types:
CSCE 314 Programming Languages Haskell: Declaring Types and Classes Dr. Hyunyoung Lee 1 Outline Declaring Data Types Class and Instance Declarations 2 Defining New Types Three constructs for defining types:
Dialects of ML. CMSC 330: Organization of Programming Languages. Dialects of ML (cont.) Features of ML. Functional Languages. Features of ML (cont.
 CMSC 330: Organization of Programming Languages OCaml 1 Functional Programming Dialects of ML ML (Meta Language) Univ. of Edinburgh,1973 Part of a theorem proving system LCF The Logic of Computable Functions
CMSC 330: Organization of Programming Languages OCaml 1 Functional Programming Dialects of ML ML (Meta Language) Univ. of Edinburgh,1973 Part of a theorem proving system LCF The Logic of Computable Functions
Standard ML. Data types. ML Datatypes.1
 Standard ML Data types ML Datatypes.1 Concrete Datatypes The datatype declaration creates new types These are concrete data types, not abstract Concrete datatypes can be inspected - constructed and taken
Standard ML Data types ML Datatypes.1 Concrete Datatypes The datatype declaration creates new types These are concrete data types, not abstract Concrete datatypes can be inspected - constructed and taken
Tuples. CMSC 330: Organization of Programming Languages. Examples With Tuples. Another Example
 CMSC 330: Organization of Programming Languages OCaml 2 Higher Order Functions Tuples Constructed using (e1,..., en) Deconstructed using pattern matching Patterns involve parens and commas, e.g., (p1,p2,
CMSC 330: Organization of Programming Languages OCaml 2 Higher Order Functions Tuples Constructed using (e1,..., en) Deconstructed using pattern matching Patterns involve parens and commas, e.g., (p1,p2,
Programming Languages Lecture 14: Sum, Product, Recursive Types
 CSE 230: Winter 200 Principles of Programming Languages Lecture 4: Sum, Product, Recursive Types The end is nigh HW 3 No HW 4 (= Final) Project (Meeting + Talk) Ranjit Jhala UC San Diego Recap Goal: Relate
CSE 230: Winter 200 Principles of Programming Languages Lecture 4: Sum, Product, Recursive Types The end is nigh HW 3 No HW 4 (= Final) Project (Meeting + Talk) Ranjit Jhala UC San Diego Recap Goal: Relate
CSE341: Programming Languages Lecture 6 Nested Patterns Exceptions Tail Recursion. Zach Tatlock Winter 2018
 CSE341: Programming Languages Lecture 6 Nested Patterns Exceptions Tail Recursion Zach Tatlock Winter 2018 Nested patterns We can nest patterns as deep as we want Just like we can nest expressions as deep
CSE341: Programming Languages Lecture 6 Nested Patterns Exceptions Tail Recursion Zach Tatlock Winter 2018 Nested patterns We can nest patterns as deep as we want Just like we can nest expressions as deep
Handout 2 August 25, 2008
 CS 502: Compiling and Programming Systems Handout 2 August 25, 2008 Project The project you will implement will be a subset of Standard ML called Mini-ML. While Mini- ML shares strong syntactic and semantic
CS 502: Compiling and Programming Systems Handout 2 August 25, 2008 Project The project you will implement will be a subset of Standard ML called Mini-ML. While Mini- ML shares strong syntactic and semantic
Any questions. Say hello to OCaml. Say hello to OCaml. Why readability matters. History, Variants. Plan (next 4 weeks)
 Any questions Say hello to OCaml? void sort(int arr[], int beg, int end){ if (end > beg + 1){ int piv = arr[beg]; int l = beg + 1; int r = end; while (l!= r-1){ if(arr[l]
Any questions Say hello to OCaml? void sort(int arr[], int beg, int end){ if (end > beg + 1){ int piv = arr[beg]; int l = beg + 1; int r = end; while (l!= r-1){ if(arr[l]
CSE 341: Programming Languages
 CSE 341: Programming Languages Hal Perkins Spring 2011 Lecture 2 Functions, pairs, and lists Hal Perkins CSE341 Spring 2011, Lecture 2 1 What is a programming language? Here are separable concepts for
CSE 341: Programming Languages Hal Perkins Spring 2011 Lecture 2 Functions, pairs, and lists Hal Perkins CSE341 Spring 2011, Lecture 2 1 What is a programming language? Here are separable concepts for
CS109A ML Notes for the Week of 1/16/96. Using ML. ML can be used as an interactive language. We. shall use a version running under UNIX, called
 CS109A ML Notes for the Week of 1/16/96 Using ML ML can be used as an interactive language. We shall use a version running under UNIX, called SML/NJ or \Standard ML of New Jersey." You can get SML/NJ by
CS109A ML Notes for the Week of 1/16/96 Using ML ML can be used as an interactive language. We shall use a version running under UNIX, called SML/NJ or \Standard ML of New Jersey." You can get SML/NJ by
So what does studying PL buy me?
 So what does studying PL buy me? Enables you to better choose the right language but isn t that decided by libraries, standards, and my boss? Yes. Chicken-and-egg. My goal: educate tomorrow s tech leaders
So what does studying PL buy me? Enables you to better choose the right language but isn t that decided by libraries, standards, and my boss? Yes. Chicken-and-egg. My goal: educate tomorrow s tech leaders
CVO103: Programming Languages. Lecture 5 Design and Implementation of PLs (1) Expressions
 CVO103: Programming Languages Lecture 5 Design and Implementation of PLs (1) Expressions Hakjoo Oh 2018 Spring Hakjoo Oh CVO103 2018 Spring, Lecture 5 April 3, 2018 1 / 23 Plan Part 1 (Preliminaries):
CVO103: Programming Languages Lecture 5 Design and Implementation of PLs (1) Expressions Hakjoo Oh 2018 Spring Hakjoo Oh CVO103 2018 Spring, Lecture 5 April 3, 2018 1 / 23 Plan Part 1 (Preliminaries):
CS 11 Haskell track: lecture 1
 CS 11 Haskell track: lecture 1 This week: Introduction/motivation/pep talk Basics of Haskell Prerequisite Knowledge of basic functional programming e.g. Scheme, Ocaml, Erlang CS 1, CS 4 "permission of
CS 11 Haskell track: lecture 1 This week: Introduction/motivation/pep talk Basics of Haskell Prerequisite Knowledge of basic functional programming e.g. Scheme, Ocaml, Erlang CS 1, CS 4 "permission of
Fall 2018 Lecture N
 15-150 Fall 2018 Lecture N Tuesday, 20 November I m too lazy to figure out the correct number Stephen Brookes midterm2 Mean: 79.5 Std Dev: 18.4 Median: 84 today or, we could procrastinate lazy functional
15-150 Fall 2018 Lecture N Tuesday, 20 November I m too lazy to figure out the correct number Stephen Brookes midterm2 Mean: 79.5 Std Dev: 18.4 Median: 84 today or, we could procrastinate lazy functional
These notes are intended exclusively for the personal usage of the students of CS352 at Cal Poly Pomona. Any other usage is prohibited without
 These notes are intended exclusively for the personal usage of the students of CS352 at Cal Poly Pomona. Any other usage is prohibited without previous written authorization. 1 2 The simplest way to create
These notes are intended exclusively for the personal usage of the students of CS352 at Cal Poly Pomona. Any other usage is prohibited without previous written authorization. 1 2 The simplest way to create
Programming with Math and Logic
 .. Programming with Math and Logic an invitation to functional programming Ed Morehouse Wesleyan University The Plan why fp? terms types interfaces The What and Why of Functional Programming Computing
.. Programming with Math and Logic an invitation to functional programming Ed Morehouse Wesleyan University The Plan why fp? terms types interfaces The What and Why of Functional Programming Computing
Computer Science CSC324 Wednesday February 13, Homework Assignment #3 Due: Thursday February 28, 2013, by 10 p.m.
 Computer Science CSC324 Wednesday February 13, 2013 St. George Campus University of Toronto Homework Assignment #3 Due: Thursday February 28, 2013, by 10 p.m. Silent Policy A silent policy takes effect
Computer Science CSC324 Wednesday February 13, 2013 St. George Campus University of Toronto Homework Assignment #3 Due: Thursday February 28, 2013, by 10 p.m. Silent Policy A silent policy takes effect
Thinking Induc,vely. COS 326 David Walker Princeton University
 Thinking Induc,vely COS 326 David Walker Princeton University slides copyright 2017 David Walker permission granted to reuse these slides for non-commercial educa,onal purposes Administra,on 2 Assignment
Thinking Induc,vely COS 326 David Walker Princeton University slides copyright 2017 David Walker permission granted to reuse these slides for non-commercial educa,onal purposes Administra,on 2 Assignment
Exercises on ML. Programming Languages. Chanseok Oh
 Exercises on ML Programming Languages Chanseok Oh chanseok@cs.nyu.edu Dejected by an arcane type error? - foldr; val it = fn : ('a * 'b -> 'b) -> 'b -> 'a list -> 'b - foldr (fn x=> fn y => fn z => (max
Exercises on ML Programming Languages Chanseok Oh chanseok@cs.nyu.edu Dejected by an arcane type error? - foldr; val it = fn : ('a * 'b -> 'b) -> 'b -> 'a list -> 'b - foldr (fn x=> fn y => fn z => (max
Functional Programming
 Functional Programming COMS W4115 Prof. Stephen A. Edwards Spring 2003 Columbia University Department of Computer Science Original version by Prof. Simon Parsons Functional vs. Imperative Imperative programming
Functional Programming COMS W4115 Prof. Stephen A. Edwards Spring 2003 Columbia University Department of Computer Science Original version by Prof. Simon Parsons Functional vs. Imperative Imperative programming
Bindings & Substitution
 Bindings & Substitution Even in our simple language, we encounter repeated expressions. 1 {* {+ 4 2} {+ 4 2}} There are several reasons to eliminate duplicated code. It introduces a redundant computation.
Bindings & Substitution Even in our simple language, we encounter repeated expressions. 1 {* {+ 4 2} {+ 4 2}} There are several reasons to eliminate duplicated code. It introduces a redundant computation.
CSE 307: Principles of Programming Languages
 CSE 307: Principles of Programming Languages Syntax R. Sekar 1 / 63 Topics 1. Introduction 2. Basics 3. Functions 4. Data Structures 5. Overview 6. OCAML Performance 2 / 63 Section 1 Introduction 3 / 63
CSE 307: Principles of Programming Languages Syntax R. Sekar 1 / 63 Topics 1. Introduction 2. Basics 3. Functions 4. Data Structures 5. Overview 6. OCAML Performance 2 / 63 Section 1 Introduction 3 / 63
Random Testing in 321
 Random Testing in 321 1 Test Cases So Far Each test relates a particular input to a particular output. (test (bound-ids (with 'x (id 'y) (id 'x))) '(x)) (test (binding-ids (with 'x (id 'y) (id 'x))) '(x))
Random Testing in 321 1 Test Cases So Far Each test relates a particular input to a particular output. (test (bound-ids (with 'x (id 'y) (id 'x))) '(x)) (test (binding-ids (with 'x (id 'y) (id 'x))) '(x))
Lab 10: OCaml sequences, comparators, stable sorting 12:00 PM, Nov 12, 2017
 Integrated Introduction to Computer Science Hughes Lab 10: OCaml sequences, comparators, stable sorting 12:00 PM, Nov 12, 2017 Contents 1 A last OCaml type, and its utility 1 1.1 Sequences in OCaml....................................
Integrated Introduction to Computer Science Hughes Lab 10: OCaml sequences, comparators, stable sorting 12:00 PM, Nov 12, 2017 Contents 1 A last OCaml type, and its utility 1 1.1 Sequences in OCaml....................................
GADTs gone mild. Code at Gabriel RADANNE 23 Mars 2017
 GADTs gone mild Code at https://tinyurl.com/irif-gadt Gabriel RADANNE 23 Mars 2017 GADT: Generalized Algebraic Data Types The least maintainable way of writing interpreters 1 1 Except maybe dependent types
GADTs gone mild Code at https://tinyurl.com/irif-gadt Gabriel RADANNE 23 Mars 2017 GADT: Generalized Algebraic Data Types The least maintainable way of writing interpreters 1 1 Except maybe dependent types
CSCI-GA Scripting Languages
 CSCI-GA.3033.003 Scripting Languages 12/02/2013 OCaml 1 Acknowledgement The material on these slides is based on notes provided by Dexter Kozen. 2 About OCaml A functional programming language All computation
CSCI-GA.3033.003 Scripting Languages 12/02/2013 OCaml 1 Acknowledgement The material on these slides is based on notes provided by Dexter Kozen. 2 About OCaml A functional programming language All computation
Lecture 2: Big-Step Semantics
 Lecture 2: Big-Step Semantics 1 Representing Abstract Syntax These are examples of arithmetic expressions: 2 * 4 1 + 2 + 3 5 * 4 * 2 1 + 2 * 3 We all know how to evaluate these expressions in our heads.
Lecture 2: Big-Step Semantics 1 Representing Abstract Syntax These are examples of arithmetic expressions: 2 * 4 1 + 2 + 3 5 * 4 * 2 1 + 2 * 3 We all know how to evaluate these expressions in our heads.
Introduction to OCaml
 Fall 2018 Introduction to OCaml Yu Zhang Course web site: http://staff.ustc.edu.cn/~yuzhang/tpl References Learn X in Y Minutes Ocaml Real World OCaml Cornell CS 3110 Spring 2018 Data Structures and Functional
Fall 2018 Introduction to OCaml Yu Zhang Course web site: http://staff.ustc.edu.cn/~yuzhang/tpl References Learn X in Y Minutes Ocaml Real World OCaml Cornell CS 3110 Spring 2018 Data Structures and Functional
Redefinition of an identifier is OK, but this is redefinition not assignment; Thus
 Redefinition of an identifier is OK, but this is redefinition not assignment; Thus val x = 100; val x = (x=100); is fine; there is no type error even though the first x is an integer and then it is a boolean.
Redefinition of an identifier is OK, but this is redefinition not assignment; Thus val x = 100; val x = (x=100); is fine; there is no type error even though the first x is an integer and then it is a boolean.
CS558 Programming Languages
 CS558 Programming Languages Fall 2017 Lecture 7b Andrew Tolmach Portland State University 1994-2017 Type Inference Some statically typed languages, like ML (and to a lesser extent Scala), offer alternative
CS558 Programming Languages Fall 2017 Lecture 7b Andrew Tolmach Portland State University 1994-2017 Type Inference Some statically typed languages, like ML (and to a lesser extent Scala), offer alternative
COMP520 - GoLite Type Checking Specification
 COMP520 - GoLite Type Checking Specification Vincent Foley February 26, 2015 1 Declarations Declarations are the primary means of introducing new identifiers in the symbol table. In Go, top-level declarations
COMP520 - GoLite Type Checking Specification Vincent Foley February 26, 2015 1 Declarations Declarations are the primary means of introducing new identifiers in the symbol table. In Go, top-level declarations
Note that pcall can be implemented using futures. That is, instead of. we can use
 Note that pcall can be implemented using futures. That is, instead of (pcall F X Y Z) we can use ((future F) (future X) (future Y) (future Z)) In fact the latter version is actually more parallel execution
Note that pcall can be implemented using futures. That is, instead of (pcall F X Y Z) we can use ((future F) (future X) (future Y) (future Z)) In fact the latter version is actually more parallel execution
CS558 Programming Languages
 CS558 Programming Languages Winter 2018 Lecture 7b Andrew Tolmach Portland State University 1994-2018 Dynamic Type Checking Static type checking offers the great advantage of catching errors early And
CS558 Programming Languages Winter 2018 Lecture 7b Andrew Tolmach Portland State University 1994-2018 Dynamic Type Checking Static type checking offers the great advantage of catching errors early And
Generic polymorphism on steroids
 Generic polymorphism on steroids or How to Solve the Expression Problem with Polymorphic Variants Claudio Sacerdoti Coen Dipartimento di Informatica Scienza e Ingegneria
Generic polymorphism on steroids or How to Solve the Expression Problem with Polymorphic Variants Claudio Sacerdoti Coen Dipartimento di Informatica Scienza e Ingegneria
CS131 Typed Lambda Calculus Worksheet Due Thursday, April 19th
 CS131 Typed Lambda Calculus Worksheet Due Thursday, April 19th Name: CAS ID (e.g., abc01234@pomona.edu): I encourage you to collaborate. collaborations below. Please record your Each question is worth
CS131 Typed Lambda Calculus Worksheet Due Thursday, April 19th Name: CAS ID (e.g., abc01234@pomona.edu): I encourage you to collaborate. collaborations below. Please record your Each question is worth
CS 360: Programming Languages Lecture 10: Introduction to Haskell
 CS 360: Programming Languages Lecture 10: Introduction to Haskell Geoffrey Mainland Drexel University Thursday, February 5, 2015 Adapted from Brent Yorgey s course Introduction to Haskell. Section 1 Administrivia
CS 360: Programming Languages Lecture 10: Introduction to Haskell Geoffrey Mainland Drexel University Thursday, February 5, 2015 Adapted from Brent Yorgey s course Introduction to Haskell. Section 1 Administrivia
Datatype declarations
 Datatype declarations datatype suit = HEARTS DIAMONDS CLUBS SPADES datatype a list = nil (* copy me NOT! *) op :: of a * a list datatype a heap = EHEAP HEAP of a * a heap * a heap type suit val HEARTS
Datatype declarations datatype suit = HEARTS DIAMONDS CLUBS SPADES datatype a list = nil (* copy me NOT! *) op :: of a * a list datatype a heap = EHEAP HEAP of a * a heap * a heap type suit val HEARTS
An introduction to functional programming. July 23, 2010
 An introduction to functional programming July 23, 2010 About Outline About About What is functional programming? What is? Why functional programming? Why? is novel. is powerful. is fun. About A brief
An introduction to functional programming July 23, 2010 About Outline About About What is functional programming? What is? Why functional programming? Why? is novel. is powerful. is fun. About A brief
COSE212: Programming Languages. Lecture 3 Functional Programming in OCaml
 COSE212: Programming Languages Lecture 3 Functional Programming in OCaml Hakjoo Oh 2017 Fall Hakjoo Oh COSE212 2017 Fall, Lecture 3 September 18, 2017 1 / 44 Why learn ML? Learning ML is a good way of
COSE212: Programming Languages Lecture 3 Functional Programming in OCaml Hakjoo Oh 2017 Fall Hakjoo Oh COSE212 2017 Fall, Lecture 3 September 18, 2017 1 / 44 Why learn ML? Learning ML is a good way of
