Chasing One s Tail: XPath Containment Under Cyclic DTDs
|
|
|
- Estella Amie Wilson
- 6 years ago
- Views:
Transcription
1 Chasing One s Tail: XPath Containment Under Cyclic DTDs Manizheh Montazerian Dept. of Computer Science and Info. Systems Birkbeck, University of London montazerian mahtab@yahoo.co.uk Peter T. Wood Dept. of Computer Science and Info. Systems Birkbeck, University of London ptw@dcs.bbk.ac.uk ABSTRACT The problem of finding subclasses of XPath queries and document type definitions (DTDs) for which containment can be tested efficiently has been much studied. Along the way, a number of constraints inferred from DTDs have been used to characterise containment in terms of the chase procedure. However, previous attempts have resulted in procedures that are non-terminating for cyclic DTDs, even when the queries include only the child and descendant operators (i.e., no predicates or wildcards). In this paper, we introduce a rewriting of such XPath queries in the presence of cyclic (but simplified) DTDs, using an operator that generalises the child and descendant operators, and show that doing so allows us to produce a complete procedure for containment using the chase and previous classes of constraints. We also characterise a set of constraints that allows for a complete chase procedure for this fragment of XPath in the case of general, non-cyclic DTDs. 1. INTRODUCTION XPath forms a crucial component in many web applications that involve the processing of XML messages. One fundamental type of static analysis for XPath queries is to determine the containment relationship between pairs of queries. A query P contains a query Q if the answers to P always include all the answers to Q. Containment tests are useful in query optimisation, query processing using views, and query cache utilisation, for example. As a result, the containment problem for XPath has been the subject of considerable study, both in general [1, 5, 7] and in the case when the XML data being queried is assumed to conform to a Document Type Definition (DTD) or other forms of constraint [2, 3, 6, 8, 10]. As has become common practice, we indicate the fragment of XPath under study by listing the operators permitted. For example, XP(/, [ ],, //) denotes the fragment in which the child, predicate, wildcard and descendant operators are permitted. It is well-known that containment can be solved Permission to make digital or hard copies of all or part of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. To copy otherwise, to republish, to post on servers or to redistribute to lists, requires prior specific permission and/or a fee. This article was presented at: DBPL 11. Copyright efficiently for each of the fragments XP(/, [ ], ), XP(/, [ ], //) and XP(/, //, ), but is conp-complete for XP(/, [],, //) [5]. In this paper, we are specifically interested in XPath queries in the presence of DTDs; that is, we assume that, along with each query (or queries) we are given a DTD, with the assumption that the queries are to be evaluated on documents conforming to the DTD. In this case, we denote the XPath fragment by including DTD in the notation, so XP(DTD, //), for example, denotes the fragment where we are given XPath expressions using only the descendant operator along with a DTD. Testing containment in the presence of DTDs is considerably harder than in the case without DTDs; even containment for XP(DTD, /, [ ]) is conp-complete [9]. A classification of tractable, intractable and even undecidable fragments is given in [6]. In this paper, we focus on XP(DTD, /, //) because containment for this fragment can be decided is in ptime and the fragment is sufficient to demonstrate the problems with previous approaches. Neven and Schwentick [6] have already shown that containment of queries in XP(DTD, /, //) can be decided in ptime by using tree automata techniques. On the other hand, for many classes of queries, including relational queries, testing whether P contains Q is done by applying the wellknown and intuitively appealing chase procedure to Q, followed by deciding whether there is a containment mapping from P to the chase of Q. So it would be of practical benefit, as well as intellectual satisfaction, to extend the use of the chase procedure and containment mappings to the case of deciding containment for XP(DTD, /, //) in ptime, as well. However, in order to achieve this, there are two problems to overcome. The first problem is that there may not be a containment mapping between two equivalent queries in XP(DTD, /, //). This is similar to the situation pointed out by Miklau and Suciu [5] in the case of XP(/, //, ). They show that, given queries P = a/ //b and Q = a// /b, there is no containment mapping from P to Q or from Q to P, despite the fact that P and Q are equivalent. A similar problem arises for XP(DTD, /, //) with queries P = a/a//a and Q = a//a/a and DTD D with the single rule a a. Note that this rule is recursive and that the DTD is therefore cyclic. The second problem is to find a suitable set of constraints with which to chase a query, while ensuring that the resulting chase procedure terminates in polynomial time. Recently, Wang and Yu [8] studied containment for the fragment XP(DTD, /, [ ], //), proposing new types of constraints inferred from DTDs and two different chase procedures. How-
2 ever, their first chase procedure does not terminate on the example above, while for a generalisation of the above query to include n descendant edges, their second chase procedure results in a set of chased queries whose size is exponential in n. In this paper (Section 4), we provide a way of ensuring that the chase of a query Q in XP(DTD, /, //) with respect to DTD D produces a single, unique result whose size is polynomial in the size of Q and D, even in the presence of cyclic DTDs. This is done by introducing a new operator into XPath, which loosely speaking denotes either / or //, and replacing certain groups of / and // operators in a query by operators. Thus the result of chasing a query Q in XP(DTD, /, //) with constraints derived from DTD D is a query in XP(DTD, /, //, ), which we call a generalised query. For example, the generalised query resulting from chasing the query a//a/a above with constraints derived from the DTD rule a a is the generalised query a a a. Given a query P in XP(DTD, /, //) and a query Q in XP(DTD, /, //, ), we then define a generalised form of containment mapping from P to Q, and present an algorithm that decides whether there is a generalised containment mapping from P to Q in time polynomial in the sizes of P and Q. The above results consider only what we term simplified DTDs, where the DTD can be represented by a simple directed graph. Simplified DTDs have also been considered in [4, 8], for example. In this paper we also consider the containment problem for queries in XP(DTD, /, //) under general but non-recursive DTDs. Many constraints for use with the chase have been introduced in previous papers [4, 8, 10] but only for restricted classes of DTDs. We show that these constraints are insufficient in the case of containment for queries in XP(DTD, /, //) with respect to general, non-recursive DTDs. To address this, we introduce a new constraint, called a family constraint, which generalises previous constraints, and show that using family constraints along with other previous constraints enables a complete chase procedure for checking containment (Section 3). 2. BACKGROUND We use the terms XPath query and tree pattern interchangeably. An XPath query in XP(/, [ ], //) can be represented by a tree pattern that uses child edges and descendant edges. For example, the tree pattern on the right of Figure 1 corresponds to the XPath query a[b//g]//e/g. We will consider only Boolean queries in this paper, and restrict ourselves to queries in XP(/, //); hence, each initial tree pattern corresponds to a path, although the chase can transform such a query into one in XP(/, [ ], //). Given a pattern P, we denote the set of nodes of P by N(P ), the set of edges of P by E(P ) (where each edge is a pair (x, y) N(P ) N(P )), the root of P by root(p ), and the label of a node x N(P ) by λ(x). The set of child edges is denoted by E / (P ), while the set of descendant edges is denoted by E // (P ). When P is in XP(/, //) we denote the single leaf node in P by leaf (P ). Tree patterns are queries to be evaluated on trees. Because we will ultimately consider only trees that conform to a given DTD, it is sufficient for now to consider trees whose node labels are drawn from a finite alphabet Σ. We denote the set of all trees whose node labels are drawn from Σ by T Σ. We use the same notation for trees as that defined for tree patterns above (except of course there are no descendant edges in a tree). Given a tree pattern P and a tree t T Σ, a homomorphism from P to t is a function h : N(P ) N(t) that is root-preserving: h(root(p )) = root(t), label-preserving: for each x N(P ), λ(x) = λ(h(x)), child-edge-preserving: for each (x, y) E / (P ), we have (h(x), h(y)) E(t), and descendant-edge-preserving: for each (x, y) E // (P ), we have (h(x), h(y)) E + (t), where E + (t) denotes the transitive closure of the edge relation E(t). Then the evaluation of a Boolean query P on tree t T Σ, denoted P (t), is true if and only if there is a homomorphism from N(P ) to N(t). We also say that t satisfies Q. We denote by SAT (Q) the set of trees in T Σ that satisfy Q. We say that query P contains query Q, denoted P Q, if and only if, for each tree t T Σ, Q(t) implies P (t). Given a pair of patterns P and Q a containment mapping from P to Q is a function h : N(P ) N(Q) satisfying the same conditions as for a homomorphism defined above (with Q substituted for t), except that in the third condition we require that (h(x), h(y)) E / (Q) (child edges must map to child edges). For queries P and Q in XP(/, [ ], //), P Q if and only if there is a containment mapping from P to Q [1]. Now assume that we are given a DTD D, and we wish to consider containment of queries under the assumption that the trees being queried satisfy D. We denote by SAT (D) the set of trees satisfying DTD D. We say that query P D-contains query Q, denoted P D Q, if and only if, for each tree t SAT (D), Q(t) implies P (t). Often when studying D-containment of queries, a simplified form of DTD, one that can be modelled by a simple directed graph G, is considered [4, 8]. Each element in D is modelled as a node in G, with an edge from node a to node b in G if an a-element can have a b-element as a child. The DTD is recursive if the graph is cyclic. Edges in G can be labelled with one of 1,?, + or *, with the usual DTD semantics, although this does capture general disjunction or grouping of elements as provided by DTDs. We will consider only the case where each edge is effectively labelled with *, similar to [4], and will call DTDs that can be modelled by such a graph simplified. One way to test D-containment is to derive a set C of constraints from D, chase Q with C, and find a containment mapping from P to the chased query. Although this method works for some classes of query and DTD [4, 8, 10], it sometimes fails to terminate for queries in XP(/, //) and simplified DTDs, as pointed out in the Introduction. For non-recursive DTDs, the following five types of constraint, which can be inferred from a DTD, have been considered. The first is from [10], while the last three are from [4]. 1. A sibling constraint (SC) is of the form a : b c and states that, whenever an a-node has a b-node as a child, then it also has a c-node as a child. A special form of SC is a : c, which states that every a-node has a c-node as a child. 2. A cousin constraint (CC) is of the form a : b c and states that, whenever an a-node has a b-node as a descendant, then it also has a c-node as a descendant. A
3 special form of CC is a : c, which states that every a-node has a c-node as a descendant. 3. A parent-child constraint (PC) is of the form a 1 b and states that, whenever a b-node is a descendant of an a-node, then it is necessarily a child. 4. An intermediate node constraint (IC) is of the form a c b and states that, whenever there is a path from an a-node to a b-node, there is a c-node on the path. While the above constraints allow for complete containment tests when the DTD is simplified and non-recursive [4], this is no longer the case for general non-recursive DTDs. For completeness in this case (as shown in Section 3), we need a new constraint that is a generalisation of sibling and cousin constraints. 5. A family constraint (FC) is of the form a[$ 1b] [$ 2c], where each of $ 1 and $ 2 is either / or //. It states that, whenever an a-node has a b-node as a child (if $ 1 is /) or descendant (if $ 1 is //), then it also has a c-node as a child (if $ 2 is /) or descendant (if $ 2 is //), respectively. As special cases, if every a-node must have a c-node as a child (or descendant), we write a [/c] (or a [//c]). When both $ 1 and $ 2 are / (respectively //), then an FC corresponds to an SC (respectively CC). Example 1. Consider the following DTD, which is not simplified because of the disjunction in the first rule: a b (c, (d e)) b c d f e f If an a-node has a c-child then it must have an f-descendant, and if an a-node has an f-descendant then it must have a c-child. So the FCs a[/c] [//f] and a[//f] [/c] hold. Note that an a-node can have a c-descendant without having an f- descendant, so a CC will not capture the first constraint. Wang and Yu [8] introduced three further types of constraint which are necessary to handle situations that arise with recursive DTDs (and are expressed with respect to the graph of a simplified DTD): 6. A child-of-first-node constraint (CFN ) is of the form a /b b and states that on every path from an a-node to a b-node, the node immediately following the a-node must be a b-node. 7. A parent-of-last-node constraint (PLN ) is of the form a a/ b and states that on every path from an a-node to a b-node, the node immediately preceding the b- node must be an a-node. 8. An essential edge constraint (EE) is of the form a / b and states that every path from an a-node to a b-node must contain an edge from an a-node to a b-node. To simplify the notation and presentation, we will say: 1. (a, b) is initial if and only if the CFN a /b b holds, 2. (a, b) is final if and only if the PLN a a/ b holds, and 3. (a, b) is essential if and only if the EE a / b holds. We collectively call these last three constraints essential constraints, abbreviated ECs. Note that a pair being initial or final implies that it is essential, although a pair can be essential without being either initial or final. For example, if E(G) = {(a, a), (a, b), (b, b)}, then (a, b) is essential but neither initial nor final. Also note that if a pair (a, b) is both initial and final, this does not imply that the only path from a to b is (a, b). For example, if E(G) = {(a, b), (b, a)}, then (a, b) is both initial and final, but there are paths of the form a(ba) b from a to b. A chasing sequence of a query Q by a set of constraints C is a sequence Q 0,..., Q k such that Q 0 = Q, for each 0 i k 1, Q i+1 is the result of applying some constraint in C to Q i, and no constraint can be applied to Q k. Given a chasing sequence Q 0,..., Q k of Q by C, we call Q k the chase of Q by C (which turns out to be unique), denoted Q C. Constraints such as PCs, ICs and FCs are applied to a query in the obvious way (we give examples in the next section). ECs, by contrast, are used to transform a query to a generalised query by replacing some occurrences of / and // by, as explained in Section NON-RECURSIVE DTDS Our goal in this section is to prove that, given a pair of queries P and Q in XP(/, //) along with a non-recursive DTD D, chasing Q with the set C of parent-child (PC), intermediate node (IC) and family constraints (FC) inferred from D to give Q C, followed by checking for a containment mapping from P to Q C gives a complete procedure for determining whether P D Q. To do so, we first show that there are trees satisfying Q and D to which there are oneto-one homomorphisms from Q C. We then show that, given such a tree t, there is a homomorphism h from P to t that maps nodes of P to nodes in t that are in the image of one of these one-to-one homomorphisms g from Q C. Then the composition of h with the inverse of g gives a containment mapping from P to Q C. It turns out that Q C needs to be minimal for the existence of such a one-to-one homomorphism from Q C to be guaranteed. Example 2. Consider the following DTD D: a b c b d c d We can infer the FCs b [/d], c [/d] and a [//d]. Given a query Q = a/b, the chase might first add a d-descendant to a followed by a d-child to b. Now there is no one-to-one homomorphism from Q C to any tree in SAT (D). The problem is that the d-descendant of a is Q C is redundant. Given a query Q in XP(DTD, /, //) and a DTD D, the models of Q with respect to D, denoted Mod(Q, D), are those trees in SAT (Q) SAT (D). Since the chase of Q with respect to a set of constraints C inferred from D preserves D-equivalence of queries, Mod(Q, D) = Mod(Q C, D). Similar to Miklau and Suciu [5], we define the set of canonical trees in Mod(Q, D) as those trees that look like Q C.
4 A tree t Mod(Q, D) is minimal if deleting any set of subtrees from t results in a tree no longer in Mod(Q, D). A minimal tree t Mod(Q, D) is canonical if t can be transformed to (a tree isomorphic to) Q C by removing entire subtrees from t and replacing paths of degree-two nodes in t by descendant edges. (Of course, the resulting tree may no longer be in Mod(Q, D).) The set of canonical trees for Q and D is denoted by CMod(Q, D). We need to prove that canonical trees exist; it turns out that this is the case when Q C is minimal. Having to work with minimal queries is not a problem, since queries in XP(/, [ ], //) can be minimised in polynomial time [1]. Lemma 1. If Q C is minimal, then CMod(Q, C). An isomorphism f from the transformed tree t for a tree t CMod(Q, D) gives rise to a one-to-one mapping from the nodes of t to the nodes of Q C. The inverse of f is a oneto-one mapping from Q C to t. We will call such a mapping a canonical homomorphism. The following example shows that there is not necessarily a unique canonical homomorphism from a minimal Q C to a canonical tree t. Example 3. Consider the following DTD D a b, b, (c d) b (e i) c e d e e h i h along with the query Q = a/b. The set of constraints C inferred from D includes (among others) a [//e], b [//h] and e [/h]. The minimal chase Q C of Q with respect to C is shown on the right of Figure 1. Note that while Q is in XP(/, //), Q C is in XP(/, [ ], //). A canonical model t CMod(Q, D) is shown on the left of Figure 1. Also shown are two canonical homomorphisms f (dotted) and g (dashed) from N(Q C ) to N(t). t: f g Q C : a f b b c b g f e i e e g h h h h h g Figure 1: Example tree t and chase Q C of query Q. We now define the notion of a node being essential in a canonical tree in CMod(Q, D). Let v be a node in a tree t. An ancestral forest of v in t is defined inductively as follows: f g f a each forest formed by the subtree rooted at v along with the subtrees rooted at zero or more siblings of v forms an ancestral forest of v, each forest formed by the subtree rooted at an ancestor u of v along with the subtrees rooted at zero or more siblings of u forms an ancestral forest of v Given a canonical tree t CMod(Q, D), a node v N(t) is inessential in t if t can be transformed to t CMod(Q, D) by replacing an ancestral forest of v by a forest in which no node is labelled λ(v). A node v N(t) is essential in t if it is not inessential. Example 4. Consider the canonical tree t in Figure 1. All the nodes labelled a, b and h are essential, as is the righthand node labelled e. The lefthand node labelled e and the nodes labelled c and i are inessential since the subtrees rooted at them can be replaced by subtrees not including nodes labelled e, c or i, respectively. In all the results that follow we assume that P and Q are queries in XP(DTD, /, //), D is a non-recursive DTD, C is the set of PCs, ICs and FCs inferred from D, Q C is the minimal chase of Q with respect to C, and t is a canonical tree in CMod(Q, D). Lemma 2. Each essential node in t is in the image of some homomorphism from N(Q C ) to N(t). Lemma 3. If P D Q, then there must be a tree t CMod(Q, D) and a homomorphism h from N(P ) to N(t) such that, for each v N(P ), h(v) is essential. Theorem 1. If P D Q, then there is a containment mapping from P to Q C. 4. RECURSIVE DTDS We now turn to considering how to use the chase to test query containment for queries in XP(DTD, /, //) with respect to a potentially recursive DTD. As pointed out in Section 2, we will restrict ourselves to simplified DTDs, ones that can be represented by simple, directed graphs. As a result, we will use the terms simplified DTD and graph interchangeably. We start our investigation by first considering the simpler setting in which the simplified DTD G is also non-recursive, that is, the directed graph G is acyclic. Note that FCs cannot arise in a simplified DTD because all children are optional and no grouping is allowed. Hence, perhaps it is not surprising that it turns out that, given queries P and Q in XP(DTD, /, //), we can test whether P G Q by first chasing Q with (only) the set of ICs and PCs implied by G to give Q C, and then checking whether there is a containment mapping from N(P ) to N(Q C ). Lemma 4. Let G be a simplified, non-recursive DTD and P and Q be in XP(DTD, /, //). Let C be the set of ICs and PCs inferred from G, and Q C be the result of chasing Q with C. If P G Q, then there is a containment mapping from P to Q C. When trying to extend the above result to queries in XP(DTD, /, //) with recursive DTDs, the situation becomes much more complicated. The problem is that, when the
5 (DTD) graph G has cycles, there can be pairs of equivalent queries without containment mappings between them. The simplest example of this situation is that given in the Introduction, namely, for queries P = a/a//a and Q = a//a/a and DTD G with rule a a. Every path through G comprises only nodes labelled a, so P G Q, but there is no containment mapping from P to Q or from Q to P. To address the above problem, we propose introducing a new notation which allows one query form to denote a number of equivalent queries in XP(DTD, /, //). First we introduce a new XPath operator which, loosely speaking, denotes either / or //. Then we allow for consecutive occurrences of in a query to be assigned to groups, indicated by superscripts, representing group numbers, on the operators. A group of operators denotes the set of subqueries obtained by replacing each within the group by either / or //, as long as at least one // remains in the group. As an example, a 1 a 1 a denotes the pair of queries a/a//a and a//a/a. We call a query using the operator a generalised query. To decide whether P G Q, for queries P and Q in XP(DTD, /, //) and potentially recursive DTD G, we will proceed as follows. We will first chase Q with the set C of PCs and ICs derived from G to give Q C. We will then form a generalised query Q C from Q C and find a containment mapping from P to Q C. In the following two subsections, we define the notion of a generalised query, and show how to transform a given query Q into a generalised query that is G-equivalent to Q. In Section 4.3 we define what it means for a containment mapping to exist from a query to a generalised query, and provide a polynomial-time algorithm for deciding whether such a containment mapping exists. 4.1 Generalised Queries A generalised query Q is an XPath query in which, in addition to the operators / and //, the operator can be used. Occurrences of in Q must be assigned to groups which are numbered using positive integers. More specifically, each occurrence of in Q must be assigned to either one group or two consecutively numbered groups: if operator is in group i, this is indicated by i ; if is in groups i and i + 1, this is written i i+1. Finally, only consecutive occurrences of can belong to the same group. A generalised query represents a set of queries defined as follows. An instantiation of a generalised query Q is a query in XP(DTD, /, //) obtained by replacing each occurrence of in Q by either / or // while ensuring that in each group at least one is replaced by a // operator. The expansion of a generalised query Q, denoted Q X, is the set of instantiations of Q. The meaning of Q X is defined as one would expect. Let Q X = {Q 1,..., Q m}. Given a tree t, Q X (t) is defined as Q 1(t) Q m(t), or, in the case of Boolean queries, as Q 1(t) Q m(t). Example 5. Q = a 1//a 2 1 a a 4 2 a 5/a 6 is a generalised query in which the operators have been placed in two groups. The expansion Q X of Q is a set of five queries, corresponding to five instantiations of groups 1 and 2. The instantiations of groups 1 and 2 are (1) a 2/a 3//a 4/a 5, (2) a 2//a 3/a 4//a 5, (3) a 2//a 3//a 4/a 5, (4) a 2/a 3//a 4//a 5 and (5) a 2//a 3//a 4//a 5. Note that a 2//a 3/a 4/a 5 is not an instantiation of groups 1 and 2 because both occurrences of in group 2 have been replaced with /. Note further that the size of Q X can be exponential in the size of Q. 4.2 Transforming a Query to a Generalised Query Let Q = a 0$ 1a 1$ 2 $ na n be a query in XP(DTD, /, //), where each $ i is either / or //. We call a sequence a i$ i+1 $ ja j, 0 i n 1 and i < j n, a query fragment of Q. In this section, we identify those fragments of a query that need to be generalised in order to ensure that we can always find a containment mapping to them. We call these fragments essential fragments, because they are identified using the essential constraints defined in Section 2. Given a simplified DTD graph G = (N(G), E(G)), we need to work with the strongly connected components (SCCs) of G. We call an SCC trivial if it is a singleton set {v} and (v, v) E(G); otherwise, it is called non-trivial. (Of course, if G is non-recursive, then every SCC in G is trivial and no part of the following transformation is performed.) Recall the definition of essential, initial and final pairs of nodes from Section 2. An essential fragment in Q is a maximal sequence of essential pairs in Q such that 1. if the first pair is not preceded by the operator // in Q, then it must be initial, 2. if the last pair is not followed by the operator // in Q, then it must be final, and 3. for each pair (x, y) in the sequence, either x or y is in a non-trivial SCC of G. Example 6. Consider the simplified DTD G shown in Figure 2, in which all nodes are in the same SCC. By definition, only pairs of nodes that correspond to edges can be essential. All such pairs, except (b, e) and (d, c), are essential. Pairs (b, e) and (d, c) are not essential because there are paths from b to e and from d to c that do not include the edges (b, e) and (d, c), respectively. In addition, (a, b), (c, d) and (e, a) are all both initial and final. (b, c) is neither initial nor final because there is a path from b to c that starts with (b, e) and ends with (d, c). For similar reasons, (d, e) is neither initial nor final. e d a Figure 2: Graph of a simplified DTD. Consider the query Q 1 = a//b//c//d. This fragment is essential because each pair is essential, and because (a, b) is initial and (c, d) is final. Now consider the query Q 2 = a//b//e//c//d. Neither (b, e) nor (e, c) is essential, the latter because there is no edge (e, c) E(G). So there are two essential fragments of length one in Q 2, namely, a//b and c//d. Allocating operators to groups in an essential fragment really only makes sense when the fragment contains at least b c
6 two operators. So we first consider the special case of an essential fragment comprising a single pair (x, y). If the operator between x and y is /, there is nothing to be done. However, if the operator is //, we can replace it by / while preserving G-equivalence in the following situations: if x is preceded by // and y is followed by //, if x is preceded by //, y is followed by / (or is the final query node), and x is in a non-trivial SCC S while y is either in a trivial SCC or also in S, if x is preceded by / (or is the first query node), y is followed by //, and y is in a non-trivial SCC S while x is either in a trivial SCC or also in S. Example 7. Recall the query Q 2 from Example 6. Since a//b is followed by // and c//d is preceded by // (and a, b, c and d are all in the same SCC), the // operator in each can be replaced by / to give the G-equivalent query a/b//e//c/d. This query is G-equivalent to Q 2 because any path from a to e via b in G must start with (a, b), while any path from e to d via c must end with (c, d) After dealing with essential fragments of length one, we can assign the operators in longer fragments to groups using the following rules for rewriting. We start with an essential fragment a 1 $ 1 a 2 $ 2 $ n 1 a n, n > 2, of Q. We now perform the following three steps: 1. (Overlapping groups) Rewrite the fragment assigning operators to groups as follows: a 1 $ 1 1 a 1 2 $ 2 2 $ n 2 n 1 an. Note that the first and last operators in the fragment are each in only one group. 2. (Extend groups) Apply the rule a j 1 i 2 $ i 1 j 1 a j i 1 $ i j a j+1 a j 1 $ i 2 j 1 a j i 2 $ i j a j+1 for any (a j 1, a j), 2 j n, that is both initial and final. 3. (Separate groups) Apply the rule a j 1 i 2 $ i 1 j 1 a j i 1 $ i j a j+1 a j 1 $ i 2 j 1 a j $ i j a j+1 for any (a j, a j+1) that is initial and (a j 1, a j) that is final, 2 j n 1. Step (1) is applied once, then step (2) as many times as possible, and finally step (3) as many times as possible. After applying each rule, we re-number the groups to ensure that their numbers remain consecutive (so that further rule applications can occur). At the end, if any group i contains only / operators, we remove the group number i from each operator in the group. For each remaining group, we replace each $ i by. We now try to give the intuition behind the above steps. For simplicity, assume that the initial essential fragment Q uses only // operators. By assigning all the operators to overlapping groups in a generalised query Q, the most specific queries in the expansion of Q are ones in which the operators / and // alternate. This is correct when all of the internal pairs of Q are only essential, but not initial nor final. If we have pairs that are both initial and final, then we can extend groups, as in step (2) above, which will allow for more occurrences of within a group to be replaced by / in an expansion. Finally, we can separate two groups by removing an intervening group as in step (3) if the last pair in the first group is final and the first pair in the second group is initial. Example 8. Recall the query Q 1 from Example 6. Step (1) of the rewriting produces a// 1 b 1 // 2 c// 2 d. Since (b, c) is neither initial nor final, steps (2) and (3) cannot be applied. Finally, each // is replaced by to give the generalised query a 1 b 1 2 c 2 d. So Q 1 is G-equivalent to each of a/b//c/d and a//b/c//d, where each group has a single // operator. Note that Q 1 is not G-equivalent to more specific queries such as a/b/c//d or a//b/c/d. Now consider the query Q 3 = a//b//c//d//e//a. Once again, the whole fragment is essential, but this time step (2) of the rewriting can be applied because (c, d) is both initial and final. So the rewriting produces a 1 b 1 2 c 2 d 2 3 e 3 a, with three operators being in group 2. Hence, Q 3 is G- equivalent to (among others) a/b//c/d/e//a, a//b/c/d//e/a and a//b/c//d/e//a. For example, in the first case, any path from b to a via c, d and e in G must pass through the sequence (c, d, e), so it is safe to separate c, d and e by / operators. Similarly, in the second case, any path from a to e via b, c and d in G must pass through the sequence (b, c, d), so it is safe to separate b, c and d by / operators. Starting with any of the three queries above would give rise to the same rewriting since both / and // operators within a group are replaced by operators. Given a query Q, we denote by Q the result of applying the above rewriting to each essential fragment of Q. Lemma 5. Let Q be in XP(/, //), G be a simplified DTD, and C be the set of PCs and ICs inferred from G. Then Q G Q C. 4.3 Generalised Containment Mappings We now need to define the notion of a containment mapping from a query P in XP(/, //) to a generalised query Q in XP(/, //, ), by taking into account how child and descendant edges in P can map to edges in Q. The basic idea is that no group in Q must have each pair in it mapped to by a child edge of P. Let P be in XP(/, //) and Q be in XP(/, //, ). A (generalised) containment mapping from P to Q is a function h : N(P ) N(Q) satisfying the root-preserving and labelpreserving properties as before, as well as: child-edge-preserving: for each (x, y) E / (P ), we have (h(x), h(y)) E / (Q) E (Q), descendant-edge-preserving: for each (x, y) E // (P ), we have (h(x), h(y)) E + (Q), and group-preserving: it is not the case that, in some group in Q, each pair (u, v) in the group has both h 1 (u) and h 1 (v) defined and has (h 1 (u), h 1 (v)) E / (P ). Theorem 2. Let P and Q be in XP(/, //), G be a simplified DTD, and C be the set of PCs and ICs inferred from G. Then P G Q if and only if there is a generalised containment mapping from P to Q C. We now present Algorithm 1 which, given queries P in XP(/, //) and Q in XP(/, //, ), checks whether there is a
7 generalised containment mapping from P to Q, and hence, by Theorem 2, whether P G Q. The algorithm is modelled after that used in [5]. Two Boolean tables C(u, x) and D(u, x), for u N(P ) and x N(Q), are constructed. C(u, x) is true if there is a containment mapping from the subtree rooted at u to the subtree rooted at x; D(u, x) is true if there is a containment mapping from the subtree rooted at u to the subtree rooted at x or one of its descendants. Of course we also need to ensure that the group-preserving property of containment mappings is satisfied. The structure of a generalised query ensures that each operator is in either one or two groups. We consider a node x in Q to be in the group(s) of the operator that follows x in Q. Two consecutive nodes in a query can have at most one group in common. A third Boolean table G(u, x, i) in Algorithm 1 denotes whether, by mapping u in P to x in Q, group i in Q has had a // operator mapped to it. We use last(x, i) to denote whether node x in group i in Q is the last node in group i (when processing nodes bottom-up or from right-to-left). Algorithm 1: Decide if P Q Input: queries P in XP(/, //), Q in XP(/, //, ) Output: whether P Q 1 foreach u N(P ) and x in group i in N(Q) do 2 G(u, x, i) false 3 foreach x N(Q) do // bottom-up 4 foreach u N(P ) do // bottom-up 5 if leaf(u) λ(u) = λ(x) then 6 foreach group i of x do G(u, x, i) true 7 C(u, x) D(u, x) true; break 8 if leaf(x) then 9 C(u, x) D(u, x) false; break 10 let y be the child of x // x is not a leaf 11 if λ(u) λ(x) then 12 C(u, x) false; D(u, x) D(u, y); break 13 let v be the child of u // u is not a leaf 14 if (u, v) E / (P ) then 15 if (x, y) E / (Q) then C(u, x) C(v, y) 16 else if (x, y) E (Q) then 17 if x and y are in the same group i then 18 G(u, x, i) G(v, y, i) 19 if last(x, i) G(u, x, i) then 20 C(u, x) false 21 else 22 C(u, x) C(v, y) 23 else C(u, x) false // (x, y) E // (Q) 24 else// (u, v) E // (P ) 25 if (x, y) E (Q) then 26 foreach group i of x do G(u, x, i) D(v, y) 27 C(u, x) D(v, y) 28 D(u, x) C(u, x) D(u, y) 29 output C(root(P ), root(q)) Example 9. Recall the query Q 1 from Examples 6 and 8, rewritten as the generalised query a 1 b 1 2 c 2 d. Let us refer to this query as Q, with P being a/b//c/d. The crucial step in applying Algorithm 1 is when processing b N(Q) and b N(P ). Since (b, c) E // (P ), line 24 applies. Since (b, c) E (Q) and b is in both groups 1 and 2, G(b, b, 1) and G(b, b, 2) are set to D(c, c), which is true, in line 26. Then when a N(Q) and a N(P ) are processed, because (a, b) E / (P ), line 14 applies. Since (a, b) E (Q) and both a and b are in group 1, G(a, a, 1) is set equal to G(b, b, 1) which is true. Then although last(a, 1) is true, G(a, a, 1) is false, so line 22 sets C(a, a) to C(b, b) which is true. Assume instead that P is simply a/b. Now when processing b N(Q) and b N(P ), because b N(P ) is a leaf, line 6 applies, setting G(b, b, 1) to true. Processing then proceeds as above for a N(Q) and a N(P ). Now assume that P is a/b//d. When processing b N(Q) and b N(P ), line 24 applies because (b, d) E // (P ). Because there is a descendant of c N(Q) to which d N(P ) can map, D(d, c) is true. Hence G(b, b, 1) is set to true in line 26. On the other hand, assume that P is a/b/c. When processing b N(Q) and b N(P ), line 16 applies because (b, c) E / (P ) and (b, c) E (Q). Nodes b and c are both in group 2, so G(b, b, 2) is set to G(c, c, 2) which is true by virtue of c being a leaf in P and line 6. Although b is last in group 2, G(b, b, 2) is true, so line 22 sets C(b, b) to C(c, c) which is true. When processing a N(Q) and a N(P ), line 16 applies again because (a, b) E / (P ) and (a, b) E (Q). Nodes a and b are both in group 1, so G(a, a, 1) is set to G(b, b, 1) which is false. Now a is last in group 1 and G(a, a, 1) is false, so C(a, a) is set to false in line 20. Proposition 1. For P in XP(/, //) and Q in XP(/, //, ), Algorithm 1 correctly determines whether there is a generalised containment mapping from P to Q. If P has n nodes and Q has m nodes, then Algorithm 1 runs in time O(nm). 5. CONCLUSION AND FUTURE WORK We have studied the problem of using the chase procedure and containment mappings to test containment of XPath queries in XP(DTD, /, //). Previous approaches considered either simplified, non-recursive DTDs [4] or simplified recursive DTDs but without the guarantee of the chase terminating [8]. Although both papers applied their techniques to XP(DTD, /, [], //), the incompleteness of the first in the presence of general non-recursive DTDs and the non-termination of the second apply also to the smaller XPath fragment XP(DTD, /, //). In this paper, we have introduced a new constraint, called a family constraint, which generalises the sibling and cousin constraints used previously and restores completeness to the chase procedure for testing containment of queries in XP(DTD, /, //) in the presence of general non-recursive DTDS. In the case of simplified recursive DTDs, we have introduced a generalised form of XPath syntax, which allows for the representation of an exponential number of equivalent queries, and a generalised form of containment mapping so that the chase can still be used as a polynomial-time test for containment. We believe these results can be combined in order to provide a polynomial-time test for containment of queries in XP(DTD, /, //) using the chase in the presence of fully general DTDs.
8 6. ACKNOWLEDGEMENTS We would like to thank the anonymous reviewers for their constructive comments which helped to improve the paper. 7. REFERENCES [1] S. Amer-Yahia, S. Cho, L. V. S. Lakshmanan, and D. Srivastava. Tree pattern query minimization. The VLDB Journal, 11(4): , [2] A. Deutsch and V. Tannen. XPath queries and constraints, containment and reformulation. Theoretical Computer Science, 336(1):57 87, [3] P. Genevès, N. Layaïda, and A. Schmitt. Efficient static analysis of XML paths and types. In Proc. ACM SIGPLAN Conf. on Programming Language Design and Implementation, pages , [4] L. V. S. Lakshmanan, H. W. Wang, and Z. J. Zhao. Answering tree pattern queries using views. In Proc. 32nd Int. Conf. on Very Large Data Bases, pages , [5] G. Miklau and D. Suciu. Containment and equivalence for a fragment of XPath. J. ACM, 51(1):2 45, January [6] F. Neven and T. Schwentick. On the complexity of XPath containment in the presence of disjunction, DTDs, and variables. Logical Methods in Computer Science, 2(3):1 30, [7] B. ten Cate and C. Lutz. The complexity of query containment in expressive fragments of XPath 2.0. J. ACM, 56(6):31:1 31:48, September [8] J. Wang and J. X. Yu. Chasing tree patterns under recursive DTDs. In Proc. 15th Int. Conf. on Database Systems for Advanced Applications, pages , [9] P. T. Wood. Minimising simple XPath expressions. In Proc. WebDB 2001: Int. Workshop on the Web and Databases, pages 13 18, [10] P. T. Wood. Containment for XPath fragments under DTD constraints. In Proc. 9th Int. Conf. on Database Theory, pages , 2003.
Treewidth and graph minors
 Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
XML and Databases. Lecture 9 Properties of XPath. Sebastian Maneth NICTA and UNSW
 XML and Databases Lecture 9 Properties of XPath Sebastian Maneth NICTA and UNSW CSE@UNSW -- Semester 1, 2009 Outline 1. XPath Equivalence 2. No Looking Back: How to Remove Backward Axes 3. Containment
XML and Databases Lecture 9 Properties of XPath Sebastian Maneth NICTA and UNSW CSE@UNSW -- Semester 1, 2009 Outline 1. XPath Equivalence 2. No Looking Back: How to Remove Backward Axes 3. Containment
Designing Views to Answer Queries under Set, Bag,and BagSet Semantics
 Designing Views to Answer Queries under Set, Bag,and BagSet Semantics Rada Chirkova Department of Computer Science, North Carolina State University Raleigh, NC 27695-7535 chirkova@csc.ncsu.edu Foto Afrati
Designing Views to Answer Queries under Set, Bag,and BagSet Semantics Rada Chirkova Department of Computer Science, North Carolina State University Raleigh, NC 27695-7535 chirkova@csc.ncsu.edu Foto Afrati
Binary Decision Diagrams
 Logic and roof Hilary 2016 James Worrell Binary Decision Diagrams A propositional formula is determined up to logical equivalence by its truth table. If the formula has n variables then its truth table
Logic and roof Hilary 2016 James Worrell Binary Decision Diagrams A propositional formula is determined up to logical equivalence by its truth table. If the formula has n variables then its truth table
Evaluating XPath Queries
 Chapter 8 Evaluating XPath Queries Peter Wood (BBK) XML Data Management 201 / 353 Introduction When XML documents are small and can fit in memory, evaluating XPath expressions can be done efficiently But
Chapter 8 Evaluating XPath Queries Peter Wood (BBK) XML Data Management 201 / 353 Introduction When XML documents are small and can fit in memory, evaluating XPath expressions can be done efficiently But
The Structure of Bull-Free Perfect Graphs
 The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
Boolean Representations and Combinatorial Equivalence
 Chapter 2 Boolean Representations and Combinatorial Equivalence This chapter introduces different representations of Boolean functions. It then discusses the applications of these representations for proving
Chapter 2 Boolean Representations and Combinatorial Equivalence This chapter introduces different representations of Boolean functions. It then discusses the applications of these representations for proving
Example using multiple predicates
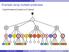 XPath Example using multiple predicates //performance[conductor][date] L C C C C p c s p p s o t d p p c p p Peter Wood (BBK) XML Data Management 162 / 366 XPath Further examples with predicates //performance[composer='frederic
XPath Example using multiple predicates //performance[conductor][date] L C C C C p c s p p s o t d p p c p p Peter Wood (BBK) XML Data Management 162 / 366 XPath Further examples with predicates //performance[composer='frederic
NP-Completeness of Minimal Width Unordered Tree Layout
 Journal of Graph Algorithms and Applications http://jgaa.info/ vol. 8, no. 3, pp. 295 312 (2004) NP-Completeness of Minimal Width Unordered Tree Layout Kim Marriott School of Computer Science and Software
Journal of Graph Algorithms and Applications http://jgaa.info/ vol. 8, no. 3, pp. 295 312 (2004) NP-Completeness of Minimal Width Unordered Tree Layout Kim Marriott School of Computer Science and Software
Conjunctive queries. Many computational problems are much easier for conjunctive queries than for general first-order queries.
 Conjunctive queries Relational calculus queries without negation and disjunction. Conjunctive queries have a normal form: ( y 1 ) ( y n )(p 1 (x 1,..., x m, y 1,..., y n ) p k (x 1,..., x m, y 1,..., y
Conjunctive queries Relational calculus queries without negation and disjunction. Conjunctive queries have a normal form: ( y 1 ) ( y n )(p 1 (x 1,..., x m, y 1,..., y n ) p k (x 1,..., x m, y 1,..., y
Joint Entity Resolution
 Joint Entity Resolution Steven Euijong Whang, Hector Garcia-Molina Computer Science Department, Stanford University 353 Serra Mall, Stanford, CA 94305, USA {swhang, hector}@cs.stanford.edu No Institute
Joint Entity Resolution Steven Euijong Whang, Hector Garcia-Molina Computer Science Department, Stanford University 353 Serra Mall, Stanford, CA 94305, USA {swhang, hector}@cs.stanford.edu No Institute
CS521 \ Notes for the Final Exam
 CS521 \ Notes for final exam 1 Ariel Stolerman Asymptotic Notations: CS521 \ Notes for the Final Exam Notation Definition Limit Big-O ( ) Small-o ( ) Big- ( ) Small- ( ) Big- ( ) Notes: ( ) ( ) ( ) ( )
CS521 \ Notes for final exam 1 Ariel Stolerman Asymptotic Notations: CS521 \ Notes for the Final Exam Notation Definition Limit Big-O ( ) Small-o ( ) Big- ( ) Small- ( ) Big- ( ) Notes: ( ) ( ) ( ) ( )
A more efficient algorithm for perfect sorting by reversals
 A more efficient algorithm for perfect sorting by reversals Sèverine Bérard 1,2, Cedric Chauve 3,4, and Christophe Paul 5 1 Département de Mathématiques et d Informatique Appliquée, INRA, Toulouse, France.
A more efficient algorithm for perfect sorting by reversals Sèverine Bérard 1,2, Cedric Chauve 3,4, and Christophe Paul 5 1 Département de Mathématiques et d Informatique Appliquée, INRA, Toulouse, France.
The Inverse of a Schema Mapping
 The Inverse of a Schema Mapping Jorge Pérez Department of Computer Science, Universidad de Chile Blanco Encalada 2120, Santiago, Chile jperez@dcc.uchile.cl Abstract The inversion of schema mappings has
The Inverse of a Schema Mapping Jorge Pérez Department of Computer Science, Universidad de Chile Blanco Encalada 2120, Santiago, Chile jperez@dcc.uchile.cl Abstract The inversion of schema mappings has
The NEXT Framework for Logical XQuery Optimization
 The NEXT Framework for Logical XQuery Optimization Alin Deutsch Yannis Papakonstantinou Yu Xu University of California, San Diego deutsch,yannis,yxu @cs.ucsd.edu Abstract Classical logical optimization
The NEXT Framework for Logical XQuery Optimization Alin Deutsch Yannis Papakonstantinou Yu Xu University of California, San Diego deutsch,yannis,yxu @cs.ucsd.edu Abstract Classical logical optimization
 This article was originally published in a journal published by Elsevier, and the attached copy is provided by Elsevier for the author s benefit and for the benefit of the author s institution, for non-commercial
This article was originally published in a journal published by Elsevier, and the attached copy is provided by Elsevier for the author s benefit and for the benefit of the author s institution, for non-commercial
Safe Stratified Datalog With Integer Order Does not Have Syntax
 Safe Stratified Datalog With Integer Order Does not Have Syntax Alexei P. Stolboushkin Department of Mathematics UCLA Los Angeles, CA 90024-1555 aps@math.ucla.edu Michael A. Taitslin Department of Computer
Safe Stratified Datalog With Integer Order Does not Have Syntax Alexei P. Stolboushkin Department of Mathematics UCLA Los Angeles, CA 90024-1555 aps@math.ucla.edu Michael A. Taitslin Department of Computer
Reasoning about XML Update Constraints
 Reasoning about XML Update Constraints Bogdan Cautis INRIA Futurs & U. Paris Sud bogdan.cautis@inria.fr Serge Abiteboul INRIA Futurs & U. Paris Sud serge.abiteboul@inria.fr Tova Milo Tel Aviv U. milo@cs.tau.ac.il
Reasoning about XML Update Constraints Bogdan Cautis INRIA Futurs & U. Paris Sud bogdan.cautis@inria.fr Serge Abiteboul INRIA Futurs & U. Paris Sud serge.abiteboul@inria.fr Tova Milo Tel Aviv U. milo@cs.tau.ac.il
XML Data Exchange. Marcelo Arenas P. Universidad Católica de Chile. Joint work with Leonid Libkin (U. of Toronto)
 XML Data Exchange Marcelo Arenas P. Universidad Católica de Chile Joint work with Leonid Libkin (U. of Toronto) Data Exchange in Relational Databases Data exchange has been extensively studied in the relational
XML Data Exchange Marcelo Arenas P. Universidad Católica de Chile Joint work with Leonid Libkin (U. of Toronto) Data Exchange in Relational Databases Data exchange has been extensively studied in the relational
COMP9319 Web Data Compression & Search. Cloud and data optimization XPath containment Distributed path expression processing
 COMP9319 Web Data Compression & Search Cloud and data optimization XPath containment Distributed path expression processing DATA OPTIMIZATION ON CLOUD Cloud Virtualization Cloud layers Cloud computing
COMP9319 Web Data Compression & Search Cloud and data optimization XPath containment Distributed path expression processing DATA OPTIMIZATION ON CLOUD Cloud Virtualization Cloud layers Cloud computing
Foundations of Schema Mapping Management
 Foundations of Schema Mapping Management Marcelo Arenas Jorge Pérez Juan Reutter Cristian Riveros PUC Chile PUC Chile University of Edinburgh Oxford University marenas@ing.puc.cl jperez@ing.puc.cl juan.reutter@ed.ac.uk
Foundations of Schema Mapping Management Marcelo Arenas Jorge Pérez Juan Reutter Cristian Riveros PUC Chile PUC Chile University of Edinburgh Oxford University marenas@ing.puc.cl jperez@ing.puc.cl juan.reutter@ed.ac.uk
Monotone Constraints in Frequent Tree Mining
 Monotone Constraints in Frequent Tree Mining Jeroen De Knijf Ad Feelders Abstract Recent studies show that using constraints that can be pushed into the mining process, substantially improves the performance
Monotone Constraints in Frequent Tree Mining Jeroen De Knijf Ad Feelders Abstract Recent studies show that using constraints that can be pushed into the mining process, substantially improves the performance
On Resolution Proofs for Combinational Equivalence Checking
 On Resolution Proofs for Combinational Equivalence Checking Satrajit Chatterjee Alan Mishchenko Robert Brayton Department of EECS U. C. Berkeley {satrajit, alanmi, brayton}@eecs.berkeley.edu Andreas Kuehlmann
On Resolution Proofs for Combinational Equivalence Checking Satrajit Chatterjee Alan Mishchenko Robert Brayton Department of EECS U. C. Berkeley {satrajit, alanmi, brayton}@eecs.berkeley.edu Andreas Kuehlmann
Introduction to Automata Theory. BİL405 - Automata Theory and Formal Languages 1
 Introduction to Automata Theory BİL405 - Automata Theory and Formal Languages 1 Automata, Computability and Complexity Automata, Computability and Complexity are linked by the question: What are the fundamental
Introduction to Automata Theory BİL405 - Automata Theory and Formal Languages 1 Automata, Computability and Complexity Automata, Computability and Complexity are linked by the question: What are the fundamental
Graphs. Part I: Basic algorithms. Laura Toma Algorithms (csci2200), Bowdoin College
 Laura Toma Algorithms (csci2200), Bowdoin College Undirected graphs Concepts: connectivity, connected components paths (undirected) cycles Basic problems, given undirected graph G: is G connected how many
Laura Toma Algorithms (csci2200), Bowdoin College Undirected graphs Concepts: connectivity, connected components paths (undirected) cycles Basic problems, given undirected graph G: is G connected how many
Semantic Characterizations of XPath
 Semantic Characterizations of XPath Maarten Marx Informatics Institute, University of Amsterdam, The Netherlands CWI, April, 2004 1 Overview Navigational XPath is a language to specify sets and paths in
Semantic Characterizations of XPath Maarten Marx Informatics Institute, University of Amsterdam, The Netherlands CWI, April, 2004 1 Overview Navigational XPath is a language to specify sets and paths in
On the Hardness of Counting the Solutions of SPARQL Queries
 On the Hardness of Counting the Solutions of SPARQL Queries Reinhard Pichler and Sebastian Skritek Vienna University of Technology, Faculty of Informatics {pichler,skritek}@dbai.tuwien.ac.at 1 Introduction
On the Hardness of Counting the Solutions of SPARQL Queries Reinhard Pichler and Sebastian Skritek Vienna University of Technology, Faculty of Informatics {pichler,skritek}@dbai.tuwien.ac.at 1 Introduction
XML databases. Jan Chomicki. University at Buffalo. Jan Chomicki (University at Buffalo) XML databases 1 / 9
 XML databases Jan Chomicki University at Buffalo Jan Chomicki (University at Buffalo) XML databases 1 / 9 Outline 1 XML data model 2 XPath 3 XQuery Jan Chomicki (University at Buffalo) XML databases 2
XML databases Jan Chomicki University at Buffalo Jan Chomicki (University at Buffalo) XML databases 1 / 9 Outline 1 XML data model 2 XPath 3 XQuery Jan Chomicki (University at Buffalo) XML databases 2
Faster parameterized algorithms for Minimum Fill-In
 Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Technical Report UU-CS-2008-042 December 2008 Department of Information and Computing Sciences Utrecht
Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Technical Report UU-CS-2008-042 December 2008 Department of Information and Computing Sciences Utrecht
Consistency and Set Intersection
 Consistency and Set Intersection Yuanlin Zhang and Roland H.C. Yap National University of Singapore 3 Science Drive 2, Singapore {zhangyl,ryap}@comp.nus.edu.sg Abstract We propose a new framework to study
Consistency and Set Intersection Yuanlin Zhang and Roland H.C. Yap National University of Singapore 3 Science Drive 2, Singapore {zhangyl,ryap}@comp.nus.edu.sg Abstract We propose a new framework to study
Answering Pattern Queries Using Views
 Answering Pattern Queries Using iews Wenfei Fan,2 Xin Wang 3 Yinghui Wu 4 University of Edinburgh 2 RCBD and SKLSDE Lab, Beihang University 3 Southwest Jiaotong University 4 Washington State University
Answering Pattern Queries Using iews Wenfei Fan,2 Xin Wang 3 Yinghui Wu 4 University of Edinburgh 2 RCBD and SKLSDE Lab, Beihang University 3 Southwest Jiaotong University 4 Washington State University
Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1
 CME 305: Discrete Mathematics and Algorithms Instructor: Professor Aaron Sidford (sidford@stanford.edu) January 11, 2018 Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1 In this lecture
CME 305: Discrete Mathematics and Algorithms Instructor: Professor Aaron Sidford (sidford@stanford.edu) January 11, 2018 Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1 In this lecture
Recoloring k-degenerate graphs
 Recoloring k-degenerate graphs Jozef Jirásek jirasekjozef@gmailcom Pavel Klavík pavel@klavikcz May 2, 2008 bstract This article presents several methods of transforming a given correct coloring of a k-degenerate
Recoloring k-degenerate graphs Jozef Jirásek jirasekjozef@gmailcom Pavel Klavík pavel@klavikcz May 2, 2008 bstract This article presents several methods of transforming a given correct coloring of a k-degenerate
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018
 Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 11 Ana Bove April 26th 2018 Recap: Regular Languages Decision properties of RL: Is it empty? Does it contain this word? Contains
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2018 Lecture 11 Ana Bove April 26th 2018 Recap: Regular Languages Decision properties of RL: Is it empty? Does it contain this word? Contains
A Structural Numbering Scheme for XML Data
 A Structural Numbering Scheme for XML Data Alfred M. Martin WS2002/2003 February/March 2003 Based on workout made during the EDBT 2002 Workshops Dao Dinh Khal, Masatoshi Yoshikawa, and Shunsuke Uemura
A Structural Numbering Scheme for XML Data Alfred M. Martin WS2002/2003 February/March 2003 Based on workout made during the EDBT 2002 Workshops Dao Dinh Khal, Masatoshi Yoshikawa, and Shunsuke Uemura
Faster parameterized algorithms for Minimum Fill-In
 Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Abstract We present two parameterized algorithms for the Minimum Fill-In problem, also known as Chordal
Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Abstract We present two parameterized algorithms for the Minimum Fill-In problem, also known as Chordal
XML Research for Formal Language Theorists
 XML Research for Formal Language Theorists Wim Martens TU Dortmund Wim Martens (TU Dortmund) XML for Formal Language Theorists May 14, 2008 1 / 65 Goal of this talk XML Research vs Formal Languages Wim
XML Research for Formal Language Theorists Wim Martens TU Dortmund Wim Martens (TU Dortmund) XML for Formal Language Theorists May 14, 2008 1 / 65 Goal of this talk XML Research vs Formal Languages Wim
Discrete Optimization. Lecture Notes 2
 Discrete Optimization. Lecture Notes 2 Disjunctive Constraints Defining variables and formulating linear constraints can be straightforward or more sophisticated, depending on the problem structure. The
Discrete Optimization. Lecture Notes 2 Disjunctive Constraints Defining variables and formulating linear constraints can be straightforward or more sophisticated, depending on the problem structure. The
On The Complexity of Virtual Topology Design for Multicasting in WDM Trees with Tap-and-Continue and Multicast-Capable Switches
 On The Complexity of Virtual Topology Design for Multicasting in WDM Trees with Tap-and-Continue and Multicast-Capable Switches E. Miller R. Libeskind-Hadas D. Barnard W. Chang K. Dresner W. M. Turner
On The Complexity of Virtual Topology Design for Multicasting in WDM Trees with Tap-and-Continue and Multicast-Capable Switches E. Miller R. Libeskind-Hadas D. Barnard W. Chang K. Dresner W. M. Turner
Applied Algorithm Design Lecture 3
 Applied Algorithm Design Lecture 3 Pietro Michiardi Eurecom Pietro Michiardi (Eurecom) Applied Algorithm Design Lecture 3 1 / 75 PART I : GREEDY ALGORITHMS Pietro Michiardi (Eurecom) Applied Algorithm
Applied Algorithm Design Lecture 3 Pietro Michiardi Eurecom Pietro Michiardi (Eurecom) Applied Algorithm Design Lecture 3 1 / 75 PART I : GREEDY ALGORITHMS Pietro Michiardi (Eurecom) Applied Algorithm
A CSP Search Algorithm with Reduced Branching Factor
 A CSP Search Algorithm with Reduced Branching Factor Igor Razgon and Amnon Meisels Department of Computer Science, Ben-Gurion University of the Negev, Beer-Sheva, 84-105, Israel {irazgon,am}@cs.bgu.ac.il
A CSP Search Algorithm with Reduced Branching Factor Igor Razgon and Amnon Meisels Department of Computer Science, Ben-Gurion University of the Negev, Beer-Sheva, 84-105, Israel {irazgon,am}@cs.bgu.ac.il
Semantics via Syntax. f (4) = if define f (x) =2 x + 55.
 1 Semantics via Syntax The specification of a programming language starts with its syntax. As every programmer knows, the syntax of a language comes in the shape of a variant of a BNF (Backus-Naur Form)
1 Semantics via Syntax The specification of a programming language starts with its syntax. As every programmer knows, the syntax of a language comes in the shape of a variant of a BNF (Backus-Naur Form)
Reduced branching-factor algorithms for constraint satisfaction problems
 Reduced branching-factor algorithms for constraint satisfaction problems Igor Razgon and Amnon Meisels Department of Computer Science, Ben-Gurion University of the Negev, Beer-Sheva, 84-105, Israel {irazgon,am}@cs.bgu.ac.il
Reduced branching-factor algorithms for constraint satisfaction problems Igor Razgon and Amnon Meisels Department of Computer Science, Ben-Gurion University of the Negev, Beer-Sheva, 84-105, Israel {irazgon,am}@cs.bgu.ac.il
Propositional Logic. Part I
 Part I Propositional Logic 1 Classical Logic and the Material Conditional 1.1 Introduction 1.1.1 The first purpose of this chapter is to review classical propositional logic, including semantic tableaux.
Part I Propositional Logic 1 Classical Logic and the Material Conditional 1.1 Introduction 1.1.1 The first purpose of this chapter is to review classical propositional logic, including semantic tableaux.
Graph Matching Based Authorization Model for Efficient Secure XML Querying
 Graph Matching Based Authorization Model for Efficient Secure XML Querying Seunghan Chang 1, Artem Chebotko 1, Shiyong Lu, and Farshad Fotouhi Department of Computer Science, Wayne State University, 5143
Graph Matching Based Authorization Model for Efficient Secure XML Querying Seunghan Chang 1, Artem Chebotko 1, Shiyong Lu, and Farshad Fotouhi Department of Computer Science, Wayne State University, 5143
Trees Rooted Trees Spanning trees and Shortest Paths. 12. Graphs and Trees 2. Aaron Tan November 2017
 12. Graphs and Trees 2 Aaron Tan 6 10 November 2017 1 10.5 Trees 2 Definition Definition Definition: Tree A graph is said to be circuit-free if, and only if, it has no circuits. A graph is called a tree
12. Graphs and Trees 2 Aaron Tan 6 10 November 2017 1 10.5 Trees 2 Definition Definition Definition: Tree A graph is said to be circuit-free if, and only if, it has no circuits. A graph is called a tree
Core Membership Computation for Succinct Representations of Coalitional Games
 Core Membership Computation for Succinct Representations of Coalitional Games Xi Alice Gao May 11, 2009 Abstract In this paper, I compare and contrast two formal results on the computational complexity
Core Membership Computation for Succinct Representations of Coalitional Games Xi Alice Gao May 11, 2009 Abstract In this paper, I compare and contrast two formal results on the computational complexity
Comparison of XPath Containment Algorithms
 Comparison of XPath Containment Algorithms Jorge Guerra 1, Luis Useche 1, Miguel Rivero 1, Imtiaz Syed 1, Hussein Orelus 1, Malek Adjouadi 1, Armando Barreto 1, Bradley Stoute 2, Scott Graham 1, Naphtali
Comparison of XPath Containment Algorithms Jorge Guerra 1, Luis Useche 1, Miguel Rivero 1, Imtiaz Syed 1, Hussein Orelus 1, Malek Adjouadi 1, Armando Barreto 1, Bradley Stoute 2, Scott Graham 1, Naphtali
Edge Colorings of Complete Multipartite Graphs Forbidding Rainbow Cycles
 Theory and Applications of Graphs Volume 4 Issue 2 Article 2 November 2017 Edge Colorings of Complete Multipartite Graphs Forbidding Rainbow Cycles Peter Johnson johnspd@auburn.edu Andrew Owens Auburn
Theory and Applications of Graphs Volume 4 Issue 2 Article 2 November 2017 Edge Colorings of Complete Multipartite Graphs Forbidding Rainbow Cycles Peter Johnson johnspd@auburn.edu Andrew Owens Auburn
DOUBLE DOMINATION CRITICAL AND STABLE GRAPHS UPON VERTEX REMOVAL 1
 Discussiones Mathematicae Graph Theory 32 (2012) 643 657 doi:10.7151/dmgt.1633 DOUBLE DOMINATION CRITICAL AND STABLE GRAPHS UPON VERTEX REMOVAL 1 Soufiane Khelifi Laboratory LMP2M, Bloc of laboratories
Discussiones Mathematicae Graph Theory 32 (2012) 643 657 doi:10.7151/dmgt.1633 DOUBLE DOMINATION CRITICAL AND STABLE GRAPHS UPON VERTEX REMOVAL 1 Soufiane Khelifi Laboratory LMP2M, Bloc of laboratories
On Universal Cycles of Labeled Graphs
 On Universal Cycles of Labeled Graphs Greg Brockman Harvard University Cambridge, MA 02138 United States brockman@hcs.harvard.edu Bill Kay University of South Carolina Columbia, SC 29208 United States
On Universal Cycles of Labeled Graphs Greg Brockman Harvard University Cambridge, MA 02138 United States brockman@hcs.harvard.edu Bill Kay University of South Carolina Columbia, SC 29208 United States
Constrained Types and their Expressiveness
 Constrained Types and their Expressiveness JENS PALSBERG Massachusetts Institute of Technology and SCOTT SMITH Johns Hopkins University A constrained type consists of both a standard type and a constraint
Constrained Types and their Expressiveness JENS PALSBERG Massachusetts Institute of Technology and SCOTT SMITH Johns Hopkins University A constrained type consists of both a standard type and a constraint
XI International PhD Workshop OWD 2009, October Fuzzy Sets as Metasets
 XI International PhD Workshop OWD 2009, 17 20 October 2009 Fuzzy Sets as Metasets Bartłomiej Starosta, Polsko-Japońska WyŜsza Szkoła Technik Komputerowych (24.01.2008, prof. Witold Kosiński, Polsko-Japońska
XI International PhD Workshop OWD 2009, 17 20 October 2009 Fuzzy Sets as Metasets Bartłomiej Starosta, Polsko-Japońska WyŜsza Szkoła Technik Komputerowych (24.01.2008, prof. Witold Kosiński, Polsko-Japońska
A Fast Algorithm for Optimal Alignment between Similar Ordered Trees
 Fundamenta Informaticae 56 (2003) 105 120 105 IOS Press A Fast Algorithm for Optimal Alignment between Similar Ordered Trees Jesper Jansson Department of Computer Science Lund University, Box 118 SE-221
Fundamenta Informaticae 56 (2003) 105 120 105 IOS Press A Fast Algorithm for Optimal Alignment between Similar Ordered Trees Jesper Jansson Department of Computer Science Lund University, Box 118 SE-221
Simpler, Linear-time Transitive Orientation via Lexicographic Breadth-First Search
 Simpler, Linear-time Transitive Orientation via Lexicographic Breadth-First Search Marc Tedder University of Toronto arxiv:1503.02773v1 [cs.ds] 10 Mar 2015 Abstract Comparability graphs are the undirected
Simpler, Linear-time Transitive Orientation via Lexicographic Breadth-First Search Marc Tedder University of Toronto arxiv:1503.02773v1 [cs.ds] 10 Mar 2015 Abstract Comparability graphs are the undirected
XPath with transitive closure
 XPath with transitive closure Logic and Databases Feb 2006 1 XPath with transitive closure Logic and Databases Feb 2006 2 Navigating XML trees XPath with transitive closure Newton Institute: Logic and
XPath with transitive closure Logic and Databases Feb 2006 1 XPath with transitive closure Logic and Databases Feb 2006 2 Navigating XML trees XPath with transitive closure Newton Institute: Logic and
Structural Characterizations of Schema-Mapping Languages
 Structural Characterizations of Schema-Mapping Languages Balder ten Cate University of Amsterdam and UC Santa Cruz balder.tencate@uva.nl Phokion G. Kolaitis UC Santa Cruz and IBM Almaden kolaitis@cs.ucsc.edu
Structural Characterizations of Schema-Mapping Languages Balder ten Cate University of Amsterdam and UC Santa Cruz balder.tencate@uva.nl Phokion G. Kolaitis UC Santa Cruz and IBM Almaden kolaitis@cs.ucsc.edu
Discrete mathematics
 Discrete mathematics Petr Kovář petr.kovar@vsb.cz VŠB Technical University of Ostrava DiM 470-2301/02, Winter term 2018/2019 About this file This file is meant to be a guideline for the lecturer. Many
Discrete mathematics Petr Kovář petr.kovar@vsb.cz VŠB Technical University of Ostrava DiM 470-2301/02, Winter term 2018/2019 About this file This file is meant to be a guideline for the lecturer. Many
Kernelization Upper Bounds for Parameterized Graph Coloring Problems
 Kernelization Upper Bounds for Parameterized Graph Coloring Problems Pim de Weijer Master Thesis: ICA-3137910 Supervisor: Hans L. Bodlaender Computing Science, Utrecht University 1 Abstract This thesis
Kernelization Upper Bounds for Parameterized Graph Coloring Problems Pim de Weijer Master Thesis: ICA-3137910 Supervisor: Hans L. Bodlaender Computing Science, Utrecht University 1 Abstract This thesis
Computing Full Disjunctions
 Computing Full Disjunctions (Extended Abstract) Yaron Kanza School of Computer Science and Engineering The Hebrew University of Jerusalem yarok@cs.huji.ac.il Yehoshua Sagiv School of Computer Science and
Computing Full Disjunctions (Extended Abstract) Yaron Kanza School of Computer Science and Engineering The Hebrew University of Jerusalem yarok@cs.huji.ac.il Yehoshua Sagiv School of Computer Science and
Fully dynamic algorithm for recognition and modular decomposition of permutation graphs
 Fully dynamic algorithm for recognition and modular decomposition of permutation graphs Christophe Crespelle Christophe Paul CNRS - Département Informatique, LIRMM, Montpellier {crespell,paul}@lirmm.fr
Fully dynamic algorithm for recognition and modular decomposition of permutation graphs Christophe Crespelle Christophe Paul CNRS - Département Informatique, LIRMM, Montpellier {crespell,paul}@lirmm.fr
A model of navigation history
 A model of navigation history Connor G. Brewster Alan Jeffrey August, 6 arxiv:68.5v [cs.se] 8 Aug 6 Abstract: Navigation has been a core component of the web since its inception: users and scripts can
A model of navigation history Connor G. Brewster Alan Jeffrey August, 6 arxiv:68.5v [cs.se] 8 Aug 6 Abstract: Navigation has been a core component of the web since its inception: users and scripts can
Distributed minimum spanning tree problem
 Distributed minimum spanning tree problem Juho-Kustaa Kangas 24th November 2012 Abstract Given a connected weighted undirected graph, the minimum spanning tree problem asks for a spanning subtree with
Distributed minimum spanning tree problem Juho-Kustaa Kangas 24th November 2012 Abstract Given a connected weighted undirected graph, the minimum spanning tree problem asks for a spanning subtree with
Introduction to Computers and Programming. Concept Question
 Introduction to Computers and Programming Prof. I. K. Lundqvist Lecture 7 April 2 2004 Concept Question G1(V1,E1) A graph G(V, where E) is V1 a finite = {}, nonempty E1 = {} set of G2(V2,E2) vertices and
Introduction to Computers and Programming Prof. I. K. Lundqvist Lecture 7 April 2 2004 Concept Question G1(V1,E1) A graph G(V, where E) is V1 a finite = {}, nonempty E1 = {} set of G2(V2,E2) vertices and
Trees, Part 1: Unbalanced Trees
 Trees, Part 1: Unbalanced Trees The first part of this chapter takes a look at trees in general and unbalanced binary trees. The second part looks at various schemes to balance trees and/or make them more
Trees, Part 1: Unbalanced Trees The first part of this chapter takes a look at trees in general and unbalanced binary trees. The second part looks at various schemes to balance trees and/or make them more
Paths, Flowers and Vertex Cover
 Paths, Flowers and Vertex Cover Venkatesh Raman M. S. Ramanujan Saket Saurabh Abstract It is well known that in a bipartite (and more generally in a König) graph, the size of the minimum vertex cover is
Paths, Flowers and Vertex Cover Venkatesh Raman M. S. Ramanujan Saket Saurabh Abstract It is well known that in a bipartite (and more generally in a König) graph, the size of the minimum vertex cover is
Representing and Querying XML with Incomplete Information
 Representing and Querying XML with Incomplete Information Serge Abiteboul INRIA Joint work with Victor Vianu, UCSD and Luc Segoufin, INRIA Organization Incomplete databases XML Motivations Setting: documents,
Representing and Querying XML with Incomplete Information Serge Abiteboul INRIA Joint work with Victor Vianu, UCSD and Luc Segoufin, INRIA Organization Incomplete databases XML Motivations Setting: documents,
2.2 Syntax Definition
 42 CHAPTER 2. A SIMPLE SYNTAX-DIRECTED TRANSLATOR sequence of "three-address" instructions; a more complete example appears in Fig. 2.2. This form of intermediate code takes its name from instructions
42 CHAPTER 2. A SIMPLE SYNTAX-DIRECTED TRANSLATOR sequence of "three-address" instructions; a more complete example appears in Fig. 2.2. This form of intermediate code takes its name from instructions
CS2 Algorithms and Data Structures Note 10. Depth-First Search and Topological Sorting
 CS2 Algorithms and Data Structures Note 10 Depth-First Search and Topological Sorting In this lecture, we will analyse the running time of DFS and discuss a few applications. 10.1 A recursive implementation
CS2 Algorithms and Data Structures Note 10 Depth-First Search and Topological Sorting In this lecture, we will analyse the running time of DFS and discuss a few applications. 10.1 A recursive implementation
Dominance Constraints and Dominance Graphs
 Dominance Constraints and Dominance Graphs David Steurer Saarland University Abstract. Dominance constraints logically describe trees in terms of their adjacency and dominance, i.e. reachability, relation.
Dominance Constraints and Dominance Graphs David Steurer Saarland University Abstract. Dominance constraints logically describe trees in terms of their adjacency and dominance, i.e. reachability, relation.
Bipartite Roots of Graphs
 Bipartite Roots of Graphs Lap Chi Lau Department of Computer Science University of Toronto Graph H is a root of graph G if there exists a positive integer k such that x and y are adjacent in G if and only
Bipartite Roots of Graphs Lap Chi Lau Department of Computer Science University of Toronto Graph H is a root of graph G if there exists a positive integer k such that x and y are adjacent in G if and only
Faster and Dynamic Algorithms For Maximal End-Component Decomposition And Related Graph Problems In Probabilistic Verification
 Faster and Dynamic Algorithms For Maximal End-Component Decomposition And Related Graph Problems In Probabilistic Verification Krishnendu Chatterjee Monika Henzinger Abstract We present faster and dynamic
Faster and Dynamic Algorithms For Maximal End-Component Decomposition And Related Graph Problems In Probabilistic Verification Krishnendu Chatterjee Monika Henzinger Abstract We present faster and dynamic
V8 Molecular decomposition of graphs
 V8 Molecular decomposition of graphs - Most cellular processes result from a cascade of events mediated by proteins that act in a cooperative manner. - Protein complexes can share components: proteins
V8 Molecular decomposition of graphs - Most cellular processes result from a cascade of events mediated by proteins that act in a cooperative manner. - Protein complexes can share components: proteins
The External Network Problem
 The External Network Problem Jan van den Heuvel and Matthew Johnson CDAM Research Report LSE-CDAM-2004-15 December 2004 Abstract The connectivity of a communications network can often be enhanced if the
The External Network Problem Jan van den Heuvel and Matthew Johnson CDAM Research Report LSE-CDAM-2004-15 December 2004 Abstract The connectivity of a communications network can often be enhanced if the
A Note on Scheduling Parallel Unit Jobs on Hypercubes
 A Note on Scheduling Parallel Unit Jobs on Hypercubes Ondřej Zajíček Abstract We study the problem of scheduling independent unit-time parallel jobs on hypercubes. A parallel job has to be scheduled between
A Note on Scheduling Parallel Unit Jobs on Hypercubes Ondřej Zajíček Abstract We study the problem of scheduling independent unit-time parallel jobs on hypercubes. A parallel job has to be scheduled between
4 Basics of Trees. Petr Hliněný, FI MU Brno 1 FI: MA010: Trees and Forests
 4 Basics of Trees Trees, actually acyclic connected simple graphs, are among the simplest graph classes. Despite their simplicity, they still have rich structure and many useful application, such as in
4 Basics of Trees Trees, actually acyclic connected simple graphs, are among the simplest graph classes. Despite their simplicity, they still have rich structure and many useful application, such as in
H2 Spring B. We can abstract out the interactions and policy points from DoDAF operational views
 1. (4 points) Of the following statements, identify all that hold about architecture. A. DoDAF specifies a number of views to capture different aspects of a system being modeled Solution: A is true: B.
1. (4 points) Of the following statements, identify all that hold about architecture. A. DoDAF specifies a number of views to capture different aspects of a system being modeled Solution: A is true: B.
XQuery Optimization Based on Rewriting
 XQuery Optimization Based on Rewriting Maxim Grinev Moscow State University Vorob evy Gory, Moscow 119992, Russia maxim@grinev.net Abstract This paper briefly describes major results of the author s dissertation
XQuery Optimization Based on Rewriting Maxim Grinev Moscow State University Vorob evy Gory, Moscow 119992, Russia maxim@grinev.net Abstract This paper briefly describes major results of the author s dissertation
Notes on Minimum Cuts and Modular Functions
 Notes on Minimum Cuts and Modular Functions 1 Introduction The following are my notes on Cunningham s paper [1]. Given a submodular function f and a set S, submodular minimisation is the problem of finding
Notes on Minimum Cuts and Modular Functions 1 Introduction The following are my notes on Cunningham s paper [1]. Given a submodular function f and a set S, submodular minimisation is the problem of finding
Chapter 3: Propositional Languages
 Chapter 3: Propositional Languages We define here a general notion of a propositional language. We show how to obtain, as specific cases, various languages for propositional classical logic and some non-classical
Chapter 3: Propositional Languages We define here a general notion of a propositional language. We show how to obtain, as specific cases, various languages for propositional classical logic and some non-classical
Module 11. Directed Graphs. Contents
 Module 11 Directed Graphs Contents 11.1 Basic concepts......................... 256 Underlying graph of a digraph................ 257 Out-degrees and in-degrees.................. 258 Isomorphism..........................
Module 11 Directed Graphs Contents 11.1 Basic concepts......................... 256 Underlying graph of a digraph................ 257 Out-degrees and in-degrees.................. 258 Isomorphism..........................
Exact Algorithms Lecture 7: FPT Hardness and the ETH
 Exact Algorithms Lecture 7: FPT Hardness and the ETH February 12, 2016 Lecturer: Michael Lampis 1 Reminder: FPT algorithms Definition 1. A parameterized problem is a function from (χ, k) {0, 1} N to {0,
Exact Algorithms Lecture 7: FPT Hardness and the ETH February 12, 2016 Lecturer: Michael Lampis 1 Reminder: FPT algorithms Definition 1. A parameterized problem is a function from (χ, k) {0, 1} N to {0,
Runtime Behavior of Conversion Interpretation of Subtyping
 Runtime Behavior of Conversion Interpretation of Subtyping Yasuhiko Minamide Institute of Information Sciences and Electronics University of Tsukuba and PRESTO, JST minamide@is.tsukuba.ac.jp Abstract.
Runtime Behavior of Conversion Interpretation of Subtyping Yasuhiko Minamide Institute of Information Sciences and Electronics University of Tsukuba and PRESTO, JST minamide@is.tsukuba.ac.jp Abstract.
CS4215 Programming Language Implementation. Martin Henz
 CS4215 Programming Language Implementation Martin Henz Thursday 26 January, 2012 2 Chapter 4 The Language simpl In this chapter, we are exting the language epl in order to provide a more powerful programming
CS4215 Programming Language Implementation Martin Henz Thursday 26 January, 2012 2 Chapter 4 The Language simpl In this chapter, we are exting the language epl in order to provide a more powerful programming
Algorithms for Learning and Teaching. Sets of Vertices in Graphs. Patricia A. Evans and Michael R. Fellows. University of Victoria
 Algorithms for Learning and Teaching Sets of Vertices in Graphs Patricia A. Evans and Michael R. Fellows Department of Computer Science University of Victoria Victoria, B.C. V8W 3P6, Canada Lane H. Clark
Algorithms for Learning and Teaching Sets of Vertices in Graphs Patricia A. Evans and Michael R. Fellows Department of Computer Science University of Victoria Victoria, B.C. V8W 3P6, Canada Lane H. Clark
Reachability in K 3,3 -free and K 5 -free Graphs is in Unambiguous Logspace
 CHICAGO JOURNAL OF THEORETICAL COMPUTER SCIENCE 2014, Article 2, pages 1 29 http://cjtcs.cs.uchicago.edu/ Reachability in K 3,3 -free and K 5 -free Graphs is in Unambiguous Logspace Thomas Thierauf Fabian
CHICAGO JOURNAL OF THEORETICAL COMPUTER SCIENCE 2014, Article 2, pages 1 29 http://cjtcs.cs.uchicago.edu/ Reachability in K 3,3 -free and K 5 -free Graphs is in Unambiguous Logspace Thomas Thierauf Fabian
The Encoding Complexity of Network Coding
 The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email: mikel,spalex,bruck @caltech.edu Abstract In the multicast network
The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email: mikel,spalex,bruck @caltech.edu Abstract In the multicast network
Data Exchange: Semantics and Query Answering
 Data Exchange: Semantics and Query Answering Ronald Fagin Phokion G. Kolaitis Renée J. Miller Lucian Popa IBM Almaden Research Center fagin,lucian @almaden.ibm.com University of California at Santa Cruz
Data Exchange: Semantics and Query Answering Ronald Fagin Phokion G. Kolaitis Renée J. Miller Lucian Popa IBM Almaden Research Center fagin,lucian @almaden.ibm.com University of California at Santa Cruz
Processing Regular Path Queries Using Views or What Do We Need for Integrating Semistructured Data?
 Processing Regular Path Queries Using Views or What Do We Need for Integrating Semistructured Data? Diego Calvanese University of Rome La Sapienza joint work with G. De Giacomo, M. Lenzerini, M.Y. Vardi
Processing Regular Path Queries Using Views or What Do We Need for Integrating Semistructured Data? Diego Calvanese University of Rome La Sapienza joint work with G. De Giacomo, M. Lenzerini, M.Y. Vardi
Nested Intervals Tree Encoding with Continued Fractions
 Nested Intervals Tree Encoding with Continued Fractions VADIM TROPASHKO Oracle Corp There is nothing like abstraction To take away your intuition Shai Simonson http://aduniorg/courses/discrete/ We introduce
Nested Intervals Tree Encoding with Continued Fractions VADIM TROPASHKO Oracle Corp There is nothing like abstraction To take away your intuition Shai Simonson http://aduniorg/courses/discrete/ We introduce
Chordal Graphs: Theory and Algorithms
 Chordal Graphs: Theory and Algorithms 1 Chordal graphs Chordal graph : Every cycle of four or more vertices has a chord in it, i.e. there is an edge between two non consecutive vertices of the cycle. Also
Chordal Graphs: Theory and Algorithms 1 Chordal graphs Chordal graph : Every cycle of four or more vertices has a chord in it, i.e. there is an edge between two non consecutive vertices of the cycle. Also
Foundations of Computer Science Spring Mathematical Preliminaries
 Foundations of Computer Science Spring 2017 Equivalence Relation, Recursive Definition, and Mathematical Induction Mathematical Preliminaries Mohammad Ashiqur Rahman Department of Computer Science College
Foundations of Computer Science Spring 2017 Equivalence Relation, Recursive Definition, and Mathematical Induction Mathematical Preliminaries Mohammad Ashiqur Rahman Department of Computer Science College
TESTING THE SATISFIABILITY OF TREE PATTERN QUERIES WITH NODE IDENTITY CONSTRAINTS. A Thesis by. Barbara Jane Gobbert
 TESTING THE SATISFIABILITY OF TREE PATTERN QUERIES WITH NODE IDENTITY CONSTRAINTS A Thesis by Barbara Jane Gobbert B. Science, University Of Queensland, 1979 B. Commerce, University Of Queensland, 1983
TESTING THE SATISFIABILITY OF TREE PATTERN QUERIES WITH NODE IDENTITY CONSTRAINTS A Thesis by Barbara Jane Gobbert B. Science, University Of Queensland, 1979 B. Commerce, University Of Queensland, 1983
Vertex 3-colorability of claw-free graphs
 Algorithmic Operations Research Vol.2 (27) 5 2 Vertex 3-colorability of claw-free graphs Marcin Kamiński a Vadim Lozin a a RUTCOR - Rutgers University Center for Operations Research, 64 Bartholomew Road,
Algorithmic Operations Research Vol.2 (27) 5 2 Vertex 3-colorability of claw-free graphs Marcin Kamiński a Vadim Lozin a a RUTCOR - Rutgers University Center for Operations Research, 64 Bartholomew Road,
COMP90051 Statistical Machine Learning
 COMP90051 Statistical Machine Learning Semester 2, 2016 Lecturer: Trevor Cohn 21. Independence in PGMs; Example PGMs Independence PGMs encode assumption of statistical independence between variables. Critical
COMP90051 Statistical Machine Learning Semester 2, 2016 Lecturer: Trevor Cohn 21. Independence in PGMs; Example PGMs Independence PGMs encode assumption of statistical independence between variables. Critical
On the Analysis of Queries with Counting Constraints
 On the Analysis of Queries with Counting Constraints Everardo Barcenas-Patino, Pierre Genevès, Nabil Layaïda To cite this version: Everardo Barcenas-Patino, Pierre Genevès, Nabil Layaïda. On the Analysis
On the Analysis of Queries with Counting Constraints Everardo Barcenas-Patino, Pierre Genevès, Nabil Layaïda To cite this version: Everardo Barcenas-Patino, Pierre Genevès, Nabil Layaïda. On the Analysis
Graph Theory Questions from Past Papers
 Graph Theory Questions from Past Papers Bilkent University, Laurence Barker, 19 October 2017 Do not forget to justify your answers in terms which could be understood by people who know the background theory
Graph Theory Questions from Past Papers Bilkent University, Laurence Barker, 19 October 2017 Do not forget to justify your answers in terms which could be understood by people who know the background theory
Containment of XPath expressions: an inference and rewriting based approach
 Extreme Markup Languages 2003 Montréal, Québec August 4-8, 2003 Containment of XPath expressions: an inference and rewriting based approach Jean-Yves Vion-Dury INRIA Rhône-Alpes Nabil Layaïda INRIA Rhône-Alpes
Extreme Markup Languages 2003 Montréal, Québec August 4-8, 2003 Containment of XPath expressions: an inference and rewriting based approach Jean-Yves Vion-Dury INRIA Rhône-Alpes Nabil Layaïda INRIA Rhône-Alpes
An Improvement of an Approach for Representation of Tree Structures in Relational Tables
 An Improvement of an Approach for Representation of Tree Structures in Relational Tables Ivaylo Atanassov Abstract: The paper introduces an improvement of an approach for tree representation in relational
An Improvement of an Approach for Representation of Tree Structures in Relational Tables Ivaylo Atanassov Abstract: The paper introduces an improvement of an approach for tree representation in relational
Incremental Adaptation of XPath Access Control Views
 Incremental Adaptation of XPath Access Control Views Abstract Materialized XPath access-control views are commonly used for enforcing access control. When access control rules defining a materialized XML
Incremental Adaptation of XPath Access Control Views Abstract Materialized XPath access-control views are commonly used for enforcing access control. When access control rules defining a materialized XML
