EEC 483 Computer Organization
|
|
|
- Oliver Kory Lewis
- 5 years ago
- Views:
Transcription
1 EEC 483 Computer Organization Chapter 3. Arithmetic for Computers Chansu Yu Table of Contents Ch.1 Introduction Ch. 2 Instruction: Machine Language Ch. 3-4 CPU Implementation Ch. 5 Cache and VM Ch. 6-7 I/O & Multiprocessors Computer CPU Programmer interface instruction set ALU, Mux, Memory, Sequential circuit,... CPU designer interface component spec. connection spec. User interface keyboard/ mouse screen/ speaker Software interface (ch.2) Hardware interface (ch.3-5) 2 Textbook subtitle 1
2 Table of Contents Ch.1 Introduction Ch. 2 Instructions: Language of the Computer Ch. 3 CPU Implementation: Arithmetic 3.1 Introduction 3.3 Multiplication 3.2 Addition and subtraction 3.4 Division 3.5 Floating point Appendix C.5 Constructing an Arithmetic Logic Unit (ALU) Ch. 4 CPU Implementation: Pipeline Software interface Hardware interface Ch. 5 Cache and Virtual Memory Ch. 6-7 I/O and Multiprocessors 3 Arithmetic Where we've been: Performance (seconds, cycles, instructions) Abstractions: Instruction Set Architecture Assembly Language and Machine Language What's up ahead: Implementing the Architecture a b 32 operation ALU 32 result
3 3.2 Addition & Subtraction Just like in grade school (carry/borrow 1s) Two's complement operations easy subtraction using addition of negative numbers Overflow (result too large for finite computer word): e.g., adding two n-bit numbers does not yield an n-bit number Detecting Overflow No overflow when adding a positive and a negative number No overflow when signs are the same for subtraction Overflow occurs when the value affects the sign: overflow when adding two positives yields a negative or, adding two negatives gives a positive or, subtract a negative from a positive and get a negative or, subtract a positive from a negative and get a positive An exception (interrupt) occurs Control jumps to predefined address for exception Interrupted address is saved for possible resumption 6 3
4 Cf. Exceptions and Interrupts MIPS exception facility Exceptions caused by errors External interrupts caused by I/O devices Exception handling CPU records information about what went wrong Software handler process the exception Error : report and halt, cure and continue (page fault), IO interrupt : data processing from/to the interrupted IO device 7 Cf. CPU Records Information Registers Cause EPC exception type and pending interrupt bits register containing address of instruction that caused exception which problem? which instruction? mfc0 (move from system control) instruction is used to copy EPC to general purpose register mfco $10, $epc 8 4
5 Cf. Exception Type (cause) 0 Int External interrupt (hardware) 4 AdEL Address error (load or instruction fetch) 5 AdES Address error (store) 6 IBE Bus error on instruction fetch 7 DBE Bus error on data load/store 8 Sys Syscall exception 9 Bp Breakpoint exception 10 RI Reserved instruction exception 11 CpU Coprocessor unimplemented 12 Ov Arithmetic overflow exception 13 Tr Trap 15 FPE Floating point exception 9 Cf. Software Handler Procedure Stop executing and Jump to fixed address 0x SPIM simulator uses 0x E.g.) CPU executes instruction whenever it is ON. If the CPU is powered on, somebody has to tell which address to start. (=reset address) 0x is the natural choice (MIPS) 0x000f fff0 for Intel CPU (ROM BIOS) 10 5
6 3.3 Multiplication More complicated than addition accomplished via shifting and addition More time and more area Let's look at 3 versions based on grade school algorithm (multiplicand) x_01011 (multiplier) Negative numbers: convert and multiply there are better techniques, we won t look at them 11 Multiplication Paper and pencil example (unsigned): Multiplicand Multiplier Product m bits x n bits = m+n bit product Binary makes it easy: 0 => place 0 1 => place a copy ( 0 x multiplicand) ( 1 x multiplicand) 12 6
7 Multiplication Paper and pencil example (unsigned): Multiplicand Multiplier Product m bits x n bits = m+n bit product Binary makes it easy: 0 => place 0 1 => place a copy ( 0 x multiplicand) ( 1 x multiplicand) 13 Product (T) =0 Multiplier 0 =1, thus, T += Multiplicand () Multiplier 1 =1, thus, T += Multiplicand<<1 (0) Multiplier 3 =1, thus, T += Multiplicand<<3 (000) Each step, shift Multiplicand one bit to the left Each step, shift Multiplier one bit to the right and check Multiplier 0 Multiplication T=0 Multiplier 0 =1 T += Multiplicand N Multiplicand<<1 Multiplier >>1 Done N 14 7
8 Multiplication: 5 () x 11 (01011) Iteration Step Multiplier (R) Multiplicand (D) Product (T) 0 Initial values 1 1: T = T + D (since R0=1) 2: Shift left D 2 1: T = T + D (since R0=1) 2: Shift left D 3 1: no operation (since R0=0) 2: Shift left D 4 1: T = T + D (since R0=1) 2: Shift left D 5 1: no operation (since R0=0) 2: Shift left D => 55 Size of register that holds Multiplier? Size of register that holds T? Size of register that holds Multiplicand? 15 Multiplication: Implementation Do addition (if 1 ) Write (if 1 ) Multiplicand 64 bits Shift left 64-bit ALU Multiplier Shift right 32 bits Product 64 bits Write Control test Number of bits??? - 32-bit architecture - Multiplier: 32-bit - Multiplicand: 64-bit!!! - Product: 64-bit!!! - ALU: 64-bit ALU!!! It is actually a series of 32-bit add operations. Replace 64-bit ALU with 32-bit ALU Shift product (res) instead of shifting m cand Next slice!!! 16 8
9 Multiplication Paper and pencil example (unsigned): Multiplicand Multiplier Product m bits x n bits = m+n bit product Binary makes it easy: 0 => place 0 1 => place a copy ( 0 x multiplicand) ( 1 x multiplicand) 17 Product (T) =0 Multiplier 0 =1, thus, T += Multiplicand () Or, T += Multiplicand<<5 () & T>>5 Multiplier 1 =1, thus, T += Multiplicand<<1 (0) Or, T += Multiplicand<<5 () & T>>4 Multiplier 3 =1, thus, T += Multiplicand<<3 (000) Or, T += Multiplicand<<5 () & T>>2 How can we improve the design? Itera tion Step Multiplier (R) Multiplicand (D) Product (T) 0 Initial values : T = T + D<<5 (since R0=1) : T = T + D<<5 (since R0=1) : no operation (since R0=0) : T = T + D<<5 (since R0=1) : no operation (since R0=0) => 55 * 32-bit additions with 5-bit D and upper part of T 18 9
10 Implementation Do addition (if 1 ) Write (if 1 ) Multiplicand 32 bits 32-bit ALU Product Shift right Write Multiplier Shift right 32 bits Control test Number of bits??? - 32-bit architecture - Multiplier: 32-bit - Multiplicand: 64-bit => 32-bit - Product: 64-bit!!! - ALU: 64-bit ALU => 32-bit ALU 64 bits Product register wastes space that exactly matches size of multiplier Multiplier space can be saved. Combine Multiplier register and Product register (Multiplier register stored in lower part of Product register will be thrown away one bit at a time) Next slice!!! 19 How can we improve the design? Itera tion Step Multiplier (R) Multiplicand (D) Product (T) 0 Initial values : T = T + D<<5 (since R0=1) : T = T + D<<5 (since R0=1) : no operation (since R0=0) : T = T + D<<5 (since R0=1) : no operation (since R0=0) => Not used 10
11 Final Version Start Product0 = 1 1. Test Product0 Product0 = 0 Multiplicand 32 bits 1a. Add multiplicand to the left half of the product and place the result in the left half of the Product register 32-bit ALU Product Shift right Write Control test 2. Shift the Product register right 1 bit 64 bits 32nd repetition? No: < 32 repetitions Just 1 step instead of 2 steps => Total of 2 steps per bit 21 Done Yes: 32 repetitions Multiply in MIPS Instruction Example Meaning Comments multiply mult $2,$3 Hi, Lo = $2 x $3 64-bit signed product multiply unsigned multu$2,$3 Hi, Lo = $2 x $3 64-bit unsigned product Move from Hi mfhi $1 $1 = Hi Used to get copy of Hi Move from Lo mflo $1 $1 = Lo Used to get copy of Lo 22 11
12 3.4 Divide: Division in MIPS Instruction Example Meaning Comments divide div $2,$3 Lo = $2 $3, Lo = quotient, Hi = remainder Hi = $2 mod $3 divide unsigned divu $2,$3 Lo = $2 $3, Unsigned quotient & remainder Hi = $2 mod $3 Move from Hi mfhi $1 $1 = Hi Used to get copy of Hi Move from Lo mflo $1 $1 = Lo Used to get copy of Lo 23 Divide $2 / $3 = quotient... remainder Is quotient 32-bit or 16-bit? Is remainder 32-bit or 16-bit? Example $2= $3= Quotient= Quotient must be 32-bit! $2= $3= Quotient=1, Remainder= Remainder must be 32-bit! 24 n-bit / n-bit n-bit quotient, n-bit remainder More hardware (wasting) n-bit / n/2-bit n/2-bit quotient, n/2-bit remainder Overflow Two basic approaches Restoring : conventional Non-restoring 12
13 Implementation: Paper & Pencil 8 Quotient Divisor Dividend Quotient Divisor Dividend We know where to start Just start from the first possible digit If the result is negative, move on to the next digit while recovering the dividend to the original value If the subtraction gives positive, Qi=1, Otherwise, Qi=0 and restore the dividend * Each step, shift right divisor * One nice thing with binary computation is that the quotient 25 bit can be 1 or 0 Implementation: Paper & Pencil Divisor Quotient 10 Dividend Remainder (or Modulo result) We know 10 is less than But ALU does not know until it subtracts and gets the negative result. If it is negative, it needs to restore the dividend to the original value by adding 1000, i.e., ( )+1000 = 10 See how big a number can be subtracted, creating quotient bit on each step Binary => 1 * divisor or 0 * divisor Dividend = Quotient x Divisor + Remainder => Dividend = Quotient + Divisor 3 versions of divide, successive refinement 26 13
14 Dividend: (11), Divisor: (5) Iteration Step Initial values 1: R = R - D 2: R<0 => Restore R, Shift left Q, Q0=0 3: Shift right D 1: R = R - D 2: R<0 => Restore R, Shift left Q, Q0=0 3: Shift right D 1: R = R - D 2: R<0 => Restore R, Shift left Q, Q0=0 3: Shift right D 1: R = R - D 2: R<0 => Restore R, Shift left Q, Q0=0 3: Shift right D 1: R = R - D 2: R>=0 => Shift left Q, Q0=1 3: Shift right D 1: R = R - D 2: R<0 => Restore R, Shift left Q, Q0=0 3: Shift right D Quotient (Q) Divisor (D) Remainder (R) Quotient = 2 remainder = 1 dividend Restored Restored Restored Restored Not restored Restored Divide Algorithm Version 1 Takes n+1 steps for n-bit Quotient & Rem. Remainder Quotient Divisor Remainder > 0 Start: Place Dividend in Remainder 1. Subtract the Divisor register from the Remainder register, and place the result in the Remainder register. Test Remainder Remainder < 0 2a. Shift the Quotient register to the left setting the new rightmost bit to 1. 2b. Restore the original value by adding the Divisor register to the Remainder register, & place the sum in the Remainder register. Also shift the Quotient register to the left, setting the new least significant bit to Shift the Divisor register right1 bit. n+1 repetition? 28 Done No: < n+1 repetitions Yes: n+1 repetitions (n = 4 here) 14
15 DIVIDE HARDWARE Version 1 64-bit Divisor reg, 64-bit ALU, 64-bit Remainder reg, 32-bit Quotient reg Divisor 64 bits Shift Right 64-bit ALU Quotient 32 bits Shift Left Remainder 64 bits Write Control 29 Observations on Divide Version 1 1/2 bits in divisor always 0 => 1/2 of 64-bit adder is wasted => 1/2 of divisor is wasted Instead of shifting divisor to right, shift remainder to left? 1st step cannot produce a 1 in quotient bit (otherwise too big) => switch order to shift first and then subtract, can save one iteration 30 15
16 DIVIDE HARDWARE Version 2 32-bit Divisor reg, 32-bit ALU, 64-bit Remainder reg, 32-bit Quotient reg Divisor 32-bit ALU 32 bits Quotient 32 bits Shift Left Remainder 64 bits Shift Left Write Control 31 Remainder Divide Algorithm Version 2 Quotient Divisor Start: Place Dividend in Remainder 1. Shift the Remainder register left 1 bit. 2. Subtract the Divisor register from the left half of the Remainder register, & place the result in the left half of the Remainder register. Remainder 0 Test Remainder Remainder < 0 3a. Shift the Quotient register to the left setting the new rightmost bit to 1. 3b. Restore the original value by adding the Divisor register to the left half of the Remainderregister, &place the sum in the left half of the Remainder register. Also shift the Quotient register to the left, setting the new least significant bit to 0. nth repetition? 32 Done No: < n repetitions Yes: n repetitions (n = 4 here) 16
17 Observations on Divide Version 2 Eliminate Quotient register by combining with Remainder as shifted left Start by shifting the Remainder left as before. Thereafter loop contains only two steps because the shifting of the Remainder register shifts both the remainder in the left half and the quotient in the right half The consequence of combining the two registers together and the new order of the operations in the loop is that the remainder will shifted left one time too many. Thus the final correction step must shift back only the remainder in the left half of the register 33 Divide Hardware: Final Version 32-bit Divisor reg, 32 -bit ALU, 64-bit Remainder reg, (0-bit Quotient reg) Divisor 32 bits 32-bit ALU HI LO Remainder (Quotient) 64 bits Shift Left Write Control 34 17
18 Remainder Divide Algorithm Version 3 Divisor Start: Place Dividend in Remainder 1. Shift the Remainder register left 1 bit. 2. Subtract the Divisor register from the left half of the Remainder register, & place the result in the left half of the Remainder register. Remainder 0 Test Remainder Remainder < 0 3a. Shift the Remainder register to the left setting the new rightmost bit to 1. 3b. Restore the original value by adding the Divisor register to the left half of the Remainderregister, &place the sum in the left half of the Remainder register. Also shift the Remainder register to the left, setting the new least significant bit to 0. nth repetition? 35 No: < n repetitions Yes: n repetitions (n = 4 here) Done. Shift left half of Remainder right 1 bit. Observations on Divide Version 3 Same Hardware as Multiply : just need ALU to add or subtract, and 63-bit register to shift left or shift right Hi and Lo registers in MIPS combine to act as 64-bit register for multiply and divide Signed Divides: Simplest is to remember signs, make positive, and complement quotient and remainder if necessary Note: Dividend and Remainder must have same sign Note: Quotient negated if Divisor sign & Dividend sign disagree e.g., 7 2 = 3, remainder = 1 Possible for quotient to be too large: if divide 64-bit interger by 1, quotient is 64 bits ( called saturation ) 36 18
COMP 303 Computer Architecture Lecture 6
 COMP 303 Computer Architecture Lecture 6 MULTIPLY (unsigned) Paper and pencil example (unsigned): Multiplicand 1000 = 8 Multiplier x 1001 = 9 1000 0000 0000 1000 Product 01001000 = 72 n bits x n bits =
COMP 303 Computer Architecture Lecture 6 MULTIPLY (unsigned) Paper and pencil example (unsigned): Multiplicand 1000 = 8 Multiplier x 1001 = 9 1000 0000 0000 1000 Product 01001000 = 72 n bits x n bits =
361 div.1. Computer Architecture EECS 361 Lecture 7: ALU Design : Division
 361 div.1 Computer Architecture EECS 361 Lecture 7: ALU Design : Division Outline of Today s Lecture Introduction to Today s Lecture Divide Questions and Administrative Matters Introduction to Single cycle
361 div.1 Computer Architecture EECS 361 Lecture 7: ALU Design : Division Outline of Today s Lecture Introduction to Today s Lecture Divide Questions and Administrative Matters Introduction to Single cycle
EECS150 - Digital Design Lecture 13 - Combinational Logic & Arithmetic Circuits Part 3
 EECS15 - Digital Design Lecture 13 - Combinational Logic & Arithmetic Circuits Part 3 October 8, 22 John Wawrzynek Fall 22 EECS15 - Lec13-cla3 Page 1 Multiplication a 3 a 2 a 1 a Multiplicand b 3 b 2 b
EECS15 - Digital Design Lecture 13 - Combinational Logic & Arithmetic Circuits Part 3 October 8, 22 John Wawrzynek Fall 22 EECS15 - Lec13-cla3 Page 1 Multiplication a 3 a 2 a 1 a Multiplicand b 3 b 2 b
Tailoring the 32-Bit ALU to MIPS
 Tailoring the 32-Bit ALU to MIPS MIPS ALU extensions Overflow detection: Carry into MSB XOR Carry out of MSB Branch instructions Shift instructions Slt instruction Immediate instructions ALU performance
Tailoring the 32-Bit ALU to MIPS MIPS ALU extensions Overflow detection: Carry into MSB XOR Carry out of MSB Branch instructions Shift instructions Slt instruction Immediate instructions ALU performance
Homework 3. Assigned on 02/15 Due time: midnight on 02/21 (1 WEEK only!) B.2 B.11 B.14 (hint: use multiplexors) CSCI 402: Computer Architectures
 Homework 3 Assigned on 02/15 Due time: midnight on 02/21 (1 WEEK only!) B.2 B.11 B.14 (hint: use multiplexors) 1 CSCI 402: Computer Architectures Arithmetic for Computers (2) Fengguang Song Department
Homework 3 Assigned on 02/15 Due time: midnight on 02/21 (1 WEEK only!) B.2 B.11 B.14 (hint: use multiplexors) 1 CSCI 402: Computer Architectures Arithmetic for Computers (2) Fengguang Song Department
Integer Arithmetic. Jinkyu Jeong Computer Systems Laboratory Sungkyunkwan University
 Integer Arithmetic Jinkyu Jeong (jinkyu@skku.edu) Computer Systems Laboratory Sungkyunkwan University http://csl.skku.edu EEE3050: Theory on Computer Architectures, Spring 2017, Jinkyu Jeong (jinkyu@skku.edu)
Integer Arithmetic Jinkyu Jeong (jinkyu@skku.edu) Computer Systems Laboratory Sungkyunkwan University http://csl.skku.edu EEE3050: Theory on Computer Architectures, Spring 2017, Jinkyu Jeong (jinkyu@skku.edu)
Review of Last lecture. Review ALU Design. Designing a Multiplier Shifter Design Review. Booth s algorithm. Today s Outline
 Today s Outline San Jose State University EE176-SJSU Computer Architecture and Organization Lecture 5 HDL, ALU, Shifter, Booth Algorithm Multiplier & Divider Instructor: Christopher H. Pham Review of Last
Today s Outline San Jose State University EE176-SJSU Computer Architecture and Organization Lecture 5 HDL, ALU, Shifter, Booth Algorithm Multiplier & Divider Instructor: Christopher H. Pham Review of Last
More complicated than addition. Let's look at 3 versions based on grade school algorithm (multiplicand) More time and more area
 Multiplication More complicated than addition accomplished via shifting and addition More time and more area Let's look at 3 versions based on grade school algorithm 01010010 (multiplicand) x01101101 (multiplier)
Multiplication More complicated than addition accomplished via shifting and addition More time and more area Let's look at 3 versions based on grade school algorithm 01010010 (multiplicand) x01101101 (multiplier)
MIPS Integer ALU Requirements
 MIPS Integer ALU Requirements Add, AddU, Sub, SubU, AddI, AddIU: 2 s complement adder/sub with overflow detection. And, Or, Andi, Ori, Xor, Xori, Nor: Logical AND, logical OR, XOR, nor. SLTI, SLTIU (set
MIPS Integer ALU Requirements Add, AddU, Sub, SubU, AddI, AddIU: 2 s complement adder/sub with overflow detection. And, Or, Andi, Ori, Xor, Xori, Nor: Logical AND, logical OR, XOR, nor. SLTI, SLTIU (set
Divide: Paper & Pencil
 Divide: Paper & Pencil 1001 Quotient Divisor 1000 1001010 Dividend -1000 10 101 1010 1000 10 Remainder See how big a number can be subtracted, creating quotient bit on each step Binary => 1 * divisor or
Divide: Paper & Pencil 1001 Quotient Divisor 1000 1001010 Dividend -1000 10 101 1010 1000 10 Remainder See how big a number can be subtracted, creating quotient bit on each step Binary => 1 * divisor or
Integer Multiplication and Division
 Integer Multiplication and Division COE 301 Computer Organization Prof. Muhamed Mudawar College of Computer Sciences and Engineering King Fahd University of Petroleum and Minerals Presentation Outline
Integer Multiplication and Division COE 301 Computer Organization Prof. Muhamed Mudawar College of Computer Sciences and Engineering King Fahd University of Petroleum and Minerals Presentation Outline
Lecture 8: Addition, Multiplication & Division
 Lecture 8: Addition, Multiplication & Division Today s topics: Signed/Unsigned Addition Multiplication Division 1 Signed / Unsigned The hardware recognizes two formats: unsigned (corresponding to the C
Lecture 8: Addition, Multiplication & Division Today s topics: Signed/Unsigned Addition Multiplication Division 1 Signed / Unsigned The hardware recognizes two formats: unsigned (corresponding to the C
Number Systems and Computer Arithmetic
 Number Systems and Computer Arithmetic Counting to four billion two fingers at a time What do all those bits mean now? bits (011011011100010...01) instruction R-format I-format... integer data number text
Number Systems and Computer Arithmetic Counting to four billion two fingers at a time What do all those bits mean now? bits (011011011100010...01) instruction R-format I-format... integer data number text
CPS 104 Computer Organization and Programming
 CPS 104 Computer Organization and Programming Lecture 9: Integer Arithmetic. Robert Wagner CPS104 IMD.1 RW Fall 2000 Overview of Today s Lecture: Integer Multiplication and Division. Read Appendix B CPS104
CPS 104 Computer Organization and Programming Lecture 9: Integer Arithmetic. Robert Wagner CPS104 IMD.1 RW Fall 2000 Overview of Today s Lecture: Integer Multiplication and Division. Read Appendix B CPS104
Outline. EEL-4713 Computer Architecture Multipliers and shifters. Deriving requirements of ALU. MIPS arithmetic instructions
 Outline EEL-4713 Computer Architecture Multipliers and shifters Multiplication and shift registers Chapter 3, section 3.4 Next lecture Division, floating-point 3.5 3.6 EEL-4713 Ann Gordon-Ross.1 EEL-4713
Outline EEL-4713 Computer Architecture Multipliers and shifters Multiplication and shift registers Chapter 3, section 3.4 Next lecture Division, floating-point 3.5 3.6 EEL-4713 Ann Gordon-Ross.1 EEL-4713
Chapter 3 Arithmetic for Computers
 Chapter 3 Arithmetic for Computers 1 Arithmetic Where we've been: Abstractions: Instruction Set Architecture Assembly Language and Machine Language What's up ahead: Implementing the Architecture operation
Chapter 3 Arithmetic for Computers 1 Arithmetic Where we've been: Abstractions: Instruction Set Architecture Assembly Language and Machine Language What's up ahead: Implementing the Architecture operation
Computer Organization and Structure. Bing-Yu Chen National Taiwan University
 Computer Organization and Structure Bing-Yu Chen National Taiwan University Arithmetic for Computers Addition and Subtraction Gate Logic and K-Map Method Constructing a Basic ALU Arithmetic Logic Unit
Computer Organization and Structure Bing-Yu Chen National Taiwan University Arithmetic for Computers Addition and Subtraction Gate Logic and K-Map Method Constructing a Basic ALU Arithmetic Logic Unit
NUMBER OPERATIONS. Mahdi Nazm Bojnordi. CS/ECE 3810: Computer Organization. Assistant Professor School of Computing University of Utah
 NUMBER OPERATIONS Mahdi Nazm Bojnordi Assistant Professor School of Computing University of Utah CS/ECE 3810: Computer Organization Overview Homework 4 is due tonight Verify your uploaded file before the
NUMBER OPERATIONS Mahdi Nazm Bojnordi Assistant Professor School of Computing University of Utah CS/ECE 3810: Computer Organization Overview Homework 4 is due tonight Verify your uploaded file before the
Computer Architecture Chapter 3. Fall 2005 Department of Computer Science Kent State University
 Computer Architecture Chapter 3 Fall 2005 Department of Computer Science Kent State University Objectives Signed and Unsigned Numbers Addition and Subtraction Multiplication and Division Floating Point
Computer Architecture Chapter 3 Fall 2005 Department of Computer Science Kent State University Objectives Signed and Unsigned Numbers Addition and Subtraction Multiplication and Division Floating Point
Chapter 3 Arithmetic for Computers. ELEC 5200/ From P-H slides
 Chapter 3 Arithmetic for Computers 1 Arithmetic for Computers Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers Representation
Chapter 3 Arithmetic for Computers 1 Arithmetic for Computers Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers Representation
Today s Outline. CS152 Computer Architecture and Engineering Lecture 5. VHDL, Multiply, Shift
 Today s Outline CS152 Computer Architecture and Engineering Lecture 5 VHDL, Multiply, Shift Feb 8, 1999 John Kubiatowicz (http.cs.berkeley.edu/~kubitron) Review of Last lecture Intro to VHDL Administrative
Today s Outline CS152 Computer Architecture and Engineering Lecture 5 VHDL, Multiply, Shift Feb 8, 1999 John Kubiatowicz (http.cs.berkeley.edu/~kubitron) Review of Last lecture Intro to VHDL Administrative
Chapter 3. Arithmetic Text: P&H rev
 Chapter 3 Arithmetic Text: P&H rev3.29.16 Arithmetic for Computers Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers Representation
Chapter 3 Arithmetic Text: P&H rev3.29.16 Arithmetic for Computers Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers Representation
COMPUTER ARITHMETIC (Part 1)
 Eastern Mediterranean University School of Computing and Technology ITEC255 Computer Organization & Architecture COMPUTER ARITHMETIC (Part 1) Introduction The two principal concerns for computer arithmetic
Eastern Mediterranean University School of Computing and Technology ITEC255 Computer Organization & Architecture COMPUTER ARITHMETIC (Part 1) Introduction The two principal concerns for computer arithmetic
Fast Arithmetic. Philipp Koehn. 19 October 2016
 Fast Arithmetic Philipp Koehn 19 October 2016 1 arithmetic Addition (Immediate) 2 Load immediately one number (s0 = 2) li $s0, 2 Add 4 ($s1 = $s0 + 4 = 6) addi $s1, $s0, 4 Subtract 3 ($s2 = $s1-3 = 3)
Fast Arithmetic Philipp Koehn 19 October 2016 1 arithmetic Addition (Immediate) 2 Load immediately one number (s0 = 2) li $s0, 2 Add 4 ($s1 = $s0 + 4 = 6) addi $s1, $s0, 4 Subtract 3 ($s2 = $s1-3 = 3)
Review from last time. CS152 Computer Architecture and Engineering Lecture 6. Verilog (finish) Multiply, Divide, Shift
 Review from last time CS152 Computer Architecture and Engineering Lecture 6 Verilog (finish) Multiply, Divide, Shift February 11, 2004 John Kubiatowicz (www.cs.berkeley.edu/~kubitron) lecture slides: http://www-inst.eecs.berkeley.edu/~cs152/
Review from last time CS152 Computer Architecture and Engineering Lecture 6 Verilog (finish) Multiply, Divide, Shift February 11, 2004 John Kubiatowicz (www.cs.berkeley.edu/~kubitron) lecture slides: http://www-inst.eecs.berkeley.edu/~cs152/
Arithmetic for Computers. Hwansoo Han
 Arithmetic for Computers Hwansoo Han Arithmetic for Computers Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers Representation
Arithmetic for Computers Hwansoo Han Arithmetic for Computers Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers Representation
Thomas Polzer Institut für Technische Informatik
 Thomas Polzer tpolzer@ecs.tuwien.ac.at Institut für Technische Informatik Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers VO
Thomas Polzer tpolzer@ecs.tuwien.ac.at Institut für Technische Informatik Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers VO
Signed Multiplication Multiply the positives Negate result if signs of operand are different
 Another Improvement Save on space: Put multiplier in product saves on speed: only single shift needed Figure: Improved hardware for multiplication Signed Multiplication Multiply the positives Negate result
Another Improvement Save on space: Put multiplier in product saves on speed: only single shift needed Figure: Improved hardware for multiplication Signed Multiplication Multiply the positives Negate result
Computer Architecture Set Four. Arithmetic
 Computer Architecture Set Four Arithmetic Arithmetic Where we ve been: Performance (seconds, cycles, instructions) Abstractions: Instruction Set Architecture Assembly Language and Machine Language What
Computer Architecture Set Four Arithmetic Arithmetic Where we ve been: Performance (seconds, cycles, instructions) Abstractions: Instruction Set Architecture Assembly Language and Machine Language What
Chapter 3: Arithmetic for Computers
 Chapter 3: Arithmetic for Computers Objectives Signed and Unsigned Numbers Addition and Subtraction Multiplication and Division Floating Point Computer Architecture CS 35101-002 2 The Binary Numbering
Chapter 3: Arithmetic for Computers Objectives Signed and Unsigned Numbers Addition and Subtraction Multiplication and Division Floating Point Computer Architecture CS 35101-002 2 The Binary Numbering
ECE260: Fundamentals of Computer Engineering
 Arithmetic for Computers James Moscola Dept. of Engineering & Computer Science York College of Pennsylvania Based on Computer Organization and Design, 5th Edition by Patterson & Hennessy Arithmetic for
Arithmetic for Computers James Moscola Dept. of Engineering & Computer Science York College of Pennsylvania Based on Computer Organization and Design, 5th Edition by Patterson & Hennessy Arithmetic for
Chapter 3 Arithmetic for Computers
 Chapter 3 Arithmetic for Computers 1 Outline Signed and unsigned numbers (Sec. 3.2) Addition and subtraction (Sec. 3.3) Multiplication (Sec. 3.4) Division (Sec. 3.5) Floating point (Sec. 3.6) 2 Representation
Chapter 3 Arithmetic for Computers 1 Outline Signed and unsigned numbers (Sec. 3.2) Addition and subtraction (Sec. 3.3) Multiplication (Sec. 3.4) Division (Sec. 3.5) Floating point (Sec. 3.6) 2 Representation
COMPUTER ORGANIZATION AND DESIGN
 COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Interface 5 th Edition Chapter 3 Arithmetic for Computers Arithmetic for Computers Operations on integers Addition and subtraction Multiplication
COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Interface 5 th Edition Chapter 3 Arithmetic for Computers Arithmetic for Computers Operations on integers Addition and subtraction Multiplication
Integer Multiplication and Division
 Integer Multiplication and Division for ENCM 369: Computer Organization Steve Norman, PhD, PEng Electrical & Computer Engineering Schulich School of Engineering University of Calgary Winter Term, 208 Integer
Integer Multiplication and Division for ENCM 369: Computer Organization Steve Norman, PhD, PEng Electrical & Computer Engineering Schulich School of Engineering University of Calgary Winter Term, 208 Integer
Math in MIPS. Subtracting a binary number from another binary number also bears an uncanny resemblance to the way it s done in decimal.
 Page < 1 > Math in MIPS Adding and Subtracting Numbers Adding two binary numbers together is very similar to the method used with decimal numbers, except simpler. When you add two binary numbers together,
Page < 1 > Math in MIPS Adding and Subtracting Numbers Adding two binary numbers together is very similar to the method used with decimal numbers, except simpler. When you add two binary numbers together,
Lecture 13: (Integer Multiplication and Division) FLOATING POINT NUMBERS
 Lecture 13: (Integer Multiplication and Division) FLOATING POINT NUMBERS Lecture 13 Floating Point I (1) Fall 2005 Integer Multiplication (1/3) Paper and pencil example (unsigned): Multiplicand 1000 8
Lecture 13: (Integer Multiplication and Division) FLOATING POINT NUMBERS Lecture 13 Floating Point I (1) Fall 2005 Integer Multiplication (1/3) Paper and pencil example (unsigned): Multiplicand 1000 8
Arithmetic for Computers
 MIPS Arithmetic Instructions Cptr280 Dr Curtis Nelson Arithmetic for Computers Operations on integers Addition and subtraction; Multiplication and division; Dealing with overflow; Signed vs. unsigned numbers.
MIPS Arithmetic Instructions Cptr280 Dr Curtis Nelson Arithmetic for Computers Operations on integers Addition and subtraction; Multiplication and division; Dealing with overflow; Signed vs. unsigned numbers.
Number Systems and Their Representations
 Number Representations Cptr280 Dr Curtis Nelson Number Systems and Their Representations In this presentation you will learn about: Representation of numbers in computers; Signed vs. unsigned numbers;
Number Representations Cptr280 Dr Curtis Nelson Number Systems and Their Representations In this presentation you will learn about: Representation of numbers in computers; Signed vs. unsigned numbers;
CSE 141 Computer Architecture Summer Session Lecture 3 ALU Part 2 Single Cycle CPU Part 1. Pramod V. Argade
 CSE 141 Computer Architecture Summer Session 1 2004 Lecture 3 ALU Part 2 Single Cycle CPU Part 1 Pramod V. Argade Reading Assignment Announcements Chapter 5: The Processor: Datapath and Control, Sec. 5.3-5.4
CSE 141 Computer Architecture Summer Session 1 2004 Lecture 3 ALU Part 2 Single Cycle CPU Part 1 Pramod V. Argade Reading Assignment Announcements Chapter 5: The Processor: Datapath and Control, Sec. 5.3-5.4
carry in carry 1101 carry carry
 Chapter Binary arithmetic Arithmetic is the process of applying a mathematical operator (such as negation or addition) to one or more operands (the values being operated upon). Binary arithmetic works
Chapter Binary arithmetic Arithmetic is the process of applying a mathematical operator (such as negation or addition) to one or more operands (the values being operated upon). Binary arithmetic works
Chapter 3 Arithmetic for Computers (Part 2)
 Department of Electr rical Eng ineering, Chapter 3 Arithmetic for Computers (Part 2) 王振傑 (Chen-Chieh Wang) ccwang@mail.ee.ncku.edu.tw ncku edu Depar rtment of Electr rical Eng ineering, Feng-Chia Unive
Department of Electr rical Eng ineering, Chapter 3 Arithmetic for Computers (Part 2) 王振傑 (Chen-Chieh Wang) ccwang@mail.ee.ncku.edu.tw ncku edu Depar rtment of Electr rical Eng ineering, Feng-Chia Unive
ECE331: Hardware Organization and Design
 ECE331: Hardware Organization and Design Lecture 9: Binary Addition & Multiplication Adapted from Computer Organization and Design, Patterson & Hennessy, UCB Pop Quiz! Using 4 bits signed integer notation:
ECE331: Hardware Organization and Design Lecture 9: Binary Addition & Multiplication Adapted from Computer Organization and Design, Patterson & Hennessy, UCB Pop Quiz! Using 4 bits signed integer notation:
xx.yyyy Lecture #11 Floating Point II Summary (single precision): Precision and Accuracy Fractional Powers of 2 Representation of Fractions
 CS61C L11 Floating Point II (1) inst.eecs.berkeley.edu/~cs61c CS61C : Machine Structures Lecture #11 Floating Point II 2007-7-12 Scott Beamer, Instructor Sony & Nintendo make E3 News www.nytimes.com Review
CS61C L11 Floating Point II (1) inst.eecs.berkeley.edu/~cs61c CS61C : Machine Structures Lecture #11 Floating Point II 2007-7-12 Scott Beamer, Instructor Sony & Nintendo make E3 News www.nytimes.com Review
Arithmetic Logic Unit
 Arithmetic Logic Unit A.R. Hurson Department of Computer Science Missouri University of Science & Technology A.R. Hurson 1 Arithmetic Logic Unit It is a functional bo designed to perform "basic" arithmetic,
Arithmetic Logic Unit A.R. Hurson Department of Computer Science Missouri University of Science & Technology A.R. Hurson 1 Arithmetic Logic Unit It is a functional bo designed to perform "basic" arithmetic,
IEEE Standard 754 for Binary Floating-Point Arithmetic.
 CS61C L11 Floating Point II (1) inst.eecs.berkeley.edu/~cs61c CS61C : Machine Structures Lecture #11 Floating Point II 2005-10-05 There is one handout today at the front and back of the room! Lecturer
CS61C L11 Floating Point II (1) inst.eecs.berkeley.edu/~cs61c CS61C : Machine Structures Lecture #11 Floating Point II 2005-10-05 There is one handout today at the front and back of the room! Lecturer
Chapter Three. Arithmetic
 Chapter Three 1 Arithmetic Where we've been: Performance (seconds, cycles, instructions) Abstractions: Instruction Set Architecture Assembly Language and Machine Language What's up ahead: Implementing
Chapter Three 1 Arithmetic Where we've been: Performance (seconds, cycles, instructions) Abstractions: Instruction Set Architecture Assembly Language and Machine Language What's up ahead: Implementing
Module 2: Computer Arithmetic
 Module 2: Computer Arithmetic 1 B O O K : C O M P U T E R O R G A N I Z A T I O N A N D D E S I G N, 3 E D, D A V I D L. P A T T E R S O N A N D J O H N L. H A N N E S S Y, M O R G A N K A U F M A N N
Module 2: Computer Arithmetic 1 B O O K : C O M P U T E R O R G A N I Z A T I O N A N D D E S I G N, 3 E D, D A V I D L. P A T T E R S O N A N D J O H N L. H A N N E S S Y, M O R G A N K A U F M A N N
CS/COE0447: Computer Organization
 CS/COE0447: Computer Organization and Assembly Language Chapter 3 Sangyeun Cho Dept. of Computer Science Five classic components I am like a control tower I am like a pack of file folders I am like a conveyor
CS/COE0447: Computer Organization and Assembly Language Chapter 3 Sangyeun Cho Dept. of Computer Science Five classic components I am like a control tower I am like a pack of file folders I am like a conveyor
CS/COE0447: Computer Organization
 Five classic components CS/COE0447: Computer Organization and Assembly Language I am like a control tower I am like a pack of file folders Chapter 3 I am like a conveyor belt + service stations I exchange
Five classic components CS/COE0447: Computer Organization and Assembly Language I am like a control tower I am like a pack of file folders Chapter 3 I am like a conveyor belt + service stations I exchange
Week 7: Assignment Solutions
 Week 7: Assignment Solutions 1. In 6-bit 2 s complement representation, when we subtract the decimal number +6 from +3, the result (in binary) will be: a. 111101 b. 000011 c. 100011 d. 111110 Correct answer
Week 7: Assignment Solutions 1. In 6-bit 2 s complement representation, when we subtract the decimal number +6 from +3, the result (in binary) will be: a. 111101 b. 000011 c. 100011 d. 111110 Correct answer
CS61C : Machine Structures
 inst.eecs.berkeley.edu/~cs61c CS61C : Machine Structures Lecture #11 Floating Point II Scott Beamer, Instructor Sony & Nintendo make E3 News 2007-7-12 CS61C L11 Floating Point II (1) www.nytimes.com Review
inst.eecs.berkeley.edu/~cs61c CS61C : Machine Structures Lecture #11 Floating Point II Scott Beamer, Instructor Sony & Nintendo make E3 News 2007-7-12 CS61C L11 Floating Point II (1) www.nytimes.com Review
Chapter 5: Computer Arithmetic. In this chapter you will learn about:
 Slide 1/29 Learning Objectives In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations using binary numbers Addition (+) Subtraction (-) Multiplication
Slide 1/29 Learning Objectives In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations using binary numbers Addition (+) Subtraction (-) Multiplication
TDT4255 Computer Design. Lecture 4. Magnus Jahre
 1 TDT4255 Computer Design Lecture 4 Magnus Jahre 2 Chapter 3 Computer Arithmetic ti Acknowledgement: Slides are adapted from Morgan Kaufmann companion material 3 Arithmetic for Computers Operations on
1 TDT4255 Computer Design Lecture 4 Magnus Jahre 2 Chapter 3 Computer Arithmetic ti Acknowledgement: Slides are adapted from Morgan Kaufmann companion material 3 Arithmetic for Computers Operations on
EE260: Logic Design, Spring n Integer multiplication. n Booth s algorithm. n Integer division. n Restoring, non-restoring
 EE 260: Introduction to Digital Design Arithmetic II Yao Zheng Department of Electrical Engineering University of Hawaiʻi at Mānoa Overview n Integer multiplication n Booth s algorithm n Integer division
EE 260: Introduction to Digital Design Arithmetic II Yao Zheng Department of Electrical Engineering University of Hawaiʻi at Mānoa Overview n Integer multiplication n Booth s algorithm n Integer division
Chapter 3. Arithmetic for Computers
 Chapter 3 Arithmetic for Computers Arithmetic for Computers Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers Representation
Chapter 3 Arithmetic for Computers Arithmetic for Computers Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers Representation
Learning Objectives. Binary over Decimal. In this chapter you will learn about:
 Ref Page Slide 1/29 Learning Objectives In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations using binary numbers Addition (+) Subtraction
Ref Page Slide 1/29 Learning Objectives In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations using binary numbers Addition (+) Subtraction
Timing for Ripple Carry Adder
 Timing for Ripple Carry Adder 1 2 3 Look Ahead Method 5 6 7 8 9 Look-Ahead, bits wide 10 11 Multiplication Simple Gradeschool Algorithm for 32 Bits (6 Bit Result) Multiplier Multiplicand AND gates 32
Timing for Ripple Carry Adder 1 2 3 Look Ahead Method 5 6 7 8 9 Look-Ahead, bits wide 10 11 Multiplication Simple Gradeschool Algorithm for 32 Bits (6 Bit Result) Multiplier Multiplicand AND gates 32
ECE331: Hardware Organization and Design
 ECE331: Hardware Organization and Design Lecture 10: Multiplication & Floating Point Representation Adapted from Computer Organization and Design, Patterson & Hennessy, UCB MIPS Division Two 32-bit registers
ECE331: Hardware Organization and Design Lecture 10: Multiplication & Floating Point Representation Adapted from Computer Organization and Design, Patterson & Hennessy, UCB MIPS Division Two 32-bit registers
Sparse Notes on an MIPS Processor s Architecture and its Assembly Language
 Sparse Notes on an MIPS Processor s Architecture and its Assembly Language February 6, 2004 1 Introduction In this notes we are not going in details with the architecture of an MIPS processor, but only
Sparse Notes on an MIPS Processor s Architecture and its Assembly Language February 6, 2004 1 Introduction In this notes we are not going in details with the architecture of an MIPS processor, but only
Divide: Paper & Pencil CS152. Computer Architecture and Engineering Lecture 7. Divide, Floating Point, Pentium Bug. DIVIDE HARDWARE Version 1
 Divide: Paper & Pencil Computer Architecture and Engineering Lecture 7 Divide, Floating Point, Pentium Bug 1001 Quotient 1000 1001010 Dividend 1000 10 101 1010 1000 10 (or Modulo result) See how big a
Divide: Paper & Pencil Computer Architecture and Engineering Lecture 7 Divide, Floating Point, Pentium Bug 1001 Quotient 1000 1001010 Dividend 1000 10 101 1010 1000 10 (or Modulo result) See how big a
CENG3420 L05: Arithmetic and Logic Unit
 CENG3420 L05: Arithmetic and Logic Unit Bei Yu byu@cse.cuhk.edu.hk (Latest update: January 25, 2018) Spring 2018 1 / 53 Overview Overview Addition Multiplication & Division Shift Floating Point Number
CENG3420 L05: Arithmetic and Logic Unit Bei Yu byu@cse.cuhk.edu.hk (Latest update: January 25, 2018) Spring 2018 1 / 53 Overview Overview Addition Multiplication & Division Shift Floating Point Number
Review: MIPS Organization
 1 MIPS Arithmetic Review: MIPS Organization Processor Memory src1 addr 5 src2 addr 5 dst addr 5 write data Register File registers ($zero - $ra) bits src1 data src2 data read/write addr 1 1100 2 30 words
1 MIPS Arithmetic Review: MIPS Organization Processor Memory src1 addr 5 src2 addr 5 dst addr 5 write data Register File registers ($zero - $ra) bits src1 data src2 data read/write addr 1 1100 2 30 words
9 Multiplication and Division
 9 Multiplication and Division Multiplication is done by doing shifts and additions. Multiplying two (unsigned) numbers of n bits each results in a product of 2n bits. Example: 0110 x 0011 (6x3) At start,
9 Multiplication and Division Multiplication is done by doing shifts and additions. Multiplying two (unsigned) numbers of n bits each results in a product of 2n bits. Example: 0110 x 0011 (6x3) At start,
Computer Architecture and Engineering Lecture 7: Divide, Floating Point, Pentium Bug
 Computer Architecture and Engineering Lecture 7: Divide, Floating Point, Pentium Bug September 17, 1997 Dave Patterson (http.cs.berkeley.edu/~patterson) lecture slides: http://www-inst.eecs.berkeley.edu/~cs152/
Computer Architecture and Engineering Lecture 7: Divide, Floating Point, Pentium Bug September 17, 1997 Dave Patterson (http.cs.berkeley.edu/~patterson) lecture slides: http://www-inst.eecs.berkeley.edu/~cs152/
MIPS ISA. 1. Data and Address Size 8-, 16-, 32-, 64-bit 2. Which instructions does the processor support
 Components of an ISA EE 357 Unit 11 MIPS ISA 1. Data and Address Size 8-, 16-, 32-, 64-bit 2. Which instructions does the processor support SUBtract instruc. vs. NEGate + ADD instrucs. 3. Registers accessible
Components of an ISA EE 357 Unit 11 MIPS ISA 1. Data and Address Size 8-, 16-, 32-, 64-bit 2. Which instructions does the processor support SUBtract instruc. vs. NEGate + ADD instrucs. 3. Registers accessible
Chapter 3. Arithmetic for Computers
 Chapter 3 Arithmetic for Computers Arithmetic for Computers Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers Representation
Chapter 3 Arithmetic for Computers Arithmetic for Computers Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers Representation
Boolean Algebra. Chapter 3. Boolean Algebra. Chapter 3 Arithmetic for Computers 1. Fundamental Boolean Operations. Arithmetic for Computers
 COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Interface 5 th Edition COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Interface 5 th Edition Chapter 3 Arithmetic for Computers Arithmetic
COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Interface 5 th Edition COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Interface 5 th Edition Chapter 3 Arithmetic for Computers Arithmetic
COMPUTER ORGANIZATION AND DESIGN. 5 th Edition. The Hardware/Software Interface. Chapter 3. Arithmetic for Computers
 COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Interface 5 th Edition Chapter 3 Arithmetic for Computers Boolean Algebra Boolean algebra is the basic math used in digital circuits and computers.
COMPUTER ORGANIZATION AND DESIGN The Hardware/Software Interface 5 th Edition Chapter 3 Arithmetic for Computers Boolean Algebra Boolean algebra is the basic math used in digital circuits and computers.
Chapter 5: Computer Arithmetic
 Slide 1/29 Learning Objectives Computer Fundamentals: Pradeep K. Sinha & Priti Sinha In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations
Slide 1/29 Learning Objectives Computer Fundamentals: Pradeep K. Sinha & Priti Sinha In this chapter you will learn about: Reasons for using binary instead of decimal numbers Basic arithmetic operations
Computer Arithmetic Ch 8
 Computer Arithmetic Ch 8 ALU Integer Representation Integer Arithmetic Floating-Point Representation Floating-Point Arithmetic 1 Arithmetic Logical Unit (ALU) (2) (aritmeettis-looginen yksikkö) Does all
Computer Arithmetic Ch 8 ALU Integer Representation Integer Arithmetic Floating-Point Representation Floating-Point Arithmetic 1 Arithmetic Logical Unit (ALU) (2) (aritmeettis-looginen yksikkö) Does all
Computer Arithmetic Ch 8
 Computer Arithmetic Ch 8 ALU Integer Representation Integer Arithmetic Floating-Point Representation Floating-Point Arithmetic 1 Arithmetic Logical Unit (ALU) (2) Does all work in CPU (aritmeettis-looginen
Computer Arithmetic Ch 8 ALU Integer Representation Integer Arithmetic Floating-Point Representation Floating-Point Arithmetic 1 Arithmetic Logical Unit (ALU) (2) Does all work in CPU (aritmeettis-looginen
ECE331: Hardware Organization and Design
 ECE331: Hardware Organization and Design Lecture 15: Midterm 1 Review Adapted from Computer Organization and Design, Patterson & Hennessy, UCB Basics Midterm to cover Book Sections (inclusive) 1.1 1.5
ECE331: Hardware Organization and Design Lecture 15: Midterm 1 Review Adapted from Computer Organization and Design, Patterson & Hennessy, UCB Basics Midterm to cover Book Sections (inclusive) 1.1 1.5
Binary Adders. Ripple-Carry Adder
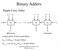 Ripple-Carry Adder Binary Adders x n y n x y x y c n FA c n - c 2 FA c FA c s n MSB position Longest delay (Critical-path delay): d c(n) = n d carry = 2n gate delays d s(n-) = (n-) d carry +d sum = 2n
Ripple-Carry Adder Binary Adders x n y n x y x y c n FA c n - c 2 FA c FA c s n MSB position Longest delay (Critical-path delay): d c(n) = n d carry = 2n gate delays d s(n-) = (n-) d carry +d sum = 2n
Review: MULTIPLY HARDWARE Version 1. ECE4680 Computer Organization & Architecture. Divide, Floating Point, Pentium Bug
 ECE468 ALU-III.1 2002-2-27 Review: MULTIPLY HARDWARE Version 1 ECE4680 Computer Organization & Architecture 64-bit Multiplicand reg, 64-bit ALU, 64-bit Product reg, 32-bit multiplier reg Divide, Floating
ECE468 ALU-III.1 2002-2-27 Review: MULTIPLY HARDWARE Version 1 ECE4680 Computer Organization & Architecture 64-bit Multiplicand reg, 64-bit ALU, 64-bit Product reg, 32-bit multiplier reg Divide, Floating
CENG 3420 Lecture 05: Arithmetic and Logic Unit
 CENG 3420 Lecture 05: Arithmetic and Logic Unit Bei Yu byu@cse.cuhk.edu.hk CENG3420 L05.1 Spring 2017 Outline q 1. Overview q 2. Addition q 3. Multiplication & Division q 4. Shift q 5. Floating Point Number
CENG 3420 Lecture 05: Arithmetic and Logic Unit Bei Yu byu@cse.cuhk.edu.hk CENG3420 L05.1 Spring 2017 Outline q 1. Overview q 2. Addition q 3. Multiplication & Division q 4. Shift q 5. Floating Point Number
Lecture Topics. Announcements. Today: Integer Arithmetic (P&H ) Next: The MIPS ISA (P&H ) Consulting hours. Milestone #1 (due 1/26)
 Lecture Topics Today: Integer Arithmetic (P&H 3.1-3.4) Next: The MIPS ISA (P&H 2.1-2.14) 1 Announcements Consulting hours Milestone #1 (due 1/26) Milestone #2 (due 2/2) 2 1 Review: Integer Operations Internal
Lecture Topics Today: Integer Arithmetic (P&H 3.1-3.4) Next: The MIPS ISA (P&H 2.1-2.14) 1 Announcements Consulting hours Milestone #1 (due 1/26) Milestone #2 (due 2/2) 2 1 Review: Integer Operations Internal
Chapter 3. Arithmetic for Computers
 Chapter 3 Arithmetic for Computers Arithmetic for Computers Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers Representation
Chapter 3 Arithmetic for Computers Arithmetic for Computers Operations on integers Addition and subtraction Multiplication and division Dealing with overflow Floating-point real numbers Representation
Exceptions and Interrupts
 Exceptions and Interrupts Unexpected events (asynchronous interrupt) requiring change in flow of control (different ISAs use the terms differently) exception Arises within the CPU e.g., undefined opcode,
Exceptions and Interrupts Unexpected events (asynchronous interrupt) requiring change in flow of control (different ISAs use the terms differently) exception Arises within the CPU e.g., undefined opcode,
Computer Arithmetic Multiplication & Shift Chapter 3.4 EEC170 FQ 2005
 Computer Arithmetic Multiplication & Shift Chapter 3.4 EEC170 FQ 200 Multiply We will start with unsigned multiply and contrast how humans and computers multiply Layout 8-bit 8 Pipelined Multiplier 1 2
Computer Arithmetic Multiplication & Shift Chapter 3.4 EEC170 FQ 200 Multiply We will start with unsigned multiply and contrast how humans and computers multiply Layout 8-bit 8 Pipelined Multiplier 1 2
COMPUTER ORGANIZATION AND ARCHITECTURE
 COMPUTER ORGANIZATION AND ARCHITECTURE For COMPUTER SCIENCE COMPUTER ORGANIZATION. SYLLABUS AND ARCHITECTURE Machine instructions and addressing modes, ALU and data-path, CPU control design, Memory interface,
COMPUTER ORGANIZATION AND ARCHITECTURE For COMPUTER SCIENCE COMPUTER ORGANIZATION. SYLLABUS AND ARCHITECTURE Machine instructions and addressing modes, ALU and data-path, CPU control design, Memory interface,
COMPUTER ORGANIZATION AND. Edition. The Hardware/Software Interface. Chapter 3. Arithmetic for Computers
 ARM D COMPUTER ORGANIZATION AND Edition The Hardware/Software Interface Chapter 3 Arithmetic for Computers Modified and extended by R.J. Leduc - 2016 In this chapter, we will investigate: How integer arithmetic
ARM D COMPUTER ORGANIZATION AND Edition The Hardware/Software Interface Chapter 3 Arithmetic for Computers Modified and extended by R.J. Leduc - 2016 In this chapter, we will investigate: How integer arithmetic
Arithmetic Processing
 CS/EE 5830/6830 VLSI ARCHITECTURE Chapter 1 Basic Number Representations and Arithmetic Algorithms Arithmetic Processing AP = (operands, operation, results, conditions, singularities) Operands are: Set
CS/EE 5830/6830 VLSI ARCHITECTURE Chapter 1 Basic Number Representations and Arithmetic Algorithms Arithmetic Processing AP = (operands, operation, results, conditions, singularities) Operands are: Set
By, Ajinkya Karande Adarsh Yoga
 By, Ajinkya Karande Adarsh Yoga Introduction Early computer designers believed saving computer time and memory were more important than programmer time. Bug in the divide algorithm used in Intel chips.
By, Ajinkya Karande Adarsh Yoga Introduction Early computer designers believed saving computer time and memory were more important than programmer time. Bug in the divide algorithm used in Intel chips.
CS/COE 0447 Example Problems for Exam 2 Spring 2011
 CS/COE 0447 Example Problems for Exam 2 Spring 2011 1) Show the steps to multiply the 4-bit numbers 3 and 5 with the fast shift-add multipler. Use the table below. List the multiplicand (M) and product
CS/COE 0447 Example Problems for Exam 2 Spring 2011 1) Show the steps to multiply the 4-bit numbers 3 and 5 with the fast shift-add multipler. Use the table below. List the multiplicand (M) and product
Computer Architecture. Chapter 3: Arithmetic for Computers
 182.092 Computer Architecture Chapter 3: Arithmetic for Computers Adapted from Computer Organization and Design, 4 th Edition, Patterson & Hennessy, 2008, Morgan Kaufmann Publishers and Mary Jane Irwin
182.092 Computer Architecture Chapter 3: Arithmetic for Computers Adapted from Computer Organization and Design, 4 th Edition, Patterson & Hennessy, 2008, Morgan Kaufmann Publishers and Mary Jane Irwin
The Operating System (OS) MicroComputer Engineering OperatingSystem slide 1!
 The Operating System (OS) MicroComputer Engineering OperatingSystem slide 1! The Operating System (OS) P1:! Editor! P2: Compiler! P3:! Quake! Arena! Operating System! MIPS! At any one time the processor
The Operating System (OS) MicroComputer Engineering OperatingSystem slide 1! The Operating System (OS) P1:! Editor! P2: Compiler! P3:! Quake! Arena! Operating System! MIPS! At any one time the processor
HW2 solutions You did this for Lab sbn temp, temp,.+1 # temp = 0; sbn temp, b,.+1 # temp = -b; sbn a, temp,.+1 # a = a (-b) = a + b;
 HW2 solutions 3.10 Pseuodinstructions What is accomplished Minimum sequence of Mips Move $t5, $t3 $t5=$t3 Add $t5, $t3, $0 Clear $t5 $t5=0 Xor $t5, $t5, $t5 Li $t5, small $t5=small Addi $t5, $0, small
HW2 solutions 3.10 Pseuodinstructions What is accomplished Minimum sequence of Mips Move $t5, $t3 $t5=$t3 Add $t5, $t3, $0 Clear $t5 $t5=0 Xor $t5, $t5, $t5 Li $t5, small $t5=small Addi $t5, $0, small
Mark Redekopp, All rights reserved. EE 357 Unit 11 MIPS ISA
 EE 357 Unit 11 MIPS ISA Components of an ISA 1. Data and Address Size 8-, 16-, 32-, 64-bit 2. Which instructions does the processor support SUBtract instruc. vs. NEGate + ADD instrucs. 3. Registers accessible
EE 357 Unit 11 MIPS ISA Components of an ISA 1. Data and Address Size 8-, 16-, 32-, 64-bit 2. Which instructions does the processor support SUBtract instruc. vs. NEGate + ADD instrucs. 3. Registers accessible
Midterm I March 12, 2003 CS152 Computer Architecture and Engineering
 University of California, Berkeley College of Engineering Computer Science Division EECS Spring 2003 John Kubiatowicz Midterm I March 2, 2003 CS52 Computer Architecture and Engineering Your Name: SID Number:
University of California, Berkeley College of Engineering Computer Science Division EECS Spring 2003 John Kubiatowicz Midterm I March 2, 2003 CS52 Computer Architecture and Engineering Your Name: SID Number:
 CS6303 COMPUTER ARCHITECTURE LESSION NOTES UNIT II ARITHMETIC OPERATIONS ALU In computing an arithmetic logic unit (ALU) is a digital circuit that performs arithmetic and logical operations. The ALU is
CS6303 COMPUTER ARCHITECTURE LESSION NOTES UNIT II ARITHMETIC OPERATIONS ALU In computing an arithmetic logic unit (ALU) is a digital circuit that performs arithmetic and logical operations. The ALU is
CS 5803 Introduction to High Performance Computer Architecture: Arithmetic Logic Unit. A.R. Hurson 323 CS Building, Missouri S&T
 CS 5803 Introduction to High Performance Computer Architecture: Arithmetic Logic Unit A.R. Hurson 323 CS Building, Missouri S&T hurson@mst.edu 1 Outline Motivation Design of a simple ALU How to design
CS 5803 Introduction to High Performance Computer Architecture: Arithmetic Logic Unit A.R. Hurson 323 CS Building, Missouri S&T hurson@mst.edu 1 Outline Motivation Design of a simple ALU How to design
Instruction Set Architecture of. MIPS Processor. MIPS Processor. MIPS Registers (continued) MIPS Registers
 CSE 675.02: Introduction to Computer Architecture MIPS Processor Memory Instruction Set Architecture of MIPS Processor CPU Arithmetic Logic unit Registers $0 $31 Multiply divide Coprocessor 1 (FPU) Registers
CSE 675.02: Introduction to Computer Architecture MIPS Processor Memory Instruction Set Architecture of MIPS Processor CPU Arithmetic Logic unit Registers $0 $31 Multiply divide Coprocessor 1 (FPU) Registers
Instruction Set Architecture of MIPS Processor
 CSE 3421/5421: Introduction to Computer Architecture Instruction Set Architecture of MIPS Processor Presentation B Study: 2.1 2.3, 2.4 2.7, 2.10 and Handout MIPS Instructions: 32-bit Core Subset Read:
CSE 3421/5421: Introduction to Computer Architecture Instruction Set Architecture of MIPS Processor Presentation B Study: 2.1 2.3, 2.4 2.7, 2.10 and Handout MIPS Instructions: 32-bit Core Subset Read:
ECE232: Hardware Organization and Design. Computer Organization - Previously covered
 ECE232: Hardware Organization and Design Part 6: MIPS Instructions II http://www.ecs.umass.edu/ece/ece232/ Adapted from Computer Organization and Design, Patterson & Hennessy, UCB Computer Organization
ECE232: Hardware Organization and Design Part 6: MIPS Instructions II http://www.ecs.umass.edu/ece/ece232/ Adapted from Computer Organization and Design, Patterson & Hennessy, UCB Computer Organization
COMPUTER ARCHITECTURE AND ORGANIZATION. Operation Add Magnitudes Subtract Magnitudes (+A) + ( B) + (A B) (B A) + (A B)
 Computer Arithmetic Data is manipulated by using the arithmetic instructions in digital computers. Data is manipulated to produce results necessary to give solution for the computation problems. The Addition,
Computer Arithmetic Data is manipulated by using the arithmetic instructions in digital computers. Data is manipulated to produce results necessary to give solution for the computation problems. The Addition,
CS 64 Week 1 Lecture 1. Kyle Dewey
 CS 64 Week 1 Lecture 1 Kyle Dewey Overview Bitwise operation wrap-up Two s complement Addition Subtraction Multiplication (if time) Bitwise Operation Wrap-up Shift Left Move all the bits N positions to
CS 64 Week 1 Lecture 1 Kyle Dewey Overview Bitwise operation wrap-up Two s complement Addition Subtraction Multiplication (if time) Bitwise Operation Wrap-up Shift Left Move all the bits N positions to
EE 109 Unit 6 Binary Arithmetic
 EE 109 Unit 6 Binary Arithmetic 1 2 Semester Transition Point At this point we are going to start to transition in our class to look more at the hardware organization and the low-level software that is
EE 109 Unit 6 Binary Arithmetic 1 2 Semester Transition Point At this point we are going to start to transition in our class to look more at the hardware organization and the low-level software that is
1010 2?= ?= CS 64 Lecture 2 Data Representation. Decimal Numbers: Base 10. Reading: FLD Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
 CS 64 Lecture 2 Data Representation Reading: FLD 1.2-1.4 Decimal Numbers: Base 10 Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Example: 3271 = (3x10 3 ) + (2x10 2 ) + (7x10 1 ) + (1x10 0 ) 1010 10?= 1010 2?= 1
CS 64 Lecture 2 Data Representation Reading: FLD 1.2-1.4 Decimal Numbers: Base 10 Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Example: 3271 = (3x10 3 ) + (2x10 2 ) + (7x10 1 ) + (1x10 0 ) 1010 10?= 1010 2?= 1
Part III The Arithmetic/Logic Unit. Oct Computer Architecture, The Arithmetic/Logic Unit Slide 1
 Part III The Arithmetic/Logic Unit Oct. 214 Computer Architecture, The Arithmetic/Logic Unit Slide 1 About This Presentation This presentation is intended to support the use of the textbook Computer Architecture:
Part III The Arithmetic/Logic Unit Oct. 214 Computer Architecture, The Arithmetic/Logic Unit Slide 1 About This Presentation This presentation is intended to support the use of the textbook Computer Architecture:
CS61C Floating Point Operations & Multiply/Divide. Lecture 9. February 17, 1999 Dave Patterson (http.cs.berkeley.edu/~patterson)
 CS61C Floating Point Operations & Multiply/Divide Lecture 9 February 17, 1999 Dave Patterson (http.cs.berkeley.edu/~patterson) www-inst.eecs.berkeley.edu/~cs61c/schedule.html cs 61C L9 FP.1 Review 1/2
CS61C Floating Point Operations & Multiply/Divide Lecture 9 February 17, 1999 Dave Patterson (http.cs.berkeley.edu/~patterson) www-inst.eecs.berkeley.edu/~cs61c/schedule.html cs 61C L9 FP.1 Review 1/2
