teacher research teach "Joe" "Joe"
|
|
|
- Drusilla Shepherd
- 5 years ago
- Views:
Transcription
1 On XML Integrity Constraints in the Presence of DTDs Wenfei Fan Bell Laboratories and Leonid Libkin University of Toronto The paper investigates XML document specifications with DTDs and integrity constraints, such as keys and foreign keys. We study the consistency problem of checking whether a given specification is meaningful: that is, whether there exists an XML document that both conforms to the DTD and satisfies the constraints. We show that DTDs interact with constraints in a highly intricate way and as a result, the consistency problem in general is undecidable. When it comes to unary keys and foreign keys, the consistency problem is shown to be NP-complete. This is done by coding DTDs and integrity constraints with linear constraints on the integers. We consider the variations of the problem (by both restricting and enlarging the class of constraints), and identify a number of tractable cases, as well as a number of additional NP-complete ones. By incorporating negations of constraints, we establish complexity bounds on the implication problem, which is shown to be conp-complete for unary keys and foreign keys. Categories and Subject Descriptors: H.2.1 [Database Management]: Data models; F.4.3 [Mathematical Logic and Formal Languages]: Decision problems; I.7.2 [Document Preparation]: Markup languages General Terms: Algorithms, Design, Languages, Theory Additional Key Words and Phrases: Integrity Constraints, DTDs, XML, Consistency, Implication Name: Wenfei Fan Address: 600 Mountain Avenue, Murray Hill, NJ 07974, USA. wenfei@research.bell-labs.com. On leave from Temple University. Supported in part by NSF Career Award IIS Name: Leonid Libkin Affiliation: Department of Computer Science Address: Department of Computer Science, University of Toronto, Toronto, Ontario, M5S 3H5, Canada. libkin@cs.toronto.edu. Supported in part by National Sciences and Engineering Research Council of Canada. Research affiliation: Bell Laboratories. Permission to make digital or hard copies of part or all of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or direct commercial advantage and that copies show this notice on the first page or initial screen of a display along with the full citation. Copyrights for components of this work owned by others than ACM must be honored. Abstracting with credit is permitted. To copy otherwise, to republish, to post on servers, to redistribute to lists, or to use any component of this work in other works, requires prior specific permission and/or a fee. Permissions may be requested from Publications Dept, ACM Inc., 1515 Broadway, New York, NY USA, fax +1 (212) , or permissions@acm.org.
2 2 Wenfei Fan and Leonid Libkin 1. INTRODUCTION Although a number of dependency formalisms were developed for relational databases, functional and inclusion dependencies are the ones used most often. More precisely, only two subclasses of functional and inclusion dependencies, namely, keys and foreign keys, are commonly found in practice. Both are fundamental to conceptual database design, and are supported by the SQL standard [30]. They provide a mechanism by which one can uniquely identify a tuple in a relation and refer to a tuple from another relation. They have proved useful in update anomaly prevention, query optimization and index design [1; 37]. XML (extensible Markup Language [6]) has become the prime standard for data exchange on the Web. XML data typically originates in databases. If XML is to represent data currently residing in databases, it should support keys and foreign keys, which are an essential part of the semantics of the data. A number of key and foreign key specifications have been proposed for XML, e.g., the XML standard (DTD) [6], XML Data [27] and XML Schema [36]. Keys and foreign keys for XML are important in, among other things, query optimization [34], data integration [21], and in data transformations between XML and database formats [28]. XML data usually comes with a DTD 1 that specifies how a document is organized. Thus, a specification of an XML document may consist of both a DTD and a set of integrity constraints, such as keys and foreign keys. A legitimate question then is whether such a specification is consistent, or meaningful: that is, whether there exists a (finite) XML document that both satisfies the constraints and conforms to the DTD. In the relational database setting, such a question would have a trivial answer: one can write arbitrary (primary) key and foreign key specifications in SQL, without worrying about consistency. However, DTDs (and other schema specifications for XML) are more complex than relational schema: in fact, XML documents are typically modeled as node-labeled trees, e.g., in XSL [15], XQL [35], XML Schema [36], XPath [16] and DOM [3]. Consequently, DTDs may interact with keys and foreign keys in a rather nontrivial way, as will be seen shortly. Thus, we shall study the following family of problems, where C ranges over classes of integrity constraints: XML SPECIFICATION CONSISTENCY (C) INPUT: A DTD D, a set ± of C-constraints. QUESTION: Is there an XML document that conforms to D and satisfies ±? In other words, we want to validate XML specifications statically. The main reason is twofold: 1 Throughout the paper, by a DTD we mean its type specification; we ignore its ID/IDREF constraints since their limitations have been well recognized [7; 19]. We shall only consider finite XML documents (trees).
3 On XML Integrity Constraints in the Presence of DTDs 3 first, complex interactions between DTDs and constraints are likely to result in inconsistent specifications, and second, an alternative dynamic approach to validation (simply check a document to see if it conforms to the DTD and satisfies the constraints) would not tell us whether repeated failures are due to a bad specification, or problems with the documents. The concept of consistency of specifications was studied for other data models, such as objectoriented [12; 13] and extended relational (e.g., with support for cardinality constraints [26]). We shall study the following four classes of constraints defined in terms of XML attributes: C : a class of keys and foreign keys; C Unary : unary keys and foreign keys in C, i.e., those defined in terms of a single attribute; C Unary K : : unary keys, unary inclusion constraints and negations of unary keys; ;IC C Unary K : ;IC :: unary keys, unary inclusion constraints and their negations. Keys and foreign keys of C are a natural generalization of their relational counterpart, and are capable of capturing those relational constraints. A foreign key is a combination of two constraints: an inclusion constraint and a key. The C Unary constraints are a special case of C constraints, which involve a single attribute. These unary keys and foreign keys are similar to but more general than XML ID and IDREF specifications. The study on simple constraints defined with XML attributes is a first step towards understanding the interaction between integrity constraints and schema specifications for XML. As will be seen shortly, the analyses of these simple constraints are already very intricate in the presence of DTDs. As generalizations of C Unary Unary constraints, C K : Unary and C ;IC K : ;IC : both allow the presence of unary inclusion constraints independent ofkeys. In addition, C Unary K : includes negations of unary keys, ;IC and C Unary K : ;IC : further permits negations of unary inclusion constraints. Negation is considered mainly for the study of implication of C Unary constraints, which is the complement of a special case of the consistency problem for C Unary K : Unary (resp. C ;IC K : ;IC :): given any DTD D and any finite set ± of unary keys and inclusion constraints, is it the case that all XML trees satisfying ± and conforming to D also satisfy some other unary key (resp. unary key or inclusion constraint)? This question is important in, among other things, data integration. For example, one may want to know whether a constraint ' holds in a mediator interface, which may use XML as a uniform data format [4; 33]. This cannot be verified directly since the mediator interface does not contain data. One way to verify ' is to show that it is implied by constraints that are known to hold [21]. These problems, however, turn out to be far more intriguing than their counterparts in relational databases. In the XML setting, DTDs do interact with keys and foreign keys, and this interaction may lead to problems with XML specifications.
4 4 Wenfei Fan and Leonid Libkin Examples. To illustrate the interaction between XML DTDs and key/foreign key constraints, consider a DTD D 1, which specifies a (nonempty) collection of teachers: <!ELEMENT teachers (teacher + )> <!ELEMENT teacher (teach, research)> <!ELEMENT teach (subject, subject)> It says that a teacher teaches two subjects. Here we omit the descriptions of elements whose type is string (e.g., PCDATA in XML). Assume that each teacher has an attribute name and each subject has an attribute taught by. Attributes are single-valued. That is, if an attribute l is defined for an element type fi in a DTD, then in a document conforming to the DTD, each element oftype fi must have a unique l attribute with a string value. Consider a set of unary key and foreign key constraints, ± 1 : teacher:name! teacher; subject:taught by! subject; subject:taught by teacher:name: That is, name is a key of teacher elements, taught by is a key of subject elements and it is also a foreign key referencing name of teacher elements. More specifically, referring to an XML tree T, the first constraint asserts that two distinct teacher nodes in T cannot have the same name attribute value: the (string) value of name attribute uniquely identifies a teacher node. It should be mentioned that two notions of equality are used in the definition of keys: we assume string value equality when comparing name attribute values, and node identity when it comes to comparing teacher elements. The second key states that taught by attribute uniquely identifies a subject node in T. The third constraint asserts that for any subject node x, there is a teacher node y in T such that the taught by attribute value of x equals the name attribute value of y. Since name is a key of teacher, the taught by attribute of any subject node refers to a unique teacher node. Obviously, there exists an XML tree conforming to D 1, as shown in Figure 1. However, there is no XML tree that both conforms to D 1 and satisfies ± 1. To see this, let us first define some notations. Given an XML tree T and an element type fi, we use ext(fi) to denote the set of all the nodes labeled fi in T. Similarly, given an attribute l of fi, we use ext(fi:l) to denote the set of l attribute values of all fi elements. Then immediately from ± 1 follows a set of dependencies: jext(teacher:name)j = jext(teacher)j; jext(subject:taught by)j = jext(subject)j; jext(subject:taught by)j» jext(teacher:name)j;
5 On XML Integrity Constraints in the Presence of DTDs 5 teachers teacher "Joe" teach research subject subject "Web DB" "Joe" "Joe" Fig. 1. An XML tree conforming to D 1 where j jis the cardinality of a set. Therefore, we have jext(subject)j»jext(teacher)j: (1) On the other hand, the DTD D 1 requires that each teacher must teach two subjects. Since no sharing of nodes is allowed in XML trees and the collection of teacher elements is nonempty, from D 1 follows: 1 < 2 jext(teacher)j = jext(subject)j: (2) Thus jext(teacher)j < jext(subject)j. Obviously, (1) and (2) contradict with each other and therefore, there exists no XML tree that both satisfies ± 1 and conforms to D 1. In particular, the XML tree in Figure 1 violates the key subject:taught by! subject. This example demonstrates that a DTD may impose dependencies on the cardinalities of certain sets of objects in XML trees. These cardinality constraints interact with keys and foreign keys. More specifically, keys and foreign keys also enforce cardinality constraints that interact with those imposed by DTD. This makes the consistency analysis of keys and foreign keys for XML far more intriguing than that for relational databases. Because of the interaction, simple key and foreign key constraints (e.g., ± 1 )may not be satisfiable by XML trees conforming to certain DTDs (e.g., D 1 ). As another example, consider the DTD D 2 given below: <!ELEMENT db (foo)> <!ELEMENT foo (foo)> Observe that there exists no finite XML tree conforming to D 2. This demonstrates that there is need for studying consistency of XML specifications even in the absence of integrity constraints.
6 6 Wenfei Fan and Leonid Libkin Contributions. The main contributions of the paper are the following: (1) For the class C of keys and foreign keys, we show that both the consistency and the implication problems are undecidable. (2) These negative results suggest that we look at the restriction C Unary of unary keys and foreign keys (which are most typical in XML documents). We provide a coding of DTDs and these unary constraints by linear constraints on the integers. This enables us to show that the consistency problem for C Unary (even under the restriction to primary keys, i.e., at most one key for each element type) is NP-complete. We further show that the problem is still in NP for an extension C Unary K :, which also allows negations of key constraints. ;IC (3) Using a different coding of constraints, we show that the consistency problem remains in NP for C Unary K : ;IC :, the class of unary keys, unary inclusion constraints and their negations. Among other things, this shows that the implication problem for unary keys and foreign keys is conp-complete. (4) We also identify several tractable cases of the consistency problem, i.e., practical situations where the consistency problem is decidable in PTIME. The undecidability of the consistency problem contrasts sharply with its trivial counterpart in relational databases. The coding of DTDs and unary constraints with linear integer constraints reveals some insight into the interaction between DTDs and unary constraints. Moreover, it allows us to use the techniques from linear integer programming in the study of XML constraints. It should be mentioned that as XML Schema and XML Data both subsume DTDs and they support keys and foreign keys which are more general than those considered here, the undecidability and NP-hardness results carry over to these schema specifications and constraint languages for XML. Related work. Keys, foreign keys and the more general inclusion and functional dependencies have been well studied for relational databases (cf. [1]). In particular, the implication problem for unary inclusion and functional dependencies is in linear time [17]. In contrast, we shall show that the XML counterpart of this problem is conp-complete. The interaction between cardinality constraints and database schemas has been studied for object-oriented [12; 13] and extended relational data models [26]. These interactions are quite different from what we explore in this paper because XML DTDs are defined in terms of extended context free grammars and they yield cardinality constraints more complex than those studied for databases. Key and foreign key specifications for XML have been proposed in the XML standard [6], XML Data [27], XML Schema [36] and in a recent proposal for XML keys [7]. The need for
7 On XML Integrity Constraints in the Presence of DTDs 7 studying XML constraints has also been advocated in [38]. DTDs in the XML standard allow one to specify limited (primary) unary keys and foreign keys with ID and IDREF attributes. However, they are not scoped: one has no control over what IDREF attributes point to. XML Data and XML Schema support more expressive specifications for keys and foreign keys with, e.g., XPath expressions. However, the consistency problems associated with constraints defined in these languages have not been studied. We consider simple XML keys and foreign keys in this paper to focus on the nature of the interaction between DTDs and constraints. The implication problem for a class of keys and foreign keys was investigated in [19], but in the absence of DTDs (in a graph model for XML), which trivializes the consistency analysis. For keys of [7], the implication problem was studied [8] in the tree model for XML, but DTDs were not considered there. To the best of our knowledge, no previous work has considered the interaction between DTDs and keys and foreign keys for XML (in the tree model). This paper is a full version of [18], providing the details and the proofs omitted there. A variety of constraints have been studied for semistructured data [2; 10; 20]. In particular, [20] also studies the consistency problem; the special form of constraints used there makes it possible to encode consistency as an instance of conjunctive query containment. The interaction between path constraints and database schemas was investigated in [9]. These constraints typically specify inclusions among certain sets of objects in edge-labeled graphs, and are not capable of expressing keys. Various generalizations of functional dependencies have also been studied [23; 25]. But these generalizations were investigated in database settings, which are quite different from the tree model for XML data. Moreover, they cannot express foreign keys. Application of constraints in data transformations was studied in [28]; usefulness of keys and foreign keys in query optimization has also been recognized [34]. Organization. The rest of the paper is organized as follows. Section 2 defines four classes of XML constraints, namely, C, C Unary, C Unary K : Unary and C ;IC K : :. Section 3 establishes the ;IC undecidability of the consistency problem for C, the class of keys and foreign keys. Section 4 provides an encoding for DTDs and unary constraints with linear integer constraints, and shows that the consistency problems are NP-complete for C Unary Unary and C K :. Section 5 further shows ;IC that the problem remains in NP for C Unary K : ;IC :, the class of unary keys, inclusion constraints and their negations. Section 6 summarizes the main results of the paper and identifies directions for further work. 2. DTDS, KEYS AND FOREIGN KEYS In this section, we first present a formalism of XML DTDs [6] and the XML tree model. We then define four classes of XML constraints.
8 8 Wenfei Fan and Leonid Libkin 2.1 DTDs and XML trees We extend the usual formalism of DTDs (as extended context free grammars [5; 11; 31]) by incorporating attributes. Definition 2.1. A DTD (Document Type Definition) is defined to be D =(E; A; P; R; r), where: E is a finite set of element types; A is a finite set of attributes, disjoint from E; P is a mapping from E to element type definitions: for each fi 2 E, P (fi) is a regular expression ff defined as follows: ff ::= S j fi 0 j ffl j ffjff j ff; ff j ff Λ where S denotes string type, fi 0 2 E, ffl is the empty word, and j", ;" and Λ" denote union, concatenation, and the Kleene closure, respectively; R is a mapping from E to P(A), the power-set of A; if l 2 R(fi) then we say l is defined for fi; r 2 E and is called the element type of the root. We normally denote element types by fi and attributes by l. Without loss of generality, assume that r does not occur in P (fi) for any fi 2 E. We also assume that each fi in Enfrg is connected to r, i.e., either fi occurs in P (r), or it appears in P (fi 0 ) for some fi 0 that is connected to r. As an example, let us consider the teacher DTD D 1 given in Section 1. In our formalism, D 1 can be represented as (E 1 ; A 1 ; P 1 ; R 1 ; r 1 ), where E 1 = fteachers; teacher; teach; research; subjectg A 1 = fname; taught byg P 1 (teachers) = teacher; teacher Λ P 1 (teacher) = teach; research P 1 (teach) = subject; subject P 1 (subject) = P 1 (research) =S R 1 (teacher) = fnameg R 1 (subject) = ftaught byg R 1 (teachers)=r 1 (teach) = R 1 (research) = ; r 1 = teachers Similarly, we represent the DTD D 2 given in Section 1as(E 2 ; A 2 ; P 2 ; R 2 ; r 2 ), where
9 On XML Integrity Constraints in the Presence of DTDs 9 E 2 = fdb; foog A 2 = ; P 2 (db) = P 2 (foo)=foo R 2 (db) = R 2 (foo)=; r 2 = db An XML document is typically modeled as a node-labeled ordered tree. Given a DTD, we define the notion of its valid documents as follows. Definition 2.2. Let D =(E; A; P; R; r) be a DTD. An XML tree T valid w.r.t. D (conforming to D) is defined to be T =(V; lab; ele; att; val; root), where V is a finite set of nodes (vertices); lab is a function that maps each node in V to a label in E [ A [fsg; a node v 2 V is called an element of fi if lab(v) = fi and fi 2 E, an attribute if lab(v) 2 A, and a text node if lab(v) =S; ele is a partial function defined on elements in V ; for any fi 2 E, it maps each element v of type fi to a (possibly empty) list [v 1 ; :::; v n ] of elements and text nodes in V such that lab(v 1 ) :::lab(v n ) is in the regular language defined by P (fi); att is a partial function from V A to V such that for any v 2 V and l 2 A, att(v; l) is defined iff lab(v) =fi, fi 2 E and l 2 R(fi); val is a partial function from V to string values such that for any node v 2 V, val(v) is defined iff lab(v) =S or lab(v) 2 A; root is the unique node in V such that lab(root) =r, called the root of T. For any element v 2 V, the nodes v 0 in ele(v) are called the subelements of v. For any l 2 A, if att(v; l) =v 0 then v 0 is called an attribute of v. In either case we say that there isaparent-child edge from v to v 0. The subelements and attributes of v are called its children. An XML tree has a tree structure, i.e., for each v 2 V, there is a unique path of parent-child edges from root to v. We write T j= D when T is valid w.r.t. D. Intuitively, V is the set of nodes of the tree T. The mapping lab labels every node of V with a symbol from E [ A [fsg. Text nodes and attributes are leaves. For an element x of type fi, the functions ele and att define the children of x, which are partitioned into subelements and attributes according to P (fi) and R(fi) in the DTD D. The subelements of x are ordered and their labels satisfy the regular expression P (fi). In contrast, its attributes are unordered and are identified by their labels (names). The function val assigns string values to attributes and text nodes. We consider single-valued attributes. That is, if l 2 R(fi) then every element of type fi has a unique l attribute with a string value. Since T has a tree structure, sharing of nodes is not allowed in T.
10 10 Wenfei Fan and Leonid Libkin For example, Figure 1 depicts an XML tree valid w.r.t. the DTD D 1 given in Section 1. Our model is simpler than the models of XQuery [14] and XML Schema [36] as DTDs support only one basic type (PCDATA or string) and do not have complex type constructs. Furthermore, we do not have nodes representing namespaces, processing instructions and references. These simplifications allow us to concentrate on the essence of the DTD/constraint interaction. It should further be noticed that they do not affect the lower bounds results in the paper. We need the following notations throughout the paper: for any fi 2 E [fsg, ext(fi) denotes the set of all the nodes in T labeled fi. For any nodex in T labeled by fi and for any attribute l 2 R(fi), we write x:l for val(att(x; l)), i.e., the value of the attribute l of node x. We define ext(fi:l) to be fx:l j x 2 ext(fi)g, which is a set of strings. For each fi element x in T and a list X =[l 1 ;:::;l n ] of attributes in R(fi), we use x[x] to denote the list of X-attribute values of x, i.e., x[x] =[x:l 1 ;:::;x:l n ]. For a set S, jsj denotes its cardinality. 2.2 XML constraints We next define our constraint languages for XML. We consider three types of constraints. Let D =(E; A; P; R; r) be a DTD, and T be an XML tree valid w.r.t. D. A constraint ' over D has one of the following forms: Key: fi[x]! fi, where fi 2 E and X is a set of attributes in R(fi). The XML tree T satisfies ', denoted by T j= ', iff in T, 8 xy 2 ext(fi) (^ l2x (x:l = y:l)! x = y): Inclusion constraint: fi 1 [X] fi 2 [Y ], where fi 1 ;fi 2 2 E, and X; Y are nonempty lists of attributes in R(fi 1 );R(fi 2 ) of the same length. We write T j= ' iff in T, 8 x 2 ext(fi 1 ) 9 y 2 ext(fi 2 )(x[x] =y[y ]): Foreign key: a combination of two constraints, namely, an inclusion constraint fi 1 [X] fi 2 [Y ] and a key fi 2 [Y ]! fi 2. We write T j= ' iff T satisfies both the key and the inclusion constraint. That is, a key fi[x]! fi indicates that the set X of attributes is a key of elements of fi, i.e., two distinct fi nodes in T cannot have the same X-attribute values; an inclusion constraint fi 1 [X] fi 2 [Y ] says that the list of X-attribute values of every fi 1 node in T must match the list of Y -attribute values of some fi 2 node in T ; and an foreign key fi 1 [X] fi 2 [Y ], fi 2 [Y ]! fi 2 indicates that X is a foreign key of fi 1 elements referencing key Y of fi 2 elements.
11 On XML Integrity Constraints in the Presence of DTDs 11 Over a DTD D, the class C of constraints consists of all the keys and foreign keys over D. They are called multi-attribute keys and foreign keys as they may be defined in terms of multiple attributes. To illustrate keys and foreign keys of C, let us consider a DTD D 3 =(E 3 ; A 3 ; P 3 ; R 3 ; r 3 ), where E 3 = fschool; student; course; enroll; name; subjectg A 3 = fstudent id; course no; deptg P 3 (school) = course Λ ; student Λ ; enroll Λ P 3 (course) = subject P 3 (student) =name P 3 (enroll) = P 3 (name) = P 3 (subject) = S R 3 (course) = fdept; course nog R 3 (student)= fstudent idg R 3 (enroll) = fstudent id; dept; course nog R 3 (school) = R 3 (name) = R 3 (subject) = ; r 3 = school Typical C constraints over D 3 include: (1) student[student id]! student, (2) course[dept; course no]! course, (3) enroll[student id; dept; course no]! enroll, (4) enroll[student id] student[student id], (5) enroll[dept; course no] course[dept; course no]. The first three constraints are keys in C, and the pairs (4, 1) and (5, 2) are foreign keys in C. The last two constraints are inclusion constraints. It is worth mentioning that two notions of equality are used to define keys: string value equality is assumed in x:l = y:l (when comparing attribute values), and x = y is true if and only if x and y are the same node (when comparing elements). This is different from the semantics of keys in relational databases. Note that a foreign key requires the presence of a key in addition to an inclusion constraint. The class of unary keys and foreign keys for XML, denoted by C Unary, is a sublanguage of C. A C Unary constraint is a C constraint defined with a single attribute. More specifically, a constraint ' of C Unary over the DTD D is either
12 12 Wenfei Fan and Leonid Libkin key: fi:l! fi, where fi 2 E and l 2 R(fi); or foreign key: fi 1 :l 1 fi 2 :l 2 and fi 2 :l 2! fi 2, where fi 1 ;fi 2 2 E, l 1 2 R(fi 1 ), and l 2 2 R(fi 2 ). For example, the constraints of ± 1 given in Section 1 are C Unary constraints over the DTD D 1. We shall also consider the following types of unary constraints over D: inclusion constraint: fi 1 :l 1 fi 2 :l 2 ; unlike a foreign key, it does not require the presence of a key; the negation of an inclusion constraint: ffi = fi 1 :l 1 6 fi 2 :l 2 ; for an XML tree T, T j= ffi iff there is a fi 1 element x in T such that for all fi 2 element y in T, x:l 1 6= y:l 2 ; the negation of a key: ' = fi:l 6! fi; T j= ' iff there are fi elements x 1 ;x 2 in T such that x 1 :l = x 2 :l, i.e., the value of the l attribute of a fi element cannot uniquely identify it in ext(fi). With these we define two extensions of C Unary Unary as follows. One is C K :, the class consisting ;IC of unary keys, unary inclusion constraints and negations of unary keys. The other, C Unary K : :, ;IC consists of unary keys, unary inclusion constraints and their negations. As mentioned earlier, we consider these classes mostly for the study of the implication problem for C Unary constraints. Finally,we describe the consistency and implication problems associated with XML constraints. Let C be one of C, C Unary, C Unary K : Unary or C ;IC K : ;IC :, D a DTD, ± a set of C constraints over D and T an XML tree valid w.r.t. D. We write T j= ± when T j= ffi for all ffi 2 ±. Let ' be another C constraint. We say that ± implies ' over D, denoted by (D; ±) ` ', if for any XML tree T such that T j= D and T j= ±,itmust be the case that T j= '. It should be noted when ' is a foreign key, ' consists of an inclusion constraint ffi 1 andakey ffi 2. In this case (D; ±) ` ' in fact means that (D; ±) ` ffi 1 ^ ffi 2. The central technical problem investigated in this paper is the consistency problem. The consistency problem for C is to determine, given any DTD D and any set ± of C constraints over D, whether there is an XML tree T such that T j= ±and T j= D. The implication problem for C is to determine, given any DTD D, any set ± and ' of C constraints over D, whether (D; ±) ` '. 3. GENERAL KEYS AND FOREIGN KEYS In this section we study C, the class of multi-attribute keys and foreign keys. We show that the consistency and implication problems for C are undecidable, but we identify several special cases of the problems and show that these cases are decidable in PTIME.
13 3.1 Undecidability of consistency analysis Our main result is negative: On XML Integrity Constraints in the Presence of DTDs 13 Theorem 3.1. The consistency problem for C constraints is undecidable. Proof: We first show that an implication problem associated with keys and foreign keys in relational databases is undecidable, and then present a reduction from (the complement of) the implication problem to the consistency problem for C constraints. Let us first review keys, foreign keys and their associated implication problems in relational databases (cf. [1]). Let R = (R 1 ; :::; R n ) be a relational schema. For each relation (schema) R i in R, we write Att(R i ) for the set of all attributes of R i, and Inst(R i ) for the set of finite instances of R i. By database instances we mean finite instances. An instance I of R has the form (I 1 ; :::; I n ), where I i 2 Inst(R i ) for all i 2 [1;n]. For an instance I i 2 Inst(R i ), a tuple t 2 I i and an attribute l 2 Att(R i ), we use t:l to denote the l attribute value of t. Keys and foreign keys over R are defined as follows: key: R[l 1 ; :::; l k ]! R, where R 2 R, and for any i 2 [1;k], l i 2 Att(R). An instance I of R satisfies the key constraint ', denoted ^ by I j= ', if ^ 8 t 1 t 2 2 I ( (t 1 :l i = t 2 :l i )! (t 1 :l = t 2 :l)); 1»i»k l2att(r) where I is the instance of R in I; foreign key: R[l 1 ; :::; l k ] R 0 [l 0 ; :::; 1 l0 ] and k R0 [l 0 ; :::; 1 l0 ]! k R0, where R, R 0 are in R, [l 1 ; :::; l k ] and [l 0 ; :::; 1 l0 ] are lists of attributes in Att(R) and in k Att(R0 ), respectively. In addition, the set consisting of l 0 ; :::; 1 l0 isakey of k R0. We write I j= ' if I j= R 0 [l 0 ; :::; 1 l0 ]! k R0 and moreover, ^ 8 t 1 2 I 9 t 2 2 I 0 ( t 1 :l j = t 2 :lj); 0 1»j»k where I and I 0 are the instances of R and R 0 in I, respectively. Let ± [f'g be a set of keys and foreign keys over R. We use ± ` ' to denote that ± implies ', i.e., for any instance I of R, ifi j= ±,then I j= '. In relational databases, the implication problem for keys and foreign keys is the problem of determining, given a relational schema R, any set ± and ' of keys and foreign keys over R, whether ± ` '. A special case of the problem is the implication problem for keys by keys and foreign keys, which is to determine whether ± ` ' where ' isakey and ±isasetof keys and foreign keys over R.
14 14 Wenfei Fan and Leonid Libkin It was shown in [19] that the implication problem for keys and foreign keys in relational databases is undecidable. The lemma below shows a stronger result. Lemma 3.2. In relational databases, the implication problem for keys by keys and foreign keys is undecidable. Proof: We prove this by reduction from the implication problem for functional dependencies by functional and inclusion dependencies, which is undecidable. Before we give the reduction, we first review functional and inclusion dependencies in relational databases. Let R be a relational schema. Functional dependencies (FDs) and inclusion dependencies (IDs) over R are defined as follows. FD. R : X! Y, where R 2 R, and X and Y are subsets of attributes in Att(R). ^ An instance (t 1 :l = t 2 :l)! (t 1 :l 0 = t 2 :l 0 )), I of R satisfies the FD, denoted by I j=, if8 t 1 t 2 2 I (^ where I is the instance of R in I. Observe that keys are a special case of FDs in which Y = Att(R). ID. R[l 1 ; :::; l k ] R 0 [l 0 ; :::; 1 l0 ], where k R; R0 2 R, [l 1 ; :::; l k ] is a list of attributes in Att(R), and [l 0 ; :::; 1 l0 ] is a list of attributes in k Att(R0 ). In contrast to foreign keys, the set consisting of l 0 ; :::; 1 l0 k is not necessarily a ^ key of R 0. An instance I of R satisfies the ID, denoted by I j=, if 8 t 1 2 I 9 t 2 2 I 0 ( t 1 :l j = t 2 :lj), 0 where I;I 0 are the instances of R; R 0 in I, respectively. 1»j»k Let ± [f g be a set of FDs and IDs over R. We use ± ` to denote that ± implies as for keys and foreign keys. The implication problem for FDs by FDs and IDs is the problem to determine, given any relational schema R, any set ± of FDs and IDs over R and a FD over R, whether ± `. This isawell-known undecidable problem (see, e.g., [1] for a proof). We encode FDs and IDs in terms of keys and foreign keys as follows. (1) FD ψ = R : X! Y. Note that every relation R has a key. In particular, Att(R), the set of all attributes of R, is a key of R. Let Z be a key for R, i.e., R[Z]! R. We define a new (fresh) relation schema R new such that Att(R new )=XY Z, i.e., the union of X, Y and Z. Intuitively, given an instance I of R, an instance I new of R new is to be constructed as a subset of Π XY Z (I) such that Π XY (I) =Π XY (I new ) and I new satisfies the key R new [XY ]! R new, where Π W (I) denotes the projection of I on attributes W. That is, we eliminate tuples in Π XY Z (I) that violate the key. Observe that XY Z is a key for both R new and R since it is the set of all attributes of R new, l2x l 0 2Y
15 On XML Integrity Constraints in the Presence of DTDs 15 and it contains the key Z of R (i.e., it is a superkey of R). Thus we encode ψ with: (2) ID ψ = R 1 [X] R 2 [Y ]. ffi 1 = R new [X]! R new ; ffi 2 = R[XY ] R new [XY ]; ffi 3 = R new [XY Z] R[XY Z]; ffi 4 = R new [XY ]! R new : Let Z be a key for R 2, i.e., R 2 [Z]! R 2. We define a new schema R new such that Att(R new )= YZ. Intuitively, given an instance I 2 of R 2, an instance I new of R new is to be constructed as a subset of Π YZ (I 2 ) by eliminating tuples that violate the key R new [Y ]! R new, such that Π Y (I 2 )=Π Y (I new ) and I new satisfies the key. Observe that YZ isakey for R 2 since it contains the key Z of R 2, i.e., it is a superkey of R 2. Thus we encode ψ with: ffi 1 = R new [Y ]! R new ; ffi 2 = R 1 [X] R new [Y ]; ffi 3 = R new [YZ] R 2 [YZ]: We next show that the encoding is indeed a reduction from the implication problem for FDs by FDs and IDs to the implication problem for keys by keys and foreign keys. Given a relational schema R, a set ± of FDs and IDs over R, and a FD = R : X! Y over R, as described above we encode ± with a set ± 1 of keys and foreign keys, and encode with ffi 1 = R new[x]! R new ; ffi 2 = R [XY ] R new[xy ]; ffi 3 = R new[xy Z] R [XY Z]; ffi 4 = R new[xy ]! R new : Let ± 0 =± 1 [fffi 2 ;ffi 3 ;ffi 4 g. It suffices to show that ± ` iff ± 0 ` ffi 1. Let R' be the relational schema that includes all relation schemas in R as well as new relations created in the encoding. We show the claim as follows. (1) Suppose that there is an instance I of R such that I j= V ± ^:. We show that there is an instance I' of R' such that I' j= V ± 0 ^:ffi 1. We construct I' such that for any R in R, the instance of R in I' is the same as the instance of R in I. We populate instances of new relations R new created in the encoding as mentioned above. (a) If R new is introduced in the encoding of afdr : X! Y then we let the instance I new of R new in I' be a subset of Π XY Z (I) such that Π XY (I) =Π XY (I new ) and I new j= R new [XY ]! R new, where I is the instance of R in I. (b) If R new is introduced in the encoding of an ID R 1 [X] R 2 [Y ] then let the instance I new of R new in I' be a subset of Π YZ (I 2 ) such that Π Y (I 2 )=Π Y (I new ) and I new j= R new [Y ]! R new, where I 2 is the instance of R 2 in I. It is easy to verify that I' j= V ± 0 ^:ffi 1. (2) Suppose that there is an instance I' of R' such that I' j= V ± 0 ^:ffi 1. We construct an instance I of R by removing from I' all instances of new relations introduced in the encoding. It is easy to verify that I j= V ± ^:.
16 16 Wenfei Fan and Leonid Libkin Therefore, the encoding is indeed a reduction from the implication problem for FDs by FDs and IDs. This shows that the implication problem for keys by keys and foreign keys is undecidable. 2 From Lemma 3.2 follows that the complement of the implication problem for keys by keys and foreign keys is also undecidable. That is to determine, given a relational schema R, a set ±of keys and foreign keys over R and a key ' over R, whether there is an instance of R satisfying V ± ^:'. We now continue with the proof of Theorem 3.1, i.e., the consistency problem for C constraints is undecidable. Given Lemma 3.2, it suffices to give a reduction from the complement of the implication problem for keys by keys and foreign keys. Let R = (R 1 ; :::; R n ) be a relational schema, be a set of keys and foreign keys over R, and ' = R[X]! R be a key over R. Let Y = Att(R) n X. We encode R, and ' in terms of a DTD D and a set ± of C constraints over D as follows. Let D =(E; A; P; R A ; r), where E = fr [ i j i 2 [1;n]g[ft i j i 2 [1;n]g [fr; D Y ; E X g A = Att(R i ) i2[1;n] P (r) = R 1 ; :::; R n ; D Y ; D Y ; E X P (R i ) = t Λ i for i 2 [1;n] P (t i ) = ffl for i 2 [1;n] P (D Y ) = P (E X )=ffl R A (t i ) = Att(R i ) for i 2 [1;n] R A (D Y ) = X [ Y R A (E X ) = X R A (r) = R A (R i ) = ; for i 2 [1;n] We denote P (R) =t Λ ' for the relation R in '. Note that R = R s and t ' = t s for some s 2 [1;n]. We encode and ' with ± = ± [ ± ', where ± is defined as follows: ± includes t i [Z]! t i if includes a key R i [Z]! R i ; ± includes t i [Z] t j [Z 0 ], t j [Z 0 ]! t j if has a foreign key R i [Z] R j [Z 0 ], R j [Z 0 ]! R j. The set ± ' consists of the following: D Y [Y ]! D Y ; E X [X]! E X ; D Y [X] E X [X]; D Y [X; Y ] t ' [X; Y ]; t ' [XY ]! t ' ; where [X; Y ] stands for the concatenation of list X and list Y, and t ' is the grammar symbol in P (R) =t Λ '. Observe that Att(R) =X [ Y and thus XY is a key of t '.
17 On XML Integrity Constraints in the Presence of DTDs 17 r R1... ti Ri Rn... ti Dy @X Fig. 2. A tree used in the proof of Theorem 3.1 As depicted in Figure 2, in any XML tree valid w.r.t. D, there are two distinct D Y nodes d 1 and d 2 that have all the attributes in X [ Y, and a single E X node having all attributes in X. If T j= ± ', then (1) d 1 [X] = d 2 [X] by D Y [X] E X [X] and the fact jext(e X )j = 1; and (2) d 1 [Y ] 6= d 2 [Y ]by D Y [Y ]! D Y. These nodes will serve as a witness for :'. Given these, we show that V ^:' can be satisfied by an instance of R if and only if ± can be satisfied by an XML tree valid w.r.t. D. Assume that there is an instance I of R satisfying V ^:'. We construct an XML tree T from I as follows. Let T have a root node r and a Ri node for each R i in R. For any R i 2 R and each tuple p in the instance of R i in I, we create a distinct t i node x such that p:l = x:l for all l 2 Att(R i ). Since I j= :', there are two tuples p and p 0 in the instance of R in I such that p[x] = p 0 [X] and p[y ] 6= p 0 [Y ]. We create two distinct D Y nodes d 1 and d 2 such that d 1 :l = p:l and d 2 :l = p 0 :l for all l 2 Att(R). In addition, we create a single E X node e such that e:l = p:l for all l 2 X. We define the edge relation of T such that T has the form shown in Figure 2. It is easy to verify that T j= D. By I j= it is easy to verify that T j= ±. By the definition of T, it is also easy to see that T j= ± '. In particular, since Att(R) = X [ Y and the set of all attributes of a relation is a key of the relation, we have T j= t ' [XY ]! t ', where t ' is the symbol in P (R) =t Λ '. Therefore, T j= ±. Conversely, suppose that D has a valid XML tree T that satisfies ±. We define an instance I of schema R as follows. For each t i node x, let (l 1 = x:l 1 ; :::; l m = x:l m ) be a tuple in the instance of R i in I, where l 1 ; :::; l m are an enumeration of Att(R i ). Obviously I is an instance of R. By T j= ±, it is easy to verify that I j=. Moreover, by T j= ± ' and the definition of I, we have I j= :' since there must be two tuples d 1 and d 2 in the instance of R in I such that d 1 [X] =d 2 [X] but d 1 [Y ] 6= d 2 [Y ]. Thus the encoding is indeed a reduction from the complement oftheimplication problem for keys by keys and foreign keys. This completes the proof of Theorem
18 18 Wenfei Fan and Leonid Libkin r Dy Dy @K 3.2 Undecidability of implication We next consider the implication problem. Fig. 3. A tree used in the proof of Lemma 3.3 Lemma 3.3. The following problems are undecidable: given any DTD D, any set ± of C constraints over D, any unary key ' 1 and unary inclusion constraint ' 2 over D, whether (1) (D; ±) ` ' 1 ; (2) (D; ±) ` ' 2. Proof: It suffices to establish a reduction from the consistency problem for C to the complement of the implication problem for C. Let the DTD D be (E; A; P; R; r). We define another DTD D 0 =(E 0 ; A 0 ; P 0 ; R 0 ; r), where E 0 = E [fd Y ; E X g where D Y, E X are fresh element types A 0 = A [fkg where K is a fresh attribute P 0 (r) = P (r); D Y ; D Y ; E X i.e., P (r) followed by two D Y elements and an E X element P 0 (fi) = P (fi) for all fi 2 E nfrg P 0 (D Y ) = P 0 (E X )=ffl R 0 (D Y ) = fkg R 0 (E X ) = fkg R 0 (fi) = R(fi) for all fi 2 E We define a unary key ' 1, a unary inclusion constraint ' 2 and another key ffi over D 0 as follows: ' 1 = D Y :K! D Y ; ' 2 = D Y :K E X :K; ffi = E X :K! E X : Clearly, ± is also a set of C constraints over D 0. We next show that (1) ± is satisfiable over D iff V ± ^ ffi ^ ' 2 ^:' 1 is satisfiable over D 0 ; (2) ± is satisfiable over D iff V ± ^ ffi ^ ' 1 ^:' 2 is satisfiable over D 0. For if these hold, then the encoding is a reduction from the consistency problem for C to the complements of the implication problems described in Lemma 3.3. V We prove (1) as follows. If there exists a tree T j= D 0 and T j= ± ^ ffi ^ ' 2 ^:' 1, then we construct another tree T 0 by removing D Y, E X elements from T. Obviously, T 0 j= D and
19 On XML Integrity Constraints in the Presence of DTDs 19 T 0 j= ±. Conversely, suppose that there is a tree T j= D and T j= ±. We construct another tree T 0 from T as shown in Figure 3. Let us refer to the two D Y elements in T 0 as d 1 ;d 2, and the E X element as e. Let d 1 :K = d 2 :K = e:k. Then it is easy to see that T 0 j= D 0, T 0 j= ± and T 0 j= ffi ^ ' 2 ^:' 1. V We now prove (2). As above, we can show that if there is a tree T j= D 0 and T j= ± ^ ffi ^ ' 1 ^:' 2, then there exists another tree T 0 such that T 0 j= D and T 0 j= ±. Conversely, suppose that there is a tree T j= D and T j= ±. We construct a tree T 0 from T as shown in Figure 3. Again we refer to the two D Y elements in T 0 as d 1 ;d 2, and the E X element ase. Now let d 1 :K 6= d 2 :K. Then it is easy to see that T 0 j= D 0, T 0 j=±and T 0 j= ffi ^ ' 1 ^:' 2. 2 From Lemma 3.3 we immediately obtain: Corollary 3.4. For C constraints, the implication problem is undecidable. 3.3 PTIME decidable cases While the general consistency and implication problems are undecidable, it is possible to identify some decidable cases of low complexity. The first one is checking whether a DTD has a valid XML tree. This is a special case of the consistency problem, namely, when the given set of C constraints is empty. A more interesting special case involves keys only. Let C K denote the set of all keys in C. The consistency problem for C K is to determine, given any DTD D and any set ± of keys in C K over D, whether there exists an XML tree valid w.r.t. D and satisfying ±. Similarly, we consider the implication problem for C : given any DTD D, any set ± and ' of keys in C K over D, whether (D; ±) ` '. The next theorem tells that all these cases are decidable. Theorem 3.5. The following problems are decidable in linear time: (1) Given any DTD D, whether there exists an XML tree valid w.r.t. D. (2) The consistency problem for C K. (3) The implication problem for C K. Proof: (1) The first problem of the theorem can be reduced to the emptiness problem for a context free grammar (CFG). Observe that a DTD D = (E; A; P; R; r) can be viewed as an extended CFG G D with r as its start symbol, S as a nonterminal with a production rule, say, S! 0, and with attributes (A and R) ignored. It is easy to verify that D has a valid XML tree if and only if G D is nonempty, i.e., it generates a terminal string (equivalently, a parse tree). Indeed, given an XML tree T valid w.r.t. D, one can construct a parse tree of G D by
20 20 Wenfei Fan and Leonid Libkin modifying T, i.e., by removing attributes from T and modifying its text nodes. Conversely, given a parse tree T 0 of G D one can construct a valid XML tree of D by modifying T 0, i.e., by adding attributes to T 0 and removing children of S nodes from T 0. It is straightforward to convert the extended CFG G D to a CFG G in linear time, by introducing new nonterminals and their (recursive) production rules to represent Kleene closures. Moreover, G D is nonempty if and only if G is nonempty. It is well known that the emptiness problem for a CFG can be determined in linear time (cf. [24]). Putting everything together, a linear algorithm for checking the validity of D works as follows: it first generates in linear time the CFG G from D, and then checks in linear time whether G is empty; it concludes that D has a valid XML tree if and only if G is nonempty. Thus the validity of DTDs can be decided in linear time. (2) We next prove the second statement of Theorem 3.5. That is, the consistency problem for C K is decidable in linear time. Given any DTD D and any set±ofkeys in C K over D, it suffices to show that ± can be satisfied by an XML tree valid w.r.t. D if and only if D hasavalid XML tree. For if it holds, then the second statement follows immediately from the first statement of Theorem 3.5. Wenow show the claim. Suppose that there exists an XML tree T 1 =(V; lab; ele; att; val; root) valid w.r.t. D. We construct another XML tree T 2 by modifying the val function in T 1 such that for any key fi[x]! fi in ±, jext(fi)j = jext(fi:l)j in T 2 for every l 2 X. That is, T 2 j= fi:l! fi for all l 2 X. More specifically, let T 2 = (V; lab; ele; att; val 0 ; root). Observe that the only difference between T 1 and T 2 is the definition of the function val 0. For any v 1 ;v 2 in V with lab(v 1 )=fi and lab(v 2 )=fi, we can make val 0 (att(v 1 ; l)) 6= val 0 (att(v 2 ; l)) for any l 2 X. Let val 0 (v) =val(v) for all other vertices in V. It is easy to verify that T 2 is valid w.r.t. D since T 1 is valid w.r.t. D. In addition, T 2 j= fi[x]! fi since for any x; y 2 ext(fi), x[x] 6= y[x]. The other direction is immediate. (3) Finally, we prove the last statement of Theorem 3.5. That is, the implication problem for C K is decidable in linear time. To show this, we need the following lemma. Lemma 3.6. For any DTD D and element type fi in D, itisdecidable in linear time whether there is an XML tree T such that T j= D and moreover, jext(fi)j > 1 in T. Proof: As in the proof of the first statement of the theorem, it is easy to show that given a DTD D, one can find in linear time a CFG G such that D has a valid XML tree in which jext(fi)j > 1 if and only if the start symbol r of G derives a terminal string w whose parse tree has at least two fi nodes. This can be transformed in linear time to the problem of checking if a given CFG derives a string with at least two occurrences of a given terminal symbol, which in turn can be solved in linear time by a minor modification of the emptiness test for CFG from [24]. 2
21 On XML Integrity Constraints in the Presence of DTDs 21 Let ± be a set of keys in C K over D, and ' = fi[x]! fi be another key in C K over D. We say that ± subsumes ' if there is ffi = fi[y ]! fi in ± such that Y X, i.e., ' is a superkey of ffi. Using this and Lemma 3.6 we can prove the following: Lemma 3.7. Let D be a DTD, ± a set of keys in C K over D, and ' = fi[x]! fi another key in C K over D. There is an XML tree T such that T j= D, T j= ±but T j= :' if and only if ± does not subsume ' and moreover, there is an XML tree T 0 such that T 0 j= D and jext(fi)j > 1 in T 0. In addition, this is decidable in linear time in the sizes of D and ± [f'g. Proof: We first show that there is an XML tree T such that T j= D, T j= ±but T j= :' iff ± does not subsume ' and moreover, there is an XML tree T 0 such that T 0 j= D and jext(fi)j > 1 in T 0. Suppose that there is an XML tree T such that T j= D, T j= ± and T j= :'. Then obviously, T is valid w.r.t. D, and moreover, there must be at least two fi elements d 1 ;d 2 in T such that d 1 [X] = d 2 [X] but d 1 6= d 2 since T j= :'. Thus there must be jext(fi)j > 1 in T. In addition, ± cannot contain fi[y ]! fi with Y X, since otherwise it would contradict T j= :' and T j= ±. Conversely, let T 0 be a tree such that T 0 j= D and jext(fi)j > 1 in T 0. Thus there are at least two fi elements d 1 ;d 2 in T 0. We construct a new tree T by modifying the string values associated with the attributes of T 0, while leaving the other functions of T 0 unchanged. More specifically, we let d 1 [X] =d 2 [X] int but all other attributes have different string values. It is easy to verify that T j= D and T j= :' by the definition of T. To show T j= ±, suppose by contradiction that there were ffi 2 ± such that T j= :ffi. Then ffi must be of the form fi[y ]! fi where Y X, i.e., ' is a superkey of ffi, since except d 1 [X] = d 2 [X], distinct nodes in T have the different attribute values by the definition of T. This contradicts the assumption that ± does not subsume '. Thus the first statement of the lemma holds. To show that this can be done in linear time, observe that by Lemma 3.6, it can be decided in linear time in the size of D whether there is a tree T such that T j= D and jext(fi)j > 1 in T. In addition, it is decidable in linear time in the size of ± [f'g whether ' is a superkey of some key in ± (see e.g., [1] for discussions about a linear time algorithm for checking implication of functional dependencies). Thus it is decidable in linear time in the sizes of D and ± [f'g whether these conditions hold. 2 This suffices to prove the third statement of Theorem 3.5 because (D; ±) ` ' iff there is no XML tree T such that T j= D, T j= ±but T j= :'. By Lemma 3.7, the latter can be decided in linear time. This completes the proof of Theorem Given Theorem 3.5, one would be tempted to think that when only foreign keys are considered, the analyses of consistency and implication could also be simpler. However, it is not the case.
teacher research teach "Joe" "Joe"
 On XML Integrity Constraints in the Presence of DTDs Wenfei Fan Bell Laboratories 600 Mountain Avenue Murray Hill, NJ 07974, USA wenfei@research.bell-labs.com Leonid Libkin Department of Computer Science
On XML Integrity Constraints in the Presence of DTDs Wenfei Fan Bell Laboratories 600 Mountain Avenue Murray Hill, NJ 07974, USA wenfei@research.bell-labs.com Leonid Libkin Department of Computer Science
Consistency of XML Specifications
 Consistency of XML Specifications Marcelo Arenas 1, Wenfei Fan 2, and Leonid Libkin 1 1 Department of Computer Science, University of Toronto {marenas, libkin}@cs.toronto.edu 2 University of Edinburgh
Consistency of XML Specifications Marcelo Arenas 1, Wenfei Fan 2, and Leonid Libkin 1 1 Department of Computer Science, University of Toronto {marenas, libkin}@cs.toronto.edu 2 University of Edinburgh
3 No-Wait Job Shops with Variable Processing Times
 3 No-Wait Job Shops with Variable Processing Times In this chapter we assume that, on top of the classical no-wait job shop setting, we are given a set of processing times for each operation. We may select
3 No-Wait Job Shops with Variable Processing Times In this chapter we assume that, on top of the classical no-wait job shop setting, we are given a set of processing times for each operation. We may select
Relative Information Completeness
 Relative Information Completeness Abstract Wenfei Fan University of Edinburgh & Bell Labs wenfei@inf.ed.ac.uk The paper investigates the question of whether a partially closed database has complete information
Relative Information Completeness Abstract Wenfei Fan University of Edinburgh & Bell Labs wenfei@inf.ed.ac.uk The paper investigates the question of whether a partially closed database has complete information
Designing Views to Answer Queries under Set, Bag,and BagSet Semantics
 Designing Views to Answer Queries under Set, Bag,and BagSet Semantics Rada Chirkova Department of Computer Science, North Carolina State University Raleigh, NC 27695-7535 chirkova@csc.ncsu.edu Foto Afrati
Designing Views to Answer Queries under Set, Bag,and BagSet Semantics Rada Chirkova Department of Computer Science, North Carolina State University Raleigh, NC 27695-7535 chirkova@csc.ncsu.edu Foto Afrati
Schema Design for Uncertain Databases
 Schema Design for Uncertain Databases Anish Das Sarma, Jeffrey Ullman, Jennifer Widom {anish,ullman,widom}@cs.stanford.edu Stanford University Abstract. We address schema design in uncertain databases.
Schema Design for Uncertain Databases Anish Das Sarma, Jeffrey Ullman, Jennifer Widom {anish,ullman,widom}@cs.stanford.edu Stanford University Abstract. We address schema design in uncertain databases.
The Encoding Complexity of Network Coding
 The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email: mikel,spalex,bruck @caltech.edu Abstract In the multicast network
The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email: mikel,spalex,bruck @caltech.edu Abstract In the multicast network
XML Data Exchange. Marcelo Arenas P. Universidad Católica de Chile. Joint work with Leonid Libkin (U. of Toronto)
 XML Data Exchange Marcelo Arenas P. Universidad Católica de Chile Joint work with Leonid Libkin (U. of Toronto) Data Exchange in Relational Databases Data exchange has been extensively studied in the relational
XML Data Exchange Marcelo Arenas P. Universidad Católica de Chile Joint work with Leonid Libkin (U. of Toronto) Data Exchange in Relational Databases Data exchange has been extensively studied in the relational
DATA MODELS FOR SEMISTRUCTURED DATA
 Chapter 2 DATA MODELS FOR SEMISTRUCTURED DATA Traditionally, real world semantics are captured in a data model, and mapped to the database schema. The real world semantics are modeled as constraints and
Chapter 2 DATA MODELS FOR SEMISTRUCTURED DATA Traditionally, real world semantics are captured in a data model, and mapped to the database schema. The real world semantics are modeled as constraints and
Chapter 3. Set Theory. 3.1 What is a Set?
 Chapter 3 Set Theory 3.1 What is a Set? A set is a well-defined collection of objects called elements or members of the set. Here, well-defined means accurately and unambiguously stated or described. Any
Chapter 3 Set Theory 3.1 What is a Set? A set is a well-defined collection of objects called elements or members of the set. Here, well-defined means accurately and unambiguously stated or described. Any
Treewidth and graph minors
 Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Core Membership Computation for Succinct Representations of Coalitional Games
 Core Membership Computation for Succinct Representations of Coalitional Games Xi Alice Gao May 11, 2009 Abstract In this paper, I compare and contrast two formal results on the computational complexity
Core Membership Computation for Succinct Representations of Coalitional Games Xi Alice Gao May 11, 2009 Abstract In this paper, I compare and contrast two formal results on the computational complexity
Path Constraints in Semistructured Databases
 Journal of Computer and System Sciences 61, 146193 (2000) doi:10.1006jcss.2000.1710, available online at http:www.idealibrary.com on Path Constraints in Semistructured Databases Peter Buneman 1 Department
Journal of Computer and System Sciences 61, 146193 (2000) doi:10.1006jcss.2000.1710, available online at http:www.idealibrary.com on Path Constraints in Semistructured Databases Peter Buneman 1 Department
Answering Pattern Queries Using Views
 Answering Pattern Queries Using iews Wenfei Fan,2 Xin Wang 3 Yinghui Wu 4 University of Edinburgh 2 RCBD and SKLSDE Lab, Beihang University 3 Southwest Jiaotong University 4 Washington State University
Answering Pattern Queries Using iews Wenfei Fan,2 Xin Wang 3 Yinghui Wu 4 University of Edinburgh 2 RCBD and SKLSDE Lab, Beihang University 3 Southwest Jiaotong University 4 Washington State University
These notes present some properties of chordal graphs, a set of undirected graphs that are important for undirected graphical models.
 Undirected Graphical Models: Chordal Graphs, Decomposable Graphs, Junction Trees, and Factorizations Peter Bartlett. October 2003. These notes present some properties of chordal graphs, a set of undirected
Undirected Graphical Models: Chordal Graphs, Decomposable Graphs, Junction Trees, and Factorizations Peter Bartlett. October 2003. These notes present some properties of chordal graphs, a set of undirected
Matching Theory. Figure 1: Is this graph bipartite?
 Matching Theory 1 Introduction A matching M of a graph is a subset of E such that no two edges in M share a vertex; edges which have this property are called independent edges. A matching M is said to
Matching Theory 1 Introduction A matching M of a graph is a subset of E such that no two edges in M share a vertex; edges which have this property are called independent edges. A matching M is said to
The Structure of Bull-Free Perfect Graphs
 The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
Consistency and Set Intersection
 Consistency and Set Intersection Yuanlin Zhang and Roland H.C. Yap National University of Singapore 3 Science Drive 2, Singapore {zhangyl,ryap}@comp.nus.edu.sg Abstract We propose a new framework to study
Consistency and Set Intersection Yuanlin Zhang and Roland H.C. Yap National University of Singapore 3 Science Drive 2, Singapore {zhangyl,ryap}@comp.nus.edu.sg Abstract We propose a new framework to study
Unifying and extending hybrid tractable classes of CSPs
 Journal of Experimental & Theoretical Artificial Intelligence Vol. 00, No. 00, Month-Month 200x, 1 16 Unifying and extending hybrid tractable classes of CSPs Wady Naanaa Faculty of sciences, University
Journal of Experimental & Theoretical Artificial Intelligence Vol. 00, No. 00, Month-Month 200x, 1 16 Unifying and extending hybrid tractable classes of CSPs Wady Naanaa Faculty of sciences, University
Byzantine Consensus in Directed Graphs
 Byzantine Consensus in Directed Graphs Lewis Tseng 1,3, and Nitin Vaidya 2,3 1 Department of Computer Science, 2 Department of Electrical and Computer Engineering, and 3 Coordinated Science Laboratory
Byzantine Consensus in Directed Graphs Lewis Tseng 1,3, and Nitin Vaidya 2,3 1 Department of Computer Science, 2 Department of Electrical and Computer Engineering, and 3 Coordinated Science Laboratory
Lecture 1. 1 Notation
 Lecture 1 (The material on mathematical logic is covered in the textbook starting with Chapter 5; however, for the first few lectures, I will be providing some required background topics and will not be
Lecture 1 (The material on mathematical logic is covered in the textbook starting with Chapter 5; however, for the first few lectures, I will be providing some required background topics and will not be
Bipartite Roots of Graphs
 Bipartite Roots of Graphs Lap Chi Lau Department of Computer Science University of Toronto Graph H is a root of graph G if there exists a positive integer k such that x and y are adjacent in G if and only
Bipartite Roots of Graphs Lap Chi Lau Department of Computer Science University of Toronto Graph H is a root of graph G if there exists a positive integer k such that x and y are adjacent in G if and only
arxiv: v1 [cs.db] 23 May 2016
![arxiv: v1 [cs.db] 23 May 2016 arxiv: v1 [cs.db] 23 May 2016](/thumbs/81/82924607.jpg) Complexity of Consistent Query Answering in Databases under Cardinality-Based and Incremental Repair Semantics (extended version) arxiv:1605.07159v1 [cs.db] 23 May 2016 Andrei Lopatenko Free University
Complexity of Consistent Query Answering in Databases under Cardinality-Based and Incremental Repair Semantics (extended version) arxiv:1605.07159v1 [cs.db] 23 May 2016 Andrei Lopatenko Free University
Removing XML Data Redundancies Using Functional and Equality-Generating Dependencies
 Removing XML Data Redundancies Using Functional and Equality-Generating Dependencies Junhu Wang 1 Rodney Topor 2 1 INT, Griffith University, Gold Coast, Australia J.Wang@griffith.edu.au 2 CIT, Griffith
Removing XML Data Redundancies Using Functional and Equality-Generating Dependencies Junhu Wang 1 Rodney Topor 2 1 INT, Griffith University, Gold Coast, Australia J.Wang@griffith.edu.au 2 CIT, Griffith
Semantics via Syntax. f (4) = if define f (x) =2 x + 55.
 1 Semantics via Syntax The specification of a programming language starts with its syntax. As every programmer knows, the syntax of a language comes in the shape of a variant of a BNF (Backus-Naur Form)
1 Semantics via Syntax The specification of a programming language starts with its syntax. As every programmer knows, the syntax of a language comes in the shape of a variant of a BNF (Backus-Naur Form)
Constrained Types and their Expressiveness
 Constrained Types and their Expressiveness JENS PALSBERG Massachusetts Institute of Technology and SCOTT SMITH Johns Hopkins University A constrained type consists of both a standard type and a constraint
Constrained Types and their Expressiveness JENS PALSBERG Massachusetts Institute of Technology and SCOTT SMITH Johns Hopkins University A constrained type consists of both a standard type and a constraint
Semantic Forcing in Disjunctive Logic Programs
 Semantic Forcing in Disjunctive Logic Programs Marina De Vos and Dirk Vermeir Dept of Computer Science Free University of Brussels, VUB Pleinlaan 2, Brussels 1050, Belgium Abstract We propose a semantics
Semantic Forcing in Disjunctive Logic Programs Marina De Vos and Dirk Vermeir Dept of Computer Science Free University of Brussels, VUB Pleinlaan 2, Brussels 1050, Belgium Abstract We propose a semantics
University of Nevada, Las Vegas Computer Science 456/656 Fall 2016
 University of Nevada, Las Vegas Computer Science 456/656 Fall 2016 The entire examination is 925 points. The real final will be much shorter. Name: No books, notes, scratch paper, or calculators. Use pen
University of Nevada, Las Vegas Computer Science 456/656 Fall 2016 The entire examination is 925 points. The real final will be much shorter. Name: No books, notes, scratch paper, or calculators. Use pen
ARELAY network consists of a pair of source and destination
 158 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL 55, NO 1, JANUARY 2009 Parity Forwarding for Multiple-Relay Networks Peyman Razaghi, Student Member, IEEE, Wei Yu, Senior Member, IEEE Abstract This paper
158 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL 55, NO 1, JANUARY 2009 Parity Forwarding for Multiple-Relay Networks Peyman Razaghi, Student Member, IEEE, Wei Yu, Senior Member, IEEE Abstract This paper
Discrete Mathematics Lecture 4. Harper Langston New York University
 Discrete Mathematics Lecture 4 Harper Langston New York University Sequences Sequence is a set of (usually infinite number of) ordered elements: a 1, a 2,, a n, Each individual element a k is called a
Discrete Mathematics Lecture 4 Harper Langston New York University Sequences Sequence is a set of (usually infinite number of) ordered elements: a 1, a 2,, a n, Each individual element a k is called a
Handout 9: Imperative Programs and State
 06-02552 Princ. of Progr. Languages (and Extended ) The University of Birmingham Spring Semester 2016-17 School of Computer Science c Uday Reddy2016-17 Handout 9: Imperative Programs and State Imperative
06-02552 Princ. of Progr. Languages (and Extended ) The University of Birmingham Spring Semester 2016-17 School of Computer Science c Uday Reddy2016-17 Handout 9: Imperative Programs and State Imperative
Recursively Enumerable Languages, Turing Machines, and Decidability
 Recursively Enumerable Languages, Turing Machines, and Decidability 1 Problem Reduction: Basic Concepts and Analogies The concept of problem reduction is simple at a high level. You simply take an algorithm
Recursively Enumerable Languages, Turing Machines, and Decidability 1 Problem Reduction: Basic Concepts and Analogies The concept of problem reduction is simple at a high level. You simply take an algorithm
9.5 Equivalence Relations
 9.5 Equivalence Relations You know from your early study of fractions that each fraction has many equivalent forms. For example, 2, 2 4, 3 6, 2, 3 6, 5 30,... are all different ways to represent the same
9.5 Equivalence Relations You know from your early study of fractions that each fraction has many equivalent forms. For example, 2, 2 4, 3 6, 2, 3 6, 5 30,... are all different ways to represent the same
CSC Discrete Math I, Spring Sets
 CSC 125 - Discrete Math I, Spring 2017 Sets Sets A set is well-defined, unordered collection of objects The objects in a set are called the elements, or members, of the set A set is said to contain its
CSC 125 - Discrete Math I, Spring 2017 Sets Sets A set is well-defined, unordered collection of objects The objects in a set are called the elements, or members, of the set A set is said to contain its
Reflection in the Chomsky Hierarchy
 Reflection in the Chomsky Hierarchy Henk Barendregt Venanzio Capretta Dexter Kozen 1 Introduction We investigate which classes of formal languages in the Chomsky hierarchy are reflexive, that is, contain
Reflection in the Chomsky Hierarchy Henk Barendregt Venanzio Capretta Dexter Kozen 1 Introduction We investigate which classes of formal languages in the Chomsky hierarchy are reflexive, that is, contain
THEORY OF COMPUTATION
 THEORY OF COMPUTATION UNIT-1 INTRODUCTION Overview This chapter begins with an overview of those areas in the theory of computation that are basic foundation of learning TOC. This unit covers the introduction
THEORY OF COMPUTATION UNIT-1 INTRODUCTION Overview This chapter begins with an overview of those areas in the theory of computation that are basic foundation of learning TOC. This unit covers the introduction
Limitations of Algorithmic Solvability In this Chapter we investigate the power of algorithms to solve problems Some can be solved algorithmically and
 Computer Language Theory Chapter 4: Decidability 1 Limitations of Algorithmic Solvability In this Chapter we investigate the power of algorithms to solve problems Some can be solved algorithmically and
Computer Language Theory Chapter 4: Decidability 1 Limitations of Algorithmic Solvability In this Chapter we investigate the power of algorithms to solve problems Some can be solved algorithmically and
Elementary Recursive Function Theory
 Chapter 6 Elementary Recursive Function Theory 6.1 Acceptable Indexings In a previous Section, we have exhibited a specific indexing of the partial recursive functions by encoding the RAM programs. Using
Chapter 6 Elementary Recursive Function Theory 6.1 Acceptable Indexings In a previous Section, we have exhibited a specific indexing of the partial recursive functions by encoding the RAM programs. Using
Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1
 CME 305: Discrete Mathematics and Algorithms Instructor: Professor Aaron Sidford (sidford@stanford.edu) January 11, 2018 Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1 In this lecture
CME 305: Discrete Mathematics and Algorithms Instructor: Professor Aaron Sidford (sidford@stanford.edu) January 11, 2018 Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1 In this lecture
1. [5 points each] True or False. If the question is currently open, write O or Open.
![1. [5 points each] True or False. If the question is currently open, write O or Open. 1. [5 points each] True or False. If the question is currently open, write O or Open.](/thumbs/89/98345819.jpg) University of Nevada, Las Vegas Computer Science 456/656 Spring 2018 Practice for the Final on May 9, 2018 The entire examination is 775 points. The real final will be much shorter. Name: No books, notes,
University of Nevada, Las Vegas Computer Science 456/656 Spring 2018 Practice for the Final on May 9, 2018 The entire examination is 775 points. The real final will be much shorter. Name: No books, notes,
Trees. 3. (Minimally Connected) G is connected and deleting any of its edges gives rise to a disconnected graph.
 Trees 1 Introduction Trees are very special kind of (undirected) graphs. Formally speaking, a tree is a connected graph that is acyclic. 1 This definition has some drawbacks: given a graph it is not trivial
Trees 1 Introduction Trees are very special kind of (undirected) graphs. Formally speaking, a tree is a connected graph that is acyclic. 1 This definition has some drawbacks: given a graph it is not trivial
We show that the composite function h, h(x) = g(f(x)) is a reduction h: A m C.
 219 Lemma J For all languages A, B, C the following hold i. A m A, (reflexive) ii. if A m B and B m C, then A m C, (transitive) iii. if A m B and B is Turing-recognizable, then so is A, and iv. if A m
219 Lemma J For all languages A, B, C the following hold i. A m A, (reflexive) ii. if A m B and B m C, then A m C, (transitive) iii. if A m B and B is Turing-recognizable, then so is A, and iv. if A m
CS525 Winter 2012 \ Class Assignment #2 Preparation
 1 CS525 Winter 2012 \ Class Assignment #2 Preparation Ariel Stolerman 2.26) Let be a CFG in Chomsky Normal Form. Following is a proof that for any ( ) of length exactly steps are required for any derivation
1 CS525 Winter 2012 \ Class Assignment #2 Preparation Ariel Stolerman 2.26) Let be a CFG in Chomsky Normal Form. Following is a proof that for any ( ) of length exactly steps are required for any derivation
PCP and Hardness of Approximation
 PCP and Hardness of Approximation January 30, 2009 Our goal herein is to define and prove basic concepts regarding hardness of approximation. We will state but obviously not prove a PCP theorem as a starting
PCP and Hardness of Approximation January 30, 2009 Our goal herein is to define and prove basic concepts regarding hardness of approximation. We will state but obviously not prove a PCP theorem as a starting
Database Theory VU , SS Codd s Theorem. Reinhard Pichler
 Database Theory Database Theory VU 181.140, SS 2011 3. Codd s Theorem Reinhard Pichler Institut für Informationssysteme Arbeitsbereich DBAI Technische Universität Wien 29 March, 2011 Pichler 29 March,
Database Theory Database Theory VU 181.140, SS 2011 3. Codd s Theorem Reinhard Pichler Institut für Informationssysteme Arbeitsbereich DBAI Technische Universität Wien 29 March, 2011 Pichler 29 March,
Relative Expressive Power of Navigational Querying on Graphs
 Relative Expressive Power of Navigational Querying on Graphs George H. L. Fletcher Eindhoven University of Technology g.h.l.fletcher@tue.nl Jan Van den Bussche Hasselt University & Transnational Univ.
Relative Expressive Power of Navigational Querying on Graphs George H. L. Fletcher Eindhoven University of Technology g.h.l.fletcher@tue.nl Jan Van den Bussche Hasselt University & Transnational Univ.
Schema Mappings and Data Exchange
 Schema Mappings and Data Exchange Lecture #2 EASSLC 2012 Southwest University August 2012 1 The Relational Data Model (E.F. Codd 1970) The Relational Data Model uses the mathematical concept of a relation
Schema Mappings and Data Exchange Lecture #2 EASSLC 2012 Southwest University August 2012 1 The Relational Data Model (E.F. Codd 1970) The Relational Data Model uses the mathematical concept of a relation
M359 Block5 - Lecture12 Eng/ Waleed Omar
 Documents and markup languages The term XML stands for extensible Markup Language. Used to label the different parts of documents. Labeling helps in: Displaying the documents in a formatted way Querying
Documents and markup languages The term XML stands for extensible Markup Language. Used to label the different parts of documents. Labeling helps in: Displaying the documents in a formatted way Querying
2 A topological interlude
 2 A topological interlude 2.1 Topological spaces Recall that a topological space is a set X with a topology: a collection T of subsets of X, known as open sets, such that and X are open, and finite intersections
2 A topological interlude 2.1 Topological spaces Recall that a topological space is a set X with a topology: a collection T of subsets of X, known as open sets, such that and X are open, and finite intersections
CSCI 403: Databases 13 - Functional Dependencies and Normalization
 CSCI 403: Databases 13 - Functional Dependencies and Normalization Introduction The point of this lecture material is to discuss some objective measures of the goodness of a database schema. The method
CSCI 403: Databases 13 - Functional Dependencies and Normalization Introduction The point of this lecture material is to discuss some objective measures of the goodness of a database schema. The method
On the Hardness of Counting the Solutions of SPARQL Queries
 On the Hardness of Counting the Solutions of SPARQL Queries Reinhard Pichler and Sebastian Skritek Vienna University of Technology, Faculty of Informatics {pichler,skritek}@dbai.tuwien.ac.at 1 Introduction
On the Hardness of Counting the Solutions of SPARQL Queries Reinhard Pichler and Sebastian Skritek Vienna University of Technology, Faculty of Informatics {pichler,skritek}@dbai.tuwien.ac.at 1 Introduction
CMPS 277 Principles of Database Systems. Lecture #4
 CMPS 277 Principles of Database Systems http://www.soe.classes.edu/cmps277/winter10 Lecture #4 1 First-Order Logic Question: What is First-Order Logic? Answer: Informally, First-Order Logic = Propositional
CMPS 277 Principles of Database Systems http://www.soe.classes.edu/cmps277/winter10 Lecture #4 1 First-Order Logic Question: What is First-Order Logic? Answer: Informally, First-Order Logic = Propositional
COMPUTABILITY THEORY AND RECURSIVELY ENUMERABLE SETS
 COMPUTABILITY THEORY AND RECURSIVELY ENUMERABLE SETS JOSHUA LENERS Abstract. An algorithm is function from ω to ω defined by a finite set of instructions to transform a given input x to the desired output
COMPUTABILITY THEORY AND RECURSIVELY ENUMERABLE SETS JOSHUA LENERS Abstract. An algorithm is function from ω to ω defined by a finite set of instructions to transform a given input x to the desired output
Justification for Inclusion Dependency Normal Form
 IEEE TRANSACTIONS ON KNOWLEDGE AND DATA ENGINEERING, VOL. 12, NO. 2, MARCH/APRIL 2000 281 Justification for Inclusion Dependency Normal Form Mark Levene and Millist W. Vincent AbstractÐFunctional dependencies
IEEE TRANSACTIONS ON KNOWLEDGE AND DATA ENGINEERING, VOL. 12, NO. 2, MARCH/APRIL 2000 281 Justification for Inclusion Dependency Normal Form Mark Levene and Millist W. Vincent AbstractÐFunctional dependencies
Data Integration: A Theoretical Perspective
 Data Integration: A Theoretical Perspective Maurizio Lenzerini Dipartimento di Informatica e Sistemistica Università di Roma La Sapienza Via Salaria 113, I 00198 Roma, Italy lenzerini@dis.uniroma1.it ABSTRACT
Data Integration: A Theoretical Perspective Maurizio Lenzerini Dipartimento di Informatica e Sistemistica Università di Roma La Sapienza Via Salaria 113, I 00198 Roma, Italy lenzerini@dis.uniroma1.it ABSTRACT
Chapter 13 XML: Extensible Markup Language
 Chapter 13 XML: Extensible Markup Language - Internet applications provide Web interfaces to databases (data sources) - Three-tier architecture Client V Application Programs Webserver V Database Server
Chapter 13 XML: Extensible Markup Language - Internet applications provide Web interfaces to databases (data sources) - Three-tier architecture Client V Application Programs Webserver V Database Server
arxiv:submit/ [math.co] 9 May 2011
![arxiv:submit/ [math.co] 9 May 2011 arxiv:submit/ [math.co] 9 May 2011](/thumbs/95/122578154.jpg) arxiv:submit/0243374 [math.co] 9 May 2011 Connectivity and tree structure in finite graphs J. Carmesin R. Diestel F. Hundertmark M. Stein 6 May, 2011 Abstract We prove that, for every integer k 0, every
arxiv:submit/0243374 [math.co] 9 May 2011 Connectivity and tree structure in finite graphs J. Carmesin R. Diestel F. Hundertmark M. Stein 6 May, 2011 Abstract We prove that, for every integer k 0, every
Database Constraints and Design
 Database Constraints and Design We know that databases are often required to satisfy some integrity constraints. The most common ones are functional and inclusion dependencies. We ll study properties of
Database Constraints and Design We know that databases are often required to satisfy some integrity constraints. The most common ones are functional and inclusion dependencies. We ll study properties of
Safe Stratified Datalog With Integer Order Does not Have Syntax
 Safe Stratified Datalog With Integer Order Does not Have Syntax Alexei P. Stolboushkin Department of Mathematics UCLA Los Angeles, CA 90024-1555 aps@math.ucla.edu Michael A. Taitslin Department of Computer
Safe Stratified Datalog With Integer Order Does not Have Syntax Alexei P. Stolboushkin Department of Mathematics UCLA Los Angeles, CA 90024-1555 aps@math.ucla.edu Michael A. Taitslin Department of Computer
On the Data Complexity of Consistent Query Answering over Graph Databases
 On the Data Complexity of Consistent Query Answering over Graph Databases Pablo Barceló and Gaëlle Fontaine Department of Computer Science University of Chile pbarcelo@dcc.uchile.cl, gaelle@dcc.uchile.cl
On the Data Complexity of Consistent Query Answering over Graph Databases Pablo Barceló and Gaëlle Fontaine Department of Computer Science University of Chile pbarcelo@dcc.uchile.cl, gaelle@dcc.uchile.cl
2.8 Universal Turing Machines and the Halting Problem
 2.8 Universal Turing Machines and the Halting Problem Through the hierarchy of Slide 74 we indirectly get a sense that Turing Machines are at least as computationally powerful as any other known model
2.8 Universal Turing Machines and the Halting Problem Through the hierarchy of Slide 74 we indirectly get a sense that Turing Machines are at least as computationally powerful as any other known model
The Relational Model
 The Relational Model David Toman School of Computer Science University of Waterloo Introduction to Databases CS348 David Toman (University of Waterloo) The Relational Model 1 / 28 The Relational Model
The Relational Model David Toman School of Computer Science University of Waterloo Introduction to Databases CS348 David Toman (University of Waterloo) The Relational Model 1 / 28 The Relational Model
Ambiguous Grammars and Compactification
 Ambiguous Grammars and Compactification Mridul Aanjaneya Stanford University July 17, 2012 Mridul Aanjaneya Automata Theory 1/ 44 Midterm Review Mathematical Induction and Pigeonhole Principle Finite Automata
Ambiguous Grammars and Compactification Mridul Aanjaneya Stanford University July 17, 2012 Mridul Aanjaneya Automata Theory 1/ 44 Midterm Review Mathematical Induction and Pigeonhole Principle Finite Automata
Fully dynamic algorithm for recognition and modular decomposition of permutation graphs
 Fully dynamic algorithm for recognition and modular decomposition of permutation graphs Christophe Crespelle Christophe Paul CNRS - Département Informatique, LIRMM, Montpellier {crespell,paul}@lirmm.fr
Fully dynamic algorithm for recognition and modular decomposition of permutation graphs Christophe Crespelle Christophe Paul CNRS - Département Informatique, LIRMM, Montpellier {crespell,paul}@lirmm.fr
Lambda Calculus and Type Inference
 Lambda Calculus and Type Inference Björn Lisper Dept. of Computer Science and Engineering Mälardalen University bjorn.lisper@mdh.se http://www.idt.mdh.se/ blr/ October 13, 2004 Lambda Calculus and Type
Lambda Calculus and Type Inference Björn Lisper Dept. of Computer Science and Engineering Mälardalen University bjorn.lisper@mdh.se http://www.idt.mdh.se/ blr/ October 13, 2004 Lambda Calculus and Type
A proof-producing CSP solver: A proof supplement
 A proof-producing CSP solver: A proof supplement Report IE/IS-2010-02 Michael Veksler Ofer Strichman mveksler@tx.technion.ac.il ofers@ie.technion.ac.il Technion Institute of Technology April 12, 2010 Abstract
A proof-producing CSP solver: A proof supplement Report IE/IS-2010-02 Michael Veksler Ofer Strichman mveksler@tx.technion.ac.il ofers@ie.technion.ac.il Technion Institute of Technology April 12, 2010 Abstract
On Codd Families of Keys over Incomplete Relations
 The Computer Journal Advance Access published September 29, 2010 The Author 2010. Published by Oxford University Press on behalf of The British Computer Society. All rights reserved. For Permissions, please
The Computer Journal Advance Access published September 29, 2010 The Author 2010. Published by Oxford University Press on behalf of The British Computer Society. All rights reserved. For Permissions, please
Math 170- Graph Theory Notes
 1 Math 170- Graph Theory Notes Michael Levet December 3, 2018 Notation: Let n be a positive integer. Denote [n] to be the set {1, 2,..., n}. So for example, [3] = {1, 2, 3}. To quote Bud Brown, Graph theory
1 Math 170- Graph Theory Notes Michael Levet December 3, 2018 Notation: Let n be a positive integer. Denote [n] to be the set {1, 2,..., n}. So for example, [3] = {1, 2, 3}. To quote Bud Brown, Graph theory
Structural Characterizations of Schema-Mapping Languages
 Structural Characterizations of Schema-Mapping Languages Balder ten Cate University of Amsterdam and UC Santa Cruz balder.tencate@uva.nl Phokion G. Kolaitis UC Santa Cruz and IBM Almaden kolaitis@cs.ucsc.edu
Structural Characterizations of Schema-Mapping Languages Balder ten Cate University of Amsterdam and UC Santa Cruz balder.tencate@uva.nl Phokion G. Kolaitis UC Santa Cruz and IBM Almaden kolaitis@cs.ucsc.edu
Course notes for Data Compression - 2 Kolmogorov complexity Fall 2005
 Course notes for Data Compression - 2 Kolmogorov complexity Fall 2005 Peter Bro Miltersen September 29, 2005 Version 2.0 1 Kolmogorov Complexity In this section, we present the concept of Kolmogorov Complexity
Course notes for Data Compression - 2 Kolmogorov complexity Fall 2005 Peter Bro Miltersen September 29, 2005 Version 2.0 1 Kolmogorov Complexity In this section, we present the concept of Kolmogorov Complexity
Indexing Keys in Hierarchical Data
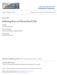 University of Pennsylvania ScholarlyCommons Technical Reports (CIS) Department of Computer & Information Science January 2001 Indexing Keys in Hierarchical Data Yi Chen University of Pennsylvania Susan
University of Pennsylvania ScholarlyCommons Technical Reports (CIS) Department of Computer & Information Science January 2001 Indexing Keys in Hierarchical Data Yi Chen University of Pennsylvania Susan
An Analysis of Approaches to XML Schema Inference
 An Analysis of Approaches to XML Schema Inference Irena Mlynkova irena.mlynkova@mff.cuni.cz Charles University Faculty of Mathematics and Physics Department of Software Engineering Prague, Czech Republic
An Analysis of Approaches to XML Schema Inference Irena Mlynkova irena.mlynkova@mff.cuni.cz Charles University Faculty of Mathematics and Physics Department of Software Engineering Prague, Czech Republic
FURTHER APPLICATIONS OF CLUTTER DOMINATION PARAMETERS TO PROJECTIVE DIMENSION
 FURTHER APPLICATIONS OF CLUTTER DOMINATION PARAMETERS TO PROJECTIVE DIMENSION HAILONG DAO AND JAY SCHWEIG Abstract. We study the relationship between the projective dimension of a squarefree monomial ideal
FURTHER APPLICATIONS OF CLUTTER DOMINATION PARAMETERS TO PROJECTIVE DIMENSION HAILONG DAO AND JAY SCHWEIG Abstract. We study the relationship between the projective dimension of a squarefree monomial ideal
On the Relationships between Zero Forcing Numbers and Certain Graph Coverings
 On the Relationships between Zero Forcing Numbers and Certain Graph Coverings Fatemeh Alinaghipour Taklimi, Shaun Fallat 1,, Karen Meagher 2 Department of Mathematics and Statistics, University of Regina,
On the Relationships between Zero Forcing Numbers and Certain Graph Coverings Fatemeh Alinaghipour Taklimi, Shaun Fallat 1,, Karen Meagher 2 Department of Mathematics and Statistics, University of Regina,
Lecture 17: Continuous Functions
 Lecture 17: Continuous Functions 1 Continuous Functions Let (X, T X ) and (Y, T Y ) be topological spaces. Definition 1.1 (Continuous Function). A function f : X Y is said to be continuous if the inverse
Lecture 17: Continuous Functions 1 Continuous Functions Let (X, T X ) and (Y, T Y ) be topological spaces. Definition 1.1 (Continuous Function). A function f : X Y is said to be continuous if the inverse
9.1 Cook-Levin Theorem
 CS787: Advanced Algorithms Scribe: Shijin Kong and David Malec Lecturer: Shuchi Chawla Topic: NP-Completeness, Approximation Algorithms Date: 10/1/2007 As we ve already seen in the preceding lecture, two
CS787: Advanced Algorithms Scribe: Shijin Kong and David Malec Lecturer: Shuchi Chawla Topic: NP-Completeness, Approximation Algorithms Date: 10/1/2007 As we ve already seen in the preceding lecture, two
PLANAR GRAPH BIPARTIZATION IN LINEAR TIME
 PLANAR GRAPH BIPARTIZATION IN LINEAR TIME SAMUEL FIORINI, NADIA HARDY, BRUCE REED, AND ADRIAN VETTA Abstract. For each constant k, we present a linear time algorithm that, given a planar graph G, either
PLANAR GRAPH BIPARTIZATION IN LINEAR TIME SAMUEL FIORINI, NADIA HARDY, BRUCE REED, AND ADRIAN VETTA Abstract. For each constant k, we present a linear time algorithm that, given a planar graph G, either
On vertex types of graphs
 On vertex types of graphs arxiv:1705.09540v1 [math.co] 26 May 2017 Pu Qiao, Xingzhi Zhan Department of Mathematics, East China Normal University, Shanghai 200241, China Abstract The vertices of a graph
On vertex types of graphs arxiv:1705.09540v1 [math.co] 26 May 2017 Pu Qiao, Xingzhi Zhan Department of Mathematics, East China Normal University, Shanghai 200241, China Abstract The vertices of a graph
SOFTWARE ENGINEERING DESIGN I
 2 SOFTWARE ENGINEERING DESIGN I 3. Schemas and Theories The aim of this course is to learn how to write formal specifications of computer systems, using classical logic. The key descriptional technique
2 SOFTWARE ENGINEERING DESIGN I 3. Schemas and Theories The aim of this course is to learn how to write formal specifications of computer systems, using classical logic. The key descriptional technique
Parameterized graph separation problems
 Parameterized graph separation problems Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary, dmarx@cs.bme.hu Abstract.
Parameterized graph separation problems Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary, dmarx@cs.bme.hu Abstract.
Fundamental Properties of Graphs
 Chapter three In many real-life situations we need to know how robust a graph that represents a certain network is, how edges or vertices can be removed without completely destroying the overall connectivity,
Chapter three In many real-life situations we need to know how robust a graph that represents a certain network is, how edges or vertices can be removed without completely destroying the overall connectivity,
Characterization of Boolean Topological Logics
 Characterization of Boolean Topological Logics Short Form: Boolean Topological Logics Anthony R. Fressola Denison University Granville, OH 43023 University of Illinois Urbana-Champaign, IL USA 61801-61802
Characterization of Boolean Topological Logics Short Form: Boolean Topological Logics Anthony R. Fressola Denison University Granville, OH 43023 University of Illinois Urbana-Champaign, IL USA 61801-61802
The Satisfiability Problem [HMU06,Chp.10b] Satisfiability (SAT) Problem Cook s Theorem: An NP-Complete Problem Restricted SAT: CSAT, k-sat, 3SAT
![The Satisfiability Problem [HMU06,Chp.10b] Satisfiability (SAT) Problem Cook s Theorem: An NP-Complete Problem Restricted SAT: CSAT, k-sat, 3SAT The Satisfiability Problem [HMU06,Chp.10b] Satisfiability (SAT) Problem Cook s Theorem: An NP-Complete Problem Restricted SAT: CSAT, k-sat, 3SAT](/thumbs/89/100203169.jpg) The Satisfiability Problem [HMU06,Chp.10b] Satisfiability (SAT) Problem Cook s Theorem: An NP-Complete Problem Restricted SAT: CSAT, k-sat, 3SAT 1 Satisfiability (SAT) Problem 2 Boolean Expressions Boolean,
The Satisfiability Problem [HMU06,Chp.10b] Satisfiability (SAT) Problem Cook s Theorem: An NP-Complete Problem Restricted SAT: CSAT, k-sat, 3SAT 1 Satisfiability (SAT) Problem 2 Boolean Expressions Boolean,
2386 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 52, NO. 6, JUNE 2006
 2386 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 52, NO. 6, JUNE 2006 The Encoding Complexity of Network Coding Michael Langberg, Member, IEEE, Alexander Sprintson, Member, IEEE, and Jehoshua Bruck,
2386 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 52, NO. 6, JUNE 2006 The Encoding Complexity of Network Coding Michael Langberg, Member, IEEE, Alexander Sprintson, Member, IEEE, and Jehoshua Bruck,
Algorithms for Learning and Teaching. Sets of Vertices in Graphs. Patricia A. Evans and Michael R. Fellows. University of Victoria
 Algorithms for Learning and Teaching Sets of Vertices in Graphs Patricia A. Evans and Michael R. Fellows Department of Computer Science University of Victoria Victoria, B.C. V8W 3P6, Canada Lane H. Clark
Algorithms for Learning and Teaching Sets of Vertices in Graphs Patricia A. Evans and Michael R. Fellows Department of Computer Science University of Victoria Victoria, B.C. V8W 3P6, Canada Lane H. Clark
Data Cleaning and Query Answering with Matching Dependencies and Matching Functions
 Data Cleaning and Query Answering with Matching Dependencies and Matching Functions Leopoldo Bertossi Carleton University Ottawa, Canada bertossi@scs.carleton.ca Solmaz Kolahi University of British Columbia
Data Cleaning and Query Answering with Matching Dependencies and Matching Functions Leopoldo Bertossi Carleton University Ottawa, Canada bertossi@scs.carleton.ca Solmaz Kolahi University of British Columbia
Copyright 2007 Ramez Elmasri and Shamkant B. Navathe. Slide 27-1
 Slide 27-1 Chapter 27 XML: Extensible Markup Language Chapter Outline Introduction Structured, Semi structured, and Unstructured Data. XML Hierarchical (Tree) Data Model. XML Documents, DTD, and XML Schema.
Slide 27-1 Chapter 27 XML: Extensible Markup Language Chapter Outline Introduction Structured, Semi structured, and Unstructured Data. XML Hierarchical (Tree) Data Model. XML Documents, DTD, and XML Schema.
9 Connectivity. Contents. 9.1 Vertex Connectivity
 9 Connectivity Contents 9.1 Vertex Connectivity.............................. 205 Connectivity and Local Connectivity............... 206 Vertex Cuts and Menger s Theorem................. 207 9.2 The Fan
9 Connectivity Contents 9.1 Vertex Connectivity.............................. 205 Connectivity and Local Connectivity............... 206 Vertex Cuts and Menger s Theorem................. 207 9.2 The Fan
 This article was originally published in a journal published by Elsevier, and the attached copy is provided by Elsevier for the author s benefit and for the benefit of the author s institution, for non-commercial
This article was originally published in a journal published by Elsevier, and the attached copy is provided by Elsevier for the author s benefit and for the benefit of the author s institution, for non-commercial
Minimal-Change Integrity Maintenance Using Tuple Deletions
 Minimal-Change Integrity Maintenance Using Tuple Deletions Jan Chomicki University at Buffalo Dept. CSE chomicki@cse.buffalo.edu Jerzy Marcinkowski Wroclaw University Instytut Informatyki jma@ii.uni.wroc.pl
Minimal-Change Integrity Maintenance Using Tuple Deletions Jan Chomicki University at Buffalo Dept. CSE chomicki@cse.buffalo.edu Jerzy Marcinkowski Wroclaw University Instytut Informatyki jma@ii.uni.wroc.pl
REPRESENTATION OF DISTRIBUTIVE LATTICES BY MEANS OF ORDERED STONE SPACES
 REPRESENTATION OF DISTRIBUTIVE LATTICES BY MEANS OF ORDERED STONE SPACES H. A. PRIESTLEY 1. Introduction Stone, in [8], developed for distributive lattices a representation theory generalizing that for
REPRESENTATION OF DISTRIBUTIVE LATTICES BY MEANS OF ORDERED STONE SPACES H. A. PRIESTLEY 1. Introduction Stone, in [8], developed for distributive lattices a representation theory generalizing that for
Finding k-paths in Cycle Free Graphs
 Finding k-paths in Cycle Free Graphs Aviv Reznik Under the Supervision of Professor Oded Goldreich Department of Computer Science and Applied Mathematics Weizmann Institute of Science Submitted for the
Finding k-paths in Cycle Free Graphs Aviv Reznik Under the Supervision of Professor Oded Goldreich Department of Computer Science and Applied Mathematics Weizmann Institute of Science Submitted for the
Review of Sets. Review. Philippe B. Laval. Current Semester. Kennesaw State University. Philippe B. Laval (KSU) Sets Current Semester 1 / 16
 Review of Sets Review Philippe B. Laval Kennesaw State University Current Semester Philippe B. Laval (KSU) Sets Current Semester 1 / 16 Outline 1 Introduction 2 Definitions, Notations and Examples 3 Special
Review of Sets Review Philippe B. Laval Kennesaw State University Current Semester Philippe B. Laval (KSU) Sets Current Semester 1 / 16 Outline 1 Introduction 2 Definitions, Notations and Examples 3 Special
6. Relational Algebra (Part II)
 6. Relational Algebra (Part II) 6.1. Introduction In the previous chapter, we introduced relational algebra as a fundamental model of relational database manipulation. In particular, we defined and discussed
6. Relational Algebra (Part II) 6.1. Introduction In the previous chapter, we introduced relational algebra as a fundamental model of relational database manipulation. In particular, we defined and discussed
Matching Algorithms. Proof. If a bipartite graph has a perfect matching, then it is easy to see that the right hand side is a necessary condition.
 18.433 Combinatorial Optimization Matching Algorithms September 9,14,16 Lecturer: Santosh Vempala Given a graph G = (V, E), a matching M is a set of edges with the property that no two of the edges have
18.433 Combinatorial Optimization Matching Algorithms September 9,14,16 Lecturer: Santosh Vempala Given a graph G = (V, E), a matching M is a set of edges with the property that no two of the edges have
Solutions to Homework 10
 CS/Math 240: Intro to Discrete Math 5/3/20 Instructor: Dieter van Melkebeek Solutions to Homework 0 Problem There were five different languages in Problem 4 of Homework 9. The Language D 0 Recall that
CS/Math 240: Intro to Discrete Math 5/3/20 Instructor: Dieter van Melkebeek Solutions to Homework 0 Problem There were five different languages in Problem 4 of Homework 9. The Language D 0 Recall that
An Attribute-Based Access Matrix Model
 An Attribute-Based Access Matrix Model Xinwen Zhang Lab for Information Security Technology George Mason University xzhang6@gmu.edu Yingjiu Li School of Information Systems Singapore Management University
An Attribute-Based Access Matrix Model Xinwen Zhang Lab for Information Security Technology George Mason University xzhang6@gmu.edu Yingjiu Li School of Information Systems Singapore Management University
Ryan Marcotte CS 475 (Advanced Topics in Databases) March 14, 2011
 Ryan Marcotte www.cs.uregina.ca/~marcottr CS 475 (Advanced Topics in Databases) March 14, 2011 Outline Introduction to XNF and motivation for its creation Analysis of XNF s link to BCNF Algorithm for converting
Ryan Marcotte www.cs.uregina.ca/~marcottr CS 475 (Advanced Topics in Databases) March 14, 2011 Outline Introduction to XNF and motivation for its creation Analysis of XNF s link to BCNF Algorithm for converting
Johns Hopkins Math Tournament Proof Round: Point Set Topology
 Johns Hopkins Math Tournament 2019 Proof Round: Point Set Topology February 9, 2019 Problem Points Score 1 3 2 6 3 6 4 6 5 10 6 6 7 8 8 6 9 8 10 8 11 9 12 10 13 14 Total 100 Instructions The exam is worth
Johns Hopkins Math Tournament 2019 Proof Round: Point Set Topology February 9, 2019 Problem Points Score 1 3 2 6 3 6 4 6 5 10 6 6 7 8 8 6 9 8 10 8 11 9 12 10 13 14 Total 100 Instructions The exam is worth
Theorem 2.9: nearest addition algorithm
 There are severe limits on our ability to compute near-optimal tours It is NP-complete to decide whether a given undirected =(,)has a Hamiltonian cycle An approximation algorithm for the TSP can be used
There are severe limits on our ability to compute near-optimal tours It is NP-complete to decide whether a given undirected =(,)has a Hamiltonian cycle An approximation algorithm for the TSP can be used
