On Infinite Groups that are Isomorphic to its Proper Infinite Subgroup. Jaymar Talledo Balihon. Abstract
|
|
|
- Leo Chandler
- 6 years ago
- Views:
Transcription
1 O Ifiite Groups that are Isomorphic to its Proper Ifiite Subgroup Jaymar Talledo Baliho Abstract Two groups are isomorphic if there exists a isomorphism betwee them Lagrage Theorem states that the order of a subgroup divides the order of the group This implies that a fiite group is ot isomorphic to its proper subgroup Some ifiite groups which are isomorphic to some of its proper subgroup are illustrated i this paper Moreover, it is show through cocepts i liear algebra that these groups really exist 1 Itroductio This chapter presets the backgroud of the study, objectives of the study, sigificace of the study, methodology ad basic cocepts i group theory Backgroud of the Study May of the studets takig itroductory abstract aim to kow whether a certai group is isomorphic to a proper subgroup of itself Fiite groups are ot isomorphic to a proper subgroup of themselves sice two groups havig differet cardialities caot be isomorphic The additive group Z of all itegers is isomorphic to the subgroup 2 Z of eve itegers via the map f : Z 2Z give by f ( x) 2x, for all Z Also, the multiplicative group Q of all positive ratioal is isomorphic to some of its proper subgroup usig the fuctio f : Q Q defied 3 by f ( x) x, for all x Q These groups show that ideed, there are ifiite groups which are isomorphic to some of their proper subgroups But beig ifiite is ot 23
2 eough because some ifiite groups are ot isomorphic to their proper subgroups Hece, this paper characterizes some ifiite groups which are isomorphic to its proper subgroup Objectives of the Study This paper will ivestigate those ifiite groups which are isomorphic to its proper subgroup Specifically, this paper aims to show the followig: 1 The additive group is isomorphic to its proper subgroup Z, where Z {0,1, 1} 2 The additive group of all ratioal umbers is ot isomorphic to ay of its proper subgroup 3 The additive group Q Z is isomorphic to its proper subgroup Q Z, where Z {0,1, 1} 4 Suppose that ad are groups, oe of which is isomorphic to some of its proper subgroup The G His also isomorphic to some of its proper subgroup 5 Let G1, G2,, G be groups If for some i{1,2,3,, }, is isomorphic to its proper subgroup the G1 G2 G is also isomorphic to its proper subgroup Sigificace of the Study G Z Q If a group is isomorphic to its proper subgroup ad this subgroup has a kow structure, the the structure of the group ca also be determied via this isomorphism Also, if oe group is kow to be isomorphic to its proper subgroup, the ay group isomorphic to this group will also be isomorphic to its proper subgroup Thus, this paper which ivolves basic cocepts of group theory is of great importace to mathematics ethusiast H G i 24
3 2 Methodology This paper exposes the work of Shau Fallat, Chi Kwo Li, David Lutzer, ad David Staford etitled O Groups That Are Isomorphic to a Proper Subgroup Defiitios, examples ad prelimiary cocepts are beig preseted i order to provide detailed proof of the mai results Prelimiaries This sectio cotais defiitios ad prelimiary cocepts that are eeded for further uderstadig of the study 11 Basic Defiitios ad Kow Results Defiitio 151 (Hugerford, 1980): A fuctio f : X Y is a relatio betwee X ad Y with the property that each x X appears as the first member of exactly oe ordered pair ( x, y) f Such a fuctio is called a map or mappig of X itoy Defiitio 152 (Hugerford, 1980): Let f : X Y be a fuctio, ad let be a subset of ad B be a subset ofy The image of i Y uder f is the set f [ A] { f ( a) : a A} The set f[x] is called the rage of A f The iverse image of B X is the set X A f 1 [ B] { x X : f ( x) B} Defiitio 153 (Maclae, Birkhoff, 1967): A fuctio f : X Y is i well defied if a bimplies f(a) = f(b) ii ijective if a, a ' A, f(a) = f(b) implies a = b iii surjective if for each b B, b = f(a) for some a A iv bijective if it is both ijective ad bijective Defiitio 154 (Fraleigh, 1994): (Priciple of Mathematical Iductio): Let P () be a statemet cocerig the positive iteger Suppose that 1 P(1) is true, ad 25
4 2 If P (k) is true, the P (k+1) is true The P () is true Z Defiitio 155 (Fraleigh, 1994): Let G be oempty set with a biary operatio The G is called a group if the followig axioms hold: [G1]: a bg, a, b G (closure property) [G2]: (a b) c = a (b c), a, b, c G (associative property) [G3]: There is a elemet e i G such thata G,ea a a e(existece of a idetity elemet i G) 1 [G4]: Correspodig to each a G, there is a elemet a G such 1 1 that a a a a e (existece of iverses i G) Defiitio 156 (Fraleigh, 1994): The order of a group G, deoted, is the umber of elemets i G A group with fiite order is called a fiite group Otherwise, it is a fiite group by G Defiitio 157 (Fraleigh, 1994): Let G be a group If H G ad is a group uder the biary operatio, the H is a subgroup of G writte H G H ig Defiitio 158 (Fraleigh, 1994): If G is a group, the the subgroup cosistig of G itself is called a improper subgroup ofg All the other subgroups of G are called proper subgroups Defiitio 159 (Fraleigh, 1994): If G is a group, a is i G ad N, the a is a product of factors each equal to a; that is, a aaa a( - factors) Defiitio 1510(Fraleigh, 1994): Let G be group If a G, the { a : } is called the cyclic subgroup of G geerated by a ad will be deoted by a If G b for someb G, the G is said to be cyclic 26
5 Defiitio 1511(Fraleigh, 1994): Let G be e group ad a G The order of a, deoted a, is the smallest positive iteger such that The order of the cyclic subgroup is equal to the order of a, that is, <a> = a a a e Theorem 1512 (Hugerford, 1980): Every ifiite cyclic group is isomorphic to the additive group Z ad every fiite cyclic group of order m is isomorphic to the additive group Z Theorem 1513 (Fraleigh, 1994): Lagrage s Theorem: Let H be subgroup of a fiite group G The the order of H divides the order of G I particular, if a G, the a divides G Defiitio 1514 (Fraleigh, 1994): Let G1, G2,, G be groups Cosider 1 Gi G1 G2 G {( g1, g2,, g) : gi G} Defie a biary operatio o by ( g, g,, g ) ( h, h,, h ) ( g h, g h,, g h ), G i gi, hi G The G1 G2 G is group called the direct sum of the groups uder the biary operatio + G i Defiitio 1515 (Fraleigh, 1994): Let G ad H be groups A fuctio f : G H is a homomorphism provided that f (a*b) = f (a)*f (b) a, b G If f is ijective, the f is called a isomorphism I this case, G ad H are said to be isomorphic writteg H The kerel of f, deoted by ker f, is the subgroup f 1 ({ e'}) where e is the idetity elemet of G Defiitio 1516 (Fraleigh, 1994): Let ad d be o-zero itegers The d divides, deoted by d/, if there exist a iteger q such that = dq 27
6 3 Results ad Discussios This chapter presets the isomorphism of group oto its proper subgroup for the case where the group is a direct sum 31 Direct Sum of Groups This sectio tells us whe the direct sum of groups is isomorphic to some of its proper subgroup Theorem 311 The additive group of itegers is isomorphic to some of its proper subgroup, where \{0,1, 1} Proof: Let f : be defied by f ( a) a, a Let a, b If a b, the f ( a) a b f ( b) Thus, f is well-defied Suppose f ( a) f ( b) The, a b which implies that a b Hece, f is oe-to-oe Also f ( a b) ( a b) a b f ( a) f ( b) Hece, f is a homomorphism Let b The b m for some m Take a m The f ( a) a m b So, f is oto Therefore, the additive group is isomorphoc to the proper subgroup The followig corollary follows from Theorem 311 ad Theorem 1512 Corollary 312 Every ifiite cyclic group is isomorphic to some of its proper subgroup Theorem 313 The additive group of all ratioal umbers is ot isomorphic to ay of its proper subgroup 28
7 Proof: Suppose that f : is a ozero homomorphism Note that ad Claim 1: f ( x) f (1) x, x, where f (1) 0 Let x The x a for some a, b, b 0 Observe that b a a a bf ( x) bf f f b b b a a f b b a f b b f( a) 1 f (1) f( a 1) f (1 1) f (1) f (1) f (1) af (1) f(1) a a Thus, f ( x) f (1) f (1) x b Moreover, f(1) 0 sice f is a ozero homomorphism Claim 2: f is oe-to-oe Let a, b with f ( a) f ( b) The f (1) a f (1) b by Claim 1 Sice f(1) 0 ad f( ) is a subgroup of, cacellatio holds, that is, a b Hece, f is oe-to-oe Claim 3: f is oto a Let x The x with a, b, b 0 Sice 0 f (1), there exist b 29
8 ozero itegers c ad b such that bc 0sice b 0 ad 0 c c f (1) d This implies that ad c ad a Let t The t ad f ( t) f (1) t x Thus, bc d bc b f is oto Therefore, is a isomorphism This meas that every homomorphism f : is a isomorphism Thus, is ot isomorphic to ay of its proper subgroup f Observe that the additive group of itegers is isomorphic to some of its proper subgroup but the additive group of ratioal umbers is ot What ca be said about? Theorem 314 The additive group is isomorphic to some if its proper subgroup, where \{0,1, 1} Proof: Note that is a proper subgroup of sice (1,1) but (1,1) Let f : be defied by f (( s, a)) ( s, a) Let ( s, a) ad ( t, b) be i with ( s, a) ( t, b) The s t ad a b Now f (( s, a)) ( s, a) ( t, b) f (( t, b)) Thus f is well-defied Suppose that f (( s, a)) f (( t, b)) The, ( s, a) ( t, b) implies that s t ad a b this shows that ( s, a) ( t, b) ad is oe-tooe Let x The, x ( s, a) for some s, a, Take ( sa, ) The, f (( s, a)) ( s, a) implyig that is oto Therefore, isomorphic to its proper subgroup Theorem 314 is geeralized i the followig theorem Theorem 315 Suppose that G ad H are groups, oe of which is isomorphic to some of its proper subgroup The G His also isomorphic to its proper subgroup f f 30
9 Proof: Sice e G G 1 1 Let G ad H 1 G1 G such that a isomorphism :G G 1 are groups, it follows that the idetity elemets say ad eh H exist Thus, ( eg, eh) G1 H ad sog 1 H ( g, h ),( g, h ) G H Now, Let ( g, h ) ( g, h ) ( g g, h h ) G H sice G ad H are closed uder additio Thus, G1 H is also closed uder + Note that ( g, h ) ( e, e ) ( g e, h e ) ( g, h ) 1 1 G1 H 1 G1 1 H 1 1 Thus ( eg, e ) 1 H is the idetity elemet ig 1 H Also, ( e, e ) ( g, h ) ( g, h ) ( g g, h h ) implies G1 H that g g e ad h h e 1 2 G1 1 2 H Thus g e g g ad 2 G1 1 1 h2 eh h1 h1 Hece (g 2h2 ) ( g1, h1 ) G1 H is the iverse (g 1, h1 ) G1 H Thus, G1 H is a subgroup ofg H Cosider the fuctio :G H G1 H defied by (( g, h)) ( ( g), h), ( g, h) G H Let ( g, h),( g ', h') G H If ( g, h) ( g ', h'), the g g ' ad h h' So, (( g, h)) ( ( g), h) ( ( g '), h') ( g ', h') well-defied Observe that, (( g, h) ( g ', h')) ( g g ', h h') Thus ( ( g g '), h h ') ( ( g) ( g '), h h ') ( ( g), h) ( ( g '), h ') (( g, h) (( g ', h')) Thus, is a homomorphism Now, if (( g, h)) (( g ', h')), the ( ( g), h) ( ( g '), h') so that ( g) ( g ') ad h h' Sice is oe-tooe, g g' Thus, ( g, h) ( g ', h') ad is oe-to-oe Let ( g1, h) G1 H Sice g 1 G 1 ad is oto, g G such that ( g) g1 Cosider ( g, h) G H The, (( g, h)) ( ( g), h) ( g1, h) 31
10 Thus, is a isomorphism ad subgroup G 1 H G H is isomorphic to its proper Corollary 316 Let G1, G2,, G be groups If for some i {1,2,, }, Gi is isomorphic to some of its proper subgroup, the G1 G2 G is also isomorphic to its proper subgroup Proof: If oe of G1 or G2is isomorphic to its proper subgroup, the by Theorem 315, G1 G2is isomorphic to its proper subgroup Assume that G1 G2 Gk is isomorphic to its proper subgroup for all k 1 The by Theorem 315, G1 G2 Gk 1 ( G1 G2 Gk ) Gk 1 is isomorphic to some of its proper subgroup Therefore, by PMI, G G G is also isomorphic to some of its proper subgroup Summary, Coclusio ad Recommedatios This chapter summarizes the results beig studied i this paper ad presets some recommedatios for further iquiries Summary ad Coclusio This paper obtaied the followig results o groups which are isomorphic to some of its proper subgroup: 1 The additive group of itegers is isomorphic to some of its proper subgroup, where \{0,1, 1} (Theorem 311) 32
11 2 Every ifiite cyclic group is isomorphic to some of its proper subgroup (Corollary 312) 3 The additive group of all ratioal umbers is ot isomorphic to ay of its proper subgroup (Theorem 313) 4 The additive group is isomorphic to some if it s proper subgroup, where \{0,1, 1} (Theorem 314) H 5 Suppose that G ad are groups, oe of which is isomorphic to some of its proper subgroup The G His also isomorphic to its proper subgroup (Theorem 315) 6 Let G1, G2,, G be groups If for some i {1,2,, }, Gi is isomorphic to some of its proper subgroup, the G1 G2 G is also isomorphic to its proper subgroup (Theorem 316) Recommedatios The author recommeds the followig questios for further ivestigatio 1 If G His isomorphic to some of its proper subgroup, will it follow that G or H is isomorphic to some of its proper subgroup? 2 How may homomorphism ad isomorphism exist from the additive group ad ito itself? 33
12 3 Oe ca show that the usual fields are ot isomorphic to proper subfields of themselves but there are fields lyig betwee them that are isomorphic to proper subfields of themselves Which fields are field isomorphic to proper subfields of themselves? ad ad List of Refereces Fraleigh, JB A First Course i Abstract Algebra 1994 Addiso Wesley Publishig Compay Ic Hugerford, T Algebra 1980 New York: Spriger-Verlag Maclae, S ad Birkhoff, G Algebra 1967 New York: Collier- Macmilla LIST OF NOTATIONS H G H is a subgroup of G H G H is a proper subgroup of G for all there exists empty set A B Direct sum of sets A ad B set of atural umber group of itegers 2 group of eve itegers group of ratioal umbers group of real umbers group of itegers modulo isomorphic to 34
Name of the Student: Unit I (Logic and Proofs) 1) Truth Table: Conjunction Disjunction Conditional Biconditional
 SUBJECT NAME : Discrete Mathematics SUBJECT CODE : MA 2265 MATERIAL NAME : Formula Material MATERIAL CODE : JM08ADM009 (Sca the above QR code for the direct dowload of this material) Name of the Studet:
SUBJECT NAME : Discrete Mathematics SUBJECT CODE : MA 2265 MATERIAL NAME : Formula Material MATERIAL CODE : JM08ADM009 (Sca the above QR code for the direct dowload of this material) Name of the Studet:
Lecture 1: Introduction and Strassen s Algorithm
 5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
5-750: Graduate Algorithms Jauary 7, 08 Lecture : Itroductio ad Strasse s Algorithm Lecturer: Gary Miller Scribe: Robert Parker Itroductio Machie models I this class, we will primarily use the Radom Access
New Results on Energy of Graphs of Small Order
 Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
Global Joural of Pure ad Applied Mathematics. ISSN 0973-1768 Volume 13, Number 7 (2017), pp. 2837-2848 Research Idia Publicatios http://www.ripublicatio.com New Results o Eergy of Graphs of Small Order
A study on Interior Domination in Graphs
 IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
IOSR Joural of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 219-765X. Volume 12, Issue 2 Ver. VI (Mar. - Apr. 2016), PP 55-59 www.iosrjourals.org A study o Iterior Domiatio i Graphs A. Ato Kisley 1,
Combination Labelings Of Graphs
 Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
Applied Mathematics E-Notes, (0), - c ISSN 0-0 Available free at mirror sites of http://wwwmaththuedutw/ame/ Combiatio Labeligs Of Graphs Pak Chig Li y Received February 0 Abstract Suppose G = (V; E) is
BOOLEAN MATHEMATICS: GENERAL THEORY
 CHAPTER 3 BOOLEAN MATHEMATICS: GENERAL THEORY 3.1 ISOMORPHIC PROPERTIES The ame Boolea Arithmetic was chose because it was discovered that literal Boolea Algebra could have a isomorphic umerical aspect.
CHAPTER 3 BOOLEAN MATHEMATICS: GENERAL THEORY 3.1 ISOMORPHIC PROPERTIES The ame Boolea Arithmetic was chose because it was discovered that literal Boolea Algebra could have a isomorphic umerical aspect.
INTERSECTION CORDIAL LABELING OF GRAPHS
 INTERSECTION CORDIAL LABELING OF GRAPHS G Meea, K Nagaraja Departmet of Mathematics, PSR Egieerig College, Sivakasi- 66 4, Virudhuagar(Dist) Tamil Nadu, INDIA meeag9@yahoocoi Departmet of Mathematics,
INTERSECTION CORDIAL LABELING OF GRAPHS G Meea, K Nagaraja Departmet of Mathematics, PSR Egieerig College, Sivakasi- 66 4, Virudhuagar(Dist) Tamil Nadu, INDIA meeag9@yahoocoi Departmet of Mathematics,
A RELATIONSHIP BETWEEN BOUNDS ON THE SUM OF SQUARES OF DEGREES OF A GRAPH
 J. Appl. Math. & Computig Vol. 21(2006), No. 1-2, pp. 233-238 Website: http://jamc.et A RELATIONSHIP BETWEEN BOUNDS ON THE SUM OF SQUARES OF DEGREES OF A GRAPH YEON SOO YOON AND JU KYUNG KIM Abstract.
J. Appl. Math. & Computig Vol. 21(2006), No. 1-2, pp. 233-238 Website: http://jamc.et A RELATIONSHIP BETWEEN BOUNDS ON THE SUM OF SQUARES OF DEGREES OF A GRAPH YEON SOO YOON AND JU KYUNG KIM Abstract.
Some cycle and path related strongly -graphs
 Some cycle ad path related strogly -graphs I. I. Jadav, G. V. Ghodasara Research Scholar, R. K. Uiversity, Rajkot, Idia. H. & H. B. Kotak Istitute of Sciece,Rajkot, Idia. jadaviram@gmail.com gaurag ejoy@yahoo.co.i
Some cycle ad path related strogly -graphs I. I. Jadav, G. V. Ghodasara Research Scholar, R. K. Uiversity, Rajkot, Idia. H. & H. B. Kotak Istitute of Sciece,Rajkot, Idia. jadaviram@gmail.com gaurag ejoy@yahoo.co.i
The isoperimetric problem on the hypercube
 The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
The isoperimetric problem o the hypercube Prepared by: Steve Butler November 2, 2005 1 The isoperimetric problem We will cosider the -dimesioal hypercube Q Recall that the hypercube Q is a graph whose
Chapter 9. Pointers and Dynamic Arrays. Copyright 2015 Pearson Education, Ltd.. All rights reserved.
 Chapter 9 Poiters ad Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 9.1 Poiters 9.2 Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Slide 9-3
Chapter 9 Poiters ad Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Overview 9.1 Poiters 9.2 Dyamic Arrays Copyright 2015 Pearso Educatio, Ltd.. All rights reserved. Slide 9-3
A Note on Chromatic Transversal Weak Domination in Graphs
 Iteratioal Joural of Mathematics Treds ad Techology Volume 17 Number 2 Ja 2015 A Note o Chromatic Trasversal Weak Domiatio i Graphs S Balamuruga 1, P Selvalakshmi 2 ad A Arivalaga 1 Assistat Professor,
Iteratioal Joural of Mathematics Treds ad Techology Volume 17 Number 2 Ja 2015 A Note o Chromatic Trasversal Weak Domiatio i Graphs S Balamuruga 1, P Selvalakshmi 2 ad A Arivalaga 1 Assistat Professor,
9.1. Sequences and Series. Sequences. What you should learn. Why you should learn it. Definition of Sequence
 _9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
_9.qxd // : AM Page Chapter 9 Sequeces, Series, ad Probability 9. Sequeces ad Series What you should lear Use sequece otatio to write the terms of sequeces. Use factorial otatio. Use summatio otatio to
CHAPTER IV: GRAPH THEORY. Section 1: Introduction to Graphs
 CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
CHAPTER IV: GRAPH THEORY Sectio : Itroductio to Graphs Sice this class is called Number-Theoretic ad Discrete Structures, it would be a crime to oly focus o umber theory regardless how woderful those topics
Module 8-7: Pascal s Triangle and the Binomial Theorem
 Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Module 8-7: Pascal s Triagle ad the Biomial Theorem Gregory V. Bard April 5, 017 A Note about Notatio Just to recall, all of the followig mea the same thig: ( 7 7C 4 C4 7 7C4 5 4 ad they are (all proouced
Strong Complementary Acyclic Domination of a Graph
 Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
Aals of Pure ad Applied Mathematics Vol 8, No, 04, 83-89 ISSN: 79-087X (P), 79-0888(olie) Published o 7 December 04 wwwresearchmathsciorg Aals of Strog Complemetary Acyclic Domiatio of a Graph NSaradha
BASED ON ITERATIVE ERROR-CORRECTION
 A COHPARISO OF CRYPTAALYTIC PRICIPLES BASED O ITERATIVE ERROR-CORRECTIO Miodrag J. MihaljeviC ad Jova Dj. GoliC Istitute of Applied Mathematics ad Electroics. Belgrade School of Electrical Egieerig. Uiversity
A COHPARISO OF CRYPTAALYTIC PRICIPLES BASED O ITERATIVE ERROR-CORRECTIO Miodrag J. MihaljeviC ad Jova Dj. GoliC Istitute of Applied Mathematics ad Electroics. Belgrade School of Electrical Egieerig. Uiversity
A New Morphological 3D Shape Decomposition: Grayscale Interframe Interpolation Method
 A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
A ew Morphological 3D Shape Decompositio: Grayscale Iterframe Iterpolatio Method D.. Vizireau Politehica Uiversity Bucharest, Romaia ae@comm.pub.ro R. M. Udrea Politehica Uiversity Bucharest, Romaia mihea@comm.pub.ro
found that now considerable work has been done in this started with some example, which motivates the later results.
 8 Iteratioal Joural of Comuter Sciece & Emergig Techologies (E-ISSN: 44-64) Volume, Issue 4, December A Study o Adjacecy Matrix for Zero-Divisor Grahs over Fiite Rig of Gaussia Iteger Prajali, Amit Sharma
8 Iteratioal Joural of Comuter Sciece & Emergig Techologies (E-ISSN: 44-64) Volume, Issue 4, December A Study o Adjacecy Matrix for Zero-Divisor Grahs over Fiite Rig of Gaussia Iteger Prajali, Amit Sharma
5.3 Recursive definitions and structural induction
 /8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
/8/05 5.3 Recursive defiitios ad structural iductio CSE03 Discrete Computatioal Structures Lecture 6 A recursively defied picture Recursive defiitios e sequece of powers of is give by a = for =0,,, Ca
ON A PROBLEM OF C. E. SHANNON IN GRAPH THEORY
 ON A PROBLEM OF C. E. SHANNON IN GRAPH THEORY m. rosefeld1 1. Itroductio. We cosider i this paper oly fiite odirected graphs without multiple edges ad we assume that o each vertex of the graph there is
ON A PROBLEM OF C. E. SHANNON IN GRAPH THEORY m. rosefeld1 1. Itroductio. We cosider i this paper oly fiite odirected graphs without multiple edges ad we assume that o each vertex of the graph there is
2 X = 2 X. The number of all permutations of a set X with n elements is. n! = n (n 1) (n 2) nn e n
 1 Discrete Mathematics revisited. Facts to remember Give set X, the umber of subsets of X is give by X = X. The umber of all permutatios of a set X with elemets is! = ( 1) ( )... 1 e π. The umber ( ) k
1 Discrete Mathematics revisited. Facts to remember Give set X, the umber of subsets of X is give by X = X. The umber of all permutatios of a set X with elemets is! = ( 1) ( )... 1 e π. The umber ( ) k
Ones Assignment Method for Solving Traveling Salesman Problem
 Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
Joural of mathematics ad computer sciece 0 (0), 58-65 Oes Assigmet Method for Solvig Travelig Salesma Problem Hadi Basirzadeh Departmet of Mathematics, Shahid Chamra Uiversity, Ahvaz, Ira Article history:
The Platonic solids The five regular polyhedra
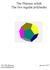 The Platoic solids The five regular polyhedra Ole Witt-Hase jauary 7 www.olewitthase.dk Cotets. Polygos.... Topologically cosideratios.... Euler s polyhedro theorem.... Regular ets o a sphere.... The dihedral
The Platoic solids The five regular polyhedra Ole Witt-Hase jauary 7 www.olewitthase.dk Cotets. Polygos.... Topologically cosideratios.... Euler s polyhedro theorem.... Regular ets o a sphere.... The dihedral
Compactness of Fuzzy Sets
 Compactess of uzzy Sets Amai E. Kadhm Departmet of Egieerig Programs, Uiversity College of Madeat Al-Elem, Baghdad, Iraq. Abstract The objective of this paper is to study the compactess of fuzzy sets i
Compactess of uzzy Sets Amai E. Kadhm Departmet of Egieerig Programs, Uiversity College of Madeat Al-Elem, Baghdad, Iraq. Abstract The objective of this paper is to study the compactess of fuzzy sets i
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Mathematical Stat I: solutions of homework 1
 Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
Mathematical Stat I: solutios of homework Name: Studet Id N:. Suppose we tur over cards simultaeously from two well shuffled decks of ordiary playig cards. We say we obtai a exact match o a particular
Theory of Fuzzy Soft Matrix and its Multi Criteria in Decision Making Based on Three Basic t-norm Operators
 Theory of Fuzzy Soft Matrix ad its Multi Criteria i Decisio Makig Based o Three Basic t-norm Operators Md. Jalilul Islam Modal 1, Dr. Tapa Kumar Roy 2 Research Scholar, Dept. of Mathematics, BESUS, Howrah-711103,
Theory of Fuzzy Soft Matrix ad its Multi Criteria i Decisio Makig Based o Three Basic t-norm Operators Md. Jalilul Islam Modal 1, Dr. Tapa Kumar Roy 2 Research Scholar, Dept. of Mathematics, BESUS, Howrah-711103,
Improved Random Graph Isomorphism
 Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
Improved Radom Graph Isomorphism Tomek Czajka Gopal Paduraga Abstract Caoical labelig of a graph cosists of assigig a uique label to each vertex such that the labels are ivariat uder isomorphism. Such
MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS
 Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
Fura Uiversity Electroic Joural of Udergraduate Matheatics Volue 00, 1996 6-16 MAXIMUM MATCHINGS IN COMPLETE MULTIPARTITE GRAPHS DAVID SITTON Abstract. How ay edges ca there be i a axiu atchig i a coplete
On (K t e)-saturated Graphs
 Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Noame mauscript No. (will be iserted by the editor O (K t e-saturated Graphs Jessica Fuller Roald J. Gould the date of receipt ad acceptace should be iserted later Abstract Give a graph H, we say a graph
Mean cordiality of some snake graphs
 Palestie Joural of Mathematics Vol. 4() (015), 49 445 Palestie Polytechic Uiversity-PPU 015 Mea cordiality of some sake graphs R. Poraj ad S. Sathish Narayaa Commuicated by Ayma Badawi MSC 010 Classificatios:
Palestie Joural of Mathematics Vol. 4() (015), 49 445 Palestie Polytechic Uiversity-PPU 015 Mea cordiality of some sake graphs R. Poraj ad S. Sathish Narayaa Commuicated by Ayma Badawi MSC 010 Classificatios:
An (or ) is a sequence in which each term after the first differs from the preceding term by a fixed constant, called the.
 Sectio.2 Arithmetic Sequeces ad Series -.2 Arithmetic Sequeces ad Series Arithmetic Sequeces Arithmetic Series Key Terms: arithmetic sequece (arithmetic progressio), commo differece, arithmetic series
Sectio.2 Arithmetic Sequeces ad Series -.2 Arithmetic Sequeces ad Series Arithmetic Sequeces Arithmetic Series Key Terms: arithmetic sequece (arithmetic progressio), commo differece, arithmetic series
Visualization of Gauss-Bonnet Theorem
 Visualizatio of Gauss-Boet Theorem Yoichi Maeda maeda@keyaki.cc.u-tokai.ac.jp Departmet of Mathematics Tokai Uiversity Japa Abstract: The sum of exteral agles of a polygo is always costat, π. There are
Visualizatio of Gauss-Boet Theorem Yoichi Maeda maeda@keyaki.cc.u-tokai.ac.jp Departmet of Mathematics Tokai Uiversity Japa Abstract: The sum of exteral agles of a polygo is always costat, π. There are
Convergence results for conditional expectations
 Beroulli 11(4), 2005, 737 745 Covergece results for coditioal expectatios IRENE CRIMALDI 1 ad LUCA PRATELLI 2 1 Departmet of Mathematics, Uiversity of Bologa, Piazza di Porta Sa Doato 5, 40126 Bologa,
Beroulli 11(4), 2005, 737 745 Covergece results for coditioal expectatios IRENE CRIMALDI 1 ad LUCA PRATELLI 2 1 Departmet of Mathematics, Uiversity of Bologa, Piazza di Porta Sa Doato 5, 40126 Bologa,
Polynomial Functions and Models. Learning Objectives. Polynomials. P (x) = a n x n + a n 1 x n a 1 x + a 0, a n 0
 Polyomial Fuctios ad Models 1 Learig Objectives 1. Idetify polyomial fuctios ad their degree 2. Graph polyomial fuctios usig trasformatios 3. Idetify the real zeros of a polyomial fuctio ad their multiplicity
Polyomial Fuctios ad Models 1 Learig Objectives 1. Idetify polyomial fuctios ad their degree 2. Graph polyomial fuctios usig trasformatios 3. Idetify the real zeros of a polyomial fuctio ad their multiplicity
Perhaps the method will give that for every e > U f() > p - 3/+e There is o o-trivial upper boud for f() ad ot eve f() < Z - e. seems to be kow, where
 ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
ON MAXIMUM CHORDAL SUBGRAPH * Paul Erdos Mathematical Istitute of the Hugaria Academy of Scieces ad Reu Laskar Clemso Uiversity 1. Let G() deote a udirected graph, with vertices ad V(G) deote the vertex
n n B. How many subsets of C are there of cardinality n. We are selecting elements for such a
 4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
4. [10] Usig a combiatorial argumet, prove that for 1: = 0 = Let A ad B be disjoit sets of cardiality each ad C = A B. How may subsets of C are there of cardiality. We are selectig elemets for such a subset
Lecture 2: Spectra of Graphs
 Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
Spectral Graph Theory ad Applicatios WS 20/202 Lecture 2: Spectra of Graphs Lecturer: Thomas Sauerwald & He Su Our goal is to use the properties of the adjacecy/laplacia matrix of graphs to first uderstad
International Journal of Pure and Applied Sciences and Technology
 It J Pure App Sci Techo 6( (0 pp7-79 Iteratioa Joura of Pure ad Appied Scieces ad Techoogy ISS 9-607 Avaiabe oie at wwwijopaasati Research Paper Reatioship Amog the Compact Subspaces of Rea Lie ad their
It J Pure App Sci Techo 6( (0 pp7-79 Iteratioa Joura of Pure ad Appied Scieces ad Techoogy ISS 9-607 Avaiabe oie at wwwijopaasati Research Paper Reatioship Amog the Compact Subspaces of Rea Lie ad their
Assignment 5; Due Friday, February 10
 Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
Assigmet 5; Due Friday, February 10 17.9b The set X is just two circles joied at a poit, ad the set X is a grid i the plae, without the iteriors of the small squares. The picture below shows that the iteriors
Protected points in ordered trees
 Applied Mathematics Letters 008 56 50 www.elsevier.com/locate/aml Protected poits i ordered trees Gi-Sag Cheo a, Louis W. Shapiro b, a Departmet of Mathematics, Sugkyukwa Uiversity, Suwo 440-746, Republic
Applied Mathematics Letters 008 56 50 www.elsevier.com/locate/aml Protected poits i ordered trees Gi-Sag Cheo a, Louis W. Shapiro b, a Departmet of Mathematics, Sugkyukwa Uiversity, Suwo 440-746, Republic
1 Enterprise Modeler
 1 Eterprise Modeler Itroductio I BaaERP, a Busiess Cotrol Model ad a Eterprise Structure Model for multi-site cofiguratios are itroduced. Eterprise Structure Model Busiess Cotrol Models Busiess Fuctio
1 Eterprise Modeler Itroductio I BaaERP, a Busiess Cotrol Model ad a Eterprise Structure Model for multi-site cofiguratios are itroduced. Eterprise Structure Model Busiess Cotrol Models Busiess Fuctio
Chapter 11. Friends, Overloaded Operators, and Arrays in Classes. Copyright 2014 Pearson Addison-Wesley. All rights reserved.
 Chapter 11 Frieds, Overloaded Operators, ad Arrays i Classes Copyright 2014 Pearso Addiso-Wesley. All rights reserved. Overview 11.1 Fried Fuctios 11.2 Overloadig Operators 11.3 Arrays ad Classes 11.4
Chapter 11 Frieds, Overloaded Operators, ad Arrays i Classes Copyright 2014 Pearso Addiso-Wesley. All rights reserved. Overview 11.1 Fried Fuctios 11.2 Overloadig Operators 11.3 Arrays ad Classes 11.4
Pseudocode ( 1.1) Analysis of Algorithms. Primitive Operations. Pseudocode Details. Running Time ( 1.1) Estimating performance
 Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
Aalysis of Algorithms Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite amout of time. Pseudocode ( 1.1) High-level descriptio of a algorithm More structured
RTG Mini-Course Perspectives in Geometry Series
 RTG Mii-Course Perspectives i Geometry Series Jacob Lurie Lecture III: The Cobordism Hypothesis (1/27/2009) A quick review of ideas from previous lectures: The origial defiitio of a -dimesioal tqft provided
RTG Mii-Course Perspectives i Geometry Series Jacob Lurie Lecture III: The Cobordism Hypothesis (1/27/2009) A quick review of ideas from previous lectures: The origial defiitio of a -dimesioal tqft provided
Improving Information Retrieval System Security via an Optimal Maximal Coding Scheme
 Improvig Iformatio Retrieval System Security via a Optimal Maximal Codig Scheme Dogyag Log Departmet of Computer Sciece, City Uiversity of Hog Kog, 8 Tat Chee Aveue Kowloo, Hog Kog SAR, PRC dylog@cs.cityu.edu.hk
Improvig Iformatio Retrieval System Security via a Optimal Maximal Codig Scheme Dogyag Log Departmet of Computer Sciece, City Uiversity of Hog Kog, 8 Tat Chee Aveue Kowloo, Hog Kog SAR, PRC dylog@cs.cityu.edu.hk
It just came to me that I 8.2 GRAPHS AND CONVERGENCE
 44 Chapter 8 Discrete Mathematics: Fuctios o the Set of Natural Numbers (a) Take several odd, positive itegers for a ad write out eough terms of the 3N sequece to reach a repeatig loop (b) Show that ot
44 Chapter 8 Discrete Mathematics: Fuctios o the Set of Natural Numbers (a) Take several odd, positive itegers for a ad write out eough terms of the 3N sequece to reach a repeatig loop (b) Show that ot
condition w i B i S maximum u i
 ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
ecture 10 Dyamic Programmig 10.1 Kapsack Problem November 1, 2004 ecturer: Kamal Jai Notes: Tobias Holgers We are give a set of items U = {a 1, a 2,..., a }. Each item has a weight w i Z + ad a utility
The Magma Database file formats
 The Magma Database file formats Adrew Gaylard, Bret Pikey, ad Mart-Mari Breedt Johaesburg, South Africa 15th May 2006 1 Summary Magma is a ope-source object database created by Chris Muller, of Kasas City,
The Magma Database file formats Adrew Gaylard, Bret Pikey, ad Mart-Mari Breedt Johaesburg, South Africa 15th May 2006 1 Summary Magma is a ope-source object database created by Chris Muller, of Kasas City,
CIS 121 Data Structures and Algorithms with Java Spring Stacks and Queues Monday, February 12 / Tuesday, February 13
 CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
CIS Data Structures ad Algorithms with Java Sprig 08 Stacks ad Queues Moday, February / Tuesday, February Learig Goals Durig this lab, you will: Review stacks ad queues. Lear amortized ruig time aalysis
Minimum Rank of Graphs Powers Family
 Oe Joural of Discrete Mathematics 0 65-69 htt://dxdoiorg/046/odm00 Published Olie Aril 0 (htt://wwwscirporg/oural/odm) Miimum Rak of rahs Powers Family Alimohammad Nazari Marzieh Karimi Radoor Deartmet
Oe Joural of Discrete Mathematics 0 65-69 htt://dxdoiorg/046/odm00 Published Olie Aril 0 (htt://wwwscirporg/oural/odm) Miimum Rak of rahs Powers Family Alimohammad Nazari Marzieh Karimi Radoor Deartmet
A Comparative Study of Positive and Negative Factorials
 A Comparative Study of Positive ad Negative Factorials A. M. Ibrahim, A. E. Ezugwu, M. Isa Departmet of Mathematics, Ahmadu Bello Uiversity, Zaria Abstract. This paper preset a comparative study of the
A Comparative Study of Positive ad Negative Factorials A. M. Ibrahim, A. E. Ezugwu, M. Isa Departmet of Mathematics, Ahmadu Bello Uiversity, Zaria Abstract. This paper preset a comparative study of the
Some New Results on Prime Graphs
 Ope Joural of Discrete Mathematics, 202, 2, 99-04 http://dxdoiorg/0426/ojdm202209 Published Olie July 202 (http://wwwscirporg/joural/ojdm) Some New Results o Prime Graphs Samir Vaidya, Udaya M Prajapati
Ope Joural of Discrete Mathematics, 202, 2, 99-04 http://dxdoiorg/0426/ojdm202209 Published Olie July 202 (http://wwwscirporg/joural/ojdm) Some New Results o Prime Graphs Samir Vaidya, Udaya M Prajapati
1 Graph Sparsfication
 CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
CME 305: Discrete Mathematics ad Algorithms 1 Graph Sparsficatio I this sectio we discuss the approximatio of a graph G(V, E) by a sparse graph H(V, F ) o the same vertex set. I particular, we cosider
. Written in factored form it is easy to see that the roots are 2, 2, i,
 CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
CMPS A Itroductio to Programmig Programmig Assigmet 4 I this assigmet you will write a java program that determies the real roots of a polyomial that lie withi a specified rage. Recall that the roots (or
CIS 121. Introduction to Trees
 CIS 121 Itroductio to Trees 1 Tree ADT Tree defiitio q A tree is a set of odes which may be empty q If ot empty, the there is a distiguished ode r, called root ad zero or more o-empty subtrees T 1, T 2,
CIS 121 Itroductio to Trees 1 Tree ADT Tree defiitio q A tree is a set of odes which may be empty q If ot empty, the there is a distiguished ode r, called root ad zero or more o-empty subtrees T 1, T 2,
Matrix Partitions of Split Graphs
 Matrix Partitios of Split Graphs Tomás Feder, Pavol Hell, Ore Shklarsky Abstract arxiv:1306.1967v2 [cs.dm] 20 Ju 2013 Matrix partitio problems geeralize a umber of atural graph partitio problems, ad have
Matrix Partitios of Split Graphs Tomás Feder, Pavol Hell, Ore Shklarsky Abstract arxiv:1306.1967v2 [cs.dm] 20 Ju 2013 Matrix partitio problems geeralize a umber of atural graph partitio problems, ad have
On Characteristic Polynomial of Directed Divisor Graphs
 Iter. J. Fuzzy Mathematical Archive Vol. 4, No., 04, 47-5 ISSN: 30 34 (P), 30 350 (olie) Published o April 04 www.researchmathsci.org Iteratioal Joural of V. Maimozhi a ad V. Kaladevi b a Departmet of
Iter. J. Fuzzy Mathematical Archive Vol. 4, No., 04, 47-5 ISSN: 30 34 (P), 30 350 (olie) Published o April 04 www.researchmathsci.org Iteratioal Joural of V. Maimozhi a ad V. Kaladevi b a Departmet of
Designing a learning system
 CS 75 Machie Learig Lecture Desigig a learig system Milos Hauskrecht milos@cs.pitt.edu 539 Seott Square, x-5 people.cs.pitt.edu/~milos/courses/cs75/ Admiistrivia No homework assigmet this week Please try
CS 75 Machie Learig Lecture Desigig a learig system Milos Hauskrecht milos@cs.pitt.edu 539 Seott Square, x-5 people.cs.pitt.edu/~milos/courses/cs75/ Admiistrivia No homework assigmet this week Please try
1.2 Binomial Coefficients and Subsets
 1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
1.2. BINOMIAL COEFFICIENTS AND SUBSETS 13 1.2 Biomial Coefficiets ad Subsets 1.2-1 The loop below is part of a program to determie the umber of triagles formed by poits i the plae. for i =1 to for j =
Pattern Recognition Systems Lab 1 Least Mean Squares
 Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
Patter Recogitio Systems Lab 1 Least Mea Squares 1. Objectives This laboratory work itroduces the OpeCV-based framework used throughout the course. I this assigmet a lie is fitted to a set of poits usig
Elementary Educational Computer
 Chapter 5 Elemetary Educatioal Computer. Geeral structure of the Elemetary Educatioal Computer (EEC) The EEC coforms to the 5 uits structure defied by vo Neuma's model (.) All uits are preseted i a simplified
Chapter 5 Elemetary Educatioal Computer. Geeral structure of the Elemetary Educatioal Computer (EEC) The EEC coforms to the 5 uits structure defied by vo Neuma's model (.) All uits are preseted i a simplified
The Closest Line to a Data Set in the Plane. David Gurney Southeastern Louisiana University Hammond, Louisiana
 The Closest Lie to a Data Set i the Plae David Gurey Southeaster Louisiaa Uiversity Hammod, Louisiaa ABSTRACT This paper looks at three differet measures of distace betwee a lie ad a data set i the plae:
The Closest Lie to a Data Set i the Plae David Gurey Southeaster Louisiaa Uiversity Hammod, Louisiaa ABSTRACT This paper looks at three differet measures of distace betwee a lie ad a data set i the plae:
4-Prime cordiality of some cycle related graphs
 Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 193-9466 Vol. 1, Issue 1 (Jue 017), pp. 30 40 Applicatios ad Applied Mathematics: A Iteratioal Joural (AAM) 4-Prime cordiality of some cycle related
Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 193-9466 Vol. 1, Issue 1 (Jue 017), pp. 30 40 Applicatios ad Applied Mathematics: A Iteratioal Joural (AAM) 4-Prime cordiality of some cycle related
UNIT 1 RECURRENCE RELATIONS
 UNIT RECURRENCE RELATIONS Structure Page No.. Itroductio 7. Objectives 7. Three Recurret Problems 8.3 More Recurreces.4 Defiitios 4.5 Divide ad Coquer 7.6 Summary 9.7 Solutios/Aswers. INTRODUCTION I the
UNIT RECURRENCE RELATIONS Structure Page No.. Itroductio 7. Objectives 7. Three Recurret Problems 8.3 More Recurreces.4 Defiitios 4.5 Divide ad Coquer 7.6 Summary 9.7 Solutios/Aswers. INTRODUCTION I the
The number n of subintervals times the length h of subintervals gives length of interval (b-a).
 Simulator with MadMath Kit: Riema Sums (Teacher s pages) I your kit: 1. GeoGebra file: Ready-to-use projector sized simulator: RiemaSumMM.ggb 2. RiemaSumMM.pdf (this file) ad RiemaSumMMEd.pdf (educator's
Simulator with MadMath Kit: Riema Sums (Teacher s pages) I your kit: 1. GeoGebra file: Ready-to-use projector sized simulator: RiemaSumMM.ggb 2. RiemaSumMM.pdf (this file) ad RiemaSumMMEd.pdf (educator's
Octahedral Graph Scaling
 Octahedral Graph Scalig Peter Russell Jauary 1, 2015 Abstract There is presetly o strog iterpretatio for the otio of -vertex graph scalig. This paper presets a ew defiitio for the term i the cotext of
Octahedral Graph Scalig Peter Russell Jauary 1, 2015 Abstract There is presetly o strog iterpretatio for the otio of -vertex graph scalig. This paper presets a ew defiitio for the term i the cotext of
Big-O Analysis. Asymptotics
 Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
Big-O Aalysis 1 Defiitio: Suppose that f() ad g() are oegative fuctios of. The we say that f() is O(g()) provided that there are costats C > 0 ad N > 0 such that for all > N, f() Cg(). Big-O expresses
NTH, GEOMETRIC, AND TELESCOPING TEST
 NTH, GEOMETRIC, AND TELESCOPING TEST Sectio 9. Calculus BC AP/Dual, Revised 08 viet.dag@humbleisd.et /4/08 0:0 PM 9.: th, Geometric, ad Telescopig Test SUMMARY OF TESTS FOR SERIES Lookig at the first few
NTH, GEOMETRIC, AND TELESCOPING TEST Sectio 9. Calculus BC AP/Dual, Revised 08 viet.dag@humbleisd.et /4/08 0:0 PM 9.: th, Geometric, ad Telescopig Test SUMMARY OF TESTS FOR SERIES Lookig at the first few
Lecture 5. Counting Sort / Radix Sort
 Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
Lecture 5. Coutig Sort / Radix Sort T. H. Corme, C. E. Leiserso ad R. L. Rivest Itroductio to Algorithms, 3rd Editio, MIT Press, 2009 Sugkyukwa Uiversity Hyuseug Choo choo@skku.edu Copyright 2000-2018
University of Waterloo Department of Electrical and Computer Engineering ECE 250 Algorithms and Data Structures
 Uiversity of Waterloo Departmet of Electrical ad Computer Egieerig ECE 250 Algorithms ad Data Structures Midterm Examiatio ( pages) Istructor: Douglas Harder February 7, 2004 7:30-9:00 Name (last, first)
Uiversity of Waterloo Departmet of Electrical ad Computer Egieerig ECE 250 Algorithms ad Data Structures Midterm Examiatio ( pages) Istructor: Douglas Harder February 7, 2004 7:30-9:00 Name (last, first)
The digraph drop polynomial
 The digraph drop polyomial Fa Chug Ro Graham Abstract For a weighted directed graph (or digraph, for short), deoted by D = (V, E, w), we defie a two-variable polyomial B D (x, y), called the drop polyomial
The digraph drop polyomial Fa Chug Ro Graham Abstract For a weighted directed graph (or digraph, for short), deoted by D = (V, E, w), we defie a two-variable polyomial B D (x, y), called the drop polyomial
Thompson s Group F (p + 1) is not Minimally Almost Convex
 Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
Thompso s Group F (p + ) is ot Miimally Almost Covex Claire Wladis Thompso s Group F (p + ). A Descriptio of F (p + ) Thompso s group F (p + ) ca be defied as the group of piecewiseliear orietatio-preservig
CIS 121 Data Structures and Algorithms with Java Spring Stacks, Queues, and Heaps Monday, February 18 / Tuesday, February 19
 CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
CIS Data Structures ad Algorithms with Java Sprig 09 Stacks, Queues, ad Heaps Moday, February 8 / Tuesday, February 9 Stacks ad Queues Recall the stack ad queue ADTs (abstract data types from lecture.
Recursion. Recursion. Mathematical induction: example. Recursion. The sum of the first n odd numbers is n 2 : Informal proof: Principle:
 Recursio Recursio Jordi Cortadella Departmet of Computer Sciece Priciple: Reduce a complex problem ito a simpler istace of the same problem Recursio Itroductio to Programmig Dept. CS, UPC 2 Mathematical
Recursio Recursio Jordi Cortadella Departmet of Computer Sciece Priciple: Reduce a complex problem ito a simpler istace of the same problem Recursio Itroductio to Programmig Dept. CS, UPC 2 Mathematical
CONTINUI TY. JEE-Mathematics. Illustration 1 : Solution : Illustration 2 : 1. CONTINUOUS FUNCTIONS :
 J-Mathematics. CONTINUOUS FUNCTIONS : CONTINUI TY A fuctio for which a small chage i the idepedet variable causes oly a small chage ad ot a sudde jump i the depedet variable are called cotiuous fuctios.
J-Mathematics. CONTINUOUS FUNCTIONS : CONTINUI TY A fuctio for which a small chage i the idepedet variable causes oly a small chage ad ot a sudde jump i the depedet variable are called cotiuous fuctios.
COSC 1P03. Ch 7 Recursion. Introduction to Data Structures 8.1
 COSC 1P03 Ch 7 Recursio Itroductio to Data Structures 8.1 COSC 1P03 Recursio Recursio I Mathematics factorial Fiboacci umbers defie ifiite set with fiite defiitio I Computer Sciece sytax rules fiite defiitio,
COSC 1P03 Ch 7 Recursio Itroductio to Data Structures 8.1 COSC 1P03 Recursio Recursio I Mathematics factorial Fiboacci umbers defie ifiite set with fiite defiitio I Computer Sciece sytax rules fiite defiitio,
On Spectral Theory Of K-n- Arithmetic Mean Idempotent Matrices On Posets
 Iteratioal Joural of Sciece, Egieerig ad echology Research (IJSER), Volume 5, Issue, February 016 O Spectral heory Of -- Arithmetic Mea Idempotet Matrices O Posets 1 Dr N Elumalai, ProfRMaikada, 3 Sythiya
Iteratioal Joural of Sciece, Egieerig ad echology Research (IJSER), Volume 5, Issue, February 016 O Spectral heory Of -- Arithmetic Mea Idempotet Matrices O Posets 1 Dr N Elumalai, ProfRMaikada, 3 Sythiya
6.854J / J Advanced Algorithms Fall 2008
 MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
MIT OpeCourseWare http://ocw.mit.edu 6.854J / 18.415J Advaced Algorithms Fall 2008 For iformatio about citig these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advaced Algorithms
CUTTING AND PASTING LIBERT E, EGALIT E, HOMOLOGIE! 1
 CUTTING AND PASTING LIBERTÉ, EGALITÉ, HOMOLOGIE! 1 1. Heegaard splittigs Makig 3-maifolds from solid hadlebodies 2. Surface homeomorphisms Gluig maifolds together alog their boudaries 3. Surgery Cuttig
CUTTING AND PASTING LIBERTÉ, EGALITÉ, HOMOLOGIE! 1 1. Heegaard splittigs Makig 3-maifolds from solid hadlebodies 2. Surface homeomorphisms Gluig maifolds together alog their boudaries 3. Surgery Cuttig
Counting the Number of Minimum Roman Dominating Functions of a Graph
 Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
Coutig the Number of Miimum Roma Domiatig Fuctios of a Graph SHI ZHENG ad KOH KHEE MENG, Natioal Uiversity of Sigapore We provide two algorithms coutig the umber of miimum Roma domiatig fuctios of a graph
Planar graphs. Definition. A graph is planar if it can be drawn on the plane in such a way that no two edges cross each other.
 Plaar graphs Defiitio. A graph is plaar if it ca be draw o the plae i such a way that o two edges cross each other. Example: Face 1 Face 2 Exercise: Which of the followig graphs are plaar? K, P, C, K,m,
Plaar graphs Defiitio. A graph is plaar if it ca be draw o the plae i such a way that o two edges cross each other. Example: Face 1 Face 2 Exercise: Which of the followig graphs are plaar? K, P, C, K,m,
The Counterchanged Crossed Cube Interconnection Network and Its Topology Properties
 WSEAS TRANSACTIONS o COMMUNICATIONS Wag Xiyag The Couterchaged Crossed Cube Itercoectio Network ad Its Topology Properties WANG XINYANG School of Computer Sciece ad Egieerig South Chia Uiversity of Techology
WSEAS TRANSACTIONS o COMMUNICATIONS Wag Xiyag The Couterchaged Crossed Cube Itercoectio Network ad Its Topology Properties WANG XINYANG School of Computer Sciece ad Egieerig South Chia Uiversity of Techology
Sum-connectivity indices of trees and unicyclic graphs of fixed maximum degree
 1 Sum-coectivity idices of trees ad uicyclic graphs of fixed maximum degree Zhibi Du a, Bo Zhou a *, Nead Triajstić b a Departmet of Mathematics, South Chia Normal Uiversity, uagzhou 510631, Chia email:
1 Sum-coectivity idices of trees ad uicyclic graphs of fixed maximum degree Zhibi Du a, Bo Zhou a *, Nead Triajstić b a Departmet of Mathematics, South Chia Normal Uiversity, uagzhou 510631, Chia email:
Sorting in Linear Time. Data Structures and Algorithms Andrei Bulatov
 Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Sortig i Liear Time Data Structures ad Algorithms Adrei Bulatov Algorithms Sortig i Liear Time 7-2 Compariso Sorts The oly test that all the algorithms we have cosidered so far is compariso The oly iformatio
Creating Exact Bezier Representations of CST Shapes. David D. Marshall. California Polytechnic State University, San Luis Obispo, CA , USA
 Creatig Exact Bezier Represetatios of CST Shapes David D. Marshall Califoria Polytechic State Uiversity, Sa Luis Obispo, CA 93407-035, USA The paper presets a method of expressig CST shapes pioeered by
Creatig Exact Bezier Represetatios of CST Shapes David D. Marshall Califoria Polytechic State Uiversity, Sa Luis Obispo, CA 93407-035, USA The paper presets a method of expressig CST shapes pioeered by
Analysis of Algorithms
 Aalysis of Algorithms Ruig Time of a algorithm Ruig Time Upper Bouds Lower Bouds Examples Mathematical facts Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite
Aalysis of Algorithms Ruig Time of a algorithm Ruig Time Upper Bouds Lower Bouds Examples Mathematical facts Iput Algorithm Output A algorithm is a step-by-step procedure for solvig a problem i a fiite
Solving Fuzzy Assignment Problem Using Fourier Elimination Method
 Global Joural of Pure ad Applied Mathematics. ISSN 0973-768 Volume 3, Number 2 (207), pp. 453-462 Research Idia Publicatios http://www.ripublicatio.com Solvig Fuzzy Assigmet Problem Usig Fourier Elimiatio
Global Joural of Pure ad Applied Mathematics. ISSN 0973-768 Volume 3, Number 2 (207), pp. 453-462 Research Idia Publicatios http://www.ripublicatio.com Solvig Fuzzy Assigmet Problem Usig Fourier Elimiatio
Some non-existence results on Leech trees
 Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
Some o-existece results o Leech trees László A.Székely Hua Wag Yog Zhag Uiversity of South Carolia This paper is dedicated to the memory of Domiique de Cae, who itroduced LAS to Leech trees.. Abstract
Force Network Analysis using Complementary Energy
 orce Network Aalysis usig Complemetary Eergy Adrew BORGART Assistat Professor Delft Uiversity of Techology Delft, The Netherlads A.Borgart@tudelft.l Yaick LIEM Studet Delft Uiversity of Techology Delft,
orce Network Aalysis usig Complemetary Eergy Adrew BORGART Assistat Professor Delft Uiversity of Techology Delft, The Netherlads A.Borgart@tudelft.l Yaick LIEM Studet Delft Uiversity of Techology Delft,
How do we evaluate algorithms?
 F2 Readig referece: chapter 2 + slides Algorithm complexity Big O ad big Ω To calculate ruig time Aalysis of recursive Algorithms Next time: Litterature: slides mostly The first Algorithm desig methods:
F2 Readig referece: chapter 2 + slides Algorithm complexity Big O ad big Ω To calculate ruig time Aalysis of recursive Algorithms Next time: Litterature: slides mostly The first Algorithm desig methods:
c-dominating Sets for Families of Graphs
 c-domiatig Sets for Families of Graphs Kelsie Syder Mathematics Uiversity of Mary Washigto April 6, 011 1 Abstract The topic of domiatio i graphs has a rich history, begiig with chess ethusiasts i the
c-domiatig Sets for Families of Graphs Kelsie Syder Mathematics Uiversity of Mary Washigto April 6, 011 1 Abstract The topic of domiatio i graphs has a rich history, begiig with chess ethusiasts i the
Super Vertex Magic and E-Super Vertex Magic. Total Labelling
 Proceedigs of the Iteratioal Coferece o Applied Mathematics ad Theoretical Computer Sciece - 03 6 Super Vertex Magic ad E-Super Vertex Magic Total Labellig C.J. Deei ad D. Atoy Xavier Abstract--- For a
Proceedigs of the Iteratioal Coferece o Applied Mathematics ad Theoretical Computer Sciece - 03 6 Super Vertex Magic ad E-Super Vertex Magic Total Labellig C.J. Deei ad D. Atoy Xavier Abstract--- For a
Fast Fourier Transform (FFT) Algorithms
 Fast Fourier Trasform FFT Algorithms Relatio to the z-trasform elsewhere, ozero, z x z X x [ ] 2 ~ elsewhere,, ~ e j x X x x π j e z z X X π 2 ~ The DFS X represets evely spaced samples of the z- trasform
Fast Fourier Trasform FFT Algorithms Relatio to the z-trasform elsewhere, ozero, z x z X x [ ] 2 ~ elsewhere,, ~ e j x X x x π j e z z X X π 2 ~ The DFS X represets evely spaced samples of the z- trasform
PLEASURE TEST SERIES (XI) - 04 By O.P. Gupta (For stuffs on Math, click at theopgupta.com)
 wwwtheopguptacom wwwimathematiciacom For all the Math-Gya Buy books by OP Gupta A Compilatio By : OP Gupta (WhatsApp @ +9-9650 350 0) For more stuffs o Maths, please visit : wwwtheopguptacom Time Allowed
wwwtheopguptacom wwwimathematiciacom For all the Math-Gya Buy books by OP Gupta A Compilatio By : OP Gupta (WhatsApp @ +9-9650 350 0) For more stuffs o Maths, please visit : wwwtheopguptacom Time Allowed
The Eigen-Cover Ratio of a Graph: Asymptotes, Domination and Areas
 The ige-cover Ratio of a Graph: Asymptotes, Domiatio ad Areas Paul August Witer ad Carol Lye Jessop Mathematics, UKZN, Durba, outh Africa-email: witerp@ukzacza Abstract The separate study of the two cocepts
The ige-cover Ratio of a Graph: Asymptotes, Domiatio ad Areas Paul August Witer ad Carol Lye Jessop Mathematics, UKZN, Durba, outh Africa-email: witerp@ukzacza Abstract The separate study of the two cocepts
Hash Tables. Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015.
 Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Hash Tables xkcd. http://xkcd.com/221/. Radom Number. Used with permissio uder Creative
Presetatio for use with the textbook Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Hash Tables xkcd. http://xkcd.com/221/. Radom Number. Used with permissio uder Creative
Symmetric Class 0 subgraphs of complete graphs
 DIMACS Techical Report 0-0 November 0 Symmetric Class 0 subgraphs of complete graphs Vi de Silva Departmet of Mathematics Pomoa College Claremot, CA, USA Chaig Verbec, Jr. Becer Friedma Istitute Booth
DIMACS Techical Report 0-0 November 0 Symmetric Class 0 subgraphs of complete graphs Vi de Silva Departmet of Mathematics Pomoa College Claremot, CA, USA Chaig Verbec, Jr. Becer Friedma Istitute Booth
Lecture 6. Lecturer: Ronitt Rubinfeld Scribes: Chen Ziv, Eliav Buchnik, Ophir Arie, Jonathan Gradstein
 068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
068.670 Subliear Time Algorithms November, 0 Lecture 6 Lecturer: Roitt Rubifeld Scribes: Che Ziv, Eliav Buchik, Ophir Arie, Joatha Gradstei Lesso overview. Usig the oracle reductio framework for approximatig
