Expected Time in Linear Space
|
|
|
- Felicity Walton
- 6 years ago
- Views:
Transcription
1 Optimizing Integer Sorting in O(n log log n) Expected Time in Linear Space Ajit Singh M. E. (Computer Science and Engineering) Department of computer Science and Engineering, Thapar University, Patiala Dr. Deepak Garg Asst. Prof. Department of Computer Science and Engineering, Thapar University, Patiala Abstract-The traditional algorithms for integer sorting give a bound of O(n log n) expected time without randomization and O(n) with randomization. Recent researches have optimized lower bound for deterministic algorithms for integer sorting [4, 5, 7]. We present a fast deterministic algorithm for integer sorting in linear space. The algorithm discussed in this paper sorts n integers in the range {0, 1, 2 m 1} in linear space in O(n log log n) expected time. This improves the traditional deterministic algorithms. The algorithm can be compared with the result of Andersson, Hagerup, Nilson and Raman which sorts n integers in O(n log log n) expected time but uses O(mᵋ ) space [2, 14]. The algorithm can also be compared with the result of Andersson which sort n integers in O( n log log n) expected time and linear space but uses randomization [2, 5]. The result of this paper can also be compared with the result of Yijie Han which sort n integers in O(n log log n) expected time and linear space but passes integers in a batch i.e. all integers at a time [8]. This paper also gives an implementation view of integer sorting in O(n log log n) in linear space. Keywords-Deterministic Algorithms; Sorting; Integer Sorting; Complexity; Space Requirement. 1. INTRODUCTION In modern computer world most of the problem is being solved by sorting. It is a classical problem which has been studied by many researchers. The traditional algorithms for sorting give a clear picture for complexity. Although the complexity for comparison sorting is now well understood, the picture for integer sorting is still not clear. The only known lower bound for integer sorting is the trivial Ω(n) bound. Many continuous research efforts have been made by many researchers on integer sorting [2, 3, 5-16]. Recent advances in the design of algorithms for integers sorting have resulted in fast algorithms [5-12, 15, 16]. However, many of these algorithms use randomization or super-linear space. The table-1 shows the comparative analysis of various traditional algorithms: Table-1: Complexity Comparison Name Best Average Worst Memory Insertion Sort O(n) O(n 2 ) O(n 2 ) O(1) Shell Sort O(n) Depends O(n logn 2 ) O(n) Binary tree sort O(n) O(nlogn) O(nlogn) O(n) Selection sort O(n 2 ) O(n 2 ) O(n 2 ) O(1) Heap sort O(nlogn) O(nlogn) O(nlogn) O(1) Bubble sort O n 2 O(n 2 ) O(n 2 ) O(1) Merge sort O(nlogn) O(nlogn) O(nlogn) Depends Quick sort O(nlogn) O(nlogn) O(n 2 ) O(log n) Randomized O(nlogn) O(nlogn) O(nlogn) Quick sort O(log n) Signature Sort O(n) O(n) O(n) Linear For sorting integers in [0, m 1] range O(mᵋ ) space is used in many algorithms. When m is large, the space used is excessive. Thus integer sorting using linear space is more important and therefore extensively studied by researchers. Fredman and Willard showed that n integers can be sorted in O n logn / log logn time in linear space [11]. Raman showed that sorting can be done in O n log n log log n time in linear space [15]. Later Andersson improved the time bound to O n log n [3]. Then Thorup improved the time bound to O(n(log log n) 2 ) [16]. Later Yijei Han showed O(n log log n log log log n) time for deterministic linear space integer sorting [6]. Yijei Han again showed improved result with O(n log log n) time and linear space [8]. In these algorithms expected time is achieved by using Andersson s exponential tree [3]. The height of such a tree is O(log log n). Also the balancing of the tree will take only O(log log n) time. Balancing does not take much time. The major time is taken by the insertion of integers as proved by the Andresson [3]. Thus we only need to reduce the insertion time of integers.
2 Andersson has shown that if we pass down integers in exponential tree one by one than the insertion takes O log n for each integer i.e. total complexity will be O n log n [3]. This is improvement over the result of Raman which takes O n log n log log n expected time [15]. Yijie Han has given an idea which reduces the complexity to O(n log log n) expected time in linear space [8]. The technique used by him is coordinated pass down of integers on the Andersson s exponential search tree [3] and the linear time multi-dividing of the bits of integers. Instead of inserting integer one at a time into the exponential search tree he passed down all integers one level of the exponential search tree at a time. Such coordinated passing down provides the chance of performing multi-dividing in linear time and therefore speeding up the algorithm. This paper will present a different idea to achieve the complexity of deterministic algorithm for integer sorting in O(n log log n) expected time and linear time which is easy to implement and very simple enough. We are also using Andersson exponential tree [3] to perform the sorting. The exponential tree can t be used as it is for our idea, so we need to modify the exponential tree. We will pass down integers one at a time but limit the comparison one per level. Thus total number of comparison for any integer will be O(log log n) i.e. total time taken for all integers insertion will be O( n log log n) as the height of the tree will be O(log log n). In order to perform this we introduce a new concept of Node word. Each node will be containing one extra word which will represent all the keys at that node. We will perform comparison of integer with this word. The tree itself is very complex to handle as number of integer increases. We are using modified concept of exponential tree for our convenience for integer sorting. Here we will say that a tree with properties of binary search tree will be the exponential tree if it has following properties: 1. Each node at level k will hold k number of keys (or integers in our case) i.e. at depth k the number of key in any node will be k keeping root at level Each node at level k will be having k + 1 children i.e. at depth k the number of children will be k All the keys in any node must be sorted. 4. An integer in child i must be greater than key i 1 and less than key i. Thus the node at root will look like as depicted in figure 1. Figure 1: Root Node of Exponential Tree And the node at it level or depth will look like as shown in figure EXPONENTIAL TREE The exponential tree was first introduced by Andersson in his research for fast deterministic algorithms for integer sorting [3]. In such a tree the number of children increases exponentially. An exponential tree is almost identical to a binary search tree, with the exception that the dimension of the tree is not the same at all levels. In a normal binary search tree, each node has a dimension (d) of 1, and has 2 d children. In an exponential tree, the dimension equals the depth of the node, with the root node having a d = 1. So the second level can hold two nodes, the third can hold eight nodes, the fourth 64 nodes, and so on. This shows that number of children at each level increased by a multiplicative factor of 2 i.e. exponential increases in number of children at each level. Figure 2: Node at it level in Exponential Tree The height of the tree will remain O(log log n) which can be proved by using induction. The modification will not only reduce the complexity of exponential tree involved in implementing it but also improves the balancing method as well as sorting technique. Integer sorting will be more convenient and fast with this modification. 2.1 Balancing The balancing of exponential tree is one of the most important and necessary task in order to achieve the O(n log log n) expected time in linear space [3]. If the tree is not balance then the worst case will happen and the expected running time will increase to undesired level. The balancing will
3 guarantee that the depth of tree will remain O(log log n) which will lead us to our target. We will say that tree is balanced if the difference between depths (or heights) of both sided children of a key will not exceed by 2. The balancing will happen on all the children of the node. Each key will play a role of a node like in binary search tree in balancing. To balance the tree we will keep track of number of keys passed through a particular node. This track will help us when to call the balancing procedure. We will find the difference between depths of two children by checking how many keys we have passed to those children. If this difference will increase the maximum number of keys the node can hold we will need the balancing. We are introducing strictly balanced tree concept. The tree will be called strictly balanced if the difference between heights (or depths) of both sided children of a key will not exceed by 1. This balancing will help us to achieve a true bound of O(n log log n) expected time. We can use the self balancing technique which is already in existence in self balancing binary tree. 3. INSERTION IN EXPONENTIAL TREE The sorting of integers will happens with inserting them into exponential tree. After inserting the integers into tree, we will trace the tree in in-order to get the sorted list as output. As proved by Andersson, insertion into exponential tree takes most of the time [3], thus our focus is to achieve the insertion in lesser expected time. As discussed above the exponential tree is a binary search tree itself, thus the insertion requires finding the appropriate place of the integer. This will be happening by comparing integer with keys presented in any node. There are at most k number of keys in any node at depth or level k, which means there will be at most k number of comparisons for passing the integer through that level. Andersson has proved that if we pass down integer to exponential tree one by one then the insertion will take O n log n expected time, which does not seem well enough optimized [3]. But in the best case scenario the insertion will take O(n log log n) time as only one comparison will required at each level. The best case happens rarely, thus we can t rely on the best case scenario. Hence we need to further modify the concept to achieve better result. As discussed passing down integers one at a time does not give well enough expected time. Yijie Han came up with the idea of passing down the integers in group [8]. He used multi-dividing technique to split the integers into smaller lists. He suggested that instead of inserting integer one at a time into the exponential search tree we can pass down all integers to one level of the exponential search tree at a time. Such coordinated passing down provides the chance of performing multi-dividing in linear time and therefore speeding up the algorithm. This technique gives an expected time of O( n log log n) in linear space. But it is very difficult to pass all integers at once if the number of integers is very large. Thus the insertion of integers in groups does not seem very good in terms of implementation and complexity associated in passing down all integers at once. We will pass down integers one by one in our design but will reduce the number of comparison required at each level. 4. SORTING IN O( n log log n log log log n) While passing down integer one by one in exponential tree, we need to perform comparison at each level in a particular node with all the keys presented in that node as the tree posses the property of binary search tree. But in our modified design of exponential tree, the keys in a particular node are sorted itself. We can use this property to enhance our algorithm. The use of this property can reduce the insertion time of integers. This property allows us to use the binary search method which is already in literature and well used. As we know that the binary search takes O(log n) expected time and uses only O(1) extra memory space. Thus if we find the position of integer to be inserted in the node or pass the integer through a level using binary search it will take O(log k) number of comparisons at each level where k is the depth of that node or level. This shows that in average case passing down all integers will take O(n log log n log k) expected time. In the best case when only one comparison will be required to perform the passing the expected reduces to O(n log log n). The worst case will happen when the number of integers is highest at any node, which is O(log log n) as there are at most O(log log n) levels in the tree. Hence in worst case the expected time with binary search will be O(n log log n log log log n) which is better than O n log n. It also uses no extra memory. The steps associated in this sorting will be: Step1: Create Exponential tree. Step2: Repeat step 3 to 7 wile tere is more integers. // Step 2 Will be repeated n times. Step3: Set l = 1. Step4: Repeat step 5 and 6 wile integer is not inserted. // Step 4 Repeated log log n times. Step5: Searc te position were integer to be inserted
4 or to be passed to at level l using binary searc. // Step 5 Takes log l comparison to find the index. Step6: if te node is full ten l = l + 1 else insert te integer in tat node. Step7: Call te balancing metod. Step8: Trace te tree in order to get te sorted list. Step9: stop. Let us discuss the algorithm given above step by step. Step1 just creates the exponential tree in which integers are supposed to be inserted. In step2 the insertion begins. Step3 to 7 find the position of integer using binary search where it is to be inserted. Now the step2 will be called n times. Step4 will be repeated log log n times and step5 will require log l number of comparisons where l is the level. Thus total number of comparisons will be O(n log log n log l). Hence when the level is highest which will be log log n then the worst case occurs. So the algorithm takes O(n log log n log log log n) expected time in linear space as discussed above. 5. NODE WORD Now we have reached up to O n log log n log log log n expected time in linear space. Here we are introducing the concept of node word. As we know that in modern era of computers, the word length i.e. bits that can be processed per instruction by a computer is very high (64 bits in general PCs). Such a high word length can be used to speed up the processing. Most of the bits of any instruction go useless as these are not used for any data. The concept is to exploit the inherent parallelism present in uniprocessor system. Instead of comparing on integer at a time we can compare multiple integers at once. This is a simple trick which is already in use in graphics. Here we will use it for integer comparison. We will achieve a time bound of O(n log log n) in linear space using this concept. In order to do so we have to limit the number of comparisons to O(1) at per node or level which means only one comparison must tell us that where to insert the integer or pass it down. To limit the number of comparisons to O(1) we will merge the all keys presented in any node to one long word. We will call it node word. When the integer needs to be passing down we will create a long word of that integer by duplicating its value. We must duplicate the value of integer by the number of keys presented in that node times. Thus only one comparison will be enough to tell us the accurate position of the integer to be passed down. Hence the node at it level or depth will look like as shown in figure 3. Figure 3: it level Node in Exponential Tree with Node Word. The creation of node word can be done by using a hash function that will convert the integers into smaller values which can be represented in lesser bits than actual integer. The lesser the bits to be merge more convenient it will be to make a node word. Now the function will also ensure that as the integer proceeds from one level to another down the tree, the node words are having all keys merged in it. This can be done by choosing the hash function in such a way that it is a function of number of keys in node, the range of key s value and the bit length of the node word. The process of creating the node word may take well enough processing time. We can reduce it by modifying the node of the tree. Now the tree node will also carry a variable to store node word. As we know that the node word once created will only needs to change when new key is inserted in that node which will happen only with leaf nodes or in balancing the tree. Hence if we store the node word in node itself we only need to create long word for the integer to be inserted. This will save a lot of processing time. Here we need to consider the time taken by the process of creation of long word for the integer to be inserted. As we know that the height of the tree will be O(n log log n), thus only O(n log log n) words will be created, one at each level. Thus the expected time for this will not exceed O(n log log n) which means we have achieved our targeted complexity. Hence by using node word we can achieve a true time bound of O(n log log n) in linear space. 6. CONCLUSION We have achieved O(n log log n log log log n) expected time in linear space using binary search in exponential tree. This result is very important in view of implementation. And also, we have achieved O(n log log n) expected time in linear
5 space for integer sorting using exponential tree. We achieved this by passing one integer at a time. This has reduced the complexity associated with passing all integers at once. REFERENCES [1] P. van Emde Boas, R. Kaas, E. Zijlstra, Design and implementation of an efficient priority queue, Math. Syst. Theory 10, [2] A. Andersson, T. Hagerup, S. Nilsson, R. Raman, Sorting in linear time?, Symposium on Theory of Computing, [3] A. Andersson, Fast deterministic sorting and searching in linear space, IEEE Symposium on Foundations of Computer Science, [4] M. Dietzfelbinger, T. Hagerup, J. Katajainen, M. Penttonen, A reliable randomized algorithm for the closest-pair problem, J. Algorithms 25, [5] M. Thorup, Randomized sorting in O(n log log n)time and linear space using addition, shift and bit-wise boolean operations, in: Proc. 8th ACM SIAM Symposium on Discrete Algorithms (SODA 97), [6] Y. Han, Improved fast integer sorting in linear space, Inform. and Comput., [7] Y. Han, M. Thorup, Sorting integers in O n log log n expected time and linear space, IEEE Symposium on Foundations of Computer Science (FOCS 02), [8] Y. Han, Deterministic sorting in O(n log log n) time and linear space, 34 th STOC, [9] T.H. Cormen, C.E. Leiserson, R.L. Rivest, C. Stein: Introduction to Algorithms, Second Edition,The MIT Press and McGraw-Hill Book Company, [10] S. Albers, T. Hagerup, Improved parallel integer sorting without concurrent writing, Inform. and Comput., [11] M.L. Fredman, D.E. Willard, Surpassing the information theoretic bound with fusion trees, J. Comput. System Sci., [12] T. Hagerup, H. Shen, Improved nonconservative sequential and parallel integer sorting, Inform. Process. Lett., [13] D. Kirkpatrick, S. Reisch, Upper bounds for sorting integers on random access machines, Theoret. Comput. Sci., [14] Y. Han, X. Shen, Conservative algorithms for parallel and sequential integer sorting, International Computing and Combinatorics Conference, [15] R. Raman, Priority queues: small, monotone and trans-dichotomous, European Symp. on Algorithms, [16] M. Thorup, Fast deterministic sorting and priority queues in linear space, ACM SIAM Symp. on Discrete Algorithms (SODA 98), 1998.
Lecture 12 March 16, 2010
 6.851: Advanced Data Structures Spring 010 Prof. Erik Demaine Lecture 1 March 16, 010 1 Overvie In the last lecture e covered the round elimination technique and loer bounds on the static predecessor problem.
6.851: Advanced Data Structures Spring 010 Prof. Erik Demaine Lecture 1 March 16, 010 1 Overvie In the last lecture e covered the round elimination technique and loer bounds on the static predecessor problem.
Running head: Integer sorting Mailing address: Yijie Han Computer Science Telecommunications Program University of Missouri - Kansas City 5100 Rockhil
 Improved Fast Integer Sorting in Linear Space 1 Yijie Han Computer Science Telecommunications Program University of Missouri Kansas City 5100 Rockhill Road Kansas City, MO 64110, USA han@cstp.umkc.edu
Improved Fast Integer Sorting in Linear Space 1 Yijie Han Computer Science Telecommunications Program University of Missouri Kansas City 5100 Rockhill Road Kansas City, MO 64110, USA han@cstp.umkc.edu
An NC Algorithm for Sorting Real Numbers
 EPiC Series in Computing Volume 58, 2019, Pages 93 98 Proceedings of 34th International Conference on Computers and Their Applications An NC Algorithm for Sorting Real Numbers in O( nlogn loglogn ) Operations
EPiC Series in Computing Volume 58, 2019, Pages 93 98 Proceedings of 34th International Conference on Computers and Their Applications An NC Algorithm for Sorting Real Numbers in O( nlogn loglogn ) Operations
Lecture 13 March 17, 2005
 6.897: Advanced Data Structures Spring 25 Prof. Erik Demaine ecture 3 March 7, 25 Scribe: Brian Jacokes Overview The sorting problem, in which we wish to sort n elements according to a given ordering,
6.897: Advanced Data Structures Spring 25 Prof. Erik Demaine ecture 3 March 7, 25 Scribe: Brian Jacokes Overview The sorting problem, in which we wish to sort n elements according to a given ordering,
Faster deterministic sorting and searching in linear space
 # %$ # %$ PREPRINT. In Proc. 37th IEEE Symposium on Foundations of Computer Science, 1996. Faster deterministic sorting and searching in linear space Arne Andersson Department of Computer Science, Lund
# %$ # %$ PREPRINT. In Proc. 37th IEEE Symposium on Foundations of Computer Science, 1996. Faster deterministic sorting and searching in linear space Arne Andersson Department of Computer Science, Lund
IMPROVED RANDOMIZED SIGNATURE SORT: IMPLEMENTATION AND PERFORMANCE ANALYSIS
 IMPROVED RANDOMIZED SIGNATURE SORT: IMPLEMENTATION AND PERFORMANCE ANALYSIS Thesis submitted in partial fulfillment of the requirements for the award of degree of Master of Engineering in Computer Science
IMPROVED RANDOMIZED SIGNATURE SORT: IMPLEMENTATION AND PERFORMANCE ANALYSIS Thesis submitted in partial fulfillment of the requirements for the award of degree of Master of Engineering in Computer Science
Planar Point Location in Sublogarithmic Time
 Planar Point Location in Sublogarithmic Time Mihai Pătraşcu (MIT) Point Location in o(log n) Time, Voronoi Diagrams in o(n log n) Time, and Other Transdichotomous Results in Computational Geometry Timothy
Planar Point Location in Sublogarithmic Time Mihai Pătraşcu (MIT) Point Location in o(log n) Time, Voronoi Diagrams in o(n log n) Time, and Other Transdichotomous Results in Computational Geometry Timothy
Spanning Trees and Optimization Problems (Excerpt)
 Bang Ye Wu and Kun-Mao Chao Spanning Trees and Optimization Problems (Excerpt) CRC PRESS Boca Raton London New York Washington, D.C. Chapter 3 Shortest-Paths Trees Consider a connected, undirected network
Bang Ye Wu and Kun-Mao Chao Spanning Trees and Optimization Problems (Excerpt) CRC PRESS Boca Raton London New York Washington, D.C. Chapter 3 Shortest-Paths Trees Consider a connected, undirected network
Applications of the Exponential Search Tree in Sweep Line Techniques
 Applications of the Exponential Search Tree in Sweep Line Techniques S. SIOUTAS, A. TSAKALIDIS, J. TSAKNAKIS. V. VASSILIADIS Department of Computer Engineering and Informatics University of Patras 2650
Applications of the Exponential Search Tree in Sweep Line Techniques S. SIOUTAS, A. TSAKALIDIS, J. TSAKNAKIS. V. VASSILIADIS Department of Computer Engineering and Informatics University of Patras 2650
Lecture 12 March 21, 2007
 6.85: Advanced Data Structures Spring 27 Oren Weimann Lecture 2 March 2, 27 Scribe: Tural Badirkhanli Overview Last lecture we saw how to perform membership quueries in O() time using hashing. Today we
6.85: Advanced Data Structures Spring 27 Oren Weimann Lecture 2 March 2, 27 Scribe: Tural Badirkhanli Overview Last lecture we saw how to perform membership quueries in O() time using hashing. Today we
ADAPTIVE SORTING WITH AVL TREES
 ADAPTIVE SORTING WITH AVL TREES Amr Elmasry Computer Science Department Alexandria University Alexandria, Egypt elmasry@alexeng.edu.eg Abstract A new adaptive sorting algorithm is introduced. The new implementation
ADAPTIVE SORTING WITH AVL TREES Amr Elmasry Computer Science Department Alexandria University Alexandria, Egypt elmasry@alexeng.edu.eg Abstract A new adaptive sorting algorithm is introduced. The new implementation
Data Structures and Algorithms. Roberto Sebastiani
 Data Structures and Algorithms Roberto Sebastiani roberto.sebastiani@disi.unitn.it http://www.disi.unitn.it/~rseba - Week 0 - B.S. In Applied Computer Science Free University of Bozen/Bolzano academic
Data Structures and Algorithms Roberto Sebastiani roberto.sebastiani@disi.unitn.it http://www.disi.unitn.it/~rseba - Week 0 - B.S. In Applied Computer Science Free University of Bozen/Bolzano academic
lecture notes September 2, How to sort?
 .30 lecture notes September 2, 203 How to sort? Lecturer: Michel Goemans The task of sorting. Setup Suppose we have n objects that we need to sort according to some ordering. These could be integers or
.30 lecture notes September 2, 203 How to sort? Lecturer: Michel Goemans The task of sorting. Setup Suppose we have n objects that we need to sort according to some ordering. These could be integers or
Quake Heaps: A Simple Alternative to Fibonacci Heaps
 Quake Heaps: A Simple Alternative to Fibonacci Heaps Timothy M. Chan Cheriton School of Computer Science, University of Waterloo, Waterloo, Ontario N2L G, Canada, tmchan@uwaterloo.ca Abstract. This note
Quake Heaps: A Simple Alternative to Fibonacci Heaps Timothy M. Chan Cheriton School of Computer Science, University of Waterloo, Waterloo, Ontario N2L G, Canada, tmchan@uwaterloo.ca Abstract. This note
Chapter 8 Sort in Linear Time
 Chapter 8 Sort in Linear Time We have so far discussed several sorting algorithms that sort a list of n numbers in O(nlog n) time. Both the space hungry merge sort and the structurely interesting heapsort
Chapter 8 Sort in Linear Time We have so far discussed several sorting algorithms that sort a list of n numbers in O(nlog n) time. Both the space hungry merge sort and the structurely interesting heapsort
Algorithms and Data Structures: Efficient and Cache-Oblivious
 7 Ritika Angrish and Dr. Deepak Garg Algorithms and Data Structures: Efficient and Cache-Oblivious Ritika Angrish* and Dr. Deepak Garg Department of Computer Science and Engineering, Thapar University,
7 Ritika Angrish and Dr. Deepak Garg Algorithms and Data Structures: Efficient and Cache-Oblivious Ritika Angrish* and Dr. Deepak Garg Department of Computer Science and Engineering, Thapar University,
Position Sort. Anuj Kumar Developer PINGA Solution Pvt. Ltd. Noida, India ABSTRACT. Keywords 1. INTRODUCTION 2. METHODS AND MATERIALS
 Position Sort International Journal of Computer Applications (0975 8887) Anuj Kumar Developer PINGA Solution Pvt. Ltd. Noida, India Mamta Former IT Faculty Ghaziabad, India ABSTRACT Computer science has
Position Sort International Journal of Computer Applications (0975 8887) Anuj Kumar Developer PINGA Solution Pvt. Ltd. Noida, India Mamta Former IT Faculty Ghaziabad, India ABSTRACT Computer science has
Data Structures Lesson 9
 Data Structures Lesson 9 BSc in Computer Science University of New York, Tirana Assoc. Prof. Marenglen Biba 1-1 Chapter 21 A Priority Queue: The Binary Heap Priority Queue The priority queue is a fundamental
Data Structures Lesson 9 BSc in Computer Science University of New York, Tirana Assoc. Prof. Marenglen Biba 1-1 Chapter 21 A Priority Queue: The Binary Heap Priority Queue The priority queue is a fundamental
Multi-Way Search Trees
 Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Lecture 8 13 March, 2012
 6.851: Advanced Data Structures Spring 2012 Prof. Erik Demaine Lecture 8 13 March, 2012 1 From Last Lectures... In the previous lecture, we discussed the External Memory and Cache Oblivious memory models.
6.851: Advanced Data Structures Spring 2012 Prof. Erik Demaine Lecture 8 13 March, 2012 1 From Last Lectures... In the previous lecture, we discussed the External Memory and Cache Oblivious memory models.
CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics
 CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics 1 Sorting 1.1 Problem Statement You are given a sequence of n numbers < a 1, a 2,..., a n >. You need to
CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics 1 Sorting 1.1 Problem Statement You are given a sequence of n numbers < a 1, a 2,..., a n >. You need to
arxiv: v3 [cs.ds] 18 Apr 2011
![arxiv: v3 [cs.ds] 18 Apr 2011 arxiv: v3 [cs.ds] 18 Apr 2011](/thumbs/84/89362283.jpg) A tight bound on the worst-case number of comparisons for Floyd s heap construction algorithm Ioannis K. Paparrizos School of Computer and Communication Sciences Ècole Polytechnique Fèdèrale de Lausanne
A tight bound on the worst-case number of comparisons for Floyd s heap construction algorithm Ioannis K. Paparrizos School of Computer and Communication Sciences Ècole Polytechnique Fèdèrale de Lausanne
Operations on Heap Tree The major operations required to be performed on a heap tree are Insertion, Deletion, and Merging.
 Priority Queue, Heap and Heap Sort In this time, we will study Priority queue, heap and heap sort. Heap is a data structure, which permits one to insert elements into a set and also to find the largest
Priority Queue, Heap and Heap Sort In this time, we will study Priority queue, heap and heap sort. Heap is a data structure, which permits one to insert elements into a set and also to find the largest
van Emde Boas trees. Dynamic algorithms F04.Q4, March 29, 2004
 Dynamic algorithms F04.Q4, March 29, 2004 van Emde Boas trees. Consider the datatype ordered dictionary. In addition to the usual dictionary operations (insert, delete, lookup) it supports operations for
Dynamic algorithms F04.Q4, March 29, 2004 van Emde Boas trees. Consider the datatype ordered dictionary. In addition to the usual dictionary operations (insert, delete, lookup) it supports operations for
Multi-Way Search Trees
 Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Lower bound for comparison-based sorting
 COMP3600/6466 Algorithms 2018 Lecture 8 1 Lower bound for comparison-based sorting Reading: Cormen et al, Section 8.1 and 8.2 Different sorting algorithms may have different running-time complexities.
COMP3600/6466 Algorithms 2018 Lecture 8 1 Lower bound for comparison-based sorting Reading: Cormen et al, Section 8.1 and 8.2 Different sorting algorithms may have different running-time complexities.
Optimal Static Range Reporting in One Dimension
 of Optimal Static Range Reporting in One Dimension Stephen Alstrup Gerth Stølting Brodal Theis Rauhe ITU Technical Report Series 2000-3 ISSN 1600 6100 November 2000 Copyright c 2000, Stephen Alstrup Gerth
of Optimal Static Range Reporting in One Dimension Stephen Alstrup Gerth Stølting Brodal Theis Rauhe ITU Technical Report Series 2000-3 ISSN 1600 6100 November 2000 Copyright c 2000, Stephen Alstrup Gerth
An Improved Thorup Shortest Paths Algorithm with a Modified Component Tree
 2013 9th International Conference on Natural Computation (ICNC 2013) An Improved Thorup Shortest Paths Algorithm with a Modified Component Tree Yusi Wei Information Systems Course, Interdisciplinary Graduate
2013 9th International Conference on Natural Computation (ICNC 2013) An Improved Thorup Shortest Paths Algorithm with a Modified Component Tree Yusi Wei Information Systems Course, Interdisciplinary Graduate
Priority Queues. T. M. Murali. January 29, 2009
 Priority Queues T. M. Murali January 29, 2009 Motivation: Sort a List of Numbers Sort INSTANCE: Nonempty list x 1, x 2,..., x n of integers. SOLUTION: A permutation y 1, y 2,..., y n of x 1, x 2,..., x
Priority Queues T. M. Murali January 29, 2009 Motivation: Sort a List of Numbers Sort INSTANCE: Nonempty list x 1, x 2,..., x n of integers. SOLUTION: A permutation y 1, y 2,..., y n of x 1, x 2,..., x
Lecture 9 March 4, 2010
 6.851: Advanced Data Structures Spring 010 Dr. André Schulz Lecture 9 March 4, 010 1 Overview Last lecture we defined the Least Common Ancestor (LCA) and Range Min Query (RMQ) problems. Recall that an
6.851: Advanced Data Structures Spring 010 Dr. André Schulz Lecture 9 March 4, 010 1 Overview Last lecture we defined the Least Common Ancestor (LCA) and Range Min Query (RMQ) problems. Recall that an
Lower Bound on Comparison-based Sorting
 Lower Bound on Comparison-based Sorting Different sorting algorithms may have different time complexity, how to know whether the running time of an algorithm is best possible? We know of several sorting
Lower Bound on Comparison-based Sorting Different sorting algorithms may have different time complexity, how to know whether the running time of an algorithm is best possible? We know of several sorting
Heap Order Property: Key stored at the parent is smaller or equal to the key stored at either child.
 A Binary Heap is a data structure that is an array object that can be viewed as a nearly complete binary tree. The tree is completely filled on all levels except the lowest, which may only be partially
A Binary Heap is a data structure that is an array object that can be viewed as a nearly complete binary tree. The tree is completely filled on all levels except the lowest, which may only be partially
Bichromatic Line Segment Intersection Counting in O(n log n) Time
 Bichromatic Line Segment Intersection Counting in O(n log n) Time Timothy M. Chan Bryan T. Wilkinson Abstract We give an algorithm for bichromatic line segment intersection counting that runs in O(n log
Bichromatic Line Segment Intersection Counting in O(n log n) Time Timothy M. Chan Bryan T. Wilkinson Abstract We give an algorithm for bichromatic line segment intersection counting that runs in O(n log
CSE 3101: Introduction to the Design and Analysis of Algorithms. Office hours: Wed 4-6 pm (CSEB 3043), or by appointment.
 CSE 3101: Introduction to the Design and Analysis of Algorithms Instructor: Suprakash Datta (datta[at]cse.yorku.ca) ext 77875 Lectures: Tues, BC 215, 7 10 PM Office hours: Wed 4-6 pm (CSEB 3043), or by
CSE 3101: Introduction to the Design and Analysis of Algorithms Instructor: Suprakash Datta (datta[at]cse.yorku.ca) ext 77875 Lectures: Tues, BC 215, 7 10 PM Office hours: Wed 4-6 pm (CSEB 3043), or by
COMP3121/3821/9101/ s1 Assignment 1
 Sample solutions to assignment 1 1. (a) Describe an O(n log n) algorithm (in the sense of the worst case performance) that, given an array S of n integers and another integer x, determines whether or not
Sample solutions to assignment 1 1. (a) Describe an O(n log n) algorithm (in the sense of the worst case performance) that, given an array S of n integers and another integer x, determines whether or not
Range Tree Applications in Computational Geometry
 Range Tree Applications in Computational Geometry ANTONIO-GABRIEL STURZU, COSTIN-ANTON BOIANGIU Computer Science Department Politehnica University of Bucharest Splaiul Independentei 313, Sector 6, Bucharest,
Range Tree Applications in Computational Geometry ANTONIO-GABRIEL STURZU, COSTIN-ANTON BOIANGIU Computer Science Department Politehnica University of Bucharest Splaiul Independentei 313, Sector 6, Bucharest,
CSCI2100B Data Structures Heaps
 CSCI2100B Data Structures Heaps Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction In some applications,
CSCI2100B Data Structures Heaps Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction In some applications,
CSE 530A. B+ Trees. Washington University Fall 2013
 CSE 530A B+ Trees Washington University Fall 2013 B Trees A B tree is an ordered (non-binary) tree where the internal nodes can have a varying number of child nodes (within some range) B Trees When a key
CSE 530A B+ Trees Washington University Fall 2013 B Trees A B tree is an ordered (non-binary) tree where the internal nodes can have a varying number of child nodes (within some range) B Trees When a key
Derandomization by Exploiting Redundancy and Mutual Independence
 Derandomization by Exploiting Redundancy and Mutual Independence Yijie Han Yoshihide Igarashi Department of Computer Science University of Kentucky Lexington, KY 40506, USA Department of Computer Science
Derandomization by Exploiting Redundancy and Mutual Independence Yijie Han Yoshihide Igarashi Department of Computer Science University of Kentucky Lexington, KY 40506, USA Department of Computer Science
HEAPS: IMPLEMENTING EFFICIENT PRIORITY QUEUES
 HEAPS: IMPLEMENTING EFFICIENT PRIORITY QUEUES 2 5 6 9 7 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H., Wiley, 2014
HEAPS: IMPLEMENTING EFFICIENT PRIORITY QUEUES 2 5 6 9 7 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H., Wiley, 2014
Data Structures and Algorithms Dr. Naveen Garg Department of Computer Science and Engineering Indian Institute of Technology, Delhi
 Data Structures and Algorithms Dr. Naveen Garg Department of Computer Science and Engineering Indian Institute of Technology, Delhi Lecture 20 Priority Queues Today we are going to look at the priority
Data Structures and Algorithms Dr. Naveen Garg Department of Computer Science and Engineering Indian Institute of Technology, Delhi Lecture 20 Priority Queues Today we are going to look at the priority
Heap: A binary heap is a complete binary tree in which each, node other than root is smaller than its parent. Heap example: Fig 1. NPTEL IIT Guwahati
 Heap sort is an efficient sorting algorithm with average and worst case time complexities are in O(n log n). Heap sort does not use any extra array, like merge sort. This method is based on a data structure
Heap sort is an efficient sorting algorithm with average and worst case time complexities are in O(n log n). Heap sort does not use any extra array, like merge sort. This method is based on a data structure
How many leaves on the decision tree? There are n! leaves, because every permutation appears at least once.
 Chapter 8. Sorting in Linear Time Types of Sort Algorithms The only operation that may be used to gain order information about a sequence is comparison of pairs of elements. Quick Sort -- comparison-based
Chapter 8. Sorting in Linear Time Types of Sort Algorithms The only operation that may be used to gain order information about a sequence is comparison of pairs of elements. Quick Sort -- comparison-based
FINALTERM EXAMINATION Fall 2009 CS301- Data Structures Question No: 1 ( Marks: 1 ) - Please choose one The data of the problem is of 2GB and the hard
 FINALTERM EXAMINATION Fall 2009 CS301- Data Structures Question No: 1 The data of the problem is of 2GB and the hard disk is of 1GB capacity, to solve this problem we should Use better data structures
FINALTERM EXAMINATION Fall 2009 CS301- Data Structures Question No: 1 The data of the problem is of 2GB and the hard disk is of 1GB capacity, to solve this problem we should Use better data structures
Data Structures. Sorting. Haim Kaplan & Uri Zwick December 2013
 Data Structures Sorting Haim Kaplan & Uri Zwick December 2013 1 Comparison based sorting key a 1 a 2 a n info Input: An array containing n items Keys belong to a totally ordered domain Two keys can be
Data Structures Sorting Haim Kaplan & Uri Zwick December 2013 1 Comparison based sorting key a 1 a 2 a n info Input: An array containing n items Keys belong to a totally ordered domain Two keys can be
Computer Science 210 Data Structures Siena College Fall Topic Notes: Priority Queues and Heaps
 Computer Science 0 Data Structures Siena College Fall 08 Topic Notes: Priority Queues and Heaps Heaps and Priority Queues From here, we will look at some ways that trees are used in other structures. First,
Computer Science 0 Data Structures Siena College Fall 08 Topic Notes: Priority Queues and Heaps Heaps and Priority Queues From here, we will look at some ways that trees are used in other structures. First,
Binary Heaps in Dynamic Arrays
 Yufei Tao ITEE University of Queensland We have already learned that the binary heap serves as an efficient implementation of a priority queue. Our previous discussion was based on pointers (for getting
Yufei Tao ITEE University of Queensland We have already learned that the binary heap serves as an efficient implementation of a priority queue. Our previous discussion was based on pointers (for getting
Data Structures and Algorithms Week 4
 Data Structures and Algorithms Week. About sorting algorithms. Heapsort Complete binary trees Heap data structure. Quicksort a popular algorithm very fast on average Previous Week Divide and conquer Merge
Data Structures and Algorithms Week. About sorting algorithms. Heapsort Complete binary trees Heap data structure. Quicksort a popular algorithm very fast on average Previous Week Divide and conquer Merge
Quick-Sort fi fi fi 7 9. Quick-Sort Goodrich, Tamassia
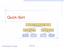 Quick-Sort 7 4 9 6 2 fi 2 4 6 7 9 4 2 fi 2 4 7 9 fi 7 9 2 fi 2 9 fi 9 Quick-Sort 1 Quick-Sort ( 10.2 text book) Quick-sort is a randomized sorting algorithm based on the divide-and-conquer paradigm: x
Quick-Sort 7 4 9 6 2 fi 2 4 6 7 9 4 2 fi 2 4 7 9 fi 7 9 2 fi 2 9 fi 9 Quick-Sort 1 Quick-Sort ( 10.2 text book) Quick-sort is a randomized sorting algorithm based on the divide-and-conquer paradigm: x
CSE100. Advanced Data Structures. Lecture 8. (Based on Paul Kube course materials)
 CSE100 Advanced Data Structures Lecture 8 (Based on Paul Kube course materials) CSE 100 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs
CSE100 Advanced Data Structures Lecture 8 (Based on Paul Kube course materials) CSE 100 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs
Programming II (CS300)
 1 Programming II (CS300) Chapter 10: Search and Heaps MOUNA KACEM mouna@cs.wisc.edu Spring 2018 Search and Heaps 2 Linear Search Binary Search Introduction to trees Priority Queues Heaps Linear Search
1 Programming II (CS300) Chapter 10: Search and Heaps MOUNA KACEM mouna@cs.wisc.edu Spring 2018 Search and Heaps 2 Linear Search Binary Search Introduction to trees Priority Queues Heaps Linear Search
Priority queues. Priority queues. Priority queue operations
 Priority queues March 30, 018 1 Priority queues The ADT priority queue stores arbitrary objects with priorities. An object with the highest priority gets served first. Objects with priorities are defined
Priority queues March 30, 018 1 Priority queues The ADT priority queue stores arbitrary objects with priorities. An object with the highest priority gets served first. Objects with priorities are defined
How much space does this routine use in the worst case for a given n? public static void use_space(int n) { int b; int [] A;
![How much space does this routine use in the worst case for a given n? public static void use_space(int n) { int b; int [] A; How much space does this routine use in the worst case for a given n? public static void use_space(int n) { int b; int [] A;](/thumbs/82/85312801.jpg) How much space does this routine use in the worst case for a given n? public static void use_space(int n) { int b; int [] A; } if (n
How much space does this routine use in the worst case for a given n? public static void use_space(int n) { int b; int [] A; } if (n
Priority Queues. 1 Introduction. 2 Naïve Implementations. CSci 335 Software Design and Analysis III Chapter 6 Priority Queues. Prof.
 Priority Queues 1 Introduction Many applications require a special type of queuing in which items are pushed onto the queue by order of arrival, but removed from the queue based on some other priority
Priority Queues 1 Introduction Many applications require a special type of queuing in which items are pushed onto the queue by order of arrival, but removed from the queue based on some other priority
Priority Queues (Heaps)
 Priority Queues (Heaps) 1 Priority Queues Many applications require that we process records with keys in order, but not necessarily in full sorted order. Often we collect a set of items and process the
Priority Queues (Heaps) 1 Priority Queues Many applications require that we process records with keys in order, but not necessarily in full sorted order. Often we collect a set of items and process the
Advanced algorithms. binary heap, d-ary heap, binomial heap, amortized analysis, Fibonacci heap. Jiří Vyskočil, Radek Mařík 2013
 binary heap, d-ary heap, binomial heap, amortized analysis, Fibonacci heap Jiří Vyskočil, Radek Mařík 2013 heap Heaps [haldy] a heap is a specialized data structure (usually tree-based) that satisfies
binary heap, d-ary heap, binomial heap, amortized analysis, Fibonacci heap Jiří Vyskočil, Radek Mařík 2013 heap Heaps [haldy] a heap is a specialized data structure (usually tree-based) that satisfies
Heaps, Heap Sort, and Priority Queues.
 Heaps, Heap Sort, and Priority Queues Sorting III / Slide 2 Background: Binary Trees Has a root at the topmost level Each node has zero, one or two children A node that has no child is called a leaf For
Heaps, Heap Sort, and Priority Queues Sorting III / Slide 2 Background: Binary Trees Has a root at the topmost level Each node has zero, one or two children A node that has no child is called a leaf For
1 Tree Sort LECTURE 4. OHSU/OGI (Winter 2009) ANALYSIS AND DESIGN OF ALGORITHMS
 OHSU/OGI (Winter 2009) CS532 ANALYSIS AND DESIGN OF ALGORITHMS LECTURE 4 1 Tree Sort Suppose a sequence of n items is given. We can sort it using TreeInsert and DeleteMin: TreeSort Initialize an empty
OHSU/OGI (Winter 2009) CS532 ANALYSIS AND DESIGN OF ALGORITHMS LECTURE 4 1 Tree Sort Suppose a sequence of n items is given. We can sort it using TreeInsert and DeleteMin: TreeSort Initialize an empty
arxiv: v2 [cs.ds] 9 Apr 2009
![arxiv: v2 [cs.ds] 9 Apr 2009 arxiv: v2 [cs.ds] 9 Apr 2009](/thumbs/72/66843812.jpg) Pairing Heaps with Costless Meld arxiv:09034130v2 [csds] 9 Apr 2009 Amr Elmasry Max-Planck Institut für Informatik Saarbrücken, Germany elmasry@mpi-infmpgde Abstract Improving the structure and analysis
Pairing Heaps with Costless Meld arxiv:09034130v2 [csds] 9 Apr 2009 Amr Elmasry Max-Planck Institut für Informatik Saarbrücken, Germany elmasry@mpi-infmpgde Abstract Improving the structure and analysis
Melding priority queues
 Melding priority queues Ran Mendelson 1, Robert E. Tarjan 2,3, Mikkel Thorup 4, and Uri Zwick 1 1 School of Computer Science, Tel Aviv University, Tel Aviv 69978, Israel 2 Department of Computer Science,
Melding priority queues Ran Mendelson 1, Robert E. Tarjan 2,3, Mikkel Thorup 4, and Uri Zwick 1 1 School of Computer Science, Tel Aviv University, Tel Aviv 69978, Israel 2 Department of Computer Science,
Heap-on-Top Priority Queues. March Abstract. We introduce the heap-on-top (hot) priority queue data structure that combines the
 Heap-on-Top Priority Queues Boris V. Cherkassky Central Economics and Mathematics Institute Krasikova St. 32 117418, Moscow, Russia cher@cemi.msk.su Andrew V. Goldberg NEC Research Institute 4 Independence
Heap-on-Top Priority Queues Boris V. Cherkassky Central Economics and Mathematics Institute Krasikova St. 32 117418, Moscow, Russia cher@cemi.msk.su Andrew V. Goldberg NEC Research Institute 4 Independence
Next. 1. Covered basics of a simple design technique (Divideand-conquer) 2. Next, more sorting algorithms.
 Next 1. Covered basics of a simple design technique (Divideand-conquer) Ch. 2 of the text. 2. Next, more sorting algorithms. Sorting Switch from design paradigms to applications. Sorting and order statistics
Next 1. Covered basics of a simple design technique (Divideand-conquer) Ch. 2 of the text. 2. Next, more sorting algorithms. Sorting Switch from design paradigms to applications. Sorting and order statistics
Chapter 2: Basic Data Structures
 Chapter 2: Basic Data Structures Basic Data Structures Stacks Queues Vectors, Linked Lists Trees (Including Balanced Trees) Priority Queues and Heaps Dictionaries and Hash Tables Spring 2014 CS 315 2 Two
Chapter 2: Basic Data Structures Basic Data Structures Stacks Queues Vectors, Linked Lists Trees (Including Balanced Trees) Priority Queues and Heaps Dictionaries and Hash Tables Spring 2014 CS 315 2 Two
A6-R3: DATA STRUCTURE THROUGH C LANGUAGE
 A6-R3: DATA STRUCTURE THROUGH C LANGUAGE NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions. 2. PART ONE is to be answered in the TEAR-OFF
A6-R3: DATA STRUCTURE THROUGH C LANGUAGE NOTE: 1. There are TWO PARTS in this Module/Paper. PART ONE contains FOUR questions and PART TWO contains FIVE questions. 2. PART ONE is to be answered in the TEAR-OFF
Priority Queues. T. M. Murali. January 23, T. M. Murali January 23, 2008 Priority Queues
 Priority Queues T. M. Murali January 23, 2008 Motivation: Sort a List of Numbers Sort INSTANCE: Nonempty list x 1, x 2,..., x n of integers. SOLUTION: A permutation y 1, y 2,..., y n of x 1, x 2,..., x
Priority Queues T. M. Murali January 23, 2008 Motivation: Sort a List of Numbers Sort INSTANCE: Nonempty list x 1, x 2,..., x n of integers. SOLUTION: A permutation y 1, y 2,..., y n of x 1, x 2,..., x
A Distribution-Sensitive Dictionary with Low Space Overhead
 A Distribution-Sensitive Dictionary with Low Space Overhead Prosenjit Bose, John Howat, and Pat Morin School of Computer Science, Carleton University 1125 Colonel By Dr., Ottawa, Ontario, CANADA, K1S 5B6
A Distribution-Sensitive Dictionary with Low Space Overhead Prosenjit Bose, John Howat, and Pat Morin School of Computer Science, Carleton University 1125 Colonel By Dr., Ottawa, Ontario, CANADA, K1S 5B6
Predecessor Data Structures. Philip Bille
 Predecessor Data Structures Philip Bille Outline Predecessor problem First tradeoffs Simple tries x-fast tries y-fast tries Predecessor Problem Predecessor Problem The predecessor problem: Maintain a set
Predecessor Data Structures Philip Bille Outline Predecessor problem First tradeoffs Simple tries x-fast tries y-fast tries Predecessor Problem Predecessor Problem The predecessor problem: Maintain a set
Lecture 5. Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs
 Lecture 5 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs Reading: Randomized Search Trees by Aragon & Seidel, Algorithmica 1996, http://sims.berkeley.edu/~aragon/pubs/rst96.pdf;
Lecture 5 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs Reading: Randomized Search Trees by Aragon & Seidel, Algorithmica 1996, http://sims.berkeley.edu/~aragon/pubs/rst96.pdf;
1. Covered basics of a simple design technique (Divideand-conquer) 2. Next, more sorting algorithms.
 Next 1. Covered basics of a simple design technique (Divideand-conquer) Ch. 2 of the text. 2. Next, more sorting algorithms. Sorting Switch from design paradigms to applications. Sorting and order statistics
Next 1. Covered basics of a simple design technique (Divideand-conquer) Ch. 2 of the text. 2. Next, more sorting algorithms. Sorting Switch from design paradigms to applications. Sorting and order statistics
/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Sorting lower bound and Linear-time sorting Date: 9/19/17
 601.433/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Sorting lower bound and Linear-time sorting Date: 9/19/17 5.1 Introduction You should all know a few ways of sorting in O(n log n)
601.433/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Sorting lower bound and Linear-time sorting Date: 9/19/17 5.1 Introduction You should all know a few ways of sorting in O(n log n)
Instructions. Definitions. Name: CMSC 341 Fall Question Points I. /12 II. /30 III. /10 IV. /12 V. /12 VI. /12 VII.
 CMSC 341 Fall 2013 Data Structures Final Exam B Name: Question Points I. /12 II. /30 III. /10 IV. /12 V. /12 VI. /12 VII. /12 TOTAL: /100 Instructions 1. This is a closed-book, closed-notes exam. 2. You
CMSC 341 Fall 2013 Data Structures Final Exam B Name: Question Points I. /12 II. /30 III. /10 IV. /12 V. /12 VI. /12 VII. /12 TOTAL: /100 Instructions 1. This is a closed-book, closed-notes exam. 2. You
Algorithms and Data Structures
 Algorithms and Data Structures CMPSC 465 LECTURES 11-12 Priority Queues and Heaps Adam Smith 1 Priority Queue ADT Dynamic set of pairs (key, data), called elements Supports operations: MakeNewPQ() Insert(S,x)
Algorithms and Data Structures CMPSC 465 LECTURES 11-12 Priority Queues and Heaps Adam Smith 1 Priority Queue ADT Dynamic set of pairs (key, data), called elements Supports operations: MakeNewPQ() Insert(S,x)
Data Structures and Algorithms Chapter 4
 Data Structures and Algorithms Chapter. About sorting algorithms. Heapsort Complete binary trees Heap data structure. Quicksort a popular algorithm very fast on average Previous Chapter Divide and conquer
Data Structures and Algorithms Chapter. About sorting algorithms. Heapsort Complete binary trees Heap data structure. Quicksort a popular algorithm very fast on average Previous Chapter Divide and conquer
Sorting and Selection
 Sorting and Selection Introduction Divide and Conquer Merge-Sort Quick-Sort Radix-Sort Bucket-Sort 10-1 Introduction Assuming we have a sequence S storing a list of keyelement entries. The key of the element
Sorting and Selection Introduction Divide and Conquer Merge-Sort Quick-Sort Radix-Sort Bucket-Sort 10-1 Introduction Assuming we have a sequence S storing a list of keyelement entries. The key of the element
Heaps. Heaps. A heap is a complete binary tree.
 A heap is a complete binary tree. 1 A max-heap is a complete binary tree in which the value in each internal node is greater than or equal to the values in the children of that node. A min-heap is defined
A heap is a complete binary tree. 1 A max-heap is a complete binary tree in which the value in each internal node is greater than or equal to the values in the children of that node. A min-heap is defined
CS-301 Data Structure. Tariq Hanif
 1. The tree data structure is a Linear data structure Non-linear data structure Graphical data structure Data structure like queue FINALTERM EXAMINATION Spring 2012 CS301- Data Structure 25-07-2012 2.
1. The tree data structure is a Linear data structure Non-linear data structure Graphical data structure Data structure like queue FINALTERM EXAMINATION Spring 2012 CS301- Data Structure 25-07-2012 2.
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, Merge Sort & Quick Sort
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Merge Sort & Quick Sort 1 Divide-and-Conquer Divide-and conquer is a general algorithm
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Merge Sort & Quick Sort 1 Divide-and-Conquer Divide-and conquer is a general algorithm
Algorithms and Applications
 Algorithms and Applications 1 Areas done in textbook: Sorting Algorithms Numerical Algorithms Image Processing Searching and Optimization 2 Chapter 10 Sorting Algorithms - rearranging a list of numbers
Algorithms and Applications 1 Areas done in textbook: Sorting Algorithms Numerical Algorithms Image Processing Searching and Optimization 2 Chapter 10 Sorting Algorithms - rearranging a list of numbers
Chapter 5 Data Structures Algorithm Theory WS 2016/17 Fabian Kuhn
 Chapter 5 Data Structures Algorithm Theory WS 06/ Fabian Kuhn Examples Dictionary: Operations: insert(key,value), delete(key), find(key) Implementations: Linked list: all operations take O(n) time (n:
Chapter 5 Data Structures Algorithm Theory WS 06/ Fabian Kuhn Examples Dictionary: Operations: insert(key,value), delete(key), find(key) Implementations: Linked list: all operations take O(n) time (n:
Treaps. 1 Binary Search Trees (BSTs) CSE341T/CSE549T 11/05/2014. Lecture 19
 CSE34T/CSE549T /05/04 Lecture 9 Treaps Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types
CSE34T/CSE549T /05/04 Lecture 9 Treaps Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types
The Union-Find Problem Is Linear
 The Union-Find Problem Is Linear Hantao Zhang Computer Science Department The University of Iowa Iowa City, IA 52242 hzhang@cs.uiowa.edu Abstract The union-find problem, also known as the disjoint set
The Union-Find Problem Is Linear Hantao Zhang Computer Science Department The University of Iowa Iowa City, IA 52242 hzhang@cs.uiowa.edu Abstract The union-find problem, also known as the disjoint set
CS301 - Data Structures Glossary By
 CS301 - Data Structures Glossary By Abstract Data Type : A set of data values and associated operations that are precisely specified independent of any particular implementation. Also known as ADT Algorithm
CS301 - Data Structures Glossary By Abstract Data Type : A set of data values and associated operations that are precisely specified independent of any particular implementation. Also known as ADT Algorithm
CS2 Algorithms and Data Structures Note 1
 CS2 Algorithms and Data Structures Note 1 Analysing Algorithms This thread of the course is concerned with the design and analysis of good algorithms and data structures. Intuitively speaking, an algorithm
CS2 Algorithms and Data Structures Note 1 Analysing Algorithms This thread of the course is concerned with the design and analysis of good algorithms and data structures. Intuitively speaking, an algorithm
9. Heap : Priority Queue
 9. Heap : Priority Queue Where We Are? Array Linked list Stack Queue Tree Binary Tree Heap Binary Search Tree Priority Queue Queue Queue operation is based on the order of arrivals of elements FIFO(First-In
9. Heap : Priority Queue Where We Are? Array Linked list Stack Queue Tree Binary Tree Heap Binary Search Tree Priority Queue Queue Queue operation is based on the order of arrivals of elements FIFO(First-In
6.856 Randomized Algorithms
 6.856 Randomized Algorithms David Karger Handout #4, September 21, 2002 Homework 1 Solutions Problem 1 MR 1.8. (a) The min-cut algorithm given in class works because at each step it is very unlikely (probability
6.856 Randomized Algorithms David Karger Handout #4, September 21, 2002 Homework 1 Solutions Problem 1 MR 1.8. (a) The min-cut algorithm given in class works because at each step it is very unlikely (probability
Priority Queues and Binary Heaps. See Chapter 21 of the text, pages
 Priority Queues and Binary Heaps See Chapter 21 of the text, pages 807-839. A priority queue is a queue-like data structure that assumes data is comparable in some way (or at least has some field on which
Priority Queues and Binary Heaps See Chapter 21 of the text, pages 807-839. A priority queue is a queue-like data structure that assumes data is comparable in some way (or at least has some field on which
Tweaking for Better Algorithmic Implementation
 Tweaking for Better Algorithmic Implementation Zirou Qiu, Ziping Liu, Xuesong Zhang Computer Science Department Southeast Missouri State University Cape Girardeau, MO, U. S. A. zqiu1s@semo.edu, zliu@semo.edu,
Tweaking for Better Algorithmic Implementation Zirou Qiu, Ziping Liu, Xuesong Zhang Computer Science Department Southeast Missouri State University Cape Girardeau, MO, U. S. A. zqiu1s@semo.edu, zliu@semo.edu,
Recall: Properties of B-Trees
 CSE 326 Lecture 10: B-Trees and Heaps It s lunch time what s cookin? B-Trees Insert/Delete Examples and Run Time Analysis Summary of Search Trees Introduction to Heaps and Priority Queues Covered in Chapters
CSE 326 Lecture 10: B-Trees and Heaps It s lunch time what s cookin? B-Trees Insert/Delete Examples and Run Time Analysis Summary of Search Trees Introduction to Heaps and Priority Queues Covered in Chapters
Computational Optimization ISE 407. Lecture 16. Dr. Ted Ralphs
 Computational Optimization ISE 407 Lecture 16 Dr. Ted Ralphs ISE 407 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms in
Computational Optimization ISE 407 Lecture 16 Dr. Ted Ralphs ISE 407 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms in
Course Review. Cpt S 223 Fall 2009
 Course Review Cpt S 223 Fall 2009 1 Final Exam When: Tuesday (12/15) 8-10am Where: in class Closed book, closed notes Comprehensive Material for preparation: Lecture slides & class notes Homeworks & program
Course Review Cpt S 223 Fall 2009 1 Final Exam When: Tuesday (12/15) 8-10am Where: in class Closed book, closed notes Comprehensive Material for preparation: Lecture slides & class notes Homeworks & program
(2,4) Trees. 2/22/2006 (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 2/22/2006 (2,4) Trees 1 Outline and Reading Multi-way search tree ( 10.4.1) Definition Search (2,4) tree ( 10.4.2) Definition Search Insertion Deletion Comparison of dictionary
(2,4) Trees 9 2 5 7 10 14 2/22/2006 (2,4) Trees 1 Outline and Reading Multi-way search tree ( 10.4.1) Definition Search (2,4) tree ( 10.4.2) Definition Search Insertion Deletion Comparison of dictionary
Data Structures and Algorithms
 Data Structures and Algorithms About the course (objectives, outline, recommended reading) Problem solving Notions of Algorithmics (growth of functions, efficiency, programming model, example analysis)
Data Structures and Algorithms About the course (objectives, outline, recommended reading) Problem solving Notions of Algorithmics (growth of functions, efficiency, programming model, example analysis)
ICS 691: Advanced Data Structures Spring Lecture 3
 ICS 691: Advanced Data Structures Spring 2016 Prof. Nodari Sitchinava Lecture 3 Scribe: Ben Karsin 1 Overview In the last lecture we started looking at self-adjusting data structures, specifically, move-to-front
ICS 691: Advanced Data Structures Spring 2016 Prof. Nodari Sitchinava Lecture 3 Scribe: Ben Karsin 1 Overview In the last lecture we started looking at self-adjusting data structures, specifically, move-to-front
Lecture 19 Apr 25, 2007
 6.851: Advanced Data Structures Spring 2007 Prof. Erik Demaine Lecture 19 Apr 25, 2007 Scribe: Aditya Rathnam 1 Overview Previously we worked in the RA or cell probe models, in which the cost of an algorithm
6.851: Advanced Data Structures Spring 2007 Prof. Erik Demaine Lecture 19 Apr 25, 2007 Scribe: Aditya Rathnam 1 Overview Previously we worked in the RA or cell probe models, in which the cost of an algorithm
Heaps and Priority Queues
 Unit 9, Part Heaps and Priority Queues Computer Science S-111 Harvard University David G. Sullivan, Ph.D. Priority Queue A priority queue (PQ) is a collection in which each item has an associated number
Unit 9, Part Heaps and Priority Queues Computer Science S-111 Harvard University David G. Sullivan, Ph.D. Priority Queue A priority queue (PQ) is a collection in which each item has an associated number
Algorithms and Data Structures for Mathematicians
 Algorithms and Data Structures for Mathematicians Lecture 5: Sorting Peter Kostolányi kostolanyi at fmph and so on Room M-258 26 October 2017 Sorting Algorithms Covered So Far Worst-case time complexity
Algorithms and Data Structures for Mathematicians Lecture 5: Sorting Peter Kostolányi kostolanyi at fmph and so on Room M-258 26 October 2017 Sorting Algorithms Covered So Far Worst-case time complexity
CE 221 Data Structures and Algorithms
 CE 2 Data Structures and Algorithms Chapter 6: Priority Queues (Binary Heaps) Text: Read Weiss, 6.1 6.3 Izmir University of Economics 1 A kind of queue Priority Queue (Heap) Dequeue gets element with the
CE 2 Data Structures and Algorithms Chapter 6: Priority Queues (Binary Heaps) Text: Read Weiss, 6.1 6.3 Izmir University of Economics 1 A kind of queue Priority Queue (Heap) Dequeue gets element with the
Binary Heaps. COL 106 Shweta Agrawal and Amit Kumar
 Binary Heaps COL Shweta Agrawal and Amit Kumar Revisiting FindMin Application: Find the smallest ( or highest priority) item quickly Operating system needs to schedule jobs according to priority instead
Binary Heaps COL Shweta Agrawal and Amit Kumar Revisiting FindMin Application: Find the smallest ( or highest priority) item quickly Operating system needs to schedule jobs according to priority instead
CSE 241 Class 17. Jeremy Buhler. October 28, Ordered collections supported both, plus total ordering operations (pred and succ)
 CSE 241 Class 17 Jeremy Buhler October 28, 2015 And now for something completely different! 1 A New Abstract Data Type So far, we ve described ordered and unordered collections. Unordered collections didn
CSE 241 Class 17 Jeremy Buhler October 28, 2015 And now for something completely different! 1 A New Abstract Data Type So far, we ve described ordered and unordered collections. Unordered collections didn
Outline. Definition. 2 Height-Balance. 3 Searches. 4 Rotations. 5 Insertion. 6 Deletions. 7 Reference. 1 Every node is either red or black.
 Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
