Chapter 3:- Divide and Conquer. Compiled By:- Sanjay Patel Assistant Professor, SVBIT.
|
|
|
- Abigail Harvey
- 5 years ago
- Views:
Transcription
1 Chapter 3:- Divide and Conquer Compiled By:- Assistant Professor, SVBIT.
2 Outline Introduction Multiplying large Integers Problem Problem Solving using divide and conquer algorithm - Binary Search Sorting (Merge Sort, Quick Sort), Matrix Multiplication, Exponential.
3 What is divide and conquer A general paradigm for algorithm design Three-step process: 1. Divide the problem into smaller problems. 2. Conquer by solving these problems. 3. Combine these results together.
4 Cont d. Many useful algorithms are recursive in structure: to solve a given problem, they call themselves recursively one or more times to deal with closely related sub problems. These algorithms typically follow a divide-andconquer approach: they break the problem into several sub problems that are similar to the original problem but smaller in size, solve the sub problems recursively, and then combine these solutions to create a solution to the original problem.
5 Cont d The divide-and-conquer paradigm involves three steps at each level of the recursion. Divide the problem into a number of sub problems. Conquer the sub problems by solving them recursively. If the sub problem sizes are small enough, however, just solve the sub problems in a straightforward manner. Combine the solutions to the sub problems into the solution for the original problem.
6 Cont d.. a problem of size n subproblem 1 of size n/2 subproblem 2 of size n/2 Solution to Sub problem 1 Solution to Sub problem 2 Solution to the original problem It general leads to a recursive algorithm!
7 Multiplying large integers numbers A small example, A B where A = 2135 and B = 4014 A = ( ), B = ( ) So, A B = ( ) ( ) = ( )
8 Generalize the Formula We can generalize the formula for multiplication of large number, C = a * b C = c2 10 n + c1 10 n/2 + c0 Where n is total number of digits in the integer c2 = a1 * b1 C0 = a0 * b0 c1 = (a1 + a0 ) * (b1+ b0 ) - ( c2+ c0 )
9 Example.. Perform multiplication with the formula 42 * 34. C= a * b so, 42 * 34 a1= 4,, a0 = 2 b1 = 3, b0= 4 Now, we have to find, c0, C1, c2.. c2 = a1 * b1 =4 * 3 = 12 C0 = a0 * b0 =2 * 4 = 8 c1 = (a1 + a0 ) * (b1+ b0 ) - ( c2+ c0 ) = (4+2) * (3+4) (12+8) = 22
10 Cont d C = c c1 10 2/2 + c0 = 12 * * = = 1428 C = a * b 1428= a * b
11 Another example Perform multiplication 0981 * 1234 C= a * b = 0981 * 1234 a1=09, a0=81, b1=12, b0= 34
12 Cont d So, c2 = 108 c0 = 2754 c1 = 1278 C = c c1 10 4/2 + c0 = 108 * * =
13 Another method Multiply by solve by divide and conquer method * 0987 = * 6543 = * 0987 = * 6543 =
14 Cont d
15 à la russe method 63 * 123 by à la russe rule Answer = = 7749
16 Another Example 64 * 125 by à la russe rule Answer= 8000
17 Another example Answer = =
18 Analysis In this method there are 3 multiplication operation This is the case for two digit multiplication, now if there are n digit to be multiplied, then multiplication of n digits require 3 multiplication of n/2 digit numbers. Hence, recurrence relation C(n) = 3 C(n/2) where n>1 C(n)= 1 where n=1 After solving this recurrence equation with backward substitution method, C(n) = 3 log 2 n = n log 2 3 so, we will get C(n) ~ n 1.5
19 Sorting Merge Quick
20 Merge Sort Divide into two halves A FirstPart SecondPart Recursively sort FirstPart SecondPart Merge A is sorted!
21 Cont d The merge sort algorithm closely follows the divideand-conquer paradigm. Intuitively, it operates as follows. Divide: Divide the n-element sequence to be sorted into two subsequences of n/2 elements each. Conquer: Sort the two subsequences recursively using merge sort. Combine: Merge the two sorted subsequences to produce the sorted answer.
22 Example
23 Cont d
24 Cont d
25 Cont d
26 Cont d
27 Cont d
28 Cont d
29 Cont d
30 Cont d
31 Cont d
32 Cont d
33 Cont d
34 Cont d
35 Cont d
36 Cont d
37 Cont d
38 Cont d
39 Cont d
40 Cont d
41 Cont d
42 Cont d
43 Cont d
44 Another approach
45 Cont d Merge
46 Cont d Merge
47 Cont d Merge
48 Cont d Merge
49 Cont d Merge
50 Cont d Merge
51 Cont d Merge
52 Cont d Merge
53 Cont d Merge
54 Another example
55 Cont d
56 Cont d
57 Cont d
58 Cont d
59 Cont d
60 Cont d
61 Cont d
62 Cont d
63 Cont d
64 Analysis We can obtain the time complexity of merge sort. T(n) = T(n/2) + T(n/2) + cn Time taken by left sub list to get sorted Time taken by right sub list to get sorted Time taken for combining two sub list T(n)= 2 T(n/2) + cn with T(1)= 0 As per master theorem. a=2, b=2 and d=1 So, T(n)= (n d log n) Hence, the time complexity of the merge sort is (nlog n)
65 Algorithm.. If(low < high) then { mid ( low + high ) / 2 Merge sort(a,low,mid) Merge sort(a,mid+1,high) Combine(A,low,mid,high) } // spilt the list //first sub list //second sub list // merging of two sub list
66 Cont d.. Algorithm Combine( A[0.n-1]) K low // k as index for array temp i low // i as index for left sublist of array A J mid+1 // J as index for right sublist of array A
67 Cont d.. While(I <= mid and J<= high) do If (A[i] <= A[J]) then // if smaller element is present in left sub list { // copy that smaller element to temp array temp[k] A[i] i i+1 k k+1 } else // smaller element is present in right sub list { // copy that smaller element in temp array temp[k] A[J] J J+1 k k+1 } }
68 Cont d.. // copy remaining element of left sub list to temp While(I <= mid) do { temp[k] A[i] i i+1 k k+1 } // copy remaining element of right sub list to temp While(J <= high) do { temp[k] A[J] J J+1 k k+1 }
69 Time complexity ( Merge sort ) Best case Average case Worst case Θ( n log2n) Θ( n log2n) Θ(n log2n)
70 Implementation There are two basic ways to implement merge sort: In Place: Merging is done with only the input array Pro: Requires only the space needed to hold the array Con: Takes longer to merge because if the next element is in the right side then all of the elements must be moved down. Double Storage: Merging is done with a temporary array of the same size as the input array. Pro: Faster than In Place since the temp array holds the resulting array until both left and right sides are merged into the temp array, then the temp array is appended over the input array. Con: The memory requirement is doubled.
71 Cont d.. There are other variants of Merge Sorts including k-way merge sorting, but the common variant is the Double Memory Merge Sort. Though the running time is O(N logn) and runs much faster than insertion sort and bubble sort, merge sort s large memory demands makes it not very practical for main memory sorting. Important things to remember for the Midterm: Best Case, Average Case, and Worst Case = O(N logn) Storage Requirement: Double that needed to hold the array to be sorted.
72 Quick sort Quick Sort is an algorithm based on the DIVIDE- AND-CONQUER paradigm that selects a pivot element and reorders the given list in such a way that all elements smaller to it are on one side and those bigger than it are on the other. Then the sub lists are recursively sorted until the list gets completely sorted. The time complexity of this algorithm is O (n log n).
73 Advantages of quick sort Pros: 1) One advantage of parallel quick sort over other parallel sort algorithms is that no synchronization is required. A new thread is started as soon as a sub list is available for it to work on and it does not communicate with other threads. When all threads complete, the sort is done. 2) All comparisons are being done with a single pivot value, which can be stored in a register. 3) The list is being traversed sequentially, which produces very good locality of reference and cache behavior for arrays.
74 Disadvantages of quick sort Cons: 1) Auxiliary space used in the average case for implementing recursive function calls is O (log n) and hence proves to be a bit space costly, especially when it comes to large data sets. 2) Its worst case has a time complexity of O (n2) which can prove very fatal for large data sets. Competitive sorting algorithms
75 Example Lets understand this algorithm with the help of some example Consider pivot element= 50
76 Example If an unsorted list (represented as vector a) originally contains: we might select the item in the middle position, a[5], as the pivot, which is 8 in our illustration. Our process would then put all values less than 8 on the left side and all values greater than 8 on the right side. This first subdivision produces Now, each sublist is subdivided in exactly the same manner. This process continues until all sublists are in order. The list is then sorted. This is a recursive process.
77 Cont d.. We choose the value in the middle for the pivot. As in binary search, the index of this value is found by (first + last) / 2, where first and last are the indices of the initial and final items in the vector representing the list. We then identify a left_arrow and right_arrow on the far left and far right, respectively. This can be envisioned as: where left_arrow and right_arrow initially represent the lowest and highest indices of the vector items.
78 Cont d.. Starting on the right, the right_arrow is moved left until a value less than or equal to the pivot is encountered. This produces In a similar manner, left_arrow is moved right until a value greater than or equal to the pivot is encountered. This is the situation just encountered. Now the contents of the two vector items are swapped to produce Mr. Dave Clausen 78
79 Cont d.. We continue by moving right_arrow left to produce and moving left_arrow right yields These values are exchanged to produce
80 Cont d.. This process stops when left_arrow > right_arrow is TRUE. Since this is still FALSE at this point, the next right_arrow move produces and the left_arrow move to the right yields
81 Cont d.. Because we are looking for a value greater than or equal to pivot when moving left, left_arrow stops moving and an exchange is made to produce Notice that the pivot, 8, has been exchanged to occupy a new position. This is acceptable because pivot is the value of the item, not the index. As before, right_arrow is moved left and left_arrow is moved right to produce
82 Cont d.. Since right_arrow < left_arrow is TRUE, the first subdivision is complete. At this stage, numbers smaller than pivot are on the left side and numbers larger than pivot are on the right side. This produces two sublists that can be envisioned as Each sublist can now be sorted by the same function. This would require a recursive call to the sorting function. In each case, the vector is passed as a parameter together with the right and left indices for the appropriate sublist.
83 Algorithm Pivot A[low] i low j high While(i<=j) do { while(a[i] <= pivot) do i= i+1 while ( A[J] >= pivot) do j= j-1 } Swap(A[low],A[j]) //when i crosses j swap A[low] and A[J]
84 Quick-Sort: Best Case Even Partition n cn n/2 n/2 2 cn/2 = cn n/4 n/4 n/4 n/4 4 c/4 = cn log n levels n/3 3c = cn Total time: (nlogn)
85 Analysis We can obtain the time complexity of quick sort. C(n) = C(n/2) + C(n/2) + n Time required to sort left sub array Time required to sort right sub array Time taken for partitioning the sub array C(n)= 2 C(n/2) + n with T(1)= 0 As per master theorem. a=2, b=2 and d=1 So, T(n)= (n d log n) Hence, the time complexity of the quick sort is (n log n)
86 Analysis with substitution method C(n)= 2 C(n/2) + n put n=2 k C(2 k ) = 2C(2 k -1 ) + 2 k.(1) Now, k= k-1 C(2 k-1 ) = 2C(2 k -2 ) + 2 k -1 Put the result of C(2 k-1 ) in equation (1) C(2 k ) = 2[2C(2 k -2 ) + 2 k -1 ] + 2 k = 2 2 C(2 k -2 ) + 2 * 2 k k = 2 2 C(2 k -2 ) + 2 k + 2 k = 2 2 C(2 k -2 ) + 2* 2 k ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
87 Cont d.. Hence above equation becomes, with C(1)= 0 C(2 k ) = 2 k C(2 k -k ) + K * 2 k = 2 k C(2 0 ) + K * 2 k = 2 k C(1) + K * 2 k = 2 k * 0 + K * 2 k As we have assumed n= 2 k Apply logarithm (base 2 ) on both side log2n = log22 k = k log22 = k (1)
88 Cont d.. K= log2n, n= 2 k C(2 k ) = 2 k * 0 + K * 2 k C(n)= n * 0 + log2n * n = n log2n thus, it is provide the best case time complexity of quick sort Θ(n log2n)
89 Quick-Sort: Worst Case Unbalanced Partition n cn n-1 c(n-1) n-2 c(n-2) Happens only if input is sortd input is reversely sorted 3 2 3c 2c Total time: (n 2 )
90 Cont d.. C(n)= C(n-1)+ n C(n)= n + (n-1) + (n-2) As we know, n= n(n+1)/2 = n(n+1)/2 = n 2 The time complexity of worst case of the quick sort is (n 2 )
91 Time complexity (quick sort) Best case Average case Worst case Θ(n log2n) Θ(n log2n) Θ(n 2 )
92 Binary Search Binary search is an efficient searching method. While searching the elements using this method the most essential thing is that the elements in the array should be sorted one. Let A[m] be the mid element of array A. Then there are three condition to be tested.(key =searched element). If KEY=A[m] then desired element in the present list. Otherwise if KEY<A[m] then search the left sub list. Otherwise if KEY>A[m] then search the right sub list
93 Example The key element is 60. Apply the formula m = (low + high)/2 so A[m] = KEY check the condition = (0+6)/2 = 3 so, A[3] = KEY. A[3] = 40
94 Cont d Now, the right sub list is Now we will again divide the list and check the mid element. m = (low + high)/2 = (4+6)/2 = 5 A[5] = KEY. A[5] = 60
95 Algorithm Low 0 High n-1 while(low<high) do { m (low + high)/2 // mid of the array is obtained if(key=a[m]) then return m else if (KEY<A[m]) then high m-1 // search left sub list else low m+1 // right sub list } return -1 // if not present in the list
96 Analysis(worst case) C(n) = C(n/2) + 1 Time required to compare left sub list or right sub list One comparison made with middle element So Recurrence relation C(n)= C(n/2) +1 Now put n= 2 k C(2 k ) = C(2 k /2) + 1 = C(2 k -1 ) + 1 Solve this equation with backward substitution
97 Cont d.. C(2 k ) = C(2 k -1 ) + 1.(1) Now, k= k-1 C(2 k-1 ) = C(2 k -2 ) + 1 Put the result of C(2 k-1 ) in equation (1) C(2 k ) = [C(2 k -2 ) + 1 ] (2) Now, k= k-2 C(2 k-2 ) = C(2 k -3 ) + 1 Put the result of C(2 k-2 ) in equation (2) C(2 k ) = [C(2 k -3 ) +1] ;;;;;;;;;;;;;;;;;;;;;;; C(2 k ) = C(2 k -k ) + k
98 Cont d C(2 k ) = C(2 k -k ) + k = C(2 0 ) + k = C(1) + k C(1)= 1 = 1 + k As we have assumed n= 2 k Apply logarithm (base 2 ) on both side log2n = log22 k = k log22 = k (1)
99 Cont d K= log2n Now, C(n) = 1 + k = 1 + log2n The worst case time complexity of binary search is (log2n)
100 Time complexity Best case Average case Worst case Θ(1) Θ(log2N) Θ(log2N)
101 pros and cons Binary search Advantage :- Binary search is an optimal searching algorithm using which we can search the desired element very efficiently. Disadvantage:- This algorithm requires the list to be sorted. Then only this method is applicable. Application:- used to search desired record from database and for solving nonlinear equation with one unknown this method is used
102 Sequential vs. Binary search technique Sequential Technique This is the simple technique of searching an element This technique does not require the list to be sorted Every element of the list may get compared with the key element The worst case time complexity of this technique is O(n) Binary search technique This is the efficient technique of searching an element This technique requires the list to be sorted. Then only this method is applicable Only the mid element of the list is compared with key element The worst case time complexity of this technique is O(log n)
103 Matrix multiplication Suppose, we want to multiply two matrices A and B each size of N. There are total 8 multiplication and 4 addition.
104 Matrix multiplication Brute-force algorithm c 00 c 01 a 00 a 01 b 00 b 01 = * c 10 c 11 a 10 a 11 b 10 b 11 = a 00 * b 00 + a 01 * b 10 a 00 * b 01 + a 01 * b 11 a 10 * b 00 + a 11 * b 10 a 10 * b 01 + a 11 * b 11 8 multiplications 4 additions
105 Strassen matrix multiplication Strassen showed that 2 * 2 matrix multiplication can be accomplished in 7 multiplication and 18 addition or subtraction. Divide:- Divide matrices into sub matrices Conquer:- Use group of matrix multiplication equation Combine:- Recursively multiply sub matrices and get the final result of multiplication after performing required addition and subtraction.
106 Cont d.. P 1 = (A 11 + A 22 )(B 11 +B 22 ) P 2 = (A 21 + A 22 ) * B 11 P 3 = A 11 * (B 12 - B 22 ) P 4 = A 22 * (B 21 - B 11 ) P 5 = (A 11 + A 12 ) * B 22 P 6 = (A 21 - A 11 ) * (B 11 + B 12 ) P 7 = (A 12 - A 22 ) * (B 21 + B 22 ) C 11 = P 1 + P 4 - P 5 + P 7 C 12 = P 3 + P 5 C 21 = P 2 + P 4 C 22 = P 1 + P 3 - P 2 + P 6
107 Cont d.. C 11 = P 1 + P 4 - P 5 + P 7 = (A 11 + A 22 )(B 11 +B 22 ) + A 22 * (B 21 - B 11 ) - (A 11 + A 12 ) * B 22 + (A 12 - A 22 ) * (B 21 + B 22 ) = A 11 B 11 + A 11 B 22 + A 22 B 11 + A 22 B 22 + A 22 B 21 A 22 B 11 - A 11 B 22 -A 12 B 22 + A 12 B 21 + A 12 B 22 A 22 B 21 A 22 B 22 = A 11 B 11 + A 12 B 21
108 Example A= B= Implement Strassen's matrix multiplication on A & B
109 Cont d A11 A12 B11 B12 A21 A22 B21 B
110 Cont d.. P 1 = (A 11 + A 22 )(B 11 +B 22 ) P 2 = (A 21 + A 22 ) * B
111 Cont d.. P 3 = A 11 * (B 12 - B 22 ) P 4 = A 22 * (B 21 - B 11 )
112 Cont d.. P 5 = (A 11 + A 12 ) * B P 6 = (A 21 - A 11 ) * (B 11 + B 12 )
113 Cont d.. P 7 = (A 12 - A 22 ) * (B 21 + B 22 )
114 Cont d.. C 11 = P 1 + P 4 - P 5 + P C 12 = P 2 + P
115 Cont d.. C 21 = P 2 + P C 22 = P 1 + P 3 - P 2 + P
116 Cont d.. Thus the final product matrix C will be
CSC Design and Analysis of Algorithms
 CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conquer Algorithm Design Technique Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide a problem instance into two
CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conquer Algorithm Design Technique Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide a problem instance into two
17/05/2018. Outline. Outline. Divide and Conquer. Control Abstraction for Divide &Conquer. Outline. Module 2: Divide and Conquer
 Module 2: Divide and Conquer Divide and Conquer Control Abstraction for Divide &Conquer 1 Recurrence equation for Divide and Conquer: If the size of problem p is n and the sizes of the k sub problems are
Module 2: Divide and Conquer Divide and Conquer Control Abstraction for Divide &Conquer 1 Recurrence equation for Divide and Conquer: If the size of problem p is n and the sizes of the k sub problems are
UNIT-2. Problem of size n. Sub-problem 1 size n/2. Sub-problem 2 size n/2. Solution to the original problem
 Divide-and-conquer method: Divide-and-conquer is probably the best known general algorithm design technique. The principle behind the Divide-and-conquer algorithm design technique is that it is easier
Divide-and-conquer method: Divide-and-conquer is probably the best known general algorithm design technique. The principle behind the Divide-and-conquer algorithm design technique is that it is easier
CSC Design and Analysis of Algorithms. Lecture 6. Divide and Conquer Algorithm Design Technique. Divide-and-Conquer
 CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conquer Algorithm Design Technique Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide a problem instance into two
CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conquer Algorithm Design Technique Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide a problem instance into two
Chapter 4. Divide-and-Conquer. Copyright 2007 Pearson Addison-Wesley. All rights reserved.
 Chapter 4 Divide-and-Conquer Copyright 2007 Pearson Addison-Wesley. All rights reserved. Divide-and-Conquer The most-well known algorithm design strategy: 2. Divide instance of problem into two or more
Chapter 4 Divide-and-Conquer Copyright 2007 Pearson Addison-Wesley. All rights reserved. Divide-and-Conquer The most-well known algorithm design strategy: 2. Divide instance of problem into two or more
DIVIDE & CONQUER. Problem of size n. Solution to sub problem 1
 DIVIDE & CONQUER Definition: Divide & conquer is a general algorithm design strategy with a general plan as follows: 1. DIVIDE: A problem s instance is divided into several smaller instances of the same
DIVIDE & CONQUER Definition: Divide & conquer is a general algorithm design strategy with a general plan as follows: 1. DIVIDE: A problem s instance is divided into several smaller instances of the same
Divide-and-Conquer. The most-well known algorithm design strategy: smaller instances. combining these solutions
 Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances recursively 3. Obtain solution to original
Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances recursively 3. Obtain solution to original
Mergesort again. 1. Split the list into two equal parts
 Quicksort Mergesort again 1. Split the list into two equal parts 5 3 9 2 8 7 3 2 1 4 5 3 9 2 8 7 3 2 1 4 Mergesort again 2. Recursively mergesort the two parts 5 3 9 2 8 7 3 2 1 4 2 3 5 8 9 1 2 3 4 7 Mergesort
Quicksort Mergesort again 1. Split the list into two equal parts 5 3 9 2 8 7 3 2 1 4 5 3 9 2 8 7 3 2 1 4 Mergesort again 2. Recursively mergesort the two parts 5 3 9 2 8 7 3 2 1 4 2 3 5 8 9 1 2 3 4 7 Mergesort
Divide-and-Conquer. Dr. Yingwu Zhu
 Divide-and-Conquer Dr. Yingwu Zhu Divide-and-Conquer The most-well known algorithm design technique: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances independently
Divide-and-Conquer Dr. Yingwu Zhu Divide-and-Conquer The most-well known algorithm design technique: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances independently
Computer Science 385 Analysis of Algorithms Siena College Spring Topic Notes: Divide and Conquer
 Computer Science 385 Analysis of Algorithms Siena College Spring 2011 Topic Notes: Divide and Conquer Divide and-conquer is a very common and very powerful algorithm design technique. The general idea:
Computer Science 385 Analysis of Algorithms Siena College Spring 2011 Topic Notes: Divide and Conquer Divide and-conquer is a very common and very powerful algorithm design technique. The general idea:
The divide-and-conquer paradigm involves three steps at each level of the recursion: Divide the problem into a number of subproblems.
 2.3 Designing algorithms There are many ways to design algorithms. Insertion sort uses an incremental approach: having sorted the subarray A[1 j - 1], we insert the single element A[j] into its proper
2.3 Designing algorithms There are many ways to design algorithms. Insertion sort uses an incremental approach: having sorted the subarray A[1 j - 1], we insert the single element A[j] into its proper
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, Merge Sort & Quick Sort
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Merge Sort & Quick Sort 1 Divide-and-Conquer Divide-and conquer is a general algorithm
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Merge Sort & Quick Sort 1 Divide-and-Conquer Divide-and conquer is a general algorithm
Quicksort. Repeat the process recursively for the left- and rightsub-blocks.
 Quicksort As the name implies, this is the fastest known sorting algorithm in practice. It is excellent for average input but bad for the worst-case input. (you will see later). Basic idea: (another divide-and-conquer
Quicksort As the name implies, this is the fastest known sorting algorithm in practice. It is excellent for average input but bad for the worst-case input. (you will see later). Basic idea: (another divide-and-conquer
ECE 2574: Data Structures and Algorithms - Basic Sorting Algorithms. C. L. Wyatt
 ECE 2574: Data Structures and Algorithms - Basic Sorting Algorithms C. L. Wyatt Today we will continue looking at sorting algorithms Bubble sort Insertion sort Merge sort Quick sort Common Sorting Algorithms
ECE 2574: Data Structures and Algorithms - Basic Sorting Algorithms C. L. Wyatt Today we will continue looking at sorting algorithms Bubble sort Insertion sort Merge sort Quick sort Common Sorting Algorithms
Analysis of Algorithms. Unit 4 - Analysis of well known Algorithms
 Analysis of Algorithms Unit 4 - Analysis of well known Algorithms 1 Analysis of well known Algorithms Brute Force Algorithms Greedy Algorithms Divide and Conquer Algorithms Decrease and Conquer Algorithms
Analysis of Algorithms Unit 4 - Analysis of well known Algorithms 1 Analysis of well known Algorithms Brute Force Algorithms Greedy Algorithms Divide and Conquer Algorithms Decrease and Conquer Algorithms
2/26/2016. Divide and Conquer. Chapter 6. The Divide and Conquer Paradigm
 Divide and Conquer Chapter 6 Divide and Conquer A divide and conquer algorithm divides the problem instance into a number of subinstances (in most cases 2), recursively solves each subinsance separately,
Divide and Conquer Chapter 6 Divide and Conquer A divide and conquer algorithm divides the problem instance into a number of subinstances (in most cases 2), recursively solves each subinsance separately,
CS Divide and Conquer
 CS483-07 Divide and Conquer Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 1:30pm - 2:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/ lifei/teaching/cs483_fall07/
CS483-07 Divide and Conquer Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 1:30pm - 2:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/ lifei/teaching/cs483_fall07/
We can use a max-heap to sort data.
 Sorting 7B N log N Sorts 1 Heap Sort We can use a max-heap to sort data. Convert an array to a max-heap. Remove the root from the heap and store it in its proper position in the same array. Repeat until
Sorting 7B N log N Sorts 1 Heap Sort We can use a max-heap to sort data. Convert an array to a max-heap. Remove the root from the heap and store it in its proper position in the same array. Repeat until
Module 2: Classical Algorithm Design Techniques
 Module 2: Classical Algorithm Design Techniques Dr. Natarajan Meghanathan Associate Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu Module
Module 2: Classical Algorithm Design Techniques Dr. Natarajan Meghanathan Associate Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu Module
Divide & Conquer. 2. Conquer the sub-problems by solving them recursively. 1. Divide the problem into number of sub-problems
 Divide & Conquer Divide & Conquer The Divide & Conquer approach breaks down the problem into multiple smaller sub-problems, solves the sub-problems recursively, then combines the solutions of the sub-problems
Divide & Conquer Divide & Conquer The Divide & Conquer approach breaks down the problem into multiple smaller sub-problems, solves the sub-problems recursively, then combines the solutions of the sub-problems
Sorting. Bubble Sort. Pseudo Code for Bubble Sorting: Sorting is ordering a list of elements.
 Sorting Sorting is ordering a list of elements. Types of sorting: There are many types of algorithms exist based on the following criteria: Based on Complexity Based on Memory usage (Internal & External
Sorting Sorting is ordering a list of elements. Types of sorting: There are many types of algorithms exist based on the following criteria: Based on Complexity Based on Memory usage (Internal & External
Quicksort (Weiss chapter 8.6)
 Quicksort (Weiss chapter 8.6) Recap of before Easter We saw a load of sorting algorithms, including mergesort To mergesort a list: Split the list into two halves Recursively mergesort the two halves Merge
Quicksort (Weiss chapter 8.6) Recap of before Easter We saw a load of sorting algorithms, including mergesort To mergesort a list: Split the list into two halves Recursively mergesort the two halves Merge
Lecture 19 Sorting Goodrich, Tamassia
 Lecture 19 Sorting 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 2004 Goodrich, Tamassia Outline Review 3 simple sorting algorithms: 1. selection Sort (in previous course) 2. insertion Sort (in previous
Lecture 19 Sorting 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 2004 Goodrich, Tamassia Outline Review 3 simple sorting algorithms: 1. selection Sort (in previous course) 2. insertion Sort (in previous
SAMPLE OF THE STUDY MATERIAL PART OF CHAPTER 6. Sorting Algorithms
 SAMPLE OF THE STUDY MATERIAL PART OF CHAPTER 6 6.0 Introduction Sorting algorithms used in computer science are often classified by: Computational complexity (worst, average and best behavior) of element
SAMPLE OF THE STUDY MATERIAL PART OF CHAPTER 6 6.0 Introduction Sorting algorithms used in computer science are often classified by: Computational complexity (worst, average and best behavior) of element
Divide and Conquer. Algorithm Fall Semester
 Divide and Conquer Algorithm 2014 Fall Semester Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances
Divide and Conquer Algorithm 2014 Fall Semester Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances
Unit-2 Divide and conquer 2016
 2 Divide and conquer Overview, Structure of divide-and-conquer algorithms, binary search, quick sort, Strassen multiplication. 13% 05 Divide-and- conquer The Divide and Conquer Paradigm, is a method of
2 Divide and conquer Overview, Structure of divide-and-conquer algorithms, binary search, quick sort, Strassen multiplication. 13% 05 Divide-and- conquer The Divide and Conquer Paradigm, is a method of
Lecture 2: Getting Started
 Lecture 2: Getting Started Insertion Sort Our first algorithm is Insertion Sort Solves the sorting problem Input: A sequence of n numbers a 1, a 2,..., a n. Output: A permutation (reordering) a 1, a 2,...,
Lecture 2: Getting Started Insertion Sort Our first algorithm is Insertion Sort Solves the sorting problem Input: A sequence of n numbers a 1, a 2,..., a n. Output: A permutation (reordering) a 1, a 2,...,
CS S-11 Sorting in Θ(nlgn) 1. Base Case: A list of length 1 or length 0 is already sorted. Recursive Case:
 CS245-2015S-11 Sorting in Θ(nlgn) 1 11-0: Merge Sort Recursive Sorting Base Case: A list of length 1 or length 0 is already sorted Recursive Case: Split the list in half Recursively sort two halves Merge
CS245-2015S-11 Sorting in Θ(nlgn) 1 11-0: Merge Sort Recursive Sorting Base Case: A list of length 1 or length 0 is already sorted Recursive Case: Split the list in half Recursively sort two halves Merge
Sorting. There exist sorting algorithms which have shown to be more efficient in practice.
 Sorting Next to storing and retrieving data, sorting of data is one of the more common algorithmic tasks, with many different ways to perform it. Whenever we perform a web search and/or view statistics
Sorting Next to storing and retrieving data, sorting of data is one of the more common algorithmic tasks, with many different ways to perform it. Whenever we perform a web search and/or view statistics
Introduction to Computers and Programming. Today
 Introduction to Computers and Programming Prof. I. K. Lundqvist Lecture 10 April 8 2004 Today How to determine Big-O Compare data structures and algorithms Sorting algorithms 2 How to determine Big-O Partition
Introduction to Computers and Programming Prof. I. K. Lundqvist Lecture 10 April 8 2004 Today How to determine Big-O Compare data structures and algorithms Sorting algorithms 2 How to determine Big-O Partition
Divide-and-Conquer. Divide-and conquer is a general algorithm design paradigm:
 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 2014 Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9
Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 2014 Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9
CSC Design and Analysis of Algorithms. Lecture 5. Decrease and Conquer Algorithm Design Technique. Decrease-and-Conquer
 CSC 8301- Design and Analysis of Algorithms Lecture 5 Decrease and Conquer Algorithm Design Technique Decrease-and-Conquer This algorithm design technique is based on exploiting a relationship between
CSC 8301- Design and Analysis of Algorithms Lecture 5 Decrease and Conquer Algorithm Design Technique Decrease-and-Conquer This algorithm design technique is based on exploiting a relationship between
Problem. Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all. 1 i j n.
![Problem. Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all. 1 i j n. Problem. Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all. 1 i j n.](/thumbs/84/89326706.jpg) Problem 5. Sorting Simple Sorting, Quicksort, Mergesort Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all 1 i j n. 98 99 Selection Sort
Problem 5. Sorting Simple Sorting, Quicksort, Mergesort Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all 1 i j n. 98 99 Selection Sort
Lecture 7. Transform-and-Conquer
 Lecture 7 Transform-and-Conquer 6-1 Transform and Conquer This group of techniques solves a problem by a transformation to a simpler/more convenient instance of the same problem (instance simplification)
Lecture 7 Transform-and-Conquer 6-1 Transform and Conquer This group of techniques solves a problem by a transformation to a simpler/more convenient instance of the same problem (instance simplification)
Multiple-choice (35 pt.)
 CS 161 Practice Midterm I Summer 2018 Released: 7/21/18 Multiple-choice (35 pt.) 1. (2 pt.) Which of the following asymptotic bounds describe the function f(n) = n 3? The bounds do not necessarily need
CS 161 Practice Midterm I Summer 2018 Released: 7/21/18 Multiple-choice (35 pt.) 1. (2 pt.) Which of the following asymptotic bounds describe the function f(n) = n 3? The bounds do not necessarily need
Divide and Conquer. Algorithm D-and-C(n: input size)
 Divide and Conquer Algorithm D-and-C(n: input size) if n n 0 /* small size problem*/ Solve problem without futher sub-division; else Divide into m sub-problems; Conquer the sub-problems by solving them
Divide and Conquer Algorithm D-and-C(n: input size) if n n 0 /* small size problem*/ Solve problem without futher sub-division; else Divide into m sub-problems; Conquer the sub-problems by solving them
IS 709/809: Computational Methods in IS Research. Algorithm Analysis (Sorting)
 IS 709/809: Computational Methods in IS Research Algorithm Analysis (Sorting) Nirmalya Roy Department of Information Systems University of Maryland Baltimore County www.umbc.edu Sorting Problem Given an
IS 709/809: Computational Methods in IS Research Algorithm Analysis (Sorting) Nirmalya Roy Department of Information Systems University of Maryland Baltimore County www.umbc.edu Sorting Problem Given an
CS Divide and Conquer
 CS483-07 Divide and Conquer Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 1:30pm - 2:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/ lifei/teaching/cs483_fall07/
CS483-07 Divide and Conquer Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 1:30pm - 2:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/ lifei/teaching/cs483_fall07/
CSCI 104 Log Structured Merge Trees. Mark Redekopp
 1 CSCI 10 Log Structured Merge Trees Mark Redekopp Series Summation Review Let n = 1 + + + + k = σk i=0 n = k+1-1 i. What is n? What is log (1) + log () + log () + log (8)++ log ( k ) = 0 + 1 + + 3+ +
1 CSCI 10 Log Structured Merge Trees Mark Redekopp Series Summation Review Let n = 1 + + + + k = σk i=0 n = k+1-1 i. What is n? What is log (1) + log () + log () + log (8)++ log ( k ) = 0 + 1 + + 3+ +
CSC Design and Analysis of Algorithms
 CSC : Lecture 7 CSC - Design and Analysis of Algorithms Lecture 7 Transform and Conquer I Algorithm Design Technique CSC : Lecture 7 Transform and Conquer This group of techniques solves a problem by a
CSC : Lecture 7 CSC - Design and Analysis of Algorithms Lecture 7 Transform and Conquer I Algorithm Design Technique CSC : Lecture 7 Transform and Conquer This group of techniques solves a problem by a
Searching, Sorting. part 1
 Searching, Sorting part 1 Week 3 Objectives Searching: binary search Comparison-based search: running time bound Sorting: bubble, selection, insertion, merge Sorting: Heapsort Comparison-based sorting
Searching, Sorting part 1 Week 3 Objectives Searching: binary search Comparison-based search: running time bound Sorting: bubble, selection, insertion, merge Sorting: Heapsort Comparison-based sorting
Divide and Conquer 4-0
 Divide and Conquer 4-0 Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances recursively 3. Obtain
Divide and Conquer 4-0 Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances recursively 3. Obtain
CSC Design and Analysis of Algorithms. Lecture 7. Transform and Conquer I Algorithm Design Technique. Transform and Conquer
 // CSC - Design and Analysis of Algorithms Lecture 7 Transform and Conquer I Algorithm Design Technique Transform and Conquer This group of techniques solves a problem by a transformation to a simpler/more
// CSC - Design and Analysis of Algorithms Lecture 7 Transform and Conquer I Algorithm Design Technique Transform and Conquer This group of techniques solves a problem by a transformation to a simpler/more
PROGRAM EFFICIENCY & COMPLEXITY ANALYSIS
 Lecture 03-04 PROGRAM EFFICIENCY & COMPLEXITY ANALYSIS By: Dr. Zahoor Jan 1 ALGORITHM DEFINITION A finite set of statements that guarantees an optimal solution in finite interval of time 2 GOOD ALGORITHMS?
Lecture 03-04 PROGRAM EFFICIENCY & COMPLEXITY ANALYSIS By: Dr. Zahoor Jan 1 ALGORITHM DEFINITION A finite set of statements that guarantees an optimal solution in finite interval of time 2 GOOD ALGORITHMS?
Divide and Conquer CISC4080, Computer Algorithms CIS, Fordham Univ. Instructor: X. Zhang
 Divide and Conquer CISC4080, Computer Algorithms CIS, Fordham Univ. Instructor: X. Zhang Acknowledgement The set of slides have use materials from the following resources Slides for textbook by Dr. Y.
Divide and Conquer CISC4080, Computer Algorithms CIS, Fordham Univ. Instructor: X. Zhang Acknowledgement The set of slides have use materials from the following resources Slides for textbook by Dr. Y.
Test 1 Review Questions with Solutions
 CS3510 Design & Analysis of Algorithms Section A Test 1 Review Questions with Solutions Instructor: Richard Peng Test 1 in class, Wednesday, Sep 13, 2017 Main Topics Asymptotic complexity: O, Ω, and Θ.
CS3510 Design & Analysis of Algorithms Section A Test 1 Review Questions with Solutions Instructor: Richard Peng Test 1 in class, Wednesday, Sep 13, 2017 Main Topics Asymptotic complexity: O, Ω, and Θ.
Divide and Conquer CISC4080, Computer Algorithms CIS, Fordham Univ. Acknowledgement. Outline
 Divide and Conquer CISC4080, Computer Algorithms CIS, Fordham Univ. Instructor: X. Zhang Acknowledgement The set of slides have use materials from the following resources Slides for textbook by Dr. Y.
Divide and Conquer CISC4080, Computer Algorithms CIS, Fordham Univ. Instructor: X. Zhang Acknowledgement The set of slides have use materials from the following resources Slides for textbook by Dr. Y.
Comparison Sorts. Chapter 9.4, 12.1, 12.2
 Comparison Sorts Chapter 9.4, 12.1, 12.2 Sorting We have seen the advantage of sorted data representations for a number of applications Sparse vectors Maps Dictionaries Here we consider the problem of
Comparison Sorts Chapter 9.4, 12.1, 12.2 Sorting We have seen the advantage of sorted data representations for a number of applications Sparse vectors Maps Dictionaries Here we consider the problem of
SORTING AND SELECTION
 2 < > 1 4 8 6 = 9 CHAPTER 12 SORTING AND SELECTION ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN JAVA, GOODRICH, TAMASSIA AND GOLDWASSER (WILEY 2016)
2 < > 1 4 8 6 = 9 CHAPTER 12 SORTING AND SELECTION ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN JAVA, GOODRICH, TAMASSIA AND GOLDWASSER (WILEY 2016)
08 A: Sorting III. CS1102S: Data Structures and Algorithms. Martin Henz. March 10, Generated on Tuesday 9 th March, 2010, 09:58
 08 A: Sorting III CS1102S: Data Structures and Algorithms Martin Henz March 10, 2010 Generated on Tuesday 9 th March, 2010, 09:58 CS1102S: Data Structures and Algorithms 08 A: Sorting III 1 1 Recap: Sorting
08 A: Sorting III CS1102S: Data Structures and Algorithms Martin Henz March 10, 2010 Generated on Tuesday 9 th March, 2010, 09:58 CS1102S: Data Structures and Algorithms 08 A: Sorting III 1 1 Recap: Sorting
EECS 2011M: Fundamentals of Data Structures
 M: Fundamentals of Data Structures Instructor: Suprakash Datta Office : LAS 3043 Course page: http://www.eecs.yorku.ca/course/2011m Also on Moodle Note: Some slides in this lecture are adopted from James
M: Fundamentals of Data Structures Instructor: Suprakash Datta Office : LAS 3043 Course page: http://www.eecs.yorku.ca/course/2011m Also on Moodle Note: Some slides in this lecture are adopted from James
7. Sorting I. 7.1 Simple Sorting. Problem. Algorithm: IsSorted(A) 1 i j n. Simple Sorting
 Simple Sorting 7. Sorting I 7.1 Simple Sorting Selection Sort, Insertion Sort, Bubblesort [Ottman/Widmayer, Kap. 2.1, Cormen et al, Kap. 2.1, 2.2, Exercise 2.2-2, Problem 2-2 19 197 Problem Algorithm:
Simple Sorting 7. Sorting I 7.1 Simple Sorting Selection Sort, Insertion Sort, Bubblesort [Ottman/Widmayer, Kap. 2.1, Cormen et al, Kap. 2.1, 2.2, Exercise 2.2-2, Problem 2-2 19 197 Problem Algorithm:
Algorithms in Systems Engineering ISE 172. Lecture 12. Dr. Ted Ralphs
 Algorithms in Systems Engineering ISE 172 Lecture 12 Dr. Ted Ralphs ISE 172 Lecture 12 1 References for Today s Lecture Required reading Chapter 6 References CLRS Chapter 7 D.E. Knuth, The Art of Computer
Algorithms in Systems Engineering ISE 172 Lecture 12 Dr. Ted Ralphs ISE 172 Lecture 12 1 References for Today s Lecture Required reading Chapter 6 References CLRS Chapter 7 D.E. Knuth, The Art of Computer
Midterm solutions. n f 3 (n) = 3
 Introduction to Computer Science 1, SE361 DGIST April 20, 2016 Professors Min-Soo Kim and Taesup Moon Midterm solutions Midterm solutions The midterm is a 1.5 hour exam (4:30pm 6:00pm). This is a closed
Introduction to Computer Science 1, SE361 DGIST April 20, 2016 Professors Min-Soo Kim and Taesup Moon Midterm solutions Midterm solutions The midterm is a 1.5 hour exam (4:30pm 6:00pm). This is a closed
Algorithm Design Techniques part I
 Algorithm Design Techniques part I Divide-and-Conquer. Dynamic Programming DSA - lecture 8 - T.U.Cluj-Napoca - M. Joldos 1 Some Algorithm Design Techniques Top-Down Algorithms: Divide-and-Conquer Bottom-Up
Algorithm Design Techniques part I Divide-and-Conquer. Dynamic Programming DSA - lecture 8 - T.U.Cluj-Napoca - M. Joldos 1 Some Algorithm Design Techniques Top-Down Algorithms: Divide-and-Conquer Bottom-Up
The Limits of Sorting Divide-and-Conquer Comparison Sorts II
 The Limits of Sorting Divide-and-Conquer Comparison Sorts II CS 311 Data Structures and Algorithms Lecture Slides Monday, October 12, 2009 Glenn G. Chappell Department of Computer Science University of
The Limits of Sorting Divide-and-Conquer Comparison Sorts II CS 311 Data Structures and Algorithms Lecture Slides Monday, October 12, 2009 Glenn G. Chappell Department of Computer Science University of
Divide and Conquer Sorting Algorithms and Noncomparison-based
 Divide and Conquer Sorting Algorithms and Noncomparison-based Sorting Algorithms COMP1927 16x1 Sedgewick Chapters 7 and 8 Sedgewick Chapter 6.10, Chapter 10 DIVIDE AND CONQUER SORTING ALGORITHMS Step 1
Divide and Conquer Sorting Algorithms and Noncomparison-based Sorting Algorithms COMP1927 16x1 Sedgewick Chapters 7 and 8 Sedgewick Chapter 6.10, Chapter 10 DIVIDE AND CONQUER SORTING ALGORITHMS Step 1
Simple Sorting Algorithms
 Simple Sorting Algorithms Outline We are going to look at three simple sorting techniques: Bubble Sort, Selection Sort, and Insertion Sort We are going to develop the notion of a loop invariant We will
Simple Sorting Algorithms Outline We are going to look at three simple sorting techniques: Bubble Sort, Selection Sort, and Insertion Sort We are going to develop the notion of a loop invariant We will
e-pg PATHSHALA- Computer Science Design and Analysis of Algorithms Module 10
 e-pg PATHSHALA- Computer Science Design and Analysis of Algorithms Module 10 Component-I (B) Description of Module Items Subject Name Computer Science Description of Module Paper Name Module Name/Title
e-pg PATHSHALA- Computer Science Design and Analysis of Algorithms Module 10 Component-I (B) Description of Module Items Subject Name Computer Science Description of Module Paper Name Module Name/Title
CSC Design and Analysis of Algorithms. Lecture 6. Divide and Conquer Algorithm Design Technique. Divide-and-Conquer
 CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conuer Algorithm Design Techniue Divide-and-Conuer The most-well known algorithm design strategy: 1. Divide a problem instance into two
CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conuer Algorithm Design Techniue Divide-and-Conuer The most-well known algorithm design strategy: 1. Divide a problem instance into two
LECTURE NOTES OF ALGORITHMS: DESIGN TECHNIQUES AND ANALYSIS
 Department of Computer Science University of Babylon LECTURE NOTES OF ALGORITHMS: DESIGN TECHNIQUES AND ANALYSIS By Faculty of Science for Women( SCIW), University of Babylon, Iraq Samaher@uobabylon.edu.iq
Department of Computer Science University of Babylon LECTURE NOTES OF ALGORITHMS: DESIGN TECHNIQUES AND ANALYSIS By Faculty of Science for Women( SCIW), University of Babylon, Iraq Samaher@uobabylon.edu.iq
The divide and conquer strategy has three basic parts. For a given problem of size n,
 1 Divide & Conquer One strategy for designing efficient algorithms is the divide and conquer approach, which is also called, more simply, a recursive approach. The analysis of recursive algorithms often
1 Divide & Conquer One strategy for designing efficient algorithms is the divide and conquer approach, which is also called, more simply, a recursive approach. The analysis of recursive algorithms often
Practical Session #11 - Sort properties, QuickSort algorithm, Selection
 Practical Session #11 - Sort properties, QuickSort algorithm, Selection Quicksort quicksort( A, low, high ) if( high > low ) pivot partition( A, low, high ) // quicksort( A, low, pivot-1 ) quicksort( A,
Practical Session #11 - Sort properties, QuickSort algorithm, Selection Quicksort quicksort( A, low, high ) if( high > low ) pivot partition( A, low, high ) // quicksort( A, low, pivot-1 ) quicksort( A,
7 Sorting Algorithms. 7.1 O n 2 sorting algorithms. 7.2 Shell sort. Reading: MAW 7.1 and 7.2. Insertion sort: Worst-case time: O n 2.
 7 Sorting Algorithms 7.1 O n 2 sorting algorithms Reading: MAW 7.1 and 7.2 Insertion sort: 1 4 3 2 1 3 4 2 Selection sort: 1 4 3 2 Bubble sort: 1 3 2 4 7.2 Shell sort Reading: MAW 7.4 Introduction: Shell
7 Sorting Algorithms 7.1 O n 2 sorting algorithms Reading: MAW 7.1 and 7.2 Insertion sort: 1 4 3 2 1 3 4 2 Selection sort: 1 4 3 2 Bubble sort: 1 3 2 4 7.2 Shell sort Reading: MAW 7.4 Introduction: Shell
CS473 - Algorithms I
 CS473 - Algorithms I Lecture 4 The Divide-and-Conquer Design Paradigm View in slide-show mode 1 Reminder: Merge Sort Input array A sort this half sort this half Divide Conquer merge two sorted halves Combine
CS473 - Algorithms I Lecture 4 The Divide-and-Conquer Design Paradigm View in slide-show mode 1 Reminder: Merge Sort Input array A sort this half sort this half Divide Conquer merge two sorted halves Combine
Assignment 1 (concept): Solutions
 CS10b Data Structures and Algorithms Due: Thursday, January 0th Assignment 1 (concept): Solutions Note, throughout Exercises 1 to 4, n denotes the input size of a problem. 1. (10%) Rank the following functions
CS10b Data Structures and Algorithms Due: Thursday, January 0th Assignment 1 (concept): Solutions Note, throughout Exercises 1 to 4, n denotes the input size of a problem. 1. (10%) Rank the following functions
g(n) time to computer answer directly from small inputs. f(n) time for dividing P and combining solution to sub problems
 .2. Divide and Conquer Divide and conquer (D&C) is an important algorithm design paradigm. It works by recursively breaking down a problem into two or more sub-problems of the same (or related) type, until
.2. Divide and Conquer Divide and conquer (D&C) is an important algorithm design paradigm. It works by recursively breaking down a problem into two or more sub-problems of the same (or related) type, until
Divide and Conquer Algorithms
 Divide and Conquer Algorithms T. M. Murali February 19, 2009 Divide and Conquer Break up a problem into several parts. Solve each part recursively. Solve base cases by brute force. Efficiently combine
Divide and Conquer Algorithms T. M. Murali February 19, 2009 Divide and Conquer Break up a problem into several parts. Solve each part recursively. Solve base cases by brute force. Efficiently combine
Lecture 9: Sorting Algorithms
 Lecture 9: Sorting Algorithms Bo Tang @ SUSTech, Spring 2018 Sorting problem Sorting Problem Input: an array A[1..n] with n integers Output: a sorted array A (in ascending order) Problem is: sort A[1..n]
Lecture 9: Sorting Algorithms Bo Tang @ SUSTech, Spring 2018 Sorting problem Sorting Problem Input: an array A[1..n] with n integers Output: a sorted array A (in ascending order) Problem is: sort A[1..n]
CS 112 Introduction to Computing II. Wayne Snyder Computer Science Department Boston University
 CS 112 Introduction to Computing II Wayne Snyder Department Boston University Today Recursive Sorting Methods and their Complexity: Mergesort Conclusions on sorting algorithms and complexity Next Time:
CS 112 Introduction to Computing II Wayne Snyder Department Boston University Today Recursive Sorting Methods and their Complexity: Mergesort Conclusions on sorting algorithms and complexity Next Time:
Plotting run-time graphically. Plotting run-time graphically. CS241 Algorithmics - week 1 review. Prefix Averages - Algorithm #1
 CS241 - week 1 review Special classes of algorithms: logarithmic: O(log n) linear: O(n) quadratic: O(n 2 ) polynomial: O(n k ), k 1 exponential: O(a n ), a > 1 Classifying algorithms is generally done
CS241 - week 1 review Special classes of algorithms: logarithmic: O(log n) linear: O(n) quadratic: O(n 2 ) polynomial: O(n k ), k 1 exponential: O(a n ), a > 1 Classifying algorithms is generally done
CS Data Structures and Algorithm Analysis
 CS 483 - Data Structures and Algorithm Analysis Lecture VI: Chapter 5, part 2; Chapter 6, part 1 R. Paul Wiegand George Mason University, Department of Computer Science March 8, 2006 Outline 1 Topological
CS 483 - Data Structures and Algorithm Analysis Lecture VI: Chapter 5, part 2; Chapter 6, part 1 R. Paul Wiegand George Mason University, Department of Computer Science March 8, 2006 Outline 1 Topological
Component 02. Algorithms and programming. Sorting Algorithms and Searching Algorithms. Matthew Robinson
 Component 02 Algorithms and programming Sorting Algorithms and Searching Algorithms 1 BUBBLE SORT Bubble sort is a brute force and iterative sorting algorithm where each adjacent item in the array is compared.
Component 02 Algorithms and programming Sorting Algorithms and Searching Algorithms 1 BUBBLE SORT Bubble sort is a brute force and iterative sorting algorithm where each adjacent item in the array is compared.
UNIT-2 DIVIDE & CONQUER
 Overview: Divide and Conquer Master theorem Master theorem based analysis for Binary Search Merge Sort Quick Sort Divide and Conquer UNIT-2 DIVIDE & CONQUER Basic Idea: 1. Decompose problems into sub instances.
Overview: Divide and Conquer Master theorem Master theorem based analysis for Binary Search Merge Sort Quick Sort Divide and Conquer UNIT-2 DIVIDE & CONQUER Basic Idea: 1. Decompose problems into sub instances.
CS 310 Advanced Data Structures and Algorithms
 CS 310 Advanced Data Structures and Algorithms Sorting June 13, 2017 Tong Wang UMass Boston CS 310 June 13, 2017 1 / 42 Sorting One of the most fundamental problems in CS Input: a series of elements with
CS 310 Advanced Data Structures and Algorithms Sorting June 13, 2017 Tong Wang UMass Boston CS 310 June 13, 2017 1 / 42 Sorting One of the most fundamental problems in CS Input: a series of elements with
Cpt S 122 Data Structures. Sorting
 Cpt S 122 Data Structures Sorting Nirmalya Roy School of Electrical Engineering and Computer Science Washington State University Sorting Process of re-arranging data in ascending or descending order Given
Cpt S 122 Data Structures Sorting Nirmalya Roy School of Electrical Engineering and Computer Science Washington State University Sorting Process of re-arranging data in ascending or descending order Given
Introduction to Algorithms
 Introduction to Algorithms An algorithm is any well-defined computational procedure that takes some value or set of values as input, and produces some value or set of values as output. 1 Why study algorithms?
Introduction to Algorithms An algorithm is any well-defined computational procedure that takes some value or set of values as input, and produces some value or set of values as output. 1 Why study algorithms?
Sorting Algorithms Day 2 4/5/17
 Sorting Algorithms Day 2 4/5/17 Agenda HW Sorting Algorithms: Review Selection Sort, Insertion Sort Introduce MergeSort Sorting Algorithms to Know Selection Sort Insertion Sort MergeSort Know their relative
Sorting Algorithms Day 2 4/5/17 Agenda HW Sorting Algorithms: Review Selection Sort, Insertion Sort Introduce MergeSort Sorting Algorithms to Know Selection Sort Insertion Sort MergeSort Know their relative
Algorithms and Data Structures (INF1) Lecture 7/15 Hua Lu
 Algorithms and Data Structures (INF1) Lecture 7/15 Hua Lu Department of Computer Science Aalborg University Fall 2007 This Lecture Merge sort Quick sort Radix sort Summary We will see more complex techniques
Algorithms and Data Structures (INF1) Lecture 7/15 Hua Lu Department of Computer Science Aalborg University Fall 2007 This Lecture Merge sort Quick sort Radix sort Summary We will see more complex techniques
Sorting Algorithms. + Analysis of the Sorting Algorithms
 Sorting Algorithms + Analysis of the Sorting Algorithms Insertion Sort What if first k elements of array are already sorted? 4, 7, 12, 5, 19, 16 We can shift the tail of the sorted elements list down and
Sorting Algorithms + Analysis of the Sorting Algorithms Insertion Sort What if first k elements of array are already sorted? 4, 7, 12, 5, 19, 16 We can shift the tail of the sorted elements list down and
A 0 A 1... A i 1 A i,..., A min,..., A n 1 in their final positions the last n i elements After n 1 passes, the list is sorted.
 CS6402 Design and Analysis of Algorithms _ Unit II 2.1 UNIT II BRUTE FORCE AND DIVIDE-AND-CONQUER 2.1 BRUTE FORCE Brute force is a straightforward approach to solving a problem, usually directly based
CS6402 Design and Analysis of Algorithms _ Unit II 2.1 UNIT II BRUTE FORCE AND DIVIDE-AND-CONQUER 2.1 BRUTE FORCE Brute force is a straightforward approach to solving a problem, usually directly based
Question And Answer.
 Q.1 What is the number of swaps required to sort n elements using selection sort, in the worst case? A. Θ(n) B. Θ(n log n) C. Θ(n2) D. Θ(n2 log n) ANSWER : Option A Θ(n) Note that we
Q.1 What is the number of swaps required to sort n elements using selection sort, in the worst case? A. Θ(n) B. Θ(n log n) C. Θ(n2) D. Θ(n2 log n) ANSWER : Option A Θ(n) Note that we
Lecture 8: Mergesort / Quicksort Steven Skiena
 Lecture 8: Mergesort / Quicksort Steven Skiena Department of Computer Science State University of New York Stony Brook, NY 11794 4400 http://www.cs.stonybrook.edu/ skiena Problem of the Day Give an efficient
Lecture 8: Mergesort / Quicksort Steven Skiena Department of Computer Science State University of New York Stony Brook, NY 11794 4400 http://www.cs.stonybrook.edu/ skiena Problem of the Day Give an efficient
Analyzing Complexity of Lists
 Analyzing Complexity of Lists Operation Sorted Array Sorted Linked List Unsorted Array Unsorted Linked List Search( L, x ) O(logn) O( n ) O( n ) O( n ) Insert( L, x ) O(logn) O( n ) + O( 1 ) O( 1 ) + O(
Analyzing Complexity of Lists Operation Sorted Array Sorted Linked List Unsorted Array Unsorted Linked List Search( L, x ) O(logn) O( n ) O( n ) O( n ) Insert( L, x ) O(logn) O( n ) + O( 1 ) O( 1 ) + O(
Classic Data Structures Introduction UNIT I
 ALGORITHM SPECIFICATION An algorithm is a finite set of instructions that, if followed, accomplishes a particular task. All algorithms must satisfy the following criteria: Input. An algorithm has zero
ALGORITHM SPECIFICATION An algorithm is a finite set of instructions that, if followed, accomplishes a particular task. All algorithms must satisfy the following criteria: Input. An algorithm has zero
Sorting & Growth of Functions
 Sorting & Growth of Functions CSci 588: Data Structures, Algorithms and Software Design Introduction to Algorithms, Cormen et al., Chapter 3 All material not from online sources or text copyright Travis
Sorting & Growth of Functions CSci 588: Data Structures, Algorithms and Software Design Introduction to Algorithms, Cormen et al., Chapter 3 All material not from online sources or text copyright Travis
Sorting. Data structures and Algorithms
 Sorting Data structures and Algorithms Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++ Goodrich, Tamassia and Mount (Wiley, 2004) Outline Bubble
Sorting Data structures and Algorithms Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++ Goodrich, Tamassia and Mount (Wiley, 2004) Outline Bubble
Divide and Conquer. Design and Analysis of Algorithms Andrei Bulatov
 Divide and Conquer Design and Analysis of Algorithms Andrei Bulatov Algorithms Divide and Conquer 4-2 Divide and Conquer, MergeSort Recursive algorithms: Call themselves on subproblem Divide and Conquer
Divide and Conquer Design and Analysis of Algorithms Andrei Bulatov Algorithms Divide and Conquer 4-2 Divide and Conquer, MergeSort Recursive algorithms: Call themselves on subproblem Divide and Conquer
n 1 x i = xn 1 x 1. i= (2n 1) = n 2.
 Questions 1. Use mathematical induction to prove that, for any n 1 n 1 x i = xn 1 x 1. (Recall that I proved it in a different way back in lecture 2.) 2. Use mathematical induction to prove that, for all
Questions 1. Use mathematical induction to prove that, for any n 1 n 1 x i = xn 1 x 1. (Recall that I proved it in a different way back in lecture 2.) 2. Use mathematical induction to prove that, for all
CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics
 CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics 1 Sorting 1.1 Problem Statement You are given a sequence of n numbers < a 1, a 2,..., a n >. You need to
CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics 1 Sorting 1.1 Problem Statement You are given a sequence of n numbers < a 1, a 2,..., a n >. You need to
Quick-Sort fi fi fi 7 9. Quick-Sort Goodrich, Tamassia
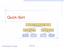 Quick-Sort 7 4 9 6 2 fi 2 4 6 7 9 4 2 fi 2 4 7 9 fi 7 9 2 fi 2 9 fi 9 Quick-Sort 1 Quick-Sort ( 10.2 text book) Quick-sort is a randomized sorting algorithm based on the divide-and-conquer paradigm: x
Quick-Sort 7 4 9 6 2 fi 2 4 6 7 9 4 2 fi 2 4 7 9 fi 7 9 2 fi 2 9 fi 9 Quick-Sort 1 Quick-Sort ( 10.2 text book) Quick-sort is a randomized sorting algorithm based on the divide-and-conquer paradigm: x
CPS 616 TRANSFORM-AND-CONQUER 7-1
 CPS 616 TRANSFORM-AND-CONQUER 7-1 TRANSFORM AND CONQUER Group of techniques to solve a problem by first transforming the problem into one of: 1. a simpler/more convenient instance of the same problem (instance
CPS 616 TRANSFORM-AND-CONQUER 7-1 TRANSFORM AND CONQUER Group of techniques to solve a problem by first transforming the problem into one of: 1. a simpler/more convenient instance of the same problem (instance
Unit 6 Chapter 15 EXAMPLES OF COMPLEXITY CALCULATION
 DESIGN AND ANALYSIS OF ALGORITHMS Unit 6 Chapter 15 EXAMPLES OF COMPLEXITY CALCULATION http://milanvachhani.blogspot.in EXAMPLES FROM THE SORTING WORLD Sorting provides a good set of examples for analyzing
DESIGN AND ANALYSIS OF ALGORITHMS Unit 6 Chapter 15 EXAMPLES OF COMPLEXITY CALCULATION http://milanvachhani.blogspot.in EXAMPLES FROM THE SORTING WORLD Sorting provides a good set of examples for analyzing
CPSC 320 Midterm 2 Thursday March 13th, 2014
 CPSC 320 Midterm 2 Thursday March 13th, 2014 [12] 1. Answer each question with True or False, and then justify your answer briefly. [2] (a) The Master theorem can be applied to the recurrence relation
CPSC 320 Midterm 2 Thursday March 13th, 2014 [12] 1. Answer each question with True or False, and then justify your answer briefly. [2] (a) The Master theorem can be applied to the recurrence relation
Fundamental problem in computing science. putting a collection of items in order. Often used as part of another algorithm
 cmpt-225 Sorting Sorting Fundamental problem in computing science putting a collection of items in order Often used as part of another algorithm e.g. sort a list, then do many binary searches e.g. looking
cmpt-225 Sorting Sorting Fundamental problem in computing science putting a collection of items in order Often used as part of another algorithm e.g. sort a list, then do many binary searches e.g. looking
Deliverables. Quick Sort. Randomized Quick Sort. Median Order statistics. Heap Sort. External Merge Sort
 More Sorting Deliverables Quick Sort Randomized Quick Sort Median Order statistics Heap Sort External Merge Sort Copyright @ gdeepak.com 2 Quick Sort Divide and conquer algorithm which relies on a partition
More Sorting Deliverables Quick Sort Randomized Quick Sort Median Order statistics Heap Sort External Merge Sort Copyright @ gdeepak.com 2 Quick Sort Divide and conquer algorithm which relies on a partition
Searching in General
 Searching in General Searching 1. using linear search on arrays, lists or files 2. using binary search trees 3. using a hash table 4. using binary search in sorted arrays (interval halving method). Data
Searching in General Searching 1. using linear search on arrays, lists or files 2. using binary search trees 3. using a hash table 4. using binary search in sorted arrays (interval halving method). Data
Data Structure Lecture#17: Internal Sorting 2 (Chapter 7) U Kang Seoul National University
 Data Structure Lecture#17: Internal Sorting 2 (Chapter 7) U Kang Seoul National University U Kang 1 In This Lecture Main ideas and analysis of Merge sort Main ideas and analysis of Quicksort U Kang 2 Merge
Data Structure Lecture#17: Internal Sorting 2 (Chapter 7) U Kang Seoul National University U Kang 1 In This Lecture Main ideas and analysis of Merge sort Main ideas and analysis of Quicksort U Kang 2 Merge
DATA STRUCTURES AND ALGORITHMS
 DATA STRUCTURES AND ALGORITHMS Fast sorting algorithms Shellsort, Mergesort, Quicksort Summary of the previous lecture Why sorting is needed? Examples from everyday life What are the basic operations in
DATA STRUCTURES AND ALGORITHMS Fast sorting algorithms Shellsort, Mergesort, Quicksort Summary of the previous lecture Why sorting is needed? Examples from everyday life What are the basic operations in
Next. 1. Covered basics of a simple design technique (Divideand-conquer) 2. Next, more sorting algorithms.
 Next 1. Covered basics of a simple design technique (Divideand-conquer) Ch. 2 of the text. 2. Next, more sorting algorithms. Sorting Switch from design paradigms to applications. Sorting and order statistics
Next 1. Covered basics of a simple design technique (Divideand-conquer) Ch. 2 of the text. 2. Next, more sorting algorithms. Sorting Switch from design paradigms to applications. Sorting and order statistics
