Transformations Part If then, the identity transformation.
|
|
|
- Vincent Perry
- 5 years ago
- Views:
Transcription
1 Transformations Part 2 Definition: Given rays with common endpoint O, we define the rotation with center O and angle as follows: 1. If then, the identity transformation. 2. If A, O, and B are noncollinear, let A be a point on such that OA = OA. Locate a point B such that B lies on the opposite side of from A,, and OB = OB. Define to be the unique isometry that takes A to A, B to B, and fixes O. 3. If are opposite rays, let A be a point on such that OA = OA. Choose a point C not on with and let C be the point on the opposite side of such that O is the midpoint of. Define to be the unique isometry that takes A to A, C to C, and fixes O. In this case called a half turn. is
2 There are several facts about rotations we did not have time to prove in class, but are basic applications of the ruler and protractor postulates, along with the fact that isometries preserve distance, angle, betweeness of points and rays, etc. Specifically: If A, B, and C are noncollinear points, then for every point P not equal to O, if P is the image of P under, then. Moreover, If, then O is the only fixed point of. We emphasize two useful theorems: First Rotation Theorem: For any rotation there exist two lines l and m such that l and m intersect at O, and lines that intersect at the center of rotation.. That is, a rotation is the product of two reflections through Outline of sketchy proof: We deal with the case where A, B, and O are non-collinear; the other cases are even easier. Let and let m be the bisector of and for convenience let. Because l and m pass through O, both and fix O. Now s l fixes A, and triangle congruent theorems and CPCF gives us that. Finally, a reflection over line l puts the image B of B on the other side of l on a ray that makes an angle of, with. A subsequent reflection over line m must place the image of B on a ray that makes an angle of with m. Use of ruler and protractor postulates show that it must map to point B. Because and agree on noncollinear points A, B, and O, they are the same isometry..
3 Note that the angle of rotation is one half the angle between the reflection lines, and that the intersection of the reflection lines is the center of rotation. Second Rotation Theorem: If there exist lines m and n such that. is a rotation and l is any line going through point O, then Thus, the lines of reflection used to create a rotation are not unique. The proof of this theorem involves some of the facts stated on the top of the previous page, together with basic properties of isometries. What is important to remember is that two lines of reflection that define a rotation can be replaced with any two lines going through the same intersection point and having the same angle. A reflection of a point across j and then k will be the same as a reflection across j and then k.
4 Definition: Given two points A and B, we define the translation T AB from A to B as follows: 1. If A = B, T AB is defined to be the identity. 2. Otherwise, let and let m be the line that is perpendicular to l at point A. Choose a point C that lies on m but not l. Locate point C such that C and C are on the same side of l,, and AC = BC. Let B be the point on l such that A and B lie on opposite sides of and AB = BB. Then, define T AB to be the unique isometry that takes A to B, B to B, and C to C. As with rotations, there are several facts about rotations we did not have time to prove in class, but are basic applications of the ruler and protractor postulates, along with the fact that isometries preserve distance, angle, betweeness of points and rays, etc. Specifically: Given points A and B and P, if P is the image of P under T AB, then PP = AB. Moreover,. T AB has no fixed points unless A = B.
5 We have two useful theorems for translations similar to those stated above for rotations: First Translation Theorem: For any translation TAB there exist two lines l and m such that l and m are parallel and. That is, a translation is the product of two reflections through parallel lines. Outline of sketchy proof: Let T AB be a translation and suppose A, B, C, B and C are as in the definition. Let and let m be the perpendicular bisector of (with M being the midpoint of ). It is easy to establish that m is also the perpendicular bisector of. Examine the composition of the two reflections. Since both A and C are fixed under a reflection in l, and since m is the perpendicular bisector of both and, it is clear that takes C to C and A to B. Now the reflection of B over l will map B to a point B on the opposite side of l a distance of AB = 2AM from A. This makes B a distance of 3AM from line m. Since B is also a distance of 3 AM from line m (since BB = 2AM), m is the perpendicular bisector of B B, so the reflection across m takes B to B. Therefore takes B to B. Since and T AB agree on the three noncollinear points A, B, and C, they are the same isometry. Note that the distance of the translation is twice the distance AM between lines of reflection, and is in the direction of.
6 Second Translation Theorem: Given distinct points A and B: For every line l that is perpendicular to there exists a line m perpendicular to such that. Thus, as with rotations, the lines of reflection used to create a translation are not unique. The proof of this theorem involves some of the facts stated following the definition of translation, together with basic properties of isometries. Again, what is important to remember is that two lines of reflection that accomplish a translation T can be replaced with any two lines perpendicular to AB that are a distance of AB apart. Summary So far we have shown that every isometry is the composition of at most three reflections. We introduced rotations and translations and waved our hands over proofs that the were the composition of two reflections. We can put what we have done together into a characterization of isometries: Isometry Number of lines of reflection Characteristics of lines Reflection 1 Rotation 2 The two lines intersect in one point Translation 2 The two lines are parallel Identity 2 The two lines are identical That exhausts the possibilities for combinations of reflections involving one or two lines. What about three lines? That is the point of the next set of notes.
Transformations and Isometries
Transformations and Isometries Definition: A transformation in absolute geometry is a function f that associates with each point P in the plane some other point P in the plane such that (1) f is one-to-one
1. A statement is a set of words and/or symbols that collectively make a claim that can be classified as true or false.
Chapter 1 Line and Angle Relationships 1.1 Sets, Statements and Reasoning Definitions 1. A statement is a set of words and/or symbols that collectively make a claim that can be classified as true or false.
Segment Addition Postulate: If B is BETWEEN A and C, then AB + BC = AC. If AB + BC = AC, then B is BETWEEN A and C.
Ruler Postulate: The points on a line can be matched one to one with the REAL numbers. The REAL number that corresponds to a point is the COORDINATE of the point. The DISTANCE between points A and B, written
Betweenness and the Crossbar Theorem. Lemma: Let A, B, and C be distinct points. If A*B*C, then neither A*C*B nor B*A*C.
Betweenness and the Crossbar Theorem Lemma: Let A, B, and C be distinct points. If A*B*C, then neither A*C*B nor B*A*C. Suppose that both A*B*C and A*C*B. Thus AB+BC =AC, and AC +CB = AB. From this we
Mth 97 Winter 2013 Sections 4.3 and 4.4
Section 4.3 Problem Solving Using Triangle Congruence Isosceles Triangles Theorem 4.5 In an isosceles triangle, the angles opposite the congruent sides are congruent. A Given: ABC with AB AC Prove: B C
(1) Page #1 24 all. (2) Page #7-21 odd, all. (3) Page #8 20 Even, Page 35 # (4) Page #1 8 all #13 23 odd
Geometry/Trigonometry Unit 1: Parallel Lines Notes Name: Date: Period: # (1) Page 25-26 #1 24 all (2) Page 33-34 #7-21 odd, 23 28 all (3) Page 33-34 #8 20 Even, Page 35 #40 44 (4) Page 60 61 #1 8 all #13
Chapter 1-2 Points, Lines, and Planes
Chapter 1-2 Points, Lines, and Planes Undefined Terms: A point has no size but is often represented by a dot and usually named by a capital letter.. A A line extends in two directions without ending. Lines
GEOMETRY POSTULATES AND THEOREMS. Postulate 1: Through any two points, there is exactly one line.
GEOMETRY POSTULATES AND THEOREMS Postulate 1: Through any two points, there is exactly one line. Postulate 2: The measure of any line segment is a unique positive number. The measure (or length) of AB
Objectives: (What You ll Learn) Identify and model points, lines, planes Identify collinear and coplanar points, intersecting lines and planes
Geometry Chapter 1 Outline: Points, Lines, Planes, & Angles A. 1-1 Points, Lines, and Planes (What You ll Learn) Identify and model points, lines, planes Identify collinear and coplanar points, intersecting
Exercises for Chapter Three You know you've got to exercise your brain just like your muscles. Will Rogers ( )
Exercises for Chapter Three You know you've got to exercise your brain just like your muscles. Will Rogers (1879 1935) Investigation Exercise 3.1. (a) Construct a tessellation. (Directions for construction.)
Postulates, Theorems, and Corollaries. Chapter 1
Chapter 1 Post. 1-1-1 Through any two points there is exactly one line. Post. 1-1-2 Through any three noncollinear points there is exactly one plane containing them. Post. 1-1-3 If two points lie in a
Geometry Reasons for Proofs Chapter 1
Geometry Reasons for Proofs Chapter 1 Lesson 1.1 Defined Terms: Undefined Terms: Point: Line: Plane: Space: Postulate 1: Postulate : terms that are explained using undefined and/or other defined terms
1.1 IDENTIFY POINTS, LINES AND PLANES
1.1 IDENTIFY POINTS, LINES AND PLANES OBJECTIVE I WILL KNOW THESE DEFINITIONS AND BE ABLE TO SKETCH THEM: POINT LINE PLANE RAY OPPOSITE RAY COLLINEAR AND COPLANAR POINTS INTERSECTIONS OF TWO LINES AND
Preparing High School Geometry Teachers to Teach the Common Core
Preparing High School Geometry Teachers to Teach the Common Core NCTM Regional Meeting Atlantic City, NJ October 22, 2014 Timothy Craine, Central Connecticut State University crainet@ccsu.edu Edward DePeau,
DE to a line parallel to Therefore
Some Proofs 1. In the figure below segment DE cuts across triangle ABC, and CD/CA = CE/CB. Prove that DE is parallel to AB. Consider the dilation with center C and scaling factor CA/CD. This dilation fixes
2-1 Transformations and Rigid Motions. ENGAGE 1 ~ Introducing Transformations REFLECT
2-1 Transformations and Rigid Motions Essential question: How do you identify transformations that are rigid motions? ENGAGE 1 ~ Introducing Transformations A transformation is a function that changes
DEFINITIONS. Perpendicular Two lines are called perpendicular if they form a right angle.
DEFINITIONS Degree A degree is the 1 th part of a straight angle. 180 Right Angle A 90 angle is called a right angle. Perpendicular Two lines are called perpendicular if they form a right angle. Congruent
Student Name: Tools of Geometry Module Review. Answer each of the following problems. Make sure to show your work. Notation
Answer each of the following problems. Make sure to show your work. Notation 1. Given the plane DGF in the diagram, which points are collinear? 2. Which point is coplanar with A, B, and C in the diagram
a triangle with all acute angles acute triangle angles that share a common side and vertex adjacent angles alternate exterior angles
acute triangle a triangle with all acute angles adjacent angles angles that share a common side and vertex alternate exterior angles two non-adjacent exterior angles on opposite sides of the transversal;
Answer each of the following problems. Make sure to show your work. Points D, E, and F are collinear because they lie on the same line in the plane.
Answer each of the following problems. Make sure to show your work. Notation 1. Given the plane DGF in the diagram, which points are collinear? Points D, E, and F are collinear because they lie on the
The angle measure at for example the vertex A is denoted by m A, or m BAC.
MT 200 ourse notes on Geometry 5 2. Triangles and congruence of triangles 2.1. asic measurements. Three distinct lines, a, b and c, no two of which are parallel, form a triangle. That is, they divide the
I can identify, name, and draw points, lines, segments, rays, and planes. I can apply basic facts about points, lines, and planes.
Page 1 of 9 Are You Ready Chapter 1 Pretest & skills Attendance Problems Graph each inequality. 1. x > 3 2. 2 < x < 6 3. x > 1 or x < 0 Vocabulary undefined term point line plane collinear coplanar segment
Geometry Lesson 1-1: Identify Points, Lines, and Planes Name Hr Pg. 5 (1, 3-22, 25, 26)
Geometry Lesson 1-1: Identify Points, Lines, and Planes Name Hr Pg. 5 (1, 3-22, 25, 26) Learning Target: At the end of today s lesson we will be able to successfully name and sketch geometric figures.
2-5 Postulates and Paragraph Proofs
Determine whether each statement is always, sometimes, or never true. Explain your reasoning. 7. The intersection of three planes is a line. If three planes intersect, then their intersection may be a
Geometry 1-1. Non-collinear Points not on the same line. Need at least 3 points to be non-collinear since two points are always collinear
Name Geometry 1-1 Undefined terms terms which cannot be defined only described. Point, line, plane Point a location in space Line a series of points that extends indefinitely in opposite directions. It
H.Geometry Chapter 3 Definition Sheet
Section 3.1 Measurement Tools Construction Tools Sketch Draw Construct Constructing the Duplicate of a Segment 1.) Start with a given segment. 2.) 3.) Constructing the Duplicate of an angle 1.) Start with
POTENTIAL REASONS: Definition of Congruence:
Sec 1.6 CC Geometry Triangle Proofs Name: POTENTIAL REASONS: Definition of Congruence: Having the exact same size and shape and there by having the exact same measures. Definition of Midpoint: The point
Geometry Definitions, Postulates, and Theorems. Chapter 3: Parallel and Perpendicular Lines. Section 3.1: Identify Pairs of Lines and Angles.
Geometry Definitions, Postulates, and Theorems Chapter : Parallel and Perpendicular Lines Section.1: Identify Pairs of Lines and Angles Standards: Prepare for 7.0 Students prove and use theorems involving
Plane Geometry: Reflection Across a Line Does It! at the Marin Math Circle 1
Plane Geometry: Reflection Across a Line Does It! at the Marin Math Circle 1 by Zvezdelina Stankova Berkeley Math Circle Director September 29 and October 13, 2010 Note: We shall work on the problems below
Geometry Cheat Sheet
Geometry Cheat Sheet Chapter 1 Postulate 1-6 Segment Addition Postulate - If three points A, B, and C are collinear and B is between A and C, then AB + BC = AC. Postulate 1-7 Angle Addition Postulate -
B. Section 1.1. Chapter 1 Review Booklet A. Vocabulary Match the vocabulary term with its definition. 3. A pair of opposite rays on line p.
A. Vocabulary Match the vocabulary term with its definition. Point Polygon Angle Sides Postulate Collinear Opposite Rays Vertical angles Coplanar Linear Pair Complementary Vertex Line Adjacent Plane Distance
Geometry IB Date: 2/18/2013 ID Check Objective: Students will identify and use medians and altitudes in triangles. Bell Ringer: Complete Constructions
Geometry IB Date: 2/18/2013 ID Check Objective: Students will identify and use medians and altitudes in triangles. Bell Ringer: Complete Constructions HW Requests: pg 327 #17-25 odds 45, 46, pg 338 #11,
An Approach to Geometry (stolen in part from Moise and Downs: Geometry)
An Approach to Geometry (stolen in part from Moise and Downs: Geometry) Undefined terms: point, line, plane The rules, axioms, theorems, etc. of elementary algebra are assumed as prior knowledge, and apply
6.2 Triangle Dilations A Solidify Understanding Task
6.2 Triangle Dilations A Solidify Understanding Task 1. Given ABC, use point M as the center of a dilation to locate the vertices of a triangle that has side lengths that are three times longer than the
Circular inversions = hyperbolic isometries
Circular inversions = hyperbolic isometries Recall how all isometries of the Euclidean plane are products of at most three line reflections. In the (Beltrami-Poincaré model of the) hyperbolic plane, we
FIGURES FOR SOLUTIONS TO SELECTED EXERCISES. V : Introduction to non Euclidean geometry
FIGURES FOR SOLUTIONS TO SELECTED EXERCISES V : Introduction to non Euclidean geometry V.1 : Facts from spherical geometry V.1.1. The objective is to show that the minor arc m does not contain a pair of
Proving Triangles and Quadrilaterals Satisfy Transformational Definitions
Proving Triangles and Quadrilaterals Satisfy Transformational Definitions 1. Definition of Isosceles Triangle: A triangle with one line of symmetry. a. If a triangle has two equal sides, it is isosceles.
Example G1: Triangles with circumcenter on a median. Prove that if the circumcenter of a triangle lies on a median, the triangle either is isosceles
1 Example G1: Triangles with circumcenter on a median. Prove that if the circumcenter of a triangle lies on a median, the triangle either is isosceles or contains a right angle. D D 2 Solution to Example
Unit 1 Unit 1 A M. M.Sigley, Baker MS. Unit 1 Unit 1. 3 M.Sigley, Baker MS
A M S 1 2 G O E A B 3 4 LINE POINT Undefined No thickness Extends infinitely in two directions Designated with two points Named with two capital letters or Undefined No size Named with a capital letter
Geometry: Semester 1 Midterm
Class: Date: Geometry: Semester 1 Midterm Multiple Choice Identify the choice that best completes the statement or answers the question. 1. The first two steps for constructing MNO that is congruent to
definition. An angle is the union of two rays with a common end point.
Chapter 3 Angles What s the secret for doing well in geometry? Knowing all the angles. As we did in the last chapter, we will introduce new terms and new notations, the building blocks for our success.
Geometry - Chapter 1 - Corrective #1
Class: Date: Geometry - Chapter 1 - Corrective #1 Short Answer 1. Sketch a figure that shows two coplanar lines that do not intersect, but one of the lines is the intersection of two planes. 2. Name two
Mth 97 Fall 2013 Chapter 4
4.1 Reasoning and Proof in Geometry Direct reasoning or reasoning is used to draw a conclusion from a series of statements. Conditional statements, if p, then q, play a central role in deductive reasoning.
Explorations of Rigid Motions and Congruence
Explorations of Rigid Motions and Congruence James King University of Washington Department of Mathematics king@uw.edu http://www.math.washington.edu/~king The Plan In this session, we will explore exploring.
theorems & postulates & stuff (mr. ko)
theorems & postulates & stuff (mr. ko) postulates 1 ruler postulate The points on a line can be matched one to one with the real numbers. The real number that corresponds to a point is the coordinate of
Lesson 9: Coordinate Proof - Quadrilaterals Learning Targets
Lesson 9: Coordinate Proof - Quadrilaterals Learning Targets Using coordinates, I can find the intersection of the medians of a triangle that meet at a point that is two-thirds of the way along each median
TRANSFORMATIONS. The original figure is called the pre-image; the new (copied) picture is called the image of the transformation.
Quiz Review Sheet A transformation is a correspondence that maps a point. TRANSFORMATIONS The original figure is called the pre-image; the new (copied) picture is called the image of the transformation.
no triangle can have more than one right angle or obtuse angle.
Congruence Theorems in Action Isosceles Triangle Theorems.3 Learning Goals In this lesson, you will: Prove the Isosceles Triangle Base Theorem. Prove the Isosceles Triangle Vertex Angle Theorem. Prove
Chapter 1 Tools of Geometry
Chapter 1 Tools of Geometry Goals: 1) learn to draw conclusions based on patterns 2) learn the building blocks for the structure of geometry 3) learn to measure line segments and angles 4) understand the
GEOMETRY is the study of points in space
CHAPTER 5 Logic and Geometry SECTION 5-1 Elements of Geometry GEOMETRY is the study of points in space POINT indicates a specific location and is represented by a dot and a letter R S T LINE is a set of
Chapter 2 Similarity and Congruence
Chapter 2 Similarity and Congruence Definitions Definition AB = CD if and only if AB = CD Remember, mab = AB. Definitions Definition AB = CD if and only if AB = CD Remember, mab = AB. Definition ABC =
Honors 213. Third Hour Exam. Name
Honors 213 Third Hour Exam Name Monday, March 27, 2000 100 points Page 1 Please note: Because of multiple exams given Monday, this exam will be returned by Thursday, March 30. 1. (5 pts.) Define what it
U4 Polygon Notes January 11, 2017 Unit 4: Polygons
Unit 4: Polygons 180 Complimentary Opposite exterior Practice Makes Perfect! Example: Example: Practice Makes Perfect! Def: Midsegment of a triangle - a segment that connects the midpoints of two sides
M2 GEOMETRY REVIEW FOR MIDTERM EXAM
M2 GEOMETRY REVIEW FOR MIDTERM EXAM #1-11: True or false? If false, replace the underlined word or phrase to make a true sentence. 1. Two lines are perpendicular if they intersect to form a right angle.
Maintaining Mathematical Proficiency
Chapter 3 Maintaining Mathematical Proficiency Find the slope of the line.. y. y 3. ( 3, 3) y (, ) (, ) x x (, ) x (, ) ( 3, 3)... (, ) y (0, 0) 8 8 x x 8 8 y (, ) (, ) y (, ) (, 0) x Write an equation
MAKE GEOMETRIC CONSTRUCTIONS
MAKE GEOMETRIC CONSTRUCTIONS KEY IDEAS 1. To copy a segment, follow the steps given: Given: AB Construct: PQ congruent to AB 1. Use a straightedge to draw a line, l. 2. Choose a point on line l and label
1stQuarterReview.nb If two parallel lines are cut by a transversal, 2. If point B is between points A and C, then AB + BC =.
1stQuarterReview.nb 1 Geometry (H) Review: First Quarter Test Part I Fill in the blank with the appropriate word or phrase. 1. If two parallel lines are cut by a transversal,. 2. If point B is between
Chapter 1. Essentials of Geometry
Chapter 1 Essentials of Geometry 1.1 Identify Points, Lines, and Planes Objective: Name and sketch geometric figures so you can use geometry terms in the real world. Essential Question: How do you name
Geometry Pre AP Graphing Linear Equations
Geometry Pre AP Graphing Linear Equations Name Date Period Find the x- and y-intercepts and slope of each equation. 1. y = -x 2. x + 3y = 6 3. x = 2 4. y = 0 5. y = 2x - 9 6. 18x 42 y = 210 Graph each
CCGPS UNIT 5 Semester 2 COORDINATE ALGEBRA Page 1 of 38. Transformations in the Coordinate Plane
CCGPS UNIT 5 Semester 2 COORDINATE ALGEBRA Page 1 of 38 Transformations in the Coordinate Plane Name: Date: MCC9-12.G.CO.1 Know precise definitions of angle, circle, perpendicular line, parallel line,
Chapter 6.1 Medians. Geometry
Chapter 6.1 Medians Identify medians of triangles Find the midpoint of a line using a compass. A median is a segment that joins a vertex of the triangle and the midpoint of the opposite side. Median AD
Unit 10 Circles 10-1 Properties of Circles Circle - the set of all points equidistant from the center of a circle. Chord - A line segment with
Unit 10 Circles 10-1 Properties of Circles Circle - the set of all points equidistant from the center of a circle. Chord - A line segment with endpoints on the circle. Diameter - A chord which passes through
2. Write the point-slope form of the equation of the line passing through the point ( 2, 4) with a slope of 3. (1 point)
Parallel and Perpendicular Lines Unit Test David Strong is taking this assessment. Multiple Choice 1. Which construction is illustrated above? a segment congruent to a given segment an angle congruent
EM225 Projective Geometry Part 2
EM225 Projective Geometry Part 2 eview In projective geometry, we regard figures as being the same if they can be made to appear the same as in the diagram below. In projective geometry: a projective point
UNIT 5 SIMILARITY AND CONGRUENCE
UNIT 5 SIMILARITY AND CONGRUENCE M2 Ch. 2, 3, 4, 6 and M1 Ch. 13 5.1 Parallel Lines Objective When parallel lines are cut by a transversal, I will be able to identify angle relationships, determine whether
Select the best answer. Bubble the corresponding choice on your scantron. Team 13. Geometry
Team Geometry . What is the sum of the interior angles of an equilateral triangle? a. 60 b. 90 c. 80 d. 60. The sine of angle A is. What is the cosine of angle A? 6 4 6 a. b. c.. A parallelogram has all
NAME DATE PER. GEOMETRY FALL SEMESTER REVIEW FIRST SIX WEEKS PART 1. A REVIEW OF ALGEBRA Find the correct answer for each of the following.
NAME ATE PER. GEOMETRY FALL SEMESTER REVIEW FIRST SIX WEEKS PART 1. A REVIEW OF ALGEBRA Find the correct answer for each of the following. 1. m = Solve for m : m 7 = -13 + m FIRST SIX-WEEKS REVIEW 2. x
GEOMETRY R Unit 4: More Transformations / Compositions. Day Classwork Homework Monday 10/16. Perpendicular Bisector Relationship to Transformations
GEOMETRY R Unit 4: More Transformations / Compositions Day Classwork Homework Monday 10/16 Perpendicular Bisector Relationship to Transformations HW 4.1 Tuesday 10/17 Construction of Parallel Lines Through
Proving Theorems about Lines and Angles
Proving Theorems about Lines and Angles Angle Vocabulary Complementary- two angles whose sum is 90 degrees. Supplementary- two angles whose sum is 180 degrees. Congruent angles- two or more angles with
Geometry Midterm Review Mr. Pisciotta
Geometry Midterm Review 2016-2017 Mr. Pisciotta Chapter 1: Essentials of Geometry Sections 1.1 1.5 1.1 Points, Lines and Planes 1.2 Use segments and Congruence 1.3 Midpoint and Distance Formulas -Be able
Unit 1: Fundamentals of Geometry
Name: 1 2 Unit 1: Fundamentals of Geometry Vocabulary Slope: m y x 2 2 Formulas- MUST KNOW THESE! y x 1 1 *Used to determine if lines are PARALLEL, PERPENDICULAR, OR NEITHER! Parallel Lines: SAME slopes
Let s use a more formal definition. An angle is the union of two rays with a common end point.
hapter 2 ngles What s the secret for doing well in geometry? Knowing all the angles. s we did in the last chapter, we will introduce new terms and new notations, the building blocks for our success. gain,
Videos, Constructions, Definitions, Postulates, Theorems, and Properties
Videos, Constructions, Definitions, Postulates, Theorems, and Properties Videos Proof Overview: http://tinyurl.com/riehlproof Modules 9 and 10: http://tinyurl.com/riehlproof2 Module 9 Review: http://tinyurl.com/module9livelesson-recording
If B is the If two angles are
If If B is between A and C, then 1 2 If P is in the interior of RST, then If B is the If two angles are midpoint of AC, vertical, then then 3 4 If angles are adjacent, then If angles are a linear pair,
Chapter 2: Transformations. Chapter 2 Transformations Page 1
Chapter 2: Transformations Chapter 2 Transformations Page 1 Unit 2: Vocabulary 1) transformation 2) pre-image 3) image 4) map(ping) 5) rigid motion (isometry) 6) orientation 7) line reflection 8) line
September 23,
1. In many ruler and compass constructions it is important to know that the perpendicular bisector of a secant to a circle is a diameter of that circle. In particular, as a limiting case, this obtains
NAME: DATE: PERIOD: 1. Find the coordinates of the midpoint of each side of the parallelogram.
NAME: DATE: PERIOD: Geometry Fall Final Exam Review 2017 1. Find the coordinates of the midpoint of each side of the parallelogram. My Exam is on: This review is due on: 2. Find the distance between the
Saccheri Quadrilaterals
Saccheri Quadrilaterals Definition: Let be any line segment, and erect two perpendiculars at the endpoints A and B. Mark off points C and D on these perpendiculars so that C and D lie on the same side
Tools of Geometry 1. X + 9 = 24 2. 25 X = 15 3. X + 3 = -2X -10 4. 3X + 4Y = 2 Place in slope intercept form. 5. Y = ½ X 2 What is the slope? What is the Y- Intercept? Inductive Reasoning is reasoning
Term Definition Figure
Notes LT 1.1 - Distinguish and apply basic terms of geometry (coplanar, collinear, bisectors, congruency, parallel, perpendicular, etc.) Term Definition Figure collinear on the same line (note: you do
VOCABULARY. Chapters 1, 2, 3, 4, 5, 9, and 8. WORD IMAGE DEFINITION An angle with measure between 0 and A triangle with three acute angles.
Acute VOCABULARY Chapters 1, 2, 3, 4, 5, 9, and 8 WORD IMAGE DEFINITION Acute angle An angle with measure between 0 and 90 56 60 70 50 A with three acute. Adjacent Alternate interior Altitude of a Angle
Geometry Notes Chapter 4: Triangles
Geometry Notes Chapter 4: Triangles Name Date Assignment Questions I have Day 1 Section 4.1: Triangle Sum, Exterior Angles, and Classifying Triangles Day 2 Assign: Finish Ch. 3 Review Sheet, WS 4.1 Section
1.1 Understanding the Undefined Terms
1.1 Understanding the Undefined Terms Undefined Terms There are three undefined terms in geometry, these words do not have a formal definition. The undefined terms are:,, and. Naming Points, Lines, and
Geometric Constructions
Materials: Compass, Straight Edge, Protractor Construction 1 Construct the perpendicular bisector of a line segment; Or construct the midpoint of a line segment. Construction 2 Given a point on a line,
Name Date Period. 1.1 Understanding the Undefined Terms
Name Date Period Lesson Objective: 1.1 Understanding the Undefined Terms Naming Points, Lines, and Planes Point Line Plane Collinear: Coplanar: 1. Give 2 other names for PQ and plane R. 2. Name 3 points
Click the mouse button or press the Space Bar to display the answers.
Click the mouse button or press the Space Bar to display the answers. 2-5 Objectives You will learn to: Identify and use basic postulates about points, lines, and planes. Write paragraph proofs. Vocabulary
Math 3315: Geometry Vocabulary Review Human Dictionary: WORD BANK
Math 3315: Geometry Vocabulary Review Human Dictionary: WORD BANK [acute angle] [acute triangle] [adjacent interior angle] [alternate exterior angles] [alternate interior angles] [altitude] [angle] [angle_addition_postulate]
Geometry HR Date: 2/13/2013 ID Check 2nd Objective: SWBAT identify and use perpendicular and angle bisectors in triangles.
Geometry HR Date: 2/13/2013 ID Check 2nd Objective: SWBAT identify and use perpendicular and angle bisectors in triangles. Bell Ringer: 5 minute check 4.6/4.7 10 minutes HW Requests: Quadratics WS 2 nd
Lesson 22: Congruence Criteria for Triangles SAS
Student Outcomes Students learn why any two triangles that satisfy the SAS congruence criterion must be congruent. Lesson Notes In, we begin to investigate criteria, or the indicators, of triangle congruence.
Review Test 1 Chapters 1 & 2 and Appendix L
ath 61 pring 2007 Review Test 1 hapters 1 & 2 and Appendix L 1 www.timetodare.com To prepare for the test, learn all definitions, be familiar with all theorems and postulates and study the following problems.
Some Comments on Leaving Certificate Geometry Work in Progress
Some Comments on Leaving Certificate Geometry Work in Progress D. R. Wilkins April 23, 2016 i Axioms for Leaving Certificate Geometry In 1932, George D. Birkhoff published a paper entitled A set of postulates
Chapter 4 - Lines in a Plane. Procedures for Detour Proofs
Chapter 4 - Lines in a Plane 4.1 Detours and Midpoints Detour proofs - To solve some problems, it is necessary to prove pair of triangles congruent. These we call detour proofs because we have to prove
Section 12.1 Translations and Rotations
Section 12.1 Translations and Rotations Any rigid motion that preserves length or distance is an isometry. We look at two types of isometries in this section: translations and rotations. Translations A
Period: Date Lesson 13: Analytic Proofs of Theorems Previously Proved by Synthetic Means
: Analytic Proofs of Theorems Previously Proved by Synthetic Means Learning Targets Using coordinates, I can find the intersection of the medians of a triangle that meet at a point that is two-thirds of
EQUATIONS OF ALTITUDES, MEDIANS, and PERPENDICULAR BISECTORS
EQUATIONS OF ALTITUDES, MEDIANS, and PERPENDICULAR BISECTORS Steps to Find the Median of a Triangle: -Find the midpoint of a segment using the midpoint formula. -Use the vertex and midpoint to find the
There are two ways to name a line. What are the two ways?
Geometry: 1-1 Points, Lines and Planes What are the Undefined Terms? The Undefined Terms are: What is a Point? How is a point named? Example: What is a Line? A line is named two ways. What are the two
Properties of a Triangle Student Activity Sheet 1; use with Overview
Student: Class: Date: Properties of a Triangle Student Activity Sheet 1; use with Overview 1. REEVVI IEEW Suppose points A, B, and C are collinear, where B is between A and C. If AB = 2x + 3, BC = 6x 5,
Mathematics For Class IX Lines and Angles
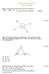Mathematics For Class IX Lines and Angles (Q.1) In Fig, lines PQ and RS intersect each other at point O. If, find angle POR and angle ROQ (1 Marks) (Q.2) An exterior angle of a triangle is 110 and one
Notes on Spherical Geometry
Notes on Spherical Geometry Abhijit Champanerkar College of Staten Island & The Graduate Center, CUNY Spring 2018 1. Vectors and planes in R 3 To review vector, dot and cross products, lines and planes
Rotate the triangle 180 degrees clockwise around center C.
Math 350 Section 5.1 Answers to lasswork lasswork 1: erform the rotations indicated below: Results in bold: Rotate the triangle 90 degrees clockwise around center. Rotate the triangle 180 degrees clockwise