A Direct Algorithm to Find a Largest Common Connected Induced Subgraph of Two Graphs
|
|
|
- Derick Todd
- 5 years ago
- Views:
Transcription
1 A Direct Algorithm to Find a Largest Common Connected Induced Subgraph of Two Graphs Bertrand Cuissart and Jean-Jacques Hébrard Groupe de Recherche en Électronique, Informatique et Imagerie de Caen, CNRS-UMR6072, Université de Caen, France {cuissart, hebrard}@info.unicaen.fr Abstract. We present a direct algorithm that computes a largest common connected induced subgraph of two given graphs. It is based on an efficient generation of the common connected induced subgraphs of the input graphs. Experimental results are provided. 1 Introduction Graphs are widely used to represent objects in various domains such as chemical information, computer imaging etc [1 p. 527]. Many applications in these domains necessitate the use of similarity measures which are often based on the calculation of a largest common subgraph of two graphs [2, 3, 4, 5, 6]. There are numerous definitions of a largest common subgraph, depending on the notions of subgraph and size of a graph taken into account. We are interested here in the case where the considered subgraphs are the connected induced subgraphs, and where the size of a graph is the number of its vertices. This notion has been successfully applied in chemistry [7]. Recall that given two graphs G 1, G 2 and a positive integer k, the problem of deciding whether there exists a common subgraph of G 1 and G 2 of size greater than k is NP-complete [8]. In fact, the problem remains NP-complete if we restrict the search to common connected induced subgraphs. However, in practice, it is useful to define specialized algorithms for this particular case, since they could be significantly more efficient than a general one. A first algorithm that computes a largest common connected subgraph of two graphs was presented by I. Koch in [9]. This algorithm can be straightforwardly adapted to compute a largest common connected induced subgraph. It reduces the problem to the search of a largest clique of a compatibility graph associated with the input graphs. In this paper, we present a direct algorithm based on a procedure that efficiently generates the common connected induced subgraphs of the two input graphs. We experimentally compare the two algorithms. 2 Preliminaries A graph G is denoted by G(V,E) where V is the set of its vertices and E the set of its edges. The subgraph of G induced by a subset of its vertices, V V, L. Brun and M. Vento (Eds.): GbRPR 2005, LNCS 3434, pp , c Springer-Verlag Berlin Heidelberg 2005
2 A Direct Algorithm to Find a LCCIS of Two Graphs 163 G 1 : G 2 : 1 a i 2 6 b 7 j h 3 5 G : (1,a) c e g 4 (2,b) (6,j) d f (3,c) (5,e) (4,d) Fig. 1. A common subgraph of two graphs is a graph consisting of V and those edges of V with both vertices in V. The subgraph of G induced by V is denoted by G[V ]. A graph G is an induced subgraph of G if there exists V V such that G[V ]=G. In all the paper, we say subgraph for induced subgraph. Two graphs G 1 (V 1,E 1 ) and G 2 (V 2,E 2 ) are isomorphic if there exists a bijection f : V 1 V 2 such that for every u 1,v 1 V 1, {u 1,v 1 } E 1 if and only if {f(u 1 ),f(v 1 )} E 2 ; f is called an isomorphism. Acommon subgraph of G 1 and G 2 is a set of ordered pairs {(u 1,v 1 ),...,(u k,v k )} such that the function f : {u 1,...,u k } {v 1,...,v k } defined by f(u i ) = v i (1 i k) isan isomorphism between G 1 [{u 1,...,u k }] and G 2 [{v 1,...,v k }]. Example 1. In Figure 1, G = {(1,a), (2,b), (3,c), (4,d), (5,e), (6,j)} is a common subgraph of G 1 and G 2. A graph G is connected if any two of its vertices are linked by a path in G. The problem LCCIS (Largest Common Connected Induced Subgraph) is to find a common connected induced subgraph C of two given graphs, such that the cardinality of C, C, is maximum. Recall that a tree is a connected graph containing no circuit. The vertices of a tree will be called nodes. Arooted tree is a tree in which one node, the root, is distinguished. In a rooted tree, any node of degree one, unless it is the root, is called a leaf. If{u, v} is an edge of a rooted tree such that u lies on the path from the root to v, then u is said to be the parent of v and v is a child of u. An ancestor of u is any node of the path from the root to u. Ifu is an ancestor of v, then v is a descendant of u, and we write u v; ifu v, we write u<v.it is convenient to denote a tree T with root r by (T,r). We present, in Section 5, an algorithm for LCCIS based on an efficient method for generating the common connected subgraphs of two graphs; this method is described in Section 4. But before generating the common connected subgraphs of two graphs, we must be able to simply generate the connected subgraphs of a graph; Section 3 is devoted to this question.
3 164 B. Cuissart and J.-J. Hébrard 3 Connected Subgraphs Generation We present a structure designed to generate the connected subgraphs of a graph. Throughout this section, G 1 (V 1,E 1 ) is a fixed graph, and (T,r) is a rooted tree in which each node, except r, is labelled by an element of {v + : v V 1 } {v : v V 1 }. The label of a node x, x r, is denoted by L(x). A label of the form v + (resp. v ) is said to be positive (resp. negative). For each node x of T, we define PL + (x) ={v V 1 : y, y r, y x and L(y) =v + } ; PL + (x) is the set of vertices of G 1 occurring in a positive label of an ancestor of x. Similarly, we define PL (x) ={v V 1 : y, y r, y x and L(y) =v }, and PL(x) =PL + (x) PL (x) ;PL(x) is the set of vertices of G 1 used for labelling the ancestors of x. In order to generate the connected subgraphs of G 1, we build T in such a way that for each node x of T, G 1 [PL + (x)] is connected. The set of vertices of G 1 that may label the children of x is denoted by F (x) and defined as follows. If PL + (x) then F (x) ={v V 1 : u PL + (x), {v, u} E 1 }\PL(x), otherwise F (x) =V 1 \ PL(x). Example 2. In Figure 2, PL + (x) ={a, b}, PL(x) ={a, b, c}, F (x) ={e}. Remark that, by definition, PL + (r) =, PL(r) = and F (r) =V 1. Definition 3. A tree of the connected subgraphs (TOCS) of G 1 is a rooted tree (T,r) such that : 1. Every node of T, except r, is labelled by an element of {v + : v V 1 } {v : v V 1 }. 2. For every node x of T,ifF(x) =, then x is a leaf, otherwise x has two children respectively labelled by v + and v, with v F (x). See Figure 2 for an example of a TOCS. We will now show that the leaves of a TOCS of G 1 and the connected subgraphs of G 1 are in a bijective correspondence. The following proposition is an immediate consequence of Definition 3. Proposition 4. Let f 1 and f 2 be two leaves of a TOCS. If f 1 f 2 then PL + (f 1 ) PL + (f 2 ). Let V V 1 and (T,r) be a TOCS of G 1. We associate with V the path of T, (x 0,...,x k ), defined as follows: x 0 = r, x k is a leaf of T, and for all i (0 i<k), x i+1 is the child of x i with a positive label v + if v V, otherwise x i+1 is the child of x i with a negative label. The leaf x k is denoted by l(v ). Example 5. In Figure 2, l({a, b, e}) =l({a, b, e, d}) =f. Remark 6. Let V V 1.WehavePL + (l(v )) V, PL (l(v )) V = and PL + (l(v )) = if and only if V =. Indeed, if PL + (l(v )) =, then F (l(v )) = V 1 \ PL(l(V )), moreover, F (l(v )) = since l(v ) is a leaf, thus PL(l(V )) = V 1, PL (l(v )) = V 1, V 1 V = and consequently V =.
4 A Direct Algorithm to Find a LCCIS of Two Graphs 165 a G 1 : b c d A TOCS of G 1 : e a + a b + x b b + b c + c c + e + c + c c e e + e d + d c + e c d + d d+ e + d d + d d + d e + e e + e d + d e + e e + f e e + e Fig. 2. A tree of the connected subgraphs of a graph Proposition 7. Let T be a TOCS of G (soundness) For every leaf f of T, G 1 [PL + (f)] is connected. 2. (completeness) Let V V 1.IfG 1 [V ] is connected, then V = PL + (l(v )). Proof. 1. Straightforward consequence of Definition If V = then PL + (l(v )) = (Remark 6) and V = PL + (l(v )). If V, then PL + (l(v )) (Remark 6). By definition of l(v ), we have PL + (l(v )) V. Let C = V \ PL + (l(v )). Suppose C. The sets C and PL + (l(v )) form a partition of V. By hypothesis, G[V ] is connected, thus there exists an edge {u, v} E 1, with u C and v PL + (l(v )). By definition of l(v ), C PL(l(V )) =, therefore u F (l(v )). Now l(v ) is a leaf of T,thus F (l(v )) =. A contradiction. Finally, C = and V = PL + (l(v )). Example 8. In Figure 2, G 1 [{a, b, e}] is connected, G 1 [{a, b, e, d}] is not connected and PL + (f) ={a, b, e}. It follows from Prop. 4 and Prop. 7 that there exists a bijection from the leaves of a TOCS of G 1 to the connected subgraphs of G 1. As a consequence, the connected subgraphs of G 1 can be generated by simply performing a depth first traversal of a TOCS of G 1 [10]. 4 Generation of the Common Connected Subgraphs of Two Graphs We present an algorithm for generating the common connected subgraphs of two graphs.
5 166 B. Cuissart and J.-J. Hébrard Throughout this section, G 1 (V 1,E 1 ) and G 2 (v 2,E 2 ) are fixed graphs and T is a TOCS of G 1. For every leaf f of T, our algorithm build simultaneously all the subgraphs of G 2 isomorphic to G 1 [PL + (f)]. We first define a rooted tree whose leaves are in a bijective correspondence with the common connected subgraphs of G 1 and G 2. Definition 9. Let (T,r) be a TOCS of G 1. The tree of the common connected subgraphs of G 1 and G 2 (TOCCS) built from T is a rooted tree (T,r ) in which each node,except r, is labelled by an element of V 1 V 2 V 1 { Excluded }. The label of a node x, x r, is denoted by L (x ). Each node x of T is associated withanodeoft, called the origin of x and denoted by Or(x ). (T,r ) and the function Or are defined by induction as follows: 1. Or(r )=r. 2. Let x beanodeoft. (a) If Or(x ) isaleafoft, then x isaleafoft. (b) Otherwise, Or(x ) has two children y and z respectively labelled by v 1+ and v 1, where v 1 V 1.LetH(x )={v 2 V 2 : for any ancestor of x labelled by (u 1,u 2 ) with u 2 V 2,v 2 u 2 and ({v 1,u 1 } E 1 {v 2,u 2 } E 2 )}, k = H(x ) and w 1,...,w k denote the elements of H(x ). Then x has k+1 children, y 1,...,y k+1, with L (y i )=(v 1,w i ) and Or(y i )=y (1 i k), L (y k+1 )=(v 1, Excluded ) and Or(y k+1 )=z. Example 10. Figure 3 displays a path from the root r toanodex in a TOCCS of the graphs G 1 and G 2. Or(x )=x, F (x) ={e}, x has two children y and z with L(y) =e + and L(z) =e. H(x )={5}, x has two children y and z with L (y )=(e, 5) and L (z )=(e, Excluded ). In a TOCCS, the labels of the form (v 1,v 2 ), with v 2 V 2, are called positive and the labels of the form (v 1, Excluded ) are called negative. For every node x of a TOCCS, we define PL +(x )={(v 1,v 2 ) V 1 V 2 : y, y r, y x and L (y )=(v 1,v 2 )}. The following proposition is an immediate consequence of Definition 9. Proposition 11. Let T be a TOCCS of G 1 and G 2, and f 1, f 2 two leaves of T.Iff 1 f 2 then PL +(f 1) PL +(f 2). We now establish the correspondence between the leaves of a TOCCS and the common connected subgraphs of G 1 and G 2. Proposition 12. Let T be a TOCCS of G 1 and G (soundness) For every leaf f of T, PL +(f ) is a common connected subgraph of G 1 and G (completeness) Let G be a common connected subgraph of G 1 and G 2. There exists a leaf f of T, such that PL +(f )=G.
6 A Direct Algorithm to Find a LCCIS of Two Graphs 167 a 1 G 1 : b c d G 2 : (T,r), a TOCS of G 1 : (a path) r e (T,r ), a TOCCS of G 1 and G 2 built from (T,r): (a path) r 5 a + a (a, 1) (a, 2),...,(a, 5) (a, E ) b + b (b, 2) (b, 3) (b, 4) (b, E ) c + c x (c, 4) (c, E ) x y e + e z y (e, 5) (e, E ) z Fig. 3. A tree of the connected subgraphs common to two graphs Proof (Sketch). 1. Straightforward consequence of Definition Let G = {(u 1,v 1 ),...,(u k,v k )} be a common connected subgraph of G 1 and G 2, u i V 1 and v i V 2 (1 i k). Let (T,r) be the TOCS of G 1 from which (T,r ) is built. By hypothesis, G 1 [{u 1,...,u k }] is connected. According to Prop. 7, we have PL + (l({u 1,...,u k })) = {u 1,...,u k }. Let (x 0,...,x p )be the path from r to l({u 1,...,u k })int. For all i, 1 i p, ifl(x i ) is a negative label, we write σ(i) = Excluded, otherwise, there exists a unique vertex v V 2 such that (L(x i ),v) G and we write σ(i) = v. Since G is a common connected subgraph of G 1 and G 2, there exists a path in T (x 0,...,x p) from r (r = x 0 ) to a leaf f (f = x p) such that L (x i )= (L(x i ),σ(i)) (1 i p). We have PL +(f )=G. It follows from Prop. 11 and Prop. 12 that there exists a bijection from the the leaves of a TOCCS of two graphs to their common connected subgraphs. Consequently, we can generate the common connected subgraphs of G 1 and G 2 by simply performing a depth first traversal of a TOCCS of G 1 and G 2. Notice that it is not necessary to compute and store the entire TOCCS. A depth first traversal only requires to store the path from the root to the node currently visited. 5 The Algorithm A first algorithm for solving LCCIS consists in generating the common connected subgraphs of the two input graphs and returning a largest one. This algorithm
7 168 B. Cuissart and J.-J. Hébrard performs a complete traversal of a TOCCS of the input graphs. We will see that, in fact, parts of the TOCCS may be ignored. Throughout this section, G 1 (V 1,E 1 ) and G 2 (V 2,E 2 ) are fixed graphs, (T,r) is a TOCS of G 1, and (T,r ) is a TOCCS of G 1 and G 2 built from (T,r). Recall that for every node x of T, PL (x) ={v V 1 : y, y r, y x and L(y) =v }. For each node x of T, we define PL (x )={(v 1, Excluded ) : y,y r,y x and L (y )=(v 1, Excluded )}. The following propositions allow us not to entirely examine the TOCCS explored by the algorithm. Proposition 13. Let m 0 be an integer and x a node of T. If V 1 PL (x ) m, then PL +(y ) m, for every descendant y of x. Remark that V 1 PL (x ) is the number of vertices of V 1 not yet excluded, when x is visited. Suppose the search has already discovered a common subgraph of size m. If V 1 PL (x ) m, then it is useless to explore the principal subtree of T at x, since, according to Prop. 13, we would not find any common subgraph of size greater than m. Proposition 14. Let x beanodeoft such that PL +(x ), and f 1 aleaf of T descending from x (x f 1). If for every y such that x <y f 1, L (y ) is positive, then, for every leaf f 2 descending from x, we have PL +(f 2) PL +(f 1 ). Proof (Sketch). Let x = Or(x ), f 1 = Or(f 1) and f 2 = Or(f 2) (Definition 9). G 1 [PL + (f 1 )] is the largest connected subgraph of G 1 that contains the vertices of PL + (x) and does not contain the vertices of PL (x). By hypothesis, PL +(x ),thuspl + (x). Consequently, G 1 [PL + (f 2 )] contains the vertices of PL + (x) and does not contain the vertices of PL (x). Hence, PL + (f 2 ) PL + (f 1 ) and PL +(f 2) PL +(f 1). Let x beanodeoft such that PL +(x ). After having explored a path p from x to a leaf f 1, such that p only contains nodes positively labelled (except x possibly), it is useless to explore the other paths beginning at x. Indeed we are sure, from Prop. 14, that these paths do not lead to any common subgraph larger than the one given by PL +(f 1). Finally, our algorithm partially explores a TOCCS in a depth first manner, ignoring parts of it that cannot provide a common subgraph larger than the current largest one already found. 6 Experimental Results It is essential to characterize graph matching algorithms by their performances [11, 12]. We experimentally compared our algorithm (T-TOCCS) with the algorithm based on the method proposed by I. Koch (C-CLIQUE) [9]. Material. The experiments were realized on a computer with 1 GB of memory and the AMD Athlon processor (2,2 GHz). We implemented both algorithms
8 A Direct Algorithm to Find a LCCIS of Two Graphs 169 Table 1. Experimental results Randomly Connected Graphs, fixed density. S M C E C M T E T S M C E C M T E T Density =0.1 Density = Density =0.5 Density = Randomly Connected Graphs, fixed size. D M C E C M T E T D M C E C M T E T Size = 18 Size = Irregular 2d Meshes. D M C E C M T E T D M C E C M T E T Size = 9 Size = S : Size of the input graphs, D : Density of the input graphs, C-CLIQUE : M C : Mean duration of the calculus (in seconds). E C : Standard deviation. T-TOCCS : M T : Mean duration of the calculus (in seconds). E T : Standard deviation.
9 170 B. Cuissart and J.-J. Hébrard in C, and compiled the code with the GNU gcc 3.3 compiler with appropriate optimizations. The algorithms were tested on two kinds of graphs : randomly connected graphs and irregular 2D meshes. These graphs are described by M. De Santo et al. in [13, 14]. Notice that they are always connected. In a randomly connected graph, the probability of an edge connecting two vertices is independant on the vertices themselves. We adopted the model proposed in [15] to generate our instances. Since it is generally agreed that irregular 2D meshes represent a worst case for general graph matching algorithms [15], we also considered these graphs. Results. We have compared the performances of the two algorithms on the same instances. The results are displayed on three tables (see Table 1). The first two tables concern the results obtained with randomly connected graphs, the third table is dedicated to irregular 2D meshes. A cell of these tables corresponds to a measure on a sample of ten instances. For example, the cell at the top left corner of the first table indicates that C-CLIQUE has taken on average seconds to find a LCCIS between two randomly connected graphs of size 21 and of density 0.1. For each series, the measures were stopped as soon as the time required to solve one instance exceeded 500 seconds. Discussion. The examination of the tables shows that T-TOCCS operates faster than C-CLIQUE on these instances. When the input graphs are randomly connected graphs of density η = 0.5, T-TOCCS solves the problem 3 times faster than C-CLIQUE. This difference increases as the density of the input graphs moves away from 0.5. T-TOCCS operates on average 10 times faster than C-CLIQUE when the density is equal to 0.1. It operates 40 times faster when the input graphs have high density (D =0.85). The observations are similar for the 2D meshes. When the density of the meshes is close to 0.5, T-TOCCS operates about 3 times faster than C-CLIQUE. This ratio rapidly increases to reach 170 when the input graphs are the regular 2D meshes with 16 vertices. On the other side, this ratio reaches 25 when the input graphs have a density of References 1. Rosen, K., ed.: 8 : Graph theory, 9: Trees. In: Handbook of discrete and combinatorial mathematics. CRC Press (2000) Koch, I., Lengauer, T., Wanke, E.: An algorithm for finding common subtopologies in a set of protein structures. J. Comput. Biol. 3 (1996) Koch, I., Lengauer, T.: Detection of distant structural similarities in a set of proteins using a fast graph based method. In Gaasterland, T., Karp, P., Karplus, K., Ouzounis, C., Sander, C., Valencia, A., eds.: Proc. 5th Int. Conf. on Intelligent systems for molecular biology, Menlo Park, AAAI Press (1997) Raymond, J., Gardiner, E., Willett, P.: Heuristics for similarity searching of chemical graphs using a maximum common edge subgraph algorithm. J. Chem. Inf. Comput. Sci. 42 (2002)
10 A Direct Algorithm to Find a LCCIS of Two Graphs Raymond, J., Gardiner, E., Willett, P.: RASCAL : calculation of graph similarity using maximum common edge subgraphs. Comp. J. 45 (2002) Garciá, G., Ruiz, I., Gómez-Nieto, M.: Step-by-step calculation of all maximum common substructures through a constraint satisfaction based algorithm. J. Chem. Inf. Comput. Sci. 44 (2004) Cuissart, B., Touffet, F., Crémilleux, B., Bureau, R., Rault, S.: The maximum common substructure as a molecular depiction in a supervised classification context: experiments in quantitative structure/biodegradability relationships. J. Chem. Inf. Comput. Sci. 42 (2002) Garey, M., Johnson, D.: Computers and Intractability: a guide to the theory of NP-completeness. Freeman (1979) 9. Koch, I.: Enumerating all connected maximal common subgraphs in two graphs. Theor. Comput. Sci. 250 (2001) Cormen, T., Leiserson, C., Rivest, R., Stein, C.: 22. Elementary graph algorithms. In: Introduction to algorithms. McGraw-Hill (2001) 11. Bunke, H., Foggia, P., Guidobaldi, C., Sansone, C., Vento, M.: A comparison of algorithms for maximum common subgraph on randomly connected graphs. In Caelli, T., Amin, A., Duin, R.P.W., Kamel, M.S., de Ridder, D., eds.: Joint IAPR International Workshops SSPR 2002 and SPR 2002, Proceedings. Volume 2396 of Lecture Notes in Computer Science., Springer-Verlag (2002) Conte, D., Guidobaldi, C., Sansone, C.: A comparison of three maximum common subgraph algorithms on a large database of labeled graphs. In Hancock, E., Vento, M., eds.: IAPR Workshop GbRPR. Volume 2726 of Lecture Notes in Computer Science., Springer-Verlag (2003) Foggia, P., Sansone, C., Vento, M.: A database of graphs for isomorphism and subgraph isomorphism benchmarking. In: Proc. 3rd IAPR TC-15 GbR Worshop. (2001) DeSanto, M., Foggia, P., Sansone, C., Vento, M.: A large database of graphs and its use for benchmarking graph isomorphism algorithms. Pattern Recogn. Lett. 24 (2003) Ullman, J.: An algorithm for subgraph isomorphism. Journal of the Association for Computing Machinery 23 (1976) 31 42
A Performance Analysis on Maximal Common Subgraph Algorithms
 A Performance Analysis on Maximal Common Subgraph Algorithms Ruud Welling University of Twente P.O. Box 217, 7500AE Enschede The Netherlands r.h.a.welling@student.utwente.nl ABSTRACT Graphs can be used
A Performance Analysis on Maximal Common Subgraph Algorithms Ruud Welling University of Twente P.O. Box 217, 7500AE Enschede The Netherlands r.h.a.welling@student.utwente.nl ABSTRACT Graphs can be used
CP Models for Maximum Common Subgraph Problems
 CP Models for Maximum Common Subgraph Problems Samba Ndojh Ndiaye and Christine Solnon Université de Lyon, CNRS Université Lyon 1, LIRIS, UMR5205, F-69622, France Abstract. The distance between two graphs
CP Models for Maximum Common Subgraph Problems Samba Ndojh Ndiaye and Christine Solnon Université de Lyon, CNRS Université Lyon 1, LIRIS, UMR5205, F-69622, France Abstract. The distance between two graphs
An Improved Algorithm for Matching Large Graphs
 An Improved Algorithm for Matching Large Graphs L. P. Cordella, P. Foggia, C. Sansone, M. Vento Dipartimento di Informatica e Sistemistica Università degli Studi di Napoli Federico II Via Claudio, 2 8025
An Improved Algorithm for Matching Large Graphs L. P. Cordella, P. Foggia, C. Sansone, M. Vento Dipartimento di Informatica e Sistemistica Università degli Studi di Napoli Federico II Via Claudio, 2 8025
A more efficient algorithm for perfect sorting by reversals
 A more efficient algorithm for perfect sorting by reversals Sèverine Bérard 1,2, Cedric Chauve 3,4, and Christophe Paul 5 1 Département de Mathématiques et d Informatique Appliquée, INRA, Toulouse, France.
A more efficient algorithm for perfect sorting by reversals Sèverine Bérard 1,2, Cedric Chauve 3,4, and Christophe Paul 5 1 Département de Mathématiques et d Informatique Appliquée, INRA, Toulouse, France.
Subgraph Isomorphism. Artem Maksov, Yong Li, Reese Butler 03/04/2015
 Subgraph Isomorphism Artem Maksov, Yong Li, Reese Butler 03/04/2015 Similar Graphs The two graphs below look different but are structurally the same. Definition What is Graph Isomorphism? An isomorphism
Subgraph Isomorphism Artem Maksov, Yong Li, Reese Butler 03/04/2015 Similar Graphs The two graphs below look different but are structurally the same. Definition What is Graph Isomorphism? An isomorphism
An Edge-Swap Heuristic for Finding Dense Spanning Trees
 Theory and Applications of Graphs Volume 3 Issue 1 Article 1 2016 An Edge-Swap Heuristic for Finding Dense Spanning Trees Mustafa Ozen Bogazici University, mustafa.ozen@boun.edu.tr Hua Wang Georgia Southern
Theory and Applications of Graphs Volume 3 Issue 1 Article 1 2016 An Edge-Swap Heuristic for Finding Dense Spanning Trees Mustafa Ozen Bogazici University, mustafa.ozen@boun.edu.tr Hua Wang Georgia Southern
Signatures of Combinatorial Maps
 Signatures of Combinatorial Maps No Author Given No Institute Given Abstract. In this paper, we address the problem of computing a canonical representation of an n-dimensional combinatorial map. For that,
Signatures of Combinatorial Maps No Author Given No Institute Given Abstract. In this paper, we address the problem of computing a canonical representation of an n-dimensional combinatorial map. For that,
Phylogenetic networks that display a tree twice
 Bulletin of Mathematical Biology manuscript No. (will be inserted by the editor) Phylogenetic networks that display a tree twice Paul Cordue Simone Linz Charles Semple Received: date / Accepted: date Abstract
Bulletin of Mathematical Biology manuscript No. (will be inserted by the editor) Phylogenetic networks that display a tree twice Paul Cordue Simone Linz Charles Semple Received: date / Accepted: date Abstract
On the Complexity of Various Parameterizations of Common Induced Subgraph Isomorphism
 On the Complexity of Various Parameterizations of Common Induced Subgraph Isomorphism Faisal N. Abu-Khzam 1, Édouard Bonnet2 and Florian Sikora 2 1 Lebanese American University, Beirut, Lebanon faisal.abukhzam@lau.edu.lb
On the Complexity of Various Parameterizations of Common Induced Subgraph Isomorphism Faisal N. Abu-Khzam 1, Édouard Bonnet2 and Florian Sikora 2 1 Lebanese American University, Beirut, Lebanon faisal.abukhzam@lau.edu.lb
The Maximum Common Subgraph Problem: Faster Solutions via Vertex Cover
 The Maximum Common Subgraph Problem: Faster Solutions via Vertex Cover Faisal N. Abu-Khzam Division of Computer Science and Mathematics Lebanese American University Beirut, Lebanon faisal.abukhzam@lau.edu.lb
The Maximum Common Subgraph Problem: Faster Solutions via Vertex Cover Faisal N. Abu-Khzam Division of Computer Science and Mathematics Lebanese American University Beirut, Lebanon faisal.abukhzam@lau.edu.lb
Treewidth and graph minors
 Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
A Performance Comparison of Five Algorithms for Graph Isomorphism
 A Performance Comparison of Five Algorithms for Graph Isomorphism P. Foggia, C.Sansone, M. Vento Dipartimento di Informatica e Sistemistica Via Claudio, 21 - I 80125 - Napoli, Italy {foggiapa, carlosan,
A Performance Comparison of Five Algorithms for Graph Isomorphism P. Foggia, C.Sansone, M. Vento Dipartimento di Informatica e Sistemistica Via Claudio, 21 - I 80125 - Napoli, Italy {foggiapa, carlosan,
ON VERTEX b-critical TREES. Mostafa Blidia, Noureddine Ikhlef Eschouf, and Frédéric Maffray
 Opuscula Math. 33, no. 1 (2013), 19 28 http://dx.doi.org/10.7494/opmath.2013.33.1.19 Opuscula Mathematica ON VERTEX b-critical TREES Mostafa Blidia, Noureddine Ikhlef Eschouf, and Frédéric Maffray Communicated
Opuscula Math. 33, no. 1 (2013), 19 28 http://dx.doi.org/10.7494/opmath.2013.33.1.19 Opuscula Mathematica ON VERTEX b-critical TREES Mostafa Blidia, Noureddine Ikhlef Eschouf, and Frédéric Maffray Communicated
Binary Decision Diagrams
 Logic and roof Hilary 2016 James Worrell Binary Decision Diagrams A propositional formula is determined up to logical equivalence by its truth table. If the formula has n variables then its truth table
Logic and roof Hilary 2016 James Worrell Binary Decision Diagrams A propositional formula is determined up to logical equivalence by its truth table. If the formula has n variables then its truth table
Parameterized coloring problems on chordal graphs
 Parameterized coloring problems on chordal graphs Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary dmarx@cs.bme.hu
Parameterized coloring problems on chordal graphs Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary dmarx@cs.bme.hu
A generalization of Mader s theorem
 A generalization of Mader s theorem Ajit A. Diwan Department of Computer Science and Engineering Indian Institute of Technology, Bombay Mumbai, 4000076, India. email: aad@cse.iitb.ac.in 18 June 2007 Abstract
A generalization of Mader s theorem Ajit A. Diwan Department of Computer Science and Engineering Indian Institute of Technology, Bombay Mumbai, 4000076, India. email: aad@cse.iitb.ac.in 18 June 2007 Abstract
Generating edge covers of path graphs
 Generating edge covers of path graphs J. Raymundo Marcial-Romero, J. A. Hernández, Vianney Muñoz-Jiménez and Héctor A. Montes-Venegas Facultad de Ingeniería, Universidad Autónoma del Estado de México,
Generating edge covers of path graphs J. Raymundo Marcial-Romero, J. A. Hernández, Vianney Muñoz-Jiménez and Héctor A. Montes-Venegas Facultad de Ingeniería, Universidad Autónoma del Estado de México,
A Performance Comparison of Five Algorithms for Graph Isomorphism
 A Performance Comparison of Five Algorithms for Graph Isomorphism P. Foggia, C.Sansone, M. Vento Dipartimento di Informatica e Sistemistica Via Claudio, 21 - I 80125 - Napoli, Italy {foggiapa, carlosan,
A Performance Comparison of Five Algorithms for Graph Isomorphism P. Foggia, C.Sansone, M. Vento Dipartimento di Informatica e Sistemistica Via Claudio, 21 - I 80125 - Napoli, Italy {foggiapa, carlosan,
γ(ɛ) (a, b) (a, d) (d, a) (a, b) (c, d) (d, d) (e, e) (e, a) (e, e) (a) Draw a picture of G.
 MAD 3105 Spring 2006 Solutions for Review for Test 2 1. Define a graph G with V (G) = {a, b, c, d, e}, E(G) = {r, s, t, u, v, w, x, y, z} and γ, the function defining the edges, is given by the table ɛ
MAD 3105 Spring 2006 Solutions for Review for Test 2 1. Define a graph G with V (G) = {a, b, c, d, e}, E(G) = {r, s, t, u, v, w, x, y, z} and γ, the function defining the edges, is given by the table ɛ
Graph Matching: Fast Candidate Elimination Using Machine Learning Techniques
 Graph Matching: Fast Candidate Elimination Using Machine Learning Techniques M. Lazarescu 1,2, H. Bunke 1, and S. Venkatesh 2 1 Computer Science Department, University of Bern, Switzerland 2 School of
Graph Matching: Fast Candidate Elimination Using Machine Learning Techniques M. Lazarescu 1,2, H. Bunke 1, and S. Venkatesh 2 1 Computer Science Department, University of Bern, Switzerland 2 School of
Trees. 3. (Minimally Connected) G is connected and deleting any of its edges gives rise to a disconnected graph.
 Trees 1 Introduction Trees are very special kind of (undirected) graphs. Formally speaking, a tree is a connected graph that is acyclic. 1 This definition has some drawbacks: given a graph it is not trivial
Trees 1 Introduction Trees are very special kind of (undirected) graphs. Formally speaking, a tree is a connected graph that is acyclic. 1 This definition has some drawbacks: given a graph it is not trivial
Map Edit Distance vs Graph Edit Distance for Matching Images
 Map Edit Distance vs Graph Edit Distance for Matching Images Camille Combier 1,2, Guillaume Damiand 3,2, and Christine Solnon 3,2 1 Université Lyon 1, LIRIS, UMR 5205 CNRS, 69622 Villeurbanne, France 2
Map Edit Distance vs Graph Edit Distance for Matching Images Camille Combier 1,2, Guillaume Damiand 3,2, and Christine Solnon 3,2 1 Université Lyon 1, LIRIS, UMR 5205 CNRS, 69622 Villeurbanne, France 2
Lecture 19 Thursday, March 29. Examples of isomorphic, and non-isomorphic graphs will be given in class.
 CIS 160 - Spring 2018 (instructor Val Tannen) Lecture 19 Thursday, March 29 GRAPH THEORY Graph isomorphism Definition 19.1 Two graphs G 1 = (V 1, E 1 ) and G 2 = (V 2, E 2 ) are isomorphic, write G 1 G
CIS 160 - Spring 2018 (instructor Val Tannen) Lecture 19 Thursday, March 29 GRAPH THEORY Graph isomorphism Definition 19.1 Two graphs G 1 = (V 1, E 1 ) and G 2 = (V 2, E 2 ) are isomorphic, write G 1 G
Trees Rooted Trees Spanning trees and Shortest Paths. 12. Graphs and Trees 2. Aaron Tan November 2017
 12. Graphs and Trees 2 Aaron Tan 6 10 November 2017 1 10.5 Trees 2 Definition Definition Definition: Tree A graph is said to be circuit-free if, and only if, it has no circuits. A graph is called a tree
12. Graphs and Trees 2 Aaron Tan 6 10 November 2017 1 10.5 Trees 2 Definition Definition Definition: Tree A graph is said to be circuit-free if, and only if, it has no circuits. A graph is called a tree
The 3-Steiner Root Problem
 The 3-Steiner Root Problem Maw-Shang Chang 1 and Ming-Tat Ko 2 1 Department of Computer Science and Information Engineering National Chung Cheng University, Chiayi 621, Taiwan, R.O.C. mschang@cs.ccu.edu.tw
The 3-Steiner Root Problem Maw-Shang Chang 1 and Ming-Tat Ko 2 1 Department of Computer Science and Information Engineering National Chung Cheng University, Chiayi 621, Taiwan, R.O.C. mschang@cs.ccu.edu.tw
A GRAPH FROM THE VIEWPOINT OF ALGEBRAIC TOPOLOGY
 A GRAPH FROM THE VIEWPOINT OF ALGEBRAIC TOPOLOGY KARL L. STRATOS Abstract. The conventional method of describing a graph as a pair (V, E), where V and E repectively denote the sets of vertices and edges,
A GRAPH FROM THE VIEWPOINT OF ALGEBRAIC TOPOLOGY KARL L. STRATOS Abstract. The conventional method of describing a graph as a pair (V, E), where V and E repectively denote the sets of vertices and edges,
REDUCING GRAPH COLORING TO CLIQUE SEARCH
 Asia Pacific Journal of Mathematics, Vol. 3, No. 1 (2016), 64-85 ISSN 2357-2205 REDUCING GRAPH COLORING TO CLIQUE SEARCH SÁNDOR SZABÓ AND BOGDÁN ZAVÁLNIJ Institute of Mathematics and Informatics, University
Asia Pacific Journal of Mathematics, Vol. 3, No. 1 (2016), 64-85 ISSN 2357-2205 REDUCING GRAPH COLORING TO CLIQUE SEARCH SÁNDOR SZABÓ AND BOGDÁN ZAVÁLNIJ Institute of Mathematics and Informatics, University
Lecture 5: Graphs. Rajat Mittal. IIT Kanpur
 Lecture : Graphs Rajat Mittal IIT Kanpur Combinatorial graphs provide a natural way to model connections between different objects. They are very useful in depicting communication networks, social networks
Lecture : Graphs Rajat Mittal IIT Kanpur Combinatorial graphs provide a natural way to model connections between different objects. They are very useful in depicting communication networks, social networks
Graph Theory. Probabilistic Graphical Models. L. Enrique Sucar, INAOE. Definitions. Types of Graphs. Trajectories and Circuits.
 Theory Probabilistic ical Models L. Enrique Sucar, INAOE and (INAOE) 1 / 32 Outline and 1 2 3 4 5 6 7 8 and 9 (INAOE) 2 / 32 A graph provides a compact way to represent binary relations between a set of
Theory Probabilistic ical Models L. Enrique Sucar, INAOE and (INAOE) 1 / 32 Outline and 1 2 3 4 5 6 7 8 and 9 (INAOE) 2 / 32 A graph provides a compact way to represent binary relations between a set of
CS 441 Discrete Mathematics for CS Lecture 26. Graphs. CS 441 Discrete mathematics for CS. Final exam
 CS 441 Discrete Mathematics for CS Lecture 26 Graphs Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Final exam Saturday, April 26, 2014 at 10:00-11:50am The same classroom as lectures The exam
CS 441 Discrete Mathematics for CS Lecture 26 Graphs Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Final exam Saturday, April 26, 2014 at 10:00-11:50am The same classroom as lectures The exam
Chordal Graphs: Theory and Algorithms
 Chordal Graphs: Theory and Algorithms 1 Chordal graphs Chordal graph : Every cycle of four or more vertices has a chord in it, i.e. there is an edge between two non consecutive vertices of the cycle. Also
Chordal Graphs: Theory and Algorithms 1 Chordal graphs Chordal graph : Every cycle of four or more vertices has a chord in it, i.e. there is an edge between two non consecutive vertices of the cycle. Also
The Structure of Bull-Free Perfect Graphs
 The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
a Steiner tree for S if S V(T) holds. For convenience, although T is not a rooted tree, we call each degree-1 vertex of T a leaf of T. We say that a l
 Reachability between Steiner Trees in a Graph Haruka Mizuta 1,2,a) Takehiro Ito 1,3,b) Xiao Zhou 1,c) Abstract: In this paper, we study the reachability between Steiner trees in a graph: Given two Steiner
Reachability between Steiner Trees in a Graph Haruka Mizuta 1,2,a) Takehiro Ito 1,3,b) Xiao Zhou 1,c) Abstract: In this paper, we study the reachability between Steiner trees in a graph: Given two Steiner
Lecture 10: Strongly Connected Components, Biconnected Graphs
 15-750: Graduate Algorithms February 8, 2016 Lecture 10: Strongly Connected Components, Biconnected Graphs Lecturer: David Witmer Scribe: Zhong Zhou 1 DFS Continued We have introduced Depth-First Search
15-750: Graduate Algorithms February 8, 2016 Lecture 10: Strongly Connected Components, Biconnected Graphs Lecturer: David Witmer Scribe: Zhong Zhou 1 DFS Continued We have introduced Depth-First Search
Discrete mathematics
 Discrete mathematics Petr Kovář petr.kovar@vsb.cz VŠB Technical University of Ostrava DiM 470-2301/02, Winter term 2018/2019 About this file This file is meant to be a guideline for the lecturer. Many
Discrete mathematics Petr Kovář petr.kovar@vsb.cz VŠB Technical University of Ostrava DiM 470-2301/02, Winter term 2018/2019 About this file This file is meant to be a guideline for the lecturer. Many
On Sequential Topogenic Graphs
 Int. J. Contemp. Math. Sciences, Vol. 5, 2010, no. 36, 1799-1805 On Sequential Topogenic Graphs Bindhu K. Thomas, K. A. Germina and Jisha Elizabath Joy Research Center & PG Department of Mathematics Mary
Int. J. Contemp. Math. Sciences, Vol. 5, 2010, no. 36, 1799-1805 On Sequential Topogenic Graphs Bindhu K. Thomas, K. A. Germina and Jisha Elizabath Joy Research Center & PG Department of Mathematics Mary
Learning Characteristic Structured Patterns in Rooted Planar Maps
 Learning Characteristic Structured Patterns in Rooted Planar Maps Satoshi Kawamoto Yusuke Suzuki Takayoshi Shoudai Abstract Exting the concept of ordered graphs, we propose a new data structure to express
Learning Characteristic Structured Patterns in Rooted Planar Maps Satoshi Kawamoto Yusuke Suzuki Takayoshi Shoudai Abstract Exting the concept of ordered graphs, we propose a new data structure to express
Theoretical Computer Science
 Theoretical Computer Science 407 (2008) 564 568 Contents lists available at ScienceDirect Theoretical Computer Science journal homepage: www.elsevier.com/locate/tcs Note A note on the problem of reporting
Theoretical Computer Science 407 (2008) 564 568 Contents lists available at ScienceDirect Theoretical Computer Science journal homepage: www.elsevier.com/locate/tcs Note A note on the problem of reporting
A Partition Method for Graph Isomorphism
 Available online at www.sciencedirect.com Physics Procedia ( ) 6 68 International Conference on Solid State Devices and Materials Science A Partition Method for Graph Isomorphism Lijun Tian, Chaoqun Liu
Available online at www.sciencedirect.com Physics Procedia ( ) 6 68 International Conference on Solid State Devices and Materials Science A Partition Method for Graph Isomorphism Lijun Tian, Chaoqun Liu
Linear time algorithms for weighted offensive and powerful alliances in trees
 Linear time algorithms for weighted offensive and powerful alliances in trees Ararat Harutyunyan Laboratoire de l Informatique du Parallélisme École Normale Supérieure de Lyon 46 Allée d Italie, 69364
Linear time algorithms for weighted offensive and powerful alliances in trees Ararat Harutyunyan Laboratoire de l Informatique du Parallélisme École Normale Supérieure de Lyon 46 Allée d Italie, 69364
Optimization I : Brute force and Greedy strategy
 Chapter 3 Optimization I : Brute force and Greedy strategy A generic definition of an optimization problem involves a set of constraints that defines a subset in some underlying space (like the Euclidean
Chapter 3 Optimization I : Brute force and Greedy strategy A generic definition of an optimization problem involves a set of constraints that defines a subset in some underlying space (like the Euclidean
Complexity Results on Graphs with Few Cliques
 Discrete Mathematics and Theoretical Computer Science DMTCS vol. 9, 2007, 127 136 Complexity Results on Graphs with Few Cliques Bill Rosgen 1 and Lorna Stewart 2 1 Institute for Quantum Computing and School
Discrete Mathematics and Theoretical Computer Science DMTCS vol. 9, 2007, 127 136 Complexity Results on Graphs with Few Cliques Bill Rosgen 1 and Lorna Stewart 2 1 Institute for Quantum Computing and School
Infinite locally random graphs
 Infinite locally random graphs Pierre Charbit and Alex D. Scott Abstract Motivated by copying models of the web graph, Bonato and Janssen [3] introduced the following simple construction: given a graph
Infinite locally random graphs Pierre Charbit and Alex D. Scott Abstract Motivated by copying models of the web graph, Bonato and Janssen [3] introduced the following simple construction: given a graph
Computing optimal total vertex covers for trees
 Computing optimal total vertex covers for trees Pak Ching Li Department of Computer Science University of Manitoba Winnipeg, Manitoba Canada R3T 2N2 Abstract. Let G = (V, E) be a simple, undirected, connected
Computing optimal total vertex covers for trees Pak Ching Li Department of Computer Science University of Manitoba Winnipeg, Manitoba Canada R3T 2N2 Abstract. Let G = (V, E) be a simple, undirected, connected
Section Summary. Introduction to Trees Rooted Trees Trees as Models Properties of Trees
 Chapter 11 Copyright McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education. Chapter Summary Introduction to Trees Applications
Chapter 11 Copyright McGraw-Hill Education. All rights reserved. No reproduction or distribution without the prior written consent of McGraw-Hill Education. Chapter Summary Introduction to Trees Applications
The Price of Connectivity for Feedback Vertex Set
 The Price of Connectivity for Feedback Vertex Set Rémy Belmonte 1,, Pim van t Hof 1,, Marcin Kamiński 2, and Daniël Paulusma 3, 1 Department of Informatics, University of Bergen, Norway {remy.belmonte,pim.vanthof}@ii.uib.no
The Price of Connectivity for Feedback Vertex Set Rémy Belmonte 1,, Pim van t Hof 1,, Marcin Kamiński 2, and Daniël Paulusma 3, 1 Department of Informatics, University of Bergen, Norway {remy.belmonte,pim.vanthof}@ii.uib.no
A Comparison of Decomposition Methods for the Maximum Common Subgraph Problem
 A Comparison of Decomposition Methods for the Maximum Common Subgraph Problem Maël MINOT LIRIS UMR 5205 CNRS Université de Lyon INSA de Lyon, France mael.minot@liris.cnrs.fr Samba Ndojh NDIAYE LIRIS UMR
A Comparison of Decomposition Methods for the Maximum Common Subgraph Problem Maël MINOT LIRIS UMR 5205 CNRS Université de Lyon INSA de Lyon, France mael.minot@liris.cnrs.fr Samba Ndojh NDIAYE LIRIS UMR
A Simplified Correctness Proof for a Well-Known Algorithm Computing Strongly Connected Components
 A Simplified Correctness Proof for a Well-Known Algorithm Computing Strongly Connected Components Ingo Wegener FB Informatik, LS2, Univ. Dortmund, 44221 Dortmund, Germany wegener@ls2.cs.uni-dortmund.de
A Simplified Correctness Proof for a Well-Known Algorithm Computing Strongly Connected Components Ingo Wegener FB Informatik, LS2, Univ. Dortmund, 44221 Dortmund, Germany wegener@ls2.cs.uni-dortmund.de
On Covering a Graph Optimally with Induced Subgraphs
 On Covering a Graph Optimally with Induced Subgraphs Shripad Thite April 1, 006 Abstract We consider the problem of covering a graph with a given number of induced subgraphs so that the maximum number
On Covering a Graph Optimally with Induced Subgraphs Shripad Thite April 1, 006 Abstract We consider the problem of covering a graph with a given number of induced subgraphs so that the maximum number
Applied Mathematics Letters. Graph triangulations and the compatibility of unrooted phylogenetic trees
 Applied Mathematics Letters 24 (2011) 719 723 Contents lists available at ScienceDirect Applied Mathematics Letters journal homepage: www.elsevier.com/locate/aml Graph triangulations and the compatibility
Applied Mathematics Letters 24 (2011) 719 723 Contents lists available at ScienceDirect Applied Mathematics Letters journal homepage: www.elsevier.com/locate/aml Graph triangulations and the compatibility
 This article was originally published in a journal published by Elsevier, and the attached copy is provided by Elsevier for the author s benefit and for the benefit of the author s institution, for non-commercial
This article was originally published in a journal published by Elsevier, and the attached copy is provided by Elsevier for the author s benefit and for the benefit of the author s institution, for non-commercial
Genetic Algorithms Based Solution To Maximum Clique Problem
 Genetic Algorithms Based Solution To Maximum Clique Problem Harsh Bhasin computergrad.com Faridabad, India i_harsh_bhasin@yahoo.com Rohan Mahajan Lingaya s University Faridabad, India mahajanr28@gmail.com
Genetic Algorithms Based Solution To Maximum Clique Problem Harsh Bhasin computergrad.com Faridabad, India i_harsh_bhasin@yahoo.com Rohan Mahajan Lingaya s University Faridabad, India mahajanr28@gmail.com
Key words. graph algorithms, chromatic number, circular arc graphs, induced cycles
 SIAM J. COMPUT. Vol. 0, No. 0, pp. 000 000 c XXXX Society for Industrial and Applied Mathematics REVISITING TUCKER S ALGORITHM TO COLOR CIRCULAR ARC GRAPHS MARIO VALENCIA-PABON Abstract. The circular arc
SIAM J. COMPUT. Vol. 0, No. 0, pp. 000 000 c XXXX Society for Industrial and Applied Mathematics REVISITING TUCKER S ALGORITHM TO COLOR CIRCULAR ARC GRAPHS MARIO VALENCIA-PABON Abstract. The circular arc
Graph Algorithms Using Depth First Search
 Graph Algorithms Using Depth First Search Analysis of Algorithms Week 8, Lecture 1 Prepared by John Reif, Ph.D. Distinguished Professor of Computer Science Duke University Graph Algorithms Using Depth
Graph Algorithms Using Depth First Search Analysis of Algorithms Week 8, Lecture 1 Prepared by John Reif, Ph.D. Distinguished Professor of Computer Science Duke University Graph Algorithms Using Depth
Extremal Graph Theory: Turán s Theorem
 Bridgewater State University Virtual Commons - Bridgewater State University Honors Program Theses and Projects Undergraduate Honors Program 5-9-07 Extremal Graph Theory: Turán s Theorem Vincent Vascimini
Bridgewater State University Virtual Commons - Bridgewater State University Honors Program Theses and Projects Undergraduate Honors Program 5-9-07 Extremal Graph Theory: Turán s Theorem Vincent Vascimini
2. CONNECTIVITY Connectivity
 2. CONNECTIVITY 70 2. Connectivity 2.1. Connectivity. Definition 2.1.1. (1) A path in a graph G = (V, E) is a sequence of vertices v 0, v 1, v 2,..., v n such that {v i 1, v i } is an edge of G for i =
2. CONNECTIVITY 70 2. Connectivity 2.1. Connectivity. Definition 2.1.1. (1) A path in a graph G = (V, E) is a sequence of vertices v 0, v 1, v 2,..., v n such that {v i 1, v i } is an edge of G for i =
Roman Domination in Complementary Prism Graphs
 International J.Math. Combin. Vol.2(2012), 24-31 Roman Domination in Complementary Prism Graphs B.Chaluvaraju and V.Chaitra 1(Department of Mathematics, Bangalore University, Central College Campus, Bangalore
International J.Math. Combin. Vol.2(2012), 24-31 Roman Domination in Complementary Prism Graphs B.Chaluvaraju and V.Chaitra 1(Department of Mathematics, Bangalore University, Central College Campus, Bangalore
PLANAR GRAPH BIPARTIZATION IN LINEAR TIME
 PLANAR GRAPH BIPARTIZATION IN LINEAR TIME SAMUEL FIORINI, NADIA HARDY, BRUCE REED, AND ADRIAN VETTA Abstract. For each constant k, we present a linear time algorithm that, given a planar graph G, either
PLANAR GRAPH BIPARTIZATION IN LINEAR TIME SAMUEL FIORINI, NADIA HARDY, BRUCE REED, AND ADRIAN VETTA Abstract. For each constant k, we present a linear time algorithm that, given a planar graph G, either
motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs { }
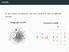 motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs G M { } 2 subgraph motifs 3 motifs Find interesting patterns in a network. 4 motifs Find
motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs G M { } 2 subgraph motifs 3 motifs Find interesting patterns in a network. 4 motifs Find
Throughout the chapter, we will assume that the reader is familiar with the basics of phylogenetic trees.
 Chapter 7 SUPERTREE ALGORITHMS FOR NESTED TAXA Philip Daniel and Charles Semple Abstract: Keywords: Most supertree algorithms combine collections of rooted phylogenetic trees with overlapping leaf sets
Chapter 7 SUPERTREE ALGORITHMS FOR NESTED TAXA Philip Daniel and Charles Semple Abstract: Keywords: Most supertree algorithms combine collections of rooted phylogenetic trees with overlapping leaf sets
Fast Skew Partition Recognition
 Fast Skew Partition Recognition William S. Kennedy 1, and Bruce Reed 2, 1 Department of Mathematics and Statistics, McGill University, Montréal, Canada, H3A2K6 kennedy@math.mcgill.ca 2 School of Computer
Fast Skew Partition Recognition William S. Kennedy 1, and Bruce Reed 2, 1 Department of Mathematics and Statistics, McGill University, Montréal, Canada, H3A2K6 kennedy@math.mcgill.ca 2 School of Computer
A Note On The Sparing Number Of The Sieve Graphs Of Certain Graphs
 Applied Mathematics E-Notes, 15(015), 9-37 c ISSN 1607-510 Available free at mirror sites of http://www.math.nthu.edu.tw/ amen/ A Note On The Sparing Number Of The Sieve Graphs Of Certain Graphs Naduvath
Applied Mathematics E-Notes, 15(015), 9-37 c ISSN 1607-510 Available free at mirror sites of http://www.math.nthu.edu.tw/ amen/ A Note On The Sparing Number Of The Sieve Graphs Of Certain Graphs Naduvath
Routing in Unidirectional (n, k)-star graphs
 Routing in Unidirectional (n, k)-star graphs Eddie CHENG Department of Mathematics and Statistics, Oakland University, Rochester,Michigan USA 48309 and Serge KRUK Department of Mathematics and Statistics,
Routing in Unidirectional (n, k)-star graphs Eddie CHENG Department of Mathematics and Statistics, Oakland University, Rochester,Michigan USA 48309 and Serge KRUK Department of Mathematics and Statistics,
A 2k-Kernelization Algorithm for Vertex Cover Based on Crown Decomposition
 A 2k-Kernelization Algorithm for Vertex Cover Based on Crown Decomposition Wenjun Li a, Binhai Zhu b, a Hunan Provincial Key Laboratory of Intelligent Processing of Big Data on Transportation, Changsha
A 2k-Kernelization Algorithm for Vertex Cover Based on Crown Decomposition Wenjun Li a, Binhai Zhu b, a Hunan Provincial Key Laboratory of Intelligent Processing of Big Data on Transportation, Changsha
Chapter 4. square sum graphs. 4.1 Introduction
 Chapter 4 square sum graphs In this Chapter we introduce a new type of labeling of graphs which is closely related to the Diophantine Equation x 2 + y 2 = n and report results of our preliminary investigations
Chapter 4 square sum graphs In this Chapter we introduce a new type of labeling of graphs which is closely related to the Diophantine Equation x 2 + y 2 = n and report results of our preliminary investigations
A note on the subgraphs of the (2 )-grid
 A note on the subgraphs of the (2 )-grid Josep Díaz a,2,1 a Departament de Llenguatges i Sistemes Informàtics, Universitat Politècnica de Catalunya Campus Nord, Edifici Ω, c/ Jordi Girona Salgado 1-3,
A note on the subgraphs of the (2 )-grid Josep Díaz a,2,1 a Departament de Llenguatges i Sistemes Informàtics, Universitat Politècnica de Catalunya Campus Nord, Edifici Ω, c/ Jordi Girona Salgado 1-3,
Localization in Graphs. Richardson, TX Azriel Rosenfeld. Center for Automation Research. College Park, MD
 CAR-TR-728 CS-TR-3326 UMIACS-TR-94-92 Samir Khuller Department of Computer Science Institute for Advanced Computer Studies University of Maryland College Park, MD 20742-3255 Localization in Graphs Azriel
CAR-TR-728 CS-TR-3326 UMIACS-TR-94-92 Samir Khuller Department of Computer Science Institute for Advanced Computer Studies University of Maryland College Park, MD 20742-3255 Localization in Graphs Azriel
The strong chromatic number of a graph
 The strong chromatic number of a graph Noga Alon Abstract It is shown that there is an absolute constant c with the following property: For any two graphs G 1 = (V, E 1 ) and G 2 = (V, E 2 ) on the same
The strong chromatic number of a graph Noga Alon Abstract It is shown that there is an absolute constant c with the following property: For any two graphs G 1 = (V, E 1 ) and G 2 = (V, E 2 ) on the same
On Universal Cycles of Labeled Graphs
 On Universal Cycles of Labeled Graphs Greg Brockman Harvard University Cambridge, MA 02138 United States brockman@hcs.harvard.edu Bill Kay University of South Carolina Columbia, SC 29208 United States
On Universal Cycles of Labeled Graphs Greg Brockman Harvard University Cambridge, MA 02138 United States brockman@hcs.harvard.edu Bill Kay University of South Carolina Columbia, SC 29208 United States
Chordal deletion is fixed-parameter tractable
 Chordal deletion is fixed-parameter tractable Dániel Marx Institut für Informatik, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. dmarx@informatik.hu-berlin.de Abstract. It
Chordal deletion is fixed-parameter tractable Dániel Marx Institut für Informatik, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. dmarx@informatik.hu-berlin.de Abstract. It
Discrete Applied Mathematics. A revision and extension of results on 4-regular, 4-connected, claw-free graphs
 Discrete Applied Mathematics 159 (2011) 1225 1230 Contents lists available at ScienceDirect Discrete Applied Mathematics journal homepage: www.elsevier.com/locate/dam A revision and extension of results
Discrete Applied Mathematics 159 (2011) 1225 1230 Contents lists available at ScienceDirect Discrete Applied Mathematics journal homepage: www.elsevier.com/locate/dam A revision and extension of results
On some subclasses of circular-arc graphs
 On some subclasses of circular-arc graphs Guillermo Durán - Min Chih Lin Departamento de Computación Facultad de Ciencias Exactas y Naturales Universidad de Buenos Aires e-mail: {willy,oscarlin}@dc.uba.ar
On some subclasses of circular-arc graphs Guillermo Durán - Min Chih Lin Departamento de Computación Facultad de Ciencias Exactas y Naturales Universidad de Buenos Aires e-mail: {willy,oscarlin}@dc.uba.ar
Symbol Detection Using Region Adjacency Graphs and Integer Linear Programming
 2009 10th International Conference on Document Analysis and Recognition Symbol Detection Using Region Adjacency Graphs and Integer Linear Programming Pierre Le Bodic LRI UMR 8623 Using Université Paris-Sud
2009 10th International Conference on Document Analysis and Recognition Symbol Detection Using Region Adjacency Graphs and Integer Linear Programming Pierre Le Bodic LRI UMR 8623 Using Université Paris-Sud
Contracting Chordal Graphs and Bipartite Graphs to Paths and Trees
 Contracting Chordal Graphs and Bipartite Graphs to Paths and Trees Pinar Heggernes Pim van t Hof Benjamin Léveque Christophe Paul Abstract We study the following two graph modification problems: given
Contracting Chordal Graphs and Bipartite Graphs to Paths and Trees Pinar Heggernes Pim van t Hof Benjamin Léveque Christophe Paul Abstract We study the following two graph modification problems: given
MAL 376: Graph Algorithms I Semester Lecture 1: July 24
 MAL 376: Graph Algorithms I Semester 2014-2015 Lecture 1: July 24 Course Coordinator: Prof. B. S. Panda Scribes: Raghuvansh, Himanshu, Mohit, Abhishek Disclaimer: These notes have not been subjected to
MAL 376: Graph Algorithms I Semester 2014-2015 Lecture 1: July 24 Course Coordinator: Prof. B. S. Panda Scribes: Raghuvansh, Himanshu, Mohit, Abhishek Disclaimer: These notes have not been subjected to
On the Page Number of Upward Planar Directed Acyclic Graphs
 Journal of Graph Algorithms and Applications http://jgaa.info/ vol. 17, no. 3, pp. 221 244 (2013) DOI: 10.7155/jgaa.00292 On the Page Number of Upward Planar Directed Acyclic Graphs Fabrizio Frati 1 Radoslav
Journal of Graph Algorithms and Applications http://jgaa.info/ vol. 17, no. 3, pp. 221 244 (2013) DOI: 10.7155/jgaa.00292 On the Page Number of Upward Planar Directed Acyclic Graphs Fabrizio Frati 1 Radoslav
Maximizing edge-ratio is NP-complete
 Maximizing edge-ratio is NP-complete Steven D Noble, Pierre Hansen and Nenad Mladenović February 7, 01 Abstract Given a graph G and a bipartition of its vertices, the edge-ratio is the minimum for both
Maximizing edge-ratio is NP-complete Steven D Noble, Pierre Hansen and Nenad Mladenović February 7, 01 Abstract Given a graph G and a bipartition of its vertices, the edge-ratio is the minimum for both
The Fibonacci hypercube
 AUSTRALASIAN JOURNAL OF COMBINATORICS Volume 40 (2008), Pages 187 196 The Fibonacci hypercube Fred J. Rispoli Department of Mathematics and Computer Science Dowling College, Oakdale, NY 11769 U.S.A. Steven
AUSTRALASIAN JOURNAL OF COMBINATORICS Volume 40 (2008), Pages 187 196 The Fibonacci hypercube Fred J. Rispoli Department of Mathematics and Computer Science Dowling College, Oakdale, NY 11769 U.S.A. Steven
An exact algorithm for max-cut in sparse graphs
 An exact algorithm for max-cut in sparse graphs F. Della Croce a M. J. Kaminski b, V. Th. Paschos c a D.A.I., Politecnico di Torino, Italy b RUTCOR, Rutgers University c LAMSADE, CNRS UMR 7024 and Université
An exact algorithm for max-cut in sparse graphs F. Della Croce a M. J. Kaminski b, V. Th. Paschos c a D.A.I., Politecnico di Torino, Italy b RUTCOR, Rutgers University c LAMSADE, CNRS UMR 7024 and Université
Noncrossing Trees and Noncrossing Graphs
 Noncrossing Trees and Noncrossing Graphs William Y. C. Chen and Sherry H. F. Yan 2 Center for Combinatorics, LPMC, Nanai University, 30007 Tianjin, P.R. China chen@nanai.edu.cn, 2 huifangyan@eyou.com Mathematics
Noncrossing Trees and Noncrossing Graphs William Y. C. Chen and Sherry H. F. Yan 2 Center for Combinatorics, LPMC, Nanai University, 30007 Tianjin, P.R. China chen@nanai.edu.cn, 2 huifangyan@eyou.com Mathematics
Basics of Graph Theory
 Basics of Graph Theory 1 Basic notions A simple graph G = (V, E) consists of V, a nonempty set of vertices, and E, a set of unordered pairs of distinct elements of V called edges. Simple graphs have their
Basics of Graph Theory 1 Basic notions A simple graph G = (V, E) consists of V, a nonempty set of vertices, and E, a set of unordered pairs of distinct elements of V called edges. Simple graphs have their
Vertex-Colouring Edge-Weightings
 Vertex-Colouring Edge-Weightings L. Addario-Berry a, K. Dalal a, C. McDiarmid b, B. A. Reed a and A. Thomason c a School of Computer Science, McGill University, University St. Montreal, QC, H3A A7, Canada
Vertex-Colouring Edge-Weightings L. Addario-Berry a, K. Dalal a, C. McDiarmid b, B. A. Reed a and A. Thomason c a School of Computer Science, McGill University, University St. Montreal, QC, H3A A7, Canada
Minimum Cycle Bases of Halin Graphs
 Minimum Cycle Bases of Halin Graphs Peter F. Stadler INSTITUTE FOR THEORETICAL CHEMISTRY AND MOLECULAR STRUCTURAL BIOLOGY, UNIVERSITY OF VIENNA WÄHRINGERSTRASSE 17, A-1090 VIENNA, AUSTRIA, & THE SANTA
Minimum Cycle Bases of Halin Graphs Peter F. Stadler INSTITUTE FOR THEORETICAL CHEMISTRY AND MOLECULAR STRUCTURAL BIOLOGY, UNIVERSITY OF VIENNA WÄHRINGERSTRASSE 17, A-1090 VIENNA, AUSTRIA, & THE SANTA
Lecture 20 : Trees DRAFT
 CS/Math 240: Introduction to Discrete Mathematics 4/12/2011 Lecture 20 : Trees Instructor: Dieter van Melkebeek Scribe: Dalibor Zelený DRAFT Last time we discussed graphs. Today we continue this discussion,
CS/Math 240: Introduction to Discrete Mathematics 4/12/2011 Lecture 20 : Trees Instructor: Dieter van Melkebeek Scribe: Dalibor Zelený DRAFT Last time we discussed graphs. Today we continue this discussion,
Maximum flows & Maximum Matchings
 Chapter 9 Maximum flows & Maximum Matchings This chapter analyzes flows and matchings. We will define flows and maximum flows and present an algorithm that solves the maximum flow problem. Then matchings
Chapter 9 Maximum flows & Maximum Matchings This chapter analyzes flows and matchings. We will define flows and maximum flows and present an algorithm that solves the maximum flow problem. Then matchings
CLAW-FREE 3-CONNECTED P 11 -FREE GRAPHS ARE HAMILTONIAN
 CLAW-FREE 3-CONNECTED P 11 -FREE GRAPHS ARE HAMILTONIAN TOMASZ LUCZAK AND FLORIAN PFENDER Abstract. We show that every 3-connected claw-free graph which contains no induced copy of P 11 is hamiltonian.
CLAW-FREE 3-CONNECTED P 11 -FREE GRAPHS ARE HAMILTONIAN TOMASZ LUCZAK AND FLORIAN PFENDER Abstract. We show that every 3-connected claw-free graph which contains no induced copy of P 11 is hamiltonian.
List colorings of K 5 -minor-free graphs with special list assignments
 List colorings of K 5 -minor-free graphs with special list assignments Daniel W. Cranston, Anja Pruchnewski, Zsolt Tuza, Margit Voigt 22 March 2010 Abstract A list assignment L of a graph G is a function
List colorings of K 5 -minor-free graphs with special list assignments Daniel W. Cranston, Anja Pruchnewski, Zsolt Tuza, Margit Voigt 22 March 2010 Abstract A list assignment L of a graph G is a function
A SIMPLE APPROXIMATION ALGORITHM FOR NONOVERLAPPING LOCAL ALIGNMENTS (WEIGHTED INDEPENDENT SETS OF AXIS PARALLEL RECTANGLES)
 Chapter 1 A SIMPLE APPROXIMATION ALGORITHM FOR NONOVERLAPPING LOCAL ALIGNMENTS (WEIGHTED INDEPENDENT SETS OF AXIS PARALLEL RECTANGLES) Piotr Berman Department of Computer Science & Engineering Pennsylvania
Chapter 1 A SIMPLE APPROXIMATION ALGORITHM FOR NONOVERLAPPING LOCAL ALIGNMENTS (WEIGHTED INDEPENDENT SETS OF AXIS PARALLEL RECTANGLES) Piotr Berman Department of Computer Science & Engineering Pennsylvania
Winning Positions in Simplicial Nim
 Winning Positions in Simplicial Nim David Horrocks Department of Mathematics and Statistics University of Prince Edward Island Charlottetown, Prince Edward Island, Canada, C1A 4P3 dhorrocks@upei.ca Submitted:
Winning Positions in Simplicial Nim David Horrocks Department of Mathematics and Statistics University of Prince Edward Island Charlottetown, Prince Edward Island, Canada, C1A 4P3 dhorrocks@upei.ca Submitted:
Characterization of Super Strongly Perfect Graphs in Chordal and Strongly Chordal Graphs
 ISSN 0975-3303 Mapana J Sci, 11, 4(2012), 121-131 https://doi.org/10.12725/mjs.23.10 Characterization of Super Strongly Perfect Graphs in Chordal and Strongly Chordal Graphs R Mary Jeya Jothi * and A Amutha
ISSN 0975-3303 Mapana J Sci, 11, 4(2012), 121-131 https://doi.org/10.12725/mjs.23.10 Characterization of Super Strongly Perfect Graphs in Chordal and Strongly Chordal Graphs R Mary Jeya Jothi * and A Amutha
Parameterized graph separation problems
 Parameterized graph separation problems Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary, dmarx@cs.bme.hu Abstract.
Parameterized graph separation problems Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary, dmarx@cs.bme.hu Abstract.
Finding two vertex connected components in linear time
 TO 1 Finding two vertex connected components in linear time Guy Kortsarz TO 2 ackward edges Please read the DFS algorithm (its in the lecture notes). The DFS gives a tree. The edges on the tree are called
TO 1 Finding two vertex connected components in linear time Guy Kortsarz TO 2 ackward edges Please read the DFS algorithm (its in the lecture notes). The DFS gives a tree. The edges on the tree are called
Complexity and approximation of satisfactory partition problems
 Complexity and approximation of satisfactory partition problems Cristina Bazgan, Zsolt Tuza, and Daniel Vanderpooten LAMSADE, Université Paris-Dauphine, France {bazgan,vdp}@lamsade.dauphine.fr Computer
Complexity and approximation of satisfactory partition problems Cristina Bazgan, Zsolt Tuza, and Daniel Vanderpooten LAMSADE, Université Paris-Dauphine, France {bazgan,vdp}@lamsade.dauphine.fr Computer
4 Basics of Trees. Petr Hliněný, FI MU Brno 1 FI: MA010: Trees and Forests
 4 Basics of Trees Trees, actually acyclic connected simple graphs, are among the simplest graph classes. Despite their simplicity, they still have rich structure and many useful application, such as in
4 Basics of Trees Trees, actually acyclic connected simple graphs, are among the simplest graph classes. Despite their simplicity, they still have rich structure and many useful application, such as in
DOUBLE DOMINATION CRITICAL AND STABLE GRAPHS UPON VERTEX REMOVAL 1
 Discussiones Mathematicae Graph Theory 32 (2012) 643 657 doi:10.7151/dmgt.1633 DOUBLE DOMINATION CRITICAL AND STABLE GRAPHS UPON VERTEX REMOVAL 1 Soufiane Khelifi Laboratory LMP2M, Bloc of laboratories
Discussiones Mathematicae Graph Theory 32 (2012) 643 657 doi:10.7151/dmgt.1633 DOUBLE DOMINATION CRITICAL AND STABLE GRAPHS UPON VERTEX REMOVAL 1 Soufiane Khelifi Laboratory LMP2M, Bloc of laboratories
9 About Intersection Graphs
 9 About Intersection Graphs Since this lecture we focus on selected detailed topics in Graph theory that are close to your teacher s heart... The first selected topic is that of intersection graphs, i.e.
9 About Intersection Graphs Since this lecture we focus on selected detailed topics in Graph theory that are close to your teacher s heart... The first selected topic is that of intersection graphs, i.e.
1 Introduction and Results
 On the Structure of Graphs with Large Minimum Bisection Cristina G. Fernandes 1,, Tina Janne Schmidt,, and Anusch Taraz, 1 Instituto de Matemática e Estatística, Universidade de São Paulo, Brazil, cris@ime.usp.br
On the Structure of Graphs with Large Minimum Bisection Cristina G. Fernandes 1,, Tina Janne Schmidt,, and Anusch Taraz, 1 Instituto de Matemática e Estatística, Universidade de São Paulo, Brazil, cris@ime.usp.br
Generalized Convex Set-Valued Maps
 Generalized Convex Set-Valued Maps September 20, 2008 Joël Benoist Department of Mathematics LACO URA-CNRS 1586 University of Limoges 87060 Limoges, France E-mail: benoist@unilim.fr Nicolae Popovici Faculty
Generalized Convex Set-Valued Maps September 20, 2008 Joël Benoist Department of Mathematics LACO URA-CNRS 1586 University of Limoges 87060 Limoges, France E-mail: benoist@unilim.fr Nicolae Popovici Faculty
Scaling limit of random planar maps Lecture 1.
 Scaling limit of random planar maps Lecture. Olivier Bernardi, CNRS, Université Paris-Sud Workshop on randomness and enumeration Temuco, Olivier Bernardi p./3 Planar maps A planar map is a connected planar
Scaling limit of random planar maps Lecture. Olivier Bernardi, CNRS, Université Paris-Sud Workshop on randomness and enumeration Temuco, Olivier Bernardi p./3 Planar maps A planar map is a connected planar
Rainbow game domination subdivision number of a graph
 Rainbow game domination subdivision number of a graph J. Amjadi Department of Mathematics Azarbaijan Shahid Madani University Tabriz, I.R. Iran j-amjadi@azaruniv.edu Abstract The rainbow game domination
Rainbow game domination subdivision number of a graph J. Amjadi Department of Mathematics Azarbaijan Shahid Madani University Tabriz, I.R. Iran j-amjadi@azaruniv.edu Abstract The rainbow game domination
