A New Game Invariant of Graphs: the Game Distinguishing Number
|
|
|
- Kristopher Harrington
- 5 years ago
- Views:
Transcription
1 Discrete Mathematics and Theoretical Computer Science DMTCS vol. 19:1, 017, # A New Game Invariant of Graphs: the Game Distinguishing Number arxiv: v7 [math.co] 7 Feb 017 Sylvain Gravier 1 Kahina Meslem 3 Simon Schmidt Souad Slimani,3 1 CNRS, Institut Fourier, UMR 558, S.F.R. Maths à Modeler, Université Grenoble Alpes, France Institut Fourier, S.F.R. Maths à Modeler, Université Grenoble Alpes, France 3 LaROMaD, S.F.R. Maths à Modeler, Faculté des Mathématiques, U.S.T.H.B, Alger, Algeria received 0 th Oct. 015, revised nd Oct. 015, 1 st Aug. 016, 8 th Nov. 016, accepted 30 th Jan The distinguishing number of a graph G is a symmetry related graph invariant whose study started two decades ago. The distinguishing number D(G) is the least integer d such that G has a distinguishing d-coloring. A distinguishing d-coloring is a coloring c : V (G) {1,, d} invariant only under the trivial automorphism. In this paper, we introduce a game variant of the distinguishing number. The distinguishing game is a game with two players, the Gentle and the Rascal, with antagonist goals. This game is played on a graph G with a set of d N colors. Alternately, the two players choose a vertex of G and color it with one of the d colors. The game ends when all the vertices have been colored. Then the Gentle wins if the coloring is distinguishing and the Rascal wins otherwise. This game leads to define two new invariants for a graph G, which are the minimum numbers of colors needed to ensure that the Gentle has a winning strategy, depending on who starts. These invariants could be infinite, thus we start by giving sufficient conditions to have infinite game distinguishing numbers. We also show that for graphs with cyclic automorphism group of prime odd order, both game invariants are finite. After that, we define a class of graphs, the involutive graphs, for which the game distinguishing number can be quadratically bounded above by the classical distinguishing number. The definition of this class is closely related to imprimitive actions whose blocks have size. Then, we apply results on involutive graphs to compute the exact value of these invariants for hypercubes and even cycles. Finally, we study odd cycles, for which we are able to compute the exact value when their order is not prime. In the prime order case, we give an upper bound of 3. Keywords: distinguishing number, graph automorphism, combinatorial game, hypercube 1 Background and definition of the game The distinguishing number of a graph G is a symmetry related graph invariant. Its study started two decades ago in a work by Albertson and Collins [1]. Given a graph G the distinguishing number D(G) is the least integer d such that G has a distinguishing d-coloring. A distinguishing d-coloring is a coloring c : V (G) {1,, d} invariant only under the trivial automorphism. More generally, we say that an automorphism σ of a graph G preserves the coloring c or is a color preserving automorphism, if c(u) = c(σ(u)) for all u V (G). We denote by Aut(G), the automorphism group of G. Clearly, for each coloring c of the vertex set of G, the set Aut c (G) = {σ Aut(G) : c σ = c} is a subgroup of ISSN c 017 by the author(s) Distributed under a Creative Commons Attribution 4.0 International License
2 Sylvain Gravier, Kahina Meslem, Simon Schmidt, Souad Slimani Aut(G). A coloring c is distinguishing if Aut c (G) is trivial. The group Aut(G) acts naturally on the vertex set of G and this action induces a partition of the vertex set V (G) into orbits. If H is a subgroup of Aut c (G) then the action of H on V (G) is such that each orbit induced by this action is monochromatic. In particular, an automorphism σ preserves the coloring if and only if the orbits under the action of the subgroup < σ > generated by σ, are all monochromatic. In the last couple of years the study of this invariant was particularly flourishing. See [10, 11] for the work of Imrich, Jerebic and Klavžar on the distinguishing number of the Cartesian products or [7] for an analog of Brook s theorem. In [7] Collins and Trenk also introduce a distinguishing coloring which must be a proper coloring. The distinguishing number is also studied in a more general context than graphs [6, 13]. Our goal in this paper is to introduce a game variant of this invariant in the spirit of the game chromatic number χ G introduced by Brahms in 1981 (see [8]) or of the most recent domination game (see [4]). Even if inventing new game invariants could raise a lot of promising and interesting questions, it might seem artificial at first glance. To defend our approach, we recall that game invariants have already proved useful to give a new insight on the classical invariant they are related. We cite in particular [5], where a greedy like strategy used in the study of the domination game is used to improve several upper bounds on the domination number. See also [1] for an application of the coloring game to the graph packing problem. The distinguishing game is a game with two players, the Gentle and the Rascal, with antagonist goals. This game is played on a graph G with a set of d N colors. Alternately, the two players choose a vertex of G and color it with one of the d colors. The game ends when all the vertices have been colored. Then the Gentle wins if the coloring is distinguishing and the Rascal wins otherwise. This game leads to two new invariants for a graph G. The G-game distinguishing number D G (G) is the minimum of colors needed to ensure that the Gentle has a winning strategy for the game on G, assuming he is playing first. If the Rascal is sure to win whatever the number of colors we allow, then D G (G) =. Similarly, the R-game distinguishing number D R (G) is the minimum number of colors needed to ensure that the Gentle has a winning strategy, assuming the Rascal is playing first. In Section, some basic results about the distinguishing games are given. In particular, we study when the distinguishing numbers are finite or not. This question is far from being easy in general. The third section is devoted to introduce the class of involutive graphs, for which we prove that the R-game distinguishing number is finite and more precisely, quadratically bounded above by the classical distinguishing number of the graph. This class, closely related to imprimitive action of group with complete block system whose blocks have size, contains a variety of graphs such as hypercubes, even cycles, spherical graphs and even graphs [9, 15]. In Section 4, the general result on involutive graphs is used to compute the exact values of the game invariants for hypercubes. Theorem 1.1 Let Q n be the hypercube of dimension n. 1. We have D G (Q n ) =.. If n 5, then D R (Q n ) =. Moreover D R (Q ) = D R (Q 3 ) = We have D R (Q 4 ) 3. Finally, in Section 5, we solve the problem for cycles, except when the number of vertices is prime. For even cycles, it is a straightforward application of a result on involutive graphs, but for odd cycles new ideas are needed.
3 A New Game Invariant of Graphs: the Game Distinguishing Number 3 Theorem 1. Let C n be a cycle of order n If n is even, then D G (C n ) =. If n is odd, then D R (C n ) =.. If n is even and n 8, then D R (C n ) =. Moreover D R (C 4 ) = D R (C 6 ) = If n is odd, not prime and n 9, then D G (C n ) =. 4. If n is prime and n 5, then D G (C n ) 3. Moreover D G (C 3 ) = and D G (C 5 ) = D G (C 7 ) = 3. Basic results This section is devoted to basic results about the distinguishing games. Especially, we are interested in determining when the G-game and R-game distinguishing numbers are infinite. It arises directly from the definition that D(G) D G (G) and D(G) D R (G), for any graph G. Another straightforward remark is that the game distinguishing number of a graph and its complement are equal. One first natural question is, if having a winning strategy with k colors is a growing property. In other words, has the Gentle a winning strategy if k D G or k D R colors are allowed? The answer is not as obvious as it looks at first glance. We recall that for the game chromatic number χ g, it is not known if there is always a winning strategy if we play with k χ g colors. However, for the game distinguishing numbers we easily show they both have this growing property. Proposition.1 Let G be a graph and k a positive integer. If k D G (G) (resp. k D R (G)), then the Gentle has a winning strategy with k colors, if he starts (resp. the Rascal starts). Proof: In order to win with k colors, the Gentle plays the same winning strategy he would have played with D G (G) (resp. D R (G)) colors, except when the Rascal chooses a color strictly greater than D G (G) (resp. D R (G)). In that case, the Gentle plays the winning move he would have played if the Rascal had played the color 1. Let c be the final coloring in the game with k colors with respect to the above strategy. Let c be the coloring defined for all v V (G) as follows: { c(v) if c(v) D G (G) (resp. c(v) D R (G)) c(v) =. 1 otherwise The coloring c is a distinguishing coloring since it is obtained by following a winning strategy for the game with only D G (G) (resp. D R (G)) colors. Let σ be an automorphism which preserves c. It is clear that σ preserves c too. Since c is distinguishing, σ must be the identity. This shows that c is a distinguishing k-coloring and that the Gentle has a winning strategy with k colors. As mentioned in the definition, D G and D R could possibly be infinite. For example, if the graph has an automorphism of order two, the Rascal can win using a strategy close to the Tweedledee Tweedledum one for the sum of opposite combinatorial games. He uses the involutive automorphism to copy the move the Gentle just made. Proposition. If G is a graph with a nontrivial automorphism of order, then: 1. D G (G) = if V (G) is even,. D R (G) =, if V (G) is odd.
4 4 Sylvain Gravier, Kahina Meslem, Simon Schmidt, Souad Slimani Proof: Let A be the set of vertices fixed by σ: A = {v G : σ(v) = v}. Note that V (G) and A have the same parity. We denote by r i and s i the i-th vertex played by the Rascal and the Gentle respectively. First, assume A is even and the Gentle starts. The winning strategy for the Rascal is as follows. If s i is in A, then the Rascal plays another vertex r i in A and does not pay attention to the color. This is always possible since A is even. Else the Rascal plays such that r i = σ(s i ) and c(r i ) = c(s i ). Since σ has order, the vertices outside A can be grouped in pairs (u, v) with σ(u) = v and σ(v) = u. Moreover the Gentle will be the first to play outside A. Hence, such a move is always available for the Rascal. Now suppose A is odd and the Rascal begins. His first move is to color a vertex in A. The number of uncolored vertices in A are now even and it is the Gentle s turn. Then the Rascal wins with exactly the same strategy as above. For example, for cycles C n or paths P n on n vertices, we have D G (C n ) = D G (P n ) =, if n is even, and D R (C n ) = D R (P n ) =, if n is odd. Note that Proposition. tells nothing about the possible values of D G (resp. D R ) when the number of fixed points is odd (resp. even). For cycles the question is rather complicated. We partially solve it in Section 5. But for paths P n, with n, it is easy to show that D G (P n ) = (resp. D R (P n ) = ) if n is odd (resp. even). There are also graphs with both D G and D R infinite, for example graphs with two transpositions moving a common vertex, like the complete graphs on more than 3 vertices. Finding graphs with both invariants finite, is a bit less obvious. Before stating the result, we recall that for a given finite group Γ, there are infinitely many non-isomorphic graphs whose automorphism group is Γ. Proposition.3 If G is a graph such that Aut(G) = Z/pZ, where p is prime and p 3, then D G (G) = D R (G) =. Proof: Since Aut(G) is prime all the orbits under the action of the whole group have either size 1 or size p. Let O 1,, O l, with l > 0 be the orbits of size p. Since there are at least three distinct vertices in each orbit O i and two colors are allowed, the Gentle can always play, whoever starts, in a manner which ensures that at least one of the O i is not monochromatic. Let σ be a nontrivial automorphism of G. Since Aut(G) is prime, σ generates Aut(G) and the orbits under Aut(G) and < σ > are the same. The automorphism σ cannot preserve the coloring because in that case all the orbits O i have to be monochromatic. This shows that the above strategy is winning for the Gentle and that D G (G) = D R (G) =. 3 Involutive graphs In this section, we introduce the new class of involutive graphs. This class contains well known graphs such as hypercubes, even cycles, even toroidal grids and even graphs [9, 15]. For graphs in this class, we are going to prove that their R-game distinguishing number is quadratically bounded above by the distinguishing number. An involutive graph G is a graph together with an involution, Bar : V (G) V (G), which commutes with all automorphisms and has no fixed point. In others words: u = u and u u for every u V (G) σ(u) = σ(u) for every σ Aut(G) and u V (G).
5 A New Game Invariant of Graphs: the Game Distinguishing Number 5 The set {u, u} will be called a block and ū will be called the opposite of u. An important remark is that, since Bar commutes with all automorphisms, the image of a block under an automorphism is also a block. The block terminology comes from imprimitive group action theory. Indeed, if we add the condition that the automorphism group of the graph acts transitively, then an involutive graph is a graph such that this action has a complete block system, whose blocks have size. Let G be an involutive graph on n vertices. We define G as the graph obtained from G by deleting all the edges and putting a new edge between all vertices and their opposites. The resulting graph is a disjoint union of n/ copies of K. Moreover, it is also an involutive graph and it has the same blocks as G. The next proposition states that these graphs are in a sense the worst involutive graphs for the Gentle. Proposition 3.1 If G is an involutive graph then D(G) D(G ) and D R (G) D R (G ). Proof: It is enough to prove that any distinguishing coloring c of G is also a distinguishing coloring of G. Let σ be a nontrivial automorphism of G. Assume first, there are two disjoint blocks {u, ū} and {v, v}, with u, v V (G), such that σ({u, ū}) = {v, v}. Since the coloring c is distinguishing for G, we have c({u, ū}) c({v, v}). Hence, σ does not preserve c. Suppose now that there are no two such blocks. Since σ is not trivial, there exists u V (G) such that σ(u) = ū. But u and ū must have distinct colors, otherwise the transposition which switch them would be a nontrivial color preserving automorphism of G. Therefore, σ is not a color preserving automorphism. We conclude that c is also a distinguishing coloring for G. For graphs which are disjoint union of K, we are able to compute the exact value of D G and D R. Proposition 3. If G is the disjoint union of n 1 copies of K, then D G (G) = and D R (G) = n+1. Proof: Such a graph G has an automorphism of order, with no fixed point, the one which exchanges the two vertices in each copy of K. By Proposition., we directly conclude that D G (G) =. We are now going to prove that D R (G) = n + 1. First, assume that only k < n + 1 colors are allowed during the game. The Rascal s strategy is to play always the color 1 in a way that at least one vertex of each copy of K is colored with 1. Since there is strictly less than n + 1 different colors, whatever the Gentle plays there will be two distinct K colored with the same pair of colors or there will be a monochromatic K. If there is a monochromatic K, the transposition which permutes its two vertices is clearly a color preserving automorphism. In the other case, there are four distinct vertices u 1, u, v 1, v V (G), such that u 1 and u (resp. v 1 and v ) are in the same K. Moreover, u 1 and v 1 (resp. u and v ) share the same color. The automorphism σ, defined by σ(u i ) = v i, σ(v i ) = u i, with i {1, }, and σ(w) = w for w V (G) \ {u 1, u, v 1, v } preserves the coloring. Hence, the strategy described is winning for the Rascal. In conclusion, D R (G) n + 1. We now allow n + 1 colors. We recall that the Rascal plays first. The winning strategy for the Gentle is as follows. He always colors the remaining uncolored vertex in the copy of K, where the Rascal has just played before. He chooses his color such that the pair of colors for this K is different from all the pairs of colors of the previously totally colored copies of K. Moreover, he ensures that no K is monochromatic. Let σ be a nontrivial automorphism of G and let u V (G) be such that σ(u) u. If u and σ(u) belong to the same copy of K, σ does not preserve the coloring. Otherwise, the copy of K which contains u is sent by σ to another one. This implies that σ is not a color preserving automorphism. This shows that the Gentle has a winning strategy with n + 1 colors. In conclusion, D R (G) = n + 1.
6 6 Sylvain Gravier, Kahina Meslem, Simon Schmidt, Souad Slimani It is shown in [7], that if G consists of n disjoint copies of K, then D(G) = 1 + 8n + 1. Hence, we get examples of graphs for which the R-game distinguishing number is quadratic in the classical one. The following results are straightforward consequences of Proposition 3.1 and Proposition 3.. Proposition 3.3 If G is an involutive graph on n vertices, then: D(G) 1 + 4n + 1 and D R (G) n + 1. This result shows that involutive graphs have finite R-game distinguishing number. But the bound we obtained does not depend on the classical distinguishing number of the graph. If the Gentle knows this number, having in mind a distinguishing coloring, he can use it to play in a smarter way. In other words, for an involutive graph G, we can bound the game distinguishing number D R using the classical one. It turns out that D R (G) is in this case at most of order D(G). Theorem 3.4 If G is an involutive graph with D(G), then D R (G) D(G) + D(G). Proof: We set d = D(G). We are going to give a winning strategy for the Gentle with d + d colors. Note that, since the Rascal starts the game, the Gentle can play in a way he is never the first to color a vertex in a block. When the Rascal colors a vertex u V (G), the Gentle s strategy is to always answer by coloring the vertex u in the same block. Before stating how he chooses the color, we need some definitions. Let c be a distinguishing coloring of G with d colors. We set k = d + d. For all i, j {1,, d}, we define the following sets of vertices: V ij = {u V (G) c(u) = i and c(u) = j}. There are d(d 1) sets V ij, with 1 i < j d, and d sets V ii, with i {1,...d}. To each set V ij, with 1 i < j d, we associate a specific number δ ij in {1,, d(d 1) }. For each V ij, with i, j {1,...d}, we define r ij as follows: δ ij if 1 i < j d k r ji if 1 j < i d r ij = d(d 1) + i if i = j and 1 i d 1 0 if i = j = d This defines only d distinct numbers. However, we need d + d colors to ensure the second of the following properties. (i) For every i, i, j, j {1,, d}, we have r ij r i j (mod k) if and only if i = i and j = j. (ii) For every i, j {1,, d}, we have r ij r ji (mod k) if i j. (iii) For every i, j {1,, d}, we have r ii r jj (mod k) if i j. Let now c : V (G) {1,, k} be the coloring built during the game. The Gentle chooses the color as follows. When the Rascal colors u V ij with c (u), he colors u such that c (u) c (u) r ij (mod k).
7 A New Game Invariant of Graphs: the Game Distinguishing Number 7 To prove this strategy is winning, it is enough to show that for any automorphism σ which preserves c, we have σ(v ij ) = V ij. Since all V ij are monochromatic for the distinguishing coloring c, this will show that σ also preserves c, and σ must therefore be the identity. Let u be a vertex of G and i, j {1,, d}. Properties (i), (ii), and (iii) easily imply the following facts. (a) If i j, then u V ij if and only if c (u) c (u) r ij (b) u V ii if and only if c (u) c (u) ±r ii (mod k). (mod k). Let σ be an automorphism which preserves c. For any vertex u V ij, with i, j {1,, d}, we have c (u) c (u) c (σ(u)) c (σ(u)) (mod k). By (a), we get that c (σ(u)) c (σ(u)) r ik (mod k), and by (b), we have that σ(u) is in the same set V ij as u. In the above proof, decreasing the number of sets V ij tightens the bound. In particular, we have the following corollary. Corollary 3.5 Let G be an involutive graph. If there is a coloring with d colors, such that Bar is the only nontrivial automorphism which preserves this coloring, then D R (G) d. Proof: We use the same notations as in the proof of Theorem 3.4. As in this proof, the Gentle uses a coloring c with d colors which is only preserved by Bar to build his strategy. Since we ask that Bar preserves c, all the sets V ij with i j are empty. So the Gentle needs only d colors to apply his strategy. Indeed, he plays in a way that for all u V (G), c (ū) c (u) i 1 (mod (d )), where i {1, d} is such that u V ii. As for the proof of the previous theorem, we can prove that an automorphism which preserves the coloring c must also preserve the coloring c. Thus, it is either the identity or the Bar involution. All blocks whose vertices do not belong to V 11 are not monochromatic. Hence, the Bar involution cannot preserve the coloring c. In conclusion, c is a distinguishing coloring and the Gentle has a winning strategy with d colors. 4 Hypercubes In this section, we use Corollary 3.5 to study the game distinguishing number of Q n, the hypercube of dimension n where n, and prove Theorem 1.1. The vertices of Q n will be denoted by words of length n on the binary alphabet {0, 1}. Let u(i) denote its i-th letter of a vertex u. For the classical distinguishing number the question is solved in []: D(Q 3 ) = D(Q ) = 3 and D(Q n ) = for n 4. As mentioned before, hypercubes are involutive graphs. The Bar involution can be defined as the operation which switches all the letters 0 to 1 and all the letters 1 to 0. Hence, by Proposition., we know that D G (Q n ) =, for all n. If we apply directly Theorem 3.4, we obtain that D R (Q n ) 4, for n. To improve this bound in order to prove the first item of Theorem 1.1, we are going to use Corollary 3.5. We will have to design nice distinguishing coloring of the hypercube with colors. For this purpose, we introduce determining sets. A subset S of vertices of a graph G is a determining set if the identity is the only automorphism of G whose restriction to S is the identity on S. Determining sets are introduced and studied in [3]. In the following lemma, we give a sufficient condition for a subset of Q n to be determining. Lemma 4.1 Let S be a subset of vertices of Q n, with n. If for all i {1,, n}, there are two vertices v i 0 and v i 1 in S such that v i 0(i) = 0, v i 1(i) = 1 and all the other letters are the same, then S is a determining set of Q n.
8 8 Sylvain Gravier, Kahina Meslem, Simon Schmidt, Souad Slimani Proof: Let σ Aut(G), which is the identity on S. Suppose for a contradiction that there exists a vertex u in Q n \ S such that σ(u) u. Then, there exists k {1,, n} such that u(k) σ(u)(k). Without loss of generality, we suppose that u(k) = 0. The vertices u and v0 k differ on l letters, with l {1,...n 1}. This means that the distance between u and v0 k is equal to l. Since σ fixes v0 k the distance between σ(u) and v0 k must be l, too. Therefore, the vertices u and v1 k have l+1 distinct letters, whereas the vertices σ(u) and v1 k have only l 1 distinct letters. This is impossible because the distance between u and v1 k must be the same as the distance between σ(u) and v1 k. Therefore σ(u) = u for all u V (Q n ). In conclusion, S is a determining set. Proposition 4. Let Q n be the n-dimensional hypercube with n 5. Then D R (Q n ) =. Proof: For i {0,, n 1}, let v i be the vertex with the i first letters equal to 1 and the n i other letters equal to 0. We define also the following vertices in Q n : f = , c 1 = and c = The subgraph S will be the graph induced by {v i, v i 0 i < n} {f, f, c 1, c 1, c, c } (see Figure 1 ). Let c be the coloring with two colors defined by: c(u) = 1 if u V (S) and c(u) = otherwise. We will show that this coloring fits hypothesis of Corollary 3.5. This would imply that D R (Q n ) = =. Clearly, Bar preserves the coloring c and we prove now this is the only nontrivial color preserving automorphism. An automorphisms σ which preserves this coloring fixes S setwise : σ(s) = S. The restriction of σ to S, say σ S, is an automorphism of S. The vertices v 0,, v n 1, and v 0 show that the hypothesis of Lemma 4.1 holds for the subgraph S. Hence σ is totally determined by the images of the elements of S. The two vertices f and f are the only vertices of degree 1 in S. So, either σ(f) = f and σ(f) = f or both are fixed. In the first case, this implies that σ(v 1 ) = v 1 and σ(v 1 ) = v 1. In the second case, v 1 and v 1 are also fixed by σ. This is because they are respectively the only neighbors of f and f in S. The vertices v 0 and v are the two remaining neighbors of v 1. Since they have not the same degree in S, they cannot be switched by σ. Hence, in the first case, σ(v i ) = v i and σ(v i ) = v i, with i {0, }. In the second case, v i and v i, with i {0, }, are fixed by σ. There is exactly one path of size n between v 0 and v (resp. v and v 0 ). Hence, in the first case these paths are switched, whereas they are fixed pointwise in the second. After that, it is easy to show that σ S is either the identity or the Bar involution. The above proof fails for Q 4 because the subgraph S will have automorphisms other than the Bar involution (see Figure ). Nevertheless, we can decrease the upper bound from 4 to 3. Proposition 4.3 We have D R (Q 4 ) 3. Proof: Let S be the subgraph of Q 4 induced by the five vertices 0000, 1000, 1100, 1110 and Let S be the subgraph induced by the opposite vertices of those in S. Note that S and S are disjoint. The Gentle s strategy is as follows. When the Rascal colors a vertex u in V (G), the Gentle colors u. He chooses the coloring c according to these rules: if u is in V (S), then c(u) c(u) 1 (mod 3), if u is in V (S), then c(u) c(u) 1 (mod 3), c(u) c(u) 0 (mod 3) otherwise. Let σ be a color preserving automorphism. Since c(ū) c(u) 1 (mod 3) if and only if u S, we have that S is fixed setwise by σ. Let σ S be the restriction of σ to S. The vertices 0000 and 1110
9 A New Game Invariant of Graphs: the Game Distinguishing Number 9 f v 0 v 1 v 4 v c 1 c c v 3 v 3 c 1 v v 4 v 1 v 0 f Fig. 1: The induced subgraph S in Q 5 are the only vertices of degree 1 in S. Then either σ S fixes them or switches them. But in Q 4, we have d(0000, 1011) d(1110, 1011). Since σ S comes from an automorphism of Q n, it must preserve distances in Q n. But, the vertex 1011 is fixed by σ S because it is the only isolated vertex of S. Hence, we have that σ S fixes 0000 and Moreover, it is clear that all the vertices of S are fixed by σ S and hence by σ. The vertex 1111 is also fixed by σ, because it is the opposite vertex of Finally, all the vertices of V (S) {1111} are fixed by σ and this subset fits hypothesis of Lemma 4.1. This shows that σ is the identity of Q 4. To complete the proof of Theorem 1.1, it remains to settle the case of hypercubes of dimension and 3. For the square Q, isomorphic to C 4, an easy computation shows that D R (Q ) = 3. For Q 3, it turns out that D R (Q 3 ) is also equal to 3. It comes from the fact that the complementary graph of Q 3 is isomorphic to K 4 K and from the following proposition. We will write the vertices of K 4 K as couples (i, x), with i {1,, 4} and x {l, r}. The first coordinate is the one associated to K 4 and the second the one associated to K. We denote by K i the K - fiber whose two vertices have i {1,, 4} as first coordinate. Let c be a coloring of K 4 K. We say that two distinct K -fibers, K i and K j, with i, j {1,, 4} are colored the same if c(ki ) = c(k j ). Moreover, if c((i, l)) = c((j, l)), we say that the two fibers are strictly colored the same. Proposition 4.4 We have D R (K 4 K ) = 3. Proof: Since D(K 4 K ) = 3, we only have to prove that the Gentle has a winning strategy with 3 colors. The Rascal starts by coloring the vertex (1, l) with 1. The Gentle replies by coloring with the vertex (, l). Now, there are two cases. Case 1: The Rascal colors the second vertex of K 1 or K with a colors δ {1,, 3}. Without loss of generality we assume he colors (1, r). There are two subcases. Subcase 1.1: δ {1, 3}. The Gentle colors (, r) with. The Gentle s strategy is now to play in the same K -fiber as Rascal. Since the two K -fibers K 1 and K share no color, the Gentle can ensure that at
10 v v 3 c c v 3 c 1 v v 4 v 1 v 0 f 10 Sylvain Gravier, Kahina Meslem, Simon Schmidt, Souad Slimani Figure 1: The induced subgraph S in Q 5. v 0 v 1 f c v 3 v c 1 c 1 v c v 3 v 1 f v 0 Figure : The induced subgraph S in Q 4. Fig. : The induced subgraph S in Q 4 if u is in V (S), c(u) c(u) 1[3], the end of the game if u no is inpair V (S) of Kc(u) -fibers c(u) are 1[3], colored the same and K 3 is not monochromatic. This shows that a color preserving automorphism σ cannot switch the K -fibers. Hence σ(k) 3 = K 3 and, since this fiber is not monochromatic, c(u) c(u) we0[3] have otherwise. that σ cannot switch the K 4 -fibers, too. Finally, σ is the identity. SubcaseLet 1.: σ δ be= a colors. Thepreserving Gentle colors automorphism. (, r) withthen colors 1. is stable By coloring under σ: theσ(s) vertices = S. in the same K -fiber aslet theσ vertices S be the the restriction Rascal will of σ play, to S. the TheGentle vertices can 0000 ensure and 1110 that at arethe thend only ofvertices the game K 1 and K are theof only degree K -fibers 1 in S. colored Then either same. σ S fixes Moreover, them orheswitches can ensure them. that But oneink Q 4 -fiber,, we have say K, 3 is not monochromatic. d(0000, Let 1011) σ be ad(1110, color 1011). preserving Sinceautomorphism. σ S comes fromthe an automorphism fibers K of Q n, it must 3 and K 4 are fixed setwise by σ. Since Kpreserve distances in Q n. But, the vertex 1011 is fixed by σ S because it is the only 3 is not monochromatic, σ cannot switch the K 4 -fibers. We conclude that every K -fibers are fixed pointwise isolated by σ, vertex which of means S. Hence, σ is we trivial. have that σ S fixed 0000 and After that, it is Case : The Rascal colors the vertex (3, x), with x {l, r}. The Gentle answers by coloring the vertex 11 (4, x). The Gentle chooses his colors such that we can assume (1, l) and (3, x) are colored with 1, (, l) is colored with and (4, x) is colored with 3 (maybe we need to permute colors 1 and ). We only deal with the case where x = l. The case where x = r is very similar. When the Rascal s move is to color (1, r) (resp. (3, r)), the Gentle answers by coloring (3, r) (resp. (1, r)). When the Rascal s move is to color (, r) (resp. (4, r)), the Gentle answers by coloring (4, r) (resp. (, r)). He can choose the colors he uses, such that no pair of K -fibers is strictly colored the same. Moreover, one of the four K -fibers is not monochromatic and is not colored the same as each of the three other K -fibers. At the end of the game, we are in the same situation as in subcase 1.. In conclusion, the coloring built in this case is also 3-distinguishing. 5 Cycles In this section, we prove Theorem 1. about cycles. We start with even cycles which are involutive graphs. For such graphs, the opposite of a vertex can be defined as the unique vertex at maximal distance. Corollary 3.5 enables us to conclude when the size of the even cycle is greater or equal to 1. For C 4, it is easy to verify that D R (C 4 ) = 3. Using the fact that the coloring shown in Figure 3 is the only distinguishing -coloring of C 6, it is easy to see that D R (C 6 ) = 3. For C 8 and C 10, the Gentle s strategies are less obvious. We give them in the below proposition.
11 A New Game Invariant of Graphs: the Game Distinguishing Number Fig. 3: The unique distinguishing -coloring of C 6 Proposition 5.1 We have D R (C 8 ) = D R (C 10 ) =. Proof: We start with Gentle s winning strategy for C 8. Let (x 1,, x 8 ) be the cycle of order 8. Let c be a -coloring with exactly three vertices colored with color. If these three vertices do not induce a stable set or a P 3, then c is -distinguishing. The Rascal starts by coloring x 1 with color 1. The Gentle replies by coloring x 1 with the same color. Gentle s strategy is now to use the other color than the one the Rascal played just before. In this way, the number of vertices colored with color will be exactly three. To avoid that these three vertices induce a stable set or a P 3, he plays exactly one move in each of the pairs {x, x 4 }, {x 6, x 8 }, {x 3, x 7 }. Now, we give Gentle s strategy for C 10. Let (x 1,, x 10 ) be the cycle of order 10. Rascal s first move is to color x 1 with color 1. The Gentle replies by coloring x 1 with the same color. After that there are two cases. Case 1: The Rascal uses color 1 for his second move. Using symmetries, we obtain only two subcases. In both subcases, the Gentle answers first with color 1. Then, he uses the other color than the one used by the Rascal just before. Subcase 1.1: The Rascal colors x with 1. The Gentle colors x 7 with 1. Then, he plays using the pairs {x 3, x 5 }, {x 8, x 10 }, {x 4, x 7 }. Subcase 1.: The Rascal colors x 3 with 1. The Gentle answers by coloring x 4 with 1. Then, he plays following the pairs {x, x 5 }, {x 7, x 9 }, {x 8, x 10 }. Case : The Rascal use color for his second move. The Gentle answers by coloring a vertex with color, too. By symmetry, we assume that x and x 3 are colored with. The Gentle plays according to the pairs s 1 = {x 4, x 5 }, d = {x 7, x 8 } and s = {x 9, x 10 }. If the Rascal plays in s 1 or s, the Gentle copies the color he used, whereas, when the Rascal plays in d, the Gentle plays the other color. We let the reader check that the strategies for C 8 and C 10 are indeed winning. Proposition 5. For n 6, we have D R (C n ) =. Proof: Let u, v, w be vertices of C n such that d(u, v) = 1, d(u, w) = 3 and d(v, w) =. We set S = {u, ū, v, v, w, w} and define the coloring c with colors as follows: c(x) = 1 if x S and c(x) = 0 otherwise. Let σ be a nontrivial color preserving automorphism. The subgroup < σ > acts on the set of the three blocks contained in S. If σ is an axial reflection then one block must be stable under σ. This
12 1 Sylvain Gravier, Kahina Meslem, Simon Schmidt, Souad Slimani block is the axis of the reflection. Since n 1, we easily check that the two other blocks cannot be map to each other by this reflection. Since σ cannot be a reflection, σ must be a rotation. The only possibility for a rotation to let S stable is to map each vertex to its opposite. Hence σ restricted to S is the Bar involution. But it is straightforward to show that σ must be the Bar involution on the whole cycle. This shows that the coloring c fits Corollary 3.5 hypothesis. We conclude that D R (C n ). We compute now the G-game distinguishing number for odd, but not prime cycles. Odd cycles are not involutive graphs, but when the number n of vertices is not prime, the action of the automorphism group is not primitive. We are going to use a complete block system, with blocks of size equal to the least prime divisor of n. Proposition 5.3 If C n is an odd cycle such that n > 9 and n is not prime, then D G (C n ) =. Proof: Let p be the least prime divisor of n. Since n 15, we have n = kp, with k 5. Let (x 1,, x n ) be the cycle C n. We define k disjoint subsets of vertices V j = {x j+lk l {0,, p 1}}, with j {1,, k}. The set V 1 will play a particular role. We denote by i, with i {1,, p}, the reflection with fixed point x 1+(i 1)k. Note that the automorphisms i, with i {1,, p}, moves the sets V j, with j {1,, k}, in the following way: i (V 1 ) = V 1 and for j 1, i (V j ) = V k+ j. Since k is odd, j k + j and i (V j ) V j, if j 1. We describe the Gentle s strategy. He starts by coloring x 1 with color 1. More precisely, he chooses the fixed point of 1. If the Rascal colors a vertex x in V 1, he answers by coloring the vertex 1 (x) in V 1 with the other color. Note that since the Gentle starts the game by coloring the fixed point of 1, this is always possible. Therefore, 1 is broken and there will be exactly 1 + p 1 vertices colored with 1 in V 1 at the end of the game. If the Rascal plays in V j, with j 1, then he plays in V k+ j. Except if the Rascal just colors the penultimate vertex of V j. In that case he plays in V j too, and colors the last vertex in a way the parity of the number of 1 in V j is not the same as the parity of 1 + p 1. The vertex he chooses to color in V k+ j is determined as follows. If at least one reflection i, with i {,, p}, is not already broken by the coloring, he chooses one of them, say i0. We call V j the set of already colored vertices in V j. There is exactly one more colored vertex in V j than in V k+ j. Hence i0 (V j ) has at least an uncolored vertex, say u. The Gentle colors u such as u and 1 i 0 (u) are not of the same color. If all the symmetries i are already broken, he plays randomly in V k+ j. At the end of the game, there are exactly 1 + p 1 vertices colored with 1 in V 1. It is clear that Gentle s strategy leads him to play the last vertex of any set V j. Hence, in all sets V j, with j 1, the number of 1s has not the same parity as in V 1. This proves that the only possible color preserving automorphisms are those under which V 1 is stable. The Gentle plays (k 1)p moves outside V 1. There are only k 1 moves used to control the parity of 1s. The number of remaining moves to break the p 1 symmetries,, p is (p )(k 1). Since k p and k 5, this number is greater or equal to p 1. This shows that all the symmetries under which V 1 is stable are broken. A color preserving automorphism σ is finally either a rotation under which V 1 is stable or the identity. Assume σ is a rotation. The subgroup < σ > acts naturally on V 1. Since V 1 is prime, < σ > must be of order p and acts transitively on V 1. This is impossible because V 1 is not monochromatic. In conclusion, σ must be the identity and the Gentle has a winning strategy with two colors.
13 A New Game Invariant of Graphs: the Game Distinguishing Number 13 For C 9, the general strategy fails but two colors are still enough for Gentle to win. Proposition 5.4 We have D G (C 9 ) =. Proof: Let (x 1,, x 9 ) be the cycle of order 9 and c the coloring built throughout the game. The Gentle can play such that after his second move, the game is in one of the following cases. Case 1: c(x 1 ) = c(x 4 ) = 1 and c(x 7 ) =. The Gentle applies the same strategy as in Proposition 5.3. For the other cases, the Gentle defines three pairs S, O, O of uncolored vertices. He plays in a way the pairs O and O have vertices of different colors, and the pair S is monochromatic. Case : c(x 1 ) = c(x ) = 1 and c(x 6 ) =. The pairs are defined by O = {x 3, x 9 }, O = {x 5, x 7 } and S = {x 4, x 8 }. Case 3: c(x 1 ) = c(x 3 ) = 1 and c(x ) =. He defines S = {x 4, x 6 }, O = {x 5, x 8 } and O = {x 7, x 9 }. Case 4: c(x 1 ) = c(x 5 ) = 1 and c(x 3 ) =. He makes S = {x, x 4 }, O = {x 6, x 9 } and O = {x 7, x 8 }. To finish the proof of Theorem 1., we deal with prime cycles. Note that, in that case, the automorphism group action is primitive. Once more, the small case C 5 does not fit the general strategy. By computation, we get D G (C 5 ) = 3. Proposition 5.5 If C p is a cycle of prime order p > 5, then D G (C p ) 3. Proof: Assume that three colors are allowed during the game. We begin the proof by showing the Rascal cannot win if he does not always play the same color as the one used by the Gentle just before. We denote respectively by n 1, n and n 3, the number of vertices colored with 1, and 3 during the game. As long as the Rascal copies the color played by the Gentle just before, the three numbers n 1, n and n 3 are even at the end of the Rascal s turn. The first time the Rascal plays a different color, two of the three numbers, n 1, n and n 3 are odd at the end of his turn. Without loss of generality, we can say n 1 and n are odd. Then the Gentle colors a vertex with 3. The numbers n 1, n and n 3 are now all odd. Until the end of the game, the Gentle strategy is now to play the same color as the one the Rascal just used before him. In this way, he preserves the parity of n 1, n and n 3. At the end of the game, the coloring is such that n 1, n and n 3 are odd. We show that this coloring is a distinguishing coloring. Let σ be a color preserving automorphism. The size of an orbit O under the action of < σ > must divide < σ >. But the cardinality of < σ > is either 1, or p. Then, this orbit has 1, or p as its size. None of n 1, n and n 3 are null, so the coloring is not monochromatic and then the size of O cannot be p. The automorphism σ cannot be a rotation because, for prime cycle, a rotation acts transitively and has an orbit of size p. Assume σ is a reflection. Then, there is exactly one fixed point. Without loss of generality, we suppose it is colored 1. All the vertices colored with are in orbits of size. Since n is not null, there are k > 0 such orbits. We get n = k, which is a contradiction. Hence σ must be the identity. We can now assume that the Rascal always copies the color played by the Gentle just before. Playing a different move will actually lead him to defeat, whatever has happened before. The winning strategy for the Gentle is as follows. He starts with 1 and his second move is to color a vertex with. The Rascal s second move must also be. Let σ be the reflection which switches the two vertices colored with and v the vertex fixed by σ. If v is already colored, the Gentle plays 1 wherever he wants. If not, he colors v with 1. After that, the Gentle always uses the color 1, except for his last turn, where he will play 3. Since p > 5, he really has enough turns to play this 3. At the end of the game, the coloring has the following properties: exactly two vertices are colored with and exactly one vertex is colored with 3. Since there
14 14 Sylvain Gravier, Kahina Meslem, Simon Schmidt, Souad Slimani is only one vertex colored with 3 no rotation can preserve the coloring. Since there are only two vertices colored with, the only possible colors preserving reflection is σ. But the Gentle played in a manner that the unique 3 is not the fixed point of this reflection. In conclusion, the coloring is distinguishing and the Gentle wins with 3 colors. 6 Conclusion and further works In this article, we have defined two new game invariants of graphs, in the same spirit as the game chromatic number or as the game domination number. Since these invariants could be infinite, we started by giving some sufficient conditions for a graph to have infinite game distinguishing numbers. But a total characterization seems far to be found and sounds like a very challenging open problem. We propose the following conjecture. Conjecture 6.1 If G is a graph with no automorphism of order, then D G (G) and D R (G) are both finite. After that, we defined a new class of graphs, the involutive graphs, for which we can bound quadratically the G-game distinguishing number using informations on the classical one. Results on this class are then applied to compute the exact value of the game distinguishing number of hypercubes and even cycles. For the hypercube of dimension 4, determining if D R (Q 4 ) is equal to or 3 remains open. For odd but not prime cycles, we were also able to compute the exact value of the two game invariants. The Gentle strategy made an intensive use of the imprimitivity of the automorphism group action. When the cycle is prime, we only know that D G is bounded above by 3. This bound is sharp for small cases. Indeed, D G (C 5 ) = D G (C 7 ) = 3. But, it seems this is more related to the small size of these cycles than to the primality of their order. Supported by computer experimentation, we state the following conjecture. Conjecture 6. If C p is a cycle of prime order p 11, then D G (C p ) =. Remark that for prime cycles, the automorphism group action is primitive. It would be interesting to study other graphs for which it is the case. It seems that the question is harder than in the imprimitive case. Acknowledgements The research was financed by the ANR-14-CE project of the French National Research Agency. References [1] M.O. Albertson and K.L. Collins. Symmetry breaking in graphs, Electron. J. Combin., 3 (1996). [] B. Bogstad and L. Cowen. The distinguishing number of hypercubes, Discrete Math., 383 (004) [3] D.L. Boutin. Identifying graph automorphisms using determining sets, Electron. J. Combin., 13 (006). [4] B. Brešar, S. Klavžar, D.F. Rall. Domination game and an imagination strategy, SIAM J. Discrete Math., 4 (010)
15 A New Game Invariant of Graphs: the Game Distinguishing Number 15 [5] C. Bujtás, S. Klavžar. Improved upper bounds on the domination number of graphs with minimum degree at least five, Graphs Combin., 3, Issue (016) [6] M. Chan. The maximum distinguishing number of a group, Electron. J. Combin., 70 (006). [7] K.L. Collins and A.N. Trenk. The Distinguishing chromatic number, Electron. J. Combin., 13 (006). [8] U. Faigle, U. Kern, H. Kierstead and W.T. Trotter. On the game chromatic number of some classes of graphs, Ars Combin., 35 (1993) [9] F. Göbel and H.J. Veldman. Even graphs, J. Graph Theory, 10 (1986) [10] W. Imrich, J. Jerebic and S. Klavžar. The distinguishing number of Cartesian products of complete graphs, European J. Combin., 45 (009) [11] W. Imrich and S. Klavžar. Distinguishing Cartesian powers of graphs, J. Graph Theory 53 (006) [1] H.A. Kierstead, A.V. Kostochka. Efficient graph packing via game coloring, Combin. Probab. Comput., 18 (009) [13] S. Klavžar, T.L. Wong and X. Zhu. Distinguishing labellings of group action on vector spaces and graphs, J. Algebra 15 Issue (006) [14] S. Klavžar and X. Zhu. Cartesian powers of graphs can be distinguished by two labels, European J. Combin., 8 (007) [15] J.H. Koolen, V. Moulton and D. Stevanović. The structure of spherical graphs, European J. Combin., 5 (004)
On the computational complexity of the domination game
 On the computational complexity of the domination game Sandi Klavžar a,b,c Gašper Košmrlj d Simon Schmidt e e Faculty of Mathematics and Physics, University of Ljubljana, Slovenia b Faculty of Natural
On the computational complexity of the domination game Sandi Klavžar a,b,c Gašper Košmrlj d Simon Schmidt e e Faculty of Mathematics and Physics, University of Ljubljana, Slovenia b Faculty of Natural
EDGE-COLOURED GRAPHS AND SWITCHING WITH S m, A m AND D m
 EDGE-COLOURED GRAPHS AND SWITCHING WITH S m, A m AND D m GARY MACGILLIVRAY BEN TREMBLAY Abstract. We consider homomorphisms and vertex colourings of m-edge-coloured graphs that have a switching operation
EDGE-COLOURED GRAPHS AND SWITCHING WITH S m, A m AND D m GARY MACGILLIVRAY BEN TREMBLAY Abstract. We consider homomorphisms and vertex colourings of m-edge-coloured graphs that have a switching operation
The domination game on split graphs
 The domination game on split graphs Tijo James a,b Sandi Klavžar c,d,e Ambat Vijayakumar b August 6, 018 a Department of Mathematics, Pavanatma College, Murickassery, India tijojames@gmail.com b Department
The domination game on split graphs Tijo James a,b Sandi Klavžar c,d,e Ambat Vijayakumar b August 6, 018 a Department of Mathematics, Pavanatma College, Murickassery, India tijojames@gmail.com b Department
Progress Towards the Total Domination Game 3 4 -Conjecture
 Progress Towards the Total Domination Game 3 4 -Conjecture 1 Michael A. Henning and 2 Douglas F. Rall 1 Department of Pure and Applied Mathematics University of Johannesburg Auckland Park, 2006 South Africa
Progress Towards the Total Domination Game 3 4 -Conjecture 1 Michael A. Henning and 2 Douglas F. Rall 1 Department of Pure and Applied Mathematics University of Johannesburg Auckland Park, 2006 South Africa
Note Asymmetric Directed Graph Coloring Games
 Note Asymmetric Directed Graph Coloring Games Stephan Dominique Andres Zentrum für angewandte Informatik Köln, University of Cologne, Weyertal 80, 50931 Köln, Germany Abstract This note generalizes the
Note Asymmetric Directed Graph Coloring Games Stephan Dominique Andres Zentrum für angewandte Informatik Köln, University of Cologne, Weyertal 80, 50931 Köln, Germany Abstract This note generalizes the
The Game Chromatic Number of Some Classes of Graphs
 The Game Chromatic Number of Some Classes of Graphs Casper Joseph Destacamento 1, Andre Dominic Rodriguez 1 and Leonor Aquino-Ruivivar 1,* 1 Mathematics Department, De La Salle University *leonorruivivar@dlsueduph
The Game Chromatic Number of Some Classes of Graphs Casper Joseph Destacamento 1, Andre Dominic Rodriguez 1 and Leonor Aquino-Ruivivar 1,* 1 Mathematics Department, De La Salle University *leonorruivivar@dlsueduph
Domination game on split graphs
 Domination game on split graphs Tijo James a,b Sandi Klavžar c,d,e Ambat Vijayakumar b May 1, 018 a Department of Mathematics, Pavanatma College, Murickassery, India tijojames@gmail.com b Department of
Domination game on split graphs Tijo James a,b Sandi Klavžar c,d,e Ambat Vijayakumar b May 1, 018 a Department of Mathematics, Pavanatma College, Murickassery, India tijojames@gmail.com b Department of
Endomorphisms and synchronization, 2: Graphs and transformation monoids
 Endomorphisms and synchronization, 2: Graphs and transformation monoids Peter J. Cameron BIRS, November 2014 Relations and algebras Given a relational structure R, there are several similar ways to produce
Endomorphisms and synchronization, 2: Graphs and transformation monoids Peter J. Cameron BIRS, November 2014 Relations and algebras Given a relational structure R, there are several similar ways to produce
GAME CHROMATIC NUMBER OF CARTESIAN PRODUCT GRAPHS. 1. Introduction
 GAME CHROMATIC NUMBER OF CARTESIAN PRODUCT GRAPHS T. BARTNICKI, B. BREŠAR, J. GRYTCZUK, M. KOVŠE, Z. MIECHOWICZ, AND I. PETERIN Abstract. The game chromatic number χ g is considered for the Cartesian product
GAME CHROMATIC NUMBER OF CARTESIAN PRODUCT GRAPHS T. BARTNICKI, B. BREŠAR, J. GRYTCZUK, M. KOVŠE, Z. MIECHOWICZ, AND I. PETERIN Abstract. The game chromatic number χ g is considered for the Cartesian product
Two Characterizations of Hypercubes
 Two Characterizations of Hypercubes Juhani Nieminen, Matti Peltola and Pasi Ruotsalainen Department of Mathematics, University of Oulu University of Oulu, Faculty of Technology, Mathematics Division, P.O.
Two Characterizations of Hypercubes Juhani Nieminen, Matti Peltola and Pasi Ruotsalainen Department of Mathematics, University of Oulu University of Oulu, Faculty of Technology, Mathematics Division, P.O.
 This article was originally published in a journal published by Elsevier, and the attached copy is provided by Elsevier for the author s benefit and for the benefit of the author s institution, for non-commercial
This article was originally published in a journal published by Elsevier, and the attached copy is provided by Elsevier for the author s benefit and for the benefit of the author s institution, for non-commercial
On the packing chromatic number of some lattices
 On the packing chromatic number of some lattices Arthur S. Finbow Department of Mathematics and Computing Science Saint Mary s University Halifax, Canada BH C art.finbow@stmarys.ca Douglas F. Rall Department
On the packing chromatic number of some lattices Arthur S. Finbow Department of Mathematics and Computing Science Saint Mary s University Halifax, Canada BH C art.finbow@stmarys.ca Douglas F. Rall Department
Diskrete Mathematik und Optimierung
 Diskrete Mathematik und Optimierung Stephan Dominique Andres: Game-perfect digraphs paths and cycles Technical Report feu-dmo015.09 Contact: dominique.andres@fernuni-hagen.de FernUniversität in Hagen Fakultät
Diskrete Mathematik und Optimierung Stephan Dominique Andres: Game-perfect digraphs paths and cycles Technical Report feu-dmo015.09 Contact: dominique.andres@fernuni-hagen.de FernUniversität in Hagen Fakultät
LOCAL CONNECTIVE CHROMATIC NUMBER OF DIRECT PRODUCT OF PATHS AND CYCLES
 BULLETIN OF THE INTERNATIONAL MATHEMATICAL VIRTUAL INSTITUTE ISSN (p) 303-4874, ISSN (o) 303-4955 www.imvibl.org /JOURNALS / BULLETIN Vol. 7(017), 561-57 DOI: 10.751/BIMVI1703561Ç Former BULLETIN OF THE
BULLETIN OF THE INTERNATIONAL MATHEMATICAL VIRTUAL INSTITUTE ISSN (p) 303-4874, ISSN (o) 303-4955 www.imvibl.org /JOURNALS / BULLETIN Vol. 7(017), 561-57 DOI: 10.751/BIMVI1703561Ç Former BULLETIN OF THE
COUNTING THE NUMBER OF WINNING BINARY STRINGS IN THE 1-DIMENSIONAL SAME GAME. Department of Mathematics Oberlin College Oberlin OH 44074
 COUNTING THE NUMBER OF WINNING BINARY STRINGS IN THE 1-DIMENSIONAL SAME GAME CHRIS BURNS AND BENJAMIN PURCELL Department of Mathematics Oberlin College Oberlin OH 44074 Abstract. Ralf Stephan recently
COUNTING THE NUMBER OF WINNING BINARY STRINGS IN THE 1-DIMENSIONAL SAME GAME CHRIS BURNS AND BENJAMIN PURCELL Department of Mathematics Oberlin College Oberlin OH 44074 Abstract. Ralf Stephan recently
The strong chromatic number of a graph
 The strong chromatic number of a graph Noga Alon Abstract It is shown that there is an absolute constant c with the following property: For any two graphs G 1 = (V, E 1 ) and G 2 = (V, E 2 ) on the same
The strong chromatic number of a graph Noga Alon Abstract It is shown that there is an absolute constant c with the following property: For any two graphs G 1 = (V, E 1 ) and G 2 = (V, E 2 ) on the same
On vertex-coloring edge-weighting of graphs
 Front. Math. China DOI 10.1007/s11464-009-0014-8 On vertex-coloring edge-weighting of graphs Hongliang LU 1, Xu YANG 1, Qinglin YU 1,2 1 Center for Combinatorics, Key Laboratory of Pure Mathematics and
Front. Math. China DOI 10.1007/s11464-009-0014-8 On vertex-coloring edge-weighting of graphs Hongliang LU 1, Xu YANG 1, Qinglin YU 1,2 1 Center for Combinatorics, Key Laboratory of Pure Mathematics and
A graph is finite if its vertex set and edge set are finite. We call a graph with just one vertex trivial and all other graphs nontrivial.
 2301-670 Graph theory 1.1 What is a graph? 1 st semester 2550 1 1.1. What is a graph? 1.1.2. Definition. A graph G is a triple (V(G), E(G), ψ G ) consisting of V(G) of vertices, a set E(G), disjoint from
2301-670 Graph theory 1.1 What is a graph? 1 st semester 2550 1 1.1. What is a graph? 1.1.2. Definition. A graph G is a triple (V(G), E(G), ψ G ) consisting of V(G) of vertices, a set E(G), disjoint from
Minimum Number of Palettes in Edge Colorings
 Graphs and Combinatorics (2014) 30:619 626 DOI 10.1007/s00373-013-1298-8 ORIGINAL PAPER Minimum Number of Palettes in Edge Colorings Mirko Horňák Rafał Kalinowski Mariusz Meszka Mariusz Woźniak Received:
Graphs and Combinatorics (2014) 30:619 626 DOI 10.1007/s00373-013-1298-8 ORIGINAL PAPER Minimum Number of Palettes in Edge Colorings Mirko Horňák Rafał Kalinowski Mariusz Meszka Mariusz Woźniak Received:
On the automorphism group of the m-coloured random graph
 On the automorphism group of the m-coloured random graph Peter J. Cameron and Sam Tarzi School of Mathematical Sciences Queen Mary, University of London Mile End Road London E1 4NS, UK p.j.cameron@qmul.ac.uk
On the automorphism group of the m-coloured random graph Peter J. Cameron and Sam Tarzi School of Mathematical Sciences Queen Mary, University of London Mile End Road London E1 4NS, UK p.j.cameron@qmul.ac.uk
Endomorphisms and synchronization, 2: Graphs and transformation monoids. Peter J. Cameron
 Endomorphisms and synchronization, 2: Graphs and transformation monoids Peter J. Cameron BIRS, November 2014 Relations and algebras From algebras to relations Given a relational structure R, there are
Endomorphisms and synchronization, 2: Graphs and transformation monoids Peter J. Cameron BIRS, November 2014 Relations and algebras From algebras to relations Given a relational structure R, there are
Module 11. Directed Graphs. Contents
 Module 11 Directed Graphs Contents 11.1 Basic concepts......................... 256 Underlying graph of a digraph................ 257 Out-degrees and in-degrees.................. 258 Isomorphism..........................
Module 11 Directed Graphs Contents 11.1 Basic concepts......................... 256 Underlying graph of a digraph................ 257 Out-degrees and in-degrees.................. 258 Isomorphism..........................
Math 776 Graph Theory Lecture Note 1 Basic concepts
 Math 776 Graph Theory Lecture Note 1 Basic concepts Lectured by Lincoln Lu Transcribed by Lincoln Lu Graph theory was founded by the great Swiss mathematician Leonhard Euler (1707-178) after he solved
Math 776 Graph Theory Lecture Note 1 Basic concepts Lectured by Lincoln Lu Transcribed by Lincoln Lu Graph theory was founded by the great Swiss mathematician Leonhard Euler (1707-178) after he solved
Discrete Mathematics
 Discrete Mathematics 310 (2010) 2769 2775 Contents lists available at ScienceDirect Discrete Mathematics journal homepage: www.elsevier.com/locate/disc Optimal acyclic edge colouring of grid like graphs
Discrete Mathematics 310 (2010) 2769 2775 Contents lists available at ScienceDirect Discrete Mathematics journal homepage: www.elsevier.com/locate/disc Optimal acyclic edge colouring of grid like graphs
FOUR EDGE-INDEPENDENT SPANNING TREES 1
 FOUR EDGE-INDEPENDENT SPANNING TREES 1 Alexander Hoyer and Robin Thomas School of Mathematics Georgia Institute of Technology Atlanta, Georgia 30332-0160, USA ABSTRACT We prove an ear-decomposition theorem
FOUR EDGE-INDEPENDENT SPANNING TREES 1 Alexander Hoyer and Robin Thomas School of Mathematics Georgia Institute of Technology Atlanta, Georgia 30332-0160, USA ABSTRACT We prove an ear-decomposition theorem
DOUBLE DOMINATION CRITICAL AND STABLE GRAPHS UPON VERTEX REMOVAL 1
 Discussiones Mathematicae Graph Theory 32 (2012) 643 657 doi:10.7151/dmgt.1633 DOUBLE DOMINATION CRITICAL AND STABLE GRAPHS UPON VERTEX REMOVAL 1 Soufiane Khelifi Laboratory LMP2M, Bloc of laboratories
Discussiones Mathematicae Graph Theory 32 (2012) 643 657 doi:10.7151/dmgt.1633 DOUBLE DOMINATION CRITICAL AND STABLE GRAPHS UPON VERTEX REMOVAL 1 Soufiane Khelifi Laboratory LMP2M, Bloc of laboratories
DOMINATION GAME: EXTREMAL FAMILIES FOR THE 3/5-CONJECTURE FOR FORESTS
 Discussiones Mathematicae Graph Theory 37 (2017) 369 381 doi:10.7151/dmgt.1931 DOMINATION GAME: EXTREMAL FAMILIES FOR THE 3/5-CONJECTURE FOR FORESTS Michael A. Henning 1 Department of Pure and Applied
Discussiones Mathematicae Graph Theory 37 (2017) 369 381 doi:10.7151/dmgt.1931 DOMINATION GAME: EXTREMAL FAMILIES FOR THE 3/5-CONJECTURE FOR FORESTS Michael A. Henning 1 Department of Pure and Applied
arxiv: v1 [math.co] 4 Apr 2011
![arxiv: v1 [math.co] 4 Apr 2011 arxiv: v1 [math.co] 4 Apr 2011](/thumbs/94/118782109.jpg) arxiv:1104.0510v1 [math.co] 4 Apr 2011 Minimal non-extensible precolorings and implicit-relations José Antonio Martín H. Abstract. In this paper I study a variant of the general vertex coloring problem
arxiv:1104.0510v1 [math.co] 4 Apr 2011 Minimal non-extensible precolorings and implicit-relations José Antonio Martín H. Abstract. In this paper I study a variant of the general vertex coloring problem
An Eternal Domination Problem in Grids
 Theory and Applications of Graphs Volume Issue 1 Article 2 2017 An Eternal Domination Problem in Grids William Klostermeyer University of North Florida, klostermeyer@hotmail.com Margaret-Ellen Messinger
Theory and Applications of Graphs Volume Issue 1 Article 2 2017 An Eternal Domination Problem in Grids William Klostermeyer University of North Florida, klostermeyer@hotmail.com Margaret-Ellen Messinger
The incidence game chromatic number
 The incidence game chromatic number Stephan Dominique Andres Zentrum für angewandte Informatik Köln, University of Cologne, Weyertal 80, 50931 Köln, Germany Abstract We introduce the incidence game chromatic
The incidence game chromatic number Stephan Dominique Andres Zentrum für angewandte Informatik Köln, University of Cologne, Weyertal 80, 50931 Köln, Germany Abstract We introduce the incidence game chromatic
Abstract. A graph G is perfect if for every induced subgraph H of G, the chromatic number of H is equal to the size of the largest clique of H.
 Abstract We discuss a class of graphs called perfect graphs. After defining them and getting intuition with a few simple examples (and one less simple example), we present a proof of the Weak Perfect Graph
Abstract We discuss a class of graphs called perfect graphs. After defining them and getting intuition with a few simple examples (and one less simple example), we present a proof of the Weak Perfect Graph
The Structure of Bull-Free Perfect Graphs
 The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
Base size and separation number
 Base size and separation number Peter J. Cameron CSG notes, April 2005 Brief history The concept of a base for a permutation group was introduced by Sims in the 1960s in connection with computational group
Base size and separation number Peter J. Cameron CSG notes, April 2005 Brief history The concept of a base for a permutation group was introduced by Sims in the 1960s in connection with computational group
arxiv: v1 [math.co] 7 Dec 2018
![arxiv: v1 [math.co] 7 Dec 2018 arxiv: v1 [math.co] 7 Dec 2018](/thumbs/92/108223845.jpg) SEQUENTIALLY EMBEDDABLE GRAPHS JACKSON AUTRY AND CHRISTOPHER O NEILL arxiv:1812.02904v1 [math.co] 7 Dec 2018 Abstract. We call a (not necessarily planar) embedding of a graph G in the plane sequential
SEQUENTIALLY EMBEDDABLE GRAPHS JACKSON AUTRY AND CHRISTOPHER O NEILL arxiv:1812.02904v1 [math.co] 7 Dec 2018 Abstract. We call a (not necessarily planar) embedding of a graph G in the plane sequential
The Probabilistic Method
 The Probabilistic Method Po-Shen Loh June 2010 1 Warm-up 1. (Russia 1996/4 In the Duma there are 1600 delegates, who have formed 16000 committees of 80 persons each. Prove that one can find two committees
The Probabilistic Method Po-Shen Loh June 2010 1 Warm-up 1. (Russia 1996/4 In the Duma there are 1600 delegates, who have formed 16000 committees of 80 persons each. Prove that one can find two committees
On the Relationships between Zero Forcing Numbers and Certain Graph Coverings
 On the Relationships between Zero Forcing Numbers and Certain Graph Coverings Fatemeh Alinaghipour Taklimi, Shaun Fallat 1,, Karen Meagher 2 Department of Mathematics and Statistics, University of Regina,
On the Relationships between Zero Forcing Numbers and Certain Graph Coverings Fatemeh Alinaghipour Taklimi, Shaun Fallat 1,, Karen Meagher 2 Department of Mathematics and Statistics, University of Regina,
Packing chromatic number of base-3 Sierpiński graphs
 Noname manuscript No. (will be inserted by the editor) Packing chromatic number of base-3 Sierpiński graphs Boštjan Brešar Sandi Klavžar Douglas F. Rall Received: date / Accepted: date Abstract The packing
Noname manuscript No. (will be inserted by the editor) Packing chromatic number of base-3 Sierpiński graphs Boštjan Brešar Sandi Klavžar Douglas F. Rall Received: date / Accepted: date Abstract The packing
ON VERTEX b-critical TREES. Mostafa Blidia, Noureddine Ikhlef Eschouf, and Frédéric Maffray
 Opuscula Math. 33, no. 1 (2013), 19 28 http://dx.doi.org/10.7494/opmath.2013.33.1.19 Opuscula Mathematica ON VERTEX b-critical TREES Mostafa Blidia, Noureddine Ikhlef Eschouf, and Frédéric Maffray Communicated
Opuscula Math. 33, no. 1 (2013), 19 28 http://dx.doi.org/10.7494/opmath.2013.33.1.19 Opuscula Mathematica ON VERTEX b-critical TREES Mostafa Blidia, Noureddine Ikhlef Eschouf, and Frédéric Maffray Communicated
Product constructions for transitive decompositions of graphs
 116 Product constructions for transitive decompositions of graphs Geoffrey Pearce Abstract A decomposition of a graph is a partition of the edge set, giving a set of subgraphs. A transitive decomposition
116 Product constructions for transitive decompositions of graphs Geoffrey Pearce Abstract A decomposition of a graph is a partition of the edge set, giving a set of subgraphs. A transitive decomposition
PACKING DIGRAPHS WITH DIRECTED CLOSED TRAILS
 PACKING DIGRAPHS WITH DIRECTED CLOSED TRAILS PAUL BALISTER Abstract It has been shown [Balister, 2001] that if n is odd and m 1,, m t are integers with m i 3 and t i=1 m i = E(K n) then K n can be decomposed
PACKING DIGRAPHS WITH DIRECTED CLOSED TRAILS PAUL BALISTER Abstract It has been shown [Balister, 2001] that if n is odd and m 1,, m t are integers with m i 3 and t i=1 m i = E(K n) then K n can be decomposed
REU 2006 Discrete Math Lecture 5
 REU 2006 Discrete Math Lecture 5 Instructor: László Babai Scribe: Megan Guichard Editors: Duru Türkoğlu and Megan Guichard June 30, 2006. Last updated July 3, 2006 at 11:30pm. 1 Review Recall the definitions
REU 2006 Discrete Math Lecture 5 Instructor: László Babai Scribe: Megan Guichard Editors: Duru Türkoğlu and Megan Guichard June 30, 2006. Last updated July 3, 2006 at 11:30pm. 1 Review Recall the definitions
Domination Game. Sandi Klavžar. Faculty of Mathematics and Physics, University of Ljubljana, Slovenia
 Sandi Klavžar Faculty of Mathematics and Physics, University of Ljubljana, Slovenia Faculty of Natural Sciences and Mathematics, University of Maribor, Slovenia Institute of Mathematics, Physics and Mechanics,
Sandi Klavžar Faculty of Mathematics and Physics, University of Ljubljana, Slovenia Faculty of Natural Sciences and Mathematics, University of Maribor, Slovenia Institute of Mathematics, Physics and Mechanics,
HW Graph Theory SOLUTIONS (hbovik) - Q
 1, Diestel 9.3: An arithmetic progression is an increasing sequence of numbers of the form a, a+d, a+ d, a + 3d.... Van der Waerden s theorem says that no matter how we partition the natural numbers into
1, Diestel 9.3: An arithmetic progression is an increasing sequence of numbers of the form a, a+d, a+ d, a + 3d.... Van der Waerden s theorem says that no matter how we partition the natural numbers into
FINDING SEMI-TRANSITIVE ORIENTATIONS OF GRAPHS
 FINDING SEMI-TRANSITIVE ORIENTATIONS OF GRAPHS MEGAN GALLANT Abstract. Given any graph, how do we determine whether it is semi-transitive or not. In this paper, I give a method to determine the semi-transitive
FINDING SEMI-TRANSITIVE ORIENTATIONS OF GRAPHS MEGAN GALLANT Abstract. Given any graph, how do we determine whether it is semi-transitive or not. In this paper, I give a method to determine the semi-transitive
Is there a McLaughlin geometry?
 Is there a McLaughlin geometry? Leonard H. Soicher School of Mathematical Sciences Queen Mary, University of London Mile End Road, London E1 4NS, UK email: L.H.Soicher@qmul.ac.uk February 9, 2006 Dedicated
Is there a McLaughlin geometry? Leonard H. Soicher School of Mathematical Sciences Queen Mary, University of London Mile End Road, London E1 4NS, UK email: L.H.Soicher@qmul.ac.uk February 9, 2006 Dedicated
Lecture 1. 1 Notation
 Lecture 1 (The material on mathematical logic is covered in the textbook starting with Chapter 5; however, for the first few lectures, I will be providing some required background topics and will not be
Lecture 1 (The material on mathematical logic is covered in the textbook starting with Chapter 5; however, for the first few lectures, I will be providing some required background topics and will not be
Nim-Regularity of Graphs
 Nim-Regularity of Graphs Nathan Reading School of Mathematics, University of Minnesota Minneapolis, MN 55455 reading@math.umn.edu Submitted: November 24, 1998; Accepted: January 22, 1999 Abstract. Ehrenborg
Nim-Regularity of Graphs Nathan Reading School of Mathematics, University of Minnesota Minneapolis, MN 55455 reading@math.umn.edu Submitted: November 24, 1998; Accepted: January 22, 1999 Abstract. Ehrenborg
Chromatic Transversal Domatic Number of Graphs
 International Mathematical Forum, 5, 010, no. 13, 639-648 Chromatic Transversal Domatic Number of Graphs L. Benedict Michael Raj 1, S. K. Ayyaswamy and I. Sahul Hamid 3 1 Department of Mathematics, St.
International Mathematical Forum, 5, 010, no. 13, 639-648 Chromatic Transversal Domatic Number of Graphs L. Benedict Michael Raj 1, S. K. Ayyaswamy and I. Sahul Hamid 3 1 Department of Mathematics, St.
On Universal Cycles of Labeled Graphs
 On Universal Cycles of Labeled Graphs Greg Brockman Harvard University Cambridge, MA 02138 United States brockman@hcs.harvard.edu Bill Kay University of South Carolina Columbia, SC 29208 United States
On Universal Cycles of Labeled Graphs Greg Brockman Harvard University Cambridge, MA 02138 United States brockman@hcs.harvard.edu Bill Kay University of South Carolina Columbia, SC 29208 United States
A GRAPH FROM THE VIEWPOINT OF ALGEBRAIC TOPOLOGY
 A GRAPH FROM THE VIEWPOINT OF ALGEBRAIC TOPOLOGY KARL L. STRATOS Abstract. The conventional method of describing a graph as a pair (V, E), where V and E repectively denote the sets of vertices and edges,
A GRAPH FROM THE VIEWPOINT OF ALGEBRAIC TOPOLOGY KARL L. STRATOS Abstract. The conventional method of describing a graph as a pair (V, E), where V and E repectively denote the sets of vertices and edges,
Vertex Deletion games with Parity rules
 Vertex Deletion games with Parity rules Richard J. Nowakowski 1 Department of Mathematics, Dalhousie University, Halifax, Nova Scotia, Canada rjn@mathstat.dal.ca Paul Ottaway Department of Mathematics,
Vertex Deletion games with Parity rules Richard J. Nowakowski 1 Department of Mathematics, Dalhousie University, Halifax, Nova Scotia, Canada rjn@mathstat.dal.ca Paul Ottaway Department of Mathematics,
Treewidth and graph minors
 Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Computation with No Memory, and Rearrangeable Multicast Networks
 Discrete Mathematics and Theoretical Computer Science DMTCS vol. 16:1, 2014, 121 142 Computation with No Memory, and Rearrangeable Multicast Networks Serge Burckel 1 Emeric Gioan 2 Emmanuel Thomé 3 1 ERMIT,
Discrete Mathematics and Theoretical Computer Science DMTCS vol. 16:1, 2014, 121 142 Computation with No Memory, and Rearrangeable Multicast Networks Serge Burckel 1 Emeric Gioan 2 Emmanuel Thomé 3 1 ERMIT,
The 4/5 Upper Bound on the Game Total Domination Number
 The 4/ Upper Bound on the Game Total Domination Number Michael A. Henning a Sandi Klavžar b,c,d Douglas F. Rall e a Department of Mathematics, University of Johannesburg, South Africa mahenning@uj.ac.za
The 4/ Upper Bound on the Game Total Domination Number Michael A. Henning a Sandi Klavžar b,c,d Douglas F. Rall e a Department of Mathematics, University of Johannesburg, South Africa mahenning@uj.ac.za
Sparse Hypercube 3-Spanners
 Sparse Hypercube 3-Spanners W. Duckworth and M. Zito Department of Mathematics and Statistics, University of Melbourne, Parkville, Victoria 3052, Australia Department of Computer Science, University of
Sparse Hypercube 3-Spanners W. Duckworth and M. Zito Department of Mathematics and Statistics, University of Melbourne, Parkville, Victoria 3052, Australia Department of Computer Science, University of
Complexity of the Game Domination Problem
 Complexity of the Game Domination Problem Boštjan Brešar a,b Paul Dorbec c,d Sandi Klavžar e,a,b Gašper Košmrlj e Gabriel Renault c,d a Faculty of Natural Sciences and Mathematics, University of Maribor,
Complexity of the Game Domination Problem Boštjan Brešar a,b Paul Dorbec c,d Sandi Klavžar e,a,b Gašper Košmrlj e Gabriel Renault c,d a Faculty of Natural Sciences and Mathematics, University of Maribor,
arxiv: v1 [math.co] 1 Nov 2017
![arxiv: v1 [math.co] 1 Nov 2017 arxiv: v1 [math.co] 1 Nov 2017](/thumbs/87/96929175.jpg) The multiset dimension of graphs Rinovia Simanjuntak a, Tomáš Vetrík b, Presli Bintang Mulia a arxiv:1711.00225v1 [math.co] 1 Nov 2017 Abstract a Combinatorial Mathematics Research Group Institut Teknologi
The multiset dimension of graphs Rinovia Simanjuntak a, Tomáš Vetrík b, Presli Bintang Mulia a arxiv:1711.00225v1 [math.co] 1 Nov 2017 Abstract a Combinatorial Mathematics Research Group Institut Teknologi
PLANAR GRAPH BIPARTIZATION IN LINEAR TIME
 PLANAR GRAPH BIPARTIZATION IN LINEAR TIME SAMUEL FIORINI, NADIA HARDY, BRUCE REED, AND ADRIAN VETTA Abstract. For each constant k, we present a linear time algorithm that, given a planar graph G, either
PLANAR GRAPH BIPARTIZATION IN LINEAR TIME SAMUEL FIORINI, NADIA HARDY, BRUCE REED, AND ADRIAN VETTA Abstract. For each constant k, we present a linear time algorithm that, given a planar graph G, either
The 3/5-conjecture for weakly S(K_1, 3)-free forests
 The 3/-conjecture for weakly S(K_1, 3)-free forests Simon Schmidt To cite this version: Simon Schmidt. The 3/-conjecture for weakly S(K_1, 3)-free forests. 201. HAL Id: hal-0121891 https://hal.archives-ouvertes.fr/hal-0121891
The 3/-conjecture for weakly S(K_1, 3)-free forests Simon Schmidt To cite this version: Simon Schmidt. The 3/-conjecture for weakly S(K_1, 3)-free forests. 201. HAL Id: hal-0121891 https://hal.archives-ouvertes.fr/hal-0121891
arxiv: v1 [math.co] 28 Nov 2016
![arxiv: v1 [math.co] 28 Nov 2016 arxiv: v1 [math.co] 28 Nov 2016](/thumbs/89/98247778.jpg) Trees with distinguishing number two arxiv:1611.09291v1 [math.co] 28 Nov 2016 Saeid Alikhani May 15, 2018 Samaneh Soltani Department of Mathematics, Yazd University, 89195-741, Yazd, Iran alikhani@yazd.ac.ir,
Trees with distinguishing number two arxiv:1611.09291v1 [math.co] 28 Nov 2016 Saeid Alikhani May 15, 2018 Samaneh Soltani Department of Mathematics, Yazd University, 89195-741, Yazd, Iran alikhani@yazd.ac.ir,
Global Alliance Partition in Trees
 Global Alliance Partition in Trees Linda Eroh Department of Mathematics University of Wisconsin Oshkosh, Oshkosh, WI, 54901 eroh@uwoshedu and Ralucca Gera Department of Applied Mathematics Naval Postgraduate
Global Alliance Partition in Trees Linda Eroh Department of Mathematics University of Wisconsin Oshkosh, Oshkosh, WI, 54901 eroh@uwoshedu and Ralucca Gera Department of Applied Mathematics Naval Postgraduate
Star Decompositions of the Complete Split Graph
 University of Dayton ecommons Honors Theses University Honors Program 4-016 Star Decompositions of the Complete Split Graph Adam C. Volk Follow this and additional works at: https://ecommons.udayton.edu/uhp_theses
University of Dayton ecommons Honors Theses University Honors Program 4-016 Star Decompositions of the Complete Split Graph Adam C. Volk Follow this and additional works at: https://ecommons.udayton.edu/uhp_theses
A Vizing-like theorem for union vertex-distinguishing edge coloring
 A Vizing-like theorem for union vertex-distinguishing edge coloring Nicolas Bousquet, Antoine Dailly, Éric Duchêne, Hamamache Kheddouci, Aline Parreau Abstract We introduce a variant of the vertex-distinguishing
A Vizing-like theorem for union vertex-distinguishing edge coloring Nicolas Bousquet, Antoine Dailly, Éric Duchêne, Hamamache Kheddouci, Aline Parreau Abstract We introduce a variant of the vertex-distinguishing
Neighbor Sum Distinguishing Index
 Graphs and Combinatorics (2013) 29:1329 1336 DOI 10.1007/s00373-012-1191-x ORIGINAL PAPER Neighbor Sum Distinguishing Index Evelyne Flandrin Antoni Marczyk Jakub Przybyło Jean-François Saclé Mariusz Woźniak
Graphs and Combinatorics (2013) 29:1329 1336 DOI 10.1007/s00373-012-1191-x ORIGINAL PAPER Neighbor Sum Distinguishing Index Evelyne Flandrin Antoni Marczyk Jakub Przybyło Jean-François Saclé Mariusz Woźniak
Subdivided graphs have linear Ramsey numbers
 Subdivided graphs have linear Ramsey numbers Noga Alon Bellcore, Morristown, NJ 07960, USA and Department of Mathematics Raymond and Beverly Sackler Faculty of Exact Sciences Tel Aviv University, Tel Aviv,
Subdivided graphs have linear Ramsey numbers Noga Alon Bellcore, Morristown, NJ 07960, USA and Department of Mathematics Raymond and Beverly Sackler Faculty of Exact Sciences Tel Aviv University, Tel Aviv,
On Acyclic Vertex Coloring of Grid like graphs
 On Acyclic Vertex Coloring of Grid like graphs Bharat Joshi and Kishore Kothapalli {bharatj@research., kkishore@}iiit.ac.in Center for Security, Theory and Algorithmic Research International Institute
On Acyclic Vertex Coloring of Grid like graphs Bharat Joshi and Kishore Kothapalli {bharatj@research., kkishore@}iiit.ac.in Center for Security, Theory and Algorithmic Research International Institute
Math 170- Graph Theory Notes
 1 Math 170- Graph Theory Notes Michael Levet December 3, 2018 Notation: Let n be a positive integer. Denote [n] to be the set {1, 2,..., n}. So for example, [3] = {1, 2, 3}. To quote Bud Brown, Graph theory
1 Math 170- Graph Theory Notes Michael Levet December 3, 2018 Notation: Let n be a positive integer. Denote [n] to be the set {1, 2,..., n}. So for example, [3] = {1, 2, 3}. To quote Bud Brown, Graph theory
Vertex 3-colorability of claw-free graphs
 Algorithmic Operations Research Vol.2 (27) 5 2 Vertex 3-colorability of claw-free graphs Marcin Kamiński a Vadim Lozin a a RUTCOR - Rutgers University Center for Operations Research, 64 Bartholomew Road,
Algorithmic Operations Research Vol.2 (27) 5 2 Vertex 3-colorability of claw-free graphs Marcin Kamiński a Vadim Lozin a a RUTCOR - Rutgers University Center for Operations Research, 64 Bartholomew Road,
Discrete Applied Mathematics. A revision and extension of results on 4-regular, 4-connected, claw-free graphs
 Discrete Applied Mathematics 159 (2011) 1225 1230 Contents lists available at ScienceDirect Discrete Applied Mathematics journal homepage: www.elsevier.com/locate/dam A revision and extension of results
Discrete Applied Mathematics 159 (2011) 1225 1230 Contents lists available at ScienceDirect Discrete Applied Mathematics journal homepage: www.elsevier.com/locate/dam A revision and extension of results
The Encoding Complexity of Network Coding
 The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email: mikel,spalex,bruck @caltech.edu Abstract In the multicast network
The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email: mikel,spalex,bruck @caltech.edu Abstract In the multicast network
Paths partition with prescribed beginnings in digraphs: a Chvátal-Erdős condition approach.
 Paths partition with prescribed beginnings in digraphs: a Chvátal-Erdős condition approach. S. Bessy, Projet Mascotte, CNRS/INRIA/UNSA, INRIA Sophia-Antipolis, 2004 route des Lucioles BP 93, 06902 Sophia-Antipolis
Paths partition with prescribed beginnings in digraphs: a Chvátal-Erdős condition approach. S. Bessy, Projet Mascotte, CNRS/INRIA/UNSA, INRIA Sophia-Antipolis, 2004 route des Lucioles BP 93, 06902 Sophia-Antipolis
Small Survey on Perfect Graphs
 Small Survey on Perfect Graphs Michele Alberti ENS Lyon December 8, 2010 Abstract This is a small survey on the exciting world of Perfect Graphs. We will see when a graph is perfect and which are families
Small Survey on Perfect Graphs Michele Alberti ENS Lyon December 8, 2010 Abstract This is a small survey on the exciting world of Perfect Graphs. We will see when a graph is perfect and which are families
Graph Adjacency Matrix Automata Joshua Abbott, Phyllis Z. Chinn, Tyler Evans, Allen J. Stewart Humboldt State University, Arcata, California
 Graph Adjacency Matrix Automata Joshua Abbott, Phyllis Z. Chinn, Tyler Evans, Allen J. Stewart Humboldt State University, Arcata, California Abstract We define a graph adjacency matrix automaton (GAMA)
Graph Adjacency Matrix Automata Joshua Abbott, Phyllis Z. Chinn, Tyler Evans, Allen J. Stewart Humboldt State University, Arcata, California Abstract We define a graph adjacency matrix automaton (GAMA)
The optimal routing of augmented cubes.
 The optimal routing of augmented cubes. Meirun Chen, Reza Naserasr To cite this version: Meirun Chen, Reza Naserasr. The optimal routing of augmented cubes.. Information Processing Letters, Elsevier, 28.
The optimal routing of augmented cubes. Meirun Chen, Reza Naserasr To cite this version: Meirun Chen, Reza Naserasr. The optimal routing of augmented cubes.. Information Processing Letters, Elsevier, 28.
Acyclic Coloring of Graphs of Maximum Degree
 Acyclic Coloring of Graphs of Maximum Degree Guillaume Fertin, André Raspaud To cite this version: Guillaume Fertin, André Raspaud. Acyclic Coloring of Graphs of Maximum Degree. Stefan Felsner. 005 European
Acyclic Coloring of Graphs of Maximum Degree Guillaume Fertin, André Raspaud To cite this version: Guillaume Fertin, André Raspaud. Acyclic Coloring of Graphs of Maximum Degree. Stefan Felsner. 005 European
Infinite locally random graphs
 Infinite locally random graphs Pierre Charbit and Alex D. Scott Abstract Motivated by copying models of the web graph, Bonato and Janssen [3] introduced the following simple construction: given a graph
Infinite locally random graphs Pierre Charbit and Alex D. Scott Abstract Motivated by copying models of the web graph, Bonato and Janssen [3] introduced the following simple construction: given a graph
ON THE STRONGLY REGULAR GRAPH OF PARAMETERS
 ON THE STRONGLY REGULAR GRAPH OF PARAMETERS (99, 14, 1, 2) SUZY LOU AND MAX MURIN Abstract. In an attempt to find a strongly regular graph of parameters (99, 14, 1, 2) or to disprove its existence, we
ON THE STRONGLY REGULAR GRAPH OF PARAMETERS (99, 14, 1, 2) SUZY LOU AND MAX MURIN Abstract. In an attempt to find a strongly regular graph of parameters (99, 14, 1, 2) or to disprove its existence, we
arxiv: v4 [math.co] 4 Apr 2011
![arxiv: v4 [math.co] 4 Apr 2011 arxiv: v4 [math.co] 4 Apr 2011](/thumbs/86/94422941.jpg) Upper-critical graphs (complete k-partite graphs) José Antonio Martín H. Faculty of Computer Science, Complutense University of Madrid, Spain arxiv:1011.4124v4 [math.co] 4 Apr 2011 Abstract This work introduces
Upper-critical graphs (complete k-partite graphs) José Antonio Martín H. Faculty of Computer Science, Complutense University of Madrid, Spain arxiv:1011.4124v4 [math.co] 4 Apr 2011 Abstract This work introduces
FURTHER APPLICATIONS OF CLUTTER DOMINATION PARAMETERS TO PROJECTIVE DIMENSION
 FURTHER APPLICATIONS OF CLUTTER DOMINATION PARAMETERS TO PROJECTIVE DIMENSION HAILONG DAO AND JAY SCHWEIG Abstract. We study the relationship between the projective dimension of a squarefree monomial ideal
FURTHER APPLICATIONS OF CLUTTER DOMINATION PARAMETERS TO PROJECTIVE DIMENSION HAILONG DAO AND JAY SCHWEIG Abstract. We study the relationship between the projective dimension of a squarefree monomial ideal
Discrete mathematics , Fall Instructor: prof. János Pach
 Discrete mathematics 2016-2017, Fall Instructor: prof. János Pach - covered material - Lecture 1. Counting problems To read: [Lov]: 1.2. Sets, 1.3. Number of subsets, 1.5. Sequences, 1.6. Permutations,
Discrete mathematics 2016-2017, Fall Instructor: prof. János Pach - covered material - Lecture 1. Counting problems To read: [Lov]: 1.2. Sets, 1.3. Number of subsets, 1.5. Sequences, 1.6. Permutations,
On vertex types of graphs
 On vertex types of graphs arxiv:1705.09540v1 [math.co] 26 May 2017 Pu Qiao, Xingzhi Zhan Department of Mathematics, East China Normal University, Shanghai 200241, China Abstract The vertices of a graph
On vertex types of graphs arxiv:1705.09540v1 [math.co] 26 May 2017 Pu Qiao, Xingzhi Zhan Department of Mathematics, East China Normal University, Shanghai 200241, China Abstract The vertices of a graph
CHAPTER 2. Graphs. 1. Introduction to Graphs and Graph Isomorphism
 CHAPTER 2 Graphs 1. Introduction to Graphs and Graph Isomorphism 1.1. The Graph Menagerie. Definition 1.1.1. A simple graph G = (V, E) consists of a set V of vertices and a set E of edges, represented
CHAPTER 2 Graphs 1. Introduction to Graphs and Graph Isomorphism 1.1. The Graph Menagerie. Definition 1.1.1. A simple graph G = (V, E) consists of a set V of vertices and a set E of edges, represented
arxiv: v1 [math.co] 13 Aug 2017
![arxiv: v1 [math.co] 13 Aug 2017 arxiv: v1 [math.co] 13 Aug 2017](/thumbs/81/83700452.jpg) Strong geodetic problem in grid like architectures arxiv:170803869v1 [mathco] 13 Aug 017 Sandi Klavžar a,b,c April 11, 018 Paul Manuel d a Faculty of Mathematics and Physics, University of Ljubljana, Slovenia
Strong geodetic problem in grid like architectures arxiv:170803869v1 [mathco] 13 Aug 017 Sandi Klavžar a,b,c April 11, 018 Paul Manuel d a Faculty of Mathematics and Physics, University of Ljubljana, Slovenia
Mirrors of reflections of regular maps
 ISSN 1855-3966 (printed edn), ISSN 1855-3974 (electronic edn) ARS MATHEMATICA CONTEMPORANEA 15 (018) 347 354 https://doiorg/106493/1855-3974145911d (Also available at http://amc-journaleu) Mirrors of reflections
ISSN 1855-3966 (printed edn), ISSN 1855-3974 (electronic edn) ARS MATHEMATICA CONTEMPORANEA 15 (018) 347 354 https://doiorg/106493/1855-3974145911d (Also available at http://amc-journaleu) Mirrors of reflections
DISTINGUISHING NUMBER AND ADJACENCY PROPERTIES
 DISTINGUISHING NUMBER AND ADJACENCY PROPERTIES ANTHONY BONATO AND DEJAN DELIĆ Dedicated to the memory of Roland Fraïssé. Abstract. The distinguishing number of countably infinite graphs and relational
DISTINGUISHING NUMBER AND ADJACENCY PROPERTIES ANTHONY BONATO AND DEJAN DELIĆ Dedicated to the memory of Roland Fraïssé. Abstract. The distinguishing number of countably infinite graphs and relational
A more efficient algorithm for perfect sorting by reversals
 A more efficient algorithm for perfect sorting by reversals Sèverine Bérard 1,2, Cedric Chauve 3,4, and Christophe Paul 5 1 Département de Mathématiques et d Informatique Appliquée, INRA, Toulouse, France.
A more efficient algorithm for perfect sorting by reversals Sèverine Bérard 1,2, Cedric Chauve 3,4, and Christophe Paul 5 1 Département de Mathématiques et d Informatique Appliquée, INRA, Toulouse, France.
Symmetric Product Graphs
 Rochester Institute of Technology RIT Scholar Works Theses Thesis/Dissertation Collections 5-20-2015 Symmetric Product Graphs Evan Witz Follow this and additional works at: http://scholarworks.rit.edu/theses
Rochester Institute of Technology RIT Scholar Works Theses Thesis/Dissertation Collections 5-20-2015 Symmetric Product Graphs Evan Witz Follow this and additional works at: http://scholarworks.rit.edu/theses
Universal Cycles for Permutations
 arxiv:0710.5611v1 [math.co] 30 Oct 2007 Universal Cycles for Permutations J Robert Johnson School of Mathematical Sciences Queen Mary, University of London Mile End Road, London E1 4NS, UK Email: r.johnson@qmul.ac.uk
arxiv:0710.5611v1 [math.co] 30 Oct 2007 Universal Cycles for Permutations J Robert Johnson School of Mathematical Sciences Queen Mary, University of London Mile End Road, London E1 4NS, UK Email: r.johnson@qmul.ac.uk
Rainbow game domination subdivision number of a graph
 Rainbow game domination subdivision number of a graph J. Amjadi Department of Mathematics Azarbaijan Shahid Madani University Tabriz, I.R. Iran j-amjadi@azaruniv.edu Abstract The rainbow game domination
Rainbow game domination subdivision number of a graph J. Amjadi Department of Mathematics Azarbaijan Shahid Madani University Tabriz, I.R. Iran j-amjadi@azaruniv.edu Abstract The rainbow game domination
Coloring Subgraphs with Restricted Amounts of Hues
 Coloring Subgraphs with Restricted Amounts of Hues Wayne Goddard School of Computing and Dept of Mathematical Sciences Clemson University goddard@clemson.edu Robert Melville Dept of Mathematics Abstract
Coloring Subgraphs with Restricted Amounts of Hues Wayne Goddard School of Computing and Dept of Mathematical Sciences Clemson University goddard@clemson.edu Robert Melville Dept of Mathematics Abstract
Packing Chromatic Number of Distance Graphs
 Packing Chromatic Number of Distance Graphs Jan Ekstein Premysl Holub Bernard Lidicky y May 25, 2011 Abstract The packing chromatic number (G) of a graph G is the smallest integer k such that vertices
Packing Chromatic Number of Distance Graphs Jan Ekstein Premysl Holub Bernard Lidicky y May 25, 2011 Abstract The packing chromatic number (G) of a graph G is the smallest integer k such that vertices
DISTINGUISHING NUMBER AND ADJACENCY PROPERTIES
 DISTINGUISHING NUMBER AND ADJACENCY PROPERTIES ANTHONY BONATO AND DEJAN DELIĆ Dedicated to the memory of Roland Fraïssé. Abstract. The distinguishing number of countably infinite graphs and relational
DISTINGUISHING NUMBER AND ADJACENCY PROPERTIES ANTHONY BONATO AND DEJAN DELIĆ Dedicated to the memory of Roland Fraïssé. Abstract. The distinguishing number of countably infinite graphs and relational
CUT VERTICES IN ZERO-DIVISOR GRAPHS OF FINITE COMMUTATIVE RINGS
 CUT VERTICES IN ZERO-DIVISOR GRAPHS OF FINITE COMMUTATIVE RINGS M. AXTELL, N. BAETH, AND J. STICKLES Abstract. A cut vertex of a connected graph is a vertex whose removal would result in a graph having
CUT VERTICES IN ZERO-DIVISOR GRAPHS OF FINITE COMMUTATIVE RINGS M. AXTELL, N. BAETH, AND J. STICKLES Abstract. A cut vertex of a connected graph is a vertex whose removal would result in a graph having
CSE 20 DISCRETE MATH WINTER
 CSE 20 DISCRETE MATH WINTER 2016 http://cseweb.ucsd.edu/classes/wi16/cse20-ab/ Today's learning goals Explain the steps in a proof by (strong) mathematical induction Use (strong) mathematical induction
CSE 20 DISCRETE MATH WINTER 2016 http://cseweb.ucsd.edu/classes/wi16/cse20-ab/ Today's learning goals Explain the steps in a proof by (strong) mathematical induction Use (strong) mathematical induction
Trail Making Game. Hyun Sung Jun Jaehoon Kim Sang-il Oum Department of Mathematical Sciences KAIST, Daejeon, , Republic of Korea.
 Trail Making Game Hyun Sung Jun Jaehoon Kim Sang-il Oum Department of Mathematical Sciences KAIST, Daejeon, 305-701, Republic of Korea. May 7, 2009 Abstract Trail Making is a game played on a graph with
Trail Making Game Hyun Sung Jun Jaehoon Kim Sang-il Oum Department of Mathematical Sciences KAIST, Daejeon, 305-701, Republic of Korea. May 7, 2009 Abstract Trail Making is a game played on a graph with
LOCAL CONNECTIVE CHROMATIC NUMBER OF CARTESIAN PRODUCT OF SOME GRAPHS
 LOCAL CONNECTIVE CHROMATIC NUMBER OF CARTESIAN PRODUCT OF SOME GRAPHS ROMANIAN JOURNAL OF MATHEMATICS AND COMPUTER SCIENCE, 08, VOLUME 8, ISSUE, p-7 CANAN C IFTC I AND PINAR DU NDAR Abstract A local connective
LOCAL CONNECTIVE CHROMATIC NUMBER OF CARTESIAN PRODUCT OF SOME GRAPHS ROMANIAN JOURNAL OF MATHEMATICS AND COMPUTER SCIENCE, 08, VOLUME 8, ISSUE, p-7 CANAN C IFTC I AND PINAR DU NDAR Abstract A local connective
The Game Chromatic Number of Trees and Forests
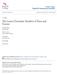 Linfield College DigitalCommons@Linfield Faculty Publications Faculty Scholarship & Creative Works 1-1-2015 The Game Chromatic Number of Trees and Forests Charles Dunn Linfield College Victor Larsen Kennesaw
Linfield College DigitalCommons@Linfield Faculty Publications Faculty Scholarship & Creative Works 1-1-2015 The Game Chromatic Number of Trees and Forests Charles Dunn Linfield College Victor Larsen Kennesaw
Matching Algorithms. Proof. If a bipartite graph has a perfect matching, then it is easy to see that the right hand side is a necessary condition.
 18.433 Combinatorial Optimization Matching Algorithms September 9,14,16 Lecturer: Santosh Vempala Given a graph G = (V, E), a matching M is a set of edges with the property that no two of the edges have
18.433 Combinatorial Optimization Matching Algorithms September 9,14,16 Lecturer: Santosh Vempala Given a graph G = (V, E), a matching M is a set of edges with the property that no two of the edges have
Winning Positions in Simplicial Nim
 Winning Positions in Simplicial Nim David Horrocks Department of Mathematics and Statistics University of Prince Edward Island Charlottetown, Prince Edward Island, Canada, C1A 4P3 dhorrocks@upei.ca Submitted:
Winning Positions in Simplicial Nim David Horrocks Department of Mathematics and Statistics University of Prince Edward Island Charlottetown, Prince Edward Island, Canada, C1A 4P3 dhorrocks@upei.ca Submitted:
Coloring edges and vertices of graphs without short or long cycles
 Coloring edges and vertices of graphs without short or long cycles Marcin Kamiński and Vadim Lozin Abstract Vertex and edge colorability are two graph problems that are NPhard in general. We show that
Coloring edges and vertices of graphs without short or long cycles Marcin Kamiński and Vadim Lozin Abstract Vertex and edge colorability are two graph problems that are NPhard in general. We show that
