Combinational Circuits
|
|
|
- Augustine Dixon
- 5 years ago
- Views:
Transcription
1 Combinational Circuits Combinational circuit consists of an interconnection of logic gates They react to their inputs and produce their outputs by transforming binary information n input binary variables come from a source for which m output variables are produced by the combinational logic go to a destination Typically the source and destination are storage registers If registers are included then the circuit is considered to be sequential 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 1
2 Combinational Circuits For n input variables there are 2 n possible combinations of the binary inputs For each possible input combination there is one possible value for each output variable A combinational circuit can be specified with a truth table that lists the output values for each combination of input variables A combinational circuit also can be described by m Boolean functions, one for each output variable Each output function is expressed in terms of the n input variables 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 2
3 Combinational Circuits Have learned: Binary numbers and binary codes that represent discrete quantities of information Boolean algebra as a way to express logic functions algebraically Simplify Boolean functions to achieve economical (simpler) gate implementations Will now formulate systematic analysis and design procedures for combinational circuits Will build a useful catalog of elementary functions that are important for the understanding of digital systems 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 3
4 Analysis Procedure To analyze a combinational circuit we need to determine the function that the circuit implements First make sure that the given circuit is combinational and not sequential No feedback or memory elements Inspect the logic diagram and then create a set of Boolean functions, a truth table, or an explanation of the circuit operation If we are told what the function does then the analysis problem reduces to just verification 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 4
5 Analysis Procedure To obtain the output Boolean functions from a logic diagram: 1. Label all gate outputs that are a function of input variables with arbitrary symbols 2. Determine the Boolean functions for each gate output 3. Label the gates that are a function of previously labeled gates with other arbitrary symbols 4. Find the Boolean functions for these gates 5. Repeat steps 3 to 4 until the outputs of the circuit are obtained 6. By repeated substitution of previously defined functions, obtain the output Boolean functions in terms of input variables 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 5
6 Analysis Procedure: Example T 4 = AB T 5 = AC T 6 = BC T 1 = A + B + C T 2 = ABC F 2 = T 4 + T 5 + T 6 T 3 = F' 2 T 1 F 1 = T 3 + T 2 = F' 2 T 1 + ABC = A'BC' + A'B'C + AB'C' + ABC 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 6
7 Analysis Procedure: Example 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 7
8 Design Procedure Steps required: 1. From the specifications, determine the required number of inputs and outputs Assign a symbol to each 2. Derive the truth table that defines the required relationship between inputs and outputs 3. Obtain the simplified Boolean functions for each output as a function of the input variables 4. Draw the logic diagram and verify the correctness of the design Manually or by simulation 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 8
9 Design Procedure: Example Convert binary coded decimal (BCD) to excess-3 code Input variables: A, B, C, & D Output variables: w, x, y, & z 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 9
10 Design Procedure: Example x = B'C + B'D + BC'D' = B'(C + D) + BC'D' = B'(C + D) + B(C + D)' w = A + BC + BD = A + B(C + D) 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 10
11 Design Procedure: Example z = D' y = CD + C'D' = CD + (C + D)' 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 11
12 Design Procedure: Example 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 12
13 Binary Adder - Half Adder Addition of 2 bits Sum: S = x'y + xy' or S = x y Carry: C = xy 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 13
14 Binary Adder - Full Adder Full adder is required for n-bit binary numbers After the least significant bit (where only 2 bits are added), addition needs to consider the carry (3 total bits) Resulting carry is passed onto next fulladder 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 14
15 Binary Adder - Full Adder 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 15
16 Binary Adder - Full Adder Can be implemented with 2 HAs and an OR gate: S = z ( x y ) C = ( x y ) z + xy 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 16
17 Binary Adder Binary adder can add 2 n- bit binary numbers Cascade n FAs where each carry feeds into next FA Ripple Carry Slow carry propagation 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 17
18 Binary Adder - Carry Lookahead P i = A i B i G i = A i B i G i is carry generate P i is carry propagate S i = P i C i C i+1 = G i + P i C i C 0 = input carry C 1 = G 0 + P 0 C 0 C 2 = G 1 + P 1 C 1 = G 1 + P 1 (G 0 + P 0 C 0 ) = G 1 + P 1 G 0 + P 1 P 0 C 0 C 3 = G 2 + P 2 C 2 = G 2 + P 2 G 1 + P 2 P 1 G 0 + P 2 P 1 P 0 C Roberto Muscedere Images 2013 Pearson Education Inc. 18
19 Binary Adder - Carry Lookahead 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 19
20 Binary Adder - Carry Lookahead 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 20
21 Binary Subtraction Subtraction of unsigned binary numbers can be done by using complements A - B is done by taking the 2's complement of B and adding it to A 2's complement can be obtained by taking the 1's complement and adding 1 1's complement can be implemented with inverters 1 can be added to the sum through the input carry Addition and subtraction operations can be combined into one circuit (for both signed and unsigned values) 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 21
22 Binary Subtraction Input M controls the operation: When M = 0, the circuit is an adder Input is B M = B 0 = B, C 0 = M = 0 When M = 1, the circuit is a subtractor Input is B M = B 1 = B', C 0 = M = 1 Output V is for detecting an overflow 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 22
23 Binary Addition/Subtraction: Overflow When two numbers with n digits are added and the sum is a number occupying n+1 digits, then an overflow occurred Problem since we have finite storage With unsigned numbers an overflow is detected by looking at the carry out With signed numbers, an overflow may occur if the two numbers added are both positive or both negative Determine by looking at 2 upper most carries, if they are different, overflow occurred 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 23
24 BCD Adder Example Addition of two decimal digits in BCD and an input carry Each input digit and output digits don't exceed 9 ie = 19 (both 1's are in and out carry respectively) Apply two BCD digits to a four-bit binary adder Sum ranges from 0 through 19, in output Z and carry K Apply a correction to Z to generate the proper BCD representation in output S When Z is greater than 9, add 6 to Z with another adder 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 24
25 BCD Adder Example 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 25
26 BCD Adder Example When Z is greater than 9, we also have a carry, C, to forward to next adder C = K + Z 8 Z 4 + Z 8 Z 2 Multiply C by 6 and add to Z to get proper BCD sum S 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 26
27 Binary Multiplier Done the same way as decimal numbers Multiplicand (B) is multiplied by each bit of the multiplier (A) starting from the LSB Each such multiplication forms a partial product Successive partial products are shifted one position to the left Sum up the partial products 2-bit multiplier shown One bit multiplication is an AND operation Partial products can be implemented with AND gates Partial products are added with two halfadders 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 27
28 Binary Multiplier In general a bit of the multiplier (A) is ANDed with each bit of the multiplicand (B) in as many levels as there are bits in the multiplier The binary output in each level of AND gates is added with the partial product of the previous level to form a new partial product The last level produces the product For J multiplier bits and K multiplicand bits, we need (J * K) AND gates and (J -1) K-bit adders to produce a product of (J + K) bits 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 28
29 Binary Multiplier: Example K = 4 and J = 3 Multiplicand: (B 3 B 2 B 1 B 0 ) Multiplier: (A 2 A 1 A 0 ) Needs 12 AND gates and two 4- bit adders to produce a product of seven bits 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 29
30 Magnitude Comparator Magnitude comparator compares two numbers A and B and determines their relative magnitudes A > B, A = B, or A < B For comparing two n-bit numbers, truth table has 2 2n entries Circuit possesses a certain amount of regularity Can be designed by means of an algorithm x i = A i B i + A' i B' i = (A i B i )' (i = 0 for LSB) (A=B) = x n-1 x n-2...x 1 x 0 (A>B) = A n-1 B' n-1 +x n-1 A n-2 B' n x n-1...x 2 A 1 B' 1 +x n-1...x 1 A 0 B' 0 (B>A) = A' n-1 B n-1 +x n-1 A' n-2 B n x n-1...x 2 A' 1 B 1 +x n-1...x 1 A' 0 B Roberto Muscedere Images 2013 Pearson Education Inc. 30
31 Magnitude Comparator Gate implementation is simpler as it involves a certain amount of repetition x i generated with exclusive-nor > and < can use internal XNOR values to further simplify implementation Can simplify further: (A<=B)=(A<B)+(A=B) (A>B)=(A<=B)' (A>B)=((A<B)+(A=B))' (A>B)=(A<B)'(A=B)' 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 31
32 Decoders A binary code of n bits is capable of representing up to 2 n distinct elements of coded information A decoder is a combinational circuit that converts binary information from n input lines to a maximum of 2 n unique output lines If the n-bit coded information has unused combinations, the decoder may have fewer outputs Called n-to-m-line decoders, where m <= 2 n They generate 2 n (or fewer) minterms of n input variables Each combination of inputs will assert a unique output 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 32
33 Decoders: Example 3-to3 to-8 Three inputs are decoded into eight outputs, each representing one of the minterms of the three input variables Inverters provide the complement of the inputs AND gates generates one of the minterms 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 33
34 Decoders: NAND Implementation Decoders can be constructed with NAND gates Output in complement form because of NAND Can include one or more enable inputs (/E) to control the circuit operation 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 34
35 Decoders Decoders with enable inputs can be connected together to form a larger decoder circuit Two 3-to-8-line decoders (w/ enable) form a 4-to-16-line decoder When w=0, the top decoder is enabled (outputs generate minterms 0000 to 0111) and the other is disabled (outputs all 0's) When w=1, the top decoder is disabled (outputs all 0's) and the other is enabled (outputs generate minterms 1000 to 1111) Demonstrates the usefulness of enable inputs in decoders and other combinational logic components 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 35
36 Decoders: Function Implementation Decoder provides the 2 n minterms of n input variables Each output is associated with a unique pattern of input bits Adding an OR gate to a decoder allows any Boolean function (in sum-of-minterms form) to be implemented Any combinational circuit with n inputs and m outputs can be implemented with an n-to-2 n - line decoder and m OR gates Example: S(x, y, z) = (1, 2, 4, 7) C(x, y, z) = (3, 5, 6, 7) 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 36
37 Encoders An encoder is a digital circuit that performs the inverse operation of a decoder An encoder has 2 n (or fewer) input lines and n output lines The output lines generate the binary code corresponding to the input value It is assumed that only one input has a value of 1 at any given time Otherwise the output produces an undefined combination Eg. When all inputs 0, output is 0 Can be implemented with OR gates whose inputs are determined directly from the truth table 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 37
38 Encoders: Octal-to to-binary Example Can be expressed by the following Boolean output functions (ORs only): z = D 1 + D 3 + D 5 + D 7 y = D 2 + D 3 + D 6 + D 7 x = D 4 + D 5 + D 6 + D Roberto Muscedere Images 2013 Pearson Education Inc. 38
39 Priority Encoder A priority encoder solves the encoders undefined combination situations by ignoring inputs less than the placement of the most significant 1 Valid indicator, V, is set when one or more inputs are equal to 1, otherwise it is 0 If not set, other outputs should not be inspected X's in the input columns represent the truth table in condensed form Don't have to list all 16 minterms 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 39
40 Priority Encoder V is an OR of all inputs Inputs, XX10 for example, represent 0010, 0110, 1010, and Roberto Muscedere Images 2013 Pearson Education Inc. 40
41 Multiplexers Multiplexer is a circuit that selects binary information from one of many input lines and directs it to a single output line Selection is controlled by a set of selection lines There are 2 n input lines and n selection lines whose bit combinations determine which input is selected Two-to-one-line multiplexer connects one of two sources to a common destination When S = 0, the upper AND gate is enabled and I 0 goes to the output When S = 1, the lower AND gate is enabled and I 1 goes to the output 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 41
42 Multiplexers Four-to-one-line multiplexer shown Function table lists the input that is passed to the output for each combination of the binary selection values Also called a data selector Multiplexer resemble a decoder since they decode the selection input lines and AND it with the data 2 n -to-1-line multiplexer is constructed from an n-to-2 n decoder by adding 2 n input lines to it, one to each AND gate Outputs of the AND gates are applied to a single OR gate May have an enable input to control the operation of the unit 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 42
43 Multiplexers Multiplexer can be combined with common selection inputs to provide multiple-bit selection logic Quadruple (or 4-bit) 2-to-1- line multiplexer shown Four multiplexers, each capable of selecting one of two input lines When E=0 and S=0, Y=A When E=0 and S=1, Y=B When E=1, Y=all 0's 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 43
44 Multiplexers: Function Implementation Multiplexer is essentially a decoder (minterms generated by selection inputs) that includes the final OR gate Minterms can be selected by the data inputs, thereby providing a method of implementing a Boolean function of n variables with a multiplexer with n-1 selection inputs and 2 n-1 data inputs General procedure for implementing: 1. Generate truth table of Boolean function 2. First n-1 variables in the table are applied to the selection inputs 3. Evaluate the output as a function of the last variable for each combination of the selection variables This function can be 0, 1, the variable, or the complement of the variable 4. Values are then applied to the data inputs in the proper order 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 44
45 Multiplexers: Function Implementation F (x, y, z) = (1, 2, 6, 7) Function of three variables can be implemented with a four-to-one-line multiplexer x, and y connected to inputs S 1, and S 0, respectively When xy=00 then F=z When xy=01 then F=z' When xy=10 then F=0 When xy=11 then F= Roberto Muscedere Images 2013 Pearson Education Inc. 45
46 Multiplexers: Function Implementation F(A,B,C,D) = (1,3,4,11,12,13,14, 15) A, B, and C connected to inputs S 2, S 1, and S 0, respectively When ABC=000, 001, and 101 then F=D When ABC=010 then F=D' When ABC=011, and 100 then F=0 When ABC=110, and 111 then F= Roberto Muscedere Images 2013 Pearson Education Inc. 46
47 Three-state or Tri-state Gate Three-state or tri-state gate is a digital circuit that exhibits three states Two are 1 and 0, but the third state is a high-impedance state or an open circuit Graphic symbol shown below Like a normal buffer but has an input control line entering the bottom When the control input, C, is 1, the gate acts like a buffer When C is 0, the output is disabled by going to a highimpedance state Large number of three-state gate outputs can be connected together 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 47
48 Multiplexers: Three-state or Tri-state Implementation Multiplexers can be made with three-state buffers Two-to-one-line multiplexer with 2 three-state buffers The two outputs are connected together to form a single output line Four-to-one-line multiplexer with 4 three-state buffers Decoder ensures no more than one three-state buffer may be in the active at any given time When the enable of the decoder is 0, all of its four outputs are 0 then this circuit is not driving Y Y can be driven by more than one circuit, but only one can be active 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 48
49 Decoders: Demultiplexer Implementation A decoder with enable input can function as a demultiplexer Circuit that receives information from a single line and directs it to one of 2 n possible output lines Decoder can function as a one-to-four-line demultiplexer E is data input line and A and B are taken as the selection inputs Decoder and demultiplexer operations are taken from the same circuit Decoder with an enable input is referred to as a decoder demultiplexer 2018 Roberto Muscedere Images 2013 Pearson Education Inc. 49
Chapter 4. Combinational Logic
 Chapter 4. Combinational Logic Tong In Oh 1 4.1 Introduction Combinational logic: Logic gates Output determined from only the present combination of inputs Specified by a set of Boolean functions Sequential
Chapter 4. Combinational Logic Tong In Oh 1 4.1 Introduction Combinational logic: Logic gates Output determined from only the present combination of inputs Specified by a set of Boolean functions Sequential
Combinational Logic. Prof. Wangrok Oh. Dept. of Information Communications Eng. Chungnam National University. Prof. Wangrok Oh(CNU) 1 / 93
 Combinational Logic Prof. Wangrok Oh Dept. of Information Communications Eng. Chungnam National University Prof. Wangrok Oh(CNU) / 93 Overview Introduction 2 Combinational Circuits 3 Analysis Procedure
Combinational Logic Prof. Wangrok Oh Dept. of Information Communications Eng. Chungnam National University Prof. Wangrok Oh(CNU) / 93 Overview Introduction 2 Combinational Circuits 3 Analysis Procedure
EE 8351 Digital Logic Circuits Ms.J.Jayaudhaya, ASP/EEE
 EE 8351 Digital Logic Circuits Ms.J.Jayaudhaya, ASP/EEE 1 Logic circuits for digital systems may be combinational or sequential. A combinational circuit consists of input variables, logic gates, and output
EE 8351 Digital Logic Circuits Ms.J.Jayaudhaya, ASP/EEE 1 Logic circuits for digital systems may be combinational or sequential. A combinational circuit consists of input variables, logic gates, and output
DLD VIDYA SAGAR P. potharajuvidyasagar.wordpress.com. Vignana Bharathi Institute of Technology UNIT 3 DLD P VIDYA SAGAR
 DLD UNIT III Combinational Circuits (CC), Analysis procedure, Design Procedure, Combinational circuit for different code converters and other problems, Binary Adder- Subtractor, Decimal Adder, Binary Multiplier,
DLD UNIT III Combinational Circuits (CC), Analysis procedure, Design Procedure, Combinational circuit for different code converters and other problems, Binary Adder- Subtractor, Decimal Adder, Binary Multiplier,
Combinational Logic Circuits
 Combinational Logic Circuits By Dr. M. Hebaishy Digital Logic Design Ch- Rem.!) Types of Logic Circuits Combinational Logic Memoryless Outputs determined by current values of inputs Sequential Logic Has
Combinational Logic Circuits By Dr. M. Hebaishy Digital Logic Design Ch- Rem.!) Types of Logic Circuits Combinational Logic Memoryless Outputs determined by current values of inputs Sequential Logic Has
Combinational Logic II
 Combinational Logic II Ranga Rodrigo July 26, 2009 1 Binary Adder-Subtractor Digital computers perform variety of information processing tasks. Among the functions encountered are the various arithmetic
Combinational Logic II Ranga Rodrigo July 26, 2009 1 Binary Adder-Subtractor Digital computers perform variety of information processing tasks. Among the functions encountered are the various arithmetic
Chap.3 3. Chap reduces the complexity required to represent the schematic diagram of a circuit Library
 3.1 Combinational Circuits 2 Chap 3. logic circuits for digital systems: combinational vs sequential Combinational Logic Design Combinational Circuit (Chap 3) outputs are determined by the present applied
3.1 Combinational Circuits 2 Chap 3. logic circuits for digital systems: combinational vs sequential Combinational Logic Design Combinational Circuit (Chap 3) outputs are determined by the present applied
NH 67, Karur Trichy Highways, Puliyur C.F, Karur District UNIT-II COMBINATIONAL CIRCUITS
 NH 67, Karur Trichy Highways, Puliyur C.F, 639 114 Karur District DEPARTMENT OF ELETRONICS AND COMMUNICATION ENGINEERING COURSE NOTES SUBJECT: DIGITAL ELECTRONICS CLASS: II YEAR ECE SUBJECT CODE: EC2203
NH 67, Karur Trichy Highways, Puliyur C.F, 639 114 Karur District DEPARTMENT OF ELETRONICS AND COMMUNICATION ENGINEERING COURSE NOTES SUBJECT: DIGITAL ELECTRONICS CLASS: II YEAR ECE SUBJECT CODE: EC2203
COMBINATIONAL LOGIC CIRCUITS
 COMBINATIONAL LOGIC CIRCUITS 4.1 INTRODUCTION The digital system consists of two types of circuits, namely: (i) Combinational circuits and (ii) Sequential circuits A combinational circuit consists of logic
COMBINATIONAL LOGIC CIRCUITS 4.1 INTRODUCTION The digital system consists of two types of circuits, namely: (i) Combinational circuits and (ii) Sequential circuits A combinational circuit consists of logic
UNIT- V COMBINATIONAL LOGIC DESIGN
 UNIT- V COMBINATIONAL LOGIC DESIGN NOTE: This is UNIT-V in JNTUK and UNIT-III and HALF PART OF UNIT-IV in JNTUA SYLLABUS (JNTUK)UNIT-V: Combinational Logic Design: Adders & Subtractors, Ripple Adder, Look
UNIT- V COMBINATIONAL LOGIC DESIGN NOTE: This is UNIT-V in JNTUK and UNIT-III and HALF PART OF UNIT-IV in JNTUA SYLLABUS (JNTUK)UNIT-V: Combinational Logic Design: Adders & Subtractors, Ripple Adder, Look
B.Tech II Year I Semester (R13) Regular Examinations December 2014 DIGITAL LOGIC DESIGN
 B.Tech II Year I Semester () Regular Examinations December 2014 (Common to IT and CSE) (a) If 1010 2 + 10 2 = X 10, then X is ----- Write the first 9 decimal digits in base 3. (c) What is meant by don
B.Tech II Year I Semester () Regular Examinations December 2014 (Common to IT and CSE) (a) If 1010 2 + 10 2 = X 10, then X is ----- Write the first 9 decimal digits in base 3. (c) What is meant by don
Gate Level Minimization Map Method
 Gate Level Minimization Map Method Complexity of hardware implementation is directly related to the complexity of the algebraic expression Truth table representation of a function is unique Algebraically
Gate Level Minimization Map Method Complexity of hardware implementation is directly related to the complexity of the algebraic expression Truth table representation of a function is unique Algebraically
Code No: R Set No. 1
 Code No: R059210504 Set No. 1 II B.Tech I Semester Regular Examinations, November 2006 DIGITAL LOGIC DESIGN ( Common to Computer Science & Engineering, Information Technology and Computer Science & Systems
Code No: R059210504 Set No. 1 II B.Tech I Semester Regular Examinations, November 2006 DIGITAL LOGIC DESIGN ( Common to Computer Science & Engineering, Information Technology and Computer Science & Systems
1. Mark the correct statement(s)
 1. Mark the correct statement(s) 1.1 A theorem in Boolean algebra: a) Can easily be proved by e.g. logic induction b) Is a logical statement that is assumed to be true, c) Can be contradicted by another
1. Mark the correct statement(s) 1.1 A theorem in Boolean algebra: a) Can easily be proved by e.g. logic induction b) Is a logical statement that is assumed to be true, c) Can be contradicted by another
Boolean Algebra and Logic Gates
 Boolean Algebra and Logic Gates Binary logic is used in all of today's digital computers and devices Cost of the circuits is an important factor Finding simpler and cheaper but equivalent circuits can
Boolean Algebra and Logic Gates Binary logic is used in all of today's digital computers and devices Cost of the circuits is an important factor Finding simpler and cheaper but equivalent circuits can
Injntu.com Injntu.com Injntu.com R16
 1. a) What are the three methods of obtaining the 2 s complement of a given binary (3M) number? b) What do you mean by K-map? Name it advantages and disadvantages. (3M) c) Distinguish between a half-adder
1. a) What are the three methods of obtaining the 2 s complement of a given binary (3M) number? b) What do you mean by K-map? Name it advantages and disadvantages. (3M) c) Distinguish between a half-adder
Code No: R Set No. 1
 Code No: R059210504 Set No. 1 II B.Tech I Semester Regular Examinations, November 2007 DIGITAL LOGIC DESIGN ( Common to Computer Science & Engineering, Information Technology and Computer Science & Systems
Code No: R059210504 Set No. 1 II B.Tech I Semester Regular Examinations, November 2007 DIGITAL LOGIC DESIGN ( Common to Computer Science & Engineering, Information Technology and Computer Science & Systems
IT 201 Digital System Design Module II Notes
 IT 201 Digital System Design Module II Notes BOOLEAN OPERATIONS AND EXPRESSIONS Variable, complement, and literal are terms used in Boolean algebra. A variable is a symbol used to represent a logical quantity.
IT 201 Digital System Design Module II Notes BOOLEAN OPERATIONS AND EXPRESSIONS Variable, complement, and literal are terms used in Boolean algebra. A variable is a symbol used to represent a logical quantity.
Department of Electrical and Computer Engineering University of Wisconsin - Madison. ECE/CS 352 Digital System Fundamentals.
 Department of Electrical and Computer Engineering University of Wisconsin - Madison ECE/C 352 Digital ystem Fundamentals Quiz #2 Thursday, March 7, 22, 7:15--8:3PM 1. (15 points) (a) (5 points) NAND, NOR
Department of Electrical and Computer Engineering University of Wisconsin - Madison ECE/C 352 Digital ystem Fundamentals Quiz #2 Thursday, March 7, 22, 7:15--8:3PM 1. (15 points) (a) (5 points) NAND, NOR
Chapter Three. Digital Components
 Chapter Three 3.1. Combinational Circuit A combinational circuit is a connected arrangement of logic gates with a set of inputs and outputs. The binary values of the outputs are a function of the binary
Chapter Three 3.1. Combinational Circuit A combinational circuit is a connected arrangement of logic gates with a set of inputs and outputs. The binary values of the outputs are a function of the binary
Combinational Logic Use the Boolean Algebra and the minimization techniques to design useful circuits No feedback, no memory Just n inputs, m outputs
 Combinational Logic Use the Boolean Algebra and the minimization techniques to design useful circuits No feedback, no memory Just n inputs, m outputs and an arbitrary truth table Analysis Procedure We
Combinational Logic Use the Boolean Algebra and the minimization techniques to design useful circuits No feedback, no memory Just n inputs, m outputs and an arbitrary truth table Analysis Procedure We
2008 The McGraw-Hill Companies, Inc. All rights reserved.
 28 The McGraw-Hill Companies, Inc. All rights reserved. 28 The McGraw-Hill Companies, Inc. All rights reserved. All or Nothing Gate Boolean Expression: A B = Y Truth Table (ee next slide) or AB = Y 28
28 The McGraw-Hill Companies, Inc. All rights reserved. 28 The McGraw-Hill Companies, Inc. All rights reserved. All or Nothing Gate Boolean Expression: A B = Y Truth Table (ee next slide) or AB = Y 28
CS/COE 0447 Example Problems for Exam 2 Spring 2011
 CS/COE 0447 Example Problems for Exam 2 Spring 2011 1) Show the steps to multiply the 4-bit numbers 3 and 5 with the fast shift-add multipler. Use the table below. List the multiplicand (M) and product
CS/COE 0447 Example Problems for Exam 2 Spring 2011 1) Show the steps to multiply the 4-bit numbers 3 and 5 with the fast shift-add multipler. Use the table below. List the multiplicand (M) and product
Combinational Logic with MSI and LSI
 1010101010101010101010101010101010101010101010101010101010101010101010101010101010 1010101010101010101010101010101010101010101010101010101010101010101010101010101010 1010101010101010101010101010101010101010101010101010101010101010101010101010101010
1010101010101010101010101010101010101010101010101010101010101010101010101010101010 1010101010101010101010101010101010101010101010101010101010101010101010101010101010 1010101010101010101010101010101010101010101010101010101010101010101010101010101010
Objectives: 1. Design procedure. 2. Fundamental circuits. 1. Design procedure
 Objectives: 1. Design procedure. 2. undamental circuits. 1. Design procedure Design procedure has five steps: o Specification. o ormulation. o Optimization. o Technology mapping. o Verification. Specification:
Objectives: 1. Design procedure. 2. undamental circuits. 1. Design procedure Design procedure has five steps: o Specification. o ormulation. o Optimization. o Technology mapping. o Verification. Specification:
SIDDHARTH GROUP OF INSTITUTIONS :: PUTTUR Siddharth Nagar, Narayanavanam Road QUESTION BANK (DESCRIPTIVE)
 SIDDHARTH GROUP OF INSTITUTIONS :: PUTTUR Siddharth Nagar, Narayanavanam Road 517583 QUESTION BANK (DESCRIPTIVE) Subject with Code : STLD(16EC402) Year & Sem: II-B.Tech & I-Sem Course & Branch: B.Tech
SIDDHARTH GROUP OF INSTITUTIONS :: PUTTUR Siddharth Nagar, Narayanavanam Road 517583 QUESTION BANK (DESCRIPTIVE) Subject with Code : STLD(16EC402) Year & Sem: II-B.Tech & I-Sem Course & Branch: B.Tech
VALLIAMMAI ENGINEERING COLLEGE. SRM Nagar, Kattankulathur DEPARTMENT OF ELECTRONICS AND COMMUNICATION ENGINEERING EC6302 DIGITAL ELECTRONICS
 VALLIAMMAI ENGINEERING COLLEGE SRM Nagar, Kattankulathur-603 203 DEPARTMENT OF ELECTRONICS AND COMMUNICATION ENGINEERING EC6302 DIGITAL ELECTRONICS YEAR / SEMESTER: II / III ACADEMIC YEAR: 2015-2016 (ODD
VALLIAMMAI ENGINEERING COLLEGE SRM Nagar, Kattankulathur-603 203 DEPARTMENT OF ELECTRONICS AND COMMUNICATION ENGINEERING EC6302 DIGITAL ELECTRONICS YEAR / SEMESTER: II / III ACADEMIC YEAR: 2015-2016 (ODD
HANSABA COLLEGE OF ENGINEERING & TECHNOLOGY (098) SUBJECT: DIGITAL ELECTRONICS ( ) Assignment
 Assignment 1. What is multiplexer? With logic circuit and function table explain the working of 4 to 1 line multiplexer. 2. Implement following Boolean function using 8: 1 multiplexer. F(A,B,C,D) = (2,3,5,7,8,9,12,13,14,15)
Assignment 1. What is multiplexer? With logic circuit and function table explain the working of 4 to 1 line multiplexer. 2. Implement following Boolean function using 8: 1 multiplexer. F(A,B,C,D) = (2,3,5,7,8,9,12,13,14,15)
 www.vidyarthiplus.com Question Paper Code : 31298 B.E./B.Tech. DEGREE EXAMINATION, NOVEMBER/DECEMBER 2013. Third Semester Computer Science and Engineering CS 2202/CS 34/EC 1206 A/10144 CS 303/080230012--DIGITAL
www.vidyarthiplus.com Question Paper Code : 31298 B.E./B.Tech. DEGREE EXAMINATION, NOVEMBER/DECEMBER 2013. Third Semester Computer Science and Engineering CS 2202/CS 34/EC 1206 A/10144 CS 303/080230012--DIGITAL
UNIT-III REGISTER TRANSFER LANGUAGE AND DESIGN OF CONTROL UNIT
 UNIT-III 1 KNREDDY UNIT-III REGISTER TRANSFER LANGUAGE AND DESIGN OF CONTROL UNIT Register Transfer: Register Transfer Language Register Transfer Bus and Memory Transfers Arithmetic Micro operations Logic
UNIT-III 1 KNREDDY UNIT-III REGISTER TRANSFER LANGUAGE AND DESIGN OF CONTROL UNIT Register Transfer: Register Transfer Language Register Transfer Bus and Memory Transfers Arithmetic Micro operations Logic
R10. II B. Tech I Semester, Supplementary Examinations, May
 SET - 1 1. a) Convert the following decimal numbers into an equivalent binary numbers. i) 53.625 ii) 4097.188 iii) 167 iv) 0.4475 b) Add the following numbers using 2 s complement method. i) -48 and +31
SET - 1 1. a) Convert the following decimal numbers into an equivalent binary numbers. i) 53.625 ii) 4097.188 iii) 167 iv) 0.4475 b) Add the following numbers using 2 s complement method. i) -48 and +31
Department of Electrical Engineering McGill University ECSE 221 Introduction to Computer Engineering Assignment 2 Combinational Logic
 Department of Electrical Engineering McGill University ECSE 221 Introduction to Computer Engineering Assignment 2 Combinational Logic Question 1: Due October 19 th, 2009 A convenient shorthand for specifying
Department of Electrical Engineering McGill University ECSE 221 Introduction to Computer Engineering Assignment 2 Combinational Logic Question 1: Due October 19 th, 2009 A convenient shorthand for specifying
 UNIT II - COMBINATIONAL LOGIC Part A 2 Marks. 1. Define Combinational circuit A combinational circuit consist of logic gates whose outputs at anytime are determined directly from the present combination
UNIT II - COMBINATIONAL LOGIC Part A 2 Marks. 1. Define Combinational circuit A combinational circuit consist of logic gates whose outputs at anytime are determined directly from the present combination
Assignment (3-6) Boolean Algebra and Logic Simplification - General Questions
 Assignment (3-6) Boolean Algebra and Logic Simplification - General Questions 1. Convert the following SOP expression to an equivalent POS expression. 2. Determine the values of A, B, C, and D that make
Assignment (3-6) Boolean Algebra and Logic Simplification - General Questions 1. Convert the following SOP expression to an equivalent POS expression. 2. Determine the values of A, B, C, and D that make
R07. Code No: V0423. II B. Tech II Semester, Supplementary Examinations, April
 SET - 1 II B. Tech II Semester, Supplementary Examinations, April - 2012 SWITCHING THEORY AND LOGIC DESIGN (Electronics and Communications Engineering) Time: 3 hours Max Marks: 80 Answer any FIVE Questions
SET - 1 II B. Tech II Semester, Supplementary Examinations, April - 2012 SWITCHING THEORY AND LOGIC DESIGN (Electronics and Communications Engineering) Time: 3 hours Max Marks: 80 Answer any FIVE Questions
SIR C.R.REDDY COLLEGE OF ENGINEERING, ELURU DEPARTMENT OF INFORMATION TECHNOLOGY LESSON PLAN
 SIR C.R.REDDY COLLEGE OF ENGINEERING, ELURU DEPARTMENT OF INFORMATION TECHNOLOGY LESSON PLAN SUBJECT: CSE 2.1.6 DIGITAL LOGIC DESIGN CLASS: 2/4 B.Tech., I SEMESTER, A.Y.2017-18 INSTRUCTOR: Sri A.M.K.KANNA
SIR C.R.REDDY COLLEGE OF ENGINEERING, ELURU DEPARTMENT OF INFORMATION TECHNOLOGY LESSON PLAN SUBJECT: CSE 2.1.6 DIGITAL LOGIC DESIGN CLASS: 2/4 B.Tech., I SEMESTER, A.Y.2017-18 INSTRUCTOR: Sri A.M.K.KANNA
R a) Simplify the logic functions from binary to seven segment display code converter (8M) b) Simplify the following using Tabular method
 SET - 1 1. a) Convert the decimal number 250.5 to base 3, base 4 b) Write and prove de-morgan laws c) Implement two input EX-OR gate from 2 to 1 multiplexer (3M) d) Write the demerits of PROM (3M) e) What
SET - 1 1. a) Convert the decimal number 250.5 to base 3, base 4 b) Write and prove de-morgan laws c) Implement two input EX-OR gate from 2 to 1 multiplexer (3M) d) Write the demerits of PROM (3M) e) What
CS8803: Advanced Digital Design for Embedded Hardware
 CS883: Advanced Digital Design for Embedded Hardware Lecture 2: Boolean Algebra, Gate Network, and Combinational Blocks Instructor: Sung Kyu Lim (limsk@ece.gatech.edu) Website: http://users.ece.gatech.edu/limsk/course/cs883
CS883: Advanced Digital Design for Embedded Hardware Lecture 2: Boolean Algebra, Gate Network, and Combinational Blocks Instructor: Sung Kyu Lim (limsk@ece.gatech.edu) Website: http://users.ece.gatech.edu/limsk/course/cs883
Code No: R Set No. 1
 Code No: R059210504 Set No. 1 II B.Tech I Semester Supplementary Examinations, February 2007 DIGITAL LOGIC DESIGN ( Common to Computer Science & Engineering, Information Technology and Computer Science
Code No: R059210504 Set No. 1 II B.Tech I Semester Supplementary Examinations, February 2007 DIGITAL LOGIC DESIGN ( Common to Computer Science & Engineering, Information Technology and Computer Science
END-TERM EXAMINATION
 (Please Write your Exam Roll No. immediately) END-TERM EXAMINATION DECEMBER 2006 Exam. Roll No... Exam Series code: 100919DEC06200963 Paper Code: MCA-103 Subject: Digital Electronics Time: 3 Hours Maximum
(Please Write your Exam Roll No. immediately) END-TERM EXAMINATION DECEMBER 2006 Exam. Roll No... Exam Series code: 100919DEC06200963 Paper Code: MCA-103 Subject: Digital Electronics Time: 3 Hours Maximum
Addition and multiplication
 Addition and multiplication Arithmetic is the most basic thing you can do with a computer, but it s not as easy as you might expect! These next few lectures focus on addition, subtraction, multiplication
Addition and multiplication Arithmetic is the most basic thing you can do with a computer, but it s not as easy as you might expect! These next few lectures focus on addition, subtraction, multiplication
SWITCHING THEORY AND LOGIC CIRCUITS
 SWITCHING THEORY AND LOGIC CIRCUITS COURSE OBJECTIVES. To understand the concepts and techniques associated with the number systems and codes 2. To understand the simplification methods (Boolean algebra
SWITCHING THEORY AND LOGIC CIRCUITS COURSE OBJECTIVES. To understand the concepts and techniques associated with the number systems and codes 2. To understand the simplification methods (Boolean algebra
Combinational Circuit Design
 Modeling Combinational Circuits with Verilog Prof. Chien-Nan Liu TEL: 3-42275 ext:34534 Email: jimmy@ee.ncu.edu.tw 3- Combinational Circuit Design Outputs are functions of inputs inputs Combinational Circuit
Modeling Combinational Circuits with Verilog Prof. Chien-Nan Liu TEL: 3-42275 ext:34534 Email: jimmy@ee.ncu.edu.tw 3- Combinational Circuit Design Outputs are functions of inputs inputs Combinational Circuit
Question No: 1 ( Marks: 1 ) - Please choose one A SOP expression is equal to 1
 ASSALAM O ALAIKUM all fellows ALL IN ONE Mega File CS302 Midterm PAPERS, MCQz & subjective Created BY Farhan& Ali BS (cs) 3rd sem Hackers Group Mandi Bahauddin Remember us in your prayers Mindhacker124@gmail.com
ASSALAM O ALAIKUM all fellows ALL IN ONE Mega File CS302 Midterm PAPERS, MCQz & subjective Created BY Farhan& Ali BS (cs) 3rd sem Hackers Group Mandi Bahauddin Remember us in your prayers Mindhacker124@gmail.com
Logic Gates and Boolean Algebra ENT263
 Logic Gates and Boolean Algebra ENT263 Logic Gates and Boolean Algebra Now that we understand the concept of binary numbers, we will study ways of describing how systems using binary logic levels make
Logic Gates and Boolean Algebra ENT263 Logic Gates and Boolean Algebra Now that we understand the concept of binary numbers, we will study ways of describing how systems using binary logic levels make
LOGIC CIRCUITS. Kirti P_Didital Design 1
 LOGIC CIRCUITS Kirti P_Didital Design 1 Introduction The digital system consists of two types of circuits, namely (i) Combinational circuits and (ii) Sequential circuit A combinational circuit consists
LOGIC CIRCUITS Kirti P_Didital Design 1 Introduction The digital system consists of two types of circuits, namely (i) Combinational circuits and (ii) Sequential circuit A combinational circuit consists
QUESTION BANK FOR TEST
 CSCI 2121 Computer Organization and Assembly Language PRACTICE QUESTION BANK FOR TEST 1 Note: This represents a sample set. Please study all the topics from the lecture notes. Question 1. Multiple Choice
CSCI 2121 Computer Organization and Assembly Language PRACTICE QUESTION BANK FOR TEST 1 Note: This represents a sample set. Please study all the topics from the lecture notes. Question 1. Multiple Choice
Microcomputers. Outline. Number Systems and Digital Logic Review
 Microcomputers Number Systems and Digital Logic Review Lecture 1-1 Outline Number systems and formats Common number systems Base Conversion Integer representation Signed integer representation Binary coded
Microcomputers Number Systems and Digital Logic Review Lecture 1-1 Outline Number systems and formats Common number systems Base Conversion Integer representation Signed integer representation Binary coded
Programmable Logic Devices
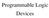 Programmable Logic Devices Programmable Logic Devices Fig. (1) General structure of PLDs Programmable Logic Device (PLD): is an integrated circuit with internal logic gates and/or connections that can
Programmable Logic Devices Programmable Logic Devices Fig. (1) General structure of PLDs Programmable Logic Device (PLD): is an integrated circuit with internal logic gates and/or connections that can
3. The high voltage level of a digital signal in positive logic is : a) 1 b) 0 c) either 1 or 0
 1. The number of level in a digital signal is: a) one b) two c) four d) ten 2. A pure sine wave is : a) a digital signal b) analog signal c) can be digital or analog signal d) neither digital nor analog
1. The number of level in a digital signal is: a) one b) two c) four d) ten 2. A pure sine wave is : a) a digital signal b) analog signal c) can be digital or analog signal d) neither digital nor analog
Combinational Logic Circuits
 Chapter 3 Combinational Logic Circuits 12 Hours 24 Marks 3.1 Standard representation for logical functions Boolean expressions / logic expressions / logical functions are expressed in terms of logical
Chapter 3 Combinational Logic Circuits 12 Hours 24 Marks 3.1 Standard representation for logical functions Boolean expressions / logic expressions / logical functions are expressed in terms of logical
CS470: Computer Architecture. AMD Quad Core
 CS470: Computer Architecture Yashwant K. Malaiya, Professor malaiya@cs.colostate.edu AMD Quad Core 1 Architecture Layers Building blocks Gates, flip-flops Functional bocks: Combinational, Sequential Instruction
CS470: Computer Architecture Yashwant K. Malaiya, Professor malaiya@cs.colostate.edu AMD Quad Core 1 Architecture Layers Building blocks Gates, flip-flops Functional bocks: Combinational, Sequential Instruction
Digital logic fundamentals. Question Bank. Unit I
 Digital logic fundamentals Question Bank Subject Name : Digital Logic Fundamentals Subject code: CA102T Staff Name: R.Roseline Unit I 1. What is Number system? 2. Define binary logic. 3. Show how negative
Digital logic fundamentals Question Bank Subject Name : Digital Logic Fundamentals Subject code: CA102T Staff Name: R.Roseline Unit I 1. What is Number system? 2. Define binary logic. 3. Show how negative
Bawar Abid Abdalla. Assistant Lecturer Software Engineering Department Koya University
 Logic Design First Stage Lecture No.5 Boolean Algebra Bawar Abid Abdalla Assistant Lecturer Software Engineering Department Koya University Boolean Operations Laws of Boolean Algebra Rules of Boolean Algebra
Logic Design First Stage Lecture No.5 Boolean Algebra Bawar Abid Abdalla Assistant Lecturer Software Engineering Department Koya University Boolean Operations Laws of Boolean Algebra Rules of Boolean Algebra
Chapter 2 Combinational
 Computer Engineering 1 (ECE290) Chapter 2 Combinational Logic Circuits Part 2 Circuit Optimization HOANG Trang 2008 Pearson Education, Inc. Overview Part 1 Gate Circuits and Boolean Equations Binary Logic
Computer Engineering 1 (ECE290) Chapter 2 Combinational Logic Circuits Part 2 Circuit Optimization HOANG Trang 2008 Pearson Education, Inc. Overview Part 1 Gate Circuits and Boolean Equations Binary Logic
 Get Free notes at Module-I One s Complement: Complement all the bits.i.e. makes all 1s as 0s and all 0s as 1s Two s Complement: One s complement+1 SIGNED BINARY NUMBERS Positive integers (including zero)
Get Free notes at Module-I One s Complement: Complement all the bits.i.e. makes all 1s as 0s and all 0s as 1s Two s Complement: One s complement+1 SIGNED BINARY NUMBERS Positive integers (including zero)
Chapter 4: Combinational Logic
 Chapter 4: Combinational Logic Combinational Circuit Design Analysis Procedure (Find out nature of O/P) Boolean Expression Approach Truth Table Approach Design Procedure Example : BCD to Excess-3 code
Chapter 4: Combinational Logic Combinational Circuit Design Analysis Procedure (Find out nature of O/P) Boolean Expression Approach Truth Table Approach Design Procedure Example : BCD to Excess-3 code
Memory and Programmable Logic
 Memory and Programmable Logic Memory units allow us to store and/or retrieve information Essentially look-up tables Good for storing data, not for function implementation Programmable logic device (PLD),
Memory and Programmable Logic Memory units allow us to store and/or retrieve information Essentially look-up tables Good for storing data, not for function implementation Programmable logic device (PLD),
DIGITAL ARITHMETIC: OPERATIONS AND CIRCUITS
 C H A P T E R 6 DIGITAL ARITHMETIC: OPERATIONS AND CIRCUITS OUTLINE 6- Binary Addition 6-2 Representing Signed Numbers 6-3 Addition in the 2 s- Complement System 6-4 Subtraction in the 2 s- Complement
C H A P T E R 6 DIGITAL ARITHMETIC: OPERATIONS AND CIRCUITS OUTLINE 6- Binary Addition 6-2 Representing Signed Numbers 6-3 Addition in the 2 s- Complement System 6-4 Subtraction in the 2 s- Complement
10EC33: DIGITAL ELECTRONICS QUESTION BANK
 10EC33: DIGITAL ELECTRONICS Faculty: Dr.Bajarangbali E Examination QuestionS QUESTION BANK 1. Discuss canonical & standard forms of Boolean functions with an example. 2. Convert the following Boolean function
10EC33: DIGITAL ELECTRONICS Faculty: Dr.Bajarangbali E Examination QuestionS QUESTION BANK 1. Discuss canonical & standard forms of Boolean functions with an example. 2. Convert the following Boolean function
DIGITAL ELECTRONICS. P41l 3 HOURS
 UNIVERSITY OF SWAZILAND FACUL TY OF SCIENCE AND ENGINEERING DEPARTMENT OF PHYSICS MAIN EXAMINATION 2015/16 TITLE OF PAPER: COURSE NUMBER: TIME ALLOWED: INSTRUCTIONS: DIGITAL ELECTRONICS P41l 3 HOURS ANSWER
UNIVERSITY OF SWAZILAND FACUL TY OF SCIENCE AND ENGINEERING DEPARTMENT OF PHYSICS MAIN EXAMINATION 2015/16 TITLE OF PAPER: COURSE NUMBER: TIME ALLOWED: INSTRUCTIONS: DIGITAL ELECTRONICS P41l 3 HOURS ANSWER
R07
 www..com www..com SET - 1 II B. Tech I Semester Supplementary Examinations May 2013 SWITCHING THEORY AND LOGIC DESIGN (Com. to EEE, EIE, BME, ECC) Time: 3 hours Max. Marks: 80 Answer any FIVE Questions
www..com www..com SET - 1 II B. Tech I Semester Supplementary Examinations May 2013 SWITCHING THEORY AND LOGIC DESIGN (Com. to EEE, EIE, BME, ECC) Time: 3 hours Max. Marks: 80 Answer any FIVE Questions
NH 67, Karur Trichy Highways, Puliyur C.F, Karur District DEPARTMENT OF INFORMATION TECHNOLOGY CS 2202 DIGITAL PRINCIPLES AND SYSTEM DESIGN
 NH 67, Karur Trichy Highways, Puliyur C.F, 639 114 Karur District DEPARTMENT OF INFORMATION TECHNOLOGY CS 2202 DIGITAL PRINCIPLES AND SYSTEM DESIGN UNIT 2 COMBINATIONAL LOGIC Combinational circuits Analysis
NH 67, Karur Trichy Highways, Puliyur C.F, 639 114 Karur District DEPARTMENT OF INFORMATION TECHNOLOGY CS 2202 DIGITAL PRINCIPLES AND SYSTEM DESIGN UNIT 2 COMBINATIONAL LOGIC Combinational circuits Analysis
2. (a) Compare the characteristics of a floppy disk and a hard disk. (b) Discuss in detail memory interleaving. [8+7]
![2. (a) Compare the characteristics of a floppy disk and a hard disk. (b) Discuss in detail memory interleaving. [8+7] 2. (a) Compare the characteristics of a floppy disk and a hard disk. (b) Discuss in detail memory interleaving. [8+7]](/thumbs/96/127320205.jpg) Code No: A109211202 R09 Set No. 2 1. (a) Explain the purpose of the following registers: i. IR ii. PC iii. MDR iv. MAR. (b) Explain with an example the steps in subtraction of two n-digit unsigned numbers.
Code No: A109211202 R09 Set No. 2 1. (a) Explain the purpose of the following registers: i. IR ii. PC iii. MDR iv. MAR. (b) Explain with an example the steps in subtraction of two n-digit unsigned numbers.
Basic Arithmetic (adding and subtracting)
 Basic Arithmetic (adding and subtracting) Digital logic to show add/subtract Boolean algebra abstraction of physical, analog circuit behavior 1 0 CPU components ALU logic circuits logic gates transistors
Basic Arithmetic (adding and subtracting) Digital logic to show add/subtract Boolean algebra abstraction of physical, analog circuit behavior 1 0 CPU components ALU logic circuits logic gates transistors
Chapter 3 Part 2 Combinational Logic Design
 University of Wisconsin - Madison ECE/Comp Sci 352 Digital Systems Fundamentals Kewal K. Saluja and Yu Hen Hu Spring 2002 Chapter 3 Part 2 Combinational Logic Design Originals by: Charles R. Kime and Tom
University of Wisconsin - Madison ECE/Comp Sci 352 Digital Systems Fundamentals Kewal K. Saluja and Yu Hen Hu Spring 2002 Chapter 3 Part 2 Combinational Logic Design Originals by: Charles R. Kime and Tom
Week 7: Assignment Solutions
 Week 7: Assignment Solutions 1. In 6-bit 2 s complement representation, when we subtract the decimal number +6 from +3, the result (in binary) will be: a. 111101 b. 000011 c. 100011 d. 111110 Correct answer
Week 7: Assignment Solutions 1. In 6-bit 2 s complement representation, when we subtract the decimal number +6 from +3, the result (in binary) will be: a. 111101 b. 000011 c. 100011 d. 111110 Correct answer
CONTENTS CHAPTER 1: NUMBER SYSTEM. Foreword...(vii) Preface... (ix) Acknowledgement... (xi) About the Author...(xxiii)
 CONTENTS Foreword...(vii) Preface... (ix) Acknowledgement... (xi) About the Author...(xxiii) CHAPTER 1: NUMBER SYSTEM 1.1 Digital Electronics... 1 1.1.1 Introduction... 1 1.1.2 Advantages of Digital Systems...
CONTENTS Foreword...(vii) Preface... (ix) Acknowledgement... (xi) About the Author...(xxiii) CHAPTER 1: NUMBER SYSTEM 1.1 Digital Electronics... 1 1.1.1 Introduction... 1 1.1.2 Advantages of Digital Systems...
SUBJECT CODE: IT T35 DIGITAL SYSTEM DESIGN YEAR / SEM : 2 / 3
 UNIT - I PART A (2 Marks) 1. Using Demorgan s theorem convert the following Boolean expression to an equivalent expression that has only OR and complement operations. Show the function can be implemented
UNIT - I PART A (2 Marks) 1. Using Demorgan s theorem convert the following Boolean expression to an equivalent expression that has only OR and complement operations. Show the function can be implemented
REGISTER TRANSFER LANGUAGE
 REGISTER TRANSFER LANGUAGE The operations executed on the data stored in the registers are called micro operations. Classifications of micro operations Register transfer micro operations Arithmetic micro
REGISTER TRANSFER LANGUAGE The operations executed on the data stored in the registers are called micro operations. Classifications of micro operations Register transfer micro operations Arithmetic micro
Code No: 07A3EC03 Set No. 1
 Code No: 07A3EC03 Set No. 1 II B.Tech I Semester Regular Examinations, November 2008 SWITCHING THEORY AND LOGIC DESIGN ( Common to Electrical & Electronic Engineering, Electronics & Instrumentation Engineering,
Code No: 07A3EC03 Set No. 1 II B.Tech I Semester Regular Examinations, November 2008 SWITCHING THEORY AND LOGIC DESIGN ( Common to Electrical & Electronic Engineering, Electronics & Instrumentation Engineering,
DIGITAL ELECTRONICS. Vayu Education of India
 DIGITAL ELECTRONICS ARUN RANA Assistant Professor Department of Electronics & Communication Engineering Doon Valley Institute of Engineering & Technology Karnal, Haryana (An ISO 9001:2008 ) Vayu Education
DIGITAL ELECTRONICS ARUN RANA Assistant Professor Department of Electronics & Communication Engineering Doon Valley Institute of Engineering & Technology Karnal, Haryana (An ISO 9001:2008 ) Vayu Education
PART B. 3. Minimize the following function using K-map and also verify through tabulation method. F (A, B, C, D) = +d (0, 3, 6, 10).
 II B. Tech II Semester Regular Examinations, May/June 2015 SWITCHING THEORY AND LOGIC DESIGN (Com. to EEE, ECE, ECC, EIE.) Time: 3 hours Max. Marks: 70 Note: 1. Question Paper consists of two parts (Part-A
II B. Tech II Semester Regular Examinations, May/June 2015 SWITCHING THEORY AND LOGIC DESIGN (Com. to EEE, ECE, ECC, EIE.) Time: 3 hours Max. Marks: 70 Note: 1. Question Paper consists of two parts (Part-A
Principles of Digital Techniques PDT (17320) Assignment No State advantages of digital system over analog system.
 Assignment No. 1 1. State advantages of digital system over analog system. 2. Convert following numbers a. (138.56) 10 = (?) 2 = (?) 8 = (?) 16 b. (1110011.011) 2 = (?) 10 = (?) 8 = (?) 16 c. (3004.06)
Assignment No. 1 1. State advantages of digital system over analog system. 2. Convert following numbers a. (138.56) 10 = (?) 2 = (?) 8 = (?) 16 b. (1110011.011) 2 = (?) 10 = (?) 8 = (?) 16 c. (3004.06)
DHANALAKSHMI SRINIVASAN COLLEGE OF ENGINEERING AND TECHNOLOGY
 DHANALAKSHMI SRINIVASAN COLLEGE OF ENGINEERING AND TECHNOLOGY Dept/Sem: II CSE/03 DEPARTMENT OF ECE CS8351 DIGITAL PRINCIPLES AND SYSTEM DESIGN UNIT I BOOLEAN ALGEBRA AND LOGIC GATES PART A 1. How many
DHANALAKSHMI SRINIVASAN COLLEGE OF ENGINEERING AND TECHNOLOGY Dept/Sem: II CSE/03 DEPARTMENT OF ECE CS8351 DIGITAL PRINCIPLES AND SYSTEM DESIGN UNIT I BOOLEAN ALGEBRA AND LOGIC GATES PART A 1. How many
UNIT - V MEMORY P.VIDYA SAGAR ( ASSOCIATE PROFESSOR) Department of Electronics and Communication Engineering, VBIT
 UNIT - V MEMORY P.VIDYA SAGAR ( ASSOCIATE PROFESSOR) contents Memory: Introduction, Random-Access memory, Memory decoding, ROM, Programmable Logic Array, Programmable Array Logic, Sequential programmable
UNIT - V MEMORY P.VIDYA SAGAR ( ASSOCIATE PROFESSOR) contents Memory: Introduction, Random-Access memory, Memory decoding, ROM, Programmable Logic Array, Programmable Array Logic, Sequential programmable
Chapter 2 Combinational Logic Circuits
 Logic and Computer Design Fundamentals Chapter 2 Combinational Logic Circuits Part 2 Circuit Optimization Charles Kime & Thomas Kaminski 2008 Pearson Education, Inc. (Hyperlinks are active in View Show
Logic and Computer Design Fundamentals Chapter 2 Combinational Logic Circuits Part 2 Circuit Optimization Charles Kime & Thomas Kaminski 2008 Pearson Education, Inc. (Hyperlinks are active in View Show
Summary. Boolean Addition
 Summary Boolean Addition In Boolean algebra, a variable is a symbol used to represent an action, a condition, or data. A single variable can only have a value of or 0. The complement represents the inverse
Summary Boolean Addition In Boolean algebra, a variable is a symbol used to represent an action, a condition, or data. A single variable can only have a value of or 0. The complement represents the inverse
COMPUTER ARCHITECTURE AND ORGANIZATION Register Transfer and Micro-operations 1. Introduction A digital system is an interconnection of digital
 Register Transfer and Micro-operations 1. Introduction A digital system is an interconnection of digital hardware modules that accomplish a specific information-processing task. Digital systems vary in
Register Transfer and Micro-operations 1. Introduction A digital system is an interconnection of digital hardware modules that accomplish a specific information-processing task. Digital systems vary in
VALLIAMMAI ENGINEERING COLLEGE
 VALLIAMMAI ENGINEERING COLLEGE SRM Nagar, Kattankulathur 603 203 DEPARTMENT OF INFORMATION TECHNOLOGY & COMPUTER SCIENCE AND ENGINEERING QUESTION BANK II SEMESTER CS6201- DIGITAL PRINCIPLE AND SYSTEM DESIGN
VALLIAMMAI ENGINEERING COLLEGE SRM Nagar, Kattankulathur 603 203 DEPARTMENT OF INFORMATION TECHNOLOGY & COMPUTER SCIENCE AND ENGINEERING QUESTION BANK II SEMESTER CS6201- DIGITAL PRINCIPLE AND SYSTEM DESIGN
COPYRIGHTED MATERIAL INDEX
 INDEX Absorption law, 31, 38 Acyclic graph, 35 tree, 36 Addition operators, in VHDL (VHSIC hardware description language), 192 Algebraic division, 105 AND gate, 48 49 Antisymmetric, 34 Applicable input
INDEX Absorption law, 31, 38 Acyclic graph, 35 tree, 36 Addition operators, in VHDL (VHSIC hardware description language), 192 Algebraic division, 105 AND gate, 48 49 Antisymmetric, 34 Applicable input
Chapter 2 Combinational Logic Circuits
 Logic and Computer Design Fundamentals Chapter 2 Combinational Logic Circuits Part 2 Circuit Optimization Overview Part Gate Circuits and Boolean Equations Binary Logic and Gates Boolean Algebra Standard
Logic and Computer Design Fundamentals Chapter 2 Combinational Logic Circuits Part 2 Circuit Optimization Overview Part Gate Circuits and Boolean Equations Binary Logic and Gates Boolean Algebra Standard
Experiment 3: Logic Simplification
 Module: Logic Design Name:... University no:.. Group no:. Lab Partner Name: Mr. Mohamed El-Saied Experiment : Logic Simplification Objective: How to implement and verify the operation of the logical functions
Module: Logic Design Name:... University no:.. Group no:. Lab Partner Name: Mr. Mohamed El-Saied Experiment : Logic Simplification Objective: How to implement and verify the operation of the logical functions
Lecture 6: Signed Numbers & Arithmetic Circuits. BCD (Binary Coded Decimal) Points Addressed in this Lecture
 Points ddressed in this Lecture Lecture 6: Signed Numbers rithmetic Circuits Professor Peter Cheung Department of EEE, Imperial College London (Floyd 2.5-2.7, 6.1-6.7) (Tocci 6.1-6.11, 9.1-9.2, 9.4) Representing
Points ddressed in this Lecture Lecture 6: Signed Numbers rithmetic Circuits Professor Peter Cheung Department of EEE, Imperial College London (Floyd 2.5-2.7, 6.1-6.7) (Tocci 6.1-6.11, 9.1-9.2, 9.4) Representing
Computer Logical Organization Tutorial
 Computer Logical Organization Tutorial COMPUTER LOGICAL ORGANIZATION TUTORIAL Simply Easy Learning by tutorialspoint.com tutorialspoint.com i ABOUT THE TUTORIAL Computer Logical Organization Tutorial Computer
Computer Logical Organization Tutorial COMPUTER LOGICAL ORGANIZATION TUTORIAL Simply Easy Learning by tutorialspoint.com tutorialspoint.com i ABOUT THE TUTORIAL Computer Logical Organization Tutorial Computer
LECTURE 4. Logic Design
 LECTURE 4 Logic Design LOGIC DESIGN The language of the machine is binary that is, sequences of 1 s and 0 s. But why? At the hardware level, computers are streams of signals. These signals only have two
LECTURE 4 Logic Design LOGIC DESIGN The language of the machine is binary that is, sequences of 1 s and 0 s. But why? At the hardware level, computers are streams of signals. These signals only have two
This tutorial gives a complete understanding on Computer Logical Organization starting from basic computer overview till its advanced architecture.
 About the Tutorial Computer Logical Organization refers to the level of abstraction above the digital logic level, but below the operating system level. At this level, the major components are functional
About the Tutorial Computer Logical Organization refers to the level of abstraction above the digital logic level, but below the operating system level. At this level, the major components are functional
DE Solution Set QP Code : 00904
 DE Solution Set QP Code : 00904 1. Attempt any three of the following: 15 a. Define digital signal. (1M) With respect to digital signal explain the terms digits and bits.(2m) Also discuss active high and
DE Solution Set QP Code : 00904 1. Attempt any three of the following: 15 a. Define digital signal. (1M) With respect to digital signal explain the terms digits and bits.(2m) Also discuss active high and
Chapter 3: part 3 Binary Subtraction
 Chapter 3: part 3 Binary Subtraction Iterative combinational circuits Binary adders Half and full adders Ripple carry and carry lookahead adders Binary subtraction Binary adder-subtractors Signed binary
Chapter 3: part 3 Binary Subtraction Iterative combinational circuits Binary adders Half and full adders Ripple carry and carry lookahead adders Binary subtraction Binary adder-subtractors Signed binary
1. Draw general diagram of computer showing different logical components (3)
 Tutorial 1 1. Draw general diagram of computer showing different logical components (3) 2. List at least three input devices (1.5) 3. List any three output devices (1.5) 4. Fill the blank cells of the
Tutorial 1 1. Draw general diagram of computer showing different logical components (3) 2. List at least three input devices (1.5) 3. List any three output devices (1.5) 4. Fill the blank cells of the
CO Computer Architecture and Programming Languages CAPL. Lecture 9
 CO20-320241 Computer Architecture and Programming Languages CAPL Lecture 9 Dr. Kinga Lipskoch Fall 2017 A Four-bit Number Circle CAPL Fall 2017 2 / 38 Functional Parts of an ALU CAPL Fall 2017 3 / 38 Addition
CO20-320241 Computer Architecture and Programming Languages CAPL Lecture 9 Dr. Kinga Lipskoch Fall 2017 A Four-bit Number Circle CAPL Fall 2017 2 / 38 Functional Parts of an ALU CAPL Fall 2017 3 / 38 Addition
INSTITUTE OF AERONAUTICAL ENGINEERING (Autonomous) Dundigal, Hyderabad
 INSTITUTE OF AERONAUTICAL ENGINEERING (Autonomous) Dundigal, Hyderabad - 500 043 COMPUTER SCIENCE AND ENGINEERING TUTORIAL QUESTION BANK Name : DIGITAL LOGIC DESISN Code : AEC020 Class : B Tech III Semester
INSTITUTE OF AERONAUTICAL ENGINEERING (Autonomous) Dundigal, Hyderabad - 500 043 COMPUTER SCIENCE AND ENGINEERING TUTORIAL QUESTION BANK Name : DIGITAL LOGIC DESISN Code : AEC020 Class : B Tech III Semester
EE292: Fundamentals of ECE
 EE292: Fundamentals of ECE Fall 2012 TTh 10:00-11:15 SEB 1242 Lecture 22 121115 http://www.ee.unlv.edu/~b1morris/ee292/ 2 Outline Review Binary Number Representation Binary Arithmetic Combinatorial Logic
EE292: Fundamentals of ECE Fall 2012 TTh 10:00-11:15 SEB 1242 Lecture 22 121115 http://www.ee.unlv.edu/~b1morris/ee292/ 2 Outline Review Binary Number Representation Binary Arithmetic Combinatorial Logic
Boolean Analysis of Logic Circuits
 Course: B.Sc. Applied Physical Science (Computer Science) Year & Sem.: IInd Year, Sem - IIIrd Subject: Computer Science Paper No.: IX Paper Title: Computer System Architecture Lecture No.: 7 Lecture Title:
Course: B.Sc. Applied Physical Science (Computer Science) Year & Sem.: IInd Year, Sem - IIIrd Subject: Computer Science Paper No.: IX Paper Title: Computer System Architecture Lecture No.: 7 Lecture Title:
VALLIAMMAI ENGINEERING COLLEGE
 VALLIAMMAI ENGINEERING COLLEGE SRM Nagar, Kattankulathur 603 203 DEPARTMENT OF INFORMATION TECHNOLOGY QUESTION BANK Academic Year 2018 19 III SEMESTER CS8351-DIGITAL PRINCIPLES AND SYSTEM DESIGN Regulation
VALLIAMMAI ENGINEERING COLLEGE SRM Nagar, Kattankulathur 603 203 DEPARTMENT OF INFORMATION TECHNOLOGY QUESTION BANK Academic Year 2018 19 III SEMESTER CS8351-DIGITAL PRINCIPLES AND SYSTEM DESIGN Regulation
Combinational Logic Circuits
 Chapter 2 Combinational Logic Circuits J.J. Shann (Slightly trimmed by C.P. Chung) Chapter Overview 2-1 Binary Logic and Gates 2-2 Boolean Algebra 2-3 Standard Forms 2-4 Two-Level Circuit Optimization
Chapter 2 Combinational Logic Circuits J.J. Shann (Slightly trimmed by C.P. Chung) Chapter Overview 2-1 Binary Logic and Gates 2-2 Boolean Algebra 2-3 Standard Forms 2-4 Two-Level Circuit Optimization
Hours / 100 Marks Seat No.
 17333 13141 3 Hours / 100 Seat No. Instructions (1) All Questions are Compulsory. (2) Answer each next main Question on a new page. (3) Illustrate your answers with neat sketches wherever necessary. (4)
17333 13141 3 Hours / 100 Seat No. Instructions (1) All Questions are Compulsory. (2) Answer each next main Question on a new page. (3) Illustrate your answers with neat sketches wherever necessary. (4)
Binary Adders: Half Adders and Full Adders
 Binary Adders: Half Adders and Full Adders In this set of slides, we present the two basic types of adders: 1. Half adders, and 2. Full adders. Each type of adder functions to add two binary bits. In order
Binary Adders: Half Adders and Full Adders In this set of slides, we present the two basic types of adders: 1. Half adders, and 2. Full adders. Each type of adder functions to add two binary bits. In order
INSTITUTE OF AERONAUTICAL ENGINEERING (Autonomous) Dundigal, Hyderabad
 INSTITUTE OF AERONAUTICAL ENGINEERING (Autonomous) Dundigal, Hyderabad - 500043 Course Name : DIGITAL LOGIC DESISN Course Code : AEC020 Class : B Tech III Semester Branch : CSE Academic Year : 2018 2019
INSTITUTE OF AERONAUTICAL ENGINEERING (Autonomous) Dundigal, Hyderabad - 500043 Course Name : DIGITAL LOGIC DESISN Course Code : AEC020 Class : B Tech III Semester Branch : CSE Academic Year : 2018 2019
II/IV B.Tech (Regular/Supplementary) DEGREE EXAMINATION. Answer ONE question from each unit.
 Hall Ticket Number: 14CS IT303 November, 2017 Third Semester Time: Three Hours Answer Question No.1 compulsorily. II/IV B.Tech (Regular/Supplementary) DEGREE EXAMINATION Common for CSE & IT Digital Logic
Hall Ticket Number: 14CS IT303 November, 2017 Third Semester Time: Three Hours Answer Question No.1 compulsorily. II/IV B.Tech (Regular/Supplementary) DEGREE EXAMINATION Common for CSE & IT Digital Logic
