Arc Length, Curvature and The TNB Frame
|
|
|
- Anne Collins
- 5 years ago
- Views:
Transcription
1 Arc Length, Curvature and The TNB Frame Introduction and Goals: The main goal of this lab will help you visualize the tools we use to describe the geometry of vector-valued functions. Moreover, we want you to begin to view the tangent, normal and binormal vectors of a curve and their relationship to the movement of the curve. We will also investigate arc length, curvature, normal planes, osculating planes and osculating circles. Before You Start: Make sure that you read and understand the mathematics from the corresponding sections in your textbook. It would also help if you looked over the lab on Lines and Planes. Textbook Correspondence: Stewart 5 th Edition: 4.3. Stewart 5 th Edition Early Transcendentals: 3.3. Thomas Calculus 0 th Edition Early Transcendentals: 0.7. Maple Commands and Packages Used: Packages: plots, linalg, VectorCalculus. Commands: ArcLength, Curvature, simplify, TangentVector, evalf, plot, PrincipalNormal, Binormal, subs, norm,., &x, read. User Defined Commands: plotvvf, plotvvftn, plotvvft, plotvvftseq, plotvvfnn, plotvvfn, plotvvfnseq, plotvvfbn, plotvvfb, plotvvfbseq, plotvvftnbn, plotvvftnb, plotvvftnbseq, plotvvftnbn, plotvvftnb, plotvvftnbseq, plotvvftn, plotvvft, plotvvftseq, plotvvfnn, plotvvfn, plotvvfnseq, plotvvfbn, plotvvfb, plotvvfbseq, normplot, plotvvfocn, plotvvfoc, plotvvfocseq, plotvvfnpn, plotvvfnp, plotvvfnpseq, plotvvfopn, plotvvfop, plotvvfopseq. History & Biographies: Maple Commands: The new Maple commands are a combination between special commands in the Vector Calculus package and some user-defined commands we have built for the more complex graphs. Most of the commands in this lab are in or need the three packages plots, linalg and VectorCalculus, load these into your worksheet..
2 > with(plots): Warning, the name changecoords has been redefined > with(linalg): Warning, the protected names norm and trace have been redefined and unprotected > with(vectorcalculus): Warning, the assigned names <,>, < > and Wronskian now have a global binding Warning, these protected names have been redefined and unprotected: *, +,., Vector, diff, int, limit, series We will start out with some of the commands in the Vector Calculus package that calculate some of the standard quantities of interest. Let s begin with defining a couple vector valued functions. > w:=t-><t,t^,t^3>; w := t VectorCalculus:-`<,>` ( t, t, t 3 ) > v:=t-><sin(t),cos(t),t>; v := t VectorCalculus:-`<,>` ( sin( t ), cos( t), t ) > r:=t-><t*sin(t),t*cos(t),t/0>; r := t VectorCalculus:-`<,>` VectorCalculus:-`*` ( t, sin( t )), VectorCalculus:-`*` ( t, cos( t) ), VectorCalculus:-`*` t, 0 To find the arc length we use the ArcLength command which takes the curve and parameter range as inputs. For example, > ArcLength(r(t),t=-5*Pi..5*Pi); π π 0 + ln ( 50 0 π π + 00 ) 00 0 ln( 50 0 π π + 00 ) 00 > evalf(arclength(r(t),t=-5*pi..5*pi)); The curvature is calculated simply using the Curvature command, for example, > Curvature(v(t));
3 4 sin( t) + cos( t ) > simplify(%,assume=real); > Curvature(r(t)); ( sin( t) + t cos( t )) t 0 ( cos( t ) t sin( t) ) + ( t ) ) t 000 ( cos( t) t sin( t )) t 0 ( sin( t ) t cos( t) ) ( t ) ) t ( / ) t 0000 t ( t ) 3 ^ > cr:=simplify(%,assume=real); t t cr := ( t ) ) > plot(cr,t=-0..0); To find the general tangent, normal and binormal vector equations we use the TangentVector, PrincipalNormal and Binormal commands. For example, > TangentVector(w(t)); e + t e + 3 t e x y z > PrincipalNormal(w(t));
4 8 t + 36 t 3 t ( 8 t + 36 t e 3 ) + ( + 4 t + 9 t 4 ) ) x + e + ( + 4 t + 9 t 4 ) ) + 4 t + 9 t 4 y 3 t ( 8 t + 36 t 3 ) 6 t + e ( + 4 t + 9 t 4 ) ) + 4 t + 9 t 4 z > Binormal(w(t)); t 3 t ( 8 t + 36 t 3 ) 6 t + ( + 4 t + 9 t 4 ) ) + 4 t + 9 t t + 9 t 4 3 t t ( 8 t + 36 t 3 ) + ( + 4 t + 9 t 4 ) ) + 4 t + 9 t t + 9 t 4 e x + 3 t ( 8 t + 36 t 3 ) 6 t + 3 t ( 8 t + 36 t 3 ) ( + 4 t + 9 t 4 ) ) + 4 t + 9 t 4 ( + 4 t + 9 t 4 ) e + 4 t + 9 t 4 + y t ( 8 t + 36 t 3 ) + ( + 4 t + 9 t 4 ) ) + 4 t + 9 t 4 t ( 8 t + 36 t 3 ) + e + 4 t + 9 t 4 ( + 4 t + 9 t 4 ) z One thing to be careful with is that these are not the unit tangent, unit normal or unit binormal vectors, as can be seen by the following calculation which finds the length of the tangent vector to w(t) at t=5, > evalf(subs(t=5,norm(tangentvector(w(t)),))); Had this been the unit tangent the calculation would have resulted in a. The unit tangent, normal and binormal vectors can be calculated with the above commands if we further divide by the norm of the vector but there is another way to do the same calculation in Maple. We can find all three at once using the command TNBFrame. For example, > TNBFrame(v(t)); + cos( t ) e x sin( t) e y e, sin( t) e cos( t) e, z x y + cos( t) e x sin( t ) e y cos( t ) sin( t ) e z
5 Note that the output of this command is a list of three vectors. The first is the unit tangent, the second is the unit normal and the third is the unit binormal. To extract the desired vector we simply use the index of the vector. For example, to extract the unit normal vector we execute the command, > TNBFrame(v(t))[]; sin( t ) e x cos( t) e y we can also convert it to a vector valued function using the unapply command. > nv:=unapply(tnbframe(v(t))[],t); nv := t rtable (.. 3, { ( ) = sin( t ), ( ) = cos( t ) }, datatype = anything, subtype = Vector column, storage = rectangular, order = Fortran_order, attributes = [ coords = cartesian ] ) > nv(pi); e y We can easily check that these are in fact unit vectors by taking the norms of each of them. Note that they all simplify to length. > norm(tnbframe(v(t))[],); + cos( t) + sin( t) > simplify(%,assume=real); > norm(tnbframe(v(t))[],); sin( t ) + cos( t) > simplify(%,assume=real); > norm(tnbframe(v(t))[3],); cos( t) + sin( t ) cos( t ) sin( t ) > simplify(%,assume=real); There are also a few quick shortcut commands that are loaded with the VectorCalculus package. The dot product can be done with a period, for example,
6 > a:=<,,3>; > b:=<5,9,6>; > a.b; a := e + e + 3 e x y z b := 5 e + 9 e + 6 e x y z 4 and the cross product can be done with the &x operator, like the following, > a &x b; (-5) e + 9 e e x y z There are several other commands in the VectorCalculus package that will be of interest to us later but we have enough for this lab. The remainder of the commands used for this lab are contained in one of two files TNB.mpl or CalcIIIProcs.mpl. The TNB.mpl file contains all of the commands used in this lab and the CalcIIIProcs.mpl file contains all of the commands we have created for multivariable Calculus. To load these commands we use the Maple read command. The read command simply requires a string that has the path and filename of the file to be loaded. In the path a backslash is created with two backslashes and a forward slash is created with a single forward slash. So if the TNB.mpl file is in the root directory of a PC (c:\) the command would be > read("c:\\tnb.mpl"); and if it were in the directory C:\My Documents\Word\MapleLabs the command would be > read("c:\\my Documents\\Word\\MapleLabs\\TNB.mpl"); We would suggest that you store your maple files on your personal network drive and read them in from there. When you read this file in you will not get any output from Maple but the commands will have been loaded. The following is the list of commands that are in the TNB.mpl file. plotvvf, plotvvftn, plotvvft, plotvvftseq, plotvvfnn, plotvvfn, plotvvfnseq, plotvvfbn, plotvvfb, plotvvfbseq, plotvvftnbn, plotvvftnb, plotvvftnbseq, plotvvftnbn, plotvvftnb, plotvvftnbseq, plotvvftn, plotvvft, plotvvftseq, plotvvfnn, plotvvfn, plotvvfnseq, plotvvfbn, plotvvfb, plotvvfbseq, normplot, plotvvfocn, plotvvfoc, plotvvfocseq, plotvvfnpn, plotvvfnp, plotvvfnpseq, plotvvfopn, plotvvfop, plotvvfopseq
7 You will notice that all of these commands are for graphing and that the names of most of these commands come in triplets, *, *n and *seq. The * commands graph one copy of the item of interest, the *n commands graph n copies of the item of interest evenly spaced along the curve. Finally the *seq commands graph the item of interest at each point in a user-defined list. We will discuss each of the commands and when we encounter the triplet functions we will discuss the three of them together. The plotvvf command is similar to the one created in a previous lab but with an added feature of taking any list of options. The plotvvf command will plot a vector valued function, it requires the input of a vector valued function and parameter range. Further options may be input as well, as long as they are options that apply to spacecurves. > plotvvf(r(t),t=-5*pi..5*pi); > plotvvf(r(t),t=- 5*Pi..5*Pi,color=black,numpoints=00,axes=boxed,labels=[x,y,z]);
8 The nornplot command plots the norm of the vector valued function over the input range of the parameter, it requires the input of a vector valued function and parameter range. Further options may be input as well, as long as they are options that apply to the plot command. > normplot(w(t),t=-..); > normplot(r(s),s=-..,y=0..0.5,color=black,thickness=3); The plotvvftn, plotvvft and plotvvftseq commands plot a vector valued function along with its tangent vectors. The first, second and fourth parameters of each of these commands are the same. The first parameter is the vector valued function, the second parameter is the range in which to ploy the curve and the fourth is the color of the tangent vectors. With the plotvvft command the third parameter is the position, in terms of the curve s parameter, of the tangent vector. For example, the following command plots the curve from 5 to 5 and a tangent vector at 3. Further options may be input as well, as long as they are options that apply to the spacecurve command and will only affect the vector valued function. > plotvvft(r(t),t=-5..5,3,red);
9 > plotvvft(r(t),t=-5..5,3,red,axes=boxed,color=black); With the plotvvftn command the third parameter is the number of tangent vectors that will be graphed. For example, the following command plots the curve from 5 to 5 and 0 tangent vectors evenly spaced from 5 to 5. Further options may be input as well, as long as they are options that apply to the spacecurve command and will only affect the vector valued function. > plotvvftn(r(t),t=-5..5,0,red);
10 > plotvvftn(r(t),t=-5..5,0,red,axes=boxed,color=black); With the plotvvftseq command the third parameter is a list of all of the positions where the tangent vectors that will be graphed. For example, the following command plots the curve from 5 to 5 and tangent vectors at, 0,.5,.9, 3 and 5. Further options may be input as well, as long as they are options that apply to the spacecurve command and will only affect the vector valued function. > plotvvftseq(r(t),t=-5..5,[-,0,.5,.9,3,5],red);
11 > plotvvftseq(r(t),t=-5..5,[-,0,.5,.9,3,5],red,axes=boxed,color=black); Note that these tangent vectors are not the unit tangent vectors. To graph the unit tangents, use the commands plotvvftn, plotvvft and plotvvftseq using the same syntax as above. For example, > plotvvftn(r(s),s=-5..5,50,red,axes=boxed,color=black);
12 To graph the normal vectors use the commands plotvvfnn, plotvvfn and plotvvfnseq with the same syntax. To graph the unit normal vectors use the commands plotvvfn, plotvvfnseq, plotvvfbn with the same syntax. To graph the binormal vectors use the commands plotvvfbn, plotvvfb and plotvvfbseq with the same syntax. Finally, to graph the unit binormal vectors use the commands plotvvfbn, plotvvfb and plotvvfbseq again with the same syntax. You can create graphs of the tangent, normal and binormal vectors together by using the display command with the commands we have discussed above but we have created six functions to do that automatically. To graph the tangent, normal and binormal together use the commands plotvvftnbn, plotvvftnb and plotvvftnbseq. To graph the unit tangent, normal and binormal together use the commands plotvvftnbn, plotvvftnb and plotvvftnbseq. The only difference between these and the above commands is that instead of requiring one color for the color of the vector they require three colors in the order of tangent, normal and binormal. For example, > plotvvftnb(r(t),t=- 5..5,3,red,green,blue,axes=boxed,color=black);
13 > plotvvftnb(r(t),t=- 5..5,3,red,green,blue,axes=boxed,color=black); > plotvvftnbn(r(t),t=- 5..5,50,red,green,blue,axes=boxed,color=black);
14 The remainder of the supplementary commands deal with osculating circles, osculating planes and normal planes. As before these commands come in triples. For osculating circles we use the commands plotvvfocn, plotvvfoc and plotvvfocseq. Each of these commands take four parameters, the first is the curve, the second is the range, the third is a position, number of vectors or list depending on which command is being used and the fourth parameter is the color of the circles. Additional options can be used for the curve, as in the previous commands. For example, > plotvvfocn(v(t),t=- 5..5,5,red,axes=boxed,color=black,thickness=3); The normal planes are produced from the commands plotvvfnpn, plotvvfnp and plotvvfnpseq. These commands each take three parameters, the curve, the range and either a position, number of vectors or list depending on which command is being used. As with the other commands, further curve options may be used. For example,
15 > plotvvfnpn(w(t),t=0..,4,axes=boxed,color=black,thickness=3 ); The osculating plane commands plotvvfopn, plotvvfop and plotvvfopseq are similar. > plotvvfopn(w(t),t=0..,3,axes=boxed,color=black,thickness=3 ); Exercises:. The following exercises concern the vector-valued function b ( t) = sin t,cos t,sin t. ( ) ( ) ( ) t b =. a. Define the vector-valued function ( t) sin( t),cos( t),sin ( t) t b. Plot the curve on the interval [0,3].
16 c. Describe the path made by the curve. Where are the largest changes in direction? How many of those direction changes are there? d. Graph the curve along with 0 evenly spaced normal vectors. e. Where are these vectors the largest? Where are these vectors the smallest? What is the relationship between the size of the normal vector and the geometry of the curve? f. Use the normplot command to plot the PrincipalNormal vector over the interval [0,3]. Where is this function a maximum? Where is this function a minimum? How do the positions of the maximum and minimum relate to your observations above? g. Plot the curvature function of the curve on [0,3]. Is there a relationship between the curvature and the normal vector graphs for this curve? If so, what? Be specific. h. Plot the curve on the interval [0,3] along with 5 osculating circles. Where are the circles large and where are they small? What is the curve doing where the circles are large and what is the curve doing where the circles are small? Be specific. i. Where do you expect the circles to be the largest? Where do you expect the circles to be the smallest? Why?. The following exercises deal with parameterizations with respect to arc length. r ( t) = t,sinh t, cosh t. a. Define the vector valued function ( ) ( ) b. Graph the vector valued function ( t) = t,sinh( t), cosh( t) r on the interval [0,5]. c. Use the command ArcLength(r(t),t=0..s); to get a function for the arc length of s. You will want to simplify the result with the command simplify(%,assume=real);. d. Set the variable c equal to the result of the last exercise and solve the equation for s. e. Define a vector valued function that takes c to the expression of r(t) with the result of the above exercise substituted for t. f. Evaluate the expression evalf(arclength(d(t),t=0..)); what is the result? Do the same with the replaced by, 3, 5, 0 and 5. What are the results? What does this say about the vector valued function d(t)? g. Using the display command plot the two curves r and d together on the same axes, graph r on [0,5] and d on [0,00]. You may wish to make the color of d red and its thickness 3. What do you observe about the two curves? t t r ( t ) = sin e,cos e, e. h. Do a similar analysis (i.e. repeat a-f) with the curve ( ) ( ) t 3. The following exercises deal with parameterizations of curves. More specifically, the motion of a child having fun, and then possibly getting sick. a. We will think of the parameter t as time. Say that a child is sitting on the edge of a merry-go-round in say a city park. The merry-go-round is 5 feet in diameter and is revolving at a rate of one revolution every two seconds. Find a threedimensional vector valued function that describes the position of the child at any time t. Graph the function with its tangent, normal and binormal vectors. Also use the normplot command to graph the norms of the tangent and normal vectors through one revolution of the merry-go-round. Use all of this information to
17 describe in detail the path and forces on the child. Find minimum and maximum velocities of the child as well as where they occur. b. As in the above exercise, a child is sitting on the edge of a 5 foot diameter merry-go-round revolving at a rate of one revolution every two seconds. This time there is a hobbyhorse bolted to the edge of the merry-go-round. The hobbyhorse is one of those that sits on a single large spring and can sway back and forth in a circular arc. The hobbyhorse is positioned so that it will sway toward and away from the center of the merry-go-round. The horse is three feet tall, rocks a total arc length of 45 degrees and has a period of ½ second. Find a three-dimensional vector valued function that describes the position of the child at any time t. Graph the function with its tangent, normal and binormal vectors. Also use the normplot command to graph the norms of the tangent and normal vectors through one revolution of the merry-go-round. Use all of this information to describe in detail the path and forces on the child. Find minimum and maximum velocities of the child as well as where they occur. c. Now we move on to bigger and better things. We go to an amusement park where there is a true merry-go-round. The merry-go-round is 60 feet in diameter and our child is on a horse that is 5 feet from the edge. The horse goes from a height of four feet to a height of 5.5 feet three times per revolution and the merry-go-round is revolving once every 5 seconds. Find a three-dimensional vector valued function that describes the position of the child at any time t. Graph the function with its tangent, normal and binormal vectors. Also use the normplot command to graph the norms of the tangent and normal vectors through one revolution of the merry-go-round. Use all of this information to describe in detail the path and forces on the child. Find minimum and maximum velocities of the child as well as where they occur. d. Now we get to the sick part. Same scenario as the previous problem but this time we place the hobbyhorse on the back of the horse on the merry-go-round. Again the hobbyhorse sways along a radius of the merry-go-round. Find a threedimensional vector valued function that describes the position of the child at any time t. Graph the function with its tangent, normal and binormal vectors. Also use the normplot command to graph the norms of the tangent and normal vectors through one revolution of the merry-go-round. Use all of this information to describe in detail the path and forces on the child. Find minimum and maximum velocities of the child as well as where they occur. e. If the last one wasn t bad enough, try this. Same scenario as the previous problem but this time we place the hobbyhorse sways along the perpendicular line to a radius of the merry-go-round. Find a three-dimensional vector valued function that describes the position of the child at any time t. Graph the function with its tangent, normal and binormal vectors. Also use the normplot command to graph the norms of the tangent and normal vectors through one revolution of the merrygo-round. Use all of this information to describe in detail the path and forces on the child. Find minimum and maximum velocities of the child as well as where they occur. f. Historically, the merry-go-round was first used to train knights in the art of jousting. A knight would sit on the fake horse and a small brass ring would hang
18 off to the side of the merry-go-round. The knight would attempt to spear the ring when it came around. Some amusement parks have merry-go-rounds with a brass ring dispenser off to the side in honor of the origins of the merry-go-round. Riders would try to grab one of the rings as they came by. Hence the saying, Grabbing the brass ring. In some cases children can exchange the rings they grab for prize tokens that can be exchanged for prizes at the arcade. If you wish to experience this please go to Knoebels Grove amusement park in Elysburg Pennsylvania. Say that the ring dispenser is seven feet off the ground and 6 inches away from the edge of the merry-go-round. In each of the three previous scenarios find a three-dimensional vector valued function that describes the position of the ring with respect to the child at any time t. What is the velocity and speed of the ring, with respect to the child, when the ring is the closest to the child? 4. The torsion of a curve can be calculated with the equation, ( r' r'' ) r'' ' τ = r' r'' a. Create a new Maple command that finds the torsion of a curve. r ( t) = t, t sin t, t cos t. Graph the torsion function b. Find the torsion of the curve ( ) ( ) on the interval [,4π ] 0. Graph the curve with 0 sets of TBN frame vectors evenly spaced along the curve. What is happening to the TBN frame vectors when the torsion is large? What is happening to the TBN frame vectors when the torsion is small? c. Find the torsion of the curve r ( t) = cos( t),sin( t), t cos( t) function on the interval [,π ]. Graph the torsion 0. Graph the curve with 0 sets of TBN frame vectors evenly spaced along the curve. What is happening to the TBN frame vectors when the torsion is large? What is happening to the TBN frame vectors when the torsion is small? 3 d. Find the torsion of the curve r ( t) = 4 t, t + 7, t 5t + 6. Graph the torsion function on the interval [,5]. Graph the curve with 0 sets of TBN frame vectors evenly spaced along the curve. What is happening to the TBN frame vectors when the torsion is large? What is happening to the TBN frame vectors when the torsion is small? e. Find the torsion of the curve r ( t) = cos( t ),sin( t ), t on the interval [.,]. Graph the torsion function 0. Graph the curve with 0 sets of TBN frame vectors evenly spaced along the curve. What is happening to the TBN frame vectors when the torsion is large? What is happening to the TBN frame vectors when the torsion is small? f. Find the torsion of the curve r ( t) = t,sin( t),sin( t) cos( t) function on the interval [,π ]. Graph the torsion 0. Graph the curve with 0 sets of TBN frame vectors evenly spaced along the curve. Note that you may need to do two graphs and join them together with the display command. What is happening to the TBN
19 frame vectors when the torsion is large? What is happening to the TBN frame vectors when the torsion is small? g. From your observations above what does torsion measure?
Lagrange Multipliers
 Lagrange Multipliers Introduction and Goals: The goal of this lab is to become more familiar with the process and workings of Lagrange multipliers. This lab is designed more to help you understand the
Lagrange Multipliers Introduction and Goals: The goal of this lab is to become more familiar with the process and workings of Lagrange multipliers. This lab is designed more to help you understand the
Functions of Several Variables, Limits and Derivatives
 Functions of Several Variables, Limits and Derivatives Introduction and Goals: The main goal of this lab is to help you visualize surfaces in three dimensions. We investigate how one can use Maple to evaluate
Functions of Several Variables, Limits and Derivatives Introduction and Goals: The main goal of this lab is to help you visualize surfaces in three dimensions. We investigate how one can use Maple to evaluate
ds dt ds 1 dt 1 dt v v v dt ds and the normal vector is given by N
 Normal Vectors and Curvature In the last section, we stated that reparameterization by arc length would help us analyze the twisting and turning of a curve. In this section, we ll see precisely how to
Normal Vectors and Curvature In the last section, we stated that reparameterization by arc length would help us analyze the twisting and turning of a curve. In this section, we ll see precisely how to
Name Class. (a) (b) (c) 2. Find the volume of the solid formed by revolving the region bounded by the graphs of
 Applications of Integration Test Form A. Determine the area of the region bounded by the graphs of y x 4x and y x 4. (a) 9 9 (b) 6 (c). Find the volume of the solid formed by revolving the region bounded
Applications of Integration Test Form A. Determine the area of the region bounded by the graphs of y x 4x and y x 4. (a) 9 9 (b) 6 (c). Find the volume of the solid formed by revolving the region bounded
Tutorial 4. Differential Geometry I - Curves
 23686 Numerical Geometry of Images Tutorial 4 Differential Geometry I - Curves Anastasia Dubrovina c 22 / 2 Anastasia Dubrovina CS 23686 - Tutorial 4 - Differential Geometry I - Curves Differential Geometry
23686 Numerical Geometry of Images Tutorial 4 Differential Geometry I - Curves Anastasia Dubrovina c 22 / 2 Anastasia Dubrovina CS 23686 - Tutorial 4 - Differential Geometry I - Curves Differential Geometry
Practice problems from old exams for math 233
 Practice problems from old exams for math 233 William H. Meeks III October 26, 2012 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Practice problems from old exams for math 233 William H. Meeks III October 26, 2012 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
MATH11007 NOTES 12: PARAMETRIC CURVES, ARCLENGTH ETC.
 MATH117 NOTES 12: PARAMETRIC CURVES, ARCLENGTH ETC. 1. Parametric representation of curves The position of a particle moving in three-dimensional space is often specified by an equation of the form For
MATH117 NOTES 12: PARAMETRIC CURVES, ARCLENGTH ETC. 1. Parametric representation of curves The position of a particle moving in three-dimensional space is often specified by an equation of the form For
Calculators ARE NOT Permitted On This Portion Of The Exam 28 Questions - 55 Minutes
 1 of 11 1) Give f(g(1)), given that Calculators ARE NOT Permitted On This Portion Of The Exam 28 Questions - 55 Minutes 2) Find the slope of the tangent line to the graph of f at x = 4, given that 3) Determine
1 of 11 1) Give f(g(1)), given that Calculators ARE NOT Permitted On This Portion Of The Exam 28 Questions - 55 Minutes 2) Find the slope of the tangent line to the graph of f at x = 4, given that 3) Determine
MATH11007 NOTES 15: PARAMETRIC CURVES, ARCLENGTH ETC.
 MATH117 NOTES 15: PARAMETRIC CURVES, ARCLENGTH ETC. 1. Parametric representation of curves The position of a particle moving in three-dimensional space is often specified by an equation of the form For
MATH117 NOTES 15: PARAMETRIC CURVES, ARCLENGTH ETC. 1. Parametric representation of curves The position of a particle moving in three-dimensional space is often specified by an equation of the form For
Goals: Course Unit: Describing Moving Objects Different Ways of Representing Functions Vector-valued Functions, or Parametric Curves
 Block #1: Vector-Valued Functions Goals: Course Unit: Describing Moving Objects Different Ways of Representing Functions Vector-valued Functions, or Parametric Curves 1 The Calculus of Moving Objects Problem.
Block #1: Vector-Valued Functions Goals: Course Unit: Describing Moving Objects Different Ways of Representing Functions Vector-valued Functions, or Parametric Curves 1 The Calculus of Moving Objects Problem.
Functions of Several Variables
 Jim Lambers MAT 280 Spring Semester 2009-10 Lecture 2 Notes These notes correspond to Section 11.1 in Stewart and Section 2.1 in Marsden and Tromba. Functions of Several Variables Multi-variable calculus
Jim Lambers MAT 280 Spring Semester 2009-10 Lecture 2 Notes These notes correspond to Section 11.1 in Stewart and Section 2.1 in Marsden and Tromba. Functions of Several Variables Multi-variable calculus
Vectors in the Plane
 Vectors in the Plane restart:with(plots): We need to input the VectorCalculus package to get the vector commands we need. with(vectorcalculus); &x, `*`, `C`, `-`, `.`,!,,!, About, AddCoordinates, ArcLength,
Vectors in the Plane restart:with(plots): We need to input the VectorCalculus package to get the vector commands we need. with(vectorcalculus); &x, `*`, `C`, `-`, `.`,!,,!, About, AddCoordinates, ArcLength,
Trigonometry Final Review Exercises
 1 The exam will last 2 hours and will be entirely short answer. Be sure to provide adequate written work to justify your answers in order to receive full credit. You will be provided with a basic trig
1 The exam will last 2 hours and will be entirely short answer. Be sure to provide adequate written work to justify your answers in order to receive full credit. You will be provided with a basic trig
6. Find the equation of the plane that passes through the point (-1,2,1) and contains the line x = y = z.
 Week 1 Worksheet Sections from Thomas 13 th edition: 12.4, 12.5, 12.6, 13.1 1. A plane is a set of points that satisfies an equation of the form c 1 x + c 2 y + c 3 z = c 4. (a) Find any three distinct
Week 1 Worksheet Sections from Thomas 13 th edition: 12.4, 12.5, 12.6, 13.1 1. A plane is a set of points that satisfies an equation of the form c 1 x + c 2 y + c 3 z = c 4. (a) Find any three distinct
Midterm Review II Math , Fall 2018
 Midterm Review II Math 2433-3, Fall 218 The test will cover section 12.5 of chapter 12 and section 13.1-13.3 of chapter 13. Examples in class, quizzes and homework problems are the best practice for the
Midterm Review II Math 2433-3, Fall 218 The test will cover section 12.5 of chapter 12 and section 13.1-13.3 of chapter 13. Examples in class, quizzes and homework problems are the best practice for the
You are not expected to transform y = tan(x) or solve problems that involve the tangent function.
 In this unit, we will develop the graphs for y = sin(x), y = cos(x), and later y = tan(x), and identify the characteristic features of each. Transformations of y = sin(x) and y = cos(x) are performed and
In this unit, we will develop the graphs for y = sin(x), y = cos(x), and later y = tan(x), and identify the characteristic features of each. Transformations of y = sin(x) and y = cos(x) are performed and
PARAMETERIZATIONS OF PLANE CURVES
 PARAMETERIZATIONS OF PLANE CURVES Suppose we want to plot the path of a particle moving in a plane. This path looks like a curve, but we cannot plot it like we would plot any other type of curve in the
PARAMETERIZATIONS OF PLANE CURVES Suppose we want to plot the path of a particle moving in a plane. This path looks like a curve, but we cannot plot it like we would plot any other type of curve in the
Solution 2. ((3)(1) (2)(1), (4 3), (4)(2) (3)(3)) = (1, 1, 1) D u (f) = (6x + 2yz, 2y + 2xz, 2xy) (0,1,1) = = 4 14
 Vector and Multivariable Calculus L Marizza A Bailey Practice Trimester Final Exam Name: Problem 1. To prepare for true/false and multiple choice: Compute the following (a) (4, 3) ( 3, 2) Solution 1. (4)(
Vector and Multivariable Calculus L Marizza A Bailey Practice Trimester Final Exam Name: Problem 1. To prepare for true/false and multiple choice: Compute the following (a) (4, 3) ( 3, 2) Solution 1. (4)(
Math Section 4.2 Radians, Arc Length, and Area of a Sector
 Math 1330 - Section 4.2 Radians, Arc Length, and Area of a Sector The word trigonometry comes from two Greek roots, trigonon, meaning having three sides, and meter, meaning measure. We have already defined
Math 1330 - Section 4.2 Radians, Arc Length, and Area of a Sector The word trigonometry comes from two Greek roots, trigonon, meaning having three sides, and meter, meaning measure. We have already defined
MA 243 Calculus III Fall Assignment 1. Reading assignments are found in James Stewart s Calculus (Early Transcendentals)
 MA 43 Calculus III Fall 8 Dr. E. Jacobs Assignments Reading assignments are found in James Stewart s Calculus (Early Transcendentals) Assignment. Spheres and Other Surfaces Read. -. and.6 Section./Problems
MA 43 Calculus III Fall 8 Dr. E. Jacobs Assignments Reading assignments are found in James Stewart s Calculus (Early Transcendentals) Assignment. Spheres and Other Surfaces Read. -. and.6 Section./Problems
INTRODUCTION TO LINE INTEGRALS
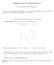 INTRODUTION TO LINE INTEGRALS PROF. MIHAEL VANVALKENBURGH Last week we discussed triple integrals. This week we will study a new topic of great importance in mathematics and physics: line integrals. 1.
INTRODUTION TO LINE INTEGRALS PROF. MIHAEL VANVALKENBURGH Last week we discussed triple integrals. This week we will study a new topic of great importance in mathematics and physics: line integrals. 1.
10.2 Calculus with Parametric Curves
 CHAPTER 1. PARAMETRIC AND POLAR 1 1.2 Calculus with Parametric Curves Example 1. Return to the parametric equations in Example 2 from the previous section: x t +sin() y t + cos() (a) Find the cartesian
CHAPTER 1. PARAMETRIC AND POLAR 1 1.2 Calculus with Parametric Curves Example 1. Return to the parametric equations in Example 2 from the previous section: x t +sin() y t + cos() (a) Find the cartesian
Section 4.2 Radians, Arc Length, and Area of a Sector
 1330 - Section 4.2 Radians, Arc Length, and Area of a Sector Two rays that have a common endpoint (vertex) form an angle. One ray is the initial side and the other is the terminal side. We typically will
1330 - Section 4.2 Radians, Arc Length, and Area of a Sector Two rays that have a common endpoint (vertex) form an angle. One ray is the initial side and the other is the terminal side. We typically will
Section 5: Introduction to Trigonometry and Graphs
 Section 5: Introduction to Trigonometry and Graphs The following maps the videos in this section to the Texas Essential Knowledge and Skills for Mathematics TAC 111.42(c). 5.01 Radians and Degree Measurements
Section 5: Introduction to Trigonometry and Graphs The following maps the videos in this section to the Texas Essential Knowledge and Skills for Mathematics TAC 111.42(c). 5.01 Radians and Degree Measurements
First of all, we need to know what it means for a parameterize curve to be differentiable. FACT:
 CALCULUS WITH PARAMETERIZED CURVES In calculus I we learned how to differentiate and integrate functions. In the chapter covering the applications of the integral, we learned how to find the length of
CALCULUS WITH PARAMETERIZED CURVES In calculus I we learned how to differentiate and integrate functions. In the chapter covering the applications of the integral, we learned how to find the length of
MA 114 Worksheet #17: Average value of a function
 Spring 2019 MA 114 Worksheet 17 Thursday, 7 March 2019 MA 114 Worksheet #17: Average value of a function 1. Write down the equation for the average value of an integrable function f(x) on [a, b]. 2. Find
Spring 2019 MA 114 Worksheet 17 Thursday, 7 March 2019 MA 114 Worksheet #17: Average value of a function 1. Write down the equation for the average value of an integrable function f(x) on [a, b]. 2. Find
Lecture 34: Curves defined by Parametric equations
 Curves defined by Parametric equations When the path of a particle moving in the plane is not the graph of a function, we cannot describe it using a formula that express y directly in terms of x, or x
Curves defined by Parametric equations When the path of a particle moving in the plane is not the graph of a function, we cannot describe it using a formula that express y directly in terms of x, or x
Measuring Lengths The First Fundamental Form
 Differential Geometry Lia Vas Measuring Lengths The First Fundamental Form Patching up the Coordinate Patches. Recall that a proper coordinate patch of a surface is given by parametric equations x = (x(u,
Differential Geometry Lia Vas Measuring Lengths The First Fundamental Form Patching up the Coordinate Patches. Recall that a proper coordinate patch of a surface is given by parametric equations x = (x(u,
Moore Catholic High School Math Department
 Moore Catholic High School Math Department Geometry Vocabulary The following is a list of terms and properties which are necessary for success in a Geometry class. You will be tested on these terms during
Moore Catholic High School Math Department Geometry Vocabulary The following is a list of terms and properties which are necessary for success in a Geometry class. You will be tested on these terms during
MATH 31A HOMEWORK 9 (DUE 12/6) PARTS (A) AND (B) SECTION 5.4. f(x) = x + 1 x 2 + 9, F (7) = 0
 FROM ROGAWSKI S CALCULUS (2ND ED.) SECTION 5.4 18.) Express the antiderivative F (x) of f(x) satisfying the given initial condition as an integral. f(x) = x + 1 x 2 + 9, F (7) = 28.) Find G (1), where
FROM ROGAWSKI S CALCULUS (2ND ED.) SECTION 5.4 18.) Express the antiderivative F (x) of f(x) satisfying the given initial condition as an integral. f(x) = x + 1 x 2 + 9, F (7) = 28.) Find G (1), where
Columbus State Community College Mathematics Department Public Syllabus. Course and Number: MATH 1172 Engineering Mathematics A
 Columbus State Community College Mathematics Department Public Syllabus Course and Number: MATH 1172 Engineering Mathematics A CREDITS: 5 CLASS HOURS PER WEEK: 5 PREREQUISITES: MATH 1151 with a C or higher
Columbus State Community College Mathematics Department Public Syllabus Course and Number: MATH 1172 Engineering Mathematics A CREDITS: 5 CLASS HOURS PER WEEK: 5 PREREQUISITES: MATH 1151 with a C or higher
9.1 Parametric Curves
 Math 172 Chapter 9A notes Page 1 of 20 9.1 Parametric Curves So far we have discussed equations in the form. Sometimes and are given as functions of a parameter. Example. Projectile Motion Sketch and axes,
Math 172 Chapter 9A notes Page 1 of 20 9.1 Parametric Curves So far we have discussed equations in the form. Sometimes and are given as functions of a parameter. Example. Projectile Motion Sketch and axes,
P1 REVISION EXERCISE: 1
 P1 REVISION EXERCISE: 1 1. Solve the simultaneous equations: x + y = x +y = 11. For what values of p does the equation px +4x +(p 3) = 0 have equal roots? 3. Solve the equation 3 x 1 =7. Give your answer
P1 REVISION EXERCISE: 1 1. Solve the simultaneous equations: x + y = x +y = 11. For what values of p does the equation px +4x +(p 3) = 0 have equal roots? 3. Solve the equation 3 x 1 =7. Give your answer
t dt ds Then, in the last class, we showed that F(s) = <2s/3, 1 2s/3, s/3> is arclength parametrization. Therefore,
 13.4. Curvature Curvature Let F(t) be a vector values function. We say it is regular if F (t)=0 Let F(t) be a vector valued function which is arclength parametrized, which means F t 1 for all t. Then,
13.4. Curvature Curvature Let F(t) be a vector values function. We say it is regular if F (t)=0 Let F(t) be a vector valued function which is arclength parametrized, which means F t 1 for all t. Then,
Differential Geometry MAT WEEKLY PROGRAM 1-2
 15.09.014 WEEKLY PROGRAM 1- The first week, we will talk about the contents of this course and mentioned the theory of curves and surfaces by giving the relation and differences between them with aid of
15.09.014 WEEKLY PROGRAM 1- The first week, we will talk about the contents of this course and mentioned the theory of curves and surfaces by giving the relation and differences between them with aid of
2. A circle is inscribed in a square of diagonal length 12 inches. What is the area of the circle?
 March 24, 2011 1. When a square is cut into two congruent rectangles, each has a perimeter of P feet. When the square is cut into three congruent rectangles, each has a perimeter of P 6 feet. Determine
March 24, 2011 1. When a square is cut into two congruent rectangles, each has a perimeter of P feet. When the square is cut into three congruent rectangles, each has a perimeter of P 6 feet. Determine
d f(g(t), h(t)) = x dt + f ( y dt = 0. Notice that we can rewrite the relationship on the left hand side of the equality using the dot product: ( f
 Gradients and the Directional Derivative In 14.3, we discussed the partial derivatives f f and, which tell us the rate of change of the x y height of the surface defined by f in the x direction and the
Gradients and the Directional Derivative In 14.3, we discussed the partial derivatives f f and, which tell us the rate of change of the x y height of the surface defined by f in the x direction and the
Practice with Parameterizing Curves and Surfaces. (Part 1)
 M:8 Spring 7 J. Simon Practice with Parameterizing Curves and Surfaces (Part ) A "parameter" is a number used to measure something. In particular, if we want to describe and analyzie some curve or surface
M:8 Spring 7 J. Simon Practice with Parameterizing Curves and Surfaces (Part ) A "parameter" is a number used to measure something. In particular, if we want to describe and analyzie some curve or surface
Mathematically, the path or the trajectory of a particle moving in space in described by a function of time.
 Module 15 : Vector fields, Gradient, Divergence and Curl Lecture 45 : Curves in space [Section 45.1] Objectives In this section you will learn the following : Concept of curve in space. Parametrization
Module 15 : Vector fields, Gradient, Divergence and Curl Lecture 45 : Curves in space [Section 45.1] Objectives In this section you will learn the following : Concept of curve in space. Parametrization
f xx (x, y) = 6 + 6x f xy (x, y) = 0 f yy (x, y) = y In general, the quantity that we re interested in is
 1. Let f(x, y) = 5 + 3x 2 + 3y 2 + 2y 3 + x 3. (a) Final all critical points of f. (b) Use the second derivatives test to classify the critical points you found in (a) as a local maximum, local minimum,
1. Let f(x, y) = 5 + 3x 2 + 3y 2 + 2y 3 + x 3. (a) Final all critical points of f. (b) Use the second derivatives test to classify the critical points you found in (a) as a local maximum, local minimum,
Chapter 8: Applications of Definite Integrals
 Name: Date: Period: AP Calc AB Mr. Mellina Chapter 8: Applications of Definite Integrals v v Sections: 8.1 Integral as Net Change 8.2 Areas in the Plane v 8.3 Volumes HW Sets Set A (Section 8.1) Pages
Name: Date: Period: AP Calc AB Mr. Mellina Chapter 8: Applications of Definite Integrals v v Sections: 8.1 Integral as Net Change 8.2 Areas in the Plane v 8.3 Volumes HW Sets Set A (Section 8.1) Pages
Practice problems. 1. Given a = 3i 2j and b = 2i + j. Write c = i + j in terms of a and b.
 Practice problems 1. Given a = 3i 2j and b = 2i + j. Write c = i + j in terms of a and b. 1, 1 = c 1 3, 2 + c 2 2, 1. Solve c 1, c 2. 2. Suppose a is a vector in the plane. If the component of the a in
Practice problems 1. Given a = 3i 2j and b = 2i + j. Write c = i + j in terms of a and b. 1, 1 = c 1 3, 2 + c 2 2, 1. Solve c 1, c 2. 2. Suppose a is a vector in the plane. If the component of the a in
Background for Surface Integration
 Background for urface Integration 1 urface Integrals We have seen in previous work how to define and compute line integrals in R 2. You should remember the basic surface integrals that we will need to
Background for urface Integration 1 urface Integrals We have seen in previous work how to define and compute line integrals in R 2. You should remember the basic surface integrals that we will need to
12 m. 30 m. The Volume of a sphere is 36 cubic units. Find the length of the radius.
 NAME DATE PER. REVIEW #18: SPHERES, COMPOSITE FIGURES, & CHANGING DIMENSIONS PART 1: SURFACE AREA & VOLUME OF SPHERES Find the measure(s) indicated. Answers to even numbered problems should be rounded
NAME DATE PER. REVIEW #18: SPHERES, COMPOSITE FIGURES, & CHANGING DIMENSIONS PART 1: SURFACE AREA & VOLUME OF SPHERES Find the measure(s) indicated. Answers to even numbered problems should be rounded
In this chapter, we will investigate what have become the standard applications of the integral:
 Chapter 8 Overview: Applications of Integrals Calculus, like most mathematical fields, began with trying to solve everyday problems. The theory and operations were formalized later. As early as 70 BC,
Chapter 8 Overview: Applications of Integrals Calculus, like most mathematical fields, began with trying to solve everyday problems. The theory and operations were formalized later. As early as 70 BC,
MAT1B01: Curves defined by parametric equations
 MAT1B01: Curves defined by parametric equations Dr Craig 24 October 2016 My details: acraig@uj.ac.za Consulting hours: Thursday 11h20 12h55 Friday 11h30 13h00 Office C-Ring 508 https://andrewcraigmaths.wordpress.com/
MAT1B01: Curves defined by parametric equations Dr Craig 24 October 2016 My details: acraig@uj.ac.za Consulting hours: Thursday 11h20 12h55 Friday 11h30 13h00 Office C-Ring 508 https://andrewcraigmaths.wordpress.com/
Look up partial Decomposition to use for problems #65-67 Do Not solve problems #78,79
 Franklin Township Summer Assignment 2017 AP calculus AB Summer assignment Students should use the Mathematics summer assignment to identify subject areas that need attention in preparation for the study
Franklin Township Summer Assignment 2017 AP calculus AB Summer assignment Students should use the Mathematics summer assignment to identify subject areas that need attention in preparation for the study
Volumes of Solids of Revolution Lecture #6 a
 Volumes of Solids of Revolution Lecture #6 a Sphereoid Parabaloid Hyperboloid Whateveroid Volumes Calculating 3-D Space an Object Occupies Take a cross-sectional slice. Compute the area of the slice. Multiply
Volumes of Solids of Revolution Lecture #6 a Sphereoid Parabaloid Hyperboloid Whateveroid Volumes Calculating 3-D Space an Object Occupies Take a cross-sectional slice. Compute the area of the slice. Multiply
Review 1. Richard Koch. April 23, 2005
 Review Richard Koch April 3, 5 Curves From the chapter on curves, you should know. the formula for arc length in section.;. the definition of T (s), κ(s), N(s), B(s) in section.4. 3. the fact that κ =
Review Richard Koch April 3, 5 Curves From the chapter on curves, you should know. the formula for arc length in section.;. the definition of T (s), κ(s), N(s), B(s) in section.4. 3. the fact that κ =
MATHEMATICS 105 Plane Trigonometry
 Chapter I THE TRIGONOMETRIC FUNCTIONS MATHEMATICS 105 Plane Trigonometry INTRODUCTION The word trigonometry literally means triangle measurement. It is concerned with the measurement of the parts, sides,
Chapter I THE TRIGONOMETRIC FUNCTIONS MATHEMATICS 105 Plane Trigonometry INTRODUCTION The word trigonometry literally means triangle measurement. It is concerned with the measurement of the parts, sides,
15. PARAMETRIZED CURVES AND GEOMETRY
 15. PARAMETRIZED CURVES AND GEOMETRY Parametric or parametrized curves are based on introducing a parameter which increases as we imagine travelling along the curve. Any graph can be recast as a parametrized
15. PARAMETRIZED CURVES AND GEOMETRY Parametric or parametrized curves are based on introducing a parameter which increases as we imagine travelling along the curve. Any graph can be recast as a parametrized
15.1 Justifying Circumference and Area of a Circle
 Name Class Date 15.1 Justifying Circumference and Area of a Circle Essential Question: How can you justify and use the formulas for the circumference and area of a circle? Explore G.10.B Determine and
Name Class Date 15.1 Justifying Circumference and Area of a Circle Essential Question: How can you justify and use the formulas for the circumference and area of a circle? Explore G.10.B Determine and
Functions of Several Variables
 Chapter 3 Functions of Several Variables 3.1 Definitions and Examples of Functions of two or More Variables In this section, we extend the definition of a function of one variable to functions of two or
Chapter 3 Functions of Several Variables 3.1 Definitions and Examples of Functions of two or More Variables In this section, we extend the definition of a function of one variable to functions of two or
Unit 4. Applications of integration
 Unit 4. Applications of integration 4A. Areas between curves. 4A-1 Find the area between the following curves a) y = 2x 2 and y = 3x 1 b) y = x 3 and y = ax; assume a > 0 c) y = x + 1/x and y = 5/2. d)
Unit 4. Applications of integration 4A. Areas between curves. 4A-1 Find the area between the following curves a) y = 2x 2 and y = 3x 1 b) y = x 3 and y = ax; assume a > 0 c) y = x + 1/x and y = 5/2. d)
Student Multivariate Calculus
 Student Multivariate Calculus Six new commands have been added and two previous commands have been augmented. The new commands are: CrossProduct diff DotProduct Norm Normalize TripleScalarProduct The modified
Student Multivariate Calculus Six new commands have been added and two previous commands have been augmented. The new commands are: CrossProduct diff DotProduct Norm Normalize TripleScalarProduct The modified
Imagine a car is traveling along the highway and you look down at the placements situation from high above: highway curve (static)
 Chapter 22 Parametric Equations Imagine a car is traveling along the highway and you look down at the placements situation from high above: highway curve (static) car moving point (dynamic) Figure 22.1:
Chapter 22 Parametric Equations Imagine a car is traveling along the highway and you look down at the placements situation from high above: highway curve (static) car moving point (dynamic) Figure 22.1:
PARAMETRIC EQUATIONS AND POLAR COORDINATES
 10 PARAMETRIC EQUATIONS AND POLAR COORDINATES PARAMETRIC EQUATIONS & POLAR COORDINATES A coordinate system represents a point in the plane by an ordered pair of numbers called coordinates. PARAMETRIC EQUATIONS
10 PARAMETRIC EQUATIONS AND POLAR COORDINATES PARAMETRIC EQUATIONS & POLAR COORDINATES A coordinate system represents a point in the plane by an ordered pair of numbers called coordinates. PARAMETRIC EQUATIONS
Exploring AP Calculus With Colorful Calculator Investigations Deedee Stanfield
 Eploring AP Calculus With Colorful Calculator Investigations Deedee Stanfield dstanfield.oh@oford.k12.al.us Eplore Limits, Derivatives, and Integration through hands-on activities that involve color-enhanced
Eploring AP Calculus With Colorful Calculator Investigations Deedee Stanfield dstanfield.oh@oford.k12.al.us Eplore Limits, Derivatives, and Integration through hands-on activities that involve color-enhanced
48. Logistic Growth (BC) Classwork
 48. Logistic Growth (BC) Classwork Using the exponential growth model, the growth of a population is proportion to its current size. The differential equation for exponential growth is dp = kp leading
48. Logistic Growth (BC) Classwork Using the exponential growth model, the growth of a population is proportion to its current size. The differential equation for exponential growth is dp = kp leading
If ( ) is approximated by a left sum using three inscribed rectangles of equal width on the x-axis, then the approximation is
 More Integration Page 1 Directions: Solve the following problems using the available space for scratchwork. Indicate your answers on the front page. Do not spend too much time on any one problem. Note:
More Integration Page 1 Directions: Solve the following problems using the available space for scratchwork. Indicate your answers on the front page. Do not spend too much time on any one problem. Note:
Unit 4. Applications of integration
 18.01 EXERCISES Unit 4. Applications of integration 4A. Areas between curves. 4A-1 Find the area between the following curves a) y = 2x 2 and y = 3x 1 b) y = x 3 and y = ax; assume a > 0 c) y = x + 1/x
18.01 EXERCISES Unit 4. Applications of integration 4A. Areas between curves. 4A-1 Find the area between the following curves a) y = 2x 2 and y = 3x 1 b) y = x 3 and y = ax; assume a > 0 c) y = x + 1/x
7-5 Parametric Equations
 3. Sketch the curve given by each pair of parametric equations over the given interval. Make a table of values for 6 t 6. t x y 6 19 28 5 16.5 17 4 14 8 3 11.5 1 2 9 4 1 6.5 7 0 4 8 1 1.5 7 2 1 4 3 3.5
3. Sketch the curve given by each pair of parametric equations over the given interval. Make a table of values for 6 t 6. t x y 6 19 28 5 16.5 17 4 14 8 3 11.5 1 2 9 4 1 6.5 7 0 4 8 1 1.5 7 2 1 4 3 3.5
Math 1330 Section 4.2 Section 4.2: Radians, Arc Length, and Area of a Sector
 Section 4.: Radians, Arc Length, and Area of a Sector An angle is formed by two rays that have a common endpoint (vertex). One ray is the initial side and the other is the terminal side. We typically will
Section 4.: Radians, Arc Length, and Area of a Sector An angle is formed by two rays that have a common endpoint (vertex). One ray is the initial side and the other is the terminal side. We typically will
Moore Catholic High School Math Department
 Moore Catholic High School Math Department Geometry Vocabulary The following is a list of terms and properties which are necessary for success in a Geometry class. You will be tested on these terms during
Moore Catholic High School Math Department Geometry Vocabulary The following is a list of terms and properties which are necessary for success in a Geometry class. You will be tested on these terms during
LECTURE 3-1 AREA OF A REGION BOUNDED BY CURVES
 7 CALCULUS II DR. YOU 98 LECTURE 3- AREA OF A REGION BOUNDED BY CURVES If y = f(x) and y = g(x) are continuous on an interval [a, b] and f(x) g(x) for all x in [a, b], then the area of the region between
7 CALCULUS II DR. YOU 98 LECTURE 3- AREA OF A REGION BOUNDED BY CURVES If y = f(x) and y = g(x) are continuous on an interval [a, b] and f(x) g(x) for all x in [a, b], then the area of the region between
5 Applications of Definite Integrals
 5 Applications of Definite Integrals The previous chapter introduced the concepts of a definite integral as an area and as a limit of Riemann sums, demonstrated some of the properties of integrals, introduced
5 Applications of Definite Integrals The previous chapter introduced the concepts of a definite integral as an area and as a limit of Riemann sums, demonstrated some of the properties of integrals, introduced
MATH 1020 WORKSHEET 10.1 Parametric Equations
 MATH WORKSHEET. Parametric Equations If f and g are continuous functions on an interval I, then the equations x ft) and y gt) are called parametric equations. The parametric equations along with the graph
MATH WORKSHEET. Parametric Equations If f and g are continuous functions on an interval I, then the equations x ft) and y gt) are called parametric equations. The parametric equations along with the graph
Chapter 5. An Introduction to Trigonometric Functions 1-1
 Chapter 5 An Introduction to Trigonometric Functions Copyright (c) The McGraw-Hill Companies, Inc. Permission required for reproduction or display. 1-1 5.1 A half line or all points extended from a single
Chapter 5 An Introduction to Trigonometric Functions Copyright (c) The McGraw-Hill Companies, Inc. Permission required for reproduction or display. 1-1 5.1 A half line or all points extended from a single
PRACTICE FINAL - MATH 1210, Spring 2012 CHAPTER 1
 PRACTICE FINAL - MATH 2, Spring 22 The Final will have more material from Chapter 4 than other chapters. To study for chapters -3 you should review the old practice eams IN ADDITION TO what appears here.
PRACTICE FINAL - MATH 2, Spring 22 The Final will have more material from Chapter 4 than other chapters. To study for chapters -3 you should review the old practice eams IN ADDITION TO what appears here.
Conics, Parametric Equations, and Polar Coordinates. Copyright Cengage Learning. All rights reserved.
 10 Conics, Parametric Equations, and Polar Coordinates Copyright Cengage Learning. All rights reserved. 10.5 Area and Arc Length in Polar Coordinates Copyright Cengage Learning. All rights reserved. Objectives
10 Conics, Parametric Equations, and Polar Coordinates Copyright Cengage Learning. All rights reserved. 10.5 Area and Arc Length in Polar Coordinates Copyright Cengage Learning. All rights reserved. Objectives
Exam 3 SCORE. MA 114 Exam 3 Spring Section and/or TA:
 MA 114 Exam 3 Spring 217 Exam 3 Name: Section and/or TA: Last Four Digits of Student ID: Do not remove this answer page you will return the whole exam. You will be allowed two hours to complete this test.
MA 114 Exam 3 Spring 217 Exam 3 Name: Section and/or TA: Last Four Digits of Student ID: Do not remove this answer page you will return the whole exam. You will be allowed two hours to complete this test.
For Test #1 study these problems, the examples in your notes, and the homework.
 Mth 74 - Review Problems for Test Test covers Sections 6.-6.5, 7. and 7. For Test # study these problems, the examples in your notes, and the homework.. The base of a solid is the region inside the circle
Mth 74 - Review Problems for Test Test covers Sections 6.-6.5, 7. and 7. For Test # study these problems, the examples in your notes, and the homework.. The base of a solid is the region inside the circle
Geometry: Angle Relationships
 Geometry: Angle Relationships I. Define the following angles (in degrees) and draw an example of each. 1. Acute 3. Right 2. Obtuse 4. Straight Complementary angles: Supplementary angles: a + b = c + d
Geometry: Angle Relationships I. Define the following angles (in degrees) and draw an example of each. 1. Acute 3. Right 2. Obtuse 4. Straight Complementary angles: Supplementary angles: a + b = c + d
Digging deeper using GeoGebra: An exploration of quadratics and more.
 Digging deeper using GeoGebra: An exploration of quadratics and more. Abstract Using GeoGebra students can explore in far more depth topics that have until recently been given a standard treatment. One
Digging deeper using GeoGebra: An exploration of quadratics and more. Abstract Using GeoGebra students can explore in far more depth topics that have until recently been given a standard treatment. One
COMPASS/ESL Sample Test Questions A Guide for Students and Parents Mathematics
 COMPASS/ESL Sample Test Questions A Guide for Students and Parents Mathematics College Algebra Geometry Trigonometry An ACT Program for Educational Planning Note to Students Welcome to the COMPASS Sample
COMPASS/ESL Sample Test Questions A Guide for Students and Parents Mathematics College Algebra Geometry Trigonometry An ACT Program for Educational Planning Note to Students Welcome to the COMPASS Sample
Vectors and the Geometry of Space
 Vectors and the Geometry of Space In Figure 11.43, consider the line L through the point P(x 1, y 1, z 1 ) and parallel to the vector. The vector v is a direction vector for the line L, and a, b, and c
Vectors and the Geometry of Space In Figure 11.43, consider the line L through the point P(x 1, y 1, z 1 ) and parallel to the vector. The vector v is a direction vector for the line L, and a, b, and c
sin30 = sin60 = cos30 = cos60 = tan30 = tan60 =
 Precalculus Notes Trig-Day 1 x Right Triangle 5 How do we find the hypotenuse? 1 sinθ = cosθ = tanθ = Reciprocals: Hint: Every function pair has a co in it. sinθ = cscθ = sinθ = cscθ = cosθ = secθ = cosθ
Precalculus Notes Trig-Day 1 x Right Triangle 5 How do we find the hypotenuse? 1 sinθ = cosθ = tanθ = Reciprocals: Hint: Every function pair has a co in it. sinθ = cscθ = sinθ = cscθ = cosθ = secθ = cosθ
Math 2260 Exam #1 Practice Problem Solutions
 Math 6 Exam # Practice Problem Solutions. What is the area bounded by the curves y x and y x + 7? Answer: As we can see in the figure, the line y x + 7 lies above the parabola y x in the region we care
Math 6 Exam # Practice Problem Solutions. What is the area bounded by the curves y x and y x + 7? Answer: As we can see in the figure, the line y x + 7 lies above the parabola y x in the region we care
Quiz 6 Practice Problems
 Quiz 6 Practice Problems Practice problems are similar, both in difficulty and in scope, to the type of problems you will see on the quiz. Problems marked with a are for your entertainment and are not
Quiz 6 Practice Problems Practice problems are similar, both in difficulty and in scope, to the type of problems you will see on the quiz. Problems marked with a are for your entertainment and are not
Classroom Tips and Techniques: Drawing a Normal and Tangent Plane on a Surface
 Classroom Tips and Techniques: Drawing a Normal and Tangent Plane on a Surface Robert J. Lopez Emeritus Professor of Mathematics and Maple Fellow Maplesoft Introduction A question posted to MaplePrimes
Classroom Tips and Techniques: Drawing a Normal and Tangent Plane on a Surface Robert J. Lopez Emeritus Professor of Mathematics and Maple Fellow Maplesoft Introduction A question posted to MaplePrimes
Proof of Constant Width of Spheroform with Tetrahedral Symmetry
 Proof of Constant Width of Spheroform with Tetrahedral Symmetry Patrick Roberts Corvallis, Oregon August 20, 2012 The four faces of the Reuleaux tetrahedron are sections of sphere surface, each centered
Proof of Constant Width of Spheroform with Tetrahedral Symmetry Patrick Roberts Corvallis, Oregon August 20, 2012 The four faces of the Reuleaux tetrahedron are sections of sphere surface, each centered
The Geometry of Solids
 CONDENSED LESSON 10.1 The Geometry of Solids In this lesson you will Learn about polyhedrons, including prisms and pyramids Learn about solids with curved surfaces, including cylinders, cones, and spheres
CONDENSED LESSON 10.1 The Geometry of Solids In this lesson you will Learn about polyhedrons, including prisms and pyramids Learn about solids with curved surfaces, including cylinders, cones, and spheres
I IS II. = 2y"\ V= n{ay 2 l 3 -\y 2 )dy. Jo n [fy 5 ' 3 1
 r Exercises 5.2 Figure 530 (a) EXAMPLE'S The region in the first quadrant bounded by the graphs of y = i* and y = 2x is revolved about the y-axis. Find the volume of the resulting solid. SOLUTON The region
r Exercises 5.2 Figure 530 (a) EXAMPLE'S The region in the first quadrant bounded by the graphs of y = i* and y = 2x is revolved about the y-axis. Find the volume of the resulting solid. SOLUTON The region
Lecture 11 Differentiable Parametric Curves
 Lecture 11 Differentiable Parametric Curves 11.1 Definitions and Examples. 11.1.1 Definition. A differentiable parametric curve in R n of class C k (k 1) is a C k map t α(t) = (α 1 (t),..., α n (t)) of
Lecture 11 Differentiable Parametric Curves 11.1 Definitions and Examples. 11.1.1 Definition. A differentiable parametric curve in R n of class C k (k 1) is a C k map t α(t) = (α 1 (t),..., α n (t)) of
Conics, Parametric Equations, and Polar Coordinates. Copyright Cengage Learning. All rights reserved.
 10 Conics, Parametric Equations, and Polar Coordinates Copyright Cengage Learning. All rights reserved. 10.5 Area and Arc Length in Polar Coordinates Copyright Cengage Learning. All rights reserved. Objectives
10 Conics, Parametric Equations, and Polar Coordinates Copyright Cengage Learning. All rights reserved. 10.5 Area and Arc Length in Polar Coordinates Copyright Cengage Learning. All rights reserved. Objectives
Trigonometry and the Unit Circle. Chapter 4
 Trigonometry and the Unit Circle Chapter 4 Topics Demonstrate an understanding of angles in standard position, expressed in degrees and radians. Develop and apply the equation of the unit circle. Solve
Trigonometry and the Unit Circle Chapter 4 Topics Demonstrate an understanding of angles in standard position, expressed in degrees and radians. Develop and apply the equation of the unit circle. Solve
Topics in Analytic Geometry Part II
 Name Chapter 9 Topics in Analytic Geometry Part II Section 9.4 Parametric Equations Objective: In this lesson you learned how to evaluate sets of parametric equations for given values of the parameter
Name Chapter 9 Topics in Analytic Geometry Part II Section 9.4 Parametric Equations Objective: In this lesson you learned how to evaluate sets of parametric equations for given values of the parameter
Be able to properly use the following terminology:
 Be able to properly use the following terminology: Initial Side Terminal Side Positive Angle Negative Angle Standard Position Quadrantal Angles Coterminal Angles Expressions generating coterminal angles
Be able to properly use the following terminology: Initial Side Terminal Side Positive Angle Negative Angle Standard Position Quadrantal Angles Coterminal Angles Expressions generating coterminal angles
Geometry / Integrated II TMTA Test units.
 1. An isosceles triangle has a side of length 2 units and another side of length 3 units. Which of the following best completes the statement The length of the third side of this triangle? (a) is (b) is
1. An isosceles triangle has a side of length 2 units and another side of length 3 units. Which of the following best completes the statement The length of the third side of this triangle? (a) is (b) is
Volume by Slicing (Disks & Washers)
 Volume by Slicing (Disks & Washers) SUGGESTED REFERENCE MATERIAL: As you work through the problems listed below, you should reference Chapter 6.2 of the recommended textbook (or the equivalent chapter
Volume by Slicing (Disks & Washers) SUGGESTED REFERENCE MATERIAL: As you work through the problems listed below, you should reference Chapter 6.2 of the recommended textbook (or the equivalent chapter
9/30/2014 FIRST HOURLY PRACTICE VIII Math 21a, Fall Name:
 9/30/2014 FIRST HOURLY PRACTICE VIII Math 21a, Fall 2014 Name: MWF 9 Oliver Knill MWF 9 Chao Li MWF 10 Gijs Heuts MWF 10 Yu-Wen Hsu MWF 10 Yong-Suk Moon MWF 11 Rosalie Belanger-Rioux MWF 11 Gijs Heuts
9/30/2014 FIRST HOURLY PRACTICE VIII Math 21a, Fall 2014 Name: MWF 9 Oliver Knill MWF 9 Chao Li MWF 10 Gijs Heuts MWF 10 Yu-Wen Hsu MWF 10 Yong-Suk Moon MWF 11 Rosalie Belanger-Rioux MWF 11 Gijs Heuts
Outcomes List for Math Multivariable Calculus (9 th edition of text) Spring
 Outcomes List for Math 200-200935 Multivariable Calculus (9 th edition of text) Spring 2009-2010 The purpose of the Outcomes List is to give you a concrete summary of the material you should know, and
Outcomes List for Math 200-200935 Multivariable Calculus (9 th edition of text) Spring 2009-2010 The purpose of the Outcomes List is to give you a concrete summary of the material you should know, and
Topic 6: Calculus Integration Volume of Revolution Paper 2
 Topic 6: Calculus Integration Standard Level 6.1 Volume of Revolution Paper 1. Let f(x) = x ln(4 x ), for < x
Topic 6: Calculus Integration Standard Level 6.1 Volume of Revolution Paper 1. Let f(x) = x ln(4 x ), for < x
INSTRUCTIONS FOR THE USE OF THE SUPER RULE TM
 INSTRUCTIONS FOR THE USE OF THE SUPER RULE TM NOTE: All images in this booklet are scale drawings only of template shapes and scales. Preparation: Your SUPER RULE TM is a valuable acquisition for classroom
INSTRUCTIONS FOR THE USE OF THE SUPER RULE TM NOTE: All images in this booklet are scale drawings only of template shapes and scales. Preparation: Your SUPER RULE TM is a valuable acquisition for classroom
What you will learn today
 What you will learn today Tangent Planes and Linear Approximation and the Gradient Vector Vector Functions 1/21 Recall in one-variable calculus, as we zoom in toward a point on a curve, the graph becomes
What you will learn today Tangent Planes and Linear Approximation and the Gradient Vector Vector Functions 1/21 Recall in one-variable calculus, as we zoom in toward a point on a curve, the graph becomes
Motivation. Parametric Curves (later Surfaces) Outline. Tangents, Normals, Binormals. Arclength. Advanced Computer Graphics (Fall 2010)
 Advanced Computer Graphics (Fall 2010) CS 283, Lecture 19: Basic Geometric Concepts and Rotations Ravi Ramamoorthi http://inst.eecs.berkeley.edu/~cs283/fa10 Motivation Moving from rendering to simulation,
Advanced Computer Graphics (Fall 2010) CS 283, Lecture 19: Basic Geometric Concepts and Rotations Ravi Ramamoorthi http://inst.eecs.berkeley.edu/~cs283/fa10 Motivation Moving from rendering to simulation,
Math 124 Final Examination Winter 2015 !!! READ...INSTRUCTIONS...READ!!!
 1 Math 124 Final Examination Winter 2015 Print Your Name Signature Student ID Number Quiz Section Professor s Name TA s Name!!! READ...INSTRUCTIONS...READ!!! 1. Your exam contains 7 problems and 11 pages;
1 Math 124 Final Examination Winter 2015 Print Your Name Signature Student ID Number Quiz Section Professor s Name TA s Name!!! READ...INSTRUCTIONS...READ!!! 1. Your exam contains 7 problems and 11 pages;
Number/Computation. addend Any number being added. digit Any one of the ten symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, or 9
 14 Number/Computation addend Any number being added algorithm A step-by-step method for computing array A picture that shows a number of items arranged in rows and columns to form a rectangle associative
14 Number/Computation addend Any number being added algorithm A step-by-step method for computing array A picture that shows a number of items arranged in rows and columns to form a rectangle associative
Math (Spring 2009): Lecture 5 Planes. Parametric equations of curves and lines
 Math 18.02 (Spring 2009): Lecture 5 Planes. Parametric equations of curves and lines February 12 Reading Material: From Simmons: 17.1 and 17.2. Last time: Square Systems. Word problem. How many solutions?
Math 18.02 (Spring 2009): Lecture 5 Planes. Parametric equations of curves and lines February 12 Reading Material: From Simmons: 17.1 and 17.2. Last time: Square Systems. Word problem. How many solutions?
Use of Number Maths Statement Code no: 1 Student: Class: At Junior Certificate level the student can: Apply the knowledge and skills necessary to perf
 Use of Number Statement Code no: 1 Apply the knowledge and skills necessary to perform mathematical calculations 1 Recognise simple fractions, for example 1 /4, 1 /2, 3 /4 shown in picture or numerical
Use of Number Statement Code no: 1 Apply the knowledge and skills necessary to perform mathematical calculations 1 Recognise simple fractions, for example 1 /4, 1 /2, 3 /4 shown in picture or numerical
