Trees. Reading: Weiss, Chapter 4. Cpt S 223, Fall 2007 Copyright: Washington State University
|
|
|
- Leslie Anthony
- 5 years ago
- Views:
Transcription
1 Trees Reading: Weiss, Chapter 4 1
2 Generic Rooted Trees 2
3 Terms Node, Edge Internal node Root Leaf Child Sibling Descendant Ancestor 3
4 Tree Representations n-ary trees Each internal node can have at most n children Representation #1 Each node stores pointers to all of its children O(n 2 ) space complexity How? Representation #2 Each node stores only two pointers: Leftmost child pointer Right sibling pointer O(n) space How? 4
5 Child-Sibling Representation Space is O(n) What about access run-times? Accessing a child from a parent is not constant time anymore 5
6 Traversals Decide on the tree representation based on how you plan to access/traverse it Access patterns Depth-first Breadth-first Top-down Bottom-up Traversals Pre-order Post-order In-order Eulerian 6
7 Pre-order Traversal (node, left, right) Visit parent first And then recursively traverse each child from left to right Example: Pseudocode for a binary tree: Pre-order(T: root of an input binary tree) BEGIN Print T->contents; IF T is a leaf RETURN; Pre-order (T->left); Pre-order (T->right); END 7
8 Unix Directory - Preorder listing 8
9 Post-order Traversal (left, right, node) First recursively traverse each child from left to right Visit Parent last Example: Pseudocode for a binary tree: Post-order(T: root of an input binary tree) BEGIN IF T is an internal node THEN Post-order (T->left); Post-order (T->right); END IF Print T->Contents; END 9
10 Unix Directory Size - Post-order Listing 10
11 In-order Traversal (left, node, right) Recursively traverse each child from left to right Between each consecutive children s traversal, visit the parent Example: Pseudocode for a binary tree: In-order(T: root of an input binary tree) BEGIN IF T is an internal node THEN Post-order (T->left); Print T->Contents; Post-order (T->right); ELSE Print T->Contents; END IF END 11
12 An Example a b g c f h d Fill up the blanks: e i Pre-order: _ Post-order: _ In-order: _ 12
13 Example: Evaluating Post-fix Expressions a b + c d e + * * ==> In-fix expression: (a + b) * (c * (d + e)) * a + b * c + Q) Does a post-order traversal, in general, always lead to a unique binary tree? d e 13
14 Tree Retrieval from Traversals Example Pre-order: a b c d e In-order: b a d c e What is the tree? (if one exists) 14
15 Tree Retrieval from Traversals Example Post-order: b e d c a In-order: b a e d c What is the tree? (if one exists) 15
16 Tree Retrieval from Traversals Example Pre-order: a b c d Post-order: c d b a What is the tree? (if one exists) 16
17 More Traversal Patterns Depth-first Eg., Eulerian Tour Breadth-first Access Patterns Top-down Bottom-up Eg., Tree accumulations 17
18 Binary Search Tree 18
19 BST: Definition Binary search tree is a binary tree such that: For every node u, the values of the nodes in the left (alternatively, right) subtree of u are strictly less (alternatively, greater) than the value at u = < > 19
20 Examples BST T 1 T 2 Not a BST because of 20
21 21
22 22
23 23
24 BST: Insert() Insert (X: new node, T: Tree) BEGIN IF T==NULL THEN T=X; ELSE IF X < T->element THEN Insert(X,T->left); ELSE IF X > T->element THEN Insert (X,T->right); ELSE Report Duplicate Error; END 24
25 Insertion Example T: before Insert(5, T) T: after 25
26 BST: Deletion 26
27 Deletion of node 4 T: before T: after Removed edge& node 27
28 Deletion of node 2 T: before T: after Removed edge& node 28
29 Run-time Analysis Find (x) Insert (x) Delete (x) Expected O(lg n) O(lg n) O(lg n) Worst-case O(n) O(n) O(n) 29
30 Average Case Analysis of BST Assumption: Every possible input sequence is equally likely Define: height of a node u is the number of levels away from the root Let D(n) = sum of heights of all nodes in a n- node tree Average height = D avg (n)/n ==> this will be the average number of hops required for an access Goal: Compute D avg (n) for an average input 30
31 Average height calculation D(n) = D(i) + D(n-i+1) + n-1 On average: D(n) root D(i)=D(n-i+1)=1/n j=0 n-1 D(j) Therefore: D(n)=2/n j=0 n-1 D(j) + n-1 D(i) D(n-i+1) O(n lg n) Average height = O(log n) i nodes n-i-1 nodes 31
32 A bad binary tree 32
33 Randomly Generated BST 33
34 AVL Trees Height-Balanced Binary Search Tree 34
35 AVL Trees AVL: Adelson-Velskii and Landis How to maintain the tree heightbalanced? Keep both sides of the root roughly balanced 35
36 AVL Trees: Definition An AVL tree is also a binary search tree but with the following additional property: For every node in the tree, the heights of the left and right subtrees can differ at most by 1 Every subtree in an AVL tree is also an AVL tree h l -h r <=1 h l h r 36
37 AVL Not an AVL Both are binary search trees 37
38 An AVL tree with 143 nodes Height=9 38
39 Height Bound of an AVL Tree The height of an n-node AVL tree can be at most 1.44 log (n+2) (not proven here) O(log n) Main idea: Let S(h) be the minimum number of nodes in an AVL tree of height h For the root S(h) = S(h-1) + S(h-2) +1 Similar to Fibonacci numbers 39
40 Operations Insert(x) into an AVL tree Condition: Inserting a new element should not disturb the height property If it does, then restructure the tree until the property is satisfied More involved insert procedure Same for remove/delete 40
41 Run-time Analysis Find (x) Insert (x) Delete (x) Expected O(lg n) O(lg n) O(lg n) Worst-case O(lg n) O(lg n) O(lg n) 41
42 Insert () into an AVL Tree root path The first stage of the algorithm is same as insertion into a binary search tree Rebalancing: x If the tree becomes unbalanced because of the new insertion, then it needs to be fixed Only the nodes that are on the path from the newly inserted node to the root may have their height altered 42
43 Rebalancing through Rotation Height of any of the green nodes could have been altered Take the bottommost such green node, u Rebalance u The rest will be automatically balanced as a consequence root x u 43
44 Rebalancing u Four cases for insertion under u: 1. X is inserted into the left subtree of the left child of u 2. X is inserted into the right subtree of the left child of u 3. X is inserted into the left subtree of the right child of u 4. X is inserted into the right subtree of the right child of u Case 1 & 4 are mirrored equivalents Case 2 & 3 are mirrored equivalents 44
45 Case 1: Single Rotation node to be rebalanced New node Inserted here PS: Case 4 is handled in a mirror-equivalent manner 45
46 Example: Single Rotation for Case 1 Problem node 46
47 Case 4: Single Rotation Problem node 47
48 In-class Exercise Insertion sequence: 3, 2, 1, 4, 6, 7 Incremental build procedure: Start with an empty tree and insert elements, one at a time 48
49 Case 2 Cases 2 & 3: Single Rotation Does NOT work Problem node Problem node Case 3 Reason: We are not lifting subtree Y up! 49
50 Case 2: Double Rotation Case 2 Problem node Y Logic: Lift up subtrees B and C one level without affecting subtrees A and D 50
51 Case 2: Why is it Double Rotation? Problem node k 3 k 3 k 2 k 1 k 2 D Rotate k 2 k 1 D Rotate k 2 k 3 k 3 k 1 A k 2 k 1 C A B C D B C A B 1. Rotate problem node s grandchild with its child 2. Rotate problem node with its new child 51
52 Case 3: Double Rotation Case 3 Problem node Y 52
53 In-class Exercise Insert sequence: 3, 2, 1, 4, 6, 7, 16, 15, 14, 13, 12, 11, 10, 8, 9 53
54 54
55 55
56 56
57 57
58 58
59 B-Trees A Data Structure for Disks 59
60 Data Structures for Disks Hardware Storage capacity Data persistence Data access speeds Primary Storage RAM (main memory), cache ~ >100 MB to 2-3GB Transient (erased after process terminates) ~ a few clock cycles (ie., x 10-9 seconds) Secondary Storage Disk (ie., I/O) Giga (10 9 ) to Terabytes (10 12 ) Persistent (permanently stored) milliseconds (10-3 sec) = Data seek time + read time could be million times slower than main memory read 60
61 Need for Different Disk-based Why? Data Structures BST, AVL trees at best have heights O(lg n) N=10 6 lg 10 6 is roughly disk seeks for each level would be too much! So reduce the height! How? Increase the log base beyond 2 Eg., log is < 9 Instead of binary (2-ary) trees, use m-ary search trees s.t. m>2 61
62 5-ary tree of 31 nodes has only 3 levels Index to the Data Real Data Items stored at leaves as disk blocks 62
63 B+ trees: Definition A B+ tree of order M is an M-ary tree with the following properties: 1. Leaves store the real data items 2. Internal nodes store up to M-1 keys s.t., key i is the smallest key in subtree i+1 3. Root can have between 2 to M children 4. Each internal node (except root) has between ceil(m/2) to M children 5. All leaves are at the same depth 6. All leaves have between ceil(l/2) and L data items, for some L 63
64 B+ tree of order 5 Root Internal nodes Leaves M=5 (order of the B+ tree) L=5 (#data items bound for leaves) 64
65 B+ tree of order 5 Index to the Data Each internal node = 1 disk block Data items stored at leaves Each leaf = 1 disk block 65
66 Node Data Structures Root & internal nodes M child pointers 4 x M bytes Leaf node L data items in the worst-case L x D bytes M-1 key entries (M-1) x K bytes D denotes the size of each data item K denotes the size of a key (ie., K <= D) 66
67 How to choose M and L? Choose M and L based on the size of each data item Example: Let 1 disk block = 8,192 bytes We will denote this by the symbol B So, B = 8 KB Let each data item be an integer So, D = 4 bytes Also, K = 4 bytes 67
68 Example K=4 bytes, B=8 KB How to calculate M? Each internal node needs 4 x M + (M-1) x K bytes Each internal node has to fit inside a disk block So we have B bytes Solving the above: M = floor[ (B+K) / (4+K) ] For K=4, B=8 KB: M = 1,024 Alternatively, if K=32 M=228 68
69 Example D=4 bytes, B=8 KB How to calculate L for leaves? L = floor[ B / D ] For D=4, B = 8 KB: L = 2,048 ie., each leaf has to store 1,024 to 2,048 data items Alternatively, if D=32: L = 256 data items / leaf 69
70 B+ trees: Other Counters Let N be the total number of data items Number of leaves = ceil [ N / L ] to ceil [ 2N / L] Height = O ( log M #leaves) 70
71 Example: Find (81)? - O(log M #leaves) disk block reads - Within the leaf: O(L) or - or even better, O(log L) if data items are kept sorted - we can use binary search within each leaf node - 71
72 B+ tree: Insertion Have to maintain all leaves at the same level before and after insertion Note that this could mean increasing the height of the tree Height vs. Level 72
73 Example: Insert (57) before Insert here, there is space! 73
74 Example: Insert (57) after Next: Insert(55) Empty now So, split the previous leaf into 2 parts 74
75 Example.. Insert (55) after Split parent node There is one empty room here Next: Insert (40) Hmm.. Leaf already full, and no empty neighbors! 75
76 Example.. Insert (40) after Note: Splitting the root itself would mean we are increasing the height by 1 76
77 Example.. Delete (99) before Too few (<3 data items) after delete Will be left with too few keys (<2) after move Borrow leaf from left neighbor 77
78 Example.. Delete (99) after 78
9/29/2016. Chapter 4 Trees. Introduction. Terminology. Terminology. Terminology. Terminology
 Introduction Chapter 4 Trees for large input, even linear access time may be prohibitive we need data structures that exhibit average running times closer to O(log N) binary search tree 2 Terminology recursive
Introduction Chapter 4 Trees for large input, even linear access time may be prohibitive we need data structures that exhibit average running times closer to O(log N) binary search tree 2 Terminology recursive
Introduction. for large input, even access time may be prohibitive we need data structures that exhibit times closer to O(log N) binary search tree
 Chapter 4 Trees 2 Introduction for large input, even access time may be prohibitive we need data structures that exhibit running times closer to O(log N) binary search tree 3 Terminology recursive definition
Chapter 4 Trees 2 Introduction for large input, even access time may be prohibitive we need data structures that exhibit running times closer to O(log N) binary search tree 3 Terminology recursive definition
Overview. Tree data structure Binary search trees. STL set and map classes B-trees for accessing secondary storage Applications
 Trees 1 Overview Tree data structure Binary search trees Support O(log 2 N) operations Balanced trees STL set and map classes B-trees for accessing secondary storage Applications 2 Trees G is parent of
Trees 1 Overview Tree data structure Binary search trees Support O(log 2 N) operations Balanced trees STL set and map classes B-trees for accessing secondary storage Applications 2 Trees G is parent of
Algorithms. AVL Tree
 Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Overview. Tree data structure Binary search trees. STL set and map classes B-trees for accessing secondary storage Applications
 Trees 1 Overview Tree data structure Binary search trees Support O(log 2 N) operations Balanced trees STL set and map classes B-trees for accessing secondary storage Applications 2 Trees G is parent of
Trees 1 Overview Tree data structure Binary search trees Support O(log 2 N) operations Balanced trees STL set and map classes B-trees for accessing secondary storage Applications 2 Trees G is parent of
CSCI2100B Data Structures Trees
 CSCI2100B Data Structures Trees Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction General Tree
CSCI2100B Data Structures Trees Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction General Tree
Module 4: Index Structures Lecture 13: Index structure. The Lecture Contains: Index structure. Binary search tree (BST) B-tree. B+-tree.
 The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
C SCI 335 Software Analysis & Design III Lecture Notes Prof. Stewart Weiss Chapter 4: B Trees
 B-Trees AVL trees and other binary search trees are suitable for organizing data that is entirely contained within computer memory. When the amount of data is too large to fit entirely in memory, i.e.,
B-Trees AVL trees and other binary search trees are suitable for organizing data that is entirely contained within computer memory. When the amount of data is too large to fit entirely in memory, i.e.,
CSE 530A. B+ Trees. Washington University Fall 2013
 CSE 530A B+ Trees Washington University Fall 2013 B Trees A B tree is an ordered (non-binary) tree where the internal nodes can have a varying number of child nodes (within some range) B Trees When a key
CSE 530A B+ Trees Washington University Fall 2013 B Trees A B tree is an ordered (non-binary) tree where the internal nodes can have a varying number of child nodes (within some range) B Trees When a key
Trees. Eric McCreath
 Trees Eric McCreath 2 Overview In this lecture we will explore: general trees, binary trees, binary search trees, and AVL and B-Trees. 3 Trees Trees are recursive data structures. They are useful for:
Trees Eric McCreath 2 Overview In this lecture we will explore: general trees, binary trees, binary search trees, and AVL and B-Trees. 3 Trees Trees are recursive data structures. They are useful for:
CS350: Data Structures B-Trees
 B-Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Introduction All of the data structures that we ve looked at thus far have been memory-based
B-Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Introduction All of the data structures that we ve looked at thus far have been memory-based
Trees. R. J. Renka 10/14/2011. Department of Computer Science & Engineering University of North Texas. R. J. Renka Trees
 Trees R. J. Renka Department of Computer Science & Engineering University of North Texas 10/14/2011 4.1 Preliminaries Defn: A (rooted) tree is a directed graph (set of nodes and edges) with a particular
Trees R. J. Renka Department of Computer Science & Engineering University of North Texas 10/14/2011 4.1 Preliminaries Defn: A (rooted) tree is a directed graph (set of nodes and edges) with a particular
Balanced Search Trees. CS 3110 Fall 2010
 Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
COMP171. AVL-Trees (Part 1)
 COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
Trees. (Trees) Data Structures and Programming Spring / 28
 Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
CS 350 : Data Structures B-Trees
 CS 350 : Data Structures B-Trees David Babcock (courtesy of James Moscola) Department of Physical Sciences York College of Pennsylvania James Moscola Introduction All of the data structures that we ve
CS 350 : Data Structures B-Trees David Babcock (courtesy of James Moscola) Department of Physical Sciences York College of Pennsylvania James Moscola Introduction All of the data structures that we ve
Uses for Trees About Trees Binary Trees. Trees. Seth Long. January 31, 2010
 Uses for About Binary January 31, 2010 Uses for About Binary Uses for Uses for About Basic Idea Implementing Binary Example: Expression Binary Search Uses for Uses for About Binary Uses for Storage Binary
Uses for About Binary January 31, 2010 Uses for About Binary Uses for Uses for About Basic Idea Implementing Binary Example: Expression Binary Search Uses for Uses for About Binary Uses for Storage Binary
AVL Tree Definition. An example of an AVL tree where the heights are shown next to the nodes. Adelson-Velsky and Landis
 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 AVL Trees v 6 3 8 z 0 Goodrich, Tamassia, Goldwasser
Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 AVL Trees v 6 3 8 z 0 Goodrich, Tamassia, Goldwasser
CS350: Data Structures AVL Trees
 S35: Data Structures VL Trees James Moscola Department of Engineering & omputer Science York ollege of Pennsylvania S35: Data Structures James Moscola Balanced Search Trees Binary search trees are not
S35: Data Structures VL Trees James Moscola Department of Engineering & omputer Science York ollege of Pennsylvania S35: Data Structures James Moscola Balanced Search Trees Binary search trees are not
Analysis of Algorithms
 Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
COSC160: Data Structures Balanced Trees. Jeremy Bolton, PhD Assistant Teaching Professor
 COSC160: Data Structures Balanced Trees Jeremy Bolton, PhD Assistant Teaching Professor Outline I. Balanced Trees I. AVL Trees I. Balance Constraint II. Examples III. Searching IV. Insertions V. Removals
COSC160: Data Structures Balanced Trees Jeremy Bolton, PhD Assistant Teaching Professor Outline I. Balanced Trees I. AVL Trees I. Balance Constraint II. Examples III. Searching IV. Insertions V. Removals
AVL Trees Goodrich, Tamassia, Goldwasser AVL Trees 1
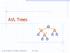 AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
Part 2: Balanced Trees
 Part 2: Balanced Trees 1 AVL Trees We could dene a perfectly balanced binary search tree with N nodes to be a complete binary search tree, one in which every level except the last is completely full. A
Part 2: Balanced Trees 1 AVL Trees We could dene a perfectly balanced binary search tree with N nodes to be a complete binary search tree, one in which every level except the last is completely full. A
Binary Trees, Binary Search Trees
 Binary Trees, Binary Search Trees Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search, insert, delete)
Binary Trees, Binary Search Trees Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search, insert, delete)
CISC 235: Topic 4. Balanced Binary Search Trees
 CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
An AVL tree with N nodes is an excellent data. The Big-Oh analysis shows that most operations finish within O(log N) time
 B + -TREES MOTIVATION An AVL tree with N nodes is an excellent data structure for searching, indexing, etc. The Big-Oh analysis shows that most operations finish within O(log N) time The theoretical conclusion
B + -TREES MOTIVATION An AVL tree with N nodes is an excellent data structure for searching, indexing, etc. The Big-Oh analysis shows that most operations finish within O(log N) time The theoretical conclusion
AVL Trees / Slide 2. AVL Trees / Slide 4. Let N h be the minimum number of nodes in an AVL tree of height h. AVL Trees / Slide 6
 COMP11 Spring 008 AVL Trees / Slide Balanced Binary Search Tree AVL-Trees Worst case height of binary search tree: N-1 Insertion, deletion can be O(N) in the worst case We want a binary search tree with
COMP11 Spring 008 AVL Trees / Slide Balanced Binary Search Tree AVL-Trees Worst case height of binary search tree: N-1 Insertion, deletion can be O(N) in the worst case We want a binary search tree with
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
Comp 335 File Structures. B - Trees
 Comp 335 File Structures B - Trees Introduction Simple indexes provided a way to directly access a record in an entry sequenced file thereby decreasing the number of seeks to disk. WE ASSUMED THE INDEX
Comp 335 File Structures B - Trees Introduction Simple indexes provided a way to directly access a record in an entry sequenced file thereby decreasing the number of seeks to disk. WE ASSUMED THE INDEX
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba 1 / 12 Binary Search Trees (review) Structure
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba 1 / 12 Binary Search Trees (review) Structure
Trees. CptS 223 Advanced Data Structures. Larry Holder School of Electrical Engineering and Computer Science Washington State University
 Trees CptS 223 Advanced Data Structures Larry Holder School of Electrical Engineering and Computer Science Washington State University 1 Overview Tree data structure Binary search trees Support O(log 2
Trees CptS 223 Advanced Data Structures Larry Holder School of Electrical Engineering and Computer Science Washington State University 1 Overview Tree data structure Binary search trees Support O(log 2
DATA STRUCTURES AND ALGORITHMS. Hierarchical data structures: AVL tree, Bayer tree, Heap
 DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
Trees : Part 1. Section 4.1. Theory and Terminology. A Tree? A Tree? Theory and Terminology. Theory and Terminology
 Trees : Part Section. () (2) Preorder, Postorder and Levelorder Traversals Definition: A tree is a connected graph with no cycles Consequences: Between any two vertices, there is exactly one unique path
Trees : Part Section. () (2) Preorder, Postorder and Levelorder Traversals Definition: A tree is a connected graph with no cycles Consequences: Between any two vertices, there is exactly one unique path
CSE 326: Data Structures B-Trees and B+ Trees
 Announcements (2/4/09) CSE 26: Data Structures B-Trees and B+ Trees Midterm on Friday Special office hour: 4:00-5:00 Thursday in Jaech Gallery (6 th floor of CSE building) This is in addition to my usual
Announcements (2/4/09) CSE 26: Data Structures B-Trees and B+ Trees Midterm on Friday Special office hour: 4:00-5:00 Thursday in Jaech Gallery (6 th floor of CSE building) This is in addition to my usual
Data Structures Lesson 7
 Data Structures Lesson 7 BSc in Computer Science University of New York, Tirana Assoc. Prof. Dr. Marenglen Biba 1-1 Binary Search Trees For large amounts of input, the linear access time of linked lists
Data Structures Lesson 7 BSc in Computer Science University of New York, Tirana Assoc. Prof. Dr. Marenglen Biba 1-1 Binary Search Trees For large amounts of input, the linear access time of linked lists
Sorted Arrays. Operation Access Search Selection Predecessor Successor Output (print) Insert Delete Extract-Min
 Binary Search Trees FRIDAY ALGORITHMS Sorted Arrays Operation Access Search Selection Predecessor Successor Output (print) Insert Delete Extract-Min 6 10 11 17 2 0 6 Running Time O(1) O(lg n) O(1) O(1)
Binary Search Trees FRIDAY ALGORITHMS Sorted Arrays Operation Access Search Selection Predecessor Successor Output (print) Insert Delete Extract-Min 6 10 11 17 2 0 6 Running Time O(1) O(lg n) O(1) O(1)
M-ary Search Tree. B-Trees. Solution: B-Trees. B-Tree: Example. B-Tree Properties. B-Trees (4.7 in Weiss)
 M-ary Search Tree B-Trees (4.7 in Weiss) Maximum branching factor of M Tree with N values has height = # disk accesses for find: Runtime of find: 1/21/2011 1 1/21/2011 2 Solution: B-Trees specialized M-ary
M-ary Search Tree B-Trees (4.7 in Weiss) Maximum branching factor of M Tree with N values has height = # disk accesses for find: Runtime of find: 1/21/2011 1 1/21/2011 2 Solution: B-Trees specialized M-ary
Dynamic Access Binary Search Trees
 Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
CMPE 160: Introduction to Object Oriented Programming
 CMPE 6: Introduction to Object Oriented Programming General Tree Concepts Binary Trees Trees Definitions Representation Binary trees Traversals Expression trees These are the slides of the textbook by
CMPE 6: Introduction to Object Oriented Programming General Tree Concepts Binary Trees Trees Definitions Representation Binary trees Traversals Expression trees These are the slides of the textbook by
Some Search Structures. Balanced Search Trees. Binary Search Trees. A Binary Search Tree. Review Binary Search Trees
 Some Search Structures Balanced Search Trees Lecture 8 CS Fall Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Some Search Structures Balanced Search Trees Lecture 8 CS Fall Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Dynamic Access Binary Search Trees
 Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Trees, Binary Trees, and Binary Search Trees
 COMP171 Trees, Binary Trees, and Binary Search Trees 2 Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search,
COMP171 Trees, Binary Trees, and Binary Search Trees 2 Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search,
10/23/2013. AVL Trees. Height of an AVL Tree. Height of an AVL Tree. AVL Trees
 // AVL Trees AVL Trees An AVL tree is a binary search tree with a balance condition. AVL is named for its inventors: Adel son-vel skii and Landis AVL tree approximates the ideal tree (completely balanced
// AVL Trees AVL Trees An AVL tree is a binary search tree with a balance condition. AVL is named for its inventors: Adel son-vel skii and Landis AVL tree approximates the ideal tree (completely balanced
ECE250: Algorithms and Data Structures AVL Trees (Part A)
 ECE250: Algorithms and Data Structures AVL Trees (Part A) Ladan Tahvildari, PEng, SMIEEE Associate Professor Software Technologies Applied Research (STAR) Group Dept. of Elect. & Comp. Eng. University
ECE250: Algorithms and Data Structures AVL Trees (Part A) Ladan Tahvildari, PEng, SMIEEE Associate Professor Software Technologies Applied Research (STAR) Group Dept. of Elect. & Comp. Eng. University
Advanced Set Representation Methods
 Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
M-ary Search Tree. B-Trees. B-Trees. Solution: B-Trees. B-Tree: Example. B-Tree Properties. Maximum branching factor of M Complete tree has height =
 M-ary Search Tree B-Trees Section 4.7 in Weiss Maximum branching factor of M Complete tree has height = # disk accesses for find: Runtime of find: 2 Solution: B-Trees specialized M-ary search trees Each
M-ary Search Tree B-Trees Section 4.7 in Weiss Maximum branching factor of M Complete tree has height = # disk accesses for find: Runtime of find: 2 Solution: B-Trees specialized M-ary search trees Each
Augmenting Data Structures
 Augmenting Data Structures [Not in G &T Text. In CLRS chapter 14.] An AVL tree by itself is not very useful. To support more useful queries we need more structure. General Definition: An augmented data
Augmenting Data Structures [Not in G &T Text. In CLRS chapter 14.] An AVL tree by itself is not very useful. To support more useful queries we need more structure. General Definition: An augmented data
Algorithms in Systems Engineering ISE 172. Lecture 16. Dr. Ted Ralphs
 Algorithms in Systems Engineering ISE 172 Lecture 16 Dr. Ted Ralphs ISE 172 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms
Algorithms in Systems Engineering ISE 172 Lecture 16 Dr. Ted Ralphs ISE 172 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms
CS60020: Foundations of Algorithm Design and Machine Learning. Sourangshu Bhattacharya
 CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Binary Search Tree - Best Time All BST operations are O(d), where d is tree depth minimum d is d = ëlog for a binary tree
CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Binary Search Tree - Best Time All BST operations are O(d), where d is tree depth minimum d is d = ëlog for a binary tree
CS60020: Foundations of Algorithm Design and Machine Learning. Sourangshu Bhattacharya
 CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when
CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when
Background: disk access vs. main memory access (1/2)
 4.4 B-trees Disk access vs. main memory access: background B-tree concept Node structure Structural properties Insertion operation Deletion operation Running time 66 Background: disk access vs. main memory
4.4 B-trees Disk access vs. main memory access: background B-tree concept Node structure Structural properties Insertion operation Deletion operation Running time 66 Background: disk access vs. main memory
B-Trees. Version of October 2, B-Trees Version of October 2, / 22
 B-Trees Version of October 2, 2014 B-Trees Version of October 2, 2014 1 / 22 Motivation An AVL tree can be an excellent data structure for implementing dictionary search, insertion and deletion Each operation
B-Trees Version of October 2, 2014 B-Trees Version of October 2, 2014 1 / 22 Motivation An AVL tree can be an excellent data structure for implementing dictionary search, insertion and deletion Each operation
Trees, Part 1: Unbalanced Trees
 Trees, Part 1: Unbalanced Trees The first part of this chapter takes a look at trees in general and unbalanced binary trees. The second part looks at various schemes to balance trees and/or make them more
Trees, Part 1: Unbalanced Trees The first part of this chapter takes a look at trees in general and unbalanced binary trees. The second part looks at various schemes to balance trees and/or make them more
Lecture 3: B-Trees. October Lecture 3: B-Trees
 October 2017 Remarks Search trees The dynamic set operations search, minimum, maximum, successor, predecessor, insert and del can be performed efficiently (in O(log n) time) if the search tree is balanced.
October 2017 Remarks Search trees The dynamic set operations search, minimum, maximum, successor, predecessor, insert and del can be performed efficiently (in O(log n) time) if the search tree is balanced.
CS350: Data Structures Red-Black Trees
 Red-Black Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Red-Black Tree An alternative to AVL trees Insertion can be done in a bottom-up or
Red-Black Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Red-Black Tree An alternative to AVL trees Insertion can be done in a bottom-up or
Red-black trees (19.5), B-trees (19.8), trees
 Red-black trees (19.5), B-trees (19.8), 2-3-4 trees Red-black trees A red-black tree is a balanced BST It has a more complicated invariant than an AVL tree: Each node is coloured red or black A red node
Red-black trees (19.5), B-trees (19.8), 2-3-4 trees Red-black trees A red-black tree is a balanced BST It has a more complicated invariant than an AVL tree: Each node is coloured red or black A red node
Balanced Search Trees
 Balanced Search Trees Computer Science E-22 Harvard Extension School David G. Sullivan, Ph.D. Review: Balanced Trees A tree is balanced if, for each node, the node s subtrees have the same height or have
Balanced Search Trees Computer Science E-22 Harvard Extension School David G. Sullivan, Ph.D. Review: Balanced Trees A tree is balanced if, for each node, the node s subtrees have the same height or have
Lec 17 April 8. Topics: binary Trees expression trees. (Chapter 5 of text)
 Lec 17 April 8 Topics: binary Trees expression trees Binary Search Trees (Chapter 5 of text) Trees Linear access time of linked lists is prohibitive Heap can t support search in O(log N) time. (takes O(N)
Lec 17 April 8 Topics: binary Trees expression trees Binary Search Trees (Chapter 5 of text) Trees Linear access time of linked lists is prohibitive Heap can t support search in O(log N) time. (takes O(N)
Advanced Tree Data Structures
 Advanced Tree Data Structures Fawzi Emad Chau-Wen Tseng Department of Computer Science University of Maryland, College Park Binary trees Traversal order Balance Rotation Multi-way trees Search Insert Overview
Advanced Tree Data Structures Fawzi Emad Chau-Wen Tseng Department of Computer Science University of Maryland, College Park Binary trees Traversal order Balance Rotation Multi-way trees Search Insert Overview
Computational Optimization ISE 407. Lecture 16. Dr. Ted Ralphs
 Computational Optimization ISE 407 Lecture 16 Dr. Ted Ralphs ISE 407 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms in
Computational Optimization ISE 407 Lecture 16 Dr. Ted Ralphs ISE 407 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms in
Data Structures Week #6. Special Trees
 Data Structures Week #6 Special Trees Outline Adelson-Velskii-Landis (AVL) Trees Splay Trees B-Trees October 5, 2015 Borahan Tümer, Ph.D. 2 AVL Trees October 5, 2015 Borahan Tümer, Ph.D. 3 Motivation for
Data Structures Week #6 Special Trees Outline Adelson-Velskii-Landis (AVL) Trees Splay Trees B-Trees October 5, 2015 Borahan Tümer, Ph.D. 2 AVL Trees October 5, 2015 Borahan Tümer, Ph.D. 3 Motivation for
Binary Search Trees. Analysis of Algorithms
 Binary Search Trees Analysis of Algorithms Binary Search Trees A BST is a binary tree in symmetric order 31 Each node has a key and every node s key is: 19 23 25 35 38 40 larger than all keys in its left
Binary Search Trees Analysis of Algorithms Binary Search Trees A BST is a binary tree in symmetric order 31 Each node has a key and every node s key is: 19 23 25 35 38 40 larger than all keys in its left
Data Structures and Algorithms
 Data Structures and Algorithms CS245-2008S-19 B-Trees David Galles Department of Computer Science University of San Francisco 19-0: Indexing Operations: Add an element Remove an element Find an element,
Data Structures and Algorithms CS245-2008S-19 B-Trees David Galles Department of Computer Science University of San Francisco 19-0: Indexing Operations: Add an element Remove an element Find an element,
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
Search Trees - 1 Venkatanatha Sarma Y
 Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Binary Trees
 Binary Trees 4-7-2005 Opening Discussion What did we talk about last class? Do you have any code to show? Do you have any questions about the assignment? What is a Tree? You are all familiar with what
Binary Trees 4-7-2005 Opening Discussion What did we talk about last class? Do you have any code to show? Do you have any questions about the assignment? What is a Tree? You are all familiar with what
Laboratory Module X B TREES
 Purpose: Purpose 1... Purpose 2 Purpose 3. Laboratory Module X B TREES 1. Preparation Before Lab When working with large sets of data, it is often not possible or desirable to maintain the entire structure
Purpose: Purpose 1... Purpose 2 Purpose 3. Laboratory Module X B TREES 1. Preparation Before Lab When working with large sets of data, it is often not possible or desirable to maintain the entire structure
Data Structures and Algorithms
 Data Structures and Algorithms Spring 2009-2010 Outline BST Trees (contd.) 1 BST Trees (contd.) Outline BST Trees (contd.) 1 BST Trees (contd.) The bad news about BSTs... Problem with BSTs is that there
Data Structures and Algorithms Spring 2009-2010 Outline BST Trees (contd.) 1 BST Trees (contd.) Outline BST Trees (contd.) 1 BST Trees (contd.) The bad news about BSTs... Problem with BSTs is that there
AVL Trees (10.2) AVL Trees
 AVL Trees (0.) CSE 0 Winter 0 8 February 0 AVL Trees AVL trees are balanced. An AVL Tree is a binary search tree such that for every internal node v of T, the heights of the children of v can differ by
AVL Trees (0.) CSE 0 Winter 0 8 February 0 AVL Trees AVL trees are balanced. An AVL Tree is a binary search tree such that for every internal node v of T, the heights of the children of v can differ by
Inf 2B: AVL Trees. Lecture 5 of ADS thread. Kyriakos Kalorkoti. School of Informatics University of Edinburgh
 Inf 2B: AVL Trees Lecture 5 of ADS thread Kyriakos Kalorkoti School of Informatics University of Edinburgh Dictionaries A Dictionary stores key element pairs, called items. Several elements might have
Inf 2B: AVL Trees Lecture 5 of ADS thread Kyriakos Kalorkoti School of Informatics University of Edinburgh Dictionaries A Dictionary stores key element pairs, called items. Several elements might have
CSI33 Data Structures
 Outline Department of Mathematics and Computer Science Bronx Community College November 21, 2018 Outline Outline 1 C++ Supplement 1.3: Balanced Binary Search Trees Balanced Binary Search Trees Outline
Outline Department of Mathematics and Computer Science Bronx Community College November 21, 2018 Outline Outline 1 C++ Supplement 1.3: Balanced Binary Search Trees Balanced Binary Search Trees Outline
AVL Trees. (AVL Trees) Data Structures and Programming Spring / 17
 AVL Trees (AVL Trees) Data Structures and Programming Spring 2017 1 / 17 Balanced Binary Tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time
AVL Trees (AVL Trees) Data Structures and Programming Spring 2017 1 / 17 Balanced Binary Tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time
THE B+ TREE INDEX. CS 564- Spring ACKs: Jignesh Patel, AnHai Doan
 THE B+ TREE INDEX CS 564- Spring 2018 ACKs: Jignesh Patel, AnHai Doan WHAT IS THIS LECTURE ABOUT? The B+ tree index Basics Search/Insertion/Deletion Design & Cost 2 INDEX RECAP We have the following query:
THE B+ TREE INDEX CS 564- Spring 2018 ACKs: Jignesh Patel, AnHai Doan WHAT IS THIS LECTURE ABOUT? The B+ tree index Basics Search/Insertion/Deletion Design & Cost 2 INDEX RECAP We have the following query:
CS 261 Data Structures. AVL Trees
 CS 261 Data Structures AVL Trees 1 Binary Search Tree Complexity of BST operations: proportional to the length of the path from a node to the root Unbalanced tree: operations may be O(n) E.g.: adding elements
CS 261 Data Structures AVL Trees 1 Binary Search Tree Complexity of BST operations: proportional to the length of the path from a node to the root Unbalanced tree: operations may be O(n) E.g.: adding elements
Module 4: Dictionaries and Balanced Search Trees
 Module 4: Dictionaries and Balanced Search Trees CS 24 - Data Structures and Data Management Jason Hinek and Arne Storjohann Based on lecture notes by R. Dorrigiv and D. Roche David R. Cheriton School
Module 4: Dictionaries and Balanced Search Trees CS 24 - Data Structures and Data Management Jason Hinek and Arne Storjohann Based on lecture notes by R. Dorrigiv and D. Roche David R. Cheriton School
CSE332: Data Abstractions Lecture 7: B Trees. James Fogarty Winter 2012
 CSE2: Data Abstractions Lecture 7: B Trees James Fogarty Winter 20 The Dictionary (a.k.a. Map) ADT Data: Set of (key, value) pairs keys must be comparable insert(jfogarty,.) Operations: insert(key,value)
CSE2: Data Abstractions Lecture 7: B Trees James Fogarty Winter 20 The Dictionary (a.k.a. Map) ADT Data: Set of (key, value) pairs keys must be comparable insert(jfogarty,.) Operations: insert(key,value)
Multi-way Search Trees! M-Way Search! M-Way Search Trees Representation!
 Lecture 10: Multi-way Search Trees: intro to B-trees 2-3 trees 2-3-4 trees Multi-way Search Trees A node on an M-way search tree with M 1 distinct and ordered keys: k 1 < k 2 < k 3
Lecture 10: Multi-way Search Trees: intro to B-trees 2-3 trees 2-3-4 trees Multi-way Search Trees A node on an M-way search tree with M 1 distinct and ordered keys: k 1 < k 2 < k 3
Data Structures Week #6. Special Trees
 Data Structures Week #6 Special Trees Outline Adelson-Velskii-Landis (AVL) Trees Splay Trees B-Trees 21.Aralık.2010 Borahan Tümer, Ph.D. 2 AVL Trees 21.Aralık.2010 Borahan Tümer, Ph.D. 3 Motivation for
Data Structures Week #6 Special Trees Outline Adelson-Velskii-Landis (AVL) Trees Splay Trees B-Trees 21.Aralık.2010 Borahan Tümer, Ph.D. 2 AVL Trees 21.Aralık.2010 Borahan Tümer, Ph.D. 3 Motivation for
Quiz 1 Solutions. (a) f(n) = n g(n) = log n Circle all that apply: f = O(g) f = Θ(g) f = Ω(g)
 Introduction to Algorithms March 11, 2009 Massachusetts Institute of Technology 6.006 Spring 2009 Professors Sivan Toledo and Alan Edelman Quiz 1 Solutions Problem 1. Quiz 1 Solutions Asymptotic orders
Introduction to Algorithms March 11, 2009 Massachusetts Institute of Technology 6.006 Spring 2009 Professors Sivan Toledo and Alan Edelman Quiz 1 Solutions Problem 1. Quiz 1 Solutions Asymptotic orders
Course Review for. Cpt S 223 Fall Cpt S 223. School of EECS, WSU
 Course Review for Midterm Exam 1 Cpt S 223 Fall 2011 1 Midterm Exam 1 When: Friday (10/14) 1:10-2pm Where: in class Closed book, closed notes Comprehensive Material for preparation: Lecture slides & in-class
Course Review for Midterm Exam 1 Cpt S 223 Fall 2011 1 Midterm Exam 1 When: Friday (10/14) 1:10-2pm Where: in class Closed book, closed notes Comprehensive Material for preparation: Lecture slides & in-class
Data Structure - Advanced Topics in Tree -
 Data Structure - Advanced Topics in Tree - AVL, Red-Black, B-tree Hanyang University Jong-Il Park AVL TREE Division of Computer Science and Engineering, Hanyang University Balanced binary trees Non-random
Data Structure - Advanced Topics in Tree - AVL, Red-Black, B-tree Hanyang University Jong-Il Park AVL TREE Division of Computer Science and Engineering, Hanyang University Balanced binary trees Non-random
Algorithms. Deleting from Red-Black Trees B-Trees
 Algorithms Deleting from Red-Black Trees B-Trees Recall the rules for BST deletion 1. If vertex to be deleted is a leaf, just delete it. 2. If vertex to be deleted has just one child, replace it with that
Algorithms Deleting from Red-Black Trees B-Trees Recall the rules for BST deletion 1. If vertex to be deleted is a leaf, just delete it. 2. If vertex to be deleted has just one child, replace it with that
More Binary Search Trees AVL Trees. CS300 Data Structures (Fall 2013)
 More Binary Search Trees AVL Trees bstdelete if (key not found) return else if (either subtree is empty) { delete the node replacing the parents link with the ptr to the nonempty subtree or NULL if both
More Binary Search Trees AVL Trees bstdelete if (key not found) return else if (either subtree is empty) { delete the node replacing the parents link with the ptr to the nonempty subtree or NULL if both
CSE 373 OCTOBER 25 TH B-TREES
 CSE 373 OCTOBER 25 TH S ASSORTED MINUTIAE Project 2 is due tonight Make canvas group submissions Load factor: total number of elements / current table size Can select any load factor (but since we don
CSE 373 OCTOBER 25 TH S ASSORTED MINUTIAE Project 2 is due tonight Make canvas group submissions Load factor: total number of elements / current table size Can select any load factor (but since we don
CS 206 Introduction to Computer Science II
 CS 206 Introduction to Computer Science II 04 / 26 / 2017 Instructor: Michael Eckmann Today s Topics Questions? Comments? Balanced Binary Search trees AVL trees Michael Eckmann - Skidmore College - CS
CS 206 Introduction to Computer Science II 04 / 26 / 2017 Instructor: Michael Eckmann Today s Topics Questions? Comments? Balanced Binary Search trees AVL trees Michael Eckmann - Skidmore College - CS
Trees (Part 1, Theoretical) CSE 2320 Algorithms and Data Structures University of Texas at Arlington
 Trees (Part 1, Theoretical) CSE 2320 Algorithms and Data Structures University of Texas at Arlington 1 Trees Trees are a natural data structure for representing specific data. Family trees. Organizational
Trees (Part 1, Theoretical) CSE 2320 Algorithms and Data Structures University of Texas at Arlington 1 Trees Trees are a natural data structure for representing specific data. Family trees. Organizational
More BSTs & AVL Trees bstdelete
 More BSTs & AVL Trees bstdelete if (key not found) return else if (either subtree is empty) { delete the node replacing the parents link with the ptr to the nonempty subtree or NULL if both subtrees are
More BSTs & AVL Trees bstdelete if (key not found) return else if (either subtree is empty) { delete the node replacing the parents link with the ptr to the nonempty subtree or NULL if both subtrees are
Intro to DB CHAPTER 12 INDEXING & HASHING
 Intro to DB CHAPTER 12 INDEXING & HASHING Chapter 12: Indexing and Hashing Basic Concepts Ordered Indices B+-Tree Index Files B-Tree Index Files Static Hashing Dynamic Hashing Comparison of Ordered Indexing
Intro to DB CHAPTER 12 INDEXING & HASHING Chapter 12: Indexing and Hashing Basic Concepts Ordered Indices B+-Tree Index Files B-Tree Index Files Static Hashing Dynamic Hashing Comparison of Ordered Indexing
Extra: B+ Trees. Motivations. Differences between BST and B+ 10/27/2017. CS1: Java Programming Colorado State University
 Extra: B+ Trees CS1: Java Programming Colorado State University Slides by Wim Bohm and Russ Wakefield 1 Motivations Many times you want to minimize the disk accesses while doing a search. A binary search
Extra: B+ Trees CS1: Java Programming Colorado State University Slides by Wim Bohm and Russ Wakefield 1 Motivations Many times you want to minimize the disk accesses while doing a search. A binary search
CE 221 Data Structures and Algorithms
 CE 221 Data Structures and Algorithms Chapter 4: Trees (Binary) Text: Read Weiss, 4.1 4.2 Izmir University of Economics 1 Preliminaries - I (Recursive) Definition: A tree is a collection of nodes. The
CE 221 Data Structures and Algorithms Chapter 4: Trees (Binary) Text: Read Weiss, 4.1 4.2 Izmir University of Economics 1 Preliminaries - I (Recursive) Definition: A tree is a collection of nodes. The
Section 4 SOLUTION: AVL Trees & B-Trees
 Section 4 SOLUTION: AVL Trees & B-Trees 1. What 3 properties must an AVL tree have? a. Be a binary tree b. Have Binary Search Tree ordering property (left children < parent, right children > parent) c.
Section 4 SOLUTION: AVL Trees & B-Trees 1. What 3 properties must an AVL tree have? a. Be a binary tree b. Have Binary Search Tree ordering property (left children < parent, right children > parent) c.
Ch04 Balanced Search Trees
 Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
B-Trees and External Memory
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 and External Memory 1 1 (2, 4) Trees: Generalization of BSTs Each internal node
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 and External Memory 1 1 (2, 4) Trees: Generalization of BSTs Each internal node
Motivation for B-Trees
 1 Motivation for Assume that we use an AVL tree to store about 20 million records We end up with a very deep binary tree with lots of different disk accesses; log2 20,000,000 is about 24, so this takes
1 Motivation for Assume that we use an AVL tree to store about 20 million records We end up with a very deep binary tree with lots of different disk accesses; log2 20,000,000 is about 24, so this takes
AVL trees and rotations
 AVL trees and rotations Part of written assignment 5 Examine the Code of Ethics of the ACM Focus on property rights Write a short reaction (up to 1 page single-spaced) Details are in the assignment Operations
AVL trees and rotations Part of written assignment 5 Examine the Code of Ethics of the ACM Focus on property rights Write a short reaction (up to 1 page single-spaced) Details are in the assignment Operations
Binary search trees (chapters )
 Binary search trees (chapters 18.1 18.3) Binary search trees In a binary search tree (BST), every node is greater than all its left descendants, and less than all its right descendants (recall that this
Binary search trees (chapters 18.1 18.3) Binary search trees In a binary search tree (BST), every node is greater than all its left descendants, and less than all its right descendants (recall that this
B-Trees and External Memory
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 B-Trees and External Memory 1 (2, 4) Trees: Generalization of BSTs Each internal
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 B-Trees and External Memory 1 (2, 4) Trees: Generalization of BSTs Each internal
Self-Balancing Search Trees. Chapter 11
 Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
UNIT III BALANCED SEARCH TREES AND INDEXING
 UNIT III BALANCED SEARCH TREES AND INDEXING OBJECTIVE The implementation of hash tables is frequently called hashing. Hashing is a technique used for performing insertions, deletions and finds in constant
UNIT III BALANCED SEARCH TREES AND INDEXING OBJECTIVE The implementation of hash tables is frequently called hashing. Hashing is a technique used for performing insertions, deletions and finds in constant
Lecture 13: AVL Trees and Binary Heaps
 Data Structures Brett Bernstein Lecture 13: AVL Trees and Binary Heaps Review Exercises 1. ( ) Interview question: Given an array show how to shue it randomly so that any possible reordering is equally
Data Structures Brett Bernstein Lecture 13: AVL Trees and Binary Heaps Review Exercises 1. ( ) Interview question: Given an array show how to shue it randomly so that any possible reordering is equally
