This matrix is not TU since the submatrix shown below has determinant of
|
|
|
- Alicia Robinson
- 5 years ago
- Views:
Transcription
1 EMIS 8373: Integer Programming [Homework 5 Solutions] 1 Problem 1 Problem 1 on page 50 of the Wolsey text book. (a) A 1 = This matrix is not TU since the submatrix shown below has determinant of 2. A 1 =
2 EMIS 8373: Integer Programming [Homework 5 Solutions] 2 (b) A 2 = Partition the rows such that M 1 = {1, 2} and M 2 = {3, 4, 5}. A 2 =
3 EMIS 8373: Integer Programming [Homework 5 Solutions] 3 For column 1, 2 i=1 a i1 5 i=3 a i1 = 1 ( 1) = 0. For column j {2, 3, 4, 7}, 2 i=1 a ij 5 i=3 a ij = 1 1 = 0. For column j {5, 6}, 2 i=1 a ij 5 i=3 a ij = 0 0 = 0. Thus, A 2 is TU by Proposition 3.2
4 EMIS 8373: Integer Programming [Homework 5 Solutions] 4 Is this matrix TU?
5 EMIS 8373: Integer Programming [Homework 5 Solutions] 5 Problem 2 (i) For each pair of employees (i, j) let c ij be a compatibility score for putting employees i and j in the same room. If we let x ij = 1 if and only if employees i and j are assigned to the same room. A valid IP formulation for the general case where there are n employees is max s.t. n 1 i=1 n j=i+1 c ij x ij x ji + x ij = 1 j<i j>i x ij {0, 1}. i = 1, 2,..., n Notice the constraint matrix for this IP is a 0-1 matrix such that each column has exactly two non-zero elements. This matrix appears to be TU. It turns out, however, that it is not in all cases.
6 EMIS 8373: Integer Programming [Homework 5 Solutions] 6 For example, suppose that the compatibility score is either 0 or 1 and that employees 1, 2, and 3, are compatible with each other. In this case the formulation would contain the constraints listed below. x 12 + x = 1 (Employee 1) x 12 + x = 1 (Employee 2) x 13 + x = 1 (Employee 3) Since the constraints above are part of the formulation, the constraint matrix would contain the submatrix shown below which has a determinant of Thus, the matrix is not TU
7 EMIS 8373: Integer Programming [Homework 5 Solutions] 7 This problem can also be formulated as matching problem. Let G = (V, E) be a graph with one node for each employee and edge (i, j) in E if employees i and j are compatible. A rooming assignment is possible if and only the maximum cardinality matching in G has size V 2. Recall from our discussion of the solutions to Homework 4 that the matching problem in a non-bipartite graph cannot be solved as an LP.
8 EMIS 8373: Integer Programming [Homework 5 Solutions] 8 (ii) This can be formulated as a minimum-cost network flow problem. Specifically, it is an assignment problem. Nodes: The network has nodes E1, E2,... En for the English children, each with a supply of 1, and nodes F 1, F 2,... F n for the French children each with a demand of 1. Arcs: For each potential pair (i, j) there is a unit-capacity arc (Ei, F j) with cost w ij where w ij is the willingness of that pair to form a team. Since this is a network flow problem, the constraint matrix is TU which means that we can solve it as a linear program and the optimal values of the flow variables will all be in {0, 1}. If there is flow on arc (i, j), that indicates English child i is teamed with French child j.
9 EMIS 8373: Integer Programming [Homework 5 Solutions] 9 Problem 3 (a) This is a minimum spanning tree (MST) problem which can be solved with Kruskal s algorithm. The minimum length of a spanning three in the given graph is 93. The edges of a MST are shown below. (1,2) (3,4) (3,6) (6,10) (7,11) (9,12) (1,4) (3,5) (5,8) (7,8) (8,9) (12,13)
10 EMIS 8373: Integer Programming [Homework 5 Solutions] 10 (b) We can use the following integer programming model to solve this problem. # AMPL model for the minimum cost tree problem. set V; # nodes in the network set E within {V,V}; # undirected edges in the network param c {E} default 0; # cost of edge (i,j) param b {V} default 0; # supply/demand for node i # Let U be the subset of nodes that are to be # connected by the tree. # Pick a root node r in U and let b[r] = card(u) - 1; # Let b[i] = -1 for every node in U\{r} and # let b[i] = 0 for every node in V\U.
11 EMIS 8373: Integer Programming [Homework 5 Solutions] 11 param M := sum{i in V: b[i] > 0} b[i]; # Maximum amount of flow that would be on any arc. var y {E} binary; # y[i,j] = 1 if edge (i,j) is in the tree var x {i in V, j in V: (i,j) in E or (j,i) in E} >= 0; # x[i,j] represents the "flow" on edge (i,j) minimize cost: sum{(i,j) in E} c[i,j] * y[i,j]; subject to flow_balance {i in V}: sum{j in V: (i,j) in E or (j,i) in E} x[i,j] - sum{j in V: (i,j) in E or (j,i) in E} x[j,i] = b[i]; subject to fixed_cost {(i,j) in E}: M * y[i,j] >= (x[i,j] + x[j,i]);
12 EMIS 8373: Integer Programming [Homework 5 Solutions] 12 This model is essentially a MCNFP model, but with a fixed (rather than variable) cost for putting flow on an arc. The following script uses the model to solve the MST problem from part (a) and then the suggested problems from part (b). # prob3_run.txt model tree_model.txt; data smu_data.txt; # set the supply/demand parameters for the MST problem let {i in V} b[i] := -1; let b[1] := (card(v) -1); solve; display {(i,j) in E: (x[i,j] + x[j,i]) > 0};
13 EMIS 8373: Integer Programming [Homework 5 Solutions] 13 # set the supply/demand parameters for the MST problem # where we only need to connect the odd-numbered nodes set U; let U := {1, 3, 5, 7, 9, 11, 13}; let b[1] := (card(u) -1); let {i in U diff {1}} b[i] := -1; let {i in V diff U} b[i] := 0; solve; display {(i,j) in E: (x[i,j] + x[j,i]) > 0}; # set the supply/demand parameters for the MST problem # where we only need to connect the prime-numbered nodes let U := {1, 2, 3, 5, 7, 11, 13}; let b[1] := (card(u) -1); let {i in U diff {1}} b[i] := -1; let {i in V diff U} b[i] := 0; solve; display {(i,j) in E: (x[i,j] + x[j,i]) > 0};
14 EMIS 8373: Integer Programming [Homework 5 Solutions] 14 % ampl < prob3_run.txt ILOG AMPL 8.000, licensed to "southern methodist-dallas, tx". AMPL Version (OSF1 V4.0) CPLEX 8.0.0: optimal integer solution; objective MIP simplex iterations 358 branch-and-bound nodes set {(i,j) in E: x[i,j] + x[j,i] > 0} := (1,2) (3,4) (3,6) (6,10) (7,11) (9,12) (1,4) (3,5) (5,8) (7,8) (8,9) (12,13); CPLEX 8.0.0: optimal integer solution; objective MIP simplex iterations 23 branch-and-bound nodes set {(i,j) in E: x[i,j] + x[j,i] > 0} := (1,4) (3,4) (3,5) (5,8) (7,8) (7,11) (8,9) (
15 EMIS 8373: Integer Programming [Homework 5 Solutions] 15 CPLEX 8.0.0: optimal integer solution; objective MIP simplex iterations 12 branch-and-bound nodes set {(i,j) in E: x[i,j] + x[j,i] > 0} := (1,2) (2,3) (3,5) (5,8) (7,8) (7,11) (8,13);
Final Exam Spring 2003
 .8 Final Exam Spring Name Instructions.. Please answer all questions in the exam books that are provided.. Please budget your time carefully. It is often a good idea to read the entire exam first, so that
.8 Final Exam Spring Name Instructions.. Please answer all questions in the exam books that are provided.. Please budget your time carefully. It is often a good idea to read the entire exam first, so that
Methods and Models for Combinatorial Optimization Exact methods for the Traveling Salesman Problem
 Methods and Models for Combinatorial Optimization Exact methods for the Traveling Salesman Problem L. De Giovanni M. Di Summa The Traveling Salesman Problem (TSP) is an optimization problem on a directed
Methods and Models for Combinatorial Optimization Exact methods for the Traveling Salesman Problem L. De Giovanni M. Di Summa The Traveling Salesman Problem (TSP) is an optimization problem on a directed
Mathematical Tools for Engineering and Management
 Mathematical Tools for Engineering and Management Lecture 8 8 Dec 0 Overview Models, Data and Algorithms Linear Optimization Mathematical Background: Polyhedra, Simplex-Algorithm Sensitivity Analysis;
Mathematical Tools for Engineering and Management Lecture 8 8 Dec 0 Overview Models, Data and Algorithms Linear Optimization Mathematical Background: Polyhedra, Simplex-Algorithm Sensitivity Analysis;
Solving problems on graph algorithms
 Solving problems on graph algorithms Workshop Organized by: ACM Unit, Indian Statistical Institute, Kolkata. Tutorial-3 Date: 06.07.2017 Let G = (V, E) be an undirected graph. For a vertex v V, G {v} is
Solving problems on graph algorithms Workshop Organized by: ACM Unit, Indian Statistical Institute, Kolkata. Tutorial-3 Date: 06.07.2017 Let G = (V, E) be an undirected graph. For a vertex v V, G {v} is
6.854J / J Advanced Algorithms Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 6.854J / 18.415J Advanced Algorithms Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advanced
MIT OpenCourseWare http://ocw.mit.edu 6.854J / 18.415J Advanced Algorithms Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advanced
Graphs and Network Flows IE411. Lecture 21. Dr. Ted Ralphs
 Graphs and Network Flows IE411 Lecture 21 Dr. Ted Ralphs IE411 Lecture 21 1 Combinatorial Optimization and Network Flows In general, most combinatorial optimization and integer programming problems are
Graphs and Network Flows IE411 Lecture 21 Dr. Ted Ralphs IE411 Lecture 21 1 Combinatorial Optimization and Network Flows In general, most combinatorial optimization and integer programming problems are
Graphs and Network Flows IE411. Lecture 20. Dr. Ted Ralphs
 Graphs and Network Flows IE411 Lecture 20 Dr. Ted Ralphs IE411 Lecture 20 1 Network Simplex Algorithm Input: A network G = (N, A), a vector of capacities u Z A, a vector of costs c Z A, and a vector of
Graphs and Network Flows IE411 Lecture 20 Dr. Ted Ralphs IE411 Lecture 20 1 Network Simplex Algorithm Input: A network G = (N, A), a vector of capacities u Z A, a vector of costs c Z A, and a vector of
Introduction to Mathematical Programming IE406. Lecture 20. Dr. Ted Ralphs
 Introduction to Mathematical Programming IE406 Lecture 20 Dr. Ted Ralphs IE406 Lecture 20 1 Reading for This Lecture Bertsimas Sections 10.1, 11.4 IE406 Lecture 20 2 Integer Linear Programming An integer
Introduction to Mathematical Programming IE406 Lecture 20 Dr. Ted Ralphs IE406 Lecture 20 1 Reading for This Lecture Bertsimas Sections 10.1, 11.4 IE406 Lecture 20 2 Integer Linear Programming An integer
Fundamentals of Integer Programming
 Fundamentals of Integer Programming Di Yuan Department of Information Technology, Uppsala University January 2018 Outline Definition of integer programming Formulating some classical problems with integer
Fundamentals of Integer Programming Di Yuan Department of Information Technology, Uppsala University January 2018 Outline Definition of integer programming Formulating some classical problems with integer
Assignment 5: Solutions
 Algorithm Design Techniques Assignment 5: Solutions () Port Authority. [This problem is more commonly called the Bin Packing Problem.] (a) Suppose K = 3 and (w, w, w 3, w 4 ) = (,,, ). The optimal solution
Algorithm Design Techniques Assignment 5: Solutions () Port Authority. [This problem is more commonly called the Bin Packing Problem.] (a) Suppose K = 3 and (w, w, w 3, w 4 ) = (,,, ). The optimal solution
Module 10. Network Simplex Method:
 Module 10 1 Network Simplex Method: In this lecture we shall study a specialized simplex method specifically designed to solve network structured linear programming problems. This specialized algorithm
Module 10 1 Network Simplex Method: In this lecture we shall study a specialized simplex method specifically designed to solve network structured linear programming problems. This specialized algorithm
Graphs and Network Flows IE411. Lecture 13. Dr. Ted Ralphs
 Graphs and Network Flows IE411 Lecture 13 Dr. Ted Ralphs IE411 Lecture 13 1 References for Today s Lecture IE411 Lecture 13 2 References for Today s Lecture Required reading Sections 21.1 21.2 References
Graphs and Network Flows IE411 Lecture 13 Dr. Ted Ralphs IE411 Lecture 13 1 References for Today s Lecture IE411 Lecture 13 2 References for Today s Lecture Required reading Sections 21.1 21.2 References
15.082J and 6.855J. Lagrangian Relaxation 2 Algorithms Application to LPs
 15.082J and 6.855J Lagrangian Relaxation 2 Algorithms Application to LPs 1 The Constrained Shortest Path Problem (1,10) 2 (1,1) 4 (2,3) (1,7) 1 (10,3) (1,2) (10,1) (5,7) 3 (12,3) 5 (2,2) 6 Find the shortest
15.082J and 6.855J Lagrangian Relaxation 2 Algorithms Application to LPs 1 The Constrained Shortest Path Problem (1,10) 2 (1,1) 4 (2,3) (1,7) 1 (10,3) (1,2) (10,1) (5,7) 3 (12,3) 5 (2,2) 6 Find the shortest
Discrete Optimization and Network Flows (laboratory 15 h)
 Business Information Systems Adam Kasperski Discrete Optimization and Network Flows (laboratory 15 h) Project co-financed by the European Union within the European Social Fund A mixed integer linear programming
Business Information Systems Adam Kasperski Discrete Optimization and Network Flows (laboratory 15 h) Project co-financed by the European Union within the European Social Fund A mixed integer linear programming
Lecture 3: Totally Unimodularity and Network Flows
 Lecture 3: Totally Unimodularity and Network Flows (3 units) Outline Properties of Easy Problems Totally Unimodular Matrix Minimum Cost Network Flows Dijkstra Algorithm for Shortest Path Problem Ford-Fulkerson
Lecture 3: Totally Unimodularity and Network Flows (3 units) Outline Properties of Easy Problems Totally Unimodular Matrix Minimum Cost Network Flows Dijkstra Algorithm for Shortest Path Problem Ford-Fulkerson
Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn
 Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn Graphs Extremely important concept in computer science Graph, : node (or vertex) set : edge set Simple graph: no self loops, no multiple
Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn Graphs Extremely important concept in computer science Graph, : node (or vertex) set : edge set Simple graph: no self loops, no multiple
Graph Algorithms (part 3 of CSC 282),
 Graph Algorithms (part of CSC 8), http://www.cs.rochester.edu/~stefanko/teaching/10cs8 1 Schedule Homework is due Thursday, Oct 1. The QUIZ will be on Tuesday, Oct. 6. List of algorithms covered in the
Graph Algorithms (part of CSC 8), http://www.cs.rochester.edu/~stefanko/teaching/10cs8 1 Schedule Homework is due Thursday, Oct 1. The QUIZ will be on Tuesday, Oct. 6. List of algorithms covered in the
Lecture 10,11: General Matching Polytope, Maximum Flow. 1 Perfect Matching and Matching Polytope on General Graphs
 CMPUT 675: Topics in Algorithms and Combinatorial Optimization (Fall 2009) Lecture 10,11: General Matching Polytope, Maximum Flow Lecturer: Mohammad R Salavatipour Date: Oct 6 and 8, 2009 Scriber: Mohammad
CMPUT 675: Topics in Algorithms and Combinatorial Optimization (Fall 2009) Lecture 10,11: General Matching Polytope, Maximum Flow Lecturer: Mohammad R Salavatipour Date: Oct 6 and 8, 2009 Scriber: Mohammad
DS UNIT 4. Matoshri College of Engineering and Research Center Nasik Department of Computer Engineering Discrete Structutre UNIT - IV
 Sr.No. Question Option A Option B Option C Option D 1 2 3 4 5 6 Class : S.E.Comp Which one of the following is the example of non linear data structure Let A be an adjacency matrix of a graph G. The ij
Sr.No. Question Option A Option B Option C Option D 1 2 3 4 5 6 Class : S.E.Comp Which one of the following is the example of non linear data structure Let A be an adjacency matrix of a graph G. The ij
Discrete Optimization 2010 Lecture 5 Min-Cost Flows & Total Unimodularity
 Discrete Optimization 2010 Lecture 5 Min-Cost Flows & Total Unimodularity Marc Uetz University of Twente m.uetz@utwente.nl Lecture 5: sheet 1 / 26 Marc Uetz Discrete Optimization Outline 1 Min-Cost Flows
Discrete Optimization 2010 Lecture 5 Min-Cost Flows & Total Unimodularity Marc Uetz University of Twente m.uetz@utwente.nl Lecture 5: sheet 1 / 26 Marc Uetz Discrete Optimization Outline 1 Min-Cost Flows
implementing the breadth-first search algorithm implementing the depth-first search algorithm
 Graph Traversals 1 Graph Traversals representing graphs adjacency matrices and adjacency lists 2 Implementing the Breadth-First and Depth-First Search Algorithms implementing the breadth-first search algorithm
Graph Traversals 1 Graph Traversals representing graphs adjacency matrices and adjacency lists 2 Implementing the Breadth-First and Depth-First Search Algorithms implementing the breadth-first search algorithm
Minimum Weight Constrained Forest Problems. Problem Definition
 Slide 1 s Xiaoyun Ji, John E. Mitchell Department of Mathematical Sciences Rensselaer Polytechnic Institute Troy, NY, USA jix@rpi.edu, mitchj@rpi.edu 2005 Optimization Days Montreal, Canada May 09, 2005
Slide 1 s Xiaoyun Ji, John E. Mitchell Department of Mathematical Sciences Rensselaer Polytechnic Institute Troy, NY, USA jix@rpi.edu, mitchj@rpi.edu 2005 Optimization Days Montreal, Canada May 09, 2005
Advanced Operations Research Techniques IE316. Lecture 10. Dr. Ted Ralphs
 Advanced Operations Research Techniques IE316 Lecture 10 Dr. Ted Ralphs IE316 Lecture 10 1 Reading for This Lecture AMPL Book: Chapter 1 AMPL: A Mathematical Programming Language IE316 Lecture 10 2 Software
Advanced Operations Research Techniques IE316 Lecture 10 Dr. Ted Ralphs IE316 Lecture 10 1 Reading for This Lecture AMPL Book: Chapter 1 AMPL: A Mathematical Programming Language IE316 Lecture 10 2 Software
University of Toronto Department of Mathematics
 University of Toronto Department of Mathematics MAT332H1F, Graph Theory Midterm, October 21, 2014 Instructor: Kasra Rafi First Last Student Number Instructions: No aids allowed. Write solutions on the
University of Toronto Department of Mathematics MAT332H1F, Graph Theory Midterm, October 21, 2014 Instructor: Kasra Rafi First Last Student Number Instructions: No aids allowed. Write solutions on the
Minimum Spanning Trees
 Minimum Spanning Trees Overview Problem A town has a set of houses and a set of roads. A road connects and only houses. A road connecting houses u and v has a repair cost w(u, v). Goal: Repair enough (and
Minimum Spanning Trees Overview Problem A town has a set of houses and a set of roads. A road connects and only houses. A road connecting houses u and v has a repair cost w(u, v). Goal: Repair enough (and
Graphs and Network Flows ISE 411. Lecture 7. Dr. Ted Ralphs
 Graphs and Network Flows ISE 411 Lecture 7 Dr. Ted Ralphs ISE 411 Lecture 7 1 References for Today s Lecture Required reading Chapter 20 References AMO Chapter 13 CLRS Chapter 23 ISE 411 Lecture 7 2 Minimum
Graphs and Network Flows ISE 411 Lecture 7 Dr. Ted Ralphs ISE 411 Lecture 7 1 References for Today s Lecture Required reading Chapter 20 References AMO Chapter 13 CLRS Chapter 23 ISE 411 Lecture 7 2 Minimum
CS 441 Discrete Mathematics for CS Lecture 26. Graphs. CS 441 Discrete mathematics for CS. Final exam
 CS 441 Discrete Mathematics for CS Lecture 26 Graphs Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Final exam Saturday, April 26, 2014 at 10:00-11:50am The same classroom as lectures The exam
CS 441 Discrete Mathematics for CS Lecture 26 Graphs Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Final exam Saturday, April 26, 2014 at 10:00-11:50am The same classroom as lectures The exam
Undirected Graphs. Hwansoo Han
 Undirected Graphs Hwansoo Han Definitions Undirected graph (simply graph) G = (V, E) V : set of vertexes (vertices, nodes, points) E : set of edges (lines) An edge is an unordered pair Edge (v, w) = (w,
Undirected Graphs Hwansoo Han Definitions Undirected graph (simply graph) G = (V, E) V : set of vertexes (vertices, nodes, points) E : set of edges (lines) An edge is an unordered pair Edge (v, w) = (w,
Introduction to Mathematical Programming IE406. Lecture 9. Dr. Ted Ralphs
 Introduction to Mathematical Programming IE406 Lecture 9 Dr. Ted Ralphs IE406 Lecture 9 1 Reading for This Lecture AMPL Book: Chapter 1 AMPL: A Mathematical Programming Language GMPL User s Guide ZIMPL
Introduction to Mathematical Programming IE406 Lecture 9 Dr. Ted Ralphs IE406 Lecture 9 1 Reading for This Lecture AMPL Book: Chapter 1 AMPL: A Mathematical Programming Language GMPL User s Guide ZIMPL
Graphs and Network Flows IE411 Lecture 20
 Graphs and Network Flows IE411 Lecture 20 Dr. Ted Ralphs IE411 Lecture 20 1 Network Simplex Algorithm Input: A network G = (N, A), a vector of capacities u Z A, a vector of costs c Z A, and a vector of
Graphs and Network Flows IE411 Lecture 20 Dr. Ted Ralphs IE411 Lecture 20 1 Network Simplex Algorithm Input: A network G = (N, A), a vector of capacities u Z A, a vector of costs c Z A, and a vector of
Tuesday, April 10. The Network Simplex Method for Solving the Minimum Cost Flow Problem
 . Tuesday, April The Network Simplex Method for Solving the Minimum Cost Flow Problem Quotes of the day I think that I shall never see A poem lovely as a tree. -- Joyce Kilmer Knowing trees, I understand
. Tuesday, April The Network Simplex Method for Solving the Minimum Cost Flow Problem Quotes of the day I think that I shall never see A poem lovely as a tree. -- Joyce Kilmer Knowing trees, I understand
Decision Problems. Observation: Many polynomial algorithms. Questions: Can we solve all problems in polynomial time? Answer: No, absolutely not.
 Decision Problems Observation: Many polynomial algorithms. Questions: Can we solve all problems in polynomial time? Answer: No, absolutely not. Definition: The class of problems that can be solved by polynomial-time
Decision Problems Observation: Many polynomial algorithms. Questions: Can we solve all problems in polynomial time? Answer: No, absolutely not. Definition: The class of problems that can be solved by polynomial-time
Notes on AMPL for and (Adapted from notes by Sommer Gentry)
 Notes on AMPL for 16.410 and 16.413 (Adapted from notes by Sommer Gentry) User Guides for MS-Dos and UNIX: http://www.ampl.com/refs/index.html#os_links About AMPL/CPLEX AMPL stands for A Mathematical Programming
Notes on AMPL for 16.410 and 16.413 (Adapted from notes by Sommer Gentry) User Guides for MS-Dos and UNIX: http://www.ampl.com/refs/index.html#os_links About AMPL/CPLEX AMPL stands for A Mathematical Programming
Minimum Spanning Trees My T. UF
 Introduction to Algorithms Minimum Spanning Trees @ UF Problem Find a low cost network connecting a set of locations Any pair of locations are connected There is no cycle Some applications: Communication
Introduction to Algorithms Minimum Spanning Trees @ UF Problem Find a low cost network connecting a set of locations Any pair of locations are connected There is no cycle Some applications: Communication
Outline. 1 The matching problem. 2 The Chinese Postman Problem
 Outline The matching problem Maximum-cardinality matchings in bipartite graphs Maximum-cardinality matchings in bipartite graphs: The augmenting path algorithm 2 Let G = (V, E) be an undirected graph.
Outline The matching problem Maximum-cardinality matchings in bipartite graphs Maximum-cardinality matchings in bipartite graphs: The augmenting path algorithm 2 Let G = (V, E) be an undirected graph.
The Matrix-Tree Theorem and Its Applications to Complete and Complete Bipartite Graphs
 The Matrix-Tree Theorem and Its Applications to Complete and Complete Bipartite Graphs Frankie Smith Nebraska Wesleyan University fsmith@nebrwesleyan.edu May 11, 2015 Abstract We will look at how to represent
The Matrix-Tree Theorem and Its Applications to Complete and Complete Bipartite Graphs Frankie Smith Nebraska Wesleyan University fsmith@nebrwesleyan.edu May 11, 2015 Abstract We will look at how to represent
In this lecture, we ll look at applications of duality to three problems:
 Lecture 7 Duality Applications (Part II) In this lecture, we ll look at applications of duality to three problems: 1. Finding maximum spanning trees (MST). We know that Kruskal s algorithm finds this,
Lecture 7 Duality Applications (Part II) In this lecture, we ll look at applications of duality to three problems: 1. Finding maximum spanning trees (MST). We know that Kruskal s algorithm finds this,
MVE165/MMG631 Linear and integer optimization with applications Lecture 7 Discrete optimization models and applications; complexity
 MVE165/MMG631 Linear and integer optimization with applications Lecture 7 Discrete optimization models and applications; complexity Ann-Brith Strömberg 2019 04 09 Lecture 7 Linear and integer optimization
MVE165/MMG631 Linear and integer optimization with applications Lecture 7 Discrete optimization models and applications; complexity Ann-Brith Strömberg 2019 04 09 Lecture 7 Linear and integer optimization
Material handling and Transportation in Logistics. Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena
 Material handling and Transportation in Logistics Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Introduction to Graph Theory Graph Theory As Mathematical
Material handling and Transportation in Logistics Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Introduction to Graph Theory Graph Theory As Mathematical
The Simplex Algorithm
 The Simplex Algorithm April 25, 2005 We seek x 1,..., x n 0 which mini- Problem. mizes C(x 1,..., x n ) = c 1 x 1 + + c n x n, subject to the constraint Ax b, where A is m n, b = m 1. Through the introduction
The Simplex Algorithm April 25, 2005 We seek x 1,..., x n 0 which mini- Problem. mizes C(x 1,..., x n ) = c 1 x 1 + + c n x n, subject to the constraint Ax b, where A is m n, b = m 1. Through the introduction
56:272 Integer Programming & Network Flows Final Exam -- December 16, 1997
 56:272 Integer Programming & Network Flows Final Exam -- December 16, 1997 Answer #1 and any five of the remaining six problems! possible score 1. Multiple Choice 25 2. Traveling Salesman Problem 15 3.
56:272 Integer Programming & Network Flows Final Exam -- December 16, 1997 Answer #1 and any five of the remaining six problems! possible score 1. Multiple Choice 25 2. Traveling Salesman Problem 15 3.
Exam problems for the course Combinatorial Optimization I (DM208)
 Exam problems for the course Combinatorial Optimization I (DM208) Jørgen Bang-Jensen Department of Mathematics and Computer Science University of Southern Denmark The problems are available form the course
Exam problems for the course Combinatorial Optimization I (DM208) Jørgen Bang-Jensen Department of Mathematics and Computer Science University of Southern Denmark The problems are available form the course
COMP9334: Capacity Planning of Computer Systems and Networks
 COMP9334: Capacity Planning of Computer Systems and Networks Week 10: Optimisation (1) A/Prof Chun Tung Chou CSE, UNSW COMP9334, Chun Tung Chou, 2016 Three Weeks of Optimisation The lectures for these
COMP9334: Capacity Planning of Computer Systems and Networks Week 10: Optimisation (1) A/Prof Chun Tung Chou CSE, UNSW COMP9334, Chun Tung Chou, 2016 Three Weeks of Optimisation The lectures for these
: Principles of Automated Reasoning and Decision Making Midterm
 16.410-13: Principles of Automated Reasoning and Decision Making Midterm October 20 th, 2003 Name E-mail Note: Budget your time wisely. Some parts of this quiz could take you much longer than others. Move
16.410-13: Principles of Automated Reasoning and Decision Making Midterm October 20 th, 2003 Name E-mail Note: Budget your time wisely. Some parts of this quiz could take you much longer than others. Move
An iteration of Branch and Bound One iteration of Branch and Bound consists of the following four steps: Some definitions. Branch and Bound.
 ranch and ound xamples and xtensions jesla@man.dtu.dk epartment of Management ngineering Technical University of enmark ounding ow do we get ourselves a bounding function? Relaxation. Leave out some constraints.
ranch and ound xamples and xtensions jesla@man.dtu.dk epartment of Management ngineering Technical University of enmark ounding ow do we get ourselves a bounding function? Relaxation. Leave out some constraints.
CSE 21 Mathematics for Algorithm and System Analysis
 CSE 21 Mathematics for Algorithm and System Analysis Unit 4: Basic Concepts in Graph Theory Section 3: Trees 1 Review : Decision Tree (DT-Section 1) Root of the decision tree on the left: 1 Leaves of the
CSE 21 Mathematics for Algorithm and System Analysis Unit 4: Basic Concepts in Graph Theory Section 3: Trees 1 Review : Decision Tree (DT-Section 1) Root of the decision tree on the left: 1 Leaves of the
Lecture Notes for IEOR 266: Graph Algorithms and Network Flows
 Lecture Notes for IEOR 266: Graph Algorithms and Network Flows Professor Dorit S. Hochbaum Contents 1 Introduction 1 1.1 Assignment problem.................................... 1 1.2 Basic graph definitions...................................
Lecture Notes for IEOR 266: Graph Algorithms and Network Flows Professor Dorit S. Hochbaum Contents 1 Introduction 1 1.1 Assignment problem.................................... 1 1.2 Basic graph definitions...................................
Foundations of Operations Research Introduction to AMPL and Modellisation
 Foundations of Operations Research Introduction to AMPL and Modellisation Pierre Hosteins hosteins@di.unito.it Politecnico di Milano November 14th 2013 Transportation Problem and Integrality Property Graph
Foundations of Operations Research Introduction to AMPL and Modellisation Pierre Hosteins hosteins@di.unito.it Politecnico di Milano November 14th 2013 Transportation Problem and Integrality Property Graph
Backtracking and Branch-and-Bound
 Backtracking and Branch-and-Bound Usually for problems with high complexity Exhaustive Search is too time consuming Cut down on some search using special methods Idea: Construct partial solutions and extend
Backtracking and Branch-and-Bound Usually for problems with high complexity Exhaustive Search is too time consuming Cut down on some search using special methods Idea: Construct partial solutions and extend
Integer and Combinatorial Optimization: Clustering Problems
 Integer and Combinatorial Optimization: Clustering Problems John E. Mitchell Department of Mathematical Sciences RPI, Troy, NY 12180 USA February 2019 Mitchell Clustering Problems 1 / 14 Clustering Clustering
Integer and Combinatorial Optimization: Clustering Problems John E. Mitchell Department of Mathematical Sciences RPI, Troy, NY 12180 USA February 2019 Mitchell Clustering Problems 1 / 14 Clustering Clustering
Linear Programming. Slides by Carl Kingsford. Apr. 14, 2014
 Linear Programming Slides by Carl Kingsford Apr. 14, 2014 Linear Programming Suppose you are given: A matrix A with m rows and n columns. A vector b of length m. A vector c of length n. Find a length-n
Linear Programming Slides by Carl Kingsford Apr. 14, 2014 Linear Programming Suppose you are given: A matrix A with m rows and n columns. A vector b of length m. A vector c of length n. Find a length-n
CME 305: Discrete Mathematics and Algorithms Instructor: Reza Zadeh HW#3 Due at the beginning of class Thursday 02/26/15
 CME 305: Discrete Mathematics and Algorithms Instructor: Reza Zadeh (rezab@stanford.edu) HW#3 Due at the beginning of class Thursday 02/26/15 1. Consider a model of a nonbipartite undirected graph in which
CME 305: Discrete Mathematics and Algorithms Instructor: Reza Zadeh (rezab@stanford.edu) HW#3 Due at the beginning of class Thursday 02/26/15 1. Consider a model of a nonbipartite undirected graph in which
Branch and Bound. Live-node: A node that has not been expanded. It is similar to backtracking technique but uses BFS-like search.
 Branch and Bound Definitions: Branch and Bound is a state space search method in which all the children of a node are generated before expanding any of its children. Live-node: A node that has not been
Branch and Bound Definitions: Branch and Bound is a state space search method in which all the children of a node are generated before expanding any of its children. Live-node: A node that has not been
Graph Algorithms (part 3 of CSC 282),
 Graph Algorithms (part of CSC 8), http://www.cs.rochester.edu/~stefanko/teaching/11cs8 Homework problem sessions are in CSB 601, 6:1-7:1pm on Oct. (Wednesday), Oct. 1 (Wednesday), and on Oct. 19 (Wednesday);
Graph Algorithms (part of CSC 8), http://www.cs.rochester.edu/~stefanko/teaching/11cs8 Homework problem sessions are in CSB 601, 6:1-7:1pm on Oct. (Wednesday), Oct. 1 (Wednesday), and on Oct. 19 (Wednesday);
Linear Programming. Course review MS-E2140. v. 1.1
 Linear Programming MS-E2140 Course review v. 1.1 Course structure Modeling techniques Linear programming theory and the Simplex method Duality theory Dual Simplex algorithm and sensitivity analysis Integer
Linear Programming MS-E2140 Course review v. 1.1 Course structure Modeling techniques Linear programming theory and the Simplex method Duality theory Dual Simplex algorithm and sensitivity analysis Integer
Greedy algorithms is another useful way for solving optimization problems.
 Greedy Algorithms Greedy algorithms is another useful way for solving optimization problems. Optimization Problems For the given input, we are seeking solutions that must satisfy certain conditions. These
Greedy Algorithms Greedy algorithms is another useful way for solving optimization problems. Optimization Problems For the given input, we are seeking solutions that must satisfy certain conditions. These
LECTURES 3 and 4: Flows and Matchings
 LECTURES 3 and 4: Flows and Matchings 1 Max Flow MAX FLOW (SP). Instance: Directed graph N = (V,A), two nodes s,t V, and capacities on the arcs c : A R +. A flow is a set of numbers on the arcs such that
LECTURES 3 and 4: Flows and Matchings 1 Max Flow MAX FLOW (SP). Instance: Directed graph N = (V,A), two nodes s,t V, and capacities on the arcs c : A R +. A flow is a set of numbers on the arcs such that
Design and Analysis of Algorithms
 CSE 101, Winter 018 D/Q Greed SP s DP LP, Flow B&B, Backtrack Metaheuristics P, NP Design and Analysis of Algorithms Lecture 8: Greed Class URL: http://vlsicad.ucsd.edu/courses/cse101-w18/ Optimization
CSE 101, Winter 018 D/Q Greed SP s DP LP, Flow B&B, Backtrack Metaheuristics P, NP Design and Analysis of Algorithms Lecture 8: Greed Class URL: http://vlsicad.ucsd.edu/courses/cse101-w18/ Optimization
Practice Final Exam 1
 Algorithm esign Techniques Practice Final xam Instructions. The exam is hours long and contains 6 questions. Write your answers clearly. You may quote any result/theorem seen in the lectures or in the
Algorithm esign Techniques Practice Final xam Instructions. The exam is hours long and contains 6 questions. Write your answers clearly. You may quote any result/theorem seen in the lectures or in the
AMPL Integer Linear Programming. ORLAB Operations Research Laboratory. Borzou Rostami. Politecnico di Milano, Italy.
 AMPL Integer Linear Programming ORLAB Operations Research Laboratory Borzou Rostami Politecnico di Milano, Italy January 18, 2012 Integer Programming: Many linear programming problems require certain variables
AMPL Integer Linear Programming ORLAB Operations Research Laboratory Borzou Rostami Politecnico di Milano, Italy January 18, 2012 Integer Programming: Many linear programming problems require certain variables
56:272 Integer Programming & Network Flows Final Examination -- December 14, 1998
 56:272 Integer Programming & Network Flows Final Examination -- December 14, 1998 Part A: Answer any four of the five problems. (15 points each) 1. Transportation problem 2. Integer LP Model Formulation
56:272 Integer Programming & Network Flows Final Examination -- December 14, 1998 Part A: Answer any four of the five problems. (15 points each) 1. Transportation problem 2. Integer LP Model Formulation
CSci 231 Final Review
 CSci 231 Final Review Here is a list of topics for the final. Generally you are responsible for anything discussed in class (except topics that appear italicized), and anything appearing on the homeworks.
CSci 231 Final Review Here is a list of topics for the final. Generally you are responsible for anything discussed in class (except topics that appear italicized), and anything appearing on the homeworks.
Strategies for Using Algebraic Modeling Languages to Formulate Second-Order Cone Programs
 Strategies for Using Algebraic Modeling Languages to Formulate Second-Order Cone Programs Robert Fourer, Jared Erickson Industrial Engineering & Management Sciences Northwestern University 4er@northwestern.edu,
Strategies for Using Algebraic Modeling Languages to Formulate Second-Order Cone Programs Robert Fourer, Jared Erickson Industrial Engineering & Management Sciences Northwestern University 4er@northwestern.edu,
A New Quick Algorithm for Finding the Minimal Spanning Tree
 A New Quick Algorithm for Finding the Minimal Spanning Tree Mai Mismar Al-Quds Open University, Nablus-Palestine ABSTRACT In this paper, I propose a new Algorithm for finding the minimal spanning tree
A New Quick Algorithm for Finding the Minimal Spanning Tree Mai Mismar Al-Quds Open University, Nablus-Palestine ABSTRACT In this paper, I propose a new Algorithm for finding the minimal spanning tree
1. Chapter 1, # 1: Prove that for all sets A, B, C, the formula
 Homework 1 MTH 4590 Spring 2018 1. Chapter 1, # 1: Prove that for all sets,, C, the formula ( C) = ( ) ( C) is true. Proof : It suffices to show that ( C) ( ) ( C) and ( ) ( C) ( C). ssume that x ( C),
Homework 1 MTH 4590 Spring 2018 1. Chapter 1, # 1: Prove that for all sets,, C, the formula ( C) = ( ) ( C) is true. Proof : It suffices to show that ( C) ( ) ( C) and ( ) ( C) ( C). ssume that x ( C),
Notes for Lecture 24
 U.C. Berkeley CS170: Intro to CS Theory Handout N24 Professor Luca Trevisan December 4, 2001 Notes for Lecture 24 1 Some NP-complete Numerical Problems 1.1 Subset Sum The Subset Sum problem is defined
U.C. Berkeley CS170: Intro to CS Theory Handout N24 Professor Luca Trevisan December 4, 2001 Notes for Lecture 24 1 Some NP-complete Numerical Problems 1.1 Subset Sum The Subset Sum problem is defined
Introduction to Mathematical Programming IE406. Lecture 16. Dr. Ted Ralphs
 Introduction to Mathematical Programming IE406 Lecture 16 Dr. Ted Ralphs IE406 Lecture 16 1 Reading for This Lecture Bertsimas 7.1-7.3 IE406 Lecture 16 2 Network Flow Problems Networks are used to model
Introduction to Mathematical Programming IE406 Lecture 16 Dr. Ted Ralphs IE406 Lecture 16 1 Reading for This Lecture Bertsimas 7.1-7.3 IE406 Lecture 16 2 Network Flow Problems Networks are used to model
LECTURE 26 PRIM S ALGORITHM
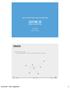 DATA STRUCTURES AND ALGORITHMS LECTURE 26 IMRAN IHSAN ASSISTANT PROFESSOR AIR UNIVERSITY, ISLAMABAD STRATEGY Suppose we take a vertex Given a single vertex v 1, it forms a minimum spanning tree on one
DATA STRUCTURES AND ALGORITHMS LECTURE 26 IMRAN IHSAN ASSISTANT PROFESSOR AIR UNIVERSITY, ISLAMABAD STRATEGY Suppose we take a vertex Given a single vertex v 1, it forms a minimum spanning tree on one
Math 485, Graph Theory: Homework #3
 Math 485, Graph Theory: Homework #3 Stephen G Simpson Due Monday, October 26, 2009 The assignment consists of Exercises 2129, 2135, 2137, 2218, 238, 2310, 2313, 2314, 2315 in the West textbook, plus the
Math 485, Graph Theory: Homework #3 Stephen G Simpson Due Monday, October 26, 2009 The assignment consists of Exercises 2129, 2135, 2137, 2218, 238, 2310, 2313, 2314, 2315 in the West textbook, plus the
Approximation Algorithms
 18.433 Combinatorial Optimization Approximation Algorithms November 20,25 Lecturer: Santosh Vempala 1 Approximation Algorithms Any known algorithm that finds the solution to an NP-hard optimization problem
18.433 Combinatorial Optimization Approximation Algorithms November 20,25 Lecturer: Santosh Vempala 1 Approximation Algorithms Any known algorithm that finds the solution to an NP-hard optimization problem
CME 305: Discrete Mathematics and Algorithms Instructor: Reza Zadeh HW#3 Due at the beginning of class Thursday 03/02/17
 CME 305: Discrete Mathematics and Algorithms Instructor: Reza Zadeh (rezab@stanford.edu) HW#3 Due at the beginning of class Thursday 03/02/17 1. Consider a model of a nonbipartite undirected graph in which
CME 305: Discrete Mathematics and Algorithms Instructor: Reza Zadeh (rezab@stanford.edu) HW#3 Due at the beginning of class Thursday 03/02/17 1. Consider a model of a nonbipartite undirected graph in which
6. Lecture notes on matroid intersection
 Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans May 2, 2017 6. Lecture notes on matroid intersection One nice feature about matroids is that a simple greedy algorithm
Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans May 2, 2017 6. Lecture notes on matroid intersection One nice feature about matroids is that a simple greedy algorithm
Small Survey on Perfect Graphs
 Small Survey on Perfect Graphs Michele Alberti ENS Lyon December 8, 2010 Abstract This is a small survey on the exciting world of Perfect Graphs. We will see when a graph is perfect and which are families
Small Survey on Perfect Graphs Michele Alberti ENS Lyon December 8, 2010 Abstract This is a small survey on the exciting world of Perfect Graphs. We will see when a graph is perfect and which are families
Algorithm Design and Analysis
 Algorithm Design and Analysis LECTURE 29 Approximation Algorithms Load Balancing Weighted Vertex Cover Reminder: Fill out SRTEs online Don t forget to click submit Sofya Raskhodnikova 12/7/2016 Approximation
Algorithm Design and Analysis LECTURE 29 Approximation Algorithms Load Balancing Weighted Vertex Cover Reminder: Fill out SRTEs online Don t forget to click submit Sofya Raskhodnikova 12/7/2016 Approximation
2 is not feasible if rounded. x =0,x 2
 Integer Programming Definitions Pure Integer Programming all variables should be integers Mied integer Programming Some variables should be integers Binary integer programming The integer variables are
Integer Programming Definitions Pure Integer Programming all variables should be integers Mied integer Programming Some variables should be integers Binary integer programming The integer variables are
CS256 Applied Theory of Computation
 CS256 Applied Theory of Computation Parallel Computation IV John E Savage Overview PRAM Work-time framework for parallel algorithms Prefix computations Finding roots of trees in a forest Parallel merging
CS256 Applied Theory of Computation Parallel Computation IV John E Savage Overview PRAM Work-time framework for parallel algorithms Prefix computations Finding roots of trees in a forest Parallel merging
AMS /672: Graph Theory Homework Problems - Week V. Problems to be handed in on Wednesday, March 2: 6, 8, 9, 11, 12.
 AMS 550.47/67: Graph Theory Homework Problems - Week V Problems to be handed in on Wednesday, March : 6, 8, 9,,.. Assignment Problem. Suppose we have a set {J, J,..., J r } of r jobs to be filled by a
AMS 550.47/67: Graph Theory Homework Problems - Week V Problems to be handed in on Wednesday, March : 6, 8, 9,,.. Assignment Problem. Suppose we have a set {J, J,..., J r } of r jobs to be filled by a
Blossom Algorithms for 1-Matching/Edge Covering Problems in Undirected Networks
 Contents 10 Blossom Algorithms for 1-Matching/Edge Covering Problems in Undirected Networks 669 10.1The1-MatchingProblems... 681 10.1.1 Blossom Algorithm for the Maximum CardinalityMatchingProblem... 714
Contents 10 Blossom Algorithms for 1-Matching/Edge Covering Problems in Undirected Networks 669 10.1The1-MatchingProblems... 681 10.1.1 Blossom Algorithm for the Maximum CardinalityMatchingProblem... 714
1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1
![1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1 1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1](/thumbs/80/82301067.jpg) Asymptotics, Recurrence and Basic Algorithms 1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1 1. O(logn) 2. O(n) 3. O(nlogn) 4. O(n 2 ) 5. O(2 n ) 2. [1 pt] What is the solution
Asymptotics, Recurrence and Basic Algorithms 1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1 1. O(logn) 2. O(n) 3. O(nlogn) 4. O(n 2 ) 5. O(2 n ) 2. [1 pt] What is the solution
CMSC 451: Linear Programming
 CMSC 451: Linear Programming Slides By: Carl Kingsford Department of Computer Science University of Maryland, College Park Linear Programming Suppose you are given: A matrix A with m rows and n columns.
CMSC 451: Linear Programming Slides By: Carl Kingsford Department of Computer Science University of Maryland, College Park Linear Programming Suppose you are given: A matrix A with m rows and n columns.
SOLVING LARGE CARPOOLING PROBLEMS USING GRAPH THEORETIC TOOLS
 July, 2014 1 SOLVING LARGE CARPOOLING PROBLEMS USING GRAPH THEORETIC TOOLS Irith Ben-Arroyo Hartman Datasim project - (joint work with Abed Abu dbai, Elad Cohen, Daniel Keren) University of Haifa, Israel
July, 2014 1 SOLVING LARGE CARPOOLING PROBLEMS USING GRAPH THEORETIC TOOLS Irith Ben-Arroyo Hartman Datasim project - (joint work with Abed Abu dbai, Elad Cohen, Daniel Keren) University of Haifa, Israel
Copyright 2007 Pearson Addison-Wesley. All rights reserved. A. Levitin Introduction to the Design & Analysis of Algorithms, 2 nd ed., Ch.
 Iterative Improvement Algorithm design technique for solving optimization problems Start with a feasible solution Repeat the following step until no improvement can be found: change the current feasible
Iterative Improvement Algorithm design technique for solving optimization problems Start with a feasible solution Repeat the following step until no improvement can be found: change the current feasible
Homework 3 Solutions
 CS3510 Design & Analysis of Algorithms Section A Homework 3 Solutions Released: 7pm, Wednesday Nov 8, 2017 This homework has a total of 4 problems on 4 pages. Solutions should be submitted to GradeScope
CS3510 Design & Analysis of Algorithms Section A Homework 3 Solutions Released: 7pm, Wednesday Nov 8, 2017 This homework has a total of 4 problems on 4 pages. Solutions should be submitted to GradeScope
CSE 21 Summer 2017 Homework 4
 CSE 21 Summer 201 Homework Key Concepts Minimum Spanning Trees, Directed Acyclic Graphs, Topological Sorting, Single source shortest paths, Counting, Basic probability principles, Independence, Linearity
CSE 21 Summer 201 Homework Key Concepts Minimum Spanning Trees, Directed Acyclic Graphs, Topological Sorting, Single source shortest paths, Counting, Basic probability principles, Independence, Linearity
1 Unweighted Set Cover
 Comp 60: Advanced Algorithms Tufts University, Spring 018 Prof. Lenore Cowen Scribe: Yuelin Liu Lecture 7: Approximation Algorithms: Set Cover and Max Cut 1 Unweighted Set Cover 1.1 Formulations There
Comp 60: Advanced Algorithms Tufts University, Spring 018 Prof. Lenore Cowen Scribe: Yuelin Liu Lecture 7: Approximation Algorithms: Set Cover and Max Cut 1 Unweighted Set Cover 1.1 Formulations There
Combinatorial Optimization
 Combinatorial Optimization Frank de Zeeuw EPFL 2012 Today Introduction Graph problems - What combinatorial things will we be optimizing? Algorithms - What kind of solution are we looking for? Linear Programming
Combinatorial Optimization Frank de Zeeuw EPFL 2012 Today Introduction Graph problems - What combinatorial things will we be optimizing? Algorithms - What kind of solution are we looking for? Linear Programming
0 0 1/20 1/20 1/20 1/20 1/20
 CS 6212 October 2018 Youssef Homework 3 Due Date: November 7, 2018 Problem 1: (15 points) Let a1< a2< a3< a4< a5< a6 be 6 numbers accessible with the following probabilities: p1 = 4/20, p2 = 2/20, p3 =
CS 6212 October 2018 Youssef Homework 3 Due Date: November 7, 2018 Problem 1: (15 points) Let a1< a2< a3< a4< a5< a6 be 6 numbers accessible with the following probabilities: p1 = 4/20, p2 = 2/20, p3 =
Exercise 1. D-ary Tree
 CSE 101: Design and Analysis of Algorithms Winter 2018 Homework 1 Solutions Due: 01/19/2018, 11.59 PM Exercise 1. D-ary Tree A d-ary tree is a rooted tree in which each node has at most d children. Show
CSE 101: Design and Analysis of Algorithms Winter 2018 Homework 1 Solutions Due: 01/19/2018, 11.59 PM Exercise 1. D-ary Tree A d-ary tree is a rooted tree in which each node has at most d children. Show
Construction of Minimum-Weight Spanners Mikkel Sigurd Martin Zachariasen
 Construction of Minimum-Weight Spanners Mikkel Sigurd Martin Zachariasen University of Copenhagen Outline Motivation and Background Minimum-Weight Spanner Problem Greedy Spanner Algorithm Exact Algorithm:
Construction of Minimum-Weight Spanners Mikkel Sigurd Martin Zachariasen University of Copenhagen Outline Motivation and Background Minimum-Weight Spanner Problem Greedy Spanner Algorithm Exact Algorithm:
Iterative Methods in Combinatorial Optimization. R. Ravi Carnegie Bosch Professor Tepper School of Business Carnegie Mellon University
 Iterative Methods in Combinatorial Optimization R. Ravi Carnegie Bosch Professor Tepper School of Business Carnegie Mellon University ravi@cmu.edu Combinatorial Optimization Easy Problems : polynomial
Iterative Methods in Combinatorial Optimization R. Ravi Carnegie Bosch Professor Tepper School of Business Carnegie Mellon University ravi@cmu.edu Combinatorial Optimization Easy Problems : polynomial
Design and Analysis of Algorithms - - Assessment
 X Courses» Design and Analysis of Algorithms Week 1 Quiz 1) In the code fragment below, start and end are integer values and prime(x) is a function that returns true if x is a prime number and false otherwise.
X Courses» Design and Analysis of Algorithms Week 1 Quiz 1) In the code fragment below, start and end are integer values and prime(x) is a function that returns true if x is a prime number and false otherwise.
Financial Optimization ISE 347/447. Lecture 13. Dr. Ted Ralphs
 Financial Optimization ISE 347/447 Lecture 13 Dr. Ted Ralphs ISE 347/447 Lecture 13 1 Reading for This Lecture C&T Chapter 11 ISE 347/447 Lecture 13 2 Integer Linear Optimization An integer linear optimization
Financial Optimization ISE 347/447 Lecture 13 Dr. Ted Ralphs ISE 347/447 Lecture 13 1 Reading for This Lecture C&T Chapter 11 ISE 347/447 Lecture 13 2 Integer Linear Optimization An integer linear optimization
Ryerson Polytechnic University Department of Mathematics, Physics, and Computer Science Final Examinations, April, 2003
 Ryerson Polytechnic University Department of Mathematics, Physics, and Computer Science Final Examinations, April, 2003 MTH 503 - Operations Research I Duration: 3 Hours. Aids allowed: Two sheets of notes
Ryerson Polytechnic University Department of Mathematics, Physics, and Computer Science Final Examinations, April, 2003 MTH 503 - Operations Research I Duration: 3 Hours. Aids allowed: Two sheets of notes
Network Optimization
 Université Paris Sud Laboratoire de Recherche en Informatique Network Optimization Fabio Martignon 1 Lecture overview Multi-commodity flow problem Network design problem Node positioning Users coverage
Université Paris Sud Laboratoire de Recherche en Informatique Network Optimization Fabio Martignon 1 Lecture overview Multi-commodity flow problem Network design problem Node positioning Users coverage
Undirected Graphs. DSA - lecture 6 - T.U.Cluj-Napoca - M. Joldos 1
 Undirected Graphs Terminology. Free Trees. Representations. Minimum Spanning Trees (algorithms: Prim, Kruskal). Graph Traversals (dfs, bfs). Articulation points & Biconnected Components. Graph Matching
Undirected Graphs Terminology. Free Trees. Representations. Minimum Spanning Trees (algorithms: Prim, Kruskal). Graph Traversals (dfs, bfs). Articulation points & Biconnected Components. Graph Matching
Paths, Flowers and Vertex Cover
 Paths, Flowers and Vertex Cover Venkatesh Raman, M.S. Ramanujan, and Saket Saurabh Presenting: Hen Sender 1 Introduction 2 Abstract. It is well known that in a bipartite (and more generally in a Konig)
Paths, Flowers and Vertex Cover Venkatesh Raman, M.S. Ramanujan, and Saket Saurabh Presenting: Hen Sender 1 Introduction 2 Abstract. It is well known that in a bipartite (and more generally in a Konig)
1. What do you get as the integer and noninteger parts if you factor this as we did with our cutting planes:
 1. What do you get as the integer and noninteger parts if you factor this as we did with our cutting planes: x 1 = -8.75-3.1 x 2 + 4.2 x 3 + 7 x 5-8 x 6 2. What constraint is added? 3. What do you need
1. What do you get as the integer and noninteger parts if you factor this as we did with our cutting planes: x 1 = -8.75-3.1 x 2 + 4.2 x 3 + 7 x 5-8 x 6 2. What constraint is added? 3. What do you need
Lecture 13. Reading: Weiss, Ch. 9, Ch 8 CSE 100, UCSD: LEC 13. Page 1 of 29
 Lecture 13 Connectedness in graphs Spanning trees in graphs Finding a minimal spanning tree Time costs of graph problems and NP-completeness Finding a minimal spanning tree: Prim s and Kruskal s algorithms
Lecture 13 Connectedness in graphs Spanning trees in graphs Finding a minimal spanning tree Time costs of graph problems and NP-completeness Finding a minimal spanning tree: Prim s and Kruskal s algorithms
Lecture 2 of Artificial Intelligence. Problem formulation. Produced by Qiangfu Zhao (Since 2008), All rights reserved
 Lecture 2 of Artificial Intelligence Problem formulation AI Lec02/1 Topics of this lecture Review of tree structure Review of graph structure Graph implementation State space representation Search graph
Lecture 2 of Artificial Intelligence Problem formulation AI Lec02/1 Topics of this lecture Review of tree structure Review of graph structure Graph implementation State space representation Search graph
AMPL Integer Linear Programming And Sensitivity Analysis for LP. ORLAB Operations Research Laboratory. Borzou Rostami. Politecnico di Milano, Italy
 AMPL Integer Linear Programming And Sensitivity Analysis for LP ORLAB Operations Research Laboratory Borzou Rostami Politecnico di Milano, Italy December 6, 2012 Integer Programming: Many linear programming
AMPL Integer Linear Programming And Sensitivity Analysis for LP ORLAB Operations Research Laboratory Borzou Rostami Politecnico di Milano, Italy December 6, 2012 Integer Programming: Many linear programming
