DEPARTMENT OF MATHS, MJ COLLEGE
|
|
|
- Lauren Willis
- 5 years ago
- Views:
Transcription
1 T. Y. B.Sc. Mathematics MTH- 356 (A) : Programming in C Unit 1 : Basic Concepts Syllabus : Introduction, Character set, C token, Keywords, Constants, Variables, Data types, Symbolic constants, Over flow, under flow, Operators of arithmetic, Relational, Logical, Assignment, Increment and decrement, Conditional and special type. In C-language the English characters are used to write any type of program. Uses small case alphabets of English language a,b,c,------,z. Uses basic nos. from mathematics 0,1,2,3,4, ,9. Uses diff. types of characters. Such as + plus, minus, * star, / slash, = equal to, % percent,! exclamation, & and,, comma, [ ] { } brackets, : colon,. dot, ; semicolon, # hash, inverted comma C tokens : C tokens are the basic bulidings blocks in C language which are constructed together to write a C program. Each and every smallest individual units in a C program are known as C tokens. C tokens are of six types. They are C tokens example program : main() } { Where, 1. Keywords ( eg. Int, while ) 2. Identifiers ( eg. main, total ) 3. Constants ( eg. 10, 20 ) 4. Strings ( eg. total, Hello ) 5. Special symbols ( eg. (), {} ) 6. Operators ( eg. +,,, / ) Int x, y, total; x = 10, y = 20; total = x + y; printf("total=%d", total); main identifier ( ) { } - special symbol Int - keyword 1
2 x, y, total identifier Main, (), { }, int, x, y, total C tokens Keywords in C language : There are 32 keywords in C programming language auto double int struct break else long switch case enum register typedef char extern return union const float short unsigned continue for signed void default goto sizeof volatile do if static while Constant : It is a single or multiple digit number formed by using basic numbers whose value Is constant throughout the program. eg. 128, 58.0, 20, The negative number assigned with a negative sign. These are four types of constant used in C language. 1) Float constant : It is a string of number containing decimal values. 2) Integer constant : This constant is a string of numbers. without any decimal values. 3) Exponent constant : The floating point constant can be written in the exponent form if the value is too long or small. 4) Single Character constant : It is constant whose value is a character which may be alphabets number or special character. for eg. 5, a, X 5) String constant : A string constant is a sequence of characters enclosed in double quotes. It consist of any combination of digits, letters, escaped sequences and spaces. for eg. SA, "5+3", "hello". Ex. Following are valid or invalid string constants i) valid string constant ii) 24, Janpath Road - valid string constant iii) W - invalid string constant iv) Modi - invalid string constant. 2
3 Difference between single character constant and string constant. Single Character constant Enclosed within single inverted commas The maximum length of a character constant can be one character The character constant A consists of only character A A single character constant occupies one byte. String constant A sequence of characters enclosed in double quotes. A string constant can be any length The character constant A consists of character A and 0. A single string constant occupies two bytes. Variables : A value which varies continuously during the exaction of program in a variable of the program. A variable can be written by a variable name formed by string of alphabets underscore & digits. But the variable name must start with alphabet or underscore. It should not start with digit. The digit can be inserted in the variable name any where. for e.g. sum, piece_ flat, i, number_ of_ movies, whatsapp, hike4 - are valid variable names. Invalid variable names : i) sum value : This is invalid variable due to blank space ii) face book : This is invalid variable due to blank space. iii) 5modi : This is invalid variable because it start with a digit. There are diff. types of variables 1) Integer variable : It is variable whose value during the execution of the program remains as an integer value. This variable can be declared at the starting of the program by the word int eg. int a,b,c; These variable accept the value between to ) Float variable: It is a variable name whose value remains real a decimal during execution of the program. This variable name can be declared at the starting of the program by a word float. Eg. float extra, count These variable have up to 6 decimal accuracy. 3) Double variable : This is similar to float variable. It is used when the accuracy provided by a float variable is not sufficient & more accuracy is expected. These are declared by the word double. eg. double second, time; These variable have up to 12 decimal accuracy. 3
4 4) Character variable: These variable contains a string of alphabets or characters or number as character. These can be declared by using the word char. eg. char call, make These variable accept are character. 5) Long variable: It the word long is placed before any declaration of variable then the declared will be extended accuracy as many computer system for double & integer variable. If long is used for the int variable then the variable accepts the value up to to eg. Long int factorial If long is used for the double variable then the variable accept the value up to 24 decimal accuracy. 6) Short variable : If the word short is place before any declaration, then the declared variable will be used to store fairly small accurate value. eg. short int factorial ; 7) Unsigned variable: If the word unsigned is placed before any declaration then the declared variable will be used to store positive number. eg. unsigned int counter; The following are the ranges of variable data types for the variable. Data types char unsigned char Ranges Characters char signed char 128 to 127 int to unsigned int 0 to signed int to unsigned shot int 0 to 235 sign short int 0 to 235 long int to unsigned long int 0 to singed long int same or long int float double float 6 decimal place 12 decimal place 4
5 long double float 4 decimal place Symbolic Constant : A symbolic constant is same that substitute for a sequence of character that can t be changed. The character may represent a numeric constant, a character constant or a string. When the program is compiled each occurrence of a symbolic constant is replaced by its corresponding character sequence. They are usually define at the beginning of the program. The symbolic constant may then appear later in the program in place of the numeric constants, character constant etc. that the symbolic constant represent. for eg : C program consists of the following symbolic constant define PI define TRUE 1 define FALSE 0 Overflow : In C programming an integer overflow occurs when an arithmetic operation attempts to create a numeric value that is too large to be represented within the available storage space. For instance, adding 1 to the largest value that can be represented constitutes an integer overflow. Underflow : The condition in a C program that can occur when the true result of a floating point operation is smaller in magnitude ( that is closer to zero ) than the smallest value representable as a normal floating point number in the target data type. Arithmetic operators : The arithmetic operators perform arithmetic operations and can be classified in to unary and binary arithmetic operations. The following are the list of the arithmetic operators. Operator Meaning + Addition _ Minus * Multiplication / Division % Modulus 1) Unary minus operators : If the value of any variable is negative then it is assigned with a negative sign by the use of unary minus operators. eg : a ; where negative sign is a unary minus operator. 2) Modulus operator : The modulus operator is indicated by % sign. This operator provides as a reminder of any value between divisions of the two integer variable. eg. a%b. This means that a is divided by b & remainder is the result. Relational Operators : The relational operators are used to compare arithmetic, logical and character expressions. We often compare two quantities and depending upon that we take a decision. 5
6 Operator Meaning < less than > greater than <= less than or equal to >= greater than or equal to == equal to! = not equal to Logical operator : These operators are used to compare the logical and relational expressions. Operator Meaning && Logical AND Logical OR! Logical NOT Bitwise operator : These operators operate on each bit of data. They are used for testing, complementing or shifting of bits to right or left. Usually they are not useful in the case of float and double variables. Operator Meaning & bitwise AND bitwise OR ^ Bitwise XOR Shift left Shift right ~ Bitwise complement Assignment Operator : This operator evaluates the expression on the right and assigns the resulting value to the variable on the left side. " = " is called as assignment operator. Increment and Decrement Operators : These operators are very much used in C language. They are extensively used in loops Syntex : Increment : ++< variable name > < variablename > + + Decrement : < variable name > < variablename > The + + operator adds 1 to the operand and operator subtract 1 from the operand. Conditional Operator : This operator consists of two symbols : the question mark (? ) and colon ( : ) Syntax : variable = (test expression)? true: false; It has three components the expression, true part and false part. If the expression is true it evaluates to true part after? else it evaluates false part after colon. Method of writing C program : Every column of screen accepts one character on one line. Each character of the statement should be written on one line on the program. At the end of every statement semicolon ; must be provided. Which indicates that the statement is complete. If the space for statement is not sufficient, it can be written an next line. The statement instruction should be written in continuation of the 6
7 sequence of the statement. If the program is a main program then it is to be written by the first statement as main ( ) main ( ) - main program { - start of program - Program statement } - end of program The opening { brace denotes the start of the program an one line & written below main ( ) statement. The statement are inserted after opening brace & at the end of program. It is closed by } closing brace on one single line.. Comment statement : The comment statement is enclosed in the two states / with * on both sides of the statement is useful for the reading of the program by the operator. It can be used for giving a tittle to the program. The comment statement can be inserted any where in the program. It is non-executable statement of the program. Eg. /* India is my country */ Ex.1] Explain whether following variable names are valid or invalid, if invalid why? 1) n_3_5 valid 2) 5-next invalid because it start with digit. 3) x > y 8 invalid due to > symbol. 4) w.l.o. invalid due to. symbol. 5) x$ invalid due to special symbol $ 6) y invalid due to special symbol Xl. 7) beg invalid due to 8) _beg valid 9) raman valid 10) Raman invalid due to start with capital letter. Ex.2] Correct the following statement in C. 1) float c, d Sol: correct is float c, d; 2) int a, b float c; Sol: correct is int a, b, float c; 3) /* This is a c program. 7
8 Sol: correct /* This is a c program */ 4) c = ((a + b) c)/d Sol: correct c = ((a + b) c)/d; 5) int a, b, c; sol: correct is int a, b, c; 6) / This is a best program */ Sol: correct /* This is a best program */ Ex.3. Write a C program to print our name with comment statement /* write a program to print our name */ main( ) } { printf ( my name is xyz ); Output: my name is xyz Ex.4 Write a C program to print Hi I am using whatsaap with comment statement. /* write a program to print Hi I am using whatsaap */ main( ) } { printf ( Hi I am using whatsaap ); Output: I am using whatsaap ( 1 mark questions ) Exercise 1. State whether the following statements are TRUE or FALSE : i) Every line in a C program should end with a semicolon. ii) Every C program ends with an END word. iii) In C language, lowercase letters are significant. iv) A line in a C program may have more than one statement. v) The closing brace of the main( ) in a program is the logical end of the program. 2. Write any four keywords in C language. 3. How many keywords in C languages, write any two keywords. 4. Following constant are which type of constant. i) 20,
9 ii) a, hello 5. Define string constant. 6. Define single character constant. 7. How to write the comment statement in C. 8. Write the syntax of Increment. 9. Write the syntax of decrement. 10. Write the syntax of conditional operator. ( 2 marks questions ) 1. Write types of C tokens. 2. Write any eight keywords in C language. 3. Write types of constant in C. 4. Write types of variable in C. 5. Define string constant. Give some example? 6. Write any two difference between single character constant and string constant. 7. Define symbolic constant 8. Write any two arithmetic operator and their meaning in C. 9. Write any two logical operator and their meaning in C. 10. Write any two relational operator and their meaning in C. 11. Write the syntax of Increment and decrement. 12. Write the syntax of conditional operator and its meaning. ( 3 marks questions ) 1. Write short note on C tokens. 2. Write short note on keywords in C language. 3. Write short note on constant in C. 4. Write short note on variable in C. 5. Write short note on arithmetic operator in C. 6. Explain the method of writing C program 9
Character Set. The character set of C represents alphabet, digit or any symbol used to represent information. Digits 0, 1, 2, 3, 9
 Character Set The character set of C represents alphabet, digit or any symbol used to represent information. Types Uppercase Alphabets Lowercase Alphabets Character Set A, B, C, Y, Z a, b, c, y, z Digits
Character Set The character set of C represents alphabet, digit or any symbol used to represent information. Types Uppercase Alphabets Lowercase Alphabets Character Set A, B, C, Y, Z a, b, c, y, z Digits
Data Types and Variables in C language
 Data Types and Variables in C language Basic structure of C programming To write a C program, we first create functions and then put them together. A C program may contain one or more sections. They are
Data Types and Variables in C language Basic structure of C programming To write a C program, we first create functions and then put them together. A C program may contain one or more sections. They are
Fundamentals of Programming
 Fundamentals of Programming Lecture 3 - Constants, Variables, Data Types, And Operations Lecturer : Ebrahim Jahandar Borrowed from lecturer notes by Omid Jafarinezhad Outline C Program Data types Variables
Fundamentals of Programming Lecture 3 - Constants, Variables, Data Types, And Operations Lecturer : Ebrahim Jahandar Borrowed from lecturer notes by Omid Jafarinezhad Outline C Program Data types Variables
Expressions and Data Types CSC 121 Spring 2015 Howard Rosenthal
 Expressions and Data Types CSC 121 Spring 2015 Howard Rosenthal Lesson Goals Understand the basic constructs of a Java Program Understand how to use basic identifiers Understand simple Java data types
Expressions and Data Types CSC 121 Spring 2015 Howard Rosenthal Lesson Goals Understand the basic constructs of a Java Program Understand how to use basic identifiers Understand simple Java data types
LESSON 1. A C program is constructed as a sequence of characters. Among the characters that can be used in a program are:
 LESSON 1 FUNDAMENTALS OF C The purpose of this lesson is to explain the fundamental elements of the C programming language. C like other languages has all alphabet and rules for putting together words
LESSON 1 FUNDAMENTALS OF C The purpose of this lesson is to explain the fundamental elements of the C programming language. C like other languages has all alphabet and rules for putting together words
Fundamental of Programming (C)
 Borrowed from lecturer notes by Omid Jafarinezhad Fundamental of Programming (C) Lecturer: Vahid Khodabakhshi Lecture 3 Constants, Variables, Data Types, And Operations Department of Computer Engineering
Borrowed from lecturer notes by Omid Jafarinezhad Fundamental of Programming (C) Lecturer: Vahid Khodabakhshi Lecture 3 Constants, Variables, Data Types, And Operations Department of Computer Engineering
6.096 Introduction to C++ January (IAP) 2009
 MIT OpenCourseWare http://ocw.mit.edu 6.096 Introduction to C++ January (IAP) 2009 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. Welcome to 6.096 Lecture
MIT OpenCourseWare http://ocw.mit.edu 6.096 Introduction to C++ January (IAP) 2009 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. Welcome to 6.096 Lecture
Unit-II Programming and Problem Solving (BE1/4 CSE-2)
 Unit-II Programming and Problem Solving (BE1/4 CSE-2) Problem Solving: Algorithm: It is a part of the plan for the computer program. An algorithm is an effective procedure for solving a problem in a finite
Unit-II Programming and Problem Solving (BE1/4 CSE-2) Problem Solving: Algorithm: It is a part of the plan for the computer program. An algorithm is an effective procedure for solving a problem in a finite
VARIABLES AND CONSTANTS
 UNIT 3 Structure VARIABLES AND CONSTANTS Variables and Constants 3.0 Introduction 3.1 Objectives 3.2 Character Set 3.3 Identifiers and Keywords 3.3.1 Rules for Forming Identifiers 3.3.2 Keywords 3.4 Data
UNIT 3 Structure VARIABLES AND CONSTANTS Variables and Constants 3.0 Introduction 3.1 Objectives 3.2 Character Set 3.3 Identifiers and Keywords 3.3.1 Rules for Forming Identifiers 3.3.2 Keywords 3.4 Data
UNIT- 3 Introduction to C++
 UNIT- 3 Introduction to C++ C++ Character Sets: Letters A-Z, a-z Digits 0-9 Special Symbols Space + - * / ^ \ ( ) [ ] =!= . $, ; : %! &? _ # = @ White Spaces Blank spaces, horizontal tab, carriage
UNIT- 3 Introduction to C++ C++ Character Sets: Letters A-Z, a-z Digits 0-9 Special Symbols Space + - * / ^ \ ( ) [ ] =!= . $, ; : %! &? _ # = @ White Spaces Blank spaces, horizontal tab, carriage
ANSI C Programming Simple Programs
 ANSI C Programming Simple Programs /* This program computes the distance between two points */ #include #include #include main() { /* Declare and initialize variables */ double
ANSI C Programming Simple Programs /* This program computes the distance between two points */ #include #include #include main() { /* Declare and initialize variables */ double
Expressions and Data Types CSC 121 Fall 2015 Howard Rosenthal
 Expressions and Data Types CSC 121 Fall 2015 Howard Rosenthal Lesson Goals Understand the basic constructs of a Java Program Understand how to use basic identifiers Understand simple Java data types and
Expressions and Data Types CSC 121 Fall 2015 Howard Rosenthal Lesson Goals Understand the basic constructs of a Java Program Understand how to use basic identifiers Understand simple Java data types and
Programming in C++ 5. Integral data types
 Programming in C++ 5. Integral data types! Introduction! Type int! Integer multiplication & division! Increment & decrement operators! Associativity & precedence of operators! Some common operators! Long
Programming in C++ 5. Integral data types! Introduction! Type int! Integer multiplication & division! Increment & decrement operators! Associativity & precedence of operators! Some common operators! Long
Programming and Data Structures
 Programming and Data Structures Teacher: Sudeshna Sarkar sudeshna@cse.iitkgp.ernet.in Department of Computer Science and Engineering Indian Institute of Technology Kharagpur #include int main()
Programming and Data Structures Teacher: Sudeshna Sarkar sudeshna@cse.iitkgp.ernet.in Department of Computer Science and Engineering Indian Institute of Technology Kharagpur #include int main()
Fundamental Data Types. CSE 130: Introduction to Programming in C Stony Brook University
 Fundamental Data Types CSE 130: Introduction to Programming in C Stony Brook University Program Organization in C The C System C consists of several parts: The C language The preprocessor The compiler
Fundamental Data Types CSE 130: Introduction to Programming in C Stony Brook University Program Organization in C The C System C consists of several parts: The C language The preprocessor The compiler
C: How to Program. Week /Mar/05
 1 C: How to Program Week 2 2007/Mar/05 Chapter 2 - Introduction to C Programming 2 Outline 2.1 Introduction 2.2 A Simple C Program: Printing a Line of Text 2.3 Another Simple C Program: Adding Two Integers
1 C: How to Program Week 2 2007/Mar/05 Chapter 2 - Introduction to C Programming 2 Outline 2.1 Introduction 2.2 A Simple C Program: Printing a Line of Text 2.3 Another Simple C Program: Adding Two Integers
Variables Data types Variable I/O. C introduction. Variables. Variables 1 / 14
 C introduction Variables Variables 1 / 14 Contents Variables Data types Variable I/O Variables 2 / 14 Usage Declaration: t y p e i d e n t i f i e r ; Assignment: i d e n t i f i e r = v a l u e ; Definition
C introduction Variables Variables 1 / 14 Contents Variables Data types Variable I/O Variables 2 / 14 Usage Declaration: t y p e i d e n t i f i e r ; Assignment: i d e n t i f i e r = v a l u e ; Definition
BASIC ELEMENTS OF A COMPUTER PROGRAM
 BASIC ELEMENTS OF A COMPUTER PROGRAM CSC128 FUNDAMENTALS OF COMPUTER PROBLEM SOLVING LOGO Contents 1 Identifier 2 3 Rules for naming and declaring data variables Basic data types 4 Arithmetic operators
BASIC ELEMENTS OF A COMPUTER PROGRAM CSC128 FUNDAMENTALS OF COMPUTER PROBLEM SOLVING LOGO Contents 1 Identifier 2 3 Rules for naming and declaring data variables Basic data types 4 Arithmetic operators
Java Notes. 10th ICSE. Saravanan Ganesh
 Java Notes 10th ICSE Saravanan Ganesh 13 Java Character Set Character set is a set of valid characters that a language can recognise A character represents any letter, digit or any other sign Java uses
Java Notes 10th ICSE Saravanan Ganesh 13 Java Character Set Character set is a set of valid characters that a language can recognise A character represents any letter, digit or any other sign Java uses
Chapter 2 - Introduction to C Programming
 Chapter 2 - Introduction to C Programming 2 Outline 2.1 Introduction 2.2 A Simple C Program: Printing a Line of Text 2.3 Another Simple C Program: Adding Two Integers 2.4 Memory Concepts 2.5 Arithmetic
Chapter 2 - Introduction to C Programming 2 Outline 2.1 Introduction 2.2 A Simple C Program: Printing a Line of Text 2.3 Another Simple C Program: Adding Two Integers 2.4 Memory Concepts 2.5 Arithmetic
JAVA Programming Fundamentals
 Chapter 4 JAVA Programming Fundamentals By: Deepak Bhinde PGT Comp.Sc. JAVA character set Character set is a set of valid characters that a language can recognize. It may be any letter, digit or any symbol
Chapter 4 JAVA Programming Fundamentals By: Deepak Bhinde PGT Comp.Sc. JAVA character set Character set is a set of valid characters that a language can recognize. It may be any letter, digit or any symbol
Creating a C++ Program
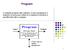 Program A computer program (also software, or just a program) is a sequence of instructions written in a sequence to perform a specified task with a computer. 1 Creating a C++ Program created using an
Program A computer program (also software, or just a program) is a sequence of instructions written in a sequence to perform a specified task with a computer. 1 Creating a C++ Program created using an
Programming in C++ 4. The lexical basis of C++
 Programming in C++ 4. The lexical basis of C++! Characters and tokens! Permissible characters! Comments & white spaces! Identifiers! Keywords! Constants! Operators! Summary 1 Characters and tokens A C++
Programming in C++ 4. The lexical basis of C++! Characters and tokens! Permissible characters! Comments & white spaces! Identifiers! Keywords! Constants! Operators! Summary 1 Characters and tokens A C++
Chapter 2: Introduction to C++
 Chapter 2: Introduction to C++ Copyright 2010 Pearson Education, Inc. Copyright Publishing as 2010 Pearson Pearson Addison-Wesley Education, Inc. Publishing as Pearson Addison-Wesley 2.1 Parts of a C++
Chapter 2: Introduction to C++ Copyright 2010 Pearson Education, Inc. Copyright Publishing as 2010 Pearson Pearson Addison-Wesley Education, Inc. Publishing as Pearson Addison-Wesley 2.1 Parts of a C++
Chapter 2: Special Characters. Parts of a C++ Program. Introduction to C++ Displays output on the computer screen
 Chapter 2: Introduction to C++ 2.1 Parts of a C++ Program Copyright 2009 Pearson Education, Inc. Copyright 2009 Publishing Pearson as Pearson Education, Addison-Wesley Inc. Publishing as Pearson Addison-Wesley
Chapter 2: Introduction to C++ 2.1 Parts of a C++ Program Copyright 2009 Pearson Education, Inc. Copyright 2009 Publishing Pearson as Pearson Education, Addison-Wesley Inc. Publishing as Pearson Addison-Wesley
C Language, Token, Keywords, Constant, variable
 C Language, Token, Keywords, Constant, variable A language written by Brian Kernighan and Dennis Ritchie. This was to be the language that UNIX was written in to become the first "portable" language. C
C Language, Token, Keywords, Constant, variable A language written by Brian Kernighan and Dennis Ritchie. This was to be the language that UNIX was written in to become the first "portable" language. C
UNIT IV 2 MARKS. ( Word to PDF Converter - Unregistered ) FUNDAMENTALS OF COMPUTING & COMPUTER PROGRAMMING
 ( Word to PDF Converter - Unregistered ) http://www.word-to-pdf-converter.net FUNDAMENTALS OF COMPUTING & COMPUTER PROGRAMMING INTRODUCTION TO C UNIT IV Overview of C Constants, Variables and Data Types
( Word to PDF Converter - Unregistered ) http://www.word-to-pdf-converter.net FUNDAMENTALS OF COMPUTING & COMPUTER PROGRAMMING INTRODUCTION TO C UNIT IV Overview of C Constants, Variables and Data Types
CS5000: Foundations of Programming. Mingon Kang, PhD Computer Science, Kennesaw State University
 CS5000: Foundations of Programming Mingon Kang, PhD Computer Science, Kennesaw State University Overview of Source Code Components Comments Library declaration Classes Functions Variables Comments Can
CS5000: Foundations of Programming Mingon Kang, PhD Computer Science, Kennesaw State University Overview of Source Code Components Comments Library declaration Classes Functions Variables Comments Can
Introduction. Following are the types of operators: Unary requires a single operand Binary requires two operands Ternary requires three operands
 Introduction Operators are the symbols which operates on value or a variable. It tells the compiler to perform certain mathematical or logical manipulations. Can be of following categories: Unary requires
Introduction Operators are the symbols which operates on value or a variable. It tells the compiler to perform certain mathematical or logical manipulations. Can be of following categories: Unary requires
Presented By : Gaurav Juneja
 Presented By : Gaurav Juneja Introduction C is a general purpose language which is very closely associated with UNIX for which it was developed in Bell Laboratories. Most of the programs of UNIX are written
Presented By : Gaurav Juneja Introduction C is a general purpose language which is very closely associated with UNIX for which it was developed in Bell Laboratories. Most of the programs of UNIX are written
Computer Science & Information Technology (CS) Rank under AIR 100. Examination Oriented Theory, Practice Set Key concepts, Analysis & Summary
 GATE- 2016-17 Postal Correspondence 1 C-Programming Computer Science & Information Technology (CS) 20 Rank under AIR 100 Postal Correspondence Examination Oriented Theory, Practice Set Key concepts, Analysis
GATE- 2016-17 Postal Correspondence 1 C-Programming Computer Science & Information Technology (CS) 20 Rank under AIR 100 Postal Correspondence Examination Oriented Theory, Practice Set Key concepts, Analysis
PART I. Part II Answer to all the questions 1. What is meant by a token? Name the token available in C++.
 Unit - III CHAPTER - 9 INTRODUCTION TO C++ Choose the correct answer. PART I 1. Who developed C++? (a) Charles Babbage (b) Bjarne Stroustrup (c) Bill Gates (d) Sundar Pichai 2. What was the original name
Unit - III CHAPTER - 9 INTRODUCTION TO C++ Choose the correct answer. PART I 1. Who developed C++? (a) Charles Babbage (b) Bjarne Stroustrup (c) Bill Gates (d) Sundar Pichai 2. What was the original name
Syntax and Variables
 Syntax and Variables What the Compiler needs to understand your program, and managing data 1 Pre-Processing Any line that starts with # is a pre-processor directive Pre-processor consumes that entire line
Syntax and Variables What the Compiler needs to understand your program, and managing data 1 Pre-Processing Any line that starts with # is a pre-processor directive Pre-processor consumes that entire line
Java Programming Fundamentals. Visit for more.
 Chapter 4: Java Programming Fundamentals Informatics Practices Class XI (CBSE Board) Revised as per CBSE Curriculum 2015 Visit www.ip4you.blogspot.com for more. Authored By:- Rajesh Kumar Mishra, PGT (Comp.Sc.)
Chapter 4: Java Programming Fundamentals Informatics Practices Class XI (CBSE Board) Revised as per CBSE Curriculum 2015 Visit www.ip4you.blogspot.com for more. Authored By:- Rajesh Kumar Mishra, PGT (Comp.Sc.)
Programming Fundamentals (CS 302 ) Dr. Ihsan Ullah. Lecturer Department of Computer Science & IT University of Balochistan
 Programming Fundamentals (CS 302 ) Dr. Ihsan Ullah Lecturer Department of Computer Science & IT University of Balochistan 1 Outline p Introduction p Program development p C language and beginning with
Programming Fundamentals (CS 302 ) Dr. Ihsan Ullah Lecturer Department of Computer Science & IT University of Balochistan 1 Outline p Introduction p Program development p C language and beginning with
Lecture 02 C FUNDAMENTALS
 Lecture 02 C FUNDAMENTALS 1 Keywords C Fundamentals auto double int struct break else long switch case enum register typedef char extern return union const float short unsigned continue for signed void
Lecture 02 C FUNDAMENTALS 1 Keywords C Fundamentals auto double int struct break else long switch case enum register typedef char extern return union const float short unsigned continue for signed void
Basic operators, Arithmetic, Relational, Bitwise, Logical, Assignment, Conditional operators. JAVA Standard Edition
 Basic operators, Arithmetic, Relational, Bitwise, Logical, Assignment, Conditional operators JAVA Standard Edition Java - Basic Operators Java provides a rich set of operators to manipulate variables.
Basic operators, Arithmetic, Relational, Bitwise, Logical, Assignment, Conditional operators JAVA Standard Edition Java - Basic Operators Java provides a rich set of operators to manipulate variables.
Basic Elements of C. Staff Incharge: S.Sasirekha
 Basic Elements of C Staff Incharge: S.Sasirekha Basic Elements of C Character Set Identifiers & Keywords Constants Variables Data Types Declaration Expressions & Statements C Character Set Letters Uppercase
Basic Elements of C Staff Incharge: S.Sasirekha Basic Elements of C Character Set Identifiers & Keywords Constants Variables Data Types Declaration Expressions & Statements C Character Set Letters Uppercase
Basics of Programming
 Unit 2 Basics of Programming Problem Analysis When we are going to develop any solution to the problem, we must fully understand the nature of the problem and what we want the program to do. Without the
Unit 2 Basics of Programming Problem Analysis When we are going to develop any solution to the problem, we must fully understand the nature of the problem and what we want the program to do. Without the
Operators in C. Staff Incharge: S.Sasirekha
 Operators in C Staff Incharge: S.Sasirekha Operators An operator is a symbol which helps the user to command the computer to do a certain mathematical or logical manipulations. Operators are used in C
Operators in C Staff Incharge: S.Sasirekha Operators An operator is a symbol which helps the user to command the computer to do a certain mathematical or logical manipulations. Operators are used in C
BCA-105 C Language What is C? History of C
 C Language What is C? C is a programming language developed at AT & T s Bell Laboratories of USA in 1972. It was designed and written by a man named Dennis Ritchie. C seems so popular is because it is
C Language What is C? C is a programming language developed at AT & T s Bell Laboratories of USA in 1972. It was designed and written by a man named Dennis Ritchie. C seems so popular is because it is
UNIT - I. Introduction to C Programming. BY A. Vijay Bharath
 UNIT - I Introduction to C Programming Introduction to C C was originally developed in the year 1970s by Dennis Ritchie at Bell Laboratories, Inc. C is a general-purpose programming language. It has been
UNIT - I Introduction to C Programming Introduction to C C was originally developed in the year 1970s by Dennis Ritchie at Bell Laboratories, Inc. C is a general-purpose programming language. It has been
C OVERVIEW. C Overview. Goals speed portability allow access to features of the architecture speed
 C Overview C OVERVIEW Goals speed portability allow access to features of the architecture speed C fast executables allows high-level structure without losing access to machine features many popular languages
C Overview C OVERVIEW Goals speed portability allow access to features of the architecture speed C fast executables allows high-level structure without losing access to machine features many popular languages
DECLARATIONS. Character Set, Keywords, Identifiers, Constants, Variables. Designed by Parul Khurana, LIECA.
 DECLARATIONS Character Set, Keywords, Identifiers, Constants, Variables Character Set C uses the uppercase letters A to Z. C uses the lowercase letters a to z. C uses digits 0 to 9. C uses certain Special
DECLARATIONS Character Set, Keywords, Identifiers, Constants, Variables Character Set C uses the uppercase letters A to Z. C uses the lowercase letters a to z. C uses digits 0 to 9. C uses certain Special
A complex expression to evaluate we need to reduce it to a series of simple expressions. E.g * 7 =>2+ 35 => 37. E.g.
 1.3a Expressions Expressions An Expression is a sequence of operands and operators that reduces to a single value. An operator is a syntactical token that requires an action be taken An operand is an object
1.3a Expressions Expressions An Expression is a sequence of operands and operators that reduces to a single value. An operator is a syntactical token that requires an action be taken An operand is an object
Objectives. Chapter 2: Basic Elements of C++ Introduction. Objectives (cont d.) A C++ Program (cont d.) A C++ Program
 Objectives Chapter 2: Basic Elements of C++ In this chapter, you will: Become familiar with functions, special symbols, and identifiers in C++ Explore simple data types Discover how a program evaluates
Objectives Chapter 2: Basic Elements of C++ In this chapter, you will: Become familiar with functions, special symbols, and identifiers in C++ Explore simple data types Discover how a program evaluates
Chapter 2: Basic Elements of C++
 Chapter 2: Basic Elements of C++ Objectives In this chapter, you will: Become familiar with functions, special symbols, and identifiers in C++ Explore simple data types Discover how a program evaluates
Chapter 2: Basic Elements of C++ Objectives In this chapter, you will: Become familiar with functions, special symbols, and identifiers in C++ Explore simple data types Discover how a program evaluates
Chapter 2: Basic Elements of C++ Objectives. Objectives (cont d.) A C++ Program. Introduction
 Chapter 2: Basic Elements of C++ C++ Programming: From Problem Analysis to Program Design, Fifth Edition 1 Objectives In this chapter, you will: Become familiar with functions, special symbols, and identifiers
Chapter 2: Basic Elements of C++ C++ Programming: From Problem Analysis to Program Design, Fifth Edition 1 Objectives In this chapter, you will: Become familiar with functions, special symbols, and identifiers
Fundamental of C programming. - Ompal Singh
 Fundamental of C programming - Ompal Singh HISTORY OF C LANGUAGE IN 1960 ALGOL BY INTERNATIONAL COMMITTEE. IT WAS TOO GENERAL AND ABSTRUCT. IN 1963 CPL(COMBINED PROGRAMMING LANGUAGE) WAS DEVELOPED AT CAMBRIDGE
Fundamental of C programming - Ompal Singh HISTORY OF C LANGUAGE IN 1960 ALGOL BY INTERNATIONAL COMMITTEE. IT WAS TOO GENERAL AND ABSTRUCT. IN 1963 CPL(COMBINED PROGRAMMING LANGUAGE) WAS DEVELOPED AT CAMBRIDGE
C OVERVIEW BASIC C PROGRAM STRUCTURE. C Overview. Basic C Program Structure
 C Overview Basic C Program Structure C OVERVIEW BASIC C PROGRAM STRUCTURE Goals The function main( )is found in every C program and is where every C program begins speed execution portability C uses braces
C Overview Basic C Program Structure C OVERVIEW BASIC C PROGRAM STRUCTURE Goals The function main( )is found in every C program and is where every C program begins speed execution portability C uses braces
These are reserved words of the C language. For example int, float, if, else, for, while etc.
 Tokens in C Keywords These are reserved words of the C language. For example int, float, if, else, for, while etc. Identifiers An Identifier is a sequence of letters and digits, but must start with a letter.
Tokens in C Keywords These are reserved words of the C language. For example int, float, if, else, for, while etc. Identifiers An Identifier is a sequence of letters and digits, but must start with a letter.
Guide for The C Programming Language Chapter 1. Q1. Explain the structure of a C program Answer: Structure of the C program is shown below:
 Q1. Explain the structure of a C program Structure of the C program is shown below: Preprocessor Directives Global Declarations Int main (void) Local Declarations Statements Other functions as required
Q1. Explain the structure of a C program Structure of the C program is shown below: Preprocessor Directives Global Declarations Int main (void) Local Declarations Statements Other functions as required
C/Java Syntax. January 13, Slides by Mark Hancock (adapted from notes by Craig Schock)
 C/Java Syntax 1 Lecture 02 Summary Keywords Variable Declarations Data Types Operators Statements if, switch, while, do-while, for Functions 2 By the end of this lecture, you will be able to identify the
C/Java Syntax 1 Lecture 02 Summary Keywords Variable Declarations Data Types Operators Statements if, switch, while, do-while, for Functions 2 By the end of this lecture, you will be able to identify the
C/Java Syntax. Lecture 02 Summary. Keywords Variable Declarations Data Types Operators Statements. Functions. if, switch, while, do-while, for
 C/Java Syntax 1 Lecture 02 Summary Keywords Variable Declarations Data Types Operators Statements if, switch, while, do-while, for Functions 2 1 By the end of this lecture, you will be able to identify
C/Java Syntax 1 Lecture 02 Summary Keywords Variable Declarations Data Types Operators Statements if, switch, while, do-while, for Functions 2 1 By the end of this lecture, you will be able to identify
2.1. Chapter 2: Parts of a C++ Program. Parts of a C++ Program. Introduction to C++ Parts of a C++ Program
 Chapter 2: Introduction to C++ 2.1 Parts of a C++ Program Copyright 2009 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 2-1 Parts of a C++ Program Parts of a C++ Program // sample C++ program
Chapter 2: Introduction to C++ 2.1 Parts of a C++ Program Copyright 2009 Pearson Education, Inc. Publishing as Pearson Addison-Wesley 2-1 Parts of a C++ Program Parts of a C++ Program // sample C++ program
CprE 288 Introduction to Embedded Systems Exam 1 Review. 1
 CprE 288 Introduction to Embedded Systems Exam 1 Review http://class.ece.iastate.edu/cpre288 1 Overview of Today s Lecture Announcements Exam 1 Review http://class.ece.iastate.edu/cpre288 2 Announcements
CprE 288 Introduction to Embedded Systems Exam 1 Review http://class.ece.iastate.edu/cpre288 1 Overview of Today s Lecture Announcements Exam 1 Review http://class.ece.iastate.edu/cpre288 2 Announcements
CHAPTER 3 BASIC INSTRUCTION OF C++
 CHAPTER 3 BASIC INSTRUCTION OF C++ MOHD HATTA BIN HJ MOHAMED ALI Computer programming (BFC 20802) Subtopics 2 Parts of a C++ Program Classes and Objects The #include Directive Variables and Literals Identifiers
CHAPTER 3 BASIC INSTRUCTION OF C++ MOHD HATTA BIN HJ MOHAMED ALI Computer programming (BFC 20802) Subtopics 2 Parts of a C++ Program Classes and Objects The #include Directive Variables and Literals Identifiers
Introduction to C Programming. Chih-Wei Tang ( 唐之瑋 ) Department of Communication Engineering National Central University JhongLi, Taiwan
 Introduction to C Programming Chih-Wei Tang ( 唐之瑋 ) Department of Communication Engineering National Central University JhongLi, Taiwan Outline Printing texts Adding 2 integers Comparing 2 integers C.E.,
Introduction to C Programming Chih-Wei Tang ( 唐之瑋 ) Department of Communication Engineering National Central University JhongLi, Taiwan Outline Printing texts Adding 2 integers Comparing 2 integers C.E.,
CS102: Variables and Expressions
 CS102: Variables and Expressions The topic of variables is one of the most important in C or any other high-level programming language. We will start with a simple example: int x; printf("the value of
CS102: Variables and Expressions The topic of variables is one of the most important in C or any other high-level programming language. We will start with a simple example: int x; printf("the value of
Le L c e t c ur u e e 2 To T p o i p c i s c t o o b e b e co c v o e v r e ed e Variables Operators
 Course Name: Advanced Java Lecture 2 Topics to be covered Variables Operators Variables -Introduction A variables can be considered as a name given to the location in memory where values are stored. One
Course Name: Advanced Java Lecture 2 Topics to be covered Variables Operators Variables -Introduction A variables can be considered as a name given to the location in memory where values are stored. One
Computers Programming Course 5. Iulian Năstac
 Computers Programming Course 5 Iulian Năstac Recap from previous course Classification of the programming languages High level (Ada, Pascal, Fortran, etc.) programming languages with strong abstraction
Computers Programming Course 5 Iulian Năstac Recap from previous course Classification of the programming languages High level (Ada, Pascal, Fortran, etc.) programming languages with strong abstraction
C++ character set Letters:- A-Z, a-z Digits:- 0 to 9 Special Symbols:- space + - / ( ) [ ] =! = < >, $ # ; :? & White Spaces:- Blank Space, Horizontal
![C++ character set Letters:- A-Z, a-z Digits:- 0 to 9 Special Symbols:- space + - / ( ) [ ] =! = < >, $ # ; :? & White Spaces:- Blank Space, Horizontal C++ character set Letters:- A-Z, a-z Digits:- 0 to 9 Special Symbols:- space + - / ( ) [ ] =! = < >, $ # ; :? & White Spaces:- Blank Space, Horizontal](/thumbs/79/80252285.jpg) TOKENS C++ character set Letters:- A-Z, a-z Digits:- 0 to 9 Special Symbols:- space + - / ( ) [ ] =! = < >, $ # ; :? & White Spaces:- Blank Space, Horizontal Tab, Vertical tab, Carriage Return. Other Characters:-
TOKENS C++ character set Letters:- A-Z, a-z Digits:- 0 to 9 Special Symbols:- space + - / ( ) [ ] =! = < >, $ # ; :? & White Spaces:- Blank Space, Horizontal Tab, Vertical tab, Carriage Return. Other Characters:-
Lecture 02 Summary. C/Java Syntax 1/14/2009. Keywords Variable Declarations Data Types Operators Statements. Functions
 Lecture 02 Summary C/Java Syntax Keywords Variable Declarations Data Types Operators Statements if, switch, while, do-while, for Functions 1 2 By the end of this lecture, you will be able to identify the
Lecture 02 Summary C/Java Syntax Keywords Variable Declarations Data Types Operators Statements if, switch, while, do-while, for Functions 1 2 By the end of this lecture, you will be able to identify the
The C++ Language. Arizona State University 1
 The C++ Language CSE100 Principles of Programming with C++ (based off Chapter 2 slides by Pearson) Ryan Dougherty Arizona State University http://www.public.asu.edu/~redoughe/ Arizona State University
The C++ Language CSE100 Principles of Programming with C++ (based off Chapter 2 slides by Pearson) Ryan Dougherty Arizona State University http://www.public.asu.edu/~redoughe/ Arizona State University
I Internal Examination Sept Class: - BCA I Subject: - Principles of Programming Lang. (BCA 104) MM: 40 Set: A Time: 1 ½ Hrs.
 I Internal Examination Sept. 2018 Class: - BCA I Subject: - Principles of Programming Lang. (BCA 104) MM: 40 Set: A Time: 1 ½ Hrs. [I]Very short answer questions (Max 40 words). (5 * 2 = 10) 1. What is
I Internal Examination Sept. 2018 Class: - BCA I Subject: - Principles of Programming Lang. (BCA 104) MM: 40 Set: A Time: 1 ½ Hrs. [I]Very short answer questions (Max 40 words). (5 * 2 = 10) 1. What is
Operators. Java operators are classified into three categories:
 Operators Operators are symbols that perform arithmetic and logical operations on operands and provide a meaningful result. Operands are data values (variables or constants) which are involved in operations.
Operators Operators are symbols that perform arithmetic and logical operations on operands and provide a meaningful result. Operands are data values (variables or constants) which are involved in operations.
LECTURE 02 INTRODUCTION TO C++
 PowerPoint Slides adapted from *Starting Out with C++: From Control Structures through Objects, 7/E* by *Tony Gaddis* Copyright 2012 Pearson Education Inc. COMPUTER PROGRAMMING LECTURE 02 INTRODUCTION
PowerPoint Slides adapted from *Starting Out with C++: From Control Structures through Objects, 7/E* by *Tony Gaddis* Copyright 2012 Pearson Education Inc. COMPUTER PROGRAMMING LECTURE 02 INTRODUCTION
Review: Exam 1. Your First C++ Program. Declaration Statements. Tells the compiler. Examples of declaration statements
 Review: Exam 1 9/20/06 CS150 Introduction to Computer Science 1 1 Your First C++ Program 1 //*********************************************************** 2 // File name: hello.cpp 3 // Author: Shereen Khoja
Review: Exam 1 9/20/06 CS150 Introduction to Computer Science 1 1 Your First C++ Program 1 //*********************************************************** 2 // File name: hello.cpp 3 // Author: Shereen Khoja
Language Fundamentals Summary
 Language Fundamentals Summary Claudia Niederée, Joachim W. Schmidt, Michael Skusa Software Systems Institute Object-oriented Analysis and Design 1999/2000 c.niederee@tu-harburg.de http://www.sts.tu-harburg.de
Language Fundamentals Summary Claudia Niederée, Joachim W. Schmidt, Michael Skusa Software Systems Institute Object-oriented Analysis and Design 1999/2000 c.niederee@tu-harburg.de http://www.sts.tu-harburg.de
GO - OPERATORS. This tutorial will explain the arithmetic, relational, logical, bitwise, assignment and other operators one by one.
 http://www.tutorialspoint.com/go/go_operators.htm GO - OPERATORS Copyright tutorialspoint.com An operator is a symbol that tells the compiler to perform specific mathematical or logical manipulations.
http://www.tutorialspoint.com/go/go_operators.htm GO - OPERATORS Copyright tutorialspoint.com An operator is a symbol that tells the compiler to perform specific mathematical or logical manipulations.
C - Basic Introduction
 C - Basic Introduction C is a general-purpose high level language that was originally developed by Dennis Ritchie for the UNIX operating system. It was first implemented on the Digital Equipment Corporation
C - Basic Introduction C is a general-purpose high level language that was originally developed by Dennis Ritchie for the UNIX operating system. It was first implemented on the Digital Equipment Corporation
CSc 10200! Introduction to Computing. Lecture 2-3 Edgardo Molina Fall 2013 City College of New York
 CSc 10200! Introduction to Computing Lecture 2-3 Edgardo Molina Fall 2013 City College of New York 1 C++ for Engineers and Scientists Third Edition Chapter 2 Problem Solving Using C++ 2 Objectives In this
CSc 10200! Introduction to Computing Lecture 2-3 Edgardo Molina Fall 2013 City College of New York 1 C++ for Engineers and Scientists Third Edition Chapter 2 Problem Solving Using C++ 2 Objectives In this
Informatics Ingeniería en Electrónica y Automática Industrial
 Informatics Ingeniería en Electrónica y Automática Industrial Operators and expressions in C Operators and expressions in C Numerical expressions and operators Arithmetical operators Relational and logical
Informatics Ingeniería en Electrónica y Automática Industrial Operators and expressions in C Operators and expressions in C Numerical expressions and operators Arithmetical operators Relational and logical
Data types, variables, constants
 Data types, variables, constants Outline 2.1 Introduction 2.2 A Simple C Program: Printing a Line of Text 2.3 Another Simple C Program: Adding Two Integers 2.4 Memory Concepts 2.5 Arithmetic in C 2.6 Decision
Data types, variables, constants Outline 2.1 Introduction 2.2 A Simple C Program: Printing a Line of Text 2.3 Another Simple C Program: Adding Two Integers 2.4 Memory Concepts 2.5 Arithmetic in C 2.6 Decision
A flow chart is a graphical or symbolic representation of a process.
 Q1. Define Algorithm with example? Answer:- A sequential solution of any program that written in human language, called algorithm. Algorithm is first step of the solution process, after the analysis of
Q1. Define Algorithm with example? Answer:- A sequential solution of any program that written in human language, called algorithm. Algorithm is first step of the solution process, after the analysis of
C Programming Multiple. Choice
 C Programming Multiple Choice Questions 1.) Developer of C language is. a.) Dennis Richie c.) Bill Gates b.) Ken Thompson d.) Peter Norton 2.) C language developed in. a.) 1970 c.) 1976 b.) 1972 d.) 1980
C Programming Multiple Choice Questions 1.) Developer of C language is. a.) Dennis Richie c.) Bill Gates b.) Ken Thompson d.) Peter Norton 2.) C language developed in. a.) 1970 c.) 1976 b.) 1972 d.) 1980
2/29/2016. Definition: Computer Program. A simple model of the computer. Example: Computer Program. Data types, variables, constants
 Data types, variables, constants Outline.1 Introduction. Text.3 Memory Concepts.4 Naming Convention of Variables.5 Arithmetic in C.6 Type Conversion Definition: Computer Program A Computer program is a
Data types, variables, constants Outline.1 Introduction. Text.3 Memory Concepts.4 Naming Convention of Variables.5 Arithmetic in C.6 Type Conversion Definition: Computer Program A Computer program is a
Computer System and programming in C
 1 Basic Data Types Integral Types Integers are stored in various sizes. They can be signed or unsigned. Example Suppose an integer is represented by a byte (8 bits). Leftmost bit is sign bit. If the sign
1 Basic Data Types Integral Types Integers are stored in various sizes. They can be signed or unsigned. Example Suppose an integer is represented by a byte (8 bits). Leftmost bit is sign bit. If the sign
Computer Programming : C++
 The Islamic University of Gaza Engineering Faculty Department of Computer Engineering Fall 2017 ECOM 2003 Muath i.alnabris Computer Programming : C++ Experiment #1 Basics Contents Structure of a program
The Islamic University of Gaza Engineering Faculty Department of Computer Engineering Fall 2017 ECOM 2003 Muath i.alnabris Computer Programming : C++ Experiment #1 Basics Contents Structure of a program
Differentiate Between Keywords and Identifiers
 History of C? Why we use C programming language Martin Richards developed a high-level computer language called BCPL in the year 1967. The intention was to develop a language for writing an operating system(os)
History of C? Why we use C programming language Martin Richards developed a high-level computer language called BCPL in the year 1967. The intention was to develop a language for writing an operating system(os)
Expressions and Data Types CSC 121 Spring 2017 Howard Rosenthal
 Expressions and Data Types CSC 121 Spring 2017 Howard Rosenthal Lesson Goals Understand the basic constructs of a Java Program Understand how to use basic identifiers Understand simple Java data types
Expressions and Data Types CSC 121 Spring 2017 Howard Rosenthal Lesson Goals Understand the basic constructs of a Java Program Understand how to use basic identifiers Understand simple Java data types
Features of C. Portable Procedural / Modular Structured Language Statically typed Middle level language
 1 History C is a general-purpose, high-level language that was originally developed by Dennis M. Ritchie to develop the UNIX operating system at Bell Labs. C was originally first implemented on the DEC
1 History C is a general-purpose, high-level language that was originally developed by Dennis M. Ritchie to develop the UNIX operating system at Bell Labs. C was originally first implemented on the DEC
C++ Programming: From Problem Analysis to Program Design, Third Edition
 C++ Programming: From Problem Analysis to Program Design, Third Edition Chapter 2: Basic Elements of C++ Objectives (continued) Become familiar with the use of increment and decrement operators Examine
C++ Programming: From Problem Analysis to Program Design, Third Edition Chapter 2: Basic Elements of C++ Objectives (continued) Become familiar with the use of increment and decrement operators Examine
Main Program. C Programming Notes. #include <stdio.h> main() { printf( Hello ); } Comments: /* comment */ //comment. Dr. Karne Towson University
 C Programming Notes Dr. Karne Towson University Reference for C http://www.cplusplus.com/reference/ Main Program #include main() printf( Hello ); Comments: /* comment */ //comment 1 Data Types
C Programming Notes Dr. Karne Towson University Reference for C http://www.cplusplus.com/reference/ Main Program #include main() printf( Hello ); Comments: /* comment */ //comment 1 Data Types
Objectives. In this chapter, you will:
 Objectives In this chapter, you will: Become familiar with functions, special symbols, and identifiers in C++ Explore simple data types Discover how a program evaluates arithmetic expressions Learn about
Objectives In this chapter, you will: Become familiar with functions, special symbols, and identifiers in C++ Explore simple data types Discover how a program evaluates arithmetic expressions Learn about
Introduction to C# Applications
 1 2 3 Introduction to C# Applications OBJECTIVES To write simple C# applications To write statements that input and output data to the screen. To declare and use data of various types. To write decision-making
1 2 3 Introduction to C# Applications OBJECTIVES To write simple C# applications To write statements that input and output data to the screen. To declare and use data of various types. To write decision-making
University of Technology. Laser & Optoelectronics Engineering Department. C++ Lab.
 University of Technology Laser & Optoelectronics Engineering Department C++ Lab. Second week Variables Data Types. The usefulness of the "Hello World" programs shown in the previous section is quite questionable.
University of Technology Laser & Optoelectronics Engineering Department C++ Lab. Second week Variables Data Types. The usefulness of the "Hello World" programs shown in the previous section is quite questionable.
The component base of C language. Nguyễn Dũng Faculty of IT Hue College of Science
 The component base of C language Nguyễn Dũng Faculty of IT Hue College of Science Content A brief history of C Standard of C Characteristics of C The C compilation model Character set and keyword Data
The component base of C language Nguyễn Dũng Faculty of IT Hue College of Science Content A brief history of C Standard of C Characteristics of C The C compilation model Character set and keyword Data
Overview of C. Basic Data Types Constants Variables Identifiers Keywords Basic I/O
 Overview of C Basic Data Types Constants Variables Identifiers Keywords Basic I/O NOTE: There are six classes of tokens: identifiers, keywords, constants, string literals, operators, and other separators.
Overview of C Basic Data Types Constants Variables Identifiers Keywords Basic I/O NOTE: There are six classes of tokens: identifiers, keywords, constants, string literals, operators, and other separators.
Quick Reference Guide
 SOFTWARE AND HARDWARE SOLUTIONS FOR THE EMBEDDED WORLD mikroelektronika Development tools - Books - Compilers Quick Reference Quick Reference Guide with EXAMPLES for Basic language This reference guide
SOFTWARE AND HARDWARE SOLUTIONS FOR THE EMBEDDED WORLD mikroelektronika Development tools - Books - Compilers Quick Reference Quick Reference Guide with EXAMPLES for Basic language This reference guide
3. Java - Language Constructs I
 Educational Objectives 3. Java - Language Constructs I Names and Identifiers, Variables, Assignments, Constants, Datatypes, Operations, Evaluation of Expressions, Type Conversions You know the basic blocks
Educational Objectives 3. Java - Language Constructs I Names and Identifiers, Variables, Assignments, Constants, Datatypes, Operations, Evaluation of Expressions, Type Conversions You know the basic blocks
.. Cal Poly CPE 101: Fundamentals of Computer Science I Alexander Dekhtyar..
 .. Cal Poly CPE 101: Fundamentals of Computer Science I Alexander Dekhtyar.. A Simple Program. simple.c: Basics of C /* CPE 101 Fall 2008 */ /* Alex Dekhtyar */ /* A simple program */ /* This is a comment!
.. Cal Poly CPE 101: Fundamentals of Computer Science I Alexander Dekhtyar.. A Simple Program. simple.c: Basics of C /* CPE 101 Fall 2008 */ /* Alex Dekhtyar */ /* A simple program */ /* This is a comment!
UNIT-2 Introduction to C++
 UNIT-2 Introduction to C++ C++ CHARACTER SET Character set is asset of valid characters that a language can recognize. A character can represents any letter, digit, or any other sign. Following are some
UNIT-2 Introduction to C++ C++ CHARACTER SET Character set is asset of valid characters that a language can recognize. A character can represents any letter, digit, or any other sign. Following are some
Operators & Expressions
 Operators & Expressions Operator An operator is a symbol used to indicate a specific operation on variables in a program. Example : symbol + is an add operator that adds two data items called operands.
Operators & Expressions Operator An operator is a symbol used to indicate a specific operation on variables in a program. Example : symbol + is an add operator that adds two data items called operands.
INTRODUCTION 1 AND REVIEW
 INTRODUTION 1 AND REVIEW hapter SYS-ED/ OMPUTER EDUATION TEHNIQUES, IN. Programming: Advanced Objectives You will learn: Program structure. Program statements. Datatypes. Pointers. Arrays. Structures.
INTRODUTION 1 AND REVIEW hapter SYS-ED/ OMPUTER EDUATION TEHNIQUES, IN. Programming: Advanced Objectives You will learn: Program structure. Program statements. Datatypes. Pointers. Arrays. Structures.
Programming in C and Data Structures [15PCD13/23] 1. PROGRAMMING IN C AND DATA STRUCTURES [As per Choice Based Credit System (CBCS) scheme]
![Programming in C and Data Structures [15PCD13/23] 1. PROGRAMMING IN C AND DATA STRUCTURES [As per Choice Based Credit System (CBCS) scheme] Programming in C and Data Structures [15PCD13/23] 1. PROGRAMMING IN C AND DATA STRUCTURES [As per Choice Based Credit System (CBCS) scheme]](/thumbs/75/71821793.jpg) Programming in C and Data Structures [15PCD13/23] 1 PROGRAMMING IN C AND DATA STRUCTURES [As per Choice Based Credit System (CBCS) scheme] Course objectives: The objectives of this course is to make students
Programming in C and Data Structures [15PCD13/23] 1 PROGRAMMING IN C AND DATA STRUCTURES [As per Choice Based Credit System (CBCS) scheme] Course objectives: The objectives of this course is to make students
Programming Lecture 3
 Programming Lecture 3 Expressions (Chapter 3) Primitive types Aside: Context Free Grammars Constants, variables Identifiers Variable declarations Arithmetic expressions Operator precedence Assignment statements
Programming Lecture 3 Expressions (Chapter 3) Primitive types Aside: Context Free Grammars Constants, variables Identifiers Variable declarations Arithmetic expressions Operator precedence Assignment statements
Basics of Java Programming
 Basics of Java Programming Lecture 2 COP 3252 Summer 2017 May 16, 2017 Components of a Java Program statements - A statement is some action or sequence of actions, given as a command in code. A statement
Basics of Java Programming Lecture 2 COP 3252 Summer 2017 May 16, 2017 Components of a Java Program statements - A statement is some action or sequence of actions, given as a command in code. A statement
BITG 1233: Introduction to C++
 BITG 1233: Introduction to C++ 1 Learning Outcomes At the end of this lecture, you should be able to: Identify basic structure of C++ program (pg 3) Describe the concepts of : Character set. (pg 11) Token
BITG 1233: Introduction to C++ 1 Learning Outcomes At the end of this lecture, you should be able to: Identify basic structure of C++ program (pg 3) Describe the concepts of : Character set. (pg 11) Token
A Fast Review of C Essentials Part I
 A Fast Review of C Essentials Part I Structural Programming by Z. Cihan TAYSI Outline Program development C Essentials Functions Variables & constants Names Formatting Comments Preprocessor Data types
A Fast Review of C Essentials Part I Structural Programming by Z. Cihan TAYSI Outline Program development C Essentials Functions Variables & constants Names Formatting Comments Preprocessor Data types
