On Complexity of Equivalence Checking
|
|
|
- Logan Cain
- 5 years ago
- Views:
Transcription
1 On Complexity of Equivalence Checking Cadence Berkeley Labs 1995 University Ave.,Suite 460, Berkeley, California,94704 phone: (510) , fax: (510) CDNL-TR August 2003 Eugene Goldberg (Cadence Berkeley Labs), Yakov Novikov (National Academy of Science, Belarus), Abstract We introduce the notion of a common specification (CS) that is the key to understanding the complexity of equivalence checking. A CS S of functionally equivalent Boolean circuits N 1 is a circuit of multi-valued blocks where N 1 can be obtained from this CS by encoding the values of multi-valued variables of S. We show that the performance of an equivalence checking algorithm heavily depends on whether a non-trivial CS S is known. If it is, then there exists an algorithm we describe whose run time is linear in the number of blocks in S. However, there are good reasons to believe that for any algorithm that does not have information about such a CS, equivalence checking is hard (if not infeasible). We experimentally show that even equivalence checking of circuits with a very fine CS is hard for a representative collection of methods while CS driven equivalence checking takes only a few seconds. 1. Introduction In electronic CAD one has to face computationally hard problems very often. One of the examples of such problems is equivalence checking of combinational circuits that is a conpcomplete problem. In complexity theory an algorithm solving a conp-complete problem has to return an easily checkable proof that is a solution of this problem. In terms of equivalence checking, an algorithm testing the equivalence of Boolean circuits N 1 has to return a proof that N 1 are equivalent. Currently, researchers in complexity theory study two types of complexity. In terms of equivalence checking, a class T of equivalence checking problems has complexity of the first type in a proof system D, if in D there is no polynomial size proof for the problems of T. A class T of equivalence checking problems has complexity of the second type in a proof system D, if for the problems of T there is no polynomial time algorithm to find polynomial size proofs even such proofs exist in D. (In that case the proof system D is called non-automatizable [2].) Complexity of the second type is weaker than that of the first type because it suggests that the problems of T can be efficiently solved if the proof system D is supplied with some extra information about the structure of short proofs. In this paper we show that there are good reasons to believe that equivalence checking problems occurring in practice have complexity of the second type in proof systems like general resolution or BDDs [4]. These are proof systems that are commonly used in existing equivalence checkers. (The general resolution system is the basis of existing SAT-solvers.). This means that these problems have short proofs of equivalence that cannot be found by existing (and probably any possible) equivalence checkers unless some extra information about the structure about short proofs is given. Let N 1 be two Boolean circuits to be checked for equivalence. The extra information mentioned above is a common specification (CS) of circuits N 1. A CS S is just a circuit of multi-valued gates further referred to as blocks such that N 1 (or N 2 ) can be obtained from S by replacing each block G of S with its implementation I 1 (G) (or I 2 (G)). The circuit I 1 (G) (or I 2 (G)) implements a multi-output Boolean function obtained from the
2 truth table of G after encoding the values of multi-valued variables with binary codes. Any pair of functionally equivalent circuits N 1,N 2 has a CS S. If N 1,N 2 are identical copies of a circuit N*, then N* can be considered as their CS. Each block of the specification N* is implemented with only one gate of N 1 or N 2. So N* is the finest possible CS. If N 1 are completely structurally dissimilar, they have a trivial CS consisting of only one block where N 1 are implementations of this block. If circuits N 1 are structurally similar they have a set of non-trivial CSs (i.e. ones different from a trivial single block CS mentioned above). Let S be a CS of circuits N 1 consisting of n blocks. We describe a procedure of equivalence checking of N 1 whose run time is n Compl(p). Here p is the maximal number of gates used in the implementation of a block of S. The value of p characterizes the granularity of S. (Henceforth, when we say that a CS if fine we mean that the value of p is small.) The function Compl(p) describes the complexity of computing filtering and correlation functions for the block of S that has the largest implementation (of p gates). The procedure computes these functions for each block of S proceeding in topological order from inputs to outputs. In this paper we use general resolution as the instrumental proof system. In particular, for general resolution we give an upper bound (a very conservative one) on the value of function Compl(p) which is 3 6p. The result above leads to the following two conclusions. First, if there is a non-trivial CS S of circuits N 1 consisting of n blocks, then equivalence checking of N 1 splits into n subproblems. (Henceforth, when we say that N 1 have a CS S we mean that S is non-trivial.) If the truth table of each block G of S is known along with the codes of values of multivalued variables used when obtaining N 1 from S, such problem decomposition is obvious. One just needs to check that each block G of S is correctly implemented by subcircuits I 1 (G) and I 2 (G) of N 1 respectively. The key point however is that the procedure we introduce needs neither any knowledge of the functionality of blocks nor the codes of values of multi-valued variables. It only needs information about the topology of S (i.e. how blocks are connected to each other) and the correspondence between the gates of N 1 and the blocks of S. The second conclusion is that finer CSs mean more efficient equivalence checking. In particular, if one needs to solve equivalence checking problems from a class where each pair of circuits N 1,N 2 has a CS with the granularity p bounded by a constant, equivalence checking is linear in the size of circuits N 1 no matter how large they are. A natural question is whether equivalence checking of circuits N 1 having a fine CS S is easy if the latter is unknown. (Henceforth, if we say that a CS of N 1 is known or unknown, we mean the finest possible CS of N 1, see Definition 9, or a good approximation of it.) The theory that addresses these issues has only started [13] and so cannot answer our question yet. However, there is a very good reason to believe that no procedure can efficiently check equivalence of circuits having even a very fine CS, if the latter is not known. On the one hand, the problem of finding the finest CS S of circuits N 1 (or a good approximation of S) is most likely NPcomplete. On the other hand, given a short proof of equivalence of N 1 one could recover a good CS from this proof. So the existence of an efficient procedure for finding a short proof of equivalence would mean that there is an efficient algorithm for solving an NP-complete problem. Due to lack of theory, we substantiate our claim experimentally. Namely, we show that if a CS S of circuits N 1,N 2 is unknown then their verification is very difficult. However, if S is known, N 1 can be checked for equivalence in a few seconds using the procedure we introduce in this paper. 2. Some Background and Possible Applications of Our Theory The most successful equivalence checkers try to make full use of structural similarity of circuits N 1,N 2 to be compared. In particular, they try to establish some strong relationships (like equivalence or implication) between internal points of N 1,N 2 [3], [7],[8]. These relationships are deduced in topological order proceeding from inputs to outputs until the equivalence of corresponding primary outputs of N 1 is deduced. Circuits are considered to be structurally similar and so easy for equivalence checking if they have many internal points that are related by these strong relationships. Our theory generalizes the notion of structural similarity that has been used so far. Namely, we show that if N 1 have a CS S of small granularity, then the equivalence checking of N 1 can be very easy even though no internal points are related by strong relationships. A new approach developed in [9],[11] is to implicitly compute the set R(C) of all the satisfiable combinations of values for the variables of a cut C. (C is a cut in the miter of N 1,N 2 [3]). This cut gradually moves from inputs to outputs until it reaches the output of the miter. Every move of the cut is accompanied by recompilation of R(C). The main flaw of this approach is that one has to compute the set R(C) exactly which may be infeasible even if this set is represented implicitly. The techniques of [9],[11] allows one to simplify the BDDs representing the functionality of cut points. This is done by grouping a set of cut points and introducing new variables in BDDs representing the functionality of these points so that the set of satisfiable combinations for this set of cut points does not change. The problem here is that it is hard (if not impossible) to find a good variable grouping not knowing a CS of N 1. The procedure we introduce can also be considered as computation of a set R of satisfiable combinations for a cut C which gradually moves from inputs to outputs. The difference is that the knowledge of a CS S allows to approximate the set R(C) by a set of filtering and correlation functions. Besides, knowing S, one can optimally group variables by putting together ones that correspond to the implementation of a block of S. Of course, the current state-of-the-art tools due to the creativity and ingenuity of their developers are able to check equivalence of the majority of circuits produced by the existing synthesis tools. This can be attributed to the fact that synthesis procedures tend to introduce only local changes because a nonlocal change is hard to verify. So the structure of the synthesized circuit is very similar to the original one. However, the theory we develop suggests that one can efficiently verify even non-local changes. Suppose that N 1 is a circuit is another circuit obtained from N 1 by a synthesis step. As long as N 1 share a predefined CS S, they can be efficiently checked for equivalence.
3 (A natural candidate for such a predefined specification is the initial high-level description of the circuit.) An example of specification preserving synthesis steps are transformations that correspond to re-encoding values of a variable C associated with the output of a block G of S. This transformation is non-local because all the circuit in the fan-out cone of the implementation of G is affected up to the primary outputs. A synthesis tool making such transformations would generate various implementations of the same specification. Then equivalence checking of the initial circuit N 1 and the resulting circuit N 2 would be impossible without any knowledge of S. Probably, the best way to describe the relation between N 1,N 2 and S is as follows. The initial circuit N 1 can be viewed as the original message and the synthesis procedure as an encryption process. The circuit N 2 is the result of encryption where S is a key. Then equivalence checking is just restoring the original message N 1 from N 2 i.e. a decryption process. If the key is known, then decryption can be performed very efficiently. Otherwise, equivalence checking is nothing else but code breaking. So no matter how powerful an equivalence checker is, without the key it can decrypt N 2 only if the latter is very similar to N 1. The notion of a CS can also be helpful in reducing the complexity of equivalence checking of the circuits produced by existing synthesis tools. The idea is to keep a CS S of the initial circuit N 1 and the current circuit N 2 and recompute S incrementally after each change of N 2. Initially N 1,N 2 and S are identical (since N 1 are identical they have a CS that is a copy of N 1 or N 2 ). Each synthesis step changing N 2 is accompanied by recomputation of S. The synthesis procedure produces a synthesized circuit N 2 and a CS S of N 1. If the current specification S becomes too coarse during synthesis one can output S and the circuit synthesized so far and start computing a CS anew considering the current circuit as initial. Then equivalence checking of the initial circuit and the synthesized one is performed in a number of steps. At each step one verifies the equivalence of some intermediate circuits N i and N i+1 using their CS S i,i+1 output in the middle of synthesis. Of course, there is much to be done to realize ideas sketched above. In this paper we just make a first step providing an efficient procedure for equivalence checking of circuits with a known CS. 3. Common Specification of Boolean Circuits In this section, we introduce the notion of a common specification of Boolean circuits. Let S be a combinational circuit of multi-valued blocks (further referred to as a specification) specified by a directed acyclic graph H. The sources and sinks of H correspond to primary inputs and outputs of S. Each non-source node of H corresponds to a multi-valued block computing a multi-valued function of multi-valued arguments. Each node of n of H is associated with a multi-valued variable V. If n is a source of H, then the corresponding variable specifies values taken by the corresponding primary input of S. If n is a non-source node of S then the corresponding variable describes the values taken by the output of the block specified by n. If n is a source (respectively a sink), then the corresponding variable is called a primary input variable (respectively primary output variable). We will use the notation C=G(A,B) to indicate that a) the output of a block G is associated with a variable C; b) the function computed by the block G is G(A,B); c) only two nodes of H are connected to the node n in H and these nodes are associated with variables A and B. Denote by D(V) the domain of a variable V associated with a node of H. The value of D(V) is called the multiplicity of V. If the multiplicity of every variable V of S is equal to 2 then S is a Boolean circuit. Now we describe how a Boolean circuit N can be produced from a specification S by encoding the multi-valued variables. Let D(V)={v 1,,v t } be the domain of a variable V of S. Denote by q(v) a Boolean encoding of the values of D(V) that is a mapping q:d(v) {0,1} m. Denote by length(q(v)) the number of bits in q that is the value of m. The value of q(v i ), v i D(V) is called the code of v i. Given an encoding q of length m of a variable V associated with a block of S, denote by v(v) the set of m coding Boolean variables. In the following exposition we make the assumptions below. Assumption 1. Each gate of a Boolean circuit and each block of a specification has two inputs and one output. Assumption 2. The multiplicity of each primary input (or output) variable of a specification is a power of 2. Assumption 3. If V is a primary input (or output) variable of a specification, then length(q(v))=log 2 ( D(V) ) Assumption 4. If v 1 and v 2 are values of a variable V of a specification and v 1 v 2, then q(v 1 ) q(v 2 ). Assumption 5. If A and B are two different variables of a specification, then v(a) v(b) =. Remark 1. From Assumption 2, Assumption 3 and Assumption 4 it follows that if A is a primary input (or output) variable, a mapping q:d(a) {0,1} m is bijective. In particular, any assignment to the variables of v(a) is a code of some value a D(A). Definition 1. Given a Boolean circuit I, denote by Inp(I) (respectively Out(I)) the set of variables associated with primary inputs (respectively primary outputs) of I. Definition 2. Let X 1 and X 2 be sets of Boolean variables and X 2 X 1. Let y be an assignment to the variables of X 1. Denote by proj(y ) the projection of y on X 2 i.e. the part of y that consists of the assignments to the variables of X 2. Definition 3. Let C=G(A,B) be a block of specification S. Let q(a),q(b),q(c) be encodings of variables A,B, and C respectively. A Boolean circuit I is said to implement the block G if the following three conditions hold: 1) The set Inp(I) is a subset of v(a) v(b). 2) The set Out(I) is equal to v(c). 3) If the set of values assigned to v(a) and v(b) form codes q(a) and q(b) respectively where a D(A), b D(B), then I(z )=q(c) where z is the projection of the assignment z=(q(a),q(b)) on Inp(I), I(z ) is the value taken by I at z, and c=g(a,b). Remark 2. The reason why Inp(I) may not include all the variables of v(a) and/or v(b) is that the function G(A,B) may not distinguish some values of A or B. (G(A,B) does not distinguish, say, values a 1,a 2 D(A), if for any b D(B), G(a 1,b)=G(a 2,b).) So to implement G(A,B) the circuit I may need only a subset of variables of v(a) v(b). This said, for the sake of simplicity, we
4 will write I(q(a),q(b)) meaning I(q (a),q (b)), q (a)= proj(q(a),inp(i)) and q (b)=proj(q(b),inp(i)). Definition 4. Let S be a multi-valued circuit. A Boolean circuit N is said to implement the specification S, if it is built according to the following two rules. 1) Each block G of S is replaced with an implementation I of G. 2) Let the output of block G 1 (specified by variable R) be connected to an input of block G 2 (specified by the same variable R) in S. Then the outputs of the circuit I 1 implementing G 1 are properly connected to inputs of circuit I 2 implementing G 2. Namely, the primary output of I 1 specified by a Boolean variable q i v(r) is connected to the input of I 2 specified by the same variable of v(r) if q i Inp(I 2 ). C=G 1 (A,B) C G 3 A B F E K G 1 G 2 (a) I 1 (q 1 (A),q 1 (B)) q 1(A) q 1(B) q 1(C) (c) A B C a 0 b 0 c 0 a 0 b 1 c 1 a 0 b 2 c 1 a 0 b 3 c 0 a 1 b 0 c 1 a 1 b 1 c 2 a 1 b 2 c 2 a 1 b 3 c 0 q 2(A) q 2(B) q 2(C) Figure 1. A specification and the functionality of two implementations of a block In Fig. 1a a specification of three blocks if shown. The functionality of two different implementations of the block C=G 1 (A,B) (Fig. 1b) are shown in Fig. 1c and 1d. Here D(A)={a 0,a 1 }, D(B)={b 0,b 1,b 2,b 3 } and D(C)={c 0,c 1,c 2 }. Since A and B are primary input variables they are encoded with a minimum code length and q 1 (A)=q 2 (A) and q 1 (B)=q 2 (B) where q 1 (a 0 )=0, q 1 (a 1 )=1, q 1 (b 0 )=00, q 1 (b 1 )=01, q 1 (b 2 )=10, q 1 (b 3 )=11. Finally, the encodings q 1 (C) and q 2 (C) are q 1 (c 0 )=00, q 1 (c 1 )=10, q 1 (c 2 )=01 and q 2 (c 0 )=100, q 2 (c 1 )=010, q 2 (c 2 )=001. (d) (b) I 2 (q 2 (A),q 2 (B)) Remark 3. Let N be an implementation of a specification S. Let p be the largest number of gates used in an implementation of a multi-valued block of S in N. We will say that S is a specification of granularity p for N. Definition 5. The topological level of a block G in a specification S is the length of the longest path from a primary input of S to G. (The length of a path is measured in the number of blocks on it. The topological level of a primary input is assumed to be 0.) Denote by level(g) the topological level of G in S. Let N be an implementation of a specification S. From Remark 1 it follows that for any value assignment h to the input variables of N there is a unique set of values (x 1,,x k ), where x i D(X i ) such that h=(q(x 1 ),,q(x k )). That is there is one-to-one correspondence between assignments to primary inputs of S and N. The same applies to primary outputs of S and N. Definition 6. Let N be an implementation of S. Given a Boolean vector y of assignments to the primary inputs of N, the corresponding vector Y=(x 1,..,x k ) such that y=(q(x 1 ),,q(x k )) is called the pre-image of y. Proposition 1. Let N be a circuit implementing specification S. Let I(G) be the implementation of a block C=G(A,B) of S in N. Let y be a value assignment to the primary input variables of N and Y be the pre-image of y. Then the values of primary outputs of I(G) form the code q(c) where c is the value taken by the output of G when the inputs of S take the values specified by Y. Proposition 2. Let N 1, N 2 be circuits implementing a specification S. Let each primary input (or output) variable X of S have the same encoding in N 1. Then Boolean circuits N 1 are functionally equivalent. Proof. The proofs of Proposition 1 and Proposition 2 are simple and so we omit them to save space. Definition 7. Let N 1, N 2 be two functionally equivalent Boolean circuits. Let N 1, N 2 implement a specification S so that for every primary input (output) variable X encodings q 1 (X) and q 2 (X) (used when producing N 1 respectively) are identical. Then S is called a common specification (CS) of N 1. Remark 4. Let S be a CS of N 1,N 2 and C be a variable of S. We will assume that v 1 (C) =v 2 (C) if C is a primary input variable and v 1 (C) v 2 (C) = otherwise. Definition 8. Let S be a CS of N 1,N 2. Let p 1 (respectively p 2 ) be the granularity of S with respect to N 1 (respectively N 2 ). Then we will say that S is a CS of N 1,N 2 of granularity p = max(p 1,p 2 ). Definition 9. Given two functionally equivalent Boolean circuits N 1, N 2, S is called the finest common specification if it has the smallest granularity p among all the CSs of N Equivalence Checking as SAT Since in this paper we formulate the complexity of equivalence checking in terms of resolution proofs, we recall a common way of reducing equivalence checking to the satisfiability problem. Definition 10. A disjunction of literals of Boolean variables not containing two literals of the same variable is called a clause. A conjunction of clauses is called a conjunctive normal form (CNF).
5 Definition 11. Given a CNF F, the satisfiability problem (SAT) is to find a value assignment to the variables of F for which F evaluates to 1 (also called a satisfying assignment) or to prove that such an assignment does not exist. A clause K of F is said to be satisfied by a value assignment y if K(y)=1. The standard conversion of an equivalence checking problem into an instance of SAT is performed in two steps. Let N 1 be Boolean circuits to be checked for equivalence. At the first step of this conversion, a circuit M called a miter [3] is formed from N 1. The miter M is obtained by 1) identifying the corresponding primary inputs of N 1 ; 2) XORing each pair of corresponding primary outputs of N 1 ; 3) ORing the outputs of the added XOR gates. So the miter of N 1 evaluates to 1 if and only if for some input assignment a primary output of N 1 and the corresponding output of N 2 evaluate to different values. Therefore, the problem of checking the equivalence of N 1 is equivalent to testing the satisfiability of the miter of N 1. At the second step of conversion, the satisfiability of the miter is reduced to that of a CNF formula F. This formula is a conjunction of CNF formulas F 1,..,F n specifying the functionality of the gates of M and a one-literal clause that is satisfied only if the output of M is set to 1. The CNF F i specifies the i-th gate g i of M. Any assignment to the variables of F i that is inconsistent with the functionality of g i falsifies a clause of F i (and vice versa, a consistent assignment satisfies all the clauses of F i.) For instance, the AND gate y=x 1 x 2 is specified by the following three clauses ~x 1 ~x 2 y, x 1 ~y, x 2 ~y. 5. Equivalence Checking in General Resolution In this section, we prove some results about the complexity of equivalence checking of circuits with a CS of granularity p. The main idea of the proof is that if S is a CS of N 1, then their equivalence checking reduces to computing filtering and correlation functions for each variable of S. The two main properties of these functions are that They can be built based only on the information about the topology of S and about assignment of gates of N 1 to blocks of S. Filtering and correlation functions for a variable C specifying the output of a block G(A,B) can be computed locally from filtering and correlation functions of variables A and B and CNFs specifying implementations I 1 (G) and I 2 (G). So these functions can be computed in topological order starting with inputs and proceeding to outputs. In this paper we consider computation of filtering and correlation functions as CNFs in the general resolution system. However, these functions can be computed in many other ways, for example, by using BDDs (see Remark 10). Definition 12. Given a constant p, a CNF formula F is a member of the class M(p) if and only if it satisfies the following two conditions. F is the CNF formula (obtained by the procedure described in Section 4) specifying the miter of a pair of functionally equivalent circuits N 1,N 2. N 1,N 2 has a CS of granularity p. Definition 13. Let K and K be clauses having opposite literals of a variable (say variable x) and there is only one such variable. The resolvent of K, K in variable x is the clause that contains all the literals of K and K but the positive (i.e. literal x) and negative (i.e. literal ~x) literals of x. The operation of producing the resolvent of K and K is called resolution. Definition 14. General resolution is a proof system of propositional logic that has only one inference rule. This rule is to resolve two existing clauses to produce a new one. Given a CNF formula F, a proof L(F) of unsatisfiability of F in the general resolution system consists of a sequence of resolutions resulting in the derivation of an empty clause (i.e. a clause without literals). General resolution is complete, which means that given an unsatisfiable formula F there is always a proof L(F) that derives an empty clause. Definition 15. Let F(X 1 ) be a Boolean function where X 1 and X 2 are sets of Boolean variables. The function H(X 2 ) is called existentially implied by F if F(X 1 ) H(X 2 ) if H(z)=1 where z is an assignment to the variables of X 2, then there is an assignment y to the variables of X 1 such that F(y,z)=1. Remark 5. Given a function F(X 1 ), the function H(X 2 ) existentially implied by F is unique. It can be obtained by from F by existentially quantifying away the variables of X 1. The definition of existential implication is important for understanding how filtering and correlation functions are obtained. Proposition 3. Let F(X 1 ) and H(X 2 ) be CNF formulas where H(X 2 ) consists of all the clauses depending only on variables from X 2 that can be derived from F(X 1 ) by general resolution. Then H(X 2 ) is existentially implied by F(X 1 ). Proof. The CNF F(X 1 ) implies H(X 2 ) because each clause of H is implied by F since it is derived by resolution. Assume that H is not existentially implied by F. Then there is an assignment z to the variables of X 2 such that H(z)=1 and for any assignment y to the variables of X 1, F(y,z)=0. However, this means that F implies a clause K depending only on variables of X 2 such that K(z)=0. Since K should be in H, then H(z) should be equal to 0, which leads to a contradiction. Definition 16. Let F be a set of clauses. Denote by supp(f) the set of variables whose literals occur in clauses of F. To estimate the complexity of obtaining the function existentially implied by F in general resolution, we need the following proposition. Proposition 4. Let F be a set of clauses that implies a clause K. Then there is a sequence of at most 3 supp(f) resolution steps that results in the derivation of the clause K or a clause that implies K. Proof. Denote by F the formula that is obtained from F by making the assignments that set the literals of K to 0 (and removing the satisfied clauses and the literals set to 0). It is not hard to see that F is unsatisfiable since it implies an empty clause. So there is a resolution proof L(F ) that results in deducing an empty clause. Then by replacing each clause of F involved in L(F ) with its parent clause from F we get a sequence of resolutions resulting in deducing either the clause K or a clause that implies K. The number of resolvents in L(F ) cannot be more than 3 supp(f ) (i.e. the total number of clauses of supp(f ) variables) and so it cannot be more than 3 supp(f).
6 Remark 6. From Proposition 3 and Proposition 4 it follows that given a CNF F(X 1 ) one can obtain the function H(X 2 ) existentially implied by F in no more than 3 supp(f ) resolution steps. Definition 17. Let N be an implementation of a specification S. Let C be a variable of S. A function Ff is called a filtering function if: supp(ff) v(c). If an assignment z to the variables of v(c) is a code q(c), c D(C), then Ff(z)=1. Otherwise, Ff(z)=0. Remark 7. If C is a primary input variable of S, then Ff(v(C)) 1. Indeed, as it follows from Remark 1 any assignment to C is the code of a value c D(C). Proposition 5. Let N be an implementation of a specification S. Let C=G(A,B) be a block of S. Let F be the CNF formula specifying N built as described in Section 4 and F(I(G)) be the part of F specifying the implementation I(G) of G in N. Then P existentially implies Ff(v(C)) where P=Ff(v(A)) Ff(v(B)) F(I(G)). Proof. To prove that P Ff(v(C)) one needs to show that any assignment that sets P to 1 also sets Ff(v(C)) to 1. It is not hard to see that the support of all the functions of the expression P Ff(v(C)) is a subset of supp(f(i(g))). Let h=(x,y,z) be an assignment that sets P to 1 where x,y,z are assignments to the variables from v(a),v(b) and v(c) respectively. Then h has to set to 1 the functions Ff(v(A)), Ff(v(B), F(I(G)). Since h sets Ff(v(A)) to 1, then x=q(a), a D(A). Since h sets Ff(v(B)) to 1, then y=q(b), b D(B). So h=(q(a),q(b),z). To set to 1 F(I(G)) assignment z has to be equal to q(c), where c=g(a,b). Then h sets Ff(v(C)) to 1. Assume that Ff(v(C)) is not existentially implied by P. Then there exists an assignment z=q(c), c D(C) such that Ff(z)=1 and for any assignments x and y to the variables of v(a) and v(b) respectively, P(x,y,z)=0. However, P(q(a), q(b), z) = 1 where a and b are values of A and B such that G(a,b)=c, which leads to a contradiction. Definition 18. Let S be a CS of circuits N 1 and C be a variable of S. A function Cf is called a correlation function for encodings q 1 and q 2 of the values of C (used when producing N 1 ) if : supp(cf ) v 1 (C) v 2 (C). Cf(z 1, z 2 )=1 for any assignment z 1 to v 1 (C) and z 2 to v 2 (C) such that z 1 =q 1 (c) and z 2 =q 2 (c) where c D(C). Otherwise Cf(z 1, z 2 )=0. Remark 8. If C is a primary input variable of S, then Cf(v 1 (C)) 1. Indeed, as it follows from Remark 1 any assignment to v 1 (C) or v 2 (C) is the code of a value c D(C). Besides, from the definition of CS it follows that q 1 (C)=q 2 (C). Finally, from Remark 4 it follows that v 1 (C)=v 2 (C). So any assignment (x,y) to the variables of v 1 (C) can be represented as (q 1 (c),q 2 (c)), c D(C). Proposition 6. Let S be a CS of circuits N 1,N 2. Let C=G(A,B) be a block of S. Let F be the CNF formula specifying the miter of N 1,N 2 built as described in Section 4. Let F(I 1 (G)) and F(I 2 (G)) be the part of F specifying the implementation I 1 (G) and I 2 (G) of G in N 1 respectively. Then P existentially implies Cf(v 1 (C)). Here P = Filtering Correlation Implementation and Filtering = Ff(v 1 (A)) Ff(v 1 (B)) Ff(v 2 (A)) Ff(v 2 (B)), Correlation = Cf(v 1 (A),v 2 (A)) Cf(v 1 (B),v 2 (B)), Implementation = F(I 1 (G)) F(I 2 (G)). Proof. To prove that P implies Cf(v 1 (C)) one needs to show that any assignment that sets P to 1 also sets Cf(v 1 (C)) to 1. It is not hard to see that the support of all the functions of the expression P Cf(v 1 (C)) is a subset of supp(f(i 1 (G)) supp(f(i 2 (G)). Let h=(x 1, x 2, y 1, y 2, z 1, z 2 ) be an assignment that sets P to 1 where x 1, x 2, y 1, y 2, z 1, z 2 are assignments to v 1 (A), v 2 (A), v 1 (B), v 2 (B), v 1 (C), v 2 (C) respectively. Then h has to set to 1 all the functions the conjunction of which forms P. Since h has to set the function Filtering to 1, then x 1 =q 1 (a 1 ), x 2 =q 2 (a 2 ) where a 1,a 2 D(A) and y 1 =q 1 (b 1 ), y 2 =q 2 (b 2 ), where b 1,b 2 D(B). So h=(q 1 (a 1 ),q 2 (a 2 ), q 1 (b 1 ),q 2 (b 2 ), z 1, z 2 ). Since h sets the function Correlation to 1 then a 1 has to be equal to a 2 and b 1 has to be equal to b 2. So h can be represented as (q 1 (a),q 2 (a), q 1 (b),q 2 (b), z 1, z 2 ) where a D(A) and b D(B). Since h sets the function Implementation to 1, then z 1 has to be equal to q 1 (c), c=g(a,b) and z 2 has to be equal to q 2 (c). So h is equal to (q 1 (a),q 2 (a),q 1 (b),q 2 (b),q 1 (c),q 2 (c)) and hence it sets the correlation function Cf(v 1 (C)) to 1. Assume that Cf(v 1 (C)) is not existentially implied by P. Then there exists an assignment z 1 =q 1 (c), z 2 =q 2 (c) to the variables of v 1 (C) and v 2 (C) respectively such that Cf(z 1, z 2 )=1 and for any assignment x 1, x 2, y 1, y 2 to the variables of v 1 (A), v 2 (A), v 1 (B), v 2 (B) respectively, P(x 1, x 2, y 1, y 2, z 1, z 2 )=0. However, P(q 1 (a), q 2 (a), q 1 (b), q 2 (b), z 1, z 2 )=1 where a, b are the values of A and B respectively for which c=g(a,b). This leads to a contradiction. Proposition 7. Let F be a formula of M(p) specifying the miter of circuits N 1,N 2 obtained from a CS S of granularity p. The unsatisfiability of F can be proven by a resolution proof of no more than d n 3 6p resolution steps where n is the number of blocks in S and d is a constant. Proof. From Proposition 5 and Proposition 6 it follows that one can deduce correlation and filtering functions for all the variables of S starting with blocks of topological level 1 and proceeding in topological order. Indeed, let C=G(A,B) be a block of topological level 1. Then A and B are primary input variables and the filtering and correlation functions for them are known (they are tautologies). Then Ff(v 1 (C)) and Ff(v 2 (C)) are existentially implied by F(I 1 (G)) and F(I 2 (G)) respectively. According to Proposition 5, Ff(v 1 (C)) (respectively Ff(v 2 (C))) can be derived by resolving clauses of F(I 1 (G)) (respectively F(I 2 (G))). Similarly, the correlation function Cf(v 1 (C)) is existentially implied by F(I 1 (G)) F(I 2 (G)). So it can be derived from the latter by resolution. After filtering and correlation functions are computed for all the variables of level 1, the same procedure can be applied to variables of topological level 2 and so on. If S consists of n blocks, then in n steps one can deduce correlation functions for the primary output variables of S. At each step two filtering and one correlation function are computed for a variable C=G(A,B) of S. The complexity of this step is no more than 3 6p. Indeed, the support of all functions mentioned in Proposition 5 and Proposition 6 needed for computing Ff(v 1 (C)), Ff(v 2 (C)) and Cf(v 1 (C)) is a subset of A=supp(F(I 1 (G))) supp(f(i 2 (G))).
7 The total number of gates in I 1 (G) and I 2 (G) is bounded by 2p, each gate having 2 inputs and 1 output. So the total number of variables in A cannot be more than 6p. Then according to Remark 6, in no more than 3 6p steps one can deduce CNFs Ff(v 1 (C)), Ff(v 2 (C)) and Cf(v 1 (C)). Then the total number of resolution steps one needs to deduce correlation functions for primary output variables of S is bounded by n 3 6p. Now we show that from the correlation functions for primary output variables of S one can deduce an empty clause in the number of resolution steps linear in n p. Let C be a primary output variable specifying the output of a block G of N. Let I 1 (G) and I 2 (G) be the implementations of G in N 1 respectively. Let D(C) =2 k (By Assumption 2 the multiplicity of C is a power of 2.) Then length(q 1 (C))= length(q 2 (C))=k. (By Assumption 3, values of S are encoded by a minimal length encoding.) Now we show that there is always a correlation function Cf(v 1 (C)) specified by the CNF consisting of k pairs of two literal clauses specifying the equivalence of corresponding outputs of I 1 (G) and I 2 (G). Let f 1 and f 2 be two Boolean variables of v 1 (C) and v 2 (C) respectively that specify corresponding outputs of N 1. Since S is a CS of N 1, then q 1 (C)=q 2 (C). So any assignment q 1 (c),q 2 (c) to v 1 (C) and v 2 (C) that satisfies Cf(v 1 (C)) also satisfies clauses K =f 1 ~f 2 and K =~f 1 f 2. So K and K are implied by Cf(v 1 (C)) and can be deduced by the procedure described in the proof of Proposition 6. (The resolution steps one needs to deduce equivalence clauses are already counted in the expression n 3 6p ) Using each pair of equivalence clauses K and K and the clauses specifying the gate g=xor(f 1,f 2 ) of the miter, one can deduce a single literal clause ~g. This clause requires setting the output of this XOR gate to 0. Each such a clause can be deduced in the number of resolutions bounded by a constant and the total number of such clauses cannot be more than n p. Finally, from these unit clauses and the clauses specifying the final OR gate of the miter, the empty clause can be deduced in the number of resolutions bounded by n p. So the empty clause is deduced in no more than n 3 6p + d n p steps where d is a constant. Finally, one can pick a constant d such n 3 6p + d n p d n 3 6p Remark 9. In Proposition 7 we give a very conservative estimate of the complexity of deducing filtering and correlation functions. In practice this complexity can be much lower. In a sense, the best way to interpret the theory developed in this section is that the problem of equivalence checking of circuits N 1,N 2 with a CS S of n blocks can be partitioned into n subproblems of computing filtering and correlation functions for each variable of S. 6. A Procedure of Equivalence Checking for Circuits with a Known CS In Section 5 we considered equivalence checking in general resolution that is a non-deterministic proof system. This means that the proof is guided by an oracle that points to the next pair of clauses to be resolved. In this section, we summarize the results of Section 5 as a deterministic procedure of equivalence checking of circuits with a known CS. Let S be a CS of granularity p of Boolean circuits N 1. Let F be the CNF formula specifying the miter of N 1. Our procedure of equivalence checking consists of two stages: 1. For each variable C of S compute filtering functions Ff(v 1 (C)), Ff(v 2 (C)) and the correlation function Cf(v 1 (C), v 2 (C)) proceeding in topological order of variables. If C is a primary input variable, then Ff(v 1 (C)), Ff(v 2 (C)) and Cf(v 1 (C), v 2 (C)) are tautologies. Let C=G(A,B). Then Ff(v 1 (C)) is built by computing the function existentially implied (see Definition 15) by Ff(v 1 (A)) Ff(v 1 (B)) F(I 1 (G)). (F(I 1 (G)) is a subset of F specifying the implementation of G in N 1. The function Ff(v 2 (C) is built similarly to Ff(v 1 (C)).) The function Cf(v 1 (C)) is built by computing the function existentially implied by Ff(v 1 (A)) Ff(v 1 (B)) Ff(v 2 (A)) Ff(v 2 (B)) Cf(v 1 (A), v 2 (A)) Cf(v 1 (B), v 2 (B)) F(I 1 (G)) F(I 2 (G)). 2. Once the correlation functions are computed for every primary output variable of S, finish the proof of unsatisfiabiby of F by invoking a SAT-solver like [6],[12]. (This SAT-solver is applied to the CNF consisting of the clauses describing the correlation functions for the primary output variables of S, the clauses specifying the gates XORing primary outputs of N 1 and the final OR gate of the miter.) The complexity of this procedure is the same as in general resolution i.e. d n 3 6p where d is a constant. This procedure is flexible with respect to the method of computing existentially implied functions. Below we describe a few options. Let F be a CNF and supp(f) = X 1 X 2. Suppose one needs to compute a CNF H(X 2 ) that is existentially implied by F. If the value of X 2 is small, one can compute H(X 2 ) by running 2 k SATchecks where k= X 2. For every assignment z to the variables of X 2 one needs to check if there is an assignment y to the variables of X 1 such that (y,z) satisfies F. If such an assignment exists then the next assignment is checked. Otherwise, a clause consisting of literals of variables from X 2 that is falsified by the assignment z is added to the clauses of H(X 2 ). If the size of X 2 is large, one can compute filtering and correlation functions by existential quantification of the variables of X 1. In terms of SAT, existential quantification of a CNF F in a variable w of X 1 means adding to F all the resolvents that can be produced by resolving clauses of F in w. Of course, existential quantification in all the variables of X 1 is very expensive in SAT and so it works only for blocks of a small size. However, less expensive methods for computing G(X 2 ) in terms of SAT can be and should be developed. Remark 10. For the sake of completeness, we should mention that nothing prevents one from computing filtering and correlation functions using BDDs. This especially makes sense when existential quantification by BDDs is more efficient that in SAT. 7. Experimental Results The objective of experiments was to show that equivalence checking of circuits with a fine CS S is easy if S is known and is hard otherwise. To produce circuits having a fine CS we used the following procedure. To get multi-valued specifications with realistic topologies we borrowed them from MCNC-91 benchmark circuits as follows. First, all the benchmarks were
8 technology mapped using SIS [14] to get circuits consisting only of two-input AND gates. Then from each obtained circuit N a multi-valued specification S was produced by replacing each twoinput binary gate with a two-input single output block of fourvalued variables. (In other words, S changes the functionality of N while preserving its topology.) Then from S two functionally equivalent Boolean circuits N 1, N 2 implementing S were produced using two different sets of two-bit encodings of four-valued values. The encodings were picked in such a way that the two different implementations of the same four-valued block in N 1 and N 2 had no functionally equivalent outputs. This way we guaranteed that internal functionally equivalent points in N 1 and N 2 may occur only by accident. Note that after encoding, the number of inputs and outputs in N 1 is twice the number of inputs and outputs in the original Boolean circuit N. For instance, the two circuits produced from C6288 used as a specification have the topology of a 16- bit multiplier and the number of inputs and outputs of a 32-bit multiplier. In experiments we used the best tools that were available to us. Namely, we used the SAT-solver BerkMin downloaded from [1], the program Nanotrav built on top of the Colorado University Decision Diagram (CUDD) package [5] and a SAT-based equivalence checker CSAT [10] (courtesy of Prof. Li of UCSB). We also tried the SAT-solver Zchaff [12], but BerkMin was up to three orders of magnitude faster on our formulas. In the experiments we used the special mode of BerkMin designed for equivalence checking that is described at [1]. BerkMin was run on the formula specifying the miter M of N 1 as described in Section 4. Nanotrav was used to build a BDD for the miter M and CSAT checked the satisfiabilty of the miter s output. To check the suitability of the tools for equivalence checking, we first ran them on regular MCNC benchmarks to verify optimized versus non-optimized circuits. (We do not report these results). The tools showed quite decent performance. For example, BerkMin was able to quickly verify all the instances including the multiplier C6288. The same kind of performance was shown by CSAT. Nanotrav was able to build BDDs for all the miters except C6288 very quickly (in a few seconds). In all the experiments we ran Nanotrav using settings suggested by Fabio Somenzi (private communication). In particular, the variable sifting option was on. In Table 1 we give runtimes of the three programs shown in our experiments. All the programs were run on a SUNW Ultra-80 system with clock frequency 450MHz. In all the experiments the time limit was set to 60,000 sec. (16.6 hours). The results of the best out of the three programs is shown in black. In the last column we report run times of a trivial CS driven procedure. This procedure computes filtering and correlation function of blocks in terms of SAT by existentially quantifying variables (as it was described in Section 6) and eventually deduces an empty clause. It is not hard to see that run times of the CS driven procedure are linear in the size of circuits to be checked for equivalence. This is due to the fact that the size of specification blocks is fixed (and very small). On the other hand, the instances we generated turned out to be hard for the three chosen tools. Even if one compares the best run times with run times of the CS driven procedure, it is not hard to see that the former quickly increased as the size of the instances grew. Table 1. Equivalence checking of circuits with a fine CS Name of specification CSAT (sec.) Nanotrav (BDDs) (sec.) BerkMin (sec.) C , ttt x i term1 1, c , c , , rot , symml frg2 13, frg , i10 60,000 60, CS driven (sec.) des 12, dalu 17, , x1 13, , alu4 8, i8 60, , c ,000 60,000 1, k2 60,000 59, , too_large 60,000 60,000 60, t481 60,000 60,000 60, It is unlikely that an industrial strength equivalence checker would do much better on the circuits we generated because they have no functionally equivalent points. Besides, one can always produce much harder equivalence checking problems by using a slightly more coarse specification (Recall that in the experiments we used a very fine CS S consisting of four-valued blocks. That is the circuits produced from S were almost identical.) As we mentioned in the introduction, the problem of finding a short proof of equivalence of N 1,N 2 if a CS is not known, comes down to recovering this CS from the description of N 1,N 2 which is computationally very hard (if not infeasible). 8. Conclusions We introduce the notion of a common specification (CS) S of Boolean circuits N 1, N 2 as a measure of complexity for equivalence checking of N 1,N 2. We show that if a CS S of n blocks is known, the problem of equivalence checking of N 1,N 2 reduces to n much simpler subproblems. The complexity of each subproblem (that is to compute filtering and correlation functions for a block of S) heavily depends on the granularity p
9 of S. If p is small then each subproblem is very simple and so equivalence checking of N 1 is extremely fast. On the other hand, equivalence checking of N 1 without any knowledge of a CS is most likely hard for any equivalence checker. We experimentally show that circuits having a fine CS S can be checked for equivalence in a few seconds if S is known, while they cannot be verified in many hours by a representative set of tools. These results suggest that the granularity of CSs can be considered as the backbone of complexity of equivalence checking. Hence the notion of a CS should be taken into account when designing efficient synthesis and verification procedures. References [1] BerkMin web page. [2] Bonet M. e.a. On interpolation and automatization for Frege systems. SIAM Journal on Computing, 29(6): , [3] Brand D. Verification of large synthesized designs. Proceedings of ICCAD-1993,pp [4] Bryant R. Graph based algorithms for Boolean function manipulation. IEEE Trans. on Computers, C(35): [5] CUDD web page. [6] Goldberg E.,Novikov,Y. BerkMin: A fast and robust SATsolver. Design, Automation, and Test in Europe (DATE 02), pages , March [7] Kuehlmann A., Krohm, F. Equivalence checking using cuts and heaps. Proceedings of DAC [8] Kunz W., Pradhan, D., Recursive learning: a new implication technique for efficient solutions to cad problems - test, verification and optimization. IEEE Tran. on CAD 13(9) Sep [9] Kwak H.H e.a. Combinational equivalence checking through function transformation. Proc. of ICCAD,1992, pp [10] Lu F. e.a. A circuit SAT solver with signal correlation guided learning,.date-2003, pp [11] Moondanos J. e.a. Clever: Divide and conquer combinational logic equivalence verification with false negative elimination. CAV-2001, pp [12] Moskewicz M. e.a. Chaff: Engineering an efficient SATsolver. Proceedings of DAC [13] Razborov A., Alekhnovich M. Resolution is not automatizable unless W[p] is tractable. Proc. of the 42 nd IEEE FOCS- 2001, pages [14] Sentovich E. e.a. Sequential circuit design using synthesis and optimization. Proceedings of ICCAD, pp , October 1992.
On Resolution Proofs for Combinational Equivalence
 33.4 On Resolution Proofs for Combinational Equivalence Satrajit Chatterjee Alan Mishchenko Robert Brayton Department of EECS U. C. Berkeley {satrajit, alanmi, brayton}@eecs.berkeley.edu Andreas Kuehlmann
33.4 On Resolution Proofs for Combinational Equivalence Satrajit Chatterjee Alan Mishchenko Robert Brayton Department of EECS U. C. Berkeley {satrajit, alanmi, brayton}@eecs.berkeley.edu Andreas Kuehlmann
Verification of Proofs of Unsatisfiability for CNF Formulas
 Verification of Proofs of Unsatisfiability for CNF Formulas Evgueni Goldberg Cadence Berkeley Labs (USA), Email: egold@cadence.com Yakov Novikov The United Institute of Informatics Problems, National Academy
Verification of Proofs of Unsatisfiability for CNF Formulas Evgueni Goldberg Cadence Berkeley Labs (USA), Email: egold@cadence.com Yakov Novikov The United Institute of Informatics Problems, National Academy
On Resolution Proofs for Combinational Equivalence Checking
 On Resolution Proofs for Combinational Equivalence Checking Satrajit Chatterjee Alan Mishchenko Robert Brayton Department of EECS U. C. Berkeley {satrajit, alanmi, brayton}@eecs.berkeley.edu Andreas Kuehlmann
On Resolution Proofs for Combinational Equivalence Checking Satrajit Chatterjee Alan Mishchenko Robert Brayton Department of EECS U. C. Berkeley {satrajit, alanmi, brayton}@eecs.berkeley.edu Andreas Kuehlmann
Boolean Representations and Combinatorial Equivalence
 Chapter 2 Boolean Representations and Combinatorial Equivalence This chapter introduces different representations of Boolean functions. It then discusses the applications of these representations for proving
Chapter 2 Boolean Representations and Combinatorial Equivalence This chapter introduces different representations of Boolean functions. It then discusses the applications of these representations for proving
Local Two-Level And-Inverter Graph Minimization without Blowup
 Local Two-Level And-Inverter Graph Minimization without Blowup Robert Brummayer and Armin Biere Institute for Formal Models and Verification Johannes Kepler University Linz, Austria {robert.brummayer,
Local Two-Level And-Inverter Graph Minimization without Blowup Robert Brummayer and Armin Biere Institute for Formal Models and Verification Johannes Kepler University Linz, Austria {robert.brummayer,
9.1 Cook-Levin Theorem
 CS787: Advanced Algorithms Scribe: Shijin Kong and David Malec Lecturer: Shuchi Chawla Topic: NP-Completeness, Approximation Algorithms Date: 10/1/2007 As we ve already seen in the preceding lecture, two
CS787: Advanced Algorithms Scribe: Shijin Kong and David Malec Lecturer: Shuchi Chawla Topic: NP-Completeness, Approximation Algorithms Date: 10/1/2007 As we ve already seen in the preceding lecture, two
Escaping Local Minima in Logic Synthesis ( and some other problems of logic synthesis preserving specification)
 Escaping Local Minima in Logic Synthesis ( and some other problems of logic synthesis preserving specification) Cadence Berkeley Labs 1995 University Ave.,Suite 460, Berkeley, California,94704 phone: (510)-647-2825,
Escaping Local Minima in Logic Synthesis ( and some other problems of logic synthesis preserving specification) Cadence Berkeley Labs 1995 University Ave.,Suite 460, Berkeley, California,94704 phone: (510)-647-2825,
Formal Verification using Probabilistic Techniques
 Formal Verification using Probabilistic Techniques René Krenz Elena Dubrova Department of Microelectronic and Information Technology Royal Institute of Technology Stockholm, Sweden rene,elena @ele.kth.se
Formal Verification using Probabilistic Techniques René Krenz Elena Dubrova Department of Microelectronic and Information Technology Royal Institute of Technology Stockholm, Sweden rene,elena @ele.kth.se
ABC basics (compilation from different articles)
 1. AIG construction 2. AIG optimization 3. Technology mapping ABC basics (compilation from different articles) 1. BACKGROUND An And-Inverter Graph (AIG) is a directed acyclic graph (DAG), in which a node
1. AIG construction 2. AIG optimization 3. Technology mapping ABC basics (compilation from different articles) 1. BACKGROUND An And-Inverter Graph (AIG) is a directed acyclic graph (DAG), in which a node
1 Definition of Reduction
 1 Definition of Reduction Problem A is reducible, or more technically Turing reducible, to problem B, denoted A B if there a main program M to solve problem A that lacks only a procedure to solve problem
1 Definition of Reduction Problem A is reducible, or more technically Turing reducible, to problem B, denoted A B if there a main program M to solve problem A that lacks only a procedure to solve problem
Combinational Equivalence Checking
 Combinational Equivalence Checking Virendra Singh Associate Professor Computer Architecture and Dependable Systems Lab. Dept. of Electrical Engineering Indian Institute of Technology Bombay viren@ee.iitb.ac.in
Combinational Equivalence Checking Virendra Singh Associate Professor Computer Architecture and Dependable Systems Lab. Dept. of Electrical Engineering Indian Institute of Technology Bombay viren@ee.iitb.ac.in
2SAT Andreas Klappenecker
 2SAT Andreas Klappenecker The Problem Can we make the following boolean formula true? ( x y) ( y z) (z y)! Terminology A boolean variable is a variable that can be assigned the values true (T) or false
2SAT Andreas Klappenecker The Problem Can we make the following boolean formula true? ( x y) ( y z) (z y)! Terminology A boolean variable is a variable that can be assigned the values true (T) or false
NP-Hardness. We start by defining types of problem, and then move on to defining the polynomial-time reductions.
 CS 787: Advanced Algorithms NP-Hardness Instructor: Dieter van Melkebeek We review the concept of polynomial-time reductions, define various classes of problems including NP-complete, and show that 3-SAT
CS 787: Advanced Algorithms NP-Hardness Instructor: Dieter van Melkebeek We review the concept of polynomial-time reductions, define various classes of problems including NP-complete, and show that 3-SAT
Lecture 14: Lower Bounds for Tree Resolution
 IAS/PCMI Summer Session 2000 Clay Mathematics Undergraduate Program Advanced Course on Computational Complexity Lecture 14: Lower Bounds for Tree Resolution David Mix Barrington and Alexis Maciel August
IAS/PCMI Summer Session 2000 Clay Mathematics Undergraduate Program Advanced Course on Computational Complexity Lecture 14: Lower Bounds for Tree Resolution David Mix Barrington and Alexis Maciel August
(a) (4 pts) Prove that if a and b are rational, then ab is rational. Since a and b are rational they can be written as the ratio of integers a 1
 CS 70 Discrete Mathematics for CS Fall 2000 Wagner MT1 Sol Solutions to Midterm 1 1. (16 pts.) Theorems and proofs (a) (4 pts) Prove that if a and b are rational, then ab is rational. Since a and b are
CS 70 Discrete Mathematics for CS Fall 2000 Wagner MT1 Sol Solutions to Midterm 1 1. (16 pts.) Theorems and proofs (a) (4 pts) Prove that if a and b are rational, then ab is rational. Since a and b are
The Resolution Algorithm
 The Resolution Algorithm Introduction In this lecture we introduce the Resolution algorithm for solving instances of the NP-complete CNF- SAT decision problem. Although the algorithm does not run in polynomial
The Resolution Algorithm Introduction In this lecture we introduce the Resolution algorithm for solving instances of the NP-complete CNF- SAT decision problem. Although the algorithm does not run in polynomial
A Simplied NP-complete MAXSAT Problem. Abstract. It is shown that the MAX2SAT problem is NP-complete even if every variable
 A Simplied NP-complete MAXSAT Problem Venkatesh Raman 1, B. Ravikumar 2 and S. Srinivasa Rao 1 1 The Institute of Mathematical Sciences, C. I. T. Campus, Chennai 600 113. India 2 Department of Computer
A Simplied NP-complete MAXSAT Problem Venkatesh Raman 1, B. Ravikumar 2 and S. Srinivasa Rao 1 1 The Institute of Mathematical Sciences, C. I. T. Campus, Chennai 600 113. India 2 Department of Computer
A Satisfiability Procedure for Quantified Boolean Formulae
 A Satisfiability Procedure for Quantified Boolean Formulae David A. Plaisted Computer Science Department, University of North Carolina Chapel Hill, NC 27599-3175, USA Armin Biere ETH Zürich, Computer Systems
A Satisfiability Procedure for Quantified Boolean Formulae David A. Plaisted Computer Science Department, University of North Carolina Chapel Hill, NC 27599-3175, USA Armin Biere ETH Zürich, Computer Systems
Combinational Equivalence Checking Using Satisfiability and Recursive Learning
 Combinational Equivalence Checking Using Satisfiability and Recursive Learning João Marques-Silva Thomas Glass Instituto Superior Técnico Siemens AG Cadence European Labs/INESC Corporate Technology 1000
Combinational Equivalence Checking Using Satisfiability and Recursive Learning João Marques-Silva Thomas Glass Instituto Superior Técnico Siemens AG Cadence European Labs/INESC Corporate Technology 1000
P Is Not Equal to NP. ScholarlyCommons. University of Pennsylvania. Jon Freeman University of Pennsylvania. October 1989
 University of Pennsylvania ScholarlyCommons Technical Reports (CIS) Department of Computer & Information Science October 1989 P Is Not Equal to NP Jon Freeman University of Pennsylvania Follow this and
University of Pennsylvania ScholarlyCommons Technical Reports (CIS) Department of Computer & Information Science October 1989 P Is Not Equal to NP Jon Freeman University of Pennsylvania Follow this and
Homework 1. Due Date: Wednesday 11/26/07 - at the beginning of the lecture
 Homework 1 Due Date: Wednesday 11/26/07 - at the beginning of the lecture Problems marked with a [*] are a littlebit harder and count as extra credit. Note 1. For any of the given problems make sure that
Homework 1 Due Date: Wednesday 11/26/07 - at the beginning of the lecture Problems marked with a [*] are a littlebit harder and count as extra credit. Note 1. For any of the given problems make sure that
Checking Equivalence for Circuits Containing Incompletely Specified Boxes
 Freiburg, Germany, September 00 Checking Equivalence for Circuits Containing Incompletely Specified Boxes Christoph Scholl Bernd Becker Institute of Computer Science Albert Ludwigs University D 79110 Freiburg
Freiburg, Germany, September 00 Checking Equivalence for Circuits Containing Incompletely Specified Boxes Christoph Scholl Bernd Becker Institute of Computer Science Albert Ludwigs University D 79110 Freiburg
Joint Entity Resolution
 Joint Entity Resolution Steven Euijong Whang, Hector Garcia-Molina Computer Science Department, Stanford University 353 Serra Mall, Stanford, CA 94305, USA {swhang, hector}@cs.stanford.edu No Institute
Joint Entity Resolution Steven Euijong Whang, Hector Garcia-Molina Computer Science Department, Stanford University 353 Serra Mall, Stanford, CA 94305, USA {swhang, hector}@cs.stanford.edu No Institute
NP and computational intractability. Kleinberg and Tardos, chapter 8
 NP and computational intractability Kleinberg and Tardos, chapter 8 1 Major Transition So far we have studied certain algorithmic patterns Greedy, Divide and conquer, Dynamic programming to develop efficient
NP and computational intractability Kleinberg and Tardos, chapter 8 1 Major Transition So far we have studied certain algorithmic patterns Greedy, Divide and conquer, Dynamic programming to develop efficient
Learning Techniques for Pseudo-Boolean Solving and Optimization
 Learning Techniques for Pseudo-Boolean Solving and Optimization José Faustino Fragoso Fremenin dos Santos September 29, 2008 Abstract The extension of conflict-based learning from Propositional Satisfiability
Learning Techniques for Pseudo-Boolean Solving and Optimization José Faustino Fragoso Fremenin dos Santos September 29, 2008 Abstract The extension of conflict-based learning from Propositional Satisfiability
The Satisfiability Problem [HMU06,Chp.10b] Satisfiability (SAT) Problem Cook s Theorem: An NP-Complete Problem Restricted SAT: CSAT, k-sat, 3SAT
![The Satisfiability Problem [HMU06,Chp.10b] Satisfiability (SAT) Problem Cook s Theorem: An NP-Complete Problem Restricted SAT: CSAT, k-sat, 3SAT The Satisfiability Problem [HMU06,Chp.10b] Satisfiability (SAT) Problem Cook s Theorem: An NP-Complete Problem Restricted SAT: CSAT, k-sat, 3SAT](/thumbs/89/100203169.jpg) The Satisfiability Problem [HMU06,Chp.10b] Satisfiability (SAT) Problem Cook s Theorem: An NP-Complete Problem Restricted SAT: CSAT, k-sat, 3SAT 1 Satisfiability (SAT) Problem 2 Boolean Expressions Boolean,
The Satisfiability Problem [HMU06,Chp.10b] Satisfiability (SAT) Problem Cook s Theorem: An NP-Complete Problem Restricted SAT: CSAT, k-sat, 3SAT 1 Satisfiability (SAT) Problem 2 Boolean Expressions Boolean,
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science Algorithms For Inference Fall 2014
 Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.438 Algorithms For Inference Fall 2014 Recitation-6: Hardness of Inference Contents 1 NP-Hardness Part-II
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.438 Algorithms For Inference Fall 2014 Recitation-6: Hardness of Inference Contents 1 NP-Hardness Part-II
A Toolbox for Counter-Example Analysis and Optimization
 A Toolbox for Counter-Example Analysis and Optimization Alan Mishchenko Niklas Een Robert Brayton Department of EECS, University of California, Berkeley {alanmi, een, brayton}@eecs.berkeley.edu Abstract
A Toolbox for Counter-Example Analysis and Optimization Alan Mishchenko Niklas Een Robert Brayton Department of EECS, University of California, Berkeley {alanmi, een, brayton}@eecs.berkeley.edu Abstract
W4231: Analysis of Algorithms
 W4231: Analysis of Algorithms 11/23/99 NP-completeness of 3SAT, Minimum Vertex Cover, Maximum Independent Set, Boolean Formulae A Boolean formula is an expression that we can build starting from Boolean
W4231: Analysis of Algorithms 11/23/99 NP-completeness of 3SAT, Minimum Vertex Cover, Maximum Independent Set, Boolean Formulae A Boolean formula is an expression that we can build starting from Boolean
Chapter 2 PRELIMINARIES
 8 Chapter 2 PRELIMINARIES Throughout this thesis, we work with propositional or Boolean variables, that is, variables that take value in the set {true, false}. A propositional formula F representing a
8 Chapter 2 PRELIMINARIES Throughout this thesis, we work with propositional or Boolean variables, that is, variables that take value in the set {true, false}. A propositional formula F representing a
Boolean Functions (Formulas) and Propositional Logic
 EECS 219C: Computer-Aided Verification Boolean Satisfiability Solving Part I: Basics Sanjit A. Seshia EECS, UC Berkeley Boolean Functions (Formulas) and Propositional Logic Variables: x 1, x 2, x 3,, x
EECS 219C: Computer-Aided Verification Boolean Satisfiability Solving Part I: Basics Sanjit A. Seshia EECS, UC Berkeley Boolean Functions (Formulas) and Propositional Logic Variables: x 1, x 2, x 3,, x
The Encoding Complexity of Network Coding
 The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email: mikel,spalex,bruck @caltech.edu Abstract In the multicast network
The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email: mikel,spalex,bruck @caltech.edu Abstract In the multicast network
Using Synthesis Techniques in SAT Solvers
 1. Introduction Using Synthesis Techniques in SAT Solvers Rolf Drechsler Institute of Computer Science University of Bremen 28359 Bremen, Germany drechsle@informatik.uni-bremen.de Abstract In many application
1. Introduction Using Synthesis Techniques in SAT Solvers Rolf Drechsler Institute of Computer Science University of Bremen 28359 Bremen, Germany drechsle@informatik.uni-bremen.de Abstract In many application
Exact Algorithms Lecture 7: FPT Hardness and the ETH
 Exact Algorithms Lecture 7: FPT Hardness and the ETH February 12, 2016 Lecturer: Michael Lampis 1 Reminder: FPT algorithms Definition 1. A parameterized problem is a function from (χ, k) {0, 1} N to {0,
Exact Algorithms Lecture 7: FPT Hardness and the ETH February 12, 2016 Lecturer: Michael Lampis 1 Reminder: FPT algorithms Definition 1. A parameterized problem is a function from (χ, k) {0, 1} N to {0,
Propositional Calculus: Boolean Algebra and Simplification. CS 270: Mathematical Foundations of Computer Science Jeremy Johnson
 Propositional Calculus: Boolean Algebra and Simplification CS 270: Mathematical Foundations of Computer Science Jeremy Johnson Propositional Calculus Topics Motivation: Simplifying Conditional Expressions
Propositional Calculus: Boolean Algebra and Simplification CS 270: Mathematical Foundations of Computer Science Jeremy Johnson Propositional Calculus Topics Motivation: Simplifying Conditional Expressions
On the Relation between SAT and BDDs for Equivalence Checking
 On the Relation between SAT and BDDs for Equivalence Checking Sherief Reda 1 Rolf Drechsler 2 Alex Orailoglu 1 1 Computer Science & Engineering Department University of California, San Diego La Jolla,
On the Relation between SAT and BDDs for Equivalence Checking Sherief Reda 1 Rolf Drechsler 2 Alex Orailoglu 1 1 Computer Science & Engineering Department University of California, San Diego La Jolla,
Bipartite Roots of Graphs
 Bipartite Roots of Graphs Lap Chi Lau Department of Computer Science University of Toronto Graph H is a root of graph G if there exists a positive integer k such that x and y are adjacent in G if and only
Bipartite Roots of Graphs Lap Chi Lau Department of Computer Science University of Toronto Graph H is a root of graph G if there exists a positive integer k such that x and y are adjacent in G if and only
To prove something about all Boolean expressions, we will need the following induction principle: Axiom 7.1 (Induction over Boolean expressions):
 CS 70 Discrete Mathematics for CS Fall 2003 Wagner Lecture 7 This lecture returns to the topic of propositional logic. Whereas in Lecture 1 we studied this topic as a way of understanding proper reasoning
CS 70 Discrete Mathematics for CS Fall 2003 Wagner Lecture 7 This lecture returns to the topic of propositional logic. Whereas in Lecture 1 we studied this topic as a way of understanding proper reasoning
Normal Forms for Boolean Expressions
 Normal Forms for Boolean Expressions A NORMAL FORM defines a class expressions s.t. a. Satisfy certain structural properties b. Are usually universal: able to express every boolean function 1. Disjunctive
Normal Forms for Boolean Expressions A NORMAL FORM defines a class expressions s.t. a. Satisfy certain structural properties b. Are usually universal: able to express every boolean function 1. Disjunctive
8 Matroid Intersection
 8 Matroid Intersection 8.1 Definition and examples 8.2 Matroid Intersection Algorithm 8.1 Definitions Given two matroids M 1 = (X, I 1 ) and M 2 = (X, I 2 ) on the same set X, their intersection is M 1
8 Matroid Intersection 8.1 Definition and examples 8.2 Matroid Intersection Algorithm 8.1 Definitions Given two matroids M 1 = (X, I 1 ) and M 2 = (X, I 2 ) on the same set X, their intersection is M 1
CSE 20 DISCRETE MATH. Fall
 CSE 20 DISCRETE MATH Fall 2017 http://cseweb.ucsd.edu/classes/fa17/cse20-ab/ Final exam The final exam is Saturday December 16 11:30am-2:30pm. Lecture A will take the exam in Lecture B will take the exam
CSE 20 DISCRETE MATH Fall 2017 http://cseweb.ucsd.edu/classes/fa17/cse20-ab/ Final exam The final exam is Saturday December 16 11:30am-2:30pm. Lecture A will take the exam in Lecture B will take the exam
4.1 Review - the DPLL procedure
 Applied Logic Lecture 4: Efficient SAT solving CS 4860 Spring 2009 Thursday, January 29, 2009 The main purpose of these notes is to help me organize the material that I used to teach today s lecture. They
Applied Logic Lecture 4: Efficient SAT solving CS 4860 Spring 2009 Thursday, January 29, 2009 The main purpose of these notes is to help me organize the material that I used to teach today s lecture. They
Functional extension of structural logic optimization techniques
 Functional extension of structural logic optimization techniques J. A. Espejo, L. Entrena, E. San Millán, E. Olías Universidad Carlos III de Madrid # e-mail: { ppespejo, entrena, quique, olias}@ing.uc3m.es
Functional extension of structural logic optimization techniques J. A. Espejo, L. Entrena, E. San Millán, E. Olías Universidad Carlos III de Madrid # e-mail: { ppespejo, entrena, quique, olias}@ing.uc3m.es
Disjoint Support Decompositions
 Chapter 4 Disjoint Support Decompositions We introduce now a new property of logic functions which will be useful to further improve the quality of parameterizations in symbolic simulation. In informal
Chapter 4 Disjoint Support Decompositions We introduce now a new property of logic functions which will be useful to further improve the quality of parameterizations in symbolic simulation. In informal
Some Hardness Proofs
 Some Hardness Proofs Magnus Lie Hetland January 2011 This is a very brief overview of some well-known hard (NP Hard and NP complete) problems, and the main ideas behind their hardness proofs. The document
Some Hardness Proofs Magnus Lie Hetland January 2011 This is a very brief overview of some well-known hard (NP Hard and NP complete) problems, and the main ideas behind their hardness proofs. The document
8.1 Polynomial-Time Reductions
 8.1 Polynomial-Time Reductions Classify Problems According to Computational Requirements Q. Which problems will we be able to solve in practice? A working definition. Those with polynomial-time algorithms.
8.1 Polynomial-Time Reductions Classify Problems According to Computational Requirements Q. Which problems will we be able to solve in practice? A working definition. Those with polynomial-time algorithms.
Bootcamp. Christoph Thiele. Summer An example of a primitive universe
 Bootcamp Christoph Thiele Summer 2012 0.1 An example of a primitive universe A primitive universe consists of primitive objects and primitive sets. This allows to form primitive statements as to which
Bootcamp Christoph Thiele Summer 2012 0.1 An example of a primitive universe A primitive universe consists of primitive objects and primitive sets. This allows to form primitive statements as to which
3 No-Wait Job Shops with Variable Processing Times
 3 No-Wait Job Shops with Variable Processing Times In this chapter we assume that, on top of the classical no-wait job shop setting, we are given a set of processing times for each operation. We may select
3 No-Wait Job Shops with Variable Processing Times In this chapter we assume that, on top of the classical no-wait job shop setting, we are given a set of processing times for each operation. We may select
BerkMin: a Fast and Robust Sat-Solver
 BerkMin: a Fast and Robust Sat-Solver Evgueni Goldberg Cadence Berkeley Labs(USA), Email: egold@cadence.com Yakov Novikov Academy of Sciences (Belarus), Email: nov@newman.bas-net.by Abstract We describe
BerkMin: a Fast and Robust Sat-Solver Evgueni Goldberg Cadence Berkeley Labs(USA), Email: egold@cadence.com Yakov Novikov Academy of Sciences (Belarus), Email: nov@newman.bas-net.by Abstract We describe
Chapter 8. NP-complete problems
 Chapter 8. NP-complete problems Search problems E cient algorithms We have developed algorithms for I I I I I finding shortest paths in graphs, minimum spanning trees in graphs, matchings in bipartite
Chapter 8. NP-complete problems Search problems E cient algorithms We have developed algorithms for I I I I I finding shortest paths in graphs, minimum spanning trees in graphs, matchings in bipartite
Introduction to Algorithms / Algorithms I Lecturer: Michael Dinitz Topic: Approximation algorithms Date: 11/18/14
 600.363 Introduction to Algorithms / 600.463 Algorithms I Lecturer: Michael Dinitz Topic: Approximation algorithms Date: 11/18/14 23.1 Introduction We spent last week proving that for certain problems,
600.363 Introduction to Algorithms / 600.463 Algorithms I Lecturer: Michael Dinitz Topic: Approximation algorithms Date: 11/18/14 23.1 Introduction We spent last week proving that for certain problems,
/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Approximation algorithms Date: 11/27/18
 601.433/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Approximation algorithms Date: 11/27/18 22.1 Introduction We spent the last two lectures proving that for certain problems, we can
601.433/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Approximation algorithms Date: 11/27/18 22.1 Introduction We spent the last two lectures proving that for certain problems, we can
A Novel SAT All-Solutions Solver for Efficient Preimage Computation
 A Novel SAT All-Solutions Solver for Efficient Preimage Computation Bin Li Department of ECE Virginia Tech. Blacksburg, VA, 24061 Michael S. Hsiao Department of ECE Virginia Tech. Blacksburg, VA, 24061
A Novel SAT All-Solutions Solver for Efficient Preimage Computation Bin Li Department of ECE Virginia Tech. Blacksburg, VA, 24061 Michael S. Hsiao Department of ECE Virginia Tech. Blacksburg, VA, 24061
Acceleration of SAT-based Iterative Property Checking
 Acceleration of SAT-based Iterative Property Checking Daniel Große Rolf Drechsler Institute of Computer Science University of Bremen 28359 Bremen, Germany {grosse, drechsle}@informatik.uni-bremen.de Abstract
Acceleration of SAT-based Iterative Property Checking Daniel Große Rolf Drechsler Institute of Computer Science University of Bremen 28359 Bremen, Germany {grosse, drechsle}@informatik.uni-bremen.de Abstract
1.4 Normal Forms. We define conjunctions of formulas as follows: and analogously disjunctions: Literals and Clauses
 1.4 Normal Forms We define conjunctions of formulas as follows: 0 i=1 F i =. 1 i=1 F i = F 1. n+1 i=1 F i = n i=1 F i F n+1. and analogously disjunctions: 0 i=1 F i =. 1 i=1 F i = F 1. n+1 i=1 F i = n
1.4 Normal Forms We define conjunctions of formulas as follows: 0 i=1 F i =. 1 i=1 F i = F 1. n+1 i=1 F i = n i=1 F i F n+1. and analogously disjunctions: 0 i=1 F i =. 1 i=1 F i = F 1. n+1 i=1 F i = n
Massively Parallel Seesaw Search for MAX-SAT
 Massively Parallel Seesaw Search for MAX-SAT Harshad Paradkar Rochester Institute of Technology hp7212@rit.edu Prof. Alan Kaminsky (Advisor) Rochester Institute of Technology ark@cs.rit.edu Abstract The
Massively Parallel Seesaw Search for MAX-SAT Harshad Paradkar Rochester Institute of Technology hp7212@rit.edu Prof. Alan Kaminsky (Advisor) Rochester Institute of Technology ark@cs.rit.edu Abstract The
Parallel and Distributed Computing
 Parallel and Distributed Computing Project Assignment MAX-SAT SOLVER Version 1.0 (07/03/2016) 2015/2016 2nd Semester CONTENTS Contents 1 Introduction 2 2 Problem Description 2 2.1 Illustrative Example...................................
Parallel and Distributed Computing Project Assignment MAX-SAT SOLVER Version 1.0 (07/03/2016) 2015/2016 2nd Semester CONTENTS Contents 1 Introduction 2 2 Problem Description 2 2.1 Illustrative Example...................................
Solving 3-SAT. Radboud University Nijmegen. Bachelor Thesis. Supervisors: Henk Barendregt Alexandra Silva. Author: Peter Maandag s
 Solving 3-SAT Radboud University Nijmegen Bachelor Thesis Author: Peter Maandag s3047121 Supervisors: Henk Barendregt Alexandra Silva July 2, 2012 Contents 1 Introduction 2 1.1 Problem context............................
Solving 3-SAT Radboud University Nijmegen Bachelor Thesis Author: Peter Maandag s3047121 Supervisors: Henk Barendregt Alexandra Silva July 2, 2012 Contents 1 Introduction 2 1.1 Problem context............................
CMPSCI 311: Introduction to Algorithms Practice Final Exam
 CMPSCI 311: Introduction to Algorithms Practice Final Exam Name: ID: Instructions: Answer the questions directly on the exam pages. Show all your work for each question. Providing more detail including
CMPSCI 311: Introduction to Algorithms Practice Final Exam Name: ID: Instructions: Answer the questions directly on the exam pages. Show all your work for each question. Providing more detail including
BOOLEAN ALGEBRA AND CIRCUITS
 UNIT 3 Structure BOOLEAN ALGEBRA AND CIRCUITS Boolean Algebra and 3. Introduction 3. Objectives 3.2 Boolean Algebras 3.3 Logic 3.4 Boolean Functions 3.5 Summary 3.6 Solutions/ Answers 3. INTRODUCTION This
UNIT 3 Structure BOOLEAN ALGEBRA AND CIRCUITS Boolean Algebra and 3. Introduction 3. Objectives 3.2 Boolean Algebras 3.3 Logic 3.4 Boolean Functions 3.5 Summary 3.6 Solutions/ Answers 3. INTRODUCTION This
CS 395T Computational Learning Theory. Scribe: Wei Tang
 CS 395T Computational Learning Theory Lecture 1: September 5th, 2007 Lecturer: Adam Klivans Scribe: Wei Tang 1.1 Introduction Many tasks from real application domain can be described as a process of learning.
CS 395T Computational Learning Theory Lecture 1: September 5th, 2007 Lecturer: Adam Klivans Scribe: Wei Tang 1.1 Introduction Many tasks from real application domain can be described as a process of learning.
Computational problems. Lecture 2: Combinatorial search and optimisation problems. Computational problems. Examples. Example
 Lecture 2: Combinatorial search and optimisation problems Different types of computational problems Examples of computational problems Relationships between problems Computational properties of different
Lecture 2: Combinatorial search and optimisation problems Different types of computational problems Examples of computational problems Relationships between problems Computational properties of different
Example of a Demonstration that a Problem is NP-Complete by reduction from CNF-SAT
 20170926 CNF-SAT: CNF-SAT is a problem in NP, defined as follows: Let E be a Boolean expression with m clauses and n literals (literals = variables, possibly negated), in which - each clause contains only
20170926 CNF-SAT: CNF-SAT is a problem in NP, defined as follows: Let E be a Boolean expression with m clauses and n literals (literals = variables, possibly negated), in which - each clause contains only
Full CNF Encoding: The Counting Constraints Case
 Full CNF Encoding: The Counting Constraints Case Olivier Bailleux 1 and Yacine Boufkhad 2 1 LERSIA, Université de Bourgogne Avenue Alain Savary, BP 47870 21078 Dijon Cedex olivier.bailleux@u-bourgogne.fr
Full CNF Encoding: The Counting Constraints Case Olivier Bailleux 1 and Yacine Boufkhad 2 1 LERSIA, Université de Bourgogne Avenue Alain Savary, BP 47870 21078 Dijon Cedex olivier.bailleux@u-bourgogne.fr
NP-Complete Reductions 2
 x 1 x 1 x 2 x 2 x 3 x 3 x 4 x 4 12 22 32 CS 447 11 13 21 23 31 33 Algorithms NP-Complete Reductions 2 Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline NP-Complete
x 1 x 1 x 2 x 2 x 3 x 3 x 4 x 4 12 22 32 CS 447 11 13 21 23 31 33 Algorithms NP-Complete Reductions 2 Prof. Gregory Provan Department of Computer Science University College Cork 1 Lecture Outline NP-Complete
Model Checking I Binary Decision Diagrams
 /42 Model Checking I Binary Decision Diagrams Edmund M. Clarke, Jr. School of Computer Science Carnegie Mellon University Pittsburgh, PA 523 2/42 Binary Decision Diagrams Ordered binary decision diagrams
/42 Model Checking I Binary Decision Diagrams Edmund M. Clarke, Jr. School of Computer Science Carnegie Mellon University Pittsburgh, PA 523 2/42 Binary Decision Diagrams Ordered binary decision diagrams
NiVER: Non Increasing Variable Elimination Resolution for Preprocessing SAT instances
 NiVER: Non Increasing Variable Elimination Resolution for Preprocessing SAT instances Sathiamoorthy Subbarayan 1 and Dhiraj K Pradhan 2 1 Department of Innovation, IT-University of Copenhagen, Copenhagen,
NiVER: Non Increasing Variable Elimination Resolution for Preprocessing SAT instances Sathiamoorthy Subbarayan 1 and Dhiraj K Pradhan 2 1 Department of Innovation, IT-University of Copenhagen, Copenhagen,
EECS 219C: Formal Methods Binary Decision Diagrams (BDDs) Sanjit A. Seshia EECS, UC Berkeley
 EECS 219C: Formal Methods Binary Decision Diagrams (BDDs) Sanjit A. Seshia EECS, UC Berkeley Boolean Function Representations Syntactic: e.g.: CNF, DNF (SOP), Circuit Semantic: e.g.: Truth table, Binary
EECS 219C: Formal Methods Binary Decision Diagrams (BDDs) Sanjit A. Seshia EECS, UC Berkeley Boolean Function Representations Syntactic: e.g.: CNF, DNF (SOP), Circuit Semantic: e.g.: Truth table, Binary
Algorithms for SAT and k-sat problems
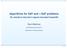 Algorithms for SAT and k-sat problems On solutions that don t require bounded treewidth Pauli Miettinen Pauli.Miettinen@cs.Helsinki.FI Department of Computer Science - p. 1/23 - p. 2/23 Problem definitions
Algorithms for SAT and k-sat problems On solutions that don t require bounded treewidth Pauli Miettinen Pauli.Miettinen@cs.Helsinki.FI Department of Computer Science - p. 1/23 - p. 2/23 Problem definitions
Set Manipulation with Boolean Functional Vectors for Symbolic Reachability Analysis
 Set Manipulation with Boolean Functional Vectors for Symbolic Reachability Analysis Amit Goel Department of ECE, Carnegie Mellon University, PA. 15213. USA. agoel@ece.cmu.edu Randal E. Bryant Computer
Set Manipulation with Boolean Functional Vectors for Symbolic Reachability Analysis Amit Goel Department of ECE, Carnegie Mellon University, PA. 15213. USA. agoel@ece.cmu.edu Randal E. Bryant Computer
COMP4418 Knowledge Representation and Reasoning
 COMP4418 Knowledge Representation and Reasoning Week 3 Practical Reasoning David Rajaratnam Click to edit Present s Name Practical Reasoning - My Interests Cognitive Robotics. Connect high level cognition
COMP4418 Knowledge Representation and Reasoning Week 3 Practical Reasoning David Rajaratnam Click to edit Present s Name Practical Reasoning - My Interests Cognitive Robotics. Connect high level cognition
Treewidth and graph minors
 Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Binary Decision Diagrams
 Binary Decision Diagrams 2-CS-626- Formal Verification Department of Computer Science University of Cincinnati Introduction Binary Decision Diagrams (BDD) [, 8] are a general, graphical representation
Binary Decision Diagrams 2-CS-626- Formal Verification Department of Computer Science University of Cincinnati Introduction Binary Decision Diagrams (BDD) [, 8] are a general, graphical representation
! Greed. O(n log n) interval scheduling. ! Divide-and-conquer. O(n log n) FFT. ! Dynamic programming. O(n 2 ) edit distance.
 Algorithm Design Patterns and Anti-Patterns Chapter 8 NP and Computational Intractability Algorithm design patterns. Ex.! Greed. O(n log n) interval scheduling.! Divide-and-conquer. O(n log n) FFT.! Dynamic
Algorithm Design Patterns and Anti-Patterns Chapter 8 NP and Computational Intractability Algorithm design patterns. Ex.! Greed. O(n log n) interval scheduling.! Divide-and-conquer. O(n log n) FFT.! Dynamic
8 NP-complete problem Hard problems: demo
 Ch8 NPC Millennium Prize Problems http://en.wikipedia.org/wiki/millennium_prize_problems 8 NP-complete problem Hard problems: demo NP-hard (Non-deterministic Polynomial-time hard), in computational complexity
Ch8 NPC Millennium Prize Problems http://en.wikipedia.org/wiki/millennium_prize_problems 8 NP-complete problem Hard problems: demo NP-hard (Non-deterministic Polynomial-time hard), in computational complexity
EECS 219C: Formal Methods Boolean Satisfiability Solving. Sanjit A. Seshia EECS, UC Berkeley
 EECS 219C: Formal Methods Boolean Satisfiability Solving Sanjit A. Seshia EECS, UC Berkeley The Boolean Satisfiability Problem (SAT) Given: A Boolean formula F(x 1, x 2, x 3,, x n ) Can F evaluate to 1
EECS 219C: Formal Methods Boolean Satisfiability Solving Sanjit A. Seshia EECS, UC Berkeley The Boolean Satisfiability Problem (SAT) Given: A Boolean formula F(x 1, x 2, x 3,, x n ) Can F evaluate to 1
CSE Theory of Computing Fall 2017 Project 1-SAT Solving
 CSE 30151 Theory of Computing Fall 2017 Project 1-SAT Solving Version 3: Sept. 21, 2017 The purpose of this project is to gain an understanding of one of the most central problems of computing: Boolean
CSE 30151 Theory of Computing Fall 2017 Project 1-SAT Solving Version 3: Sept. 21, 2017 The purpose of this project is to gain an understanding of one of the most central problems of computing: Boolean
Computer Science Technical Report
 Computer Science Technical Report Feasibility of Stepwise Addition of Multitolerance to High Atomicity Programs Ali Ebnenasir and Sandeep S. Kulkarni Michigan Technological University Computer Science
Computer Science Technical Report Feasibility of Stepwise Addition of Multitolerance to High Atomicity Programs Ali Ebnenasir and Sandeep S. Kulkarni Michigan Technological University Computer Science
A Scalable Algorithm for Minimal Unsatisfiable Core Extraction
 A Scalable Algorithm for Minimal Unsatisfiable Core Extraction Nachum Dershowitz 1, Ziyad Hanna 2, and Alexander Nadel 1,2 1 School of Computer Science, Tel Aviv University, Ramat Aviv, Israel {nachumd,
A Scalable Algorithm for Minimal Unsatisfiable Core Extraction Nachum Dershowitz 1, Ziyad Hanna 2, and Alexander Nadel 1,2 1 School of Computer Science, Tel Aviv University, Ramat Aviv, Israel {nachumd,
Lecture 2: Symbolic Model Checking With SAT
 Lecture 2: Symbolic Model Checking With SAT Edmund M. Clarke, Jr. School of Computer Science Carnegie Mellon University Pittsburgh, PA 15213 (Joint work over several years with: A. Biere, A. Cimatti, Y.
Lecture 2: Symbolic Model Checking With SAT Edmund M. Clarke, Jr. School of Computer Science Carnegie Mellon University Pittsburgh, PA 15213 (Joint work over several years with: A. Biere, A. Cimatti, Y.
Integrity Constraints (Chapter 7.3) Overview. Bottom-Up. Top-Down. Integrity Constraint. Disjunctive & Negative Knowledge. Proof by Refutation
 CSE560 Class 10: 1 c P. Heeman, 2010 Integrity Constraints Overview Disjunctive & Negative Knowledge Resolution Rule Bottom-Up Proof by Refutation Top-Down CSE560 Class 10: 2 c P. Heeman, 2010 Integrity
CSE560 Class 10: 1 c P. Heeman, 2010 Integrity Constraints Overview Disjunctive & Negative Knowledge Resolution Rule Bottom-Up Proof by Refutation Top-Down CSE560 Class 10: 2 c P. Heeman, 2010 Integrity
Paths, Flowers and Vertex Cover
 Paths, Flowers and Vertex Cover Venkatesh Raman M. S. Ramanujan Saket Saurabh Abstract It is well known that in a bipartite (and more generally in a König) graph, the size of the minimum vertex cover is
Paths, Flowers and Vertex Cover Venkatesh Raman M. S. Ramanujan Saket Saurabh Abstract It is well known that in a bipartite (and more generally in a König) graph, the size of the minimum vertex cover is
Propositional Logic. Andreas Klappenecker
 Propositional Logic Andreas Klappenecker Propositions A proposition is a declarative sentence that is either true or false (but not both). Examples: College Station is the capital of the USA. There are
Propositional Logic Andreas Klappenecker Propositions A proposition is a declarative sentence that is either true or false (but not both). Examples: College Station is the capital of the USA. There are
1. Suppose you are given a magic black box that somehow answers the following decision problem in polynomial time:
 1. Suppose you are given a magic black box that somehow answers the following decision problem in polynomial time: Input: A CNF formula ϕ with n variables x 1, x 2,..., x n. Output: True if there is an
1. Suppose you are given a magic black box that somehow answers the following decision problem in polynomial time: Input: A CNF formula ϕ with n variables x 1, x 2,..., x n. Output: True if there is an
FRAIGs: A Unifying Representation for Logic Synthesis and Verification
 FRAIGs: A Unifying Representation for Logic Synthesis and Verification Alan Mishchenko, Satrajit Chatterjee, Roland Jiang, Robert Brayton Department of EECS, University of California, Berkeley {alanmi,
FRAIGs: A Unifying Representation for Logic Synthesis and Verification Alan Mishchenko, Satrajit Chatterjee, Roland Jiang, Robert Brayton Department of EECS, University of California, Berkeley {alanmi,
ALGORITHMS EXAMINATION Department of Computer Science New York University December 17, 2007
 ALGORITHMS EXAMINATION Department of Computer Science New York University December 17, 2007 This examination is a three hour exam. All questions carry the same weight. Answer all of the following six questions.
ALGORITHMS EXAMINATION Department of Computer Science New York University December 17, 2007 This examination is a three hour exam. All questions carry the same weight. Answer all of the following six questions.
Module 11. Directed Graphs. Contents
 Module 11 Directed Graphs Contents 11.1 Basic concepts......................... 256 Underlying graph of a digraph................ 257 Out-degrees and in-degrees.................. 258 Isomorphism..........................
Module 11 Directed Graphs Contents 11.1 Basic concepts......................... 256 Underlying graph of a digraph................ 257 Out-degrees and in-degrees.................. 258 Isomorphism..........................
Chapter 8. NP and Computational Intractability. Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved.
 Chapter 8 NP and Computational Intractability Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved. 1 Algorithm Design Patterns and Anti-Patterns Algorithm design patterns.
Chapter 8 NP and Computational Intractability Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved. 1 Algorithm Design Patterns and Anti-Patterns Algorithm design patterns.
An Efficient Learning Procedure for Multiple Implication Checks
 An Efficient Learning Procedure for Multiple Implication Checks Yakov Novikov, Academy of ciences (elarus), email: NOV@newman.bas-net.by Evgueni Goldberg,Cadence erkeley Labs (UA) email: egold@cadence.com
An Efficient Learning Procedure for Multiple Implication Checks Yakov Novikov, Academy of ciences (elarus), email: NOV@newman.bas-net.by Evgueni Goldberg,Cadence erkeley Labs (UA) email: egold@cadence.com
Reductions and Satisfiability
 Reductions and Satisfiability 1 Polynomial-Time Reductions reformulating problems reformulating a problem in polynomial time independent set and vertex cover reducing vertex cover to set cover 2 The Satisfiability
Reductions and Satisfiability 1 Polynomial-Time Reductions reformulating problems reformulating a problem in polynomial time independent set and vertex cover reducing vertex cover to set cover 2 The Satisfiability
Watching Clauses in Quantified Boolean Formulae
 Watching Clauses in Quantified Boolean Formulae Andrew G D Rowley University of St. Andrews, Fife, Scotland agdr@dcs.st-and.ac.uk Abstract. I present a way to speed up the detection of pure literals and
Watching Clauses in Quantified Boolean Formulae Andrew G D Rowley University of St. Andrews, Fife, Scotland agdr@dcs.st-and.ac.uk Abstract. I present a way to speed up the detection of pure literals and
Linear Time Unit Propagation, Horn-SAT and 2-SAT
 Notes on Satisfiability-Based Problem Solving Linear Time Unit Propagation, Horn-SAT and 2-SAT David Mitchell mitchell@cs.sfu.ca September 25, 2013 This is a preliminary draft of these notes. Please do
Notes on Satisfiability-Based Problem Solving Linear Time Unit Propagation, Horn-SAT and 2-SAT David Mitchell mitchell@cs.sfu.ca September 25, 2013 This is a preliminary draft of these notes. Please do
VLSI Logic Test, Validation and Verification Lecture 7 Properties & Applications of Binary Decision Diagrams
 VLSI Logic Test, Validation and Verification Lecture 7 Properties & Applications of Binary Decision Diagrams 1 Instructor: Priyank Kalla Department of Electrical and Computer Engineering University of
VLSI Logic Test, Validation and Verification Lecture 7 Properties & Applications of Binary Decision Diagrams 1 Instructor: Priyank Kalla Department of Electrical and Computer Engineering University of
Complexity and approximation of satisfactory partition problems
 Complexity and approximation of satisfactory partition problems Cristina Bazgan, Zsolt Tuza, and Daniel Vanderpooten LAMSADE, Université Paris-Dauphine, France {bazgan,vdp}@lamsade.dauphine.fr Computer
Complexity and approximation of satisfactory partition problems Cristina Bazgan, Zsolt Tuza, and Daniel Vanderpooten LAMSADE, Université Paris-Dauphine, France {bazgan,vdp}@lamsade.dauphine.fr Computer
Combining Abstraction Refinement and SAT-Based Model Checking
 Combining Abstraction Refinement and SAT-Based Model Checking Nina Amla and Kenneth L. McMillan Cadence Design Systems Abstract. Unbounded model checking methods based on Boolean satisfiability (SAT) solvers
Combining Abstraction Refinement and SAT-Based Model Checking Nina Amla and Kenneth L. McMillan Cadence Design Systems Abstract. Unbounded model checking methods based on Boolean satisfiability (SAT) solvers
CS-E3220 Declarative Programming
 CS-E3220 Declarative Programming Lecture 5: Premises for Modern SAT Solving Aalto University School of Science Department of Computer Science Spring 2018 Motivation The Davis-Putnam-Logemann-Loveland (DPLL)
CS-E3220 Declarative Programming Lecture 5: Premises for Modern SAT Solving Aalto University School of Science Department of Computer Science Spring 2018 Motivation The Davis-Putnam-Logemann-Loveland (DPLL)
Complexity Classes and Polynomial-time Reductions
 COMPSCI 330: Design and Analysis of Algorithms April 19, 2016 Complexity Classes and Polynomial-time Reductions Lecturer: Debmalya Panigrahi Scribe: Tianqi Song 1 Overview In this lecture, we introduce
COMPSCI 330: Design and Analysis of Algorithms April 19, 2016 Complexity Classes and Polynomial-time Reductions Lecturer: Debmalya Panigrahi Scribe: Tianqi Song 1 Overview In this lecture, we introduce
QuteSat. A Robust Circuit-Based SAT Solver for Complex Circuit Structure. Chung-Yang (Ric) Huang National Taiwan University
 QuteSat A Robust Circuit-Based SAT Solver for Complex Circuit Structure Chung-Yang (Ric) Huang National Taiwan University To appear: DATE 27 2/1/27 Fact Sheet (Background) Boolean Satisfiability (SAT)
QuteSat A Robust Circuit-Based SAT Solver for Complex Circuit Structure Chung-Yang (Ric) Huang National Taiwan University To appear: DATE 27 2/1/27 Fact Sheet (Background) Boolean Satisfiability (SAT)
6. Lecture notes on matroid intersection
 Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans May 2, 2017 6. Lecture notes on matroid intersection One nice feature about matroids is that a simple greedy algorithm
Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans May 2, 2017 6. Lecture notes on matroid intersection One nice feature about matroids is that a simple greedy algorithm
PCP and Hardness of Approximation
 PCP and Hardness of Approximation January 30, 2009 Our goal herein is to define and prove basic concepts regarding hardness of approximation. We will state but obviously not prove a PCP theorem as a starting
PCP and Hardness of Approximation January 30, 2009 Our goal herein is to define and prove basic concepts regarding hardness of approximation. We will state but obviously not prove a PCP theorem as a starting
