Threshold DSS Signatures without a Trusted Party
|
|
|
- Charity Norman
- 6 years ago
- Views:
Transcription
1 Threshold DSS Signatures without a Trusted Party Susan K. Langford* Department of Electrical Engineering Stanford University Stanford CA Abstract. A t-out-of-l threshold signature scheme allows 1 members of a group to own shares of a private key such that any t of them can create a signature, while fewer than t cannot. Most of these schemes require a single trusted party to create the secret key and calculate the 1 shares. Harn [lo] and Li, Hwang, and Lee [13] have devised threshold schemes based on the difficulty of solving the discrete logarithm problem which do not require such a trusted party. This paper extends that property to 2-out-of4 threshold signatures based on the Digital Signature Standard and describes two possible generalizations to a t-out-of4 scheme. 1 Introduction A digital signature, like a handwritten signature, is used to verify the sender of a particular message. The signer is generally a single person. However, when the message is on behalf of an organization, a valid message may require the approval of several people. A common example of this policy is a large bank transaction, which requires signatures from two people. Such a policy could be implemented by having a separate digital signature for every required signer, but this solution increases the effort to verify the message linearly with the number of signers. An alternative method is a threshold signature scheme. In a t-out-of4 threshold signature scheme, there is one public key for the group while the private key is shared among the 1 members of the group. Any t members can cooperate to create a digital signature without revealing their shares of the private key. Fewer than t members cannot create a valid signature. Threshold signatures are closely related to the concept of threshold cryptography, first introduced by Desmedt [5]. A number of group oriented systems have been proposed and, for an overview of the field, t,he reader is referred to [6]. Threshold signature schemes have been proposed using RSA signatures [7, 11, 91. These schemes require the use of a trusted center to generate the private key and calculate the share values. While the existence of such a center is not an unreasonable assumption, there are two potential problems. First, for many * This work was supported by the National Semiconductor Corporation under the Fellow/Mentor/Advisor [FMA] program of Stanford University Center for Integrated Systems. D. Coppersmith (Ed.): Advances in Cryptology - CRYPT0 '95, LNCS 963, pp , Spnnger-Verlag Berlin Heidelberg 1995
2 398 applications, there is no one person or device which can be completely trusted by all members of the group. Second, the use of a key center creates a single point failure. Any security lapse at the key center can reveal the private key. Once the shares are distributed, careless handling of any one share reveals no information about the private key. At least t shares must be compromised before an attacker has any useful information. To avoid these problems, Harn [lo] introduced a scheme based on a modified ElGamal signature which does not require a trusted key center. Li, Hwang, and Lee used Harn's scheme to allow the receiver to verify which members of the group signed a given message [13]. These schemes show that it is possible to generate threshold signatures without a trusted party, but leave open the question of how to create such schemes.for other signature algorithms. This paper extends the idea of distributed generation of the private key by proposing three threshold schemes based on the Digital Signature Standard (DSS). The first is a 2-out-of-l threshold scheme which requires a small amount of interaction between the co-signers, but does not require the use of a trusted center to generate the shares. This scheme does need a third person as combiner, but the combiner need not be any more trusted than other members of the group. In fact, the combiner may be a member of the group who is not a co-signer. The second scheme uses precomputed values to create t-out-of-1 threshold signatures. The key generation center for this scheme can be distributed into three centers, any two of which must be compromised to expose the private key. The third scheme does not require the use of a semi-trusted combiner or precomputed lists. However, the scheme requires t2 -t + 1 signers for t-out-of-l security. These three schemes are the first threshold schemes to be proposed using DSS. 2 Digital Signature Standard The Digital Signature Standard (DSS) [l] is based on the difficulty of computing discrete logs. For this algorithm, we need the following parameters. 1. p = a prime modulus, L bits long, where L , and L is a multiple of q = a 160-bit prime divisor of p g = h(p-')/q mod p, where h is any integer with 0 < h < p such that g mod p > 1 (g is an element of order q in GF(p)). 4. x = an integer with 0 < x < q. 5. y =gx modp. 6. M = a one-way hash of the message to be signed. 7. k = a random integer with 0 < k < q. The system parameters p, q, and g are public. The user's public key and private key are y and 2, respectively. To create a signature, the user chooses a random k, computes IC-' mod q, and calculates T = (gk-l mod p) mod q,
3 399 and s = Ic(M + m) mod q. The pair (r, s) is the desired signature. A new value for k must be generated for each new signature. Note: For this paper, k and k-' are switched from the standard DSS nota- tion. This is merely to simplify the following discussion. Since k is random, this interchange is immaterial. To verify a signature, the recipient calculates gma-'yrs-' mod p and checks that the result equals P. Since y = gz, when we multiply the two values together, the exponent becomes Ms-' + trs-l = (M + 2r)s-l mod q. This expression reduces to k-' in the exponent, yielding the desired result r as in equation (1). 3 Secret Sharing of Sums and Products Shamir [15] developed a secret sharing scheme based on polynomials over a finite field. A polynomial f of degree t - 1 is chosen such that f(0) is the secret. Every participant i, (i # 0), in the scheme is given f(i), a share of the secret. Any t of these shares can be used to calculate f(0). Further, if any t - 1 of these shares are combined, then no information is revealed about f(0). In general, from any t distinct points of a degree t - 1 polynomial, we can calculate the value of any other point of the polynomial by interpolation. For a set T oft shareholders with shares f(zj), over the field GF(q), the formula for this interpolation is Therefore the formula for calculating the secret f(0) is the linear combination of the shares, where is a constant which can be publicly determined because its value does not depend on any secret information. Although generally defined over a field, this scheme can be defined mod n, where n is not prime, if the quantities zi - zj have inverses for all i and j. If the shareholders are numbered from 1 to I, this is equivalent to requiring that n has no prime factors less than 1. It is natural to think of secret sharing in terms of an existing secret owned by an individual or device. The owner of the secret then creates and distributes the shares. However, we can also implement secret sharing so that the secret is created as part of the process of creating the shares. The value of the secret is determined by the value of the shares, but the secret itself is not explicitly calculated at the time the shares are created. This process will be useful for creating threshold signatures, where we want to create shares of a private key.
4 400 The private key itself is never used directly, so there is no reason that it ever needs to be explicitly calculated. Shamir's scheme can be used to implement this idea of implicitly creating the secret. Suppose that a group wishes to create shares in a secret which is the sum of two numbers, without any one person ever knowing that sum. Person A creates a secret sharing polynomial f ~(2) with secret SA (i.e., f ~(0) = SA)] and distributes the shares. Similarly, person B creates fg (x) with secret Sg and distributes the resulting shares. Then f(z) = f~(t) + fg(z) is a new polynomial with secret f(0) = f~(0) + fg(0) = SA + SB. If shareholder i has received fa(i) and fg(i), he can create the share of the new polynomial by adding the two shares, f(i) = f~(i) + fg(i). Clearly, this scheme is not limited to two equations, the only requirement for additional equations is that the numbering of the shareholders remains consistent. Shareholder i must receive the polynomial evaluated at point i for all polynomials involved. If we use these polynomials in the exponent, then we create shares which multiply together] rather than add. Given a prime q and an element,o of order n in GF(q), we can create a polynomial f(z) mod n and define the secret mod q. The secret can be recovered by exponentiating the normal linear interpolation formula. As explained above, n must not have any small prime factors or this interpolation is not possible. We will use this multiplicativesharing technique to create the shares of the private key in our threshold scheme. The methods for creating additive or multiplicative shares without a trusted center are well known. However, generating DSS threshold signatures leads to a new problem-creating shares of an arbitrary product. We would like to be able to have every member of a group generate a number and calculate shares which combine linearly to form the product of those numbers. We have not solved this problem in general. The remainder of this section explains the solution for the case of the product of two numbers. Suppose Alice knows secret A and Bob knows secret B. Together, they would like to create shares which can produce the secret AB mod q. However, they would like to create these shares without having any one person know the secret AB. To do this, they need the help of a third person, Charles. 1. Alice generates a random number RA and Bob generates RB, where 0 5 RA,RE < q. 2. Alice privately sends Charles A - RA mod q and privately sends Bob RA. Bob privately sends Charles B - Rg mod q and privately sends Alice RE. 3. Alice calculates SA = ARB - ~ RARB mod q, and Bob calculates SB = BRA - ~RARB mod q. Charles calculates Sc = (A- RA)(B - RE) mod q. The sum of the three secrets, SA, SB, and Sc, is the desired product, AB. Notice that no single person has sufficient information to calculate AB, but that any two of the three can work together to recover the secret. Thus, Charles must be trusted exactly the same amount as Alice or Bob.
5 out-of-l Threshold Signature Algorithm 4.1 DSS Parameters The 2-out-of-I threshold signature scheme places an additional requirement on the parameters of DSS. We require that (q - 1)/2 has no prime divisors smaller than I, the number of shareholders.2 This requirement will slow the generation of the system parameters slightly. We will also need an additional parameter, p, where p is the square of a primitive element mod q. (p has order (q - 1)/2.) 4.2 Creating the Shares To create the 2-out-of-! threshold signature algorithm, every shareholder needs a multiplicative share of the secret key, x. We will define 2 = /3fco) mod q, where f is a secret sharing polynomial. Since p is the square of a primitive element, arithmetic in the exponent is done mod (q - 1)/2. Therefore, we will define f mod (q - 1)/2. All necessary inverses exist since q has been chosen such that (q - 1)/2 has no prime factors less than 1. As described in Section 3, the generation of the secret sharing polynomial f can be accomplished cooperatively, rather than relying on a trusted center. Each member of the group generates a degree one polynomial mod (q - 1)/2. For instance, if Alice is member number 1, she generates fl(z) = ylz + 61 mod (q - 1)/2, where 71 and 61 are random. She now generates shares of f1 and distributes them privately to each member of the group, taking care to give each member i the share fi (i). When every member of the group has generated and distributed shares of their polynomial, Alice has fi (1), f2( l),... fi (1). She now adds them together. Since the polynomials are linear, the result gives her f(l), where f(z) = fl(z) + fz(z)+...+fi(z). Now everyone.has a share of the polynomial f, yet no single person knows f( 0). To calculate the public key, member a computes za = T*,-f(') modq and member b computes Zb = pbgrf(b) mod q. The product of these two numbers is the secret key since ZaZb = T02*f(a)+cb*wf(b) = pf(o) = mod q. Members a and b can use their values of x, and zb in a Diffie-Hellman exchange to calculate y = gxacb modp. This process can be repeated for any pair, allowing group members to check their shares without revealing them. 4.3 Creating the Signature The signature is created using the method for creating shares of a product described in Section 3. We will be creating shares of the values k and kx. Creating a signature requires two shareholders, Alice and Bob, and a trusted combiner, Charles. Any two of these three can cooperate to recover the secret, so Charles must be trusted the same amount as any shareholder. For simplicity, we could require that (q - 1)/2 be prime. However, this stronger requirement is not necessary.
6 402 To create a signature, Alice generates three independent random numbers, ka, RA~, and RA~, uniformly between 0 and q - 1. She then sends gka- mod p, RA~, and RA~ privately to Bob. Similarly, Bob sends gkb- mod pi RBI, and Rg2 privately to Alice. Alice and Bob can avoid the need for a Secure channel by generating RA~, RA~, RBI, and RB~ by a Diffie-Hellman exchange. Alice and Bob can now calculate r = (gka- *B- mod p) mod q, and send the result publicly to Charles. Alice calculates XA =, FA,if(A) mod q for her private use. Note that X A X ~ = x mod q and kakg = k mod q. So Alice can use the number ka and the method of Section 3 to create a sharing scheme for k. Similarly, she can create a sharing scheme for kx. Let sa1 be Alice s share of k and SA~ be Alice s share of kx. Alice computes She then sends SA, k~ - RA~, and kaza - RA~ privately to Charles. Similarly, Bob computes and sends SB, kg - RBI, and kgzg - Rs2 privately to Charles. Charles now computes his shares of k and kz, Sci = ( k - ~ R~i)(kg - Rsi) mod q and sc2 = (kaza - RA2)(kBZB - RB2) mod Q. He can now calculate s = SA + 8~ + (SclM + Scar) mod q. The result (r, s) is a valid DSS signature, since = (sa1 + SBl + SCl)M + (sa2 + sb2 + sc2)r (9) = km + kxr (10) = k (M + zr) mod q. (11) 4.4 Maintenance of Shares One of the benefits of a threshold scheme is that if a single share is compromised, the private key is not revealed. If the shareholders know that a share has been compromised, for security they should generate a new public key and shares of the private key. However, the shareholders may not realize that a share has been compromised, or the cost of changing the public key may be quite high. To help preserve the security of the system in these cases, we can change the shares in such a way that although the public and private keys do not change, the old shares and the new shares are incompatible. This process is similar to the disenrollment capability described in [2] and [3]. To create the new shares, one of the shareholders should distribute shares of a polynomial with a secret of zero (ie., gz(z) = R x + 0 mod (q - 1)/2, (7) (8)
7 403 where R is random). Each shareholder then adds the share of gz to the share of the private key. Adding the two polynomials does not change the secret, but does change the value of all shares. Visualizing the secret sharing polynomial as a line, we have changed the slope of the line, but not the intercept. Once the shareholders confirm that their shares are still valid, they destroy their shares of gz. Since the old shares and the new shares now correspond to two different polynomials, they cannot be combined to calculate the private key. The private key is only compromised if someone has access to two shares which are valid at the same time. Any two shareholders can cooperate to replace a lost or damaged share without revealing their shares or calculating the secret. To create share i, the two shareholders use the interpolation formula (3) to calculate the value of f(i). Each calculates one of the terms of this sum and adds a share of a polynomial with secret zero as described in the preceding paragraph. The result is transmitted secretly to shareholder i. Share i is the sum of the these two results. The two shareholders generating these pieces must use independent polynomials. Otherwise, shareholder i would have sufficient information to calculate the secret. Once share i is created, shares of the two polynomials with secret zero should be distributed to the remaining shareholders. 4.5 Security of 2-out-of-Z Scheme Because the partial signer, Alice (or by symmetry Bob), knows only a share of x, a share of k, and four random numbers, she has no information that could not be simulated by an external attacker. She therefore cannot break the system faster than an attacker who sees only the final DSS signature which is a result of this scheme. The only participant with information which cannot be simulated by an attacker is the combiner. Coppersmith [4] has observed that the combiner Charles can compute quadratic residues involving ZA and XB, but that this does not seem to lead to an attack. Essentially, this attack manipulates the equations Charles knows to generate a quantity which is a function of XA and XB and known information. Charles does not know the quantity itself, merely that it is a quadratic residue. This information does not appear to help Charles calculate XA and ZB. For a description of the method for calculating quadratic residues, see [12]. 5 t-out-of4 Threshold Signatures To create general t-out-of4 threshold signaturesi we will precompute and store information for each signature. While this approach raises non-trivial implementation problems, it may be suitable for certain applications.
8 With a Trusted Center For simplicity, we will first assume the existence of a trusted center to create the shares. The next section will show how to remove this requirement. The center creates the private key x, and the public key y. For a single signature, the center generates a random k and creates two independent secret sharing schemes, one with secret k and the other with secret kx. Then the centef privately gives Alice her share of k, her share of kx, and the quantity r = (gk- mod p ) mod q. Since the sharing schemes for k and kx are both mod q, and q is 160 bits long, the entire share is 480 bits. The center repeats the process for the other shareholders. Notice that, unlike the 2-out-of-l scheme, this scheme does not place any additional restrictions on the parameters of the system. In order to sign a message, any t of the shareholders must create a partial signature. Let UA be Alice s share of k and VA be Alice s share of kx. Then her partial signature would be SA = UAM + VAT. She sends this partial signature to a combiner. Once the combiner has accumulated t partial signatures for a message, he can combine them into a single signature using equation (3), = k M + kxr = k(m + ZV). (14) The interpolation constant ci,% can be calculated by the combiner, so the signers do not need to know who else is signing. Notice that unlike the method from Section 4, this method does not require trusting the combiner or keeping the partial signatures secret. Once the share has been used to create a signature, it must never be used to create another signature. Therefore, the center will create a list of shares, with each share to be used exactly once. Since about 20,000 shares would fit on a floppy disk, the storage requirements for this are not unreasonable. However, using these lists creates a new problem. The shareholders need some system to insure that two messages are never signed using the same k. One of the simplest methods would be to have one person in charge of sending out message signing requests which include the number of the share to be used to create the signature. Each signing request would be signed by the individual. The shareholders could then keep track of what requests had been sent. If the requester cheats and requests that two different messages be signed with the same k, the shareholders records will show this, and he will be eventually caught. Other protocols may be possible depending on the individual application. For example, the following protocol might be acceptable for a small group of shareholders which creates signatures infrequently. Whenever a message to be signed is sent to the group, each member signs with her personal key an acknowledgement giving the message and the current k value. Group members wait to receive acknowledgements from all members before partially signing the message.
9 Distributing the Share Generation To avoid the single point failure of Section 5.1, we can replace the single trusted center with three share creation centers. The three centers use the method of sharing a product described in section 3 to create additive shares of k and kx, then create t-out-of-i secret sharing schemes and distribute these shares to the shareholders. This method requires a great deal of interaction between the share creation centers at the time when they create all of the shares. If t > 2 then this system puts more trust in the centers than in the shareholders since any two of the centers can compromise the private key, while two shareholders cannot reveal any information about it. As in Section 4, we need some method for checking the validity of the shares. The shareholders can check their shares by choosing random shares within the list and computing y" = riyc'..u* mod P, (15) ies a function of their shares of k, and a function of their shares of kx. Since y = gx modp, if equation (15) equals equation (16), then the shares are legitimate. 5.3 Security of t-out-of4 Scheme The security of this scheme depends critically on preventing shareholders from signing more than one message with the same k. If the protocol for determining the current k value is not secure, then two messages may be signed using the same k, revealing the private key. While the reliance on lists is clearly a disadvantage of this system, the t-out-of-l scheme does have the nice property that the partial signatures are zero-knowledge. Therefore, we can prove the following theorem. Theorem 1. If the Shareholders never partially sign different messages with the same k value, then breaking the t-out-of4 signature scheme is equivalent to breaking DSS. To prove this theorem, we need to show that an external attacker, Eve, can simulate the threshold signature scheme given a standard DSS signature. Without loss of generality, we show that Eve can simulate a threshold signature scheme in which she knows the t - 1 shares f( l),..., f(i- 1). Eve generates t - 1 random numbers, U1,..., Ut-1, which are shares of k. For every possible value of k, there is exactly one degree t - 1 polynomial, f(r), such that f (i) = Ui and f (0) = k. Eve's "shares" are therefore perfectly legitimate shares of the secret k. Similarly, Eve generates t - 1 random numbers, &,...,&-I, which are shares of kx. Let sj = f(j)m + g(j). mod q, where f is the polynomial determined by Eve's choice of U, and the value of k, and g is the polynomial determined
10 406 by Eve's choice of Vi and the value of kz. Eve creates t - 1 partial signatures, s; = U;M + Vir mod q, for i = 1,..., t - 1. Eve does not know f(j) or g(j) for t 5 j 5 I, but she does know that t-1 s = cj,=sj + C Cj,rsj mod q. (17) i=l Therefore, using s, she can solve for sj, for any j of interest. Eve can thus simulate a threshold signature scheme in which she knows t - 1 of the shares and sees partial signatures created by all shareholders. Therefore, she can use any attack on the threshold scheme to attack standard DSS signatures. 6 (itz - t + 1)-out-of4 Scheme This section presents an alternate way to generalize the 2-out-of-2 signature scheme. This method avoids the precomputed lists of the previous section, but requires ta-t+l signers to participate in a signature which has t-out-of4 security. The additional signers are required because we are multiplying secret sharing polynomials. Let h(z) = f(z) x g(z), then h(0) = f(0) x g(o), and the degree of h is equal to the degree off plus the degree of g. For the signature algorithm, t people generate shares of k, and multiply the secret sharing polynomials. While this method is clearly impractical for large t, it may be usable for small values. For example, a scheme with 2-out-of-I security requires only three signers. For this algorithm, we will place the same requirements on q as those of Section 4 and create the private key as described in that section. An individual signature is created by the following steps: 1. Identify t of the signers to act as dealers for 12. Let T represent this group. 2. Each dealer, i, generates ki and k;' mod q. 3. The dealers calculate r = (gk;'k;''..k;' mod p) mod q. 4. Each dealer generates and distributes shares of the following polynomials mod q: Kj(t), degree t - 1 polynomial, Kj(0) = ki. X~(Z), degree t - 1 polynomial, Xj(0) = kizj, where xi = ~ ~~*f(o). Ti(.), degree t2 - t polynomial, Ti(0) = 0. di(z), degree t2 - t polynomial, di(0) = Signer j creates the shares ier ier and
11 Signer j creates the partial signature ~j = UjM + Vjr, (20) and sends the result to the combiner. (Note: the combiner is not trusted as in Section 4.) 7. After receiving t2 - t + 1 partial signatures, the combiner calculates 6.1 where p is the set of t2 - t + 1 signers and the cjlp s are the interpolation constants for a t2 - t degree polynomial. Security of the (t - t + 1)-out-of-I Scheme Like the algorithm of Section 5, the partial signatures of this algorithm are zero-knowledge. Therefore, we can prove the following theorem. Theorem2. If t - 1 or fewer of the shareholders collude, then breaking the (ta-t+l)-out-of-z signature scheme is no more than twice as daficult as breaking a standard DSS signature with the same pj qj and g pammeters. Again, to prove this theorem, we need to show that an external attacker, Eve, can simulate the threshold signature scheme given a standard DSS signature. Recall that the method for creating the private key, z, caused z to be a quadratic residue mod q. Since z may not be a quadratic residue for a standard DSS signature, Eve first conducts her simulation using the signature (r, a), then if the attack fails she repeats the attack using the value (r, as). This value corresponds to a signature with message am and private key az. Let a be a primitive element mod q, so either 2: or az must be a quadratic residue, and one of Eve s simulations should succeed. Now Eve can simulate the knowledge oft - 1 signers of the threshold ~cheme.~ For 1 5 j < t and 1 E A, Eve generates ~,(j), A;(j), yj(j), and %(j) randomly. For every value of kj and kizj, and any t - 1 values for rci(j) and Ai(j), there is exactly one polynomial K; such that ~j(0) = kj and one polynomial A, such that Ai(0) = kizj. Eve then computes Uj and Vj according to equations (18) and (19) and calculates the partial signatures sj. Now she generates t2-2t + 1 additional independent, random sj, where j = t,..., t2 - t. We need to show that these are valid partial signatures for those t2-2t + 1 signers. Let X(z) be a ta - t degree polynomial with X(0) = 0 r;(j). Similarly, let Y(z) be a t2 - t degree polynomial with Y(0) = 0 and Y(j) = ct=, &(j). Rewriting the formula for the partial signature, and X(j) = CT=, equation (20), we have The proof that Eve can simulate t - 1 dealers is a straightforward extension of this, but is more complicated to follow.
12 408 The values of ~i(j) and Xi(j) were fixed for all j by the random numbers Eve generated. The polynomials X(z) and y(z) each have degree t2 - t, and t2 - t unknown terms. (The zeroth order term is fixed at zero.) For arbitrary Sj, j = t,..., t2 - t, there are t2-2t + 1 linear equations in these unknowns created by equation (22). There are an additional 2(t - 1) equations from our above definitions of X(r) and y(z). Therefore, there are a total of t2-1 linear equations in 2t2-2t unknowns. Since 2t2-2t > t2-1 for all t > 1, the number of unknowns is greater than the number of equations, and there must be a solution for the system. Therefore, the random sj s are legitimate partial signatures. Eve now has t2 - t valid partial signatures. She can use the equation to find any other partial signature, si. Therefore, she can perfectly simulate the threshold signature scheme using a standard DSS signature. 7 Conclusion This paper describes three threshold signature schemes for the Digital Signature Standard. The 2-out-of-l scheme does not require a trusted party to create the shares or to recreate lost shares. The more general t-out-of4 scheme is less practical, requiring precomputation and storage of shares for each individual signature. The (t2 - t + 1)-out-of-l scheme does not require precomputed lists, but approximately t2 signers are required or t-out-of-z security. Both generalized schemes have provable levels of security. Acknowledgements The author would like to thank Jimmy Upton for suggesting this problem and Don Coppersmith and Rajeev Motwani for their helpful comments. References 1. A proposed federal information processing standard for digital signature standard (DSS), Federal Register, August B. Blakley, G. Blakley, A. Chan, and J. Massey. Threshold schemes with &senrollment. Advances in Cryptology-Crypto 92 proceedings, Springer-Verlag, p C. Charnes, J. Pieprzyk, and R. Safavi-Naini, Conditionally secure secret sharing schemes with disenrollment capability, 2nd ACM conference on Computer and Communications Security, Fairfax, Virginia, Nov. 2-4, 1994, pp D. Coppersmith, personal communication. 5. Y. Desmedt, Society and group oriented cryptography, Advances in Cryptology- Crypto 87 proceedings, Springer-Verlag, 1988, pp
13 Y. Desmedt, Threshold Cryptography, European Transactions on Telecommunications and Related Technologies, Vol. 5, No. 4, July-August 1994, pp Y. Desmedt and Y. Frankel, Shared generation of authenticators and signatures, Advances in Cryptology-Crypto 91 proceedings, Springer-Verlag, 1992, pp T. EIGamal, A public key cryptosystem and a signature scheme based on discrete logarithms, IEEE Trans. Inform. Theory, Vol. 31, 1985, pp Y. F rankel and Y. Desmedt, Parallel reliable threshold multisignature, Tech. Report TR-92-U4-U2, Dep. of EE & CS, Univ. of Wisconsin-Milwaukee, April L. Harn, Grouporiented (t, n) threshold digital signature scheme and digital multisignature, IEE Proc.-Comput. Digit. Tech., Vol. 141, No. 5, September 1994, pp C. Laih and L. Ham, Generalized threshold cyrptosystems, Advances in Cryptology - Asiacrypt 91 proceedings, Springer-Verlag, 1993, pp S. Langford, Differential-Linear Cryptanalysis and Threshold Signatures, Ph.D. Thesis, Stanford University, June C. Li, T. Hwang, N. Lee, (t,n)-threshold signature scheme based on discrete logarithm, Advances in Cryptology - Eurocrypt 94 proceedings, to appear. 14. R. Rivest, A. Shamir, L. Adleman, A method for obtaining digital signatures and public key cryptosystems, Communications of the ACM, Vol. 21, April 1978, pp A. Shamir, How to share a secret, Commun. ACM, 22: , November 1979.
An Z-Span Generalized Secret Sharing Scheme
 An Z-Span Generalized Secret Sharing Scheme Computer Science Telecommunications Program University of Missouri - Kansas City Kansas City, MO 64110 Abstract. For some secret sharing applications, the secret
An Z-Span Generalized Secret Sharing Scheme Computer Science Telecommunications Program University of Missouri - Kansas City Kansas City, MO 64110 Abstract. For some secret sharing applications, the secret
Remark on the Threshold RSA Signature Scheme
 Remark on the Threshold RSA Signature Scheme Chuan-Ming Li, Tzonelih Hwang, Narn-Yih Lee Institute of Information Engineering National Cheng-Kung University Tainan, Taiwan, R.O.C. Abstract Shared generation
Remark on the Threshold RSA Signature Scheme Chuan-Ming Li, Tzonelih Hwang, Narn-Yih Lee Institute of Information Engineering National Cheng-Kung University Tainan, Taiwan, R.O.C. Abstract Shared generation
Threshold-Multisignature Schemes where Suspected Forgery Implies Traceability of Adversarial Shareholders
 Threshold-Multisignature Schemes where Suspected Forgery Implies Traceability of Adversarial Shareholders Chuan-Ming Li, Tzonelih Hwang and Narn-Yih Lee Institute of Information Engineering, National Cheng-Kung
Threshold-Multisignature Schemes where Suspected Forgery Implies Traceability of Adversarial Shareholders Chuan-Ming Li, Tzonelih Hwang and Narn-Yih Lee Institute of Information Engineering, National Cheng-Kung
CSCI 454/554 Computer and Network Security. Topic 5.2 Public Key Cryptography
 CSCI 454/554 Computer and Network Security Topic 5.2 Public Key Cryptography Outline 1. Introduction 2. RSA 3. Diffie-Hellman Key Exchange 4. Digital Signature Standard 2 Introduction Public Key Cryptography
CSCI 454/554 Computer and Network Security Topic 5.2 Public Key Cryptography Outline 1. Introduction 2. RSA 3. Diffie-Hellman Key Exchange 4. Digital Signature Standard 2 Introduction Public Key Cryptography
Outline. CSCI 454/554 Computer and Network Security. Introduction. Topic 5.2 Public Key Cryptography. 1. Introduction 2. RSA
 CSCI 454/554 Computer and Network Security Topic 5.2 Public Key Cryptography 1. Introduction 2. RSA Outline 3. Diffie-Hellman Key Exchange 4. Digital Signature Standard 2 Introduction Public Key Cryptography
CSCI 454/554 Computer and Network Security Topic 5.2 Public Key Cryptography 1. Introduction 2. RSA Outline 3. Diffie-Hellman Key Exchange 4. Digital Signature Standard 2 Introduction Public Key Cryptography
A SIGNATURE ALGORITHM BASED ON DLP AND COMPUTING SQUARE ROOTS
 A SIGNATURE ALGORITHM BASED ON DLP AND COMPUTING SQUARE ROOTS Ounasser Abid 1 and Omar Khadir 2 1, 2 Laboratory of Mathematics, Cryptography and Mechanics, FSTM University Hassan II of Casablanca, Morocco
A SIGNATURE ALGORITHM BASED ON DLP AND COMPUTING SQUARE ROOTS Ounasser Abid 1 and Omar Khadir 2 1, 2 Laboratory of Mathematics, Cryptography and Mechanics, FSTM University Hassan II of Casablanca, Morocco
Key Management and Distribution
 CPE 542: CRYPTOGRAPHY & NETWORK SECURITY Chapter 10 Key Management; Other Public Key Cryptosystems Dr. Lo ai Tawalbeh Computer Engineering Department Jordan University of Science and Technology Jordan
CPE 542: CRYPTOGRAPHY & NETWORK SECURITY Chapter 10 Key Management; Other Public Key Cryptosystems Dr. Lo ai Tawalbeh Computer Engineering Department Jordan University of Science and Technology Jordan
Outline. Public Key Cryptography. Applications of Public Key Crypto. Applications (Cont d)
 Outline AIT 682: Network and Systems Security 1. Introduction 2. RSA 3. Diffie-Hellman Key Exchange 4. Digital Signature Standard Topic 5.2 Public Key Cryptography Instructor: Dr. Kun Sun 2 Public Key
Outline AIT 682: Network and Systems Security 1. Introduction 2. RSA 3. Diffie-Hellman Key Exchange 4. Digital Signature Standard Topic 5.2 Public Key Cryptography Instructor: Dr. Kun Sun 2 Public Key
Public Key Algorithms
 Public Key Algorithms 1 Public Key Algorithms It is necessary to know some number theory to really understand how and why public key algorithms work Most of the public key algorithms are based on modular
Public Key Algorithms 1 Public Key Algorithms It is necessary to know some number theory to really understand how and why public key algorithms work Most of the public key algorithms are based on modular
The most important development from the work on public-key cryptography is the digital signature. Message authentication protects two parties who
 1 The most important development from the work on public-key cryptography is the digital signature. Message authentication protects two parties who exchange messages from any third party. However, it does
1 The most important development from the work on public-key cryptography is the digital signature. Message authentication protects two parties who exchange messages from any third party. However, it does
On the Diculty of Software Key Escrow. Abstract. At Eurocrypt'95, Desmedt suggested a scheme which allows individuals to encrypt
 On the Diculty of Software Key Escrow Lars R. Knudsen Katholieke Universiteit Leuven Dept. Elektrotechniek-ESAT Kardinaal Mercierlaan 94 B-3001 Heverlee Torben P. Pedersen y Cryptomathic Arhus Science
On the Diculty of Software Key Escrow Lars R. Knudsen Katholieke Universiteit Leuven Dept. Elektrotechniek-ESAT Kardinaal Mercierlaan 94 B-3001 Heverlee Torben P. Pedersen y Cryptomathic Arhus Science
Public Key Cryptography and the RSA Cryptosystem
 Public Key Cryptography and the RSA Cryptosystem Two people, say Alice and Bob, would like to exchange secret messages; however, Eve is eavesdropping: One technique would be to use an encryption technique
Public Key Cryptography and the RSA Cryptosystem Two people, say Alice and Bob, would like to exchange secret messages; however, Eve is eavesdropping: One technique would be to use an encryption technique
Cryptanalysis of the Lee-Hwang Group-Oriented Undeniable Signature Schemes
 Cryptanalysis of the Lee-Hwang Group-Oriented Undeniable Signature Schemes Guilin Wang, Jianying Zhou, and Robert H. Deng Laboratories for Information Technology 21 Heng Mui Keng Terrace, Singapore 119613
Cryptanalysis of the Lee-Hwang Group-Oriented Undeniable Signature Schemes Guilin Wang, Jianying Zhou, and Robert H. Deng Laboratories for Information Technology 21 Heng Mui Keng Terrace, Singapore 119613
Efficient identity-based GQ multisignatures
 Int. J. Inf. Secur. DOI 10.1007/s10207-008-0072-z REGULAR CONTRIBUTION Efficient identity-based GQ multisignatures Lein Harn Jian Ren Changlu Lin Springer-Verlag 2008 Abstract ISO/IEC 14888 specifies a
Int. J. Inf. Secur. DOI 10.1007/s10207-008-0072-z REGULAR CONTRIBUTION Efficient identity-based GQ multisignatures Lein Harn Jian Ren Changlu Lin Springer-Verlag 2008 Abstract ISO/IEC 14888 specifies a
Overview. Public Key Algorithms I
 Public Key Algorithms I Dr. Arjan Durresi Louisiana State University Baton Rouge, LA 70810 Durresi@csc.lsu.Edu These slides are available at: http://www.csc.lsu.edu/~durresi/csc4601-04/ Louisiana State
Public Key Algorithms I Dr. Arjan Durresi Louisiana State University Baton Rouge, LA 70810 Durresi@csc.lsu.Edu These slides are available at: http://www.csc.lsu.edu/~durresi/csc4601-04/ Louisiana State
Digital Multi Signature Schemes Premalatha A Grandhi
 Digital Multi Signature Schemes Premalatha A Grandhi (pgrandhi@cise.ufl.edu) Digital Signatures can be classified into o Single Signatures o Multiple Signatures (multi-signatures) Types of Multiple Signatures
Digital Multi Signature Schemes Premalatha A Grandhi (pgrandhi@cise.ufl.edu) Digital Signatures can be classified into o Single Signatures o Multiple Signatures (multi-signatures) Types of Multiple Signatures
Lecture 2 Applied Cryptography (Part 2)
 Lecture 2 Applied Cryptography (Part 2) Patrick P. C. Lee Tsinghua Summer Course 2010 2-1 Roadmap Number theory Public key cryptography RSA Diffie-Hellman DSA Certificates Tsinghua Summer Course 2010 2-2
Lecture 2 Applied Cryptography (Part 2) Patrick P. C. Lee Tsinghua Summer Course 2010 2-1 Roadmap Number theory Public key cryptography RSA Diffie-Hellman DSA Certificates Tsinghua Summer Course 2010 2-2
CSC 474/574 Information Systems Security
 CSC 474/574 Information Systems Security Topic 2.5 Public Key Algorithms CSC 474/574 Dr. Peng Ning 1 Public Key Algorithms Public key algorithms covered in this class RSA: encryption and digital signature
CSC 474/574 Information Systems Security Topic 2.5 Public Key Algorithms CSC 474/574 Dr. Peng Ning 1 Public Key Algorithms Public key algorithms covered in this class RSA: encryption and digital signature
1. Diffie-Hellman Key Exchange
 e-pgpathshala Subject : Computer Science Paper: Cryptography and Network Security Module: Diffie-Hellman Key Exchange Module No: CS/CNS/26 Quadrant 1 e-text Cryptography and Network Security Objectives
e-pgpathshala Subject : Computer Science Paper: Cryptography and Network Security Module: Diffie-Hellman Key Exchange Module No: CS/CNS/26 Quadrant 1 e-text Cryptography and Network Security Objectives
Sharing Several Secrets based on Lagrange s Interpolation formula and Cipher Feedback Mode
 Int. J. Nonlinear Anal. Appl. 5 (2014) No. 2, 60-66 ISSN: 2008-6822 (electronic) http://www.ijnaa.semnan.ac.ir Sharing Several Secrets based on Lagrange s Interpolation formula and Cipher Feedback Mode
Int. J. Nonlinear Anal. Appl. 5 (2014) No. 2, 60-66 ISSN: 2008-6822 (electronic) http://www.ijnaa.semnan.ac.ir Sharing Several Secrets based on Lagrange s Interpolation formula and Cipher Feedback Mode
Digital Signatures. KG November 3, Introduction 1. 2 Digital Signatures 2
 Digital Signatures KG November 3, 2017 Contents 1 Introduction 1 2 Digital Signatures 2 3 Hash Functions 3 3.1 Attacks.................................... 4 3.2 Compression Functions............................
Digital Signatures KG November 3, 2017 Contents 1 Introduction 1 2 Digital Signatures 2 3 Hash Functions 3 3.1 Attacks.................................... 4 3.2 Compression Functions............................
Chapter 9. Public Key Cryptography, RSA And Key Management
 Chapter 9 Public Key Cryptography, RSA And Key Management RSA by Rivest, Shamir & Adleman of MIT in 1977 The most widely used public-key cryptosystem is RSA. The difficulty of attacking RSA is based on
Chapter 9 Public Key Cryptography, RSA And Key Management RSA by Rivest, Shamir & Adleman of MIT in 1977 The most widely used public-key cryptosystem is RSA. The difficulty of attacking RSA is based on
Distributed Systems. 26. Cryptographic Systems: An Introduction. Paul Krzyzanowski. Rutgers University. Fall 2015
 Distributed Systems 26. Cryptographic Systems: An Introduction Paul Krzyzanowski Rutgers University Fall 2015 1 Cryptography Security Cryptography may be a component of a secure system Adding cryptography
Distributed Systems 26. Cryptographic Systems: An Introduction Paul Krzyzanowski Rutgers University Fall 2015 1 Cryptography Security Cryptography may be a component of a secure system Adding cryptography
An IBE Scheme to Exchange Authenticated Secret Keys
 An IBE Scheme to Exchange Authenticated Secret Keys Waldyr Dias Benits Júnior 1, Routo Terada (Advisor) 1 1 Instituto de Matemática e Estatística Universidade de São Paulo R. do Matão, 1010 Cidade Universitária
An IBE Scheme to Exchange Authenticated Secret Keys Waldyr Dias Benits Júnior 1, Routo Terada (Advisor) 1 1 Instituto de Matemática e Estatística Universidade de São Paulo R. do Matão, 1010 Cidade Universitária
What did we talk about last time? Public key cryptography A little number theory
 Week 4 - Friday What did we talk about last time? Public key cryptography A little number theory If p is prime and a is a positive integer not divisible by p, then: a p 1 1 (mod p) Assume a is positive
Week 4 - Friday What did we talk about last time? Public key cryptography A little number theory If p is prime and a is a positive integer not divisible by p, then: a p 1 1 (mod p) Assume a is positive
Public Key Algorithms
 CSE597B: Special Topics in Network and Systems Security Public Key Cryptography Instructor: Sencun Zhu The Pennsylvania State University Public Key Algorithms Public key algorithms RSA: encryption and
CSE597B: Special Topics in Network and Systems Security Public Key Cryptography Instructor: Sencun Zhu The Pennsylvania State University Public Key Algorithms Public key algorithms RSA: encryption and
A PUBLIC KEY CRYPTOSYSTEM AND A SIGNATURE
 A PUBLIC KEY CRYPTOSYSTEM AND A SIGNATURE SCHEME BASED ON DISCRETE LOGARITHMS TaherElGamal' Hewlett-Packard Labs 1501 Page Mill Rd Palo Alto CA 94301 A new signature scheme is proposed together with an
A PUBLIC KEY CRYPTOSYSTEM AND A SIGNATURE SCHEME BASED ON DISCRETE LOGARITHMS TaherElGamal' Hewlett-Packard Labs 1501 Page Mill Rd Palo Alto CA 94301 A new signature scheme is proposed together with an
Verifiably Encrypted Signature Scheme with Threshold Adjudication
 Verifiably Encrypted Signature Scheme with Threshold Adjudication M. Choudary Gorantla and Ashutosh Saxena Institute for Development and Research in Banking Technology Road No. 1, Castle Hills, Masab Tank,
Verifiably Encrypted Signature Scheme with Threshold Adjudication M. Choudary Gorantla and Ashutosh Saxena Institute for Development and Research in Banking Technology Road No. 1, Castle Hills, Masab Tank,
- 0 - CryptoLib: Cryptography in Software John B. Lacy 1 Donald P. Mitchell 2 William M. Schell 3 AT&T Bell Laboratories ABSTRACT
 - 0 - CryptoLib: Cryptography in Software John B. Lacy 1 Donald P. Mitchell 2 William M. Schell 3 AT&T Bell Laboratories ABSTRACT With the capacity of communications channels increasing at the current
- 0 - CryptoLib: Cryptography in Software John B. Lacy 1 Donald P. Mitchell 2 William M. Schell 3 AT&T Bell Laboratories ABSTRACT With the capacity of communications channels increasing at the current
Chapter 9 Public Key Cryptography. WANG YANG
 Chapter 9 Public Key Cryptography WANG YANG wyang@njnet.edu.cn Content Introduction RSA Diffie-Hellman Key Exchange Introduction Public Key Cryptography plaintext encryption ciphertext decryption plaintext
Chapter 9 Public Key Cryptography WANG YANG wyang@njnet.edu.cn Content Introduction RSA Diffie-Hellman Key Exchange Introduction Public Key Cryptography plaintext encryption ciphertext decryption plaintext
Key Exchange. References: Applied Cryptography, Bruce Schneier Cryptography and Network Securiy, Willian Stallings
 Key Exchange References: Applied Cryptography, Bruce Schneier Cryptography and Network Securiy, Willian Stallings Outlines Primitives Root Discrete Logarithm Diffie-Hellman ElGamal Shamir s Three Pass
Key Exchange References: Applied Cryptography, Bruce Schneier Cryptography and Network Securiy, Willian Stallings Outlines Primitives Root Discrete Logarithm Diffie-Hellman ElGamal Shamir s Three Pass
Dr. Jinyuan (Stella) Sun Dept. of Electrical Engineering and Computer Science University of Tennessee Fall 2010
 CS 494/594 Computer and Network Security Dr. Jinyuan (Stella) Sun Dept. of Electrical Engineering and Computer Science University of Tennessee Fall 2010 1 Public Key Cryptography Modular Arithmetic RSA
CS 494/594 Computer and Network Security Dr. Jinyuan (Stella) Sun Dept. of Electrical Engineering and Computer Science University of Tennessee Fall 2010 1 Public Key Cryptography Modular Arithmetic RSA
Cryptography and Network Security Chapter 10. Fourth Edition by William Stallings
 Cryptography and Network Security Chapter 10 Fourth Edition by William Stallings Chapter 10 Key Management; Other Public Key Cryptosystems No Singhalese, whether man or woman, would venture out of the
Cryptography and Network Security Chapter 10 Fourth Edition by William Stallings Chapter 10 Key Management; Other Public Key Cryptosystems No Singhalese, whether man or woman, would venture out of the
INTERNATIONAL JOURNAL OF ELECTRONICS AND COMMUNICATION ENGINEERING & TECHNOLOGY (IJECET)
 INTERNATIONAL JOURNAL OF ELECTRONICS AND COMMUNICATION ENGINEERING & TECHNOLOGY (IJECET) International Journal of Electronics and Communication Engineering & Technology (IJECET), ISSN 0976 ISSN 0976 6464(Print)
INTERNATIONAL JOURNAL OF ELECTRONICS AND COMMUNICATION ENGINEERING & TECHNOLOGY (IJECET) International Journal of Electronics and Communication Engineering & Technology (IJECET), ISSN 0976 ISSN 0976 6464(Print)
Elements of Cryptography and Computer and Networking Security Computer Science 134 (COMPSCI 134) Fall 2016 Instructor: Karim ElDefrawy
 Elements of Cryptography and Computer and Networking Security Computer Science 134 (COMPSCI 134) Fall 2016 Instructor: Karim ElDefrawy Homework 2 Due: Friday, 10/28/2016 at 11:55pm PT Will be posted on
Elements of Cryptography and Computer and Networking Security Computer Science 134 (COMPSCI 134) Fall 2016 Instructor: Karim ElDefrawy Homework 2 Due: Friday, 10/28/2016 at 11:55pm PT Will be posted on
Public-key Cryptography: Theory and Practice
 Public-key Cryptography Theory and Practice Department of Computer Science and Engineering Indian Institute of Technology Kharagpur Chapter 1: Overview What is Cryptography? Cryptography is the study of
Public-key Cryptography Theory and Practice Department of Computer Science and Engineering Indian Institute of Technology Kharagpur Chapter 1: Overview What is Cryptography? Cryptography is the study of
CS 161 Computer Security
 Paxson Spring 2013 CS 161 Computer Security 3/14 Asymmetric cryptography Previously we saw symmetric-key cryptography, where Alice and Bob share a secret key K. However, symmetric-key cryptography can
Paxson Spring 2013 CS 161 Computer Security 3/14 Asymmetric cryptography Previously we saw symmetric-key cryptography, where Alice and Bob share a secret key K. However, symmetric-key cryptography can
Provable Partial Key Escrow
 Provable Partial Key Escrow Kooshiar Azimian Electronic Research Center, Sharif University of Technology, and Computer Engineering Department, Sharif University of Technology Tehran, Iran Email: Azimian@ce.sharif.edu
Provable Partial Key Escrow Kooshiar Azimian Electronic Research Center, Sharif University of Technology, and Computer Engineering Department, Sharif University of Technology Tehran, Iran Email: Azimian@ce.sharif.edu
Research Issues and Challenges for Multiple Digital Signatures
 INTERNATION JOURNAL OF NETWORK SECURITY, VOL.1, NO.1,PP. 1-6, 2005 1 Research Issues and Challenges for Multiple Digital Signatures Min-Shiang Hwang, and Cheng-Chi Lee, Abstract In this paper, we survey
INTERNATION JOURNAL OF NETWORK SECURITY, VOL.1, NO.1,PP. 1-6, 2005 1 Research Issues and Challenges for Multiple Digital Signatures Min-Shiang Hwang, and Cheng-Chi Lee, Abstract In this paper, we survey
Cryptography and Network Security
 Cryptography and Network Security Third Edition by William Stallings Lecture slides by Lawrie Brown Chapter 10 Key Management; Other Public Key Cryptosystems No Singhalese, whether man or woman, would
Cryptography and Network Security Third Edition by William Stallings Lecture slides by Lawrie Brown Chapter 10 Key Management; Other Public Key Cryptosystems No Singhalese, whether man or woman, would
Introduction to Cryptography Lecture 7
 Introduction to Cryptography Lecture 7 Public-Key Encryption: El-Gamal, RSA Benny Pinkas page 1 1 Public key encryption Alice publishes a public key PK Alice. Alice has a secret key SK Alice. Anyone knowing
Introduction to Cryptography Lecture 7 Public-Key Encryption: El-Gamal, RSA Benny Pinkas page 1 1 Public key encryption Alice publishes a public key PK Alice. Alice has a secret key SK Alice. Anyone knowing
Elliptic Curve Cryptosystem
 UDC 681.8 Elliptic Curve Cryptosystem VNaoya Torii VKazuhiro Yokoyama (Manuscript received June 6, 2000) This paper describes elliptic curve cryptosystems (ECCs), which are expected to become the next-generation
UDC 681.8 Elliptic Curve Cryptosystem VNaoya Torii VKazuhiro Yokoyama (Manuscript received June 6, 2000) This paper describes elliptic curve cryptosystems (ECCs), which are expected to become the next-generation
Public-key encipherment concept
 Date: onday, October 21, 2002 Prof.: Dr Jean-Yves Chouinard Design of Secure Computer Systems CSI4138/CEG4394 Notes on Public Key Cryptography Public-key encipherment concept Each user in a secure communication
Date: onday, October 21, 2002 Prof.: Dr Jean-Yves Chouinard Design of Secure Computer Systems CSI4138/CEG4394 Notes on Public Key Cryptography Public-key encipherment concept Each user in a secure communication
CS669 Network Security
 UNIT II PUBLIC KEY ENCRYPTION Uniqueness Number Theory concepts Primality Modular Arithmetic Fermet & Euler Theorem Euclid Algorithm RSA Elliptic Curve Cryptography Diffie Hellman Key Exchange Uniqueness
UNIT II PUBLIC KEY ENCRYPTION Uniqueness Number Theory concepts Primality Modular Arithmetic Fermet & Euler Theorem Euclid Algorithm RSA Elliptic Curve Cryptography Diffie Hellman Key Exchange Uniqueness
Introduction to Cryptography Lecture 7
 Introduction to Cryptography Lecture 7 El Gamal Encryption RSA Encryption Benny Pinkas page 1 1 Public key encryption Alice publishes a public key PK Alice. Alice has a secret key SK Alice. Anyone knowing
Introduction to Cryptography Lecture 7 El Gamal Encryption RSA Encryption Benny Pinkas page 1 1 Public key encryption Alice publishes a public key PK Alice. Alice has a secret key SK Alice. Anyone knowing
Digital Signature. Raj Jain
 Digital Signature Raj Jain Washington University in Saint Louis Saint Louis, MO 63130 Jain@cse.wustl.edu Audio/Video recordings of this lecture are available at: http://www.cse.wustl.edu/~jain/cse571-14/
Digital Signature Raj Jain Washington University in Saint Louis Saint Louis, MO 63130 Jain@cse.wustl.edu Audio/Video recordings of this lecture are available at: http://www.cse.wustl.edu/~jain/cse571-14/
Chapter 7 Public Key Cryptography and Digital Signatures
 Chapter 7 Public Key Cryptography and Digital Signatures Every Egyptian received two names, which were known respectively as the true name and the good name, or the great name and the little name; and
Chapter 7 Public Key Cryptography and Digital Signatures Every Egyptian received two names, which were known respectively as the true name and the good name, or the great name and the little name; and
This chapter continues our overview of public-key cryptography systems (PKCSs), and begins with a description of one of the earliest and simplest
 1 2 3 This chapter continues our overview of public-key cryptography systems (PKCSs), and begins with a description of one of the earliest and simplest PKCS, Diffie- Hellman key exchange. This first published
1 2 3 This chapter continues our overview of public-key cryptography systems (PKCSs), and begins with a description of one of the earliest and simplest PKCS, Diffie- Hellman key exchange. This first published
ASYMMETRIC CRYPTOGRAPHY
 ASYMMETRIC CRYPTOGRAPHY CONTENT: 1. Number Theory 2. One Way Function 3. Hash Function 4. Digital Signature 5. RSA (Rivest-Shamir Adleman) References: 1. Applied Cryptography, Bruce Schneier 2. Cryptography
ASYMMETRIC CRYPTOGRAPHY CONTENT: 1. Number Theory 2. One Way Function 3. Hash Function 4. Digital Signature 5. RSA (Rivest-Shamir Adleman) References: 1. Applied Cryptography, Bruce Schneier 2. Cryptography
Algorithms (III) Yijia Chen Shanghai Jiaotong University
 Algorithms (III) Yijia Chen Shanghai Jiaotong University Review of the Previous Lecture Factoring: Given a number N, express it as a product of its prime factors. Many security protocols are based on the
Algorithms (III) Yijia Chen Shanghai Jiaotong University Review of the Previous Lecture Factoring: Given a number N, express it as a product of its prime factors. Many security protocols are based on the
Using Commutative Encryption to Share a Secret
 Using Commutative Encryption to Share a Secret Saied Hosseini Khayat August 18, 2008 Abstract It is shown how to use commutative encryption to share a secret. Suppose Alice wants to share a secret with
Using Commutative Encryption to Share a Secret Saied Hosseini Khayat August 18, 2008 Abstract It is shown how to use commutative encryption to share a secret. Suppose Alice wants to share a secret with
Kurose & Ross, Chapters (5 th ed.)
 Kurose & Ross, Chapters 8.2-8.3 (5 th ed.) Slides adapted from: J. Kurose & K. Ross \ Computer Networking: A Top Down Approach (5 th ed.) Addison-Wesley, April 2009. Copyright 1996-2010, J.F Kurose and
Kurose & Ross, Chapters 8.2-8.3 (5 th ed.) Slides adapted from: J. Kurose & K. Ross \ Computer Networking: A Top Down Approach (5 th ed.) Addison-Wesley, April 2009. Copyright 1996-2010, J.F Kurose and
Algorithms (III) Yu Yu. Shanghai Jiaotong University
 Algorithms (III) Yu Yu Shanghai Jiaotong University Review of the Previous Lecture Factoring: Given a number N, express it as a product of its prime factors. Many security protocols are based on the assumed
Algorithms (III) Yu Yu Shanghai Jiaotong University Review of the Previous Lecture Factoring: Given a number N, express it as a product of its prime factors. Many security protocols are based on the assumed
Spring 2010: CS419 Computer Security
 Spring 2010: CS419 Computer Security Vinod Ganapathy Lecture 7 Topic: Key exchange protocols Material: Class handout (lecture7_handout.pdf) Chapter 2 in Anderson's book. Today s agenda Key exchange basics
Spring 2010: CS419 Computer Security Vinod Ganapathy Lecture 7 Topic: Key exchange protocols Material: Class handout (lecture7_handout.pdf) Chapter 2 in Anderson's book. Today s agenda Key exchange basics
Public Key Algorithms
 Public Key Algorithms CS 472 Spring 13 Lecture 6 Mohammad Almalag 2/19/2013 Public Key Algorithms - Introduction Public key algorithms are a motley crew, how? All hash algorithms do the same thing: Take
Public Key Algorithms CS 472 Spring 13 Lecture 6 Mohammad Almalag 2/19/2013 Public Key Algorithms - Introduction Public key algorithms are a motley crew, how? All hash algorithms do the same thing: Take
1. Digital Signatures 2. ElGamal Digital Signature Scheme 3. Schnorr Digital Signature Scheme 4. Digital Signature Standard (DSS)
 Digital Signature Overview Raj Jain Washington University in Saint Louis Saint Louis, MO 63130 Jain@cse.wustl.edu Audio/Video recordings of this lecture are available at: 13-1 1. Digital Signatures 2.
Digital Signature Overview Raj Jain Washington University in Saint Louis Saint Louis, MO 63130 Jain@cse.wustl.edu Audio/Video recordings of this lecture are available at: 13-1 1. Digital Signatures 2.
Computer Security. 08. Cryptography Part II. Paul Krzyzanowski. Rutgers University. Spring 2018
 Computer Security 08. Cryptography Part II Paul Krzyzanowski Rutgers University Spring 2018 March 23, 2018 CS 419 2018 Paul Krzyzanowski 1 Block ciphers Block ciphers encrypt a block of plaintext at a
Computer Security 08. Cryptography Part II Paul Krzyzanowski Rutgers University Spring 2018 March 23, 2018 CS 419 2018 Paul Krzyzanowski 1 Block ciphers Block ciphers encrypt a block of plaintext at a
RSA (algorithm) History
 RSA (algorithm) RSA is an algorithm for public-key cryptography that is based on the presumed difficulty of factoring large integers, the factoring problem. RSA stands for Ron Rivest, Adi Shamir and Leonard
RSA (algorithm) RSA is an algorithm for public-key cryptography that is based on the presumed difficulty of factoring large integers, the factoring problem. RSA stands for Ron Rivest, Adi Shamir and Leonard
Understanding Cryptography A Textbook for Students and Practitioners by Christof Paar and Jan Pelzl. Chapter 6 Introduction to Public-Key Cryptography
 Understanding Cryptography A Textbook for Students and Practitioners by Christof Paar and Jan Pelzl www.crypto-textbook.com Chapter 6 Introduction to Public-Key Cryptography ver. November 18, 2010 These
Understanding Cryptography A Textbook for Students and Practitioners by Christof Paar and Jan Pelzl www.crypto-textbook.com Chapter 6 Introduction to Public-Key Cryptography ver. November 18, 2010 These
(t, n) Multi-Secret Sharing Scheme Based on Bivariate Polynomial
 Wireless Pers Commun DOI 10.1007/s11277-016-3862-z (t, n) Multi-Secret Sharing Scheme Based on Bivariate Polynomial Lein Harn 1 Ching-Fang Hsu 1,2 Springer Science+Business Media New York 2016 Abstract
Wireless Pers Commun DOI 10.1007/s11277-016-3862-z (t, n) Multi-Secret Sharing Scheme Based on Bivariate Polynomial Lein Harn 1 Ching-Fang Hsu 1,2 Springer Science+Business Media New York 2016 Abstract
Introduction to Cryptography and Security Mechanisms: Unit 5. Public-Key Encryption
 Introduction to Cryptography and Security Mechanisms: Unit 5 Public-Key Encryption Learning Outcomes Explain the basic principles behind public-key cryptography Recognise the fundamental problems that
Introduction to Cryptography and Security Mechanisms: Unit 5 Public-Key Encryption Learning Outcomes Explain the basic principles behind public-key cryptography Recognise the fundamental problems that
Public Key Cryptography
 Public Key Cryptography Giuseppe F. Italiano Universita` di Roma Tor Vergata italiano@disp.uniroma2.it Motivation Until early 70s, cryptography was mostly owned by government and military Symmetric cryptography
Public Key Cryptography Giuseppe F. Italiano Universita` di Roma Tor Vergata italiano@disp.uniroma2.it Motivation Until early 70s, cryptography was mostly owned by government and military Symmetric cryptography
Public-Key Cryptography. Professor Yanmin Gong Week 3: Sep. 7
 Public-Key Cryptography Professor Yanmin Gong Week 3: Sep. 7 Outline Key exchange and Diffie-Hellman protocol Mathematical backgrounds for modular arithmetic RSA Digital Signatures Key management Problem:
Public-Key Cryptography Professor Yanmin Gong Week 3: Sep. 7 Outline Key exchange and Diffie-Hellman protocol Mathematical backgrounds for modular arithmetic RSA Digital Signatures Key management Problem:
Public-Key Cryptanalysis
 http://www.di.ens.fr/ pnguyen INRIA and École normale supérieure, Paris, France MPRI, 2010 Outline 1 Introduction Asymmetric Cryptology Course Overview 2 Textbook RSA 3 Euclid s Algorithm Applications
http://www.di.ens.fr/ pnguyen INRIA and École normale supérieure, Paris, France MPRI, 2010 Outline 1 Introduction Asymmetric Cryptology Course Overview 2 Textbook RSA 3 Euclid s Algorithm Applications
Key Exchange. Secure Software Systems
 1 Key Exchange 2 Challenge Exchanging Keys &!"#h%&'() & & 1 2 6(6 1) 2 15! $ The more parties in communication, the more keys that need to be securely exchanged " # Do we have to use out-of-band methods?
1 Key Exchange 2 Challenge Exchanging Keys &!"#h%&'() & & 1 2 6(6 1) 2 15! $ The more parties in communication, the more keys that need to be securely exchanged " # Do we have to use out-of-band methods?
Lecture 10, Zero Knowledge Proofs, Secure Computation
 CS 4501-6501 Topics in Cryptography 30 Mar 2018 Lecture 10, Zero Knowledge Proofs, Secure Computation Lecturer: Mahmoody Scribe: Bella Vice-Van Heyde, Derrick Blakely, Bobby Andris 1 Introduction Last
CS 4501-6501 Topics in Cryptography 30 Mar 2018 Lecture 10, Zero Knowledge Proofs, Secure Computation Lecturer: Mahmoody Scribe: Bella Vice-Van Heyde, Derrick Blakely, Bobby Andris 1 Introduction Last
E-cash. Cryptography. Professor: Marius Zimand. e-cash. Benefits of cash: anonymous. difficult to copy. divisible (you can get change)
 Cryptography E-cash Professor: Marius Zimand e-cash Benefits of cash: anonymous difficult to copy divisible (you can get change) easily transferable There are several protocols for e-cash. We will discuss
Cryptography E-cash Professor: Marius Zimand e-cash Benefits of cash: anonymous difficult to copy divisible (you can get change) easily transferable There are several protocols for e-cash. We will discuss
International Journal of Scientific Research and Reviews
 Research article Available online www.ijsrr.org ISSN: 2279 0543 International Journal of Scientific Research and Reviews Asymmetric Digital Signature Algorithm Based on Discrete Logarithm Concept with
Research article Available online www.ijsrr.org ISSN: 2279 0543 International Journal of Scientific Research and Reviews Asymmetric Digital Signature Algorithm Based on Discrete Logarithm Concept with
Linear (k, n) secret sharing scheme with cheating detection
 SECURITY AND COMMUNICATION NETWORKS Security Comm. Networks 2016; 9:2115 2121 Published online 20 March 2016 in Wiley Online Library (wileyonlinelibrary.com)..1467 RESEARCH ARTICLE Linear (k, n) secret
SECURITY AND COMMUNICATION NETWORKS Security Comm. Networks 2016; 9:2115 2121 Published online 20 March 2016 in Wiley Online Library (wileyonlinelibrary.com)..1467 RESEARCH ARTICLE Linear (k, n) secret
Algorithms (III) Yijia Chen Shanghai Jiaotong University
 Algorithms (III) Yijia Chen Shanghai Jiaotong University Review of the Previous Lecture Factoring: Given a number N, express it as a product of its prime factors. Many security protocols are based on the
Algorithms (III) Yijia Chen Shanghai Jiaotong University Review of the Previous Lecture Factoring: Given a number N, express it as a product of its prime factors. Many security protocols are based on the
ח'/סיון/תשע "א. RSA: getting ready. Public Key Cryptography. Public key cryptography. Public key encryption algorithms
 Public Key Cryptography Kurose & Ross, Chapters 8.28.3 (5 th ed.) Slides adapted from: J. Kurose & K. Ross \ Computer Networking: A Top Down Approach (5 th ed.) AddisonWesley, April 2009. Copyright 19962010,
Public Key Cryptography Kurose & Ross, Chapters 8.28.3 (5 th ed.) Slides adapted from: J. Kurose & K. Ross \ Computer Networking: A Top Down Approach (5 th ed.) AddisonWesley, April 2009. Copyright 19962010,
UNIT III 3.1DISCRETE LOGARITHMS
 UNIT III Discrete Logarithms Computing discrete logs Diffie-Hellman key exchange ElGamal Public key cryptosystems Hash functions Secure Hash - MD5 Digital signatures RSA ElGamal Digital signature scheme.
UNIT III Discrete Logarithms Computing discrete logs Diffie-Hellman key exchange ElGamal Public key cryptosystems Hash functions Secure Hash - MD5 Digital signatures RSA ElGamal Digital signature scheme.
CPSC 467b: Cryptography and Computer Security
 CPSC 467b: Cryptography and Computer Security Michael J. Fischer Lecture 7 January 30, 2012 CPSC 467b, Lecture 7 1/44 Public-key cryptography RSA Factoring Assumption Computing with Big Numbers Fast Exponentiation
CPSC 467b: Cryptography and Computer Security Michael J. Fischer Lecture 7 January 30, 2012 CPSC 467b, Lecture 7 1/44 Public-key cryptography RSA Factoring Assumption Computing with Big Numbers Fast Exponentiation
Forward-Secure Signatures for Unbounded Time Periods in Mobile Computing Applications
 208 Forward-Secure Signatures for Unbounded Time Periods in Mobile Computing Applications N..Sunitha B.B.Amberker Prashant Koulgi Department of Computer Science Department of Computer Science Department
208 Forward-Secure Signatures for Unbounded Time Periods in Mobile Computing Applications N..Sunitha B.B.Amberker Prashant Koulgi Department of Computer Science Department of Computer Science Department
k Anonymous Private Query Based on Blind Signature and Oblivious Transfer
 Edith Cowan University Research Online International Cyber Resilience conference Conferences, Symposia and Campus Events 2011 k Anonymous Private Query Based on Blind Signature and Oblivious Transfer Russell
Edith Cowan University Research Online International Cyber Resilience conference Conferences, Symposia and Campus Events 2011 k Anonymous Private Query Based on Blind Signature and Oblivious Transfer Russell
CS 161 Computer Security
 Popa & Wagner Spring 2016 CS 161 Computer Security Discussion 5 Week of February 19, 2017 Question 1 Diffie Hellman key exchange (15 min) Recall that in a Diffie-Hellman key exchange, there are values
Popa & Wagner Spring 2016 CS 161 Computer Security Discussion 5 Week of February 19, 2017 Question 1 Diffie Hellman key exchange (15 min) Recall that in a Diffie-Hellman key exchange, there are values
An overview and Cryptographic Challenges of RSA Bhawana
 An overview and Cryptographic Challenges of RSA Bhawana Department of CSE, Shanti Devi Institute of Technology & Management, Israna, Haryana India ABSTRACT: With the introduction of the computer, the need
An overview and Cryptographic Challenges of RSA Bhawana Department of CSE, Shanti Devi Institute of Technology & Management, Israna, Haryana India ABSTRACT: With the introduction of the computer, the need
Module: Cryptographic Protocols. Professor Patrick McDaniel Spring CMPSC443 - Introduction to Computer and Network Security
 CMPSC443 - Introduction to Computer and Network Security Module: Cryptographic Protocols Professor Patrick McDaniel Spring 2009 1 Key Distribution/Agreement Key Distribution is the process where we assign
CMPSC443 - Introduction to Computer and Network Security Module: Cryptographic Protocols Professor Patrick McDaniel Spring 2009 1 Key Distribution/Agreement Key Distribution is the process where we assign
Uzzah and the Ark of the Covenant
 Uzzah and the Ark of the Covenant And when they came to the threshing floor of Chidon, Uzzah put out his hand to take hold of the ark, for the oxen stumbled. 10 And the anger of the LORD was kindled against
Uzzah and the Ark of the Covenant And when they came to the threshing floor of Chidon, Uzzah put out his hand to take hold of the ark, for the oxen stumbled. 10 And the anger of the LORD was kindled against
Crypto Basics. Recent block cipher: AES Public Key Cryptography Public key exchange: Diffie-Hellmann Homework suggestion
 Crypto Basics Recent block cipher: AES Public Key Cryptography Public key exchange: Diffie-Hellmann Homework suggestion 1 What is a cryptosystem? K = {0,1} l P = {0,1} m C = {0,1} n, C C E: P K C D: C
Crypto Basics Recent block cipher: AES Public Key Cryptography Public key exchange: Diffie-Hellmann Homework suggestion 1 What is a cryptosystem? K = {0,1} l P = {0,1} m C = {0,1} n, C C E: P K C D: C
Channel Coding and Cryptography Part II: Introduction to Cryptography
 Channel Coding and Cryptography Part II: Introduction to Cryptography Prof. Dr.-Ing. habil. Andreas Ahrens Communications Signal Processing Group, University of Technology, Business and Design Email: andreas.ahrens@hs-wismar.de
Channel Coding and Cryptography Part II: Introduction to Cryptography Prof. Dr.-Ing. habil. Andreas Ahrens Communications Signal Processing Group, University of Technology, Business and Design Email: andreas.ahrens@hs-wismar.de
The Beta Cryptosystem
 Bulletin of Electrical Engineering and Informatics Vol. 4, No. 2, June 2015, pp. 155~159 ISSN: 2089-3191 155 The Beta Cryptosystem Chandrashekhar Meshram Department of Mathematics, RTM Nagpur University,
Bulletin of Electrical Engineering and Informatics Vol. 4, No. 2, June 2015, pp. 155~159 ISSN: 2089-3191 155 The Beta Cryptosystem Chandrashekhar Meshram Department of Mathematics, RTM Nagpur University,
Diffie-Hellman. Part 1 Cryptography 136
 Diffie-Hellman Part 1 Cryptography 136 Diffie-Hellman Invented by Williamson (GCHQ) and, independently, by D and H (Stanford) A key exchange algorithm o Used to establish a shared symmetric key Not for
Diffie-Hellman Part 1 Cryptography 136 Diffie-Hellman Invented by Williamson (GCHQ) and, independently, by D and H (Stanford) A key exchange algorithm o Used to establish a shared symmetric key Not for
COIN FLIPPING BY TELEPHONE
 COIN FLIPPING BY TELEPHONE A protocol for solving impossible problems Based on Manuel Blum's Paper from 1981 Proved useful for: - Mental poker - Certified Mail - Exchange of Secrets Table of Contents Application
COIN FLIPPING BY TELEPHONE A protocol for solving impossible problems Based on Manuel Blum's Paper from 1981 Proved useful for: - Mental poker - Certified Mail - Exchange of Secrets Table of Contents Application
A Mathematical Proof. Zero Knowledge Protocols. Interactive Proof System. Other Kinds of Proofs. When referring to a proof in logic we usually mean:
 A Mathematical Proof When referring to a proof in logic we usually mean: 1. A sequence of statements. 2. Based on axioms. Zero Knowledge Protocols 3. Each statement is derived via the derivation rules.
A Mathematical Proof When referring to a proof in logic we usually mean: 1. A sequence of statements. 2. Based on axioms. Zero Knowledge Protocols 3. Each statement is derived via the derivation rules.
Zero Knowledge Protocols. c Eli Biham - May 3, Zero Knowledge Protocols (16)
 Zero Knowledge Protocols c Eli Biham - May 3, 2005 442 Zero Knowledge Protocols (16) A Mathematical Proof When referring to a proof in logic we usually mean: 1. A sequence of statements. 2. Based on axioms.
Zero Knowledge Protocols c Eli Biham - May 3, 2005 442 Zero Knowledge Protocols (16) A Mathematical Proof When referring to a proof in logic we usually mean: 1. A sequence of statements. 2. Based on axioms.
Primitive Elements. Samuel Slocum, Evan Wall April 27, a p 1 1(modp)
 Primitive Elements Samuel Slocum, Evan Wall April 27, 2015 1 Introduction A Primitive element is a number a Z p given a prime p such that it has order p 1 and therefore the following equation holds. a
Primitive Elements Samuel Slocum, Evan Wall April 27, 2015 1 Introduction A Primitive element is a number a Z p given a prime p such that it has order p 1 and therefore the following equation holds. a
ICS 180 May 4th, Guest Lecturer: Einar Mykletun
 ICS 180 May 4th, 2004 Guest Lecturer: Einar Mykletun 1 Symmetric Key Crypto 2 Symmetric Key Two users who wish to communicate share a secret key Properties High encryption speed Limited applications: encryption
ICS 180 May 4th, 2004 Guest Lecturer: Einar Mykletun 1 Symmetric Key Crypto 2 Symmetric Key Two users who wish to communicate share a secret key Properties High encryption speed Limited applications: encryption
Introduction to Cryptography and Security Mechanisms. Abdul Hameed
 Introduction to Cryptography and Security Mechanisms Abdul Hameed http://informationtechnology.pk Before we start 3 Quiz 1 From a security perspective, rather than an efficiency perspective, which of the
Introduction to Cryptography and Security Mechanisms Abdul Hameed http://informationtechnology.pk Before we start 3 Quiz 1 From a security perspective, rather than an efficiency perspective, which of the
CS Computer Networks 1: Authentication
 CS 3251- Computer Networks 1: Authentication Professor Patrick Traynor 4/14/11 Lecture 25 Announcements Homework 3 is due next class. Submit via T-Square or in person. Project 3 has been graded. Scores
CS 3251- Computer Networks 1: Authentication Professor Patrick Traynor 4/14/11 Lecture 25 Announcements Homework 3 is due next class. Submit via T-Square or in person. Project 3 has been graded. Scores
Secure Multiparty Computation
 CS573 Data Privacy and Security Secure Multiparty Computation Problem and security definitions Li Xiong Outline Cryptographic primitives Symmetric Encryption Public Key Encryption Secure Multiparty Computation
CS573 Data Privacy and Security Secure Multiparty Computation Problem and security definitions Li Xiong Outline Cryptographic primitives Symmetric Encryption Public Key Encryption Secure Multiparty Computation
Flexible Access Control with Master Keys
 Flexible Access Control with Master Keys Gerald C. Chick and Stafford E. Tavares Queen s University at Kingston Abstract. We show how to create a master key scheme for controlling access to a set of services.
Flexible Access Control with Master Keys Gerald C. Chick and Stafford E. Tavares Queen s University at Kingston Abstract. We show how to create a master key scheme for controlling access to a set of services.
Information Security. message M. fingerprint f = H(M) one-way hash. 4/19/2006 Information Security 1
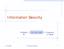 Information Security message M one-way hash fingerprint f = H(M) 4/19/2006 Information Security 1 Outline and Reading Digital signatures Definition RSA signature and verification One-way hash functions
Information Security message M one-way hash fingerprint f = H(M) 4/19/2006 Information Security 1 Outline and Reading Digital signatures Definition RSA signature and verification One-way hash functions
Public Key Cryptography and RSA
 Public Key Cryptography and RSA Major topics Principles of public key cryptosystems The RSA algorithm The Security of RSA Motivations A public key system is asymmetric, there does not have to be an exchange
Public Key Cryptography and RSA Major topics Principles of public key cryptosystems The RSA algorithm The Security of RSA Motivations A public key system is asymmetric, there does not have to be an exchange
CS408 Cryptography & Internet Security
 CS408 Cryptography & Internet Security Lectures 16, 17: Security of RSA El Gamal Cryptosystem Announcement Final exam will be on May 11, 2015 between 11:30am 2:00pm in FMH 319 http://www.njit.edu/registrar/exams/finalexams.php
CS408 Cryptography & Internet Security Lectures 16, 17: Security of RSA El Gamal Cryptosystem Announcement Final exam will be on May 11, 2015 between 11:30am 2:00pm in FMH 319 http://www.njit.edu/registrar/exams/finalexams.php
Security Analysis of Batch Verification on Identity-based Signature Schemes
 Proceedings of the 11th WSEAS International Conference on COMPUTERS, Agios Nikolaos, Crete Island, Greece, July 26-28, 2007 50 Security Analysis of Batch Verification on Identity-based Signature Schemes
Proceedings of the 11th WSEAS International Conference on COMPUTERS, Agios Nikolaos, Crete Island, Greece, July 26-28, 2007 50 Security Analysis of Batch Verification on Identity-based Signature Schemes
Improved Delegation Of Computation Using Somewhat Homomorphic Encryption To Reduce Storage Space
 Improved Delegation Of Computation Using Somewhat Homomorphic Encryption To Reduce Storage Space Dhivya.S (PG Scholar) M.E Computer Science and Engineering Institute of Road and Transport Technology Erode,
Improved Delegation Of Computation Using Somewhat Homomorphic Encryption To Reduce Storage Space Dhivya.S (PG Scholar) M.E Computer Science and Engineering Institute of Road and Transport Technology Erode,
Digital Signatures. Luke Anderson. 7 th April University Of Sydney.
 Digital Signatures Luke Anderson luke@lukeanderson.com.au 7 th April 2017 University Of Sydney Overview 1. Digital Signatures 1.1 Background 1.2 Basic Operation 1.3 Attack Models Replay Naïve RSA 2. PKCS#1
Digital Signatures Luke Anderson luke@lukeanderson.com.au 7 th April 2017 University Of Sydney Overview 1. Digital Signatures 1.1 Background 1.2 Basic Operation 1.3 Attack Models Replay Naïve RSA 2. PKCS#1
CPSC 467: Cryptography and Computer Security
 CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 11 October 4, 2017 CPSC 467, Lecture 11 1/39 ElGamal Cryptosystem Message Integrity and Authenticity Message authentication codes
CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 11 October 4, 2017 CPSC 467, Lecture 11 1/39 ElGamal Cryptosystem Message Integrity and Authenticity Message authentication codes
On the Importance of Memory Resources in the Security of Key Exchange Protocols
 On the Importance of Memory Resources in the Security of Key Exchange Protocols (Extended Abstract) George Davida Yvo Desmedt RenQ Peralta* Dept. EE & CS, Univ. of Wisconsin - Milwaukee P.O. Box 784 WI
On the Importance of Memory Resources in the Security of Key Exchange Protocols (Extended Abstract) George Davida Yvo Desmedt RenQ Peralta* Dept. EE & CS, Univ. of Wisconsin - Milwaukee P.O. Box 784 WI
