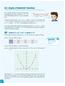
SECTION 8.2 the hyperbola Wake created from shock wave. Portion of a hyperbola

Transcription

1 SECTION 8. the hperola learning OjeCTIveS In this section, ou will: Locate a hperola s vertices and foci. Write equations of hperolas in standard form. Graph hperolas centered at the origin. Graph hperolas not centered at the origin. Solve applied prolems involving hperolas. 8. The hperola What do paths of comets, supersonic ooms, ancient Grecian pillars, and natural draft cooling towers have in common? The can all e modeled the same tpe of conic. For instance, when something moves faster than the speed of sound, a shock wave in the form of a cone is created. A portion of a conic is formed when the wave intersects the ground, resulting in a sonic oom. See Figure 1. Wake created from shock wave Portion of a hperola Figure 1 A shock wave intersecting the ground forms a portion of a conic and results in a sonic oom. Most people are familiar with the sonic oom created supersonic aircraft, ut humans were reaking the sound arrier long efore the first supersonic flight. The crack of a whip occurs ecause the tip is eceeding the speed of sound. The ullets shot from man firearms also reak the sound arrier, although the ang of the gun usuall supersedes the sound of the sonic oom. locating the vertices and Foci of a hperola In analtic geometr, a hperola is a conic section formed intersecting a right circular cone with a plane at an angle such that oth halves of the cone are intersected. This intersection produces two separate unounded curves that are mirror images of each other. See Figure. Figure A hperola Like the ellipse, the hperola can also e defined as a set of points in the coordinate plane. A hperola is the set of all points (, ) in a plane such that the difference of the distances etween (, ) and the foci is a positive constant.

2 698 CHAPTER 8 ANAltic geometr Notice that the definition of a hperola is ver similar to that of an ellipse. The distinction is that the hperola is defined in terms of the difference of two distances, whereas the ellipse is defined in terms of the sum of two distances. As with the ellipse, ever hperola has two aes of smmetr. The transverse ais is a line segment that passes through the center of the hperola and has vertices as its endpoints. The foci lie on the line that contains the transverse ais. The conjugate ais is perpendicular to the transverse ais and has the co-vertices as its endpoints. The center of a hperola is the midpoint of oth the transverse and conjugate aes, where the intersect. Ever hperola also has two asmptotes that pass through its center. As a hperola recedes from the center, its ranches approach these asmptotes. The central rectangle of the hperola is centered at the origin with sides that pass through each verte and co-verte; it is a useful tool for graphing the hperola and its asmptotes. To sketch the asmptotes of the hperola, simpl sketch and etend the diagonals of the central rectangle. See Figure 3. Conjugate ais Co-verte Transverse ais Focus Verte Verte Focus Co-verte Asmptote Center Asmptote Figure 3 Ke features of the hperola In this section, we will limit our discussion to hperolas that are positioned verticall or horizontall in the coordinate plane; the aes will either lie on or e parallel to the - and -aes. We will consider two cases: those that are centered at the origin, and those that are centered at a point other than the origin. Deriving the Equation of an Ellipse Centered at the Origin Let (c, 0) and (c, 0) e the foci of a hperola centered at the origin. The hperola is the set of all points (, ) such that the difference of the distances from (, ) to the foci is constant. See Figure 4. d (, ) d1 ( c, 0) (c, 0) ( a, 0) (a, 0) Figure 4 If (a, 0) is a verte of the hperola, the distance from (c, 0) to (a, 0) is a (c) = a + c. The distance from (c, 0) to (a, 0) is c a. The sum of the distances from the foci to the verte is (a + c) (c a) = a

3 SECTION 8. the hperola If (, ) is a point on the hperola, we can define the following variales: d = the distance from (c, 0) to (, ) d 1 = the distance from (c, 0) to (, ) B definition of a hperola, d d 1 is constant for an point (, ) on the hperola. We know that the difference of these distances is a for the verte (a, 0). It follows that d d 1 = a for an point on the hperola. As with the derivation of the equation of an ellipse, we will egin appling the distance formula. The rest of the derivation is algeraic. Compare this derivation with the one from the previous section for ellipses. ( + c) + ( c) + = a d d 1 = ( ( c)) + ( 0) ( c) + ( 0) = a Distance formula Simplif epressions. ( + c) + = a + ( c) + Move radical to opposite side. ( + c) + = (a + ( c) + ) Square oth sides. + c + c + = 4a + 4a ( c) + + ( c) + + c + c + = 4a + 4a ( c) + + c + c + c = 4a + 4a ( c) + c 4c 4a = 4a ( c) + Epand the squares. Epand remaining square. Comine like terms. Isolate the radical. c a = a ( c) + Divide 4. (c a ) = a ( c) + Square oth sides. c a c + a 4 = a ( c + c + ) Epand the squares. c a c + a 4 = a a c + a c + a Distriute a. a 4 + c = a + a c + a c a a = a c a 4 (c a ) a = a (c a ) Comine like terms. Rearrange terms. Factor common terms a = a Set = c a. a a a = a a Divide oth sides a. a = 1 This equation defines a hperola centered at the origin with vertices (±a, 0) and co-vertices (0 ± ). standard forms of the equation of a hperola with center (0, 0) The standard form of the equation of a hperola with center (0, 0) and major ais on the -ais is a = 1 where the length of the transverse ais is a the coordinates of the vertices are (±a, 0) the length of the conjugate ais is the coordinates of the co-vertices are (0, ±) the distance etween the foci is c, where c = a + the coordinates of the foci are (±c, 0) the equations of the asmptotes are = ± a

4 700 CHAPTER 8 ANAltic geometr See Figure 5a. The standard form of the equation of a hperola with center (0, 0) and transverse ais on the -ais is a = 1 where the length of the transverse ais is a the coordinates of the vertices are (0, ± a) the length of the conjugate ais is the coordinates of the co-vertices are (±, 0) the distance etween the foci is c, where c = a + the coordinates of the foci are (0, ± c) the equations of the asmptotes are = ± a See Figure 5. Note that the vertices, co-vertices, and foci are related the equation c = a +. When we are given the equation of a hperola, we can use this relationship to identif its vertices and foci. = a (0, ) = a = a (0, c ) (0, a) = a (c, 0) (a, 0) (0, 0) (a, 0) (c, 0) (, 0) (0, 0) (, 0) (0, ) (0, c) (0, a) (a) Figure 5 (a) horizontal hperola with center (0, 0) () vertical hperola with center (0, 0) () How To Given the equation of a hperola in standard form, locate its vertices and foci. 1. Determine whether the transverse ais lies on the - or -ais. Notice that a is alwas under the variale with the positive coefficient. So, if ou set the other variale equal to zero, ou can easil find the intercepts. In the case where the hperola is centered at the origin, the intercepts coincide with the vertices. a. If the equation has the form a = 1, then the transverse ais lies on the -ais. The vertices are located at ( ± a, 0), and the foci are located at (± c, 0).. If the equation has the form a = 1, then the transverse ais lies on the -ais. The vertices are located at (0, ± a), and the foci are located at (0, ± c).. Solve for a using the equation a = a. 3. Solve for c using the equation c = a +.

5 SECTION 8. the hperola Eample 1 Locating a Hperola s Vertices and Foci Identif the vertices and foci of the hperola with equation 49 3 = 1. Solution The equation has the form a = 1, so the transverse ais lies on the -ais. The hperola is centered at the origin, so the vertices serve as the -intercepts of the graph. To find the vertices, set = 0, and solve for. 1 = = = 49 = 49 = ± 49 = ± 7 The foci are located at (0, ± c). Solving for c, c = a + = = 81 = 9 Therefore, the vertices are located at (0, ± 7), and the foci are located at (0, 9). Tr It #1 Identif the vertices and foci of the hperola with equation 9 5 = 1. Writing equations of hperolas in Standard Form Just as with ellipses, writing the equation for a hperola in standard form allows us to calculate the ke features: its center, vertices, co-vertices, foci, asmptotes, and the lengths and positions of the transverse and conjugate aes. Conversel, an equation for a hperola can e found given its ke features. We egin finding standard equations for hperolas centered at the origin. Then we will turn our attention to finding standard equations for hperolas centered at some point other than the origin. Hperolas Centered at the Origin Reviewing the standard forms given for hperolas centered at (0, 0), we see that the vertices, co-vertices, and foci are related the equation c = a +. Note that this equation can also e rewritten as = c a. This relationship is used to write the equation for a hperola when given the coordinates of its foci and vertices. How To Given the vertices and foci of a hperola centered at (0, 0), write its equation in standard form. 1. Determine whether the transverse ais lies on the - or -ais. a. If the given coordinates of the vertices and foci have the form (± a, 0) and (± c, 0), respectivel, then the transverse ais is the -ais. Use the standard form a = 1.. If the given coordinates of the vertices and foci have the form (0, ± a) and (0, ± c), respectivel, then the transverse ais is the -ais. Use the standard form a = 1.. Find using the equation = c a. 3. Sustitute the values for a and into the standard form of the equation determined in Step 1.

6 70 CHAPTER 8 ANAltic geometr Eample Finding the Equation of a Hperola Centered at (0, 0) Given its Foci and Vertices What is the standard form equation of the hperola that has vertices (±6, 0) and foci (± 10, 0)? Solution The vertices and foci are on the -ais. Thus, the equation for the hperola will have the form a = 1. The vertices are (±6, 0), so a = 6 and a = 36. The foci are (± 10, 0), so c = 10 and c = 40. Solving for, we have = c a = Sustitute for c and a. = 4 Sutract. Finall, we sustitute a = 36 and = 4 into the standard form of the equation, a hperola is 36 = 1, as shown in Figure = 1. The equation of the Figure 6 Tr It # What is the standard form equation of the hperola that has vertices (0, ± ) and foci (0, ± 5 )? Hperolas Not Centered at the Origin Like the graphs for other equations, the graph of a hperola can e translated. If a hperola is translated h units horizontall and k units verticall, the center of the hperola will e (h, k). This translation results in the standard form of the equation we saw previousl, with replaced ( h) and replaced ( k). standard forms of the equation of a hperola with center (h, k) The standard form of the equation of a hperola with center (h, k) and transverse ais parallel to the -ais is ( h) ( k) a = 1 where the length of the transverse ais is a the coordinates of the vertices are (h ± a, k) the length of the conjugate ais is the coordinates of the co-vertices are (h, k ± ) the distance etween the foci is c, where c = a + the coordinates of the foci are (h ± c, k)

7 SECTION 8. the hperola The asmptotes of the hperola coincide with the diagonals of the central rectangle. The length of the rectangle is a and its width is. The slopes of the diagonals are ±, and each diagonal passes through the center (h, k). a Using the point-slope formula, it is simple to show that the equations of the asmptotes are = ± ( h) + k. a See Figure 7a. The standard form of the equation of a hperola with center (h, k) and transverse ais parallel to the -ais is ( k) ( h) a = 1 where the length of the transverse ais is a the coordinates of the vertices are (h, k ± a) the length of the conjugate ais is the coordinates of the co-vertices are (h ±, k) the distance etween the foci is c, where c = a + the coordinates of the foci are (h, k ± c) Using the reasoning aove, the equations of the asmptotes are = ± a ( h) + k. See Figure 7. = ( h) + k a (h, k + ) (h, k + c) (h, k + a) = a ( h) + k (h c, k) (h + c, k) (h a, k) (h, k) (h + a, k) (h, k ) (h, k) (h +, k) (h, k) (h, k a) (h, k c) = a ( h) + k = a ( h) + k (a) () Figure 7 (a) horizontal hperola with center (h, k) () vertical hperola with center (h, k) Like hperolas centered at the origin, hperolas centered at a point (h, k) have vertices, co-vertices, and foci that are related the equation c = a +. We can use this relationship along with the midpoint and distance formulas to find the standard equation of a hperola when the vertices and foci are given. How To Given the vertices and foci of a hperola centered at (h, k), write its equation in standard form. 1. Determine whether the transverse ais is parallel to the - or -ais. a. If the -coordinates of the given vertices and foci are the same, then the transverse ais is parallel to the -ais. ( h) ( k) Use the standard form a = 1.. If the -coordinates of the given vertices and foci are the same, then the transverse ais is parallel to the -ais. ( k) Use the standard form ( h) a = 1.. Identif the center of the hperola, (h, k), using the midpoint formula and the given coordinates for the vertices.

8 704 CHAPTER 8 ANAltic geometr 3. Find a solving for the length of the transverse ais, a, which is the distance etween the given vertices. 4. Find c using h and k found in Step along with the given coordinates for the foci. 5. Solve for using the equation = c a. 6. Sustitute the values for h, k, a, and into the standard form of the equation determined in Step 1. Eample 3 Finding the Equation of a Hperola Centered at (h, k) Given its Foci and Vertices What is the standard form equation of the hperola that has vertices at (0, ) and (6, ) and foci at (, ) and (8, )? Solution The -coordinates of the vertices and foci are the same, so the transverse ais is parallel to the -ais. Thus, the equation of the hperola will have the form ( h) ( k) a = 1 First, we identif the center, (h, k). The center is halfwa etween the vertices (0, ) and (6, ). Appling the midpoint formula, we have (h, k) = 0 + 6, + () = (3, ) Net, we find a. The length of the transverse ais, a, is ounded the vertices. So, we can find a finding the distance etween the -coordinates of the vertices. a = 0 6 a = 6 a = 3 a = 9 Now we need to find c. The coordinates of the foci are (h ± c, k). So (h c, k) = (, ) and (h + c, k) = (8, ). We can use the -coordinate from either of these points to solve for c. Using the point (8, ), and sustituting h = 3, Net, solve for using the equation = c a : h + c = c = 8 c = 5 c = 5 = c a = 5 9 = 16 Finall, sustitute the values found for h, k, a, and into the standard form of the equation. ( 3) ( + ) = Tr It #3 What is the standard form equation of the hperola that has vertices (1, ) and (1, 8) and foci (1, 10) and (1, 16)? graphing hperolas Centered at the Origin When we have an equation in standard form for a hperola centered at the origin, we can interpret its parts to identif the ke features of its graph: the center, vertices, co-vertices, asmptotes, foci, and lengths and positions of the transverse and conjugate aes. To graph hperolas centered at the origin, we use the standard form a = 1 for horizontal hperolas and the standard form a = 1 for vertical hperolas.

9 SECTION 8. the hperola How To Given a standard form equation for a hperola centered at (0, 0), sketch the graph. 1. Determine which of the standard forms applies to the given equation.. Use the standard form identified in Step 1 to determine the position of the transverse ais; coordinates for the vertices, co-vertices, and foci; and the equations for the asmptotes. a. If the equation is in the form a = 1, then the transverse ais is on the -ais the coordinates of the vertices are (±a, 0) the coordinates of the co-vertices are (0, ± ) the coordinates of the foci are (±c, 0) the equations of the asmptotes are = ± a. If the equation is in the form a = 1, then the transverse ais is on the -ais the coordinates of the vertices are (0, ± a) the coordinates of the co-vertices are (±, 0) the coordinates of the foci are (0, ± c) the equations of the asmptotes are = ± a 3. Solve for the coordinates of the foci using the equation c = ± a Plot the vertices, co-vertices, foci, and asmptotes in the coordinate plane, and draw a smooth curve to form the hperola. Eample 4 Graphing a Hperola Centered at (0, 0) Given an Equation in Standard Form Graph the hperola given the equation = 1. Identif and lael the vertices, co-vertices, foci, and asmptotes. Solution The standard form that applies to the given equation is a = 1. Thus, the transverse ais is on the -ais The coordinates of the vertices are (0, ± a) = (0, ± 64 ) = (0, ± 8) The coordinates of the co-vertices are (±, 0) = (± 36, 0) = (±6, 0) The coordinates of the foci are (0, ± c), where c = ± a +. Solving for c, we have Therefore, the coordinates of the foci are (0, ± 10) c = ± a + = ± = ± 100 = ± 10 The equations of the asmptotes are = ± a = ± 8 6 = ± 4 3 Plot and lael the vertices and co-vertices, and then sketch the central rectangle. Sides of the rectangle are parallel to the aes and pass through the vertices and co-vertices. Sketch and etend the diagonals of the central rectangle to show the asmptotes. The central rectangle and asmptotes provide the framework needed to sketch an accurate graph of the hperola. Lael the foci and asmptotes, and draw a smooth curve to form the hperola, as shown in Figure 8.

10 706 CHAPTER 8 ANAltic geometr = 4 3 (0, 10) (0, 8) = 4 3 (6, 8) (0, 8) (6, 8) ( 6, 0) (0, 0) (6, 0) (6, 0) (0, 0) (6, 0) (0, 8) (0, 8) (6, 8) (6, 8) (0, 10) Tr It #4 Figure 8 Graph the hperola given the equation 144 = 1. Identif and lael the vertices, co-vertices, foci, and 81 asmptotes. graphing hperolas not Centered at the Origin Graphing hperolas centered at a point (h, k) other than the origin is similar to graphing ellipses centered at a ( h) ( k) point other than the origin. We use the standard forms = 1 for horizontal hperolas, and ( k) a ( h) = 1 for vertical hperolas. From these standard form equations we can easil calculate and plot a ke features of the graph: the coordinates of its center, vertices, co-vertices, and foci; the equations of its asmptotes; and the positions of the transverse and conjugate aes. How To Given a general form for a hperola centered at (h, k), sketch the graph. 1. Determine which of the standard forms applies to the given equation. Convert the general form to that standard form.. Use the standard form identified in Step 1 to determine the position of the transverse ais; coordinates for the center, vertices, co-vertices, foci; and equations for the asmptotes. ( h) ( k) a. If the equation is in the form a the transverse ais is parallel to the -ais the center is (h, k) the coordinates of the vertices are (h ± a, k) the coordinates of the co-vertices are (h, k ± ) the coordinates of the foci are (h ± c, k) = 1, then the equations of the asmptotes are = ± ( h) + k a

11 SECTION 8. the hperola If the equation is in the form the transverse ais is parallel to the -ais the center is (h, k) the coordinates of the vertices are (h, k ± a) ( k) a ( h) = 1, then the coordinates of the co-vertices are (h ±, k) the coordinates of the foci are (h, k ± c) the equations of the asmptotes are = ± a ( h) + k 3. Solve for the coordinates of the foci using the equation c = ± a Plot the center, vertices, co-vertices, foci, and asmptotes in the coordinate plane and draw a smooth curve to form the hperola. Eample 5 Graphing a Hperola Centered at (h, k) Given an Equation in General Form Graph the hperola given the equation = 0. Identif and lael the center, vertices, co-vertices, foci, and asmptotes. Solution Start epressing the equation in standard form. Group terms that contain the same variale, and move the constant to the opposite side of the equation. Factor the leading coefficient of each epression. (9 36) (4 + 40) = 388 9( 4) 4( + 10) = 388 Complete the square twice. Rememer to alance the equation adding the same constants to each side. Rewrite as perfect squares. 9( 4 + 4) 4( ) = ( ) 4( + 5) = 34 Divide oth sides the constant term to place the equation in standard form. ( ) ( + 5) = ( h) ( k) The standard form that applies to the given equation is a = 1, where a = 36 and = 81, or a = 6 and = 9. Thus, the transverse ais is parallel to the -ais. It follows that: the center of the ellipse is (h, k) = (, 5) the coordinates of the vertices are (h ± a, k) = ( ± 6, 5), or (4, 5) and (8, 5) the coordinates of the co-vertices are (h, k ± ) = (, 5 ± 9), or (, 14) and (, 4) the coordinates of the foci are (h ± c, k), where c = ± a +. Solving for c, we have c = ± = ± 117 = ± 3 13 Therefore, the coordinates of the foci are ( 3 13, 5) and ( , 5). The equations of the asmptotes are = ± a ( h) + k = ± 3 ( ) 5. Net, we plot and lael the center, vertices, co-vertices, foci, and asmptotes and draw smooth curves to form the hperola, as shown in Figure 9.

12 708 CHAPTER 8 ANAltic geometr (, 4) (4, 5) (8, 5) (, 14) (, 5) Figure 9 Tr It #5 ( + 4) Graph the hperola given the standard form of an equation ( 3) = 1. Identif and lael the center, vertices, co-vertices, foci, and asmptotes. Solving Applied Prolems Involving hperolas As we discussed at the eginning of this section, hperolas have real-world applications in man fields, such as astronom, phsics, engineering, and architecture. The design efficienc of hperolic cooling towers is particularl interesting. Cooling towers are used to transfer waste heat to the atmosphere and are often touted for their ailit to generate power efficientl. Because of their hperolic form, these structures are ale to withstand etreme winds while requiring less material than an other forms of their size and strength. See Figure 10. For eample, a 500-foot tower can e made of a reinforced concrete shell onl 6 or 8 inches wide! Figure 10 Cooling towers at the dra power station in north orkshire, United Kingdom (credit: les haines, Flickr) The first hperolic towers were designed in 1914 and were 35 meters high. Toda, the tallest cooling towers are in France, standing a remarkale 170 meters tall. In Eample 6 we will use the design laout of a cooling tower to find a hperolic equation that models its sides.

13 Eample 6 SECTION 8. the hperola Solving Applied Prolems Involving Hperolas The design laout of a cooling tower is shown in Figure 11. The tower stands meters tall. The diameter of the top is 7 meters. At their closest, the sides of the tower are 60 meters apart. 7 m 79.6 m 60 m m Figure 11 Project design for a natural draft cooling tower Find the equation of the hperola that models the sides of the cooling tower. Assume that the center of the hperola indicated the intersection of dashed perpendicular lines in the figure is the origin of the coordinate plane. Round final values to four decimal places. Solution We are assuming the center of the tower is at the origin, so we can use the standard form of a horizontal hperola centered at the origin: a = 1, where the ranches of the hperola form the sides of the cooling tower. We must find the values of a and to complete the model. First, we find a. Recall that the length of the transverse ais of a hperola is a. This length is represented the distance where the sides are closest, which is given as 65.3 meters. So, a = 60. Therefore, a = 30 and a = 900. To solve for, we need to sustitute for and in our equation using a known point. To do this, we can use the dimensions of the tower to find some point (, ) that lies on the hperola. We will use the top right corner of the tower to represent that point. Since the -ais isects the tower, our -value can e represented the radius of the top, or 36 meters. The -value is represented the distance from the origin to the top, which is given as 79.6 meters. Therefore, a = 1 = = a 1 (79.6) (36) Standard form of horizontal hperola. Isolate Sustitute for a,, and Round to four decimal places The sides of the tower can e modeled the hperolic equation = 1, or = 1

14 710 CHAPTER 8 ANAltic geometr Tr It #6 A design for a cooling tower project is shown in Figure 1. Find the equation of the hperola that models the sides of the cooling tower. Assume that the center of the hperola indicated the intersection of dashed perpendicular lines in the figure is the origin of the coordinate plane. Round final values to four decimal places. 60 m m 40 m m Figure 1 Access these online resources for additional instruction and practice with hperolas. Conic Sections: The hperola Part 1 of ( Conic Sections: The hperola Part of ( graph a hperola with Center at Origin ( graph a hperola with Center not at Origin (

15 SECTION 8. section eercises SeCTIOn eercises veral 1. Define a hperola in terms of its foci.. What can we conclude aout a hperola if its asmptotes intersect at the origin? 3. What must e true of the foci of a hperola? 4. If the transverse ais of a hperola is vertical, what do we know aout the graph? 5. Where must the center of hperola e relative to its foci? AlgeRAIC For the following eercises, determine whether the following equations represent hperolas. If so, write in standard form = = = = = 0 For the following eercises, write the equation for the hperola in standard form if it is not alread, and identif the vertices and foci, and write equations of asmptotes = = = = ( 1) 9 ( ) 16 = ( 6) 36 ( + 1) = 1 16 ( ) ( + 7) = = = = = = = = = 0 For the following eercises, find the equations of the asmptotes for each hperola = 1 7. ( 3) ( + 4) 5 = 1 ( 3) 8. ( + 5) 3 6 = = = 0 graphical For the following eercises, sketch a graph of the hperola, laeling vertices and foci = = = = ( + 5) 9 ( 4) = ( ) 8 ( + 3) = 1 7 ( 3) ( 3) = = 0

16 7 1 CHAPTER 8 ANAltic geometr = = = = = = 0 For the following eercises, given information aout the graph of the hperola, find its equation. 45. Vertices at (3, 0) and (3, 0) and one focus at (5, 0). 46. Vertices at (0, 6) and (0, 6) and one focus at (0, 8). 47. Vertices at (1, 1) and (11, 1) and one focus at (1, 1). 48. Center: (0, 0); verte: (0, 13); one focus: (0, 313 ). 49. Center: (4, ); verte: (9, ); one focus: (4 + 6, ). 50. Center: (3, 5); verte: (3, 11); one focus: (3, ). For the following eercises, given the graph of the hperola, find its equation Foci Vertices Center (1, 1) Foci 53. Foci 54. Foci (1, 3) Vertices Center (1, 0) Center (3, 1) Vertices (1, 3) Foci Foci 55. Foci Foci ( 3, 3) ( 8, 3) Center (, 3) Vertices

17 etensions SECTION 8. section eercises For the following eercises, epress the equation for the hperola as two functions, with as a function of. Epress as simpl as possile. Use a graphing calculator to sketch the graph of the two functions on the same aes = = ( ) ( + 3) = = = 0 ReAl-WORld APPlICATIOnS For the following eercises, a hedge is to e constructed in the shape of a hperola near a fountain at the center of the ard. Find the equation of the hperola and sketch the graph. 61. The hedge will follow the asmptotes = and =, and its closest distance to the center fountain is 5 ards. 6. The hedge will follow the asmptotes = and =, and its closest distance to the center fountain is 6 ards. 63. The hedge will follow the asmptotes = 1 and = 1, and its closest distance to the center fountain is 10 ards. 64. The hedge will follow the asmptotes = 3 and =, and its closest distance to the center 3 fountain is 1 ards. 65. The hedge will follow the asmptotes = 3 4 and = 3, and its closest distance to the center 4 fountain is 0 ards. For the following eercises, assume an oject enters our solar sstem and we want to graph its path on a coordinate sstem with the sun at the origin and the -ais as the ais of smmetr for the oject's path. Give the equation of the flight path of each oject using the given information. 66. The oject enters along a path approimated the line = and passes within 1 au (astronomical unit) of the sun at its closest approach, so that the sun is one focus of the hperola. It then departs the solar sstem along a path approimated the line = The oject enters along a path approimated the line = and passes within 1 au of the sun at its closest approach, so the sun is one focus of the hperola. It then departs the solar sstem along a path approimated the line = The oject enters along a path approimated the line = 3 9 and passes within 1 au of the sun at its closest approach, so the sun is one focus of the hperola. It then departs the solar sstem along a path approimated the line = The oject enters along a path approimated the line = and passes within 0.5 au of the sun at its closest approach, so the sun is one focus of the hperola. It then departs the solar sstem along a path approimated the line = The oject enters along a path approimated the line = 1 1 and passes within 1 au of the sun 3 at its closest approach, so the sun is one focus of the hperola. It then departs the solar sstem along a path approimated the line =