Substituting a 2 b 2 for c 2 and using a little algebra, we can then derive the standard equation for an ellipse centred at the origin,
|
|
|
- Jonah Jennings
- 5 years ago
- Views:
Transcription
1 Conics onic sections are the curves which result from the intersection of a plane with a cone. These curves were studied and revered by the ancient Greeks, and were written about extensively by both Euclid and Appolonius. They remain important today, partly for their many and diverse applications. Although to most people the word cone conjures up an image of a solid figure with a round base and a pointed top, to a mathematician a cone is a surface, one which is obtained in a very precise way. Imagine a vertical line, and a second line intersecting it at some angle (phi). We will call the vertical line the axis, and the second line the generator. The angle between them is called the vertex angle. Now imagine grasping the axis between thumb and forefinger on either side of its point of intersection with the generator, and twirling it. The generator will sweep out a surface, as shown in the diagram. It is this surface which we call a cone. Notice that a cone has an upper half and a lower half (called the nappes), and that these are joined at a single point, called the vertex. Notice also that the nappes extend indefinitely far both upwards and downwards. A cone is thus completely determined by its vertex angle. Now, in intersecting a flat plane with a cone, we have three choices, depending on the angle the plane makes to the vertical axis of the cone. First, we may choose our plane to have a greater angle to the vertical than does the generator of the cone, in which case the plane must cut right through one of the nappes. This results in a closed curve called an ellipse. Second, our plane may have exactly the same angle to the vertical axis as the generator of the cone, so that it is parallel to the side of the cone. The resulting open curve is called a parabola. Finally, the plane may have a smaller angle to the vertical axis (that is, the plane is steeper than the generator), in which case the plane will cut both nappes of the cone. The resulting curve is called a hyperbola, and has two disjoint branches.
2 Notice that if the plane is actually perpendicular to the axis (that is, it is horizontal) then we get a circle showing that a circle is really a special kind of ellipse. Also, if the intersecting plane passes through the vertex then we get the so-called degenerate conics; a single point in the case of an ellipse, a line in the case of a parabola, and two intersecting lines in the case of a hyperbola. ELLIPSE The set of all points in the plane, the sum of whose distances from two fixed points, called the foci, is a constant. ( Foci is the plural of focus) For reasons that will become apparent, we will denote the sum of these distances by 2a. We see from the definition that an ellipse has two axes of symmetry, the larger of which we call the major axis and the smaller the minor axis. The two points at the ends of the ellipse (on the major axis) are called the vertices. It happens that the length of the major axis is 2a, the sum of the distances from any point on the ellipse to its foci. If we call the length of the
3 minor axis 2b and the distance between the foci 2c (where c = e, called eccentricity), then the Pythagorean Theorem yields the relationship b 2 + c 2 = a 2 : By imposing coordinate axes in this convenient manner, we see that the vertices are at the x intercepts, at a and -a, and that the y-intercepts are at b and -b. Let the variable point P on the ellipse be given the coordinates (x, y). We may then apply the distance formula for the distances from P to F 1 and from P to F 2 to express our geometrical definition of the ellipse in the language of algebra: Substituting a 2 b 2 for c 2 and using a little algebra, we can then derive the standard equation for an ellipse centred at the origin, where a and b are the lengths of the semimajor and semiminor axes, respectively. (If the major axis of the ellipse is vertical, exchange a and b in the equation.) The points (a, 0) and (-a, 0) are called the vertices of the ellipse. If the ellipse is translated up/down or left/right, so that its centre is at (h, k), then the equation takes the form
4 If a = b, we have the special case of an ellipse whose foci coincide at the centre that is, a circle of radius a. The ellipse has the following remarkable reflection property. Let P be any point on the ellipse, and construct the line segments joining P to the foci. Then these lines make equal angles to the tangent line at P. Consequently, any ray emanating from one focus will always reflect off of the inside of the ellipse in such a way as to go straight to the other focus. Architects have exploited this property in many famous buildings. The whisper chamber in the United States Capitol is one; stand at one focus and whisper, and anyone at the other focus can hear you with perfect clarity, even though they are much too far away from you to hear a whisper normally. The Mormon Tabernacle in Salt Lake City was also designed as an ellipse (indeed, it is the top half of an ellipsoid), to provide a perfect acoustical environment for choral and organ music. Geometric Construction The geometric construction of an ellipse can easily be accomplished with some very simple tools: a piece of string, a pencil, two pins, and a piece of paper. Simply stick the two pieces of string into the piece of paper using the two pins. Pull the string tight (using the pencil) until a triangle is built with the pencil and the two pins as vertices. Now, keeping the string pulled tight, move the pencil around until the ellipse is traced out. (See the enclosed FIGURE E2.)
5 Some other terms need to be introduced at this point of the discussion. The line through the foci intersects the ellipse at two points, known as vertices. (Vertices is the plural of the term vertex.) This line segment joining the vertices is called the major axis and its midpoint is called the centre of the ellipse. The minor axis is the line segment perpendicular to the major axis which also goes through the centre and crosses the ellipse at two points. (By the way, these two points are called minor vertices in the Slovak literature) See FIGURE E3 for a graphical view of some of these key terms. Example 1 Consider the equation Given our comments above, this equation yields an ellipse. We see that a = 5 and b = 3 and the graph of this ellipse is the following:
6 Note the relationship of a and b to the graph. We see that the value of a yields half the length of the major axis. Equivalently, we can say that the vertices are found by travelling down the major axis exactly a units from the centre. We also see that half the length of the minor axis is exactly b. Example 2 It turns out that this ellipse looks very similar to the ellipse in Example 1. The major difference is that this ellipse is now oriented along the vertical axis as opposed to the horizontal. In other words, the major axis of this ellipse is vertical, not horizontal. See FIGURE E5. Example 3 Find the standard form of the equation of the ellipse with foci at (0, 5) and (0, -5) and with a major axis of length 26.
7 We must interpret the information given to us in the above problem. First, we see that the foci are 10 units apart (and live on the y-axis). Thus, we have e = 5 and a = 13, since the length of the major axis is 26. Since the centre of the ellipse is at (0, 0), the vertices of the ellipse must be at (0, 13) and (0, -13). Finally, we just need to find out the value of b. From the relationship e 2 = a 2 b 2 we know that 5 2 = 13 2 b 2 This can be simplified to b 2 = = 144 Thus we see that b = 12 Now we can write the standard equation of the ellipse. It is Example 4: Sketch the graph of the ellipse whose equation is Again, let's pull as much information out of the equation as possible. We see that the centre of the ellipse is (3, -1). Next, note that a = 7 and b = 5 Since a is in the denominator of the term involving the variable x, we know that the major axis of this ellipse is horizontal (parallel with the x-axis). Moreover, we know that the major axis has length 14 and the vertices occur at points which are 7 units in either direction from the centre. This all implies that the vertices are at (3 + 7, -1) and (3 7, -1), which could also be written as (10, -1) and (-4, -1). As a sidelight, we also know that the endpoints of the minor axis are exactly 5 units above and below the centre, which places them at the points (3, 4) and (3, -6). From this information, we can easily plot the ellipse in question. For the sake of completion, let's quickly determine the location of the foci. Again using the relationship we know that Thus, the foci are exactly Finally, a sketch of the graph is given in Figure E7. 24 units to the left and right of the centre of the ellipse.
8 Example 5 Sketch the graph of the ellipse whose equation is At this stage of our conics development, we really have not dealt with the equation of a conic in non-standard form. Recall that this is, however, a valid equation for a conic and it happens to be an ellipse. Our first goal is to rewrite this equation into standard form and then to interpret this equation as we sketch the graph. The technique involved in rewriting this equation into standard form is known as completing the square. We see that is equivalent to Now we want to fill in the apparent gaps that have been inserted in the parentheses above. This filling in is completing the square. We want to write in the number that will make each set of parentheses a perfect square. We do that now: Note that, when we add 9 to the left-hand side of the equation, we must also add it to the right-hand side. Also, we are not really adding 1 to the left-hand side; we are really adding 4 since we multiply the 1 by the 4 that is outside the parentheses. Hence, we must also add 4 to the right-hand side. Rewriting our equation now yields or
9 and we have successfully transformed the equation originally given to us into the standard equation of an ellipse. This ellipse has centre (3, -1) and has values a = 2, b = 1 As noted in previous examples, because a is in the denominator of the term involving the variable x, we know that the major axis of this ellipse is horizontal (parallel with the x-axis). HYPERBOLA The set of all points in the plane, the difference of whose distances from two fixed points, called the foci, remains constant. Mimicking our procedure with ellipses, we will choose the constant 2a to represent the difference of these distances, that is, PF 1 PF 2 = 2a. We will call the two points of the hyperbola which lie on the line connecting the foci the vertices, and we then see that the distance between the vertices must be 2a. Also, we will call the distance between the foci 2e. Finally, we will define the constant b by e 2 = a 2 + b 2. (We may do this since evidently e > a.) Placing coordinate axes at the centre as before, we obtain this picture:
10 Applying the distance formulas and substituting for e as we did in the previous cases, we can derive the standard formula of a hyperbola: We note that solving this equation for y yields and letting x become arbitrarily large causes this expression to become arbitrarily close to Thus we see that the crisscrossing lines in the diagram above are asymptotes for the hyperbola, that is, the curve becomes indefinitely close to these lines as the absolute value of x grows without bound. As before, if the principal axis of the hyperbola is vertical instead of horizontal, we switch the roles of a and b. We may also translate the hyperbola up/down and back/forth, placing the centre at (h, k) by modifying our equation thusly: The reflection property of the hyperbola is of great importance in optics. Let P be any
11 point on one branch of the hyperbola. Then the line segments joining P to each of the foci form an angle which is bisected by the tangent line at P. Each hyperbola consists of two branches. The line segment which connects the two foci intersects the hyperbola at two points, called the vertices. The line segment which ends at these vertices is called the transverse axis and the midpoint of this line is called the centre of the hyperbola. See Figure H1 for a sketch of a hyperbola with these pieces identified. Note that, as in the case of the ellipse, a hyperbola can have a vertical or horizontal orientation. We now turn our attention to the standard equation of a hyperbola. We say that the standard equation of a hyperbola cantered at the origin is given by if the transverse axis is horizontal, or if the transverse axis is vertical.
12 Notice a very important difference in the notation of the equation of a hyperbola compared to that of the ellipse. We see that a always corresponds to the positive term in the equation of the ellipse. The relationship of a and b does not determine the orientation of the hyperbola. (Recall that the size of a and b was used in the section on the ellipse to determine the orientation of the ellipse.) In the case of the hyperbola, the variable in the positive term of the equation determines the orientation of the hyperbola. Hence, if the variable x is in the positive term of the equation, as it is in the equation then the hyperbola is oriented as follows: If the variable y is in the positive term of the equation, as it is in the equation then we see the following type of hyperbola:
13 Note that the vertices are always a units from the centre of the hyperbola, and the distance e of the foci from the centre of the hyperbola can be determined using a, b, and the following equality: e 2 = a 2 + b 2 We will use this relationship often, so keep it in mind. The next question you might ask is this: What happens to the equation if the centre of the hyperbola is not (0,0)? As in the case of the ellipse, if the centre of the hyperbola is (h, k), then the equation of the hyperbola becomes if the transverse axis is horizontal, or if the transverse axis is vertical. Now in the case of a hyperbola, the distance between the foci is greater than the distance between the vertices. Hence, in the case of a hyperbola, Recall that for the ellipse, Two final terms that we must mention are asymptotes and the conjugate axis. The two branches of a hyperbola are bounded by two straight lines, known as asymptotes. These asymptotes are easily drawn once one plots the vertices and the points (h, k + b) and (h, k b) and draws the rectangle which goes through these four points. The line segment joining (h, k + b) and (h, k b) is called the conjugate axis. The asymptotes then are simply the lines which go through the corners of the rectangle. (See FIGURE H4.)
14 Example 1: Consider the equation Given our comments above, this equation yields a hyperbola. (Note the difference between this equation and that in Example 1 of the section on ellipses.) We see that a =5, and b = 3 and the graph of this hyperbola is the following: Note also, as we finish this example, that the equations of the asymptotes for this hyperbola are and Example 2 Consider the equation Note that the only difference between this example and the previous one is that the 9 and 25 have traded places. How does this change the shape of the hyperbola? Is there a change in the orientation from horizontal to vertical? The answer is no. Recall that orientation of a hyperbola is not determined by the sizes of the denominators in the terms of the standard equation of the hyperbola. Rather, orientation is determined by which variable (x or y) is in the ``positive'' term. Hence, as is the case in the previous example, this hyperbola is also horizontally oriented. The switch between the 9 and 25 simply changes the shape of the branches. The openings of the branches appear to be wider. See FIGURE H5.
15 Note that difference in shape (between this example and the previous) can also be seen in the equations of the asymptotes. Now we see that and 5 3 Thus, the slope of the asymptotes is now, not as in the previous example. 3 5 Example 3 Find the standard form of the equation of the hyperbola with foci at (0, 9) and (0, -9) and transverse axis of length 6. We must interpret the information given to us in the above problem. First, we see that the foci are 18 units apart (and live on the y--axis). Thus, we have e = 9. Moreover, a = 3 since the length of the transverse axis is 6. Since the centre of the hyperbola is at (0, 0), the vertices of the hyperbola must be at (0, 3) and (0, -3). Finally, we just need to find out the value of b. From the relationship we know that This can be simplified to Thus we see that Now we can write the standard equation of the hyperbola. It is
16 Example 4 Sketch the graph of the hyperbola whose equation is Again, let's pull as much information out of the equation as possible. We see that the centre of the hyperbola is (3, -1). Next, note that a = 7 and b = 5. Since the ``positive'' term in the equation involves the variable x, we know that the transverse axis of this hyperbola is horizontal (parallel with the x--axis). Moreover, we know that the transverse axis has length 14 and the vertices occur at points which are 7 units in either direction of the centre. This all implies that the vertices are at (3 + 7, -1) and (3 7, -1), which could also be written as (10, -1) and (-4, -1). As a sidelight, we also know that the endpoints of the conjugate axis are exactly 5 units above and below the centre, which places them at the points (3, 4) and (3, -6). From this information, we can easily plot the hyperbola in question. For the sake of completion, let's quickly determine the location of the foci. Again using the relationship we know that Thus, the foci are exactly Finally, a sketch of the graph is given in Figure H7. 74 units to the left and right of the centre of the hyperbola. Example 5 Sketch the graph of the hyperbola whose equation is
17 Note that this is a valid equation for a hyperbola, even though it is not in standard form. Our first goal is to rewrite this equation into standard form and then to interpret this equation as we sketch the graph. As we have seen in previous work, we need to use the technique of ``completing the square'' to work this out. We see that is equivalent to Now we want to fill in the apparent gaps that have been inserted in the parentheses above. This ``filling in'' is completing the square. We want to write in the number that will make each set of parentheses a perfect square. We do that now: Note that, when we add 9 to the left--hand side of the equation, we must also add it to the right--hand side. Also, we are not really adding 1 to the left--hand side; we are really subtracting 4 since we multiply the 1 by the -4 that is outside the parentheses. Hence, we must also subtract 4 from the right--hand side. Rewriting our equation now yields or and we have successfully transformed the equation originally given to us into the standard equation of a hyperbola. This hyperbola has centre (3, -1) and has values a = 4 and b = 2. Since the variable y is in the ``positive'' term here, we know that the transverse axis of this hyperbola is vertical (parallel with the y--axis). The graph of this hyperbola is given in Figure H8.
18 PARABOLA The set of all points in the plane whose distances from a fixed point, called the focus, and a fixed line, called the directrix, are always equal. The point directly between and hence closest to the focus and the directrix is called the vertex of the parabola. To derive the equation of a parabola in rectangular coordinates, we again choose a convenient location for the axes, placing the origin at the vertex so that the y-axis is the axis of symmetry. We denote the distance from the focus to the directrix by p (called parameter). p Then distance from the vertex to the focus and to the directrix is the same, i.e.. 2 Then the standard equation of a parabola is y 2 = ± 2px (when axis is coincident with x axis) or x 2 = ± 2py (when axis is coincident with y- axis). This one is the equation of a parabola opening upwards, with its vertex at the origin. If we
19 introduce a negative sign, we get a parabola opening downwards. If we interchange the roles of x and y, we get a parabola opening to the right (or to the left if there is a negative). We may translate the parabola up/down or back/forth, putting the vertex at the point (h, k) if we write our equation as (x h) 2 = 2 p (y k) The reflection property of parabolas is very important because it has so many practical uses. Let P be any point on the parabola. Construct the line segment joining P to the focus, and a ray through P that is parallel to the axis of symmetry. The line segment and ray will always make equal angles to the tangent line at P. Consequently, any ray emanating from the focus will reflect off of the parabola so as to point directly outwards, parallel to the axis. This property is made use of in the design of flashlights, headlights, and spotlights, for instance. Conversely, any ray entering the parabola that is parallel to the axis will be reflected to the focus. This property is exploited in the design of radio and satellite receiving dishes, and solar collectors. The reflection property of parabolas is related to the curious property that the tangent lines at the endpoints of any chord through the focus (as shown above) intersect on the directrix, and always do so in a right angle. Parabolas are also important in the study of ballistics, the movement of a body under the force of gravity. Note that the graph of a parabola is similar to one branch of a hyperbola. However, you should realize that a parabola is not simply one branch of a hyperbola. Indeed, the branches of a hyperbola approach linear asymptotes, while a parabola does not do so.
20 Several other terms exist which are associated with a parabola. The midpoint between the focus and directrix of the parabola is called the vertex and the line passing through the focus and vertex is called the axis of the parabola. (This is similar to the major axis of the ellipse and the transverse axis of the hyperbola.) See Figure P2. Thus, we see that there are four different orientations of parabolas, which depend on a) which variable is squared (x or y) and b) whether d is positive or negative. Example 1 Consider the equation Given our comments above, this equation yields a parabola. (Note that this equation only has one square term. This indicates that we have a parabola here, as opposed to an ellipse or hyperbola.)
21 The value of p in this case is fairly clear; namely, p = 4 The vertex of this parabola is at (0, 0) and the axis of this parabola is vertical (since the variable x is the squared variable.) Thus, the focus of this parabola is situated at the point (0, 2) and the directrix is the horizontal line 4 units below the vertex. Thus, the equation of the directrix is given by See Figure P7 for a sketch of this parabola. Example 2 Again, realize that this is a parabola (as opposed to an ellipse or a hyperbola) because it only has one squared term (as opposed to two). Because the y is squared instead of the x, we automatically know that this parabola has a horizontal axis. The only other question dealing with orientation is whether the parabola opens to the left or to the right. We note here that p = -8. This indicates that the parabola will indeed open to the left. The vertex is again (0, 0), as in the first example, and the focus will now occur at the point (-4, 0). Finally, the equation of the directrix is x = 4. See Figure P8 for the graph of this parabola.
22 Example 3 Consider the equation This is the standard equation of the parabola with vertex (3, 5) and p = 12. Hence, because the axis is vertical, we know that the focus is exactly 6 units above the vertex, placing it at (3, 11). A sketch of this parabola can be found in Figure P9. Example 4 Find the standard form of the equation of the parabola with vertex (2, 1) and focus (5, 1). We see several things from the information given. First, note that the axis of this parabola is oriented horizontally. Next, note that p = 6. Thus, we can quickly write down the standard equation of this parabola. It is See Figure P10 for a sketch of this parabola.
23 Example 5 Determine the vertex, focus, and directrix of the parabola given by the equation In order to accomplish this task, we need to rewrite the equation in standard form. This will again involve completing the square. We see that this is accomplished by the following: so Factoring out -8 from the right--hand side leaves We have now rewritten our equation into standard form. Note that the vertex is (-2, -3) and p = -4. We also see that the axis is horizontal and that the parabola opens to the left (since p is negative.) Thus, the directrix is the vertical line that lies 2 units to the right of the vertex, yielding the equation x = 0. Finally, the focus is the point 2 units to the right of the vertex, which in this case is the point.
Conic Sections. College Algebra
 Conic Sections College Algebra Conic Sections A conic section, or conic, is a shape resulting from intersecting a right circular cone with a plane. The angle at which the plane intersects the cone determines
Conic Sections College Algebra Conic Sections A conic section, or conic, is a shape resulting from intersecting a right circular cone with a plane. The angle at which the plane intersects the cone determines
Chapter 10. Exploring Conic Sections
 Chapter 10 Exploring Conic Sections Conics A conic section is a curve formed by the intersection of a plane and a hollow cone. Each of these shapes are made by slicing the cone and observing the shape
Chapter 10 Exploring Conic Sections Conics A conic section is a curve formed by the intersection of a plane and a hollow cone. Each of these shapes are made by slicing the cone and observing the shape
Unit 12 Topics in Analytic Geometry - Classwork
 Unit 1 Topics in Analytic Geometry - Classwork Back in Unit 7, we delved into the algebra and geometry of lines. We showed that lines can be written in several forms: a) the general form: Ax + By + C =
Unit 1 Topics in Analytic Geometry - Classwork Back in Unit 7, we delved into the algebra and geometry of lines. We showed that lines can be written in several forms: a) the general form: Ax + By + C =
The point (x, y) lies on the circle of radius r and center (h, k) iff. x h y k r
 NOTES +: ANALYTIC GEOMETRY NAME LESSON. GRAPHS OF EQUATIONS IN TWO VARIABLES (CIRCLES). Standard form of a Circle The point (x, y) lies on the circle of radius r and center (h, k) iff x h y k r Center:
NOTES +: ANALYTIC GEOMETRY NAME LESSON. GRAPHS OF EQUATIONS IN TWO VARIABLES (CIRCLES). Standard form of a Circle The point (x, y) lies on the circle of radius r and center (h, k) iff x h y k r Center:
Multivariable Calculus
 Multivariable Calculus Chapter 10 Topics in Analytic Geometry (Optional) 1. Inclination of a line p. 5. Circles p. 4 9. Determining Conic Type p. 13. Angle between lines p. 6. Parabolas p. 5 10. Rotation
Multivariable Calculus Chapter 10 Topics in Analytic Geometry (Optional) 1. Inclination of a line p. 5. Circles p. 4 9. Determining Conic Type p. 13. Angle between lines p. 6. Parabolas p. 5 10. Rotation
9.3 Hyperbolas and Rotation of Conics
 9.3 Hyperbolas and Rotation of Conics Copyright Cengage Learning. All rights reserved. What You Should Learn Write equations of hyperbolas in standard form. Find asymptotes of and graph hyperbolas. Use
9.3 Hyperbolas and Rotation of Conics Copyright Cengage Learning. All rights reserved. What You Should Learn Write equations of hyperbolas in standard form. Find asymptotes of and graph hyperbolas. Use
Standard Equation of a Circle
 Math 335 Trigonometry Conics We will study all 4 types of conic sections, which are curves that result from the intersection of a right circular cone and a plane that does not contain the vertex. (If the
Math 335 Trigonometry Conics We will study all 4 types of conic sections, which are curves that result from the intersection of a right circular cone and a plane that does not contain the vertex. (If the
CHAPTER 8 QUADRATIC RELATIONS AND CONIC SECTIONS
 CHAPTER 8 QUADRATIC RELATIONS AND CONIC SECTIONS Big IDEAS: 1) Writing equations of conic sections ) Graphing equations of conic sections 3) Solving quadratic systems Section: Essential Question 8-1 Apply
CHAPTER 8 QUADRATIC RELATIONS AND CONIC SECTIONS Big IDEAS: 1) Writing equations of conic sections ) Graphing equations of conic sections 3) Solving quadratic systems Section: Essential Question 8-1 Apply
KEMATH1 Calculus for Chemistry and Biochemistry Students. Francis Joseph H. Campeña, De La Salle University Manila
 KEMATH1 Calculus for Chemistry and Biochemistry Students Francis Joseph H Campeña, De La Salle University Manila January 26, 2015 Contents 1 Conic Sections 2 11 A review of the coordinate system 2 12 Conic
KEMATH1 Calculus for Chemistry and Biochemistry Students Francis Joseph H Campeña, De La Salle University Manila January 26, 2015 Contents 1 Conic Sections 2 11 A review of the coordinate system 2 12 Conic
Chapter 11. Parametric Equations And Polar Coordinates
 Instructor: Prof. Dr. Ayman H. Sakka Chapter 11 Parametric Equations And Polar Coordinates In this chapter we study new ways to define curves in the plane, give geometric definitions of parabolas, ellipses,
Instructor: Prof. Dr. Ayman H. Sakka Chapter 11 Parametric Equations And Polar Coordinates In this chapter we study new ways to define curves in the plane, give geometric definitions of parabolas, ellipses,
Math 155, Lecture Notes- Bonds
 Math 155, Lecture Notes- Bonds Name Section 10.1 Conics and Calculus In this section, we will study conic sections from a few different perspectives. We will consider the geometry-based idea that conics
Math 155, Lecture Notes- Bonds Name Section 10.1 Conics and Calculus In this section, we will study conic sections from a few different perspectives. We will consider the geometry-based idea that conics
Geometry: Conic Sections
 Conic Sections Introduction When a right circular cone is intersected by a plane, as in figure 1 below, a family of four types of curves results. Because of their relationship to the cone, they are called
Conic Sections Introduction When a right circular cone is intersected by a plane, as in figure 1 below, a family of four types of curves results. Because of their relationship to the cone, they are called
Algebra II. Slide 1 / 181. Slide 2 / 181. Slide 3 / 181. Conic Sections Table of Contents
 Slide 1 / 181 Algebra II Slide 2 / 181 Conic Sections 2015-04-21 www.njctl.org Table of Contents click on the topic to go to that section Slide 3 / 181 Review of Midpoint and Distance Formulas Introduction
Slide 1 / 181 Algebra II Slide 2 / 181 Conic Sections 2015-04-21 www.njctl.org Table of Contents click on the topic to go to that section Slide 3 / 181 Review of Midpoint and Distance Formulas Introduction
Rewrite the equation in the left column into the format in the middle column. The answers are in the third column. 1. y 4y 4x 4 0 y k 4p x h y 2 4 x 0
 Pre-Calculus Section 1.1 Completing the Square Rewrite the equation in the left column into the format in the middle column. The answers are in the third column. 1. y 4y 4x 4 0 y k 4p x h y 4 x 0. 3x 3y
Pre-Calculus Section 1.1 Completing the Square Rewrite the equation in the left column into the format in the middle column. The answers are in the third column. 1. y 4y 4x 4 0 y k 4p x h y 4 x 0. 3x 3y
Pre-Calculus Guided Notes: Chapter 10 Conics. A circle is
 Name: Pre-Calculus Guided Notes: Chapter 10 Conics Section Circles A circle is _ Example 1 Write an equation for the circle with center (3, ) and radius 5. To do this, we ll need the x1 y y1 distance formula:
Name: Pre-Calculus Guided Notes: Chapter 10 Conics Section Circles A circle is _ Example 1 Write an equation for the circle with center (3, ) and radius 5. To do this, we ll need the x1 y y1 distance formula:
Module 3: Stand Up Conics
 MATH55 Module 3: Stand Up Conics Main Math concepts: Conic Sections (i.e. Parabolas, Ellipses, Hyperbolas), nd degree equations Auxilliary ideas: Analytic vs. Co-ordinate-free Geometry, Parameters, Calculus.
MATH55 Module 3: Stand Up Conics Main Math concepts: Conic Sections (i.e. Parabolas, Ellipses, Hyperbolas), nd degree equations Auxilliary ideas: Analytic vs. Co-ordinate-free Geometry, Parameters, Calculus.
Chapter 9 Topics in Analytic Geometry
 Chapter 9 Topics in Analytic Geometry What You ll Learn: 9.1 Introduction to Conics: Parabolas 9.2 Ellipses 9.3 Hyperbolas 9.5 Parametric Equations 9.6 Polar Coordinates 9.7 Graphs of Polar Equations 9.1
Chapter 9 Topics in Analytic Geometry What You ll Learn: 9.1 Introduction to Conics: Parabolas 9.2 Ellipses 9.3 Hyperbolas 9.5 Parametric Equations 9.6 Polar Coordinates 9.7 Graphs of Polar Equations 9.1
Algebra II Lesson 10-5: Hyperbolas Mrs. Snow, Instructor
 Algebra II Lesson 10-5: Hyperbolas Mrs. Snow, Instructor In this section, we will look at the hyperbola. A hyperbola is a set of points P in a plane such that the absolute value of the difference between
Algebra II Lesson 10-5: Hyperbolas Mrs. Snow, Instructor In this section, we will look at the hyperbola. A hyperbola is a set of points P in a plane such that the absolute value of the difference between
ALGEBRA II UNIT X: Conic Sections Unit Notes Packet
 Name: Period: ALGEBRA II UNIT X: Conic Sections Unit Notes Packet Algebra II Unit 10 Plan: This plan is subject to change at the teacher s discretion. Section Topic Formative Work Due Date 10.3 Circles
Name: Period: ALGEBRA II UNIT X: Conic Sections Unit Notes Packet Algebra II Unit 10 Plan: This plan is subject to change at the teacher s discretion. Section Topic Formative Work Due Date 10.3 Circles
13.1 2/20/2018. Conic Sections. Conic Sections: Parabolas and Circles
 13 Conic Sections 13.1 Conic Sections: Parabolas and Circles 13.2 Conic Sections: Ellipses 13.3 Conic Sections: Hyperbolas 13.4 Nonlinear Systems of Equations 13.1 Conic Sections: Parabolas and Circles
13 Conic Sections 13.1 Conic Sections: Parabolas and Circles 13.2 Conic Sections: Ellipses 13.3 Conic Sections: Hyperbolas 13.4 Nonlinear Systems of Equations 13.1 Conic Sections: Parabolas and Circles
Figures adapted from Mathworld.wolfram.com and vectosite.net.
 MTH 11 CONIC SECTIONS 1 The four basic types of conic sections we will discuss are: circles, parabolas, ellipses, and hyperbolas. They were named conic by the Greeks who used them to describe the intersection
MTH 11 CONIC SECTIONS 1 The four basic types of conic sections we will discuss are: circles, parabolas, ellipses, and hyperbolas. They were named conic by the Greeks who used them to describe the intersection
1.) Write the equation of a circle in standard form with radius 3 and center (-3,4). Then graph the circle.
 Welcome to the world of conic sections! http://www.youtube.com/watch?v=bfonicn4bbg Some examples of conics in the real world: Parabolas Ellipse Hyperbola Your Assignment: Circle -Find at least four pictures
Welcome to the world of conic sections! http://www.youtube.com/watch?v=bfonicn4bbg Some examples of conics in the real world: Parabolas Ellipse Hyperbola Your Assignment: Circle -Find at least four pictures
We start by looking at a double cone. Think of this as two pointy ice cream cones that are connected at the small tips:
 Math 1330 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text. We start
Math 1330 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text. We start
Conics. By: Maya, Dietrich, and Jesse
 Conics By: Maya, Dietrich, and Jesse Exploring Conics (This is basically the summary too) A conic section curve formed by intersection of a plane and double cone: by changing plane, one can create parabola,
Conics By: Maya, Dietrich, and Jesse Exploring Conics (This is basically the summary too) A conic section curve formed by intersection of a plane and double cone: by changing plane, one can create parabola,
Conic Sections and Analytic Geometry
 Chapter 9 Conic Sections and Analytic Geometry Chapter 9 Conic Sections and Analytic Geometry 9.1 The Ellipse 9.2 The Hyperbola 9.3 The Parabola 9.4 Rotation of Axes 9.5 Parametric Equations 9.6 Conic
Chapter 9 Conic Sections and Analytic Geometry Chapter 9 Conic Sections and Analytic Geometry 9.1 The Ellipse 9.2 The Hyperbola 9.3 The Parabola 9.4 Rotation of Axes 9.5 Parametric Equations 9.6 Conic
OpenStax-CNX module: m The Ellipse. OpenStax College. Abstract
 OpenStax-CNX module: m49438 1 The Ellipse OpenStax College This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 4.0 In this section, you will: Write equations
OpenStax-CNX module: m49438 1 The Ellipse OpenStax College This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 4.0 In this section, you will: Write equations
Mid-Chapter Quiz: Lessons 7-1 through 7-3
 Write an equation for and graph a parabola with the given focus F and vertex V 1. F(1, 5), V(1, 3) Because the focus and vertex share the same x coordinate, the graph is vertical. The focus is (h, k +
Write an equation for and graph a parabola with the given focus F and vertex V 1. F(1, 5), V(1, 3) Because the focus and vertex share the same x coordinate, the graph is vertical. The focus is (h, k +
Unit 8, Ongoing Activity, Little Black Book of Algebra II Properties
 Unit 8, Ongoing Activity, Little Black Book of Algebra II Properties Little Black Book of Algebra II Properties Unit 8 Conic Sections 8.1 Circle write the definition, provide examples of both the standard
Unit 8, Ongoing Activity, Little Black Book of Algebra II Properties Little Black Book of Algebra II Properties Unit 8 Conic Sections 8.1 Circle write the definition, provide examples of both the standard
What you will learn today
 What you will learn today Conic Sections (in 2D coordinates) Cylinders (3D) Quadric Surfaces (3D) Vectors and the Geometry of Space 1/24 Parabolas ellipses Hyperbolas Shifted Conics Conic sections result
What you will learn today Conic Sections (in 2D coordinates) Cylinders (3D) Quadric Surfaces (3D) Vectors and the Geometry of Space 1/24 Parabolas ellipses Hyperbolas Shifted Conics Conic sections result
Algebra II. Midpoint and Distance Formula. Slide 1 / 181 Slide 2 / 181. Slide 3 / 181. Slide 4 / 181. Slide 6 / 181. Slide 5 / 181.
 Slide 1 / 181 Slide 2 / 181 lgebra II onic Sections 2015-04-21 www.njctl.org Slide 3 / 181 Slide 4 / 181 Table of ontents click on the topic to go to that section Review of Midpoint and istance Formulas
Slide 1 / 181 Slide 2 / 181 lgebra II onic Sections 2015-04-21 www.njctl.org Slide 3 / 181 Slide 4 / 181 Table of ontents click on the topic to go to that section Review of Midpoint and istance Formulas
Each point P in the xy-plane corresponds to an ordered pair (x, y) of real numbers called the coordinates of P.
 Lecture 7, Part I: Section 1.1 Rectangular Coordinates Rectangular or Cartesian coordinate system Pythagorean theorem Distance formula Midpoint formula Lecture 7, Part II: Section 1.2 Graph of Equations
Lecture 7, Part I: Section 1.1 Rectangular Coordinates Rectangular or Cartesian coordinate system Pythagorean theorem Distance formula Midpoint formula Lecture 7, Part II: Section 1.2 Graph of Equations
Pre-Calculus. 2) Find the equation of the circle having (2, 5) and (-2, -1) as endpoints of the diameter.
 Pre-Calculus Conic Review Name Block Date Circles: 1) Determine the center and radius of each circle. a) ( x 5) + ( y + 6) = 11 b) x y x y + 6 + 16 + 56 = 0 ) Find the equation of the circle having (,
Pre-Calculus Conic Review Name Block Date Circles: 1) Determine the center and radius of each circle. a) ( x 5) + ( y + 6) = 11 b) x y x y + 6 + 16 + 56 = 0 ) Find the equation of the circle having (,
Name. Center axis. Introduction to Conic Sections
 Name Introduction to Conic Sections Center axis This introduction to conic sections is going to focus on what they some of the skills needed to work with their equations and graphs. year, we will only
Name Introduction to Conic Sections Center axis This introduction to conic sections is going to focus on what they some of the skills needed to work with their equations and graphs. year, we will only
PreCalculus Chapter 9 Practice Test Name:
 This ellipse has foci 0,, and therefore has a vertical major axis. The standard form for an ellipse with a vertical major axis is: 1 Note: graphs of conic sections for problems 1 to 1 were made with the
This ellipse has foci 0,, and therefore has a vertical major axis. The standard form for an ellipse with a vertical major axis is: 1 Note: graphs of conic sections for problems 1 to 1 were made with the
8.2 Graph and Write Equations of Parabolas
 8.2 Graph and Write Equations of Parabolas Where is the focus and directrix compared to the vertex? How do you know what direction a parabola opens? How do you write the equation of a parabola given the
8.2 Graph and Write Equations of Parabolas Where is the focus and directrix compared to the vertex? How do you know what direction a parabola opens? How do you write the equation of a parabola given the
7. r = r = r = r = r = 2 5
 Exercise a: I. Write the equation in standard form of each circle with its center at the origin and the given radius.. r = 4. r = 6 3. r = 7 r = 5 5. r = 6. r = 6 7. r = 0.3 8. r =.5 9. r = 4 0. r = 3.
Exercise a: I. Write the equation in standard form of each circle with its center at the origin and the given radius.. r = 4. r = 6 3. r = 7 r = 5 5. r = 6. r = 6 7. r = 0.3 8. r =.5 9. r = 4 0. r = 3.
Chapter 10. Homework
 Chapter 0 Homework Lesson 0- pages 538 5 Exercises. 2. Hyperbola: center (0, 0), y-intercepts at ±, no x-intercepts, the lines of symmetry are the x- and y-axes; domain: all real numbers, range: y 5 3
Chapter 0 Homework Lesson 0- pages 538 5 Exercises. 2. Hyperbola: center (0, 0), y-intercepts at ±, no x-intercepts, the lines of symmetry are the x- and y-axes; domain: all real numbers, range: y 5 3
Flash Light Reflectors. Fountains and Projectiles. Algebraically, parabolas are usually defined in two different forms: Standard Form and Vertex Form
 Sec 6.1 Conic Sections Parabolas Name: What is a parabola? It is geometrically defined by a set of points or locus of points that are equidistant from a point (the focus) and a line (the directrix). To
Sec 6.1 Conic Sections Parabolas Name: What is a parabola? It is geometrically defined by a set of points or locus of points that are equidistant from a point (the focus) and a line (the directrix). To
P.5 Rational Expressions
 P.5 Rational Expressions I Domain Domain: Rational expressions : Finding domain a. polynomials: b. Radicals: keep it real! i. sqrt(x-2) x>=2 [2, inf) ii. cubert(x-2) all reals since cube rootscan be positive
P.5 Rational Expressions I Domain Domain: Rational expressions : Finding domain a. polynomials: b. Radicals: keep it real! i. sqrt(x-2) x>=2 [2, inf) ii. cubert(x-2) all reals since cube rootscan be positive
Summary of Formulas: see
 To review the Conic Sections, Identify them and sketch them from the given equations, watch the following set of YouTube videos. They are followed by several practice problems for you to try, covering
To review the Conic Sections, Identify them and sketch them from the given equations, watch the following set of YouTube videos. They are followed by several practice problems for you to try, covering
, minor axis of length 12. , asymptotes y 2x. 16y
 Math 4 Midterm 1 Review CONICS [1] Find the equations of the following conics. If the equation corresponds to a circle find its center & radius. If the equation corresponds to a parabola find its focus
Math 4 Midterm 1 Review CONICS [1] Find the equations of the following conics. If the equation corresponds to a circle find its center & radius. If the equation corresponds to a parabola find its focus
Algebra II Chapter 10 Conics Notes Packet. Student Name Teacher Name
 Algebra II Chapter 10 Conics Notes Packet Student Name Teacher Name 1 Conic Sections 2 Identifying Conics Ave both variables squared?' No PARABOLA y = a(x- h)z + k x = a(y- k)z + h YEs Put l'h squared!'erms
Algebra II Chapter 10 Conics Notes Packet Student Name Teacher Name 1 Conic Sections 2 Identifying Conics Ave both variables squared?' No PARABOLA y = a(x- h)z + k x = a(y- k)z + h YEs Put l'h squared!'erms
Conic Sections: Parabolas
 Conic Sections: Parabolas Why are the graphs of parabolas, ellipses, and hyperbolas called 'conic sections'? Because if you pass a plane through a double cone, the intersection of the plane and the cone
Conic Sections: Parabolas Why are the graphs of parabolas, ellipses, and hyperbolas called 'conic sections'? Because if you pass a plane through a double cone, the intersection of the plane and the cone
Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts
 Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
Conic Sections. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Conic Sections MATH 211, Calculus II J. Robert Buchanan Department o Mathematics Spring 2018 Introduction The conic sections include the parabola, the ellipse, and the hyperbola. y y y x x x Parabola A
Conic Sections MATH 211, Calculus II J. Robert Buchanan Department o Mathematics Spring 2018 Introduction The conic sections include the parabola, the ellipse, and the hyperbola. y y y x x x Parabola A
Common Core Cluster. Experiment with transformations in the plane. Unpacking What does this standard mean that a student will know and be able to do?
 Congruence G.CO Experiment with transformations in the plane. G.CO.1 Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point,
Congruence G.CO Experiment with transformations in the plane. G.CO.1 Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point,
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
 Pre-Calculus Mid Term Review. January 2014 Name SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Use the graph of the function f, plotted with a solid
Pre-Calculus Mid Term Review. January 2014 Name SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Use the graph of the function f, plotted with a solid
Assignment 3/17/15. Section 10.2(p 568) 2 12 (E) (E)
 Section 10.2 Warm Up Assignment 3/17/15 Section 10.2(p 568) 2 12 (E) 24 40 (E) Objective We are going to find equations for parabolas identify the vertex, focus, and directrix of a parabola The parabola
Section 10.2 Warm Up Assignment 3/17/15 Section 10.2(p 568) 2 12 (E) 24 40 (E) Objective We are going to find equations for parabolas identify the vertex, focus, and directrix of a parabola The parabola
Geometry. Cluster: Experiment with transformations in the plane. G.CO.1 G.CO.2. Common Core Institute
 Geometry Cluster: Experiment with transformations in the plane. G.CO.1: Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of
Geometry Cluster: Experiment with transformations in the plane. G.CO.1: Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of
Chapter 8.1 Conic Sections/Parabolas. Honors Pre-Calculus Rogers High School
 Chapter 8.1 Conic Sections/Parabolas Honors Pre-Calculus Rogers High School Introduction to Conic Sections Conic sections are defined geometrically as the result of the intersection of a plane with a right
Chapter 8.1 Conic Sections/Parabolas Honors Pre-Calculus Rogers High School Introduction to Conic Sections Conic sections are defined geometrically as the result of the intersection of a plane with a right
Mathematics High School Geometry
 Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
Honors Precalculus: Solving equations and inequalities graphically and algebraically. Page 1
 Solving equations and inequalities graphically and algebraically 1. Plot points on the Cartesian coordinate plane. P.1 2. Represent data graphically using scatter plots, bar graphs, & line graphs. P.1
Solving equations and inequalities graphically and algebraically 1. Plot points on the Cartesian coordinate plane. P.1 2. Represent data graphically using scatter plots, bar graphs, & line graphs. P.1
Log1 Contest Round 2 Theta Circles, Parabolas and Polygons. 4 points each
 Name: Units do not have to be included. 016 017 Log1 Contest Round Theta Circles, Parabolas and Polygons 4 points each 1 Find the value of x given that 8 x 30 Find the area of a triangle given that it
Name: Units do not have to be included. 016 017 Log1 Contest Round Theta Circles, Parabolas and Polygons 4 points each 1 Find the value of x given that 8 x 30 Find the area of a triangle given that it
Ex. 1-3: Put each circle below in the correct equation form as listed!! above, then determine the center and radius of each circle.
 Day 1 Conics - Circles Equation of a Circle The circle with center (h, k) and radius r is the set of all points (x, y) that satisfies!! (x h) 2 + (y k) 2 = r 2 Ex. 1-3: Put each circle below in the correct
Day 1 Conics - Circles Equation of a Circle The circle with center (h, k) and radius r is the set of all points (x, y) that satisfies!! (x h) 2 + (y k) 2 = r 2 Ex. 1-3: Put each circle below in the correct
A function: A mathematical relationship between two variables (x and y), where every input value (usually x) has one output value (usually y)
 SESSION 9: FUNCTIONS KEY CONCEPTS: Definitions & Terminology Graphs of Functions - Straight line - Parabola - Hyperbola - Exponential Sketching graphs Finding Equations Combinations of graphs TERMINOLOGY
SESSION 9: FUNCTIONS KEY CONCEPTS: Definitions & Terminology Graphs of Functions - Straight line - Parabola - Hyperbola - Exponential Sketching graphs Finding Equations Combinations of graphs TERMINOLOGY
Unit 5: Quadratic Functions
 Unit 5: Quadratic Functions LESSON #5: THE PARABOLA GEOMETRIC DEFINITION DIRECTRIX FOCUS LATUS RECTUM Geometric Definition of a Parabola Quadratic Functions Geometrically, a parabola is the set of all
Unit 5: Quadratic Functions LESSON #5: THE PARABOLA GEOMETRIC DEFINITION DIRECTRIX FOCUS LATUS RECTUM Geometric Definition of a Parabola Quadratic Functions Geometrically, a parabola is the set of all
Math 2 Coordinate Geometry Part 3 Inequalities & Quadratics
 Math 2 Coordinate Geometry Part 3 Inequalities & Quadratics 1 DISTANCE BETWEEN TWO POINTS - REVIEW To find the distance between two points, use the Pythagorean theorem. The difference between x 1 and x
Math 2 Coordinate Geometry Part 3 Inequalities & Quadratics 1 DISTANCE BETWEEN TWO POINTS - REVIEW To find the distance between two points, use the Pythagorean theorem. The difference between x 1 and x
2.) Write the standard form of the equation of a circle whose endpoints of diameter are (4, 7) and (2,3).
 Ch 10: Conic Sections Name: Objectives: Students will be able to: -graph parabolas, hyperbolas and ellipses and answer characteristic questions about these graphs. -write equations of conic sections Dec
Ch 10: Conic Sections Name: Objectives: Students will be able to: -graph parabolas, hyperbolas and ellipses and answer characteristic questions about these graphs. -write equations of conic sections Dec
Chapter 10 Test Review
 Name: Class: Date: Chapter 10 Test Review Short Answer 1. Write an equation of a parabola with a vertex at the origin and a focus at ( 2, 0). 2. Write an equation of a parabola with a vertex at the origin
Name: Class: Date: Chapter 10 Test Review Short Answer 1. Write an equation of a parabola with a vertex at the origin and a focus at ( 2, 0). 2. Write an equation of a parabola with a vertex at the origin
Common Core Specifications for Geometry
 1 Common Core Specifications for Geometry Examples of how to read the red references: Congruence (G-Co) 2-03 indicates this spec is implemented in Unit 3, Lesson 2. IDT_C indicates that this spec is implemented
1 Common Core Specifications for Geometry Examples of how to read the red references: Congruence (G-Co) 2-03 indicates this spec is implemented in Unit 3, Lesson 2. IDT_C indicates that this spec is implemented
3.1. 3x 4y = 12 3(0) 4y = 12. 3x 4y = 12 3x 4(0) = y = x 0 = 12. 4y = 12 y = 3. 3x = 12 x = 4. The Rectangular Coordinate System
 3. The Rectangular Coordinate System Interpret a line graph. Objectives Interpret a line graph. Plot ordered pairs. 3 Find ordered pairs that satisfy a given equation. 4 Graph lines. 5 Find x- and y-intercepts.
3. The Rectangular Coordinate System Interpret a line graph. Objectives Interpret a line graph. Plot ordered pairs. 3 Find ordered pairs that satisfy a given equation. 4 Graph lines. 5 Find x- and y-intercepts.
Study Guide and Review
 Graph the hyperbola given by each equation. 30. = 1 The equation is in standard form, and h = 6 and k = 3. Because a 2 = 30 and b 2 = 8, a = 5.5 and b =. The values of a and b can be used to find c. c
Graph the hyperbola given by each equation. 30. = 1 The equation is in standard form, and h = 6 and k = 3. Because a 2 = 30 and b 2 = 8, a = 5.5 and b =. The values of a and b can be used to find c. c
Honors Geometry Pacing Guide Honors Geometry Pacing First Nine Weeks
 Unit Topic To recognize points, lines and planes. To be able to recognize and measure segments and angles. To classify angles and name the parts of a degree To recognize collinearity and betweenness of
Unit Topic To recognize points, lines and planes. To be able to recognize and measure segments and angles. To classify angles and name the parts of a degree To recognize collinearity and betweenness of
Preview Notes. Systems of Equations. Linear Functions. Let y = y. Solve for x then solve for y
 Preview Notes Linear Functions A linear function is a straight line that has a slope (m) and a y-intercept (b). Systems of Equations 1. Comparison Method Let y = y x1 y1 x2 y2 Solve for x then solve for
Preview Notes Linear Functions A linear function is a straight line that has a slope (m) and a y-intercept (b). Systems of Equations 1. Comparison Method Let y = y x1 y1 x2 y2 Solve for x then solve for
MATH 110 analytic geometry Conics. The Parabola
 1 MATH 11 analytic geometry Conics The graph of a second-degree equation in the coordinates x and y is called a conic section or, more simply, a conic. This designation derives from the fact that the curve
1 MATH 11 analytic geometry Conics The graph of a second-degree equation in the coordinates x and y is called a conic section or, more simply, a conic. This designation derives from the fact that the curve
Z+z 1 X2 Y2. or y, Graph / 4 25 jj y=±x. x2+y 2=
 Conic Sections Understanding the graphs of conic sections is made easier if you first begin with the simplest form of a conic section. These would be the graphs that are centered at the origin. If we can
Conic Sections Understanding the graphs of conic sections is made easier if you first begin with the simplest form of a conic section. These would be the graphs that are centered at the origin. If we can
3 Identify shapes as two-dimensional (lying in a plane, flat ) or three-dimensional ( solid ).
 Geometry Kindergarten Identify and describe shapes (squares, circles, triangles, rectangles, hexagons, cubes, cones, cylinders, and spheres). 1 Describe objects in the environment using names of shapes,
Geometry Kindergarten Identify and describe shapes (squares, circles, triangles, rectangles, hexagons, cubes, cones, cylinders, and spheres). 1 Describe objects in the environment using names of shapes,
MATH 1113 Exam 1 Review. Fall 2017
 MATH 1113 Exam 1 Review Fall 2017 Topics Covered Section 1.1: Rectangular Coordinate System Section 1.2: Circles Section 1.3: Functions and Relations Section 1.4: Linear Equations in Two Variables and
MATH 1113 Exam 1 Review Fall 2017 Topics Covered Section 1.1: Rectangular Coordinate System Section 1.2: Circles Section 1.3: Functions and Relations Section 1.4: Linear Equations in Two Variables and
Warm-Up. Write the standard equation of the circle with the given radius and center. 1) 9; (0,0) 2) 1; (0,5) 3) 4; (-8,-1) 4) 5; (4,2)
 Warm-Up Write the standard equation of the circle with the given radius and center. 1) 9; (0,0) ) 1; (0,5) 3) 4; (-8,-1) 4) 5; (4,) 8.4 Graph and Write Equations of Ellipses What are the major parts of
Warm-Up Write the standard equation of the circle with the given radius and center. 1) 9; (0,0) ) 1; (0,5) 3) 4; (-8,-1) 4) 5; (4,) 8.4 Graph and Write Equations of Ellipses What are the major parts of
K-12 Geometry Standards
 Geometry K.G Identify and describe shapes (squares, circles, triangles, rectangles, hexagons, cubes, cones, cylinders, and spheres). 1. Describe objects in the environment using names of shapes, and describe
Geometry K.G Identify and describe shapes (squares, circles, triangles, rectangles, hexagons, cubes, cones, cylinders, and spheres). 1. Describe objects in the environment using names of shapes, and describe
Chapter 1. Linear Equations and Straight Lines. 2 of 71. Copyright 2014, 2010, 2007 Pearson Education, Inc.
 Chapter 1 Linear Equations and Straight Lines 2 of 71 Outline 1.1 Coordinate Systems and Graphs 1.4 The Slope of a Straight Line 1.3 The Intersection Point of a Pair of Lines 1.2 Linear Inequalities 1.5
Chapter 1 Linear Equations and Straight Lines 2 of 71 Outline 1.1 Coordinate Systems and Graphs 1.4 The Slope of a Straight Line 1.3 The Intersection Point of a Pair of Lines 1.2 Linear Inequalities 1.5
Assignment Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Assignment.1-.3 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. 1) The arch beneath a bridge is semi-elliptical, a one-way
Assignment.1-.3 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Solve the problem. 1) The arch beneath a bridge is semi-elliptical, a one-way
WHAT YOU SHOULD LEARN
 GRAPHS OF EQUATIONS WHAT YOU SHOULD LEARN Sketch graphs of equations. Find x- and y-intercepts of graphs of equations. Use symmetry to sketch graphs of equations. Find equations of and sketch graphs of
GRAPHS OF EQUATIONS WHAT YOU SHOULD LEARN Sketch graphs of equations. Find x- and y-intercepts of graphs of equations. Use symmetry to sketch graphs of equations. Find equations of and sketch graphs of
HYPERBOLA. Going off on a TANGENT!
 HYPERBOLA Going off on a TANGENT! RECALL THAT THE HYPERBOLA IS A CONIC SECTION A LAMP CASTS A HYPERBOLIC BEAM OF LIGHT NUCLEAR COOLING TOWERS TORNADO TOWER, QATAR KOBE PORT TOWER, JAPAN RULED HYPERBOLOID
HYPERBOLA Going off on a TANGENT! RECALL THAT THE HYPERBOLA IS A CONIC SECTION A LAMP CASTS A HYPERBOLIC BEAM OF LIGHT NUCLEAR COOLING TOWERS TORNADO TOWER, QATAR KOBE PORT TOWER, JAPAN RULED HYPERBOLOID
Practice Test - Chapter 7
 Write an equation for an ellipse with each set of characteristics. 1. vertices (7, 4), ( 3, 4); foci (6, 4), ( 2, 4) The distance between the vertices is 2a. 2a = 7 ( 3) a = 5; a 2 = 25 The distance between
Write an equation for an ellipse with each set of characteristics. 1. vertices (7, 4), ( 3, 4); foci (6, 4), ( 2, 4) The distance between the vertices is 2a. 2a = 7 ( 3) a = 5; a 2 = 25 The distance between
Analytic Geometry Vocabulary Cards and Word Walls Important Notes for Teachers:
 Analytic Geometry Vocabulary Cards and Word Walls Important Notes for Teachers: The vocabulary cards in this file reflect the vocabulary students taking Coordinate Algebra will need to know and be able
Analytic Geometry Vocabulary Cards and Word Walls Important Notes for Teachers: The vocabulary cards in this file reflect the vocabulary students taking Coordinate Algebra will need to know and be able
Ohio s Learning Standards-Extended. Mathematics. Congruence Standards Complexity a Complexity b Complexity c
 Ohio s Learning Standards-Extended Mathematics Congruence Standards Complexity a Complexity b Complexity c Most Complex Least Complex Experiment with transformations in the plane G.CO.1 Know precise definitions
Ohio s Learning Standards-Extended Mathematics Congruence Standards Complexity a Complexity b Complexity c Most Complex Least Complex Experiment with transformations in the plane G.CO.1 Know precise definitions
1.8 Coordinate Geometry. Copyright Cengage Learning. All rights reserved.
 1.8 Coordinate Geometry Copyright Cengage Learning. All rights reserved. Objectives The Coordinate Plane The Distance and Midpoint Formulas Graphs of Equations in Two Variables Intercepts Circles Symmetry
1.8 Coordinate Geometry Copyright Cengage Learning. All rights reserved. Objectives The Coordinate Plane The Distance and Midpoint Formulas Graphs of Equations in Two Variables Intercepts Circles Symmetry
Geometry Common Core State Standard (CCSS) Math
 = ntroduced R=Reinforced/Reviewed HGH SCHOOL GEOMETRY MATH STANDARDS 1 2 3 4 Congruence Experiment with transformations in the plane G.CO.1 Know precise definitions of angle, circle, perpendicular line,
= ntroduced R=Reinforced/Reviewed HGH SCHOOL GEOMETRY MATH STANDARDS 1 2 3 4 Congruence Experiment with transformations in the plane G.CO.1 Know precise definitions of angle, circle, perpendicular line,
Moore Catholic High School Math Department
 Moore Catholic High School Math Department Geometry Vocabulary The following is a list of terms and properties which are necessary for success in a Geometry class. You will be tested on these terms during
Moore Catholic High School Math Department Geometry Vocabulary The following is a list of terms and properties which are necessary for success in a Geometry class. You will be tested on these terms during
We start by looking at a double cone. Think of this as two pointy ice cream cones that are connected at the small tips:
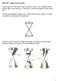 Math 1330 Chapter 8 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text.
Math 1330 Chapter 8 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text.
Name: Class: Date: Conics Multiple Choice Pre-Test. Multiple Choice Identify the choice that best completes the statement or answers the question.
 Name: Class: Date: Conics Multiple Choice Pre-Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1 Graph the equation x 2 + y 2 = 36. Then describe the
Name: Class: Date: Conics Multiple Choice Pre-Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1 Graph the equation x 2 + y 2 = 36. Then describe the
8.5 Graph and Write Equations of Hyperbolas p.518 What are the parts of a hyperbola? What are the standard form equations of a hyperbola?
 8.5 Graph and Write Equations of Hyperbolas p.518 What are the parts of a hyperbola? What are the standard form equations of a hyperbola? How do you know which way it opens? Given a & b, how do you find
8.5 Graph and Write Equations of Hyperbolas p.518 What are the parts of a hyperbola? What are the standard form equations of a hyperbola? How do you know which way it opens? Given a & b, how do you find
Lecture 5. If, as shown in figure, we form a right triangle With P1 and P2 as vertices, then length of the horizontal
 Distance; Circles; Equations of the form Lecture 5 y = ax + bx + c In this lecture we shall derive a formula for the distance between two points in a coordinate plane, and we shall use that formula to
Distance; Circles; Equations of the form Lecture 5 y = ax + bx + c In this lecture we shall derive a formula for the distance between two points in a coordinate plane, and we shall use that formula to
DISCOVERING CONICS WITH. Dr Toh Pee Choon NIE 2 June 2016
 DISCOVERING CONICS WITH Dr Toh Pee Choon MTC @ NIE 2 June 2016 Introduction GeoGebra is a dynamic mathematics software that integrates both geometry and algebra Open source and free to download www.geogebra.org
DISCOVERING CONICS WITH Dr Toh Pee Choon MTC @ NIE 2 June 2016 Introduction GeoGebra is a dynamic mathematics software that integrates both geometry and algebra Open source and free to download www.geogebra.org
Math 8 Honors Coordinate Geometry part 3 Unit Updated July 29, 2016
 Review how to find the distance between two points To find the distance between two points, use the Pythagorean theorem. The difference between is one leg and the difference between and is the other leg.
Review how to find the distance between two points To find the distance between two points, use the Pythagorean theorem. The difference between is one leg and the difference between and is the other leg.
Quadric Surfaces. Six basic types of quadric surfaces: ellipsoid. cone. elliptic paraboloid. hyperboloid of one sheet. hyperboloid of two sheets
 Quadric Surfaces Six basic types of quadric surfaces: ellipsoid cone elliptic paraboloid hyperboloid of one sheet hyperboloid of two sheets hyperbolic paraboloid (A) (B) (C) (D) (E) (F) 1. For each surface,
Quadric Surfaces Six basic types of quadric surfaces: ellipsoid cone elliptic paraboloid hyperboloid of one sheet hyperboloid of two sheets hyperbolic paraboloid (A) (B) (C) (D) (E) (F) 1. For each surface,
Polynomial and Rational Functions. Copyright Cengage Learning. All rights reserved.
 2 Polynomial and Rational Functions Copyright Cengage Learning. All rights reserved. 2.1 Quadratic Functions Copyright Cengage Learning. All rights reserved. What You Should Learn Analyze graphs of quadratic
2 Polynomial and Rational Functions Copyright Cengage Learning. All rights reserved. 2.1 Quadratic Functions Copyright Cengage Learning. All rights reserved. What You Should Learn Analyze graphs of quadratic
Grade 9 Math Terminology
 Unit 1 Basic Skills Review BEDMAS a way of remembering order of operations: Brackets, Exponents, Division, Multiplication, Addition, Subtraction Collect like terms gather all like terms and simplify as
Unit 1 Basic Skills Review BEDMAS a way of remembering order of operations: Brackets, Exponents, Division, Multiplication, Addition, Subtraction Collect like terms gather all like terms and simplify as
Chapter 10: Parametric And Polar Curves; Conic Sections
 206 Chapter 10: Parametric And Polar Curves; Conic Sections Summary: This chapter begins by introducing the idea of representing curves using parameters. These parametric equations of the curves can then
206 Chapter 10: Parametric And Polar Curves; Conic Sections Summary: This chapter begins by introducing the idea of representing curves using parameters. These parametric equations of the curves can then
Polar Coordinates. OpenStax. 1 Dening Polar Coordinates
 OpenStax-CNX module: m53852 1 Polar Coordinates OpenStax This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License 4.0 Abstract Locate points
OpenStax-CNX module: m53852 1 Polar Coordinates OpenStax This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution-NonCommercial-ShareAlike License 4.0 Abstract Locate points
8.3 Technology: Loci and Conics
 8.3 Technology: Loci and Conics The diagram shows a double cone. The two cones have one point in common. The intersection of a double cone and a plane is called a conic section or a conic. The circle,
8.3 Technology: Loci and Conics The diagram shows a double cone. The two cones have one point in common. The intersection of a double cone and a plane is called a conic section or a conic. The circle,
Buds Public School, Dubai
 Buds Public School, Dubai Subject: Maths Grade: 11 AB Topic: Statistics, Probability, Trigonometry, 3D, Conic Section, Straight lines and Limits and Derivatives Statistics and Probability: 1. Find the
Buds Public School, Dubai Subject: Maths Grade: 11 AB Topic: Statistics, Probability, Trigonometry, 3D, Conic Section, Straight lines and Limits and Derivatives Statistics and Probability: 1. Find the
Appendix. Correlation to the High School Geometry Standards of the Common Core State Standards for Mathematics
 Appendix Correlation to the High School Geometry Standards of the Common Core State Standards for Mathematics The correlation shows how the activities in Exploring Geometry with The Geometer s Sketchpad
Appendix Correlation to the High School Geometry Standards of the Common Core State Standards for Mathematics The correlation shows how the activities in Exploring Geometry with The Geometer s Sketchpad
MATH 1020 WORKSHEET 10.1 Parametric Equations
 MATH WORKSHEET. Parametric Equations If f and g are continuous functions on an interval I, then the equations x ft) and y gt) are called parametric equations. The parametric equations along with the graph
MATH WORKSHEET. Parametric Equations If f and g are continuous functions on an interval I, then the equations x ft) and y gt) are called parametric equations. The parametric equations along with the graph
Topics in Two-Dimensional Analytic Geometry
 Chapter Topics in Two-Dimensional Analytic Geometry In this chapter we look at topics in analytic geometry so we can use our calculus in many new settings. Most of the discussion will involve developing
Chapter Topics in Two-Dimensional Analytic Geometry In this chapter we look at topics in analytic geometry so we can use our calculus in many new settings. Most of the discussion will involve developing
Videos, Constructions, Definitions, Postulates, Theorems, and Properties
 Videos, Constructions, Definitions, Postulates, Theorems, and Properties Videos Proof Overview: http://tinyurl.com/riehlproof Modules 9 and 10: http://tinyurl.com/riehlproof2 Module 9 Review: http://tinyurl.com/module9livelesson-recording
Videos, Constructions, Definitions, Postulates, Theorems, and Properties Videos Proof Overview: http://tinyurl.com/riehlproof Modules 9 and 10: http://tinyurl.com/riehlproof2 Module 9 Review: http://tinyurl.com/module9livelesson-recording
1. Use the Trapezium Rule with five ordinates to find an approximate value for the integral
 1. Use the Trapezium Rule with five ordinates to find an approximate value for the integral Show your working and give your answer correct to three decimal places. 2 2.5 3 3.5 4 When When When When When
1. Use the Trapezium Rule with five ordinates to find an approximate value for the integral Show your working and give your answer correct to three decimal places. 2 2.5 3 3.5 4 When When When When When
Assignment Assignment for Lesson 11.1
 Assignment Assignment for Lesson.1 Name Date Conics? Conics as Cross Sections Determine the conic section that results from the intersection of the double-napped cone shown and each plane described. 1.
Assignment Assignment for Lesson.1 Name Date Conics? Conics as Cross Sections Determine the conic section that results from the intersection of the double-napped cone shown and each plane described. 1.
) 2 + (y 2. x 1. y c x2 = y
 Graphing Parabola Parabolas A parabola is a set of points P whose distance from a fixed point, called the focus, is equal to the perpendicular distance from P to a line, called the directrix. Since this
Graphing Parabola Parabolas A parabola is a set of points P whose distance from a fixed point, called the focus, is equal to the perpendicular distance from P to a line, called the directrix. Since this
