2.8 An application of Dynamic Programming to machine renewal
|
|
|
- Margaret Hill
- 5 years ago
- Views:
Transcription
1 ex-.6-. Foundations of Operations Research Prof. E. Amaldi.6 Shortest paths with nonnegative costs Given the following directed graph, find a set of shortest paths from node to all the other nodes, using Dijkstra s algorithm. Can we solve the problem with Dynamic Programming? If yes, do so..7 Shortest paths with negative costs and ill-posedness Given the following directed graph, find the shortest paths between all pairs of nodes, or show that the problem is ill-posed by exhibiting a circuit of total negative cost An application of Dynamic Programming to machine renewal A company must buy a new machine and then determine a renewal (maintenance-replacement) plan for the next years, making sure that, at any point in time, the available machine works properly. At the beginning of each year of the planning horizon, the company must decide whether to keep the old machine or to substitute it with a new machine. The maintenance costs and the expected revenue (when the machine is sold) clearly depend on how old the machine is and they are indicated in the following table. years maintenance (keuro) revenue when sold (keuro) Document prepared by L. Liberti, S. Bosio, S. Coniglio. Translation to English by S. Coniglio
2 ex-.6-. Foundations of Operations Research Prof. E. Amaldi To avoid high maintenance costs of an old machine, the machine can be sold at the beginning of the second, third, fourth, and fifth year, and an new one can be bought. For the sake of simplicity, we suppose that a new machine always costs K Euro. Show that the problem of determing a machine renewal plan of minimum total net cost (total cost for buying/rebuying the machine + maintenance costs - total revenue) can be solved via Dynamic Programming by finding a shortest path in an ad hoc directed acyclic graph. Find an optimal renewal plan. Is it unique?.9 Project planning The preparation of the apple pie has long been a tradition at Rossi s family. First the weight of the ingredients has to be determined: flour, sugar, butter, eggs, apples, cream. The butter must then be melted down, and added to a mixture of flour, sugar, and eggs. Apples must be added to this new mixture, once they have been peeled and cut into thin slices. The mixture can then be cooked, in the already heated oven. It is advisable to whip the cream only after the apple slices have been added to the mixture. Once the cake is cooked, the cream is used to garnish it. The following table reports the time needed for each activity. Activity Time (minutes) A Weight the ingredients B Melt the butter C Mix flour, eggs and sugar D Peel the apples and cut them into slices E Heat the oven F Add butter to the mixture 8 G Add apples to the mixture H Cook the mixture in the oven I Whip the cream L Garnish Draw the graph (with activities associated to arcs) which represents the project precedence relations. Determine the minimum total completion time of the project as well as the earliest times and latest times associated to each node. Identify the critical activities and draw Gantt s chart at earliest.. Shortest paths with negative costs Given the following directed graph, find the shortest paths between all pairs of nodes, or show that the problem is ill-posed, by exhibiting a circuit of total negative cost. Document prepared by L. Liberti, S. Bosio, S. Coniglio. Translation to English by S. Coniglio
3 ex-.6-. Foundations of Operations Research Prof. E. Amaldi - - Document prepared by L. Liberti, S. Bosio, S. Coniglio. Translation to English by S. Coniglio
4 ex-.6-. Foundations of Operations Research Prof. E. Amaldi Solution.6 Shortest paths with nonnegative costs Dijkstra s algorithm determines a set of shortest paths from a given node s to all the other nodes in the graph. It can be applied to any (directed) graph with nonnegative arc costs. Data structures: subset S V of nodes with fixed labels (initialization S = {s}); n- dimensionalvectorlwherel(i)isthecostofashortestpathfromstoi(initialization L(s) = ); n-dimensional vector p where p(i) is the predecessor of node i in the shortest path from s to i (initialization p(s) = s). Description: at each iteration, we identify in the outgoing cut induced by S, δ + (S), an arc (v,h) such that L(v)+c vh is minimum, where c vh is the cost of the arc (v,h). Then we set S := S {h}, L(h) := L(v) + c vh and p(h) := v. The algorithm halts when S = V. Iterations: Initialization: S = {},L() =,p() = ; (v,h) = (,), L() =, p() =, S = {,}; (v,h) = (,), L() =, p() =, S = {,,}; (v,h) = (,), L() =, p() =, S = {,,,}; (v,h) = (,), L() =, p() =, S = {,,,,}; (v,h) = (,), L() =, p() =, S = {,,,,,}; (v,h) = (,7), L(7) =, p(7) =, S = {,,,,,,7}; (v,h) = (,6), L(6) =, p(6) =, S = G: STOP; The behaviour of the algorithm can be summarized as follows. In the pictures, a node is highlighted if it belongs to S, while an arc is represented with a dashed line if it can be selected in the current iteration (if it belongs to δ + (S)), and in a solid line when it is chosen. The labels on the nodes in S indicate the cost of the shortest path from node. When a dashed arc is incident to two nodes in S, it is removed. This way, the dashed arcs always belongs to the cut induced by S. The arc (i,j) that is selected is always that with minimum cost L(i)+c ij. : L: : L: L: Document prepared by L. Liberti, S. Bosio, S. Coniglio. Translation to English by S. Coniglio
5 ex-.6-. Foundations of Operations Research Prof. E. Amaldi : L: L: L: L: L: L: : L: L: L: L: L: L: L: L: : 7: L: L: L: L: L: L: L: L: L: 6: 8: 6 L: 7 L: L: L: L: L: L: L: L: L: A topological order can be obtained as follows. At iteration i, for i = {,...,n}, pick a node with no incoming arcs, label it as node i, remove it from the graph, iterate until all nodes are removed, or there is no node with no incident arcs in this case the graph is not acyclic. The graph we are dealing with is acyclic, and its node indices already correspond to a topological order. The Dynamic Programming technique can therefore be applied. It has complexity O(m), smaller than that of the Dijkstra algorithm of O(n ). L() =, p() = ; L() = L()+c =, p() = ; L() = min{l()+c,l()+c } = min{+,+} =, p() = ; L() = min{l()+c,l()+c } = min{+,+} =, p() = ; L() = min{l()+c,l()+c } = min{+,+} =, p() = ; L() = min{l()+c,l()+c } = min{+,+} =, p() = ; L(6) = min{l()+c 6,L()+c 6 } = min{+,+} =, p(6) = ; L(7) = min{l()+c 7,L()+c 7,L(6)+c 67 } = min{+,+,+} =,p(7) = ; Document prepared by L. Liberti, S. Bosio, S. Coniglio. Translation to English by S. Coniglio
6 ex-.6-. Foundations of Operations Research Prof. E. Amaldi.7 Shortest paths with negative costs and ill-posedness Since the graph contains negative arc costs, we use Floyd-Warshall s algorithm that finds a shortest path between each pair of nodes, or establishes that the problem is ill-posed by exhibiting a circuit of negative cost. The graph can contain cycles, but such cycles have to be of nonnegative cost. It has complexity O(n ), where n is the number of nodes in the graph. Data structures: let D be an n n matrix whose element d ij is, at the beginning of the algorithm, the cost c ij of arc (i,j) and, at the end, the cost of a shortest path from i to j. Let P be an n n matrix whose element p ij is the precedecessor of node j in the shortest path from i to j. Description: We consider in turn each node of the graph according to the order of the indices. At iteration h, we consider the node with index h and, for every pair of nodes (i,j) with i h and j h (but including the case i = j), we compare the length of the path via h, that is, d ih +d hj, with the current d ij. If d ih +d hj < d ij, the matrices D and P are updated: we set d ij = d ih +d hj and p ij is updated to p hj. The algorithm halts when one of the following conditions holds () all nodes have been selected for the triangulation operation, () a circuit of negative cost has been found: the problem of finding a shortest path (not necessarily simple!) it not well defined. Indeed, it is possible to go through the negative cost circuit an arbitrary number of times, reducing the cost of the path containing such circuit at each iteration. The problem is, evidently, unbounded. (a) Initial configuration D P Document prepared by L. Liberti, S. Bosio, S. Coniglio. Translation to English by S. Coniglio 6
7 ex-.6-. Foundations of Operations Research Prof. E. Amaldi (b) Iteration h = (triangulation on node ) d +d = 8 > d = d +d = > d = d +d = 8 < d = update d,p d +d = < d = update d,p d +d = 6 > d = d +d = < d = update d,p d +d ij = ( i,j) D P (c) Iteration h = (triangulation on node ) d +d = 8 > d = d +d = 7 < d = 8 update d,p d +d = > d = d +d = 6 > d = d +d = > d = d +d = 9 > d = d +d = < d = update d,p d +d = < d = D P update d,p d +d = > d = Document prepared by L. Liberti, S. Bosio, S. Coniglio. Translation to English by S. Coniglio 7
8 ex-.6-. Foundations of Operations Research Prof. E. Amaldi (d) Iteration h = (triangulation on node ) d +d = > d = d +d = 8 > d = d +d = 8 > d = d +d = < d = update d,p d +d = > d = d +d = < d = 8 update d,p d +d = < d = update d,p d +d = > d = 7 d +d = < d = D P update d,p We obtain d = < and the algorithm halts: we found a circuit with a total negative cost of - ( )..8 An application of Dynamic Programming to machine renewal Consider a directed graph with six nodes: nodes to are associated to the beginning of each year, while node 6 corresponds to the end of the year time horizon. For each pair i,j, with i,j =,..., and i < j, the arc (i,j) that represents the choice of bying a machine at the beginning of year i and selling it at the beginning of year j. The cost c ij of arc (i,j) is defined as the net cost of the corresponding partial renewal plan from the beginning of year i to the beginning of year j, namely j i c ij = c b +( m k ) r j i, k= where c b is the buying cost of Euro, m k is the annual maintenance cost for a machine that is k years old, and r k is the selling price of a machine which is k years old. We obtain the following directed acyclic graph: Document prepared by L. Liberti, S. Bosio, S. Coniglio. Translation to English by S. Coniglio 8
9 ex-.6-. Foundations of Operations Research Prof. E. Amaldi Any path from node to node 6 corresponds to a (complete) renewal plan whose total net cost is equivalent to the total cost of the path. To look for a shortest path from node to node 6, we apply the Dynamic Programming algorithm, obtaining (a) L() = (b) L() = 7, pred() = (c) L() =, pred() = (d) L() = 9, pred() = (e) L() =, pred() = (f) L(6) =, pred(6) =. A shortest path (of cost ) is 6. It amounts to buy a new machine every years. Note that there are two other optimal solutions: path 6 and path 6..9 Project planning The following table indicates the duration of each activity and the related precedence relations: Activities Duration Predecessors A Weight the ingredients - B Meld the butter down A C Mix flour, eggs, and sugar A D Peel and cut the apples into slices A E Heaten the oven - F Add butter to the mixture 8 B,C G Add apples to the mixture D,F H Cook the mixture in the oven E,G I Whip the cream G L Garnish H,I We derive the directed graph represeting the precedence relations as follows. For each activity, we introduce an arc whose cost is equivalent to the duration of the activity (its two nodes represent the beginning and the end of the activity). For each precedence relation A i < A j, a fictitious arc (i,j) of duration is introduced (dashed line) between the ending node of the arc associated to A i and the beginning node of the arc associated to A j. We include a node s and, for each activity without predecessors associated to arc (v,w), we add the arc (s,v) of cost. Similarly, we include a node t and, for each activity without successors associated to arc (v.w), we add the arc (w,t) of cost. B F A C I s D G L t E H Document prepared by L. Liberti, S. Bosio, S. Coniglio. Translation to English by S. Coniglio 9
10 ex-.6-. Foundations of Operations Research Prof. E. Amaldi By contracting (deleting) some of the fictitious arcs while paying attention not to create any unwanted precedence relations, we obtain the following more compact directed acyclic graph representing the project: B F s A C G I E D H L t We use the Critical Path Method (CPM) to determine, for each node v of the graph, the at earliest and at latest times, denoted by T min (v) and respectively T max (v). The algorithm exploits the topological order of the nodes and consists of two phases where Dynamic Programing is applied considering the n nodes in the increasing/decreasing order of the indices. Here is the pseudocode of the algorithm: (a) Sort the nodes in topological order; (b) T min () = ; (c) FOR h =,...,n DO T min (h) := max{t min (i)+d ih (i,h) δ (h)}; (d) T max (n) = T min (n); (e) FOR h = n,..., DO T max (h) := min{t max (i) d hi (h,i) δ + (h)}. After ordering topologically the nodes, we obtain the following earliest times and latest times: [,] [8,8] [,] F G 6 8 I B [.] [,] A C [,] H D E 7 [,] [6,6] [67,67] L 8 9 which are summarized in the following table: Document prepared by L. Liberti, S. Bosio, S. Coniglio. Translation to English by S. Coniglio
11 ex-.6-. Foundations of Operations Research Prof. E. Amaldi The slacks for the activities are: attivity T min (i) T max (i) slack A B 7 C D 8 E F G 8 8 H I L 6 6 σ(a) = T max () T min () d = = σ(b) = T max () T min () d = = σ(c) = T max () T min () d = = σ(d) = T max () T min () d = 8 = σ(e) = T max (6) T min () d 6 = = σ(f) = T max () T min () d = 8 8 = σ(g) = T max (6) T min () d 6 = 8 = σ(h) = T max (8) T min (7) d 78 = 6 = σ(i) = T max (8) T min (6) d 68 = 6 = σ(l) = T max (9) T min (8) d 89 = =. The critical activities are A,C,F,G,H,L. The Gantt chart at earliest (where each activity (i,j) starts at the earliest time T min (i)): A B C D E F G H I L 6 67 Document prepared by L. Liberti, S. Bosio, S. Coniglio. Translation to English by S. Coniglio
12 ex-.6-. Foundations of Operations Research Prof. E. Amaldi. Shortest paths with negative costs. We apply Floyd-Warshall s algorithm. (a) Initialization D - - P (b) Iteration h = (triangulation on node ) d +d = + = 6 > d = d +d = + = = d = d +d = + = > d = d +d = + = > d = D - - P (c) Iteration h = (triangulation on node ) d +d = + = 6 > d = d +d = + = 9 > d = d +d = + = > d = d +d = + = = d = D - - P (d) Iteration h = (triangulation on node ) d +d = = > d = d +d = = < d = update d,p d +d = = > d = d +d = = > d = D P Document prepared by L. Liberti, S. Bosio, S. Coniglio. Translation to English by S. Coniglio
2.3 Optimal paths. Optimal (shortest or longest) paths have a wide range of applications:
 . Optimal paths Optimal (shortest or longest) paths have a wide range of applications: Google maps, GPS navigators planning and management of transportation, electrical and telecommunication networks project
. Optimal paths Optimal (shortest or longest) paths have a wide range of applications: Google maps, GPS navigators planning and management of transportation, electrical and telecommunication networks project
2.3 Optimal paths. E. Amaldi Foundations of Operations Research Politecnico di Milano 1
 . Optimal paths E. Amaldi Foundations of Operations Research Politecnico di Milano Optimal (minimum or maximum) paths have a wide range of applications: Google maps, GPS navigators planning and management
. Optimal paths E. Amaldi Foundations of Operations Research Politecnico di Milano Optimal (minimum or maximum) paths have a wide range of applications: Google maps, GPS navigators planning and management
2.3.4 Optimal paths in directed acyclic graphs
 .3.4 Optimal paths in directed acyclic graphs Definition: A directed graph G = (N, A) is acyclic if it contains no circuits. A directed acyclic graph is referred to as DAG. circuit Problem Given a directed
.3.4 Optimal paths in directed acyclic graphs Definition: A directed graph G = (N, A) is acyclic if it contains no circuits. A directed acyclic graph is referred to as DAG. circuit Problem Given a directed
2.3.5 Project planning
 efinitions:..5 Project planning project consists of a set of m activities with their duration: activity i has duration d i, i = 1,..., m. estimate Some pairs of activities are subject to a precedence constraint:
efinitions:..5 Project planning project consists of a set of m activities with their duration: activity i has duration d i, i = 1,..., m. estimate Some pairs of activities are subject to a precedence constraint:
2.2 Optimal cost spanning trees
 . Optimal cost spanning trees Spanning trees have a number of applications: network design (communication, electrical,...) IP network protocols compact memory storage (DNA)... E. Amaldi Foundations of
. Optimal cost spanning trees Spanning trees have a number of applications: network design (communication, electrical,...) IP network protocols compact memory storage (DNA)... E. Amaldi Foundations of
Foundations of Operations Research (Prof. Roberto Cordone) September 11th, 2014 Time available: 2 hours and 30 minutes
 Foundations of Operations Research (Prof. Roberto Cordone) September 11th, 2014 Time available: 2 hours and 30 minutes Note: Report all computational passages (unmotivated results will be ignored). Exercise
Foundations of Operations Research (Prof. Roberto Cordone) September 11th, 2014 Time available: 2 hours and 30 minutes Note: Report all computational passages (unmotivated results will be ignored). Exercise
These are not polished as solutions, but ought to give a correct idea of solutions that work. Note that most problems have multiple good solutions.
 CSE 591 HW Sketch Sample Solutions These are not polished as solutions, but ought to give a correct idea of solutions that work. Note that most problems have multiple good solutions. Problem 1 (a) Any
CSE 591 HW Sketch Sample Solutions These are not polished as solutions, but ought to give a correct idea of solutions that work. Note that most problems have multiple good solutions. Problem 1 (a) Any
Lecture 18 Solving Shortest Path Problem: Dijkstra s Algorithm. October 23, 2009
 Solving Shortest Path Problem: Dijkstra s Algorithm October 23, 2009 Outline Lecture 18 Focus on Dijkstra s Algorithm Importance: Where it has been used? Algorithm s general description Algorithm steps
Solving Shortest Path Problem: Dijkstra s Algorithm October 23, 2009 Outline Lecture 18 Focus on Dijkstra s Algorithm Importance: Where it has been used? Algorithm s general description Algorithm steps
Chapter 15 Introduction to Linear Programming
 Chapter 15 Introduction to Linear Programming An Introduction to Optimization Spring, 2015 Wei-Ta Chu 1 Brief History of Linear Programming The goal of linear programming is to determine the values of
Chapter 15 Introduction to Linear Programming An Introduction to Optimization Spring, 2015 Wei-Ta Chu 1 Brief History of Linear Programming The goal of linear programming is to determine the values of
LECTURES 3 and 4: Flows and Matchings
 LECTURES 3 and 4: Flows and Matchings 1 Max Flow MAX FLOW (SP). Instance: Directed graph N = (V,A), two nodes s,t V, and capacities on the arcs c : A R +. A flow is a set of numbers on the arcs such that
LECTURES 3 and 4: Flows and Matchings 1 Max Flow MAX FLOW (SP). Instance: Directed graph N = (V,A), two nodes s,t V, and capacities on the arcs c : A R +. A flow is a set of numbers on the arcs such that
2. True or false: even though BFS and DFS have the same space complexity, they do not always have the same worst case asymptotic time complexity.
 1. T F: Consider a directed graph G = (V, E) and a vertex s V. Suppose that for all v V, there exists a directed path in G from s to v. Suppose that a DFS is run on G, starting from s. Then, true or false:
1. T F: Consider a directed graph G = (V, E) and a vertex s V. Suppose that for all v V, there exists a directed path in G from s to v. Suppose that a DFS is run on G, starting from s. Then, true or false:
Dynamic-Programming algorithms for shortest path problems: Bellman-Ford (for singlesource) and Floyd-Warshall (for all-pairs).
 Lecture 13 Graph Algorithms I 13.1 Overview This is the first of several lectures on graph algorithms. We will see how simple algorithms like depth-first-search can be used in clever ways (for a problem
Lecture 13 Graph Algorithms I 13.1 Overview This is the first of several lectures on graph algorithms. We will see how simple algorithms like depth-first-search can be used in clever ways (for a problem
7.3 Spanning trees Spanning trees [ ] 61
![7.3 Spanning trees Spanning trees [ ] 61 7.3 Spanning trees Spanning trees [ ] 61](/thumbs/77/75523634.jpg) 7.3. Spanning trees [161211-1348 ] 61 7.3 Spanning trees We know that trees are connected graphs with the minimal number of edges. Hence trees become very useful in applications where our goal is to connect
7.3. Spanning trees [161211-1348 ] 61 7.3 Spanning trees We know that trees are connected graphs with the minimal number of edges. Hence trees become very useful in applications where our goal is to connect
Graph Algorithms (part 3 of CSC 282),
 Graph Algorithms (part of CSC 8), http://www.cs.rochester.edu/~stefanko/teaching/10cs8 1 Schedule Homework is due Thursday, Oct 1. The QUIZ will be on Tuesday, Oct. 6. List of algorithms covered in the
Graph Algorithms (part of CSC 8), http://www.cs.rochester.edu/~stefanko/teaching/10cs8 1 Schedule Homework is due Thursday, Oct 1. The QUIZ will be on Tuesday, Oct. 6. List of algorithms covered in the
Chapter 9 Graph Algorithms
 Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be if not careful with data structures 3 Definitions an undirected graph G = (V, E) is a
Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be if not careful with data structures 3 Definitions an undirected graph G = (V, E) is a
Project and Production Management Prof. Arun Kanda Department of Mechanical Engineering Indian Institute of Technology, Delhi
 Project and Production Management Prof. Arun Kanda Department of Mechanical Engineering Indian Institute of Technology, Delhi Lecture - 8 Consistency and Redundancy in Project networks In today s lecture
Project and Production Management Prof. Arun Kanda Department of Mechanical Engineering Indian Institute of Technology, Delhi Lecture - 8 Consistency and Redundancy in Project networks In today s lecture
The diagram below is only partially complete. Use the terms in the word list to complete the empty boxes. Make dinner
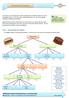 Decomposing Problems As we have seen, decomposition means breaking down a difficult problem into more manageable pieces. A common way to tackle this process is to use a tree diagram showing increasing
Decomposing Problems As we have seen, decomposition means breaking down a difficult problem into more manageable pieces. A common way to tackle this process is to use a tree diagram showing increasing
MOST attention in the literature of network codes has
 3862 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 56, NO. 8, AUGUST 2010 Efficient Network Code Design for Cyclic Networks Elona Erez, Member, IEEE, and Meir Feder, Fellow, IEEE Abstract This paper introduces
3862 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 56, NO. 8, AUGUST 2010 Efficient Network Code Design for Cyclic Networks Elona Erez, Member, IEEE, and Meir Feder, Fellow, IEEE Abstract This paper introduces
Minimum Spanning Trees
 Minimum Spanning Trees Problem A town has a set of houses and a set of roads. A road connects 2 and only 2 houses. A road connecting houses u and v has a repair cost w(u, v). Goal: Repair enough (and no
Minimum Spanning Trees Problem A town has a set of houses and a set of roads. A road connects 2 and only 2 houses. A road connecting houses u and v has a repair cost w(u, v). Goal: Repair enough (and no
Chapter 9 Graph Algorithms
 Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 3 Definitions an undirected graph G = (V, E)
Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 3 Definitions an undirected graph G = (V, E)
11/22/2016. Chapter 9 Graph Algorithms. Introduction. Definitions. Definitions. Definitions. Definitions
 Introduction Chapter 9 Graph Algorithms graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 2 Definitions an undirected graph G = (V, E) is
Introduction Chapter 9 Graph Algorithms graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 2 Definitions an undirected graph G = (V, E) is
CS 341: Algorithms. Douglas R. Stinson. David R. Cheriton School of Computer Science University of Waterloo. February 26, 2019
 CS 341: Algorithms Douglas R. Stinson David R. Cheriton School of Computer Science University of Waterloo February 26, 2019 D.R. Stinson (SCS) CS 341 February 26, 2019 1 / 296 1 Course Information 2 Introduction
CS 341: Algorithms Douglas R. Stinson David R. Cheriton School of Computer Science University of Waterloo February 26, 2019 D.R. Stinson (SCS) CS 341 February 26, 2019 1 / 296 1 Course Information 2 Introduction
4.1 Graphical solution of a linear program and standard form
 4.1 Graphical solution of a linear program and standard form Consider the problem min c T x Ax b x where x = ( x1 x ) ( 16, c = 5 ), b = 4 5 9, A = 1 7 1 5 1. Solve the problem graphically and determine
4.1 Graphical solution of a linear program and standard form Consider the problem min c T x Ax b x where x = ( x1 x ) ( 16, c = 5 ), b = 4 5 9, A = 1 7 1 5 1. Solve the problem graphically and determine
Chapter 9 Graph Algorithms
 Introduction graph theory useful in practice represent many real-life problems can be if not careful with data structures Chapter 9 Graph s 2 Definitions Definitions an undirected graph is a finite set
Introduction graph theory useful in practice represent many real-life problems can be if not careful with data structures Chapter 9 Graph s 2 Definitions Definitions an undirected graph is a finite set
6. Lecture notes on matroid intersection
 Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans May 2, 2017 6. Lecture notes on matroid intersection One nice feature about matroids is that a simple greedy algorithm
Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans May 2, 2017 6. Lecture notes on matroid intersection One nice feature about matroids is that a simple greedy algorithm
Graph definitions. There are two kinds of graphs: directed graphs (sometimes called digraphs) and undirected graphs. An undirected graph
 Graphs Graph definitions There are two kinds of graphs: directed graphs (sometimes called digraphs) and undirected graphs start Birmingham 60 Rugby fill pan with water add salt to water take egg from fridge
Graphs Graph definitions There are two kinds of graphs: directed graphs (sometimes called digraphs) and undirected graphs start Birmingham 60 Rugby fill pan with water add salt to water take egg from fridge
Graph Algorithms (part 3 of CSC 282),
 Graph Algorithms (part of CSC 8), http://www.cs.rochester.edu/~stefanko/teaching/11cs8 Homework problem sessions are in CSB 601, 6:1-7:1pm on Oct. (Wednesday), Oct. 1 (Wednesday), and on Oct. 19 (Wednesday);
Graph Algorithms (part of CSC 8), http://www.cs.rochester.edu/~stefanko/teaching/11cs8 Homework problem sessions are in CSB 601, 6:1-7:1pm on Oct. (Wednesday), Oct. 1 (Wednesday), and on Oct. 19 (Wednesday);
EXERCISES SHORTEST PATHS: APPLICATIONS, OPTIMIZATION, VARIATIONS, AND SOLVING THE CONSTRAINED SHORTEST PATH PROBLEM. 1 Applications and Modelling
 SHORTEST PATHS: APPLICATIONS, OPTIMIZATION, VARIATIONS, AND SOLVING THE CONSTRAINED SHORTEST PATH PROBLEM EXERCISES Prepared by Natashia Boland 1 and Irina Dumitrescu 2 1 Applications and Modelling 1.1
SHORTEST PATHS: APPLICATIONS, OPTIMIZATION, VARIATIONS, AND SOLVING THE CONSTRAINED SHORTEST PATH PROBLEM EXERCISES Prepared by Natashia Boland 1 and Irina Dumitrescu 2 1 Applications and Modelling 1.1
Analysis of Algorithms, I
 Analysis of Algorithms, I CSOR W4231.002 Eleni Drinea Computer Science Department Columbia University Thursday, March 8, 2016 Outline 1 Recap Single-source shortest paths in graphs with real edge weights:
Analysis of Algorithms, I CSOR W4231.002 Eleni Drinea Computer Science Department Columbia University Thursday, March 8, 2016 Outline 1 Recap Single-source shortest paths in graphs with real edge weights:
Directed Graphs. DSA - lecture 5 - T.U.Cluj-Napoca - M. Joldos 1
 Directed Graphs Definitions. Representations. ADT s. Single Source Shortest Path Problem (Dijkstra, Bellman-Ford, Floyd-Warshall). Traversals for DGs. Parenthesis Lemma. DAGs. Strong Components. Topological
Directed Graphs Definitions. Representations. ADT s. Single Source Shortest Path Problem (Dijkstra, Bellman-Ford, Floyd-Warshall). Traversals for DGs. Parenthesis Lemma. DAGs. Strong Components. Topological
Job-shop scheduling with limited capacity buffers
 Job-shop scheduling with limited capacity buffers Peter Brucker, Silvia Heitmann University of Osnabrück, Department of Mathematics/Informatics Albrechtstr. 28, D-49069 Osnabrück, Germany {peter,sheitman}@mathematik.uni-osnabrueck.de
Job-shop scheduling with limited capacity buffers Peter Brucker, Silvia Heitmann University of Osnabrück, Department of Mathematics/Informatics Albrechtstr. 28, D-49069 Osnabrück, Germany {peter,sheitman}@mathematik.uni-osnabrueck.de
Shortest Paths. March 21, CTU in Prague. Z. Hanzálek (CTU) Shortest Paths March 21, / 44
 Shortest Paths Zdeněk Hanzálek hanzalek@fel.cvut.cz CTU in Prague March 21, 2017 Z. Hanzálek (CTU) Shortest Paths March 21, 2017 1 / 44 Table of contents 1 Introduction Problem Statement Negative Weights
Shortest Paths Zdeněk Hanzálek hanzalek@fel.cvut.cz CTU in Prague March 21, 2017 Z. Hanzálek (CTU) Shortest Paths March 21, 2017 1 / 44 Table of contents 1 Introduction Problem Statement Negative Weights
The Shortest Path Problem. The Shortest Path Problem. Mathematical Model. Integer Programming Formulation
 The Shortest Path Problem jla,jc@imm.dtu.dk Department of Management Engineering Technical University of Denmark The Shortest Path Problem Given a directed network G = (V,E,w) for which the underlying
The Shortest Path Problem jla,jc@imm.dtu.dk Department of Management Engineering Technical University of Denmark The Shortest Path Problem Given a directed network G = (V,E,w) for which the underlying
Chalmers University of Technology. Network Models. April 11, Birgit Grohe
 Chalmers University of Technology Applied Optimisation lp 4 VT08 Network Models April 11, 2008 Birgit Grohe Network Models - Examples Many different problems can be formulated as graph/network models:
Chalmers University of Technology Applied Optimisation lp 4 VT08 Network Models April 11, 2008 Birgit Grohe Network Models - Examples Many different problems can be formulated as graph/network models:
Network Models - Examples. Network Models. Definition and Terminology. The Minimum Spanning Tree (MST) Problem
 Chalmers University of Technology Applied Optimisa- Network Models - Examples tion lp 4 VT08 Network Models April 11, 2008 Birgit Grohe Many different problems can be formulated as graph/network models:
Chalmers University of Technology Applied Optimisa- Network Models - Examples tion lp 4 VT08 Network Models April 11, 2008 Birgit Grohe Many different problems can be formulated as graph/network models:
UNIT 5 GRAPH. Application of Graph Structure in real world:- Graph Terminologies:
 UNIT 5 CSE 103 - Unit V- Graph GRAPH Graph is another important non-linear data structure. In tree Structure, there is a hierarchical relationship between, parent and children that is one-to-many relationship.
UNIT 5 CSE 103 - Unit V- Graph GRAPH Graph is another important non-linear data structure. In tree Structure, there is a hierarchical relationship between, parent and children that is one-to-many relationship.
PBW 654 Applied Statistics - I Urban Operations Research. Unit 3. Network Modelling
 PBW 54 Applied Statistics - I Urban Operations Research Unit 3 Network Modelling Background So far, we treated urban space as a continuum, where an entity could travel from any point to any other point
PBW 54 Applied Statistics - I Urban Operations Research Unit 3 Network Modelling Background So far, we treated urban space as a continuum, where an entity could travel from any point to any other point
8. The Postman Problems
 8. The Postman Problems The Chinese postman problem (CPP) A postal carrier must pick up the mail at the post office, deliver the mail along blocks on the route, and finally return to the post office. To
8. The Postman Problems The Chinese postman problem (CPP) A postal carrier must pick up the mail at the post office, deliver the mail along blocks on the route, and finally return to the post office. To
CS261: Problem Set #1
 CS261: Problem Set #1 Due by 11:59 PM on Tuesday, April 21, 2015 Instructions: (1) Form a group of 1-3 students. You should turn in only one write-up for your entire group. (2) Turn in your solutions by
CS261: Problem Set #1 Due by 11:59 PM on Tuesday, April 21, 2015 Instructions: (1) Form a group of 1-3 students. You should turn in only one write-up for your entire group. (2) Turn in your solutions by
YEAR 12 FURTHER MATHS UNIT 4 MODULE 2 NETWORKS AND DECISION MATHEMATICS CRITICAL PATH ANALYSIS
 YEAR 12 FURTHER MATHS UNIT 4 MODULE 2 NETWORKS AND DECISION MATHEMATICS CRITICAL PATH ANALYSIS Directed graphs or digraphs can be used to model situations where an order or direction is implied. For example,
YEAR 12 FURTHER MATHS UNIT 4 MODULE 2 NETWORKS AND DECISION MATHEMATICS CRITICAL PATH ANALYSIS Directed graphs or digraphs can be used to model situations where an order or direction is implied. For example,
Shortest Path Problem
 Shortest Path Problem CLRS Chapters 24.1 3, 24.5, 25.2 Shortest path problem Shortest path problem (and variants) Properties of shortest paths Algorithmic framework Bellman-Ford algorithm Shortest paths
Shortest Path Problem CLRS Chapters 24.1 3, 24.5, 25.2 Shortest path problem Shortest path problem (and variants) Properties of shortest paths Algorithmic framework Bellman-Ford algorithm Shortest paths
The Encoding Complexity of Network Coding
 The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email: mikel,spalex,bruck @caltech.edu Abstract In the multicast network
The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email: mikel,spalex,bruck @caltech.edu Abstract In the multicast network
OPTIMIZATION: Linear Programming
 May 21, 2013 OPTIMIZATION: Linear Programming Linear programming (OPTIMIZATION) is the process of taking various linear inequalities (constraints) related to some situation, and finding the "best" value
May 21, 2013 OPTIMIZATION: Linear Programming Linear programming (OPTIMIZATION) is the process of taking various linear inequalities (constraints) related to some situation, and finding the "best" value
Unweighted Graphs & Algorithms
 Unweighted Graphs & Algorithms Zachary Friggstad Programming Club Meeting References Chapter 4: Graph (Section 4.2) Chapter 22: Elementary Graph Algorithms Graphs Features: vertices/nodes/dots and edges/links/lines
Unweighted Graphs & Algorithms Zachary Friggstad Programming Club Meeting References Chapter 4: Graph (Section 4.2) Chapter 22: Elementary Graph Algorithms Graphs Features: vertices/nodes/dots and edges/links/lines
Basics of Graph Theory
 Basics of Graph Theory 1 Basic notions A simple graph G = (V, E) consists of V, a nonempty set of vertices, and E, a set of unordered pairs of distinct elements of V called edges. Simple graphs have their
Basics of Graph Theory 1 Basic notions A simple graph G = (V, E) consists of V, a nonempty set of vertices, and E, a set of unordered pairs of distinct elements of V called edges. Simple graphs have their
Solution for Homework set 3
 TTIC 300 and CMSC 37000 Algorithms Winter 07 Solution for Homework set 3 Question (0 points) We are given a directed graph G = (V, E), with two special vertices s and t, and non-negative integral capacities
TTIC 300 and CMSC 37000 Algorithms Winter 07 Solution for Homework set 3 Question (0 points) We are given a directed graph G = (V, E), with two special vertices s and t, and non-negative integral capacities
Lecture 22 Tuesday, April 10
 CIS 160 - Spring 2018 (instructor Val Tannen) Lecture 22 Tuesday, April 10 GRAPH THEORY Directed Graphs Directed graphs (a.k.a. digraphs) are an important mathematical modeling tool in Computer Science,
CIS 160 - Spring 2018 (instructor Val Tannen) Lecture 22 Tuesday, April 10 GRAPH THEORY Directed Graphs Directed graphs (a.k.a. digraphs) are an important mathematical modeling tool in Computer Science,
Graph Representations and Traversal
 COMPSCI 330: Design and Analysis of Algorithms 02/08/2017-02/20/2017 Graph Representations and Traversal Lecturer: Debmalya Panigrahi Scribe: Tianqi Song, Fred Zhang, Tianyu Wang 1 Overview This lecture
COMPSCI 330: Design and Analysis of Algorithms 02/08/2017-02/20/2017 Graph Representations and Traversal Lecturer: Debmalya Panigrahi Scribe: Tianqi Song, Fred Zhang, Tianyu Wang 1 Overview This lecture
A Unicorn Named Sparkle Word Search. A New Friend for Sparkle Coloring Sheet. A Unicorn Named Sparkle s First Christmas Coloring Sheet
 Table of Contents Page 1 Page 2 Page 3 Page 4 Page 5 Page 6 Page 7 Pages 8 9 Page 10 Page 11 Page 12 Page 13 Page 14 Page 15 Name Tags A Unicorn Named Sparkle Word Search Draw and Name Your Unicorn Connect
Table of Contents Page 1 Page 2 Page 3 Page 4 Page 5 Page 6 Page 7 Pages 8 9 Page 10 Page 11 Page 12 Page 13 Page 14 Page 15 Name Tags A Unicorn Named Sparkle Word Search Draw and Name Your Unicorn Connect
Dynamic Programming Shabsi Walfish NYU - Fundamental Algorithms Summer 2006
 Dynamic Programming What is Dynamic Programming? Technique for avoiding redundant work in recursive algorithms Works best with optimization problems that have a nice underlying structure Can often be used
Dynamic Programming What is Dynamic Programming? Technique for avoiding redundant work in recursive algorithms Works best with optimization problems that have a nice underlying structure Can often be used
x ji = s i, i N, (1.1)
 Dual Ascent Methods. DUAL ASCENT In this chapter we focus on the minimum cost flow problem minimize subject to (i,j) A {j (i,j) A} a ij x ij x ij {j (j,i) A} (MCF) x ji = s i, i N, (.) b ij x ij c ij,
Dual Ascent Methods. DUAL ASCENT In this chapter we focus on the minimum cost flow problem minimize subject to (i,j) A {j (i,j) A} a ij x ij x ij {j (j,i) A} (MCF) x ji = s i, i N, (.) b ij x ij c ij,
Introductory Remarks
 Chapter 8: Graphs Introductory Remarks Although trees are quite flexible, they have an inherent limitation in that they can only express hierarchical structures Fortunately, we can generalize a tree to
Chapter 8: Graphs Introductory Remarks Although trees are quite flexible, they have an inherent limitation in that they can only express hierarchical structures Fortunately, we can generalize a tree to
Dijkstra s Algorithm. Dijkstra s algorithm is a natural, greedy approach towards
 CPSC-320: Intermediate Algorithm Design and Analysis 128 CPSC-320: Intermediate Algorithm Design and Analysis 129 Dijkstra s Algorithm Dijkstra s algorithm is a natural, greedy approach towards solving
CPSC-320: Intermediate Algorithm Design and Analysis 128 CPSC-320: Intermediate Algorithm Design and Analysis 129 Dijkstra s Algorithm Dijkstra s algorithm is a natural, greedy approach towards solving
Simulation. Lecture O1 Optimization: Linear Programming. Saeed Bastani April 2016
 Simulation Lecture O Optimization: Linear Programming Saeed Bastani April 06 Outline of the course Linear Programming ( lecture) Integer Programming ( lecture) Heuristics and Metaheursitics (3 lectures)
Simulation Lecture O Optimization: Linear Programming Saeed Bastani April 06 Outline of the course Linear Programming ( lecture) Integer Programming ( lecture) Heuristics and Metaheursitics (3 lectures)
CS170 Discussion Section 4: 9/18
 CS170 Discussion Section 4: 9/18 1. Alien alphabet. Suppose you have a dictionary of an alien language which lists words in some sorted lexicographical ordering. For example, given the following list of
CS170 Discussion Section 4: 9/18 1. Alien alphabet. Suppose you have a dictionary of an alien language which lists words in some sorted lexicographical ordering. For example, given the following list of
CS490 Quiz 1. This is the written part of Quiz 1. The quiz is closed book; in particular, no notes, calculators and cell phones are allowed.
 CS490 Quiz 1 NAME: STUDENT NO: SIGNATURE: This is the written part of Quiz 1. The quiz is closed book; in particular, no notes, calculators and cell phones are allowed. Not all questions are of the same
CS490 Quiz 1 NAME: STUDENT NO: SIGNATURE: This is the written part of Quiz 1. The quiz is closed book; in particular, no notes, calculators and cell phones are allowed. Not all questions are of the same
Dependency Table Example. Task ID Name Predecessors 1 A 2 B 3 C 4 D 1 5 E 1;2 6 F 1;2 7 G 5;6 8 H 4;5
 Dependency Table Example Task ID Name Predecessors 1 A 2 B 3 C 4 D 1 5 E 1;2 6 F 1;2 7 G 5;6 8 H 4;5 Dependent tasks Dependency Matrix 1 2 3 4 5 6 7 8 9 10 1 x 2 x x 3 x x 4 x 5 x x 6 x 7 x 8 x 9 x x 10
Dependency Table Example Task ID Name Predecessors 1 A 2 B 3 C 4 D 1 5 E 1;2 6 F 1;2 7 G 5;6 8 H 4;5 Dependent tasks Dependency Matrix 1 2 3 4 5 6 7 8 9 10 1 x 2 x x 3 x x 4 x 5 x x 6 x 7 x 8 x 9 x x 10
1 Non greedy algorithms (which we should have covered
 1 Non greedy algorithms (which we should have covered earlier) 1.1 Floyd Warshall algorithm This algorithm solves the all-pairs shortest paths problem, which is a problem where we want to find the shortest
1 Non greedy algorithms (which we should have covered earlier) 1.1 Floyd Warshall algorithm This algorithm solves the all-pairs shortest paths problem, which is a problem where we want to find the shortest
More Graph Algorithms: Topological Sort and Shortest Distance
 More Graph Algorithms: Topological Sort and Shortest Distance Topological Sort The goal of a topological sort is given a list of items with dependencies, (ie. item 5 must be completed before item 3, etc.)
More Graph Algorithms: Topological Sort and Shortest Distance Topological Sort The goal of a topological sort is given a list of items with dependencies, (ie. item 5 must be completed before item 3, etc.)
Routing. Information Networks p.1/35
 Routing Routing is done by the network layer protocol to guide packets through the communication subnet to their destinations The time when routing decisions are made depends on whether we are using virtual
Routing Routing is done by the network layer protocol to guide packets through the communication subnet to their destinations The time when routing decisions are made depends on whether we are using virtual
The Shortest Path Problem
 The Shortest Path Problem 1 Shortest-Path Algorithms Find the shortest path from point A to point B Shortest in time, distance, cost, Numerous applications Map navigation Flight itineraries Circuit wiring
The Shortest Path Problem 1 Shortest-Path Algorithms Find the shortest path from point A to point B Shortest in time, distance, cost, Numerous applications Map navigation Flight itineraries Circuit wiring
Algorithms for Data Science
 Algorithms for Data Science CSOR W4246 Eleni Drinea Computer Science Department Columbia University Shortest paths in weighted graphs (Bellman-Ford, Floyd-Warshall) Outline 1 Shortest paths in graphs with
Algorithms for Data Science CSOR W4246 Eleni Drinea Computer Science Department Columbia University Shortest paths in weighted graphs (Bellman-Ford, Floyd-Warshall) Outline 1 Shortest paths in graphs with
Graph Algorithms. 1 Preliminary Denitions. CSci 335 Software Design and Analysis III Chapter 9 Graph Algorithms. Prof.
 Preliminary Denitions Graph Algorithms There is a lot of terminology associated with graphs and graph algorithms, and so we start by dening the terms we will use for the remainder of this chapter. Denition.
Preliminary Denitions Graph Algorithms There is a lot of terminology associated with graphs and graph algorithms, and so we start by dening the terms we will use for the remainder of this chapter. Denition.
Lecture 3: Totally Unimodularity and Network Flows
 Lecture 3: Totally Unimodularity and Network Flows (3 units) Outline Properties of Easy Problems Totally Unimodular Matrix Minimum Cost Network Flows Dijkstra Algorithm for Shortest Path Problem Ford-Fulkerson
Lecture 3: Totally Unimodularity and Network Flows (3 units) Outline Properties of Easy Problems Totally Unimodular Matrix Minimum Cost Network Flows Dijkstra Algorithm for Shortest Path Problem Ford-Fulkerson
All Shortest Paths. Questions from exercises and exams
 All Shortest Paths Questions from exercises and exams The Problem: G = (V, E, w) is a weighted directed graph. We want to find the shortest path between any pair of vertices in G. Example: find the distance
All Shortest Paths Questions from exercises and exams The Problem: G = (V, E, w) is a weighted directed graph. We want to find the shortest path between any pair of vertices in G. Example: find the distance
Lecture I: Shortest Path Algorithms
 Lecture I: Shortest Path Algorithms Dr Kieran T. Herley Department of Computer Science University College Cork October 201 KH (21/10/1) Lecture I: Shortest Path Algorithms October 201 1 / 28 Background
Lecture I: Shortest Path Algorithms Dr Kieran T. Herley Department of Computer Science University College Cork October 201 KH (21/10/1) Lecture I: Shortest Path Algorithms October 201 1 / 28 Background
Chapter 6. Planar Orientations. 6.1 Numberings of Digraphs
 Chapter 6 Planar Orientations In this chapter we will focus on algorithms and techniques used for drawing planar graphs. The algorithms we will use are based on numbering the vertices and orienting the
Chapter 6 Planar Orientations In this chapter we will focus on algorithms and techniques used for drawing planar graphs. The algorithms we will use are based on numbering the vertices and orienting the
Datenstrukturen & Algorithmen Blatt P13 HS 18
 Eidgenössische Technische Hochschule Zürich Ecole polytechnique fédérale de Zurich Politecnico federale di Zurigo Federal Institute of Technology at Zurich Departement of Computer Science 3. December 08
Eidgenössische Technische Hochschule Zürich Ecole polytechnique fédérale de Zurich Politecnico federale di Zurigo Federal Institute of Technology at Zurich Departement of Computer Science 3. December 08
Advanced Algorithms Linear Programming
 Reading: Advanced Algorithms Linear Programming CLRS, Chapter29 (2 nd ed. onward). Linear Algebra and Its Applications, by Gilbert Strang, chapter 8 Linear Programming, by Vasek Chvatal Introduction to
Reading: Advanced Algorithms Linear Programming CLRS, Chapter29 (2 nd ed. onward). Linear Algebra and Its Applications, by Gilbert Strang, chapter 8 Linear Programming, by Vasek Chvatal Introduction to
Solving problems on graph algorithms
 Solving problems on graph algorithms Workshop Organized by: ACM Unit, Indian Statistical Institute, Kolkata. Tutorial-3 Date: 06.07.2017 Let G = (V, E) be an undirected graph. For a vertex v V, G {v} is
Solving problems on graph algorithms Workshop Organized by: ACM Unit, Indian Statistical Institute, Kolkata. Tutorial-3 Date: 06.07.2017 Let G = (V, E) be an undirected graph. For a vertex v V, G {v} is
Konigsberg Bridge Problem
 Graphs Konigsberg Bridge Problem c C d g A Kneiphof e D a B b f c A C d e g D a b f B Euler s Graph Degree of a vertex: the number of edges incident to it Euler showed that there is a walk starting at
Graphs Konigsberg Bridge Problem c C d g A Kneiphof e D a B b f c A C d e g D a b f B Euler s Graph Degree of a vertex: the number of edges incident to it Euler showed that there is a walk starting at
1. What do you get as the integer and noninteger parts if you factor this as we did with our cutting planes:
 1. What do you get as the integer and noninteger parts if you factor this as we did with our cutting planes: x 1 = -8.75-3.1 x 2 + 4.2 x 3 + 7 x 5-8 x 6 2. What constraint is added? 3. What do you need
1. What do you get as the integer and noninteger parts if you factor this as we did with our cutting planes: x 1 = -8.75-3.1 x 2 + 4.2 x 3 + 7 x 5-8 x 6 2. What constraint is added? 3. What do you need
Communication Networks I December 4, 2001 Agenda Graph theory notation Trees Shortest path algorithms Distributed, asynchronous algorithms Page 1
 Communication Networks I December, Agenda Graph theory notation Trees Shortest path algorithms Distributed, asynchronous algorithms Page Communication Networks I December, Notation G = (V,E) denotes a
Communication Networks I December, Agenda Graph theory notation Trees Shortest path algorithms Distributed, asynchronous algorithms Page Communication Networks I December, Notation G = (V,E) denotes a
Material handling and Transportation in Logistics. Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena
 Material handling and Transportation in Logistics Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Introduction to Graph Theory Graph Theory As Mathematical
Material handling and Transportation in Logistics Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Introduction to Graph Theory Graph Theory As Mathematical
Discrete Mathematics. Kruskal, order, sorting, induction
 Discrete Mathematics wwwmifvult/~algis Kruskal, order, sorting, induction Kruskal algorithm Kruskal s Algorithm for Minimal Spanning Trees The algorithm constructs a minimal spanning tree as follows: Starting
Discrete Mathematics wwwmifvult/~algis Kruskal, order, sorting, induction Kruskal algorithm Kruskal s Algorithm for Minimal Spanning Trees The algorithm constructs a minimal spanning tree as follows: Starting
Quiz 2 CS 3510 October 22, 2004
 Quiz 2 CS 3510 October 22, 2004 NAME : (Remember to fill in your name!) For grading purposes, please leave blank: (1) Short Answer (40 points) (2) Cycle Length (20 points) (3) Bottleneck (20 points) (4)
Quiz 2 CS 3510 October 22, 2004 NAME : (Remember to fill in your name!) For grading purposes, please leave blank: (1) Short Answer (40 points) (2) Cycle Length (20 points) (3) Bottleneck (20 points) (4)
22 Elementary Graph Algorithms. There are two standard ways to represent a
 VI Graph Algorithms Elementary Graph Algorithms Minimum Spanning Trees Single-Source Shortest Paths All-Pairs Shortest Paths 22 Elementary Graph Algorithms There are two standard ways to represent a graph
VI Graph Algorithms Elementary Graph Algorithms Minimum Spanning Trees Single-Source Shortest Paths All-Pairs Shortest Paths 22 Elementary Graph Algorithms There are two standard ways to represent a graph
Introduction to Graphs. CS2110, Spring 2011 Cornell University
 Introduction to Graphs CS2110, Spring 2011 Cornell University A graph is a data structure for representing relationships. Each graph is a set of nodes connected by edges. Synonym Graph Hostile Slick Icy
Introduction to Graphs CS2110, Spring 2011 Cornell University A graph is a data structure for representing relationships. Each graph is a set of nodes connected by edges. Synonym Graph Hostile Slick Icy
Algorithms: The recipe for computation
 Algorithms: The recipe for computation 2A What is an algorithm? 15-105 Principles of Computation, Carnegie Mellon University - CORTINA 1 Algorithms An algorithm is a precise rule (or set of rules) specifying
Algorithms: The recipe for computation 2A What is an algorithm? 15-105 Principles of Computation, Carnegie Mellon University - CORTINA 1 Algorithms An algorithm is a precise rule (or set of rules) specifying
COT 6936: Topics in Algorithms! Giri Narasimhan. ECS 254A / EC 2443; Phone: x3748
 COT 6936: Topics in Algorithms! Giri Narasimhan ECS 254A / EC 2443; Phone: x3748 giri@cs.fiu.edu http://www.cs.fiu.edu/~giri/teach/cot6936_s12.html https://moodle.cis.fiu.edu/v2.1/course/view.php?id=174
COT 6936: Topics in Algorithms! Giri Narasimhan ECS 254A / EC 2443; Phone: x3748 giri@cs.fiu.edu http://www.cs.fiu.edu/~giri/teach/cot6936_s12.html https://moodle.cis.fiu.edu/v2.1/course/view.php?id=174
FastA & the chaining problem
 FastA & the chaining problem We will discuss: Heuristics used by the FastA program for sequence alignment Chaining problem 1 Sources for this lecture: Lectures by Volker Heun, Daniel Huson and Knut Reinert,
FastA & the chaining problem We will discuss: Heuristics used by the FastA program for sequence alignment Chaining problem 1 Sources for this lecture: Lectures by Volker Heun, Daniel Huson and Knut Reinert,
Advanced Algorithm Design and Analysis (Lecture 5) SW5 fall 2007 Simonas Šaltenis
 Advanced Algorithm Design and Analysis (Lecture 5) SW5 fall 2007 Simonas Šaltenis 3.2.12 simas@cs.aau.dk All-pairs shortest paths Main goals of the lecture: to go through one more example of dynamic programming
Advanced Algorithm Design and Analysis (Lecture 5) SW5 fall 2007 Simonas Šaltenis 3.2.12 simas@cs.aau.dk All-pairs shortest paths Main goals of the lecture: to go through one more example of dynamic programming
FastA and the chaining problem, Gunnar Klau, December 1, 2005, 10:
 FastA and the chaining problem, Gunnar Klau, December 1, 2005, 10:56 4001 4 FastA and the chaining problem We will discuss: Heuristics used by the FastA program for sequence alignment Chaining problem
FastA and the chaining problem, Gunnar Klau, December 1, 2005, 10:56 4001 4 FastA and the chaining problem We will discuss: Heuristics used by the FastA program for sequence alignment Chaining problem
Methods and Models for Combinatorial Optimization Modeling by Linear Programming
 Methods and Models for Combinatorial Optimization Modeling by Linear Programming Luigi De Giovanni, Marco Di Summa 1 Linear programming models Linear programming models are a special class of mathematical
Methods and Models for Combinatorial Optimization Modeling by Linear Programming Luigi De Giovanni, Marco Di Summa 1 Linear programming models Linear programming models are a special class of mathematical
Test 1 Last 4 Digits of Mav ID # Multiple Choice. Write your answer to the LEFT of each problem. 2 points each t 1
 CSE 0 Name Test Fall 00 Last Digits of Mav ID # Multiple Choice. Write your answer to the LEFT of each problem. points each t. What is the value of k? k=0 A. k B. t C. t+ D. t+ +. Suppose that you have
CSE 0 Name Test Fall 00 Last Digits of Mav ID # Multiple Choice. Write your answer to the LEFT of each problem. points each t. What is the value of k? k=0 A. k B. t C. t+ D. t+ +. Suppose that you have
Graph Theory. Part of Texas Counties.
 Graph Theory Part of Texas Counties. We would like to visit each of the above counties, crossing each county only once, starting from Harris county. Is this possible? This problem can be modeled as a graph.
Graph Theory Part of Texas Counties. We would like to visit each of the above counties, crossing each county only once, starting from Harris county. Is this possible? This problem can be modeled as a graph.
CIS 121 Data Structures and Algorithms Minimum Spanning Trees
 CIS 121 Data Structures and Algorithms Minimum Spanning Trees March 19, 2019 Introduction and Background Consider a very natural problem: we are given a set of locations V = {v 1, v 2,..., v n }. We want
CIS 121 Data Structures and Algorithms Minimum Spanning Trees March 19, 2019 Introduction and Background Consider a very natural problem: we are given a set of locations V = {v 1, v 2,..., v n }. We want
Shortest path problems
 Next... Shortest path problems Single-source shortest paths in weighted graphs Shortest-Path Problems Properties of Shortest Paths, Relaxation Dijkstra s Algorithm Bellman-Ford Algorithm Shortest-Paths
Next... Shortest path problems Single-source shortest paths in weighted graphs Shortest-Path Problems Properties of Shortest Paths, Relaxation Dijkstra s Algorithm Bellman-Ford Algorithm Shortest-Paths
Taking Stock. Last Time Flows. This Time Review! 1 Characterize the structure of an optimal solution
 Taking Stock IE170: Algorithms in Systems Engineering: Lecture 26 Jeff Linderoth Last Time Department of Industrial and Systems Engineering Lehigh University April 2, 2007 This Time Review! Jeff Linderoth
Taking Stock IE170: Algorithms in Systems Engineering: Lecture 26 Jeff Linderoth Last Time Department of Industrial and Systems Engineering Lehigh University April 2, 2007 This Time Review! Jeff Linderoth
LINEAR PROGRAMMING: A GEOMETRIC APPROACH. Copyright Cengage Learning. All rights reserved.
 3 LINEAR PROGRAMMING: A GEOMETRIC APPROACH Copyright Cengage Learning. All rights reserved. 3.1 Graphing Systems of Linear Inequalities in Two Variables Copyright Cengage Learning. All rights reserved.
3 LINEAR PROGRAMMING: A GEOMETRIC APPROACH Copyright Cengage Learning. All rights reserved. 3.1 Graphing Systems of Linear Inequalities in Two Variables Copyright Cengage Learning. All rights reserved.
Monday 23 January 2012 Morning
 Monday 2 January 202 Morning AS GCE MATHEMATICS (MEI) 477 Decision Mathematics QUESTION PAPER *472202* Candidates answer on the Printed Answer Book. OCR supplied materials: Printed Answer Book 477 MEI
Monday 2 January 202 Morning AS GCE MATHEMATICS (MEI) 477 Decision Mathematics QUESTION PAPER *472202* Candidates answer on the Printed Answer Book. OCR supplied materials: Printed Answer Book 477 MEI
Notes on Minimum Cuts and Modular Functions
 Notes on Minimum Cuts and Modular Functions 1 Introduction The following are my notes on Cunningham s paper [1]. Given a submodular function f and a set S, submodular minimisation is the problem of finding
Notes on Minimum Cuts and Modular Functions 1 Introduction The following are my notes on Cunningham s paper [1]. Given a submodular function f and a set S, submodular minimisation is the problem of finding
Tuesday, April 10. The Network Simplex Method for Solving the Minimum Cost Flow Problem
 . Tuesday, April The Network Simplex Method for Solving the Minimum Cost Flow Problem Quotes of the day I think that I shall never see A poem lovely as a tree. -- Joyce Kilmer Knowing trees, I understand
. Tuesday, April The Network Simplex Method for Solving the Minimum Cost Flow Problem Quotes of the day I think that I shall never see A poem lovely as a tree. -- Joyce Kilmer Knowing trees, I understand
Unit-5 Dynamic Programming 2016
 5 Dynamic programming Overview, Applications - shortest path in graph, matrix multiplication, travelling salesman problem, Fibonacci Series. 20% 12 Origin: Richard Bellman, 1957 Programming referred to
5 Dynamic programming Overview, Applications - shortest path in graph, matrix multiplication, travelling salesman problem, Fibonacci Series. 20% 12 Origin: Richard Bellman, 1957 Programming referred to
Problem 1. Which of the following is true of functions =100 +log and = + log? Problem 2. Which of the following is true of functions = 2 and =3?
 Multiple-choice Problems: Problem 1. Which of the following is true of functions =100+log and =+log? a) = b) =Ω c) =Θ d) All of the above e) None of the above Problem 2. Which of the following is true
Multiple-choice Problems: Problem 1. Which of the following is true of functions =100+log and =+log? a) = b) =Ω c) =Θ d) All of the above e) None of the above Problem 2. Which of the following is true
Introduction to Algorithms / Algorithms I Lecturer: Michael Dinitz Topic: Shortest Paths Date: 10/13/15
 600.363 Introduction to Algorithms / 600.463 Algorithms I Lecturer: Michael Dinitz Topic: Shortest Paths Date: 10/13/15 14.1 Introduction Today we re going to talk about algorithms for computing shortest
600.363 Introduction to Algorithms / 600.463 Algorithms I Lecturer: Michael Dinitz Topic: Shortest Paths Date: 10/13/15 14.1 Introduction Today we re going to talk about algorithms for computing shortest
Dynamic Programming II
 Lecture 11 Dynamic Programming II 11.1 Overview In this lecture we continue our discussion of dynamic programming, focusing on using it for a variety of path-finding problems in graphs. Topics in this
Lecture 11 Dynamic Programming II 11.1 Overview In this lecture we continue our discussion of dynamic programming, focusing on using it for a variety of path-finding problems in graphs. Topics in this
Classic Graph Theory Problems
 Classic Graph Theory Problems Hiroki Sayama sayama@binghamton.edu The Origin Königsberg bridge problem Pregel River (Solved negatively by Euler in 176) Representation in a graph Can all the seven edges
Classic Graph Theory Problems Hiroki Sayama sayama@binghamton.edu The Origin Königsberg bridge problem Pregel River (Solved negatively by Euler in 176) Representation in a graph Can all the seven edges
Introduction to Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras
 Introduction to Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Module 03 Simplex Algorithm Lecture - 03 Tabular form (Minimization) In this
Introduction to Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Module 03 Simplex Algorithm Lecture - 03 Tabular form (Minimization) In this
3x + y 50. y=10. x=15 3x+y=50. 2x + 3y = 40
 Section 3.3: Linear programming: A geometric approach In addition to constraints, linear programming problems usually involve some quantity to maximize or minimize such as profits or costs. The quantity
Section 3.3: Linear programming: A geometric approach In addition to constraints, linear programming problems usually involve some quantity to maximize or minimize such as profits or costs. The quantity
