5 Segments Properties Segment Trajectory Force Fields
|
|
|
- Neal Daniel
- 5 years ago
- Views:
Transcription
1 Neuron Developmental Modeling and Structural Representation: The Statistical Model Richard W. DeVaul Bruce H. McCormick Λ Technical Report Scientific Visualization Laboratory Department of Computer Science Texas A&M University, College Station, TX, USA June 30, 1997 Revision: 1.8 fi Contents 1 Abstract 4 2 Introduction Purpose Document Structure Properties Probability Density Functions Somata Properties Probability Density Functions Arbors Properties Probability Density Functions Λ This material is based in part on work supported by the Texas Advanced Technology Program under Grant No (McCormick) 1
2 5 Segments Properties Segment Trajectory Force Fields Properties list Probability Density Functions Spines Properties Probability Density Functions Junctions Properties Relative Angle Junction Geometry Representation Quaternion Junction Rotation Representation Hierarchical Daughter Segment Dependency Properties List Probability Density Functions Auxiliary Properties Introduction Auxiliary Property Definition Auxiliary Property Record Literature Cited 27 2
3 List of Figures 1 The discrete Frenet frame at P i, with interpolating spline Example hierarchical dependency relationships Dendritic branching with three levels of daughter dependency 21 List of Tables 1 Schematic properties Schematic probability density functions Somata properties Soma probability density functions Arbor properties Segment properties Segment probability density functions Spine properties spine probability density functions Junction properties Junction probability density functions Auxiliary Property Definition Auxiliary Property Record
4 1 Abstract This is the second in a series of papers describing a set of tools for the developmental modeling, visualization, and statistical analysis of neuron populations. Paper two covers the statistical model used by the N++ tools and the probability density functions which accompany it. The statistical model is described as a an essential set of properties describing neuron morphology, auxiliary properties which derive from the essential properties, and a simple indexed flat file" organization suitable for import into a spreadsheet or similar statistical analysis package. Probability density functions are described both in terms of the properties they relate to and the parametric statistical forms used in the N++ stochastic neuron generation process. 4
5 2 Introduction 2.1 Purpose The purpose of the statistical model is to create a framework for the description and statistical analysis of neurons and neuron populations. The statistical model specifies an indexed flat file organization suitable for import into a spreadsheet or other statistical analysis tool. The purpose of such analysis is twofold: 1. To derive probability density functions for neuron morphological properties. 2. To distinguish between different types of neurons or between variant types of neuron within an inhomogeneous neuronal population. The probability density functions for neuron properties are of interest because they allow for the statistical description of neuron properties and for the synthetic generation of neuron populations through the stochastic modeling tools of N++. Our objective here is to stochastically generate neuron populations which are visually and statistically indistinguishable in morphology from the modeled neuron database. 2.2 Document Structure This document is based on the N++ nneuron anatomical model, as described in the first paper in this series, An Introduction to the N++ Language, an Open Stochastic L-System. In this model a neuron is subdivided into a soma, one or more dendritic arbors, and one or possibly two axonal arbors. Arbors are subdivided into junctions and segments. Segments are subdivided into generalized cylinders (which will be referred to simply as segments") and spines, which are small, regularly spaced protrusions on the sides of the segment. In each of the following sections a subdivision of the neuron morphological model is described. Section 3 deals with somata, Section 4 with arbors, Section 5 with segments, Section 6 with spines, and Section 7 deals with junctions. Each section is divided into a Properties subsection and Probability Density Functions subsection. Auxiliary properties are discussed in Section 8. 5
6 Description Symbol Type Representation A position property P 1 < 3 (p 1 p 2 p 3 ) 2< 3 An orientation property P 2 Q unit (q 0 q 1 q 2 q 3 ) 2< 4 Table 1: Schematic properties Properties The term property roughly corresponds to Mulchandani's[2] morphological variable" except that a distinction is made between properties, which provide a primary or essential representation, and auxiliary properties which are derived properties. Auxiliary properties are given their own treatment in Section 8 1. The term property is also used to refer to synthetic" values (such asan ID number) which are essential to the organization of the statistical data in a flat file but which do not have a direct anatomical basis. Associated with each Properties subsection is a table summarizing the properties, a schematic representation of which is found in Table 1. Note that a distinction is made between the property and its representation. In Table 1 P 1 is a vector but its representation is as three scalar values. Likewise, P 2 is a quaternion but it is represented as four scalars. This distinction is important for representing data in a spreadsheet or other application which may not directly support data types like vectors or quaternions Probability Density Functions A probability density function describes the statistical distribution of a property. All properties meaningful to the stochastic generation of neurons have associated probability density functions. Each Probability Density Functions subsection contains a brief description of the probability density functions associated with each non-synthetic property. These are summarized in a table like Table 2. 1 In many cases there is a direct correspondence between one of Mulchandani's morphological variables and a given property, but in a few cases there are significant differences. In every case the morphological variable can be reconstructed as an auxiliary property. 6
7 Description Representation Distribution of positions p(p 1 ) Distribution of orientations, conditional on P 1 p(p 2 j P 1 ) Table 2: Schematic probability density functions 7
8 Description Symbol Type Representation cell ID ID cell I 100; 000 I soma position P soma < 3 (p 1 p 2 p 3 ) 2< 3 soma orientation O soma Q unit (q 0 q 1 q 2 q 3 ) 2< 4 soma diameter D soma < < 3 Somata 3.1 Properties Table 3: Somata properties The soma is the root of the dendritic and axonal arbors. For the purposes of the neuron morphology model the soma is a three-dimensional solid positioned and oriented in anatomical space. As such the soma has three important properties: cell ID A unique identifier which distinguishes one neuron cell from every other neuron cell in a population. Since there is only one soma per cell, this also uniquely identifies each soma. Cell ID is represented as a six digit integer counting upwards from 100,000. soma position The soma's position in anatomical (rostral lateral dorsal) space. Position is represented by a< 3 position vector. soma orientation The soma's orientation in anatomical space. The soma's orientation is represented by a unit quaternion relative to the anatomical space. soma diameter The diameter of a circle with the same cross sectional area as a 2D projection of the soma onto the sagittal plane. Soma diameter is represented as a real number. These properties are summarized in Table Probability Density Functions In order to statistically model somata the following probability density functions are necessary: ffl p(p soma ) A probability density function for the position of somata in anatomical space. 8
9 Description Representation distribution of soma positions p(p soma ) distribution of soma orientations p(o soma j P soma ) distribution of soma diameters p(d soma j P soma ) Table 4: Soma probability density functions ffl p(o soma j P soma ) A probability density function for the orientation of somata in anatomical space, conditional on soma position. ffl p(d soma j P soma ) A probability density function for the diameter of somata, conditional on soma position. These are summarized in Table 4. 9
10 Description Symbol Type Representation arbor ID ID arbor I 1 I cell ID ID cell I 100; 000 I arbor type T fdendritic; axonalg fdendritic; axonalg number of segments N seg I 1 I number of junctions N junction I 1 I arbor depth D I 1 I 4 Arbors 4.1 Properties Table 5: Arbor properties An arbor is a collection of dendritic or axonal segments which share a common predecessor segment. Arbors have the following properties: arbor ID An identifier which distinguishes one arbor from every other arbor belonging to the same cell. This is represented as an integer value counting upwards from 1. cell ID The identifier of the neuron to which the arbor belongs. arbor type A symbolic designator for the type of arbor, s 2fdendritic; axonalg. number of segments The number of segments in the arbor. number of junctions The number of junctions in the arbor. arbor depth The maximum junction order of the arbor. The root Soma Arbor junction is order 0. These properties are summarized in Table Probability Density Functions None. 10
11 5 Segments 5.1 Properties Segments are modeled as a trajectory in space and a diameter which may change as a function of length. Empirically measured segment trajectory data is usually in the form of a series of sampled points, which mayormay not be regularly spaced. For the purposes of statistical modeling such data is re-sampled at a user-specified resolution. This results in a set of uniformly spaced data points representing the segment trajectory. The sampled data points are referred to as P i ; 1» i» n. By linearly interpolating between these points, a piecewise linear representation of the trajectory may be constructed. Each linear portion of the piecewise trajectory is referred to as a section, and is defined as: Segment Trajectory s i = P i+1 P i j 1» i<n (1) The Frenet Frame To statistically model the segment trajectory, it is useful to introduce the Frenet frame of the trajectory at each sampled data point P i j 1» i<n. The Frenet frame of a parametric curve x = f(s); x 2 < 3 provides a local frame of reference defined by the direction and curvature of f at s. The Frenet frame is defined as the triplet of orthonormal vectors (t mb) t = _x k _xk ; m = b ^ t; b = _x ^ ẍ (2) k _x ^ ẍk where _x is the first derivative of x with respect to s, and ẍ is the second derivative of x with respect to s, and both of these derivatives exist and are non-zero[1, 2]. The Discrete Frenet Frame Since sampled data points themselves are not a continuous curve, it is necessary to use other information to approximate the true Frenet frame at a sampled data point. One way of doing this would be to refer to the Frenet frame of an interpolating spline constructed through the data points. However, this would require the use of a C2 continuous interpolating spline so that the required derivatives exist. There is no a priori reason to believe that real segment trajectories are C2 continuous. Further, the curvature of an interpolating spline depends on anumber of factors other than the data points. Thus it is desirable to find 11
12 b t P i m S i S i-1 Figure 1: The discrete Frenet frame at P i, with interpolating spline. a representation which approximates the true Frenet frame of the trajectory but is discrete and depends only on the sampled data points. To accomplish this, the discrete Frenet frame (Figure 1) at P i j 1 <i<n is defined as: t = s i 1 + s i ks i 1 + s i k ; m = b t; b = s i s i 1 ks i s i 1 k (3) For the special case of P 1 the discrete Frenet frame is defined as: t = RF t + s 1 ;m= b t; b = s krf t + s 1 k 1 RF t ks 1 RF t k (4) where RF t is the t vector of the initial segment reference frame. A succession of discrete Frenet frames may be described in terms of a series of rotations of the initial segment coordinate frame. A Continuous Reconstruction A continuous reconstruction of the segment trajectory may occasionally be useful for resampling or visualization. Using an interpolating spline with a Catmull-Rom interpolant results in curvature at the control points which matches the discrete Frenet frame at that point. 12
13 Description Symbol Type Representation segment ID ID segment I 200; 000 I cell ID ID cell I 100; 000 I arbor ID ID arbor I 1 I segment type t fnonterminal ; terminal g fnonterminal ; terminal g parent junction ID ID j0 I 300; 000 I daughter junction ID ID j1 I 300; 000 I initial diameter d i < > 0 < initial taper d 0 i < > 0 < final diameter d f < > 0 < final taper d 0 f < > 0 < diameter interpolation method I method flinear ; Hermiteg flinear ; Hermiteg segment arc length l arc < > 0 < segment electrotonic length l e < > 0 < total rotation R total Q unit (q 0 q 1 q 2 q 3 ) 2< 4 number of sampled data points n I 2 I sampling interval l s L arc l s > 0 < trajectory T (P 1 P 2 ::: P n ) P i =(p i0 p i1 p i2 ) 2< 3 discrete Frenet frames D (Q P1 Q P2 ::: Q Pn ) Q P i =(q Pi0 q Pi1 q Pi2 q ) Pi3 2<4 segment growth force field rffi ( rffi P1 rffi P2 ::: rffi Pn ) rffi P Table 6: ) 2< Force Fields To model the growth of neuron segments it is necessary to take into account the effects of chemical force fields" which attract or repel the neuron growth cone. The statistical model assumes that such a field can be approximated as a constant gradient with respect to the growth of a single section, but can vary over the length of the segment. The further assumption is that the field effects segment growth by applying a torque to the Frenet frame of the growth tip equal to the cross product of the t vector and the gradient. The presence of such a field is therefor detectable through analysis of the discrete Frenet frame data Properties list Segments have the following properties: segment ID A unique identifier which distinguishes one segment from ev- 13
14 ery other segment in a neuron. Segment ID is represented as a six digit integer counting upwards from 200,000. cell ID The identifier of the cell in which the segment resides. arbor ID The identifier of the arbor in which the segment resides. segment type There are two types of segments, nonterminal and terminal. Nonterminal segments have daughter junctions; terminal segments do not. parent junction ID The identifier of the parent junction of the segment. daughter junction ID The identifier of the daughter junction of the segment. initial diameter The initial diameter of the segment. initial taper The negative slope of the diameter as a function of length at the beginning of the segment. This is used as the initial tangent for cubic Hermitian diameter interpolation. final diameter The final diameter of the segment. final taper The negative slope of the diameter as a function of length at the end of the segment. This is used as the final tangent for cubic Hermitian diameter interpolation. diameter interpolation method The method used to interpolate between the initial and final diameter. The choices are linear and hermite. segment arc length The path length of the trajectory of segment. segment electrotonic length The electrotonic length of the segment. total rotation The rotation of the final reference frame of the trajectory with respect to the initial reference frame, i.e. RF initial ) RF final number of sampled data points The number of data points in the trajectory. sampling interval The sampling interval for the data points. 14
15 Description Representation Distribution of nonterminal segments p(t) Distribution of initial segment diameter p(d i ) Distribution of initial segment taper p( d 0 i ) Distribution of final segment diameter p(d f ) Distribution of final segment taper p( d 0 f ) Distribution of segment arc length p(l arc ) Distribution of segment electrotonic length p(l e j l arc j d i j d f ) Distribution of successive discrete Frenet frame rotations p(q P ) Distribution of segment growth force field p( rffi) Table 7: Segment probability density functions trajectory A sequence of sampled data points representing the segment trajectory. These are < 3 vectors relative to the initial reference frame of the segment. discrete Frenet frames The discrete Frenet frames at points P i j 1» i» n expressed as a series of successive rotations of the initial segment reference frame. segment growth force field The negative gradient of the chemical concentration effecting the growth of the segment, as measured at each sampled data point. These properties are summarized in Table Probability Density Functions A segment may be statistically modeled using the following probability density functions: ffl p(t) A probability density function for the distribution of nonterminal segments. ffl p(d i ) A probability density function for the distribution of initial segment diameter. ffl p( d 0 i ) A probability density function for the distribution of initial segment taper. 15
16 ffl p(d f ) A probability density function for the distribution of final segment diameter. ffl p( d 0 f ) A probability density function for the distribution of final segment taper. ffl p(l arc ) A probability density function for the distribution of segment arc length. ffl p(l e ) A probability density function for the distribution of segment electrotonic length. It is assumed that electrotonic length can be computed from l arc, d i, and d f, and for segments adjacent to the soma, additionally from d 0 i and d0 f. ffl p(q P ) A probability density function for the distribution of successive discrete Frenet frame rotations independent of segment growth force field. ffl p( rffi) A probability density function for the distribution of segment growth force field. These probability density functions are summarized in Table 7. 16
17 Description Symbol Type Representation segment ID ID segment I 200; 000 I cell ID ID cell I 100; 000 I number of spines n spine I 0 I spine distances d spines (d 1 d 2 ::: d nspine ) d i 2< spine rotations spines ( 1 2 ::: nspine ) i 2< 6 Spines 6.1 Properties Table 8: Spine properties Spines are small protrusions found on the sides of segments. The precise measurement of individual spines is difficult and time consuming given their small scale these structures are barely visible at the limit of optical resolution. However, an attempt must be made to accurately measure the position and orientation of individual spines on at least some segments for statistical modeling purposes. Spines have the following properties: segment ID The ID of the segment being described. cell ID The identifier of the cell in which the segment resides. number of spines The observed number of spines on the segment. spine distances A list of the distances of each spine from the parent junction. spine rotations A list of the rotations of each spine (in radians) relative to the b vector of the Frenet frame. These properties are summarized in Table Probability Density Functions Spines may be statistically modeled using the following probability density functions: ffl p(n spine j l arc ) a probability density function for the distribution of the number of spines, conditional on segment length. 17
18 Description Representation Distribution of number of spines p(n spine j l arc ) Distribution of spine distances p(d spines j n spine j l arc ) Distribution of spine rotations p( spines ) Table 9: spine probability density functions ffl p(d spines ) a probability density function for the distribution of the distance of spines from the segment junction. ffl p( spines ) a probability density function for the distribution of spine rotations relative to the b vector of the local Frenet frame. These probability density functions are summarized in Table 9. 18
19 7 Junctions 7.1 Properties A junction is a branch point in an axon or dendrite. A single segment, referred to as the parent, branches into two or more daughter segments. In the case where there are two daughter segments the junction is termed a bifurcation, otherwise it is called a multifurcation. The statistical model directly accommodates bifurcations and multifurcations of three daughter segments. For multifurcations of more than three daughter segments, additional junctions may be used. Junctions are defined by the intersection of parent and daughter segments. The parent segment is referred to as S 0 and the daughter segments as S 1 :::S n ; n 2f2; 3g. Daughter segments are designated S 1, S 2, etc. in order of decreasing diameter, unless dependency relationships dictate otherwise (see below) Relative Angle Junction Geometry Representation Mulchandani[2] describes bifurcation junction geometry in terms of three relative angles ( 01, 02, and 12 ) and a chirility factor which indicates the handedness" of the structure. Unfortunately this is adequate only for a bifurcation. For a trifurcation the number of relative angles needed increases to six ( 01, 02, 03, 12, 13, and 23.) Further, an additional twist" angle must be calculated for each daughter segment trajectory to orient the initial reference frame of the daughter segment Quaternion Junction Rotation Representation The relative angle representation treats the junction as a rigid body. More generally, the neuron morphology model treats the junction as a set of branching trajectories, each with its own reference frame. This means that the initial trajectory of each S i ; 1» i» n may be described in terms of a rotation of the final trajectory reference frame of S 0. This junction rotation may be conveniently represented as a unit quaternion q i. The quaternion representation has several advantages: 1. A quaternion completely specifies the initial reference frame of a daughter segment trajectory. Additional factors such as chirility and twist" are derived attributes. 19
20 S 0 final A S S S 1initial 2initial 3initial S 0 final S 0 final B S 1initial C S 1initial S 2initial S 2initial S 3initial S 3initial Figure 2: Example hierarchical dependency relationships 2. The quaternion representation allows junction branch angles to be easily decoupled or made dependent. (See below.) 3. The quaternion representation supports the neuron morphology model paradigm of treating junctions as branching segment trajectories, each with its own coordinate frame. This paradigm is not supported by using relative angles. 4. Figuring out twist" angles in the relative angle approach requires analyzing a junction in terms of segment trajectories and reference frames anyway. Thus, no work is saved by using this representation Hierarchical Daughter Segment Dependency In the simplest case the initial frame of reference and the trajectory of daughter segment S n depends only on the final reference frame of S 0. In other words, the initial trajectories of all daughter segments are influenced only by the final trajectory of the parent. There is no a priori reason to believe that this is true in every case; it is possible that the initial trajectory of daughter segments could influence each other. Leaving aside the problem of detecting such influences, it is possible to represent this kind of complex trajectory dependency in the statistical model through hierarchical daughter dependency relationships. 20
21 S 1 S3 S 0 Junction S 2 Figure 3: Dendritic branching with three levels of daughter dependency Figure 2 graphically represents three possible dependency relationships. In A, all daughter segments depend only on the parent segment the simplest case. The junction rotations of each daughter segment are specified relative to the final reference frame of S 0. In B, the initial trajectory (junction rotation) of daughter segment S 2 depends on the junction rotation of daughter segment S 1, which in turn depends on the final trajectory of S 0. The dependency relationship in C is a three level hierarchy, and is geometrically illustrated in Figure Properties List A junction has the following properties: junction ID Junction ID is a unique identifier which distinguishes one junction from every other junction in a neuron. Junction ID is represented as a six digit integer counting upwards from 300,000. cell ID The identifier of the cell in which the junction resides. arbor ID The identifier of the arbor in which the junction resides. junction order The order of the junction. path length The total length of the shortest path from the branch point of the junction back to the root of the arbor. electrotonic path length The total electrotonic length of the shortest path from the branch point of the junction back to the root of the arbor. 21
22 Description Symbol Type Representation junction ID ID junction I 300; 000 I cell ID ID cell I 100; 000 I arbor ID ID arbor I 1 I junction order O I 1 I path length l path < > 0 < electrotonic path length l e < > 0 < number of segments N seg f3,4g I parent segment ID ID S0 I 200; 000 I S 1 ID ID S1 I 200; 000 I S 2 ID ID S2 I 200; 000 I S 3 ID ID S3 I 200; 000 I S 1 rotation dependency D S1 f0g I S 2 rotation dependency D S2 f0; 1g I S 3 rotation dependency D S3 f0; 1; 2g I S 1 junction rotation R S1 Q unit (q 0 q 1 q 2 q 3 ) 2< 4 S 2 junction rotation R S2 Q unit (q 0 q 1 q 2 q 3 ) 2< 4 S 3 junction rotation R S3 Q unit (q 0 q 1 q 2 q 3 ) 2< 4 Table 10: Junction properties 22
23 Description Representation Distribution of S 1 junction rotations. p(r S1 ) Distribution of S 2 dependencies. p(d S2 ) Distribution of S 2 junction rotations dependent ons 0. p(r S2 jd S2 =0) Distribution of S 2 junction rotations dependent ons 1. p(r S2 jd S2 =1) Distribution of S 3 dependencies. p(d S2 ) Distribution of S 3 junction rotations dependent ons 0. p(r S3 jd S3 =0) Distribution of S 3 junction rotations dependent ons 1. p(r S3 jd S3 =1) Distribution of S 3 junction rotations dependent ons 2. p(r S3 jd S3 =2) Table 11: Junction probability density functions number of segments The number of segments intersecting at the junction. parent ID The identifier of the S 0 (parent) segment. S i ID Three segment identifiers corresponding to daughter segments S 1, S 2, and S 3. For a bifurcation only S 1 and S 2 will be non-zero. S i rotation dependency Three dependency identifiers designating the rotation dependencies of the daughter segments S 1, S 2, and S 3 respectively. S i junction rotation Three rotations specified as unit quaternions representing the junction rotations of the daughter segments S 1, S 2, and S 3 respectively. These properties are summarized in Table Probability Density Functions The probability density functions which govern the junction all relate to the initial junction rotation and hierarchical dependency relationships of the daughter segments. Separate probability density functions for junction rotation are specified for each daughter segment dependency case. A junction may be statistically modeled using the following probability density functions: ffl p(r S1 ) A probability density function for the junction rotation of S 1. By definition, S 1 always depends on S 0. 23
24 ffl p(d S2 ) A probability density function for the dependency of the junction rotation of S 2. Segment S 2 may depend on either the parent or the first daughter segment. ffl p(r S2 jd S2 = 0) A probability density function for the junction rotation of S 2 when S 2 depends on S 0. ffl p(r S2 jd S2 = 1) A probability density function for the junction rotation of S 2 when S 2 depends on S 1. ffl p(d S3 ) A probability density function for the dependency of the junction rotation of S 3. Segment S 3 may depend on either the parent, the first, or the second daughter segment. ffl p(r S3 jd S3 = 0) A probability density function for the junction rotation of S 3 when S 3 depends on S 0. ffl p(r S3 jd S3 = 1) A probability density function for the junction rotation of S 3 when S 3 depends on S 1. ffl p(r S3 jd S3 = 2) A probability density function for the junction rotation of S 3 when S 3 depends on S 2. These probability density functions are summarized in Table
25 Description Type Representation auxiliary property name [A:::Z a:::z] n text string auxiliary property type fsoma arbor segment spine junctiong fsoma arbor segment spine junctiong auxiliary property description descriptive text text string Table 12: Auxiliary Property Definition 8 Auxiliary Properties 8.1 Introduction Auxiliary properties provide an alternate or elaborated representation of neuron morphology. An auxiliary property derives from one or more of the fundamental properties of a morphological element. On example of an auxiliary property is the Mulchandani relative angle representation for junction geometry. There are two components to the N++ aauxiliary property framework: an auxiliary property definition, and zero or more auxiliary property records. The auxiliary property definition provides a label for the auxiliary property and a description of how the property is calculated. An auxiliary property record is a individual instance of an auxiliary property. 8.2 Auxiliary Property Definition In the flat file representation, auxiliary property definitions are placed after all other data except auxiliary property records. An auxiliary property definition is composed of the following elements: auxiliary property name A unique text string identifying the property. This string is composed of the letters A Z and a z. auxiliary property type The type of morphology to which this auxiliary property relates. auxiliary property description A text string describing the property. This description could take the form of a symbolic expression or descriptive text. If a symbolic expression is used it should be humanreadable, since the N++ model does not specify a standard for parsing such expressions and a data-set may be evaluated in a wide range of software applications. The auxiliary property definition is summarized in Table
26 Description Symbol Type Representation record ID ID record I 400; 000 I cell ID ID cell I 100; 000 I arbor ID ID arbor I 1 I segment ID ID segment I 200; 000 I junction ID ID junction I 300; 000 I property X record any text string Table 13: Auxiliary Property Record 8.3 Auxiliary Property Record An auxiliary property record is an instance of an auxiliary property which refers to a particular soma, arbor, segment, or junction. In the flat file representation, auxiliary property records are placed after all auxiliary property definitions. An auxiliary property record is composed of the following elements: record ID A unique identifier which distinguishes this auxiliary property record from every other auxiliary property record in the flat file. Record ID is represented as a six digit number counting upwards from 400,000. record type The type of auxiliary property record. This string must match a defined auxiliary property name. cell ID The ID of the neuron to which the auxiliary property record refers. arbor ID The identifier of the arbor to which the auxiliary property record refers, if relevant. Zero otherwise. segment ID The identifier of the segment to which the auxiliary property refers, if appropriate. Zero otherwise. junction ID The identifier of the junction to which the auxiliary property refers, if appropriate. Zero otherwise. property A text string representation of the value of the auxiliary property. The use of a text string representation allows the greatest flexibility for the contents of this field. 26
27 9 Literature Cited References [1] G. Farin. Curves and Surfaces for Computer-Aided Geometric Design: A Practical Guide. Academic Press, San Diego, 4th edition, [2] K. Mulchandani. Morphological modeling of neurons. Master's thesis, Texas A&M University, College Station, TX,
Central issues in modelling
 Central issues in modelling Construct families of curves, surfaces and volumes that can represent common objects usefully; are easy to interact with; interaction includes: manual modelling; fitting to
Central issues in modelling Construct families of curves, surfaces and volumes that can represent common objects usefully; are easy to interact with; interaction includes: manual modelling; fitting to
Neurolucida v1.4 to Matlab v6.0 Converter
 Neurolucida v1. to Matlab v6.0 Converter February 1, 200 Convert.m reads the ASCII data produced by Neurolucida and outputs arrays and vectors of the imaged cell s information for later use by the algorithum.
Neurolucida v1. to Matlab v6.0 Converter February 1, 200 Convert.m reads the ASCII data produced by Neurolucida and outputs arrays and vectors of the imaged cell s information for later use by the algorithum.
3.3 Interpolation of rotations represented by quaternions
 3 S 3.3 Interpolation of rotations represented by quaternions : set of unit quaternions ; S :set of unit 3D vectors Interpolation will be performed on 3 S (direct linear interpolation produces nonlinear
3 S 3.3 Interpolation of rotations represented by quaternions : set of unit quaternions ; S :set of unit 3D vectors Interpolation will be performed on 3 S (direct linear interpolation produces nonlinear
Flank Millable Surface Design with Conical and Barrel Tools
 461 Computer-Aided Design and Applications 2008 CAD Solutions, LLC http://www.cadanda.com Flank Millable Surface Design with Conical and Barrel Tools Chenggang Li 1, Sanjeev Bedi 2 and Stephen Mann 3 1
461 Computer-Aided Design and Applications 2008 CAD Solutions, LLC http://www.cadanda.com Flank Millable Surface Design with Conical and Barrel Tools Chenggang Li 1, Sanjeev Bedi 2 and Stephen Mann 3 1
Mathematically, the path or the trajectory of a particle moving in space in described by a function of time.
 Module 15 : Vector fields, Gradient, Divergence and Curl Lecture 45 : Curves in space [Section 45.1] Objectives In this section you will learn the following : Concept of curve in space. Parametrization
Module 15 : Vector fields, Gradient, Divergence and Curl Lecture 45 : Curves in space [Section 45.1] Objectives In this section you will learn the following : Concept of curve in space. Parametrization
Computer Graphics Curves and Surfaces. Matthias Teschner
 Computer Graphics Curves and Surfaces Matthias Teschner Outline Introduction Polynomial curves Bézier curves Matrix notation Curve subdivision Differential curve properties Piecewise polynomial curves
Computer Graphics Curves and Surfaces Matthias Teschner Outline Introduction Polynomial curves Bézier curves Matrix notation Curve subdivision Differential curve properties Piecewise polynomial curves
Know it. Control points. B Spline surfaces. Implicit surfaces
 Know it 15 B Spline Cur 14 13 12 11 Parametric curves Catmull clark subdivision Parametric surfaces Interpolating curves 10 9 8 7 6 5 4 3 2 Control points B Spline surfaces Implicit surfaces Bezier surfaces
Know it 15 B Spline Cur 14 13 12 11 Parametric curves Catmull clark subdivision Parametric surfaces Interpolating curves 10 9 8 7 6 5 4 3 2 Control points B Spline surfaces Implicit surfaces Bezier surfaces
Freeform Curves on Spheres of Arbitrary Dimension
 Freeform Curves on Spheres of Arbitrary Dimension Scott Schaefer and Ron Goldman Rice University 6100 Main St. Houston, TX 77005 sschaefe@rice.edu and rng@rice.edu Abstract Recursive evaluation procedures
Freeform Curves on Spheres of Arbitrary Dimension Scott Schaefer and Ron Goldman Rice University 6100 Main St. Houston, TX 77005 sschaefe@rice.edu and rng@rice.edu Abstract Recursive evaluation procedures
Curve Representation ME761A Instructor in Charge Prof. J. Ramkumar Department of Mechanical Engineering, IIT Kanpur
 Curve Representation ME761A Instructor in Charge Prof. J. Ramkumar Department of Mechanical Engineering, IIT Kanpur Email: jrkumar@iitk.ac.in Curve representation 1. Wireframe models There are three types
Curve Representation ME761A Instructor in Charge Prof. J. Ramkumar Department of Mechanical Engineering, IIT Kanpur Email: jrkumar@iitk.ac.in Curve representation 1. Wireframe models There are three types
Curves D.A. Forsyth, with slides from John Hart
 Curves D.A. Forsyth, with slides from John Hart Central issues in modelling Construct families of curves, surfaces and volumes that can represent common objects usefully; are easy to interact with; interaction
Curves D.A. Forsyth, with slides from John Hart Central issues in modelling Construct families of curves, surfaces and volumes that can represent common objects usefully; are easy to interact with; interaction
2D Spline Curves. CS 4620 Lecture 18
 2D Spline Curves CS 4620 Lecture 18 2014 Steve Marschner 1 Motivation: smoothness In many applications we need smooth shapes that is, without discontinuities So far we can make things with corners (lines,
2D Spline Curves CS 4620 Lecture 18 2014 Steve Marschner 1 Motivation: smoothness In many applications we need smooth shapes that is, without discontinuities So far we can make things with corners (lines,
Geometric and Solid Modeling. Problems
 Geometric and Solid Modeling Problems Define a Solid Define Representation Schemes Devise Data Structures Construct Solids Page 1 Mathematical Models Points Curves Surfaces Solids A shape is a set of Points
Geometric and Solid Modeling Problems Define a Solid Define Representation Schemes Devise Data Structures Construct Solids Page 1 Mathematical Models Points Curves Surfaces Solids A shape is a set of Points
COMPUTER AIDED ENGINEERING DESIGN (BFF2612)
 COMPUTER AIDED ENGINEERING DESIGN (BFF2612) BASIC MATHEMATICAL CONCEPTS IN CAED by Dr. Mohd Nizar Mhd Razali Faculty of Manufacturing Engineering mnizar@ump.edu.my COORDINATE SYSTEM y+ y+ z+ z+ x+ RIGHT
COMPUTER AIDED ENGINEERING DESIGN (BFF2612) BASIC MATHEMATICAL CONCEPTS IN CAED by Dr. Mohd Nizar Mhd Razali Faculty of Manufacturing Engineering mnizar@ump.edu.my COORDINATE SYSTEM y+ y+ z+ z+ x+ RIGHT
Visual Recognition: Image Formation
 Visual Recognition: Image Formation Raquel Urtasun TTI Chicago Jan 5, 2012 Raquel Urtasun (TTI-C) Visual Recognition Jan 5, 2012 1 / 61 Today s lecture... Fundamentals of image formation You should know
Visual Recognition: Image Formation Raquel Urtasun TTI Chicago Jan 5, 2012 Raquel Urtasun (TTI-C) Visual Recognition Jan 5, 2012 1 / 61 Today s lecture... Fundamentals of image formation You should know
Ohio Tutorials are designed specifically for the Ohio Learning Standards to prepare students for the Ohio State Tests and end-ofcourse
 Tutorial Outline Ohio Tutorials are designed specifically for the Ohio Learning Standards to prepare students for the Ohio State Tests and end-ofcourse exams. Math Tutorials offer targeted instruction,
Tutorial Outline Ohio Tutorials are designed specifically for the Ohio Learning Standards to prepare students for the Ohio State Tests and end-ofcourse exams. Math Tutorials offer targeted instruction,
Inventor 201. Work Planes, Features & Constraints: Advanced part features and constraints
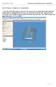 Work Planes, Features & Constraints: 1. Select the Work Plane feature tool, move the cursor to the rim of the base so that inside and outside edges are highlighted and click once on the bottom rim of the
Work Planes, Features & Constraints: 1. Select the Work Plane feature tool, move the cursor to the rim of the base so that inside and outside edges are highlighted and click once on the bottom rim of the
Using Isosurface Methods for Visualizing the Envelope of a Swept Trivariate Solid
 Using Isosurface Methods for Visualizing the Envelope of a Swept Trivariate Solid Jason Conkey Kenneth I. Joy Center for Image Processing and Integrated Computing Department of Computer Science University
Using Isosurface Methods for Visualizing the Envelope of a Swept Trivariate Solid Jason Conkey Kenneth I. Joy Center for Image Processing and Integrated Computing Department of Computer Science University
Lecture 2.2 Cubic Splines
 Lecture. Cubic Splines Cubic Spline The equation for a single parametric cubic spline segment is given by 4 i t Bit t t t i (..) where t and t are the parameter values at the beginning and end of the segment.
Lecture. Cubic Splines Cubic Spline The equation for a single parametric cubic spline segment is given by 4 i t Bit t t t i (..) where t and t are the parameter values at the beginning and end of the segment.
For each question, indicate whether the statement is true or false by circling T or F, respectively.
 True/False For each question, indicate whether the statement is true or false by circling T or F, respectively. 1. (T/F) Rasterization occurs before vertex transformation in the graphics pipeline. 2. (T/F)
True/False For each question, indicate whether the statement is true or false by circling T or F, respectively. 1. (T/F) Rasterization occurs before vertex transformation in the graphics pipeline. 2. (T/F)
Optimization of a two-link Robotic Manipulator
 Optimization of a two-link Robotic Manipulator Zachary Renwick, Yalım Yıldırım April 22, 2016 Abstract Although robots are used in many processes in research and industry, they are generally not customized
Optimization of a two-link Robotic Manipulator Zachary Renwick, Yalım Yıldırım April 22, 2016 Abstract Although robots are used in many processes in research and industry, they are generally not customized
3 Identify shapes as two-dimensional (lying in a plane, flat ) or three-dimensional ( solid ).
 Geometry Kindergarten Identify and describe shapes (squares, circles, triangles, rectangles, hexagons, cubes, cones, cylinders, and spheres). 1 Describe objects in the environment using names of shapes,
Geometry Kindergarten Identify and describe shapes (squares, circles, triangles, rectangles, hexagons, cubes, cones, cylinders, and spheres). 1 Describe objects in the environment using names of shapes,
Geometric Modeling of Curves
 Curves Locus of a point moving with one degree of freedom Locus of a one-dimensional parameter family of point Mathematically defined using: Explicit equations Implicit equations Parametric equations (Hermite,
Curves Locus of a point moving with one degree of freedom Locus of a one-dimensional parameter family of point Mathematically defined using: Explicit equations Implicit equations Parametric equations (Hermite,
Shape modeling Modeling technique Shape representation! 3D Graphics Modeling Techniques
 D Graphics http://chamilo2.grenet.fr/inp/courses/ensimag4mmgd6/ Shape Modeling technique Shape representation! Part : Basic techniques. Projective rendering pipeline 2. Procedural Modeling techniques Shape
D Graphics http://chamilo2.grenet.fr/inp/courses/ensimag4mmgd6/ Shape Modeling technique Shape representation! Part : Basic techniques. Projective rendering pipeline 2. Procedural Modeling techniques Shape
Computer Animation. Rick Parent
 Algorithms and Techniques Interpolating Values Animation Animator specified interpolation key frame Algorithmically controlled Physics-based Behavioral Data-driven motion capture Motivation Common problem:
Algorithms and Techniques Interpolating Values Animation Animator specified interpolation key frame Algorithmically controlled Physics-based Behavioral Data-driven motion capture Motivation Common problem:
Guidelines for proper use of Plate elements
 Guidelines for proper use of Plate elements In structural analysis using finite element method, the analysis model is created by dividing the entire structure into finite elements. This procedure is known
Guidelines for proper use of Plate elements In structural analysis using finite element method, the analysis model is created by dividing the entire structure into finite elements. This procedure is known
ALGEBRA II A CURRICULUM OUTLINE
 ALGEBRA II A CURRICULUM OUTLINE 2013-2014 OVERVIEW: 1. Linear Equations and Inequalities 2. Polynomial Expressions and Equations 3. Rational Expressions and Equations 4. Radical Expressions and Equations
ALGEBRA II A CURRICULUM OUTLINE 2013-2014 OVERVIEW: 1. Linear Equations and Inequalities 2. Polynomial Expressions and Equations 3. Rational Expressions and Equations 4. Radical Expressions and Equations
Geometric Modeling Mortenson Chapter 11. Complex Model Construction
 Geometric Modeling 91.580.201 Mortenson Chapter 11 Complex Model Construction Topics Topology of Models Connectivity and other intrinsic properties Graph-Based Models Emphasize topological structure Boolean
Geometric Modeling 91.580.201 Mortenson Chapter 11 Complex Model Construction Topics Topology of Models Connectivity and other intrinsic properties Graph-Based Models Emphasize topological structure Boolean
Shape Modeling and Geometry Processing
 252-0538-00L, Spring 2018 Shape Modeling and Geometry Processing Discrete Differential Geometry Differential Geometry Motivation Formalize geometric properties of shapes Roi Poranne # 2 Differential Geometry
252-0538-00L, Spring 2018 Shape Modeling and Geometry Processing Discrete Differential Geometry Differential Geometry Motivation Formalize geometric properties of shapes Roi Poranne # 2 Differential Geometry
Almost Curvature Continuous Fitting of B-Spline Surfaces
 Journal for Geometry and Graphics Volume 2 (1998), No. 1, 33 43 Almost Curvature Continuous Fitting of B-Spline Surfaces Márta Szilvási-Nagy Department of Geometry, Mathematical Institute, Technical University
Journal for Geometry and Graphics Volume 2 (1998), No. 1, 33 43 Almost Curvature Continuous Fitting of B-Spline Surfaces Márta Szilvási-Nagy Department of Geometry, Mathematical Institute, Technical University
(Discrete) Differential Geometry
 (Discrete) Differential Geometry Motivation Understand the structure of the surface Properties: smoothness, curviness, important directions How to modify the surface to change these properties What properties
(Discrete) Differential Geometry Motivation Understand the structure of the surface Properties: smoothness, curviness, important directions How to modify the surface to change these properties What properties
A Continuous 3-D Medial Shape Model with Branching
 A Continuous 3-D Medial Shape Model with Branching Timothy B. Terriberry Guido Gerig Outline Introduction The Generic 3-D Medial Axis Review of Subdivision Surfaces Boundary Reconstruction Edge Curves
A Continuous 3-D Medial Shape Model with Branching Timothy B. Terriberry Guido Gerig Outline Introduction The Generic 3-D Medial Axis Review of Subdivision Surfaces Boundary Reconstruction Edge Curves
Design considerations
 Curves Design considerations local control of shape design each segment independently smoothness and continuity ability to evaluate derivatives stability small change in input leads to small change in
Curves Design considerations local control of shape design each segment independently smoothness and continuity ability to evaluate derivatives stability small change in input leads to small change in
Sung-Eui Yoon ( 윤성의 )
 CS480: Computer Graphics Curves and Surfaces Sung-Eui Yoon ( 윤성의 ) Course URL: http://jupiter.kaist.ac.kr/~sungeui/cg Today s Topics Surface representations Smooth curves Subdivision 2 Smooth Curves and
CS480: Computer Graphics Curves and Surfaces Sung-Eui Yoon ( 윤성의 ) Course URL: http://jupiter.kaist.ac.kr/~sungeui/cg Today s Topics Surface representations Smooth curves Subdivision 2 Smooth Curves and
From curves to surfaces. Parametric surfaces and solid modeling. Extrusions. Surfaces of revolution. So far have discussed spline curves in 2D
 From curves to surfaces Parametric surfaces and solid modeling CS 465 Lecture 12 2007 Doug James & Steve Marschner 1 So far have discussed spline curves in 2D it turns out that this already provides of
From curves to surfaces Parametric surfaces and solid modeling CS 465 Lecture 12 2007 Doug James & Steve Marschner 1 So far have discussed spline curves in 2D it turns out that this already provides of
Bellman s Escape Problem for Convex Polygons
 Bellman s Escape Problem for Convex Polygons Philip Gibbs philegibbs@gmail.com Abstract: Bellman s challenge to find the shortest path to escape from a forest of known shape is notoriously difficult. Apart
Bellman s Escape Problem for Convex Polygons Philip Gibbs philegibbs@gmail.com Abstract: Bellman s challenge to find the shortest path to escape from a forest of known shape is notoriously difficult. Apart
Scheme of Work Form 4 (Scheme A)
 Scheme of Work Form 4 (Scheme A) Topic A revision of number work Directed Numbers Content Factors and Multiples Expressing a number as a product of prime factors LCM and HCF Objectives - Core and Paper
Scheme of Work Form 4 (Scheme A) Topic A revision of number work Directed Numbers Content Factors and Multiples Expressing a number as a product of prime factors LCM and HCF Objectives - Core and Paper
KS4 3 Year scheme of Work Year 10 Higher
 KS4 3 Year scheme of Work Year 10 Higher Review: Equations A2 Substitute numerical values into formulae and expressions, including scientific formulae unfamiliar formulae will be given in the question
KS4 3 Year scheme of Work Year 10 Higher Review: Equations A2 Substitute numerical values into formulae and expressions, including scientific formulae unfamiliar formulae will be given in the question
Motivation. Parametric Curves (later Surfaces) Outline. Tangents, Normals, Binormals. Arclength. Advanced Computer Graphics (Fall 2010)
 Advanced Computer Graphics (Fall 2010) CS 283, Lecture 19: Basic Geometric Concepts and Rotations Ravi Ramamoorthi http://inst.eecs.berkeley.edu/~cs283/fa10 Motivation Moving from rendering to simulation,
Advanced Computer Graphics (Fall 2010) CS 283, Lecture 19: Basic Geometric Concepts and Rotations Ravi Ramamoorthi http://inst.eecs.berkeley.edu/~cs283/fa10 Motivation Moving from rendering to simulation,
VALLIAMMAI ENGINEERING COLLEGE
 VALLIAMMAI ENGINEERING COLLEGE SRM Nagar, Kattankulathur 603 203 DEPARTMENT OF MECHANICAL ENGINEERING QUESTION BANK M.E: CAD/CAM I SEMESTER ED5151 COMPUTER APPLICATIONS IN DESIGN Regulation 2017 Academic
VALLIAMMAI ENGINEERING COLLEGE SRM Nagar, Kattankulathur 603 203 DEPARTMENT OF MECHANICAL ENGINEERING QUESTION BANK M.E: CAD/CAM I SEMESTER ED5151 COMPUTER APPLICATIONS IN DESIGN Regulation 2017 Academic
Geometry. Chapter 5. Types of Curves and Surfaces
 Chapter 5. Geometry Geometry refers to the physical items represented by the model (such as points, curves, and surfaces), independent of their spatial or topological relationships. The ACIS free form
Chapter 5. Geometry Geometry refers to the physical items represented by the model (such as points, curves, and surfaces), independent of their spatial or topological relationships. The ACIS free form
Glossary of dictionary terms in the AP geometry units
 Glossary of dictionary terms in the AP geometry units affine linear equation: an equation in which both sides are sums of terms that are either a number times y or a number times x or just a number [SlL2-D5]
Glossary of dictionary terms in the AP geometry units affine linear equation: an equation in which both sides are sums of terms that are either a number times y or a number times x or just a number [SlL2-D5]
arxiv:cs/ v1 [cs.gr] 22 Mar 2005
![arxiv:cs/ v1 [cs.gr] 22 Mar 2005 arxiv:cs/ v1 [cs.gr] 22 Mar 2005](/thumbs/83/88367215.jpg) arxiv:cs/0503054v1 [cs.gr] 22 Mar 2005 ANALYTIC DEFINITION OF CURVES AND SURFACES BY PARABOLIC BLENDING by A.W. Overhauser Mathematical and Theoretical Sciences Department Scientific Laboratory, Ford Motor
arxiv:cs/0503054v1 [cs.gr] 22 Mar 2005 ANALYTIC DEFINITION OF CURVES AND SURFACES BY PARABOLIC BLENDING by A.W. Overhauser Mathematical and Theoretical Sciences Department Scientific Laboratory, Ford Motor
In this course we will need a set of techniques to represent curves and surfaces in 2-d and 3-d. Some reasons for this include
 Parametric Curves and Surfaces In this course we will need a set of techniques to represent curves and surfaces in 2-d and 3-d. Some reasons for this include Describing curves in space that objects move
Parametric Curves and Surfaces In this course we will need a set of techniques to represent curves and surfaces in 2-d and 3-d. Some reasons for this include Describing curves in space that objects move
Curves and Surfaces for Computer-Aided Geometric Design
 Curves and Surfaces for Computer-Aided Geometric Design A Practical Guide Fourth Edition Gerald Farin Department of Computer Science Arizona State University Tempe, Arizona /ACADEMIC PRESS I San Diego
Curves and Surfaces for Computer-Aided Geometric Design A Practical Guide Fourth Edition Gerald Farin Department of Computer Science Arizona State University Tempe, Arizona /ACADEMIC PRESS I San Diego
Make geometric constructions. (Formalize and explain processes)
 Standard 5: Geometry Pre-Algebra Plus Algebra Geometry Algebra II Fourth Course Benchmark 1 - Benchmark 1 - Benchmark 1 - Part 3 Draw construct, and describe geometrical figures and describe the relationships
Standard 5: Geometry Pre-Algebra Plus Algebra Geometry Algebra II Fourth Course Benchmark 1 - Benchmark 1 - Benchmark 1 - Part 3 Draw construct, and describe geometrical figures and describe the relationships
Suggested Foundation Topics for Paper 2
 Suggested Foundation Topics for Paper 2 Number N a N b N b N c N d Add, subtract, multiply and divide any positive and negative integers Order decimals and integers Order rational numbers Use the concepts
Suggested Foundation Topics for Paper 2 Number N a N b N b N c N d Add, subtract, multiply and divide any positive and negative integers Order decimals and integers Order rational numbers Use the concepts
Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts
 Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
JEFFERSON COUNTY SCHOOLS 8th Grade Pacing Guide Suggested 9 Weeks Splits
 JEFFERSON COUNTY SCHOOLS 8th Grade Pacing Guide 2011-2012 Suggested 9 Weeks Splits Lessons 1 thru 6 (pages 4-20) May cover before starting chapter 1 or as 1.1-1.6, Start Smart needed 1.3 2.3,3.2 3.1, 5.4
JEFFERSON COUNTY SCHOOLS 8th Grade Pacing Guide 2011-2012 Suggested 9 Weeks Splits Lessons 1 thru 6 (pages 4-20) May cover before starting chapter 1 or as 1.1-1.6, Start Smart needed 1.3 2.3,3.2 3.1, 5.4
COMPUTER AIDED GEOMETRIC DESIGN. Thomas W. Sederberg
 COMPUTER AIDED GEOMETRIC DESIGN Thomas W. Sederberg January 31, 2011 ii T. W. Sederberg iii Preface This semester is the 24 th time I have taught a course at Brigham Young University titled, Computer Aided
COMPUTER AIDED GEOMETRIC DESIGN Thomas W. Sederberg January 31, 2011 ii T. W. Sederberg iii Preface This semester is the 24 th time I have taught a course at Brigham Young University titled, Computer Aided
Foundation tier knowledge, skills and understanding
 Foundation tier knowledge, skills and understanding 1. Number Structure and calculation N1 N2 N3 N4 N5 N6 N7 N8 order positive and negative integers, decimals and fractions; use the symbols =,, ,,
Foundation tier knowledge, skills and understanding 1. Number Structure and calculation N1 N2 N3 N4 N5 N6 N7 N8 order positive and negative integers, decimals and fractions; use the symbols =,, ,,
Fall CSCI 420: Computer Graphics. 4.2 Splines. Hao Li.
 Fall 2014 CSCI 420: Computer Graphics 4.2 Splines Hao Li http://cs420.hao-li.com 1 Roller coaster Next programming assignment involves creating a 3D roller coaster animation We must model the 3D curve
Fall 2014 CSCI 420: Computer Graphics 4.2 Splines Hao Li http://cs420.hao-li.com 1 Roller coaster Next programming assignment involves creating a 3D roller coaster animation We must model the 3D curve
PITSCO Math Individualized Prescriptive Lessons (IPLs)
 Orientation Integers 10-10 Orientation I 20-10 Speaking Math Define common math vocabulary. Explore the four basic operations and their solutions. Form equations and expressions. 20-20 Place Value Define
Orientation Integers 10-10 Orientation I 20-10 Speaking Math Define common math vocabulary. Explore the four basic operations and their solutions. Form equations and expressions. 20-20 Place Value Define
2D Spline Curves. CS 4620 Lecture 13
 2D Spline Curves CS 4620 Lecture 13 2008 Steve Marschner 1 Motivation: smoothness In many applications we need smooth shapes [Boeing] that is, without discontinuities So far we can make things with corners
2D Spline Curves CS 4620 Lecture 13 2008 Steve Marschner 1 Motivation: smoothness In many applications we need smooth shapes [Boeing] that is, without discontinuities So far we can make things with corners
Distance Functions 1
 Distance Functions 1 Distance function Given: geometric object F (curve, surface, solid, ) Assigns to each point the shortest distance from F Level sets of the distance function are trimmed offsets F p
Distance Functions 1 Distance function Given: geometric object F (curve, surface, solid, ) Assigns to each point the shortest distance from F Level sets of the distance function are trimmed offsets F p
APS Seventh Grade Math District Benchmark Assessment NM Math Standards Alignment
 APS Seventh Grade Math District Benchmark NM Math Standards Alignment SEVENTH GRADE NM STANDARDS Strand: NUMBER AND OPERATIONS Standard: Students will understand numerical concepts and mathematical operations.
APS Seventh Grade Math District Benchmark NM Math Standards Alignment SEVENTH GRADE NM STANDARDS Strand: NUMBER AND OPERATIONS Standard: Students will understand numerical concepts and mathematical operations.
Geometric Modeling Systems
 Geometric Modeling Systems Wireframe Modeling use lines/curves and points for 2D or 3D largely replaced by surface and solid models Surface Modeling wireframe information plus surface definitions supports
Geometric Modeling Systems Wireframe Modeling use lines/curves and points for 2D or 3D largely replaced by surface and solid models Surface Modeling wireframe information plus surface definitions supports
Development of Reverse Engineering System for Machine Engineering Using 3D Bit-map Data. Tatsuro Yashiki* and Tarou Takagi*
 Development of Reverse Engineering System for Machine Engineering Using 3D Bit-map Data Tatsuro Yashiki* and Tarou Takagi* *Power & Industrial Systems R&D Laboratory, Hitachi, Ltd. Abstract In this paper,
Development of Reverse Engineering System for Machine Engineering Using 3D Bit-map Data Tatsuro Yashiki* and Tarou Takagi* *Power & Industrial Systems R&D Laboratory, Hitachi, Ltd. Abstract In this paper,
Technical Report. Removing polar rendering artifacts in subdivision surfaces. Ursula H. Augsdörfer, Neil A. Dodgson, Malcolm A. Sabin.
 Technical Report UCAM-CL-TR-689 ISSN 1476-2986 Number 689 Computer Laboratory Removing polar rendering artifacts in subdivision surfaces Ursula H. Augsdörfer, Neil A. Dodgson, Malcolm A. Sabin June 2007
Technical Report UCAM-CL-TR-689 ISSN 1476-2986 Number 689 Computer Laboratory Removing polar rendering artifacts in subdivision surfaces Ursula H. Augsdörfer, Neil A. Dodgson, Malcolm A. Sabin June 2007
Planes Intersecting Cones: Static Hypertext Version
 Page 1 of 12 Planes Intersecting Cones: Static Hypertext Version On this page, we develop some of the details of the plane-slicing-cone picture discussed in the introduction. The relationship between the
Page 1 of 12 Planes Intersecting Cones: Static Hypertext Version On this page, we develop some of the details of the plane-slicing-cone picture discussed in the introduction. The relationship between the
Mathematics - Grade 7: Introduction Math 7
 Mathematics - Grade 7: Introduction Math 7 In Grade 7, instructional time should focus on four critical areas: (1) developing understanding of and applying proportional relationships; (2) developing understanding
Mathematics - Grade 7: Introduction Math 7 In Grade 7, instructional time should focus on four critical areas: (1) developing understanding of and applying proportional relationships; (2) developing understanding
Interpolating/approximating pp gcurves
 Chap 3 Interpolating Values 1 Outline Interpolating/approximating pp gcurves Controlling the motion of a point along a curve Interpolation of orientation Working with paths Interpolation between key frames
Chap 3 Interpolating Values 1 Outline Interpolating/approximating pp gcurves Controlling the motion of a point along a curve Interpolation of orientation Working with paths Interpolation between key frames
SPLITTING THE CUBIC UNIFORM B-SPLINE CURVE
 On-Line Geometric odeling Notes SPLITTING THE CUBIC UNIFOR B-SPLINE CURVE Kenneth I. Joy Visualization and Graphics Research Group Department of Computer Science University of California, Davis Overview
On-Line Geometric odeling Notes SPLITTING THE CUBIC UNIFOR B-SPLINE CURVE Kenneth I. Joy Visualization and Graphics Research Group Department of Computer Science University of California, Davis Overview
MOTION OF A LINE SEGMENT WHOSE ENDPOINT PATHS HAVE EQUAL ARC LENGTH. Anton GFRERRER 1 1 University of Technology, Graz, Austria
 MOTION OF A LINE SEGMENT WHOSE ENDPOINT PATHS HAVE EQUAL ARC LENGTH Anton GFRERRER 1 1 University of Technology, Graz, Austria Abstract. The following geometric problem originating from an engineering
MOTION OF A LINE SEGMENT WHOSE ENDPOINT PATHS HAVE EQUAL ARC LENGTH Anton GFRERRER 1 1 University of Technology, Graz, Austria Abstract. The following geometric problem originating from an engineering
Curriculum Area: Mathematics Year: 9
 Reviewed in the light of the new national curriculum July 2014 TOPICS YEAR CURRICULUM HOW YOU CAN SUPPORT LEARNING AT HOME, EG. BOOKS, WEBSITES, FAMILY LEARNING THROUGH VISITS. Term 1 1. Number Properties
Reviewed in the light of the new national curriculum July 2014 TOPICS YEAR CURRICULUM HOW YOU CAN SUPPORT LEARNING AT HOME, EG. BOOKS, WEBSITES, FAMILY LEARNING THROUGH VISITS. Term 1 1. Number Properties
Free-Form Deformation and Other Deformation Techniques
 Free-Form Deformation and Other Deformation Techniques Deformation Deformation Basic Definition Deformation: A transformation/mapping of the positions of every particle in the original object to those
Free-Form Deformation and Other Deformation Techniques Deformation Deformation Basic Definition Deformation: A transformation/mapping of the positions of every particle in the original object to those
Positivity Preserving Interpolation of Positive Data by Rational Quadratic Trigonometric Spline
 IOSR Journal of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn:2319-765x. Volume 10, Issue 2 Ver. IV (Mar-Apr. 2014), PP 42-47 Positivity Preserving Interpolation of Positive Data by Rational Quadratic
IOSR Journal of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn:2319-765x. Volume 10, Issue 2 Ver. IV (Mar-Apr. 2014), PP 42-47 Positivity Preserving Interpolation of Positive Data by Rational Quadratic
Geometric approximation of curves and singularities of secant maps Ghosh, Sunayana
 University of Groningen Geometric approximation of curves and singularities of secant maps Ghosh, Sunayana IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you wish
University of Groningen Geometric approximation of curves and singularities of secant maps Ghosh, Sunayana IMPORTANT NOTE: You are advised to consult the publisher's version (publisher's PDF) if you wish
Themes in the Texas CCRS - Mathematics
 1. Compare real numbers. a. Classify numbers as natural, whole, integers, rational, irrational, real, imaginary, &/or complex. b. Use and apply the relative magnitude of real numbers by using inequality
1. Compare real numbers. a. Classify numbers as natural, whole, integers, rational, irrational, real, imaginary, &/or complex. b. Use and apply the relative magnitude of real numbers by using inequality
Computer Graphics I Lecture 11
 15-462 Computer Graphics I Lecture 11 Midterm Review Assignment 3 Movie Midterm Review Midterm Preview February 26, 2002 Frank Pfenning Carnegie Mellon University http://www.cs.cmu.edu/~fp/courses/graphics/
15-462 Computer Graphics I Lecture 11 Midterm Review Assignment 3 Movie Midterm Review Midterm Preview February 26, 2002 Frank Pfenning Carnegie Mellon University http://www.cs.cmu.edu/~fp/courses/graphics/
Structural & Thermal Analysis Using the ANSYS Workbench Release 12.1 Environment
 ANSYS Workbench Tutorial Structural & Thermal Analysis Using the ANSYS Workbench Release 12.1 Environment Kent L. Lawrence Mechanical and Aerospace Engineering University of Texas at Arlington SDC PUBLICATIONS
ANSYS Workbench Tutorial Structural & Thermal Analysis Using the ANSYS Workbench Release 12.1 Environment Kent L. Lawrence Mechanical and Aerospace Engineering University of Texas at Arlington SDC PUBLICATIONS
1. Introduction to Constructive Solid Geometry (CSG)
 opyright@010, YZU Optimal Design Laboratory. All rights reserved. Last updated: Yeh-Liang Hsu (010-1-10). Note: This is the course material for ME550 Geometric modeling and computer graphics, Yuan Ze University.
opyright@010, YZU Optimal Design Laboratory. All rights reserved. Last updated: Yeh-Liang Hsu (010-1-10). Note: This is the course material for ME550 Geometric modeling and computer graphics, Yuan Ze University.
Subdivision Surfaces. Homework 1: Last Time? Today. Bilinear Patch. Tensor Product. Spline Surfaces / Patches
 Homework 1: Questions/Comments? Subdivision Surfaces Last Time? Curves & Surfaces Continuity Definitions Spline Surfaces / Patches Tensor Product Bilinear Patches Bezier Patches Trimming Curves C0, G1,
Homework 1: Questions/Comments? Subdivision Surfaces Last Time? Curves & Surfaces Continuity Definitions Spline Surfaces / Patches Tensor Product Bilinear Patches Bezier Patches Trimming Curves C0, G1,
Mathematics High School Geometry
 Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
A VERTICAL LOOK AT KEY CONCEPTS AND PROCEDURES GEOMETRY. Texas Education Agency
 A VERTICAL LOOK AT KEY CONCEPTS AND PROCEDURES GEOMETRY Texas Education Agency The materials are copyrighted (c) and trademarked (tm) as the property of the Texas Education Agency (TEA) and may not be
A VERTICAL LOOK AT KEY CONCEPTS AND PROCEDURES GEOMETRY Texas Education Agency The materials are copyrighted (c) and trademarked (tm) as the property of the Texas Education Agency (TEA) and may not be
Name: Let the Catmull-Rom curve q(u) be defined by the following control points: p 1 = 0, 1 p 2 = 1, 1 p 3 = 1, 0. p 2. p 1.
 Name: 2 1. Let the Catmull-Rom curve q(u) be defined by the following control points: p 0 = 0, 0 p 1 = 0, 1 p 2 = 1, 1 p 3 = 1, 0 p 4 = 2, 0 y p 1 p 2 p 0 p 3 p 4 x Thus, q(i) =p i for i =1, 2, 3. For
Name: 2 1. Let the Catmull-Rom curve q(u) be defined by the following control points: p 0 = 0, 0 p 1 = 0, 1 p 2 = 1, 1 p 3 = 1, 0 p 4 = 2, 0 y p 1 p 2 p 0 p 3 p 4 x Thus, q(i) =p i for i =1, 2, 3. For
Edexcel Linear GCSE Higher Checklist
 Number Add, subtract, multiply and divide whole numbers integers and decimals Multiply and divide fractions Order integers and decimals Order rational numbers Use the concepts and vocabulary of factor
Number Add, subtract, multiply and divide whole numbers integers and decimals Multiply and divide fractions Order integers and decimals Order rational numbers Use the concepts and vocabulary of factor
Particle-Based Volume Rendering of Unstructured Volume Data
 Particle-Based Volume Rendering of Unstructured Volume Data Takuma KAWAMURA 1)*) Jorji NONAKA 3) Naohisa SAKAMOTO 2),3) Koji KOYAMADA 2) 1) Graduate School of Engineering, Kyoto University 2) Center for
Particle-Based Volume Rendering of Unstructured Volume Data Takuma KAWAMURA 1)*) Jorji NONAKA 3) Naohisa SAKAMOTO 2),3) Koji KOYAMADA 2) 1) Graduate School of Engineering, Kyoto University 2) Center for
CGT 581 G Geometric Modeling Curves
 CGT 581 G Geometric Modeling Curves Bedrich Benes, Ph.D. Purdue University Department of Computer Graphics Technology Curves What is a curve? Mathematical definition 1) The continuous image of an interval
CGT 581 G Geometric Modeling Curves Bedrich Benes, Ph.D. Purdue University Department of Computer Graphics Technology Curves What is a curve? Mathematical definition 1) The continuous image of an interval
Design by Subdivision
 Bridges 2010: Mathematics, Music, Art, Architecture, Culture Design by Subdivision Michael Hansmeyer Department for CAAD - Institute for Technology in Architecture Swiss Federal Institute of Technology
Bridges 2010: Mathematics, Music, Art, Architecture, Culture Design by Subdivision Michael Hansmeyer Department for CAAD - Institute for Technology in Architecture Swiss Federal Institute of Technology
Surface and Solid Geometry. 3D Polygons
 Surface and Solid Geometry D olygons Once we know our plane equation: Ax + By + Cz + D = 0, we still need to manage the truncation which leads to the polygon itself Functionally, we will need to do this
Surface and Solid Geometry D olygons Once we know our plane equation: Ax + By + Cz + D = 0, we still need to manage the truncation which leads to the polygon itself Functionally, we will need to do this
Ohio Tutorials are designed specifically for the Ohio Learning Standards to prepare students for the Ohio State Tests and end-ofcourse
 Tutorial Outline Ohio Tutorials are designed specifically for the Ohio Learning Standards to prepare students for the Ohio State Tests and end-ofcourse exams. Math Tutorials offer targeted instruction,
Tutorial Outline Ohio Tutorials are designed specifically for the Ohio Learning Standards to prepare students for the Ohio State Tests and end-ofcourse exams. Math Tutorials offer targeted instruction,
BODMAS and Standard Form. Integers. Understand and use coordinates. Decimals. Introduction to algebra, linear equations
 HIGHER REVISION LIST FOUNDATION REVISION LIST Topic Objectives Topic Objectives BODMAS and Standard Form * Add, subtract, multiply and divide whole numbers, integers and decimals * Order integers and decimals
HIGHER REVISION LIST FOUNDATION REVISION LIST Topic Objectives Topic Objectives BODMAS and Standard Form * Add, subtract, multiply and divide whole numbers, integers and decimals * Order integers and decimals
Geometry Vocabulary Math Fundamentals Reference Sheet Page 1
 Math Fundamentals Reference Sheet Page 1 Acute Angle An angle whose measure is between 0 and 90 Acute Triangle A that has all acute Adjacent Alternate Interior Angle Two coplanar with a common vertex and
Math Fundamentals Reference Sheet Page 1 Acute Angle An angle whose measure is between 0 and 90 Acute Triangle A that has all acute Adjacent Alternate Interior Angle Two coplanar with a common vertex and
Connected Minimal Acceleration Trigonometric Curves
 Connected Minimal Acceleration Trigonometric Curves Tony Barrera Barrera Kristiansen AB Anders Hast Creative Media Lab, University of Gävle Ewert Bengtsson Centre for Image Analysis Uppsala University
Connected Minimal Acceleration Trigonometric Curves Tony Barrera Barrera Kristiansen AB Anders Hast Creative Media Lab, University of Gävle Ewert Bengtsson Centre for Image Analysis Uppsala University
Research Article A Family of Even-Point Ternary Approximating Schemes
 International Scholarly Research Network ISRN Applied Mathematics Volume, Article ID 97, pages doi:.5//97 Research Article A Family of Even-Point Ternary Approximating Schemes Abdul Ghaffar and Ghulam
International Scholarly Research Network ISRN Applied Mathematics Volume, Article ID 97, pages doi:.5//97 Research Article A Family of Even-Point Ternary Approximating Schemes Abdul Ghaffar and Ghulam
A VERTICAL LOOK AT KEY CONCEPTS AND PROCEDURES GEOMETRY
 A VERTICAL LOOK AT KEY CONCEPTS AND PROCEDURES GEOMETRY Revised TEKS (2012): Building to Geometry Coordinate and Transformational Geometry A Vertical Look at Key Concepts and Procedures Derive and use
A VERTICAL LOOK AT KEY CONCEPTS AND PROCEDURES GEOMETRY Revised TEKS (2012): Building to Geometry Coordinate and Transformational Geometry A Vertical Look at Key Concepts and Procedures Derive and use
Mathematics Scope & Sequence Grade 8 Revised: June 2015
 Mathematics Scope & Sequence 2015-16 Grade 8 Revised: June 2015 Readiness Standard(s) First Six Weeks (29 ) 8.2D Order a set of real numbers arising from mathematical and real-world contexts Convert between
Mathematics Scope & Sequence 2015-16 Grade 8 Revised: June 2015 Readiness Standard(s) First Six Weeks (29 ) 8.2D Order a set of real numbers arising from mathematical and real-world contexts Convert between
CS 465 Program 4: Modeller
 CS 465 Program 4: Modeller out: 30 October 2004 due: 16 November 2004 1 Introduction In this assignment you will work on a simple 3D modelling system that uses simple primitives and curved surfaces organized
CS 465 Program 4: Modeller out: 30 October 2004 due: 16 November 2004 1 Introduction In this assignment you will work on a simple 3D modelling system that uses simple primitives and curved surfaces organized
Prentice Hall Pre-Algebra 2004 Correlated to: Hawaii Mathematics Content and Performance Standards (HCPS) II (Grades 9-12)
 Hawaii Mathematics Content and Performance Standards (HCPS) II (Grades 9-12) NUMBER AND OPERATIONS STANDARD 1: Students understand numbers, ways of representing numbers, relationships among numbers, and
Hawaii Mathematics Content and Performance Standards (HCPS) II (Grades 9-12) NUMBER AND OPERATIONS STANDARD 1: Students understand numbers, ways of representing numbers, relationships among numbers, and
3D Modeling Parametric Curves & Surfaces
 3D Modeling Parametric Curves & Surfaces Shandong University Spring 2012 3D Object Representations Raw data Point cloud Range image Polygon soup Solids Voxels BSP tree CSG Sweep Surfaces Mesh Subdivision
3D Modeling Parametric Curves & Surfaces Shandong University Spring 2012 3D Object Representations Raw data Point cloud Range image Polygon soup Solids Voxels BSP tree CSG Sweep Surfaces Mesh Subdivision
Side-by-Side Comparison of the Texas Educational Knowledge and Skills (TEKS) and Louisiana Grade Level Expectations (GLEs) MATHEMATICS: Geometry
 Side-by-Side Comparison of the Texas Educational Knowledge and Skills (TEKS) and Louisiana Grade Level Expectations (GLEs) MATHEMATICS: Geometry TEKS Comments Louisiana GLE (G.1) Geometric Structure. The
Side-by-Side Comparison of the Texas Educational Knowledge and Skills (TEKS) and Louisiana Grade Level Expectations (GLEs) MATHEMATICS: Geometry TEKS Comments Louisiana GLE (G.1) Geometric Structure. The
Columbus State Community College Mathematics Department Public Syllabus. Course and Number: MATH 1172 Engineering Mathematics A
 Columbus State Community College Mathematics Department Public Syllabus Course and Number: MATH 1172 Engineering Mathematics A CREDITS: 5 CLASS HOURS PER WEEK: 5 PREREQUISITES: MATH 1151 with a C or higher
Columbus State Community College Mathematics Department Public Syllabus Course and Number: MATH 1172 Engineering Mathematics A CREDITS: 5 CLASS HOURS PER WEEK: 5 PREREQUISITES: MATH 1151 with a C or higher
CS-184: Computer Graphics
 CS-184: Computer Graphics Lecture #12: Curves and Surfaces Prof. James O Brien University of California, Berkeley V2007-F-12-1.0 Today General curve and surface representations Splines and other polynomial
CS-184: Computer Graphics Lecture #12: Curves and Surfaces Prof. James O Brien University of California, Berkeley V2007-F-12-1.0 Today General curve and surface representations Splines and other polynomial
Integers & Absolute Value Properties of Addition Add Integers Subtract Integers. Add & Subtract Like Fractions Add & Subtract Unlike Fractions
 Unit 1: Rational Numbers & Exponents M07.A-N & M08.A-N, M08.B-E Essential Questions Standards Content Skills Vocabulary What happens when you add, subtract, multiply and divide integers? What happens when
Unit 1: Rational Numbers & Exponents M07.A-N & M08.A-N, M08.B-E Essential Questions Standards Content Skills Vocabulary What happens when you add, subtract, multiply and divide integers? What happens when
Mathematics - Grade 7: Introduction Math 7A
 Mathematics - Grade 7: Introduction Math 7A In Grade 7, instructional time should focus on four critical areas: (1) developing understanding of and applying proportional relationships; (2) developing understanding
Mathematics - Grade 7: Introduction Math 7A In Grade 7, instructional time should focus on four critical areas: (1) developing understanding of and applying proportional relationships; (2) developing understanding
CS 130 Final. Fall 2015
 CS 130 Final Fall 2015 Name Student ID Signature You may not ask any questions during the test. If you believe that there is something wrong with a question, write down what you think the question is trying
CS 130 Final Fall 2015 Name Student ID Signature You may not ask any questions during the test. If you believe that there is something wrong with a question, write down what you think the question is trying
Adaptive Tessellation for Trimmed NURBS Surface
 Adaptive Tessellation for Trimmed NURBS Surface Ma YingLiang and Terry Hewitt 2 Manchester Visualization Centre, University of Manchester, Manchester, M3 9PL, U.K. may@cs.man.ac.uk 2 W.T.Hewitt@man.ac.uk
Adaptive Tessellation for Trimmed NURBS Surface Ma YingLiang and Terry Hewitt 2 Manchester Visualization Centre, University of Manchester, Manchester, M3 9PL, U.K. may@cs.man.ac.uk 2 W.T.Hewitt@man.ac.uk
(Refer Slide Time: 00:02:24 min)
 CAD / CAM Prof. Dr. P. V. Madhusudhan Rao Department of Mechanical Engineering Indian Institute of Technology, Delhi Lecture No. # 9 Parametric Surfaces II So these days, we are discussing the subject
CAD / CAM Prof. Dr. P. V. Madhusudhan Rao Department of Mechanical Engineering Indian Institute of Technology, Delhi Lecture No. # 9 Parametric Surfaces II So these days, we are discussing the subject
Mathematical Tools in Computer Graphics with C# Implementations Table of Contents
 Mathematical Tools in Computer Graphics with C# Implementations by Hardy Alexandre, Willi-Hans Steeb, World Scientific Publishing Company, Incorporated, 2008 Table of Contents List of Figures Notation
Mathematical Tools in Computer Graphics with C# Implementations by Hardy Alexandre, Willi-Hans Steeb, World Scientific Publishing Company, Incorporated, 2008 Table of Contents List of Figures Notation
6-12 Math Course Sequence Effective
 6-12 Math Course Sequence Effective 2009-2010 Regular Single Acceleration Double Acceleration Grade 6 Everyday Math Pre- Algebra Linear Algebra I Grade 7 Pre-Algebra Linear Algebra I Intermediate Algebra
6-12 Math Course Sequence Effective 2009-2010 Regular Single Acceleration Double Acceleration Grade 6 Everyday Math Pre- Algebra Linear Algebra I Grade 7 Pre-Algebra Linear Algebra I Intermediate Algebra
