COMP Parallel Computing. PRAM (2) PRAM algorithm design techniques
|
|
|
- Lester Wells
- 6 years ago
- Views:
Transcription
1 COMP Parallel Computing Lecture 3 Aug 29, 2017 PRAM algorithm design techniques Reading for next class (Thu Aug 31): PRAM handout secns 3.6, 4.1, skim section 5. Written assignment 1 is posted, due Tue Sep 19 1
2 Topics PRAM Algorithm design techniques pointer jumping algorithm cascading parallel divide and conquer 2
3 Design Technique: Pointer Jumping Fast parallel processing of linked data structures linked lists Membership, reduction and prefix sum of linked lists graphs (adjacency lists, edge lists) connected components minimum spanning trees 3
4 Example: Finding the roots of a forest Input G = (V,E) a forest of directed trees Output s[1:n] where for each vertex j, s[j] is the root of the tree containing j Representation of G in a directed tree the root has no parent every other vertex has a unique parent V = {1,..., n} E is defined by s: V V s(u) = v if v is parent of u in G s(r) = r if r is a root in G s is represented using an array s[1:n] s
5 Pointer jumping operation Let (n, s[1..n]) be the representation of directed forest G Pointer jumping operation every vertex directs its edge to its grandparent also called pointer doubling forall i in 1:n do s[i] := s[s[i]] enddo s before ptr jumping s following ptr jumping 5
6 Analysis of pointer jumping pointer jumping halves distance to the root in s let d be the distance in s from vertex u to the root after pointer jumping distance in s from u to root is d/2 S(n) = forall i in 1:n do enddo s[i] := s[s[i]] W(n) = PRAM model s s 6
7 Pointer jumping in a forest Initial Forest after 1 doubling after 2 doublings All vertices point to the root of their tree COMP 203 J. F. Prins [Lec 3]
8 Finding roots of a forest pointer jumping reaches a fixed point when forest has max height 1 vertex i is distance 1 or less from root when s[i] = s[s[i]] forest height 1 s[i] = root of tree containing i forall i in 1:n do while s[i]!= s[s[i]] do s[i] := s[s[i]] end do enddo 8
9 Problem: find distance to root in directed forest Construct an algorithm for the following problem Let (n, s[1..n]) be directed forest G For each vertex 1 i n, set d[i] to be the distance from i to the root of its tree Invariant: let d[i] be the distance in G from i to s[i] establish initially maintain property with each pointer doubling termination implies result Complexity W(n) = S(n) = forall i in 1:n do end do d[i] := (s[i]== i)? 0 : 1 for i := 1 to (lg n) do end do forall i in 1:n do d[i] := d[i] + d[s[i]] s[i] := s[s[i]] end do 10
10 Design Technique: Algorithm Cascading Technique for improving work efficiency of an algorithm work-inefficient but fast parallel algorithm A work-efficient but slow algorithm B (typically sequential) combine ( cascade ) A and B to get best of both Speeding up by slowing down 11
11 Example: histogram values in a sequence Input Sequence L[1..n] with integer values in the range 1..k, where k = lg n Output R[1..k] with R[i] = # occurrences of i in L[1..n] L R Sequential algorithm R[1:k] := 0 for i := 1 to n do R[L[i]] := R[L[i]] + 1 end do T s (n) = 12
12 Parallel Algorithm: First try C i, j 1, 0, if L i j otherwise R j i1: n C i, j L C k integer C[1:n,1:k] forall i in 1:n, j in 1:k do end do C[i,j] := (L[i]==j)? 1 : 0 forall j in 1:k do end do R[k] := REDUCE(C[1:n,j], + ) n 5 6 PRAM W(n) = R S(n) = model 13
13 Cascading the histogram algorithm partition L into m chunks of size (lg n) k = lg n (assume k divides n) m = n / lg n compute mini-histogram sequentially within a chunk S chunk = W chunk = compute all m mini-histograms in parallel S all = S chunk W all = m W chunk combine histograms by summing S combine = W combine = integer C[1:m,1:k] forall i in 1:m, j in 1:k do C[i,j] := 0 end do forall i in 1:m do for j := 1 to k do C[i, L[(i-1)k+j] ] += 1 end do end do forall j in 1:k do R[k] := REDUCE(C[1:m,j], +) end do W(n) = S(n) = PRAM model? 14
14 Parallel Divide and Conquer To solve problem instance P using parallel divide-and-conquer divide P into subproblems (possibly in parallel) apply D&C recursively to each subproblem in parallel combine subsolutions to produce solution (possibly in parallel) Example: sorting mergesort combining quicksort subproblems: left/right half of array sort each subproblem merge results partitioning subproblems: values less than pivot, values greater than or equal to pivot sort each subproblem concatenate results 15
15 Parallel Mergesort (parallel divide and conquer) Assume parallel EREW merge(a,b) for A = B = O(n) with W merge (n) = O(n) S merge (n) = O(lg n) mergesort(v[1:n]) = if n 1 then S[1:n] := V[1:n] else m := n/2 { R[1:m] = mergesort V[1:m] R[m+1:n] = mergesort V[m+1:n] } S[1:n] := merge( R[1:m], R[m+1:n] ) endif return S[1:n] 16
16 Parallel Mergesort (forall) Assume parallel EREW merge(a,b) for A = B = O(n) with W merge (n) = O(n) S merge (n) = O(lg n) mergesort(v[1:n]) = if n 1 then S[1:n] := V[1:n] else m := n/2 forall i in 0:1 do R[i*m+1 : (i+1)*m] = mergesort V[i*m+1 : (i+1)*m] end do S[1:n] := merge( R[1:m], R[m+1:2*m] ) endif return S[1:n] S mergesort (n) = W mergesort (n) = 17
17 Parallel Quicksort Assume parallel EREW partition(a,p) for A = O(n) with W partition (n) = O(n) S partition (n) = O(lg n) quicksort(v[1:n]) = if n 1 then S[1:n] := V[1:n] else p := V[ random(1:n) ] R[1:n], m := partition (V[1:n], p) h[0:2] := [0, m, n] forall i in 0:1 do S[h(i)+1 : h(i+1)] = quicksort R[h(i)+1 : h(i+1)] end do end if return S[1:n] S quicksort (n) = W quicksort (n) = 18
18 Planar Convex Hull Problem Input S = {(x i, y i )} set of n points in the plane assume x i distinct, y i distinct, and no three points co-linear Output tour of smallest convex polygon containing all points of S Complexity T s (n) = Θ(n lg n) 19
19 Two Parallel Algorithms for Planar Convex Hull two divide and conquer algorithms combining approach partitioning approach combining algorithm (like mergesort) assume input points presented in order of increasing x coordinate obtained using O(n lg n) work, O(lg 2 n) step sorting algorithm optimal worst case performance partitioning algorithm (like quicksort) no assumptions about order of input points suboptimal worst case performance very good expected case performance 20
20 D&C algorithm via combining 1. Divide S into US, LS by P 1 -P n 2. Compute Upper Convex Path and Lower Convex Path using D&C algorithm 3. Combine UCP, LCP to construct convex hull US UCP P 1 P n LCP LS 21
21 Construction of upper convex path P n/2+1 P 1 Divide P n/2 P n Recur Combine (1): find upper common tangent Combine (2): create upper convex path 22
22 Analysis (Combining algorithm) Upper/Lower Convex path Find common tangent (UCT/LCT) binary search of convex paths to find tangent points [Overmars & van Leeuwen] Sequential: S(n) = W(n) = O(lg n) Connect paths CREW: S(n) = O(1), W(n) = O(n) EREW: S(n) = O(lg n), W(n) = O(n) Convex Hull S(n) = S(n/2) + O(lg n) S(n) = O(lg 2 n) W(n) = 2 W(n/2) + O(n) W(n) = O(n lg n) Work-efficient, since T S (n) = (n lg n) 23
23 D&C algorithm via partitioning 1. Divide S into US, LS by line P i -P j where P i, P j have extremal x coordinates 2. Compute Upper Convex Path and Lower Convex Path using D&C algorithm 3. Combine UCP, LCP to construct convex hull US UCP P i P j LCP LS 24
24 Construction of upper convex path d max d max US 2 US 1 P i Locate point at max distance from P i - P j P j P i Discard interior points and partition remaining points P j UCP 2 d max UCP UCP 1 P i P j P i P j Recur: find upper convex paths Combine upper convex paths 25
25 Analysis (Partitioning algorithm) Upper/Lower Convex path for n points above baseline Find point at maximum distance from baseline S(n) = O(lg n), W(n) = O(n) Partition S(n) = O(lg n), W(n) = O(n) Combine S(n) = O(lg n), W(n) = O(n) Convex Hull Find extremal points for initial baseline S(n) = O(lg n), W(n) = O(n) Construct UCP, LCP S(n) = max( S(n 1 ), S(n 2 ) ) + O(lg n) W(n) = W(n 1 ) + W(n 2 ) + O(n) n 1 + n 2 n Combine paths S(n)=O(1), W(n) = O(n) 26
26 Analysis of parallel partitioning algorithm Analysis Expected partition, no points eliminated S(n) = S(n/2) + O(lgn) S(n) = O(lg 2 n) W(n) = 2 W(n/2) + O(n) W(n) = O(n lg n) Worst-case partition, no points eliminated S(n) = S(n 1) + O(lg n) S(n) = O(n lg n) W(n) = W(1) + W(n 1) + O(n) W(n) = O(n 2 ) Expected partition, random points in the unit square S(n) = O(lg n (lg lg n)) W(n) = O(n lg lg n) 27
27 Reminder: asymptotic growth for recurrence relations Recurrence form H ( n) ah H (1) O(1) n b f ( n) where a 1, b 1 Solution H ( n) where a k k log n b k 1 i0 a i f n i b 28
EE/CSCI 451 Spring 2018 Homework 8 Total Points: [10 points] Explain the following terms: EREW PRAM CRCW PRAM. Brent s Theorem.
![EE/CSCI 451 Spring 2018 Homework 8 Total Points: [10 points] Explain the following terms: EREW PRAM CRCW PRAM. Brent s Theorem. EE/CSCI 451 Spring 2018 Homework 8 Total Points: [10 points] Explain the following terms: EREW PRAM CRCW PRAM. Brent s Theorem.](/thumbs/86/94254637.jpg) EE/CSCI 451 Spring 2018 Homework 8 Total Points: 100 1 [10 points] Explain the following terms: EREW PRAM CRCW PRAM Brent s Theorem BSP model 1 2 [15 points] Assume two sorted sequences of size n can be
EE/CSCI 451 Spring 2018 Homework 8 Total Points: 100 1 [10 points] Explain the following terms: EREW PRAM CRCW PRAM Brent s Theorem BSP model 1 2 [15 points] Assume two sorted sequences of size n can be
COMP Parallel Computing. PRAM (3) PRAM algorithm design techniques
 COMP 633 - Parallel Computing Lecture 4 August 30, 2018 PRAM algorithm design techniques Reading for next class PRAM handout section 5 1 Topics Parallel connected components algorithm representation of
COMP 633 - Parallel Computing Lecture 4 August 30, 2018 PRAM algorithm design techniques Reading for next class PRAM handout section 5 1 Topics Parallel connected components algorithm representation of
The PRAM model. A. V. Gerbessiotis CIS 485/Spring 1999 Handout 2 Week 2
 The PRAM model A. V. Gerbessiotis CIS 485/Spring 1999 Handout 2 Week 2 Introduction The Parallel Random Access Machine (PRAM) is one of the simplest ways to model a parallel computer. A PRAM consists of
The PRAM model A. V. Gerbessiotis CIS 485/Spring 1999 Handout 2 Week 2 Introduction The Parallel Random Access Machine (PRAM) is one of the simplest ways to model a parallel computer. A PRAM consists of
A Sophomoric Introduction to Shared-Memory Parallelism and Concurrency Lecture 3 Parallel Prefix, Pack, and Sorting
 A Sophomoric Introduction to Shared-Memory Parallelism and Concurrency Lecture 3 Parallel Prefix, Pack, and Sorting Steve Wolfman, based on work by Dan Grossman LICENSE: This file is licensed under a Creative
A Sophomoric Introduction to Shared-Memory Parallelism and Concurrency Lecture 3 Parallel Prefix, Pack, and Sorting Steve Wolfman, based on work by Dan Grossman LICENSE: This file is licensed under a Creative
Chapter 1 Divide and Conquer Algorithm Theory WS 2014/15 Fabian Kuhn
 Chapter 1 Divide and Conquer Algorithm Theory WS 2014/15 Fabian Kuhn Divide And Conquer Principle Important algorithm design method Examples from Informatik 2: Sorting: Mergesort, Quicksort Binary search
Chapter 1 Divide and Conquer Algorithm Theory WS 2014/15 Fabian Kuhn Divide And Conquer Principle Important algorithm design method Examples from Informatik 2: Sorting: Mergesort, Quicksort Binary search
Divide and Conquer Algorithms
 CSE341T 09/13/2017 Lecture 5 Divide and Conquer Algorithms We have already seen a couple of divide and conquer algorithms in this lecture. The reduce algorithm and the algorithm to copy elements of the
CSE341T 09/13/2017 Lecture 5 Divide and Conquer Algorithms We have already seen a couple of divide and conquer algorithms in this lecture. The reduce algorithm and the algorithm to copy elements of the
PRAM Divide and Conquer Algorithms
 PRAM Divide and Conquer Algorithms (Chapter Five) Introduction: Really three fundamental operations: Divide is the partitioning process Conquer the the process of (eventually) solving the eventual base
PRAM Divide and Conquer Algorithms (Chapter Five) Introduction: Really three fundamental operations: Divide is the partitioning process Conquer the the process of (eventually) solving the eventual base
Chapter 4. Divide-and-Conquer. Copyright 2007 Pearson Addison-Wesley. All rights reserved.
 Chapter 4 Divide-and-Conquer Copyright 2007 Pearson Addison-Wesley. All rights reserved. Divide-and-Conquer The most-well known algorithm design strategy: 2. Divide instance of problem into two or more
Chapter 4 Divide-and-Conquer Copyright 2007 Pearson Addison-Wesley. All rights reserved. Divide-and-Conquer The most-well known algorithm design strategy: 2. Divide instance of problem into two or more
Divide-and-Conquer. The most-well known algorithm design strategy: smaller instances. combining these solutions
 Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances recursively 3. Obtain solution to original
Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances recursively 3. Obtain solution to original
Divide and Conquer. Algorithm Fall Semester
 Divide and Conquer Algorithm 2014 Fall Semester Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances
Divide and Conquer Algorithm 2014 Fall Semester Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances
COMP Parallel Computing. PRAM (4) PRAM models and complexity
 COMP 633 - Parallel Computing Lecture 5 September 4, 2018 PRAM models and complexity Reading for Thursday Memory hierarchy and cache-based systems Topics Comparison of PRAM models relative performance
COMP 633 - Parallel Computing Lecture 5 September 4, 2018 PRAM models and complexity Reading for Thursday Memory hierarchy and cache-based systems Topics Comparison of PRAM models relative performance
Scan and Quicksort. 1 Scan. 1.1 Contraction CSE341T 09/20/2017. Lecture 7
 CSE341T 09/20/2017 Lecture 7 Scan and Quicksort 1 Scan Scan is a very useful primitive for parallel programming. We will use it all the time in this class. First, lets start by thinking about what other
CSE341T 09/20/2017 Lecture 7 Scan and Quicksort 1 Scan Scan is a very useful primitive for parallel programming. We will use it all the time in this class. First, lets start by thinking about what other
CSC Design and Analysis of Algorithms
 CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conquer Algorithm Design Technique Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide a problem instance into two
CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conquer Algorithm Design Technique Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide a problem instance into two
CSC Design and Analysis of Algorithms. Lecture 6. Divide and Conquer Algorithm Design Technique. Divide-and-Conquer
 CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conquer Algorithm Design Technique Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide a problem instance into two
CSC 8301- Design and Analysis of Algorithms Lecture 6 Divide and Conquer Algorithm Design Technique Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide a problem instance into two
Programming II (CS300)
 1 Programming II (CS300) Chapter 12: Sorting Algorithms MOUNA KACEM mouna@cs.wisc.edu Spring 2018 Outline 2 Last week Implementation of the three tree depth-traversal algorithms Implementation of the BinarySearchTree
1 Programming II (CS300) Chapter 12: Sorting Algorithms MOUNA KACEM mouna@cs.wisc.edu Spring 2018 Outline 2 Last week Implementation of the three tree depth-traversal algorithms Implementation of the BinarySearchTree
Divide-and-Conquer. Dr. Yingwu Zhu
 Divide-and-Conquer Dr. Yingwu Zhu Divide-and-Conquer The most-well known algorithm design technique: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances independently
Divide-and-Conquer Dr. Yingwu Zhu Divide-and-Conquer The most-well known algorithm design technique: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances independently
Parallel Algorithms for (PRAM) Computers & Some Parallel Algorithms. Reference : Horowitz, Sahni and Rajasekaran, Computer Algorithms
 Parallel Algorithms for (PRAM) Computers & Some Parallel Algorithms Reference : Horowitz, Sahni and Rajasekaran, Computer Algorithms Part 2 1 3 Maximum Selection Problem : Given n numbers, x 1, x 2,, x
Parallel Algorithms for (PRAM) Computers & Some Parallel Algorithms Reference : Horowitz, Sahni and Rajasekaran, Computer Algorithms Part 2 1 3 Maximum Selection Problem : Given n numbers, x 1, x 2,, x
Lecture 5: Sorting Part A
 Lecture 5: Sorting Part A Heapsort Running time O(n lg n), like merge sort Sorts in place (as insertion sort), only constant number of array elements are stored outside the input array at any time Combines
Lecture 5: Sorting Part A Heapsort Running time O(n lg n), like merge sort Sorts in place (as insertion sort), only constant number of array elements are stored outside the input array at any time Combines
Sorting. Data structures and Algorithms
 Sorting Data structures and Algorithms Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++ Goodrich, Tamassia and Mount (Wiley, 2004) Outline Bubble
Sorting Data structures and Algorithms Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++ Goodrich, Tamassia and Mount (Wiley, 2004) Outline Bubble
Scan and its Uses. 1 Scan. 1.1 Contraction CSE341T/CSE549T 09/17/2014. Lecture 8
 CSE341T/CSE549T 09/17/2014 Lecture 8 Scan and its Uses 1 Scan Today, we start by learning a very useful primitive. First, lets start by thinking about what other primitives we have learned so far? The
CSE341T/CSE549T 09/17/2014 Lecture 8 Scan and its Uses 1 Scan Today, we start by learning a very useful primitive. First, lets start by thinking about what other primitives we have learned so far? The
CSL 730: Parallel Programming
 CSL 73: Parallel Programming General Algorithmic Techniques Balance binary tree Partitioning Divid and conquer Fractional cascading Recursive doubling Symmetry breaking Pipelining 2 PARALLEL ALGORITHM
CSL 73: Parallel Programming General Algorithmic Techniques Balance binary tree Partitioning Divid and conquer Fractional cascading Recursive doubling Symmetry breaking Pipelining 2 PARALLEL ALGORITHM
Sorting and Selection
 Sorting and Selection Introduction Divide and Conquer Merge-Sort Quick-Sort Radix-Sort Bucket-Sort 10-1 Introduction Assuming we have a sequence S storing a list of keyelement entries. The key of the element
Sorting and Selection Introduction Divide and Conquer Merge-Sort Quick-Sort Radix-Sort Bucket-Sort 10-1 Introduction Assuming we have a sequence S storing a list of keyelement entries. The key of the element
CSE 613: Parallel Programming. Lecture 6 ( Basic Parallel Algorithmic Techniques )
 CSE 613: Parallel Programming Lecture 6 ( Basic Parallel Algorithmic Techniques ) Rezaul A. Chowdhury Department of Computer Science SUNY Stony Brook Spring 2017 Some Basic Techniques 1. Divide-and-Conquer
CSE 613: Parallel Programming Lecture 6 ( Basic Parallel Algorithmic Techniques ) Rezaul A. Chowdhury Department of Computer Science SUNY Stony Brook Spring 2017 Some Basic Techniques 1. Divide-and-Conquer
CS256 Applied Theory of Computation
 CS256 Applied Theory of Computation Parallel Computation IV John E Savage Overview PRAM Work-time framework for parallel algorithms Prefix computations Finding roots of trees in a forest Parallel merging
CS256 Applied Theory of Computation Parallel Computation IV John E Savage Overview PRAM Work-time framework for parallel algorithms Prefix computations Finding roots of trees in a forest Parallel merging
DIVIDE & CONQUER. Problem of size n. Solution to sub problem 1
 DIVIDE & CONQUER Definition: Divide & conquer is a general algorithm design strategy with a general plan as follows: 1. DIVIDE: A problem s instance is divided into several smaller instances of the same
DIVIDE & CONQUER Definition: Divide & conquer is a general algorithm design strategy with a general plan as follows: 1. DIVIDE: A problem s instance is divided into several smaller instances of the same
Chapter 1 Divide and Conquer Algorithm Theory WS 2013/14 Fabian Kuhn
 Chapter 1 Divide and Conquer Algorithm Theory WS 2013/14 Fabian Kuhn Divide And Conquer Principle Important algorithm design method Examples from Informatik 2: Sorting: Mergesort, Quicksort Binary search
Chapter 1 Divide and Conquer Algorithm Theory WS 2013/14 Fabian Kuhn Divide And Conquer Principle Important algorithm design method Examples from Informatik 2: Sorting: Mergesort, Quicksort Binary search
Sorting Goodrich, Tamassia Sorting 1
 Sorting Put array A of n numbers in increasing order. A core algorithm with many applications. Simple algorithms are O(n 2 ). Optimal algorithms are O(n log n). We will see O(n) for restricted input in
Sorting Put array A of n numbers in increasing order. A core algorithm with many applications. Simple algorithms are O(n 2 ). Optimal algorithms are O(n log n). We will see O(n) for restricted input in
COMP 352 FALL Tutorial 10
 1 COMP 352 FALL 2016 Tutorial 10 SESSION OUTLINE Divide-and-Conquer Method Sort Algorithm Properties Quick Overview on Sorting Algorithms Merge Sort Quick Sort Bucket Sort Radix Sort Problem Solving 2
1 COMP 352 FALL 2016 Tutorial 10 SESSION OUTLINE Divide-and-Conquer Method Sort Algorithm Properties Quick Overview on Sorting Algorithms Merge Sort Quick Sort Bucket Sort Radix Sort Problem Solving 2
Chapter 1 Divide and Conquer Algorithm Theory WS 2015/16 Fabian Kuhn
 Chapter 1 Divide and Conquer Algorithm Theory WS 2015/16 Fabian Kuhn Divide And Conquer Principle Important algorithm design method Examples from Informatik 2: Sorting: Mergesort, Quicksort Binary search
Chapter 1 Divide and Conquer Algorithm Theory WS 2015/16 Fabian Kuhn Divide And Conquer Principle Important algorithm design method Examples from Informatik 2: Sorting: Mergesort, Quicksort Binary search
We can use a max-heap to sort data.
 Sorting 7B N log N Sorts 1 Heap Sort We can use a max-heap to sort data. Convert an array to a max-heap. Remove the root from the heap and store it in its proper position in the same array. Repeat until
Sorting 7B N log N Sorts 1 Heap Sort We can use a max-heap to sort data. Convert an array to a max-heap. Remove the root from the heap and store it in its proper position in the same array. Repeat until
Lecture 19 Sorting Goodrich, Tamassia
 Lecture 19 Sorting 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 2004 Goodrich, Tamassia Outline Review 3 simple sorting algorithms: 1. selection Sort (in previous course) 2. insertion Sort (in previous
Lecture 19 Sorting 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 2004 Goodrich, Tamassia Outline Review 3 simple sorting algorithms: 1. selection Sort (in previous course) 2. insertion Sort (in previous
The divide-and-conquer paradigm involves three steps at each level of the recursion: Divide the problem into a number of subproblems.
 2.3 Designing algorithms There are many ways to design algorithms. Insertion sort uses an incremental approach: having sorted the subarray A[1 j - 1], we insert the single element A[j] into its proper
2.3 Designing algorithms There are many ways to design algorithms. Insertion sort uses an incremental approach: having sorted the subarray A[1 j - 1], we insert the single element A[j] into its proper
CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics
 CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics 1 Sorting 1.1 Problem Statement You are given a sequence of n numbers < a 1, a 2,..., a n >. You need to
CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics 1 Sorting 1.1 Problem Statement You are given a sequence of n numbers < a 1, a 2,..., a n >. You need to
Algorithms and Data Structures (INF1) Lecture 7/15 Hua Lu
 Algorithms and Data Structures (INF1) Lecture 7/15 Hua Lu Department of Computer Science Aalborg University Fall 2007 This Lecture Merge sort Quick sort Radix sort Summary We will see more complex techniques
Algorithms and Data Structures (INF1) Lecture 7/15 Hua Lu Department of Computer Science Aalborg University Fall 2007 This Lecture Merge sort Quick sort Radix sort Summary We will see more complex techniques
Algorithm Efficiency & Sorting. Algorithm efficiency Big-O notation Searching algorithms Sorting algorithms
 Algorithm Efficiency & Sorting Algorithm efficiency Big-O notation Searching algorithms Sorting algorithms Overview Writing programs to solve problem consists of a large number of decisions how to represent
Algorithm Efficiency & Sorting Algorithm efficiency Big-O notation Searching algorithms Sorting algorithms Overview Writing programs to solve problem consists of a large number of decisions how to represent
CIS 121 Data Structures and Algorithms with Java Spring Code Snippets and Recurrences Monday, January 29/Tuesday, January 30
 CIS 11 Data Structures and Algorithms with Java Spring 018 Code Snippets and Recurrences Monday, January 9/Tuesday, January 30 Learning Goals Practice solving recurrences and proving asymptotic bounds
CIS 11 Data Structures and Algorithms with Java Spring 018 Code Snippets and Recurrences Monday, January 9/Tuesday, January 30 Learning Goals Practice solving recurrences and proving asymptotic bounds
CSL 860: Modern Parallel
 CSL 860: Modern Parallel Computation PARALLEL ALGORITHM TECHNIQUES: BALANCED BINARY TREE Reduction n operands => log n steps Total work = O(n) How do you map? Balance Binary tree technique Reduction n
CSL 860: Modern Parallel Computation PARALLEL ALGORITHM TECHNIQUES: BALANCED BINARY TREE Reduction n operands => log n steps Total work = O(n) How do you map? Balance Binary tree technique Reduction n
Computer Science 385 Analysis of Algorithms Siena College Spring Topic Notes: Divide and Conquer
 Computer Science 385 Analysis of Algorithms Siena College Spring 2011 Topic Notes: Divide and Conquer Divide and-conquer is a very common and very powerful algorithm design technique. The general idea:
Computer Science 385 Analysis of Algorithms Siena College Spring 2011 Topic Notes: Divide and Conquer Divide and-conquer is a very common and very powerful algorithm design technique. The general idea:
Divide-and-Conquer CSE 680
 Divide-and-Conquer CSE 680 1 Introduction Given an instance x of a problem, the divide-and-conquer method works as follows. function DAQ(x) if x is sufficiently small or simple then solve it directly else
Divide-and-Conquer CSE 680 1 Introduction Given an instance x of a problem, the divide-and-conquer method works as follows. function DAQ(x) if x is sufficiently small or simple then solve it directly else
would be included in is small: to be exact. Thus with probability1, the same partition n+1 n+1 would be produced regardless of whether p is in the inp
 1 Introduction 1.1 Parallel Randomized Algorihtms Using Sampling A fundamental strategy used in designing ecient algorithms is divide-and-conquer, where that input data is partitioned into several subproblems
1 Introduction 1.1 Parallel Randomized Algorihtms Using Sampling A fundamental strategy used in designing ecient algorithms is divide-and-conquer, where that input data is partitioned into several subproblems
CS 6463: AT Computational Geometry Spring 2006 Convex Hulls Carola Wenk
 CS 6463: AT Computational Geometry Spring 2006 Convex Hulls Carola Wenk 8/29/06 CS 6463: AT Computational Geometry 1 Convex Hull Problem Given a set of pins on a pinboard and a rubber band around them.
CS 6463: AT Computational Geometry Spring 2006 Convex Hulls Carola Wenk 8/29/06 CS 6463: AT Computational Geometry 1 Convex Hull Problem Given a set of pins on a pinboard and a rubber band around them.
Parallel Models. Hypercube Butterfly Fully Connected Other Networks Shared Memory v.s. Distributed Memory SIMD v.s. MIMD
 Parallel Algorithms Parallel Models Hypercube Butterfly Fully Connected Other Networks Shared Memory v.s. Distributed Memory SIMD v.s. MIMD The PRAM Model Parallel Random Access Machine All processors
Parallel Algorithms Parallel Models Hypercube Butterfly Fully Connected Other Networks Shared Memory v.s. Distributed Memory SIMD v.s. MIMD The PRAM Model Parallel Random Access Machine All processors
DIVIDE AND CONQUER ALGORITHMS ANALYSIS WITH RECURRENCE EQUATIONS
 CHAPTER 11 SORTING ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY M. AMATO AND
CHAPTER 11 SORTING ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY M. AMATO AND
Convex Hull Algorithms
 Convex Hull Algorithms Design and Analysis of Algorithms prof. F. Malucelli Villa Andrea e Ceriani Simone Outline Problem Definition Basic Concepts Bruteforce Algorithm Graham Scan Algorithm Divide and
Convex Hull Algorithms Design and Analysis of Algorithms prof. F. Malucelli Villa Andrea e Ceriani Simone Outline Problem Definition Basic Concepts Bruteforce Algorithm Graham Scan Algorithm Divide and
QuickSort
 QuickSort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 1 QuickSort QuickSort on an input sequence S with n elements consists of three steps: n n n Divide: partition S into two sequences S 1 and S 2 of about
QuickSort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 1 QuickSort QuickSort on an input sequence S with n elements consists of three steps: n n n Divide: partition S into two sequences S 1 and S 2 of about
1/60. Geometric Algorithms. Lecture 1: Introduction. Convex Hulls
 1/60 Geometric Algorithms Lecture 1: Introduction Convex Hulls Geometric algorithms scope 2/60 Geometry algorithms (practice): Study of geometric problems that arise in various applications and how algorithms
1/60 Geometric Algorithms Lecture 1: Introduction Convex Hulls Geometric algorithms scope 2/60 Geometry algorithms (practice): Study of geometric problems that arise in various applications and how algorithms
II (Sorting and) Order Statistics
 II (Sorting and) Order Statistics Heapsort Quicksort Sorting in Linear Time Medians and Order Statistics 8 Sorting in Linear Time The sorting algorithms introduced thus far are comparison sorts Any comparison
II (Sorting and) Order Statistics Heapsort Quicksort Sorting in Linear Time Medians and Order Statistics 8 Sorting in Linear Time The sorting algorithms introduced thus far are comparison sorts Any comparison
Lecture 2: Divide and Conquer
 Lecture 2: Divide and Conquer Paradigm Convex Hull Median finding Paradigm Given a problem of size n divide it into subproblems of size n, a 1, b >1. Solve each b subproblem recursively. Combine solutions
Lecture 2: Divide and Conquer Paradigm Convex Hull Median finding Paradigm Given a problem of size n divide it into subproblems of size n, a 1, b >1. Solve each b subproblem recursively. Combine solutions
: Parallel Algorithms Exercises, Batch 1. Exercise Day, Tuesday 18.11, 10:00. Hand-in before or at Exercise Day
 184.727: Parallel Algorithms Exercises, Batch 1. Exercise Day, Tuesday 18.11, 10:00. Hand-in before or at Exercise Day Jesper Larsson Träff, Francesco Versaci Parallel Computing Group TU Wien October 16,
184.727: Parallel Algorithms Exercises, Batch 1. Exercise Day, Tuesday 18.11, 10:00. Hand-in before or at Exercise Day Jesper Larsson Träff, Francesco Versaci Parallel Computing Group TU Wien October 16,
Lecture 2: Getting Started
 Lecture 2: Getting Started Insertion Sort Our first algorithm is Insertion Sort Solves the sorting problem Input: A sequence of n numbers a 1, a 2,..., a n. Output: A permutation (reordering) a 1, a 2,...,
Lecture 2: Getting Started Insertion Sort Our first algorithm is Insertion Sort Solves the sorting problem Input: A sequence of n numbers a 1, a 2,..., a n. Output: A permutation (reordering) a 1, a 2,...,
Merge Sort Goodrich, Tamassia Merge Sort 1
 Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 2004 Goodrich, Tamassia Merge Sort 1 Review of Sorting Selection-sort: Search: search through remaining unsorted elements for min Remove: remove
Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 2004 Goodrich, Tamassia Merge Sort 1 Review of Sorting Selection-sort: Search: search through remaining unsorted elements for min Remove: remove
Sorting. Sorting in Arrays. SelectionSort. SelectionSort. Binary search works great, but how do we create a sorted array in the first place?
 Sorting Binary search works great, but how do we create a sorted array in the first place? Sorting in Arrays Sorting algorithms: Selection sort: O(n 2 ) time Merge sort: O(nlog 2 (n)) time Quicksort: O(n
Sorting Binary search works great, but how do we create a sorted array in the first place? Sorting in Arrays Sorting algorithms: Selection sort: O(n 2 ) time Merge sort: O(nlog 2 (n)) time Quicksort: O(n
More PRAM Algorithms. Techniques Covered
 More PRAM Algorithms Arvind Krishnamurthy Fall 24 Analysis technique: Brent s scheduling lemma Techniques Covered Parallel algorithm is simply characterized by W(n) and S(n) Parallel techniques: Scans
More PRAM Algorithms Arvind Krishnamurthy Fall 24 Analysis technique: Brent s scheduling lemma Techniques Covered Parallel algorithm is simply characterized by W(n) and S(n) Parallel techniques: Scans
Divide and Conquer 4-0
 Divide and Conquer 4-0 Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances recursively 3. Obtain
Divide and Conquer 4-0 Divide-and-Conquer The most-well known algorithm design strategy: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances recursively 3. Obtain
Sorting Algorithms. + Analysis of the Sorting Algorithms
 Sorting Algorithms + Analysis of the Sorting Algorithms Insertion Sort What if first k elements of array are already sorted? 4, 7, 12, 5, 19, 16 We can shift the tail of the sorted elements list down and
Sorting Algorithms + Analysis of the Sorting Algorithms Insertion Sort What if first k elements of array are already sorted? 4, 7, 12, 5, 19, 16 We can shift the tail of the sorted elements list down and
CSE 373: Data Structures and Algorithms
 CSE 373: Data Structures and Algorithms Lecture 20: More Sorting Instructor: Lilian de Greef Quarter: Summer 2017 Today: More sorting algorithms! Merge sort analysis Quicksort Bucket sort Radix sort Divide
CSE 373: Data Structures and Algorithms Lecture 20: More Sorting Instructor: Lilian de Greef Quarter: Summer 2017 Today: More sorting algorithms! Merge sort analysis Quicksort Bucket sort Radix sort Divide
Unit-2 Divide and conquer 2016
 2 Divide and conquer Overview, Structure of divide-and-conquer algorithms, binary search, quick sort, Strassen multiplication. 13% 05 Divide-and- conquer The Divide and Conquer Paradigm, is a method of
2 Divide and conquer Overview, Structure of divide-and-conquer algorithms, binary search, quick sort, Strassen multiplication. 13% 05 Divide-and- conquer The Divide and Conquer Paradigm, is a method of
Divide-and-Conquer. Divide-and conquer is a general algorithm design paradigm:
 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 2014 Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9
Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 2014 Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9
Merge Sort fi fi fi 4 9. Merge Sort Goodrich, Tamassia
 Merge Sort 7 9 4 fi 4 7 9 7 fi 7 9 4 fi 4 9 7 fi 7 fi 9 fi 9 4 fi 4 Merge Sort 1 Divide-and-Conquer ( 10.1.1) Divide-and conquer is a general algorithm design paradigm: Divide: divide the input data S
Merge Sort 7 9 4 fi 4 7 9 7 fi 7 9 4 fi 4 9 7 fi 7 fi 9 fi 9 4 fi 4 Merge Sort 1 Divide-and-Conquer ( 10.1.1) Divide-and conquer is a general algorithm design paradigm: Divide: divide the input data S
5. DIVIDE AND CONQUER I
 5. DIVIDE AND CONQUER I mergesort counting inversions closest pair of points randomized quicksort median and selection Lecture slides by Kevin Wayne Copyright 2005 Pearson-Addison Wesley Copyright 2013
5. DIVIDE AND CONQUER I mergesort counting inversions closest pair of points randomized quicksort median and selection Lecture slides by Kevin Wayne Copyright 2005 Pearson-Addison Wesley Copyright 2013
CS473 - Algorithms I
 CS473 - Algorithms I Lecture 4 The Divide-and-Conquer Design Paradigm View in slide-show mode 1 Reminder: Merge Sort Input array A sort this half sort this half Divide Conquer merge two sorted halves Combine
CS473 - Algorithms I Lecture 4 The Divide-and-Conquer Design Paradigm View in slide-show mode 1 Reminder: Merge Sort Input array A sort this half sort this half Divide Conquer merge two sorted halves Combine
CS Divide and Conquer
 CS483-07 Divide and Conquer Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 1:30pm - 2:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/ lifei/teaching/cs483_fall07/
CS483-07 Divide and Conquer Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 1:30pm - 2:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/ lifei/teaching/cs483_fall07/
Complexity and Advanced Algorithms Monsoon Parallel Algorithms Lecture 2
 Complexity and Advanced Algorithms Monsoon 2011 Parallel Algorithms Lecture 2 Trivia ISRO has a new supercomputer rated at 220 Tflops Can be extended to Pflops. Consumes only 150 KW of power. LINPACK is
Complexity and Advanced Algorithms Monsoon 2011 Parallel Algorithms Lecture 2 Trivia ISRO has a new supercomputer rated at 220 Tflops Can be extended to Pflops. Consumes only 150 KW of power. LINPACK is
Quick Sort. CSE Data Structures May 15, 2002
 Quick Sort CSE 373 - Data Structures May 15, 2002 Readings and References Reading Section 7.7, Data Structures and Algorithm Analysis in C, Weiss Other References C LR 15-May-02 CSE 373 - Data Structures
Quick Sort CSE 373 - Data Structures May 15, 2002 Readings and References Reading Section 7.7, Data Structures and Algorithm Analysis in C, Weiss Other References C LR 15-May-02 CSE 373 - Data Structures
Quick-Sort. Quick-Sort 1
 Quick-Sort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 Quick-Sort 1 Outline and Reading Quick-sort ( 4.3) Algorithm Partition step Quick-sort tree Execution example Analysis of quick-sort (4.3.1) In-place
Quick-Sort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 Quick-Sort 1 Outline and Reading Quick-sort ( 4.3) Algorithm Partition step Quick-sort tree Execution example Analysis of quick-sort (4.3.1) In-place
Sorting Algorithms. CptS 223 Advanced Data Structures. Larry Holder School of Electrical Engineering and Computer Science Washington State University
 Sorting Algorithms CptS 223 Advanced Data Structures Larry Holder School of Electrical Engineering and Computer Science Washington State University 1 QuickSort Divide-and-conquer approach to sorting Like
Sorting Algorithms CptS 223 Advanced Data Structures Larry Holder School of Electrical Engineering and Computer Science Washington State University 1 QuickSort Divide-and-conquer approach to sorting Like
Introduction to Computers and Programming. Today
 Introduction to Computers and Programming Prof. I. K. Lundqvist Lecture 10 April 8 2004 Today How to determine Big-O Compare data structures and algorithms Sorting algorithms 2 How to determine Big-O Partition
Introduction to Computers and Programming Prof. I. K. Lundqvist Lecture 10 April 8 2004 Today How to determine Big-O Compare data structures and algorithms Sorting algorithms 2 How to determine Big-O Partition
Solutions to Exam Data structures (X and NV)
 Solutions to Exam Data structures X and NV 2005102. 1. a Insert the keys 9, 6, 2,, 97, 1 into a binary search tree BST. Draw the final tree. See Figure 1. b Add NIL nodes to the tree of 1a and color it
Solutions to Exam Data structures X and NV 2005102. 1. a Insert the keys 9, 6, 2,, 97, 1 into a binary search tree BST. Draw the final tree. See Figure 1. b Add NIL nodes to the tree of 1a and color it
CSE373: Data Structure & Algorithms Lecture 21: More Comparison Sorting. Aaron Bauer Winter 2014
 CSE373: Data Structure & Algorithms Lecture 21: More Comparison Sorting Aaron Bauer Winter 2014 The main problem, stated carefully For now, assume we have n comparable elements in an array and we want
CSE373: Data Structure & Algorithms Lecture 21: More Comparison Sorting Aaron Bauer Winter 2014 The main problem, stated carefully For now, assume we have n comparable elements in an array and we want
A 0 A 1... A i 1 A i,..., A min,..., A n 1 in their final positions the last n i elements After n 1 passes, the list is sorted.
 CS6402 Design and Analysis of Algorithms _ Unit II 2.1 UNIT II BRUTE FORCE AND DIVIDE-AND-CONQUER 2.1 BRUTE FORCE Brute force is a straightforward approach to solving a problem, usually directly based
CS6402 Design and Analysis of Algorithms _ Unit II 2.1 UNIT II BRUTE FORCE AND DIVIDE-AND-CONQUER 2.1 BRUTE FORCE Brute force is a straightforward approach to solving a problem, usually directly based
SORTING, SETS, AND SELECTION
 CHAPTER 11 SORTING, SETS, AND SELECTION ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM
CHAPTER 11 SORTING, SETS, AND SELECTION ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM
Planar convex hulls (I) Computational Geometry [csci 3250] Laura Toma Bowdoin College
![Planar convex hulls (I) Computational Geometry [csci 3250] Laura Toma Bowdoin College Planar convex hulls (I) Computational Geometry [csci 3250] Laura Toma Bowdoin College](/thumbs/86/93358306.jpg) Planar convex hulls (I) Computational Geometry [csci 3250] Laura Toma Bowdoin College Convex Hull Given a set P of points in 2D, their convex hull is the smallest convex polygon that contains all points
Planar convex hulls (I) Computational Geometry [csci 3250] Laura Toma Bowdoin College Convex Hull Given a set P of points in 2D, their convex hull is the smallest convex polygon that contains all points
Lecture 8: Mergesort / Quicksort Steven Skiena
 Lecture 8: Mergesort / Quicksort Steven Skiena Department of Computer Science State University of New York Stony Brook, NY 11794 4400 http://www.cs.stonybrook.edu/ skiena Problem of the Day Give an efficient
Lecture 8: Mergesort / Quicksort Steven Skiena Department of Computer Science State University of New York Stony Brook, NY 11794 4400 http://www.cs.stonybrook.edu/ skiena Problem of the Day Give an efficient
EECS 2011M: Fundamentals of Data Structures
 M: Fundamentals of Data Structures Instructor: Suprakash Datta Office : LAS 3043 Course page: http://www.eecs.yorku.ca/course/2011m Also on Moodle Note: Some slides in this lecture are adopted from James
M: Fundamentals of Data Structures Instructor: Suprakash Datta Office : LAS 3043 Course page: http://www.eecs.yorku.ca/course/2011m Also on Moodle Note: Some slides in this lecture are adopted from James
Outline. Disjoint set data structure Applications Implementation
 Disjoint Data Sets Outline Disjoint set data structure Applications Implementation Data Structures for Disjoint Sets A disjoint-set data structure is a collection of sets S = {S 1 S k }, such that S i
Disjoint Data Sets Outline Disjoint set data structure Applications Implementation Data Structures for Disjoint Sets A disjoint-set data structure is a collection of sets S = {S 1 S k }, such that S i
Sorting. Task Description. Selection Sort. Should we worry about speed?
 Sorting Should we worry about speed? Task Description We have an array of n values in any order We need to have the array sorted in ascending or descending order of values 2 Selection Sort Select the smallest
Sorting Should we worry about speed? Task Description We have an array of n values in any order We need to have the array sorted in ascending or descending order of values 2 Selection Sort Select the smallest
17/05/2018. Outline. Outline. Divide and Conquer. Control Abstraction for Divide &Conquer. Outline. Module 2: Divide and Conquer
 Module 2: Divide and Conquer Divide and Conquer Control Abstraction for Divide &Conquer 1 Recurrence equation for Divide and Conquer: If the size of problem p is n and the sizes of the k sub problems are
Module 2: Divide and Conquer Divide and Conquer Control Abstraction for Divide &Conquer 1 Recurrence equation for Divide and Conquer: If the size of problem p is n and the sizes of the k sub problems are
CSE 421 Closest Pair of Points, Master Theorem, Integer Multiplication
 CSE 421 Closest Pair of Points, Master Theorem, Integer Multiplication Shayan Oveis Gharan 1 Finding the Closest Pair of Points Closest Pair of Points (non geometric) Given n points and arbitrary distances
CSE 421 Closest Pair of Points, Master Theorem, Integer Multiplication Shayan Oveis Gharan 1 Finding the Closest Pair of Points Closest Pair of Points (non geometric) Given n points and arbitrary distances
Advanced Algorithm Homework 4 Results and Solutions
 Advanced Algorithm Homework 4 Results and Solutions ID 1 2 3 4 5 Av Ex 2554 6288 9919 10 6 10 10 9.5 8.9 10-1 4208 10 10 9 8.5 10 9.5 9 0996 10 10 10 10 10 10 10 8239 10 10 10 10 10 10 10 7388 8 8.5 9
Advanced Algorithm Homework 4 Results and Solutions ID 1 2 3 4 5 Av Ex 2554 6288 9919 10 6 10 10 9.5 8.9 10-1 4208 10 10 9 8.5 10 9.5 9 0996 10 10 10 10 10 10 10 8239 10 10 10 10 10 10 10 7388 8 8.5 9
CS Divide and Conquer
 CS483-07 Divide and Conquer Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 1:30pm - 2:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/ lifei/teaching/cs483_fall07/
CS483-07 Divide and Conquer Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 1:30pm - 2:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/ lifei/teaching/cs483_fall07/
Lecture 16: Sorting. CS178: Programming Parallel and Distributed Systems. April 2, 2001 Steven P. Reiss
 Lecture 16: Sorting CS178: Programming Parallel and Distributed Systems April 2, 2001 Steven P. Reiss I. Overview A. Before break we started talking about parallel computing and MPI 1. Basic idea of a
Lecture 16: Sorting CS178: Programming Parallel and Distributed Systems April 2, 2001 Steven P. Reiss I. Overview A. Before break we started talking about parallel computing and MPI 1. Basic idea of a
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 6 - Jan. 15, 2018 CLRS 7.1, 7-4, 9.1, 9.3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures 1 / 12 Quick-sort
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 6 - Jan. 15, 2018 CLRS 7.1, 7-4, 9.1, 9.3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures 1 / 12 Quick-sort
Lecture 4: Dynamic programming I
 Lecture : Dynamic programming I Dynamic programming is a powerful, tabular method that solves problems by combining solutions to subproblems. It was introduced by Bellman in the 950 s (when programming
Lecture : Dynamic programming I Dynamic programming is a powerful, tabular method that solves problems by combining solutions to subproblems. It was introduced by Bellman in the 950 s (when programming
Lower bound for comparison-based sorting
 COMP3600/6466 Algorithms 2018 Lecture 8 1 Lower bound for comparison-based sorting Reading: Cormen et al, Section 8.1 and 8.2 Different sorting algorithms may have different running-time complexities.
COMP3600/6466 Algorithms 2018 Lecture 8 1 Lower bound for comparison-based sorting Reading: Cormen et al, Section 8.1 and 8.2 Different sorting algorithms may have different running-time complexities.
Parallel Models RAM. Parallel RAM aka PRAM. Variants of CRCW PRAM. Advanced Algorithms
 Parallel Models Advanced Algorithms Piyush Kumar (Lecture 10: Parallel Algorithms) An abstract description of a real world parallel machine. Attempts to capture essential features (and suppress details?)
Parallel Models Advanced Algorithms Piyush Kumar (Lecture 10: Parallel Algorithms) An abstract description of a real world parallel machine. Attempts to capture essential features (and suppress details?)
COMP Data Structures
 COMP 2140 - Data Structures Shahin Kamali Topic 5 - Sorting University of Manitoba Based on notes by S. Durocher. COMP 2140 - Data Structures 1 / 55 Overview Review: Insertion Sort Merge Sort Quicksort
COMP 2140 - Data Structures Shahin Kamali Topic 5 - Sorting University of Manitoba Based on notes by S. Durocher. COMP 2140 - Data Structures 1 / 55 Overview Review: Insertion Sort Merge Sort Quicksort
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Quick-Sort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 2015 Goodrich and Tamassia
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Quick-Sort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 2015 Goodrich and Tamassia
7. Sorting I. 7.1 Simple Sorting. Problem. Algorithm: IsSorted(A) 1 i j n. Simple Sorting
 Simple Sorting 7. Sorting I 7.1 Simple Sorting Selection Sort, Insertion Sort, Bubblesort [Ottman/Widmayer, Kap. 2.1, Cormen et al, Kap. 2.1, 2.2, Exercise 2.2-2, Problem 2-2 19 197 Problem Algorithm:
Simple Sorting 7. Sorting I 7.1 Simple Sorting Selection Sort, Insertion Sort, Bubblesort [Ottman/Widmayer, Kap. 2.1, Cormen et al, Kap. 2.1, 2.2, Exercise 2.2-2, Problem 2-2 19 197 Problem Algorithm:
9/10/12. Outline. Part 5. Computational Complexity (2) Examples. (revisit) Properties of Growth-rate functions(1/3)
 Outline Part 5. Computational Complexity (2) Complexity of Algorithms Efficiency of Searching Algorithms Sorting Algorithms and Their Efficiencies CS 200 Algorithms and Data Structures 1 2 (revisit) Properties
Outline Part 5. Computational Complexity (2) Complexity of Algorithms Efficiency of Searching Algorithms Sorting Algorithms and Their Efficiencies CS 200 Algorithms and Data Structures 1 2 (revisit) Properties
Advanced Algorithms and Data Structures
 Advanced Algorithms and Data Structures Prof. Tapio Elomaa Course Basics A new 7 credit unit course Replaces OHJ-2156 Analysis of Algorithms We take things a bit further than OHJ-2156 We will assume familiarity
Advanced Algorithms and Data Structures Prof. Tapio Elomaa Course Basics A new 7 credit unit course Replaces OHJ-2156 Analysis of Algorithms We take things a bit further than OHJ-2156 We will assume familiarity
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Merge Sort 2015 Goodrich and Tamassia Merge Sort 1 Application: Internet Search
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Merge Sort 2015 Goodrich and Tamassia Merge Sort 1 Application: Internet Search
Problem. Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all. 1 i j n.
![Problem. Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all. 1 i j n. Problem. Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all. 1 i j n.](/thumbs/84/89326706.jpg) Problem 5. Sorting Simple Sorting, Quicksort, Mergesort Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all 1 i j n. 98 99 Selection Sort
Problem 5. Sorting Simple Sorting, Quicksort, Mergesort Input: An array A = (A[1],..., A[n]) with length n. Output: a permutation A of A, that is sorted: A [i] A [j] for all 1 i j n. 98 99 Selection Sort
Divide and Conquer Algorithms
 Divide and Conquer Algorithms T. M. Murali February 19, 2009 Divide and Conquer Break up a problem into several parts. Solve each part recursively. Solve base cases by brute force. Efficiently combine
Divide and Conquer Algorithms T. M. Murali February 19, 2009 Divide and Conquer Break up a problem into several parts. Solve each part recursively. Solve base cases by brute force. Efficiently combine
CSci 231 Final Review
 CSci 231 Final Review Here is a list of topics for the final. Generally you are responsible for anything discussed in class (except topics that appear italicized), and anything appearing on the homeworks.
CSci 231 Final Review Here is a list of topics for the final. Generally you are responsible for anything discussed in class (except topics that appear italicized), and anything appearing on the homeworks.
Quick-Sort fi fi fi 7 9. Quick-Sort Goodrich, Tamassia
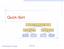 Quick-Sort 7 4 9 6 2 fi 2 4 6 7 9 4 2 fi 2 4 7 9 fi 7 9 2 fi 2 9 fi 9 Quick-Sort 1 Quick-Sort ( 10.2 text book) Quick-sort is a randomized sorting algorithm based on the divide-and-conquer paradigm: x
Quick-Sort 7 4 9 6 2 fi 2 4 6 7 9 4 2 fi 2 4 7 9 fi 7 9 2 fi 2 9 fi 9 Quick-Sort 1 Quick-Sort ( 10.2 text book) Quick-sort is a randomized sorting algorithm based on the divide-and-conquer paradigm: x
MergeSort. Algorithm : Design & Analysis [5]
![MergeSort. Algorithm : Design & Analysis [5] MergeSort. Algorithm : Design & Analysis [5]](/thumbs/72/66691138.jpg) MergeSort Algorithm : Design & Analysis [5] In the last class Insertion sort Analysis of insertion sorting algorithm Lower bound of local comparison based sorting algorithm General pattern of divide-and-conquer
MergeSort Algorithm : Design & Analysis [5] In the last class Insertion sort Analysis of insertion sorting algorithm Lower bound of local comparison based sorting algorithm General pattern of divide-and-conquer
The divide and conquer strategy has three basic parts. For a given problem of size n,
 1 Divide & Conquer One strategy for designing efficient algorithms is the divide and conquer approach, which is also called, more simply, a recursive approach. The analysis of recursive algorithms often
1 Divide & Conquer One strategy for designing efficient algorithms is the divide and conquer approach, which is also called, more simply, a recursive approach. The analysis of recursive algorithms often
Merge Sort. Yufei Tao. Department of Computer Science and Engineering Chinese University of Hong Kong
 Department of Computer Science and Engineering Chinese University of Hong Kong In this lecture, we will design the merge sort which sorts n elements in O(n log n) time. The algorithm illustrates a technique
Department of Computer Science and Engineering Chinese University of Hong Kong In this lecture, we will design the merge sort which sorts n elements in O(n log n) time. The algorithm illustrates a technique
Recursive Sorts. Recursive Sorts. Divide-and-Conquer. Divide-and-Conquer. Divide-and-conquer paradigm:
 Recursive Sorts Recursive Sorts Recursive sorts divide the data roughly in half and are called again on the smaller data sets. This is called the Divide-and-Conquer paradigm. We will see 2 recursive sorts:
Recursive Sorts Recursive Sorts Recursive sorts divide the data roughly in half and are called again on the smaller data sets. This is called the Divide-and-Conquer paradigm. We will see 2 recursive sorts:
Lecture #2. 1 Overview. 2 Worst-Case Analysis vs. Average Case Analysis. 3 Divide-and-Conquer Design Paradigm. 4 Quicksort. 4.
 COMPSCI 330: Design and Analysis of Algorithms 8/28/2014 Lecturer: Debmalya Panigrahi Lecture #2 Scribe: Yilun Zhou 1 Overview This lecture presents two sorting algorithms, quicksort and mergesort, that
COMPSCI 330: Design and Analysis of Algorithms 8/28/2014 Lecturer: Debmalya Panigrahi Lecture #2 Scribe: Yilun Zhou 1 Overview This lecture presents two sorting algorithms, quicksort and mergesort, that
