Dominating Set on Bipartite Graphs
|
|
|
- Rosaline Cobb
- 6 years ago
- Views:
Transcription
1 Dominating Set on Bipartite Graphs Mathieu Liedloff Abstract Finding a dominating set of minimum cardinality is an NP-hard graph problem, even when the graph is bipartite. In this paper we are interested in solving the problem on graphs having a large independent set. Given a graph G with an independent set of size z, we show that the problem can be solved in time O (2 n z ), where n is the number of vertices of G. As a consequence, our algorithm is able to solve the dominating set problem on bipartite graphs in time O (2 n/2 ). Another implication is an algorithm for general graphs whose running time is O( n ). 1 Introduction In the last years, we experience a growing interest in the design and analysis of exact exponential time algorithms to solve NP-hard problems. Several surveys have been published recently (see e.g. [3, 14, 15]). Known results. Given a graph G = (V, E), a subset D V is a dominating set of G if every vertex of V either belongs to D or has at least one neighbor in D. The minimum dominating set problem requires to find a dominating set of minimum cardinality of a given graph. This problem is well known to be NP-hard and several exact exponential time algorithms for solving it on general graphs, as well as on some graph classes, have been published during the last years. The first non trivial algorithms for the problem was proposed in In [6], Fomin et al. provided an O( n ) time algorithm for general graphs and algorithms for split graphs, bipartite graphs and graphs of maximum degree three. The running time of these algorithms are O( n ), O( n ) and O( n ) respectively. Independently and using different approaches, Laboratoire d Informatique Théorique et Appliquée, Université Paul Verlaine - Metz, Metz Cedex 01, France. liedloff (at) univ-metz.fr 1
2 Randerath and Schiermeyer published an O( n ) time algorithm [10], and Grandoni gave an O( n ) time algorithm [8, 9], both for general graphs. By refining the analysis of this latter algorithm, Fomin et al. [2] established an O( n ) time algorithm using polynomial space and an O( n ) time algorithm using exponential space. By now, the best known algorithm is due to van Rooij and Bodlaender [13]. They obtained an O( n ) time and polynomial space algorithm, and an O( n ) time algorithm that uses exponential space. We are insterested in exact algorithms to find a minimum dominating set on special graph classes. As already mentioned, Fomin et al. provide in [6] algorithms for split graphs, bipartite graphs and graphs of maximum degree three. In [5], Fomin and Høie give an O( n ) time algorithm for graphs of maximum degree three. In [1], Dorn shows that a minimum dominating set in a planar graph can be found in sub-exponential time giving an O( n ) time algorithm. In [7], Gaspers et al. provide algorithms for chordal graphs, circle graphs and dense graphs Concerning bipartite graphs, the only previously known algorithm is the one published in [6] having running time O( n ). Since by now the general algorithm of Fomin et al. [2] has worst case running time O( n ), it has been asked whether there is an algorithm finding a minimum dominating set on bipartite graphs in time O(α n ), with α < 1.5. Our results. In this paper, we provide an algorithm computing a minimum dominating set on graphs having a large independent set. Given a graph G with an independent set of size z, the worst case running time of our algorithm is O (2 n z ). Moreover, the algorithm leads to two interesting results. First, we show that a minimum dominating set of a bipartite graph can be computed in time O( n ), providing the best known algorithm for this graph class. The second consequence is a new algorithm for arbitrary graphs having running time O( n ). Besides the O( n ) time algorithm of Fomin et al. using the Branch & Reduce paradigm, our Dynamic Programming based algorithm is the best known for general graphs. 2 Preliminaries Let G = (V, E) be an undirected and simple graph. The number of its vertices is denoted by n. For a vertex v V, we denote by N(v) the neighborhood of v and by N[v] = N(v) {v} the closed neighborhood of v. Given a subset of vertices S V, N[S] denotes the set v S N[S] and N(S) denotes the set N[S] \ S. A subset D V such that every vertex of V \D has at least one neighbor 2
3 in D is a dominating set of G. The minimum cardinality of a dominating set of a graph G is denoted by γ(g). A subset of vertices S V is an independent set of a graph G = (V, E) if the vertices of S are pairwise non adjacent. The problem asking to find an independent set of maximum size is well known to be NP-hard. An independent set S of a graph G is maximal if S is not properly contained in an other independent set. It is well-known that each maximal independent set of a graph G is also a dominating set of G. A graph G = (V, E) is bipartite if the set of its vertices can be partitioned into two independent sets. Through out this paper, we use the (by now standard) O notation introduced by Woeginger [14]. We write f(n) = O (g(n)) if f(n) p(n) g(n) for some polynomial p(n). 3 Solving the dominating set problem on graphs with a large independent set Let G be a graph with an independent set of size z with 1 z n. In this section we show that a minimum dominating set of a such graph can be found in time O (2 n z ). Note that although the maximum independent set problem is NP-hard, there exists several exponential time algorithms for solving this problem exactly [12, 11, 4]. E.g. the one by Fomin et al. has running time O( n ) [4]. Theorem 1 Given a graph G and an independent set of size z of G, a minimum dominating set of G can be computed in time O (2 n z ). Proof. Let G = (V, E) be a graph and I = {v 1, v 2,..., v z } V an independent set of size z. We denote by J the set V \ I. To compute a dominating set of minimum size, the presented algorithm uses two stages. The first one, called preprocessing, computes for each subset X J a subset D X I of minimum cardinality such that X N[D X ]. The second stage, called Domination, computes for each set D J J a dominating set D of smallest size for G fulfilling the condition D J = D J. The calculations done during the preprocessing stage will be used to speed up the execution of the domination stage. In the next, we describe this two stages, prove their correctness and study their running times. Stage : Preprocessing For each subset X J and each integer k, 1 k z, we denote by Opt[X, k] a set D X,k of smallest size, if any, such that : 3
4 (i) D X,k {v 1, v 2,..., v k }, and (ii) X N[D X,k ]. The computation of Opt[X, k] is done by using a dynamic programming approach. The algorithm starts by initializing Opt so that for all k, 1 k z, we let and for all subsets X J we let : Opt[, k] = (1) { {v1 } if X N[v Opt[X, 1] = 1 ], { } otherwise. (2) The special set { } denotes a sentinel meaning that a subset fulfilling the requested properties does not exist. Moreover, we let the cardinality of { } be. The computation of Opt[X, k] is done by considering the sets X by increasing order of cardinality and the values of k by increasing order. Finally, for every non empty subset X J and every integer k 2, the set Opt[X, k] is obtained from the following formula: Opt[X, k] = { The set of minimum cardinality chosen amongst Opt[X, k 1] and {v k } Opt[X \ N[v k ], k 1]. } (3) It is not hard to show that this stage computes for each subset X J and each integer k, 1 k z, a set D X,k = Opt[X, k] of smallest size such that (i) D X,k {v 1, v 2,..., v k } and (ii) X N[D X,k ]. Consider the initializations (1) and (2). If the set X is empty then a set D X,k = is clearly a set of minimum cardinality fulfilling (i) and (ii) for every k. If k is equal to 1, for every subset X, the only way to have X N[D X,k ] is to take v 1 in D X,k. However in that case, either X N[v 1 ] and D X,k = {v 1 } is a solution of minimum size fulfilling (i) and (ii), or X N[v 1 ] and thus no set D X,k {v 1 } can fulfill the condition (ii). As previously explained, in the latter case we store the sentinel { }. We consider now the formula (3). When Opt[X, k] is computed, all the sets Opt[X, k ] with k < k and X J were previously computed. There are two possibilities: either v k belongs to Opt[X, k], or v k Opt[X, k]. If v k Opt[X, k] then it sufficient to know an optimal solution for the subproblem X = X \N[v k ] and k = k 1, which is given by Opt[X, k ]. If v k Opt[X, k] then we have Opt[X, k] = Opt[X, k 1]. Finally, we keep the set having the smallest cardinality amongst these two possibilities. 4
5 Given a set X and an integer k, the computation of Opt[X, k] require no more than polynomial time. Since the computation of Opt[X, k] is done for every X J and every integer k, 1 k z, the running time of the preprocessing stage is O (z2 J ) = O (2 n z ). We note that the storage of all the sets Opt[X, k] request space bounded by O (2 n z ). Stage: Domination Given a set D J J, in this stage we compute a set D = D J D I of minimum size such that D is a dominating set of G respecting the condition D J = D J. As we will show in the next, the set D I I is given by D I = DI 1 D2 I where D1 I = I \ N(D J) and DI 2 = Opt[J \ (N[D J] N(DI 1 )), z] (see Fig. 1). J I D J D I 2 D I 1 Figure 1: An example of a graph having an independent set I together with sets D J, DI 1 and D2 I. (Dashed lines represent neighborhoods of the sets.) Claim 2 Amongst all dominating sets S of G such that S J = D J, the set D = D J DI 1 D2 I is one of smallest cardinality. Proof. First, we show that D = D J DI 1 D2 I is a dominating set. Let v be a vertex in J. If v N[D J ] then v has at least one neighbor in D J or belongs to D J. If v N[D J ], we distinguish two cases. (1) If v N(DI 1) then v has at least one neighbor in DI 1. (2) If v N(D1 I ) then v belongs to J \ (N[D J ] N(DI 1)) and thus, by definition of Opt[J \ (N[D J] N(DI 1 )), z], v has at least one neighbor in DI 2. Consider now v being a vertex of I. Then either v N(D J ) and thus v has at least one neighbor in D J, or v (I \ N(D J )) and then v is in DI 1. Now we show that D is of minimum cardinality amongst all dominating sets S fulfilling S J = D J. Since D J = D J and I is an independent set of G, the vertices of I \ N(D J ) cannot have any neighbor in the dominating set and thus should belong to the dominating set. Consequently, for any dominating set S we have DI 1 S. Then, since D J = D J, the vertices of J \ (N[D J ] N(DI 1 )) can only be dominated by some vertices of I. A 5
6 subset DI 2 I of minimum size such that J \ (N[D J] N(DI 1)) N[D2 I ] was computed during the preprocessing stage. Namely, DI 2 is given by Opt[J \ (N[D J ] N(DI 1)), z]. Note that by the minimality of D2 I, it follows that D1 I and DI 2 are disjoint. Consequently, D = D J DI 1 D2 I is a dominating set of minimum size fulfulling D J = D J. Note that given a set D J J, and using the results coming from the preprocessing stage, the computation of D = D J DI 1 D2 I can be done in polynomial time. Finally, by enumerating all the 2 J = 2 n z possible subsets for D J = D J, the algorithm finds a minimum dominating set D of the graph G in time O (2 n z ). Since every bipartite graph has an independent set of size at least n/2, as an immediate consequence of Theorem 1, we obtain the following corollary. Corollary 3 Given a bipartite graph G, a minimum dominating set of G can be computed in time O (2 n/2 ) = O( n ). 4 Dominating set on general graphs The algorithm described in the previous section can be used to solve the minimum dominating set problem on general graphs. By using a simple greedy strategy, we start by computing in polynomial time a maximal independent set I of the given graph G. (E.g. choose a vertex v of G, add it to I, remove N[v] from G, and continue this process until G is empty.) Let z = n. If I z then we use the algorithm of Theorem 1 to compute a minimum dominating set in time O ( n ) = O( n ). If I < z then γ(g) < z since I is also a (not necessary minimum) dominating set of G. In that case, we enumerate all subsets of vertices of G of size at most z and keep the one being a dominating set of minimum size. By using the Stirling approximation and standard calculations, we state that the time needed for a such enumeration is bounded by z ( ) ( ) n n n! ( ( n ) z ( n ) n z ) z = z k z (z)!(n z)! = O z = O( n ). z n z k=0 Since given a set D, checking whether it is a dominating set require a polynomial time, the overall running time is O( n ) which prove the following Theorem. Theorem 4 Given a graph G, a minimum dominating set of G can be computed in time O( n ). 6
7 References [1] Dorn, F., Designing Subexponential Algorithms: Problems, Techniques & Structures, Ph.D. thesis, University of Bergen, Norway, July [2] Fomin, F.V., F. Grandoni, and D. Kratsch, Measure and conquer: Domination - A case study, Proceedings of ICALP 2005, Springer-Verlag, 2006, Berlin, LNCS 3380, pp [3] Fomin, F.V., F. Grandoni, and D. Kratsch, Some new techniques in design and analysis of exact (exponential) algorithms, Bull. EATCS, 87 (2005), pp [4] Fomin, F.V., F. Grandoni, D. Kratsch, Measure and conquer: A simple O( n ) independent set algorithm, Proceedings of SODA 2006, (2006), pp [5] Fomin, F.V., and K. Høie, Pathwidth of cubic graphs and exact algorithms, Inform. Process. Lett. 97 (2006), pp [6] Fomin, F.V., D. Kratsch, and G. J. Woeginger, Exact (exponential) algorithms for the dominating set problem, Proceedings of WG 2004, Springer-Verlag, Berlin, 2004, LNCS 3353, pp [7] Gaspers, S., D. Kratsch, M. Liedloff, Exponential Time Algorithms for the Minimum Dominating Set Problem on Some Graph Classes, Proceedings of SWAT 2006, LNCS 4059, (2006), pp [8] Grandoni, F., Exact algorithms for hard graph problems, Ph.D. thesis, University of Rome Tor Vergata, Italy, March [9] Grandoni, F., A note on the complexity of minimum dominating set, J. Discrete Algorithms 4 (2006), pp [10] Randerath, B., and I. Schiermeyer, Exact algorithms for Minimum Dominating Set, Technical Report zaik-469, Zentrum fur Angewandte Informatik, Köln, Germany, [11] Robson, J. M., Algorithms for maximum independent sets, Journal of Algorithms 7 (1986), pp [12] Tarjan, R. E., A. E. Trojanowski, Finding a maximum independent set, SIAM Journal on Computing, 6, (1977), pp
8 [13] van Rooij, J. M. M., H. L. Bodlaender, Design by measure and conquer: a faster exact algorithm for dominating set, Proceedings of STACS 2008, to appear. [14] Woeginger, G. J., Exact algorithms for NP-hard problems: A survey, Combinatorial Optimization - Eureka, You Shrink!, Springer-Verlag, 2003, Berlin, LNCS 2570, pp [15] Woeginger, G. J., Space and time complexity of exact algorithms: Some open problems, Proceedings of IWPEC 2004, Springer-Verlag, 2004, Berlin, LNCS 3162, pp
Exponential time algorithms for the minimum dominating set problem on some graph classes
 Exponential time algorithms for the minimum dominating set problem on some graph classes Serge Gaspers University of Bergen Department of Informatics N-500 Bergen, Norway. gaspers@ii.uib.no Dieter Kratsch
Exponential time algorithms for the minimum dominating set problem on some graph classes Serge Gaspers University of Bergen Department of Informatics N-500 Bergen, Norway. gaspers@ii.uib.no Dieter Kratsch
Exponential time algorithms for the minimum dominating set problem on some graph classes
 Exponential time algorithms for the minimum dominating set problem on some graph classes SERGE GASPERS University of Bergen, Norway and DIETER KRATSCH Université Paul Verlaine - Metz, France and MATHIEU
Exponential time algorithms for the minimum dominating set problem on some graph classes SERGE GASPERS University of Bergen, Norway and DIETER KRATSCH Université Paul Verlaine - Metz, France and MATHIEU
Minimal dominating sets in graph classes: combinatorial bounds and enumeration
 Minimal dominating sets in graph classes: combinatorial bounds and enumeration Jean-François Couturier 1, Pinar Heggernes 2, Pim van t Hof 2, and Dieter Kratsch 1 1 LITA, Université Paul Verlaine - Metz,
Minimal dominating sets in graph classes: combinatorial bounds and enumeration Jean-François Couturier 1, Pinar Heggernes 2, Pim van t Hof 2, and Dieter Kratsch 1 1 LITA, Université Paul Verlaine - Metz,
Iterative Compression and Exact Algorithms
 Iterative Compression and Exact Algorithms Fedor V Fomin Serge Gaspers Dieter Kratsch Mathieu Liedloff Saket Saurabh Abstract Iterative Compression has recently led to a number of breakthroughs in parameterized
Iterative Compression and Exact Algorithms Fedor V Fomin Serge Gaspers Dieter Kratsch Mathieu Liedloff Saket Saurabh Abstract Iterative Compression has recently led to a number of breakthroughs in parameterized
Further Improvement on Maximum Independent Set in Degree-4 Graphs
 Further Improvement on Maximum Independent Set in Degree-4 Graphs Mingyu Xiao School of Computer Science and Engineering, University of Electronic Science and Technology of China, China, myxiao@gmail.com
Further Improvement on Maximum Independent Set in Degree-4 Graphs Mingyu Xiao School of Computer Science and Engineering, University of Electronic Science and Technology of China, China, myxiao@gmail.com
Parameterized Algorithm for Eternal Vertex Cover
 Parameterized Algorithm for Eternal Vertex Cover Fedor V. Fomin a,1, Serge Gaspers b, Petr A. Golovach c, Dieter Kratsch d, Saket Saurabh e, a Department of Informatics, University of Bergen, N-5020 Bergen,
Parameterized Algorithm for Eternal Vertex Cover Fedor V. Fomin a,1, Serge Gaspers b, Petr A. Golovach c, Dieter Kratsch d, Saket Saurabh e, a Department of Informatics, University of Bergen, N-5020 Bergen,
Exact Algorithms for Graph Homomorphisms
 Exact Algorithms for Graph Homomorphisms Fedor V. Fomin Pinar Heggernes Dieter Kratsch Abstract Graph homomorphism, also called H-coloring, is a natural generalization of graph coloring: There is a homomorphism
Exact Algorithms for Graph Homomorphisms Fedor V. Fomin Pinar Heggernes Dieter Kratsch Abstract Graph homomorphism, also called H-coloring, is a natural generalization of graph coloring: There is a homomorphism
Minimal Dominating Sets in Graphs: Enumeration, Combinatorial Bounds and Graph Classes
 Minimal Dominating Sets in Graphs: Enumeration, Combinatorial Bounds and Graph Classes J.-F. Couturier 1 P. Heggernes 2 D. Kratsch 1 P. van t Hof 2 1 LITA Université de Lorraine F-57045 Metz France 2 University
Minimal Dominating Sets in Graphs: Enumeration, Combinatorial Bounds and Graph Classes J.-F. Couturier 1 P. Heggernes 2 D. Kratsch 1 P. van t Hof 2 1 LITA Université de Lorraine F-57045 Metz France 2 University
On the minimum feedback vertex set problem: Exact and enumeration algorithms
 On the minimum feedback vertex set problem: Exact and enumeration algorithms Fedor V. Fomin Serge Gaspers Artem V. Pyatkin Igor Razgon November 26, 2007 Abstract We present a time O(1.7548 n ) algorithm
On the minimum feedback vertex set problem: Exact and enumeration algorithms Fedor V. Fomin Serge Gaspers Artem V. Pyatkin Igor Razgon November 26, 2007 Abstract We present a time O(1.7548 n ) algorithm
Minimal dominating sets in interval graphs and trees
 Minimal dominating sets in interval graphs and trees Petr A. Golovach a, Pinar Heggernes a, Mamadou Moustapha Kanté b, Dieter Kratsch c,, Yngve Villanger a a Department of Informatics, University of Bergen,
Minimal dominating sets in interval graphs and trees Petr A. Golovach a, Pinar Heggernes a, Mamadou Moustapha Kanté b, Dieter Kratsch c,, Yngve Villanger a a Department of Informatics, University of Bergen,
Faster parameterized algorithms for Minimum Fill-In
 Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Abstract We present two parameterized algorithms for the Minimum Fill-In problem, also known as Chordal
Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Abstract We present two parameterized algorithms for the Minimum Fill-In problem, also known as Chordal
A Moderately Exponential Time Algorithm for Full Degree Spanning Tree
 A Moderately Exponential Time Algorithm for Full Degree Spanning Tree Serge Gaspers Saket Saurabh Alexey A. Stepanov Abstract We present a moderately exponential time exact algorithm for the wellstudied
A Moderately Exponential Time Algorithm for Full Degree Spanning Tree Serge Gaspers Saket Saurabh Alexey A. Stepanov Abstract We present a moderately exponential time exact algorithm for the wellstudied
Faster parameterized algorithms for Minimum Fill-In
 Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Technical Report UU-CS-2008-042 December 2008 Department of Information and Computing Sciences Utrecht
Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Technical Report UU-CS-2008-042 December 2008 Department of Information and Computing Sciences Utrecht
Chordal deletion is fixed-parameter tractable
 Chordal deletion is fixed-parameter tractable Dániel Marx Institut für Informatik, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. dmarx@informatik.hu-berlin.de Abstract. It
Chordal deletion is fixed-parameter tractable Dániel Marx Institut für Informatik, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. dmarx@informatik.hu-berlin.de Abstract. It
An exact algorithm for max-cut in sparse graphs
 An exact algorithm for max-cut in sparse graphs F. Della Croce a M. J. Kaminski b, V. Th. Paschos c a D.A.I., Politecnico di Torino, Italy b RUTCOR, Rutgers University c LAMSADE, CNRS UMR 7024 and Université
An exact algorithm for max-cut in sparse graphs F. Della Croce a M. J. Kaminski b, V. Th. Paschos c a D.A.I., Politecnico di Torino, Italy b RUTCOR, Rutgers University c LAMSADE, CNRS UMR 7024 and Université
Exact algorithms for L(2, 1)-labeling of graphs
 Exact algorithms for L(, 1)-labeling of graphs Frédéric Havet Martin Klazar Jan Kratochvíl Dieter Kratsch Mathieu Liedloff Abstract The notion of distance constrained graph labelings, motivated by the
Exact algorithms for L(, 1)-labeling of graphs Frédéric Havet Martin Klazar Jan Kratochvíl Dieter Kratsch Mathieu Liedloff Abstract The notion of distance constrained graph labelings, motivated by the
Contracting Chordal Graphs and Bipartite Graphs to Paths and Trees
 Contracting Chordal Graphs and Bipartite Graphs to Paths and Trees Pinar Heggernes Pim van t Hof Benjamin Léveque Christophe Paul Abstract We study the following two graph modification problems: given
Contracting Chordal Graphs and Bipartite Graphs to Paths and Trees Pinar Heggernes Pim van t Hof Benjamin Léveque Christophe Paul Abstract We study the following two graph modification problems: given
Improved Upper Bounds for Partial Vertex Cover
 Improved Upper Bounds for Partial Vertex Cover Joachim Kneis, Alexander Langer, Peter Rossmanith Dept. of Computer Science, RWTH Aachen University, Germany Abstract. The Partial Vertex Cover problem is
Improved Upper Bounds for Partial Vertex Cover Joachim Kneis, Alexander Langer, Peter Rossmanith Dept. of Computer Science, RWTH Aachen University, Germany Abstract. The Partial Vertex Cover problem is
arxiv: v1 [cs.ds] 8 Jan 2019
![arxiv: v1 [cs.ds] 8 Jan 2019 arxiv: v1 [cs.ds] 8 Jan 2019](/thumbs/93/113547113.jpg) Subset Feedback Vertex Set in Chordal and Split Graphs Geevarghese Philip 1, Varun Rajan 2, Saket Saurabh 3,4, and Prafullkumar Tale 5 arxiv:1901.02209v1 [cs.ds] 8 Jan 2019 1 Chennai Mathematical Institute,
Subset Feedback Vertex Set in Chordal and Split Graphs Geevarghese Philip 1, Varun Rajan 2, Saket Saurabh 3,4, and Prafullkumar Tale 5 arxiv:1901.02209v1 [cs.ds] 8 Jan 2019 1 Chennai Mathematical Institute,
Parameterized graph separation problems
 Parameterized graph separation problems Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary, dmarx@cs.bme.hu Abstract.
Parameterized graph separation problems Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary, dmarx@cs.bme.hu Abstract.
The Price of Connectivity for Feedback Vertex Set
 The Price of Connectivity for Feedback Vertex Set Rémy Belmonte 1,, Pim van t Hof 1,, Marcin Kamiński 2, and Daniël Paulusma 3, 1 Department of Informatics, University of Bergen, Norway {remy.belmonte,pim.vanthof}@ii.uib.no
The Price of Connectivity for Feedback Vertex Set Rémy Belmonte 1,, Pim van t Hof 1,, Marcin Kamiński 2, and Daniël Paulusma 3, 1 Department of Informatics, University of Bergen, Norway {remy.belmonte,pim.vanthof}@ii.uib.no
Branch and Recharge: Exact algorithms for generalized domination
 Branch and Recharge: Exact algorithms for generalized domination Fedor V. Fomin Petr A. Golovach Jan Kratochvíl Dieter Kratsch Mathieu Liedloff February 28, 2010 Abstract In this paper we present branching
Branch and Recharge: Exact algorithms for generalized domination Fedor V. Fomin Petr A. Golovach Jan Kratochvíl Dieter Kratsch Mathieu Liedloff February 28, 2010 Abstract In this paper we present branching
arxiv: v1 [cs.dm] 21 Dec 2015
![arxiv: v1 [cs.dm] 21 Dec 2015 arxiv: v1 [cs.dm] 21 Dec 2015](/thumbs/84/90806310.jpg) The Maximum Cardinality Cut Problem is Polynomial in Proper Interval Graphs Arman Boyacı 1, Tinaz Ekim 1, and Mordechai Shalom 1 Department of Industrial Engineering, Boğaziçi University, Istanbul, Turkey
The Maximum Cardinality Cut Problem is Polynomial in Proper Interval Graphs Arman Boyacı 1, Tinaz Ekim 1, and Mordechai Shalom 1 Department of Industrial Engineering, Boğaziçi University, Istanbul, Turkey
A Linear Vertex Kernel for Maximum Internal Spanning Tree
 A Linear Vertex Kernel for Maximum Internal Spanning Tree Fedor V. Fomin Serge Gaspers Saket Saurabh Stéphan Thomassé Abstract We present a polynomial time algorithm that for any graph G and integer k
A Linear Vertex Kernel for Maximum Internal Spanning Tree Fedor V. Fomin Serge Gaspers Saket Saurabh Stéphan Thomassé Abstract We present a polynomial time algorithm that for any graph G and integer k
nonblocker: Parameterized Algorithmics for minimum dominating set
 nonblocker: Parameterized Algorithmics for minimum dominating set Frank Dehne 1, Michael Fellows 2, Henning Fernau 2,3, Elena Prieto 2, Frances Rosamond 2 1 School of Computer Science Carleton University,
nonblocker: Parameterized Algorithmics for minimum dominating set Frank Dehne 1, Michael Fellows 2, Henning Fernau 2,3, Elena Prieto 2, Frances Rosamond 2 1 School of Computer Science Carleton University,
Certifying Algorithms and Forbidden Induced Subgraphs
 /32 and P. Heggernes 1 D. Kratsch 2 1 Institutt for Informatikk Universitetet i Bergen Norway 2 Laboratoire d Informatique Théorique et Appliquée Université Paul Verlaine - Metz France Dagstuhl - Germany
/32 and P. Heggernes 1 D. Kratsch 2 1 Institutt for Informatikk Universitetet i Bergen Norway 2 Laboratoire d Informatique Théorique et Appliquée Université Paul Verlaine - Metz France Dagstuhl - Germany
On Structural Parameterizations of the Matching Cut Problem
 On Structural Parameterizations of the Matching Cut Problem N. R. Aravind, Subrahmanyam Kalyanasundaram, and Anjeneya Swami Kare Department of Computer Science and Engineering, IIT Hyderabad, Hyderabad,
On Structural Parameterizations of the Matching Cut Problem N. R. Aravind, Subrahmanyam Kalyanasundaram, and Anjeneya Swami Kare Department of Computer Science and Engineering, IIT Hyderabad, Hyderabad,
The Parameterized Complexity of the Rainbow Subgraph Problem
 The Parameterized Complexity of the Rainbow Subgraph Problem Falk Hüffner, Christian Komusiewicz, Rolf Niedermeier, and Martin Rötzschke Institut für Softwaretechnik und Theoretische Informatik, TU Berlin,
The Parameterized Complexity of the Rainbow Subgraph Problem Falk Hüffner, Christian Komusiewicz, Rolf Niedermeier, and Martin Rötzschke Institut für Softwaretechnik und Theoretische Informatik, TU Berlin,
Optimal Linear Arrangement of Interval Graphs
 /5 Optimal Linear Arrangement of Interval Graphs Johanne Cohen Fedor Fomin Pinar Heggernes Dieter Kratsch Gregory Kucherov 4 LORIA/CNRS, Nancy, France. Department of Informatics, University of Bergen,
/5 Optimal Linear Arrangement of Interval Graphs Johanne Cohen Fedor Fomin Pinar Heggernes Dieter Kratsch Gregory Kucherov 4 LORIA/CNRS, Nancy, France. Department of Informatics, University of Bergen,
XLVI Pesquisa Operacional na Gestão da Segurança Pública
 Setembro de 014 Approximation algorithms for simple maxcut of split graphs Rubens Sucupira 1 Luerbio Faria 1 Sulamita Klein 1- IME/UERJ UERJ, Rio de JaneiroRJ, Brasil rasucupira@oi.com.br, luerbio@cos.ufrj.br
Setembro de 014 Approximation algorithms for simple maxcut of split graphs Rubens Sucupira 1 Luerbio Faria 1 Sulamita Klein 1- IME/UERJ UERJ, Rio de JaneiroRJ, Brasil rasucupira@oi.com.br, luerbio@cos.ufrj.br
Convex Recoloring Revisited: Complexity and Exact Algorithms
 Convex Recoloring Revisited: Complexity and Exact Algorithms Iyad A. Kanj Dieter Kratsch Abstract We take a new look at the convex path recoloring (CPR), convex tree recoloring (CTR), and convex leaf recoloring
Convex Recoloring Revisited: Complexity and Exact Algorithms Iyad A. Kanj Dieter Kratsch Abstract We take a new look at the convex path recoloring (CPR), convex tree recoloring (CTR), and convex leaf recoloring
On Covering a Graph Optimally with Induced Subgraphs
 On Covering a Graph Optimally with Induced Subgraphs Shripad Thite April 1, 006 Abstract We consider the problem of covering a graph with a given number of induced subgraphs so that the maximum number
On Covering a Graph Optimally with Induced Subgraphs Shripad Thite April 1, 006 Abstract We consider the problem of covering a graph with a given number of induced subgraphs so that the maximum number
Improved algorithms for constructing fault-tolerant spanners
 Improved algorithms for constructing fault-tolerant spanners Christos Levcopoulos Giri Narasimhan Michiel Smid December 8, 2000 Abstract Let S be a set of n points in a metric space, and k a positive integer.
Improved algorithms for constructing fault-tolerant spanners Christos Levcopoulos Giri Narasimhan Michiel Smid December 8, 2000 Abstract Let S be a set of n points in a metric space, and k a positive integer.
Computing optimal total vertex covers for trees
 Computing optimal total vertex covers for trees Pak Ching Li Department of Computer Science University of Manitoba Winnipeg, Manitoba Canada R3T 2N2 Abstract. Let G = (V, E) be a simple, undirected, connected
Computing optimal total vertex covers for trees Pak Ching Li Department of Computer Science University of Manitoba Winnipeg, Manitoba Canada R3T 2N2 Abstract. Let G = (V, E) be a simple, undirected, connected
Complexity Results on Graphs with Few Cliques
 Discrete Mathematics and Theoretical Computer Science DMTCS vol. 9, 2007, 127 136 Complexity Results on Graphs with Few Cliques Bill Rosgen 1 and Lorna Stewart 2 1 Institute for Quantum Computing and School
Discrete Mathematics and Theoretical Computer Science DMTCS vol. 9, 2007, 127 136 Complexity Results on Graphs with Few Cliques Bill Rosgen 1 and Lorna Stewart 2 1 Institute for Quantum Computing and School
Coloring edges and vertices of graphs without short or long cycles
 Coloring edges and vertices of graphs without short or long cycles Marcin Kamiński and Vadim Lozin Abstract Vertex and edge colorability are two graph problems that are NPhard in general. We show that
Coloring edges and vertices of graphs without short or long cycles Marcin Kamiński and Vadim Lozin Abstract Vertex and edge colorability are two graph problems that are NPhard in general. We show that
COLORING EDGES AND VERTICES OF GRAPHS WITHOUT SHORT OR LONG CYCLES
 Volume 2, Number 1, Pages 61 66 ISSN 1715-0868 COLORING EDGES AND VERTICES OF GRAPHS WITHOUT SHORT OR LONG CYCLES MARCIN KAMIŃSKI AND VADIM LOZIN Abstract. Vertex and edge colorability are two graph problems
Volume 2, Number 1, Pages 61 66 ISSN 1715-0868 COLORING EDGES AND VERTICES OF GRAPHS WITHOUT SHORT OR LONG CYCLES MARCIN KAMIŃSKI AND VADIM LOZIN Abstract. Vertex and edge colorability are two graph problems
The 3-Steiner Root Problem
 The 3-Steiner Root Problem Maw-Shang Chang 1 and Ming-Tat Ko 2 1 Department of Computer Science and Information Engineering National Chung Cheng University, Chiayi 621, Taiwan, R.O.C. mschang@cs.ccu.edu.tw
The 3-Steiner Root Problem Maw-Shang Chang 1 and Ming-Tat Ko 2 1 Department of Computer Science and Information Engineering National Chung Cheng University, Chiayi 621, Taiwan, R.O.C. mschang@cs.ccu.edu.tw
THE INDEPENDENCE NUMBER PROJECT:
 THE INDEPENDENCE NUMBER PROJECT: α-properties AND α-reductions C. E. LARSON DEPARTMENT OF MATHEMATICS AND APPLIED MATHEMATICS VIRGINIA COMMONWEALTH UNIVERSITY 1. Introduction A graph property P is an α-property
THE INDEPENDENCE NUMBER PROJECT: α-properties AND α-reductions C. E. LARSON DEPARTMENT OF MATHEMATICS AND APPLIED MATHEMATICS VIRGINIA COMMONWEALTH UNIVERSITY 1. Introduction A graph property P is an α-property
Feedback Arc Set in Bipartite Tournaments is NP-Complete
 Feedback Arc Set in Bipartite Tournaments is NP-Complete Jiong Guo 1 Falk Hüffner 1 Hannes Moser 2 Institut für Informatik, Friedrich-Schiller-Universität Jena, Ernst-Abbe-Platz 2, D-07743 Jena, Germany
Feedback Arc Set in Bipartite Tournaments is NP-Complete Jiong Guo 1 Falk Hüffner 1 Hannes Moser 2 Institut für Informatik, Friedrich-Schiller-Universität Jena, Ernst-Abbe-Platz 2, D-07743 Jena, Germany
Bounds for the m-eternal Domination Number of a Graph
 Bounds for the m-eternal Domination Number of a Graph Michael A. Henning Department of Pure and Applied Mathematics University of Johannesburg South Africa mahenning@uj.ac.za Gary MacGillivray Department
Bounds for the m-eternal Domination Number of a Graph Michael A. Henning Department of Pure and Applied Mathematics University of Johannesburg South Africa mahenning@uj.ac.za Gary MacGillivray Department
Branching Algorithms
 Lecture 01 05.10.01 Branching Algorithms Author: Arkadiusz Soca la 1 Motivation Definition 1. Decision problem L Σ is called NP problem if there exists a predicate ψ P computable in polynomial time such
Lecture 01 05.10.01 Branching Algorithms Author: Arkadiusz Soca la 1 Motivation Definition 1. Decision problem L Σ is called NP problem if there exists a predicate ψ P computable in polynomial time such
Fast algorithms for max independent set
 Fast algorithms for max independent set N. Bourgeois 1 B. Escoffier 1 V. Th. Paschos 1 J.M.M. van Rooij 2 1 LAMSADE, CNRS and Université Paris-Dauphine, France {bourgeois,escoffier,paschos}@lamsade.dauphine.fr
Fast algorithms for max independent set N. Bourgeois 1 B. Escoffier 1 V. Th. Paschos 1 J.M.M. van Rooij 2 1 LAMSADE, CNRS and Université Paris-Dauphine, France {bourgeois,escoffier,paschos}@lamsade.dauphine.fr
Linear Kernel for Planar Connected Dominating Set
 Linear Kernel for Planar Connected Dominating Set Daniel Lokshtanov Matthias Mnich Saket Saurabh Abstract We provide polynomial time data reduction rules for Connected Dominating Set on planar graphs and
Linear Kernel for Planar Connected Dominating Set Daniel Lokshtanov Matthias Mnich Saket Saurabh Abstract We provide polynomial time data reduction rules for Connected Dominating Set on planar graphs and
Algorithm and Complexity of Disjointed Connected Dominating Set Problem on Trees
 Algorithm and Complexity of Disjointed Connected Dominating Set Problem on Trees Wei Wang joint with Zishen Yang, Xianliang Liu School of Mathematics and Statistics, Xi an Jiaotong University Dec 20, 2016
Algorithm and Complexity of Disjointed Connected Dominating Set Problem on Trees Wei Wang joint with Zishen Yang, Xianliang Liu School of Mathematics and Statistics, Xi an Jiaotong University Dec 20, 2016
Vertex 3-colorability of claw-free graphs
 Algorithmic Operations Research Vol.2 (27) 5 2 Vertex 3-colorability of claw-free graphs Marcin Kamiński a Vadim Lozin a a RUTCOR - Rutgers University Center for Operations Research, 64 Bartholomew Road,
Algorithmic Operations Research Vol.2 (27) 5 2 Vertex 3-colorability of claw-free graphs Marcin Kamiński a Vadim Lozin a a RUTCOR - Rutgers University Center for Operations Research, 64 Bartholomew Road,
Exact Algorithms for NP-hard problems
 24 mai 2012 1 Why do we need exponential algorithms? 2 3 Why the P-border? 1 Practical reasons (Jack Edmonds, 1965) For practical purposes the difference between algebraic and exponential order is more
24 mai 2012 1 Why do we need exponential algorithms? 2 3 Why the P-border? 1 Practical reasons (Jack Edmonds, 1965) For practical purposes the difference between algebraic and exponential order is more
Eternal Domination: Criticality and Reachability
 Eternal Domination: Criticality and Reachability William F. Klostermeyer School of Computing University of North Florida Jacksonville, FL 32224-2669 wkloster@unf.edu Gary MacGillivray Department of Mathematics
Eternal Domination: Criticality and Reachability William F. Klostermeyer School of Computing University of North Florida Jacksonville, FL 32224-2669 wkloster@unf.edu Gary MacGillivray Department of Mathematics
CS 598CSC: Approximation Algorithms Lecture date: March 2, 2011 Instructor: Chandra Chekuri
 CS 598CSC: Approximation Algorithms Lecture date: March, 011 Instructor: Chandra Chekuri Scribe: CC Local search is a powerful and widely used heuristic method (with various extensions). In this lecture
CS 598CSC: Approximation Algorithms Lecture date: March, 011 Instructor: Chandra Chekuri Scribe: CC Local search is a powerful and widely used heuristic method (with various extensions). In this lecture
Solving Dominating Set in Larger Classes of Graphs: FPT Algorithms and Polynomial Kernels
 Solving Dominating Set in Larger Classes of Graphs: FPT Algorithms and Polynomial Kernels Geevarghese Philip, Venkatesh Raman, and Somnath Sikdar The Institute of Mathematical Sciences, Chennai, India.
Solving Dominating Set in Larger Classes of Graphs: FPT Algorithms and Polynomial Kernels Geevarghese Philip, Venkatesh Raman, and Somnath Sikdar The Institute of Mathematical Sciences, Chennai, India.
Dynamic programming. Trivial problems are solved first More complex solutions are composed from the simpler solutions already computed
 Dynamic programming Solves a complex problem by breaking it down into subproblems Each subproblem is broken down recursively until a trivial problem is reached Computation itself is not recursive: problems
Dynamic programming Solves a complex problem by breaking it down into subproblems Each subproblem is broken down recursively until a trivial problem is reached Computation itself is not recursive: problems
Minimal comparability completions of arbitrary graphs
 Minimal comparability completions of arbitrary graphs Pinar Heggernes Federico Mancini Charis Papadopoulos Abstract A transitive orientation of an undirected graph is an assignment of directions to its
Minimal comparability completions of arbitrary graphs Pinar Heggernes Federico Mancini Charis Papadopoulos Abstract A transitive orientation of an undirected graph is an assignment of directions to its
On vertex types of graphs
 On vertex types of graphs arxiv:1705.09540v1 [math.co] 26 May 2017 Pu Qiao, Xingzhi Zhan Department of Mathematics, East China Normal University, Shanghai 200241, China Abstract The vertices of a graph
On vertex types of graphs arxiv:1705.09540v1 [math.co] 26 May 2017 Pu Qiao, Xingzhi Zhan Department of Mathematics, East China Normal University, Shanghai 200241, China Abstract The vertices of a graph
Maximum number of edges in claw-free graphs whose maximum degree and matching number are bounded
 Maximum number of edges in claw-free graphs whose maximum degree and matching number are bounded Cemil Dibek Tınaz Ekim Pinar Heggernes Abstract We determine the maximum number of edges that a claw-free
Maximum number of edges in claw-free graphs whose maximum degree and matching number are bounded Cemil Dibek Tınaz Ekim Pinar Heggernes Abstract We determine the maximum number of edges that a claw-free
Generating edge covers of path graphs
 Generating edge covers of path graphs J. Raymundo Marcial-Romero, J. A. Hernández, Vianney Muñoz-Jiménez and Héctor A. Montes-Venegas Facultad de Ingeniería, Universidad Autónoma del Estado de México,
Generating edge covers of path graphs J. Raymundo Marcial-Romero, J. A. Hernández, Vianney Muñoz-Jiménez and Héctor A. Montes-Venegas Facultad de Ingeniería, Universidad Autónoma del Estado de México,
Finding Dense Subgraphs of Sparse Graphs
 Finding Dense Subgraphs of Sparse Graphs Christian Komusiewicz and Manuel Sorge Institut für Softwaretechnik und Theoretische Informatik, TU Berlin {christian.komusiewicz,manuel.sorge}@tu-berlin.de Abstract.
Finding Dense Subgraphs of Sparse Graphs Christian Komusiewicz and Manuel Sorge Institut für Softwaretechnik und Theoretische Informatik, TU Berlin {christian.komusiewicz,manuel.sorge}@tu-berlin.de Abstract.
Bounds on the k-domination Number of a Graph
 Bounds on the k-domination Number of a Graph Ermelinda DeLaViña a,1, Wayne Goddard b, Michael A. Henning c,, Ryan Pepper a,1, Emil R. Vaughan d a University of Houston Downtown b Clemson University c University
Bounds on the k-domination Number of a Graph Ermelinda DeLaViña a,1, Wayne Goddard b, Michael A. Henning c,, Ryan Pepper a,1, Emil R. Vaughan d a University of Houston Downtown b Clemson University c University
Ton Kloks and Yue-Li Wang. Advances in Graph Algorithms. October 10, y X z
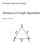 Ton Kloks and Yue-Li Wang Advances in Graph Algorithms October 10, 2013 x Z Y < y X z
Ton Kloks and Yue-Li Wang Advances in Graph Algorithms October 10, 2013 x Z Y < y X z
arxiv: v3 [cs.ds] 28 Apr 2017
![arxiv: v3 [cs.ds] 28 Apr 2017 arxiv: v3 [cs.ds] 28 Apr 2017](/thumbs/87/95726476.jpg) A Linear Kernel for Planar Red-Blue Dominating Set Valentin Garnero, Ignasi Sau, and Dimitrios M. Thilikos arxiv:1408.6388v3 [cs.ds] 28 Apr 2017 Abstract In the Red-Blue Dominating Set problem, we are
A Linear Kernel for Planar Red-Blue Dominating Set Valentin Garnero, Ignasi Sau, and Dimitrios M. Thilikos arxiv:1408.6388v3 [cs.ds] 28 Apr 2017 Abstract In the Red-Blue Dominating Set problem, we are
THE RAINBOW DOMINATION SUBDIVISION NUMBERS OF GRAPHS. N. Dehgardi, S. M. Sheikholeslami and L. Volkmann. 1. Introduction
 MATEMATIQKI VESNIK 67, 2 (2015), 102 114 June 2015 originalni nauqni rad research paper THE RAINBOW DOMINATION SUBDIVISION NUMBERS OF GRAPHS N. Dehgardi, S. M. Sheikholeslami and L. Volkmann Abstract.
MATEMATIQKI VESNIK 67, 2 (2015), 102 114 June 2015 originalni nauqni rad research paper THE RAINBOW DOMINATION SUBDIVISION NUMBERS OF GRAPHS N. Dehgardi, S. M. Sheikholeslami and L. Volkmann Abstract.
Bipartite Roots of Graphs
 Bipartite Roots of Graphs Lap Chi Lau Department of Computer Science University of Toronto Graph H is a root of graph G if there exists a positive integer k such that x and y are adjacent in G if and only
Bipartite Roots of Graphs Lap Chi Lau Department of Computer Science University of Toronto Graph H is a root of graph G if there exists a positive integer k such that x and y are adjacent in G if and only
Dominated colorings of graphs
 Noname manuscript No. (will be inserted by the editor) Dominated colorings of graphs Houcine Boumediene Merouane Mohammed Haddad Mustapha Chellali Hamamache Kheddouci Received: date / Accepted: date Abstract
Noname manuscript No. (will be inserted by the editor) Dominated colorings of graphs Houcine Boumediene Merouane Mohammed Haddad Mustapha Chellali Hamamache Kheddouci Received: date / Accepted: date Abstract
arxiv:cs/ v1 [cs.ds] 20 Feb 2003
![arxiv:cs/ v1 [cs.ds] 20 Feb 2003 arxiv:cs/ v1 [cs.ds] 20 Feb 2003](/thumbs/82/85921811.jpg) The Traveling Salesman Problem for Cubic Graphs David Eppstein School of Information & Computer Science University of California, Irvine Irvine, CA 92697-3425, USA eppstein@ics.uci.edu arxiv:cs/0302030v1
The Traveling Salesman Problem for Cubic Graphs David Eppstein School of Information & Computer Science University of California, Irvine Irvine, CA 92697-3425, USA eppstein@ics.uci.edu arxiv:cs/0302030v1
Matching Algorithms. Proof. If a bipartite graph has a perfect matching, then it is easy to see that the right hand side is a necessary condition.
 18.433 Combinatorial Optimization Matching Algorithms September 9,14,16 Lecturer: Santosh Vempala Given a graph G = (V, E), a matching M is a set of edges with the property that no two of the edges have
18.433 Combinatorial Optimization Matching Algorithms September 9,14,16 Lecturer: Santosh Vempala Given a graph G = (V, E), a matching M is a set of edges with the property that no two of the edges have
Faster parameterized algorithm for Cluster Vertex Deletion
 Faster parameterized algorithm for Cluster Vertex Deletion Dekel Tsur arxiv:1901.07609v1 [cs.ds] 22 Jan 2019 Abstract In the Cluster Vertex Deletion problem the input is a graph G and an integer k. The
Faster parameterized algorithm for Cluster Vertex Deletion Dekel Tsur arxiv:1901.07609v1 [cs.ds] 22 Jan 2019 Abstract In the Cluster Vertex Deletion problem the input is a graph G and an integer k. The
Kernelization Upper Bounds for Parameterized Graph Coloring Problems
 Kernelization Upper Bounds for Parameterized Graph Coloring Problems Pim de Weijer Master Thesis: ICA-3137910 Supervisor: Hans L. Bodlaender Computing Science, Utrecht University 1 Abstract This thesis
Kernelization Upper Bounds for Parameterized Graph Coloring Problems Pim de Weijer Master Thesis: ICA-3137910 Supervisor: Hans L. Bodlaender Computing Science, Utrecht University 1 Abstract This thesis
Every DFS Tree of a 3-Connected Graph Contains a Contractible Edge
 Every DFS Tree of a 3-Connected Graph Contains a Contractible Edge Amr Elmasry Kurt Mehlhorn Jens M. Schmidt Abstract Let G be a 3-connected graph on more than 4 vertices. We show that every depth-first-search
Every DFS Tree of a 3-Connected Graph Contains a Contractible Edge Amr Elmasry Kurt Mehlhorn Jens M. Schmidt Abstract Let G be a 3-connected graph on more than 4 vertices. We show that every depth-first-search
On Exploring Temporal Graphs of Small Pathwidth
 On Exploring Temporal Graphs of Small Pathwidth Hans L. Bodlaender Tom C. van der Zanden arxiv:1807.11869v1 [cs.ds] 31 Jul 2018 Abstract We show that the Temporal Graph Exploration Problem is NP-complete,
On Exploring Temporal Graphs of Small Pathwidth Hans L. Bodlaender Tom C. van der Zanden arxiv:1807.11869v1 [cs.ds] 31 Jul 2018 Abstract We show that the Temporal Graph Exploration Problem is NP-complete,
Finding k Disjoint Triangles in an Arbitrary Graph
 Finding k Disjoint Triangles in an Arbitrary Graph Mike Fellows 1, Pinar Heggernes 2, Frances Rosamond 1, Christian Sloper 2, and Jan Arne Telle 2 1 School of Electrical Engineering and Computer Science
Finding k Disjoint Triangles in an Arbitrary Graph Mike Fellows 1, Pinar Heggernes 2, Frances Rosamond 1, Christian Sloper 2, and Jan Arne Telle 2 1 School of Electrical Engineering and Computer Science
Discrete mathematics , Fall Instructor: prof. János Pach
 Discrete mathematics 2016-2017, Fall Instructor: prof. János Pach - covered material - Lecture 1. Counting problems To read: [Lov]: 1.2. Sets, 1.3. Number of subsets, 1.5. Sequences, 1.6. Permutations,
Discrete mathematics 2016-2017, Fall Instructor: prof. János Pach - covered material - Lecture 1. Counting problems To read: [Lov]: 1.2. Sets, 1.3. Number of subsets, 1.5. Sequences, 1.6. Permutations,
On exact algorithms for treewidth
 Konrad-Zuse-Zentrum für Informationstechnik Berlin Takustraße 7 D-14195 Berlin-Dahlem Germany HANS L. BODLAENDER FEDOR V. FOMIN ARIE M.C.A. KOSTER DIETER KRATSCH DIMITRIOS M. THILIKOS On exact algorithms
Konrad-Zuse-Zentrum für Informationstechnik Berlin Takustraße 7 D-14195 Berlin-Dahlem Germany HANS L. BODLAENDER FEDOR V. FOMIN ARIE M.C.A. KOSTER DIETER KRATSCH DIMITRIOS M. THILIKOS On exact algorithms
Sharp Separation and Applications to Exact and Parameterized Algorithms
 Sharp Separation and Applications to Exact and Parameterized Algorithms Fedor V. Fomin 1 Daniel Lokshtanov 1 Fabrizio Grandoni 2 Saket Saurabh 3 1 Department of Informatics, University of Bergen, N-5020
Sharp Separation and Applications to Exact and Parameterized Algorithms Fedor V. Fomin 1 Daniel Lokshtanov 1 Fabrizio Grandoni 2 Saket Saurabh 3 1 Department of Informatics, University of Bergen, N-5020
The geometric generalized minimum spanning tree problem with grid clustering
 4OR (2006) 4:319 329 DOI 10.1007/s10288-006-0012-6 REGULAR PAPER The geometric generalized minimum spanning tree problem with grid clustering Corinne Feremans Alexander Grigoriev René Sitters Received:
4OR (2006) 4:319 329 DOI 10.1007/s10288-006-0012-6 REGULAR PAPER The geometric generalized minimum spanning tree problem with grid clustering Corinne Feremans Alexander Grigoriev René Sitters Received:
Hardness of r-dominating set on graphs of diameter (r + 1)
 Hardness of r-dominating set on graphs of diameter (r + 1) Daniel Lokshtanov 1, Neeldhara Misra 2, Geevarghese Philip 3, M S Ramanujan 4, Saket Saurabh 1,4 University of Bergen, Norway Indian Institute
Hardness of r-dominating set on graphs of diameter (r + 1) Daniel Lokshtanov 1, Neeldhara Misra 2, Geevarghese Philip 3, M S Ramanujan 4, Saket Saurabh 1,4 University of Bergen, Norway Indian Institute
A Note on Polyhedral Relaxations for the Maximum Cut Problem
 A Note on Polyhedral Relaxations for the Maximum Cut Problem Alantha Newman Abstract We consider three well-studied polyhedral relaxations for the maximum cut problem: the metric polytope of the complete
A Note on Polyhedral Relaxations for the Maximum Cut Problem Alantha Newman Abstract We consider three well-studied polyhedral relaxations for the maximum cut problem: the metric polytope of the complete
FPT Algorithms for Connected Feedback Vertex Set
 FPT Algorithms for Connected Feedback Vertex Set Neeldhara Misra, Geevarghese Philip, Venkatesh Raman, Saket Saurabh, and Somnath Sikdar The Institute of Mathematical Sciences, India. {neeldhara gphilip
FPT Algorithms for Connected Feedback Vertex Set Neeldhara Misra, Geevarghese Philip, Venkatesh Raman, Saket Saurabh, and Somnath Sikdar The Institute of Mathematical Sciences, India. {neeldhara gphilip
Approximating minimum cocolorings
 Information Processing Letters 84 (2002) 285 290 www.elsevier.com/locate/ipl Approximating minimum cocolorings Fedor V. Fomin a,, Dieter Kratsch b, Jean-Christophe Novelli c a Heinz Nixdorf Institute,
Information Processing Letters 84 (2002) 285 290 www.elsevier.com/locate/ipl Approximating minimum cocolorings Fedor V. Fomin a,, Dieter Kratsch b, Jean-Christophe Novelli c a Heinz Nixdorf Institute,
Grundy chromatic number of the complement of bipartite graphs
 Grundy chromatic number of the complement of bipartite graphs Manouchehr Zaker Institute for Advanced Studies in Basic Sciences P. O. BOX 45195-159 Zanjan, Iran E-mail: mzaker@iasbs.ac.ir Abstract A Grundy
Grundy chromatic number of the complement of bipartite graphs Manouchehr Zaker Institute for Advanced Studies in Basic Sciences P. O. BOX 45195-159 Zanjan, Iran E-mail: mzaker@iasbs.ac.ir Abstract A Grundy
Contracting graphs to paths and trees
 Contracting graphs to paths and trees Pinar Heggernes 1, Pim van t Hof 1, Benjamin Lévêque 2, Daniel Lokshtanov 3, and Christophe Paul 2 1 Department of Informatics, University of Bergen, N-5020 Bergen,
Contracting graphs to paths and trees Pinar Heggernes 1, Pim van t Hof 1, Benjamin Lévêque 2, Daniel Lokshtanov 3, and Christophe Paul 2 1 Department of Informatics, University of Bergen, N-5020 Bergen,
Fixed-Parameter Algorithms, IA166
 Fixed-Parameter Algorithms, IA166 Sebastian Ordyniak Faculty of Informatics Masaryk University Brno Spring Semester 2013 Introduction Outline 1 Introduction Algorithms on Locally Bounded Treewidth Layer
Fixed-Parameter Algorithms, IA166 Sebastian Ordyniak Faculty of Informatics Masaryk University Brno Spring Semester 2013 Introduction Outline 1 Introduction Algorithms on Locally Bounded Treewidth Layer
arxiv: v3 [cs.ds] 26 Sep 2013
![arxiv: v3 [cs.ds] 26 Sep 2013 arxiv: v3 [cs.ds] 26 Sep 2013](/thumbs/96/129281842.jpg) Preprocessing Subgraph and Minor Problems: When Does a Small Vertex Cover Help?, Fedor V. Fomin a, Bart M. P. Jansen a,, Micha l Pilipczuk a a Department of Informatics, University of Bergen. PO Box 7803,
Preprocessing Subgraph and Minor Problems: When Does a Small Vertex Cover Help?, Fedor V. Fomin a, Bart M. P. Jansen a,, Micha l Pilipczuk a a Department of Informatics, University of Bergen. PO Box 7803,
A linear kernel for planar red-blue dominating set
 A linear kernel for planar red-blue dominating set Valentin Garnero, Ignasi Sau, and Dimitrios M. Thilikos Version of August 24, 2013 (12:41h) Abstract In the Red-Blue Dominating Set problem, we are given
A linear kernel for planar red-blue dominating set Valentin Garnero, Ignasi Sau, and Dimitrios M. Thilikos Version of August 24, 2013 (12:41h) Abstract In the Red-Blue Dominating Set problem, we are given
Linear Problem Kernels for NP-Hard Problems on Planar Graphs
 Linear Problem Kernels for NP-Hard Problems on Planar Graphs Jiong Guo and Rolf Niedermeier Institut für Informatik, Friedrich-Schiller-Universität Jena, Ernst-Abbe-Platz 2, D-07743 Jena, Germany. {guo,niedermr}@minet.uni-jena.de
Linear Problem Kernels for NP-Hard Problems on Planar Graphs Jiong Guo and Rolf Niedermeier Institut für Informatik, Friedrich-Schiller-Universität Jena, Ernst-Abbe-Platz 2, D-07743 Jena, Germany. {guo,niedermr}@minet.uni-jena.de
Computing minimum distortion embeddings into a path for bipartite permutation graphs and threshold graphs
 Computing minimum distortion embeddings into a path for bipartite permutation graphs and threshold graphs Pinar Heggernes Daniel Meister Andrzej Proskurowski Abstract The problem of computing minimum distortion
Computing minimum distortion embeddings into a path for bipartite permutation graphs and threshold graphs Pinar Heggernes Daniel Meister Andrzej Proskurowski Abstract The problem of computing minimum distortion
Deciding k-colorability of P 5 -free graphs in polynomial time
 Deciding k-colorability of P 5 -free graphs in polynomial time Chính T. Hoàng Marcin Kamiński Vadim Lozin Joe Sawada Xiao Shu April 16, 2008 Abstract The problem of computing the chromatic number of a
Deciding k-colorability of P 5 -free graphs in polynomial time Chính T. Hoàng Marcin Kamiński Vadim Lozin Joe Sawada Xiao Shu April 16, 2008 Abstract The problem of computing the chromatic number of a
PLANAR GRAPH BIPARTIZATION IN LINEAR TIME
 PLANAR GRAPH BIPARTIZATION IN LINEAR TIME SAMUEL FIORINI, NADIA HARDY, BRUCE REED, AND ADRIAN VETTA Abstract. For each constant k, we present a linear time algorithm that, given a planar graph G, either
PLANAR GRAPH BIPARTIZATION IN LINEAR TIME SAMUEL FIORINI, NADIA HARDY, BRUCE REED, AND ADRIAN VETTA Abstract. For each constant k, we present a linear time algorithm that, given a planar graph G, either
The strong chromatic number of a graph
 The strong chromatic number of a graph Noga Alon Abstract It is shown that there is an absolute constant c with the following property: For any two graphs G 1 = (V, E 1 ) and G 2 = (V, E 2 ) on the same
The strong chromatic number of a graph Noga Alon Abstract It is shown that there is an absolute constant c with the following property: For any two graphs G 1 = (V, E 1 ) and G 2 = (V, E 2 ) on the same
Subexponential Algorithms for Partial Cover Problems
 LIPIcs Leibniz International Proceedings in Informatics Subexponential Algorithms for Partial Cover Problems Fedor V. Fomin 1, Daniel Lokshtanov 1, Venkatesh Raman 2 and Saket Saurabh 2 1 Department of
LIPIcs Leibniz International Proceedings in Informatics Subexponential Algorithms for Partial Cover Problems Fedor V. Fomin 1, Daniel Lokshtanov 1, Venkatesh Raman 2 and Saket Saurabh 2 1 Department of
Approximating Node-Weighted Multicast Trees in Wireless Ad-Hoc Networks
 Approximating Node-Weighted Multicast Trees in Wireless Ad-Hoc Networks Thomas Erlebach Department of Computer Science University of Leicester, UK te17@mcs.le.ac.uk Ambreen Shahnaz Department of Computer
Approximating Node-Weighted Multicast Trees in Wireless Ad-Hoc Networks Thomas Erlebach Department of Computer Science University of Leicester, UK te17@mcs.le.ac.uk Ambreen Shahnaz Department of Computer
Subexponential Algorithms for Partial Cover Problems
 Subexponential Algorithms for Partial Cover Problems Fedor V. Fomin Daniel Lokshtanov Venkatesh Raman Saket Saurabh July 4, 2009 Abstract Partial Cover problems are optimization versions of fundamental
Subexponential Algorithms for Partial Cover Problems Fedor V. Fomin Daniel Lokshtanov Venkatesh Raman Saket Saurabh July 4, 2009 Abstract Partial Cover problems are optimization versions of fundamental
Minimum Maximal Matching Is NP-Hard in Regular Bipartite Graphs
 Minimum Maximal Matching Is NP-Hard in Regular Bipartite Graphs M. Demange 1 and T. Ekim 2, 1 ESSEC Business School, Avenue Bernard HIRSH, BP 105, 95021 Cergy Pontoise cedex France demange@essec.fr 2 Boğaziçi
Minimum Maximal Matching Is NP-Hard in Regular Bipartite Graphs M. Demange 1 and T. Ekim 2, 1 ESSEC Business School, Avenue Bernard HIRSH, BP 105, 95021 Cergy Pontoise cedex France demange@essec.fr 2 Boğaziçi
This article appeared in a journal published by Elsevier. The attached copy is furnished to the author for internal non-commercial research and
 This article appeared in a journal published by Elsevier. The attached copy is furnished to the author for internal non-commercial research and education use, including for instruction at the authors institution
This article appeared in a journal published by Elsevier. The attached copy is furnished to the author for internal non-commercial research and education use, including for instruction at the authors institution
MAXIMAL PLANAR SUBGRAPHS OF FIXED GIRTH IN RANDOM GRAPHS
 MAXIMAL PLANAR SUBGRAPHS OF FIXED GIRTH IN RANDOM GRAPHS MANUEL FERNÁNDEZ, NICHOLAS SIEGER, AND MICHAEL TAIT Abstract. In 99, Bollobás and Frieze showed that the threshold for G n,p to contain a spanning
MAXIMAL PLANAR SUBGRAPHS OF FIXED GIRTH IN RANDOM GRAPHS MANUEL FERNÁNDEZ, NICHOLAS SIEGER, AND MICHAEL TAIT Abstract. In 99, Bollobás and Frieze showed that the threshold for G n,p to contain a spanning
Theorem 2.9: nearest addition algorithm
 There are severe limits on our ability to compute near-optimal tours It is NP-complete to decide whether a given undirected =(,)has a Hamiltonian cycle An approximation algorithm for the TSP can be used
There are severe limits on our ability to compute near-optimal tours It is NP-complete to decide whether a given undirected =(,)has a Hamiltonian cycle An approximation algorithm for the TSP can be used
Monotone Paths in Geometric Triangulations
 Monotone Paths in Geometric Triangulations Adrian Dumitrescu Ritankar Mandal Csaba D. Tóth November 19, 2017 Abstract (I) We prove that the (maximum) number of monotone paths in a geometric triangulation
Monotone Paths in Geometric Triangulations Adrian Dumitrescu Ritankar Mandal Csaba D. Tóth November 19, 2017 Abstract (I) We prove that the (maximum) number of monotone paths in a geometric triangulation
Improved Results on Geometric Hitting Set Problems
 Improved Results on Geometric Hitting Set Problems Nabil H. Mustafa nabil@lums.edu.pk Saurabh Ray saurabh@cs.uni-sb.de Abstract We consider the problem of computing minimum geometric hitting sets in which,
Improved Results on Geometric Hitting Set Problems Nabil H. Mustafa nabil@lums.edu.pk Saurabh Ray saurabh@cs.uni-sb.de Abstract We consider the problem of computing minimum geometric hitting sets in which,
NP-Hardness. We start by defining types of problem, and then move on to defining the polynomial-time reductions.
 CS 787: Advanced Algorithms NP-Hardness Instructor: Dieter van Melkebeek We review the concept of polynomial-time reductions, define various classes of problems including NP-complete, and show that 3-SAT
CS 787: Advanced Algorithms NP-Hardness Instructor: Dieter van Melkebeek We review the concept of polynomial-time reductions, define various classes of problems including NP-complete, and show that 3-SAT
Towards more efficient infection and fire fighting
 Towards more efficient infection and fire fighting Peter Floderus Andrzej Lingas Mia Persson The Centre for Mathematical Sciences, Lund University, 00 Lund, Sweden. Email: pflo@maths.lth.se Department
Towards more efficient infection and fire fighting Peter Floderus Andrzej Lingas Mia Persson The Centre for Mathematical Sciences, Lund University, 00 Lund, Sweden. Email: pflo@maths.lth.se Department
Efficient Enumeration Algorithm for Dominating Sets in Bounded Degenerate Graphs
 Efficient Enumeration Algorithm for Dominating Sets in Bounded Degenerate Graphs Kazuhiro Kurita 1, Kunihiro Wasa 2, Hiroki Arimura 1, and Takeaki Uno 2 1 IST, Hokkaido University, Sapporo, Japan 2 National
Efficient Enumeration Algorithm for Dominating Sets in Bounded Degenerate Graphs Kazuhiro Kurita 1, Kunihiro Wasa 2, Hiroki Arimura 1, and Takeaki Uno 2 1 IST, Hokkaido University, Sapporo, Japan 2 National
Parameterized Complexity of Independence and Domination on Geometric Graphs
 Parameterized Complexity of Independence and Domination on Geometric Graphs Dániel Marx Institut für Informatik, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. dmarx@informatik.hu-berlin.de
Parameterized Complexity of Independence and Domination on Geometric Graphs Dániel Marx Institut für Informatik, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. dmarx@informatik.hu-berlin.de
