1 Introduction to generation and random generation
|
|
|
- Kerry Waters
- 6 years ago
- Views:
Transcription
1 Contents 1 Introduction to generation and random generation Features we might want in an exhaustive generation algorithm What about random generation? Lexicographic ranking and unranking Binary strings Bijection to subsets k-subsets Introduction to generation and random generation Two things we might want to do given a combinatorial class A would be to generate all elements of A n or to generate a random element of A n. What does it mean to generate something at random? For a combinatorial class A, we want to describe a process (e.g. algorithm) that takes as input n, and outputs an object α from A such that any element has probability 1 A n of being generated. We call this Uniform generation. 1.1 Features we might want in an exhaustive generation algorithm We might want to be able to generate the elements of A n sequentially, so that we can step from one to the next. That is we might want a successor function which takes one element of A n and gives the next one in the order. This is useful if we want to iterate through all elements of A n and do something with each one. Given an object in A n we might want to be able to determine the position of this object in the order, that is we might want a ranking function. We also might want to be able to determine the element in position i, that is we might want an unranking function We would want to be able to do these things efficiently. Definition. Let S be a finite set. A rank function is a bijection rank : S {0, 1,..., S 1} The corresponding unrank function is the inverse bijection unrank : {0, 1,..., S 1} S So rank(s) = i if and only if unrank(i) = s. If we have a good unranking function we can generate a random element by first generating a random element of {0,..., S 1} and then unranking. If we have a good ranking and unranking function we can generate a successor function by successor(c) = unrank(rank(c) + 1). In both cases other approaches might be more efficient. 1.2 What about random generation? Why would we want to do random generation? To get a sense of what the objects in a given class look like on average: estimate parameters like average depth of a tree; average number of cycles in a permutation etc. To test a hypothesis about the class using an experimental method; MARNI MISHNA, SPRING 2011; KAREN YEATS, SPRING 2013 MATH 343: APPLIED DISCRETE MATHEMATICS PAGE 1/5
2 To feed as input into an algorithm to test the algorithm. A random labelled binary tree on 200 nodes: Hallmarks of a good random generation scheme Correct Each element of size n is generated with equal probability. Efficient How long does it take to generate an element of size n as a function of n? Space Efficiency How much space does it take to generate an element Ease of implementation How long would it take to actually code the algorithm? Re-usability Are there optimizations possible if I am going to run the algorithm multiple times? Generalizability Is this part of a wider framework, or simply an adhoc solution applicable to a single problem? Strategies 1. Consider simple models like binary strings, and make a direct argument; 2. Reduce the random generation to a very simple model via a bijection; 3. Surjective method: Find a simpler class that is in a k to one correspondence uniform generation is still preserved; 4. Ranking/unranking: Order all A n elements. Generate uniformly a random number k between 1 and A n, and determine the k-th element. 5. Rejection method: Generate a larger set and then filter the output; 6. Recursive method: Decompose the object by the counting probabilities 7. Markov method: use Markov chains; Lexicographic ranking and unranking (see Donald Kreher and Douglas Stinson, Combinatorial Algorithms, chapter 2 for a reference on this material) Definition. Let A = (a 1, a 2,..., a n ) and B = (b 1, b 2,..., b m ) be distinct lists of integers. A < B in lexicographic order, if a 1 = b 1,..., a k 1 = b k 1 and either a k < b k or n = k 1 and m k. For example (1, 2, 2) < (2, 1), (1, 2, 2) < (1, 3, 1), (1, 2, 2) < (1, 2, 2, 1). This is the usual dictionary ordering on words using alphabetical order on the letters (hence the name). If we can represent our combinatorial objects as lists, then we can use lexicographic order to order them, and from that get successor, rank, and unrank functions. MARNI MISHNA, SPRING 2011; KAREN YEATS, SPRING 2013 MATH 343: APPLIED DISCRETE MATHEMATICS PAGE 2/5
3 2.1 Binary strings Binary strings are simple enough to directly do random generation. Let us represent a binary string of length n by an array of length n with entries 0 or 1. Assume we have a random number generator. Maple > R:=rand(0..1); # picks a random integer in the range 0..1, i.e. picks 0 or 1 > Bin:= proc(n) > for i from 1 to n do : > A[i]:= R(); > od; > return (seq(a[i], i=1..10)); > end proc; Each string has probability (0.5) n of being generated, so it is uniform. There is one call made for each n, so we say that it is linear in n. It is quite easy to implement, as we see. Binary strings can also be lexicographically ordered since they are lists of 0s and 1s. It will be handiest if we do reverse lexicographic order (so start at the right), because then lexicographic order corresponds exactly to the order given by interpreting the binary string as a binary number. Conceptually ranking and unranking is just converting from a binary string to a binary number and back. So we have Algorithm: RankBin input: n (length of word), w (word) for i from 1 to n if w(i) = 1 r = r+2ˆi output: r Algorithm: UnrankBin input: n (length of word), r (rank) for i from 1 to n if r is congruent to 1 mod 2 b(i) = 1 r = floor(r/2) output: b 2.2 Bijection to subsets Now, let us apply a bijection. Let S be a set of size n. Imagine we want to generate a subset of S such that every subset is equally probable. How do we do it? Let us use a bijection to binary strings: 1. Order all elements: S = {s 1, s 2,..., s n }; 2. Generate a random binary string β = (β 1, β 2,..., β n ) 3. Create the subset {s i : β i = 1}. 2.3 k-subsets In the language of subsets it is natural to ask about ranking/unranking/randomly generating subsets of size k of {1,..., n}. We can also give these a lexicographic order, for example, list the elements of the subset from smallest to largest, and then use lexicographic order on these lists. For example the subsets of size 3 of {1, 2, 3, 4, 5} in this order are Using this we can get a successor function {1, 2, 3}, {1, 2, 4}, {1, 2, 5},{1, 3, 4}, {1, 3, 5}, {1, 4, 5} {2, 3, 4}, {2, 3, 5},{2, 4, 5}, {3, 4, 5} MARNI MISHNA, SPRING 2011; KAREN YEATS, SPRING 2013 MATH 343: APPLIED DISCRETE MATHEMATICS PAGE 3/5
4 Algorithm: SuccessorkSubset Lnew = L i = k while (i >= 1) and (L(i) = n-k+i) i=i-1 if i=0 return no successor (L was the last in the order) else for j from i to k Lnew(j) = L(i) j - i return Lnew To rank and unrank we need to count how many elements preceed a given one. Namely we need Proposition. Let {n 1,..., n k } {1, 2,..., n} with n 1 < n 2 < < n k. Write L = (n 1,..., n k ). Then rank(l) = k n i 1 i=1 j=n i 1+1 ( ) n j k i Proof. There are ( n (n i+l) ) k i 1 k-subsets (as lists in increasing order) beginning with n1, n 2,... n i, l. For l < n i+1 all such subsets preceed L in lexicographic order. Summing these completes the proof. From this we have Algorithm: RankkSubset L(0) = 0 if L(i-1)+1 <= L(i)-1 for j from L(i-1)+1 to L(i)-1 r = r + binom(n-j,k-i) output: r input: r (rank), k, n j = 1 while binom(n-j,k-i) <= r r = r - binom(n-j,k-i) j = j+1 T(i) = j j = j+1 output: T Algorithm: UnrankkSubset Successor is O(k) in the worst case, and the other two algorithms are each O(n) in the worst case. We can do better and rank in O(k). What we need to do is use the reverse lexicographic order again. Call this the corank, and apply it to lists in decreading order Proposition. Let {n 1,..., n k } {1, 2,..., n} with n 1 < n 2 < < n k. Write L = (n k,..., n 1 ). Then corank(l) = k i=1 ( ) nk i+1 1 k i + 1 Proof. There are ( n k i+1 ) 1 k i+1 lists which begin with nk, n k 1,..., n k i+2 and have all remaining elements less than n k i+1. All of these lists comes before L in the order, and so summing we get the result. MARNI MISHNA, SPRING 2011; KAREN YEATS, SPRING 2013 MATH 343: APPLIED DISCRETE MATHEMATICS PAGE 4/5
5 Proposition. Let {n 1,..., n k } {1, 2,..., n} with n 1 < n 2 < < n k. Let L = (n 1, n 2,..., n k ) and L = (n + 1 n 1, n + 1 n 2,..., n + 1 n k ). Then ( ) n rank(l) + corank( L) = 1 k Proof. Suppose (n 1, n 2,..., n k ) < (m 1, m 2,..., m k ) in lexicographic order, then (n+1 n 1,..., n+1 n k ) > (n + 1 m 1,..., n + 1 m k ) in lexicographic order. So given L, for every other k-subset M either L > M or L > M. Therefore rank(l) + corank( L) equals the number of k-subsets other than L itself. From this we can build Algorithm: Rank2kSubset L(0) = 0 r = r + binom(n-l(i), k+1-i) output: binom(n,k) r This algorithm is O(k). Exercise. Can you make a similar Unrank2kSubset? What is its runtime? MARNI MISHNA, SPRING 2011; KAREN YEATS, SPRING 2013 MATH 343: APPLIED DISCRETE MATHEMATICS PAGE 5/5
Trees. 3. (Minimally Connected) G is connected and deleting any of its edges gives rise to a disconnected graph.
 Trees 1 Introduction Trees are very special kind of (undirected) graphs. Formally speaking, a tree is a connected graph that is acyclic. 1 This definition has some drawbacks: given a graph it is not trivial
Trees 1 Introduction Trees are very special kind of (undirected) graphs. Formally speaking, a tree is a connected graph that is acyclic. 1 This definition has some drawbacks: given a graph it is not trivial
Beyond Counting. Owen Kaser. September 17, 2014
 Beyond Counting Owen Kaser September 17, 2014 1 Introduction Combinatorial objects such as permutations and combinations are frequently studied from a counting perspective. For instance, How many distinct
Beyond Counting Owen Kaser September 17, 2014 1 Introduction Combinatorial objects such as permutations and combinations are frequently studied from a counting perspective. For instance, How many distinct
1 (15 points) LexicoSort
 CS161 Homework 2 Due: 22 April 2016, 12 noon Submit on Gradescope Handed out: 15 April 2016 Instructions: Please answer the following questions to the best of your ability. If you are asked to show your
CS161 Homework 2 Due: 22 April 2016, 12 noon Submit on Gradescope Handed out: 15 April 2016 Instructions: Please answer the following questions to the best of your ability. If you are asked to show your
of characters from an alphabet, then, the hash function could be:
 Module 7: Hashing Dr. Natarajan Meghanathan Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu Hashing A very efficient method for implementing
Module 7: Hashing Dr. Natarajan Meghanathan Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu Hashing A very efficient method for implementing
1 Elementary number theory
 Math 215 - Introduction to Advanced Mathematics Spring 2019 1 Elementary number theory We assume the existence of the natural numbers and the integers N = {1, 2, 3,...} Z = {..., 3, 2, 1, 0, 1, 2, 3,...},
Math 215 - Introduction to Advanced Mathematics Spring 2019 1 Elementary number theory We assume the existence of the natural numbers and the integers N = {1, 2, 3,...} Z = {..., 3, 2, 1, 0, 1, 2, 3,...},
CHENNAI MATHEMATICAL INSTITUTE M.Sc. / Ph.D. Programme in Computer Science
 CHENNAI MATHEMATICAL INSTITUTE M.Sc. / Ph.D. Programme in Computer Science Entrance Examination, 5 May 23 This question paper has 4 printed sides. Part A has questions of 3 marks each. Part B has 7 questions
CHENNAI MATHEMATICAL INSTITUTE M.Sc. / Ph.D. Programme in Computer Science Entrance Examination, 5 May 23 This question paper has 4 printed sides. Part A has questions of 3 marks each. Part B has 7 questions
Chapter 4: Sorting. Spring 2014 Sorting Fun 1
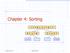 Chapter 4: Sorting 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 Spring 2014 Sorting Fun 1 What We ll Do! Quick Sort! Lower bound on runtimes for comparison based sort! Radix and Bucket sort Spring 2014
Chapter 4: Sorting 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 Spring 2014 Sorting Fun 1 What We ll Do! Quick Sort! Lower bound on runtimes for comparison based sort! Radix and Bucket sort Spring 2014
Assignment 1. Stefano Guerra. October 11, The following observation follows directly from the definition of in order and pre order traversal:
 Assignment 1 Stefano Guerra October 11, 2016 1 Problem 1 Describe a recursive algorithm to reconstruct an arbitrary binary tree, given its preorder and inorder node sequences as input. First, recall that
Assignment 1 Stefano Guerra October 11, 2016 1 Problem 1 Describe a recursive algorithm to reconstruct an arbitrary binary tree, given its preorder and inorder node sequences as input. First, recall that
Lecture 1. 1 Notation
 Lecture 1 (The material on mathematical logic is covered in the textbook starting with Chapter 5; however, for the first few lectures, I will be providing some required background topics and will not be
Lecture 1 (The material on mathematical logic is covered in the textbook starting with Chapter 5; however, for the first few lectures, I will be providing some required background topics and will not be
EDAA40 At home exercises 1
 EDAA40 At home exercises 1 1. Given, with as always the natural numbers starting at 1, let us define the following sets (with iff ): Give the number of elements in these sets as follows: 1. 23 2. 6 3.
EDAA40 At home exercises 1 1. Given, with as always the natural numbers starting at 1, let us define the following sets (with iff ): Give the number of elements in these sets as follows: 1. 23 2. 6 3.
Functions 2/1/2017. Exercises. Exercises. Exercises. and the following mathematical appetizer is about. Functions. Functions
 Exercises Question 1: Given a set A = {x, y, z} and a set B = {1, 2, 3, 4}, what is the value of 2 A 2 B? Answer: 2 A 2 B = 2 A 2 B = 2 A 2 B = 8 16 = 128 Exercises Question 2: Is it true for all sets
Exercises Question 1: Given a set A = {x, y, z} and a set B = {1, 2, 3, 4}, what is the value of 2 A 2 B? Answer: 2 A 2 B = 2 A 2 B = 2 A 2 B = 8 16 = 128 Exercises Question 2: Is it true for all sets
Discrete Mathematics. Kruskal, order, sorting, induction
 Discrete Mathematics wwwmifvult/~algis Kruskal, order, sorting, induction Kruskal algorithm Kruskal s Algorithm for Minimal Spanning Trees The algorithm constructs a minimal spanning tree as follows: Starting
Discrete Mathematics wwwmifvult/~algis Kruskal, order, sorting, induction Kruskal algorithm Kruskal s Algorithm for Minimal Spanning Trees The algorithm constructs a minimal spanning tree as follows: Starting
Module 2: Classical Algorithm Design Techniques
 Module 2: Classical Algorithm Design Techniques Dr. Natarajan Meghanathan Associate Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu Module
Module 2: Classical Algorithm Design Techniques Dr. Natarajan Meghanathan Associate Professor of Computer Science Jackson State University Jackson, MS 39217 E-mail: natarajan.meghanathan@jsums.edu Module
Introduction to Graph Theory
 Introduction to Graph Theory George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 351 George Voutsadakis (LSSU) Introduction to Graph Theory August 2018 1 /
Introduction to Graph Theory George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 351 George Voutsadakis (LSSU) Introduction to Graph Theory August 2018 1 /
CSE 20 DISCRETE MATH. Winter
 CSE 20 DISCRETE MATH Winter 2017 http://cseweb.ucsd.edu/classes/wi17/cse20-ab/ Final exam The final exam is Saturday March 18 8am-11am. Lecture A will take the exam in GH 242 Lecture B will take the exam
CSE 20 DISCRETE MATH Winter 2017 http://cseweb.ucsd.edu/classes/wi17/cse20-ab/ Final exam The final exam is Saturday March 18 8am-11am. Lecture A will take the exam in GH 242 Lecture B will take the exam
1KOd17RMoURxjn2 CSE 20 DISCRETE MATH Fall
 CSE 20 https://goo.gl/forms/1o 1KOd17RMoURxjn2 DISCRETE MATH Fall 2017 http://cseweb.ucsd.edu/classes/fa17/cse20-ab/ Today's learning goals Explain the steps in a proof by mathematical and/or structural
CSE 20 https://goo.gl/forms/1o 1KOd17RMoURxjn2 DISCRETE MATH Fall 2017 http://cseweb.ucsd.edu/classes/fa17/cse20-ab/ Today's learning goals Explain the steps in a proof by mathematical and/or structural
Principles of Algorithm Design
 Principles of Algorithm Design When you are trying to design an algorithm or a data structure, it s often hard to see how to accomplish the task. The following techniques can often be useful: 1. Experiment
Principles of Algorithm Design When you are trying to design an algorithm or a data structure, it s often hard to see how to accomplish the task. The following techniques can often be useful: 1. Experiment
Hash Table. A hash function h maps keys of a given type into integers in a fixed interval [0,m-1]
![Hash Table. A hash function h maps keys of a given type into integers in a fixed interval [0,m-1] Hash Table. A hash function h maps keys of a given type into integers in a fixed interval [0,m-1]](/thumbs/82/85322795.jpg) Exercise # 8- Hash Tables Hash Tables Hash Function Uniform Hash Hash Table Direct Addressing A hash function h maps keys of a given type into integers in a fixed interval [0,m-1] 1 Pr h( key) i, where
Exercise # 8- Hash Tables Hash Tables Hash Function Uniform Hash Hash Table Direct Addressing A hash function h maps keys of a given type into integers in a fixed interval [0,m-1] 1 Pr h( key) i, where
Outline. Introduction. 2 Proof of Correctness. 3 Final Notes. Precondition P 1 : Inputs include
 Outline Computer Science 331 Correctness of Algorithms Mike Jacobson Department of Computer Science University of Calgary Lectures #2-4 1 What is a? Applications 2 Recursive Algorithms 3 Final Notes Additional
Outline Computer Science 331 Correctness of Algorithms Mike Jacobson Department of Computer Science University of Calgary Lectures #2-4 1 What is a? Applications 2 Recursive Algorithms 3 Final Notes Additional
Analyze the obvious algorithm, 5 points Here is the most obvious algorithm for this problem: (LastLargerElement[A[1..n]:
![Analyze the obvious algorithm, 5 points Here is the most obvious algorithm for this problem: (LastLargerElement[A[1..n]: Analyze the obvious algorithm, 5 points Here is the most obvious algorithm for this problem: (LastLargerElement[A[1..n]:](/thumbs/90/104324109.jpg) CSE 101 Homework 1 Background (Order and Recurrence Relations), correctness proofs, time analysis, and speeding up algorithms with restructuring, preprocessing and data structures. Due Thursday, April
CSE 101 Homework 1 Background (Order and Recurrence Relations), correctness proofs, time analysis, and speeding up algorithms with restructuring, preprocessing and data structures. Due Thursday, April
Applied Algorithm Design Lecture 3
 Applied Algorithm Design Lecture 3 Pietro Michiardi Eurecom Pietro Michiardi (Eurecom) Applied Algorithm Design Lecture 3 1 / 75 PART I : GREEDY ALGORITHMS Pietro Michiardi (Eurecom) Applied Algorithm
Applied Algorithm Design Lecture 3 Pietro Michiardi Eurecom Pietro Michiardi (Eurecom) Applied Algorithm Design Lecture 3 1 / 75 PART I : GREEDY ALGORITHMS Pietro Michiardi (Eurecom) Applied Algorithm
MATHEMATICS 191, FALL 2004 MATHEMATICAL PROBABILITY Outline #1 (Countability and Uncountability)
 MATHEMATICS 191, FALL 2004 MATHEMATICAL PROBABILITY Outline #1 (Countability and Uncountability) Last modified: September 16, 2004 Reference: Apostol, Calculus, Vol. 2, section 13.19 (attached). The aim
MATHEMATICS 191, FALL 2004 MATHEMATICAL PROBABILITY Outline #1 (Countability and Uncountability) Last modified: September 16, 2004 Reference: Apostol, Calculus, Vol. 2, section 13.19 (attached). The aim
A Reduction of Conway s Thrackle Conjecture
 A Reduction of Conway s Thrackle Conjecture Wei Li, Karen Daniels, and Konstantin Rybnikov Department of Computer Science and Department of Mathematical Sciences University of Massachusetts, Lowell 01854
A Reduction of Conway s Thrackle Conjecture Wei Li, Karen Daniels, and Konstantin Rybnikov Department of Computer Science and Department of Mathematical Sciences University of Massachusetts, Lowell 01854
MA651 Topology. Lecture 4. Topological spaces 2
 MA651 Topology. Lecture 4. Topological spaces 2 This text is based on the following books: Linear Algebra and Analysis by Marc Zamansky Topology by James Dugundgji Fundamental concepts of topology by Peter
MA651 Topology. Lecture 4. Topological spaces 2 This text is based on the following books: Linear Algebra and Analysis by Marc Zamansky Topology by James Dugundgji Fundamental concepts of topology by Peter
On the Number of Tilings of a Square by Rectangles
 University of Tennessee, Knoxville Trace: Tennessee Research and Creative Exchange University of Tennessee Honors Thesis Projects University of Tennessee Honors Program 5-2012 On the Number of Tilings
University of Tennessee, Knoxville Trace: Tennessee Research and Creative Exchange University of Tennessee Honors Thesis Projects University of Tennessee Honors Program 5-2012 On the Number of Tilings
4&5 Binary Operations and Relations. The Integers. (part I)
 c Oksana Shatalov, Spring 2016 1 4&5 Binary Operations and Relations. The Integers. (part I) 4.1: Binary Operations DEFINITION 1. A binary operation on a nonempty set A is a function from A A to A. Addition,
c Oksana Shatalov, Spring 2016 1 4&5 Binary Operations and Relations. The Integers. (part I) 4.1: Binary Operations DEFINITION 1. A binary operation on a nonempty set A is a function from A A to A. Addition,
On Universal Cycles of Labeled Graphs
 On Universal Cycles of Labeled Graphs Greg Brockman Harvard University Cambridge, MA 02138 United States brockman@hcs.harvard.edu Bill Kay University of South Carolina Columbia, SC 29208 United States
On Universal Cycles of Labeled Graphs Greg Brockman Harvard University Cambridge, MA 02138 United States brockman@hcs.harvard.edu Bill Kay University of South Carolina Columbia, SC 29208 United States
Searching Algorithms/Time Analysis
 Searching Algorithms/Time Analysis CSE21 Fall 2017, Day 8 Oct 16, 2017 https://sites.google.com/a/eng.ucsd.edu/cse21-fall-2017-miles-jones/ (MinSort) loop invariant induction Loop invariant: After the
Searching Algorithms/Time Analysis CSE21 Fall 2017, Day 8 Oct 16, 2017 https://sites.google.com/a/eng.ucsd.edu/cse21-fall-2017-miles-jones/ (MinSort) loop invariant induction Loop invariant: After the
/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Sorting lower bound and Linear-time sorting Date: 9/19/17
 601.433/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Sorting lower bound and Linear-time sorting Date: 9/19/17 5.1 Introduction You should all know a few ways of sorting in O(n log n)
601.433/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Sorting lower bound and Linear-time sorting Date: 9/19/17 5.1 Introduction You should all know a few ways of sorting in O(n log n)
Slides for Faculty Oxford University Press All rights reserved.
 Oxford University Press 2013 Slides for Faculty Assistance Preliminaries Author: Vivek Kulkarni vivek_kulkarni@yahoo.com Outline Following topics are covered in the slides: Basic concepts, namely, symbols,
Oxford University Press 2013 Slides for Faculty Assistance Preliminaries Author: Vivek Kulkarni vivek_kulkarni@yahoo.com Outline Following topics are covered in the slides: Basic concepts, namely, symbols,
Lecture 9: Sorting Algorithms
 Lecture 9: Sorting Algorithms Bo Tang @ SUSTech, Spring 2018 Sorting problem Sorting Problem Input: an array A[1..n] with n integers Output: a sorted array A (in ascending order) Problem is: sort A[1..n]
Lecture 9: Sorting Algorithms Bo Tang @ SUSTech, Spring 2018 Sorting problem Sorting Problem Input: an array A[1..n] with n integers Output: a sorted array A (in ascending order) Problem is: sort A[1..n]
Introduction to Algorithms I
 Summer School on Algorithms and Optimization Organized by: ACM Unit, ISI and IEEE CEDA. Tutorial II Date: 05.07.017 Introduction to Algorithms I (Q1) A binary tree is a rooted tree in which each node has
Summer School on Algorithms and Optimization Organized by: ACM Unit, ISI and IEEE CEDA. Tutorial II Date: 05.07.017 Introduction to Algorithms I (Q1) A binary tree is a rooted tree in which each node has
Functions. How is this definition written in symbolic logic notation?
 functions 1 Functions Def. Let A and B be sets. A function f from A to B is an assignment of exactly one element of B to each element of A. We write f(a) = b if b is the unique element of B assigned by
functions 1 Functions Def. Let A and B be sets. A function f from A to B is an assignment of exactly one element of B to each element of A. We write f(a) = b if b is the unique element of B assigned by
Sorting and Selection
 Sorting and Selection Introduction Divide and Conquer Merge-Sort Quick-Sort Radix-Sort Bucket-Sort 10-1 Introduction Assuming we have a sequence S storing a list of keyelement entries. The key of the element
Sorting and Selection Introduction Divide and Conquer Merge-Sort Quick-Sort Radix-Sort Bucket-Sort 10-1 Introduction Assuming we have a sequence S storing a list of keyelement entries. The key of the element
PACKING DIGRAPHS WITH DIRECTED CLOSED TRAILS
 PACKING DIGRAPHS WITH DIRECTED CLOSED TRAILS PAUL BALISTER Abstract It has been shown [Balister, 2001] that if n is odd and m 1,, m t are integers with m i 3 and t i=1 m i = E(K n) then K n can be decomposed
PACKING DIGRAPHS WITH DIRECTED CLOSED TRAILS PAUL BALISTER Abstract It has been shown [Balister, 2001] that if n is odd and m 1,, m t are integers with m i 3 and t i=1 m i = E(K n) then K n can be decomposed
CS 441 Discrete Mathematics for CS Lecture 24. Relations IV. CS 441 Discrete mathematics for CS. Equivalence relation
 CS 441 Discrete Mathematics for CS Lecture 24 Relations IV Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Equivalence relation Definition: A relation R on a set A is called an equivalence relation
CS 441 Discrete Mathematics for CS Lecture 24 Relations IV Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Equivalence relation Definition: A relation R on a set A is called an equivalence relation
γ(ɛ) (a, b) (a, d) (d, a) (a, b) (c, d) (d, d) (e, e) (e, a) (e, e) (a) Draw a picture of G.
 MAD 3105 Spring 2006 Solutions for Review for Test 2 1. Define a graph G with V (G) = {a, b, c, d, e}, E(G) = {r, s, t, u, v, w, x, y, z} and γ, the function defining the edges, is given by the table ɛ
MAD 3105 Spring 2006 Solutions for Review for Test 2 1. Define a graph G with V (G) = {a, b, c, d, e}, E(G) = {r, s, t, u, v, w, x, y, z} and γ, the function defining the edges, is given by the table ɛ
An Embedded Declarative Data Transformation Language
 An Embedded Declarative Data Transformation Language Department of Computer Science and Engineering PPDP 9, Sept. 29 Motivation analogies (and analogies between analogies) emerge when we transport objects
An Embedded Declarative Data Transformation Language Department of Computer Science and Engineering PPDP 9, Sept. 29 Motivation analogies (and analogies between analogies) emerge when we transport objects
Basic Properties The Definition of Catalan Numbers
 1 Basic Properties 1.1. The Definition of Catalan Numbers There are many equivalent ways to define Catalan numbers. In fact, the main focus of this monograph is the myriad combinatorial interpretations
1 Basic Properties 1.1. The Definition of Catalan Numbers There are many equivalent ways to define Catalan numbers. In fact, the main focus of this monograph is the myriad combinatorial interpretations
CSE Winter 2015 Quiz 2 Solutions
 CSE 101 - Winter 2015 Quiz 2 s January 27, 2015 1. True or False: For any DAG G = (V, E) with at least one vertex v V, there must exist at least one topological ordering. (Answer: True) Fact (from class)
CSE 101 - Winter 2015 Quiz 2 s January 27, 2015 1. True or False: For any DAG G = (V, E) with at least one vertex v V, there must exist at least one topological ordering. (Answer: True) Fact (from class)
CSE 20 DISCRETE MATH. Fall
 CSE 20 DISCRETE MATH Fall 2017 http://cseweb.ucsd.edu/classes/fa17/cse20-ab/ Final exam The final exam is Saturday December 16 11:30am-2:30pm. Lecture A will take the exam in Lecture B will take the exam
CSE 20 DISCRETE MATH Fall 2017 http://cseweb.ucsd.edu/classes/fa17/cse20-ab/ Final exam The final exam is Saturday December 16 11:30am-2:30pm. Lecture A will take the exam in Lecture B will take the exam
Generell Topologi. Richard Williamson. May 6, 2013
 Generell Topologi Richard Williamson May 6, 2013 1 8 Thursday 7th February 8.1 Using connectedness to distinguish between topological spaces I Proposition 8.1. Let (, O ) and (Y, O Y ) be topological spaces.
Generell Topologi Richard Williamson May 6, 2013 1 8 Thursday 7th February 8.1 Using connectedness to distinguish between topological spaces I Proposition 8.1. Let (, O ) and (Y, O Y ) be topological spaces.
III Data Structures. Dynamic sets
 III Data Structures Elementary Data Structures Hash Tables Binary Search Trees Red-Black Trees Dynamic sets Sets are fundamental to computer science Algorithms may require several different types of operations
III Data Structures Elementary Data Structures Hash Tables Binary Search Trees Red-Black Trees Dynamic sets Sets are fundamental to computer science Algorithms may require several different types of operations
Randomly Generated Numerical Semigroups
 Randomly Generated Numerical Semigroups By Zachary J. Spaulding Abstract. Numerical semigroups are subsemigroups of N, that is, subsets of the natural numbers closed under addition. In this paper, we will
Randomly Generated Numerical Semigroups By Zachary J. Spaulding Abstract. Numerical semigroups are subsemigroups of N, that is, subsets of the natural numbers closed under addition. In this paper, we will
Lecture 5: Formation Tree and Parsing Algorithm
 Discrete Mathematics (II) Spring 2012 Lecture 5: Formation Tree and Parsing Algorithm Lecturer: Yi Li 1 Overview In this lecture, we completely focus on syntax of proposition. And the term proposition
Discrete Mathematics (II) Spring 2012 Lecture 5: Formation Tree and Parsing Algorithm Lecturer: Yi Li 1 Overview In this lecture, we completely focus on syntax of proposition. And the term proposition
15.4 Longest common subsequence
 15.4 Longest common subsequence Biological applications often need to compare the DNA of two (or more) different organisms A strand of DNA consists of a string of molecules called bases, where the possible
15.4 Longest common subsequence Biological applications often need to compare the DNA of two (or more) different organisms A strand of DNA consists of a string of molecules called bases, where the possible
Discrete mathematics , Fall Instructor: prof. János Pach
 Discrete mathematics 2016-2017, Fall Instructor: prof. János Pach - covered material - Lecture 1. Counting problems To read: [Lov]: 1.2. Sets, 1.3. Number of subsets, 1.5. Sequences, 1.6. Permutations,
Discrete mathematics 2016-2017, Fall Instructor: prof. János Pach - covered material - Lecture 1. Counting problems To read: [Lov]: 1.2. Sets, 1.3. Number of subsets, 1.5. Sequences, 1.6. Permutations,
Definition: A graph G = (V, E) is called a tree if G is connected and acyclic. The following theorem captures many important facts about trees.
 Tree 1. Trees and their Properties. Spanning trees 3. Minimum Spanning Trees 4. Applications of Minimum Spanning Trees 5. Minimum Spanning Tree Algorithms 1.1 Properties of Trees: Definition: A graph G
Tree 1. Trees and their Properties. Spanning trees 3. Minimum Spanning Trees 4. Applications of Minimum Spanning Trees 5. Minimum Spanning Tree Algorithms 1.1 Properties of Trees: Definition: A graph G
csci 210: Data Structures Program Analysis
 csci 210: Data Structures Program Analysis Summary Summary analysis of algorithms asymptotic analysis and notation big-o big-omega big-theta commonly used functions discrete math refresher Analysis of
csci 210: Data Structures Program Analysis Summary Summary analysis of algorithms asymptotic analysis and notation big-o big-omega big-theta commonly used functions discrete math refresher Analysis of
Suffix Array Construction
 Suffix Array Construction Suffix array construction means simply sorting the set of all suffixes. Using standard sorting or string sorting the time complexity is Ω(DP (T [0..n] )). Another possibility
Suffix Array Construction Suffix array construction means simply sorting the set of all suffixes. Using standard sorting or string sorting the time complexity is Ω(DP (T [0..n] )). Another possibility
MATH20902: Discrete Maths, Solutions to Problem Set 1. These solutions, as well as the corresponding problems, are available at
 MATH20902: Discrete Maths, Solutions to Problem Set 1 These solutions, as well as the corresponding problems, are available at https://bit.ly/mancmathsdiscrete.. (1). The upper panel in the figure below
MATH20902: Discrete Maths, Solutions to Problem Set 1 These solutions, as well as the corresponding problems, are available at https://bit.ly/mancmathsdiscrete.. (1). The upper panel in the figure below
Worst-case running time for RANDOMIZED-SELECT
 Worst-case running time for RANDOMIZED-SELECT is ), even to nd the minimum The algorithm has a linear expected running time, though, and because it is randomized, no particular input elicits the worst-case
Worst-case running time for RANDOMIZED-SELECT is ), even to nd the minimum The algorithm has a linear expected running time, though, and because it is randomized, no particular input elicits the worst-case
Theorem 2.9: nearest addition algorithm
 There are severe limits on our ability to compute near-optimal tours It is NP-complete to decide whether a given undirected =(,)has a Hamiltonian cycle An approximation algorithm for the TSP can be used
There are severe limits on our ability to compute near-optimal tours It is NP-complete to decide whether a given undirected =(,)has a Hamiltonian cycle An approximation algorithm for the TSP can be used
Lecture 12 March 4th
 Math 239: Discrete Mathematics for the Life Sciences Spring 2008 Lecture 12 March 4th Lecturer: Lior Pachter Scribe/ Editor: Wenjing Zheng/ Shaowei Lin 12.1 Alignment Polytopes Recall that the alignment
Math 239: Discrete Mathematics for the Life Sciences Spring 2008 Lecture 12 March 4th Lecturer: Lior Pachter Scribe/ Editor: Wenjing Zheng/ Shaowei Lin 12.1 Alignment Polytopes Recall that the alignment
or else take their intersection. Now define
 Samuel Lee Algebraic Topology Homework #5 May 10, 2016 Problem 1: ( 1.3: #3). Let p : X X be a covering space with p 1 (x) finite and nonempty for all x X. Show that X is compact Hausdorff if and only
Samuel Lee Algebraic Topology Homework #5 May 10, 2016 Problem 1: ( 1.3: #3). Let p : X X be a covering space with p 1 (x) finite and nonempty for all x X. Show that X is compact Hausdorff if and only
CS 137 Part 8. Merge Sort, Quick Sort, Binary Search. November 20th, 2017
 CS 137 Part 8 Merge Sort, Quick Sort, Binary Search November 20th, 2017 This Week We re going to see two more complicated sorting algorithms that will be our first introduction to O(n log n) sorting algorithms.
CS 137 Part 8 Merge Sort, Quick Sort, Binary Search November 20th, 2017 This Week We re going to see two more complicated sorting algorithms that will be our first introduction to O(n log n) sorting algorithms.
Chapter 3. Set Theory. 3.1 What is a Set?
 Chapter 3 Set Theory 3.1 What is a Set? A set is a well-defined collection of objects called elements or members of the set. Here, well-defined means accurately and unambiguously stated or described. Any
Chapter 3 Set Theory 3.1 What is a Set? A set is a well-defined collection of objects called elements or members of the set. Here, well-defined means accurately and unambiguously stated or described. Any
1. Find f(1), f(2), f(3), and f(4) if f(n) is defined recursively by f(0) = 1 and for n = 0, 1, 2,
 Exercises Exercises 1. Find f(1), f(2), f(3), and f(4) if f(n) is defined recursively by f(0) = 1 and for n = 0, 1, 2, a) f(n + 1) = f(n) + 2. b) f(n + 1) = 3f(n). c) f(n + 1) = 2f(n). d) f(n + 1) = f(n)2
Exercises Exercises 1. Find f(1), f(2), f(3), and f(4) if f(n) is defined recursively by f(0) = 1 and for n = 0, 1, 2, a) f(n + 1) = f(n) + 2. b) f(n + 1) = 3f(n). c) f(n + 1) = 2f(n). d) f(n + 1) = f(n)2
CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics
 CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics 1 Sorting 1.1 Problem Statement You are given a sequence of n numbers < a 1, a 2,..., a n >. You need to
CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics 1 Sorting 1.1 Problem Statement You are given a sequence of n numbers < a 1, a 2,..., a n >. You need to
Dyck-Eulerian digraphs
 Dyck-Eulerian digraphs Pietro Codara 1,2 Ottavio M. D Antona 3 Dipartimento di Informatica Università degli Studi di Milano Via Comelico 39, I-20135 Milan, Italy Abstract We introduce a family of Eulerian
Dyck-Eulerian digraphs Pietro Codara 1,2 Ottavio M. D Antona 3 Dipartimento di Informatica Università degli Studi di Milano Via Comelico 39, I-20135 Milan, Italy Abstract We introduce a family of Eulerian
MATH 54 - LECTURE 4 DAN CRYTSER
 MATH 54 - LECTURE 4 DAN CRYTSER Introduction In this lecture we review properties and examples of bases and subbases. Then we consider ordered sets and the natural order topology that one can lay on an
MATH 54 - LECTURE 4 DAN CRYTSER Introduction In this lecture we review properties and examples of bases and subbases. Then we consider ordered sets and the natural order topology that one can lay on an
Functional Programming in Haskell Prof. Madhavan Mukund and S. P. Suresh Chennai Mathematical Institute
 Functional Programming in Haskell Prof. Madhavan Mukund and S. P. Suresh Chennai Mathematical Institute Module # 02 Lecture - 03 Characters and Strings So, let us turn our attention to a data type we have
Functional Programming in Haskell Prof. Madhavan Mukund and S. P. Suresh Chennai Mathematical Institute Module # 02 Lecture - 03 Characters and Strings So, let us turn our attention to a data type we have
Solutions to Homework 10
 CS/Math 240: Intro to Discrete Math 5/3/20 Instructor: Dieter van Melkebeek Solutions to Homework 0 Problem There were five different languages in Problem 4 of Homework 9. The Language D 0 Recall that
CS/Math 240: Intro to Discrete Math 5/3/20 Instructor: Dieter van Melkebeek Solutions to Homework 0 Problem There were five different languages in Problem 4 of Homework 9. The Language D 0 Recall that
Topics Applications Most Common Methods Serial Search Binary Search Search by Hashing (next lecture) Run-Time Analysis Average-time analysis Time anal
 CSC212 Data Structure t Lecture 18 Searching Instructor: George Wolberg Department of Computer Science City College of New York @ George Wolberg, 2016 1 Topics Applications Most Common Methods Serial Search
CSC212 Data Structure t Lecture 18 Searching Instructor: George Wolberg Department of Computer Science City College of New York @ George Wolberg, 2016 1 Topics Applications Most Common Methods Serial Search
CIS 121 Data Structures and Algorithms Midterm 3 Review Solution Sketches Fall 2018
 CIS 121 Data Structures and Algorithms Midterm 3 Review Solution Sketches Fall 2018 Q1: Prove or disprove: You are given a connected undirected graph G = (V, E) with a weight function w defined over its
CIS 121 Data Structures and Algorithms Midterm 3 Review Solution Sketches Fall 2018 Q1: Prove or disprove: You are given a connected undirected graph G = (V, E) with a weight function w defined over its
II (Sorting and) Order Statistics
 II (Sorting and) Order Statistics Heapsort Quicksort Sorting in Linear Time Medians and Order Statistics 8 Sorting in Linear Time The sorting algorithms introduced thus far are comparison sorts Any comparison
II (Sorting and) Order Statistics Heapsort Quicksort Sorting in Linear Time Medians and Order Statistics 8 Sorting in Linear Time The sorting algorithms introduced thus far are comparison sorts Any comparison
Lecture 6: Hashing Steven Skiena
 Lecture 6: Hashing Steven Skiena Department of Computer Science State University of New York Stony Brook, NY 11794 4400 http://www.cs.stonybrook.edu/ skiena Dictionary / Dynamic Set Operations Perhaps
Lecture 6: Hashing Steven Skiena Department of Computer Science State University of New York Stony Brook, NY 11794 4400 http://www.cs.stonybrook.edu/ skiena Dictionary / Dynamic Set Operations Perhaps
1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1
![1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1 1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1](/thumbs/85/92778785.jpg) Asymptotics, Recurrence and Basic Algorithms 1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1 2. O(n) 2. [1 pt] What is the solution to the recurrence T(n) = T(n/2) + n, T(1)
Asymptotics, Recurrence and Basic Algorithms 1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1 2. O(n) 2. [1 pt] What is the solution to the recurrence T(n) = T(n/2) + n, T(1)
Math Introduction to Advanced Mathematics
 Math 215 - Introduction to Advanced Mathematics Number Theory Fall 2017 The following introductory guide to number theory is borrowed from Drew Shulman and is used in a couple of other Math 215 classes.
Math 215 - Introduction to Advanced Mathematics Number Theory Fall 2017 The following introductory guide to number theory is borrowed from Drew Shulman and is used in a couple of other Math 215 classes.
Isomorphisms, Hylomorphisms and Hereditarily Finite Data Types in Haskell
 Isomorphisms, Hylomorphisms and Hereditarily Finite Data Types in Haskell 1 1 Department of Computer Science and Engineering Univ of North Texas SAC 09 Motivation Figure : Shapeshifting between datatypes:
Isomorphisms, Hylomorphisms and Hereditarily Finite Data Types in Haskell 1 1 Department of Computer Science and Engineering Univ of North Texas SAC 09 Motivation Figure : Shapeshifting between datatypes:
Advanced Operations Research Techniques IE316. Quiz 1 Review. Dr. Ted Ralphs
 Advanced Operations Research Techniques IE316 Quiz 1 Review Dr. Ted Ralphs IE316 Quiz 1 Review 1 Reading for The Quiz Material covered in detail in lecture. 1.1, 1.4, 2.1-2.6, 3.1-3.3, 3.5 Background material
Advanced Operations Research Techniques IE316 Quiz 1 Review Dr. Ted Ralphs IE316 Quiz 1 Review 1 Reading for The Quiz Material covered in detail in lecture. 1.1, 1.4, 2.1-2.6, 3.1-3.3, 3.5 Background material
Constraint Satisfaction Problems (CSPs)
 Constraint Satisfaction Problems (CSPs) CPSC 322 CSP 1 Poole & Mackworth textbook: Sections 4.0-4.2 Lecturer: Alan Mackworth September 28, 2012 Problem Type Static Sequential Constraint Satisfaction Logic
Constraint Satisfaction Problems (CSPs) CPSC 322 CSP 1 Poole & Mackworth textbook: Sections 4.0-4.2 Lecturer: Alan Mackworth September 28, 2012 Problem Type Static Sequential Constraint Satisfaction Logic
Computer Science 431 Algorithms The College of Saint Rose Spring Topic Notes: Decrease and Conquer
 Computer Science 431 Algorithms The College of Saint Rose Spring 2013 Topic Notes: Decrease and Conquer Our next class of algorithms are the decrease-and-conquer group. The idea here: 1. Reduce the problem
Computer Science 431 Algorithms The College of Saint Rose Spring 2013 Topic Notes: Decrease and Conquer Our next class of algorithms are the decrease-and-conquer group. The idea here: 1. Reduce the problem
Solution for Homework set 3
 TTIC 300 and CMSC 37000 Algorithms Winter 07 Solution for Homework set 3 Question (0 points) We are given a directed graph G = (V, E), with two special vertices s and t, and non-negative integral capacities
TTIC 300 and CMSC 37000 Algorithms Winter 07 Solution for Homework set 3 Question (0 points) We are given a directed graph G = (V, E), with two special vertices s and t, and non-negative integral capacities
Hashing. Hashing Procedures
 Hashing Hashing Procedures Let us denote the set of all possible key values (i.e., the universe of keys) used in a dictionary application by U. Suppose an application requires a dictionary in which elements
Hashing Hashing Procedures Let us denote the set of all possible key values (i.e., the universe of keys) used in a dictionary application by U. Suppose an application requires a dictionary in which elements
Hashing. Yufei Tao. Department of Computer Science and Engineering Chinese University of Hong Kong
 Department of Computer Science and Engineering Chinese University of Hong Kong In this lecture, we will revisit the dictionary search problem, where we want to locate an integer v in a set of size n or
Department of Computer Science and Engineering Chinese University of Hong Kong In this lecture, we will revisit the dictionary search problem, where we want to locate an integer v in a set of size n or
The complexity of Sorting and sorting in linear-time. Median and Order Statistics. Chapter 8 and Chapter 9
 Subject 6 Spring 2017 The complexity of Sorting and sorting in linear-time Median and Order Statistics Chapter 8 and Chapter 9 Disclaimer: These abbreviated notes DO NOT substitute the textbook for this
Subject 6 Spring 2017 The complexity of Sorting and sorting in linear-time Median and Order Statistics Chapter 8 and Chapter 9 Disclaimer: These abbreviated notes DO NOT substitute the textbook for this
Branch-and-bound: an example
 Branch-and-bound: an example Giovanni Righini Università degli Studi di Milano Operations Research Complements The Linear Ordering Problem The Linear Ordering Problem (LOP) is an N P-hard combinatorial
Branch-and-bound: an example Giovanni Righini Università degli Studi di Milano Operations Research Complements The Linear Ordering Problem The Linear Ordering Problem (LOP) is an N P-hard combinatorial
Directed Graph for Finite-State Machine
 Directed Graph for Finite-State Machine Tito D. Kesumo Siregar (13511018) 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132,
Directed Graph for Finite-State Machine Tito D. Kesumo Siregar (13511018) 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132,
Greedy algorithms is another useful way for solving optimization problems.
 Greedy Algorithms Greedy algorithms is another useful way for solving optimization problems. Optimization Problems For the given input, we are seeking solutions that must satisfy certain conditions. These
Greedy Algorithms Greedy algorithms is another useful way for solving optimization problems. Optimization Problems For the given input, we are seeking solutions that must satisfy certain conditions. These
A SHARKOVSKY THEOREM FOR VERTEX MAPS ON TREES
 A SHARKOVSKY THEOREM FOR VERTEX MAPS ON TREES CHRIS BERNHARDT Abstract. Let T be a tree with n vertices. Let f : T T be continuous and suppose that the n vertices form a periodic orbit under f. We show:
A SHARKOVSKY THEOREM FOR VERTEX MAPS ON TREES CHRIS BERNHARDT Abstract. Let T be a tree with n vertices. Let f : T T be continuous and suppose that the n vertices form a periodic orbit under f. We show:
INTRODUCTION TO THE HOMOLOGY GROUPS OF COMPLEXES
 INTRODUCTION TO THE HOMOLOGY GROUPS OF COMPLEXES RACHEL CARANDANG Abstract. This paper provides an overview of the homology groups of a 2- dimensional complex. It then demonstrates a proof of the Invariance
INTRODUCTION TO THE HOMOLOGY GROUPS OF COMPLEXES RACHEL CARANDANG Abstract. This paper provides an overview of the homology groups of a 2- dimensional complex. It then demonstrates a proof of the Invariance
CS446: Machine Learning Fall Problem Set 4. Handed Out: October 17, 2013 Due: October 31 th, w T x i w
 CS446: Machine Learning Fall 2013 Problem Set 4 Handed Out: October 17, 2013 Due: October 31 th, 2013 Feel free to talk to other members of the class in doing the homework. I am more concerned that you
CS446: Machine Learning Fall 2013 Problem Set 4 Handed Out: October 17, 2013 Due: October 31 th, 2013 Feel free to talk to other members of the class in doing the homework. I am more concerned that you
Burrows Wheeler Transform
 Burrows Wheeler Transform The Burrows Wheeler transform (BWT) is an important technique for text compression, text indexing, and their combination compressed text indexing. Let T [0..n] be the text with
Burrows Wheeler Transform The Burrows Wheeler transform (BWT) is an important technique for text compression, text indexing, and their combination compressed text indexing. Let T [0..n] be the text with
CSE 421 Greedy: Huffman Codes
 CSE 421 Greedy: Huffman Codes Yin Tat Lee 1 Compression Example 100k file, 6 letter alphabet: File Size: ASCII, 8 bits/char: 800kbits 2 3 > 6; 3 bits/char: 300kbits a 45% b 13% c 12% d 16% e 9% f 5% Why?
CSE 421 Greedy: Huffman Codes Yin Tat Lee 1 Compression Example 100k file, 6 letter alphabet: File Size: ASCII, 8 bits/char: 800kbits 2 3 > 6; 3 bits/char: 300kbits a 45% b 13% c 12% d 16% e 9% f 5% Why?
1. Suppose you are given a magic black box that somehow answers the following decision problem in polynomial time:
 1. Suppose you are given a magic black box that somehow answers the following decision problem in polynomial time: Input: A CNF formula ϕ with n variables x 1, x 2,..., x n. Output: True if there is an
1. Suppose you are given a magic black box that somehow answers the following decision problem in polynomial time: Input: A CNF formula ϕ with n variables x 1, x 2,..., x n. Output: True if there is an
13 th Annual Johns Hopkins Math Tournament Saturday, February 19, 2011 Automata Theory EUR solutions
 13 th Annual Johns Hopkins Math Tournament Saturday, February 19, 011 Automata Theory EUR solutions Problem 1 (5 points). Prove that any surjective map between finite sets of the same cardinality is a
13 th Annual Johns Hopkins Math Tournament Saturday, February 19, 011 Automata Theory EUR solutions Problem 1 (5 points). Prove that any surjective map between finite sets of the same cardinality is a
Introduction to Algorithms
 Introduction to Algorithms An algorithm is any well-defined computational procedure that takes some value or set of values as input, and produces some value or set of values as output. 1 Why study algorithms?
Introduction to Algorithms An algorithm is any well-defined computational procedure that takes some value or set of values as input, and produces some value or set of values as output. 1 Why study algorithms?
TOPOLOGY, DR. BLOCK, FALL 2015, NOTES, PART 3.
 TOPOLOGY, DR. BLOCK, FALL 2015, NOTES, PART 3. 301. Definition. Let m be a positive integer, and let X be a set. An m-tuple of elements of X is a function x : {1,..., m} X. We sometimes use x i instead
TOPOLOGY, DR. BLOCK, FALL 2015, NOTES, PART 3. 301. Definition. Let m be a positive integer, and let X be a set. An m-tuple of elements of X is a function x : {1,..., m} X. We sometimes use x i instead
Problem Set 4 Solutions
 Design and Analysis of Algorithms March 5, 205 Massachusetts Institute of Technology 6.046J/8.40J Profs. Erik Demaine, Srini Devadas, and Nancy Lynch Problem Set 4 Solutions Problem Set 4 Solutions This
Design and Analysis of Algorithms March 5, 205 Massachusetts Institute of Technology 6.046J/8.40J Profs. Erik Demaine, Srini Devadas, and Nancy Lynch Problem Set 4 Solutions Problem Set 4 Solutions This
Bound Consistency for Binary Length-Lex Set Constraints
 Bound Consistency for Binary Length-Lex Set Constraints Pascal Van Hentenryck and Justin Yip Brown University, Box 1910 Carmen Gervet Boston University, Providence, RI 02912 808 Commonwealth Av. Boston,
Bound Consistency for Binary Length-Lex Set Constraints Pascal Van Hentenryck and Justin Yip Brown University, Box 1910 Carmen Gervet Boston University, Providence, RI 02912 808 Commonwealth Av. Boston,
Hashing. 7- Hashing. Hashing. Transform Keys into Integers in [[0, M 1]] The steps in hashing:
![Hashing. 7- Hashing. Hashing. Transform Keys into Integers in [[0, M 1]] The steps in hashing: Hashing. 7- Hashing. Hashing. Transform Keys into Integers in [[0, M 1]] The steps in hashing:](/thumbs/82/85614926.jpg) Hashing 7- Hashing Bruno MARTI, University of ice - Sophia Antipolis mailto:bruno.martin@unice.fr http://www.i3s.unice.fr/~bmartin/mathmods.html The steps in hashing: 1 compute a hash function which maps
Hashing 7- Hashing Bruno MARTI, University of ice - Sophia Antipolis mailto:bruno.martin@unice.fr http://www.i3s.unice.fr/~bmartin/mathmods.html The steps in hashing: 1 compute a hash function which maps
H. W. Kuhn. Bryn Mawr College
 VARIANTS OF THE HUNGARIAN METHOD FOR ASSIGNMENT PROBLEMS' H. W. Kuhn Bryn Mawr College The author presents a geometrical modelwhich illuminates variants of the Hungarian method for the solution of the
VARIANTS OF THE HUNGARIAN METHOD FOR ASSIGNMENT PROBLEMS' H. W. Kuhn Bryn Mawr College The author presents a geometrical modelwhich illuminates variants of the Hungarian method for the solution of the
Case by Case. Chapter 3
 Chapter 3 Case by Case In the previous chapter, we used the conditional expression if... then... else to define functions whose results depend on their arguments. For some of them we had to nest the conditional
Chapter 3 Case by Case In the previous chapter, we used the conditional expression if... then... else to define functions whose results depend on their arguments. For some of them we had to nest the conditional
Problem Set 4: Streams and Lazy Evaluation
 Due Friday, March 24 Computer Science (1)21b (Spring Term, 2017) Structure and Interpretation of Computer Programs Problem Set 4: Streams and Lazy Evaluation Reading Assignment: Chapter 3, Section 3.5.
Due Friday, March 24 Computer Science (1)21b (Spring Term, 2017) Structure and Interpretation of Computer Programs Problem Set 4: Streams and Lazy Evaluation Reading Assignment: Chapter 3, Section 3.5.
Dictionary. Dictionary. stores key-value pairs. Find(k) Insert(k, v) Delete(k) List O(n) O(1) O(n) Sorted Array O(log n) O(n) O(n)
 Hash-Tables Introduction Dictionary Dictionary stores key-value pairs Find(k) Insert(k, v) Delete(k) List O(n) O(1) O(n) Sorted Array O(log n) O(n) O(n) Balanced BST O(log n) O(log n) O(log n) Dictionary
Hash-Tables Introduction Dictionary Dictionary stores key-value pairs Find(k) Insert(k, v) Delete(k) List O(n) O(1) O(n) Sorted Array O(log n) O(n) O(n) Balanced BST O(log n) O(log n) O(log n) Dictionary
The PRAM (Parallel Random Access Memory) model. All processors operate synchronously under the control of a common CPU.
 The PRAM (Parallel Random Access Memory) model All processors operate synchronously under the control of a common CPU. The PRAM (Parallel Random Access Memory) model All processors operate synchronously
The PRAM (Parallel Random Access Memory) model All processors operate synchronously under the control of a common CPU. The PRAM (Parallel Random Access Memory) model All processors operate synchronously
ALGORITHMS ALGORITHMS ALGORITHMS ALGORITHMS ALGORITHMS ALGORITHMS. Reference: Discrete Math by Rosen
 Reference: Discrete Math by Rosen Example: Finding the Maximum Element in a Finite Sequence. procedure max(a 1, a 2,..., a n : integers) max : = a 1 f i : = 2 to n if max < a i then max := a i return max
Reference: Discrete Math by Rosen Example: Finding the Maximum Element in a Finite Sequence. procedure max(a 1, a 2,..., a n : integers) max : = a 1 f i : = 2 to n if max < a i then max := a i return max
NOI 2012 TASKS OVERVIEW
 NOI 2012 TASKS OVERVIEW Tasks Task 1: MODSUM Task 2: PANCAKE Task 3: FORENSIC Task 4: WALKING Notes: 1. Each task is worth 25 marks. 2. Each task will be tested on a few sets of input instances. Each set
NOI 2012 TASKS OVERVIEW Tasks Task 1: MODSUM Task 2: PANCAKE Task 3: FORENSIC Task 4: WALKING Notes: 1. Each task is worth 25 marks. 2. Each task will be tested on a few sets of input instances. Each set
1 Probability Review. CS 124 Section #8 Hashing, Skip Lists 3/20/17. Expectation (weighted average): the expectation of a random quantity X is:
 CS 124 Section #8 Hashing, Skip Lists 3/20/17 1 Probability Review Expectation (weighted average): the expectation of a random quantity X is: x= x P (X = x) For each value x that X can take on, we look
CS 124 Section #8 Hashing, Skip Lists 3/20/17 1 Probability Review Expectation (weighted average): the expectation of a random quantity X is: x= x P (X = x) For each value x that X can take on, we look
